- Department of Computer and System Science, Mid Sweden University, Östersund, Sweden
Introduction: An ongoing trend on a global scale is the integration of computer science and programming in K-12 education. The integration has been motivated by the needs of the present and future labor market but also by the assumption that skills related to computer science and programming are valuable for citizens to navigate an increasingly digitalized society. Computational thinking (CT) is a concept that aims to define and summarize skills associated with programming and computer science and has received wide recognition within research and education. But how do the teachers perceive this concept, and how do they relate it to their own teaching and learning activities? This study aims to investigate and discuss teachers' perceptions of CT in grades 7–12 mathematics and technology.
Methods: Data have been collected from essay assignments in three instances of a professional development course on fundamental programming for grades 7–12 teachers in mathematics and technology. In the essays, the teachers reflect on CT in relation to mathematics and technology and teaching and learning activities in these subjects. With a theoretical framework for CT, the collected data have been analyzed with a directed content analysis approach to identify categories of interests for CT in relation to grades 7–12 mathematics and technology.
Results: The results of the study show that the teachers perceive both opportunities and challenges in applying the CT concept in their teaching and learning activities. For example, it can strengthen the subjects through new practices and reinforce old practices, but it could be too complex and perceived as difficult by some students. Furthermore, many of the teachers perceive CT not only to be relevant for mathematics and technology but also for learning in general.
Discussion: The conclusion of the study is that CT has the potential to enhance teaching and learning activities in mathematics, technology, and other STEM subjects. If this should be successful, CT must not be involved too abstractly or too superficially. This study contributes to the discussion on CT in K-12 education, adding the teachers' perspective. The findings of this study can be used by teachers and other stakeholders in the design of classroom activities that apply the CT concept.
Introduction
The integration of computer science and programming in kindergarten to grade 12 (K-12) settings is an ongoing and worldwide process (Balanskat and Engelhardt, 2015; Tran, 2018; Irons and Hartnett, 2020). Initiatives have been started for various reasons, but often with the labor market demand for system developers in mind (Smit et al., 2020; Wolz et al., 2022). At the same time, the rapidly increasing digitalization has created a need for more general computer science skills with computational thinking (CT) as an interesting core part of 21st-century skills. As presented in the study by Tikva and Tambouris (2021, p. 1) that CT “through programming attracts increased attention as it is considered an ideal medium for the development of 21st-century skills.” Some examples of important 21st-century skills are critical thinking, creativity, and collaboration (Van Laar et al., 2017; Tzagkaraki et al., 2021).
In the Swedish context, a revised curriculum was presented in 2017, where programming and general digital proficiency should be introduced. The special focus should be on CT and fundamental programming for secondary school mathematics and technology (Heintz et al., 2017). In the subjects of mathematics and technology, secondary school teachers are supposed to use programming as a tool for problem-solving in their daily teaching. An inevitable first step in the process of introducing programming was to arrange tailored professional development for teachers in mathematics and technology. Previous research studies have found that most K-12 teachers were poorly prepared for the introduction of programming with no, or little, previous programming skills, general computer science knowledge, or technical knowledge (Royal Society, 2017; Humble et al., 2019; Mozelius and Hoff, 2019; Pörn et al., 2021; Tzagkaraki et al., 2021).
CT could be traced back to the 1980s, with an origin in ideas by Papert (1980) and the creation of the LOGO programming language for introducing programming to a younger audience. Two and a half decades later, CT was defined briefly by Wing (2006) as a necessary skill for everyone that “involves solving problems, designing systems, and understanding human behavior, by drawing on the concepts fundamental to computer science.” During the last decade, CT has rapidly increased as a research field with a large number of extended definitions and the creation of various CT frameworks (Brennan and Resnick, 2012; Shute et al., 2017; Dolgopolovas et al., 2019). As pointed out in the study by Tikva and Tambouris (2021), this leaves us with the problem that teachers do not have a decent overview of the CT field and how to involve CT in curricula.
This study has the aim of investigating and discussing teachers' perceptions of CT in grades 7–12 mathematics and technology. The main question to answer was: How do the teachers perceive CT and how do they relate it to their own teaching and learning activities in grade 7–12 mathematics and technology?
Computational thinking
The concept of CT is in several studies described with an origin in the short four-page article by Wing (2006). CT was there described as a concept built around the possibilities and limitations of computing processes that could be executed both by humans and by machines. Furthermore, the use of computational methods would enable new possibilities to solve problems and to design systems (Wing, 2006). However, as highlighted by Cansu and Cansu (2019), this concept had been referred to earlier by Seymour Papert as Procedural Thinking, and something that Papert used in the development of Turtle graphics and the Logo programming language (Brims, 1999). In computer science, the concept can be traced further back to the 1950s and 1960s, when the term algorithmic thinking was used to formulate problems as conversions of an input to an adequate output, with algorithms to perform the desired conversions (Denning, 2009).
As stated by Cansu and Cansu (2019), CT and computer science are not one and the same and should not be used as synonyms. The original definition by Wing (2006) that computational thinking is to think like a computer scientist has several times been criticized. The argument has been that CT has many interesting applications for solving real-world problems outside the field of Computer science (Denning, 2009; Hemmendinger, 2010). Later in 2014, Wing redefined CT as “The thought processes used to formulate a problem and express its solution or solutions in terms a computer can apply effectively.” Later the same year, CT was defined by Yadav et al. (2014) as “The mental process for abstraction of problems and the creation of automatable solutions” (Wing, 2014; Yadav et al., 2014; Cansu and Cansu, 2019). In addition to the various definitions of CT, there have also been different suggestions for which components that CT should involve. Some examples are: (1) Abstraction, Automation, and Analysis (Lee et al., 2011), (2) Abstraction, Algorithms, Automation, Problem Decomposition, and Generalization (Wing, 2006, 2008, 2011), and (3) Abstraction, Algorithmic Thinking, Decomposition, Evaluation, and Generalization (Selby and Woollard, 2013).
Shute et al. (2017) synthesize the findings from previous research on CT in a literature review to produce a definition and framework of how CT can be used by K-12 teachers to build a strong foundation for students' learning. Shute et al. (2017) define CT as “the conceptual foundation required to solve problems effectively and efficiently (i.e., algorithmically, with or without the assistance of computers) with solutions that are reusable in different contexts.” They further divided CT into six facets: (1) decomposition, (2) abstraction, (3) algorithms, (4) debugging, (5) iteration, and (6) generalization (Shute et al., 2017). Each of these facets is accompanied by its own definitions, which are provided in Table 1.
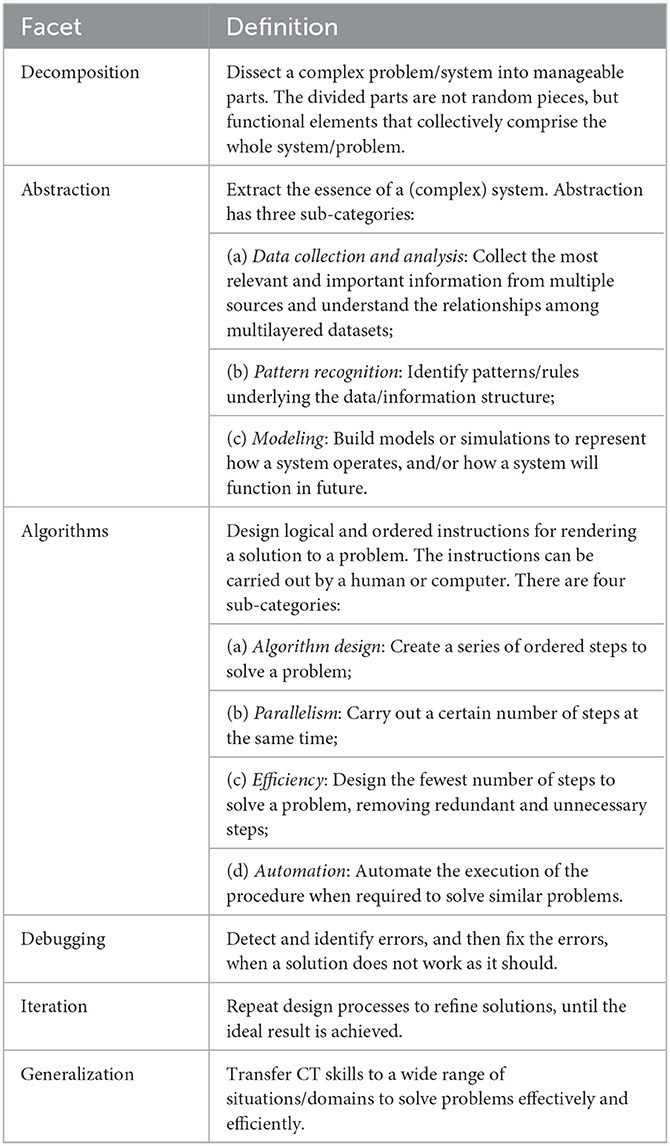
Table 1. Summary of CT framework (Shute et al., 2017).
The idea of using decomposition to break down large and complex tasks into manageable smaller units was a component in Wing's (2006) first presentation of the CT concept. Decomposition was also a part of the CT concept presented by Barr and Stephenson, where decomposition was defined as “breaking problems down into smaller parts that may be more easily solved” (Barr and Stephenson, 2011, p. 52). It could be argued that this idea is far older, with the principle of divide and conquer that often is presented in university courses on artificial intelligence and computer science. The term is often traced back to Julius Caesar and his brutal leadership. However, an even older idea of applying divide and conquer is the Euclidean algorithm on how to compute the greatest common divisor of two numbers. The challenge that remains is that “a student who scores well on tests to explain and illustrate abstraction and decomposition can still be an incompetent or insensitive algorithm designer” (Denning, 2017, Question 2).
To involve abstraction, defined as finding the essential structure of complex systems, has also a long and rich tradition in STEM. As pointed out in the seminal article by Wing (2006), abstraction is an aligned complement to decomposition in the solving of large and complex problems. In Wing's very optimistic view of abstraction, it is described as “It is having the confidence we can safely use, modify, and influence a large complex system without understanding its every detail.” The objection could be the same as for decomposition, and that abstraction by itself could lead to incorrectly designed algorithms (Denning, 2017, Question 2). The famous quote from Friedrich Wilhelm Nietzsche that the devil is in the details is still a very present challenge in computer science. A teacher that uses too much abstraction in teaching and learning activities risks misleading students.
In the early versions of CT, algorithms were very broadly defined and often more of heuristic recipes. In the seminal article by Wing (2006, p. 34), CT concepts are presented as everyday examples with algorithms exemplified as “At what point do you stop renting skis and buy yourself a pair?; that's online algorithms.” To be compared with the stricter definition used in mathematics and computer science, where an algorithm ought to be a finite sequence of well-defined instructions that solves a problem or a class of problems. Moreover, the classic definition for mathematics and computer science should have proof that shows that the algorithm solves the problem in a finite number of instructions. Without proof of a solution in a finite sequence of steps, the solving approach should be classified as heuristics. However, as highlighted by Wing (2006), the heuristic approach is also valuable. However, if the aim should be to bring computational thinking to K-12 settings, as in Barr and Stephenson (2011), algorithms have to be introduced with a more loosely defined. These loose definitions have been criticized in the article by Denning (2017), asking the question: “Is it really true that any sequence of steps is an algorithm? That procedures of daily life are algorithms?” If the algorithm part of CT should be useful in K-12 students' future life, algorithms should probably be introduced, as recommended by Denning (2017), as a series of steps. However, the steps must not be arbitrary, and they should control a computational model.
The component of debugging was not a component of the very first CT model (Wing, 2006). On the other hand, Wing (2006) brought up damage containment and error correction. For the K-12 audience, this was exemplified by the rather complex concepts of gridlock, deadlock, and contract interfaces. Concepts in computer science at the university level, in general, are omitted in the two first programming courses in a Bachelor's program. However, the handling of the deadlock problem could also be illustrated as an everyday issue: “It is learning to avoid race conditions when synchronizing meetings with one another” (Wing, 2006, p. 34). Notably, years later, debugging is still not a concept in the comparison by Barr and Stephenson (2011), where different existing CT concepts were analyzed and discussed. However, in their attempt to develop an operational definition of computational thinking for K-12 settings, test and debug is brought up as core concept. In another study from the same year, debugging is suggested as a part of a CT concept suitable for K-12 teachers (Yadav et al., 2011). However, in computer science, debugging has a more exact definition than how it is related to by Yadav et al.'s (2011) “debugging was discussed by asking students to troubleshoot the scenario of a lamp not working when they get home from school, but was working in the morning. A series of ordered steps to solve a problem.” The question that remains with the definition of debugging in Table 1 is as follows: What does CT debugging include that is not a part of traditional troubleshooting in K-12 STEM subjects?
Like debugging, iteration is a CT component that has been added relatively late. The term was not mentioned by Wing (2006) and was not presented as a CT component by Barr and Stephenson (2011). However, in the same article, Barr and Stephenson (2011) pointed out iteration as a way of envisioning computational thinking in K-12 classrooms and an important component in the strive to make students tool builders and not merely tool users. On the one hand, it could be argued that iteration is a relatively basic programming technique with a structure not more complex than selection. On the other hand, it could be claimed that iteration has been a powerful technique for solving complex mathematical problems and has been used for centuries in numeric analysis. One well-known example is the Newton–Raphson Method to solve non-square and non-linear problems, with the idea of iteratively finding improvingly better approximations (Akram and Ann, 2015). Another field in mathematics where iteration is an important component is in the solving of number series problems (Folger et al., 2012; Schmid and Ragni, 2015). The mathematic tradition of iteratively creating improved approximations, like in a Fibonacci series, is also reflected in the definition above in Table 1 “Repeat design processes to refine solutions, until the ideal result is achieved” (Shute et al., 2017). In computer programming, iteration can be used for solving a wide variety of other tasks, such as file handling, searching and traversing data structures, and for image handling. With this wider computer science perspective, iteration could have more suitable applications, both for a younger audience (Brennan and Resnick, 2012) and for other types of problem-solving in STEM (Fields et al., 2019).
Finally, and what seems to be the last added of the six CT components, is a generalization. The term was neither mentioned by Wing (2006) nor by Barr and Stephenson (2011). In the more computer science-oriented discussion in the article by Denning (2017), the term is discussed as “Generalizing and transferring to other domains.” It could be argued that generalization could be interpreted as transferring from many domains to many other domains, and more like how problem-solving strategies were outlined in the classic book by Polya (1945). Including the idea that complex problems are easier solved by persons that earlier have solved similar but less complex problems. At the same time as Polya's ideas in the book have become a praised theory, it has been pointed out that younger students do not improve their problem-solving by reading this book. They improve their problem-solving skills by solving a lot of different problems (Schoenfeld, 1987). Transferred to the CT concept, this could be interpreted as that generalization is best learned by practicing other CT concepts. Regarding the definition of generalization in Table 1, “Transfer CT skills to a wide range of situations/domains to solve problems effectively and efficiently” (Shute et al., 2017), the stepwise and systematic approach in CT could be applied in several other domains, and preferably in other STEM subjects. Finally, as claimed in the white article by Einhorn (2012), CT could be seen as a general and essential 21st-century skill and a skill that is best learned by learning to program. “Computational thinking is a learnt approach and there's no better way to learn it than through programming. Programming employs all the components of computational thinking” (Einhorn, 2012, p. 2).
Materials and methods
The study was carried out with a qualitative approach to acquire data that have the potential to answer the research question and to fulfill the aim of investigating and discussing teachers' perceptions of CT in grades 7–12 mathematics and technology. Data have been gathered from essays that were submitted to an assignment in three batches of a teacher training course on fundamental programming. The course was tailored for grades 7–12 teachers in mathematics and technology with assignments that have the purpose of supporting teachers in their daily teaching and learning activities. In the submitted essays, teachers have reflected on CT in relation to their subject matters and how CT could be used in their future teaching and learning activities. The course has been designed with the idea of combining theoretical course content on didactic concepts, with concrete assignments on programming and CT (Mozelius, 2018).
Data collection
Collected data in the study consist of documents, which can be a valuable source for insights and information on a studied topic (Bowen, 2009). Using existing material such as documents is, compared to many other sources, convenient since the material can be accessed directly (Karppinen and Moe, 2019). Similar to other qualitative methods, the use of documents for analysis emphasizes the description and discovery of underlying patterns and meanings (Altheide, 2000). The documents are written by teachers in the form of essays during three instances of a professional development course on programming for grades 7–12 teachers in mathematics and technology. A total of 38 essays were written by the teacher participants (20 women and 18 men) during the course instances and collected for the study. 12 essays were collected from the course instance in the autumn semester of 2020, 10 were collected from the course instance in the spring semester of 2021, and 16 from the course instance in the autumn semester of 2021 (Table 2).
Data analysis
Collected data were analyzed with directed content analysis to extend the knowledge of teachers' perceptions of CT for grades 7–12 mathematics and technology (Hsieh and Shannon, 2005). Content analysis provides a systematic coding approach for interpreting and describing textual data (Assarroudi et al., 2018). To enhance the trustworthiness of the study, the analysis has been conducted in accordance with Assarroudi et al. (2018) 16 steps for directed qualitative content analysis, where the first seven cover the preparation phase of the study and the last nine cover the organization and reporting phase of the study. The last nine steps are described in this section.
In the first step of the analysis, the main categories were selected from the CT facets described in the section Computational Thinking. This was deductively performed using a theoretical framework related to the studied topic (Mayring, 2000). In the second and third steps, definitions and coding rules for the categories were decided based on the CT framework and related research for objectivity and accuracy (Mayring, 2000; Assarroudi et al., 2018). In the fourth step, a small sample of the collected data was analyzed with the selected categories and discussed between the authors. The rationale behind this was to test and evaluate the chosen categories and modify them if necessary (Elo et al., 2014), which was not deemed necessary. Discussions between the authors on the applicability of categories and theoretical framework continued throughout the analysis. In the fifth step, anchor examples for categories were chosen and specified (Assarroudi et al., 2018). This was done by adding related research to the facets of the CT framework, which were used as the basis for the categories. The related research could be seen as expectancy for the categories.
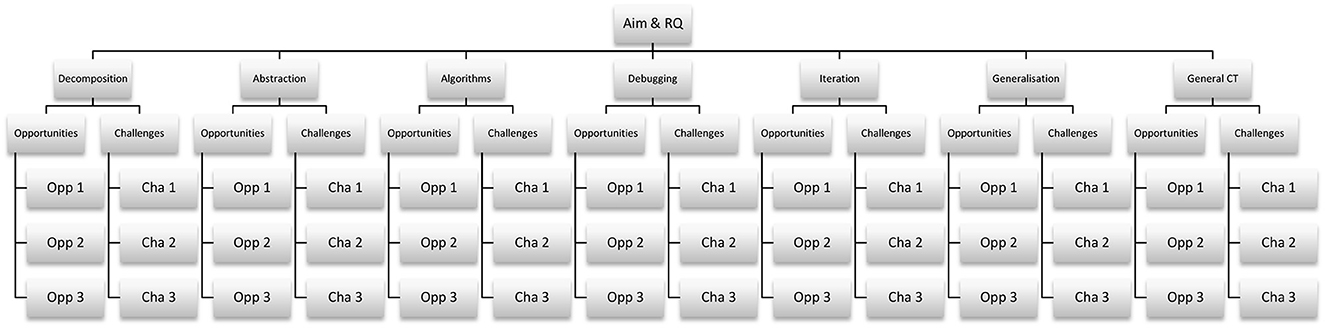
In the sixth step, the main data analysis was performed with a spreadsheet document to identify the content of interest for the categories and to select preliminary codes (Assarroudi et al., 2018). In the seventh step, sub-categories were derived from the categories through an inductive approach of grouping codes together based on their differences, similarities, and meanings (Assarroudi et al., 2018). This also resulted in a new category with new sub-categories of codes that related to CT in a more general sense than the initial categories provided by the theory. In the eighth step, comparisons were made between the categories, sub-categories, and codes to establish a logical link between them (Assarroudi et al., 2018). This was performed through multiple cycles where sub-categories and codes were grouped and re-grouped for logical consistency. This resulted in a coding tree (Figure 1) consisting of seven main categories (related to the aim and research question of the study), with two sub-categories of opportunities and challenges for each category and six main opportunities/challenges (three opportunities and three challenges) for each sub-category.
The main opportunities/challenges for each sub-category were identified by comparing codes for similarities, differences, and their relevance for the study aim, the research question, and their support in collected data. In the last step, the reporting of the findings was structured in the section Results and Analysis, with the categories for analysis used as sub-headings. In the sub-headings, the first parts were devoted to the sub-category of opportunities and the three identified main opportunities. The second part of the sub-headings was devoted to the sub-category of challenges, and the three identified main challenges.
Trustworthiness
To ensure trustworthiness in the study, the authors have worked according to the criteria of trustworthiness (credibility, transferability, dependability, and confirmability) provided by Schwandt et al. (2007), with the aim to make these visible throughout the study. Trustworthiness can be described as an alternative to reliability and validity, developed to be more applicable for judging and evaluating qualitative research (Bryman, 2016, p. 383–384). To ensure credibility, the study has been conducted with data from three iterations of a teacher professional development course on programming, spanning over a total of 1.5 years. Courses where both authors have been engaged in data collection and analysis and, at the same time, have worked as course facilitators. Both authors have earlier experience in research on the CT concept (Nouri and Mozelius, 2018; Humble, 2019, 2020). The collected data, the purpose behind the data, and the context for collection have been described in the Method section for transferability. To ensure dependability and confirmability, a detailed description of the analysis is provided in the Method section, and examples from the data are provided in the Results and Analysis section to show the connection between the collected material and the analysis.
Ethical considerations
The study followed the recommendation by Shaw (2003) about informed consent. Course participants were, in the introduction meetings for the various course instances, informed about the teachers' intention of using course content and submitted essays as parts of research studies. Furthermore, course participants were informed about the principle that they, at any time and without discussion, have the right to withdraw consent and quit without motivating why. The information was provided both orally in the introduction meetings and in written postings on the course discussion forum. As pointed out by Shaw (2003) and Pietilä et al. (2020), the strive for confidentiality and privacy is important in qualitative research. Essayists have been kept as anonymous as possible during the research process, with all names, affiliations, and other personal details removed. Presented quotes from the essays have been translated from Swedish to English with minor changes to further protect essayists' confidentiality and privacy. Moreover, some Swedish idioms have been rewritten with the aim of improving readability but without changing the core meaning. Finally, in these courses, where authors also have had the roles of instructors and facilitators, the principle of practitioner research was considered (Shaw, 2003).
Results and analysis
This section presents the results of the analysis in sub-headings related to each facet of the theoretical framework: decomposition, abstraction, algorithms, debugging, iteration, and generalization. The section is concluded with a sub-heading on the general perceptions of CT that teachers expressed in the study. Quotes from the collected data are presented in the sub-headings to exemplify the results and analysis of the study.
Decomposition
Results of the study show that teachers perceived CT decomposition as related to general problem-solving and that it can be used for exercising students in understanding instructions. It was also mentioned that it is a practice frequently used by teachers to break down subject content for students, and teachers express that there is a clear connection between CT decomposition and how teachers divide problems into their subjects into manageable parts. This is perceived as an important skill for students to develop. Teachers further expressed that being exposed to CT decomposition can enhance students' ability to understand instructions. Instructions that otherwise would be complex or difficult can be broken down into smaller and more understandable parts. Exercising CT decomposition through programming is perceived to also have positive effects on students' performance in other subjects. Teachers further expressed that their own practice of breaking down a subject into manageable teaching and learning parts for the students resembles the decomposition concept.
Teachers in the study perceived several challenges for CT decomposition in mathematics and technology. Some examples are that students' challenges in CT decomposition correlate with similar difficulties in mathematics, that decomposition is an unfamiliar practice for many students, and that decomposition is easier to understand than to apply for many students. According to teachers in the study, students that find mathematics challenging in general often also find decomposition challenging. Teachers expressed that decomposition is perceived as complicated by students but that this also depends on how the practice is introduced by the teacher. Furthermore, many students are not familiar with the practice of breaking down a problem and get frustrated when the answer does not appear immediately and give up, as expressed by one teacher in the study (Quote 1). According to teachers in the study, the practice of breaking down a problem is much easier to understand than it is to apply. Decomposition requires practice, an understanding of the whole problem, and how everything is connected and affects each other. According to teachers in the study, decomposition is fundamental for problem-solving but also one of the most difficult skills to master.
“I perceive that many students get frustrated when they get stuck and the answer does not appear, and sometimes they give up. They don't know how to break down the problem to progress. The majority are not familiar with addressing a problem through a computational approach and need to exercise more to be able to solve more difficult assignments. By exercising with, for example, programming, their patience and understanding for how quick and easy you can arrive at a solution should increase.”
Quote 1. Teacher about students' frustration with decomposition.
Abstraction
Regarding CT abstraction, teachers in the study perceived that finding patterns is a common practice for problem-solving in their subjects, that abstraction is a crucial skill for distinguishing between what is important and what is less important, and that abstraction is a crucial skill to develop for generalization. Teachers expressed that CT abstraction is connected to highlighting important parts of instructions and finding general patterns to solve problems in their subjects. According to teachers in the study, mathematics is about finding patterns and causality, and abstraction is reinforced by both mathematics and programming. Abstraction is also perceived by teachers to be the most common CT skill addressed in the teaching and learning of mathematics. A teacher in the study expressed that abstraction is an important first step in general problem-solving, that is, identifying the most important parts of a problem to form a picture of the whole solution (Quote 2). Teachers in the study further expressed that abstraction is vital for the ability to generalize. Students first need to understand the patterns to then be able to generalize those patterns to another context.
“Take problem-solving for example, it is important that the student first and foremost can understand the assignment and identify the content of a text. This is so that they know what kind of solution is being asked for and they can choose an appropriate method for the assignment. That is abstraction.”
Quote 2. Teacher about abstraction for problem-solving.
Teachers in the study perceived challenges for abstraction in mathematics and technology, such as abstraction is perceived to take a lot of time and practice to learn, abstraction is a challenging practice for teachers, and that abstraction can be a challenge for students that already find mathematics difficult. Teachers expressed that abstraction is a skill that develops over time and takes a lot of practice, which can be a challenge for many students. Teachers further expressed that abstraction can be a challenge for many teachers since it is not as common in teaching and learning activities as many of the other CT skills. Teachers also highlighted that abstraction is something that many students can understand and find easy when the teacher explains and shows, but they still fail to use the concept. Both CT abstraction and generalization are perceived by teachers in the study to be especially challenging for students since they also are aspects of mathematics that many students find difficult. However, teachers expressed that some students that struggle with abstraction and generalization in mathematics find it easier to handle in programming.
Algorithms
Results show that teachers in the study perceived that CT algorithms could foster students to be precise in their work, encourage them to be structured, and that algorithms relate to teachers' practice of creating subject instructions. Teachers expressed that the practice of being precise when working with algorithms is important in mathematics and that this practice can be developed with both mathematics and programming. Teachers also expressed hope that the precision developed by engaging with programming can make students more precise when working with mathematics. According to the teachers, algorithms are also among the first things that students learn in mathematics in their work with assignments on arithmetic. It is highlighted by teachers that if an algorithm is generalizable, it is a fantastic tool for the students and their learning. Teachers further expressed that algorithms mostly relate to the practice of creating subject instructions, by the teacher or in a book, that students should follow to solve a problem. Working with algorithms in programming by creating, manipulating, and discussing is perceived to support students to think more freely and deeper instead of viewing algorithms as a predefined recipe.
Some of the challenges that teachers in the study perceived with CT algorithms is that it can be difficult to motivate students since many want shortcuts and that CT algorithms can foster an unreflective problem-solving strategy. Teachers also expressed that some students find it pointless to write instructions for their solutions and that it, therefore, can be difficult to motivate them to do so. It takes a lot of practice and repetition to incorporate the practice among students, and teachers devote a lot of time to it. Teachers further highlighted that students tend to be careless in some steps of their solutions or calculations because they do not see the need to be precise. According to the teachers in the study, students want shortcuts and therefore have difficulties understanding that some problems need to be solved in a certain order. Teachers also expressed that algorithms can be problematic since they provide students with a strategy to solve problems without reflection. That is, following a pattern to solving a problem rather than understanding the problem. A teacher in the study expressed that this approach to problem-solving is quite common in mathematics and that students submit solutions to problems that are not reasonable and not supported by instructions because they have simply followed a pattern (Quote 3).
“Many students conduct mathematics quite unreflective. It's all too common that students submit assignments with solutions that are not reasonable. Additionally, the student provides scarce, if any, notes on how the solutions were derived at.”
Quote 3. Teacher about unreflective problem-solving in mathematics.
Debugging
CT debugging is perceived by teachers in the study to foster patience, encourage collaboration and discussion, and relate to the practice of coaching students. Teachers expressed that debugging can be a way to exercise students' patience when conducting a calculation or to search for errors. A teacher in the study also highlights that programming is a practice that can foster patience and error handling and hopefully influence students to apply this in mathematics also (Quote 4). Teachers further expressed that debugging is probably the easiest part of CT to apply with students since it can be combined with collaboration and discussion during lessons. Students can discuss different solutions to a problem and support each other in identifying and correcting errors. CT debugging is also perceived as a good approach for teachers to support students in identifying and solving their own errors instead of providing the correct answer. Debugging is perceived as a natural part of both programming and teaching since teachers coach students through their solutions.
“In programming, troubleshooting is a natural part. Additionally, it requires the student to write correctly, precise and that no steps are skipped. I have hopes for that troubleshooting will influence mathematics and become a habit. With programming, troubleshooting becomes natural.”
Quote 4. Teacher about programming as an influence on mathematics.
Regarding challenges of CT debugging, teachers in the study perceived that students can get blinded by their solutions, that it can be difficult to overcome initial failure, and that the practice of debugging is not as obvious in their subjects as it is in programming. Teachers expressed that students have difficulties identifying errors in their solutions and that they often get blinded by what they have done earlier. According to teachers in the study, this could be because teaching materials often focus more on concept, procedure, and problem-solving, rather than debugging. However, it would be better for students' mathematical development if more assignments focused on finding and correcting errors. Related to this, it is expressed that students often lack the motivation to systematically debug their solutions and rather just be told what needs to be corrected since it can be difficult to overcome the initial failure of making errors. Teachers further highlighted that motivation for debugging can be especially challenging for students that already find the subject boring or difficult. It is much easier just to give up. Teachers also expressed that debugging is not as obvious in the subject content as it is in programming since you do not get a solution that works or not. Instead, debugging becomes a question of plausibility. It is also expressed that exercising subject debugging through programming can be a challenge since students first need a certain level of programming knowledge.
Iteration
Results of the study show that teachers perceived CT iteration as similar to that of classroom feedback, repetition for learning, and the practice of reconsidering and trying different solutions to a problem. Teachers expressed that iteration resembles how a solution is passed between a student and a teacher for feedback; this is repeated until both are pleased with the outcome. However, this is more common with students that aim for higher grades. Teachers in the study also compare iteration with the practice of how students present their solutions in front of their classmates, which is followed by a discussion on the pros and cons and other potential solutions to the problem. Iteration is further compared to how equations are repeated for learning and to support students in finding shortcuts and optimizing their work. Teachers also highlighted that iteration is similar to how the four arithmetic methods are learned by students through repetition with pen and article. To reconsider solutions and try new approaches is also expressed by the teachers as important. If students do not get a satisfactory result that is not plausible, they should iterate and try again.
Teachers in the study perceived challenges regarding CT iteration, such as that students would rather be done with their assignments than iterate, that iteration is an advanced practice that is more obvious for programming, and that it is easier to ask for help than to iterate. Teachers expressed that not all students want to iterate their solutions but prefer to be done after the first try or have the teacher tell them what they need to do. Iteration is also expressed as something that teachers do not work on a lot within their subjects, but it is perceived as a relevant skill to develop and could be supported by programming. Iteration is also perceived as more applicable in programming than in mathematics. Teachers expressed that it is a more advanced practice and more difficult to teach than other parts of CT. One of the teachers wrote that iteration is important if you are a programmer and need to make your programs more efficient or competitive but that it is not that important for solving problems in school and, therefore, could be excluded when teaching and using CT (Quote 5). Iteration is also considered challenging to use since it is not a practice that many students are accustomed to. Students know what a typical lesson in mathematics looks like and feel comfortable with that, and if they are not motivated by the challenge, it is easier to ask for help.
“Iteration [...] I perceive as more advanced and difficult to teach [...]. As a professional programmer, it's important to get the optimal results which can affect a program efficiency and competitiveness. But to solve easy problems in school this can practically be neglected.”
Quote 5. Teacher about the problem with iteration for problem-solving in school.
Generalization
Regarding CT generalization, results show that teachers in the study perceived that it could support the development of interdisciplinary knowledge, methods for general problem-solving, and life skills. Teachers expressed that decomposition is a CT skill that should be generalized to all subjects since being structured and having a good study technique can help students in all subjects. Furthermore, teachers compared CT generalization with the knowledge that stretched over multiple school subjects and expressed that interdisciplinary projects in school can support the generalization of knowledge. General methods for problem-solving in mathematics are also used as examples for generalization by teachers. According to the teachers, students need a bank of methods that they can choose from and apply when they encounter problems where the solution is not obvious. A teacher in the study expressed that generalizable knowledge is something to strive for and that mathematics is not learned for the purpose of solving equations but to think logically and to solve problems (Quote 6).
“Finally, to generalize all this knowledge to other domains is certainly something to strive for. I usually say that you don't learn mathematics for solving equations but to learn logical thinking and problem-solving. I believe that the exact same reasoning can be applied for programming. Not everyone will be programmers, but to learn a structured way of thinking is an opportunity for many parts of life.”
Quote 6. Teacher about generalization as something to strive for.
Teachers perceived challenges with CT generalization in their subjects, such as: that it is difficult for students to develop, that it is mainly addressed for the higher grades and that students learn for now rather than in future. Teachers expressed that generalization is not the same in programming and mathematics and that it is more challenging in mathematics, especially if students already have difficulties in mathematics. However, using programming for exercise generalization and abstraction is mentioned as an opportunity for students that find this difficult in mathematics. It gives them the opportunity to grow. Teachers further highlighted that although generalization is considered important, it is not often taught as part of problem-solving strategies in their classrooms because it is mainly addressed in the higher grades of the subjects. According to the teachers, generalization can help students solve problems faster and more efficiently, but it also requires them to have knowledge of when to apply what. Generalization and algorithms are also considered among the CT skills that take the longest for students to develop. This becomes especially challenging when many students learn for now, rather than for the future, according to the teachers. Teachers further expressed that it can be difficult to convince students that their knowledge can be used in different contexts to solve similar problems. Students feel that the learning is finished when they have shown the teacher once that they can apply a specific strategy or method for problem-solving.
General perceptions of CT
Results of the study also show that teachers have general perceptions of CT for mathematics and technology that stretch beyond the facets of the CT framework, such as: that much of CT is already part of several school subjects but not addressed as CT, that CT can be used as a tool for motivation and changing perceptions in their subjects, and that CT is an important interdisciplinary skill for the future. Teachers in the study highlighted that they already do a lot of CT in their teaching and learning activities and that CT can be related to several subjects, for example, mathematics, technology, and natural sciences. Teachers also brought up that CT can act as the bridge between their subjects and programming, although CT is not a new practice for mathematics and technology. The associated skills can be addressed much more precisely and consciously with the concept of CT. It was also suggested by teachers that maybe CT should be addressed in mathematics rather than specifically in computer programming.
Teachers in the study expressed that CT can be a tool for changing perceptions and fostering motivation, both for students and teachers. It was suggested by a teacher in the study that CT can be used as a tool for supporting students that have a negative view of mathematics, and a history of failure, to find motivation again (Quote 7). Teachers also expressed that they feel motivated to use CT to make their teaching and learning activities more fun and up-to-date and move beyond the well-known methods and strategies in their subjects. CT skills were also perceived by teachers as relevant for all levels of education and all subjects, not only mathematics and technology. Furthermore, teachers expressed that CT is an important skill for students to develop, both for future work and everyday life. Teachers expressed that CT could foster creativity and planning and support students in being structured. Teachers in the study pointed out that not developing CT could be like having a digital handicap in future, much like the elderly today struggle with apps for parking and digital banks. According to teachers in the study, this puts the responsibility on schools to develop school culture and subjects to be up to date and in line with the needs of future society and labor market.
“Many students have developed a negative view of mathematics and have labeled it as boring and complicated. Also, a number of students have a history with years of failure in the subject. It requires enormous skills by the teacher to present the subject for these students in a way that can change their perceptions. Computational thinking can be a powerful tool that we teachers can use for supporting students in finding their motivation and learning mathematics.”
Quote 7. Teacher about CT as a powerful tool for supporting students in finding motivation.
There were also some perceived challenges for CT that were of a more general nature. Teachers perceived that CT requires a lot of time to be integrated, that it is a new way of thinking that can be difficult for many, and that it can be difficult to persuade teacher colleagues to implement CT. Teachers mentioned that it requires a lot of time, discussion, and coaching to incorporate CT in school subjects, and with limited time for teaching and big classes as it is, CT may be abandoned by many teachers. With this, teachers in the study perceive that it will take a long time before CT is a natural part of education and that the integration will continue to be a challenge for many teachers. It was also mentioned that this could be considered an inequality for education dependent on student's age since the younger students will have more time to develop CT than the older students. However, they will still live and work in the same society.
Teachers also expressed that CT is a new way of thinking that will be challenging for many students since it requires patience and a lot of work. According to teachers in the study, grown-ups tend to believe that students will find anything digitally interesting and fun, but this might not be the case for CT since it requires a lot of work. However, teachers also expressed that this trend of CT should be used by teachers to show students the importance of time and patience when engaging in problem-solving. A teacher in the study highlighted that it will be a challenge to get all teacher colleagues on board with CT since not everyone will see the importance of incorporating CT in their subjects and could still believe that CT is an isolated occurrence only affecting some subjects (Quote 8). According to teachers in the study, this could partly be explained by an unclear integration of programming by the Swedish National Agency for Education, which in turn may lead to a less thought-out integration by the teachers.
“However, I do see a challenge in converting many colleagues when this is probably going to include more subjects than technology and mathematics in the future. It will require a lesser popular movement to also get teachers in other school subjects to understand the point of programming. No previous curriculum in mathematics has, according to me, outlined such a big change. The requirements for competence in and awareness about computational thinking is something that do not only affect teachers in mathematics and technology. It is a global trend.”
Quote 8. Teacher about the challenge of getting teacher colleagues on board.
Discussion
Results of the study suggest that teachers perceived CT decomposition to be closely aligned with practices in mathematics. This can be compared to the fact that decomposition is an idea far older than its role in CT, as portrayed by Wing (2006), Barr and Stephenson (2011), and Shute et al. (2017). As a practice of divide and conquer in the Euclidean algorithm, decomposition has a clear connection to mathematics. As exemplified by Denning (2017), students who explain decomposition and abstraction well can still be poor designers of algorithms. This can be related to challenges expressed by teachers in the study, that students who find CT decomposition and abstraction difficult often have similar challenges in mathematics. According to Wing (2006), abstraction is closely aligned with decomposition to solve large and complex problems. Teachers in this study also perceived abstraction as an important skill for mathematics and as a foundation for developing generalization skills. For students that find decomposition and abstraction to be difficult, the recommendation is to practice and discuss different solutions in practical problem-solving. This could be carried out as group work, where the teacher initially presents a complex problem with details that could be abstracted. In the initial abstraction phase, the teacher asks the students how the presented problem could be abstracted to find an overall solution strategy. This is followed up with a common decomposition discussion where the given problem is divided into several smaller sub-tasks. In the next phase, students are divided into groups, where every group should work on the solution of one specific sub-task. Finally, each group presents their solution, and all groups together discuss if the solutions of the sub-tasks could be aggregated into coordinated solutions that solve the entire problem.
Computational thinking algorithms can be given more loosely defined, as in the case of Wing (2006) and Barr and Stephenson (2011). These definitions have the opportunity of making algorithms more applicable in everyday situations. As expressed by teachers in the study, CT algorithms can be used to encourage students to be more precise and structured in their work and relate to teacher practice of making step-by-step instructions for students. However, teachers also expressed concerns that CT algorithms can foster unreflective problem-solving strategies by simply following a pattern without reflecting if the answer is reasonable. This can be related to the criticism by Denning (2017) regarding defining algorithms too loosely. If algorithms are defined as any sequences of steps in everyday life, they can be easily applied almost anywhere, but what support do they then bring to larger and more complex problems? Regarding debugging, the teachers in the study perceived several opportunities for debugging in their teaching and learning practices, such as looking for errors in solutions and fostering patience among students. However, the results also show that the teachers do not use a definition of debugging that is as precise as in computer science, which is also exemplified by Yadav et al. (2011). As a part of CT, debugging has not been as obvious as many of the other facets, as can be seen in Wing (2006) and Barr and Stephenson (2011). This can be related to teacher perceptions in this study that debugging is not as obviously applicable in primary and secondary school subjects as in computer programming. The authors' recommendation is that algorithms could have a wider definition in primary school and be introduced as cooking recipes with a clear alignment to everyday activities that students can relate to. Later in secondary school, algorithms should be redefined more strictly to prepare students for future studies in programming and computer science. The same idea could be applied to debugging that it in primary school and lower secondary school, which might be presented as ‘troubleshooting' instead of debugging. Exactly when the term and definition shift should take place depends on when CT and programming are introduced. Today, this shows large variations between different schools, regions, and countries, but the guess is that students will meet these concepts at a younger age in future.
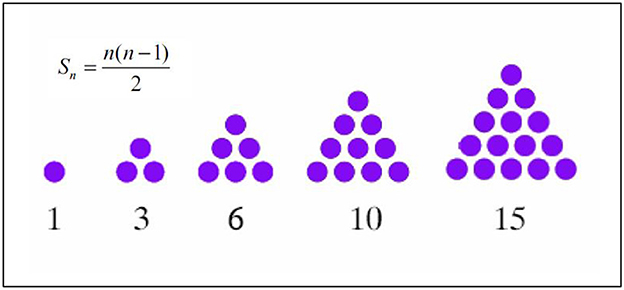
As with debugging, CT iteration is perceived by teachers in the study to not be as obvious for their subjects as for computer programming. Once again, as in the case of debugging, iteration is not a self-evident part of CT, which can be viewed in Wing (2006) and Barr and Stephenson (2011). CT iteration is further considered by the teachers to be an advanced practice that can be difficult to incorporate with students since it challenges how they are accustomed to working. This can be related to Barr and Stephenson's (2011) presentation of iteration as an important component for supporting tool building and not only tool use, which should be considered an advanced practice for primary and lower secondary school students. However, with a wider computer science perceptive on iteration, it can be used to address, for example, mathematics in the form of Newton Raphson Method (Akram and Ann, 2015), number series problems (Folger et al., 2012; Schmid and Ragni, 2015), and Fibonacci series. This could make the CT iteration concept more suitable for younger students (Brennan and Resnick, 2012) and their problem-solving in STEM subjects (Fields et al., 2019). To iteratively find approximations with the Newton Raphson Method is mathematics for upper secondary school and does not work for 7–9 grade students. For lower secondary schools, the recommendation is to build around algorithms that could be more clearly visualized. An example of this is the Fibonacci series sequence mentioned earlier, which could be visually depicted with the Golden Ratio. Another way of making the Fibonacci series more concrete is like Leonardo Fibonacci himself did, with the number series describing the growth of a rabbit population (Sinha, 2017). In another assignment, in the same courses where this study gathered data, participating teachers should submit a lesson plan where mathematical concepts were combined with programming exercises. A submitted creative lesson was built around the number series for pyramids. The lesson starts out with a calculation of two-dimensional pyramids, as illustrated in Figure 2.
In the second part of the lesson, pyramids should be three-dimensional, resulting in a pyramid with a height of 147. If the iteration is carried out correctly, the pyramid should consist of 1,069,670 blocks, which the teacher then compares to the Cheops pyramid in Giza. The real Cheops pyramid in Egypt is around 147 meters high, 280 royal cubits high, and with a total of ~2.3 million blocks with a weight of ~6 million tons. An assignment that can be clearly visualized and related to a fascinating real-world phenomenon (Mozelius and Humble, 2022). Regarding CT generalization, teachers in the study mentioned that it is considered an important skill for both education and life outside school. However, it can be challenging to integrate generalization in teaching and learning since generalization is mainly addressed for higher grades. The teachers' perceptions of generalization can be related to the ideas recommended by Denning (2017) and Polya (1945) that problem-solving strategies can be transferred to other domains and are best improved by solving many different problems (Schoenfeld, 1987). The teachers in the study perceived CT abstraction as a good foundation for developing generalization and could further be viewed as a support for this notion. Therefore, a recommendation for teachers would be to seek collaborations with other subjects in the use of CT concepts. This would give students the opportunities to apply CT-related skills to different types of problems and to generalize their knowledge to other domains and contexts. Einhorn (2012) claimed that CT is best learned through computer programming also resonates with the perceptions of many teachers in the study. Teachers in the study expressed that programming can be used to support teaching and learning in their subjects and the development of students' CT skills. A potential challenge with this is that programming can be perceived as difficult by both students and teachers. However, with the growth of programming tools targeted for educational use, and sometimes with CT in mind, searching for appropriate programming tools is easier today than just a decade ago.
Teachers also expressed more general perceptions of CT that stretch beyond the CT facets and K-12 education context. An example is that CT is considered to be an important skill for both education in general and the future life of students. These perceptions can be related to the criticism of Wing's (2006) original definition of CT and that CT could be relevant for problem-solving outside the field of computer science (Denning, 2009; Hemmendinger, 2010). Teachers in the study also expressed some general concerns about CT. For example, it will be a long and challenging process to implement CT in education and to get all colleagues onboard. Once again, the authors suggested that this challenge could be addressed through collaborations between different school subjects. Collaborations between teachers would both strengthen their own professional development in CT and provide students with the opportunity to generalize their skills and knowledge. It is further suggested that part of this challenge could be caused by unclear instructions for the use and integration of computer programming and related practices in K-12 education. This could be related to the more general body of research and theoretical frameworks for CT, where no consensus has been reached for exactly what CT is and what it incorporates. Here, the research community has a responsibility to provide more quality studies on CT in the K-12 context and to communicate these to educational stakeholders with clear recommendations.
Conclusion
The findings of this study show that teachers perceived both opportunities and challenges for CT in grades 7-12 mathematics and technology, of which many can be related to previous research on CT. Some of the more interesting findings are that teachers perceived CT, and many of its facets, as relevant to their subjects and that it can provide opportunities for teaching and learning activities. However, some parts of CT are also perceived as challenging to apply in classroom settings, and their relevance for mathematics and technology is, to some extent, questioned. This can be related to the literature on the topic, which shows a differentiated view of what CT is and what skills it contains. A scattered understanding of CT and what it encompasses makes it difficult for teachers to form an overview of the concept and what it can be used for.
The conclusion of the study is that CT has the potential to enhance teaching and learning activities in mathematics, technology, and other STEM subjects. If this should be successful, CT must not be involved too abstractly or too superficially. Abstraction is an important component in CT and, in general, problem-solving, but at the same time, the more diabolic details must also be handled. The resemblances between CT and programming are evident, with the same distinction between knowledge and skills. Regarding the knowledge part of CT, this could be presented relatively easily. However, to be an additional and useful skill in STEM subjects, more technical definitions of CT are preferred. The authors' recommendation is to provide a wider range of professional development courses for K-12 STEM teachers. There ought to be various courses on programming and computer science, where the CT components are applied in concrete problem-solving. Finally, as highlighted in several other studies, CT sharpens students' systematic and analytical thinking, which could be of value in contexts outside STEM.
This study makes an important contribution to the discussion on CT in K-12 education, adding the teachers' perspective. The findings presented in the study can be used to inform teachers and other stakeholders of the potential opportunities and challenges with CT for K-12 education.
Limitations and future research
The results of this study are based on limited material and include teacher perceptions of the studied topic that are not always based on their own experiences. Two potential future studies that could address these limitations are (1) a large-scale investigation of teacher perception of CT and its' application in K-12 education and (2) a specialized investigation with teachers that apply CT in their teaching and learning activities, for example, through computer programming. These two studies could also be combined for a more thorough investigation of the opportunities and challenges of CT, with the idea of a mixed methods approach.
Data availability statement
The datasets for this article are not publicly available due to concerns regarding participant/patient anonymity. Requests to access the datasets should be directed to the corresponding author.
Ethics statement
Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent for participation was not required for this study in accordance with the national legislation and the institutional requirements.
Author contributions
The main work of the study has been conducted by the NH. PM has contributed important insights to the study, including but not limited to: previous research, data collection and analysis, and presentation of findings. All authors contributed to the article and approved the submitted version.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Akram, S., and Ann, Q. U. (2015). Newton raphson method. Int. J. Sci. Eng. Res. 6, 1748–1752. Available online at: https://www.ijser.org/onlineResearchPaperViewer.aspx?Newton-Raphson-Method.pdf (accessed March 16, 2023).
Altheide, D. L. (2000). Tracking discourse and qualitative document analysis. Poetics 27, 287–299. doi: 10.1016/S0304-422X(00)00005-X
Assarroudi, A., Heshmati Nabavi, F., Armat, M. R., Ebadi, A., and Vaismoradi, M. (2018). Directed qualitative content analysis: the description and elaboration of its underpinning methods and data analysis process. J. Res. Nurs. 23, 42–55. doi: 10.1177/1744987117741667
Balanskat, A., and Engelhardt, K. (2015). Computing Our Future. Computer Programming and Coding. Priorities, School Curricula and Initiatives Across Europe. Brussels: European Schoolnet.
Barr, V., and Stephenson, C. (2011). Bringing computational thinking to K-12: what is involved and what is the role of the computer science education community? ACM Inroads 2, 48–54. doi: 10.1145/1929887.1929905
Bowen, G. A. (2009). Document analysis as a qualitative research method. Qualit. Res. J. 9, 27–40. doi: 10.3316/QRJ0902027
Brennan, K., and Resnick, M. (2012). “New frameworks for studying and assessing the development of computational thinking,” in Proceedings of the 2012 Annual Meeting of the American Educational Research Association, Vancouver. Canada, 25.
Brims, J. (1999). Procedural thinking and the Logo computing language (Doctoral dissertation). University of Glasgow, United Kingdom.
Cansu, S. K., and Cansu, F. K. (2019). An overview of computational thinking. Int. J. Comput. Sci. Educ. Schools 3, n1. doi: 10.21585/ijcses.v3i1.53
Denning, P. J. (2009). The profession of IT Beyond computational thinking. Commun. ACM 52, 28–30. doi: 10.1145/1516046.1516054
Denning, P. J. (2017). Remaining trouble spots with computational thinking. Commun. ACM 60, 33–39. doi: 10.1145/2998438
Dolgopolovas, V., Dagiene, V., Jasute, E., and Jevsikova, T. (2019). Design science research for computational thinking in constructionist education: a pragmatist perspective. Problemos 95, 144–159. doi: 10.15388/Problemos.95.12
Einhorn, S. (2012). “Microworlds, computational thinking, and 21st century learning,” in LCSI White Paper, 1–10.
Elo, S., Kääriäinen, M., Kanste, O., Pölkki, T., Utriainen, K., and Kyngäs, H. (2014). Qualitative content analysis: a focus on trustworthiness. SAGE Open 4, 2158244014522633. doi: 10.1177/2158244014522633
Fields, D. A., Lui, D., and Kafai, Y. B. (2019). “Teaching computational thinking with electronic textiles: modeling iterative practices and supporting personal projects in exploring computer science,” in Computational Thinking Education (Singapore: Springer), 279–294. doi: 10.1007/978-981-13-6528-7_16
Heintz, F., Mannila, L., Nordén, L. Å., Parnes, P., and Regnell, B. (2017). "Introducing programming and digital competence in Swedish K-9 education,” in International Conference on Informatics in Schools: Situation, Evolution, and Perspectives (Cham: Springer), 117–128. doi: 10.1007/978-3-319-71483-7_10
Hsieh, H. F., and Shannon, S. E. (2005). Three approaches to qualitative content analysis. Qualit. Health Res. 15, 1277–1288. doi: 10.1177/1049732305276687
Humble, N. (2019). “Developing computational thinking skills in K-12 education through block programming tools,” in Proceedings of the 12th annual International Conference of Education, Research and Innovation 2019 (ICERI 2019) (New York, NY: The International Academy of Technology, Education and Development), 4865–4873. doi: 10.21125/iceri.2019.1190
Humble, N. (2020). “Using textual programming tools to develop computational thinking skills in K-12 education,” in Proceedings of the 12th Annual International Conference on Education and New Learning Technologies (EDULEARN20) Valencia, Spain, 6th−7th of July, 2020 (New York, NY: The International Academy of Technology, Education and Development), 7188–7195. doi: 10.21125/edulearn.2020.1846
Humble, N., Mozelius, P., and Sällvin, L. (2019). “Teacher challenges and choice of programming tools for teaching k-12 technology and mathematics,” in International Conference on Education and New Developments (END 2019), Porto, Portugal, 22–24 June, 2019 (New York, NY: InScience Press), 431–435. doi: 10.36315/2019v1end099
Irons, J., and Hartnett, M. (2020). Computational thinking in junior classrooms in New Zealand. J. Open Flexible Dist. Learn. 24, 28–42. Available online at: https://search.informit.org/doi/epdf/10.3316/informit.629980776866194 (accessed March 16, 2023).
Karppinen, K., and Moe, H. (2019). “Texts as data I: document analysis,” in The Palgrave Handbook of Methods for Media Policy Research (Cham: Palgrave Macmillan), 249–262. doi: 10.1007/978-3-030-16065-4_14
Lee, I., Martin, F., Denner, J., Coulter, B., Allan, W., Erickson, J., et al. (2011). Computational thinking for youth in practice. ACM Inroads. 2, 32–37. doi: 10.1145/1929887.1929902
Mayring, P. (2000). Qualitative content analysis. Forum: Qual. Soc. Res. 1, 1–10. doi: 10.17169/fqs-1.2.1089
Mozelius, P. (2018). “Teaching the teachers to teach programming: on course design and didactic concepts,” in Proceedings of the 11th Annual International Conference of Education, Research and Innovation, Vol. 11 (New York, NY: The International Academy of Technology, Education and Development), 8031–8037. doi: 10.21125/iceri.2018.0445
Mozelius, P., and Hoff, C. (2019). “The introduction of programming in compulsory school: a multi-stakeholder perspective,” in Proceedings of the 12th Annual International Conference of Education, Research and Innovation (Sevilla: IATED). doi: 10.21125/iceri.2019.0570
Mozelius, P., and Humble, N. (2022). “Programming in K-12 mathematics: a two-step rocket,” in INTED2022 Proceedings (Sevilla: IATED), 2389–2397. doi: 10.21125/inted.2022.0704
Nouri, J., and Mozelius, P. (2018). “A framework for evaluating and orchestrating game based learning that fosters computational thinking,” in EduLearn 2018, Vol. 10 (New York, NY: The International Academy of Technology, Education and Development), 1305–1310. doi: 10.21125/edulearn.2018.0418
Papert, S. A. (1980). Mindstorms: Children, Computers, and Powerful Ideas. New York, NY: Basic Books.
Pietilä, A. M., Nurmi, S. M., Halkoaho, A., and Kyngäs, H. (2020). “Qualitative research: ethical considerations,” in The Application of Content Analysis in Nursing Science Research (Cham: Springer), 49–69. doi: 10.1007/978-3-030-30199-6_6
Pörn, R., Hemmi, K., and Kallio-Kujala, P. (2021). Inspiring or confusing: a study of Finnish 1–6 teachers' relation to teaching programming. LUMAT Int. J. Math Sci. Technol. Educ. 9, 366–396. doi: 10.31129/LUMAT.9.1.1355
Royal Society (2017). After the Reboot: Computing Education in UK Schools. Washington, DC: Policy Report.
Schmid, U., and Ragni, M. (2015). “Comparing computer models solving number series problems,” in International Conference on Artificial General Intelligence (Cham: Springer), 352–361. doi: 10.1007/978-3-319-21365-1_36
Schwandt, T. A., Lincoln, Y. S., and Guba, E. G. (2007). Judging interpretations: But is it rigorous? Trustworthiness and authenticity in naturalistic evaluation. New Direct. Eval. 2007, 11–25. doi: 10.1002/ev.223
Selby, C., and Woollard, J. (2013). Computational Thinking: The Developing Definition. University of Southampton (E-prints). Available online at: http://eprints.soton.ac.uk/id/eprint/356481 (accessed March 16, 2023).
Shaw, I. F. (2003). Ethics in qualitative research and evaluation. J. Soc. Work 3, 9–29. doi: 10.1177/1468017303003001002
Shute, V. J., Sun, C., and Asbell-Clarke, J. (2017). Demystifying computational thinking. Educ. Res. Rev. 22, 142–158. doi: 10.1016/j.edurev.2017.09.003
Sinha, S. (2017). The Fibonacci numbers and its amazing applications. Int. J. Eng. Sci. Invent. 6, 7–14. Available online at: http://www.ijesi.org/papers/Vol(6)9/Version-3/B0609030714.pdf (accessed March 16, 2023).
Smit, S., Tacke, T., Lund, S., Manyika, J., and Thiel, L. (2020). The Future of Work in Europe: Automation, Workforce Transitions, and the Shifting Geography of Employment. McKinsey Global Institute. Available online at: https://www.mckinsey.com/featured-insights/future-of-work/the-future-of-work-in-europe (accessed March 16, 2023).
Tikva, C., and Tambouris, E. (2021). Mapping computational thinking through programming in K-12 education: a conceptual model based on a systematic literature review. Comput. Educ. 162, 104083. doi: 10.1016/j.compedu.2020.104083
Tran, Y. (2018). Computer programming effects in elementary: Perceptions and career aspirations in STEM. Technol. Knowl. Learn. 23, 273–299. doi: 10.1007/s10758-018-9358-z
Tzagkaraki, E., Papadakis, S., and Kalogiannakis, M. (2021). “Exploring the use of educational robotics in primary school and its possible place in the curricula,” in Education in and with Robotics to Foster 21st-Century Skills: Proceedings of EDUROBOTICS 2020 (Cham: Springer International Publishing), 216–229. doi: 10.1007/978-3-030-77022-8_19
Van Laar, E., Van Deursen, A. J., Van Dijk, J. A., and De Haan, J. (2017). The relation between 21st-century skills and digital skills: a systematic literature review. Comput. Hum. Behav. 72, 577–588. doi: 10.1016/j.chb.2017.03.010
Wing, J. (2011). Research notebook: computational thinking-what and why. Link Mag. 6, 20–23. Available online at: https://www.cs.cmu.edu/link/research-notebook-computational-thinking-what-and-why (accessed 16 March 2023).
Wing, J. (2014). “Computational thinking benefits society,” in Proceedings of the 40th Anniversary Blog of Social Issues in Computing (New York, NY: Academic Press). Available online at: http://socialissues.cs.toronto.edu/index.html%3Fp=279.html (accessed March 16, 2023).
Wing, J. M. (2008). Computational thinking and thinking about computing. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 366, 3717–3725. doi: 10.1098/rsta.2008.0118
Wolz, S., Bergande, B., and Brune, P. (2022). Influence factors on students motivation in introductory programming lectures of computer science non-majors. Cogent. Educ. 9, 2054914. doi: 10.1080/2331186X.2022.2054914
Yadav, A., Mayfield, C., Zhou, N., Hambrusch, S., and Korb, J. T. (2014). Computational thinking in elementary and secondary teacher education. ACM Trans. Comput. Educ. 14, 1–16. doi: 10.1145/2576872
Keywords: computational thinking, teacher perspective, mathematics, technology, K-12 education
Citation: Humble N and Mozelius P (2023) Grades 7–12 teachers' perception of computational thinking for mathematics and technology. Front. Educ. 8:956618. doi: 10.3389/feduc.2023.956618
Received: 30 May 2022; Accepted: 06 March 2023;
Published: 29 March 2023.
Edited by:
Stamatios Papadakis, University of Crete, GreeceReviewed by:
Gary Wong, The University of Hong Kong, Hong Kong SAR, ChinaEffransia E. Tzagkaraki, University of Crete, Greece
Copyright © 2023 Humble and Mozelius. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Niklas Humble, bmlrbGFzLmh1bWJsZUBoaWcuc2U=
 Niklas Humble
Niklas Humble Peter Mozelius
Peter Mozelius