The importance of high school on the university students’ success in the subject of mathematics

This research examines the relationship between high school, namely, high school profiles, and students’ success during an elementary mathematics course at university. For the analysis of this relationship, a mixed methods case study was chosen as the research design. The instruments for collecting the data were a questionnaire and a semi-structured interview that provided answers to the research questions. The sample consisted of 81 students (N = 81) from the University of Applied Sciences in Ferizaj, Kosovo, who participated in the questionnaire, and 12 out of the 81 students were also interviewed. The research results indicated that a positive, not strong, correlation exists between high school and university success. Moreover, students expressed that knowledge gained in high school made them feel sufficiently prepared during the lectures on elementary mathematics. The high school profile makes a difference in the students’ success in the elementary mathematics course at the university.

Introduction

Unfortunately, in recent times, pre-university education in Kosovo has faced a lack of students who are well prepared even with basic knowledge of mathematics. According to the Program for International Student Assessment (PISA) results, Kosovar students performed worse in the 2018 PISA compared to the 2015 PISA (Shala et al., 2021). A lack of knowledge in mathematics creates gaps and difficulties in understanding the subjects taught during the first year of studies (Gjonbalaj, 2013). This is an issue that professors have expressed in various formal meetings organized by faculties, such as program/department committee meetings. They have expressed that they have noticed a decrease in the level of knowledge students are expected to have in the relevant level of studies. The research conducted by Ayebo et al. (2017), which examined the role of high school preparation in students’ success at calculus, has led us to consider addressing this problem in Kosovo as well. The results obtained from Ayebo et al. (2017) show that good preparation in pre-calculus in high school represents a link to success in calculus at university. Since calculus is not taught in the University of Applied Sciences in Ferizaj, Kosovo, we have deemed it appropriate to conduct our research on the subject of elementary mathematics (EM), because it is taught in several faculties of this university. The review of the EM syllabuses (University of Applied Science in Ferizaj, 2020) at these faculties indicates that the course content generally comprises topics covered in high school (HS) such as sets, sequences, limit of sequences and functions, derivative of functions, percentage, financial mathematics, measurement, geometry, and trigonometry. The difference is that in EM classes, this content is handled quickly because it is considered that students are already familiar with the topics and the professors focus only on students’ needs regarding certain parts of the material. In almost all the faculties, the EM course aims to equip the students with knowledge and skills regarding concepts, structures, and basic mathematical operations so they can successfully use them in other subjects as well. Another important aim of this course is to fill the gaps in previous education by developing the students’ skills and abilities to be better prepared for their field of study and better integrate mathematics with other areas. The purposes and content of the EM course indicate that preparation with basic mathematical knowledge in high school is necessary, and its importance is unquestionable. Based on our experience with students, the fact they have difficulties in successfully completing the EM course is concerning for us. Students need time to pass this exam and all the energy they should spend focusing on professional subjects is spent on learning mathematics. Furthermore, because of their difficulties in successfully completing the EM course, sometimes they drop out, whereas others engage in additional private classes (additional paid math classes taken outside the school).

In Kosovo, upper secondary education is divided into gymnasiums and vocational schools. Gymnasiums are divided into three profiles: the Gymnasium of Natural Sciences, the Gymnasium of Social Sciences and Languages, and Specialized Gymnasiums (Artistic, Mathematical, Languages, Technical). Profiles in vocational schools are created based on their core curricula (Ministry of Education Science and Technology, 2016). Mathematics is an obligatory subject in all these profiles, but the difference lies in the number of classes held per week. None of these profiles offer different branches of mathematics (algebra, analysis, geometry), neither as mandatory nor as elective courses; therefore, one of the research questions is focused on the role of HS profiles for EM courses.

This research examined students’ mathematical preparation from these profiles based on their homework and participation in various projects, as well as their private course attendance. Looking closely at the students’ poor results, especially in the first exam session, these issues have been researched as a case study at the University of Applied Sciences in Ferizaj. This university comprises five faculties, but the research was conducted in three of them because the EM course is taught only in these three faculties (during the first year of studies). This empirical research aims to examine the following questions:

Does the students’ chosen high school profile play a role in their success in the EM course?

To what extent does the high school prepare the first-year students for the EM course?

Answers to the research questions have been obtained using mixed methods.

The importance of this research lies in the fact that the results obtained can provide useful information to make the necessary interventions in the community. This means identifying the problems so students can be properly prepared in regard to the mathematical knowledge needed for their studies. In Kosovo, there is no way that high school math teachers have the opportunity to track their students’ success in mathematics during their studies. Therefore, this research can serve as an opportunity for them to get feedback in order to focus on filling the students’ gaps regarding basic mathematical concepts.

Literature review

In order to succeed in a particular area, a particular working method is obviously needed (Gjonbalaj, 2013). According to the teachers’ interactions with students on a daily basis, it was observed that a small number of students use a specific learning system or study continually. Within a classroom, such a group of students–who are almost always prepared for their classes–is immensely small. The rest of them start preparing for the course only if they have an oral or written assessment within one or 2 days. Students who are part of the group with a special work system are the potential students likely to succeed in their studies as well. In the research conducted by Edge and Friedberg (1984), three groups of students were involved in finding the factors from which success in calculus could be predicted. The results obtained indicated that the combination of algebraic skills, psychological factors such as persistence, and long-term stability, play an important role in predicting success in calculus. The knowledge that students obtain in high school is an essential factor in how prepared they feel for the calculus subject in college (Ayebo et al., 2017). Moreover, even in the first lecture, when the course syllabus is presented, students notice and self-evaluate their preparation by recalling the course syllabus topics. The students’ suggestion to their high school math teachers was to include the reviewing of limits and tell them about the specific use of the concepts so they can better prepare for university level. High school teachers, on the other hand, emphasized some difficulties that their students encounter, starting from exponential expressions, the composition of functions, and the factorization of complex fractional expressions (Godfrey, 2020). Additionally, mathematics professors at the faculty expressed their concern about the lack of their students’ knowledge and claim that this issue derives from the level of knowledge they have obtained in high school (Sadler and Sonnert, 2017). They highlight certain skills that students typically need to develop in high school and expect them to be able to interpret results, analyze phenomena, solve complex problems, and support evidence-based ideas (Conley, 2010). On the other hand, the professors of EM at the university where this research was conducted, based on their syllabuses, expect their students to have basic conceptual knowledge, to understand the elements of linear algebra, to know the concept of sequence and function, and be familiar with the limit of functions. Between what students remember from the knowledge gained in high school and what university professors expect in calculus, there is a gap that prevents them from building new knowledge (Godfrey, 2020).

The students’ transition period from high school to college is very complex and much-discussed, especially for the subject of mathematics (Burrill, 2017). Identifying the reasons for students’ challenges throughout the transition phase has been an ongoing component of many studies. According to Burrill (2017), challenges may arise from the fact that the majority of high school textbooks do not regularly incorporate practices in their approach to teaching mathematics, such as providing opportunities for students to think about mathematics by reasoning and connecting concepts, implementing algebraic processes, and developing notational fluency.

According to Bressoud (2017), if high school students choose a calculus course to enroll more easily in college rather than focus on perfecting the course content and, furthermore, if it is established that this purpose affects their ability to remember better and assimilate the information, then special attention should be paid to this students’ purpose. Choosing the right HS profile is an early and important step for good preparation for further studies. If the students in this phase have clear views and ambitions for their profession in the future, then the more dedicated they will be to the engagements that guide them to that profession, and they are more likely to be successful. The transition from high school mathematics to university mathematics can be successfully completed when everyone works toward a common goal (Bressoud, 2021).

Methodology

Research design

This research design is a case study conducted at the University of Applied Sciences in Ferizaj, Kosovo. In order to carry out this research, written permission was obtained in advance from the university management for access to student lists and data collection through research instruments, which started 4 weeks after the end of the winter semester. Based on the regular contact with students we dealt with during our lectures and exams, we noticed a lack of adequate preparation for the EM courses. Therefore, the case study with these students sheds light on the problem. The method used in this research is the mixed method because the data was collected through a questionnaire and a semi-structured interview. The questionnaire was conducted virtually through Google Forms, due to the circumstances caused by the COVID-19 pandemic, thus giving participants 2 weeks to complete it. One week after the completion of the questionnaire, physical interviews were conducted with 12 students at the university campus, respecting the anti-COVID measures in place.

Sample and data collection

The population comprises students of the Faculty of Management, the Faculty of Tourism and Environment, and the Faculty of Architecture, Design, and Wood Technology at the University of Applied Sciences in Ferizaj. The city where the research was conducted is among the top three municipalities by number of inhabitants in Kosovo. The sample (N = 81) was chosen randomly by taking every fifth student (probability sampling) from the lists of students of these faculties, generated by the UMS (University Management System). It comprised 56 women and 25 men who completed high school in one of the public schools in Kosovo. Regarding the study year, 33 of the participating students were in the first year of studies, 40 in the second year, and eight in the third year of studies. The questionnaire was conducted with the entire sample, while the interview was conducted with 12 students. Four students were randomly selected for the interview for each study year. Considering the fact that the questionnaire was conducted virtually, depending on the time students submitted the completed questionnaires, they were selected for the interview by taking the first student, then two students from the middle, and the last one.

The instrument for gathering the quantitative data was a questionnaire, while the qualitative data were gathered through a semi-structured interview. The questionnaire as a tool for data collection was chosen to include more students in the research, so their representation of characteristics of their previous education was decent. The questionnaire included 29 questions about HS, the subject of mathematics, and questions about the students’ engagement in mathematics. These categories provided the data on the profiles, the number of mathematics classes, the topics covered during their previous education, how much they felt prepared for these topics at the university, whether their knowledge from high school helped them, solving homework, and the attendance of private mathematics courses. Data on success in high school were gathered from the questionnaire through the following question: What was your average grade in the subject of mathematics during your three years of high school education? Meanwhile, the students’ grades in EM were obtained from the list generated by the UMS; consequently, direct questions in the questionnaire about their grades in EM were not included. The reliability of the questionnaire was calculated using Cronbach’s Alpha with a value of 0.807. This means the questionnaire was highly reliable; therefore, the questions had internal consistency and were closely related (Hameli, 2017). The interview contained questions that aimed to elicit more details of participants’ knowledge and their views and opinions (Creswell and Creswell, 2018). Hence, the interview was supposed to provide more detailed information about the students’ experience in high school and their mathematical knowledge using seven questions and three mathematical problems. The questions provided information regarding their liking of the subject of mathematics and the factors that influenced their success in this subject, while through the mathematical problems more detailed information was gathered regarding the students’ knowledge of formulas, concepts, and mathematical rules. Since the interview contained questions and mathematical problems, in order to increase its validity and reliability, we consulted two experts in the field of mathematics who assessed that the interview questions’ content answer the research purpose.

Data analysis

The data gathered from the questionnaire were analyzed using the SPSS program (Statistical Package for the Social Science). Via this program, the correlation between different variables was examined and the Chi-square test was used to test the raised hypotheses (Norusis, 2008). When entering the data into the SPSS program, there were questions that contained multiple selections and had to be coded as new variables; consequently, the number of items increased to 60 even though there were 29 questions in the questionnaire. Godfrey (2020) investigated students’ gaps between their high school knowledge and the knowledge obtained during mathematics lectures at university. He divided the answers of the students’ tasks during the interview into several categories to compare them with their grades. A similar analysis was used in this research by dividing the solving of tasks included in the interview into five categories, depending on the number of mistakes made during the problem-solving process. These categories indicate the level of knowledge students have about mathematical formulas, concepts, and rules.

Results

The results from the questionnaire

In order to see whether the students’ success in high school is associated with the success they achieve in their studies, the Spearman correlation coefficient was used. High school success was measured by a question included in the questionnaire where participants had to choose their grade (1–5) in mathematics based on the rounded mean during your three years of high school education. Of all the participants, 11.1% had poor grades (2), 34.6% had fair grades (3), 35.8% had good grades (4), and 18.5% had excellent grades (5). The high school grading system in Kosovo is 1–5, where 1 means “failed” and 5 means “excellent.” While the assessment at the university level is done according to the following division: “5 = failed,” “6 = sufficient,” “7 = satisfactory,” “8 = good,” “9 = very good,” and “10 = excellent.”

Success in the EM course was calculated from the grades of each participating student, derived from the lists generated by the UMS, of which the passing rate (grades 6–10) is approximately 80%, so 51.9% (6), 9.9% (7), 8.6% (8), 7.4% (9), and 2.5% (10). Approximately 20% of the students did not pass the EM exam.

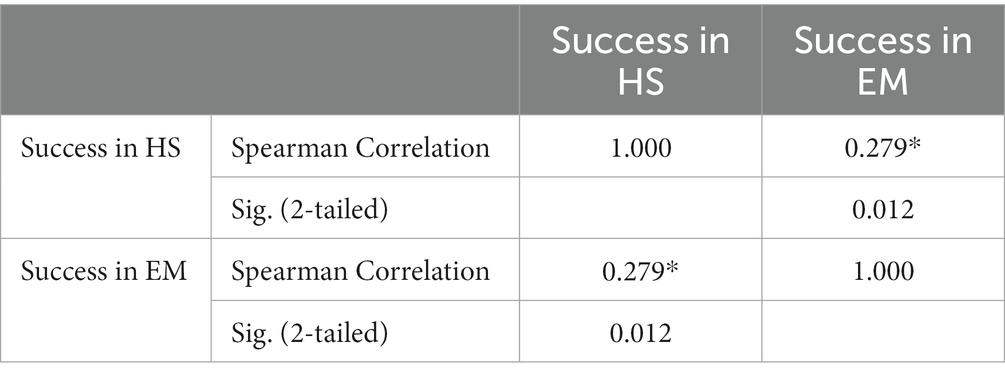
To ensure that the data are not normally distributed, the test of normality is done ( $"sig.,p=.000<.05$ ), and then a non-parametric test like the Spearman correlation can be used to measure the degree of the relationship between two ordinal variables. The Spearman coefficient is denoted by $\rho$ and takes values in the range [−1,1] and, if $\rho$ is positive, then the variables are in direct proportion (Denis, 2016).

It can be seen in Table 1 that $\rho =.279$ , therefore, there is a positive correlation between success in HS and success in EM, but this correlation is not strong. However, a coefficient of 0.279 is still statistically significant and if one of the variables increases, there is a tendency for the other to increase to a certain degree.

TABLE 1

Table 1. The Spearman correlation coefficient.

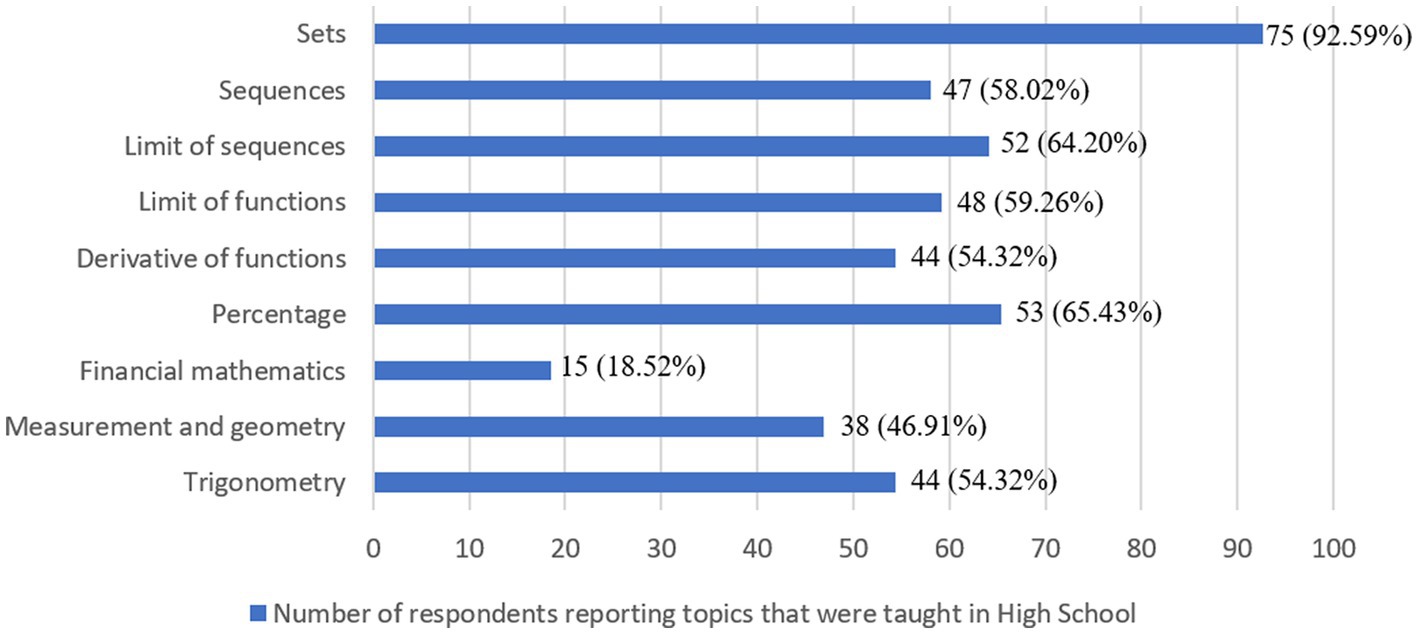
On the other hand, the EM syllabus mostly comprises topics that are taught in HS, and its purpose is to fill the gaps in the knowledge the students may have from HS. Students were asked to select the topics taught in HS and, based on their responses, the graphic below depicts an overview in percentages of students’ responses for each topic taught, e.g., 75 out of 81 students reported that the topic “Sets” was taught in high school.

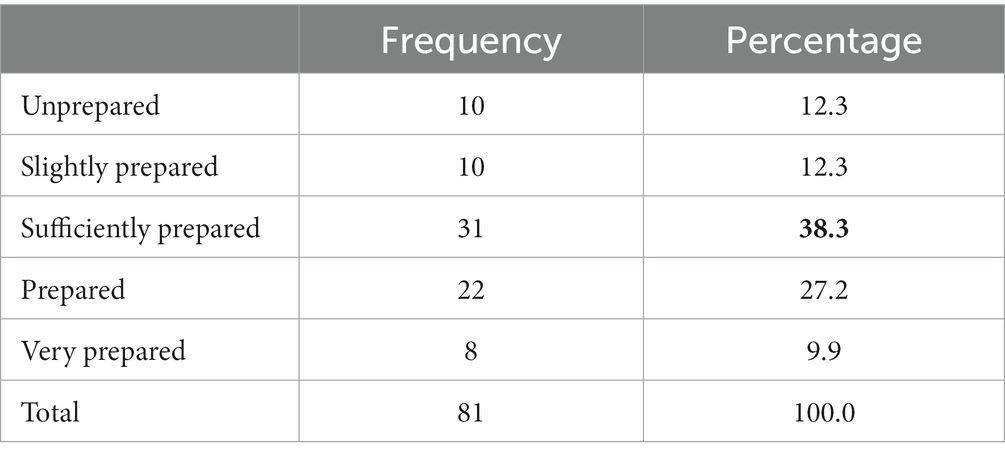
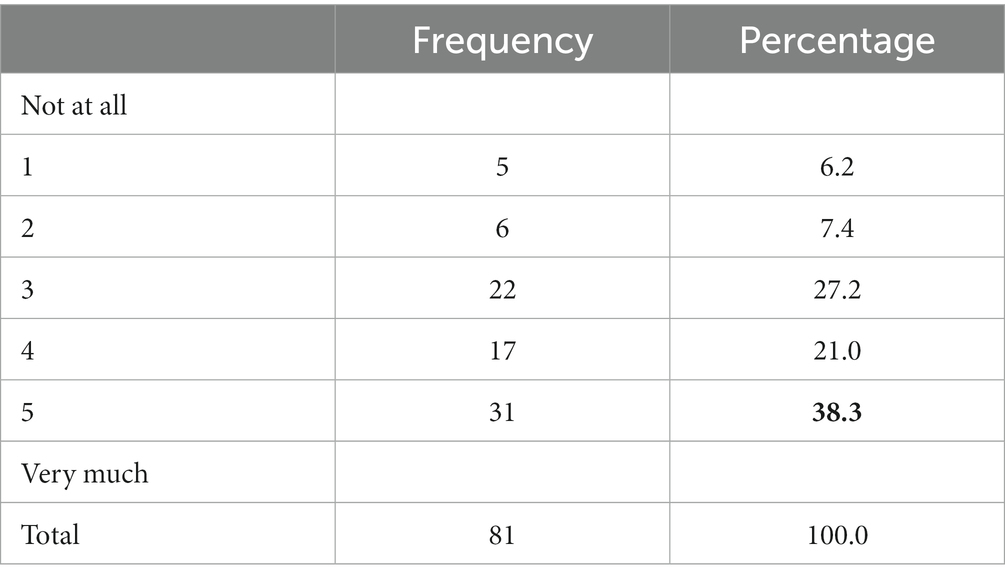
Since the topics presented in Figure 1 are also covered in the EM course, and it can be seen that seven out of nine of these topics are taught in relatively high percentage in HS, then participants were asked to answer the Likert scale (1–5) question about how well they were prepared when these topics were handled during the EM lectures. The scales were as follows: “1- Unprepared,” meaning that students feel not adequately prepared to complete the tasks or participate in the activities; “2- Slightly prepared” suggests that students may start to solve any given task but they need additional preparation; “3- Sufficiently prepared” indicates that students have only basic knowledge of the subject and may have some doubts or uncertainty about their preparation; “4- Prepared” indicates that the students feel comfortable with the material covered in the class, there is less doubt in their mind and they have modest confidence and certainty; and “5- Very prepared” implies that the students feel fully prepared and confident in their ability to complete the given task or activity successfully.

FIGURE 1

Figure 1. Overview of topics taught in high school.

As seen in Table 2, approximately 38% of the students felt sufficiently prepared during the EM lectures, indicating that they had only basic knowledge of the subject and may have some doubts or uncertainty about their preparation. The 9.9% value in the table represents students who felt very prepared during EM lectures, implying that they feel very confident and competent in their mathematical abilities and in their preparation for the course. This percentage is a relatively small value and presents a concerning situation that could be considered as an issue for further studies to identify the causes of this result.

TABLE 2

Table 2. Students’ preparation during the EM lectures.

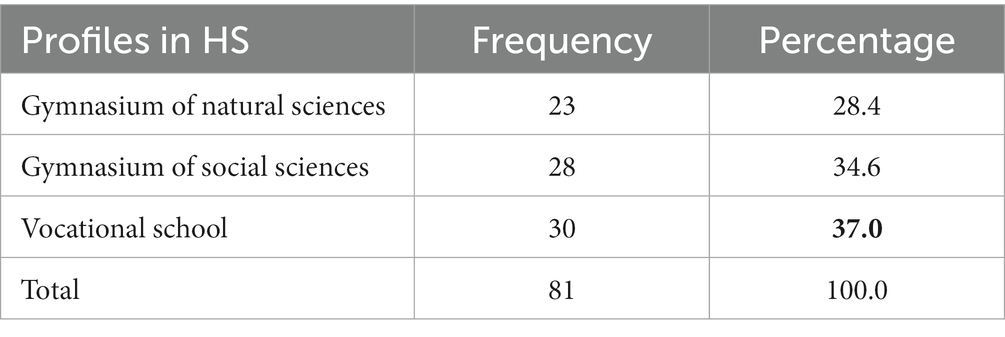
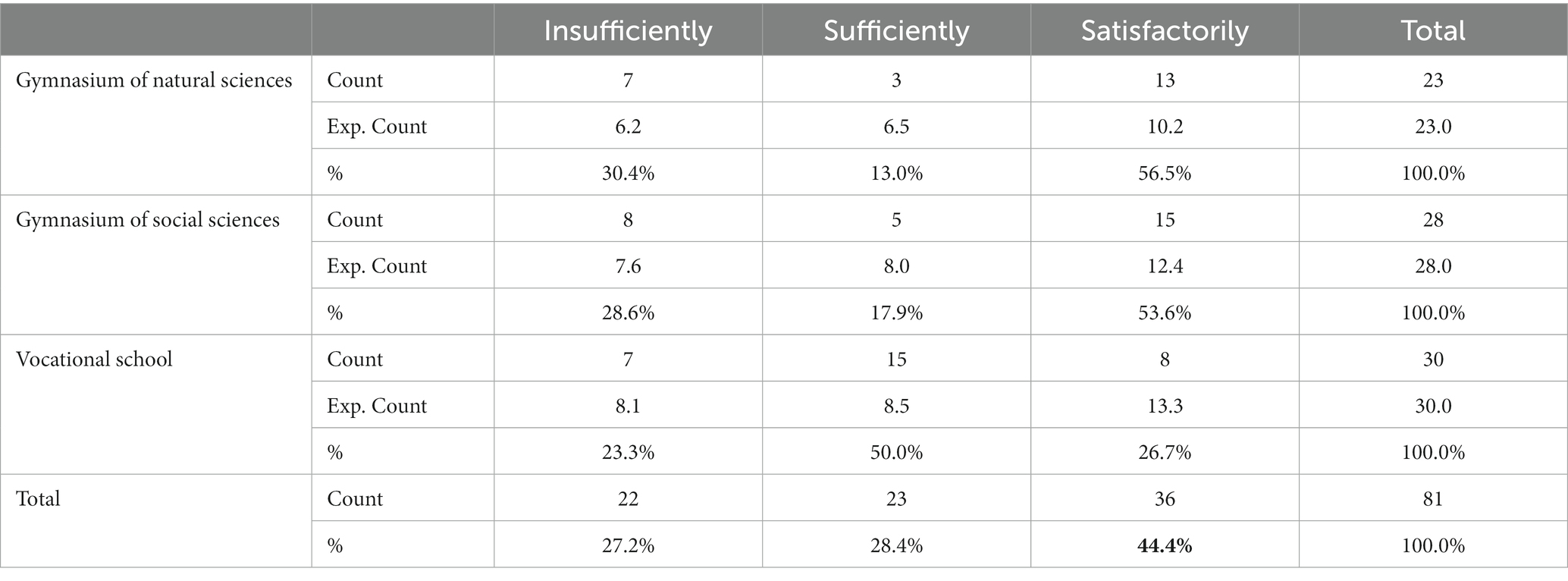
As there is a connection between HS and EM success, and the first research question concerns the high school profiles, the analysis below indicates the profiles chosen in HS and the preparation for EM. Table 3 shows the participants’ distribution according to profiles and it can be seen that the highest number of participants completed vocational school.

TABLE 3

Table 3. Distribution of participants according to profiles.

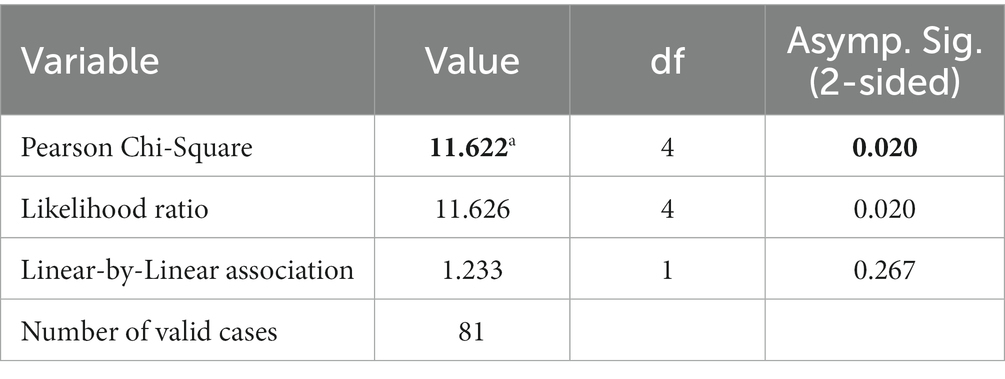
The Pearson Chi-square test is a standard statistical test used to see if there is a significant relationship between two variables, comparing the observed frequencies with the expected ones. If the standard frequencies are less than five, then the Chi-square is not a reliable test (Hameli, 2017). The Chi-square test was used to observe the role of high school profiles on the students’ preparation for the EM course and their significant relationships. Therefore, the null and the alternative hypotheses were raised:

H₀: There is no significant association between HS profiles and good preparation for the EM exam.

H_a: There is a significant association between HS profiles and good preparation for the EM exam.

If the null hypothesis is accepted, then the values of cells in Table 4 will be uniformly distributed and the asymptotic significance of Pearson Chi-square will be higher than the alpha level of 0.05. Otherwise, the alternative hypothesis will be accepted (Moore et al., 2013).

TABLE 4

Table 4. Relationship between high school profiles and students’ preparation for the EM exam.

Participants were initially asked to rate, according to a Likert scale (1–3), their opinion on how much the knowledge gained in HS helped them to prepare for the EM exam. The scales were: “1- Insufficiently,” meaning that students feel that the knowledge gained in high school did not adequately prepare them with the proper information or skills to pass the EM exam; “2- Sufficiently” suggests that the students feel that the knowledge gained in high school provided some support and preparation for the exam, but not to a level that they feel fully confident or well-prepared; and “3- Satisfactorily” implies that students feel the knowledge gained in high school has adequately prepared them with the necessary knowledge and skills to perform well in the EM exam.

Table 5 indicates that the value of p 0.02 is less than 0.05 and therefore the alternative hypothesis is accepted. In addition, there is a significant association between HS profiles and preparation for the EM exam. Considering the fact that there is a relationship between the variables, then we describe the cells that make the difference. Only eight participants from vocational schools stated that the knowledge obtained in HS helped them “satisfactorily” for the EM exam, compared to the expected value of 13.3; whereas 15 participants stated that the knowledge obtained in HS helped them “sufficiently” for the EM exam, compared to the expected value 8.5. It can be concluded from the above tables that HS profiles have an impact on the students’ opinion of their preparation for the EM exam; therefore, we can say that the chosen profile also makes a difference regarding success in EM. Moreover, 44.4% of the participants stated that the HS profile affected their preparation to the extent of “satisfactorily” for the EM exam.

TABLE 5

Table 5. Chi-squared test.

After completing their upper secondary education, students need to choose the profile for further education. Some of them look for a program with as little mathematical content as possible, others look for the appropriate profile to get the basic knowledge that will be useful to them in their bachelor’s studies, whereas the rest of them choose professional profiles for various reasons (e.g., to become a doctor, economist, or lawyer). Table 6 shows the frequency of answers to the question of how much students think their HS profile has played a role in their success in EM.

TABLE 6

Table 6. Frequency of the role of HS profile on success in EM.

After rating their opinions on the role of profiles for success in EM, in the following question, students were asked to expand on their opinions and one of the participants whose profile was Gymnasium of Natural Sciences stated: “During the math classes in high school, various topics from which I gained skills that now help me a lot in dealing with various issues in the subject of elementary mathematics were addressed.” According to the participants’ answers, regardless of the factors that led them to choose the profile of high school, they now think that the HS selected profile plays a very significant role in succeeding in EM.

During the questionnaire analysis, several potential factors that could play a role in the success of EM were examined, depending on the students’ profile in HS. To the question, if they had done their homework, 93% of the participants answered “Yes.” Since this result presents the students’ answers that belonged to all three profiles, it is obvious that engagement in homework cannot be considered as a factor in seeing the differences between profiles in the students’ success in EM. Additionally, the students’ answers were analyzed to investigate to which profile those who did not solve their homework belonged, and 50% of the “No” answers were from the Gymnasium of Natural Sciences, 33.3% from the Gymnasium of Social Sciences, and 16.7% from vocational schools. Furthermore, Pearson’s correlation was conducted $\left(sig.\mathrm{,}\mathrm{\hspace{0.33em}}\mathrm{0}.901>0.05\mathrm{,}\mathrm{\hspace{0.33em}}r=0.014\right)$ between homework engagement and success in EM and, according to the results, the relationship between these two variables is not statistically significant. However, for further studies, it would be important to investigate those variables and identify if there is any relationship between them, under certain conditions, e.g., how homework is organized, the way homework is checked, giving feedback as guidance to improve, and frequency of engagement with tasks. On the other hand, when asked if they were involved in high school working projects and whether they attended any private additional mathematics courses, 93 and 88% of the students answered “No,” respectively. The results obtained above are not influenced by these two factors, due to the high percentages of non-attendance. The correlation between engaging in additional courses and success in EM was found through the Pearson correlation with a value of 0.273, which means that there is a weak correlation between them. But, considering that 88% of participants stated that they did not attend any additional course, then: Would the Pearson correlation be stronger if the percentage of non-attendance were lower? However, we can say that the attendance of additional courses presents a factor that could affect the students’ success in mathematics. Additionally, the Pearson’s correlation was conducted to see the relationship between working projects and the success in EM and, according to the result ( $sig.,\mathrm{\hspace{0.33em}}0.256>\mathrm{\hspace{0.33em}}0.05$ ), the relationship between these variables is not statistically significant.

The results from the interview

During the interview, students were asked to address some other factors (that were not part of the questionnaire) which may have influenced their success. The most often mentioned factors were: student interest, teacher commitment, and the number of weekly classes. The following citations are some students’ opinions: “Mathematics is the same subject, wherever you go, in all schools. Therefore, if you are interested, you can learn a lot.”

“Until the 10^th grade, I was quite prepared, whereas in the 11^th and 12^th grade, the teacher’s explanation was not appropriate; therefore, I was left behind.”

The last, but not least, important factor was also the number of mathematics weekly classes. “In the Gymnasium of Natural Sciences, we dedicate only 4 h per week to the subject, and we had not the opportunity to choose specialized branches within the elective classes,” said one of the participants.

Another student of the same profile said that this number of classes enabled them to solve more tasks during their mathematics classes. Generally, other participants of this profile also appreciated the importance of a larger number of classes per week compared to other profiles whose workload of mathematics was smaller.

Since the interview, in addition to the questions, also contained three tasks (Figure 2) which had to be solved, then their categorization was done depending on the given solutions? The categorization was done in order to examine in detail the students’ mathematical knowledge.

FIGURE 2

Figure 2. The task part of the interview (translated from Albanian into English).

In the figures below, the red pencil shows the researcher’s feedback.

Category 1 includes students who solved all three tasks without any mistakes (Figure 3).

FIGURE 3

Figure 3. Problem solving of a student in Category 1.

In the first task, the student has correctly used the procedures for solving the problem, starting from equating the quadratic equation with zero to using the formula. It is worth noting here that the problem was solved without skipping even one single step. This indicates that the student had properly acquired the procedural knowledge in high school. In the second task, they did not use the formula to calculate the sum of the first nth-terms of the arithmetic sequence but used the concept of addition, thus increasing the number of cars for each month, and then finding their sum. Although the student may not be familiar with the formulas of the arithmetic sequence, they were able to find the result, indicating that their understanding of mathematical ideas is at an adequate level. While in the third task, they used the triangle rule to calculate the third-order determinant. This was also an indication that the student has sufficient knowledge to implement the rules.

Category 2 includes students who solved all the tasks but did not correctly recall the formulas (Figure 4).

It can be seen that the student started to solve the problem correctly, equating the equation with zero. They then miswrote the formula, confusing the coefficients b with b², which followed them to the end of the task. We noticed that the student did not remember the formula for finding the solutions of the quadratic equation and, moreover, they did not try to test the obtained solutions in the equation to see if they represented its roots. This means that the student did not develop work habits from previous education to validate the task solutions. The student solved tasks two and three using conceptual knowledge and knowledge of mathematical rules.

FIGURE 4

Figure 4. Problem solving of a student in Category 2.

Category 3 includes students who did not solve the first problem, while in the second and third problem they had difficulties developing concepts and rules, respectively (Figure 5).

FIGURE 5

Figure 5. Problem solving of a student in Category 3.

In the second problem, the student began to properly develop the concept of addition, presenting an arithmetic sequence of the machines’ monthly output but discontinued the task in the tenth term. This made it impossible to find the sum of the 12 terms of the sequence; consequently, they had difficulties conceptualizing the total sum of some terms. While in the third task, they used Sarrus’ rule to find the value of the determinant. During the calculations, they erred in multiplying the numbers with the sign, which made us realize that they either ignored it or had difficulties with multiplication.

Category 4 includes students who used formulas and rules but did not achieve the correct result (Figure 6).

FIGURE 6

Figure 6. Problem solving of a student in Category 4.

In the first problem, the student used the quadratic equation formula correctly but did not start the task correctly, making mistakes in the signs and adding monomials with the same exponent. In the second task, the student was noticed to have had a straightforward addition but did not complete the solution. In the third task, they marked the first step of Sarrus’ rule correctly, adding the first two columns, but did not perform the production of numbers according to this rule. This means that they did not master the rules for calculating third-order determinants.

Category 5 includes students who did not solve any of the problems (Figure 7).

FIGURE 7

Figure 7. Problem solving of a student in Category 5.

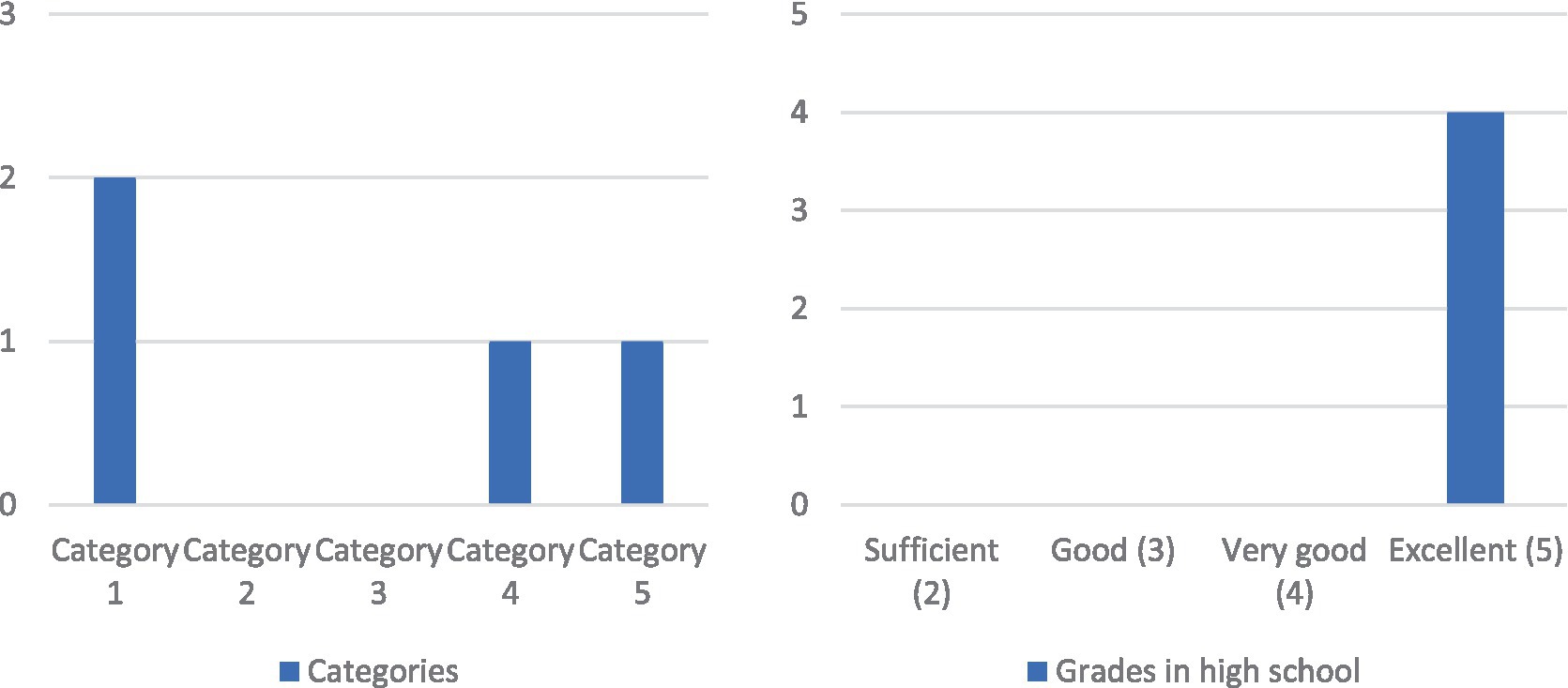
Presenting all the categories separately, we introduced the participants’ division according to these categories in Table 7, and 33.3% of them belong to the third category. This category includes the students who had no knowledge of definitions and formulas, while having difficulties in developing concepts and rules. Since first-year students still have fresh knowledge from HS and the EM course contains topics most of which are already taught in HS, we have decided to analyze these students’ division into these categories based on their success.

TABLE 7

Table 7. Distribution of participants according to categories.

Figure 8 shows that two of the first-year students belong to the first category, while one student belongs to each of the fourth and fifth categories. On the other hand, we can also see that all the students had the maximum grade in mathematics in HS. Therefore, since all the students were excellent in HS and half of them belong to the top categories, while a quarter to the categories four and five, these results make us question the HS preparation. Considering the fact that the students had the maximum grades in HS, it is assumed that they should have at least basic knowledge of formulas, concepts, and rules. However, students in Category 4 have only partially used the procedures and rules, and they have failed to obtain the correct result by making elementary mistakes while applying them, whereas those in Category 5 have not solved any task, handing in blank tests, despite their excellent grade in HS.

FIGURE 8

Figure 8. Division of first-year students into categories and their grades in high school.

Discussion

The findings of the first research question indicate that the chosen profile in HS has a significant relationship between the students’ preparation and success in the EM exam. Our findings matched with other research examining the role of high school in calculus at university level (Ayebo et al., 2017; Sadler and Sonnert, 2018; Bressoud, 2021). According to Ayebo et al. (2017), good preparation for pre-calculus in high school represents a bridge to success in calculus at university; furthermore, according to Sadler and Sonnert (2018), good preparation in calculus in HS carries advantages even for weaker students. On the other hand, according to Bressoud (2021), high schools do not need to offer pre-calculus courses on their curricula so that students to succeed in calculus at university. Instead, high schools should provide students with challenging learning experiences, confronting them with non-routine problems that help to develop mathematical skills and abilities.

Participants in this study highlighted some factors that contributed to their success: student interest, teacher commitment, and the number of math classes. One of the factors identified through the questionnaire that could affect the students’ success in mathematics was the students’ attendance in additional courses. This echoes the finding of Ayebo et al. (2017) in that the choice of elective mathematics classes had a greater impact on the students’ success than other more common factors such as socioeconomic status, ethnicity, or parents’ educational backgrounds.

Professors of mathematics at the university constantly express their concern about the students’ lack of knowledge and skills in the EM course, knowledge which they need for other fields as well. The analysis of the tasks included in the interview indicated that several students have limited knowledge of rules, formulas, and mathematical concepts. This lack of understanding from high school has also been explored by other researchers (Conley, 2010; Sadler and Sonnert, 2017; Godfrey, 2020). Students’ difficulties in mastering basic mathematical knowledge are related to their high school experience (Sadler and Sonnert, 2017). According to Conley (2010), university professors hope students have a deep conceptual understanding of mathematics as well as the ability to apply mathematical concepts to real-world problems; having basic mathematical skills, such as algebraic manipulation, graphing, geometry, and trigonometry are also some initial expectations. Godfrey (2020) emphasized that university professors expect students to have a strong mathematical background and remember the foundational algebraic concepts in order to apply those concepts more easily to higher-level math classes, which may help students acquire a deeper understanding of the material.

This research is part of the studies mosaic that emphasizes the importance of good preparation in high school. Findings from the interviews showed that some first-year students, even though they were assessed with the maximum grades in mathematics in HS, have difficulties with basic knowledge of formulas, concepts, and rules. Our results contribute to the work of high school math teachers by providing them the opportunity to evidence students’ shortcomings and the paradox that occurs between students’ grades and their expected mathematical knowledge. It is important that students complete their high school with adequate preparation for the subject of EM so that they do not have difficulties of the kind that would make them take a longer time than necessary to pass the exam, or, in the worst case, abandon their studies.

Conclusion

From the collected data, after analyzing the answers to the question about the role of the high school profile and good preparation for elementary mathematics through the Chi-square test, we can assert that there is a significant relationship between these variables. Research participants have estimated that the HS profile plays an important role in success in EM. Only 26.7% of students from vocational schools reported feeling “satisfactorily” prepared for the EM course, while for students of the natural sciences and social sciences gymnasiums, the proportions were much higher (56.5 and 53.6%, respectively). Therefore, profiles with a greater number of mathematics classes per week provide students with better preparation for EM.

The Spearman’s correlation coefficient ( $\rho =0.279$ ) indicates a positive correlation between success in high school and success in elementary mathematics, but this correlation is not strong. According to the participants of this research, the potential factors that can affect the students’ success in EM are the students’ interest in acquiring knowledge during their classes, their math teachers’ commitment, and the number of math classes. Another three factors were explored regarding their role in the students’ success in EM. According to the Pearson’s correlation, engaging in additional courses is a weak factor affecting the students’ success. Working on projects and doing homework, on the other hand, were not statistically significant variables in students’ EM success. Considering the importance of homework on students’ abilities to memorize, receive feedback, and prepare for exams, it would be important for further studies to explore how homework is organized in high schools.

Concerning the tasks included in the interview and their solution divided into categories, approximately 33% of participants did not know the definitions and formulas and had difficulties developing concepts and rules. Only 16.7% of the students solved all the tasks without errors, whereas 8.3% of them made mistakes only in the quadratic equation formula. The data analysis leads us to conclude that the participants came out of high school with limited knowledge of rules, formulas, and even mathematical concepts.

Recommendations

To the question of how prepared they felt during EM classes in regard to the topics that were taught in HS, 9.9% of respondents stated that they felt very prepared. This value is relatively small and represents a situation of concern that should be considered an issue to be studied further in order to identify the causes of such a small number of students prepared with adequate mathematical knowledge for EM. Approximately 38% of the students felt sufficiently prepared for EM, which means they had only basic knowledge of mathematics. In the future, to increase the number of students who are prepared with decent knowledge for university studies, the results of this study can serve as awareness for high school math teachers to reflect on their teaching practices and pay more attention to the students’ preparation by filling the gaps that have been observed in this research. Regarding the attention paid to a good HS preparation and its importance mentioned in other research, looking at the transition programs of other countries, we suggest a transition planning program that would support high school students to better prepare for university studies. This transition program could begin in the summer semester of the 12th grade. At that period, most of the students will have already decided on their future profile in bachelor’s studies. Initially, students should answer a questionnaire that would enable the selection of students who have chosen the faculty profiles that comprise the elementary mathematics course. This questionnaire should also include questions about the students’ experiences in learning mathematics, their difficulties, shortcomings, and advantages. High school math teachers should have 1–2 meetings per week with the selected students until the end of the summer semester. During these meetings, students would be able to improve their limited knowledge of rules, formulas, and mathematical concepts (derived from this research), raising questions about ambiguities and misunderstandings regarding the previously covered topics. At these meetings, students could also be offered the opportunity to discuss their needs regarding the subject of mathematics, which they may lack in their regular math classes because of the teachers’ time pressure to cover all the topics defined by the curriculum within a school year.

Limitations

This study has several limitations. Firstly, it is a case study at the University of Applied Sciences in Ferizaj and the results cannot be generalized to all universities in Kosovo. Further studies can expand the sample size to all universities in Kosovo that have EM courses on their study programs.

Secondly, the largest number of participants in the research were students who completed vocational high school; therefore, the results of this paper can be slightly affected by the sample content. Future studies may focus on separate research for the three profiles that were part of this study.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics statement

The studies involving human participants were reviewed and approved by University of Applied Science in Ferizaj. The patients/participants provided their written informed consent to participate in this study.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ayebo, A., Ukkelberg, S., and Assuah, C. (2017). Success in introductory calculus: the role of high school and pre-calculus preparation. Int. J. Res. Educ. Sci. 3, 11–19.

Google Scholar

Bressoud, D. (2017). The role of calculus in the transition from high school to college mathematics, pp. 1–8. Available at: https://www.maa.org/sites/default/files/RoleOfCalc_rev.pdf

Google Scholar

Bressoud, D. M. (2021). The strange role of calculus in the United States. ZDM 53, 521–533. doi: 10.1007/s11858-020-01188-0

CrossRef Full Text | Google Scholar

Burrill, G. (2017). Challenges in the transition from high school to post-secondary mathematics. Role of Calculus in the Transition from High School to College Mathematics, No. 67, pp. 1–84.

Google Scholar

Conley, D. T. (2010). College and career ready: Helping all students succeed beyond high school. New York: John Wiley & Sons.

Google Scholar

Creswell, J. W., and Creswell, J. D. (2018). Research design: qualitative, quantitative, and mixed methods approaches. (5th Edn). Thousand Oaks, CA: SAGE Publications.

Google Scholar

Denis, D. J. (2016). Applied univariate, bivariate, and multivariate statistics. New York: John Wiley & Sons.

Google Scholar

Edge, O. P., and Friedberg, S. H. (1984). Factors affecting achievement in the first course in calculus. J. Exp. Educ. 52, 136–140. doi: 10.1080/00220973.1984.11011882

CrossRef Full Text | Google Scholar

Gjonbalaj, Q. (2013). Si të rrisim interesin dhe suksesin e studentëve në lëndët matematike [How to increase students' interest and success in mathematics]. ResearchGate. Available at: https://www.researchgate.net/profile/Qefsere-Doko-Gjonbalaj/publication/258848188_SI_TE_RRISIM_INTERESIN_DHE_SUKSESIN_E_STUDENTEVE_NE_LENDET_MATEMATIKE/links/00b7d5293d86dae3ba000000/SI-TE-RRISIM-INTERESIN-DHE-SUKSESIN-E-STUDENTEVE-NE-LENDET-MATEMATIKE.pdf.

Google Scholar

Godfrey, L. (2020). Expectation gaps between high school mathematics courses and college calculus. Available at: https://commons.lib.jmu.edu/cgi/viewcontent.cgi?article=1065&context=honors202029.

Google Scholar

Hameli, K. (2017). Teknikat statistikore me shumë ndryshore me aplikim në SPSS [Multi-variable statistical techniques with application in SPSS]. ResearchGate. Available at: https://www.researchgate.net/publication/319493569_Teknikat_Statistikore_me_Shume_Ndryshore_me_Aplikim_ne_SPSS.

Google Scholar

Ministry of Education Science and Technology . (2016). Curriculum Framework of Pre-University Education of the Republic of Kosovo. Pristina. Available at: https://masht.rks-gov.net/uploads/2017/03/korniza-kurrikulare-finale.pdf.

Google Scholar

Moore, D. S., Notz, W. I., and Fligner, M. A., (2013). The basic practice of statistics (6th Edn). W. H. Freeman and Company. New York.

Google Scholar

Norusis, M. (2008). SPSS 16.0 statistical procedures companion. Hoboken, NJ: Prentice Hall Press.

Google Scholar

Sadler, P. M., and Sonnert, G. (2017). Factors influencing success in introductory college calculus. In David M. Bressoud, The role of calculus in the transition from high school to college mathematics, pp. 53–65. Available at: https://www.maa.org/sites/default/files/RoleOfCalc_rev.pdf.

Google Scholar

Sadler, P., and Sonnert, G. (2018). The path to college calculus: The impact of high school mathematics coursework. J. Res. Math. Educ. 49, 292–329. doi: 10.5951/jresematheduc.49.3.0292

CrossRef Full Text | Google Scholar

Shala, A., Grajcevci, A., and Latifi, F. (2021). Do teacher characteristics matter? Findings from the PISA performance of Kosovar students. Int. J. Manage. Educ. 15, 580–597. doi: 10.1504/IJMIE.2021.119357

CrossRef Full Text | Google Scholar

University of Applied Science in Ferizaj . (2020). Available at: https://www.ushaf.net/wp-content/uploads/2020/05/1.-Matematika-për-Biznes_syllabus_shqip.pdf.

Google Scholar