- Faculty of Education and Social Work, The University of Auckland, Auckland, New Zealand
Higher degree research students in education are largely underprepared for understanding or employing statistical data analysis methods. This is despite their need to read literature in their field which will indubitably include such research. This weakness may result in students choosing to use qualitative or interpretivist methodologies, even though education data are highly complex requiring sophisticated analysis techniques to properly evaluate the impact of nested data, multi-collinear factors, missing data, and changes over time. This paper describes a research methods course at a research-intensive university designed for students in a thesis-only degree program. The course emphasizes the logic and conceptual function of statistical methods and exposes students to hands-on tutorials in which students are required to conduct analyses with open-access data. The first half of the 12-week course focuses on core knowledge, normally taught in first-year probability and statistics courses. The second half focuses on introducing and modeling advanced statistical methods needed to handle complex problems and data. The course outline is provided along with descriptions of teaching and assessments. This exemplar functions as a potential model of how relative novices in statistical methods can be introduced to a conceptual use of statistical methods to raise the credibility of research.
Introduction
Education data are highly complex, being typically nested (e.g., students within classes within schools within districts, etc.), longitudinal (i.e., repeated measures that may or may not be equated), incomplete (i.e., many missing data points), and highly interconnected (i.e., multi-causal, multi-collinear). Thus, higher degree research (HDR) or doctoral students require advanced skills (e.g., psychometric test analysis, structural equation modeling, hierarchical level modeling, missing value analysis, or propensity score analysis) to properly analyse such data or even to read the literature in their field. Indeed, Dutt et al. (2017, p. 15991) argue that educational data mining requires “machine-learning, statistics, Data Mining (DM), psycho-pedagogy, information retrieval, cognitive psychology, and recommender systems methods and techniques,” thus increasing the range of technical data analytic skills doctoral students might need to read and/or perform to address educational issues.
A large proportion of HDR and doctoral students in education do not have strong backgrounds in statistics, probability theory, or data analysis. The emphasis in their undergraduate training is heavily on relational skills needed to design curriculum, carry out instruction, offer pastoral care, and conduct evaluative practices. Professional practitioners, upon entry to postgraduate research will generally have worked and become experienced, competent professionals in fields that require high levels of interpersonal and social skills where ‘craft’ or experience-based knowledge is most highly prized (Leder, 1995; O'Brien, 1995; Labaree, 2003; Eisenhart and DeHaan, 2005). This means that doctoral students in education tend to find quantitative methods daunting and difficult (Page, 2001) and few courses provide robust attention to statistics (Little et al., 2003). Thus, most students “have had little or no undergraduate preparation in research design or data analysis (quantitative or qualitative) and lack knowledge of the epistemological foundations for social science research” (Brown, 2014, p. 70).
Many education faculties offer HDR and doctoral students opportunities to learn about a wide panoply of qualitative research methods, often consigning scientific design and statistical data analysis methods to a small proportion of the course. For example, the general research methods course textbook at this case study’s institution (Meyer and Meissel, 2023) contains one chapter to introduce the complete field of quantitative research methods (Meissel and Brown, 2023) and another three chapters refer to statistical methods, giving 4 out of 27 chapters or 15%.
However, research students, especially at the doctoral level, need training to understand and adjudge the suitability of using longitudinal, nested, and/or multivariate data. They need to be able to evaluate the psychometric properties of various measures they read about or select for their own empirical research. They need to understand the sub-discipline in which their own research will contribute. If that field has zero quantitative or statistical knowledge methods, then perhaps they do not need that knowledge. Nonetheless, without such knowledge students would not necessarily know how or why they do not use such methods. Thus, the challenge in this context is how to design a course that exposes doctoral and HDR students to sufficient knowledge that they can understand literature they have to read, select tools and methods for their own projects, and have some idea as to what kinds of methods are most likely required for their proposed research. As Albers (2017, p. 215) puts it:
Teaching quantitative data analysis is not teaching number crunching, but teaching a way of critical thinking for how to analyze the data. The goal of data analysis is to reveal the underlying patterns, trends, and relationships of a study’s contextual situation. Learning data analysis is not learning how to use statistical tests to crunch numbers but is, instead, how to use those statistical tests as a tool to draw valid conclusions from the data. Three major pedagogical goals that must be taught as part of learning quantitative data analysis are the following: (a) determining what questions to ask during all phases of a data analysis, (b) recognizing how to judge the relevance of potential questions, and (c) deciding how to understand the deep-level relationships within the data.
Context
This case takes place at a research-intensive urban university that is globally ranked in the top 100 on the QS system. The doctoral program follows the UK-style doctoral program in being ‘thesis-only’ rather than the American model in which two years of coursework precede a comprehensive examination before students engage in thesis research. New Zealand allows doctoral students just 60 points (i.e., 4 courses of 24 h instruction) in the provisional year, meaning there is a small opportunity to provide intensive instruction prior to the full proposal students are expected to deliver at the end of 12 months preparation for thesis field or lab work. Each candidate has two or more supervisors, though the norm is just two. Monthly meetings with supervisors are the norm who are given 50 h each to provide all supervision related work. This means there is little formal mechanism for students to learn new methods and content.
Within the university’s doctoral development program, hosted by the School of Graduate Studies, there is a framework for identifying topics that a student needs to consider throughout the academic journey1. These include understanding essential processes and regulations of being a candidate, navigating the research environment, developing research knowledge and skills, disseminating and influencing the field, learning to collaborate and lead, and preparing for a career beyond graduation. Under research knowledge and skills, there are extensive links on finding and managing information, learning software tools, and developing written communication skills. However, candidates are told that they need to explore and identify appropriate research approaches early in their candidature by participating in faculty specific seminars and workshops. In other words, the university does not set central requirements for methodological competencies nor provide central resources for learning those skills. It is up to supervisors to ensure that selected candidates have appropriate background or provide the training students need.
Within the first year of provisional candidature, students are expected to complete a 10,000-word proposal which is reviewed by two academics in the faculty. The candidate has to give an oral presentation and answer questions in vivo examination by the reviewers. In addition, students are expected to complete English language testing, academic integrity training, and multiple workshops hosted by the Library Services, Centre for eResearch and the School of Graduate Studies. The faculty has a large proportion of international students in the PhD program, in part because New Zealand has a strong commitment to the Chinese One Belt, One Road framework, resulting in many doctoral students in education from China. An interesting challenge for these students is that they expect, based on their local experience, to have coursework as part of their preparation for thesis research.
This paper describes a statistics course aimed at ensuring students have exposure to principles of statistics and advanced statistical data analytic methods. A major goal of the course is to ensure that students select appropriate methods for their proposals and can give a rationale for their selection. There is no expectation that by the end of the first year, students would know how to execute the methods, only know that they exist and have some confidence to judge the suitability of those methods for their proposed empirical research.
Curriculum development: what should students be taught?
The University of Auckland is a member of several international networks (i.e., World Universities Network, Universitas 21, and Asia Pacific Rim Universities). Funding was obtained from the University’s International Central Networks Fund that supports visits to institutions belonging to any of these three networks. That resulted in visits to Prof. Bruno Zumbo at the University of British Columbia and to Prof. Mark Gierl at the University of Alberta. At the University of Alberta, additional meetings were held with Dr. Okan Bulut on the same topics. The point of the visits was to determine essential elements of a curriculum for doctoral level skill and knowledge in statistics and probability.
In discussion with Prof. Gierl, he noted that in his PhD in the USA, he had taken a 12-week course on regression analysis alone. Upon reflection, we agreed that the key concepts of regression, building on high school mathematics instruction, could be covered in 2 h. While a great deal of useful detailed information on all the ins and outs of regression analysis were covered in the longer course, the key ideas of intercept, slope, and raw/standardized values could be communicated much more quickly, especially if students could rely on software to complete calculations rather than have to learn the formula and apply it manually.
In addition, focus group discussions were held at UBC with recently graduated doctoral students and with academic staff concerning methods curriculum, pedagogy, and evaluation practices. The roundtable discussion generated a list of minimal competency topics to cover, including:
1. Describing the space of education data, which is naturalistic and complex without control, meaning that advanced nonexperimental techniques are needed (Shadish et al., 2002).
2. Foregrounding the prevalence of error and uncertainty (Brown, 2017) and the advantages of latent trait approaches (Borsboom, 2005).
3. Looking at data (e.g., exploratory data analysis; Tukey, 1977) to describe, inspect, clean, impute missing values, and treat outliers.
4. The linear model (Pearl, 2013; Fox, 2015) underlying regression, correlation, covariance, SEM, CFA, HLM, etc., meaning that assumptions of constructs, models, or data need to be understood, as well as principles around selecting and evaluating a model (e.g., Burnham and Anderson, 2004).
5. Understanding the limitations of the null hypothesis significance test and the importance of effect size over p-values (Kline, 2004).
6. Power issues related to sample size and effect size (Cohen, 1988).
7. Understanding the need for confidence intervals (Thompson, 2007).
8. Understanding the ‘so what’ significance or meaning of statistics, not calculations (Abelson, 1995).
Prior to approving the this course, a quick straw poll of currently-enrolled doctoral students (n ≈ 30) at the University of Auckland generated a number of comments speaking to the importance of the course. Note that no further processing of the data was carried out; the current analysis was used to demonstrate the importance of the course to faculty doctoral students. Students noted the importance of having an understanding of statistics:
Absolutely! it has to go without saying you need to have statistical knowledge for almost any research you do. I struggled without this knowledge, and it consumed a lot of my PhD time to get to grips with the stats.
Yes absolutely - because I have very limited understanding about quant studies.
Yes, definitely. This was not something I had access to in my undergrad degree and my Masters was a qualitative study only. Now my PhD study involves a mixed method approach, and I am out of my depth with the advance statistics required.
Yes, it is fundamental to complete a PhD research project.
Absolutely, I will take this course that will be very helpful for the research.
Yes. I feel this detailed instruction is missing at postgraduate level.
A number of students commented that this kind of material is missing in the faculty’s suite of methods courses available to postgraduate students. Situating methods instruction within the general discipline of education was also seen as a useful way of ensuring the methods made sense.
Yes. I think the faculty is lacking an intermediate-advanced statistics course and the proposed course could fill the gap.
Yes, because I have never learned stats or research methods from an education specialist. I had to go to the stats and maths department to learn it. So, it would be very useful to have a course in our faculty which gives relevant examples and implications for researching educational settings.
One student commented that because they had not experienced previous instruction in quantitative methods, they had to be a qualitative researcher.
Yes. I did not have any exposure to quantitative methods at undergrad, postgrad level. Now that I am at doctoral level, I do not feel adequately resourced if you like to engage in quant methods. Although I realize there are workshops, I can attend. Early days yet but so far have positioned myself as a qualitative researcher.
Another commented that although they were using qualitative methods, they would still want such material to be available to students in education.
I would be interested, but likely give it a low priority, because it is so different from the methods I use in my research. But I’d be happy to know it was offered, because I am aware many others are very interested.
This student feedback contributed to the Faculty’s decision to approve the course.
Course development: what happens in this course?
A new course, entitled Measurement and Advanced Statistics, was developed to introduce education postgraduate and doctoral students to the complicated problems of education and the complex models and sophisticated techniques that can provide probable answers. The course is attentive to the possibility that any model or result may be wrong but that it gives a starting point for understanding data and the real world represented by those data.
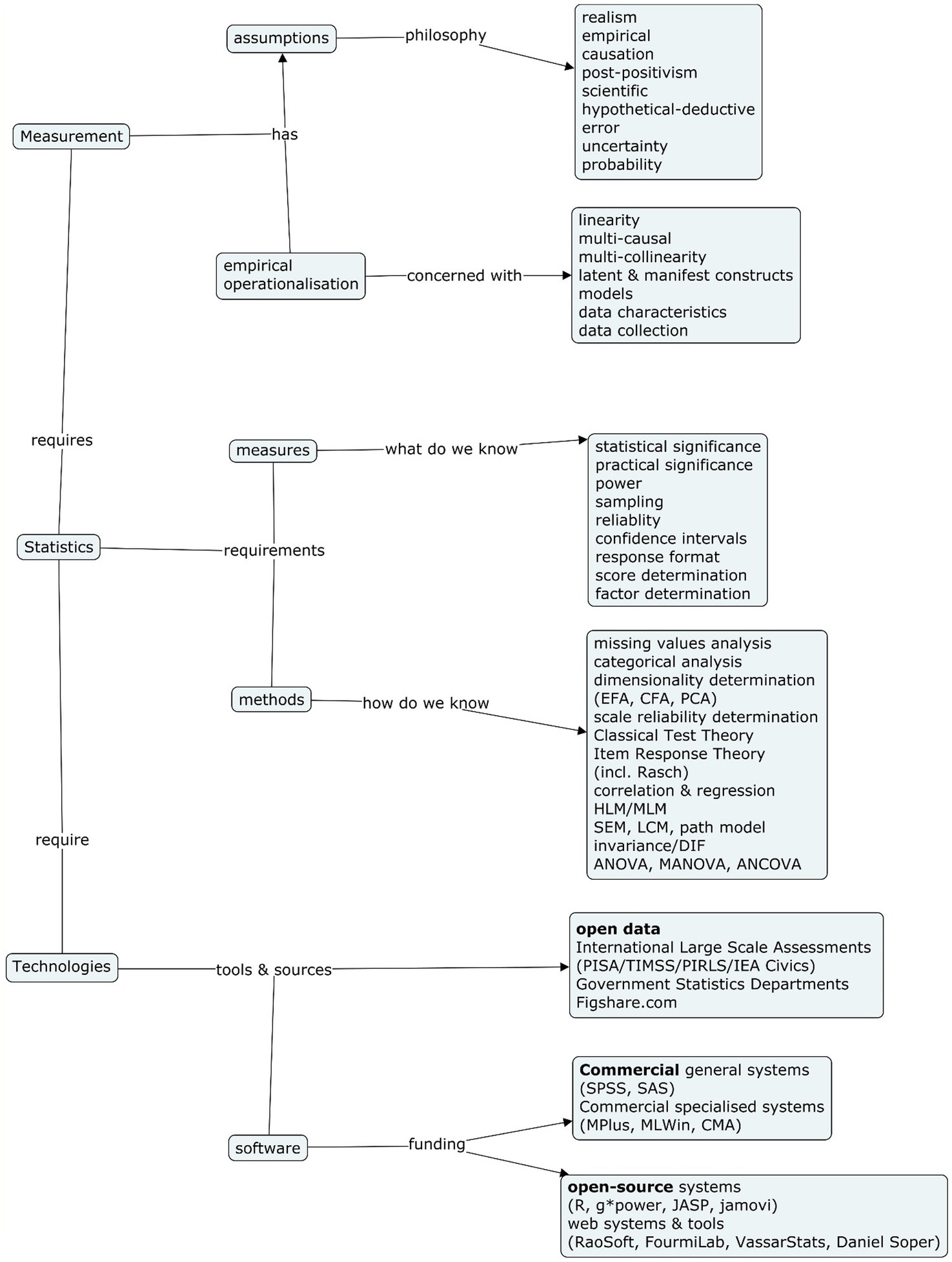
Figure 1 shows the sequential relationship imposed on the curriculum to focus on fundamental principles of probability in conjunction with methods to estimate these fundamental ideas. The course was devised around three key components: (1) principles of measurement, (2) statistical tools; and (3) technologies for carrying out components 1 and 2.
The course is based on attention to the assumptions and philosophy of measurement derived from psychometrics. Psychometrics, growing out “psychological scaling, educational and psychological measurement, and factor analysis” (Jones and Thissen, 2006, p. 8), is “the disciplinary home of a set of statistical models and methods that have been developed primarily to summarize, describe, and draw inferences from empirical data collected in psychological research” (Jones and Thissen, 2006, p. 21). An essential assumption of psychometrics, derived from classical test theory, is that all measures contain error and are imperfect operationalisation of real-world phenomena (Novick, 1966). Thus, awareness of and attention to the degree of uncertainty in every result is a sine qua non starting point for teaching statistical methods. It leads to a need for techniques to estimate that degree of reliability or accuracy (e.g., standard error, standard error of measurement, confidence intervals, power estimation, etc.).
Furthermore, consistent with scientific approaches to knowledge, the theoretical basis of our hypotheses expressed in quantitative models of psychological entities may not be true, “but we will assume it recognizing that at some point in the future someone needs to investigate it” (Michell, 2008, p. 12). The inherent uncertainty in quantitative estimation of psychological and social phenomena produces what may “be truly meaningful, and not just statistically convenient…[and] might serve as a more effective and efficient pragmatic communication tool that represents a decidedly conscious compromise between cognitive fidelity, empirical feasibility, and utilitarian practicability” (Rupp, 2008, p. 122).
While statistical methods generate uncertainty, the goal of analysis is not to just describe, but also to understand and explain how or why things happen in education. Consequently, even without full experimental control (Kim and Steiner, 2016), understanding causation and how it can be approached within theoretically-informed data analysis is necessary (Pearl and Mackenzie, 2018). That means that instruction has to move beyond the null hypothesis statistical test to estimating the size of effect (Kline, 2004) and the elimination of rival, alternative hypotheses (Huck and Sandler, 1979). This last consideration requires the analyst to consider the possibility that “I might be wrong” and build into the design of the data collection and analysis systematic evaluation of whether alternative explanations that might defeat one’s preferred solution have merit. As Popper (1979) makes clear our goal in analysis is to find theory statements that have better correspondence to the facts and that requires testing alternatives, even those that we find disagreeable. Thus, the scientific process of devising and testing hypotheses against empirical data is necessary to fulfill Abelson’s (1995) criteria for magnitude, credibility, and generalisability as necessary characteristics of research.
Having outlined the principles of measurement and statistics in six sessions (something that might be covered in undergraduate probability or statistics courses), the course proceeds to touch on major methods used in analysing non-experimental data in the social sciences (Appendix A). My choice of these methods is informed by my own work as a psychometric test developer using large-scale survey data to explore curriculum achievement and psychological attitudes. Specifically, attention is paid to analysis of categorical data, linear correlation and regression, multilevel regression modeling, dimensionality analysis, structural equation modeling, and longitudinal data analysis. The goal in this rapid traverse of methods is to establish the conceptual logic behind the method, provide skills and knowledge in interpreting the results, and exposure to working with the method.
While the goal of the course is to embed familiarity with the principles and concepts of data analysis, the course provides opportunities to use software to implement the procedures. Open-source data are obtained from my figshare account2 to provide students a chance to learn how to do the analysis. The data file has demographic variables, multiple-indicator, multiple cause self-report data, and test performance data.3 This means that almost all procedures documented in the course can be tested with the one dataset, meaning students become familiar with the dataset through multiple exposures.
The university supplies free access to MS Excel and SPSS/AMOS systems for students while enrolled. However, because not all students will have access, post-graduation, to commercial statistical software, I introduce them to the R software environment for several reasons: (1) it is free, (2) it was invented at the University of Auckland, (3) it is powerful, and (4) it has widespread acceptance. Because learning to write syntax is difficult, especially for relative novices, I take advantage of graphic user interface applications that mimic SPSS (i.e., Jamovi Project, 2022) but which are open-access interfaces that build on top of R (Abbasnasab Sardareh et al., 2021). Students find that jamovi’s feature of displaying results in APA format beside input commands a very helpful feature. Tutorials accompany each week’s lecture in a subsequent computer lab with a structured activity to mimic the instruction given in the lecture. Tutorials have been refined over several years with the input of GTAs with special acknowledgement to Dr. Anran Zhao4 and Rachel Cann5 who had both been students in the course prior to working as tutors.
In terms of assessing student learning, there are (1) four short answer/multiple choice quizzes every 3 weeks testing material taught in that block, (2) credit for completing 10 tutorial lessons, (3) a critical reading of a published manuscript to identify design and method strengths and weaknesses at mid-term, and (4) a final assignment in which students replicate the analysis of one of my own published journal papers (‘Otunuku and Brown, 2007) using the data set, with commentary as to whether their results align with the published paper and if they differ as to why that may be. The final assignment requires students to:
• organize data by selecting cases and variables;
• conduct exploratory and confirmatory factor analysis;
• calculate mean scores, analysis of variance, and effect sizes;
• compute correlations;
• conduct a block-wise regression analysis;
• conduct a simple 3 factor structural equation model.
Mastering so much content in just 12 weeks is challenging for the novices enrolled in this course. I strongly recommend Field (2016) as an excellent introduction. Field embeds teaching of statistical reasoning and computation into a narrative about Zach trying to find out why Alice has left him (from Z to A!), illustrated with cartoons. This text is extremely accessible, well-crafted, and enjoyable for anyone with a sense of the absurd or enjoyment of science fiction stories.
Possible lessons
The point of reading a case study like this is to consider if anything can be learned for one’s own situation. It is a difficult task to predict what others who want to teach quantitative methods to higher degree research students in education might take from this paper because contexts are so different. This course is positioned within a doctoral thesis model that is thesis-only. This is a very different situation to doctoral programs that contain required coursework prior to thesis work, as is seen in the North American model of doctoral education. That means, although doctoral students are presumed to be ready in terms of content knowledge and methodology, they may lack competence in the advanced methods their research requires. Consequently, the current course is aimed at achieving conceptual clarity as to what methods suit best their design. It does not guarantee they can implement those methods, but rather that they have sufficient clarity and some experience using the method on which they can build. Instructors who want students to achieve mastery level will find this rapid overview approach, somewhat akin to a tasting menu, to be deeply unsatisfactory. That is always a compromise that instructors need to make—deep vs. wide. My own stance is that once students appreciate key principles of statistical data analysis they can make rapid progress on their own. Without a doubt, having a lab environment in which more senior students can coach juniors with the techniques they have already mastered is an important adjunct to student learning.
This approach avoids teaching formulae in favor of conceptual understanding (Albers, 2017). If, as Abelson (1995) argues, statistical methods are designed to estimate magnitude and generalisability and give credibility to arguments, students need to understand what the problem is that the statistic addresses. They need to know which alternative hypotheses are associated with the statistical test and method being used, otherwise it is possible statistics would be understood as a cookbook recipe without deep understanding of the question being addressed by the method.
Whether this course would fit in another context is difficult to predict. However, it seems certain key fundamental principles apply to ensuring relative novices at any level of higher education are able to grasp statistical methods. These include:
1. The student needs to have a conceptual grasp of key statistical ideas (i.e., appreciating uncertainty and error, understanding the power of sample size on confidence intervals and p, and appreciating and estimating practical effect sizes).
2. The student needs to be able to appreciate and use statistical methods as tools for eliminating rival hypotheses and addressing research questions, while acknowledging the complex mathematical processes underlying those concepts and the importance of appropriate sample size.
3. The student needs opportunity to use real statistical software with real data in a scaffolded environment so that they can gain clarity about what the statistic does and how to operate open-source and user friendly software (e.g., jamovi, jasp within R).
Conclusion
This course has not been taken by many students, in part because it is only offered once per year, when I am available to teach it. Anecdotally, I can say that students seem to benefit from it. Most importantly, for me as a supervisor, it means that I do not have to teach the same topics individually to all my supervisees. I can assign them the course, knowing that they will have the beginning of understanding what it is they need to do and what my comments on their statistical thinking imply. I can conclude that after being run multiple times now, the course design seems to work. Students have to demonstrate conceptual and practical ability to conduct and think about data analysis. Even those qualitative researcher students who have taken or audited the course have gained a deeper appreciation of statistical methods. Perhaps, this approach demonstrates that less is more.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Ethics statement
Ethical approval was not required for the study involving human participants in accordance with the local legislation and institutional requirements. Written informed consent to participate in this study was not required in accordance with the national legislation and the institutional requirements. The individuals named within the article provided written informed consent for the publication of identifying information.
Author contributions
GB: Conceptualization, Data curation, Funding acquisition, Investigation, Methodology, Project administration, Visualization, Writing – original draft.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. APC funding was provided by the Associate Dean Research, Faculty of Education and Social Work, The University of Auckland.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2023.1302326/full#supplementary-material
Footnotes
1. ^ https://www.auckland.ac.nz/en/students/academic-information/postgraduate-students/doctoral/doctoral-opportunities/doctoral-development-framework/Using-the-DDF.html
2. ^ https://figshare.com/authors/Gavin_T_L_Brown/1192740
3. ^ doi:10.17608/k6.auckland.4557322.v1
References
Abbasnasab Sardareh, S., Brown, G. T. L., and Denny, P. (2021). Comparing four contemporary statistical software tools for introductory data science and statistics in the social sciences. Teach. Stat. 43, S157–S172. doi: 10.1111/test.12274
Albers, M. J. (2017). Quantitative data analysis—in the graduate curriculum. J. Tech. Writ. Commun. 47, 215–233. doi: 10.1177/0047281617692067
Borsboom, D. (2005). Measuring the mind: Conceptual issues in contemporary psychometrics Cambridge University Press.
Brown, G. T. (2014). What supervisors expect of education masters students before they engage in supervised research: a Delphi study. Intern J Quantitative Res Educ 2, 69–88. doi: 10.1504/IJQRE.2014.060983
Brown, G. T. L. (2017). The future of assessment as a human and social endeavor: addressing the inconvenient truth of error [specialty grand challenge]. Front Educ 2:3. doi: 10.3389/feduc.2017.00003
Burnham, K. P., and Anderson, D. R. (2004). Multimodel inference: understanding AIC and BIC in model selection. Sociol. Methods Res. 33, 261–304. doi: 10.1177/0049124104268644
Dutt, A., Ismail, M. A., and Herawan, T. (2017). A systematic review on educational data mining. IEEE Access 5, 15991–16005. doi: 10.1109/ACCESS.2017.2654247
Eisenhart, M., and DeHaan, R. L. (2005). Doctoral preparation of scientifically based education researchers. Educ. Res. 34, 3–13.
Huck, S. W., and Sandler, H. M. (1979). Rival hypothesis: Alternative interpretations of data-based conclusions Longman.
Jamovi Project . (2022). Available at: https://www.jamovi.org
Jones, L. V., and Thissen, D. (2006). “A history and overview of psychometrics” in Handbook of statistics. eds. C. R. Rao and S. Sinharay (Elsevier), 1–27.
Kim, Y., and Steiner, P. (2016). Quasi-experimental designs for causal inference. Educ. Psychol. 51, 395–405. doi: 10.1080/00461520.2016.1207177
Kline, R. B. (2004). Beyond significance testing: Reforming data analysis methods in behavioral research American Psychological Association.
Labaree, D. F. (2003). The peculiar problems of preparing educational researchers. Educ. Res. 32, 13–22. doi: 10.3102/0013189X032004013
Leder, G. C. (1995). Higher degree research supervision: a question of balance. Aust. Univ. Rev. 2, 5–8.
Little, S. G., Akin-Little, A., and Lee, H. B. (2003). Education in statistics and research Design in School Psychology. Sch. Psychol. Int. 24, 437–448. doi: 10.1177/01430343030244006
Meissel, K., and Brown, G. T. L. (2023). “Quantitative research methods” in Research methods for education and the social disciplines in Aotearoa New Zealand. eds. F. Meyer and K. Meissel (NZCER), 83–97.
Meyer, F., and Meissel, K. (Eds.) (2023). Research methods for education and the social disciplines in Aotearoa New Zealand NZCER.
Michell, J. (2008). Is psychometrics pathological science? Measurement. Interdisciplinary Res Perspectives 6, 7–24. doi: 10.1080/15366360802035489
Novick, M. R. (1966). The axioms and principal results of classical test theory. J. Math. Psychol. 3, 1–18. doi: 10.1016/0022-2496(66)90002-2
O'Brien, K. M. (1995). Enhancing research training for counseling students: interuniversity collaborative research teams. Counselor Educ Supervision 34, 187–198. doi: 10.1002/j.1556-6978.1995.tb00241.x
‘Otunuku, M. A., and Brown, G. T. (2007). Tongan students' attitudes towards their subjects in New Zealand relative to their academic achievement. Asia Pac. Educ. Rev. 8, 117–128. doi: 10.1007/BF03025838
Page, R. N. (2001). Reshaping graduate preparation in educational research methods: one school's experience. Educ. Res. 30, 19–25. doi: 10.3102/0013189X030005019
Pearl, J. (2013). Linear models: a useful “microscope” for causal analysis. J Causal Inference 1, 155–170. doi: 10.1515/jci-2013-0003
Pearl, J., and Mackenzie, D. (2018). The book of why: The new science of cause and effect Hachette Book Group.
Rupp, A. A. (2008). Lost in translation? Meaning and decision making in actual and possible worlds. Measurement: Interdisciplinary Res and Perspectives 6, 117–123. doi: 10.1080/15366360802035612
Shadish, W. R., Cook, T. D., and Campbell, D. T. (2002). Experimental and quasi-experimental designs for generalized causal inference Houghton Mifflin.
Thompson, B. (2007). Effect sizes, confidence intervals, and confidence intervals for effect sizes. Psychol. Sch. 44, 423–432. doi: 10.1002/pits
Keywords: teaching, doctoral study, novice learners, course design and curricula, quantitative methods
Citation: Brown GTL (2024) Teaching advanced statistical methods to postgraduate novices: a case example. Front. Educ. 8:1302326. doi: 10.3389/feduc.2023.1302326
Edited by:
Ben Daniel, University of Otago, New ZealandReviewed by:
Vanessa Scherman, International Baccalaureate (IBO), NetherlandsAssoc Paitoon Pimdee, King Mongkut's Institute of Technology Ladkrabang, Thailand
Copyright © 2024 Brown. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Gavin T. L. Brown, Z3QuYnJvd25AYXVja2xhbmQuYWMubno=
 Gavin T. L. Brown
Gavin T. L. Brown