The changing nature of basic skills in numeracy

The issue

Conducting large calculations manually with pen and paper following prescribed procedures or algorithms has been diminishing in significance for some time. In most cultures, and for many years already, individuals employ digital instruments for such computational tasks, when confronted with them in daily life.

Yet, a closer examination of prevalent practices in the teaching of basic numeracy skills in adult education reveals a persistent emphasis on mastering standardized manual calculation techniques, especially with abstract and decontextualized numbers. This emphasis predominantly stems from the belief that mastering these manual procedures forms the cornerstone of all numeracy abilities. Contrastingly, our research indicates that the numeracy skills most frequently utilized and required in contemporary professions and daily activities encompass higher-order capabilities (Hoogland and Stoker, 2021; Boels et al., 2022; Hoogland and Díez-Palomar, 2022). These include interpretation, reasoning, mathematizing, estimation, critical reflection on quantitative data, and the application of digital instruments for computation. It is imperative, therefore, that numeracy education for adults prioritizes these competencies to achieve efficacy.

Exploring the issue

Present-day society is profoundly infiltrated by websites, expansive data sets, computational models, interconnected data networks, hyperlinked configurations, filter systems, and online applications. These predominantly digital entities are fundamentally rooted in mathematical concepts and principles. Media communication has witnessed a surge in data utilization, evident in the proliferation of visual representations such as tables, charts, and diagrams, all underpinned by big data and data-driven indices. Algorithms, in this context, not only guide our actions but also mold the informational spheres or “bubbles” we inhabit. Succinctly, our society has undergone a significant mathematization over the past four decades, attributable to technological advancements and the digital revolution (see, for instance, Gellert and Jablonka, 2007 and Skovsmose, 2020).

Globally, there's a unanimous agreement on the necessity for individuals, whether as professionals or citizens, to possess adequate and multifaceted numeracy skills to engage effectively in the number-drenched world as described above. This is corroborated by studies on 21st-century skills and global competences (Voogt and Pareja Roblin, 2010; OECD, 2016; Schwab, 2016). Data from PIAAC underscores that a substantial number of citizens are lacking these essential numeracy competencies (OECD, 2013). This lack impedes their autonomous and effective participation in our technologically advanced, numerically saturated societies, leading to potential occupational exclusions and daily life challenges.

While adult numeracy educational practices should mirror these broad, multifaceted competencies for effectiveness, a significant portion of such practices remains anchored in manual calculations with abstract numbers. Although there's a discernible shift toward materials and strategies that align with the aforementioned broad competencies, the traditional computational approach remains deeply entrenched. Subsequent sections will elucidate the primary cause for this enduring incongruence, with a deeper exploration of the evolution of basic numeracy skills.

Basic skills: a historical and contemporary perspective

The UNESCO Glossary of Curriculum Terminology provides a comprehensive definition of basic skills. They are described as: “The fundamental knowledge (i.e., declarative and procedural) as well as operational aspects of knowledge needed for learning, work and life. Within the curriculum, literacy and numeracy are normally considered as foundational, essential or basic skills. The term can include a range of skills that individuals need to live successfully in contemporary society.” (UNESCO-IBE, 2013, p. 8)

According to this definition, basic skills are not static and everlasting, but fluid, evolving in tandem with societal demands and advancements. They are the cornerstone skills deemed indispensable in the contemporary world, underpinning personal growth, educational achievements, and career progression. What's more, these skills are broad and transferable, implying their applicability across diverse scenarios and their value in various life domains. As individuals journey through life, these basic competencies act as the starting point from which more specialized and advanced skills evolve. A skills and dispositions overview as used in the developing of the Common European Numeracy Framework (see Figure 1) is in line with this definition (Hoogland et al., 2021).

FIGURE 1

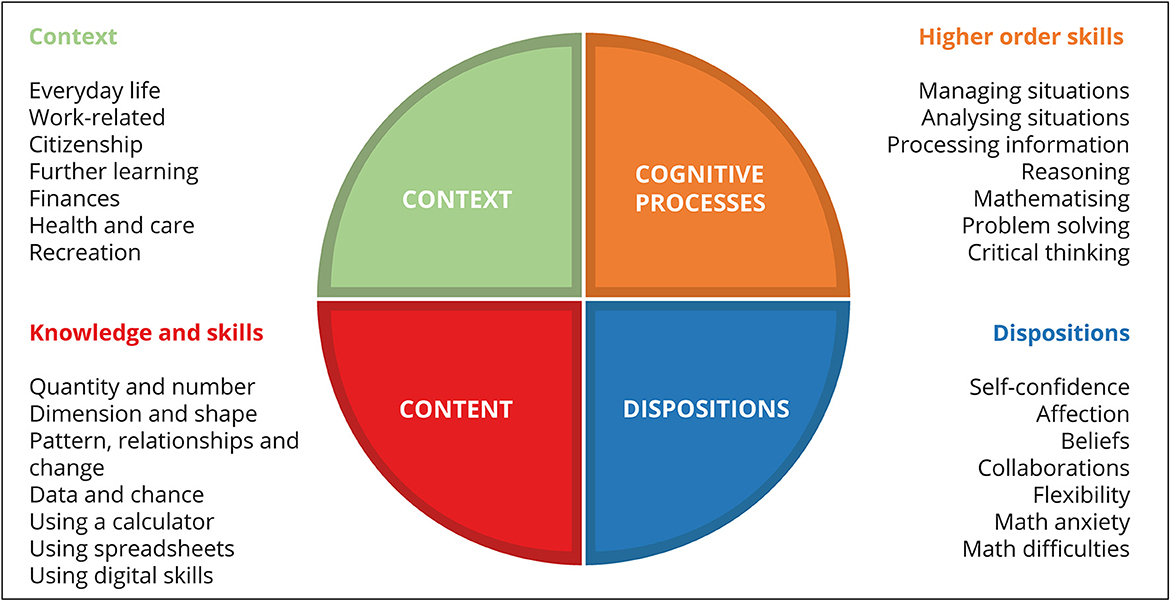
Figure 1. Common European Numeracy Framework: aspects of the quality of numerate behavior. Adapted from (Hoogland et al., 2021).

To grasp the evolving essence of numeracy as a basic skill, it's crucial to differentiate between two distinct yet related phenomena.

The first phenomenon is a mathematical mental toolkit, that individuals cultivate over their lifetime and which is used flexible and at an instant in relevant numerical situations. It encompasses basic concepts like number names, internalized, ready to use, small operations (e.g., 7 × 8 = 56, 4 × 25 = 100, 14 + 8 = 22, 12: 3 = 4 and 2 × $\frac{1}{4}$ = $\frac{1}{2}$), and strategies for flexible mathematical thinking, for instance in multiplying 6 × 99. This toolkit also includes an understanding of common measurements such as time, length, and weight. Scholars like Butterworth (1999) and Devlin (2000) posit that this mental toolkit is intrinsic to human development, shaped by our interactions with a world abundant in numerical concepts and artifacts. The depth and breadth of this toolkit can vary among individuals. Regular engagement in diverse numeracy situations can enhance and solidify this toolkit. However, factors like self-confidence, self-efficacy, and math anxiety can influence its effective utilization.

The second phenomenon is the capacity to finds answers to more complex and larger calculations, using written down procedures and algorithms. These complex mathematical operations go beyond the direct scope of the mental toolkit. Examples include more complex calculations starting from 123 × 939, 1.434.300 ÷ 171, 24/7 ÷ 5/19, and so on. Historically, to navigate these complex calculations, cultures developed specific written algorithms. Tools like pen and paper, slates, or even clay tablets were employed to break down these calculations into smaller, manageable steps that could be tackled using the mental toolkit. The mental toolkit was used in these procedures over and over again in a specific—detached from reality—way.

The distinction between the mathematical mental toolkit and procedural calculations offers a lens to comprehend the evolution of basic numeracy skills. The first phenomenon is rather universal and encompasses also the higher-order skills necessary to cope with a plethora of numeracy situations, the second one is time-bound and started loosing its relevance at the end of last century after being prominent for centuries.

Historical developments in basic skills

We will discuss in broad strokes three periods in recent times and how the phenomena described above played a role. We distinguish between roughly three periods.

Crafts numeracy in the pre-industrial revolution era (up to 1850)

In the eras spanning from Classical Antiquity to the Middle Ages, reading, writing and arithmetic were privileges reserved for a select elite. The 12th century witnessed the rise of guilds and apprenticeship systems, broadening the scope of skill acquisition. Guilds, representing various crafts such as carpentry, baking, tailoring, and masonry, played a pivotal role. Essential numeracy skills for artisans during this period encompassed measurement, geometry, estimation, time calculations, weight and volume assessments, trade-related calculations, and design patterns. These skills, a blend of basic facts and procedural calculations, often in the form of situational “ready reckoners” were predominantly imparted as situational knowledge, crucial for artisans to hone their craft (Smith, 1924; Cohen, 1982).

The rise of procedures in the industrial age (1850–1980)

The Industrial Revolution, a transformative period in history, brought about significant changes in the way society perceived and imparted basic skills. As industries grew and urbanized areas expanded, the need for a more universally applicable set of skills became evident. It became clear that this system of apprenticeships was insufficient to meet the demands of a rapidly changing workforce.

The mid-19th century, particularly the Victorian era, saw an emphasis on the so-called 3 R's of Reading, 'Riting, and 'Ritmetic. These skills were deemed essential for individuals to navigate the complexities of an industrialized society (Thomas, 1987). As the 20th century dawned, there was a global push toward mass education. Schools became the primary institutions for imparting a standardized set of skills. Subjects like language and mathematics were at the forefront, considered indispensable for personal and professional growth. Within the realm of mathematics, there was a noticeable shift in pedagogical approaches. While the emphasis on mastering basic facts remained, the procedural content became more abstract and decontextualized. The practical application of these skills in daily life was often overlooked in favor of rote learning and procedural mastery.

This abstract approach to mathematics trickled down to adult education as well. There was a prevailing belief that mastering abstract mathematical procedures was a prerequisite to harnessing one's mental toolkit in real-life situations. This often led to a disconnect, with adults learning skills that they found little to no application for in their daily lives.

Transition to the digital age (post-1980)

The late 20th century, marked by technological advancements, witnessed a seismic shift in the substantiation of basic skills, especially in the realm of numeracy. The 1980s saw the advent of calculators, revolutionizing the landscape of arithmetic. These devices, initially priced between 50 and 100 euros, were capable of executing a vast array of calculations, from basic arithmetic to advanced scientific computations. This technological leap posed a challenge to the traditional goals in education as the necessity to manually perform calculations diminished. This meant also that the “natural” environment to keep using and exercising the mental toolkit in carrying out procedures came under pressure because the need to master it to solve calculational problems dwindled rapidly.

A discernible gap emerged between real-world practice and school curricula. While calculators and digital computation tools became ubiquitous in daily life, their use was often restricted in educational settings. In primary and most secondary education this discrepancy was kept at arms length by simply not allowing calculators or other digital calculation software in the mathematics lessons.

For adult numeracy education the need to tackle this discrepancy is urgent. It simply doesn't make sense to teach adults again procedures that are not used anymore, while an abundance of challenging numeracy problems comes across in their daily life.

Conclusion

In an increasingly mathematized world, the ability to navigate and make informed decisions hinges on possessing a broad and multifaceted set of numeracy skills. These foundational mathematical competencies, often termed as basic numeracy or mathematics skills, are pivotal for adults to engage meaningfully in both their professional and personal lives. When we delve into the real-world actions and interactions of individuals, a clear pattern emerges, highlighting the quintessential mathematical competencies required in today's society (see Figure 1). Especially the higher order skills, tailored to numeracy situations, should be part of the mental toolkit.

Yet, a stark contrast is evident when we turn our gaze to the prevalent practices in adult numeracy education. The current pedagogical landscape is dominated by traditional, paper-based exercises, often emphasizing decontextualized number crunching and rigid procedural algorithms. This approach, while rooted in historical educational paradigms, seems misaligned with the dynamic demands of the contemporary world.

Labeling the prevailing calculational approach as “catastrophic teaching of skills” is not an overstatement. It epitomizes an educational scenario where a skill, despite being underscored as paramount, is incessantly drilled into learners without any tangible demonstration of its applicability outside the classroom. Such an approach not only diminishes the perceived value of the skill but also causes a disconnect between learning and real-world relevance.

To foster a versatile mathematical mindset in adults, a paradigm shift in educational practices in adult numeracy education is imperative. The focus should pivot from rote calculations to the cultivation of higher-order skills that resonate with the complexities of a mathematized society. By anchoring lesson tasks in real-world scenarios and emphasizing ánd exercising higher order skills that hold tangible relevance, we can bridge the chasm between adult classrooms and practical use, ensuring that adults are well-equipped to navigate the intricacies of the modern world.

Author contributions

KH: Writing—original draft, Writing—review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Boels, L., Hoogland, K., Kleine Deters, B., Jonker, V., and Wijers, M. (2022). Interpreting and Understanding of Contemporary Information Sources. Available online at: https://www.hu.nl/onderzoek/publicaties/het-interpreteren-en-begrijpen-van-hedendaagse--informatiebronnen (accessed September 01, 2023).

Google Scholar

Butterworth, B. (1999). The Mathematical Brain. London: Macmillan.

Google Scholar

Cohen, P. C. (1982). A Calculating People the Spread of Numeracy in Early America. Chicago, IL: The University of Chicago Press.

Google Scholar

Devlin, K. (2000). The Math Gene: How Mathematical Thinking Evolved and Why Numbers are Like Gossip. New York, NY: Basic Books.

Google Scholar

Gellert, U., and Jablonka, E. (2007). Mathematisation and Demathematisation – Social, Philosophical and Educational Ramifications. Dordrecht: Sense Publishers.

Google Scholar

Hoogland, K., and Díez-Palomar, J. (2022). “The mathematisation of society: rethinking basic skills for adults,' in Proceedings of the Twelfth Congress of the European Society for Research in Mathematics Education. Available online at: https://hal.science/hal-03745525v1 (accessed September 01, 2023).

Google Scholar

Hoogland, K., Díez-Palomar, J., and O'Meara, N. (2021). “Common European Numeracy framework – a multifaceted perspective on numeracy,” in Paper presented at the 14th International Congress on Mathematics Education (ICME14) (Shanghai). Available online at: https://www.researchgate.net/publication/368921986 (accessed September 01, 2023).

Google Scholar

Hoogland, K., and Stoker, M. (2021). The Mathematisation of Society. Available online at: https://www.youtube.com/watch?reload=9&v=8HisrNPI65E (accessed September 01, 2023).

Google Scholar

OECD (2013). Skilled for Life? Key Findings from the Survey of Adult Skills. OECD Publishing. Available online at: https://www.youtube.com/watch?v=8HisrNPI65E

Google Scholar

OECD (2016). Global Competency for an Inclusive World. OECD Publishing. Available online at: https://www.oecd.org/education/Global-competency-for-an-inclusive-world.pdf (accessed September 01, 2023).

Google Scholar

Schwab, K. (2016). “The Fourth Industrial Revolution: what it means, how to respond,” in World Economic Forum - Global Agenda, Vol. 2018 (World Economic Forum). Available online at: https://www.weforum.org/agenda/2016/01/the-fourth-industrial-revolution-what-it-means-and-how-to-respond/ (accessed September 01, 2023).

Google Scholar

Skovsmose, O. (2020). “Mathematization as social process,” in Encyclopedia of Mathematics Education, ed S. Lerman (Cham: Springer). doi: 10.1007/978-3-030-15789-0_112

CrossRef Full Text | Google Scholar

Smith, D. E. (1924). The first printed arithmetic (Treviso, 1478). Isis 6, 311–331. doi: 10.1086/358240

CrossRef Full Text | Google Scholar

Thomas, K. (1987). Numeracy in early modern England. The prothero lecture. Transact. R. Hist. Soc. 37, 103–132. doi: 10.2307/3679153

CrossRef Full Text | Google Scholar

UNESCO-IBE (2013). Glossary of Curriculum Terminology. Available online at: https://www.ibe.unesco.org/sites/default/files/resources/ibe-glossary-curriculum.pdf (accessed September 01, 2023).

Google Scholar

Voogt, J., and Pareja Roblin, N. (2010). 21st Century Skills. Enschede: Universiteit Twente.

Google Scholar