Edith Debrenti
Andrea Bordás- 1Department of Economics, Faculty of Economics and Social Science, Partium Christian University, Oradea, Romania
- 2Department of Human and Social Sciences, Faculty of Economics and Social Science, Partium Christian University, Oradea, Romania
Empirical research results show that the system of logical operations and conclusion schemes does not become complete even in adulthood. Although we know other logical models besides the classical two-valued logical reasoning model, in higher education for students it is essential to know and apply the rules of the classical reasoning model. Proofs, reasoning and refutation are necessary in the case of several subjects, as scientific language uses many of logical operations. Our 2022 end-of-year research measured general logical basic-knowledge and operations in everyday life, mathematical, physical, chemical and biological contexts based on 246 university students’ online testing. The students completed the tasks which required the correct conclusion in the highest proportion (69.02%), followed by the interpretation of ‘at most’/‘at least’ (63.41%), and at least the negation (the negation of the ‘at least’, of ‘exists’ and of ‘for all’) (29.91%). Our results show that the correct interpretation did not become dominant in the case of all logical operations for these students. The everyday life problems were solved correctly by the highest percentage of students (70.05%), followed by problems in biological, physical and mathematical context. They were least successful (28.04%) in solving logical problems related to chemistry. This shows that our data cannot be analyzed without semantic content. Based on different statistical tests, we did not find a significant difference in performance between genders, but according to the human capital theory students of more highly educated mothers performed significantly better.
1. Introduction
Universities are places of acquaintance with reality through the eyes of sciences, where students are immersed in the ‘intellectual life’ of those around them; they gain social experience through the mediation of more competent peers (Ilyash, 2008). If learning is seen as enculturation in all its forms, involvement in the culture of a community, whereby one acquires and takes possession of the culture, the set of habits, skills, methods and tools of a group, community or society (Lave and Wenger, 1991; Lave, 1997; Allal, 2001), then university life is an entry into the scientific community, into the world of science. This is what Prior and Bilbro (2012) called academic enculturation. Prior and Bilbro (2012) identifies three research directions in the study of the content of academic enculturation. Our research is most closely related to linguistic-rhetorical studies, by investigating logical thinking among university students through different logical tasks. These tasks required the ability to recognise and understand the most commonly used logical syntaxes and operations, to understand the most relevant information, scientific context of the tasks.
In today’s knowledge-based society, the role of research and science has increased, so developing higher-order thinking skills of higher education students is a priority. In a broadened concept of scientific thinking critical thinking and understanding, epistemic understanding, research skills, evidence-based reasoning skills and contextual understanding are essential for students (Murtonen and Balloo, 2019). Students need to be able to select relevant information, make research-based decisions, understand the process of knowledge construction, assess the validity of information sources, and apply reasoning skills, i.e., critical thinking skills (Seppälä et al., 2020). These higher-order thinking skills besides technical, social and behavioral skills are essential for the 21st century’s citizens, because they are transferable across different subject areas and contextual situations, different jobs, occupations, and industries (Arum and Roksa, 2011; Avvisati et al., 2013; Shavelson et al., 2019). In recent decades more and more research has focused on the assessment and development of generic skills and competencies in higher education, such as critical thinking, problem-solving and complex reasoning (Shavelson, 2007; Nusche, 2008; Arum and Roksa, 2011; Tremblay et al., 2012; Zlatkin-Troitschanskaia et al., 2015; Shavelson et al., 2019; Braun et al., 2020; Tuononen et al., 2022). Basic logical operations are at the basis of these three internationally most studied generic skills.
Logical and critical thinking contribute to students’ understanding of different disciplines (Durand-Guerrier, 2003; Cresswell and Speelman, 2020; Sobhanzadeh et al., 2021). Drawing on some other researches Adey and Shayer (1994) emphasise that formal reasoning is needed in higher education, because not only natural sciences, but social sciences also require deductive logical thinking, knowledge of the process of causal reasoning with its sub-processes as exclusion and control of variables, constructing and using formal models and logical reasoning. Many aspects of students’ intellectual abilities are stimulated and developed during the school years, and the overall development of thinking, the correct use of logical operations is an important objective in mathematics education (Cresswell and Speelman, 2020). Basic logical operations allow us to carry out mathematical proofs and then draw further conclusions from them.
Formal logic and basic logical operations are important in mathematics and science, while in everyday life discussions we use informal logic. Before learning formal logic, we use informal logic of the language. „Conventions and norms of mathematical logic are clearly not inherent in everyday rationality or non-mathematical language” (Durand-Guerrier and Dawkins, 2020, p. 482). To be able to operate the norms and rules of formal logic in different contexts, it is primarily required to recognize the linguistic register in which we have to think, because the semantic content, the mental representations evoked by the context, determine how we think about the given topic, how we interpret logical operations: according to the rules of everyday language or according to the rules of formal logic (Dawkins and Cook, 2017).
1.1. Our research
There are very few studies on measuring student performance in higher education in Romania. To fill this gap, we examined a very small slice of the content of academic enculturation in order to get an idea about students’ competences in basic logical operation skills and logical reasoning. Our research goal was to clarify what types of logical operations and tasks cause difficulties in interpretation and solving, and how much the context of the sciences influences the understanding and correct solution of problems. One of our research questions was whether the proportion of correct answers in different logical operation tasks depends on the scientific context in which the task is formulated or not. However, we also wanted to find out how the participants’ gender, age, their parents’ educational level, and involvement in teacher training influenced the success in problem-solving.
The Western Romanian region concerned is one of the ethnically and religiously most diverse peripheral regions of the country. Traditional values are highly valued in the region, the population is strongly bound to the area and the local community. Higher education institutions here are struggling to cope with the study-driven migration of youth to big cities’ elite universities and abroad, it is difficult to recruit strongly selected students here, so regional recruitment is typical. The emergence and growth of non-traditional student groups, coming from families with limited financial resources, lower social classes, and different cultural backgrounds have given rise to the so-called „third mission of higher education”: the wish to promote the cohesion of the diverse regional society (Kozma, 2010; Kozma and Ceglédi, 2010; Nyüsti and Ceglédi, 2012; Pusztai et al., 2012).
We conducted a conceptual replication study using the survey developed by Szarka et al. (2022), partially replicating their research and raising new questions. Also Slovakia and Romania are two Central and Eastern European countries, with very similar historical, cultural, and geo-political characteristics due to the ‘nationalization’ of teacher training (Kowalczuk-Walędziak, et al., 2023) there are main differences not only in teacher education policies, but in the whole educational process. Both in the initial and the replication study we found peripheral regions, with young universities which emerged around the turn of the millennium as a result of the educational policy conditions of the post-communist period and the subsequent changes in the European higher education area (Kozma, 2010, 2022). These changes have led to the development of a similar student base in both regions, which makes them comparable. We have formulated two hypotheses to test the results of the preliminary research (Szarka et al., 2022) regarding students’ performance in logical tasks embedded in different scientific contexts on a different population, within a different educational space.
H1: Students’ gender does not influence on the performance of the logical thinking tasks.
H2: Students’ age influences on the performance of the logical thinking tasks: older students perform better, than younger.
In searching for alternative explanations of the original studies’ results, two other hypotheses were formulated based on further literature review, as follows:
H3: It is assumed that the educational level of the students’ parents has an influence on students’ achievements in logical thinking tasks. Students of parents with higher educational levels perform better than students of parents with lower educational levels.
H4: Both the type of the logical task and the context of the task influence the effectiveness of the task solution.
2. Methods
Our study can be identified as a conceptual replication study, whereas by design it replicates most of the methodological features of the original study (Aguilar, 2020; Star, 2021; Perry et al., 2022). To test whether the results hold beyond the boundaries of the original study, we used a so-called scaling out model of exploration (Aguilar, 2020), using a study population with different geographical and educational characteristics than the original study.
We used the same research design and in most of the cases we followed the same statistical processing strategy as the original study to ensure comparability of the data. However there were some aspects of the original study’s methodology we changed or added. To understand deeply the relationships between performance and the differences between logical tasks, we examined whether the type of logical operations or the context of the tasks were the determinants of performance. Compared to the original study we examined the effect of parental education on student performance as an independent variable.
2.1. Participants
The data were collected online in November and December 2022. The population consisted of undergraduate and master’s students belonging to the Hungarian national minority of two universities from the Western Region of Romania: the Partium Christian University (PCU) in Oradea and Babeș–Bolyai University (BBU), the Satu-Mare extension. Random sampling was used; students completed the questionnaire online in the presence of a university lecturer.
The survey was completed by 246 students: 196 (79.7%) participants were from PCU, while 50 (20.30%) participants were from BBU. 72.76% of the participants were undergraduate students, and 27.23% were master’s students. Distribution of students according to gender: 187 female (76.01%) and 59 male (23.98%). Distribution according to age: 217 participants aged 18–25 (88.21%), and 29 participants (11.79%) older than 25 years. The majority of respondents (over 95%) study other disciplines than STEM: economics, social sciences, humanities, languages or arts, and preschool and primary school teacher training. The percentages reflect the range of subjects offered by the two institutions.
2.2. Instrument
As a research tool, we used an online questionnaire developed during the COVID by a research group in Slovakia (Szarka et al., 2021, 2022). The questionnaire is divided into three parts: sociodemographic questions, different tasks for selected elements of propositional logic embedded in everyday life and four academic disciplines (STEM) contexts, and a rating of the tasks on a 5-point Likert scale. The variables related to the social background and demographic characteristics of the respondents (gender, age, parents’ highest level of education, and characteristics of the study programmes) were identified as independent variables in the survey. The dependent variables were the results obtained in solving the tasks requiring logical thinking, basic logical operations and basic mathematical knowledge. The test compilers (Szarka et al., 2021, 2022) used three different types of logical operations: set A: understanding some quantifiers as ‘at most/at least’; Set B: the negation of ‘at least’, ‘there is’, ‘all’, and finally Set C: reasoning: ‘if … then’, ‘therefore’. All three problem sets contained problems of the same type, but were presented in different contexts. The basic general logical reasoning skills and operations were tested in the context of everyday life, mathematics, physics, chemistry, and biology. Except for one biological task, the tasks were multiple-choice questions with a single answer. The biological task was a short-answer task from set C, where students had to complete the sentence, to continue the reasoning. Each item was rated on a dichotomous scale (right/wrong). For each correct answer, 1 point was awarded. As examples we present in the Supplementary Material three tasks from the three different types of logical operations, each in different contexts.
The third set of questions (assessing the difficulty of tasks) is not included in the present study.
2.3. Statistical analysis
The statistical analysis of the data was realized with Excel and R statistical software. The tasks measuring logical operations were of nearly the same difficulty. To verify the reliability of the test we used Kuder–Richardson formula 21 (KR-21), which is a special case of Cronbach’s Alpha in which the items are binary variables, usually scored as 0 or 1, and the tasks are of nearly the same difficulty. Based on the KR-21 our test is reliable, our value is 0.7, and the results are consistent. In order to compare the standard deviation squares of different subsamples we used the F-test and Anova, and to compare the mean of subsamples, we used T-test for Two-Sample Assuming Equal Variance or T-test for Two-Sample Assuming Unequal Variance. Searching for significant correlations between parents’ educational level and students’ performance chi-square test was applied. In order to determine which variables determine the results more significantly (type of logical task or context), multiple linear regression analysis was used.
3. Results
From a maximum of 15 good answers the average test score for N = 246 participants was 8.12 (SD = 2.18). The median value was 8. The participants resolved correctly at least 3 tasks, and they resolve up to 14 tasks correctly. 54.12% of questions were correctly answered.
3.1. Overall results based on the type of the logical operations required in the tasks and their context
Our results show that the difficulty of the task types, therefore the difficulty of basic logical operations differs as presented in Table 1. As every set of tasks is composed of 5 tasks of a kind, a maximum of 5 points could be achieved. In Set A tasks at least 1 task was correctly resolved by everybody (13 students get 1 point out of 5), but in Set B, and C we found participants, who could not resolve even one of five negation or reasoning tasks. In Set B 47 students achieved 0 points, which means 19.11% of students, in Set C just 1 student. Most of the perfect solutions were in set C, in the reasoning, and conclusion-making tasks: 48 students (19.51%) solved all 5 problems correctly.
Table 1. Descriptive statistics of task sets and contexts (N = 246).
The students completed correctly in the highest proportion the tasks set C which required reasoning (69.02%, 849 good answers), followed by the interpretation of ‘at most’, ‘at least’ (63.41%, 780 good answers), and at least the negation of ‘at least’, ‘exists’ and ‘for all’ (29.91%, 368 good answers). The Single-factor ANOVA shows that there is a significant difference in the success rate of solving different sets of tasks (F = 228.83, p ≤ 0.001), and negation of different statements including quantifiers such as ‘every/everyone’, ‘at least’, ‘there are’ is the most difficult logical operation for students. The most difficult task was to negate the sentence with ‘at least’. Although, according to the rules of formal logic, a relatively simple situation from everyday life had to be negated (‘I have been to Prague at least 6 times’), from 246 participants a total of 36 correct answers were received, giving a 14.63% success rate. The same low percentage of students (19.92%) negated correctly a sentence in chemistry context: ‘2 of the elements in the periodic table are in the liquid state’.
Grouping the tasks by their context, we see that context plays a significant role in the interpretation of propositional logical operations. Table 1 presents the descriptive statistics of the tasks grouped by context. In everyday life context at least 1 task was correctly resolved by everybody (7 students get 1 point of 3), but in scientific contexts we found participants, who cannot resolve even one of three tasks. In the chemistry context 102 students achieved 0 points, which means 41.46% of students. Most of the perfect solutions were in the biology context: 62 students (25.20%) solved all 3 problems correctly.
The tasks related to everyday life were solved correctly by the highest percentage of students (70.05%), followed by problems in biological (65.85%), physical (56.78%) and mathematical (49.86%) contexts. The tasks embedded in a chemistry context were the weakest performed (28.04%) by the students. The Single-factor ANOVA shows that there is a significant difference in solving problems related to the context (F = 97.31; p ≤ 0.001). There were two tasks related to everyday life that were solved correctly by more than 95% of the participants.
Looking at the overall score achieved by the students, it can be seen that it depends both on the type of logical operation used in the task and the context of the task. Using multiple linear regression and examining all the factors simultaneously, we find that the context of the tasks has a significant effect on the student’s performance, while there is no significance for the logical operation used (R-square value is 1, p = 0.00). From this we conclude that context has a greater effect on task performance than logical operation.
3.2. Results presented by gender and age
The sample is unbalanced in terms of gender due to the high proportion of students enrolled in preschool and primary school teacher training (See Table 2). To assess the differences between the results obtained in solving the tasks, an F-test and, a T-test were used, but there were no significant differences between males’ and females’ test scores, not even in one specific type of task or context.
Table 2. Average test scores by gender and age.
The sample is unbalanced in terms of age, but represents the population of the examined Western-Romanian universities. As above an F-test and, a T-test was used to explore the differences between the specified age-groups. Table 2 shows the main descriptive statistics regarding the age-group’s achievement, and specifies two task types where there are significant differences. The understanding and usage of quantifiers tasks, were significantly better performed by younger students: the average of correct answers was 3.24 for younger students, and 2.68 for older students (t = 2.79, p ≤ 0.01). Although older students performed better in the other two types of logical operations, there are no significant differences. On the other hand, when the tasks were grouped by context, the older students performed significantly better on the tasks embedded in a chemistry context, which caused the most problems for the participants. Older students’ performance was 1.21, younger students’ 0.79 (t = −2.49, p ≤ 0.02).
3.3. Results presented by parents’ highest educational level
As an explanatory variable we used parents’ highest educational level. No significant correlations were found between parents’ highest educational attainment and students’ test scores for the three types of operational logic tasks tested. Concerning the contexts of the tasks, fathers’ educational level had no significant impact on students’ performance, but mothers’ educational level had. As Table 3 shows, students of mothers with tertiary education perform better than students of mothers with lower educational levels in all contexts. The largest difference is seen in the proportion of correct answers to the tasks embedded in the physical context: while students of mothers with tertiary education answered the questions correctly in 64.81% of cases, participants of parents with lower educational level answered correctly in 56.86% at most.
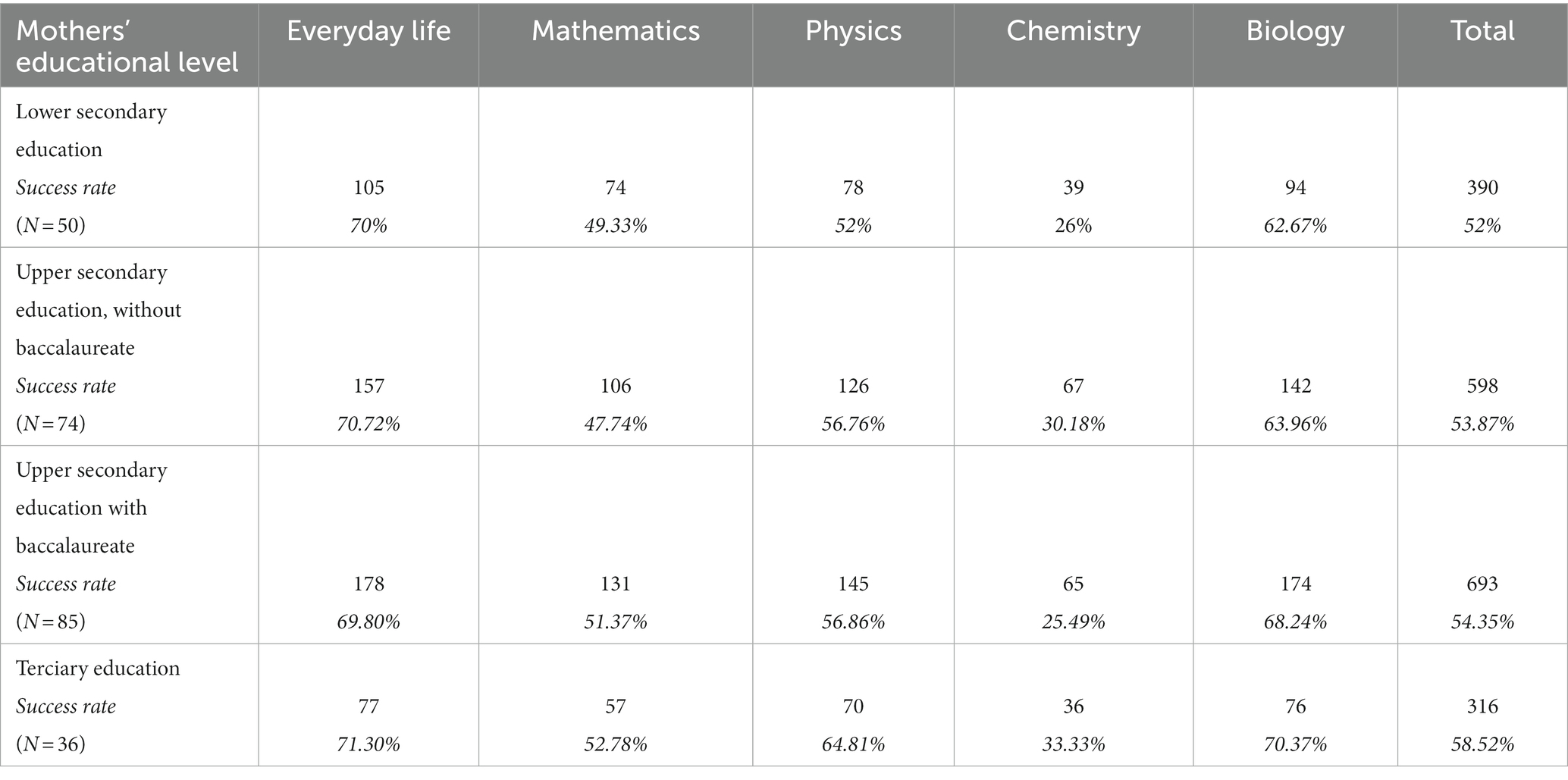
Table 3. Distribution of correct answers by mothers’ educational level and percentage of correct answers from possible answers.
Grouping participants’ correct responses by their mothers’ highest educational level, using a chi-square test (χ2 = 61.67, p ≤ 0.001), we found a significant correlation between mothers’ higher education and better students’ performance in different contexts.
4. Discussion
The significance of the present study lies in the skill assessment methodology. There is a lack of literature on the basic logical operation skills of university students, although these operations are essential for critical thinking and scientific thinking in higher education. With our conceptual replication study, we focused on the comprehension of the relationship between logical operations and context, and the conditions that led us to the presented results. Except for a few minor differences, our results confirm the lessons from the Slovak studies by Szarka et al. (2021, 2022). Based on our new sample of research from another country, we can generalise the following findings: both the types of logical operations and the contexts of the tasks determine students’ performance. We can also establish the same order of difficulty in both countries based on the type of logical operations (reasoning, understanding quantifiers, negation of quantifiers) and based on the context of the tasks (everyday life, biology, physics, mathematics, chemistry). This suggests that both the type of logical operations and the context are determined by some immanent characteristics rather than by the educational systems. Regarding the examined logical operations some researchers find that understanding quantifiers and mainly negation of quantifiers is one of the most problematic tasks (Dubinsky and Yiparaki, 2000; Ferrari, 2004; Ye and Czarnocha, 2012; Bardelle, 2013; Hazem, 2017). This is because some quantifiers have to be reformulated in a more formal language for comprehension, and students rarely encounter formal language before higher education (Mesnil, 2017), they are not familiarized with formalisations and visualizations to support logical tasks (Bronkhorst et al., 2022). Students’ difficulties with the measured logical operations, and comprehension of concepts “can be related to their epistemological complexity or to their use in the classroom” (Mesnil, 2017, p. 217), to the lack of awareness of the importance of the mathematical language used in such tasks (Bardelle, 2013). Ferrari’s (2004) and Bardelle’s (2013) experiments prove that there is a typical mistake to ignore the differences between everyday registers and mathematical ones because of the overlapping and interference between some technical terms from mathematical language and everyday language.
One of the limitations of the study is the relatively small sample of students from universities in the peripheral border region, so the results are not representative of the whole country. Compared to the performance of students in Slovakia (Szarka et al., 2021, 2022), our students’ poor results are in line with the results of the PISA surveys, where Romania’s scores are well below the OECD average in all areas year after year (Lazar, 2021; Mirea et al., 2021; European Union, 2022), while Slovakia is much closer to the OECD average. The overall development of logical thinking is an important objective in mathematics education all over the world. The mathematics curriculum is divided into different areas and topics, and almost all of them aim to develop logical thinking. The areas vary from country to country, while in the Slovak curriculum for mathematics logic, reasoning and proof are separate areas, in Romania there is no explicit inclusion of such topics in the curriculum, and elements of logic, the logic of judgement are embedded in other topics. Learning mathematics and logical thinking also depends on the pedagogical practices, the content, and the methodology used by the teachers. The differences between the teacher training systems of these countries are measurable in terms of time, curriculum, and pedagogical, psychological, and methodological knowledge (Bordás, 2015; Nagy, 2015; Luchenko and Yurchenko, 2023). In Romania, much more emphasis is placed on the scientific disciplinary training of teachers than on pedagogical-psychological subjects. These factors certainly combine to influence students’ scores on logical tests.
Neither age nor gender has a significant effect on test scores. Our results support researches showing that there is no significant difference between boys’ and girls’ performance in mathematical and logical tasks (Cassar and Musumeci, 2017; Ramírez-Uclés and Ramírez-Uclés, 2020). According to human capital theory the parents’ educational level, is one of the most important background factors in educational research on students in the peripheral area under study (Róbert, 2004; Pusztai, 2009, 2011; Ceglédi, 2015a,b,c, 2018; Pusztai and Ceglédi, 2015). Several studies have shown that the parents’ educational level, including the mother, is closely related to academic performance, especially students’ mathematics achievement (Davis-Kean, 2005; Kodippili, 2011; Crede et al., 2015; Dixson et al., 2018; Hidayatullah and Csíkos, 2023). Our study demonstrated a strong positive relationship between maternal education and students’ basic logical operation skills.
The results show that the refutation or negation of quantitative determinants is one of the most difficult logical operations, regardless of the context of the task. The different results achieved in different contexts (difficulty in solving chemistry problems) indicate that students’ thinking is context-dependent and that many of them are not able to handle abstract logical inferences independently of context. As the majority of our sample consists of students from preschool and primary school education programme, testing and developing their elementary reasoning skills is important not only for their academic enculturation but also for their future work. The results suggest that a subject should be introduced where these competencies in basic logical operation skills and logical reasoning can be practiced and developed. There is evidence that thinking skills (critical thinking, problem-solving) can be fostered in tertiary education (Saavedra and Saavedra, 2011) in theory-intensive programmes (Avvisati et al., 2013), using active and collaborative learning (Roksa and Arum, 2011), problem-based learning (Hoidn and Kärkkäinen, 2014).
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
ED: Data curation, Methodology, Writing – original draft. AB: Conceptualization, Investigation, Visualization, Writing – original draft.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The research was supported by the Pallas Athéné Domus Educationis Foundation, Hungary (PADE 113/2019.09.23.).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2023.1273602/full#supplementary-material
References
Adey, P., and Shayer, M. (1994). Really raising standards: cognitive intervention and academic achievement, London: Routledge.
Aguilar, M. S. (2020). Replication studies in mathematics education: what kind of questions would be productive to explore? Int. J. Sci. Math. Educ. 18, 37–50. doi: 10.1007/s10763-020-10069-7
Allal, L. (2001). Situated cognition and learning: from conceptual frameworks to classroom investigations. Schweizerische Zeitschrift für Bildungswissenschaften 23, 407–422. doi: 10.24452/sjer.23.3.4611
Arum, R., and Roksa, J. (2011). Academically adrift: limited learning on college campuses. Chicago, IL: University of Chicago Press.
Avvisati, F., Jacotin, G., and Vincent-Lancrin, S. (2013). Educating higher education students for innovative economies: what international data tell us. Tun. J. High. Educ. 1, 223–240. doi: 10.18543/tjhe-1(1)-2013pp223-240
Bardelle, C. (2013). “The influence of verbal language in a mathematical context: a study on negation,” in Proceedings of the 37th Conference of the International Group for the Psychology of Mathematics Education, Vol. 2, ed. A. M. Lindmeier and A Heinze. (Kiel, Germany: PME), 65–72.
Bordás, A. (2015). “Pillanatkép Románia oktatási gyakorlatáról és az intézmények közötti kapcsolatrendszerről” in Tanárképzési háromszögek: iskolák, fenntartók és képzők együttműködése. Összehasonlító országtanulmányok. ed. M. Chrappán (Debrecen: Debreceni Egyetem), 103–140.
Braun, H. I., Shavelson, R. J., Zlatkin-Troitschanskaia, O., and Borowiec, K. (2020). Performance assessment of critical thinking: conceptualization, design, and implementation. Front. Educ. 5:156. doi: 10.3389/feduc.2020.00156
Bronkhorst, H., Roorda, G., Suhre, C., and Goedhart, M. (2022). Students’ use of formalisations for improved logical reasoning. Res. Math. Educ. 24, 291–323. doi: 10.1080/14794802.2021.1991463
Cassar, J. A., and Musumeci, M. (2017). The influence of age, gender and subject choice on logical and lateral thinking skills in science students at secondary level. International conference new perspectives in science education, 6th Edition, Florence. Available at: https://www.um.edu.mt/library/oar/handle/123456789/84077
Ceglédi, T. (2015a). “Resilient teacher education students” in Professional calling in higher education. eds. G. Pusztai and T. Ceglédi (Nagyvárad & Budapest: Partium, PPS & Új Mandátum), 61–75.
Ceglédi, T. (2015b). “Felsőoktatás és társadalmi egyenlőtlenségek. Reziliens pedagógusjelöltek” in Szakmai szocializáció a felsőoktatásban. eds. G. Pusztai and T. Ceglédi (Nagyvárad & Budapest: Partium, PPS & ÚMK), 116–135.
Ceglédi, T. (2015c). Kulturális és gazdasági tőke a hallgatók családjaiban. In Pedagógusjelöltek oktatásszociológiai vizsgálata II., ed. G. Pusztai, T. Ceglédi, V. Bocsi, K. Kovács, Á. Dusa, and ZS. Márkus, et al. (Debrecen: CHERD-Hungary) 9–12.
Ceglédi, T. (2018). Ugródeszkán. Reziliencia és társadalmi egyenlőtlenségek a felsőoktatásban. Debrecen: Debreceni Egyetem – CHERD.
Crede, J., Wirthwein, L., McElvany, N., and Steinmayr, R. (2015). Adolescents’ academic achievement and life satisfaction: the role of parents’ education. Front. Psychol. 6. doi: 10.3389/fpsyg.2015.00052
Cresswell, C., and Speelman, C. P. (2020). Does mathematics training lead to better logical thinking and reasoning? A cross-sectional assessment from students to professors. PLoS One 15:e0236153. doi: 10.1371/journal.pone.0236153
Davis-Kean, P. E. (2005). The influence of parent education and family income on child achievement: the indirect role of parental expectations and the home environment. J. Fam. Psychol. 19, 294–304. doi: 10.1037/0893-3200.19.2.294
Dawkins, P. C., and Cook, J. P. (2017). Guiding reinvention of conventional tools of mathematical logic: students’ reasoning about mathematical disjunctions. Educ. Stud. Math. 94, 241–256. doi: 10.1007/s10649-016-9722-7
Dixson, D. D., Keltner, D., Worrell, F. C., and Mello, Z. (2018). The magic of Hope: hope mediates the relationship between socioeconomic status and academic achievement. J. Educ. Res. 111, 507–515. doi: 10.1080/00220671.2017.1302915
Dubinsky, E., and Yiparaki, O. (2000). On student understanding of AE and EA quantification. Res. Colleg. Math. IV, Providence, RI: American Mathematical Society. 239–289.
Durand-Guerrier, V. (2003). Which notion of implication is the right one? From logical considerations to a didactic perspective. Educ. Stud. Math. 53, 5–34. doi: 10.1023/A:1024661004375
Durand-Guerrier, V., and Dawkins, P. C. (2020). “Logic in university mathematics education” in Encyclopedia of mathematics education. ed. S. Lerman. 2nd ed (Cham: Springer), 481–485.
European Union. (2022). Education and training monitor 2022. Comparative report. European Comission: Directorate-General for Education, Youth, Sport and Culture, Luxembourg: Publications Office of the European Union.
Ferrari, P. L. (2004). “Matematical language and advanced mathematics learning,” in Proceedings of the 28th Conference of the International Group for the Psychology of Mathematics Education: PME 28, ed. M. J. Høines and A. B. Fuglestad Vol 2, Bergen: Bergen University College, 383–390.
Hazem, A. H. (2017). Using quantifiers in English university students: problems and strategies. Special Fifth Scientific Conference for the year 2017 --1 438 e Issue, 79–94. doi: 10.2139/ssrn.3881843
Hidayatullah, A., and Csíkos, C. (2023). The role of students’ beliefs, parents’ educational level, and the mediating role of attitude and motivation in students’ mathematics achievement. Asia-Pacific Edu Res. 32, 1–10. doi: 10.1007/s40299-023-00724-2
Hoidn, S., and Kärkkäinen, K.. (2014). Promoting skills for innovation in higher education: a literature review on the effectiveness of problem-based learning and of teaching Behaviours, OECD Education Working Papers, No. 100, OECD Publishing, Paris.
Kodippili, A. (2011). Parents’Education level in students’ mathematics achievement; do School factors matter? Academic Leadership The Online Journal 9 Spring. doi: 10.58809/HDJE3533
Kowalczuk-Walędziak, M., Menter, I., Sablić, M., and Valeeva, R. A. (eds.)(2023). “Setting the scene: the changing contexts of teacher education in central and eastern europe and beyond”, in The Palgrave Handbook of Teacher Education in Central and Eastern Europe. (Cham: Palgrave Macmillan), 3–24.
Kozma, T. (2010). “Felsőfokú oktatás és regionális átalakulás” in Régió és oktatás: a partium esete. eds. T. Kozma and T. Ceglédi (Debrecen: Center for Higher Educational Research and Development), 15–27.
Kozma, T, and Ceglédi, T (2010). Régió és oktatás: a Partium esete. Debrecen, CHERD-Hungary: Center for Higher Education Research and Development – Hungary [Region and education: the case of the Partium]
Lave, J. (1997). “The culture of acquisition and the practice of understanding” in Situated cognition: social, semiotic, and psychologyical perspectives. eds. D. Kirshner and J. A. Whitson (New Jersey: Lawrence Erlbaum Associates, Inc), 17–37.
Lave, J., and Wenger, E. (1991). Situated learning: legitimate Periperal participation. New York: Cambridge University Press.
Lazar, M. M. (2021). De la STEM la STEAM – O abordare inovatoare în cadrul proiectelor eTwinning ”. Revista educationala EDICT. Available at: https://edict.ro/de-la-stem-la-steam-o-abordare-inovatoare-in-cadrul-proiectelor-etwinning/ (Accessed September 2, 2023)
Luchenko, O., and Yurchenko, V. (2023). Entering the teaching profession in Slovakia. Educ. Challeng. 28, 113–127. doi: 10.34142/2709-7986.2023.28.1.09
Mirea, N., Robescu, D. F., Bogdea, C. F., and Carutasu, G. (2021). “Facts and figures about STEM education in Romania”, in Proceedings of the MakeLearn and TIIM International Conference. ed. V. Dermol (Bangkok, Celje, Lublin: ToKnowPress), Available at: https://www.toknowpress.net/ISBN/978-961-6914-27-7.pdf
Murtonen, M., and Balloo, K. (2019). Redefining scientific thinking for higher education higher-order thinking, evidence-based reasoning and research skills. Cham: Palgrave Macmillan.
Nagy, Z. (2015). “Szlovákia közoktatása és tanárképzési rendszere” in Tanárképzési háromszögek: iskolák, fenntartók és képzők együttműködése. Összehasonlító országtanulmányok. ed. M. Chrappán (Debrecen: Debreceni Egyetem), 165–190.
Nusche, D. (2008). Assessment of learning outcomes in higher education: a comparative review of selected practices OECD. Education Working Papers No. 15, EDU/WKP (2008) 2. doi: 10.1787/244257272573
Nyüsti, S., and Ceglédi, T. (2012). “Vándorló diplomások, diplomáért vándorlók – Elvándorlási mintázatok és azok magyarázata a felsőfokú tanulmányok és a végzés utáni letelepedés során” in Frissdiplomások 2011. eds. O. Garai and Z. Veroszta (Budapest: Educatio Társadalmi Szolgáltató Nonprofit Kft. Felsőoktatási Osztály), 173–207.
Perry, T., Morris, R., and Lea, R. (2022). A decade of replication study in education? A mapping review (2011–2020). Educ. Res. Eval. 27, 12–34. doi: 10.1080/13803611.2021.2022315
Prior, P., and Bilbro, R. (2012). “Academic enculturation: developing literate practices and disciplinary identities” in University writing: selves and texts in academic societies studies in writing. eds. M. Castelló and C. Donahue, vol. 24 (Bingley, UK: Emerald Group Publishing), 19–31.
Pusztai, G. (2011). A láthatatlan kéztől a baráti kezekig. Hallgatói értelmező közösségek a felsőoktatásban. Budapest: Új Mandátum.
Pusztai, G., and Ceglédi, T. (2015). Szakmai szocializáció a felsőoktatásban. A pedagógusképzés kihívásai a Kárpát-medencében. Nagyvárad, Budapest: Partium Könyvkiadó – Personal Problems Solution – Új Mandátum Kiadó
Pusztai, G., Hatos, A., and Ceglédi, T. (2012). “Foreword: what do we mean by the third Mission of higher education” in Third Mission of higher education in a cross-border region. eds. G. Pusztai, A. Hatos, and T. Ceglédi (Debrecen: Center for Higher EducationResearch and Development – Hungary), 4–14.
Ramírez-Uclés, I. M., and Ramírez-Uclés, R. (2020, 2020). Gender differences in visuospatial abilities and complex mathematical problem solving. Front. Psyhol. 11:191. doi: 10.3389/fpsyg.2020.00191
Róbert, P. (2004). “Iskolai teljesítmény és társadalmi háttér nemzetközi összehasonlításban” in Társadalmi riport 2004. eds. T. Kolosi, I. G. Tóth, and G. Vukovich (Budapest: TÁRKI), 193–205.
Roksa, J., and Arum, R. (2011). The state of undergraduate learning. Change 43, 35–38. doi: 10.1080/00091383.2011.556992
Saavedra, A. R., and Saavedra, J. E. (2011). Do colleges cultivate critical thinking, problem solving, writing and interpersonal skills? Econom. Educ. Rev. 30 2011, 1516–1526. doi: 10.1016/j.econedurev.2011.08.006
Seppälä, H., Lindblom-Ylänne, S., and Kallio, E. K. (2020). “Integrating epistemic knowledge and logical reasoning skills in adult cognitive development” in Development of adult thinking: interdisciplinary perspectives on cognitive development and adult learning. ed. E. K. Kallio (London: Routledge), 33–46.
Shavelson, R. J. (2007). Assessing student learning responsibly: from history to an audacious proposal. Change 39, 26–33. doi: 10.3200/CHNG.39.1.26-33
Shavelson, R. J., Zlatkin-Troitschanskaia, O., Beck, K., Schmidt, S., and Marino, J. P. (2019). Assessment of university students’ critical thinking: next generation performance assessment. Int. J. Test. 19, 337–362. doi: 10.1080/15305058.2018.1543309
Sobhanzadeh, M., Dharamsi, K., Strzalkowski, N., Zizler, P., and Roettger, E. (2021). Logic and the development of scientific competencies in first-year general education. Creat. Educ. 12, 2580–2593. doi: 10.4236/ce.2021.1211193
Star, J. R. (2021). In pursuit of a replication culture in mathematics education. Imp. Rep. Stud. Math. Educ. 1, 53–76. doi: 10.1163/26670127-01010003
Szarka, K., Fehér, Z., Jaruska, L., and Tóthová, Tarová E. (2021). “Investigation of the students’ solutions in tasks focused on selected elements of propositional logic in a scientific and mathematical context in teacher education”, in ICERI2021 Proceedings, 14th International Conference of Education, Research and Innovation. eds. L. G. Chova, A. L. Martínez, and I. C. Torres (Valencia: IATED Academy), 822–831. doi: 10.21125/iceri.2021.0256
Szarka, K., Fehér, Z., Jaruska, L., and Tóthová, T. E. (2022). Results of analysis of tasks solutions focused on selected elements of propositional logic in the context of science and mathematics subjects in the post-formal stage of cognitive development. Ad Alta 12, 157–161.
Tremblay, K., Lalancette, D., and Roseveare, D. (2012). “Assessment of higher education learning outcomes – AHELO – Feasibility Study Report” in Design and Implementation, Vol. 1 (OECD).
Tuononen, T., Hyytinen, H., Kleemola, K., Hailikari, T., Männikkö, I., and Toom, A. (2022). Systematic review of learning generic skills in higher education—enhancing and impeding factors. Front. Educ. 7:885917. doi: 10.3389/feduc.2022.885917
Ye, R., and Czarnocha, B. (2012). Universal and existential quantifiers revisited, PME36. Math. Teach. Res. J. 5. Taipei, Taiwan. Available at: https://commons.hostos.cuny.edu/mtrj/wp-content/uploads/sites/30/2018/12/v5n3-Universal-and-Existential-Quantifiers.pdf
Keywords: basic mathematical knowledge, logical operations, higher education, problem solving abilities, academic enculturation content
Citation: Debrenti E and Bordás A (2023) Basic logical operation skills and logical reasoning competences of university students in a Western region of Romania. Front. Educ. 8:1273602. doi: 10.3389/feduc.2023.1273602
Edited by:
Vanda Santos, University of Aveiro, PortugalReviewed by:
Tamás Kersánszki, Óbuda University, HungaryTimothy Fukawa-Connelly, Temple University, United States
Copyright © 2023 Debrenti and Bordás. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Andrea Bordás, Ym9yZGFzLmFuZHJlYUBwYXJ0aXVtLnJv