- 1Escola Básica Bernardino Machado, Joane-Vila Nova de Famalicão, Portugal
- 2Department of Integrated Studies on Literacy, Didactics and Supervision, Institute of Education, University of Minho, Braga, Portugal
- 3Research Center on Education (CIEd), Institute of Education, University of Minho, Braga, Portugal
- 4Department of Education and Psychology, University of Aveiro, Aveiro, Portugal
- 5CIDTFF—Research Center on Didactics and Technology in the Education of Trainers, University of Aveiro, Aveiro, Portugal
- 6Department of Mathematics, University of Trás-os-Montes e Alto Douro, Vila Real, Portugal
Over time, teaching materials, such as manipulatives, have acquired a key role in promoting students’ understanding of mathematical knowledge. These materials play an important resource in student learning, including a recreational role that promotes motivation and a dynamic role in the understanding of concepts in which students are involved in the learning activities. Based on these assumptions, this study aims to investigate the contribution of manipulative materials in the learning of geometric figures by elementary school students. Adopting a qualitative and interpretative approach, data were collected through students’ written records, and audio and video record of students’ activities. The results show that students explored, manipulated, and constructed representations of triangles, squares, rectangles, circles, and other geometric figures, distinguishing them from each other through shape and properties. In particular, through manipulation of shapes with manipulatives students realized that a square is a rectangle but the inverse is not true.
Introduction
The subject of mathematics, due to the inherent complexity of its concepts, has over time acquired a social status that distinguishes it from other subjects by the poor performance that students show in assessments at the national level (internal and external) and in studies that take place at international level (such as TIMSS and PISA). Such results tend to create a stigma around this subject, which often leads to the “avoidance” of effort and dedication to learning. Such a scenario requires mathematics teachers to implement strategies that promote students’ willingness to learn mathematics, from the earliest school years.
The teacher thus assumes a fundamental function in creating favorable environments for learning mathematical topics with appropriate strategies. Steffe and Thompson (2000) argue that concept formation in mathematics is essentially grounded in experience, making it possible to develop abstract thinking through experimentation. Therefore, in the early levels of learning, it is important to use means that promote this transition. Didactic materials, including manipulatives, are especially important as a means of facilitating meaningful learning of mathematical concepts and relationships (Reys, 1982; Ponte and Serrazina, 2000; Canals, 2001; Lorenzato, 2006; Hurst and Linsell, 2020), and Geometry in particular.
Several curriculum documents highlight that students should use materials in learning various Geometry concepts. The “Principles and Standards for School Mathematics” [National Council of Teachers of Mathematics (NCTM), 2000] emphasize that from an early age students develop visualization skills using concrete experiences and a variety of geometric objects. Geometry is therefore relevant for learning to mathematise reality and to make discoveries “with one’s own eyes and hands,” which fosters the development of mathematical thinking and visual reasoning. Geometry thus allows teachers to prioritize teaching by discovery through experimentation and manipulation, and—a determining contribution, as mentioned above—promoting students’ motivation. Students need to feel stimulated to explore, test, communicate, and discuss ideas and knowledge, and it is essential to involve students in their own learning and in the construction of their own knowledge. One way to promote students’ involvement in their own learning is through the use of manipulative materials because, through observing, searching, and reflecting, they acquire ways of organizing their own thinking and structuring their concepts. With these considerations as background, this study aims to investigate the contribution of manipulative materials to the learning of geometric figures by students of the first cycle of basic education.
The relevance of this work highlights the exploration of various concrete manipulatives by students in the early years of schooling, appealing to their playful and tactile dimension, learning by playing, and challenging them to build and deconstruct geometric figures. These activities, which interconnect informal and formal experiences, promote the development of visual perception capacities, considered essential for the student to understand the space around him.
Development of geometric thinking
In Portugal, the curriculum reference document “Essential Mathematics Learning for the 1st Cycle of Basic Education” regarding Geometry and Measurement, refers to “the importance of the students’ contact with a wide range of shapes, related to figures in space and in the plane, with which they produce several operations, composing and decomposing, establishing spatial relations” [Ministério da Educação e Ciência (MEC), 2021, p. 11]. Geometry involves ways of thinking and representing systems that are used to analyze spatial, physical, and imaginary environments that support the conceptualization of those systems (Battista, 2007). Indeed, Geometry provides a favorable context for the development of intuition and spatial visualization (e.g., Abrantes et al., 1999; Presmeg, 2006). For this reason, its study should begin with concrete experiences and gradually expand to more formalized processes in order to develop the capacity for logical organization of thought. Several researchers argue that to promote geometric thinking geometric activities carried out with students should involve the composition and decomposition of objects, rotating objects in the plane and in space, and exploring models and their spatial relationships (e.g., Gonzato et al., 2011; Veloso, 2012). This idea is very present in the type of concrete geometry addressed in the early years of schooling where objects are physical and the argumentation presented by students is of a perceptual nature, considering the first experiences on geometric topics are crucial in the way students sustain the development of their geometric skill (Clements and Battista, 1992; Clements and Sarama, 2000; Parzysz and Jore, 2002).
For Duval (1998, 2012), the study of Geometry involves three kinds of cognitive processes that accomplish specific epistemological functions: (i) Visualization processes, relating to the visual representation of a geometric statement, the exploration or heuristic of a complex geometric situation; (ii) Construction processes using tools, where construction can function as a model in which representative actions and observed results are related to the mathematical objects being represented; (iii) Reasoning processes in relation to discursive processes to extend knowledge, support argumentation and interpretation. Although these processes can be carried out separately, they are closely linked and their synergy is cognitively necessary for the promotion of geometric thinking. Kuzniak et al. (2018) reinforce this idea by mentioning four skills used to describe geometric thinking: reasoning; representation; visualization; and operationalization. Those authors also mention the role of activity with materials, including their manipulation, in the construction of mathematical concepts, visualization and spatial skills, language, and reasoning. Thus, in learning Geometry and the consequent development of geometric thinking, especially in the early years of schooling, the spatial ability (or spatial sense) is understood as a set of skills related to the way students perceive the World around them and their ability to interpret, modify, and anticipate transformations in objects (Levine et al., 2012).
The present study is based on the work of Frostig et al. (1989). Those researchers define visual perception as the ability to recognize and discriminate visual stimuli, and to interpret them by associating them with previous experiences. In addition to seeing a figure or object, an analysis and interpretation of what is seen is performed, establishing relationships with the observer and other objects. These authors highlight the role of language in visual perception skills and also consider the development of visual perception associated to an appropriate sensory-motor development. They identify five capacities of visual perception: visual motor coordination; figure-background perception; perceptual constancy; perception of position in space; and perception of spatial relations. Later, these capacities were expanded on by the work of Hoffer (cited in Del Grande, 1990), integrating visual discrimination and visual memory. The following table shows the seven visual perception capacities and the respective descriptors of the child’s activity (Table 1).
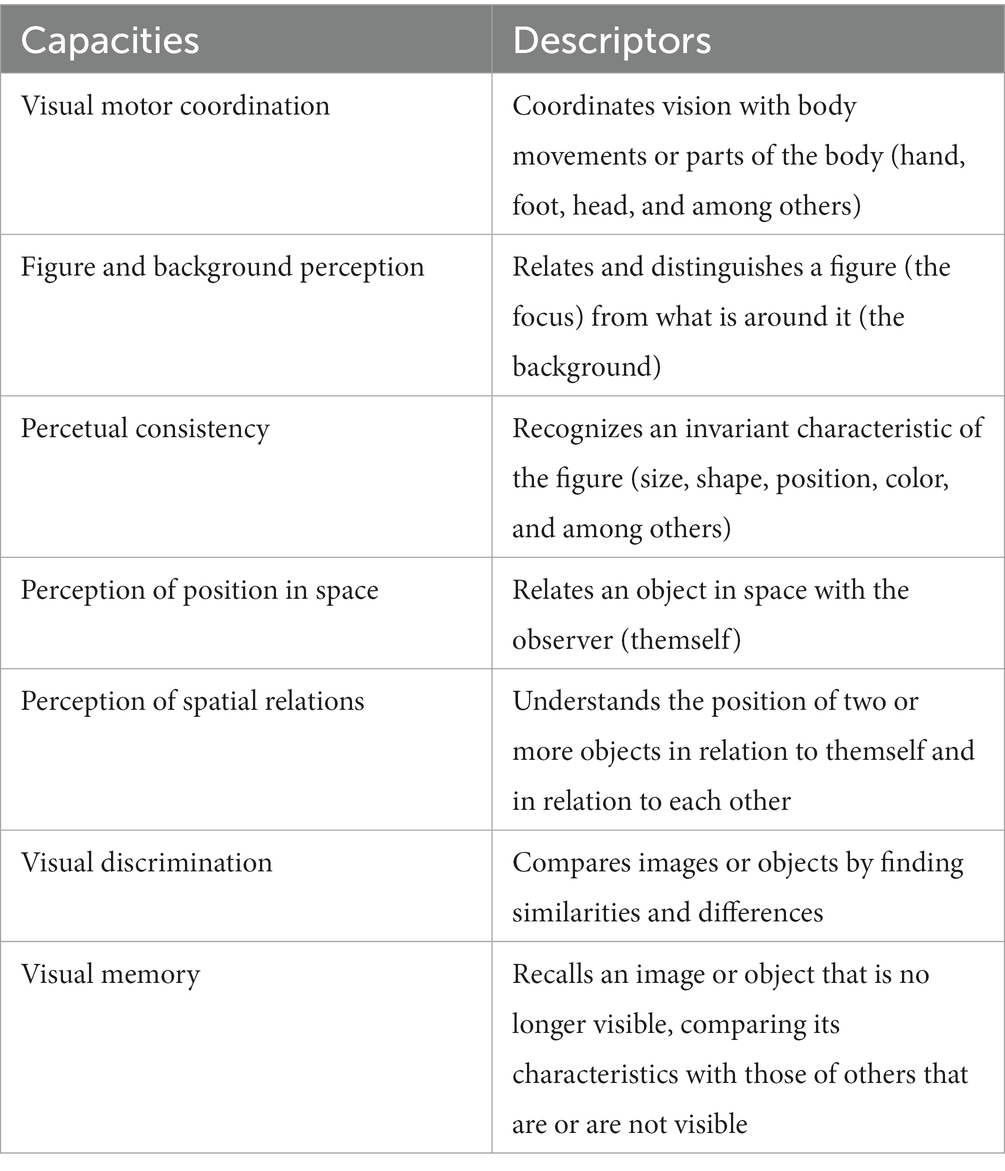
Table 1. Visual perception capacities (Frostig et al., 1989; Del Grande, 1990).
In order to analyze the development of geometric thinking, several theories have contributed to an understanding of the teaching and learning processes. van Hiele (1986, 1999) stands out for defining a precise description of the development of this thinking, structured by five descriptive and qualitative levels of geometric, sequential and hierarchical reasoning, as follows:
• Visualization or recognition, the student understands geometric figures in a global way by their appearance.
• Analysis, the student understands figures as a set of their properties and uses their components and attributes to describe and characterize them.
• Informal deduction or ordering, the student establishes relationships between properties both of a figure and between figures and orders them logically and hierarchically.
• Formal deduction, the student understands the meaning of deduction and Geometry is understood as an axiomatic system.
• Rigor, it is of all that which acquires a greater nature of abstraction, not necessarily involving, for that reason, concrete models. At this level axiomatic systems are studied.
It should also be noted that the van Hiele model allows aspects, such as recursion, sequentiality, language, continuity, and location to be used. These aspects will allow the development of geometric thinking skills.
Manipulatives in geometry learning
Geometry is an area favorable to the development of mathematical thinking since it is a privileged means to represent and give meaning to the world around us. In this sense, teaching Geometry promotes discovery and experimentation, and the development of students’ geometric thinking. One way to do this is through the use of manipulative materials that are often associated with the playful dimension of learning. These materials are part of a larger set called didactic materials, which Graells (2000) defines as all material that is created to facilitate teaching and student learning, classified into three categories: conventional materials, audio-visual materials, and new technologies. Manipulatives are considered by Graells (2000) to be conventional didactic materials, referring to them as being something that the student can manipulate in a physical way. A manipulative material is thus any concrete object that incorporates mathematical concepts, appeals to different senses, and can be touched, moved, rearranged, and manipulated by students (Graells, 2000). With similar reasoning, Swan and Marshall (2010) define a manipulative as “an object that can be handled by an individual in a sensory manner during which conscious and unconscious mathematical thinking will be fostered” (p. 14). More recently, Bartolini and Martignone (2020) consider that mathematics manipulatives are artifacts used in mathematics education that are manipulated by students to explore, learn, or investigate mathematical concepts or processes and to solve problems based on perceptual sensory evidence (e.g., visual, tactile). All of these definitions share the idea of mathematical experiences that allow the development of sensory skills, which are considered particularly relevant when learning Geometry.
Manipulatives are not exclusively concrete (physical). With advances in technology it is possible to visualize and manipulate virtually, leading to the emergence of the concept of virtual manipulatives, introduced by Moyer-Packenham et al. (2002). As a result of the technological evolution of this type of material and research associated with its use, in 2016, the same authors further developed the concept and presented an updated definition of virtual manipulatives: “an interactive, technology-enabled visual representation of a dynamic mathematical object, including all of the programmable features that allow it to be manipulated, that presents opportunities for constructing mathematical knowledge” (Moyer-Packenham and Bolyard, 2016, p. 13). In an effort to distinguish concrete manipulatives from virtual ones, Bartolini and Martignone (2020) define the former as “physical artifacts that can be concretely handled by students and offer a large and deep set of sensory experiences” (p. 486), and the latter as “digital artifacts that resemble physical objects and can be manipulated, usually with a mouse, in a similar way as their authentic, concrete counterparts” (ibid.). It is important to note that virtual manipulatives are technologies and like any technology, by themselves, do not provide learning. It is the quality of engagement that the student has with technology that presents opportunities for effective math learning (Moyer-Packenham and Bolyard, 2016).
One manipulative, whether concrete or virtual, cannot be considered better than another in educational terms, since its choice by the teacher depends on several factors, such as what is more available, what suits the students’ interests, but above all the teacher themself and the vision they have about mathematics and how students learn (Kamii et al., 2001; Bartolini and Martignone, 2020). Furthermore, one of the fundamental ideas about using manipulatives, both concrete and virtual, is that they play a key role in the construction of mathematical knowledge, but they should be considered as a means and never as an end (Batista and Clements, 1994; Clements, 1999; Simon, 2022). According to these authors, the nature of a manipulative, by itself, does not constitute a mathematical idea, and it is necessary to design rich and powerful mathematical tasks where the use of these materials can be integrated.
Methods
This study aims to investigate the contribution of manipulative materials to the learning of geometric figures by students of the first cycle of basic education. Given the nature of the research objective, we adopted a qualitative and interpretive approach in order to understand the meaning of student activity in the classroom context (McMillan and Schumacher, 2014).
Participants
In this study, one of the authors conducted a teaching experiment in the first grade class of a Portuguese primary school located in a predominantly urban area, focusing on the exploration of manipulatives, and with a duration of two lessons. The class consisted of 20 students, aged 6, of which 10 students were female and 10 were male. The class was heterogeneous since it included students with different learning abilities and paces, and no students with special educational needs. Of the 20 students in the class, 15 stated that they like the subject of mathematics and five that they did not like it, mainly because they considered that “the exercises are difficult,” “they do not like to do math,” or because “we only learn small numbers.” Regarding the students’ performance in their favorite subjects (Mathematics, Portuguese, or Environmental Studies) throughout the three terms of the school year, only one student received “Satisfactory” and “Insufficient” marks in Mathematics and Portuguese with the other students classified as “Good” and “Very Good.”
Procedures
The teaching experiment was guided by indicators concerning the role of the student, the role of the teacher, and the use of manipulatives (Figure 1).
Based on these principles, the learning activities on geometric figures involved the exploration of manipulatives in solving the proposed tasks.
Data were collected from the audio and video recording of the lessons taught and the written records that the students produced.
Method of analysis
The analysis of the data was based on the content analysis of the activities carried out by the students, some of them recorded in the form of dialogs resulting from their interaction with the teacher, following the works of Del Grande (1990) and Duval (1998, 2012). The information was analyzed using the following dimensions of analysis: (i) Figure background perception/perceptual constancy; (ii) Visual discrimination/visual memory; and (iii) Construction/composition and decomposition.
Results
The presentation of the results is based on an analysis and interpretation of the information that integrates each of the defined dimensions of analysis.
Figure background perception/perceptual constancy.
In the study of geometric figures, students were challenged to solve Task 1 aiming to understand the notion they had informally learned about some of these figures.
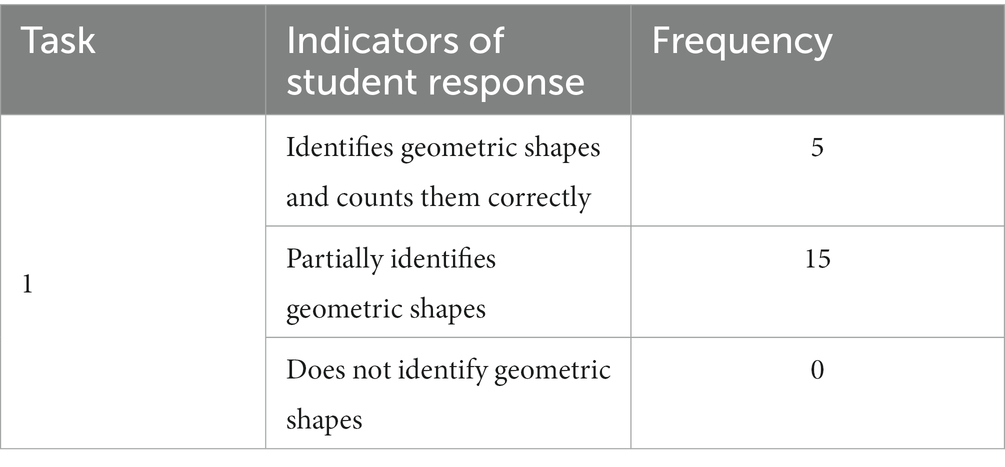
TASK 1 Identify the geometric shapes contained in the Pinocchio’s image.
Student responses were analyzed according to the following criteria: (i) Identifies geometric shapes and correctly counts them; (ii) Partially identifies geometric shapes; and (iii) Does not identify geometric shapes (Table 2).
From the answers given by the students to the proposed task it can be seen that most of them do distinguish geometric figures, partially identifying the geometric figures that make up the Pinocchio image. However, Table 2 also shows that only five students identified all of the geometric shapes that make up the Pinocchio image (Task 1), which reveals difficulties in figure-background perception capacity. Not all students were able to recognize the invariant characteristic of the rectangle figure (size, position, and color), that is they could not identify all the rectangles contained in Pinocchio’s “body.” The same happened with the triangular and circular shapes, denoting difficulties in terms of perceptual constancy.
After Task 1 was completed, the children heard a story called “The forest of plane figures” (Hall, 2009) whose content was based on geometric figures and their characteristics. During the large group discussion of the story, most students associated the geometric figures with real situations in their everyday lives, as can be seen in the following dialog:
Teacher:What is this story about?
Student:It is about geometric figures.
Teacher:And what geometric figures are those?
Student:They are triangles.
Student:Rectangles.
StudentIt also talks about squares.
Student:Is that all?
Student:Ah, and circles.
Student:Yes, our face is a circle.
When the student states that “our face is a circle” they recognize the geometric figure circle globally by the appearance of the face, which, according to van Hiele, reveals that they are at the visualization level of geometric thinking. In addition to activities to identify geometric figures, students were provided with opportunities to build them. To this end, students verified with dynamic manipulation that the physical structure of the material changes as it is deformed by those who manipulate it (Figure 2).
According to Lorenzato (2006), the manipulation and construction of geometric figures by students facilitates the perception of shape and geometric properties and the realization of rediscoveries, as illustrated in the following dialog:
Teacher:Can you say what the sides of a figure are?
Student:They are these parts here [pointing to the sides of a square].
Teacher:Yes, very good. These [pointing to the sides] are the sides. So how many sides do you have to shape to make a square?
All:Four!
Teacher:So how many sides does a square have?
Student:It has four sides.
TeacherDo you know what this is called?
Student:They are the corners.
Student:These are the corners.
Teacher:These “beaks” or “corners” are called vertices. How many vertices did you have to shape to make a triangle?
Student:Three vertices because it has three peaks.
Teacher:When you built the circle how many vertices and how many sides did you shape?
Student:The circle is round, it has zero sides and zero vertices.
The construction of geometric figures allowed students to establish the characteristics of these figures, such as the fact that the triangular shape has “three dots.” In terms of the capacity indicators, this activity and the previous one analyzing the figures in Pinocchio’s image fostered the promotion of figure-background perception and perceptual constancy, translated below in terms of respective descriptors:
• Relates and distinguishes various geometric figures (the focus) from what is around them (the background—the Pinocchio image).
• Correctly counts different figures.
• Recognizes the invariant characteristic of the rectangle figure (size, position, and color).
• Recognizes the invariant characteristic of the triangle figure (size, shape, position, and color).
• Recognizes the invariant characteristic of the circle figure (size, shape, position, and color).
Visual discrimination/visual memory
After the resolution of Task 1 and the class discussion on the “The forest of flat figures” story, the experiment focused on a free exploration of the logic blocks. This allowed students to become familiar with the material, interact and share ideas (Rêgo and Rêgo, 2006; Figure 3).
Once the free exploration of the material logic blocks was over, students were asked to solve Task 2 described below.
TASK 2 Exploration of the Logic Blocks.
In solving the first question of this task, all students correctly placed the logic block pieces in their corresponding groups, as illustrated by the following dialog:
Teacher:Where do I put this geometric figure? [holds up a square]
Student:That is a square so it is in the place of squares.
Teacher:Do I put it together with the rectangles?
Student:No, not there!
Student:That is the place of rectangles.
Teacher:A square is also a rectangle, only special. Can you tell what the difference between the two is?
Student:The sides.
Teacher:How many sides [pointing to sides] does a rectangle have? And a square?
Student:Four.
Student:Four and four.
Student:What will be the difference then?
Student:The square has these parts [pointing to the sides] all the same.
Teacher:Yes, very good, the sides are all the same.
Student:So a square is a rectangle only special because the sides are all the same.
Initially, the students were confused by the fact that a square is also a rectangle, however when asked about the difference between them they stated that the sides (“these parts”) are “all the same” in the square. At an early stage, children should be encouraged to express their geometric understandings with their own vocabulary (Crowley, 1987).
In response to the question 2 of Task 2 (Build figures with the logic blocks and count geometric shapes), students built representations of a train and Pinocchio (inspired from Task 1), and counted the geometric figures in the constructions (Figure 4).
The manipulation and observation sparked the students’ interest and curiosity about the properties of geometric figures, as the following dialog shows:
Teacher:Can you say what the sides of a figure are?
Student:They are these parts here [pointing to the sides of a square].
Teacher:Yes, very good. These [pointing to the sides] are the sides.
Teacher:So how many sides does a square have?
Student:It has four sides.
Teacher:Do you know what this is called? [pointing to vertices].
Student:Those are the corners.
Student:These are the corners.
Teacher:These “peaks” or “corners” are called vertices.
Student:Three vertices because it has three beaks.
Teacher:And the circle, how many vertices and how many sides does it have?
Student:The circle is round; it has zero sides and zero vertices.
Students showed they have acquired the capacity of visual discrimination (Del Grande, 1990), which can be seen in the moments when they are able to classify a set of objects according to a certain attribute, in this case the shape, according to the number of sides and vertices.
In question 3 of Task 2, students were asked about everyday objects that they associate with geometric shapes.
Teacher:As you said, the clock looks like a circle. Do you know any other objects from our everyday life that you associate with geometric figures?
Student:Yes, a slice of pizza looks like a triangle.
Student:And a whole pizza looks like a circle.
Student:A ruler.
Teacher:What does a ruler look like?
Student:A rectangle.
Teacher:What else?
Student:A sheet of paper also looks like a rectangle.
Student:So does a window.
Teacher:And what does the square look like?
[silence]
Teacher:So, you do not remember anything?
Student:No.
In the examples presented by the students, given their young age, the researcher felt that it was not appropriate to distinguish two-dimensional figures from three-dimensional figures. For learning to be meaningful, students must be able to relate to it.
To make the poster in question 4 of Task 2 students were distributed into four groups and each group was assigned a geometric figure and various representations of everyday objects. The correspondence between the geometric shape and the objects was evidenced in a poster (Figure 5).
To synthesize what they had learned about the shape of the geometric figures under study students were asked to solve Task 3, which consisted of verbally describing shapes and properties using appropriate language to develop their visual memory capacity.
TASK 3
In an opaque bag are triangles, rectangles, squares and circles. You are asked to remove one each of the requested shapes from the bag without looking. What will you do to know that the piece you are removing is the one you want?
Students were able to correctly draw the intended figure, as well as correctly describe it by stating its characteristics:
Teacher:I want you to draw a square.
[student looks for the geometric figure in the bag using touch]
Teacher: What are you feeling [with your hands] to know whether you remove a square or not?
Student:I am looking for four vertices.
Teacher:And what else?
Student:Four sides that all have to be equal.
Teacher:OK.
Student:[removes desired piece] I got it!
Teacher:So what features does the square have?
Student:It has four vertices and four sides that are all the same.
The tactile perception of some characteristics of geometric figures was complemented by their visual translation through an activity called “Geometric Twister” performed in a large group outside of the classroom. In this activity, students had to place their hands or feet on a mat that contained the geometric figures already discussed (Figure 6), also working on memory about laterality concepts (left and right).
Teacher:[Right foot on square] You chose that geometric figure as being a square. What reasons make you think that?
Student:Because a square has four sides.
Teacher:A rectangle also has four sides.
Student:But they are not all equal and to be a square they all have to be equal.
Teacher:“Right hand on rectangle.”
[students picks a square]
Teacher:What reasons make you choose that geometric figure?
Student:Oh teacher, a square is also a rectangle, only special.
This activity showed that the students recognized the geometric shapes, independently of size and position, which allowed them to verify their capacity of visual discrimination and visual memory of the figures, supported by empirical indicators for these capacity:
• Compares the various shapes of the logic block pieces, finding similarities, and differences.
• Compares constructions of geometric figures and identifies similarities and differences (identifies “peaks”).
• Identifies similarities between geometric shapes and everyday objects.
• Recalls a picture or object that is no longer visible, comparing its features with those of others that are or are not visible.
• Recognizes a non-visible flat figure by its shape (appealing to other sensory perception).
Construction/composition and decomposition
For the construction of geometric figures, students began by exploring the Geoplane in constructing a triangle (Figure 7).
In order to understand if students identified triangles from their characteristics and not by memorization, the teacher engaged the students in dialogs such as the following:
Teacher:So what geometric figure did you construct?
Student:A triangle.
Teacher:Why is it a triangle?
Student:Because it has three beaks [pointing to the vertices].
Teacher:Beaks? Yesterday we learned what these ‘beaks’ are called. Do not you remember?
Student:Ah, the vertices.
Teacher:That is right. And what else makes you say it is a triangle?
Student:The three sides.
Teacher:[rotates Geoplane 90°] And this, which geometric figure is it?
Student:It is still a triangle.
Teacher:[turns the Geoplane 90°] And now?
Student:It is the same, a triangle.
Teacher:If you are always rotating the Geoplane, what figure do we always get?
Student:It is always a triangle both like this, like this, like this [student rotating the Geoplane].
Following Duval (1998), we can see in the previous dialog that the representation of triangles using the Geoplane supports the process of visualization of their characteristics, as seen in the students’ arguments, allowing the expansion of geometric knowledge about the triangular figure. This was followed by the construction of triangles with the student’s choice of Tangram pieces (Figure 8). The challenge consisted of experimenting if students could get a new triangle from either two triangle pieces, or one square piece and one triangle piece.
According to the National Council of Teachers of Mathematics (NCTM) (2014), effective mathematics teaching should involve using relevant questions to evaluate and enhance students’ sense-making about mathematical ideas and relationships.
Teacher:What pieces did you use to build a triangle?
StudentTwo triangles.
Teacher:Explain to me how you did it.
Student:I thought and went like this, went like this [rotating the pieces] and I put two pieces together like this and it became a triangle like this.
Teacher:And how many sides does this triangle have?
Student:1, 2, 3 [points to sides] it has three.
Teacher:And how many vertices does it have?
Student:It has three too.
We proceeded in the same way for the construction of the rectangle and the square (Figure 9).
When constructing rectangles on the Geoplane, some students were asked what characteristics they identified in this figure.
Teacher:What geometric figures did you build?
Student:Rectangles.
Teacher:What can you tell me about these rectangles? What features do you find?
Student:They have four vertices and four sides.
Teacher:And is this geometric figure a rectangle? [Pointing to a square]
Student:Yes, a square is also a rectangle.
In order to translate these characteristics, the students were asked to construct rectangles by composition with Tangram pieces (Figure 10).
Student:It is done.
Teacher:What figure did you build with Tangram?
Student:A rectangle.
Teacher:And what pieces did you use?
Student:I used a triangle, a triangle and a square [pointing to the corresponding pieces].
Teacher:And how many sides does this rectangle have?
Student:Four.
Teacher:And how many vertices does this rectangle have?
Student:Four vertices.
The aim of constructing squares on the Geoplane (Figure 9) was for students to discover that all sides are equal because they have the same length. Simply saying that they were all the same could be due to memorization, as the below excerpt from a dialog with a student about their constructions illustrates.
Teacher:What geometric figures did you build?
Student:Squares.
Teacher:What makes you say they are squares?
Student:Because they have four vertices.
Teacher:And what else do they have?
Student:They have four equal sides.
Teacher:And how do you know that the sides are equal?
Student:Because this side is equal to this side and this side and this side.
Teacher:And how do you know that they are equal?
Student:This one has 1, 2, 3, 4…this one has 1, 2, 3, 4, this one too and this one too [pointing to the sides]. They all have four [pins]
As the pins served as guides for the student’s construction of the squares on the Geoplane, they were then asked to construct squares using the Tangram pieces instead (Figure 11).
During this construction, students were asked whether the characteristics they had identified with the constructions on the Geoplane still held:
Teacher:What figure did you build with the Tangram pieces?
Student:A square
Teacher:And what pieces did you use?
Student:A triangle and another triangle.
Teacher:Explain to me how you did it.
Student:By joining this one here [pointing to a side] with this one here and make a triang…square!
Teacher:And how many sides does this square have?
Student:Four.
Teacher:And how many corners does it have?
Student:Four.
These activities allowed students to explore various situations, taking advantage of the dynamic nature of the Geoplane and Tangram. These manipulatives enhance exploration and discussion of the characteristics of geometric shapes rather than memorization of their names.
After the constructions, students were given moments to reflect on what they had accomplished by moving from the Geoplane construction to dotted paper (Figure 12).
Overall, the students showed no difficulty in moving from constructions of rectangles and squares to dotted paper. Although the line was not very firm, their reproduction on the dotted paper was faithful to the construction on the Geoplane. For triangles, the transition to dotted paper from the construction on the Geoplane was more difficult and their reproduction on the dotted paper was not faithful to their construction on the Geoplane, although the students displayed concern in joining ‘pin’ to ‘pin’ when drawing the proposed figures. Regarding Tangram, Figure 13 illustrates some of the students’ reproductions on paper of their Tangram constructions.
In the representation of triangles, squares and rectangles on paper, in general students do not present difficulties despite an often imprecise line, and their reproduction is faithful to the constructions with Tangram. Moving to paper is a way for students to reflect on what they have learned and go beyond simple manipulation. In the activities performed, students distinguish geometric shapes in any position and of any size by enumerating their properties, developing their capacity of construction and composition and decomposition of geometric figures, through the following indicators:
• Builds triangles, squares and rectangles using the Geoplane.
• Identifies characteristics of a triangle.
• Composes figures to obtain other figures using Tangram pieces.
• Reproduces on paper the figures built on the Geoplane and with Tangram.
• Identifies the square as a particular case of rectangle.
The above activities, involving the construction and composition/decomposition of figures, supported geometric thinking about various plane figures (Gonzato et al., 2011; Veloso, 2012). For example, the construction of a square using two triangles involved a certain composition from the student: placing the two triangles so that the new figure had all equal sides and right angles (Figures 13C,D). For constructing a triangle, on the other hand, those same pieces needed a different arrangement (Figures 13A,B). In the construction of the rectangle (in the example shown in the same image) the student used three Tangram pieces, one square and two triangles, with a specific composition of these pieces (Figures 13E,F). The dialog presented by the students was supported by the drawing of the parts used.
Conclusion
The analysis and interpretation of the information coming from the dialogs between students and teacher, and the productions obtained during the teaching experience make it possible to highlight the activities that the students carried out with the manipulatives in the learning of geometric figures. The phase of exploration with manipulatives was pertinent to promote mathematical communication, alluding essentially to students’ previous ideas for the development of understandings, as their initial explanations were not always explicit and organized. In general, students appealed to their formal and informal knowledge about the geometric shapes explored. Based on this knowledge, students interpreted images, understood stories and constructed concepts. The enhancement of natural motivation, curiosity and enthusiasm were determining factors for the students to be involved in the activities developed (Coll et al., 2001).
The students began exploring manipulatives (logic blocks, tangram, and geoplane) in a free and spontaneous way, which proved to be a privileged moment to become familiar with the materials, and was crucial to activate previous knowledge about geometric figures. This free exploration served as a starting point for the subsequent exploration of more guided activities. Students subsequently performed activities aimed at discovering the characteristics of the geometric figures studied, promoting the formation of the concept image (Duval, 2012). The learning environment provided by the use of manipulatives favored the acquisition of aspects of visual perception (Frostig et al., 1989; Del Grande, 1990), in particular: relate and distinguish various geometric figures from their surroundings; recognize invariant characteristics (size, shape, position, and color) of the triangle, rectangle and square; understand the hierarchy square, rectangle; compare the various shapes of the pieces of manipulative material used, identifying similarities and differences and establishing links with everyday objects; recognize a geometric shape not visible by touch.
The Tangram was used to perform decomposition and composition activities of geometric figures, which were accompanied by representation on paper, resulting in a reinforced appropriation of the figures’ characteristics. Additionally, the composition and decomposition of geometric figures supported and promoted the development of the students’ visualization of shapes, confirming the results of previous studies (e.g., Duval, 1998, 2012; Presmeg, 2006; Gonzato et al., 2011).
As a consequence of the exploration of manipulative materials, students were challenged to reflect on the content covered, showing evidence of sharing and discussion of ideas. They carried out activities that appealed to the visual memory and senses, such as touch, in the characterization of geometric figures. The materials played a significant role in the learning of geometric figures by providing concrete representations, appealing multiple senses, promoting geometric thinking, the collaboration, and the communication.
Even though we live in a society where technology is essential and, consequently, the use of virtual manipulatives in school is a natural development, this study highlights the relevance of the use of concrete manipulatives by students in the early years of schooling. These provide physical manipulation, visualization of different characteristics through sensory-motor experiences (Del Grande, 1990), giving meaning to the formation of abstract concepts and serving as a link to virtual environments expected in a 21st century school (Simon, 2022). The didactic knowledge that comes from revisiting studies with concrete manipulatives enhances future work that connects this knowledge with didactic approaches that integrate virtual manipulatives.
The revisiting of the use of concrete manipulatives in the classroom context compares the mathematical activities carried out in the Elenic civilization, as shown in the Socratic dialogs and in the Pythagorean school, and the activities carried out in today’s world, increasingly digital, with emphasis on the use of virtual manipulatives. This comparison leads us to consider that the joint exploration of concrete manipulatives and virtual manipulatives increases the understanding of the meaning of mathematical objects under study.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
RP and FV: conceptualization, methodology, and writing—original first version. RP, FV, TN, and AA: literature review, data analysis presented, and writing—review and editing. RP: data collection.
Funding
This work is funded by CIEd—Research Center on Education, Institute of Education, University of Minho, projects UIDB/01661/2020 and UIDP/01661/2020, through national funds of FCT/MCTES-PT. And this work was financially supported by National Funds through FCT – Fundação para a Ciência e a Tecnologia, I.P., under the project UIDB/00194/2020 (CIDTFF).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abrantes, P., Serrazina, L., and Oliveira, I. (1999). A Matemática na Educação Básica. Lisboa: Ministério da Educação.
Bartolini, M. G., and Martignone, F. (2020). “Manipulatives in mathematics education” in Encyclopedia of Mathematics Education. ed. S. Lerman (Cham: Springer)
Batista, M., and Clements, D. H. (1994). Computer environments for learning geometry. J Educ Comput Res 10, 173–197. doi: 10.2190/8074-298A-KTL2-UQVW
Battista, M. (2007). “The development of geometric and spatial thinking” in Second Handbook of Research on Mathematics Teaching and Learning. ed. F. K. Lester (Greenwich: Information Age Publishing), 843–908.
Clements, D. H. (1999). Concrete manipulatives, concrete ideas. Contemp Issues Early Child 1, 45–60. doi: 10.2304/ciec.2000.1.1.7
Clements, D. H., and Battista, M. (1992). “Geometry and spatial reasoning” in Handbook of Research on Mathematics Teaching and Learning. ed. D. A. Grouws (MacMillan), 420–464.
Clements, D. H., and Sarama, J. (2000). Young children’s ideas about geometric shapes. Teach Child Math 6, 482–488. doi: 10.5951/TCM.6.8.0482
Coll, C., Martín, E., Mauri, T., Miras, M., Onrubias, J., Solé, I., et al. (2001). O construtivismo na Sala de Aula: Novas Perspetivas Para a Ação Pedagógica. Porto: Edições Asa.
Crowley, M. (1987). “The van Hiele model of development of geometric thought” in Learning and Teaching Geometry, K-12. ed. M. M. Lindquist (Reston, VA: National Council of Teachers of Mathematics), 1–16.
Duval, R. (1998). “Geometry from a cognitive point of view” in Perspectives on the Teaching of Geometry for the 21st Century: an ICMI study. eds. C. Mammana and V. Villani (Dordrecht: Kluwer)
Duval, R. (2012). Abordagem cognitiva de problemas de geometria em termos de congruencia. Rev Eletrôn Educ Matem 7, 118–138. doi: 10.5007/1981-1322.2012v7n1p118
Frostig, M., Horne, D., and Miller, A. (1989). Figuras y Formas: Programa Para el Desarollo de la Percepción Visual. Madrid: Editorial Medica Panamericana.
Gonzato, M., Godino, J. D., and Neto, T. (2011). Evaluación de conocimientos didáctico-matemáticos sobre la visualización de objetos tridimensionales. Educ Matem 23, 5–37.
Hurst, C., and Linsell, C. (2020). Manipulatives and multiplicative thinking. Eur J STEM Educ 5:4. doi: 10.20897/ejsteme/5808
Kamii, C., Lewis, B. A., and Kirkland, L. (2001). Manipulatives: when are they useful? J Math Behav 20, 21–31. doi: 10.1016/S0732-3123(01)00059-1
Kuzniak, A., Richard, P. R., and Michael, P. (2018). “From geometrical thinking to geometrical working competencies” in Developing Research in Mathematics Education—Twenty Years of Communication, Cooperation and Collaboration in Europe. eds. T. Dreyfus, M. Artigue, D. Potari, S. Prediger, and K. Ruthven (London: Routledge), 1–20.
Levine, S. C., Ratliff, K. R., Huttenlocher, J., and Cannon, J. (2012). Early puzzle play: a predictor of preschoolers' spatial transformation skill. Dev Psychol 48, 530–542. doi: 10.1037/a0025913
Lorenzato, S. (2006). “Laboratório de ensino da matemática e materiais didáticos manipuláveis” in O Laboratório de Ensino da Matemática na Formação de Professores. ed. S. Lorenzato (Campinas: Autores Associados), 3–38.
McMillan, J., and Schumacher, S. (2014). Research in Education Evidence-Based Inquiry. Harlow: Pearson Education Limited.
Ministério da Educação e Ciência (MEC) (2021). Aprendizagens Essenciais de Matemática para o Ensino Básico. Ministério da Educação, Direção Geral da Inovação e Desenvolvimento Curricular.
Moyer-Packenham, P., and Bolyard, J. (2016). “Revisiting the definition of a virtual manipulative” in International Perspectives on Teaching and Learning Mathematics With Virtual Manipulatives. ed. P. Moyer-Packenham (Logan, UT: Springer), 3–23.
Moyer-Packenham, P., Bolyard, J., and Spikell, M. (2002). What are virtual manipulatives? Teach Child Math 8, 372–377. doi: 10.5951/TCM.8.6.0372
National Council of Teachers of Mathematics (NCTM) (2000). Principles and standards for school mathematics. Reston, VA: NCTM.
National Council of Teachers of Mathematics (NCTM) (2014). Principles to Actions, Ensuring Mathematical Success for All NCTM.
Parzysz, B., and Jore, F. (2002). “What is geometry for French pre-service elementary schoolteachers?” in Proceedings of the 26th PME Conference I: 218.
Ponte, J. P., and Serrazina, L. (2000). Didáctica da Matemática no 1.° Ciclo. Lisboa: Universidade Aberta.
Presmeg, N. C. (2006). “Research on visualization in learning and teaching mathematics” in Handbook of Research on the Psychology of Mathematics Education: Past, Present and Future. eds. A. Guitierrez and P. Boero (Roterdam: Sense Publishers), 205–235.
Rêgo, R., and Rêgo, R. (2006). “Desenvolvimento e uso de materiais didáticos no ensino de matemática” in Laboratório de Ensino de Matemática na Formação de Professores. ed. S. Lorenzato (Campinas: Autoes Associados), 39–56.
Reys, R. (1982). “Considerations for teaching using manipulative materials” in Teaching Made Aids for Elementary School Mathematics. (Reston, VA: NCTM)
Simon, M. A. (2022). Contributions of the learning through activity theoretical framework to understanding and using manipulatives in the learning and teaching of mathematical concepts. J Math Behav 66:100945. doi: 10.1016/j.jmathb.2022.
Steffe, L. P., and Thompson, P. W. (2000). “Teaching experiment methodology: underlying principles and essential elements” in Research Design in Mathematics and Science Education. eds. R. Lesh and A. E. Kelly (Hillsdale, NJ: Erlbaum), 267–307.
Swan, P., and Marshall, L. (2010). Revisiting mathematics manipulative materials. Aust Prim Math Classr 15, 13–19.
van Hiele, P. M. (1986). Structure and Insight—A Theory of Mathematics Education. Orlando: Academic Press.
Keywords: manipulative materials, first grade students, geometry learning, geometric thinking, visual perception
Citation: Ponte R, Viseu F, Neto TB and Aires AP (2023) Revisiting manipulatives in the learning of geometric figures. Front. Educ. 8:1217680. doi: 10.3389/feduc.2023.1217680
Edited by:
Khathibul Umam Zaid Nugroho, State University of Semarang, IndonesiaReviewed by:
Wahyu Widada, University of Bengkulu, IndonesiaAbdurrobbil Falaq Dwi Anggoro, Siliwangi College of Education Bandung, Indonesia
Copyright © 2023 Ponte, Viseu, Neto and Aires. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Floriano Viseu, ZnZpc2V1QGllLnVtaW5oby5wdA==
 Rita Ponte1
Rita Ponte1 Floriano Viseu
Floriano Viseu Teresa B. Neto
Teresa B. Neto Ana Paula Aires
Ana Paula Aires