What’s mathematics doing here? The role of mathematics in German Physics Olympiad tasks

Physics competitions target at motivating students for engaging in physics and at promoting students talented in physics. Physics competitions also aim at conveying a picture of physics as a scientific discipline, going beyond regular physics classes in school, and should thus also include a more intense mathematization of physics problems. Given that physics students often struggle with mathematics, mathematics in the competition may pose a challenge beyond the intended physics challenge. The present paper therefore presents an analysis of theoretical tasks employed in the German Physics Olympiad. Mathematical requirements were (1) identified by analyzing sample solutions and (2) compared to mathematics curricula. Then, (3) the solutions were categorized regarding whether the mathematics employed was used in a tool-like manner, a structuring manner, or both. Findings indicate that the first competition round typically includes rather basic mathematical requirements which are addressed in lower secondary mathematics education. In the higher rounds, more advanced mathematics is needed, which is only taught in the last years of high school, or not taught at all. The structural role of mathematics proved to be essential in the analyzed tasks. Beside the (intended) physics challenges, participants thus have to deal with mathematics they have not learned at school and have to apply mathematics in a different way than is often done at school when participating in the competition. As a consequence, unintended negative effects may occur, potentially counteracting the aim to promote students talented in physics. Implications for science education and future research are discussed.

1. Introduction

Given the reported decline of students’ interest in science (e.g., Potvin and Hasni, 2014), various programs aim at increasing students’ interest and motivation for science and at fostering talented students in these fields. Competitions in STEM subjects are one means to identify and foster talented students thought to ensure a sufficient amount of highly qualified scientific and technical personnel and thus economic growth and wealth. Competitions are expected to attract extraordinarily talented students, to develop their talent, and “once developed, this talent is expected to contribute to society” (Campbell and Walberg, 2010, p. 8). International competitions (e.g., the International Biology, Chemistry, and Physics Olympiads) bring together top students in their respective domains from countries around the world to compete against each other and to get to know other students with similar interests. In the field of Physics, the International Physics Olympiad (IPhO) is the most prominent international competition with a 50-year-long tradition and participants from more than 80 countries (Gorzkowski and Tichy-Rács, 2010). Student delegations are usually selected through national Olympiad programs of one or more selection stages (Petersen and Wulff, 2017).

In Germany, the delegation for the IPhO is selected by a four-staged selection process, the so-called German Physics Olympiad (GPO). Presumably, the GPO can hardly do without mathematics as it aims to communicate a picture of physics which goes beyond regular physics classes at school. However, it is unclear whether mathematics in the competition may pose a challenge beyond the intended physics challenge. Students could get demotivated by struggling with mathematics when expecting to do physics. The present paper therefore aims at addressing this research gap and reports about a study, which (1) identified the mathematical requirements by analyzing GPO sample solutions, (2) compared them with school mathematics curricula as indicators for the mathematical knowledge which can be expected by the participants, and (3) examined if the requirements rather addressed a technical or a structural role – the two roles mathematics can take in physics (Uhden et al., 2012).

2. The role of mathematics in physics

“The description of physical processes by mathematical means is one of the most characteristic traits and most powerful tools of physics research” (Pospiech et al., 2015, p. 1). When solving physics tasks, mathematics can take a “technical role” (Uhden et al., 2012, p. 493) and a “structural role” (Uhden et al., 2012, p. 493). The technical role of mathematics refers to the “tool-like use of mathematics” (Uhden and Pospiech, 2011, p. 219). Solving physics tasks typically includes such purely mathematical calculations not connected to the phenomenon itself, for example, when polynomials are differentiated, or when an equation is rearranged into an equivalent form. In physics education, the technical role of mathematics is often quite obvious, so that mathematics is regarded a prerequisite for physics (e.g., Uhden et al., 2012; Pospiech et al., 2015; Hertel and Großmann, 2016): “[M]athematical skills alone are not sufficient to guarantee success in physics, but … unless the student has the mathematical skills, the performance in the physics will be poor” (Hudson and McIntire, 1977, p. 470). The technical role often leads students to view “mathematics as a mere tool to quantify entities and express relations between them” (Karam, 2014, p. 010119–1) and to employ a “Recursive Plug-And-Chug Game” (Tuminaro and Redish, 2007, p. 020101–7) to solve physics tasks, that is they choose the physics equations based on the givens and the unknowns and calculate some value, regardless of the physical setting.

The structural role of mathematics refers to the fact that mathematics also provides structures to represent idealized physics systems. Mathematics can serve to “order the physical phenomena according to underlying patterns (modelling and hinting at analogies) and in a further extension it enriches physical thought by the physical meanings of mathematical operations” (Pospiech et al., 2015, p. 2). For example, straight lines – abstract mathematical objects – are used in geometrical optics to describe the propagation of light. Teaching students not only to use mathematics as a tool, but also to use mathematical structures to reason in physics is regarded important for physics education (e.g., Sherin, 2001; Karam and Krey, 2015). However, often teachers directly start off from the purely mathematical operations (e.g., Hansson et al., 2015), and only seldom the mathematical structures used and the interpreting of mathematical results are emphasized (e.g., Karam, 2014). As a result, the process of mathematization and the structural role remains implicit. This might be one reason for students often struggling with structural aspects of mathematics in physics education (e.g., Rebello et al., 2007; Uhden and Pospiech, 2011).

Figure 1 visualizes the technical and the structural role of mathematics in the process of solving a physics task. The process starts with a phenomenon or situation in the real world (“World”). This phenomenon is translated into a physical–mathematical model (1); that is, it is idealized, simplified, and described by mathematical means (such as mathematical structures, terms, or formulae). The physical–mathematical model can be considered a mathematical one, when all physics-based knowledge and assumptions are considered and described by mathematics means. Then, one can restrict to the domain of mathematics, and reach a mathematical solution (2). Finally, the mathematical solution is translated back to the world (3) to evaluate whether it is a (meaningful) physics solution. The described structure of solving a physics task integrates a physics education and a mathematics education perspective, as it combines the physics modelling cycle (Uhden et al., 2012) with the inner-mathematical steps of the mathematics modelling cycle (Blum and Leiß, 2005). The structural role of mathematics in physics is located in the transitions between world and model (1, 3); and the technical role comes into play in finding a mathematical solution (2) (see Uhden et al., 2012).

FIGURE 1

Figure 1. Mathematics in solving physics tasks.

3. The German Physics Olympiad

Given the importance of mathematics in physics in general, it is very likely to assume that mathematics is also important in the GPO. The GPO is a four-staged competition taking about 1 year. In the first round, up to 1,000 participants solve theoretical tasks at home. About 300 to 600 students qualify for the second round which consists of theoretical tasks and an experimental task to be solved at home again (since 2019: written exam at the students’ schools.) The 50 best students qualify for the third round, organized as a seminar week including theoretical and experimental exams. The 15 best students from the third round qualify for the fourth round, again a seminar week with theoretical and experimental exams. Every student from a German school can participate in the competition. Most participating students (about 85%) are in grade 11–13 (about 16–19 years old), but there is also a considerable amount of participants from grades 8–10.

The goals of the GPO are twofold (Petersen and Wulff, 2017): The tasks of the first round aim at arousing interest and motivation to participate in the competition which, in turn, is hoped to create a sustained motivation for physics. Afterwards, the focus shifts towards identifying and training the national team for the IPhO. Therefore, most tasks in the first round of the GPO require physics knowledge that is mostly covered by the German physics school curriculum. In the higher rounds, as selecting and fostering become more relevant, the required level of physics knowledge increases and exceeds the high school level.

Good mathematical knowledge is emphasized as one important skill to perform successfully in the competition (GPO, 2021). Also, the IPhO syllabus (IPhO, 2015) – a guideline detailing the topics to expect in the IPhO – includes mathematical aspects, besides physics content aspects and experimental skills; such as solving linear systems of equations or knowing the properties of conic sections. However, the syllabus states: “Problems should focus on testing creativity and understanding of physics rather than testing mathematical virtuosity” (para. 1.2). The international syllabus serves as a guideline for the GPO, but the organizers emphasize that it is not necessary to know every aspect mentioned in the syllabus, especially not for the first rounds, rather training and experience in solving physics tasks is important (GPO, n.d.-a). GPO tasks usually differ from tasks in school in that they require different solution strategies, but address a more advanced level regarding physics and mathematics (Petersen, 2010). Overall, this indicates that GPO tasks include mathematical aspects, however, it is unclear whether the focus is on the technical role (as is the case in school physics) or on the structural role. Given students’ problems with the structural role of mathematics in physics education (e.g., Rebello et al., 2007; Uhden and Pospiech, 2011) such insight would be valuable to evaluate challenges GPO participants might face.

Figure 2 displays a sample task from the second round of the German Physics Olympiad 2017 and Figure 3 the corresponding sample solution, as provided by the competition organizers. Sample task and solution exemplify the structure of solving a physics task (Figure 1) and the role of mathematics in the GPO. The situation is idealized by neglecting the semiconductor’s dimensions – which corresponds to the transition from the world to the physical–mathematical model. Using the mathematical concept “point” for the semiconductor as well as the ray model of light corresponds to the structural role of mathematics (1). The phenomenon of refraction at the surface of the dome is mathematized in the law of refraction. Calculating the angle between light ray and normal vector refers to the technical role of mathematics (2); it requires, e.g., knowledge about congruent angles and trigonometric functions, but the original situation is not relevant. Additionally, the trigonometric functions are approximated, as can be seen in the sample solution in which they do not appear explicitly. Of course, a student experienced in physics reading “near the axis of symmetry” will likely know at once that the small angle approximation has to be used; but for a less experienced student (such as a participant in the Olympiad) this might not be as obvious. Finally, an equation has to be solved (which also corresponds to the technical role) and then the numerical result is connected to the physics situation again (3).

FIGURE 2

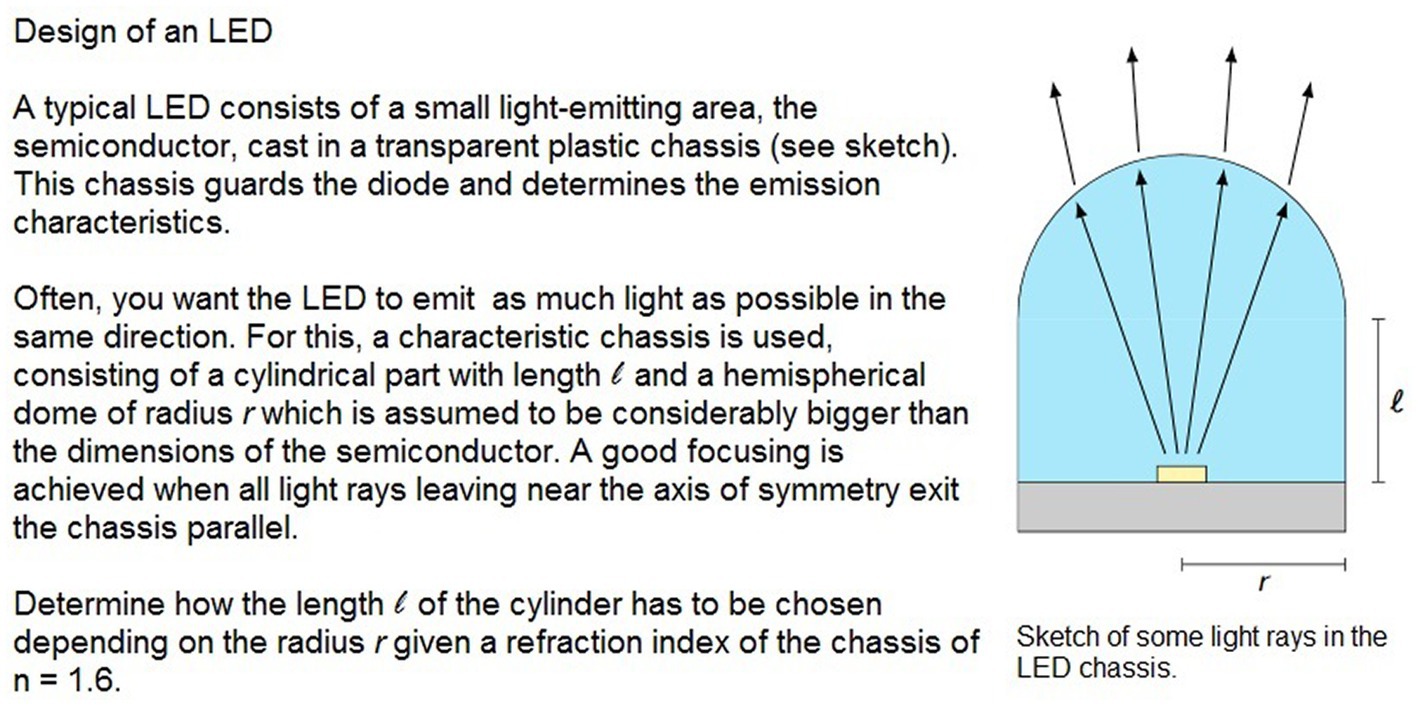
Figure 2. Task from the German Physics Olympiad 2017, second round (GPO, n.d.-b – in German; translation by the authors).

FIGURE 3

Figure 3. Sample solution to the task in Figure 2 (GPO, n.d.-b, translation by the authors).

This sample task and solution illustrate that the Physics Olympiad’s tasks require the participants to employ knowledge related both to physics and to mathematics beyond the mere calculation aspect. Task and solution moreover illustrate that a variety of mathematical aspects is required. Younger students in particular may lack knowledge about trigonometry, but even students from higher grades, who typically know sine and cosine will not have learned about the small angle approximation in school. In particular, students may be not used to applying mathematics in a structural manner. Overall, even if the participants know well the phenomenon of refraction and formula of the law of refraction (i.e., they can solve the physics challenge), they might lack knowledge on mathematical aspects or the application of mathematics in a structural manner (i.e., they fail the mathematics challenge).

4. Research questions and research design

As students often struggle with mathematical aspects in school physics (e.g., Hertel and Großmann, 2016), it is likely to assume that mathematics poses challenges to Physics Olympians, as well. It is thus important to know more about the mathematics in the competition, both regarding content and the role. For example, it is unclear whether mathematical challenges (such as in the sample task) appear regularly or only occasionally. If participants struggle with mathematics in the GPO, they might lose their motivation for physics which would counteract the goal of the competition. The present study therefore aims at investigating the role of mathematics in the GPO. In particular, the following research questions are addressed:

1. Which mathematical aspects are needed to solve the theoretical tasks in the GPO?

2. To what extent are the aspects covered by the school mathematics curriculum?

3. To what extent does the structural role of mathematics come into play?

Research question 1 was investigated by a content analysis of the theoretical tasks employed in the four rounds of 4 years of the GPO. Research question 2 was investigated by comparing the results from research question 1 with the school mathematics curriculum. Research question 3 was investigated by categorizing the mathematical aspects used in each sample solution with respect to the role.

5. Method

To investigate the role of mathematics in the GPO, we focused on the theoretical tasks for several reasons. First, theoretical tasks are required in every round of the competition, whereas experimental tasks are only required from the second round on. [With the change in the second round (from tasks to be solved at home to a written exam), the experimental task which was part of the second round before 2019, was shifted to the first round]. Second, the experimental tasks impact less the participants’ total score than do the theoretical tasks as is also the case in the international competition (see §6 of the IPhO statutes; IPhO, 2018). Third, the experimental tasks typically focus on experimental skills; in contrast, the theoretical tasks require more advanced mathematics. Finally, including also the experimental tasks into our analysis would expand our theoretical frame by adding experiments as a means to gain insights into physics beside the role of mathematics in physics which is not our intention.

To approach the first research question, we analyzed 257 sample solutions distributed over 4 years and all four competition rounds (see GPO, n.d.-b for sample solutions; in the Supplementary material a table is provided showing the distribution of the analyzed sample solutions over the competition rounds and years). An overview of the process is given in Figure 4. For the analysis, we developed a category system regarding the mathematics used in the sample solutions. As initial categories we used the set of mathematical aspects provided by the IPhO Syllabus (IPhO, 2015). That is, we read each task and respective sample solution and tagged, which mathematical aspect(s) of the IPhO Syllabus is addressed. During this process, we inductively refined the categories provided in the IPhO Syllabus bottom-up in order to generate a more detailed categorization which could later on be compared with the mathematics school curriculum (RQ2). For example, one category provided by the IPhO Syllabus is “derivatives of elementary functions” (IPhO, 2015, para. 4.7). During our analysis, we found some sample solutions requiring derivatives of polynomials as well as some sample solutions requiring derivatives of the exponential function. As these two types of derivatives are not necessarily taught in the same grade, we replaced “derivatives of elementary functions” by the categories “derivatives of polynomials” and “derivatives of the exponential function.” Additionally, some mathematical categories were added, that were not covered by the IPhO syllabus but addressed in the sample solutions (e.g., “limit of a function as the function value approaches zero requiring a formal evaluation”). Given the complexity of the tasks and thus the sample solutions, typically more than one mathematical aspect was assigned to each sample solution. For example, the sample solution provided in Figure 3 addressed the categories “introducing identifiers”, “definition of sin, cos, tan in a right triangle”, “geometric approximation” as well as “polynomial approximation based on Taylor series”, “describing a situation in terms of mathematics”, “inserting one term into another”, “equating two terms” and “rearranging an equation into an equivalent form”. Employing this procedure, we generated a highly detailed catalogue consisting of 204 mathematical categories which provides an overview of the mathematical requirements in the GPO as comprehensive as possible. The high level of detail allowed for a comparison with the mathematics school curriculum in Germany (RQ2).

FIGURE 4

Figure 4. Approach to answer research question 1.

After analyzing all sample solutions, to confirm the objectivity of the catalogue a subset of 33 (13%) sample solutions covering all years and all rounds was categorized by an independent second rater. Based on the developed catalogue, the rater indicated for each of the 33 sample solutions and each of the 204 mathematical categories whether the category was addressed in the sample solution or not. The interrater agreement (97.2%, κ_n = 0.94, accounting for free marginal due to the varying frequencies of the categories, see Brennan and Prediger, 1981) was very high indicating well-established categories and a sufficient objectivity of the classification of the sample solutions. The few disagreed cases were discussed by the two raters to reach a consensus. As a result, the descriptions for some of the aspects were refined to enhance clarity and two categories were split into two each. The resulting catalogue thus included 206 mathematical categories. When analyzing the sample solutions, we not only noted which mathematical categories are needed (at all), but also when, that is, in which year and in which round of the competition. This information helped us to better evaluate the relevance and importance of single mathematical aspects. The final catalogue including all 206 mathematical categories is provided in the Supplementary material.

To investigate to what extent the participants may reasonably be assumed to possess the required mathematical knowledge for the GPO (RQ2), we compared the catalogue of 206 mathematical aspects with the school mathematics curriculum. Since most of the participants (more than 80% participants in the first round in 2018) are in the “gymnasiale Oberstufe” (the upper level of the school track “Gymnasium”, which implements the most advanced curricula), we restricted our comparisons to the Gymnasium curriculum. Given that each federal state in Germany implements its own school system and respective curricula, the curricula vary: The mathematical contents are not assigned the same grades across the different states, but some contents are addressed in one state a year earlier or later than in another state; similarly, some curricula are written in a very precise manner and some address rather broad mathematical key ideas. We therefore assigned the mathematical aspects identified in the GPO to either (a) the lower secondary grades (grades five to ten/eleven) or (b) the last 2 years of Gymnasium, but not to single grades. As most of the Olympians are at least in grade eleven, this differentiation corresponds approximately to the classification of “mathematics known to the average participant” (a) and “possibly not known (yet)” (b).

Four federal states were chosen to represent the south-west, mid-east, and northern part of Germany as well as one city state. To compare the identified aspects with the curricula, first, each curriculum document (Baden-Württemberg, KM, 2004; Hamburg, BSB, 2011, 2015/2016; Saxony, SMK, 2004/2009/2011/2013; Schleswig-Holstein, Bimi, 2014) was read and whenever an aspect was found, it was noted. Then, the aspects which had not been found, were explicitly searched in the different curricula documents, as not all the aspects appeared literally or nearly literally in the curricula. In this step, words similar to or part of the aspects were used as key terms for the search in the digital version of the curricula. If again there was no result, the parts of the curriculum dealing with the topics possibly covering the aspect searched for were carefully read again. Sometimes, the aspects were found implicitly, sometimes, an equivalent wording was found (which then was used for searching other documents as well). For this analysis, the level of detail of the list of 206 aspects proved very helpful, as for example the derivative of the exponential function is taught in the last 2 years, whereas differentiating polynomials in some states in the lower grades.

To investigate the third research question regarding the technical or structural role of mathematics in the sample solutions, we noted for every mathematical aspect in every sample solution whether it corresponded to the technical or the structural role. To this end, we rated whether the respective step in the solution can be understood by a person knowing the prior steps and possessing good mathematical knowledge and skills, but without any physics knowledge. To confirm the objectivity of this classification, another independent second rater categorized a subset of the sample solutions. First, the rater categorized eight solutions and the differences in the categorizations were discussed. Based on the discussion, the coding rule was refined. Then, another 30 sample solutions (12%) were rated. The interrater agreement (86.3%, κ_n = 0.79, accounting for free marginal, see Brennan and Prediger, 1981) indicated a sufficient objectivity of the classification. As a result, each sample solution was categorized as (1) purely technical, (2) purely structural, or (3) both if every mathematical aspect corresponded to the technical role (1), the structural role (2), or if some aspects corresponded to the technical and some to the structural role (3). Additionally, we categorized each aspect as (1) purely technical, (2) purely structural, or (3) both if it was always used in a technical manner (1), always used in a structural manner (2), or sometimes used in a technical and sometimes in a structural manner (3).

6. Results

6.1. RQ1: mathematical aspects in the sample solutions

The 206 identified mathematical aspects cover a broad spectrum of mathematics. Many belong to the topic calculus (43 categories) or functions (39 categories), e.g., derivatives or integrals as well as properties of different types of functions. Other aspects relate to geometry and stereometry (36 categories, e.g., surface areas of different figures), to vectors (8 categories, e.g., the scalar product of a vector), and to complex numbers (8 categories, e.g., the product of two complex numbers). Aspects related to algebra (28 categories) concern mostly the handling of terms or equations like inserting one term into another or identities for exponents. And students need to use approximate methods, analyze data and uncertainties, or model mathematically, e.g., when describing a physical situation. A comprehensive list of all mathematical categories is provided in the Supplementary material.

Only seven of all 257 sample solutions did not include any mathematical requirements (like a crossword asking, e.g., for “the capability to store charge”). Based on our detailed catalogue, on average, more than eight mathematical aspects were addressed in every sample solution. The categories differed widely in their appearance over the rounds and the years, corresponding to the relevance for the competition: Aspects that appear in every year and every round are fundamental for all participants and thus the most relevant, whereas aspects occurring in some years only affect just some participants and can therefore be considered as less relevant. To draw conclusions from this extensive catalogue, we grouped the aspects with respect to their appearance in the sample solutions. An overview is given in Table 1 with the appearance as the basis for the grouping, an interpretation of each group (third column) and a short summary of the results of research question 2 (fourth column). A table containing all aspects ordered by group is provided in the Supplementary material.

TABLE 1

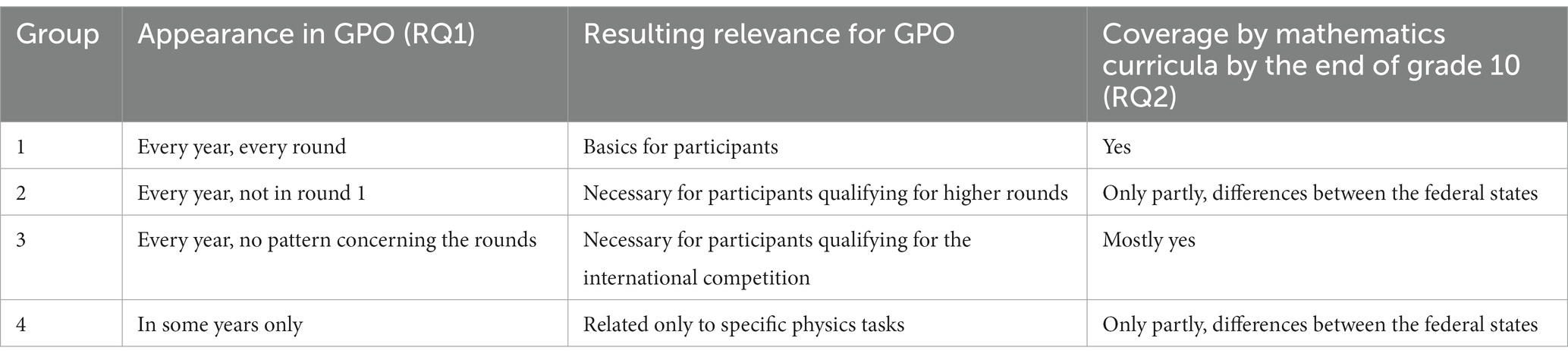
Table 1. Overview of the identified mathematical aspects, their interpretation for the competition and the availability for participants based on curricula.

6.1.1. Aspects occurring in every year and every round

Eight aspects were found every year in every round and can thus be regarded the basic mathematical requirements for the GPO. These include mostly aspects dealing with the manipulation of formulae (simplifying formulae by factorization and expansion, equating two terms, rearranging an equation into an equivalent form, inserting one term into another), calculating values (using a formula to calculate numerical values, rounding, handling measurement units), and introducing identifiers.

6.1.2. Aspects occurring every year, but not in the first round

Twenty-four aspects were found in every year, but only in higher rounds. These aspects can be regarded necessary requirements for those students who qualify for the higher rounds. Many of the aspects relate to the topic calculus, e.g., differentiating and integrating polynomials (round two and higher) or the chain rule (round three and four). Other aspects address Taylor series or logarithmic identities (round two and higher).

6.1.3. Aspects occurring every year but with varying appearance in the rounds

Twenty-six aspects were found every year, but their appearance in the rounds varied. The aspects thus represent a collection of requirements met by students who qualify for the IPhO. For example, in 1 year, the volume of a sphere had to be known in the first round, whereas in another, it occurred only in the third round. Similarly, exponential identities or the scalar product in some years occurred in round one, and in round three or four in others.

6.1.4. Aspects occurring in some years only

Finally, 148 mathematical aspects were found in some years only (see Supplementary material for details). These aspects thus highly relate to the specific physics tasks in the competition. Regarding the regular mathematical challenges in the GPO, these aspects are less crucial than the aspects of groups 1 to 3. Thus, in the following we will focus on the aspects needed every year.

Based on our results we do not expect big changes by analyzing more tasks from earlier competitions: Maybe, some single aspects would additionally be identified which did not occur in any of the 257 analyzed tasks. As we already found many aspects covered in these 4 years, especially aspects occurring in some years only, this would not change the overall result that aspects from a wide range of mathematics are important for the competition. Then, one could also imagine that the assignment of one aspect to one of the groups could change: An aspect from group 1 could be classified as not basic anymore – as these aspects present basic requirements even for physics classes we consider this as very unlikely. An aspect of group 2 could be found to also appear in first round – having in mind the second research question, such a change could at most make our results worse, namely if it is an aspect participants might not know. An aspect of group 2 or 3 could change to group 4 – a shift we do not consider as very plausible: The aspects in group 4 are those that are related to single physics tasks. In our opinion, it is very unlikely to have one task in every of four subsequent years addressing the same special mathematical aspect which would not be needed in advanced physics tasks regularly. Last, carefully inspecting our data showed that omitting the tasks of 1 year would have resulted in basically the same groups, indicating our catalogue and grouping to be quite robust.

6.2. RQ2: coverage of the mathematical aspects by mathematics curricula

As indicated before, the curricula vary regarding the level of detail. So, it was not possible to spot every single aspect in every curriculum. Nonetheless, there are some evident trends in the findings (see also Table 1).

The biggest differences are found for the topics of differentiation and integration regarding both when and what is taught. Some requirements identified in the GPO were not found in any of the curricula (e.g., Taylor series). In the following, we detail our findings for the groups of aspects identified in RQ1.

6.2.1. Aspects occurring in every year and every round

These aspects present the basic requirements for the GPO and can be found explicitly or implicitly in all of the four curricula in lower grades. For example, dealing with common measurement units (e.g., time or length units) is part of the mathematics curricula; even if the handling of more physics specific units (such as voltage) is not, we assume that the basic skill of handling units is addressed in mathematics classes. Similarly, introducing identifiers (as part of modelling) or handling terms is covered by the curricula and is as such likely known by the Physics Olympians.

6.2.2. Aspects occurring every year, but not in the first round

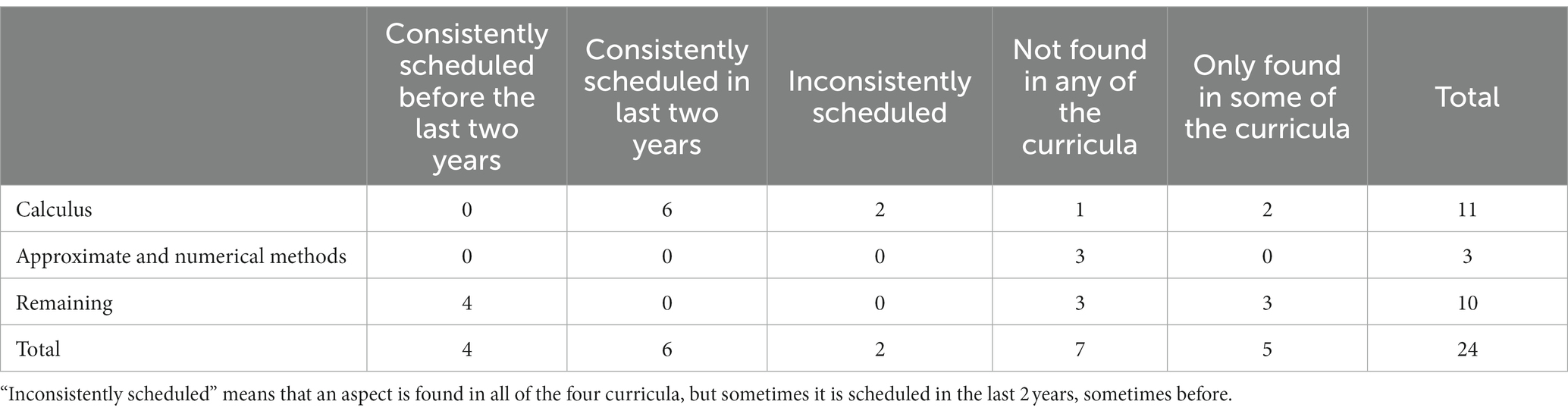
These aspects present necessary requirements for students who qualify for higher rounds. The biggest percentage is comprised by aspects dealing with calculus and, as can be seen in Table 2, this might prove as a challenge: None aspect is scheduled before the last 2 years in all of the four states, but more than half of the aspects are consistently scheduled in the last 2 years (e.g., the linearity of the integral) or not at all (the transition from an equation f(z)dz/dx = g(x) to the corresponding integral equation).

TABLE 2

Table 2. Number of group 2 aspects and their occurrence in the four considered curricula.

Two calculus aspects (derivatives of polynomials, linearity of derivatives) are not consistently scheduled in the four federal states; that is, in some federal states they are scheduled in the last 2 years, whereas in other federal states they are scheduled earlier. What is not found in any curriculum are aspects regarding approximate and numerical methods (e.g., Taylor series). Of the remaining aspects, at least some are commonly scheduled in the lower secondary grades and so should be known to an average participant. But again, some aspects are mentioned in only single curricula (e.g., the cross product), while some are not mentioned at all, such as identities for sine and cosine. Certainly, the trigonometric functions are taught in the lower secondary grades, but how much teaching time (if any) is spent, e.g., for angle addition formulae, is unclear. The German Physics Olympians may consult a formulary, but without knowing about the existence of such formulae, probably no participant will look for it.

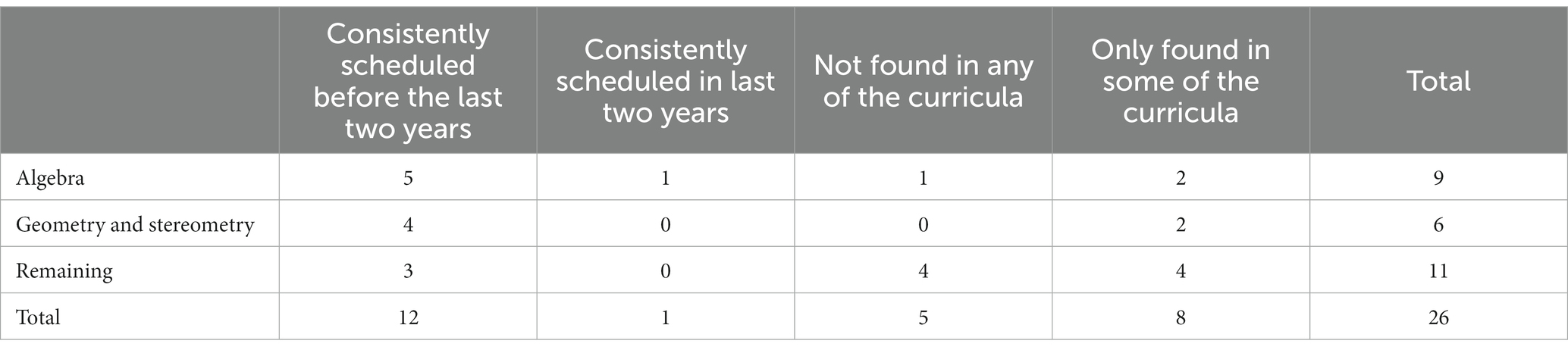
6.2.3. Aspects occurring every year but with varying appearance in the rounds

These aspects present those that will be met by any student who qualifies for the IPhO. There again are aspects not covered by any curriculum (e.g., differentials) and others show a broad variance across the states (e.g., the dot product). However, as reported in Table 3, almost half of the aspects are covered in lower grades (e.g., the area of a circle, identities for exponentiation), while only one is addressed in the last 2 years (systems of linear equations with three variables).

TABLE 3

Table 3. Number of group 3 aspects and their occurrence in the four considered curricula.

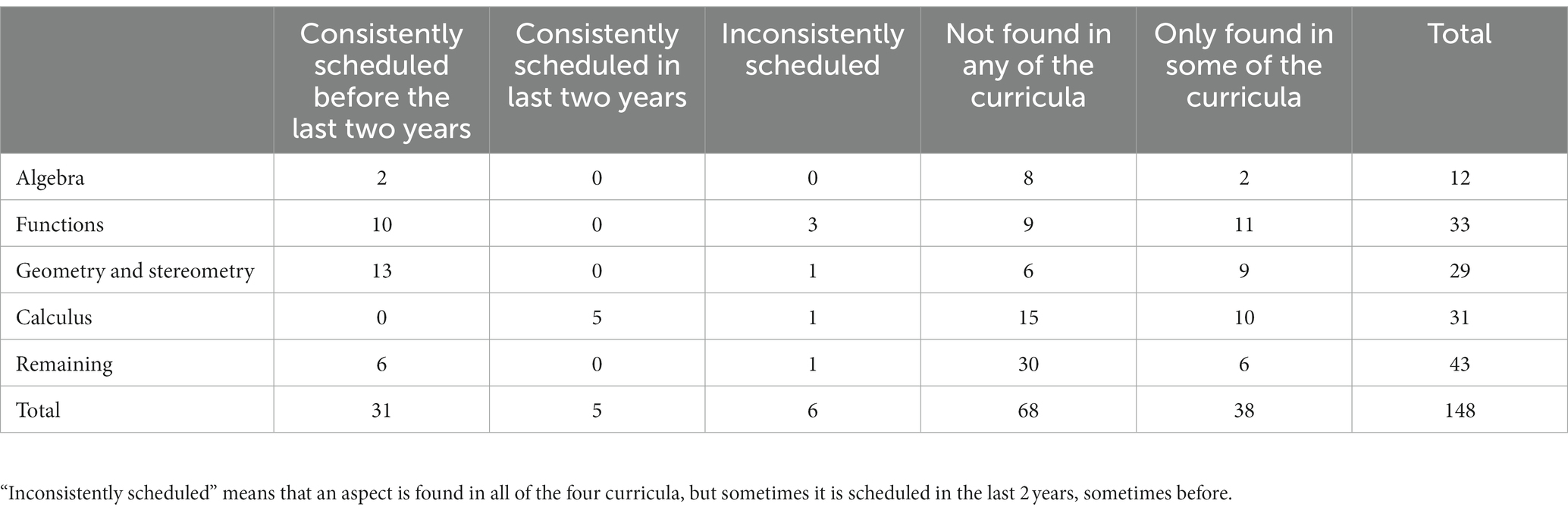
6.2.4. Aspects occurring in some years only

The comparison with the curricula yields a similarly diverse picture as the aspects of group 2 do (see Table 4 for an overview and Supplementary material for details). We do not consider this as problematic as for the aspects of group 2, because the aspects of group 4 do not appear every year in the competition, in contrast to the aspects of group 2.

TABLE 4

Table 4. Number of group 4 aspects and their occurrence in the four considered curricula.

6.3. RQ3: role of mathematics in the sample solutions

The analysis of the 250 sample solutions containing mathematics showed that less than 10% were categorized as purely technical (Table 5). That is, more than 90% of the solutions contained structural mathematics. Less than 5% of the sample solutions contained purely structural mathematics. Interestingly, solutions that were purely technical always followed a task which included structural mathematics. For example, one task asked for the relationship between two physics entities and the following task asked for calculating an entity’s value given specific values. Thus, implicitly the purely technical solutions still rely on structural mathematics.

TABLE 5

Table 5. Number of sample solutions containing purely technical mathematics, both technical and structural mathematics or purely structural mathematics.

The categorization of the single mathematical aspects showed that nearly half of the aspects (100 out of 206) were, at least in some sample solutions, used in a structural manner (Table 6). Restricting to the aspects occurring every year (groups 1–3), we found that at least half of the aspects were used in a structural manner in some or all sample solutions. The (partly) structurally used aspects covered all mathematics topics and were not restricted to aspects one would intuitively expect, e.g., equating two terms, but also included for example the formal notation of an integral. Some aspects (such as on approximate and numerical methods), which are not covered by the curriculum, might thus prove even more challenging as they are used every year in the GPO in an at least partly structural manner.

TABLE 6

Table 6. Number of purely technical, purely structural and technical and structural aspects.

7. Discussion

The aim of the present work was to investigate the role of mathematics in physics competitions by investigating tasks and sample solutions from the GPO. We found more than 200 mathematics aspects covered in the sample solutions, partly exceeding what is taught at school. Additionally, the vast amount of tasks addressed the structural role of mathematics.

Our results show that mathematics might prove as a challenge in the GPO, both regarding content and the role of mathematics. Participants may face the need for mathematics knowledge they have not learned in school yet. Indeed, there is some anecdotic evidence for participants facing this need: During the third round of the GPO 2018, we had the opportunity to talk with participants. They mentioned some mathematical aspects necessary for the competition they had not learned in mathematics classes; especially those participants who were not in their final year of schooling, had had to learn mathematics (such as integration) on their own. Given that all but two of the 50 Olympians were in grade 11 or higher, and thus already had undergone substantial mathematics education, their lacking of mathematics knowledge might be an important statement, especially regarding younger participants in the early rounds. Additionally, in the sample solutions the structural role of mathematics proved as very relevant. This is in stark contrast to physics education which typically emphasizes the technical role (e.g., Karam, 2014; Hansson et al., 2015). Thus, even if the participants possess the required mathematics knowledge, applying this knowledge to solve the competition tasks might be a problem for the students as mathematics in physics is different from pure mathematics (e.g., Redish, 2006). Consequently, it is possible that students, though talented and/or highly interested in physics, fail quite early in the competition due to a lack of mathematics knowledge or because they cannot apply their mathematics knowledge to solve the competition tasks. For example, in the interviews mentioned above, one participant reported to have been taught in mathematics lessons how to calculate with complex numbers, but not “what else could be done with them”, for example applying them to two-dimensional physics problems. Some participants said that as a part of their preparation for the competition they learned mathematics which they had not covered at school like “to integrate I’ve learned by myself” or “last year, I prepared very intensely and learned a lot by that, integral and differential calculus and approximation methods”. Mathematical aspects like these – integral and differential calculus, approximation methods – were found to occur quite often across years, and early in the competition (round 2 the latest). They thus might, in fact, pose (substantial) challenges to some participants.

7.1. Limitations

As every empirical investigation, the study comes with some limitations. First, we only analyzed sample solutions, though, surely, we cannot expect every participant to hand in a sample solution. Participants’ solutions could be less formal – this would not change the needed mathematics yet – or even more complex – this could have resulted in an even lengthier catalogue. Second, we used the mathematics curricula as indicators of what can or cannot be expected by the participants. Normative curricula and enacted curricula may differ (Stein et al., 2007), so it is possible that students lack some knowledge which we assumed them to have based on the curriculum. However, students may also possess knowledge beyond the curriculum; for example, because they already participated in previous Olympiads or because their teachers may have highlighted mathematical aspects in their physics teaching. Nevertheless, one may not expect that every Physics Olympian is supported by a designated physics teacher or experiences physics education by an engaged teacher who explicitly emphasizes mathematical tools or mathematics thinking during the physics lessons. Finally, our studies are restricted to the German Physics Olympiad. In order to generalize our findings to other physics competitions or countries, future studies are necessary.

7.2. Implications

Despite the above limitations, our study and the identified catalogue of mathematical aspects contribute implications to science (and mathematics) education research and practice. First, given that mathematics in the GPO may cause particular challenges to participants, it is possible that talented students get discouraged by mathematical challenges and turn to other domains instead. This would counteract the goal of the competition that is to foster such talented students, increase their interest and possibly motivate them to enter a STEM-related profession. If the prominent role of mathematics in physics competitions is in fact a problem to the participants remains to be investigated.

Second, it is unclear, in how far knowledge of the identified mathematical aspects implies success in the GPO and the IPhO. Future studies may use the catalogue to design tests of participants’ mathematical knowledge and skills, and to relate them with their success in the Olympiads.

Third, our study may be informative to tertiary STEM research. It is well known that mathematical challenges may lead freshmen to drop out from a STEM study (e.g., Heublein et al., 2010). In contrast, physics Olympians are known to often choose and successfully complete a STEM career (e.g., Campbell and Walberg, 2010). This may indicate that Olympians are better prepared to cope with the mathematical challenges of a STEM study. In a first step, our catalogue of identified mathematical aspects could be compared with insights from current tertiary STEM research. Mapping our catalogue against the KUMA model (Rach and Ufer, 2020) or the MaLeMINT catalogue (Deeken et al., 2020) will show in how far mathematical aspects in the GPO correspond to mathematical requirement for STEM studies. Moreover, the strong emphasis of the structural role of mathematics in the GPO may also be an important preparation for a STEM, in particular a physics, study. This, in turn, could also imply the necessity to highlight the structural role of mathematics in school physics education more strongly.

Finally, our catalogue (see Supplementary material) offers practitioners – such as Physics Olympiad organizers and teachers – the possibility to specifically foster talented students. Organizers, who aim to offer supporting material (e.g., especially for younger students), based on our results we would suggest to especially address aspects from calculus or approximate methods. Similarly, mathematics and physics teachers can strongly influence the promoting of students talented in physics, when using our catalogue to decide which topics to address or not. Providing extracurricular opportunities for the Olympians to learn mathematics in physics contexts, the students would receive a fostering in mathematics beside the intended fostering in physics. Such additional offers would benefit from joint – mathematics and physics education – expertise.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

ET, IN and AH contributed to the conception and design of the study. ET performed the analysis and wrote the first draft of the manuscript. IN and AH critically revised the manuscript. All authors contributed to the article and approved the submitted version.

Funding

The study was part of the WinnerS project funded by the Leibniz Association.

Acknowledgments

We express our gratitude to the coordinator of the GPO, Dr. Stefan Petersen, for providing us with the tasks and sample solutions analyzed in this study. We would moreover like to thank him for his valuable comments on a previous version of this manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2023.1196189/full#supplementary-material

References

Blum, W., and Leiß, D. (2005). “‘Filling Up’– The problem of independence-preserving teacher interventions in lessons with demanding modelling tasks” in CERME 4–proceedings of the fourth congress of the European Society for Research in mathematics education, 1623–1633.

Google Scholar

Brennan, R. L., and Prediger, D. J. (1981). Coefficient kappa: some uses, misuses, and alternatives. Educ. Psychol. Meas. 41, 687–699. doi: 10.1177/001316448104100307

CrossRef Full Text | Google Scholar

Campbell, J. R., and Walberg, H. J. (2010). Olympiad studies: competitions provide alternatives to developing talents that serve national interests. Roeper Rev. 33, 8–17. doi: 10.1080/02783193.2011.530202

CrossRef Full Text | Google Scholar

Deeken, C., Neumann, I., and Heinze, A. (2020). Mathematical prerequisites for STEM programs: what do university instructors expect from new STEM undergraduates? Int. J. Res. Undergrad. Math. Educ. 6, 23–41. doi: 10.1007/s40753-019-00098-1

CrossRef Full Text | Google Scholar

Freie und Hansestadt Hamburg, Behörde für Schule und Berufsbildung (BSB, Ed.). (2011). Bildungsplan Gymnasium Sekundarstufe I, Mathematika.

Google Scholar

Freie und Hansestadt Hamburg, Behörde für Schule und Berufsbildung (BSB, Ed.). (2015/2016). Bildungsplan gymnasiale Oberstufe, Anlage zum Rahmenplan Mathematik zur Umsetzung der Bildungsstandards Mathematik für die Allgemeine Hochschulreife

Google Scholar

Gorzkowski, W., and Tichy-Rács, Á. (2010). List of Winners in 1st – 41st International Physics Olympiads. Available at: http://www.ipho.org/statictics.pdf

Google Scholar

GPO (2021). Flyer of the GPO 2021. Available at: http://wettbewerbe.ipn.uni-kiel.de/ipho/data/52_IPhO_2021_1Rd_Handzettel_web.pdf (Accessed September 30, 2020).

Google Scholar

GPO (n.d.-a). Requirements. Available at: http://wettbewerbe.ipn.uni-kiel.de/ipho/anforderungen.html (Accessed September 30, 2020).

Google Scholar

GPO (n.d.-b). Sample tasks and solutions of the German Physics Olympiad. Available at: http://wettbewerbe.ipn.uni-kiel.de/ipho/aufgaben.html (Accessed September 30, 2020).

Google Scholar

Hansson, L., Hansson, Ö., Juter, K., and Redfors, A. (2015). Reality–theoretical models–mathematics: a ternary perspective on physics lessons in upper-secondary school. Sci. Educ. 24, 615–644. doi: 10.1007/s11191-015-9750-1

CrossRef Full Text | Google Scholar

Hertel, I., and Großmann, S. (2016). Physik in der Schule: Hauptteil. Eine Studie der Deutschen Physikalischen Gesellschaft (DPG). Available at: https://www.dpg-physik.de/veroeffentlichung/broschueren/studien.html

Google Scholar

Heublein, U., Hutzsch, C., Schreiber, J., Sommer, D., and Besuch, G. (2010). Ursachen des Studienabbruchs in Bachelor- und in herkömmlichen Studiengängen: Ergebnisse einer bundesweiten Befragung von Exmatrikulierten des Studienjahres 2007/08. Hannover: HIS.

Google Scholar

Hudson, H. T., and McIntire, W. R. (1977). Correlation between mathematical skills and success in physics. Am. J. Phys. 45, 470–471. doi: 10.1119/1.10823

CrossRef Full Text | Google Scholar

IPhO (2015). IPhO Syllabus. Available at: http://www.ipho.org/syllabus.html

Google Scholar

IPhO (2018). Statutes of the international physics Olympiad. Available at: https://www.ipho-new.org/statutes-syllabus/

Google Scholar

Karam, R. (2014). Framing the structural role of mathematics in physics lectures: a case study on electromagnetism. Phys. Rev. Spec. Top. 10:10119. doi: 10.1103/PhysRevSTPER.10.010119

CrossRef Full Text | Google Scholar

Karam, R., and Krey, O. (2015). Quod erat demonstrandum: understanding and explaining equations in physics teacher education. Sci. Educ. 24, 661–698. doi: 10.1007/s11191-015-9743-0

CrossRef Full Text | Google Scholar

Ministerium für Kultus, Jugend und Sport Baden-Württemberg (KM, Ed.). (2004). Bildungsplan 2004, Allgemein bildendes Gymnasium.

Google Scholar

Ministerium für Schule und Berufsbildung des Landes Schleswig-Holstein (Bimi, Ed.). (2014). Fachanforderungen Mathematik, Allgemein bildende Schulen, Sekundarstufe I, Sekundarstufe II.

Google Scholar

Petersen, S. (2010). Oberflächen- und Tiefenmerkmale von Aufgaben in der Internationalen PhysikOlympiade: Projekte zur systematischen Analyse und Entwicklung von Aufgaben in dem Wettbewerb. PhyDid B.

Google Scholar

Petersen, S., and Wulff, P. (2017). The German Physics Olympiad—identifying and inspiring talents. Eur. J. Phys. 38, 034005–034016. doi: 10.1088/1361-6404/aa538f

CrossRef Full Text | Google Scholar

Pospiech, G., Eylon, B., Bagno, E., Lehavi, Y., and Geyer, M.-A. (2015). The role of mathematics for physics teaching and understanding. Nuovo Cimento C Geophysics Space Physics C 38:110. doi: 10.1393/ncc/i2015-15110-6

CrossRef Full Text | Google Scholar

Potvin, P., and Hasni, A. (2014). Interest, motivation and attitude towards science and technology at K-12 levels: a systematic review of 12 years of educational research. Stud. Sci. Educ. 50, 85–129. doi: 10.1080/03057267.2014.881626

CrossRef Full Text | Google Scholar

Rach, S., and Ufer, S. (2020). Which prior mathematical knowledge is necessary for study success in the university study entrance phase? Results on a new model of knowledge levels based on a reanalysis of data from existing studies. Int. J. Res. Undergrad. Math. Educ. 6, 375–403. doi: 10.1007/s40753-020-00112-x

CrossRef Full Text | Google Scholar

Rebello, N. S., Cui, L., Bennet, A. G., Zollman, D. A., and Ozimek, D. J. (2007). “Transfer of learning in problem solving in the context of mathematics and physics” in Learning to solve complex scientific problems. ed. D. H. Jonassen (New York: Erlbaum), 223–246.

Google Scholar

Redish, E. F. (2006). Problem solving and the use of math in physics courses. Invited talk presented at the conference, world view on physics education in 2005: focusing on change, Delhi, August 21–26, 2005. To be published in the proceedings. Available at: https://arxiv.org/abs/physics/0608268

Google Scholar

Sächsisches Staatsministerium für Kultus (SMK, Ed.). (2004/2009/2011/2013). Lehrplan Gymnasium Mathematik.

Google Scholar

Sherin, B. L. (2001). How students understand physics equations. Cogn. Instr. 19, 479–541. doi: 10.1207/S1532690XCI1904_3

CrossRef Full Text | Google Scholar

Stein, M. K., Remillard, J., and Smith, M. S. (2007). “How curriculum influences student learning” in Second handbook of research on mathematics teaching and learning: a project of the National Council of teachers of mathematics. ed. F. K. Lester (Charlotte, NC: Information Age Publishing), 319–369.

Google Scholar

Tuminaro, J., and Redish, E. F. (2007). Elements of a cognitive model of physics problem solving: epistemic games. Phys. Rev. Spec. Top. 3, 1–22. doi: 10.1103/PhysRevSTPER.3.020101

CrossRef Full Text | Google Scholar

Uhden, O., Karam, R., Pietrocola, M., and Pospiech, G. (2012). Modelling mathematical reasoning in physics education. Sci. Educ. 21, 485–506. doi: 10.1007/s11191-011-9396-6

CrossRef Full Text | Google Scholar

Uhden, O., and Pospiech, G. (2011). “Mathematics in physics: analysis of students' difficulties” in E-book proceedings of the ESERA conference, 218–222.

Google Scholar