Mathematical knowledge for teaching as a didactic praxeology

Pansell, Anna

doi:10.3389/feduc.2023.1165977

HYPOTHESIS AND THEORY article

Front. Educ., 11 August 2023

Sec. Teacher Education

Volume 8 - 2023 | https://doi.org/10.3389/feduc.2023.1165977

This article is part of the Research Topic Theories and Theorising in Mathematics Education and How they Inform Teacher Education View all 6 articles

Mathematical knowledge for teaching as a didactic praxeology

$\r\nAnna Pansell$ Anna Pansell^*

Department of Teaching and Learning, Stockholm University, Stockholm, Sweden

It is widely acknowledged that teachers' work has both practical and theoretical dimensions, both praxis and logos, and that teacher education should address both dimensions. However, as argued in this article, existing discourses for describing the mathematical knowledge of teachers and what it takes to become competent in it are not always clear to what extent these discourses address knowledge about the practices of mathematics teaching or theories that provide arguments for the practices. Specifically, I argue for the coordination of the framework of mathematical knowledge for teaching (MKT) with the analytical distinction of logos and praxis combined in teaching practices. Moreover, I have backed this argument with examples of the proposed categories of the adjusted framework from the existing body of work in mathematics education. Each category of the proposed framework, whether concerning a teaching method or a theoretical consideration, was indeed exemplified by some concept, approach, or perspective from the field of mathematics education. The framework, I believe, would prove useful in engaging mathematics teacher education discursively, for instance, in analyzing teacher education materials to determine the extent to which they offer mere methods, theoretical arguments, or a combination of both.

1. Introduction

There have been numerous studies on teacher knowledge. The proposition of the existence of various types of teacher knowledge, in particular, pedagogical content knowledge (PCK) by Shulman (1986), is one of the most cited claims in the field of education and mathematics education, in particular, the notion of mathematical knowledge for teaching (MKT) (Ball et al., 2008) is equally well-renown. MKT and PCK have been used with both cognitive and situated approaches, yet in both cases, limitations were evident. Cognitive approaches tend to focus on teachers' understanding with little regard for contextual or affective aspects. Situated approaches lead to difficulties in articulating the relationship between PCK and classroom practices (Depaepe et al., 2013). After substantial theoretical and empirical research on mathematics teachers' actual and desired knowledge, Ball (2017) could still ask what constitutes the “special mathematical work of teaching”. In this article, I have attempted to add nuances to how both practical and theoretical ideas constitute mathematics teachers' practices and invite further discussion where the entanglement of mathematical ideas and other ideas from other domains can be part of what constitutes mathematics teaching practices.

It is a crucial premise for this study that knowing and doing go hand in hand and that know-what, know-how, and know-why are integral components of any practice (see Chevallard and Bosch, 2020a). Just as обучение in Russian refers neither to teaching nor to learning but to the interaction between the student and the teacher, the interaction between knowing and doing deserves its own term. In the Germanic tradition, some may view the term didaktik as encompassing the inseparability of both an enacted and a knowledge component when it comes to teaching. While other proposals exist and I could have simply stayed with the idea of teachers' work, I chose to draw on the notion of praxeology in this study (Chevallard, 2006). I have expanded on this term below. Suffice here to say that this notion from the Anthropological Theory of the Didactic (Chevallard and Bosch, 2020a) can address some of the aforementioned limitations by foregrounding how what a teacher knows (logos) and what a teacher does (praxis) exist in close relation to each other as two aspects of praxeology and at the same time in close relationship with the content. A move from MKT to praxeology is a move from a cognitive orientation to a systemic orientation, shifting interest from what individual teachers know to the organization of mathematics teachers' knowledge (see Scheiner et al., 2022), where MKT provides the notion of praxeology with categories.

In what follows, I have briefly touched on the main categories of MKT, subject knowledge and pedagogical content knowledge, and their subdivisions. I have then discussed the promise for the field of mathematics teacher education through the Anthropological Theory of the Didactic (ATD), particularly the notion of praxeology. These two sections serve to highlight not only the strengths but also the limitations of the existing categories. What follows from there is an introduction to the proposed framework, where the categories of MKT are coordinated with the notion of praxeology and by which the categories remain but are described as mathematical or didactical praxeologies with practical and theoretical elements that are observed to constitute each other.

2. Mathematical knowledge for teaching

The claim I put forward in this section is 2-fold. First, the MKT framework has offered the field of mathematics education valuable categories of different aspects of what a mathematics teacher knows or should know, and this deserves to be explored and developed. Second, the MKT framework, a framework of mathematical knowledge for teaching with subject matter knowledge and a pedagogical content knowledge (PCK) element, is limited since it does not clarify how different categories may have different kinds of practical enactment and theoretical grounds. Coordinating MKT with ATD may contribute to more nuances and relations, which could bridge the categories of MKT and classroom practices, as asked for in situated research.

In the following sections, I provide support for this claim by discussing two warrants. First, I have examined the categories of MKT and illustrated them with examples from the field of mathematics education. These categories are presented individually, although it is important to note that they are not rigidly defined and can overlap due to their analytical nature. The second warrant concerns the possibility of extending the MKT framework in conjunction with the notion of praxeology.

2.1. Subject matter knowledge

Subject matter knowledge is divided into common, specialized, and horizon content knowledge (Ball et al., 2008), while PCK is divided into knowledge of content and students (KCS), knowledge of content and teaching (KCT), and knowledge of curriculum. These categories of the knowledge a teacher needs to do the mathematical work in the mathematics classroom have proven useful in comparing teacher knowledge (e.g., Marcinek et al., 2023) or understanding mathematics teacher education (e.g., Borko et al., 1992) with more precision.

Common content knowledge (CCK) refers to the mathematical knowledge used in any setting, not only by mathematics teachers. Specialized content knowledge (SCK) is the mathematical knowledge special to mathematics teaching, for example, the mathematical explanation for why a standard algorithm for addition calculations works. Horizon content knowledge (HCK) is mathematical knowledge beyond what is normally taught at the grade level, but awareness of which can assist the teacher in avoiding creating obstacles to future learning. It could be formal algebra for the primary school teacher who teaches natural numbers to the first grade (see Pitta-Pantazi et al., 2020), which follows the content that is usually taught. The need for mathematics teachers to know mathematics has been argued by many (e.g., Wu, 2018), and the three categories offer a language to distinguish what mathematical knowledge teachers can advantageously lean on in their teaching practices: the SCK and the HCK (Van Bommel, 2012). This gives mathematics a position as to what constitutes mathematics teaching. What teachers know about mathematics will affect/decide/influence how they teach, but not in isolation from other types of knowledge. A negotiation across mathematics and teaching domains is crucial to mathematics teacher education if teachers know how to use mathematics in teaching (Adler and Davis, 2006). Hence, these sub-categorizations of mathematical knowledge assist in providing arguments for what content is reasonable to cover in teacher education; student teachers need to engage with mathematics in ways that go beyond what they learned in school themselves (CCK), and they need to do so not only for the content of the grades they will teach but also not to contribute to unnecessary hurdles for students.

2.2. Pedagogical content knowledge

PCK and its sub-categories similarly occupy a position as a theory for teaching. Knowledge of content and students (KCS) refers to knowledge about how students relate to, learn, and struggle with mathematics, for example, predicting what will be difficult for students to understand or what they will find motivating and fun. KCS can also be about assessing and documenting what mathematics students know (see Ball et al., 2008). While KCS appears highly relevant for teachers in their practices, it has nonetheless been difficult to concretize and, especially, assess. Understanding how students may understand a concept is beneficial for a teacher (Hill et al., 2008). Conversely, the absence of such understanding can be a limiting factor, even if the teacher is well-versed in mathematics (Johnson and Larsen, 2012). This is partially because decisions in teaching cannot be derived from KCS alone. Teachers also need knowledge of content and teaching, and we need to know more about how these different ideas work together in a teaching situation (see also Hill et al., 2008).

Knowledge of content and teaching (KCT) refers to knowledge about how to make learning mathematics possible for students. It concerns the choice and sequencing of examples or the use of models and representations to, for example, explain the multiplication of fractions (Ball et al., 2008). However, it is not unproblematic to distinguish KCT from other categories of MKT or to assess KCT, and studies focusing on KCT may end up asking for more courses on the specific subject matter (see Lestari and Juniati, 2018). Knowing how to do the mathematical work in teaching could be viewed as knowing how to teach, as a praxis dimension only. The proposal in this study is that mathematical teaching also has a knowledge component; that is, ideas that together with mathematical knowledge call for different teaching practices. The proposal is also that these ideas are not only mathematical but also didactic, as the word is used in the French tradition. I fully acknowledge that the MKT framework was originally written in another tradition and that the word didactic is used differently.

Knowledge of curriculum refers to knowledge of national policy and syllabi, encompassing stated goals for both teachers and students to achieve. Additionally, it involves familiarity with curricular materials, such as textbooks, teacher guides, digital platforms, or educational programs (Ball et al., 2008). Sleep and Eskelson (2012) distinguished between curriculum use, teachers' orientations toward curriculum, MKT, and teachers' goals for their students, illustrating again the need for considering the know-how and the knowledge components together.

2.3. The need for the development of the language of mathematics teacher knowledge

Three limitations manifest in MKT studies (see Depaepe et al., 2013). First, there are difficulties distinguishing between sub-categories in studies aiming to assess prospective teachers' MKT, showing how these categories do not work in isolation but always in relation to other categories. The categories appear to work more as a system than as separate categories, meaning that the utilization of MKT for analytical purposes is restricted. A second limitation has not, to the same extent, been explicitly addressed in existing studies. It concerns the use of the MKT framework in assessing mathematics teachers' practices. When the conclusion emphasizes the need for additional knowledge—whether it is related to mathematics, specific teaching methods, or how students comprehend a particular content—it highlights the inherent challenge of incorporating every intricacy within a finite mathematics teacher education program. Critiquing the emphasis on measuring the knowledge of individual mathematics teachers, Ball (2017) describes how this emphasis on measurement has led to a compartmentalization of what a teacher focuses on in mathematics teaching, with the example that the focus on mathematics has been separated from, for example, a focus on equity. “However, in teaching, equity concerns—who has the floor, who is being recognized, whose ideas are being valued—are entangled in the construction of mathematics, of what is asked and emphasized, and of what it means to do or be good at math” (Ball, 2017, p. 14). Critiquing frameworks based on the idea of teaching as decompressing mathematical knowledge, for example, MKT, Scheiner and Bowers (2023) ask if other perspectives, for example, the perspective of which praxeology is a part, may be a more fruitful way of seeing mathematics teacher knowledge, not as “decomposable into more elemental bits and pieces” (p. 12) but as a more holistic view of mathematics teachers' work and knowledge. A third limitation, described as a pitfall in a review of PCK in mathematics education (Depaepe et al., 2013), concerns how PCK becomes an object of study regardless of the context of its use. In such cases, cultural, affective, or other issues arising from teachers' complex practices make it difficult to know what is possible to be drawn from these studies. A situated perspective is suggested as a possible solution, but this comes with its own challenges. The connection between classroom activities and PCK is difficult to understand even when a situated perspective acknowledges the interactions between different types of knowledge, practices, and contexts. In this article, I have attempted to address this difficulty by articulating how the practical tasks relate to methods and theoretical ideas and how all these are part of a situation that sets boundaries for what is possible to do or not.

MKT and PCK have been used with both cognitive and situated approaches, revealing limitations. Cognitive approaches tend to focus on teachers' understanding with little regard for contextual or affective aspects. Situated approaches lead to difficulties in articulating the relationship between MKT/PCK and classroom practices (Depaepe et al., 2013). What mathematics teachers know is, in these studies, related to practice and sometimes observed as a reason for practice. In a sense, what teachers should know is also seen as what they should practice. This, as also discussed for the sub-categories above, suggests that it is problematic in descriptions of practice, desired student-teacher learning, and analyses of teachers' practice and learning to focus on knowledge and not how it is related to the doing, hence the foregrounding of the praxeological and didactic approach in this study. All teacher knowledge acquires its usefulness in relation to knowing how to teach. Therefore, continuous development of our specialized language is needed.

All teaching-related activity also has an element of knowing, which can be written, spoken, or enacted (see Chevallard and Bosch, 2020a). This concerns specifically knowing why, the logos aspect, as ideas, frameworks, concepts, or grand theories may support arguments for different teaching activities. However, as indicated above, there is no given road from knowledge to action, from logos to praxis. Which activities a teacher decides on depends, among other things, on what ideas are taken into account—as when Ball (2017) describes how the idea of equity affects whose ideas to value in a classroom discussion—but a mathematics teacher needs to negotiate the mathematical issues at hand with many other, sometimes, conflicting issues (Biesta, 2015). The professional judgment of mathematics teachers is not decided by their theoretical knowledge. Rather, theoretical knowledge grounds the professional judgment of what to do in a specific situation (Shalem, 2014).

My claim that MKT, and by extension, PCK, has offered the field of mathematics education valuable categories for the understanding of mathematics teacher knowledge has been backed by different studies using MKT to make important claims about parts of mathematics teacher knowledge. The other part of my claim that MKT, or at least the use of MKT in research, has limitations is also backed by several studies. The limitations from both a cognitive and a social perspective point toward a need for more articulation of the categories of MKT and the difficulties in relating the categories to practice. This, together with the limitation that it is difficult to understand what is connected to which category, leads me to suggest that it may be useful to take the idea of MKT into a situated perspective as well as a systemic approach and consider mathematics teacher knowledge as a system, an organization of knowledge. Such a shift involves viewing teacher knowledge as both doing and knowing as well as both mathematical and didactic, which brings the practices of mathematics teaching, the mathematical work of teaching, right into the framework. This is why I suggest coordinating the MKT framework with the idea of praxeology from ATD to add a didactic dimension and an articulation of the know-how and know-why of mathematics teachers in their teaching practices.

3. The promise from ATD

The claim I put forward here is that coordinating (see Prediger and Bikner-Ahsbahs, 2014) the MKT framework with the idea of didactic praxeology can serve the field of mathematics education and, more specifically, mathematics teacher education by developing the specialized language about mathematics teacher knowledge, which may help us as a field to be more specific about the nuances and different aspects of what a mathematics teacher knows. In addition, I see a wholeness of the organization of teachers' know-how and know-why, which will address some of the limitations of the MKT framework. This will also address Scheiner and Bower's (2023) question for more holistic ideas to discuss mathematics teacher knowledge. Ball et al. (2008) contributed with the idea that a mathematics teacher's work is indeed mathematical, which was shown in the categories of MKT. In the following, I have extended MKT based on the idea that mathematics teacher knowledge is didactic and that the mathematical and didactic parts of mathematics teacher knowledge are intertwined, meaning the didactics of mathematics is neither content knowledge nor pedagogic knowledge; it is the amalgam between the two. When a mathematics teacher works and makes decisions in the classroom, mathematical ideas and methods are central, but I argue that they are always negotiated together with other ideas. This is similar to when Ball (2017) describes how ideas such as equity are entangled in the construction of mathematics, of what is asked and emphasized, and of what it means to do or be good at math (14). It is this entanglement that I wish to explore and contribute to model when I coordinate MKT with the idea of mathematical and didactic praxeologies.

3.1. Anthropological theory of the didactic

The Anthropological Theory of the Didactic (ATD) is used to study didactic knowledge in social practices where teaching happens (Chevallard and Bosch, 2020a). One basic assumption is that the knowledge produced in, for example, academic institutions is not the same knowledge that is taught in a classroom. To be available for students' knowledge, it has to be changed and simplified in the process of didactic transposition (Chevallard and Bosch, 2020b). If mathematics is the theory of mathematics teaching, it is only mathematical ideas that are negotiated and transformed into classroom teaching. However, an assumption in this article is that mathematics shares the position of theory with other theoretical ideas and concepts, and they are negotiated and transformed in relation to each other, grounding different mathematics teaching practices. This infers that the theoretical ideas affect how a teacher teaches. However, another central idea in ATD, co-determination, indicates that what happens in the classroom can also affect the theory a teacher takes into account when forming their mathematics teaching. Co-determination does not only concern theory vs. practice. It concerns any institution in the school system, society, or culture. The “co” in co-determination is key here since these institutions are all seen as part of an ecology where they contribute with conditions and constraints that affect what is possible to say within the ecology (Chevallard, 2002). Chevallard describes how even the mathematics expressed in the classroom are expressed in a specific way since the classroom, teacher, and curricular materials are all part of a specific educational system and a specific cultural setting. How a mathematics teacher teaches is not decided by these external institutions but is co-determined. They affect what becomes desirable as good mathematics teaching in the specific classroom, together with the teacher and students in the classroom. This is not a one-sided process. It moves between institutions (Chevallard, 2002; see also Pansell, 2018). This ecological view resonates with the holistic perspective proposed by Scheiner et al. (2022) as an alternative way of discussing mathematics teachers' knowledge. In this study, neither didactic transposition nor didactic co-determination is the object of study. They serve here as a theoretical background to the idea of knowledge as a praxeology. A praxeology is expressed within an institution, which is part of an ecology and participates in the didactic transposition.

Coordinating MKT with an idea from ATD also brings MKT into a situated perspective and a systemic approach. This entails a need to see the particularities in teaching activities as part of something whole, and to explain a teaching activity by an individual teacher's knowledge alone becomes uninteresting. This does not mean that what a teacher knows about fractions does not matter. It only says that it is not the whole reason the teacher teaches the way they do. A didactic praxeology is always situated (see Chevallard and Bosch, 2020a), and with the idea of co-determination in the background, I have discussed what is privileged in different societies or situations and how this may affect mathematics teaching practices. In the following sections, I have unpacked the idea of mathematical and didactic praxeology as a way to view the knowledge of teachers to further back my claim that coordinating MKT and didactic praxeology will be a way to contribute to a more specialized language about mathematics teachers' knowledge for further discussions about the entanglements of mathematical and didactic ideas that a mathematics teacher uses when they work.

3.2. Praxeology

In the context of ATD, theory and practice are, as described above, not only intertwined but also co-determined. The combination of the two sides of knowledge is, in ATD, described as a praxeology, representing a method that articulates the know-how as a type of task to be solved through technology. Know-why is then articulated as a technology explaining why the method works and a theory where the assumptions and ideas behind the technology can be found (see Chevallard and Bosch, 2020a). In this study, I have focused on didactic praxeology. However, the task of a teacher is to teach mathematics, or, in ATD words, to make a mathematical praxeology available for students (Gellert et al., 2013). In the following paragraphs, I have unpacked mathematical and didactical praxeologies to build a foundation for coordination with MKT.

3.2.1. Mathematical praxeology

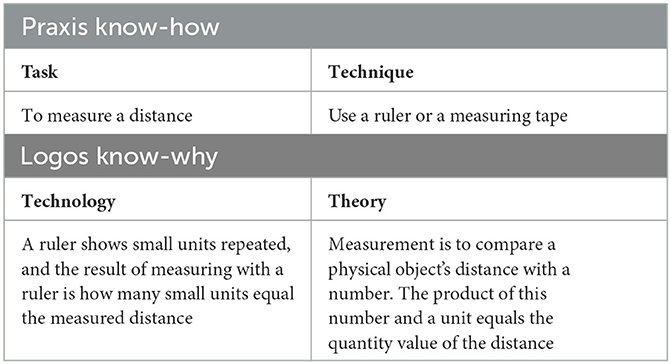
A mathematical praxeology begins with a type of mathematical task to be solved using a technique described in the study of Chevallard and Bosch (2020a). This task could be to measure a distance, decide a value in a function, or do any other mathematical task. In this section, I have given an example of praxeologies for the task of measuring a distance. How to measure a distance may, of course, vary between cultures or age groups of students. In preschool, a valid measurement of a distance could be made with shoes or stones, while in another grade level, a more sophisticated tool is required. In my example, the age group is first grade, and the technique to measure a distance is a ruler or a measuring tape. This technique can be explained and justified. In my example, it is explained with a detailed description of how the ruler, even if it is one object, still shows how the small units are repeated and how the measurement we get is an account of how many small units equal the distance. This explanation may function as a technological argument for the technique. Backing this explanation, there are mathematical assumptions about distances and measurements, which, in a mathematical praxeology, is a theory. See Table 1.

TABLE 1

Table 1. Mathematical praxeology of how to measure a distance.

A mathematical praxeology is consequently not a fixed model of mathematical knowledge. It is deeply rooted in its social setting. It is, however, possible to construct a reference model of a mathematical praxeology where possible elements are displayed and can be used as a reference in praxeological analyses (Gascòn and Nicolás, 2019). In this study, coordination with MKT will result in a reference model and not in an actual description of mathematical knowledge.

3.2.2. Didactic praxeology

In a teaching situation, there is always a didactic praxeology with the task of making a specific mathematical praxeology available for students (see Gellert et al., 2013). A didactic praxeology is a description of knowledge as a praxis (know-how), the teaching methods making mathematics available, logos (know-why), and the reasons or arguments for these methods (Chevallard and Bosch, 2020a). The practical aspect of a mathematics teacher's work, a technique in didactic praxeology, thus makes mathematics available for students with different teaching methods, such as visualization or modeling. Arguments for why a method works, such as technology in didactic praxeology, can be found in concepts describing ways of understanding mathematical concepts, such as subitizing (Mandler and Shebo, 1982), or in theoretical constructs about different phases in understanding mathematical concepts, such as van Hiele's (1984) levels. Theoretical grounds, or theory in didactic praxeology, can be found in basic assumptions, ideas, or principles about mathematics or mathematics teaching and learning.

Following the example of measuring a distance above, a didactic praxis could be to teach how to measure a distance with an understanding of why we need standardized methods and units for measuring. This type of teaching task can be solved with different teaching methods, such as demonstrating, for example, how a ruler is built of many units that repeat themselves or measuring with unstandardized units such as shoes or stones and comparing the results before introducing a standardized unit. In this example, the didactic technology could be six concepts described by Clements and Stephan (2004) to constitute an understanding of measurement. These six concepts imply arguments for different teaching methods for measuring distance. In this case, the theory is ideas about mathematics, teaching, and learning that could be the basis for the technology. It can be mathematical axioms, ideas about orchestrating group discussion in the mathematics classroom, or theories about learning, for example, realistic mathematics education (Wubbels et al., 1997). These ideas may be the basis for teaching about measuring a distance (see Barbé et al., 2005). For an overview of this praxeology, see Table 2. A praxeology is always an interpretation of the knowledge expressed in a specific situation; it is never a complete description of the knowledge of any participant.

TABLE 2

Table 2. Didactic praxeology of how to teach how to measure a distance.

TABLE 3

Table 3. Subject matter knowledge as a mathematical praxeology.

All parts of a didactic praxeology, such as making mathematics available for students (task), the teaching methods (technique), the concepts or theoretical constructs that could explain the methods (technology), and the theoretical grounds behind the technology (theory), are all functions in a math teacher's practice (Chevallard, 2015). They are all built on mathematics teachers' work and provide a language for how theoretical ideas and assumptions can be tools for mathematics teachers' practice (see Chevallard and Bosch, 2020a). In the MKT framework, categories were described, making it clear what mathematics teachers need to know, with no distinction between the methods to know or the concepts, ideas, or theories behind the methods. In this article, I add this distinction by presenting MKT as a didactic praxeology.

4. The MKT framework as praxeologies

A praxeology of what could be, rather than a praxeology of an actual situation, a so-called reference model is made to analyze data (see Wijayanti and Winsløw, 2017). Coordinating MKT and didactic praxeology is not a way to describe what mathematics teachers know or should know. It is only to draw a picture of what mathematics teachers could know if we see teachers knowing and doing as praxeology and consider praxeology an organization of knowledge embedded in a situation. Coordinating two ideas into a conceptual framework, such as the one I describe here, is a way to obtain deeper insights into MKT. This framework is a theoretical bricolage of ideas to understand more than would be possible using the two ideas separately (see Prediger and Bikner-Ahsbahs, 2014). It is consequently not placing one framework into the other but an arrangement where both frameworks contribute to a new whole. In the following sections, I describe the proposed framework, backed with examples from the field of mathematics education. This is an attempt to set up a translation device for this coordinated framework (see Maton and Doran, 2017), which also supports my claim that this coordinated framework may serve the field of mathematics education with a more specialized language about MKT.

To begin with, I present the categories of MKT and how they can be described as praxeologies. The intention is not to make a complete framework of mathematics teachers' knowledge but an attempt to continue the discussion, which was started by Ball et al., with the hope of further discussions in the future.

4.1. Subject matter knowledge as a mathematical praxeology

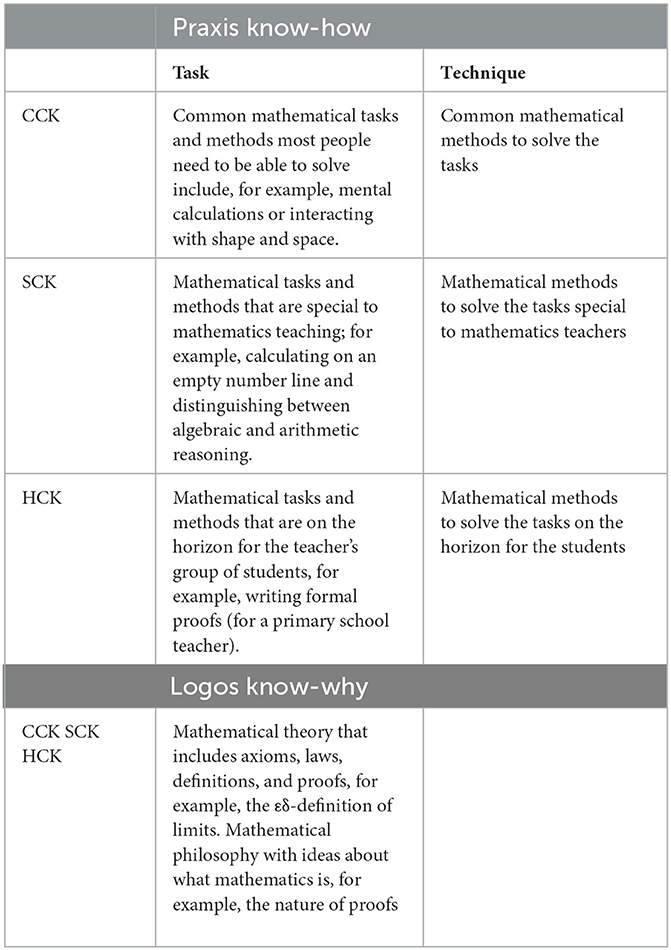
Subject matter knowledge describes the mathematical knowledge of mathematics teachers. With mathematical knowledge, it is possible to translate it into a mathematical praxeology. Praxis is a set of mathematical tasks to be completed with mathematical methods, with different tasks and methods depending on the category. Indeed, mathematics teachers need to know how to do mathematics just as well as a piano teacher needs to be able to play the piano. In the following section, I will draw mathematical praxeologies of the three parts of subject matter knowledge: CCK, SCK, and HCK.

CCK, which is what people in general need to know how to do in mathematics, has common tasks and methods. One example of a common task is to do mental calculations (Pitta-Pantazi et al., 2020) and another is to interact with shapes in everyday life (see Hershkowitz, 2020). These two mathematical activities are beneficial for all, not only mathematics teachers. Hence, they are examples of CCK mathematical praxis. SCK refers to the mathematics teachers need to know how to do and describes tasks and methods special to mathematics teaching. One example is to calculate on an empty number line (Gravemeijer, 2020), and another example is being able to distinguish between algebraic and arithmetic reasoning (Carraher and Schliemann, 2020). Not many types of teachers other than mathematics teachers need to be able to do this, even if the knowledge that comes with calculations on empty number lines and both algebraic and arithmetic reasoning could come in handy. Common to all SCK praxis was that they were all mathematical activities special to mathematics teachers, even if not for all mathematics teachers.

What a mathematics teacher needs to be able to do in mathematics depends, to some extent, on the grade they teach. What HCK does always depends on the teacher and what his/her students know. The HCK for a first-grade teacher differs from the HCK for an upper-secondary school teacher. This means that almost anything from the SCK praxis category could also be HCK, depending on who the teacher is. Writing formal mathematical proof for a lower secondary school teacher could be HCK (Winsløw, 2020), but still, not for all. The nature of HCK is always related to the situation in which mathematics teacher knowledge is discussed.

The three mathematical categories, CCK, SCK, and HCK, share theoretical ground. They are all types of mathematical knowledge grounded in mathematical laws and definitions. Their logos then become mathematical theory with ideas, definitions, axioms, and mathematical laws that may argue for different ways of solving mathematical problems. Ideas of mathematics can be properties, for example, the completeness of real numbers or definitions such as the εδ-definition of limits (Winsløw, 2020). Mathematical ideas can also be considered a form of mathematical philosophy, encompassing ideas about mathematics and the nature of mathematical concepts, such as the concept of proof (see Harel and Weber, 2020). Common for mathematical logos is that they all are ideas of mathematics, not teaching and learning. This division may be important to some extent, but for this study, it is more important to identify what could be logos for the different categories, not if the logos is theory or technology. It can be more fruitful to see logos as a continuum of theoretical weight (see Pansell and Boistrup, 2018).

In several studies, subject matter knowledge is described as what underpins mathematics teaching practices (see Borko et al., 1992) or as a prerequisite for MKT (see Van Bommel, 2012). Seeing each category of MKT in terms of praxis and logos helps us see this differently. Mathematics alone may argue for how to solve mathematical tasks, but it cannot be the only argument for how to visualize fractions or how to predict what will be difficult for students. A limitation with PCK and, by extension MKT, was the difficulty of understanding how the different categories worked together or the connection between PCK and, for example, contextual and affective ideas (Depaepe et al., 2013). The logos for the whole section of subject matter knowledge may also be logos for the PCK, but they are not the only logos. In this study, there was a need to include other concepts and ideas to discuss why we teach or relate to students' learning in different ways.

4.2. Pedagogical content knowledge as a didactic praxeology

For PCK, the task is to make mathematical knowledge available for someone else to teach mathematics. This positions PCK as a didactic domain in the language of ATD. The didactics of mathematics includes both mathematics and didactics as two domains with different types of tasks. The two cannot function without each other They are co-determined. What mathematics a teacher can do affects what mathematics they can make available, and what mathematics they need to make available affects what mathematics they need to (re)discover. It is not to separate the didactic from the mathematics that I propose this coordination between MKT and praxeology but rather to create visible entanglements between the two.

4.2.1. Knowledge of content and students as a didactic praxeology

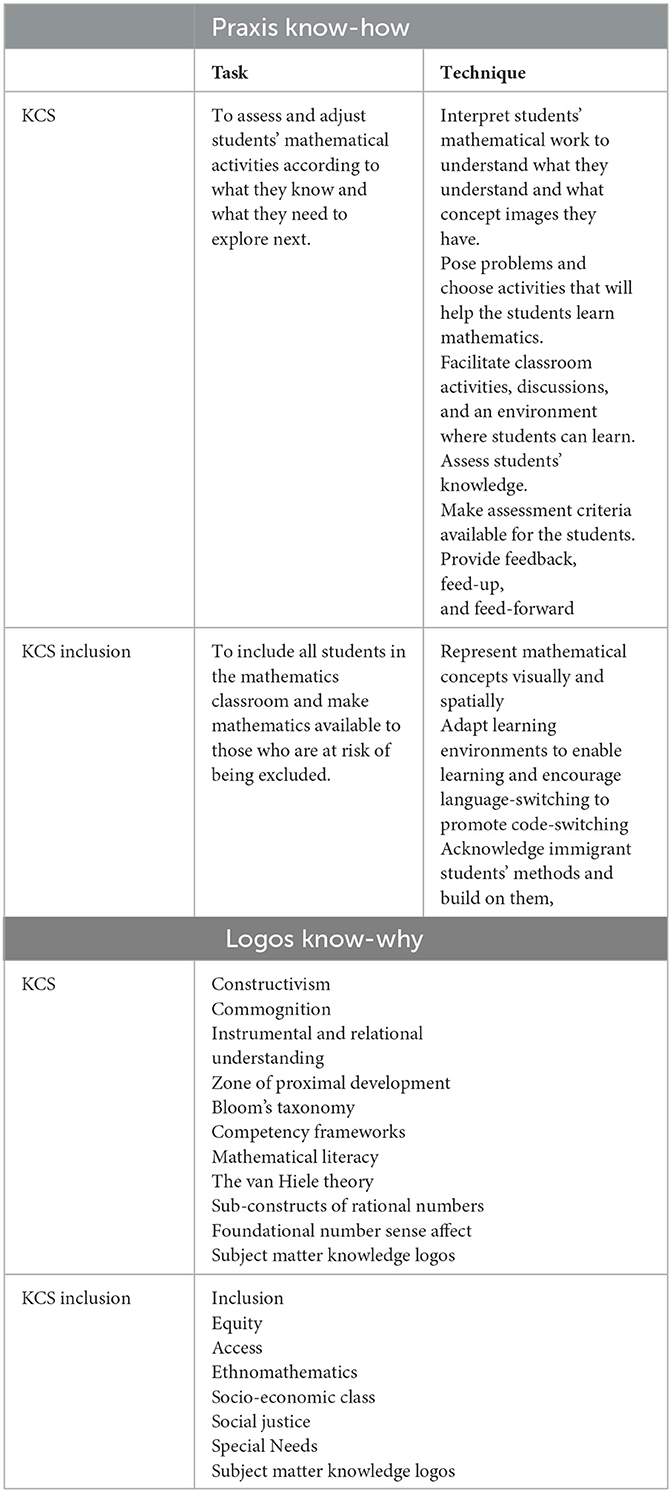
A praxis of KCS is what a teacher does in relation to their students and the content, for example, to understand, assess, or adjust to students learning of mathematics. One task for adjusting to students could be to pose genuine problems for the students, relating the problem to the students' abilities so they can engage in a meaningful way. For students to be engaged in problem-solving and classroom discussions about solutions, teachers must create safe environments relating to what they know about the students (Stephan, 2020). One task could be to interpret solutions and assess what a student knows and what will be needed for the student to move forward, that is, to assess mathematical knowledge. Teachers need to be able to draw from different forms of evidence of knowledge to interpret what they know. They also need to teach their students about what mathematical practices are valuable and provide feedback so that the students can progress (Goos, 2020), or in Hattie and Timperley's (2007) words, provide feedback, feed-up, and feed-forward so that the students know where they are, what they are striving for, and what to do next. Another task could be to interpret their students' concept images or levels of understanding to teach them so that they can reach new levels (see Hershkowitz, 2020). KCS techniques encompass methods for assessment and individualization, allowing mathematical content to be adapted and made accessible to students. These techniques facilitate the customization of teaching approaches to cater to the unique needs and abilities of individual students.

Tasks that stand out as special include specific groups of students, for example, students with special needs. It is special since it has less to do with mathematical knowledge and more with the characteristics of the student(s), still entangled with mathematics. Teachers, for example, need to visualize numbers both visually and spatially for deaf children (Nunes, 2020a). They can also encourage language switching for immigrant students (see Norén, 2011) or build on methods that immigrant students already know rather than disregard those and teach the methods common to the majority of students (Civil, 2020). These teaching activities are where a group of students is at risk of being excluded from mathematics without special engagement from teachers. Even if any child could benefit from these teaching activities, they have been placed in a sub-category of KCS called inclusive teaching activities. See Table 4. Common to these practices are activities aimed at including groups of students in mathematics teaching.

TABLE 4

Table 4. Knowledge of content and students as a didactic praxeology.

The logos of KCS then become theories, frameworks, and assumptions that may ground the methods of, for example, assessment, individualization, and inclusion. Examples of such theories, frameworks, or assumptions are van Hiele's (1984) levels, Kieren's (1993) description of what it is to understand rational numbers, or Sayer's and Andrew's (2015) framework explaining what it is to have a foundational number sense. KCS logos can also be more overarching theories and assumptions, for example, theories of learning such as constructivism (Thompson, 2020), the idea of instrumental and relational understanding (Star, 2020), commognition (Sfard, 2020), and socio-cultural perspective (e.g., Forman, 2020; Roth, 2020a), and the idea of the zone of proximal development (Roth, 2020b). Other possible theoretical ideas to ground teachers' work when relating mathematical content to their students are ideas of what it is to know in general, such as Bloom's taxonomy (Web, 2020), or more specifically to know mathematics. For example, to have mathematical competence (Kilpatrick et al., 2001) or the idea of mathematical literacy (Niss and Jablonka, 2020). Common to these theories, concepts, and ideas was that they all made claims about learning and/or knowing mathematics. Other theories/concepts/ideas with claims that may argue for practices of KCS have claimed about students' emotions such as anxiety (Hannula, 2020), attitudes, and their complex relationship to achievement (Zan and Di Martino, 2020), or motivation (Moddleton, 2020). These ideas directed toward the affective domain, still connected to learning, can also argue for different practices in the mathematics classroom when a teacher adapts and makes mathematics available for his/her students.

Logos for the inclusion practices are ideas about who has access to mathematics and what inclusion is, which is not to say that these ideas only argue for inclusive practices, even though they especially argue for such practices. The idea of inclusion argues for different inclusive practices (Jorgensen, 2020) and perspectives of equity and access to mathematics (Gates, 2020), which all make claims about access to mathematics education. The concept of special needs and the concept of learning difficulties argue for how to teach when learning does not come easy (Nunes, 2020b). Theories more distant from actual student groups but still arguing for inclusion are concepts from sociological perspectives, for example, social justice and socioeconomic class (Gellert, 2020), or ideas from anthropological perspectives connecting students learning with cultural issues, for example, bilingualism and multilingualism (Moschkovich, 2020) and ethnomathematics (D'Ambrósio and Knijnik, 2020). Common to this category are concepts and ideas arguing for inclusive practices, even though reasons for exclusion vary from, for example, deaf students to indigenous students.

Together with these theories and ideas, the logos of subject matter knowledge can also work as theoretical grounds for teaching activities regarding content and students. A teacher predicting what is helpful in the upcoming lesson about geometric figures can, on the ground of the van Hiele levels, prepare a visualization of the properties of figures to challenge students to see the general ideas of, for example, a rectangle since they already know how to talk about specific rectangles. At the same time, mathematical ideas are in play, and the same visualizations are grounded in mathematical ideas of figures and their properties. The teacher is consequently both anchored in ideas of learning and ideas of mathematics, which is why mathematical logos is also logos for KCS but not the only logos. Moreover, in this praxeology and the following paragraphs, I have drawn on technology and theory for the same reasons as in Section 4.1. See Table 4 for an overview.

Table 4 of KCS as a didactic praxeology is far from complete as a reference praxeology. It is an example of what could be. As logos, I have also included the part of the logos from subject matter knowledge, the mathematical logos, since this is always negotiated with other ideas in mathematics teaching practices.

4.2.2. Knowledge of content and teaching as a didactic praxeology

Praxis in a didactic praxeology for KCT is the teaching method a teacher can use to teach mathematics, for example, how specific content can be sequenced and how examples and exercises are selected to help students engage with mathematical content. It could also be on how to present, visualize, or model a mathematical concept so that it is accessible to students (see Ball et al., 2008). In contrast to praxis in KCS, a teacher has the option to choose from a range of methods, while in KCS, the choice of method or visualization is made in relation to the students and their learning. The categories are thus very close to each other; they entangle. It is, however, not the line between them that is helpful for those of us who want to discuss teacher knowledge but rather the ideas highlighted in each category, which are still possible to capture. In the following paragraphs, I have exemplified the praxis and logos of KCT as a didactic praxeology. For an overview, see Table 5.

TABLE 5

Table 5. Knowledge of content and teaching as a didactic praxeology.

The task of KCT is to teach mathematical concepts, which are solved with different teaching methods. One example of this is three suggestions about how to teach algebra: “(1) use solved problems to engage students in analyzing algebraic reasoning and strategies, (2) teach students to utilize the structure of algebraic representations, and (3) teach students to intentionally choose from alternative algebraic strategies when solving problems” (Kieran, 2020, p. 42). Another example comes from research about how to teach functions, where the importance of using multiple representations has been identified as important, or to use technology to help students see generalities between different types of functions and develop an object conception of functions (Niss, 2020). These techniques are related directly to a mathematical concept, even if it is possible to see general ideas, for example, the use of multiple representations, which could benefit other concepts but it has been shown to be especially important to the concept of functions. Other techniques of a more general character can be adjusted in relation to a mathematical concept. For example, scaffolding is the method of building support systems to enhance students' learning (van Oers, 2020). Teaching through project-based learning (PBL) (Lahann and Lambdin, 2020) is another possible method to teach mathematical concepts. Other examples of this type of more general technique are to know how a mathematical concept could be scaffolded or how mathematical concepts could be focused in a PBL project. These are examples of what techniques for teaching mathematical concepts could be. Choosing manipulatives to support specific concepts requires knowledge about both the concepts and how the manipulatives work (Stephan, 2020); knowing how to orchestrate whole-class discussions in problem-solving activities (see Larsson, 2015); and keeping quiet for a few seconds and giving time to thought in discussing mathematics, which is claimed to be beneficial for students as long as the questions in play are challenging and require extra thought (Ingram, 2020). All these methods and many others, which say something about how mathematics could be taught, can be observed to be used here as the techniques of KCT. A teacher may never use a specific method even if they know it, but it can still be negotiated closely with mathematical ideas and the students' and put into practice.

The logos for KCT is the theoretical ideas arguing for techniques where mathematical concepts are taught. Examples of such ideas are the theory of didactic situations, arguing for delegating the mathematical work to students (Brousseau and Warfield, 2020), ideas about visualization (Presmeg, 2020), or ideas about how to organize assessment practices (Black and Wiliam, 2010). More grounding ideas may concern what learning is (e.g., Piaget, 1964) or what it is to know mathematics, here as competencies (Kilpatrick et al., 2001), but also how teaching practices are formed (e.g., Chevallard, 2006). Realistic mathematics education (Wubbels et al., 1997) argues for mathematization and critical mathematics education, arguing for mathematics teaching to reveal how a mathematics-based action could serve different interests (Skovsmose, 2020). Similar to KCS, logos for KCT is also mathematical ideas, laws, and assumptions that, together with ideas about teaching, may argue for different ways to teach mathematical content. This way of seeing mathematical ideas alongside didactic ideas about teaching as grounds for teaching practices may, to some extent, overcome the problem of understanding PCK in relation to affect or contextual issues (Depaepe et al., 2013). Here, different influences of teaching practices are not understood separately but as an organization of knowledge instead of knowledge of separate ideas. For an overview, see Table 5.

To teach mathematical concepts based on ideas about manipulatives and the van Hiele theory compared to teaching based on critical mathematics education. In articulating theoretical and practical elements that are in action in a situation, praxeology as a tool may be a way to discuss and analyze mathematics teaching in a nuanced and explicit way. The notion of co-determination also implies that different situations privilege different theoretical grounds, which, by extension, make different teaching activities possible.

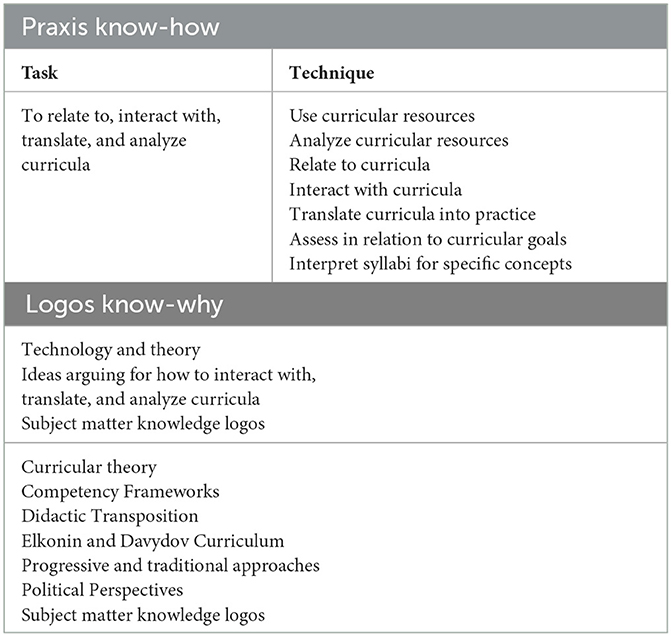
4.2.3. Knowledge of curriculum as a didactic praxeology

The task of knowledge of curriculum is to relate to, interact with, and translate curricula into practice (Llinares et al., 2020) as well as analyze curricula (Pepin et al., 2013). Textbooks, for example, may be inadequate, and a teacher needs to be able to decide what parts to use and how to engage with the structure of mathematics and mathematical concepts provided in the textbook. Teachers also need to be able to analyze textbooks to decide which books to use in the classroom. Regarding policy, it may be more difficult to use or select what to follow or not. At the very least, teachers need to be able to interpret policy so they know what to do. Teachers may also need to be able to analyze policy since, for example, the national curriculum is not always perfect (see Pansell and Andrews, 2017). Knowledge of curriculum could also be gained by using or analyzing an educational program, for example, the mathematics curriculum from Singapore (Lee, 2021), which has gained much interest in the past years. These activities are most certainly done in close relation to the activities of KCT and KCS, but the very relation to the curriculum, curricular materials, or educational programs is central to the activities of knowledge of the curriculum.

Logos of knowledge and curriculum is theoretical ideas with claims about how school mathematics is formed, for example, didactic transposition in mathematics education with claims about how mathematical knowledge is transformed from academic institutions to be accessible for students (Chevallard and Bosch, 2020b), sometimes called curricular theory (e.g., Linné, 2015), with ideas and frameworks arguing for what mathematical knowledge is valid in a specific society. Theories grounding knowledge of curriculum may also be sociological ideas about how a content matter transforms from academic institutions before it is taught in the classroom (e.g., Bernstein, 2000; Chevallard, 2006) or ideas about the role of mathematics education and, for example, political perspectives where the neutrality of mathematics education was problematized (Valero, 2020). Others have claimed for curricular programs such as the Elkonin and Davydov curriculum, arguing for teaching practices where students are engaged in deconstructing mathematical ideas from their origin (Dougherty and Simon, 2020). These ideas can be used to argue for different activities in relation to mathematics curricula. Competency frameworks may not argue directly for curricular practice, but they are included in international assessments (Osta, 2020), influencing policy and curricula, which is why they are included as a concept in this logos category. An overview of policy debates in the USA and the UK, for example, the debate between traditional and progressive approaches, may be viewed as an idea of this category, a historical insight into when and why different approaches are valued (Ernest, 2020). These theoretical ideas are, similar to the curricular practices, not specifically mathematical, but they are still closely related to mathematics. The political ideas are not ideas of any subject; they are ideas about what mathematics and school mathematics do for and to students. If this is a mathematical activity or not depends on what you see as mathematical. The policy debates are also debates about what counts as mathematics, not any subject, which is why mathematical logos from subject matter knowledge is also logos for this category.

In the above paragraphs, I have proposed a conceptual framework, a bricolage of the ideas of MKT, and didactic praxeology. The question is whether this is useful or valid in the field of mathematics education. I have claimed that this framework may offer new insights and tools for a specialized language of mathematics teachers' knowledge. As backing for this claim, I have offered examples as indicators of what each category may imply as an operationalization of the framework where the categories are exemplified with data (see Maton and Doran, 2017). This serves a double purpose. First, to see if both the praxis and logos dimensions of each category can be exemplified with methods and concepts from the field of mathematics education. Second, the field of mathematics education argues against the framework by proposing content and possible sub-categories of the framework. This is also compatible with how a reference model of praxeology is developed, always in relation to data or, as in this study, in relation to examples from a research field (see Wijayanti and Winsløw, 2017). These examples are meant to bring color to the image of MKT as a didactic praxeology, to exemplify but not to create a complete image of mathematics teachers' knowledge. This proposed framework, or reference model, is currently up for discussion and can be extended with more or other examples. It is only a model where mathematics teacher knowledge is articulated to include entanglements between mathematical and didactical elements and between practical and theoretical ideas.

5. Discussion

I have claimed that the MKT framework has offered the field of mathematics education valuable categories, but with limitations, both in articulating what each category holds and as a framework to be used in situated research. I have also claimed that a coordination of the MKT framework and the idea of didactic praxeology could serve the field of mathematics education and, more specifically, mathematics teacher education with a more specified and nuanced language of what knowledge mathematics teachers could make use of in their teaching practices, which would address some of the limitations reported from previous studies. The proposed framework (see Tables 3–6) shows how theoretical ideas and methods can be part of the same category but still be different. It also shows how each category comes with different types of tasks in teaching practices and how theoretical ideas function as grounds for the methods solving these tasks. This bricolage of MKT and didactic praxeology has created two dimensions of each category, which provides a possibility to articulate what teachers can be able to do and what they can know and how these two dimensions can be co-determined when ideas call for different practices and the need for practice calls for ideas to support them. One theoretical idea may argue for methods from all three PCK categories, while several may argue for one method. The way mathematical logos underlie all categories also shows how mathematical ideas are always present when mathematical practices are formed and how they co-exist with other theoretical ideas. At the same time, mathematical tasks and techniques are always present in a didactic praxeology since mathematics teaching aims to make mathematics accessible for students. As a didactic praxeology, MKT puts the co-determination and co-existence of different practical and theoretical ideas at the center rather than separating categories from each other.

TABLE 6

Table 6. Knowledge of curriculum as a didactic praxeology.

Distinguishing between the categories of MKT has been reported to be difficult (Depaepe et al., 2013). Assessing prospective teachers' KCS, it was unclear what knowledge constituted the other (Hill et al., 2008). The idea of praxeology contributes to seeing not what constitutes but what could be connected or engaged in Ball's (2017) words. Praxeology has its limitations: One is that it does not come with categories of knowledge but rather only with a structure of how knowledge can be observed.

MKT offers categories that make it possible to draw a reference model of mathematics teacher knowledge. This may not have clarified boundaries between categories, but in the model, the emphasis on each category comes from the type of task to solve. This takes us right back to the origin of MKT, based on the practices of mathematics teachers and their types of tasks to execute, with the extension of how didactic praxis and logos are entangled and how they function together. In the proposed framework, the same theoretical ideas occur in more than one category, for example, competency frameworks or learner-centered teaching, not to mention mathematical ideas that occur in all categories. Separating praxis from logos makes the role of these theoretical ideas visible. Competency frameworks argue for different practices in relation to the assessment of students' mathematical knowledge compared to how teachers analyze a syllabus. The boundaries are still not clear, but MKT as a didactic praxeology provides the possibility to visualize and discuss the role different ideas can play in relation to each other in mathematics education.

The proposed framework addresses the interconnections between mathematical ideas and broader concepts, such as equity, which aligns with Ball's (2017) call for understanding these entanglements. Seeing knowledge for teaching as didactic praxeologies, the task of teaching a mathematical concept can be grounded not only in mathematical ideas and definitions but also in ideas of sequencing, visualization, and orchestration of classroom discussions. Mathematics underlies all categories, which is necessary since all tasks aim at teaching mathematics. This framework visualizes that mathematics is an important part of the answer but not the only one. The concept of didactic praxeology also entails that it does not know the different kinds of ideas that are the answer. When the ideas function together, teachers can negotiate different ideas and form teaching methods on solid ground. This framework showing how praxis and logos co-exist is not meaningful as an assessment rubric. However, it can function to discuss or analyze the content of mathematics teacher education, for example, teacher education materials, to determine the extent to which they offer mere methods, theoretical arguments, or a combination of both. It may also be one step toward a more complex understanding of the mathematical work of teaching.

Researchers using PCK have struggled with the connection between PCK categories and classroom activities and with the interaction between different types of knowledge, practice, and contexts (Depaepe et al., 2013). In MKT, as a didactic praxeology, the different practices and types of tasks can be articulated. This study begins to show how such a framework can be, and how it is possible to apply, according to the situation under analysis or discussion, with the actual tasks and methods of the situation and how they may be grounded. This means that there is a system to search for in a study, and a reference praxeology, such as the one proposed here, may be used as an analytical framework to enable the understanding of how different ideas and methods interact in a situation and how theoretical ideas can function as grounds for teachers' professional judgment (see Shalem, 2014) when deciding what to do. The articulation of how theoretical grounds may argue for different practices also enables discussions of what idea to lean on in a specific situation. The entanglement of mathematical ideas and equity that Ball (2017) describes argues for what mathematical solutions to value and from whom. Exchange equity for the idea of formative assessment with feedback, feed-up, and feed-forward, which, without involving equity in the entanglement, may argue for how to answer the students so they will move forward in their mathematical learning.

If the result of studying what mathematics teachers know leads to the suggestion that they should acquire more mathematics knowledge (see Borko et al., 1992), and if we fail to distinguish between mathematical praxis and mathematical logos, we are at risk of elevating all mathematical knowledge to the position of theory. If mathematics is the answer, the ability to divide a fraction could be seen as sufficient mathematical knowledge to teach fractions in the first school years. If we assess prospective teachers' mathematical praxis but not their interpretations of mathematical ideas, we make mathematical praxis the privileged knowledge for mathematics teachers, not mathematical logos, even if a mathematics teacher in first grade may benefit more from knowing what a fraction is than from being able to divide fractions. This is an example, and one thing should not exclude the other, but at some point, we need to delimit what to include in mathematics teacher education. Both content and assessment in mathematics teacher education, at least, need to include mathematical praxis and logos, and the proposed framework, where mathematical logos serves any category as logos but not mathematical praxis, may contribute to the discussion of what and how to include mathematical ideas, practical and theoretical, to serve teachers' professional judgment well.

In this study, I have argued for the coordination of MKT and didactic praxeology to offer a different and more nuanced articulation of the categories. In the discussion, I have argued that this coordination, to some extent, was successful. I, however, realize that this is not a full picture of mathematics teachers' knowledge, nor do I wish to offer one. In exploring what could be, we can learn more about how to talk about this complex kind of knowledge. Scheiner et al. (2022), in an exploration of the same kind, promoted a more holistic view of mathematics teachers' work as ecological engineering. As in the present article, this suggestion aims to address the complexity of mathematical knowledge and mathematics teaching. All metaphors of mathematics teachers' knowledge are limited (Scheiner et al., 2022), and the one I propose here will bring some aspects to the forefront but hide others. Therefore, I do not wish to complete the discussion of mathematics teachers' knowledge but to continue the discussion.

In the end, it is the teacher who needs to decide what to do in a specific situation. What a teacher knows what to do and why will feed into his/her professional judgment, but the decision of what to lean on in a decision is also made in a situation in relation to students, parents, colleagues, and others participating in a mathematics teacher's practice (see Shalem, 2014; Biesta, 2015). Besides all a teacher may know, this teacher needs the authority to decide. If he/she learns that someone else, whether it be mathematics, Vygotsky, or a competency framework, knows better than him/her how to teach, he/she may constantly feel inadequate. Relying on superficial experts can also lead to these individuals overriding the teacher's judgment, preventing teachers from tailoring their teaching methods to suit the needs of specific students. However, when teachers grasp theoretical ideas and how they sometimes conflict (Biesta, 2015), and understand their connection to teaching methods, it provides them with the freedom to exercise their own judgment in the classroom. Teachers doing the mathematical work of teaching, knowing their students are the ones who can know what needs to be done in a particular situation. Teacher education can only provide support for their professional judgment.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

AP is the only author of the article contributing with data collection and analysis as well as writing.

Funding

This article reports on research conducted in the TRACE project (tracing mathematics teacher education in practice) with funding from the National Research Council, project 2017-03614.

Acknowledgments

Except for the Swedish National Research Council and Stockholm University, who made this research financially possible, a special thanks goes to the LUGN group. Thank you for your insightful comments early, during, and, for some of you, very late in the process. This could not have been done without you.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adler, J., and Davis, Z. (2006). Opening another black box: researching mathematics for teaching in mathematics teacher education. J. Res. Math. Educ. 37, 270–296. Available online at: https://www.jstor.org/stable/30034851 (accessed Auguat 4, 2023).