
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Educ. , 20 June 2023
Sec. Teacher Education
Volume 8 - 2023 | https://doi.org/10.3389/feduc.2023.1162681
This article is part of the Research Topic Theories and Theorising in Mathematics Education and How they Inform Teacher Education View all 6 articles
To reach for abstraction is a major but challenging goal in mathematics education: teachers struggle with finding ways how to foster abstraction in their classes. To shed light on this issue for the case of geometry education, we align theoretical perspectives on embodied learning and abstraction with practical perspectives from in-service teachers. We focus on the teaching and learning of realistic geometry, not only because this domain is apt for sensori-motor action investigations, but also because abstraction in realistic geometry is under-researched in relation to other domains of mathematics, and teachers’ knowledge of geometry and confidence in teaching it lag behind. The following research question will be addressed: how can a theoretical embodied perspective on abstraction in geometry education in the higher grades of primary school inform current teacher practices? To answer this question, we carried out a literature study and an interview study with in-service teachers (n = 6). As a result of the literature study, we consider embodied abstraction in geometry as a process of reflecting on, describing, explaining, and structuring of sensory-motor actions in the experienced world through developing and using mathematical artifacts. The results from the interview study show that teachers are potentially prepared for using aspects of embodied learning (e.g., manipulatives), but are not aware of the different aspects of enactment that may invite students’ abstraction. We conclude that theories on embodiment and abstraction do not suffice to foster students’ abstraction process in geometry. Instead, teachers’ knowledge of embodied abstraction in geometry and how to foster this grows with experience in enactment, and with the discovery that cognition emerges to serve action.
Today’s geometry education in primary school is moving away from focusing on formal spaces and shapes toward a growing role for spatial reasoning and geometric problems encountered in daily life (Clements, 2003; Jones and Tzekaki, 2016; Doorman et al., 2020). In this education inspired by “realistic geometry” (De Moor, 1999), students interpret distances, shapes and angles, orient themselves on routes using digital maps in combination with a real-life view, and discover figures and constructions. While exploring spatial and geometric phenomena, such as projections, shadows, mirrored images and symmetries, students engage in problems with the goal of grasping the underlying mathematical and geometrical concepts and structures. This process of understanding the structure of a mathematical concept is regarded as abstraction (Dreyfus, 2014). Although recognized as a key component of mathematical thinking (Drijvers, 2015), which has become increasingly important in primary education in recent years (Meijerink et al., 2009), teachers still struggle with the issue of how to foster abstraction in all their students (White et al., 2012).
Most contemporary theoretical perspectives on abstraction relate to the mathematical topics of numbers and algebra, leaving the field of geometry underexposed (Breive, 2022). Where the Van Hiele level theory of geometric understanding (Van Hiele, 1986) does relate to abstraction, its applications primarily relate to the abstraction of formal shapes, forms and solids. For a realistic geometry approach, a suitable theory on how abstraction can be fostered is lacking, as is knowledge about fruitful ways for teachers to incorporate such a theory in their teaching practices. As there is a danger of making students engage in abstraction without a concrete basis (White and Mitchelmore, 2010), teachers need to be able to invite students to take part in the process of abstraction and simultaneously maintain a strong link to the concrete situation. The question therefore arises how the process of abstraction in geometry can be brought about from such a concrete starting point.
In exploring the question of how abstraction in geometry education can be fostered, the theory of embodied cognition may provide a fruitful approach. Embodied cognition theory proposes that all cognition, including mathematic thinking skills, is rooted in bodily experience, i.e., in the actions and interaction of the body with the physical environment (Abrahamson and Lindgren, 2014). If we consider that abstraction arises from the actions the learner undertakes, teachers need to be able to acknowledge and elicit students interactions within the learning environment, which—in the case of realistic geometry—is a real-life geometric situation.
Research on the teaching and learning of geometry indicates that using manipulatives and physical manipulation is important for gaining geometrical understanding (Jones and Mooney, 2003; Clements et al., 2018). However, using manipulatives does not automatically lead to abstraction (Simon, 2022). The role of the teacher in guiding students toward abstraction is therefore essential. Fostering students toward abstraction proves to be a challenge for many teachers (White et al., 2012; Simon, 2022). For the case of geometry, this seems even more demanding, since teachers often lack sufficient knowledge of geometry for teaching (Jones and Tzekaki, 2016; Clements et al., 2018), and many of them feel insecure in teaching geometry (Kuzle, 2022). The challenge in teacher education, to prepare teachers for fostering abstraction arising from students physical manipulation, is not only to pay more attention to geometric knowledge, but also to focus on emerging perspectives in geometry education, such as embodied cognition (Jones and Tzekaki, 2016; Sinclair et al., 2016).
In this paper, we aim to explore the first steps needed for an embodied abstraction approach to geometry in teacher education. To do so, we integrate two approaches in this study. First, we investigate the theoretical perspective of embodied cognition for abstraction in geometry education. Second, we investigate teachers’ experiences and needs in their teaching toward abstraction through realistic experiences. This is done through semi-structured interviews. The following research question will be addressed: how can a theoretical embodied perspective on abstraction in geometry education in the higher grades of primary school inform current teacher practices? In answering this question, we hope to contribute to the teachers’ professional development in the fostering of abstraction in accordance with the embodied perspective.
To describe the theoretical perspective on the fostering of abstraction in geometry through the lens of embodiment, we performed a narrative review in combination with a scoping review (Arksey and O’Malley, 2005). We started with the scoping review to identify the scope of the combined field of abstraction, realistic geometry and embodiment. The research question used for the scoping review reads, what theoretical perspectives on abstraction and embodiment in realistic geometry education are relevant for the teaching and learning practice of primary school teachers? To select relevant publications we performed databases searches in Scopus, Web of Science and Eric using a single query.1 The search was completed on December 18, 2020. The combined results were organized in Mendeley Desktop (reference management software) and checked for duplicates. This resulted in 84 articles. The first selection for exclusion was done based on criteria for title and journal/publisher. The second selection for inclusion, performed by the first author, was done by reviewing the abstracts of each remaining article. The resulting articles all deal with the three themes: geometry (or mathematics), abstraction and embodiment. However, none of these describe abstraction for the case of realistic geometry. This showed that more theoretical work was needed to describe an embodied approach to abstraction relevant for teaching geometry, and to support in-service teachers’ practice. For the narrative review relevant papers were selected by using the technique of snowballing on some key articles in the previous mentioned selection. Combined with ideas from realistic geometry education and relevant theories on embodiment and action-based approaches to abstraction, this allowed for a synthesis toward a description of abstraction from an embodied perspective applicable for geometry learning.
Information about teacher practice was obtained by performing an interview study on primary school teachers’ experiences with and opportunities for embodied abstraction in geometry. The purpose of this interview is twofold: first, to investigate teachers’ views on and knowledge of geometry teaching and learning, second, to investigate experiences and needs related to the process of abstraction in geometry. For this, our view on abstraction, as it emerged from the theoretical perspective, was used and presented as a definition.
The conducted interviews were semi-structured. The questions were arranged in groups with the following topics: (1) geometry education – including the topics (1a) acting, (1b) using manipulatives and (1c) verbalizing in relation to geometry; (2) knowledge of knowing why;2 (3) the process of abstraction; (4) abstraction related to a particular geometry problem, and (5) fostering abstraction. The six interviewees were teachers from four different partner schools of the University of Applied Sciences Utrecht. They taught Grades 3 (teacher A), 3 and 4 combined (B), 4 (E, D), 4, 5 and 6 combined (C) and 6 (F). Teachers B, C and F have 10 plus years’ experience in the upper grades of primary school; teachers A and E have two plus years’ experience, and teacher D has 1 year’s experience. Teacher C is an experienced Montessori teacher. Each interview lasted between 50 and 60 minutes and was audio recorded. The recording was transcribed verbatim using the Automatic Transcription of Dutch Speech Recognition website.3
To analyze the interview data, the transcripts were coded in ATLAS.ti, using a combination of a deductive and inductive approach and in collaboration with a second researcher. First, a coding scheme was made consisting of seven code categories: abstraction, geometry, knowing why, verbalizing, reflecting, acting and using manipulatives, and general teaching and learning. These categories were based on the interview structure as well as theory presented in this study. The category “general teaching and learning” was used because we foresaw that some quotations might be relevant and would not fit the other categories per se. The actual coding process was done via inductive coding (Saldana, 2009). Relevant quotations were selected by the first author and assigned a category. They were coded further via open coding in ATLAS.ti. The final coding scheme was made in cooperation with the second author. Quotations including their assigned codes were exported into an excel sheet. The second author commented on the codes and the allocations of the quotations. This process was repeated two times, after which agreement was achieved. The final coding scheme is presented in Table 1.
In this section, the results from the theoretical study and the interview study are outlined. The synthesis of these findings will be described in the discussion section, as well as opportunities and implications for teacher education.
In this subsection, we synthesize the most relevant perspectives on abstraction, geometry in primary education and embodied cognition. We end with defining abstraction in realistic geometry through the theoretical lens of embodied cognition.
The topic of abstraction has been extensively studied throughout the history of mathematics education, and has remained popular in the last two decades (Hershkowitz et al., 2001; Ferrari, 2003; Mitchelmore and White, 2007; Nemirovsky et al., 2020). Most of these contemporary studies focus on abstraction related to the mathematical topics of numbers and algebra. Concerning the field of geometry, the field of realistic geometry remains underexposed.
Considering mathematics education, abstraction is described by Dreyfus (2014) as a process “by which learners attempt, succeed, or fail to reach an understanding of the structure of a concept or a strategy or a procedure” (p. 5). Since abstract concepts are often learned in isolation (White and Mitchelmore, 2010) “without engaging in the abstraction process” (p. 207), White and Mitchelmore suggest that the process of abstraction should keep a strong link between the mathematical concept and the experience from which it emerges. This approach to abstraction is influenced by Skemp (1987), who describes abstraction as an activity where students become aware of mathematical similarities through their experience, culminating into a concept. Denoting similarities is very similar to Piaget’s notion of empirical abstraction (Beth and Piaget, 1966). Empirical abstraction entails that common characteristics are perceived in different objects, generalizations are made accordingly and certain classes or concepts are established. However, in Mitchelmore and White’s view, abstraction differs from such a generalization idea. They claim that “abstraction creates a new mental object (a concept) whereas generalization extends the meaning of an existing concept” (Mitchelmore and White, 2000, p. 212).
According to Piaget (1971), mathematical knowledge can be established via abstraction in two possible ways: (1) from the objects that the learners acts upon and (2) from the actions itself. The first relates to empirical knowledge (on objects experienced) and is therefore regarded as empirical abstraction. The second possibility of abstraction relates to action, of which Piaget states “we can also take into account the action itself, or operation if you will, since the transformation can be carried out mentally… abstraction is drawn not from the object that is acted upon, but from the action itself” (p. 16). This type of abstraction is named reflective abstraction by Piaget. Where abstraction relates to the transfer between different hierarchical levels, the term reflective refers to the reorganization of thought on actions on these levels. Reflective abstraction, therefore, is based on the coordination of actions. An example of reflective abstraction is the discovery that the total number of objects in a set is unaffected by how the individual objects are counted. Cetin and Dubinsky (2017) describe reflective abstraction as the process by which new mental objects are formed via reflecting on actions on a lower level in order to reconstruct and integrate these on a higher level. In his later work, Piaget (1985) stated that reflective abstraction might be the mechanism by which all mathematical concepts can be constructed, and as such forms the basis for all mathematical thinking.
The importance of action leading toward abstraction is also recognized by Sfard (1991). According to Sfard, the process of learning mathematical concepts (and subsequently the process of abstraction) starts with operations on (lower level) mathematical objects. Sfard describes three stages in the process of concept formation leading to abstraction: interiorization, condensation and reification. Reaching a higher level of operating occurs already at the interiorization stage. Interiorization suggests becoming familiar with a mathematical process by operating, e.g., counting or dividing. A process has been interiorized if it “can be carried out through (mental) representations” (p. 20). During the second stage, condensation, the structure of the process becomes apparent in its totality and “a person becomes more and more capable of thinking about a given process as a whole, without feeling an urge to go into details” (p. 19). Interiorization and condensation happen gradually according to Sfard, whereas reification is an ontological shift where “a process solidifies into an object, into a static structure” (p. 20). During reification, the notion of the process is fully grasped; process and concept are merged, which finalizes the process of abstraction.
Hershkowitz et al. (2001) consider abstraction as an activity of vertically reorganizing previously constructed mathematics into a new mathematical structure. This new structure is then represented “often in a more abstract or formal form than the original” (Hershkowitz et al., 1996, p. 144). The term vertical originates from realistic mathematics education (RME) and refers to vertical mathematization. According to Freudenthal (1968), the focus in mathematics education should not be on mathematics itself (as a closed system) but on the process of mathematization. During mathematization a student re-invents mathematics by constructing mathematical relations from experienced problem situations and from there goes on to develop more formal mathematics (Freudenthal, 1991). Treffers (1987) describes two types of mathematization, horizontal and vertical; a distinction later adopted also by Freudenthal (1991). Within horizontal mathematization, “students come up with mathematical tools, which can help to organize and solve a problem located in a real-life situation” (Van den Heuvel-Panhuizen, 2001, p. 3), and during vertical mathematization, the focus is on “the process of reorganization within the mathematical system itself.” White and Mitchelmore (2010) recognize abstraction in both types of mathematization.
Considering the above, the theoretical views on abstraction emphasize (a) abstraction is a process, (b) that encompasses the developing of new mathematical concepts or structures, (c) that takes place through action, and (d) includes reaching a higher level of thinking and acting by reflecting.
Geometry in primary education is a multifaceted field of mathematics. It encompasses the study of shapes and figures and deals with spatial phenomena and their relation to mathematical concepts. This diversity of activities is clearly described by Usiskin (1987), who discerns four major themes of geometry: (a) visualizing, drawing and constructing figures; (b) studying the spatial aspects of the physical world; (c) representing nonvisual mathematical concepts and relationships; and (d) standing as a formal mathematical system. Clements (2003) describes geometry in Grades pre-K to 12 as follows: “the study of spatial objects, relationships and transformations; their mathematization and formalization; and the axiomatic mathematical systems that have been constructed to represent them” (p. 2). This definition is particularly significant because of the mentioning of both spatial objects and relations, and the process of mathematization. As we have seen in the previous section, mathematization relates to (the process of) abstraction.
Traditionally, the focus in geometry education has been on Euclidian geometry, in which the study of two-dimensional figures and shapes plays a central role (Sinclair and Bruce, 2015). In their study on abstraction where gestures are used, Kim et al. (2011) focus on such geometric shapes. Modern approaches to geometry, however, show an increasing focus on spatial reasoning (Sinclair et al., 2016). Spatial reasoning is described by Sinclair et al. as “the activity of imagining static or dynamic objects and acting on them (mentally rotating, stretching, etc.)” (p. 6) and can help a child to learn to understand basic geometric principles like: “boundedness, flatness, parallels, perpendiculars, curves, distance, and mapping” (p. 6). Clements et al. (2018) show the importance of spatial reasoning in claiming that “young children’s abilities to engage in geometric thought and spatial reasoning can support their overall mathematical and cognitive development” (p. 2). Contrary to what had long been a popular belief, Newcombe and Stieff (2012) show that spatial reasoning can be improved through education. The growing role of spatial reasoning in geometry education is also recognized in the five major trends that Sinclair and Bruce distinguish in contemporary research on geometry in primary school.
“(1) the role of spatial reasoning and its connection to school mathematics in general and school geometry in particular; (2) the function of drawing in the construction of geometric meaning; (3) the affordances of digital technologies in geometric and spatial reasoning; (4) the importance of transformational geometry in the curriculum (including symmetry as well as the isometries); and, (5) extending primary school geometry from its typical passive emphasis on vocabulary (naming and sorting shapes by properties) to a more active meaning-making orientation to geometry (including composing/ decomposing, classifying, mapping and orienting, comparing and mentally manipulating two- and three-dimensional figures).” (Sinclair and Bruce, 2015, p. 320).
The aforementioned trends and activities resonate with the realistic geometry that emerged in the Netherlands in the twentieth century (De Moor, 1999). Since the 1970s, an intuitive approach to geometry (strongly related to spatial reasoning) began to develop, focusing on (reasoning about) activities with vision lines, vision angles, sighting, rays of light and with projecting, shadowing, and perspective (De Moor and Groen, 2012). This so-called vision geometry was inspired by Freudenthal’s ideas on realistic geometry (Freudenthal, 1973). Freudenthal states: “geometry is grasping space (…) that space in which the child lives, breathes and moves. The space that the child must learn to know, explore, conquer, in order to live, breathe and move better in it” (p. 403). Per Freudenthal, geometry should be meaningful and encompass problems, tasks and activities experienced in our direct surroundings, with the aim to learn about mathematical objects and concepts. He illustrated this approach with questions like “Why does a piece of paper fold along a straight line? Why does a rolled piece of paper become rigid? Why does a tied paper ribbon show a regular pentagon? And, how do shadows originate?” (Freudenthal, 1971, p. 6). Contemporary geometry educational programs in the Netherlands are inspired on this realistic geometry, and therefore largely based on spatial orientation, with little attention for the formal study of geometric shapes and figures (Gravemeijer et al., 2007).
In summary, we focus on realistic geometry, the study of realistic situations, with an emphasis on spatial reasoning and the discovery of geometric and mathematics concepts. We leave aside the more formal studies of shape and figures and consider geometry in this study as the wide-ranging domain of studying and structuring spatial objects and phenomena in the experienced world.
As we are not focusing on traditional formal aspects of geometry, we leave aside the theory of figural concepts (Fischbein, 1993) and the theory of figural apprehension (Duval, 1998), and only briefly discuss the Van Hiele level model of geometrical thinking (Van Hiele, 1986). The Van Hiele model has been very influential in describing geometric understanding in terms of five consecutive levels. Geometrical thinking starts at the visual level, where figures are judged by appearance (in a holistic manner) only. At the second level, the descriptive level, properties of figures can be described (and analyzed) using language, not necessarily in a logical order. It then passes to informal deduction (also named abstraction), where properties are logically ordered using reasoning. At the formal deduction level, students are capable of delivering formal proofs, and at the last level, rigor, students understand the whole system of Euclidian geometry. The Van Hiele theory of geometric understanding does seem to relate to abstraction, but since it primarily applies to the properties and study of figures, we do not consider the Van Hiele levels suitable for pursuing abstraction related to realistic geometry.
Characteristic for the teaching and learning of realistic mathematics is the concept of different levels of comprehension (Van den Heuvel-Panhuizen, 2001). The same holds for realistic geometry (Freudenthal, 1971; Goffree and Jansen, 1976; De Moor, 1999; Gravemeijer et al., 2007; Doorman et al., 2020). Goffree and Jansen describe four stages of teaching and learning geometry: observing, doing, thinking and seeing. After observing, a general orientation, the student acts and uses manipulatives applicable to the concrete situation. Comprehension grows during the third stage, thinking, that can be regarded as understanding according to De Moor (2000). In the last stage, seeing, “the insight between different phenomena can be raised to a higher level” (p. 86).
Reaching a higher level is also advocated by Gravemeijer et al. (2007). Central in their approach is the concept of mathematizing space (the modeling of geometrical experiences), a process stimulated through reflecting and mental imagination, whereby students explain problems using drawings, constructions and mathematical concepts. Eventually, “a higher abstraction level will be reached” (p. 91). According to Doorman et al. (2020), at this stage “you make a model or a drawing to describe the phenomenon with geometrical means. Reasoning about these means will help you to develop mathematics and to understand the modeled phenomena” (p. 285).
The forming of concepts and structures is key in the process of abstraction. In describing learning processes in realistic geometry, Doorman and colleagues point to the creation of such structures, called “situation models,” that lead to formalization. Learners are first presented with explorative activities “through which they can further develop their geometrical intuitions” (p. 291). At this stage, preliminary structures of the geometric problem can emerge in the students’ reasoning. Next, mathematization is elicited by “focusing on the development of situation models like vision lines which bring the students from the informal to the more formal geometry” (p. 291). These models are built on the structures that emerge during the students’ reasoning.
The fostering of students’ reasoning and abstraction processes, related to realistic geometry problems also concerns the use of the right language. Both Freudenthal (1971) and Goffree (1992) emphasize the importance of language use and the teacher’s awareness thereof. Goffree describes three levels of language use. The demonstrative level, where language is used intuitively, the relational level, used in referring to movements related to certain positions or objects, and the functional level. Here, subjective elements are mostly discarded and a more formal (mathematical) terminology is used. Goffree points out that to develop mathematical discourse, a student should, when acting within a problem situation, be encouraged to use words on a functional level. Although these levels are not categorically implemented in geometry education, we expect that stimulating the use of higher levels of language could enhance students’ reasoning in geometry and therefore the process of abstraction.
In short, relevant theoretical views on the teaching and learning of geometry distinguish different levels of understanding (Van Hiele, 1986), acting (Goffree and Jansen, 1976), language use (Goffree, 1992) and mathematising and modeling (Gravemeijer et al., 2007; Doorman et al., 2020).
Based on the above, the most important elements of teaching and learning realistic geometry in primary school are: (1) acting within “realistic” problem situations, (2) mental acting and reflecting on that acting, (3) verbalizing using mathematical related language and (4) the forming of models and mathematical structures for the geometrical situation.
Concerning the process of abstraction in relation to the teaching and learning of geometry, the focus is on the discovery of mathematical structures in geometrical and spatial phenomena. This is done through a process of structuring and reflecting on students’ actions and experiences. This central role for action is highlighted in the theoretical lens of embodied cognition, which we describe in the next section.
Embodied cognition theory focuses on the interaction between the body and the environment, bringing forth the idea that cognition emerges from those interactions and is therefore not restricted to brain processes. Regarding an embodied cognition approach to mathematics and mathematics education, extensive research has been done in the last two and a half decades (Radford, 2009; Abrahamson and Sánchez-García, 2016; Mavilidi et al., 2018; Sinclair and de Freitas, 2019). Embodied cognition is an umbrella term for many theories that present a variety of claims, from conservative to radical (Hutto and Abrahamson, 2022), regarding the relationship between cognition, the body and the environment (Wilson, 2002; Barsalou, 2008; Weisberg and Newcombe, 2017). In the next section, some of the these claims will be outlined and discussed in relation to abstraction and geometry.
The core idea in embodied cognition theory is that action and engagement with the environment plays a fundamental part in cognitive processes. In conservative embodiment theories, as opposed to the strong embodiment stance, cognition is partially dependent on our interactions with the environment via the sensory and motor systems in which we live. At the basis of mild embodiment is the theory of grounded cognition (Barsalou, 2008). Grounded theory rejects the computational view of the mind. The latter holds the idea that cognition comprises amodal mental representations (detached from the concrete world) that resemble some information units, such as formal notations and symbols organized in semantic networks. Barsalou states “it is unlikely that the brain contains amodal symbols” (p. 618). Instead, cognition is grounded in modal representations (including sensual and motoric information). Cognition is thus constituted perceptually, as sensory representations of physical stimuli are captured and stored. These perceptual representations can be reenacted even when the stimuli that shaped these units in actual experience are absent. In this way, even abstract mathematical knowledge of concepts, relations and structures can be presented by reenactment.
Grounded cognition theory recognizes the possibility that cognition can be connected to sensuous experience in multiple ways, including “simulations, situated action, and on occasion, bodily states” (Barsalou, 2008, p. 619). Although grounded cognition does not deem the body necessary for cognition, it acknowledges the importance of actions (body-based and gestural) for cognition. Nathan et al. (2014) define body-based actions, performed to introduce abstract mathematical ideas as “grounding actions,” and conclude that these can indeed support mathematical reasoning and therefore abstraction.
Goldin-Meadow and Beilock (2010) propose that gestures can bridge action and abstract thought. Not only do gestures reflect the actor’s thinking, they give feedback and can alter that thinking. Alibali and Nathan (2012) argue that certain types of gestures, used when communicating about mathematical concepts, show that mathematical cognition “is based in perception and action, and it is grounded in the physical environment” (p. 251). They distinguish three types of gestures: pointing gestures, representational gestures and metaphoric gestures. Pointing gestures are used to indicate “objects, locations, or inscriptions in the physical environment” (p. 252) and are often used alongside speech. They “reflect the grounding of cognition in the physical environment” (p. 277). Representational gestures are gestures that “depict semantic content….via handshape or motion trajectory” (p. 252). They communicate mental simulations of a learner’s perceptions and actions related to mathematical knowledge. An example is the movement of one’s hand that depicts the changing slope of a mountain road. Processes related to mathematical thinking that can be noticed in students’ and teachers’ representational gestures might involve “simulations of actions on mathematical objects, simulations of visual images of mathematical ideas or inscriptions, and simulations of the real-world situations that mathematical problems address” (p. 274). The third type of gestures Alibali and Nathan describe is metaphoric gestures. These strongly relate to conceptual metaphors, described in detail by Lakoff and Núñez (2000). An example of a metaphoric gesture is a body-based action of physically taking steps on an imaginary straight line while communicating corresponding numbers. Such a gesture provides the conceptual metaphor of numbers as locations in space.
According to Nathan and Walkington (2017), gestures can be considered an expression of mathematical reasoning. In their theory of grounded and embodied mathematical cognition, Nathan and Walkington point out the necessity of the coordination between dynamic gestures and language. Dynamic gestures reflect motion-based transformations of mathematical objects. When carefully coordinated, dynamic gestures and language could together serve as a mediator of mathematical thinking, enabling students to formulate “an insightful and explicable chain of reasoning that constitutes a mathematical proof that is both externally valid and internally meaningful” (p. 8).
Hayes and Kraemer (2017) claim that abstract concepts in mathematics are better understood “when they are initially grounded in hands-on learning activities” (p. 10). Concepts are considered abstract when they refer to the emergent properties resulting from interaction with concrete materials. Understanding these abstract concepts, from a grounded cognition view, requires comprehending a relationship between the experienced concrete materials. However, no details are described on what type of sensory-motor activities is best suited for their proposed approach.
One of the rare studies on embodiment that include an experimental and quantitative approach is the one by Ng and Ye (2022). In their work, over 100 11–12-year-old students explored the properties of prisms and pyramids through making these solids with a 3D printing pen. The pre-posttest results show a significant improvement, with a large effect size (d = 1.121, p < 0.001). The analysis of the qualitative data suggest that the embodied activities with the 3D printing pen might explain this learning outcome. The topic of abstraction, however, is not addressed in this study.
The above shows that as per embodied cognition views, based on grounded cognition theory, situated body-based actions and various types of gestures can spark and display mathematical understanding and help structuring the environment in a geometrical way. Although the grounding of abstract concepts (via sensory-motor representation) can facilitate abstraction (Hayes and Kraemer, 2017), we hesitate to say whether these actions alone might be enough for engaging in and continuing the process of abstraction.
The strong embodied cognition stance has its origin in ecological psychology, theory of dynamic systems and enactivism (Chemero, 2009; Abrahamson and Sánchez-García, 2016). Strong views on embodiment deny any ideas of mental representations and the faculty of computing (Hutto and Abrahamson, 2022). Although strong embodiment has often gained criticism, in the sense that without mental representation it would be impossible to explain “real” cognition including thinking and planning, some scholars present ways that cognition can be modeled in such a radical way (Wilson and Golonka, 2013; Abrahamson and Sánchez-García, 2016; Sanches de Oliveira et al., 2021).
Wilson and Golonka (2013) argue that, since the perceptual world is very rich, perceptual information needs no further internal enrichment and thus no representation. Instead, all elements in the environment that might support complex behavior, as well as “the information that might serve to tie them together” (p. 11), should be considered in embodied research. To understand how these environmental characteristics are coupled with specific behavior, Wilson and Golonka suggest to consider four questions regarding embodied tasks. First, what is the task to be solved? Second, what are the resources that a person has access to in order to solve the task? Third, how can these resources be assembled to solve the task? And last, does this person assemble and use these resources? Considering these questions with regard to education, researchers could understand a close relation between the environment and the person’s interaction with it. More strongly, in Wilson and Golonka’s view, it is paramount to place embodiment at the center of the learner’s solution of a given task. Considering our focus on realistic geometry, this is something we agree with.
Wilson (2002) describes six views on embodied cognition, some of which indicate a radical embodiment conviction. The first reads: cognition is situated. As discussed in the above, this applies to realistic geometry, where tasks can be considered as situated cognition tasks. The second view on embodiment reads: cognition is time-pressured. Since situated tasks in realistic geometry take place in real time, coping with time pressure is a logical consequence. An important factor of time pressure in a task that demands continuous action is that “there may simply not be time to build up a full-blown mental model of the environment, from which to derive a plan of action” (p. 628). This is an important aspect to consider for the case of realistic geometry. The third view reads: we offload cognitive work onto the environment. In other words, artifacts and manipulatives do the work we otherwise would be doing in our heads. This certainly applies for the case of realistic geometry, where mathematical tools in the environment are used. Regarding such tasks, Wilson states: “the advantage is that by doing actual, physical manipulation, rather than computing a solution in our heads, we save cognitive work” (p. 629). Wilson’s fourth view reads: the environment is part of the cognitive system. This is certainly the most radical claim. Wilson describes this in more detail as: “the forces that drive cognitive activity do not reside solely inside the head of the individual, but instead are distributed across the individual and the situation as they interact” (p. 630). The idea that forces that drive cognition do not reside solely in the head, is inherent to the whole embodied cognition spectrum. The second part is problematic, according to Wilson. However, according to Clark (2012), our daily lives gives ample evidence that we can see our cognition as extended to the world. For example, we find it easier to offload cognition by storing telephone numbers and future events in our smartphone memory and calendar, instead of remembering them by heart. Not only do we offload cognition, but due to our dependency on certain tools in daily life (for example a knife to cut food with) we can argue that such a tool becomes part of our cognitive system (Shvarts et al., 2021). Therefore, to understand mathematical cognition, we must study the situation as a unified system of artifacts and the body. Wilson’s fifth view reads: cognition is for action; sometimes phrased as “cognition serves action.” Cognition evolves in service of action and is therefore based on action. Ultimately, this would mean that the only way we can come to know and understand is through our need for particular action. Certain actions thus drive the development of our cognition. This view is central in the ideas of Nemirovsky and Ferrara (2009). On the matter of grasping conceptual and mathematical knowledge, they say: “whatever we can recognize as rational, rule-based, or inferential, is fully embedded in our bodily actions” (p. 3). Regarding realistic geometry, the tasks where cognition is guided by action could be a fruitful starting point for eliciting an abstraction process. The last of the six views reads: off-line cognition is body-based. Wilson states: “even when decoupled from the environment, the activity of the mind is grounded in mechanisms that evolved for interaction with the environment—that is, mechanisms of sensory processing and motor control” (p. 626). So, even when the artifacts and mathematical tools are not physically present, the knowledge gained from these artifacts still involves the sensory-motor control processes which were active during the performance with these artifacts.
While not recognizing any representation in cognition (modal or amodal), strong embodiment cognitive theory does accept possible facilitation that motor action and perception activities can offer in embodied learning. One way is through the emergence of attentional anchors (Abrahamson and Sánchez-García, 2016) that could help in structuring the environment. An attentional anchor is a real or imaged structure, that “lies at the intermediate level of interaction between subject and environment” (p. 218). The power of such attentional anchors lies in the affordance they facilitate concerning the motor actions from which they originate. For example, in placing two objects in a reflective symmetry position on two sides of a drawn line, an imagined line between the two objects can help steering towards correct position. As an attentional anchor can function as a tool for guiding further actions, it could be helpful in structuring the environment in a mathematical way and therefore spark an abstraction process.
Particularly important for abstraction from an embodied perspective on realistic geometry is the role of artifacts and models. Artifacts are at the core of discovering new mathematical structures. Sanches de Oliveira et al. (2021) describe a way of thinking (artifactualism) where the creation and use of models play a crucial role. Models are to be understood as “artifacts that serve action-guiding purposes” (p. 131). The mathematical structures that emerge in embodied actions are expressed through and incorporated into models. These models, or artifacts, further guide the thinking process. They trigger perception of relevant mathematical structures again and again. Those artifacts create a lens for the learner that allows for seeing spatial reality structured in a new way (Shvarts et al., 2022).
To conclude, from a strong perspective on embodiment, abstraction lies in structuring the actual surroundings and phenomena in a mathematically relevant way. This might be done via the triggering of certain attentional anchors, together with the use of models and other artifacts (Sanches de Oliveira et al., 2021). Focusing on geometry education, specifically designed environments could then facilitate the actions through which such attentional anchors, models and artifacts emerge or are hinted at by teacher. From a grounded perspective on embodiment, bodily actions such as gestures, accompany the process of mathematization in the mind. From a strong perspective, they become the mechanisms of the actual fulfillment of the abstraction, namely, the transformation of the environment into mathematical structure.
Together with the questions suggested by Wilson and Golonka (2013) and Wilson’s (2002) views on embodiment, the most important considerations for a strong perspective on embodied in relation to abstraction in geometry are: (1) the central role for embodiment in the given problem situation of realistic geometry and a close (integrated) relation between the environment, a learner and the specific mathematical content, (2) tasks should be based on situated actions that are time-pressured, (3) tools (manipulatives) are purposefully used in such a way that they offload cognition and may become part of the cognitive system, (4) cognition serves action, i.e., cognition evolves in service of action, (5) propagate the emergence of attentional anchors and artifacts that drive cognition and perception.
To summarize the above, an abstraction process in geometry concerns a discovery of geometrical (or mathematical) structures in spatial phenomena. This is done through a process of acting on and structuring the environment and reflecting on these actions. The embodiment perspective on abstraction, outlined above, accentuates the role of action in this process. During the process of abstraction, actions within the geometrical environment (that might include manipulatives) play a central role in such a way that they determine the perception of environment and consequently further actions in the situation. These required actions trigger the understanding (cognition) related to that problem. The understanding is further propelled by structuring the environment that manifests as emergence of attentional anchors, which are further expressed though mathematical models and artifacts, including verbal expressions and symbols. So, while acting within the problem situation, such structures and attentional anchors will emerge to the student. These structures, when noticed and expressed, then become artifacts and can be used in further reasoning, thus they transform the environment into a more mathematical one. Reflecting on the performed actions and relating them to the discovered structures eventually results in the understanding of a geometrical concept.
The above leads us to consider abstraction in geometry from an embodied perspective as a process of reflecting on, describing, explaining, and structuring sensory-motor actions in the experienced world through developing and using mathematical artifacts.
In this section, we present the results from the semi-structured interviews. For understandability and practicality the last word of the definition of abstraction (presented in the previous section) has been changed from artifacts to words. Because of the interview being semi-structured, the dataset consists of a broad variety (in length and content) of descriptive answers. After coding the interviews, quotes are analyzed further in relation to the research question and the definition of abstraction. Since we are searching for teachers’ views and needs related to abstraction compatible with embodied cognition theory, the analysis resulted in five themes: (1) geometry, (2) acting and the use of materials and manipulatives, (3) abstraction, (4) teachers’ views on students engaging in the process of abstraction and (5) teachers’ needs. Corresponding quotes were grouped in quotation sheets from which the most interesting findings are presented below in tables and summary conclusions per theme. How the findings can help answer the research question will be part of the discussion section.
When asked about what they consider to be geometry in primary school, all teachers showed they have knowledge of the geometry curriculum. Teacher A for example says: “building plans and front and helicopter view, as if a fly hangs above it.” What stands out is that four out of six teachers mention spatial insight in their answer, which shows they tend to relate geometry to a specific skill rather than to certain topics. Frequently mentioned tasks and topics are: shapes and figures (3x), building and constructing with manipulatives (2x), spatial orientation (2x), front, side and helicopter view (2x), relating two and three dimensions to each other (2x), maps, nets and building plans and perspective (1x). These tasks and topics correspond to the (realistic) geometry curriculum in primary school in the Netherlands. It is therefore fair to say that the interviewees are well acquainted with this curriculum.
The use of manipulatives as a didactical instrument in geometry by teachers paints a versatile picture. All teachers had experience in letting students act and work with manipulatives during geometry lessons; some do this as often as possible (A and B) and others do it seldom (C, D, E, and F). Teacher A is convinced that students learn more through experiencing and working with manipulatives and also that they are able to show the solution by using materials. She says: “when I let students use manipulatives, I ask them to show how they act and think, then it will work. But finding words is difficult for them.” Teacher B uses materials to invite students to physically experience a phenomenon. Teacher D says that acting can help students greatly to discover on their own level and to try finding out. And teacher F states that acting helps students to solve a problem, more than just working on paper, which she calls volatile. In summary, benefits of acting and using manipulatives mentioned by teachers are: it helps students to see the problem concretely, to experience, to remember, to try out, to discover and to gain insight. While teachers A, D, and F are convinced that acting and working with materials helps students’ reasoning in geometry (teacher A sees acting as a preliminary stage for solving problems on paper), all teachers primarily use manipulatives with a supportive objective in mind. The general belief is that when a problem on paper is experienced as difficult, it becomes easier to solve when manipulatives are used. This might be influenced by mathematics textbooks, where geometry problems are generally presented to be solved mentally or on paper, without acting or using manipulatives. Only when a student struggles with such problem, are manipulatives used to “lift” the problem to a three-dimensional and thus more realistic situation. Teacher C describes materials used in this way as differentiative material. In conclusion, a coherent vision on the use of manipulatives is missing. On the plus side, teachers are convinced of the importance of manipulatives and use them in a variety of tasks, albeit not as frequently as they want to due to an emphasis on textbooks (paper) problems. On the downside, purposely using acting and manipulatives, other than in a supportive way, is rare.
Table 2 shows the interpretations and reactions that teachers gave before and after the definition of abstraction was presented during the interview. The table clearly shows that most teachers recognize some aspects of the process of abstraction in their teaching practice and the way their students learn. It also shows that teachers do not purposefully foster the abstraction process. As teacher A and F express: “it happens unconsciously” (A) and “it simply does occur” (F).
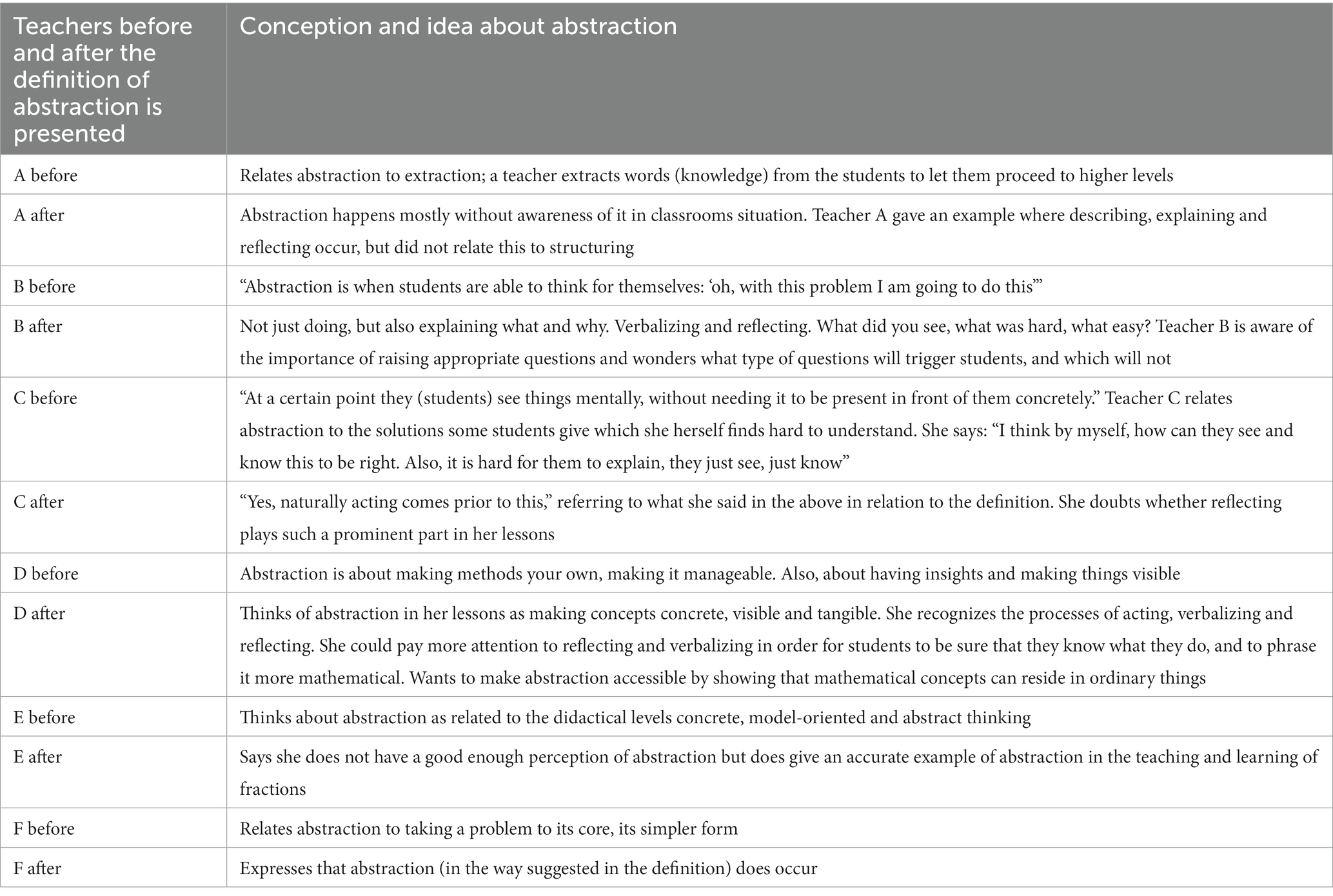
Table 2. Teachers’ conceptions and ideas about abstraction before and after the definition is presented.
Five out of the six interviewed teachers are convinced that each student will be able to proceed in the process of abstraction as presented in the interviews. Differences in students engaging in this process are related to: learning capacities, intrinsic behavior (curiosity, urge to discover), being able to consider multiple possible answers, being able to cope with large open problems, and having spatial abilities. Teacher E is convinced that some students lack the ability to reflect and structure. Being able to verbalize is generally seen by the interviewees as an indication of the capability of understanding the problem and solution. Teacher B says: “if you are able to express it, then you understand.” Verbalizing is also seen by most teachers as the biggest challenge for students engaging in the process of abstraction. This is because of a lack of vocabulary of mathematical and geometrical words. To learn to use this vocabulary, teacher D proposes to let students work on the process of abstraction not occasionally, but for several weeks in a row. Teacher F raises an important point regarding our study. She first suggests bringing in the mathematical words (concepts) herself, but then corrects herself. “I would let the student express it in his own words. Because if I would teach them a concept, I would teach them something abstract.” She means teaching something abstract without context. This resonates with the observations made by White and Mitchelmore (2010), that abstract concepts are often learned in isolation. Teacher F recognizes this pitfall and expresses her conviction, that students learn best by doing.
Table 3 shows teachers’ needs for fostering the process of abstraction. Although a versatile image emerges from this table, some results stand out. First, all teachers are in need of a better understanding of the abstraction process. Questions raised are: what does this process consist of? And how can this be fostered? Secondly, an urgent need expressed by all but one teacher is being able to ask the right questions in fostering the process of abstraction. This shows that teachers relate the fostering of abstraction to a teaching process where asking questions plays a central role. Thirdly, one in two teachers mentioned being aware of the process as an important teaching need. This shows that teachers believe that possibilities for abstraction are present, but lack the knowledge how to recognize and elicit this. Furthermore, two out of six teachers expressed a lack of mathematical and geometrical content knowledge for fostering abstraction.
This study investigates how developing theoretical perspectives may inform teachers practices concerning abstraction in geometry education. We described a theoretical viewpoint on the fostering of abstraction in geometry through the lens of embodied cognition as well as teachers’ ideas, experiences and needs concerning an embodied approach to abstraction in geometry. In this section conclusions and implications of the theoretical views in relation to the practical perspectives are shared.
Concerning geometry education, we found from literature that modern approaches to geometry in primary school emphasize spatial reasoning, with less emphasis on the formal study of shapes and solids. Inspired by the characteristics of realistic geometry that have gained importance in recent years, we consider geometry as the wide-ranging domain of studying and structuring spatial objects and phenomena in the experienced world. From the interview study, we learned that the ideas and beliefs teachers shared, match with the principles of realistic geometry. We also learned that, although many teachers are experienced in using manipulatives (and acting) to provide help to the student, this does not mean they purposely use manipulatives and acting to guide students’ reasoning. A plausible cause for this is the fact that textbooks tasks are usually not designed to be solved using manipulatives, at least in the Netherlands. From this practical perspective, combined with the theoretical ideas of realistic geometry, we believe it is necessary to create opportunities to train teachers in using manipulatives and acting to support students reasoning and abstraction in geometry.
Abstraction in geometry is a process in which structures of a geometric phenomenon are discovered, with an emphasis on acting. Piaget (1971) describes the process where abstraction is drawn from actions (physical or mental) as reflective abstraction. Reflection on these actions helps students to reach a higher level of understanding and in forming new structures. This process is similar to mathematization, where a student is invited to progress from initial discovered structures toward more formal mathematics. Taking into account the relevance of embodied action, abstraction is defined as a process of reflecting on, describing, explaining and structuring of sensory-motor actions in the experienced world through developing and using mathematical artifacts (in the definition used in the interviews, artifacts was replaced with words). As a whole, the process of abstraction was not recognized by teachers in their own practice. Elements of abstraction by students (verbalizing, acting and reflecting) are, however, familiar to most teachers. The majority of respondents trust their students to be capable in engaging in the process of abstraction, albeit without having concrete ideas (and appropriate knowledge) of how to foster this. Consciously fostering abstraction requires a transformation in their teaching practice. Taking into account these practical perspectives and the theory-driven definition of abstraction, we believe teachers need to notice that students’ reflections and descriptions are in service of students’ (structuring) actions. When familiarity is gained with idiosyncratic ways of reflecting, describing and acting, teachers will be better equipped to guide and support students during this process of abstraction.
The theoretical lens of embodied cognition brought to light new ways in which a learning environment on geometry can be organized to act as a fruitful situation for fostering abstraction. Certain types of gestures do not only expose mathematical understanding, but can also support mathematical understanding. Stronger views on embodied cognition testify that the only way we can come to know and understand is through the need for particular action. Consequently, the process of abstraction comes from and is sparked by certain (required) actions. With regards to geometry, this implies that actions are to be elicited to start the process of mathematically structuring a geometric phenomenon (abstraction). What type of actions should be elicited to foster abstraction depends largely on the type of geometry problems to which the abstraction process applies. Future research could focus on the development of such typical designs. The second important factor that the theory on embodiment brings to the fore is the role of artifacts as tools in the process of abstraction. It is assumed that when engaging in the process of abstraction, new attentional anchors are formed by the student. When students are led to use these attentional anchors to serve and guide their further actions, these attentional anchors are expressed as artifacts or tools that help to structure the reality in a mathematical way. Using artifacts in this way asks for teachers to be able to use and communicate about them, and to recognize their students’ use. Next to a thorough mathematical understanding, this requires the teacher to develop new ways of communicating. More study is needed to investigate fruitful ways of training such communication related to specific geometry problems in the classroom. Regarding the embodied approach in general, three out of six teachers are convinced that purposeful acting can indeed be used in such a way that the mathematics of a geometrical phenomenon can be discovered. Some teachers believed their students would have difficulty in finding the correct words to accompany their reasoning.
From the literature study we learned that abstraction is related to the discovery of mathematically relevant structures. The practical perspective showed that teachers experience challenges in fostering abstraction. Also, teachers are not certain if students are able to discover mathematical structures. Considering the embodied viewpoint, teachers therefore would benefit from appropriate skills in supporting action-based discoveries. Experience with such embodied activities can help teachers to see that any student can come to discover new structures through enactment.
The aim of this study is to explore the first steps needed for an embodied abstraction approach to geometry in teacher education. An apparent limitation to this study is the small number of interviewees. Although the practical perspective would have benefitted from a larger population with respect to generalization of teachers beliefs and needs, we found the perspectives raised by the teachers extensive and the implications with the presented theory informative.
Considering the implications of the theoretical perspective in relation to teachers’ perspectives as written in the above, some suggestions for in-service teacher education and teacher professional development can be made. Although theory does provide us with valuable insights, the fostering of abstraction from an embodied perspective cannot be trained from theory alone. Firstly, because the very nature of an embodiment approach to learning geometry is the acknowledgement of idiosyncratic bodily actions and interactions, which very much contradicts standard teaching practice (Alberto et al., 2022). Secondly, because different geometry problems bring different mathematical models and artifacts and require different (inter)actions. Key for learning to foster abstraction in geometry from an embodied perspective is for teachers to learn to facilitate and acknowledge learners’ unique bodily interactions and recognizes these as productive for further mathematical description. Further research is necessary to study how these objectives might be obtained. Future studies could aim to design expert-guided training arrangements, based on hypothetical teaching-learning trajectories (Bakker and Van Eerde, 2015), during which teachers practice and experience themselves and reflect on those experiences. The proposed ways for eliciting multi-modal behavior (Flood et al., 2020) and multi-modal revoicing (Flood, 2018) could be subject for such training. We also suggest making use of a wide variety of realistic geometry problems during this training, to learn about the diversity of artifacts and attentional anchors and ways these are used for structuring toward abstraction.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
KB, MK, AS, and PD contributed to the conception and design of the study. KB and MK performed the coding process. KB performed the database searches and wrote the first draft of this manuscript. MK, AS, and PD commented on it and revised it. All authors contributed to the article and approved the submitted version.
The authors thank Nathalie Kuijpers for editing the manuscript.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. ^Query: [TITLE-ABS-KEY (abstracti* OR abstractn*)] AND [TITLE-ABS-KEY (embodi* OR sensor*)] AND [TITLE-ABS-KEY (math* OR geom* OR spatia*)].
2. ^Knowledge related to understanding, explaining, formalizing, abstraction, analyzing, and giving overview (Meijerink et al., 2009, p. 6).
Abrahamson, D., and Lindgren, R. (2014). “Embodiment and embodied design,” in The Cambridge handbook of the learning sciences. ed. K. Sawyer. 2nd ed (Cambridge: Cambridge University Press), 358–376.
Abrahamson, D., and Sánchez-García, R. (2016). Learning is moving in new ways: the ecological dynamics of mathematics education. J. Learn. Sci. 25, 203–239. doi: 10.1080/10508406.2016.1143370
Alberto, R., van Helden, G., and Bakker, A. (2022). Action-Based Embodied Design for Proportions: From the Laboratory to the Classroom. Implementation and Replication Studies in Mathematics Education, 2, 174–207. doi: 10.1163/26670127-bja10008
Alibali, M. W., and Nathan, M. J. (2012). Embodiment in mathematics teaching and learning: evidence from learners’ and teachers’ gestures. J. Learn. Sci. 21, 247–286. doi: 10.1080/10508406.2011.611446
Arksey, H., and O’Malley, L. (2005). Scoping studies: towards a methodological framework. Int. J. Soc. Res. Methodol. 8, 19–32. doi: 10.1080/1364557032000119616
Bakker, A., and Van Eerde, H. A. A. (2015). “An introduction to design based research with an example from statistics education,” in Approaches to qualitative research in mathematics education. eds. A. Bikner-Ahsbahs, C. Knipping, and N. Presmeg (New York, NY: Springer), 429–466.
Barsalou, L. W. (2008). Grounded cognition. Annu. Rev. Psychol. 59, 617–645. doi: 10.1146/annurev.psych.59.103006.093639
Breive, S. (2022). Abstraction and embodiment: exploring the process of grasping a general. Educ. Stud. Math. 110, 313–329. doi: 10.1007/s10649-021-10137-x
Cetin, I., and Dubinsky, E. (2017). Reflective abstraction in computational thinking. J. Math. Behav. 47, 70–80. doi: 10.1016/j.jmathb.2017.06.004
Clark, A. (2012). “Memento’s revenge: the extended mind, extended,” in The extended mind. ed. R. Menary (Cambridge, MA: MIT Press), 43–66.
Clements, D. H. (2003). “Teaching and learning geometry,” in A research companion to principles and standards for school mathematics. eds. J. Kilpatrick, W. G. Martin, and D. Schifter (Reston, VA: National Council of Teachers of Mathematics), 151–178.
Clements, D. H., Sarama, J., and Joswick, C. (2018). Learning and teaching geometry in early childhood. Quadrante XXVII, 7–31.
De Moor, E. (2000). “Van Fröbel tot Freudenthal-realistische meetkunde voor de basisschool,” in Panama Cursusboek 18 Tien jaar PPON. Lessen voor de toekomst. eds. R. Keijzer and W. Uittenbogaard (Utrecht: Freudenthal Instituut, Universiteit Utrecht), 77–97.
De Moor, E., and Groen, W. (2012). Kijkmeetkunde, een ander uitgangspunt (1970-1980) [Vision Geometry, a different starting point (1970-1980)]. Nieuw Archief Voor Wiskunde 4, 248–253.
Doorman, M., Van den Heuvel-Panhuizen, M., and Goddijn, A. (2020). “The emergence of meaningful geometry,” in National Reflections on the Netherlands didactics of mathematics: Teaching and learning in the context of realistic mathematics education, ed. M. Van den Heuvel-Panhuizen, (Cham: Springer International Publishing.), 281–302.
Dreyfus, T. (2014). “Abstraction in mathematics education,” in Encyclopedia of mathematics education. ed. S. Lerman (Dordrecht: Springer), 5–8.
Drijvers, P. H. M. (2015). Kernaspecten van wiskundig denken [key aspects of mathematical thinking]. Euclides 90, 4–8.
Duval, R. (1998). “Geometry from a cognitive point of view,” in Perspectives on the teaching of geometry for the 21st century: An ICMI study. eds. C. Mammana and V. Villani (Dordrecht: Springer), 37–52.
Ferrari, P. L. (2003). Abstraction in mathematics. Philos. Trans. R. Soc. B Biol. Sci. 358, 1225–1230. doi: 10.1098/rstb.2003.1316
Fischbein, E. (1993). The theory of figural concepts. Educ. Stud. Math. 24, 139–162. doi: 10.1007/BF01273689
Flood, V. J. (2018). Multimodal Revoicing as an interactional mechanism for connecting scientific and everyday concepts. Hum. Dev. 61, 145–173. doi: 10.1159/000488693
Flood, V. J., Shvarts, A., and Abrahamson, D. (2020). Teaching with embodied learning technologies for mathematics: responsive teaching for embodied learning. ZDM – Math. Educ. 52, 1307–1331. doi: 10.1007/s11858-020-01165-7
Freudenthal, H. (1968). Why to teach mathematics so as to be useful. Educ. Stud. Math. 1, 3–8. doi: 10.1007/BF00426224
Freudenthal, H. (1971). Geometry between the devil and the deep sea. Educ. Stud. Math. 3, 413–435. doi: 10.1007/BF00302305
Goldin-Meadow, S., and Beilock, S. (2010). Action’s influence on thought: the case of gesture. Perspect. Psychol. Sci. 5, 664–674. doi: 10.1177/1745691610388764
Gravemeijer, K., Figueiredo, N., Feijs, E., van Galen, F., Keijzer, R., and Munk, F. (2007). Meten en meetkunde in de bovenbouw. Groningen: Wolters-Noordhoff.
Hayes, J. C., and Kraemer, D. J. M. (2017). Grounded understanding of abstract concepts: the case of STEM learning. Cogn. Res. Principles Implicat. 2:7. doi: 10.1186/s41235-016-0046-z
Hershkowitz, R., Parzysz, B., and Dormolen, J. (1996). “Space and shape” in International handbook of mathematics education. eds. A. J. Bishop, K. Clements, C. Keitel, J. Kilpatrick, and C. Laborde (Dordrecht: Springer Netherlands), 205–237.
Hershkowitz, R., Schwarz, B. B., and Dreyfus, T. (2001). Abstraction in context: epistemic actions. J. Res. Math. Educ. 32, 195–222. doi: 10.2307/749673
Hutto, D. D., and Abrahamson, D. (2022). “Embodied, enactive education: conservative versus radical approaches,” in To appear in movement matters: How embodied cognition informs teaching and learning. eds. S. L. Macrine and J. M. B. Fugate (Cambridge, MA: The MIT Press)
Jones, K., and Mooney, C. (2003). “Making space for geometry in primary mathematics,” in Enhancing primary mathematics teaching. ed. I. Thompson (Maidenhead: Open University Press), 3–15.
Jones, K., and Tzekaki, M. (2016). “Research on the teaching and learning of geometry,” in The second handbook of research on the psychology of mathematics education. eds. A. Gutiérrez, G. C. Leder, and P. Boero (Rotterdam: Sense Publishers), 109–149.
Kim, M., Roth, W. M., and Thom, J. (2011). Children’s gestures and the embodied knowledge of geometry. Int. J. Sci. Math. Educ. 9, 207–238. doi: 10.1007/s10763-010-9240-5
Kuzle, A. (2022) The teaching of geometry in primary education: Is geometry still neglected in school mathematics? [Conference paper]. CERME 12, Bolzano, Italy.
Lakoff, G., and Núñez, R. E. (2000). Where mathematics comes from: How the embodied mind brings mathematics into being. New York, NY: Basic Books.
Mavilidi, M.-F., Okely, A., Chandler, P., Louise Domazet, S., and Paas, F. (2018). Immediate and delayed effects of integrating physical activity into preschool children’s learning of numeracy skills. J. Exp. Child Psychol. 166, 502–519. doi: 10.1016/j.jecp.2017.09.009
Meijerink, H. P., Letschert, J. F., Rijlaarsdam, G. C. W., van den Bergh, H. H., and van Streun, A. (2009). Referentiekader taal en rekenen. [Reference framework language and mathematics]. Dutch Ministry of Education, Culture and Science. Available at: https://www.rijksoverheid.nl/onderwerpen/taal-en-rekenen/referentiekader-taal-en-rekenen.
Mitchelmore, M. C., and White, P. (2000). Development of angel concepts by progressive abstraction and generalisation. Educ. Stud. Math. 41, 209–238. doi: 10.1023/A:1003927811079
Mitchelmore, M. C., and White, P. (2007). Abstraction in mathematics learning. Math. Educ. Res. J. 19, 1–9. doi: 10.1007/BF03217452
Nathan, M. J., and Walkington, C. (2017). Grounded and embodied mathematical cognition: promoting mathematical insight and proof using action and language. Cogn. Res. Principles Implicat. 2:9. doi: 10.1186/s41235-016-0040-5
Nathan, M. J., Walkington, C., Boncoddo, R., Pier, E., Williams, C. C., and Alibali, M. W. (2014). Actions speak louder with words: the roles of action and pedagogical language for grounding mathematical proof. Learn. Instr. 33, 182–193. doi: 10.1016/j.learninstruc.2014.07.001
Nemirovsky, R., and Ferrara, F. (2009). Mathematical imagination and embodied cognition. Educ. Stud. Math. 70, 159–174. doi: 10.1007/s10649-008-9150-4
Nemirovsky, R., Ferrara, F., Ferrari, G., and Adamuz-Povedano, N. (2020). Body motion, early algebra and the Colours of abstraction. Educ. Stud. Math. 104, 261–283. doi: 10.1007/s10649-020-09955-2
Newcombe, N. S., and Stieff, M. (2012). Six myths about spatial thinking. Int. J. Sci. Educ. 34, 955–971. doi: 10.1080/09500693.2011.588728
Ng, O. L., and Ye, H. (2022). Mathematics learning as embodied making: primary students’ investigation of 3D geometry with handheld 3D printing technology. Asia Pacific Educ. Rev. 23, 311–323. doi: 10.1007/s12564-022-09755-8
Radford, L. (2009). Why do gestures matter? Sensuous cognition and the palpability of mathematical meanings. Educ. Stud. Math. 70, 111–126. doi: 10.1007/s10649-008-9127-3
Sanches de Oliveira, G., Raja, V., and Chemero, A. (2021). Radical embodied cognitive science and “real cognition”. Synthese 198, 115–136. doi: 10.1007/s11229-019-02475-4
Sfard, A. (1991). On the dual nature of mathematical conceptions: reflections on processes and objects as different sides of the same coin. Educ. Stud. Math. 22, 1–36. doi: 10.1007/BF00302715
Shvarts, A., Alberto, R., Bakker, A., Doorman, M., and Drijvers, P. (2021). Embodied instrumentation in learning mathematics as the genesis of a body-artifact functional system. Educ. Stud. Math. 107, 447–469. doi: 10.1007/s10649-021-10053-0
Shvarts, A., Doorman, M., and Alberto, R. (2022) Concrete–abstract–new-concrete: Freudenthal and Davydov in advancing embodied design framework. [Conference paper]. CERME 12, Bolzano, Italy.
Simon, M. A. (2022). Contributions of the learning through activity theoretical framework to understanding and using manipulatives in the learning and teaching of mathematical concepts. J. Math. Behav. 66:100945. doi: 10.1016/j.jmathb.2022.100945
Sinclair, N., Bartolini Bussi, M. G., de Villiers, M., Jones, K., Kortenkamp, U., Leung, A., et al. (2016). Recent research on geometry education: an ICME-13 survey team report. ZDM Math. Educ. 48, 691–719. doi: 10.1007/s11858-016-0796-6
Sinclair, N., and Bruce, C. D. (2015). New opportunities in geometry education at the primary school. ZDM Math. Educ. 47, 319–329. doi: 10.1007/s11858-015-0693-4
Sinclair, N., and de Freitas, E. (2019). Body studies in mathematics education: diverse scales of mattering. ZDM Math. Educ. 51, 227–237. doi: 10.1007/s11858-019-01052-w
Treffers, A. (1987). Three dimensions: A model of goal and theory description in mathematics instruction. Dordrecht: Springer.
Usiskin, Z. (1987). “Resolving the continuing dilemmas in school geometry” in Learning and teaching geometry, K-12
Van den Heuvel-Panhuizen, M. (2001). “Realistic mathematics education as work in progress” in Common sense in mathematics education. Proceedings of 2001 the Netherlands and Taiwan conference on mathematics education, Taipei, Taiwan. ed. F.-L. Lin (Taipei: National Taiwan Normal University), 1–42.
Van Hiele, P. M. (1986). Structure and insight:A theory of mathematics education. London: Academic Press.
Weisberg, S. M., and Newcombe, N. S. (2017). Embodied cognition and STEM learning: overview of a topical collection in CR:PI. Cogn. Res. Princ. Implicat. 2:38. doi: 10.1186/s41235-017-0071-6
White, P., and Mitchelmore, M. C. (2010). Teaching for abstraction: a model. Math. Think. Learn. 12, 205–226. doi: 10.1080/10986061003717476
White, P., Wilson, S., and Mitchelmore, M. (2012). “Teaching for abstraction: collaborative teacher learning,” in Mathematics education: Expanding horizons (proceedings of the 35th annual conference of the mathematics education research Group of Australasia). eds. J. Dindyal, L. P. Cheng, and S. F. Ng (Singapore: MERGA), 761–768.
Wilson, M. (2002). Six views of embodied cognition. Psychon. Bull. Rev. 9, 625–636. doi: 10.3758/BF03196322
Keywords: abstraction, geometry, embodiment, primary education, teacher—education
Citation: Boonstra K, Kool M, Shvarts A and Drijvers P (2023) Theories and practical perspectives on fostering embodied abstraction in primary school geometry education. Front. Educ. 8:1162681. doi: 10.3389/feduc.2023.1162681
Received: 09 February 2023; Accepted: 23 May 2023;
Published: 20 June 2023.
Edited by:
Claudia Corriveau, Laval University, CanadaReviewed by:
Allen Leung, Hong Kong Baptist University, Hong Kong SAR, ChinaCopyright © 2023 Boonstra, Kool, Shvarts and Drijvers. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Karel Boonstra, a2FyZWwuYm9vbnN0cmFAaHUubmw=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.