Teacher learning to teach mathematics via reasoning and proving: a discursive analysis of lesson plans modifications

Despite the importance of reasoning and proving in mathematics and mathematics education, little is known about how future teachers become proficient in integrating reasoning and proving in their teaching practices. In this article, we characterize this aspect of prospective secondary mathematics teachers’ (PSTs’) professional learning by drawing upon the commognitive theory. We offer a triple-layer conceptualization of (student) learning, teaching, and learning to teach mathematics via reasoning and proving by focusing on the discourses students participate in (learning), the opportunities for reasoning and proving afforded to them (teaching), and how PSTs design and enrich such opportunities (learning to teach). We explore PSTs’ pedagogical discourse anchored in the lesson plans they designed, enacted, and modified as part of their participation in a university-based course: Mathematical Reasoning and Proving for Secondary Teachers. We identified four types of discursive modifications: structural, mathematical, reasoning-based, and logic-based. We describe how the potential opportunities for reasoning and proving afforded to students by these lesson plans changed as a result of these modifications. Based on our triple-layered conceptualization we illustrate how the lesson modifications and the resulting alterations to student learning opportunities can be used to characterize PSTs’ professional learning. We discuss the affordances of theorizing teacher practices with the same theoretical lens (grounded in commognition) to inquire student learning and teacher learning, and how lesson plans, as a proxy of teaching practices, can be used as a methodological tool to better understand PSTs’ professional learning.

1. Introduction

The critical role of reasoning and proving in mathematics and mathematics education is broadly recognized (e.g., NCTM, 2000, 2009, 2014; Harel and Sowder, 2007; National Governors’ Association Center for Best Practices and Council of Chief State School Officers, NGA and CCSSO, 2010; Hanna and de Villiers, 2012). Policy documents and national standards around the world emphasize the importance of students learning mathematics meaningfully, understanding the reasoning behind mathematical rules, procedures, and theorems, being able to prove basic results in geometry, justify their thinking, and evaluate and critique mathematical arguments (NCTM, 2000; AAMT, 2006; National Governors’ Association Center for Best Practices and Council of Chief State School Officers, NGA and CCSSO, 2010). An underlying idea behind the emphasis on reasoning and proving is that these are the key processes by which mathematical knowledge is constructed and validated; therefore, they are important vehicles for learning and understanding mathematics. Hanna and Barbeau (2010) point out that in mathematics classrooms, proofs can be bearers of mathematical knowledge by conveying methods and strategies, and explaining why mathematical results are true. Buchbinder and McCrone (2022) refer to this perspective as teaching mathematics via reasoning and proving¹ and explain: “changing the discourse from teaching proof toward proof-based teaching, puts student learning of mathematics in focus” (p. 4). This perspective puts forward a set of principles for guiding the classroom practice of secondary mathematics teachers: (1) Reasoning and proving must be fully embedded in the existing mathematics curriculum; (2) Emphasis should be made on deductive reasoning in knowledge production and validation, while (3) Using language, notation, and representations within the conceptual reach of the students.

Despite the general acknowledgment of the importance of reasoning and proving, in the United States, proof often remains marginalized in mathematics classrooms. Reflecting on this phenomenon and the research on reasoning and proof over the last few decades, Stylianides et al. (2017) maintain that there is a vast body of knowledge on students’ difficulties with proving and teachers’ challenges in teaching it; there are also several theoretical frameworks explaining the origins of student challenges with proving. However, there is a significant knowledge gap on how teachers can successfully create learning environments that support student engagement with reasoning and proving. Further, there is little theoretical or practical knowledge on how to prepare teachers to enact this type of mathematics teaching or how teacher knowledge in this area grows and evolves. Consequently, there is also a shortage in the methodological tools that researchers can use to explore teachers’ professional growth.

Several researchers have proposed frameworks delineating various types of knowledge teachers need to teach mathematics via reasoning and proving (e.g., Stylianides, 2011; Lesseig, 2016). Buchbinder and McCrone (2020) proposed a framework: Mathematical Knowledge for Teaching Proof, which outlines the knowledge, dispositions, and practices teachers need to teach mathematics via reasoning and proving. The framework is grounded in the socio-cultural and situated perspectives on teacher learning (Lave and Wenger, 1991; Borko et al., 2000), which conceptualize knowledge and learning as situated within physical and social contexts in which they develop through active participation in social practices. According to Lave and Wenger (1991), learning itself is a type of activity based on “situated negotiation and renegotiation of meaning in the world” (p. 51). The commognitive perspective (Sfard, 2008), on which we rely in this article, allowed us to further operationalize teachers’ learning as evolving participation in the social practices of integrating reasoning and proving in teaching mathematics. By the rigorous discursive-based conceptual tools commognition provides, we step forward and conceptualize how professional learning toward reasoning and proving can be characterized and recognized in teacher practice.

The study reported herein is a part of larger, longitudinal research investigating beginning teachers’ learning to teach mathematics via reasoning and proving across several years and contexts: an undergraduate teacher education program, a year-long school-based internship, and two first years of teaching their own classroom. In this article, we examine PSTs’ professional learning in the context of the university-based capstone course² Mathematical Reasoning and Proving for Secondary Teachers. The course was uniquely designed to provide PSTs opportunities to develop their learning toward teaching mathematics via reasoning and proving. Specifically, four times during the semester, the PSTs participated in the lesson planning-enacting-reflecting cycle in which they designed and taught in local schools lessons that integrated activities requiring reasoning and proving. The PSTs recorded these lessons and reflected on them. At the end of the semester, they were asked to revise two out of four lesson plans and write an essay justifying their modifications. Building on the commognitive perspective, we offer a discursive operationalization of PSTs’ learning toward teaching mathematics via reasoning and proving. We aim to explore how PSTs’ professional learning manifests in their lesson plans – as a lens for their discourse. Thus, the data for this study is obtained from PSTs’ original and modified lesson plans.

We begin by situating our work and the focus of this study in the literature on lesson planning. Next, we outline the theoretical perspective – commognition – and the Opportunities for Reasoning and Proving (ORP) Framework grounded in it. We present our operationalization of teacher learning to teach mathematics via reasoning and proving as creating potentially richer and more ample ORP. We then illustrate how PSTs’ modifications to their lesson plans can indicate their professional growth.

2. Lesson planning

Lesson planning is a core task of teaching, and it is considered an important part of teachers’ pedagogical knowledge and practice (Hogan et al., 2003; Ball and Forzani, 2009; Zazkis et al., 2009). As such, teachers’ lesson plans have often been used as a key component in models of teacher professional learning. For example, Blömeke et al.’s (2008) model of teacher competence contains lesson planning – and lesson plans as the artifacts of this practice – as a situation-specific skill, along with noticing and assessing student learning. While lesson planning can take multiple forms for in-service teachers, student teachers and novice teachers are typically required to write lesson plans. Assessment of lesson plans as a representation of lesson planning performance is commonly used in teacher education (e.g., Buchbinder and McCrone, 2020), as well as in the process of induction of novice teachers into the teaching profession (Taylan, 2018; König et al., 2021) and in awarding advanced certification for accomplished teachers, e.g., American National Board for Professional Teaching Standards (Silver et al., 2009). In the process of lesson planning, teachers attend to multiple components, generally associated with three dimensions: content, social interactions, and time (Stigler and Miller, 2018). Along the content dimension, teachers analyze the mathematical subject matter and then select, adapt, and transform it into “teachable content” (Chevallard, 1989). They need to take into consideration the broader context of the instructional unit, curriculum objectives as well as local or national standards. In attending to the second dimension of lesson planning – social interactions, teachers consider their students’ prior knowledge and discursive practices and develop mathematical tasks that afford students the opportunities to engage in productive struggle (Warshauer, 2015). The teachers need to choose instructional strategies for enacting these tasks and supporting student learning (Watson and Ohtani, 2015). This includes attending to teacher actions for supporting student thinking and responding to student inquiries, instructional explanations, and approaches for facilitating group work (Fennema and Franke, 1992; Grossman and McDonald, 2008; Stein et al., 2008; Taylan, 2018). These processes intend to ensure that the learning and teaching processes occur within students’ zone of proximal development (Vygotsky, 1978). The third dimension – time, requires each lesson to have a clearly defined structure, organized along a timeline, with appropriately phased activities, which students can easily recognize and follow (Ball and Forzani, 2009). This may include a warm-up, an individual activity, a whole class discussion, or a lesson summary. Such an extensive list of components indicates the inherent complexity of lesson planning. Hence the challenges facing PSTs and novice teachers in developing the practice of lesson planning are understandable. Studies have shown that expert and novice teachers use different processes when planning lessons. While expert teachers tend to pay more attention to student learning processes, can better anticipate student difficulties, and plan for contingencies, novice teachers apply less-adaptive, rigid instructional approaches (Berliner, 2004; Contreras et al., 2020). In particular, these challenges apply to PSTs, who usually have limited access to mathematics classrooms (Grossman and McDonald, 2008; Stein et al., 2008; Remillard et al., 2009).

With lesson planning being an important and complex practice, teacher preparation programs extend significant efforts to helping PSTs develop proficiency with lesson and unit planning (König et al., 2021). This may involve analyzing or critiquing lesson plans, modifying existing lesson plans, synthesizing across multiple plans, sequencing, and creating original lesson plans (Lim et al., 2018). Teacher educators may also engage PSTs in enacting a part or even whole lesson with their peers, akin to microteaching or rehearsals (Lampert et al., 2013). However, in the context of university-based secondary teacher preparation programs, in particular, in the United States, PSTs seldom have an opportunity to enact full-length lessons in real classrooms prior to their student teaching experiences³ (Tatto et al., 2009). The uniqueness of the capstone course designed by Buchbinder and McCrone (2020), which provided a context for the current study, is that over the course of one semester, PSTs participated in four cycles of planning a 50-min lesson, enacting it with school students, reflecting, and redesigning the lesson plan. The learning environment of the course aimed to advance PSTs’ professional learning toward teaching mathematics via reasoning and proving.

In this paper, we aim to examine the development of PSTs’ teaching practices, as reflected in their lesson planning and the modifications they made to their lesson plans after they enacted the lesson and reflected on it. The modified lesson plans involved PSTs’ envisioned teaching actions and the potential learning opportunities with respect to reasoning and proving that can be offered to students. In this process, we rely on the robust conceptual tools of discursive learning theory, that of commognition, which allows conceptualizing learning as a change of discourse. Thus, we examine PSTs’ discourse, as reflected in the revisions they made to their lesson plans and their explanations for these modifications. We suggest these modifications and explanations to be indicators of PSTs’ professional learning.

3. Theoretical framework

3.1. Commognition: learning as becoming a sophisticated participant in discourse

The commognitive perspective (Sfard, 2008), similar to other socio-cultural theories, views learning as becoming a more proficient participant in the discourse of a particular community. This proficiency in discourse is often termed by commognitive studies as explorative participation, where learners’ participation gradually shifts from ritualistic to more goal-oriented (Lavie et al., 2019). This change in participation is captured by learners’ discourse, including their use of keywords, the routines they follow, the visual mediators used, and the narratives they produce. Most of the commognitive studies have focused on students’ mathematical discourse and the extent to which their communication about mathematical objects gradually changes over time (e.g., Lavie and Sfard, 2019; Zayyadi et al., 2019; Shinno and Fujita, 2021). Recently, some commognitive-based studies examined the teaching practices that can encourage students to participate more exploratively in mathematical discourse (e.g., Nardi et al., 2014; Viirman, 2015; Nachlieli and Tabach, 2019; Weingarden et al., 2019). Also, there has been a growing interest in examining the learning process of teachers toward teaching for explorative participation (Thoma and Nardi, 2018; Heyd-Metzuyanim and Shabtay, 2019; Zayyadi et al., 2020; Christiansen et al., 2022). Some of these studies inquire into teachers’ pedagogical discourse and the extent to which teachers adopt or value learning and teaching actions aligned with such explorative participation (e.g., Heyd-Metzuyanim and Shabtay, 2019; Nachlieli and Heyd-Metzuyanim, 2021). However, little is known about how changes in teachers’ pedagogical discourse and their expressed valuation of a particular set of teaching-learning actions are associated with changes in their teaching practices, specifically in the practices they encountered during their professional learning. In addition, there is a shortage of theoretical and methodological tools for examining changes in teachers’ pedagogical discourse and how these changes relate to their teaching practices and their professional learning around these practices.

In this study, we step forward to contribute to these recent developments and extend this body of knowledge by relating the change in teachers’ discourse to the development of their teaching practice. Specifically, we are interested in conceptualizing future teachers’ professional learning toward integrating reasoning and proving in their mathematics classrooms by relying on the discursive-based modifications they made to their original lesson plans after enacting and reflecting on these lessons. Teachers’ professional learning can thus be examined by the modifications they produced to their lesson plans and the potential opportunities for reasoning and proving embedded in these modifications.

To conceptualize teachers’ learning to teach mathematics via reasoning and proving, we need to describe what is entailed in students’ learning mathematics via reasoning and proving, as well as which teaching practices can support this type of learning. We turn now to describe these conceptualizations in detail.

3.2. Learning mathematics via reasoning and proving

3.2.1. Participating in mathematical discourse

Learning mathematics, as described by Lavie and Sfard (2019), can be viewed as a “change in discourses,” where discourse consists of certain keywords, involved in the communication (e.g., triangles, numbers), routines, which are patterns of actions that learners follow while operating on the objects of discourse (e.g., combining like terms, graphing functions), visual mediators used to mediate communication (e.g., mathematical symbols, tables, graphs), and narratives produced by the participants of discourse (e.g., the graph of $y=2x-8$ passes through a point $\left(0\mathrm{,}-8\right)$). The narratives produced by the discourse’s participants can be divided into object-level and meta-level (Sfard, 2007). The object-level narratives are produced on mathematical objects (e.g., the angles opposite to the legs of an isosceles triangle are congruent), whereas the meta-level narratives are “stories about the discourse itself [… and] about how mathematics is done” (Sfard, 2007, p. 574). Sfard and Kieran (2001) described meta-level narratives as meta-discursive utterances – discourse about discourse, that focus on discursive elements rather than on the objects of mathematics. The meta-discursive utterances concern the truth values of the utterances (“I know this is true because…”) and actions of the interlocutors (“I used a quadratic formula to solve this equation”).

Meta-discursive activity that focuses on the utterances themselves and their truth values, such as “how do you know this is true?” or “why can you say this?,” is largely related to reasoning and proving because it often requires the interlocutors to infer mathematical utterances from other mathematical utterances. For example, to generalize a pattern that they identified or to justify their argument. This relationship between the meta-discursive activity and reasoning and proving was investigated by Jeannotte and Kieran (2017), who developed a conceptual model of Mathematical Reasoning for School Mathematics. Based on the extensive review of literature on reasoning and proving, Jeannotte and Kieran defined mathematical reasoning processes as: “meta-discursive commognitive processes that derive narratives about objects or relations by exploring the relations between objects” (p. 9). The nine mathematical reasoning processes are: generalizing, conjecturing, identifying a pattern, comparing, classifying, validating, justifying, proving, and formal proving. For example, generalizing is “a process that infers narratives about a set of mathematical objects or a relation between objects of the set from a subset of this set” (Jeannotte and Kieran, 2017, p. 9). Justifying is “a mathematical reasoning process that, by searching for data, warrant, and backing, allows for modifying the epistemic value of a narrative” (Jeannotte and Kieran, 2017, p. 12). The notion of these mathematical reasoning processes has been broadly used by many researchers and mathematics educators, both to develop curricular materials (Ellis et al., 2012; Arbaugh et al., 2018) and to examine the processes underlying certain types of student mathematical activity (e.g., identifying patterns, making conjectures, providing non-proof arguments, and providing proofs) (Stylianides, 2009; Davis, 2012; Thompson et al., 2012; Otten et al., 2014).

3.2.2. Participating in meta-discourse about proof

In our previous study (Weingarden et al., 2022), we argued that in order for students to enact meta-discursive processes (e.g., mathematical reasoning processes such as validating and conjecturing), and to produce meta-level narratives (e.g., justification narratives such as “I know this is true because…”) students, often implicitly, follow logic-based principles and enact logic-based processes. Consider the following task: “Prove or refute the statement: ‘A quadrilateral with two pairs of opposite congruent sides is a parallelogram’.” To complete this task, students need to participate in mathematical discourse: produce mathematical narratives about quadrilaterals, use keywords such as “parallelogram” and “congruent,” use visual mediators such as a figure of a parallelogram and symbolic notation (e.g., $AB\parallel CD$), and follow mathematical routines such as drawing a quadrilateral with two pairs of opposite congruent sides. Since students are asked to prove or refute the statement, they also need to enact reasoning processes of proving, which are “mathematical reasoning process that, by searching for data, warrant, and backing, modifies the epistemic value of a narrative from likely to true” (Jeannotte and Kieran, 2017, p. 12). While modifying the epistemic value of mathematical narrative from likely to true or from likely to false, students, often unconsciously, follow principles like “a universal statement can be refuted by a counterexample” or “each proposition in the argument is endorsed based on those that preceded it.” These are examples of what Sfard (2007) defines as meta-level rules, which are principles that regulate the production of meta-level narratives. According to Sfard, these meta-level rules are “rarely made explicit and are usually learned from examples rather than from general verbal prescriptions” (Sfard, 2007, p. 575).

The implicitness of the meta-level rules is broadly recognized regarding proof and argumentation in the context of secondary school mathematics as well as the need to make these meta-level rules explicit and communicable among secondary teachers and students (Harel and Sowder, 2007; Buchbinder and McCrone, 2020; Cirillo and May, 2020; Harel and Weber, 2020). This need is at the core of our efforts to conceptualize the meta-discourse about proof. This discourse is not about mathematical objects. Rather, the objects at the core of this discourse are logic-based objects related to the meta-level rules about proofs. This includes the logical structure of theorems (e.g., the form of an if-then statement ‘if A then B’), the types of proof (e.g., direct proof, proof by contradictions), roles of examples (e.g., counterexample, supportive examples), rules of logic (e.g., if A then B is different from if B then A), and the derived conclusions from different types of statements (e.g., existential statements vs. universal statements). The narratives produced in this discourse are thus, the meta-level rules, such as “a universal statement can be refuted by a counterexample,” “a statement if ‘A then B’ is equivalent to ‘if not B then not A’.” The keywords used to communicate in meta-discourse about proof are logic-related terms such as “conditional statement,” “hypothesis,” “conclusion,” “truth value,” “contradiction,” and more, and the visual mediators of this discourse are, for example, $A\to B$, $\neg B\to A$, $\forall$, $\exists$. The routines of this discourse are logic-based processes, such as writing a conditional statement in the if-then form, identifying the hypothesis and conclusion of a conditional statement, determining what is needed for a statement to be proved or disproved, and others.

To conclude, from the commognitive perspective, learning mathematics via reasoning and proving can be defined as participating in two types of discourses. One is mathematical discourse while enacting reasoning processes, which we term mathematical reasoning discourse for short, and the second is participating in meta-discourse about proof or logic-based discourse (here, we use these two concepts interchangeably). Similar to mathematical discourse, where teachers can offer more or less opportunities for students to participate exploratively by enacting certain tasks or through certain teaching actions (e.g., Weingarden et al., 2019), also in meta-discourse about proof, teachers can offer different types of opportunities for learning mathematics via reasoning and proving.

3.3. Teaching mathematics via reasoning and proving as providing students with opportunities to participate in two discourses

In our previous study (Weingarden et al., 2022), we empirically identified four types of Opportunities for Reasoning and Proving (ORP) embedded in tasks designed by prospective teachers. The first type – limited ORP, involves tasks that focus solely on mathematical objects, such as “solve the following 10 equations: e.g., 2x-7 = 9.” Though it can be argued that solving any mathematical task can (and should) involve reasoning, this particular task involves limited ORP since students are not explicitly required to operate at the meta-discourse level nor to enact reasoning processes such as explaining why they can perform the same operations on both sides of the equation. The second type of ORP – reasoning-based mathematical ORP – appears in tasks that centered on a mathematical object, but in addition, in order to solve the task, students need to enact reasoning processes. For example, “explain why $\left(2\mathrm{,}-3\right)$ is not a point on the line $y=3x+4$.” This task offers students an opportunity to participate in mathematical reasoning discourse by enacting processes such as justifying and explaining around mathematical objects of linear equations and points. The third type – logic-based ORP – involves tasks characterized by logic-based objects and logic-based processes. For example, “identify hypothesis and conclusion in given statements and determine if the statements are existential or universal.” This task provides students with opportunities to participate in meta-discourse about proof. Importantly, in such a task, the mathematical content is in the background, while the object at the core of the task is the logical structure of mathematical statements. The fourth type – fully-integrated ORP – appears in tasks that involve opportunities for participating in both the mathematical reasoning discourse and meta-discourse about proof. For example, “come up with an example of a conditional statement that has to do with linear functions and equations and determine whether the statement is true or false.” The four types of ORP, summarized in Table 1, allow researchers, teachers, and teacher educators “to communicate about opportunities for reasoning and proving by operating with definite characteristics such as objects and processes, [which] may contribute to more explicit, and unambiguous communication” (Weingarden et al., 2022, p. 846).

TABLE 1

Table 1. The four types of ORP in mathematical tasks.

In this study, we use the three latter types of ORP (reasoning-based, logic-based, and fully-integrated) as a discursive-based commognitive theorization and operationalization of the principles of Teaching Mathematics via Reasoning and Proving (Buchbinder and McCrone, 2022). This theorization allows us to better communicate about and characterize the teaching practices included in teaching mathematics via reasoning and proving, and more importantly, to operationalize teachers’ professional learning around these practices. The first principle of incorporating reasoning and proving in the existing mathematics curriculum is operationalized by the reasoning-based ORP, which characterizes tasks that afford students to enact reasoning processes on mathematical objects from the school curriculum, and also by the fully-integrated ORP, which involves the reasoning-based ORP along with the logic-based ORP. The second principle of putting emphasis on deductive reasoning in knowledge production and validation can be operationalized by the logic-based ORP that affords students to participate in meta-discourse about proof. The third principle of using language, notation, and representations within the conceptual reach of the students can be viewed as a cross-cutting principle. It can be operationalized by the discourse’s characteristics, both mathematical discourse and meta-discourse about proof, including the use of keywords (e.g., “slope,” “contradiction”), the narratives produced (“the slope of $y=2x+2$ is $2$,” “the converse of $A\to B$ is $B\to A$”), the visual artifacts that mediate communications (e.g., “$y=2x+2$,” “A → B”), and the routines followed (e.g., “graphing the function,” “identifying hypothesis and conclusion of conditional statements”).

3.4. PSTs’ learning to teach mathematics via reasoning and proving

Based on the discursive-based commognitive conceptualizations of learning mathematics via reasoning and proving as participating both in meta-discourse about proof and in mathematical reasoning discourse; and based on the operationalization of teaching practices that could encourage such participation by different ORPs, we are interested in operationalizing and characterizing PSTs’ learning to create richer opportunities to such participation. We suggest identifying changes in PSTs’ discourse that could serve as indicators of PSTs’ learning to teach mathematics via reasoning and proving. Toward this end, we aim to identify the discursive modifications in the lesson plans the PSTs designed during the course and revised at the end of the course. We endeavor to explore whether or how these modifications in the PSTs’ written discourse of their lesson plans can be translated to changes in opportunities provided to students to learn mathematics via reasoning and proving. Figure 1 visualizes our theoretical and methodological aspects of examining the development of PSTs’ practices toward teaching mathematics via reasoning and proving. The theoretical and conceptual stands we developed appear in blue. As described above, student learning via reasoning and proving can be advanced by specific teaching practices – opportunities for reasoning and proving embedded in instructional tasks (ORP). The development of teaching practices is reflected in the richer and better integrated ORP they provide to students. For examining, methodologically how PSTs’ practices were developed, we suggest using PSTs’ lesson plans and the discursive modifications they made to their lesson plans as indicators of their learning to teach mathematics via reasoning and proving (represented in green cells in Figure 1).

FIGURE 1

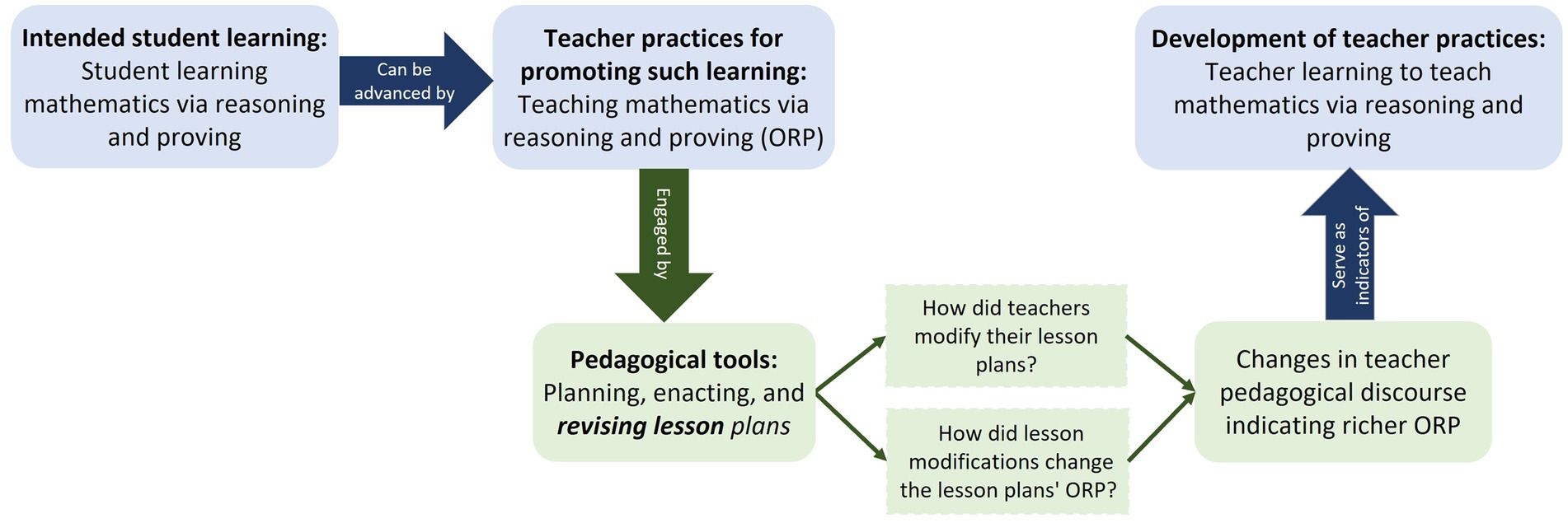
Figure 1. PSTs’ lesson plans modifications as indicators of their learning to teach via reasoning and proving.

Thus, our goal for this study is to illustrate the connection between these two layers – the theoretical and methodological. This entails showing how lesson plans can be used as a discursive methodological tool for examining teacher professional learning toward integrating reasoning and proving, conceptualized as a change in discourse and the potential ORP the teachers create. We explore the following overarching question:

How can PSTs’ learning to teach mathematics via reasoning and proving be characterized by their pedagogical discourse, as reflected in the modifications PSTs made to their lesson plans and the potential ORP provided to students by these modifications?

To respond to this question, we operationalize the discursive modifications made and their related ORP. This operationalization was guided by the following two research questions:

1. What types of discursive modifications can be identified in PSTs’ revised lesson plans?

2. How do the discursive modifications relate to the types of discourses afforded to students to participate in and to the types of ORP provided to them?

4. Methods

4.1. Context: the capstone course Mathematical Reasoning and Proving for Secondary Teachers

The setting for this study was a larger research project conducted in a large, public, four-year university in the Northeast of the United States. The project developed and studied the capstone course, Mathematical Reasoning and Proving for Secondary Teachers (Buchbinder and McCrone, 2020, 2023). The course aimed to enhance PSTs’ knowledge, skills, and dispositions for teaching mathematics via reasoning and proving. The course includes four modules, each focused on one proof theme, i.e., a proof topic that was identified in the literature as posing persistent difficulties for students to learn and for teachers to teach. The four proof themes were: (1) direct proof and argument evaluation, (2) conditional statements, (3) quantification and the role of examples in proving, and (4) indirect reasoning. In each module, the PSTs first refreshed their own mathematical knowledge of the proof theme, learned about students’ conceptions and common difficulties pertaining to this theme, and examined connections between the university-level proof topic and the secondary school curriculum. A culminating experience in each module was a lesson planning-enactment-reflection cycle. Each PST was paired up with a schoolteacher from a local school for the duration of the entire semester. Four times during the semester – once in every module – the PST reached out to the teacher to inquire about the ongoing mathematical topic of the class. Then the PST designed a 50-min-long lesson plan, which integrated the current proof theme with that mathematical topic. To support PSTs in this process, the instructor of the capstone course (the second author of this paper) devoted a two-hour class session to PSTs working in small groups, sharing their draft lesson plans and getting feedback and suggestions from their peers and the course instructor⁴. Next, the PSTs taught their lessons to small groups of students in their teachers’ classrooms. This occurred during regular class time; the PSTs taught a group of consenting students in a separate classroom while the rest of the class had a regular lesson with their teacher. The PSTs videorecorded their lessons using table-top 360-degree video cameras, which capture the PST and the students’ interactions during the lesson. Next, the PSTs watched the video of their lessons and reflected on it by writing a report (Buchbinder et al., 2021). This lesson planning-enactment-reflection cycle was repeated four times during the semester, once for each proof theme. At the end of the semester, the PSTs were asked to revise two of the four lesson plans based on their experience teaching the lesson, with regard to what they learned in the course and the feedback they received from the course instructor and their peers.

The PSTs participating in the study were secondary mathematics education majors who took the course across the five years of the project⁵. By the time of their participation in the course, most PSTs were in the fourth (on rare occasions, third) year of their program, having successfully completed the majority of their mathematical coursework, which included a course on mathematical proof and other proof-intensive courses like geometry and/or abstract algebra. The PSTs also had previously completed at least one course in mathematics education where they learned lesson planning, among other teaching methods. However, this capstone course was the only one providing a structured clinical experience of teaching mathematics in real classrooms.

4.2. PSTs’ lesson plans and their modifications

The data for this study came from the lesson plans designed by PSTs as a part of course assignments collected between 2017 and 2021. Each lesson plan had the following parts: (a) background information on the mathematical topic of the lesson and the grade level, prior knowledge required for the lesson, lesson objectives, and related curriculum standards; (b) student materials and complete solutions, (c) implementation plan outlining different parts of the lesson, the time devoted to each part, and teacher-led explanation, (d) formative assessment questions for lesson summary and (e) anticipated student difficulties and planned ways to address them. Despite the required common structure, the lesson plans varied by the level of detail in each section and the overall format. Some lesson plans were very laconic, while others were written almost as a scenario integrating planned teacher’s speech and anticipated students’ responses.

With the 44 PSTs who participated in the capstone course during the five years of the project, the resulting data corpus contained 88 pairs of original and revised lesson plans. When submitting the revised lesson plans, the PSTs were asked to indicate the revisions they made by using colored font or highlight, and crossing off text they wish to eliminate, rather than deleting it. In addition, for each revised lesson plan, the PSTs wrote a short essay explaining the rationale behind their lesson modifications.

We used the data to identify changes in PSTs’ pedagogical discourse anchored in modified teaching routines, narratives, keywords, and visual mediators. Specifically, in relation to our research questions, we sought to identify the types of modifications the PSTs made to their lesson plans following the lessons’ enactment and reflection, and to illustrate how the identified modifications affected ORP afforded to students. Our focus in this paper is not to report on the statistical trends observed in the data, but to present a theoretical model, grounded in the commognitive perspective, and a related methodological approach for characterizing PSTs’ professional learning.

As a first step of the analysis, we identified all modifications made to the lesson plans by diligently comparing the original lesson plan to its revised version, using PSTs’ own identifiers (color coding) as an initial guide. The modifications included any text that was changed, added to, or excluded from the original lesson plan. These included modifications to the lesson narratives themselves – the revised tasks, objectives, scaffolding questions, visual mediators, introducing or replacing keywords (specifically, ones related to meta-discourse on proof), as well as changes to the overall structure of the lesson, order and time duration of the tasks. In addition to the lesson plan modifications, which could be objectively observed, we analyzed PSTs’ essays describing the rationale for their modifications, and how they envision the modified lesson unfold, if they were to teach it. These essays provided us with an additional lens to teachers’ pedagogical discourse around ORP afforded to students. The pedagogical narratives that PSTs produced in these essays helped us to explicate the change in their teaching routines rooted in the modifications.

In the second stage, we used a sample of 28 original and revised lesson plans to conduct an in-depth, comprehensive analysis to develop a coding scheme classifying the types of modifications to the lesson narratives. The identified changes were characterized discursively by considering the type of keywords and visual mediators used in the modifications, the object at the core of the modifications, and the processes (routines) the teacher or students might need to enact according to the modification made. For example, when the revised lesson plan included adding a presentation explicating and explaining what a counterexample is, the modification involved keywords and objects taken from meta-discourse about proof (counterexample). The processes related to this modification – teacher explaining and explicating, are performed on a logic-based object, that of counterexample. When the PSTs, for example, indicated that they wanted to add more time to students’ activity to provide them more time to struggle with the task, we identified the object at the core of this modification to be related to more structural aspects of the lesson, including social and pedagogical elements, rather than mathematical or logic-related objects. Similarly, the keyword used in this type of modification (e.g., time, struggle, student work) and the teacher’s processes related to it (e.g., provide more time, allow group work) are not directly related to mathematics or logic-related objects. PSTs, often, modified or added a visual mediator to their lesson plan (e.g., graph of a function, proof flowchart). These visual mediators were also analyzed based on the object at the core of the visual mediator and the processes students or the teacher need to perform based on the modified mediator. The process of coding the discursive elements of the modifications in 28 lesson plans reveals four types of modifications the PSTs made to their lesson plans: structural, mathematical, logic-based, and reasoning-based. We elaborate on those four types of modifications and exemplify each of them in the Results sections. Using the inductively developed categories, we examined the rest of the data corpus to verify that the modifications indeed fall within these four categories. This process led to refining and clarifying the description of the four categories of modifications; however, no new categories emerged. In addition, we identified compelling examples of modifications that effectively illustrate the characteristics of the categories of modifications we found in our in-depth analysis.

In addition to identifying the types of modification, based on their discursive characteristics, we examined the types of ORP (limited, reasoning-based, logic-based, fully-integrated) in the original and revised lesson plans, to seek relationships between the types of ORP and types of modifications. Our goal in this stage of analysis was to capture the changes in PSTs’ discourse and to characterize them with respect to types of discourse afforded to students to participate in by these modifications. For example, whereas some of the changes provide students richer opportunities to participate in meta-discourse about proof (e.g., explicate the nature of counterexamples), other modifications involve providing students with richer opportunities to participate in mathematical reasoning discourse. Still, some modifications altered the type of ORP afforded to students, or even diminished it, as we will illustrate in the Results section.

In classifying the types of modifications, it was important to examine each modification on its own, but it was also important to keep track of all the changes in the lesson plan as a whole, so we could see how the different modifications related to each other and contributed to a bigger rationale for the whole revised lesson plan. Thus, in the third stage of our analysis, we enlarged our unit of analysis from a single modification to an entire lesson plan of one of the PSTs including multiple modifications. By this, we explored the types of ORP the PST provided to students by all lesson modifications collectively. In addition, we examined how the various modifications that appeared in different parts of the revised lesson plan (mathematical tasks, lesson objectives, discussion prompts, summative questions, and instructional explanations) related to each other and aimed to achieve a common goal.

5. Results

In this section, we first describe the types of modifications the PSTs made to their lesson plans, and by pointing out the modified routines, narratives, keywords, and visual mediators, we illustrate the opportunities for reasoning and proving afforded by them. Next, we show an example of modifications made to an entire lesson plan and the consequent changes in the ORP afforded to students. We interpret the changes in PSTs’ pedagogical discourse around reasoning and proving as reflecting their professional growth.

5.1. Types of changes in lesson plans

As mentioned above, we identified four types of modifications PSTs made to their original lesson plans. These modifications were characterized discursively as structural, mathematical, reasoning-based, and logic-based.

5.1.1. Structural modifications

The first type of modification in the PSTs’ lesson plans is characterized by modifications to the structural, pedagogical aspects of the lesson. These modifications relate to participation structures, such as students’ modes of participation, students’ interaction and their social activity, and to the lesson structure, such as allocating time to different activities, order of activities, supporting materials, and teaching strategies. These modifications are characterized by general pedagogical, social keywords (e.g., “students feel more comfortable sharing,” “have a discussion with the students,” “allow more time to discuss”) and reflect on teaching routines, intended to increase and support student engagement and improve the flow of the lesson. The discourse characteristics (narratives, keywords, routines) involved in this type of modification are not specific to student mathematical work nor the mathematical objects at the core of the discourse. Rather, they focus on improving the structural and pedagogical aspects of the lesson that aim to support and enable student engagement. This type of structural modification was very common in the PSTs’ revised lesson plans, as the following example shows.

5.1.1.1. Example: Laura’s case

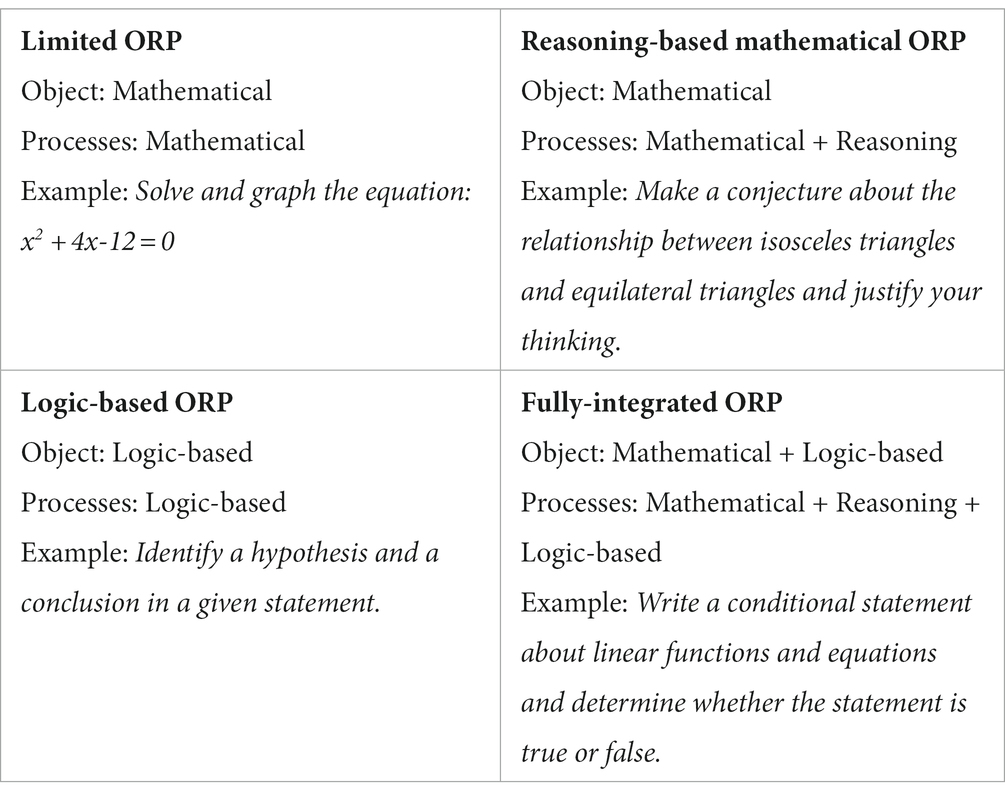
Laura chose to revise her fourth lesson plan on graphing linear equations and indirect reasoning. The original lesson plan contained three activities. The first two: (1) a word problem about two runners competing in a race, asking students when one of them will overtake the other, and (2) a review task with practice problems on graphing linear equations. The first two activities provided only limited ORP since both the objects at the core of the task and the processes that need to be enacted to solve the task are mathematical (e.g., linear equation, graphing, formulating). The third activity contained three problems in which students were asked to use indirect reasoning to explain why a certain point cannot be a solution to a given system of linear equations (Figure 2). Specifically, the students were expected to assume the given point is a solution to the system, plug it into both equations, determine that the point does not satisfy both equations and thus reject the initial assumption.

FIGURE 2

Figure 2. Indirect reasoning and systems of equations task.

Thus, in contrast to the first two activities, Activity 3 involves fully-integrated ORP. The objects at the core of this activity are systems of linear equations (mathematical) as well as indirect reasoning (logic-based). Students were asked to use mathematical reasoning processes of justifying and explaining, and since they were invited to use a particular type of reasoning, they needed to enact logic-based processes related to indirect reasoning and its structure. Thus, students were expected to participate in two types of discourses – mathematical reasoning discourse and meta-discourse about proof.

Despite considering this lesson plan as her “favorite,” after enacting the lesson, Laura decided to modify the plan. The changes she made to the lesson plan were structural: revising the timeline of the lesson, excluding Activity 2, and adding time to Activity 3. In addition, she changed the mode of student interaction with Activity 3 by breaking a class into three groups, assigning each group one question from Figure 2 above, and devoting time to group work and the whole class discussion of student solutions.

Justifying the modifications to the lesson plan, Laura suggested that Activity 2 was intended to be a “quick review, but in implementation, it took longer than expected and really did not help students in achieving my objectives.” Moreover, she mentioned that there was little time left for the indirect reasoning activity. So, in the revised lesson plan, Laura wanted to allocate more time to it. She wrote: “I decided that I really liked my original third activity and thought it was valuable in implementation even though it was a little rushed.” Her pedagogical narratives [e.g., “it (Activity 2) took longer than expected”], as well as her keywords (e.g., “little time,” “took longer,” “quick review”) and routines (“achieving my objectives,” implementing Activity 3 “even though it was a little rushed”), focused on the pedagogical aspect of the lesson and the lesson’s structure, pertaining to time management and mode of engagement with the tasks. While Activity 3 with the fully-integrated ORP was present in the original lesson plan, the time allotted to it, as Laura described, made it unrealistic to fulfill its potential. By excluding tasks with limited ORP (Activity 2), adding more time to tasks with fully-integrated ORP (Activity 3), and restructuring the mode of student interaction with the activity (assigning different tasks to different groups), Laura increased students’ opportunities to engage with reasoning and proving, specifically with fully-integrated ORP, which received more time and prominence in the revised lesson plan.

5.1.2. Mathematical modifications

The second type of modification focuses solely on the mathematical objects at the core of the lesson grounded in the school curriculum and on the mathematical routines the teacher or students are expected to follow. This includes modifications in which PSTs changed the mathematical tasks, elaborated mathematical content, and added explanations or questions intended to clarify mathematical ideas or connections between them. These changes can be viewed as modifications aimed at changing students’ mathematical discourse. In contrast to the structural modifications that indirectly affect students’ mathematical work by changing general pedagogical, and structural aspects of the lesson, the mathematical modifications relate to specific mathematical objects and processes. The teaching routines, as well as the keywords used, and the visual mediators utilized, are specifically related to the mathematical object. The mathematical modifications were less common in our analysis than the structural modifications.

The following two examples illustrate mathematical modifications. Whereas the first case – Nate’s case, depicts mathematical modifications that led to richer ORP, the second case – Molly’s case, is an example of mathematical modifications that can diminish the ORP provided to students.

5.1.2.1. Example 1: Nate’s case

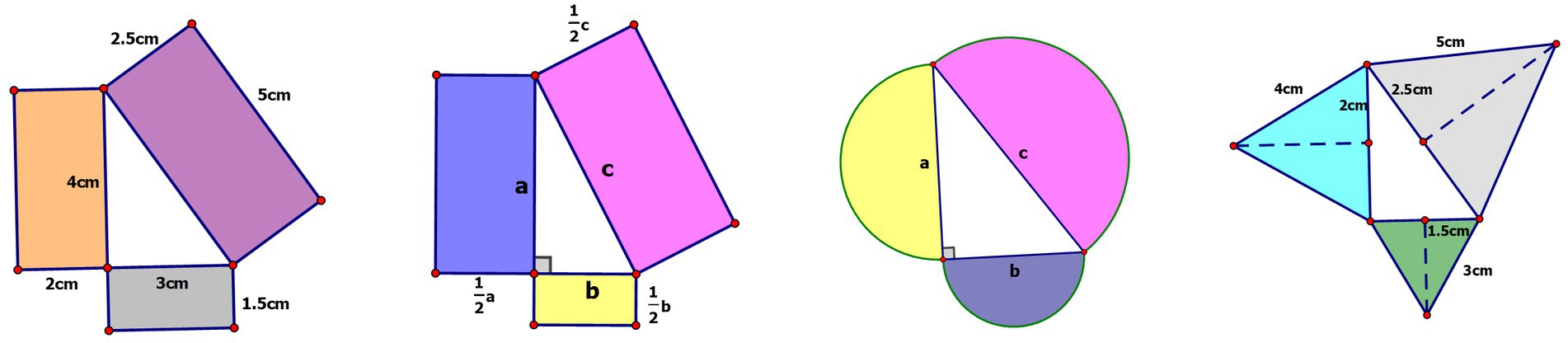
Nate designed an activity in which he had students discover the extended Pythagorean theorem, which states that areas of any similar shapes constructed on the sides of a right triangle satisfy the relationship $a^2+b^2=c^2$, where $a,b$ are the length of the legs, and $c$is the length of the hypotenuse of the right triangle. In the original lesson plan, Nate relied on students’ prior knowledge of the Pythagorean theorem and had students explore areas of rectangles, equilateral triangles, and semi-circles constructed on the sides of a right triangle (Figure 3). These calculations were supposed to set the stage for observing the pattern and generalizing the Pythagorean Theorem across the cases.

FIGURE 3

Figure 3. Sequence of explorations in the original lesson plan.

During lesson enactment, Nate discovered that algebraic manipulations with multiple parameters were difficult for students. The technical complexity of algebraic manipulations prevented students from engaging with the mathematical reasoning processes of identifying patterns and generalizing. In the revised lesson plan, Nate introduced many changes, some of which we categorized as mathematical in nature (Figure 4). First, to ease students into the task, he introduced an example of a simple calculation of areas of rectangles constructed on the sides of a right triangle with given numeric values. This was followed by an example of the same shapes but with parameters instead of numbers. The second modification was that Nate changed the order of explorations of semi-circles and equilateral triangles, moving the exploration of semi-circles immediately after rectangles since this case is easier in terms of algebraic manipulations than the one with equilateral triangles. The third modification included providing numeric values for the sides of an equilateral triangle and asking students to calculate the lengths of the altitudes as a first step of the exploration. This modification allowed students to practice applying the Pythagorean Theorem to find the length of the altitudes of the equilateral triangles prior to calculating their areas. These calculations served as a basis for a generalized case of equilateral triangles, with parameters instead of numbers, which was left for homework.

FIGURE 4

Figure 4. Sequence of explorations in the revised lesson plan.

Nate provides his rationale behind the modifications, supporting our categorization. He wrote:

… The original conjecture stays in the worksheet but the next problem about the area of rectangles changes slightly. In the original worksheet, this problem started generalized and I was made aware that doing this problem with actual numbers and then generalize it will help students understand the algebra of the next problems. The next problem is the original generalized rectangle problem to translate their work with real numbers to generalization. I then moved the area of semi circles before the area of equilateral triangles, because […] it is easier than the problem of equilateral triangles. To mitigate the issues with the area of equilateral triangles, I provided the altitude and values for the base and hypotenuse. This gives them [students] concrete numbers to work with instead of generalized values. Hopefully this will make the problem easier to understand and comprehend.

Nate’s modifications to the lesson plan are mathematical in nature. He distinguishes between the “worksheet” – the mathematical task, and the rest of the lesson plan. The objects at the core of the modifications and the routines are mathematical: introducing numeric examples and changing the order of the tasks to simplify calculations and algebraic manipulations. The aim of these changes and the rationale for changing the order of the tasks, as described by Nate, is to scaffold students’ participation toward enacting mathematical reasoning processes (“help students understand algebra,” “mitigate issues with areas”) and allow students to analyze similarities and differences between the cases to identify patterns and make conjectures (“doing this problem with actual numbers and then generalize,” “translate their work with numbers to generalization”). By this, the mathematical changes in the content of the lesson increased students’ opportunities to eventually participate in mathematical reasoning discourse.

We move now to describe Molly’s case, in which, similar to Nate’s case, mathematical modifications were identified, but these modifications did not result in increasing students’ opportunities for reasoning and proving.

5.1.2.2. Example 2: Molly’s case

In one of the tasks developed by Molly for middle school geometry class, students were given a chart reminding them of two ways to classify triangles: by sides or by angles, along with definitions of various types of triangles and their sketches (Figure 5).

FIGURE 5

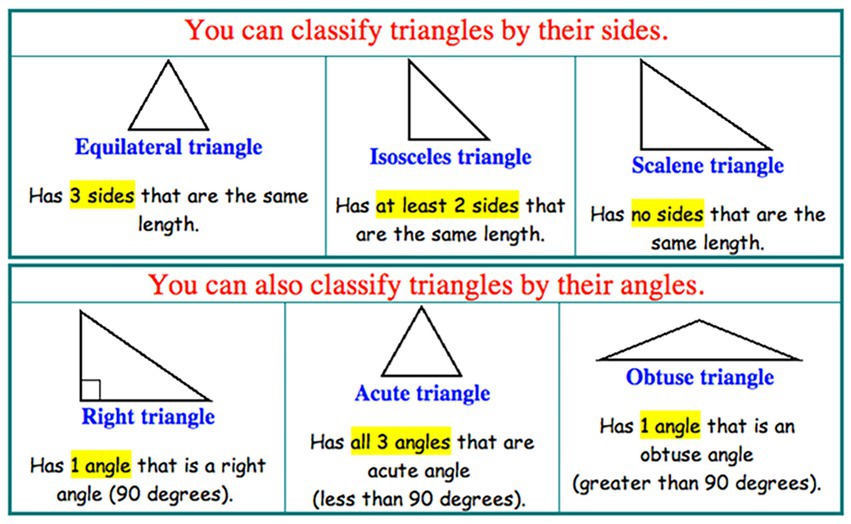
Figure 5. Ways to classify triangles (from Molly’s original lesson plan) (Copyright https://assignmentpoint.com/).

The task for students was to find relationships between different types of triangles and write them as conjectures; for example, all isosceles triangles are equilateral, or if a triangle is obtuse, then it is not equilateral. Next, students had to prove or disprove their conjectures. This task is characterized by fully-integrated ORP since it requires students to engage in mathematical reasoning processes of pattern identification and conjecturing, as well as in logic-based processes of formulating true mathematical statements on mathematical objects. In the revised lesson plan, Molly removed the table depicted in Figure 5 and substituted it with a table without images of triangles, only with definitions (Figure 6).

FIGURE 6

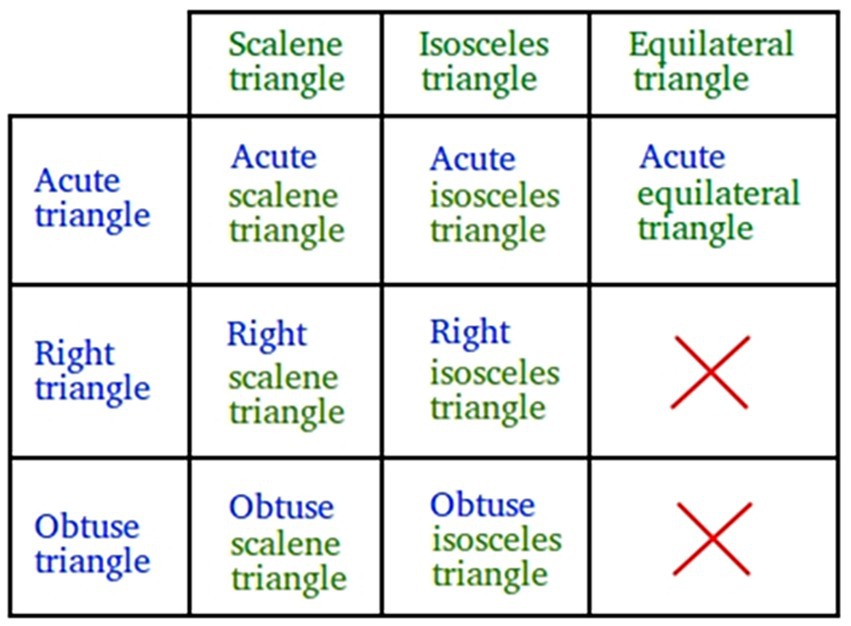
Figure 6. Summary of triangles’ relationships (from Molly’s revised lesson plan) (Copyright basic-mathematics.com).

When explaining the reason for changing the figure, Molly wrote that she found Figure 5 online and inserted it into her lesson without critically evaluating it: “At the time, I wanted a nice visual to help the students, but I realize now that we cannot trust all the information on the internet.” After enacting the lesson and receiving feedback on it, Molly realized that the diagram that she originally used “can be misleading and can cause confusion.” For example, the scalene triangle in Figure 5 looks right, and both the acute and obtuse triangles look isosceles, which is not always true. As Molly described, the use of such a “misleading” figure led her to “work a little harder and try to find a better diagram for students.”

As for the ORP in the revised task, in the revised figure (Figure 6), in contrast to the original figure (Figure 5), all the relationships between triangle types were already explicitly summarized for students. Thus, students were not required to find the relationship, generalize it and determine if their conjecture is true or false. Rather, they were only required to formulate mathematical statements in proper logical forms. Molly wrote that she “will show the students this picture to help them construct conditional statements.” Thus, the object and processes at the core of the task are no longer mathematical at the middle school curriculum level – types of triangles and finding the relationships between them. Instead, the revised object-processes are logical – formulating conditional statements from the given information. Thus, the ORP changed, or more precisely diminished, to logic-based only. Molly also noticed the differences between the figures and their mathematical affordances. She argued that the modified figure (Figure 6) “is better because it shows what happens when you “crossover” different triangles.” However, since all the relationships are already represented in the figure, this modification takes away students’ opportunities to engage with reasoning processes on mathematical objects, such as pattern identification, generalizations, and conjecturing (e.g., there exists a right triangle which is also an isosceles triangle, or there is no right triangle that is also equilateral triangle).

It can be argued that having a more mathematically precise and less ambiguous figure for students to analyze is an improvement; or that there may be pedagogical advantages for intentionally using imprecise figures. While we agree with both ideas, there is no indication in Molly’s work that she considered these issues. In terms of the ORP afforded to students, by this mathematical modification of changing the visual mediator of the types of triangles, the ORP of the task were diminished from fully-integrated ORP, which includes opportunities to participate both in mathematical reasoning and logic-based discourse, to logic-based ORP only, which includes only opportunities to participate in logic-based discourse.

5.1.3. Reasoning-based modifications

The reasoning-based modifications are characterized by narratives, routines, keyword and visual mediators that focus on the reasoning processes students need to enact, such as justifying, conjecturing, validating, or proving. The reasoning-based modifications include, for example, the teaching routine of asking more scaffolding questions or revising the existing questions during classroom discussions toward providing students more opportunities to enact reasoning processes. This type of modification also includes changes to the mathematical tasks that appear in the lesson plan, which often involve changes in the mathematical objects and sometimes even in the mathematical processes of the task. But what makes these modifications reasoning-based rather than just mathematical is that the main change was made to the mathematical reasoning processes which students need to enact. These reasoning-based modifications were intended to increase student engagement with additional reasoning processes enacted on mathematical objects. Thus, in most cases, the reasoning-based modifications led to richer reasoning-based ORP, as described in the following examples. The first example is taken from Nate’s lesson plan within Geometry curriculum, whereas the second example is taken from Phil’s Algebra’s lesson plan. Our aim in providing two examples is to illustrate how reasoning processes can be integrated in both Geometry and Algebra.

5.1.3.1. Example 1: Nate’s case

Returning to Nate’s activity with the extension of the Pythagorean Theorem (Figure 4), recall that he intended the exploration of cases with different shapes constructed on the sides of a right triangle would generate calculations that students could generalize and come up with a conjecture. In the revised lesson plan, before asking students to write a conjecture generalizing their observations, Nate included an additional task in which students were expected to work in groups to create their own case of shapes constructed on the sides of a right triangle, calculate their areas and see if the pattern of extended Pythagorean Theorem still holds. In this question, Nate intentionally did not specify that the shapes need to be similar, i.e., have proportional sides. He anticipated that some students might overgeneralize the examples examined so far without noticing that the shapes must be similar. By adding this question, Nate expected students to discover counterexamples – non-similar shapes – and then have students examine what is common in cases where the conjecture holds. This way, students could identify that the similarity of shapes constructed on the sides of a right triangle is a necessary condition for the conjecture to hold. Nate explained the changes to the lesson plan by writing:

I added a question in which the students will take the time to create their own example, this gives them time to try and find a counterexample and to explore other ideas not presented directly to them. All the problems [cases examined so far] showed the conjecture would work, and I expected students to know that there would be a counterexample. Then I ask them to look at the examples that worked and try and find the common thread of similar shapes. This is a new question that supplements the question before to really help them understand the coincidence in the worksheet and to think critically about the work they have been doing.

The object at the core of the modification – the new tasks Nate designed, are mathematical objects (shapes, algebraic expressions), and the processes students are expected to enact are both mathematical (writing an equation, calculating) and reasoning (generating examples and counterexamples, identifying patterns, generalizing and writing a conjecture). Nate’s teaching routines, as reflected in the revised lesson plan, focused on encouraging students to enact reasoning processes: “to create their own example and find counterexample,” “to explore other ideas not presented,” “find the common thread of similar shapes,” and “think critically about their work.” As a result of these changes, the revised lesson plan involves richer opportunities for students to participate in mathematical reasoning discourse. These opportunities are also reflected in Nate’s usage of keywords such as “explore,” “create,” “example,” and “counterexample,” and in his narratives focused on the importance of encouraging students to create examples and counterexamples, generalize, conjecture, and think critically.

5.1.3.2. Example 2: Phil’s case

Phil developed a 9th-grade Algebra lesson devoted to the distributive property. In the original lesson plan, Phil intended to introduce the formula representing the distributive property and to show how it can be represented with an area model (Figure 7). He wrote: “I’ll first show the general notation for the distributive property: $a\left(b+c\right)=ab+ac$. Then I’ll explore the distributive property using visual demonstration with rectangles area. Show how the visual relates to the mathematical notation, using the example $4\left(x+10\right)$.” Next, Phil wanted students to practice applying the distributive property using the area model (Figure 8 shows one out of four such exercises).

FIGURE 7

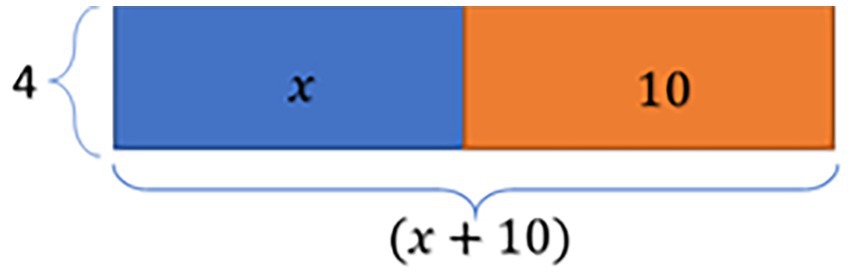
Figure 7. Excerpts from Phil’s tasks in the original lesson plan: area model illustration of distributive property.

FIGURE 8

Figure 8. Excerpts from Phil’s tasks in the original lesson plan: sample exercise (Copyright Homeschoolmath.net).

This task has limited ORP, since both the object of the task and the processes that students need to enact are school-based mathematical (distributive property, integers, calculations, area representations). Reflecting on the lesson, Phil was concerned with the fact that students had little ownership over their mathematical knowledge when the formula was simply presented to them. Phil wrote: “I felt that it would be much better to have students explore the distributive property on their own through working with the worksheet, rather than just give it to them on the board like I did.” Phil also was concerned with students “modeling distributive property expressions with subtraction.” He wrote that “it was hard for students to look at area as a negative.”

In the revised lesson plan, Phil designed a new activity where students were given colored chips: green representing positive numbers and red for negative numbers. First, the students were asked to use the chips to represent three pairs of expressions, such as 3·(2) + 3·(−1) and 3·(2–1), related to two parts of the distributive property. This task was followed by a set of questions:

1. What did you have to do differently for the subtraction example?

2. What do you notice in common for all the examples?

3. Is there a general way you can write this pattern?

4. Create your own distribution problem with four numbers and represent it with your chips. Example: 3·(2 + 1 + 2).

5. Does the pattern work with four numbers? Will it continue to work with even more?

This example again illustrates reasoning-based modification. Note that the mathematical objects of the modified activity remain the same as in the original one: integers and the distributive property. Also, in both original and modified tasks, students needed to work with representations and visual mediators. The main modification concerns the nature of the processes that students need to enact while solving the task. Whereas the original task had students writing a mathematical sentence representing the area model of the distributive property, the modified task calls for different types of reasoning processes, such as pattern identification, conjecturing, generalizing, and justifying. These types of processes were absent from the original task but are at the core of the modified one. Therefore, Phil’s reasoning-based modification changed the ORP of the task from limited to reasoning-based ORP. In addition, Phil’s pedagogical narratives and teaching routines, similar to those of Nate, focused on encouraging students to enact reasoning processes: “explore the distributive property on their own” by “noticing what is common” across examples, finding “a general way to write a pattern,” and pondering of this would be true with “more numbers.” Phil’s pedagogical discourse, including teaching routines such as “explore,” “noticing,” and “write a pattern,” supports the richer ORP provided by the task Phil revised.

5.1.4. Logic-based modifications

This category of changes is characterized by modifications to the logic-based discourse of the lesson. These changes included making the logic-based objects and processes of the lesson plan explicit to students, for example, by modifying teacher explanations, introducing logic-based vocabulary, adding questions that require students to enact logic-based processes like identifying a type of quantifier or unpacking the logical structure of a statement. Other changes included adding discussion prompts requiring students to reflect on the type of reasoning they used to solve the provided tasks, making the logical structure of this reasoning explicit and formalized. These types of changes are characterized by modifications to the logic-based objects and processes pertaining to the lesson plan and therefore intended to modify students’ participation in logic-based discourse.

5.1.4.1. Example: Zoe’s case

Zoe’s lesson for 8th-grade students intended to combine solving simple equations with quantification and the role of examples in proving them. The students were given seven equations (e.g., $2x-2\left(x-3\right)-5=4-3$, $2m+2-m\left(3-1\right)=2\left(6\right)$, $2\left(y+1\right)+\frac{4y+6}{2}=8)$, which they had to solve and sort according to the number of solutions: no solutions, one solution, and infinitely many solutions. Then students had to determine whether the following statements were true or false and explain their reasoning. The statements were: (a) An equation always has a solution, (b) There exists an equation with an infinite number of solutions. Zoe wrote in her original lesson plan that she expected students to “come up with a counterexample to prove the first sentence false and a supporting example to prove the second sentence true.” She also planned to ask them why a counterexample is enough to prove the first statement false and why a supporting example is enough to prove the second statement true. However, the lesson plan included no written explanation about how exactly Zoe planned to introduce students to the roles of examples in proving and disproving quantified statements.

After enacting the lesson and reflecting on it, Zoe noticed that in the original lesson plan, the proof-related ideas were introduced only at the end of the lesson: “the role of examples in proving was only introduced in the end […] catching students by surprise,” with “not thinking about this idea of proofs throughout the lesson.” Hence, in the revised lesson plan, Zoe added, at the very beginning of the lesson an introduction to the topic of the role of examples using familiar, non-mathematical context. Zoe wrote an explicit description of how she would introduce students to the topic of the roles of examples in proving:

To introduce the topic of the role of examples in proving, I can ask them questions about when examples are enough to prove something. I will begin by saying “All cars are red” and asking the students if they can prove me right or wrong. The goal is that the students can respond with an example of a car that is not red, which would disprove my statement. I could also say, “there exists a dog with brown fur” and ask the students if they can prove that statement. The students should be able to come up with an example of a dog with brown fur, which would prove the statement. This could lead to a discussion about using examples in proving and when an example is sufficient in proving and disproving.

When justifying her lesson modifications, Zoe explained that “when the students are asked to use examples to prove or disprove different statements about equations, they should already have some ideas of how to do this,” and the inclusion of the explicit explanation “ties the lesson together.” Zoe also expressed hope that the introductory discussion would aid student understanding and that she “can bring students back to our discussion if they are still struggling.”

Characterizing the change made to Zoe’s lesson, the object at the core of the change is logic-based. The mathematical task remained unchanged, as well as the logic-based tasks of validating and justifying the truth-value of quantified statements. When enacting the lesson, Zoe discovered that students struggled to determine if the given mathematical statements were true or false, to justify their thinking, and, in general, to participate in the discussion around this task. This was because students were missing the relevant keywords (e.g., a counterexample), the endorsed narratives (e.g., “when examples are enough to prove something?”), and the processes of meta-discourse about proof, particularly those that related to the role of examples in proving or disproving statements [e.g., using examples of solved equations as examples or counterexamples of the quantified statements (a) and (b)]. The focus of Zoe’s modifications was on introducing logic-based vocabulary and modeling the logic-based processes related to the form and structure of validating and justifying. In summary, the logic-based modifications in the revised lesson plan enhanced students’ opportunities to participate in logic-based discourse. These enhanced opportunities are also reflected in Zoe’s pedagogical discourse. Zoe’s teaching routines and her pedagogical narrative point to the explicit manner by which she planned to engage students in logic-based discourse (e.g., “ask what their solution is and what they think it means;” and if students wrongly assume that all equations have solutions, Zoe would orient them to their calculations to “see that there are some examples of equations with no solutions”).

5.2. Illustration of changes to the entire lesson plan

So far, we have described and illustrated categories of specific changes in the lesson plans. A single lesson plan may contain one or a few types of modifications, which collectively affect the learning opportunities provided to students and the types of discourses students can participate in. To better understand this phenomenon, it is important to analyze a lesson as a whole, considering not just the individual changes but also how these changes, collectively, interact with and complement each other. We illustrate this by analyzing Diane’s 9th-grade Algebra lesson plan.

5.2.1. Diane’s original lesson plan

This lesson intended to integrate the proof theme of indirect reasoning (and prove by contradiction) with the mathematical topic of the quotient rule of exponents. The lesson involved four components: introduction, individual student work, class discussion, and summary. The introduction focused on the collective recall of key vocabulary terms such as base and exponent and the meaning of natural number exponents as repeated multiplication. The individual work contained an exploration activity in which students were supposed to discover the quotient rule by observing and generalizing a pattern of calculations. The students were to fill out a table (Figure 9) and come up with the quotient rule: $\frac{x^m}{x^n}=x^{m-n}$. The task’s directions to students were: “The table is going to help you figure out a general rule about simplifying exponents that can be used when we are solving equations that have exponents in them. Work on your own to look for a pattern in the examples and try and make a more general rule.”

FIGURE 9

Figure 9. Diane’s original task.

The plan for the whole-class discussion contained two parts. First, “go over the worksheet and ask students to present their ideas of the generalized rule they created in the last row of the table.” The second part involved “Indirect Reasoning Activity,” which presented students with a set of questions about the quotient rule, whose solutions may involve indirect reasoning (Figure 10). For example, to answer question 6 (the first question in Figure 10), students may substitute $x=8$ into the equation, use the quotient rule to obtain a false statement $4^6=4^3$, and conclude that $x=8$ cannot be a solution. The mode of engagement was a whole class discussion, with students getting a few minutes of individual thinking time for each question and then justifying their answers to the class.

FIGURE 10

Figure 10. Sample questions from the indirect reasoning activity.

To summarize the lesson, Diane planned to “have a conversation about how sometimes we have to show why things are not true, and we can use contradictions to do this.” However, she did not intend to explicitly introduce the concept of indirect reasoning, asserting that “using the words ‘indirect reasoning’ is not going to be particularly helpful” to the students.

5.2.2. Diane’s modified lesson plan

Following the lesson enactment and reflection, at the end of the course, Diane introduced several types of changes to her original lesson plan. In what follows, we describe the modifications, and then we show how, collectively, these modifications lead to richer ORP in the lesson plan.

5.2.2.1. Structural modifications

To increase and support students’ active participation, Diane introduced an intermediate check of student work as they completed the first three rows of the table in Figure 9. This pedagogical change was intended, according to Diane’s explanation, to make students more comfortable and confident in the outcomes of their calculations and set the stage for pattern identification and generalization. Another structural modification, that focused on the structure of students’ participation, was explicitly reminding students about expectations for active engagement and sharing ideas. Justifying this modification Diane wrote: “This will make the lessons go smoother and more enjoyable for everyone involved. Emphasize that they (students) are not being graded, so there is really no pressure, and I would love to hear what they are thinking.”

5.2.2.2. Reasoning-based modifications

A different type of modification – reasoning-based modification, was the introduction of a slide with questions scaffolding students generalizing activity and their discovery of the quotient rule of exponents (Figure 11). The aim of the slide, as Dinae described, was for students “to start thinking of the general rule that will come from the expression in the bottom row of the table.” The intended reasoning processes of the first exploratory activity were for students to identify a pattern, notice how the values of the exponents change, and generalize the pattern they identified to any number and exponent. The processes remained unchanged between the original and revised version of the lesson. However, the way the original task was set up did not elicit the intended engagement of students with these processes. By adding this slide, Diane made the reasoning processes more explicit and provided scaffolding for students’ thinking.

FIGURE 11

Figure 11. Scaffolding questions for discovering the quotient rule.

5.2.2.3. Logic-based modifications

The third type of change in Diane’s lesson was during the Indirect Reasoning Activity and pertained to logic-based modification. In the original lesson plan, students were expected to solve questions about why certain values of variables are impossible by identifying contradictions resulting when these values are used. The lesson summary was supposed to contain a discussion of the usefulness of this type of reasoning. While Diane was aware that students are engaged with indirect reasoning, this remained implicit for the students. As she described in her essay: “I never specifically said ‘we are going to be using indirect reasoning’, nor did I ever have them complete an indirect proof.” As a result, students were missing the keywords and endorsed narratives of logic-based discourse and struggled to participate in the discussion. In the revised lesson, Diane decided to explicitly address the logic-related objects and processes. Right before the Indirect Reasoning Activity, she added a slide, which intended to help her navigate discussions about indirect reasoning and the nature of contradiction in mathematics. The slides contained two discussion questions: What is a contradiction? And why might we want to find a contradiction? Diane motivated this change by writing: “I would like to place more emphasis on the fact that we are finding contradictions as the reasoning that some of these equations cannot work. We will discuss what a contradiction is and what it tells us in mathematics.” The object at the core of this modification is logic-based: the nature of contradiction and its application. Although it is discussed in the context of exponents, these questions are meta-mathematical, anchored in logic-based discourse.

5.2.2.4. Mathematical and logic-based modifications

Another modification, characterized by a logic-based and mathematical modification, appeared when Diane modified the wording of the mathematical questions in the Indirect Reasoning Activity. The original questions only prompted students to “be ready to explain why you chose the answer that you did” without explicitly connecting student responses to indirect reasoning and proof by contradiction. In the revised lesson plan, each question was accompanied by an explicit prompt to “explain what is the contradiction here?” When students were asked to solve the second question in Figure 10 – “Determine what values of x, in general, would make $\frac{4^8}{4^2}>\frac{4^x}{4^5}$ false. And why?” – Diane added a discussion question: “What contradiction would these values lead to?” These modifications focus on both the logic-based object of contradiction and the mathematical object of exponent expressions in these questions. As opposed to the former modification – asking students what a contradiction is, which we categorized as solely logic-based modification, this modification – requiring students to identify the contradiction, also required students to operate on mathematical objects (exponent expressions) while engaging with logic-based processes (applying indirect reasoning).

The two latter types of modifications were also identified in Diane’s modified lesson summary. Similar to the logic-based modification mentioned above, Diane explicitly introduced the notion of indirect reasoning (Figure 12, slide 27), and akin to the mathematical and logic-based modification, she made indirect reasoning underlying students’ answers to the mathematical questions explicit to them (Figure 12, slides 28–30). Diane’s rationale for making these modifications to the lesson summary was:

FIGURE 12

Figure 12. Summary questions explicating indirect reasoning.

To conclude the lesson, we will talk about how the students were using indirect reasoning. I am going to take a few of the answers that students submitted to previous questions that show great examples of indirect reasoning and put them on a slide.

As opposed to the original lesson plan, rather than expecting students to learn “indirectly” about the nature and logical structure of indirect reasoning, Diane introduced changes that make these non-trivial logical elements explicit to students and connect them to their mathematical narratives.

5.3. The ORP afforded by Diane’s modifications

Diane’s original lesson plan contained opportunities for students to enact mathematical processes, such as calculating and solving, on mathematical objects: exponential expressions. The lesson also involved some opportunities to enact mathematical reasoning processes, such as identifying patterns, generalizing, and justifying when discovering the quotient rule and when justifying solutions to questions in the Indirect Reasoning Activity. The logical aspects of indirect reasoning were intentionally implicit in Diane’s original lesson plan, as she considered them unnecessary, meaning that the original lesson did not involve explicit opportunities to participate in logic-based discourse.

After enacting and reflecting on the lesson, Diane’s goal in modifying the lesson was “to try and better incorporate the Indirect Reasoning proof theme throughout the lesson.” Her revised lesson plan involved all four types of modifications: structural, mathematical, reasoning, and logic-based. Collectively, these modifications provided students with increased opportunities to participate both in mathematical reasoning discourse and in meta-discourse about proof. For example, Diane’s structural modifications described above, were intended to increase access to opportunities to participate in mathematical reasoning discourse and decrease social costs associated with this participation. As for encouraging students to participate in mathematical reasoning discourse, the reasoning-based modifications Diane made to her lesson plan increased support and scaffolding for students to enact mathematical reasoning processes when discovering the quotient rule (Figure 11). Students were encouraged to identify patterns and generalize while enacting mathematical processes (substituting and computing) on mathematical objects (exponential expressions) and producing mathematical narratives (e.g., $4^6\ne 4^3$). Thus, students were provided richer opportunities to participate in mathematical reasoning discourse.

Importantly, Diane’s logic-based modifications introduced new opportunities for students to participate in logic-based discourse on contradiction and indirect reasoning during the Indirect Reasoning Activity and the lesson discussion (Figure 12). These opportunities manifested in her modifications related to making the non-trivial logical elements of the lesson (e.g., contradiction, indirect reasoning) explicit to students. In addition, in her mathematical modifications, Diane also connected these logical elements to the mathematical narratives students produced. Thus, as a whole, Diane’s modifications generated fully-integrated ORPs, which collectively afford more ample and richer opportunities for students to participate both in mathematical reasoning discourse and logic-based discourse.

These fully-integrated ORPs are also reflected in Diane’s pedagogical narratives and teaching routines focused on the importance of explicating the logical elements (e.g., “place more emphasis on the fact that we are finding contradictions”), connecting them to mathematics (e.g., “ask students to explain what is the contradiction here”), and encouraging students to reason (e.g., “help them to start thinking of a general rule”). The fully-integrated ORP generated in her revised lesson plan, together with her modifications – reflecting her teaching routines – and her justification to these modifications – her pedagogical narratives – indicate Diane’s professional learning to teach mathematics via reasoning and proving.

6. Discussion

This article is part of a long-term study that aims to advance teachers’ professional learning toward integrating reasoning and proving in teaching mathematics and to examine how this learning develops over time (Buchbinder and McCrone, 2020, 2023). The capstone course designed in the larger study is a semester-long intervention aimed to promote PSTs’ professional competence for teaching mathematics via reasoning and proving. A literature review reveals limited theoretical and methodological tools for capturing and characterizing how teachers’ practices specific to reasoning and proving evolve (Stylianides et al., 2017; Depaepe et al., 2020). To address these challenges, we developed a conceptualization that involves a triple-layered characterization of student learning, teaching, and learning to teach mathematics via reasoning and proving. One of the key premises of our conceptualization is that teachers’ professional growth is intrinsically linked to their classroom experimentation, including the learning opportunities they provide to students and student learning processes, and reflection on the consequences of this experimentation (Clarke and Hollingsworth, 2002). We expanded Buchbinder et al. (2021) earlier conceptualization of principles for teaching mathematics via reasoning and proving and operationalized them using the commognitive perspective (Sfard, 2008). The commognitive perspective, with its robust tools for characterizing discourses in terms of objects, processes, keywords, and visual mediators, allowed us to operationalize each of the three layers of the model (Figure 13) and strengthen the theoretical connections between the layers. Specifically, our model describes which type of student learning PSTs were expected to promote in their classrooms – learning mathematics via reasoning and proving, which type of teaching practices they should enact to promote it – teaching mathematics via reasoning and proving, and how PSTs’ own learning can be cast in similar terms.

FIGURE 13

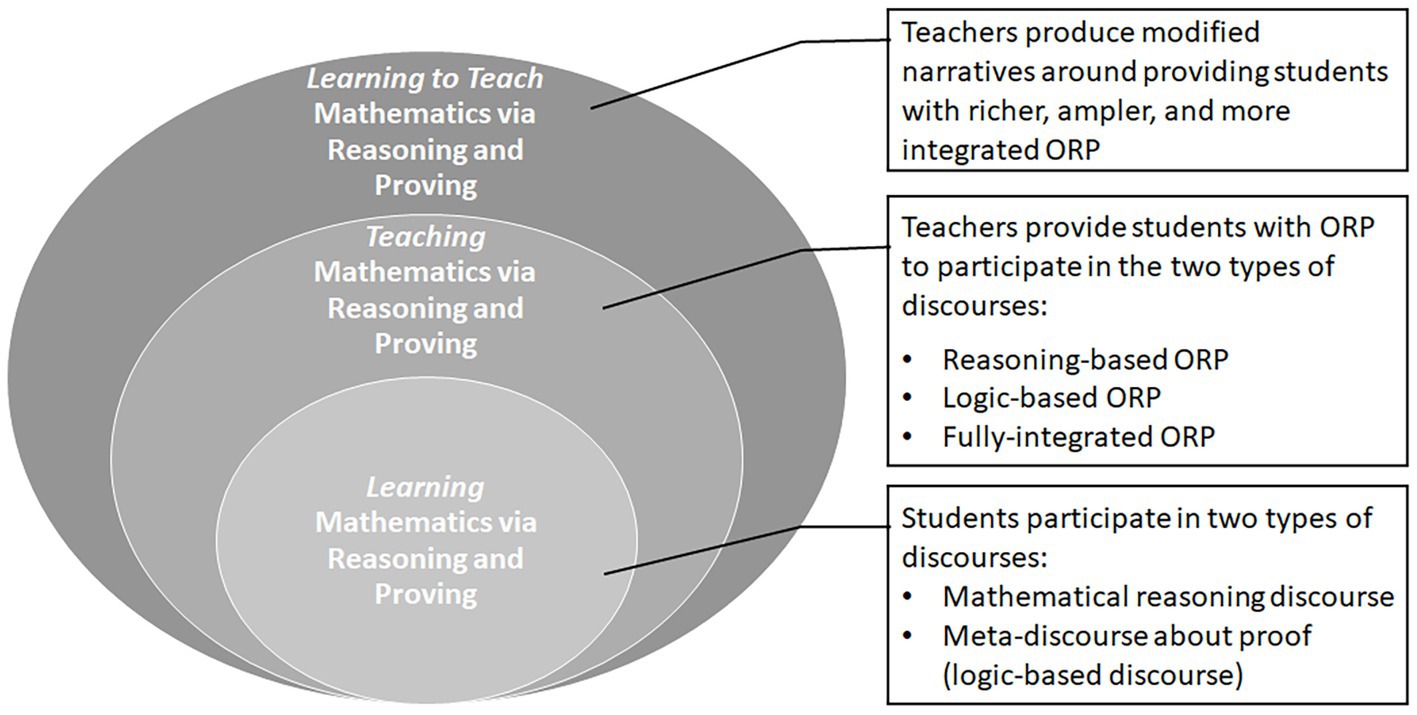
Figure 13. Triple-layer characterization of learning, teaching, and learning to teach mathematics via reasoning and proving.

Student learning mathematics via reasoning and proving is conceptualized by participating in two types of discourses: mathematical reasoning discourse and meta-discourse about proof (or logic-based discourse). Teaching mathematics via reasoning and proving entails providing opportunities for students to participate in the two types of discourses by providing reasoning-based, logic-based and fully-integrated ORP. Consequently, PSTs’ learning to teach mathematics via reasoning and proving is conceptualized as a change in their pedagogical discourse. This change is captured by the modifications they made to their lesson plans, which reflect on their teaching routines, their use of keywords and visual mediators, and the pedagogical narratives used to justify these modifications. The modifications the PSTs made and their pedagogical narratives, ideally, lead to richer, more integrated, and more ample ORP afforded to students.

We operationalized our framework methodologically by focusing on PSTs’ lesson plans as a proxy for their teaching practice (e.g., Blömeke et al., 2008) and utilized commognition to capture changes in PSTs’ practices related to teaching mathematics via reasoning and proving by examining the modifications they made to their lesson plans as a lens to their pedagogical discourse. With respect to the types of modifications made to the lesson plans (the first research question), our analysis revealed four types of modifications: structural, mathematical, reasoning-based, and logic-based. Structural modifications reflect changes to the pedagogical, structural aspects of a lesson, like timing, order of activities, supportive materials, and to the structure of students’ participation and to their interactions. Mathematical modifications aim to affect student mathematical discourse by making changes to the mathematical content of the lesson. Reasoning-based modifications intend to increase student engagement with mathematical reasoning processes, either by making the existing processes more explicit or by adding new prompts requiring students to enact reasoning processes, such as conjecturing, generalizing, validating, and justifying. The logic-based modifications are specifically aimed to explicate the logic-based objects and processes and increase student engagement with them.

Answering the second research question, we illustrated how each of these modifications in the revised lesson plan could alter the opportunities for reasoning and proving (ORP) afforded to students. Whereas most modifications provided richer ORP for students, we found some modifications that diminished or changed the nature of the ORP provided to students compared to the original lesson plan. For example, Zoe’s logic-based modifications – adding explications, definitions, and examples, which are related to logic-based objects (e.g., types of examples, the meaning of “always, sometimes, never true”), resulted in richer opportunities provided to students to participate in meta-discourse about proof. Nate’s mathematical and reasoning-based modifications, e.g., adding numeric examples before algebraic manipulations and adding questions requiring reasoning processes, increased students’ opportunities to participate in mathematical reasoning discourse. In contrast, Molly’s mathematical modification of changing the figure with the types of triangles to the figure that included the relationships that students were originally expected to notice. This modification altered the ORP afforded to students from fully-integrated to logic-related. Although students were still expected to apply logic-based processes (formulating conditional statements), Molly’s modification led to diminishing the tasks’ ORP, since it excluded the reasoning-based processes of classifying, comparing, generalizing, and conjecturing. The extended example of Diane’s lesson shows how considering all the modifications made to the entire lesson plan allowed us to characterize more holistically the ORP afforded to students. Collectively, the various modifications Diane made to her lesson plan resulted in richer, fully-integrated ORP.

We further connected the modifications PSTs made to their lesson plans and the increased (or altered ORP) afforded to students by these modifications to change in PSTs’ practices around reasoning and proving by identifying changes in their pedagogical discourse (our overarching research question). The analysis of Diane’s case illustrates how the discursive modifications and the ORP afforded by them, as well as the pedagogical narratives she produced when justifying these modifications, can indicate Diane’s evolving professional learning to teach mathematics via reasoning and proving – under the theoretical conceptualization outlined above. Similar indicators of other PSTs’ professional learning in the form of modified ORP are evident in the local revisions to the lesson plans and the related PSTs’ rationale for these revisions.

7. Contributions, implications, and future directions

Our goal in this paper, as described above, was to present the theoretical conceptualization and the related methodological approach for capturing how teachers learn to teach mathematics via reasoning and proving. One of the strengths of our conceptualization is relating teachers’ pedagogical growth to modified teaching (in our case – the envisioned teaching reflected in the modified lesson plan) and to student learning (in our data – the opportunities for student learning embedded in the lesson plan). In particular, teacher pedagogical growth is characterized as PSTs’ modified pedagogical discourse, reflected in the modifications to the lesson plans, and the modified, ideally, richer ORP afforded to students. The second strength of our approach is the reliance on the robust conceptual tools of commognition (Sfard, 2008) and its discursive conceptualization of learning. Hence, all three components of our framework – student learning, teaching, and teacher learning – are described in unified discursive elements such as keywords, routines, and visual mediators. Hence, our study contributes to the recent applications of the commognitive perspective, and other discursive perspectives for studying and advancing teacher learning (e.g., Thoma and Nardi, 2018; Zayyadi et al., 2020; Christiansen et al., 2022; Österling, 2022).

Our study contributes to the inquiry of teacher learning, specifically around integrating reasoning and proving. It is known that teachers have a central role in advancing student engagement with reasoning and proving. Yet, how teachers learn to teach mathematics via reasoning and proving remains an under researched topic (Nardi and Knuth, 2017; Stylianides et al., 2017; Buchbinder and McCrone, 2022). Capturing the development in teachers’ practice is challenging, in particular, in the context of a university teacher preparation program, where PSTs’ classroom teaching experiences are often short and limited (e.g., Jacobson, 2017). By using lesson plan modifications as a proxy for teacher practice, our study contributes to the body of knowledge exploring methodological approaches for capturing development of teacher pedagogical expertise (Depaepe et al., 2020). While lesson plans have been previously used to capture teachers’ knowledge and practices (e.g., Taylan, 2018; König et al., 2021), this study shows how teacher learning can be captured by attending to the discursive elements and characteristics of the lesson plan. This can be an invaluable asset for researchers aiming at examining PSTs’ professional learning in situations where access to classrooms is limited.

Our theoretical conceptualization and methodological approach can be used to gauge empirical patterns in the PSTs’ data. For example, the PSTs in our study modified their lesson plans in various ways, including different amounts of modifications, different types of modifications, and different types of ORP provided by these modifications. While analyzing the data, we observed clear differences between PST practical learning in the form of modified ORP. Examining each PST’s professional learning is beyond the scope of this paper, but we believe it is possible due to our theoretical and methodological work performed in this study. Quantifying the modifications and analyzing changes within and between participants may be useful in future studies for evaluating the extent of professional learning of a particular teacher or group of teachers.

It is important to note that our analysis of both the original and the modified lesson plans focused on the ORP embedded in these plans, as written by the PSTs, i.e., the intended curriculum, in Stein et al. (2007) terms. Examining the actual ORP provided to students in the enacted lessons is beyond the scope of our analysis, and our focus was on the potential ORP in both the original and revised lesson plans. However, this analysis can step forward to examine the modifications made to the lesson plan in the enacted lessons, and to compare the potential ORP as appeared in the lesson plan (intended curriculum) to the actual ORP provided to students during the enacted lesson. We began exploring this direction in our ongoing work that focuses on classroom discourse and the extent to which teachers provide students with various ORP in mathematics classrooms (Weingarden and Buchbinder, 2023).

Our analysis may be extended beyond the context of our study to professional development settings with practicing teachers or supervised teaching experiences. In regular school teaching settings, it is not often that teachers have time to deeply reflect on the enacted lessons and carefully modify their lesson plans. It may even take a full school year before a teacher has a chance to teach the same lesson again. However, teachers often need to write and/or modify lesson plans in the context of professional development programs, when being evaluated, or when seeking promotion (Silver et al., 2009; König et al., 2021). Our framework could be used in such circumstances and settings and provide clear and precise criteria for identifying and capturing teacher learning. In addition, the reliance on written artifacts, such as lesson plans, opens the possibilities for scaling up data collection and analysis, as opposed to costly and time-consuming observations (Blömeke et al., 2008). Future studies can explore these applications of our theorization.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Ethics statement

The studies involving human participants were reviewed and approved by the Dr. Julie Simpson, University of New Hampshire. The patients/participants provided their written informed consent to participate in this study.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This research was supported by the National Science Foundation, Awards No. 1711163, 1941720. The opinions expressed herein are those of the authors and do not necessarily reflect the views of the National Science Foundation.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^Similar ideas were described in Reid’s (2011) Proof-Based Teaching and Ronis’ (2008) problem-solving teaching. See Buchbinder and McCrone (2022) for comparison of the frameworks.

2. ^By capstone course, we mean a course offered toward the end of the teacher preparation program, which aims to serve as a concluding experience, linking academic training with the future professional occupation (Winsløw and Grønbæk, 2014).

3. ^Secondary education programs around the world are commonly structured as consecutive periods of university-based coursework followed by a separate period of school-based preparation. At the elementary level, a concurrent university and school-based experience is more common (Tatto et al., 2009).

4. ^The instructor provided feedback on the mathematical correctness and clarity of the lesson plan but did not tell PSTs what content or activities to include in their lesson plans.

5. ^All PSTs who took the course agreed to have their data analyzed for this research.

References

AAMT. (2006). Standards for excellence in teaching mathematics in Australian schools. Adelaide, SA, Australia: Australian Association of Mathematics Teachers.

Google Scholar

Arbaugh, F., Smith, M. P., Boyle, J., Stylianides, G. J., and Steele, M. (2018). We reason & we prove for all mathematics: building students’ critical thinking, grades 6–12. Thousand Oaks, CA: Corwin Press.

Google Scholar

Ball, D. L., and Forzani, F. (2009). The work of teaching and the challenge for teacher education. J. Teach. Educ. 60, 497–511. doi: 10.1177/0022487109348479

CrossRef Full Text | Google Scholar

Berliner, D. C. (2004). Describing the behavior and documenting the accomplishments of expert teachers. Bull. Sci. Technol. Soc. 24, 200–212. doi: 10.1177/0270467604265535

CrossRef Full Text | Google Scholar

Blömeke, S., Paine, L., Houang, R. T., Hsieh, F. J., Schmidt, W. H., Tatto, M. T., et al. (2008). Future teachers competence to plan a lesson: first results of a six-country study on the efficiency of teacher education. ZDM 40, 749–762. doi: 10.1007/s11858-008-0123-y

CrossRef Full Text | Google Scholar

Borko, H., Peressini, D., Romagnano, L., Knuth, E., Willis-Yorker, C., Wooley, C., et al. (2000). Teacher education does matter: a situative view of learning to teach secondary mathematics. Educ. Psychol. 35, 193–206. doi: 10.1207/S15326985EP3503_5

CrossRef Full Text | Google Scholar

Buchbinder, O., Brisard, S., Butler, R., and McCrone, S. (2021). Preservice secondary mathematics teachers’ reflective noticing from 360-degree video recordings of their own teaching. J. Technol. Teach. Educ. 29, 279–308.

Google Scholar

Buchbinder, O., and McCrone, S. (2020). Preservice teachers learning to teach proof through classroom implementation: successes and challenges. J. Math. Behav. 58:100779. doi: 10.1016/j.jmathb.2020.100779

CrossRef Full Text | Google Scholar

Buchbinder, O., and McCrone, S. (2022). “Guiding principles for teaching mathematics via reasoning and proving” in Proceedings of the 12th congress of European research Society in Mathematics Education (CERME12). eds. J. Hodgen, E. Geraniou, G. Bolondi, and F. Ferretti (Free University of Bozen-Bolzano and ERME), 1–8. Available at: https://hal.archives-ouvertes.fr/hal-03746878.

Google Scholar

Buchbinder, O., and McCrone, S. (2023). Prospective secondary teachers learning to teach mathematical reasoning and proof: the case of the role of examples in proving. ZDM 55, 779–792. doi: 10.1007/s11858-023-01493-4

CrossRef Full Text | Google Scholar

Chevallard, Y. (1989). On didactic transposition theory: some introductory notes. In Proceedings of the international symposium on selected domains of research and development in mathematics education (pp. 51–62). University of Bielefeld, Germany, and University of Bratislava, Slovakia. Available at: http://yves.chevallard.free.fr/spip/spip/IMG/pdf/On_Didactic_Transposition_Theory.pdf

Google Scholar

Christiansen, I. M., Corriveau, C., and Pettersson, K. (2022). Hybrids between rituals and explorative routines: opportunities to learn through guided and recreated exploration. Educ. Stud. Math. 112, 49–72. doi: 10.1007/s10649-022-10167-z

CrossRef Full Text | Google Scholar

Cirillo, M., and May, H. (2020). Decomposing proof in secondary classrooms: a promising intervention for school geometry. In Proceedings of the 14th International Congress on Mathematical Education, Shanghai, Chaina.

Google Scholar

Clarke, D., and Hollingsworth, H. (2002). Elaborating a model of teacher professional growth. Teach. Teach. Educ. 18, 947–967. doi: 10.1016/S0742-051X(02)00053-7

CrossRef Full Text | Google Scholar

Contreras, K., Arredondo, C., Díaz, C., Inostroza, M. J., and Strickland, B. (2020). Examining differences between pre-and in-service teachers’ cognition when lesson planning. System 91:102240. doi: 10.1016/j.system.2020.102240

CrossRef Full Text | Google Scholar

Davis, J. D. (2012). An examination of reasoning and proof opportunities in three differently organized secondary mathematics textbook units. Math. Educ. Res. J. 24, 467–491. doi: 10.1007/s13394-012-0047-2

CrossRef Full Text | Google Scholar

Depaepe, F., Verschaffel, L., and Star, J. (2020). Expertise in developing students’ expertise in mathematics: bridging teachers’ professional knowledge and instructional quality. ZDM 52, 179–192. doi: 10.1007/s11858-020-01148-8

CrossRef Full Text | Google Scholar

Ellis, A. B., Bieda, K., and Knuth, E. (2012). Developing essential understanding of proof and proving for teaching mathematics in grades 9–12. Reston, VA: National Council of Teachers of Mathematics (NCTM).

Google Scholar

Fennema, E., and Franke, M. L. (1992). “Teachers’ knowledge and its impact” in Handbook of research on mathematics teaching and learning. ed. D. A. Grouws (Macmillan, New York: Macmillan), 147–164.

Google Scholar

Grossman, P., and McDonald, M. (2008). Back to the future: directions for research in teaching and teacher education. Am. Educ. Res. Assoc. 45, 184–205. doi: 10.3102/0002831207312906

CrossRef Full Text | Google Scholar

Hanna, G., and Barbeau, E. (2010). Proofs as bearers of mathematical knowledge. ZDM 40, 345–353. doi: 10.1007/s11858-008-0080-5

CrossRef Full Text | Google Scholar

Hanna, G., and de Villiers, M. (2012). “Proof and proving in mathematics education: the 19th ICMI study” in New ICMI study series, vol. 15 ( Springer)

Google Scholar

Harel, G., and Sowder, L. (2007). “Toward comprehensive perspectives on the learning and teaching of proof” in Second handbook of research on mathematics teaching and learning. ed. F. K. Lester (Reston, VA: National Council of Teachers of Mathematics (NCTM)), 805–842.

Google Scholar

Harel, G., and Weber, K. (2020). “Deductive reasoning in mathematics education” in Encyclopedia of mathematics education. ed. S. Lerman (Netherlands: Springer), 183–190.

Google Scholar

Heyd-Metzuyanim, E., and Shabtay, G. (2019). Narratives of “good” instruction: teachers’ identities as drawing on exploration vs. acquisition pedagogical discourses. ZDM 51, 541–554. doi: 10.1007/s11858-018-01019-3

CrossRef Full Text | Google Scholar

Hogan, T., Rabinowitz, M., and Craven, J. A. III (2003). Problem representation in teaching: inferences from research of expert and novice teachers. Educ. Psychol. 38, 235–247. doi: 10.4324/9781315046372

CrossRef Full Text | Google Scholar

Jacobson, E. D. (2017). Field experience and prospective teachers’ mathematical knowledge and beliefs. J. Res. Math. Educ. 48, 148–190. doi: 10.5951/jresematheduc.48.2.0148

CrossRef Full Text | Google Scholar

Jeannotte, D., and Kieran, C. (2017). A conceptual model of mathematical reasoning for school mathematics. Educ. Stud. Math. 96, 1–16. doi: 10.1007/s10649-017-9761-8

CrossRef Full Text | Google Scholar

König, J., Krepf, M., Bremerich-Vos, A., and Buchholtz, C. (2021). Meeting cognitive demands of lesson planning: introducing the CODE-PLAN model to describe and analyze teachers’ planning competence. Teach. Educ. 56, 466–487. doi: 10.1080/08878730.2021.1938324

CrossRef Full Text | Google Scholar

Lampert, M., Franke, M. L., Kazemi, E., Ghousseini, H., Turrou, A. C., Beasley, H., et al. (2013). Keeping it complex: using rehearsals to support novice teacher learning of ambitious teaching. J. Teach. Educ. 64, 226–243. doi: 10.1177/0022487112473837

CrossRef Full Text | Google Scholar

Lave, J., and Wenger, E. (1991). Situated learning: Legitimate peripheral participation Cambridge, UK: Cambridge University Press.

Google Scholar

Lavie, I., and Sfard, A. (2019). How children individualize numerical routines: elements of a discursive theory in making. J. Learn. Sci. 28, 419–461. doi: 10.1080/10508406.2019.1646650

CrossRef Full Text | Google Scholar

Lavie, I., Steiner, A., and Sfard, A. (2019). Routines we live by: from ritual to exploration. Educ. Stud. Math. 101, 153–176. doi: 10.1007/s10649-018-9817-4

CrossRef Full Text | Google Scholar

Lesseig, K. (2016). Investigating mathematical knowledge for teaching proof in professional development. Int. J. Res. Educ. Sci. 2, 253–270. doi: 10.21890/ijres.13913

CrossRef Full Text | Google Scholar

Lim, W., Son, J. W., and Kim, D. J. (2018). Understanding preservice teacher skills to construct lesson plans. Int. J. Sci. Math. Educ. 16, 519–538. doi: 10.1007/s10763-016-9783-1

CrossRef Full Text | Google Scholar

Nachlieli, T., and Heyd-Metzuyanim, E. (2021). Commognitive conflicts as a learning mechanism towards explorative pedagogical discourse. J. Math. Teach. Educ. 25, 347–369. doi: 10.1007/s10857-021-09495-3

CrossRef Full Text | Google Scholar

Nachlieli, T., and Tabach, M. (2019). Ritual-enabling opportunities-to-learn in mathematics classrooms. Educ. Stud. Math. 101, 253–271. doi: 10.1007/s10649-018-9848-x

CrossRef Full Text | Google Scholar

Nardi, E., and Knuth, E. (2017). Changing classroom culture, curricula, and instruction for proof and proving: how amenable to scaling up, practicable for curricular integration, and capable of producing long-lasting effects are current interventions? Educ. Stud. Math. 96, 267–274. doi: 10.1007/s10649-017-9785-0

CrossRef Full Text | Google Scholar

Nardi, E., Ryve, A., Stadler, E., and Viirman, O. (2014). Commognitive analyses of the learning and teaching of mathematics at university level: the case of discursive shifts in the study of calculus. Res. Math. Educ. 16, 182–198. doi: 10.1080/14794802.2014.918338

CrossRef Full Text | Google Scholar

NCTM (2000). Principles and standards for school mathematics Reston, VA: NCTM.

Google Scholar

NCTM (2009). Focus in high school mathematics: Reasoning and sense making NCTM.

Google Scholar

NCTM (2014). Principles to actions NCTM.

Google Scholar

National Governors’ Association Center for Best Practices and Council of Chief State School Officers, NGA and CCSSO (2010). Common core state standards: mathematics. Washington DC: Council of Chief State School Officers. Available at: http://www. corestandards. org/assets/CCSSI_Math% 20Standards. Pdf.

Google Scholar

Österling, L. (2022). “Operationalising de-ritualisation for the analysis of teaching-as-usual” in Proceedings of the 12th congress of European research Society in Mathematics Education. eds. J. Hodgen, E. Geraniou, G. Bolondi, and F. Ferretti ( Free University of Bozen-Bolzano and ERME)

Google Scholar

Otten, S., Males, L. M., and Gilbertson, N. J. (2014). The introduction of proof in secondary geometry textbooks. Int. J. Educ. Res. 64, 107–118. doi: 10.1016/j.ijer.2013.08.006

CrossRef Full Text | Google Scholar

Reid, D. A. (2011). “Understanding proof and transforming teaching” in Proceedings of the 33rd annual meeting of the north American chapter of the International Group for the Psychology of mathematics education. eds. L. R. Wiest and T. Lamberg (Reno, NV: University of Nevada), 15–13.

Google Scholar

Remillard, J. T., Herbel-Eisenmann, B., and Lloyd, G. M. (Eds.) (2009). Mathematics teachers at work: Connecting curriculum materials and mathematics instruction. New York, NY: Routledge.

Google Scholar

Ronis, D. L. (2008). Problem-based learning for math & science: Integrating inquiry and the internet. Thousand Oaks, CA: Corwin Press.

Google Scholar

Sfard, A. (2007). When the rules of discourse change, but nobody tells you: making sense of mathematics learning from a commognitive standpoint. J. Learn. Sci. 16, 565–613. doi: 10.1080/10508400701525253

CrossRef Full Text | Google Scholar

Sfard, A. (2008). Thinking as communicating. Cambridge, UK: Cambridge University Press.

Google Scholar

Sfard, A., and Kieran, C. (2001). Cognition as communication: rethinking learning-by-talking through multi-faceted analysis of students’ mathematical interactions. Mind Cult. Act. 8, 42–76. doi: 10.1207/S15327884MCA0801_04

CrossRef Full Text | Google Scholar

Shinno, Y., and Fujita, T. (2021). Characterizing how and when a way of proving develops in a primary mathematics classroom: a commognitive approach. Int. J. Math. Educ. Sci. Technol. 53, 3326–3351. doi: 10.1080/0020739X.2021.1941365

CrossRef Full Text | Google Scholar

Silver, E. A., Mesa, V. M., Morris, K. A., Star, J. R., and Benken, B. M. (2009). Teaching mathematics for understanding: an analysis of lessons submitted by teachers seeking NBPTS certification. Am. Educ. Res. J. 46, 501–531. doi: 10.3102/0002831208326559

CrossRef Full Text | Google Scholar

Stein, M. K., Engle, R. A., Smith, M. S., and Hughes, E. K. (2008). Orchestrating productive mathematical discussions: five practices for helping teachers move beyond show and tell. Math. Think. Learn. 10, 313–340. doi: 10.1080/10986060802229675

CrossRef Full Text | Google Scholar

Stein, M. K., Remillard, J., and Smith, M. S. (2007). “How curriculum influences student learning” in Second handbook of research on mathematics teaching and learning. ed. F. K. Lester (Charlotte, NC: Information Age Publishers), 319–370.

Google Scholar

Stigler, J. W., and Miller, K. F. (2018). “Expertise and expert performance in teaching” in The Cambridge handbook of expertise and expert performance. eds. A. Ericsson, R. R. Hoffman, A. Kozbelt, and A. M. Williams. 2nd ed (Cambridge, UK: Cambridge University Press), 431–452.

Google Scholar

Stylianides, G. J. (2009). Reasoning-and-proving in school mathematics textbooks. Math. Think. Learn. 11, 258–288. doi: 10.1080/10986060903253954

CrossRef Full Text | Google Scholar

Stylianides, A. J. (2011). Towards a comprehensive knowledge package for teaching proof: a focus on the misconception that empirical arguments are proofs. Pythagoras 32, 1–10. doi: 10.4102/pythagoras.v32i1.14

CrossRef Full Text | Google Scholar

Stylianides, G. J., Stylianides, A. J., and Weber, K. (2017). “Research on the teaching and learning of proof: taking stock and moving forward” in Compendium for research in mathematics education. ed. J. Cai (Reston, VA: National Council of Teachers of Mathematics (NCTM)), 237–266.

Google Scholar

Tatto, M. T., Lerman, S., and Novotná, J. (2009). “Overview of teacher education systems across the world” in The professional education and development of teachers of mathematics: The 15th ICMI study. eds. R. Even and D. L. Ball (Boston, MA: Springer), 15–23.

Google Scholar

Taylan, R. D. (2018). The relationship between pre-service mathematics teachers’ focus on student thinking in lesson analysis and lesson planning tasks. Int. J. Sci. Math. Educ. 16, 337–356. doi: 10.1007/s10763-016-9778-y

CrossRef Full Text | Google Scholar

Thoma, A., and Nardi, E. (2018). Transition from school to university mathematics: manifestations of unresolved commognitive conflict in first year students’ examination scripts. Int. J. Res. Undergrad. Math. Educ. 4, 161–180. doi: 10.1007/s40753-017-0064-3

CrossRef Full Text | Google Scholar

Thompson, D. R., Senk, S. L., and Johnson, G. J. (2012). Opportunities to learn reasoning and proof in high school mathematics textbooks. J. Res. Math. Educ. 43, 253–295. doi: 10.5951/jresematheduc.43.3.0253

CrossRef Full Text | Google Scholar

Viirman, O. (2015). Explanation, motivation and question posing routines in university mathematics teachers’ pedagogical discourse: a commognitive analysis. Int. J. Math. Educ. Sci. Technol. 46, 1165–1181. doi: 10.1080/0020739X.2015.1034206

CrossRef Full Text | Google Scholar

Vygotsky, L. S. (1978). Mind in society: the development of higher psychological processes. Harvard, MA: Harvard University Press.

Google Scholar

Warshauer, H. K. (2015). Productive struggle in middle school mathematics classrooms. J. Math. Teach. Educ. 18, 375–400. doi: 10.1007/s10857-014-9286-3

CrossRef Full Text | Google Scholar

Watson, A., and Ohtani, M. (2015). “Task design in mathematics education: An ICMI study 22.” New ICMI Study Series. Berlin: Springer.

Google Scholar

Weingarden, M., and Buchbinder, O. (2023). “Understanding beginning teachers’ transition from university to supervised internship: implementing opportunities for reasoning and proving” in In the proceedings of the annual meeting of the American Educational Research Association (AERA) (Chicago, IL)

Google Scholar

Weingarden, M., Buchbinder, O., and Liu, J. (2022). Opportunities for reasoning-and-proving in mathematical tasks: a discursive perspective. In S Lischka, A E Dyer, E B Jones, R S Lovett, J Strayer, and J Drown (Ed.), Proceedings of the 44th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (PME-NA). Middle Tennessee State University. (pp. 839–848).

Google Scholar

Weingarden, M., Heyd-Metzuyanim, E., and Nachlieli, T. (2019). The realization tree assessment tool – examining explorative participation in mathematics lessons. J. Math. Behav. 56:100717. doi: 10.1016/j.jmathb.2019.100717

CrossRef Full Text | Google Scholar

Winsløw, C., and Grønbæk, N. (2014). Klein’s double discontinuity revisited. Recherches En Didactique Des Mathématiques 34, 59–86.

Google Scholar

Zayyadi, M., Nusantara, T., Hidayanto, E., Sulandra, I. M., and Sa’Dijah, C. (2020). Content and pedagogical knowledge of prospective teachers in mathematics learning: Commognitive. J. Educ. Gifted Young Sci 8, 515–532. doi: 10.17478/jegys.642131

CrossRef Full Text | Google Scholar

Zayyadi, M., Nusantara, T., Subanji, S., Hidayanto, E., and Sulandra, I. M. (2019). A commognitive framework: the process of solving mathematical problems of middle school students. Int. J. Learn. Teach. Educ. Res. 18, 89–102. doi: 10.26803/ijlter.18.2.7

CrossRef Full Text | Google Scholar

Zazkis, R., Liljedahl, P., and Sinclair, N. (2009). Lesson plays: planning teaching versus teaching planning. For Learn. Math. 29, 40–47.

Google Scholar