An implementation analysis of a Cognitively Guided Instruction (CGI) teacher professional development program

Information about program implementation provides critical information for the interpretation of results from randomized trials. The present study provides an evaluation of the implementation of a Cognitively Guided Instruction mathematics teacher professional development as part of a large scale randomized controlled trial with teachers in first- and second- grade in eleven elementary schools in two adjacent school districts. We developed a measure of fidelity of implementation and used it during the in-person training sessions to determine the extent to which the training program was implemented as intended. The results from this study suggest that the program was implemented with high fidelity providing context for interpretation of overall program outcomes on teachers and students.

1. Introduction

Mathematics proficiency is an important educational milestone because of its relationship to both short-term and long-term benefits (Barrett and VanDerHeyden, 2020). Every year, school leaders and educators are challenged with determining what programs they should adopt in their schools to support the development of students mathematics proficiency. Teacher professional development (PD) is often one-way schools use to improve teaching and learning. Teacher professional development is an ongoing process in which teachers’ continuous growth depends not only on their own efforts if they are to expect to see classroom practices change (Braseth, 2021), but also on the extent to which the training program was provided as intended. In this article, we describe the conceptualization and measurement of implementation fidelity for an evidence-based mathematics teacher professional development program called Cognitively Guided Instruction.

Cognitively Guided Instruction (CGI) is a mathematics teacher PD program initially developed by researchers at the University of Wisconsin-Madison with funding from the National Science Foundation in the 1980s. The goal of the CGI program was to provide an opportunity for teachers to learn a taxonomy for mathematics word problems and a related taxonomy for describing the progression of student thinking from least sophisticated to most sophisticated (Carpenter and Fennema, 1992; Carey et al., 1995). These taxonomies were based upon decades of research on how young children learn to perform operations on whole number (Carpenter, 1985; Carpenter et al., 1988, 1999). The stated aim of the CGI program in the 1980s was to incorporate scientific knowledge of how children learn mathematics into instructional practice by focusing teachers’ attention on student thinking and providing them with principled frameworks for mathematics problem solving and student thinking (Carpenter et al., 1989; Carpenter and Fennema, 1992).

The initial study of the CGI program in the 1980s reported that CGI was beneficial to both teachers and students and over the last thirty years teacher PD based on CGI has taken many different forms. Keeping with its original goal of focusing teachers’ attention on student thinking, CGI PD programs are not prescriptive and do not require the use of any specific textbook. Many CGI PD programs align well with modern curriculum standards, which have incorporated some of the same basic research on types of word problems, student understanding of the equals symbol, and other topics that teachers learn through the CGI PD program.

In 2012, a replication study of a CGI program was funded by the Institute for Educational Sciences (IES) to examine the effects of the CGI teacher PD program on a diverse set of teachers and students. The study was designed to evaluate whether the CGI program designed and delivered by Teachers Development Group, the largest provider of CGI teacher PD in the United States at the time, would result in increased student achievement in mathematics. The theory of change for the CGI program hypothesizes that if the CGI PD program is delivered as intended and teachers attend the CGI PD, their involvement in the program will lead to a change in their mathematical knowledge for teaching and their beliefs about teaching and learning. These changes occur through an interactive and iterative process as they attend multiple days of the professional development trainings and interact with their students between sessions. These interactions and changes in mathematical knowledge and beliefs can result in changes in teachers’ approaches to mathematics instruction and, ultimately, increase student learning in mathematics. Methods and measures were developed during the replication study to evaluate the program’s effects on participating teachers and students. During the measurement development process, questions arose about the need for a measure to monitor the delivery of the teacher training program. The study presented in this brief research report is driven by the following research question: To what extent was the Cognitively Guided Instruction teacher professional development program implemented with teachers as expected during the Replicating the CGI Experiment in Diverse Environments research study?

2. Fidelity of implementation

Fidelity of implementation refers to the degree to which a program is implemented as intended by the program developer and is necessary for accurate interpretation of program effects (Bond et al., 2000; O’Donnell, 2008; Gearing et al., 2011; Meyers and Brandt, 2015; Roberts et al., 2017). Traditionally used in the medical and public health literature, the measurement of fidelity developed into two related directions: treatment integrity and treatment differentiation. Treatment integrity is the degree to which a program is implemented as intended. Treatment differentiation describes the distinct differences between the program condition (i.e., between treatment/control or between several interventions under comparison) and describes how those differences would be expected to provide changes in the outcome measure (Bond et al., 2000; Gresham, 2017). While there are many slight variations to the definition of fidelity of implementation in education research, there is general agreement that implementation fidelity is a combination of both treatment integrity and treatment differentiation (Meyers and Brandt, 2015; Roberts et al., 2017).

One of the most compelling arguments for the study of implementation fidelity is to better understand when programs do not attain the intended outcomes. Without a measure of the program’s fidelity to the intended plan, there is no way to determine if unexpected results, such as when there is no discernible difference between the compared groups, reflect a failure of the program or a failure to implement the program (Bond et al., 2000; Mowbray et al., 2003; Meyers and Brandt, 2015). Studies have found that fidelity levels are significantly related to the amount of positive change achieved by a program (Durlak and DuPre, 2008). In addition, studies that incorporate fidelity data into outcome analysis often found larger effect than analyses conducted without fidelity data (Dane and Schneider, 1998; Lillehoj et al., 2004).

While the importance of measuring program implementation as a method to document deviations from the intended model in general might seem straightforward, interpreting the extent or quality of implementation can be complex. This article is the first to present an analysis of fidelity of implementation of a Cognitively Guided Instruction teacher professional development program following many of the key aspects of fidelity of implementation as defined by Dane and Schneider (1998). These key aspects of fidelity of implementation are presented in Table 1 and provide the bases for how we measured the delivery of the CGI professional development program.

TABLE 1

Table 1. Key aspects of fidelity of implementation.

3. The CGI program and the context of the study

The CGI teacher PD program that will be discussed in this article was the program as designed and delivered by the Teachers Development Group under the direction of Linda Levi, who served as the Director of CGI initiatives at the time. The program was designed to provide up to three years of teacher professional development for elementary mathematics teachers. Each year of the program consisted of eight days (forty-eight hours) of teacher PD delivered in three sets of workshops, including four consecutive days during the summer months and two 2-day follow-up PD sessions during the school year. Teachers must have completed the first year of the program before becoming eligible for the next program year.

This CGI PD program provided teachers with information about the research on student mathematical thinking and understanding. Keeping in line with the belief expressed by Carpenter and Fennema (1992) about the original CGI program “researchers and educators can bring about significant changes in classroom practices by helping teachers make informed decisions rather than by attempting to train them to perform in a specified way” (p. 460), the program offered during this project did not provide teachers with explicit information on how to teach mathematics to students on a daily basis.

The PD provider hired and trained all PD facilitators utilizing their hiring criteria and training manual. The requirements necessary to become certified by them as a CGI PD facilitator are as follows:

1. Have a strong understanding of the CGI content knowledge (i.e., problem types, solution strategies, relationship between problem types and solution strategies).

2. Have at least 5 years of experience with CGI in one of the following ways:

a. actively implementing CGI as a classroom teacher.

b. actively supporting/implementing CGI as a math coach working with expert CGI teachers.

c. actively supporting/implementing CGI as a CGI researcher working closely with expert CGI teachers.

3. Have at least 3 years of experience teaching CGI PD to teachers in their own communities.

4. Be able to design a problem in real time that would engage children with a particular property within a particular number domain.

5. Have strong pedagogical skills when working with adult learners.

The CGI PD facilitators were provided with a CGI PD facilitator’s manual containing content-specific tasks and lessons, projected questions from teachers, and specific goals and ideas that should be achieved for each session. The prescriptive and detailed nature of the facilitators manual enabled measurement of PD fidelity. Prior to each PD session, the Director of CGI initiatives and PD facilitator meet to clarify any questions they might have about the material that will be presented to the group. Due to the nature of the CGI program and differences between teachers, students, and locations that the professional developments are held, PD facilitators were allowed to modify approximately 5% of the session to fit the needs and interests of the teachers and schools attending the workshop. These changes, however, should have been small enough to not change the essence of the program. After each set of PD days, the facilitator reported back to the Director of CGI initiatives on the progress made regarding the agenda and discussed any areas of concern they experienced with delivery of the content to their specific group of teachers. This information was then used to make any necessary adjustments to the scope and sequence for the remainder of that group’s program.

The Replicating the CGI Experiment in Diverse Environments study was conducted between 2013–2015 and focused on the first two years (CGI year 1 and CGI year 2) of the three-year CGI professional development program. Enrollment criteria limited participation to only first- or second-grade teachers of mathematics in two adjacent school districts in the southeastern United States. More information about the research study design can be found in project reports (Schoen et al., 2020, 2022). The research protocol approved by the FSU Institution Review Board and the participating school districts required teachers in participating schools to voluntarily consent to participate in the program and associated study, regardless of the school’s agreement and assignment in the study. In schools assigned to the treatment condition (CGI PD), all first and second grade teachers who consented to participate were invited to attend the two-year CGI professional development program.

4. Methods

To address the research question presented in this article, it was necessary to determine if a fidelity of implementation measure for the CGI teacher PD program being delivered existed. Despite the widespread implementation of the CGI teacher PD program that served as the intervention in the study, the program had never been subject to an external evaluation or an evaluation of the extent to which the program was being delivered as planned. As a result, we needed to develop a fidelity of implementation measure that would assess the important aspects of program delivery.

4.1. The fidelity of implementation measure

The data presented in this article will focus only on the fidelity of implementation of the CGI teacher professional development sessions, which starts at teacher registration for the research study and ends at the proximal outcomes of increased teacher knowledge and changes in teacher beliefs. These training sessions are the first opportunity in the CGI program for teachers to gain information about student thinking and processes that can ultimately lead to the more distal outcomes of improved student achievement.

The development of the CGI PD fidelity of implementation measure was based on steps necessary to measure implementation fidelity as described previously in the research literature (McGrew et al., 1994; Teague et al., 1998; Mowbray et al., 2003). The first step was to identify and define key ingredients and components of the program and related mediators necessary to achieve program outcomes. Key ingredients and components of the program are program components, activities, and processes for which the developer is responsible to deliver. Program mediators are short-term outcomes through which activities as implemented are expected to lead to subsequent intended outcomes (Lorenston et al., 2015; Meyers and Brandt, 2015). Outcomes are the terminal change that the intervention is designed to achieve.

The measure of fidelity of implementation that we developed used direct observations of each professional development session to obtain data on the extent to which the CGI PD facilitators were adhering to the planned content. The observation plan was developed from the CGI PD facilitators manual and utilized a checklist to document which key sections of the planned content occurred. To document teachers’ exposure to the program, direct observation of teachers’ attendance and self-reports from teachers on the extent to which they completed out-of-workshop activities were collected. Quality of delivery and participant responsiveness were two areas in which indirect methods of data collection were the primary source of data, relying mostly on self-reports by teachers.

4.2. Data collection

Data collected using the fidelity of implementation measure was completed by trained research personnel external to Teachers Development Group. Observers were paired up during the initial four-day PD session so that they could continue training on the use of the measure while discussing with their partner any questions regarding activity completion. At the end of each day of the initial four-day PD session, the paired observers came to consensus on which activities were completed in the observation measure. Observers were also provided with an opportunity to debrief with the CGI PD facilitator after each day to discuss any questions about delivery of activities listed on the observation protocol. To reduce the reliance on the CGI PD facilitator to identify certain activities for the PD observers, the observation protocol was modified after the first live PD implementation days. These modifications to the protocol included explicit naming of handouts and providing more detailed information about the video clips that were scheduled to be played. After the initial four-day use of the fidelity measure, observers were assigned to individually observe separate CGI PD sessions. The observers were still allowed to discuss any questions about the day’s activity with their respective CGI PD facilitator and, if applicable, with any other research staff who might have been present during their PD session.

5. Results

5.1. Qualifications of the selected workshop facilitators

Three different experienced CGI PD facilitators were provided with training and support from Teachers Development Group throughout the implementation of the CGI program with teachers in the study. On average, the number of years of experience with CGI amongst the three facilitators was 22.7 years. They also averaged 16 years facilitating CGI teacher PD. The specific qualifications for each of the three facilitators at the start of the professional development program and the type and number of workshops each were assigned to deliver are provided in the Supplemental materials.

5.2. Adherence to content coverage during the professional development

Prior to the delivery of the program with teachers, analysis of the CGI PD program facilitator manual revealed that the eight-day CGI year 1 program consisted of a total of seventy-nine planned activities and the eight-day CGI year 2 program consisted of a total of sixty-seven planned activities. We sectioned these activities into seven key subcategories of CGI program components and present them in Table 2.

TABLE 2

Table 2. Seven subcategories of the CGI teacher professional development program.

Figure 1 contains a comparison of the implemented CGI year 1 PD program activities and the planned PD program activities. On average and across both years of implementation of the CGI year 1 program, about 82% of the planned activities were implemented in the workshops. A comparison of the implemented CGI year 2 PD program activities and the planned PD program activities during the 2014–2015 school year are presented in Figure 2. On average, 87% of the planned CGI year 2 PD program activities were implemented in the training workshops. These figures provide data indicating that the PD facilitators completed nearly all the activities in all the major categories.

FIGURE 1

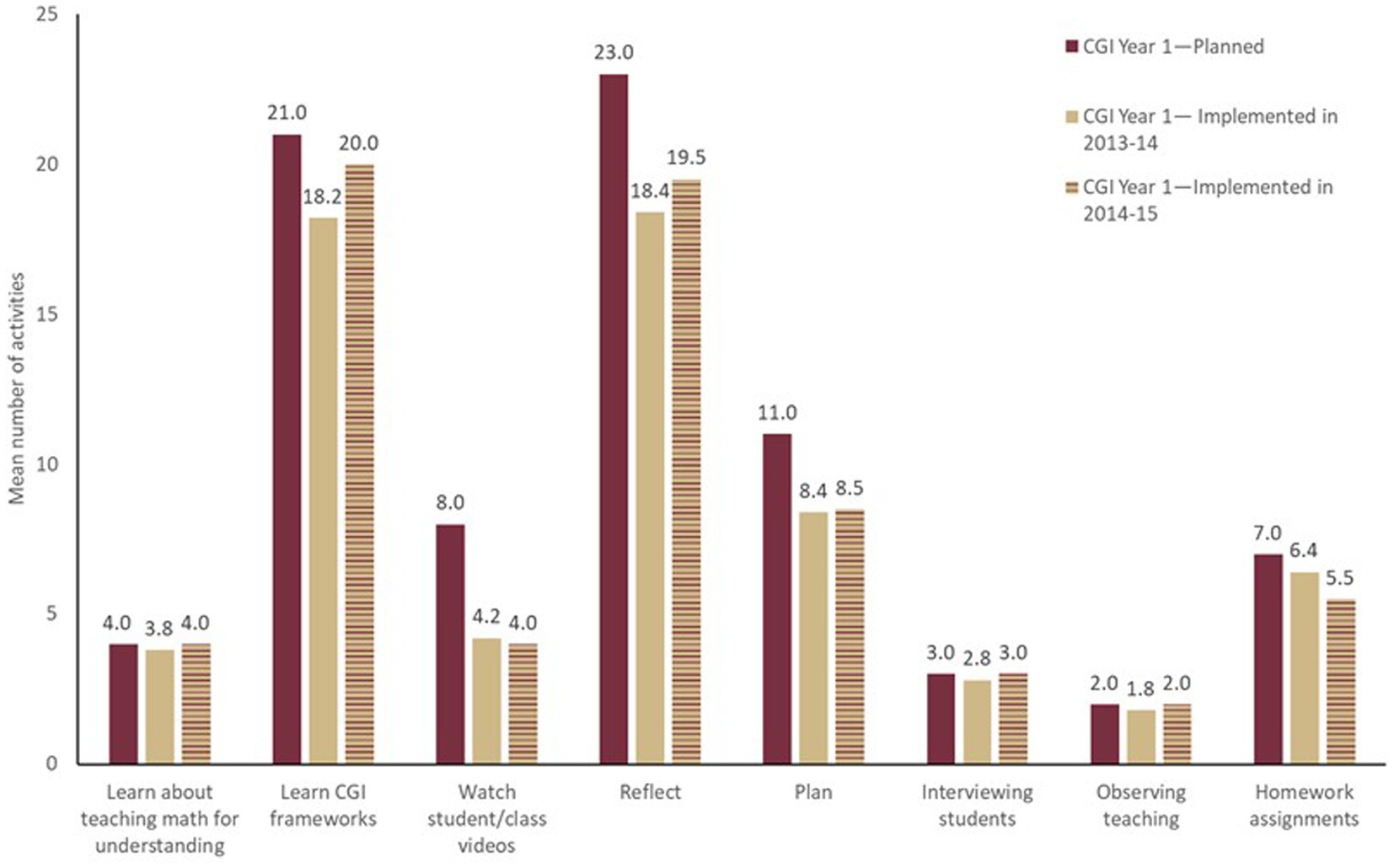
Figure 1. Comparing the plan and implementation of activities of the first year of the CGI program for groups in two subsequent school years.

FIGURE 2

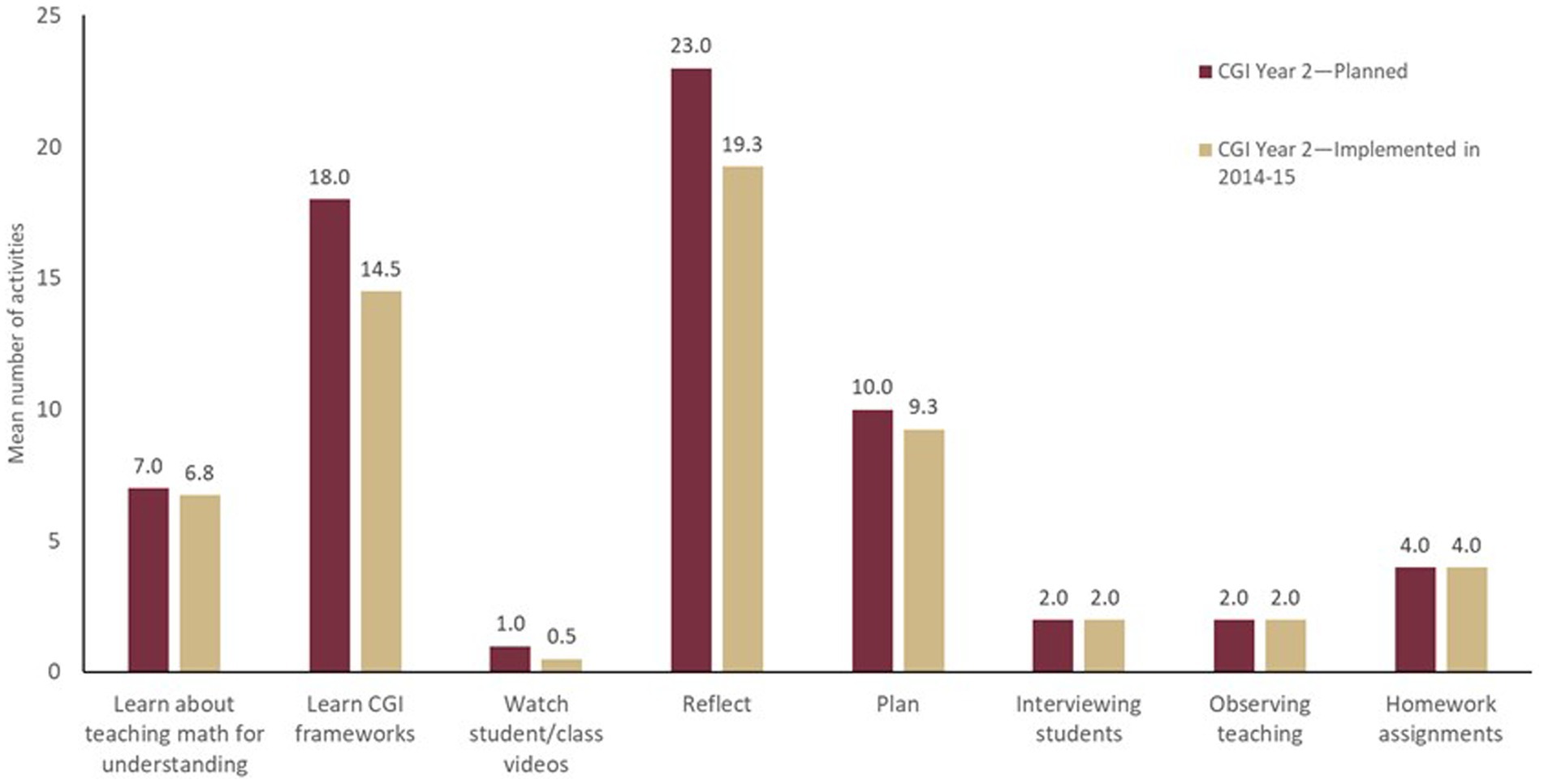
Figure 2. Comparing the plan and implementation of activities of the second year of the CGI program for groups in the 2014–2015 school year.

5.3. School level exposure to the CGI program

Overall, the voluntary participation rate amongst eligible teachers in schools randomized to participate in the CGI PD program was high. In the 2013–2014 school year, 107 of the 144 teachers at eligible schools participated in the CGI year 1 PD. In the 2014–2015 year, 103 of the 141 teachers eligible participated, of which, twenty-seven teachers were in the CGI year 1 program and seventy-six teachers were in the CGI year 2 program. Overall, approximately 75% of the eligible teachers in participating schools participated in the training program during the two-year period.

5.4. Participant exposure to the professional development

The CGI PD program offered forty-eight hours of direct contact with teachers during each year of the program (i.e., CGI year 1, CGI year 2). Attendance records collected by the research team showed that program completion rates (teachers completing between 37–48 h) for the CGI year 1 and CGI year 2 program were 80 and 64.5%, respectively. During the 2014–2015 year, thirteen teachers missed the CGI year 2 program completion cutoff criterion by missing two days of training due to a variety of reasons (e.g., illness, maternity leave, substitute teacher no-shows, family obligations, religious conflicts with Saturday trainings).

5.5. Participant responsiveness to the professional development

Participant responsiveness is a measure of how participants are engaged by the CGI training. We did not directly ask participants questions about their level of engagement; however, engagement levels were derived using the participants attendance records and their responses to a self-report survey about their perception of the quality of the program.

On days four, six, and eight of the PD program, we asked teachers to report on their perception of the overall quality of the program using a five-point scale, with one indicating “poor” and five indicating “excellent.” The average score across all the training days for CGI year 1 and the CGI year 2 program was around a score of four. This suggests that on average teachers perceived the workshops offered to be of high quality.

Combining the number of teachers who voluntarily agreed to participate in the program, the high level of completion by teachers of all the training hours over the school year, and the teachers positive self-report on the quality of the professional development all indicate that the teachers perceived value in the program.

5.6. Limitations

There are a few limitations in this study that we would like to note. The first limitation exists due to the flexibility in the implementation of program activities by the PD facilitator to meet the needs of teachers in the group. Future measures of fidelity of implementation of CGI PD should include asking PD facilitators questions regarding decisions to omit program activities. A second limitation exists due to the derivation of participant responsiveness from attendance records and teachers self-report of quality of the program. While we believe our conclusions of a positive participant responsiveness to the CGI teacher professional development program was warranted from the analysis of teacher enrollment, teacher attendance, and teacher self-report of quality of instruction, future measures of fidelity of implementation of CGI PD should include the collection of observational data on teacher engagement in the program during program activities, as well as, the collection of data that directly asks teachers to report on their level of enthusiasm for the program.

6. Conclusion

This study was the first to utilize key aspects of implementation fidelity to analyze a Cognitively Guided Instruction teacher professional development program. Although the program had been in place and implemented for many years there was not a way for school leaders and educators to really know if the CGI program purchased was, in fact, the program their teachers received. Using the developed fidelity of implementation measure we found that the CGI teacher PD program provided during the Replicating the CGI Experiment in Diverse Environments study was delivered to the teachers in the research study by highly qualified facilitators who adhered to the program implementation plan resulting in teachers receiving the program as intended by the program developer. The collection and evaluation of data about the implementation of the PD program is important for the CGI replication study because it provides context to the extent to which the participating teachers were exposed to the intended training program. These data are currently being used by researchers to provide additional context for the overall reporting on the program’s effects on teachers and students.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics statement

The studies involving humans were approved by the Institutional Review Board at Florida State University and the cognizant authorities in the two participating school districts. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants.

Author contributions

AT and RS contributed to conception and design of the study. AT organized the database and performed the analysis and wrote the first draft of the manuscript. All authors contributed to the article and approved the submitted version.

Funding

The research reported here was supported by the Institute of Education Sciences, U.S. Department of Education, through grant award numbers R305A120781 and R305A180429 to Florida State University.

Acknowledgments

The authors wish to thank the teachers, schools, and school districts who participated in the randomized controlled trial study, without them this research could not be conducted. The authors would also like to thank Alain Bengochea, Charity Buntin, Kristopher Childs, Kristy Farina, Laura Tapp, Naomi Iuhasz-Velez, Nesrin Sahin, Uma Gadge, Vernita Glenn-White, Wendy Bray, and Zachary Champagne for assisting with data collection.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Author disclaimer

The opinions expressed are those of the authors and do not represent the views of the Institute or the U.S. Department of Education.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2023.1150229/full#supplementary-material

References

Barrett, C. A., and VanDerHeyden, A. M. (2020). A cost-effectiveness analysis of classwide math intervention. J. Sch. Psychol. 80, 54–65. doi: 10.1016/j.jsp.2020.04.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Bond, G. R., Evans, L., Salyers, M. P., Williams, J., and Kim, H.-W. (2000). Measurement of Fidelity in psychiatric rehabilitation. Ment. Health Serv. Res. 2, 75–87. doi: 10.1023/A:1010153020697

CrossRef Full Text | Google Scholar

Braseth, E. A. (2021). Principals’ leadership of mathematics teachers’ professional development. Front. Educ. 6:697231. doi: 10.3389/feduc.2021.697231

CrossRef Full Text | Google Scholar

Carey, D., Fennema, E., Carpenter, T. P., and Franke, M. L. (1995). “Equity and mathematics education” in New directions for equity in mathematics education. eds. W. G. Secada, E. Fennema, L. B. Adajian, and L. Byrd (New York, NY: Cambridge University Press), 93–125.

Google Scholar

Carpenter, T. P. (1985). “Learning to add and subtract: an exercise in problem solving” in Teaching and learning mathematical problem solving: Multiple research perspectives. ed. E. A. Silver (Hillsdale, New Jersey: Lawrence Erlbaum Associates, Inc.), 17–40.

Google Scholar

Carpenter, T. P., and Fennema, E. (1992). Chapter 4 cognitively guided instruction: building on the knowledge of students and teachers. Int. J. Educ. Res. 17, 457–470. doi: 10.1016/S0883-0355(05)80005-9

CrossRef Full Text | Google Scholar

Carpenter, T. P., Fennema, E., Franke, M. L., Levi, L., and Empson, S. B. (1999). Children's mathematics: cognitively guided instruction. Portsmouth, NH: Heinemann.

Google Scholar

Carpenter, T. P., Fennema, E., Peterson, P. L., Chiang, C.-P., and Loef, M. (1989). Using knowledge of children’s mathematics thinking in classroom teaching: an experimental study. Am. Educ. Res. J. 26, 499–531. doi: 10.3102/00028312026004499

CrossRef Full Text | Google Scholar

Carpenter, T. P., Moser, J. M., and Bebout, H. C. (1988). Representation of addition and subtraction word problems. J. Res. Math. Educ. 19, 345–357. doi: 10.2307/749545

CrossRef Full Text | Google Scholar

Dane, A. V., and Schneider, B. H. (1998). Program integrity in primary and early secondary prevention: are implementation effects out of control? Clin. Psychol. Rev. 18, 23–45. doi: 10.1016/S0272-7358(97)00043-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Durlak, J. A., and DuPre, E. P. (2008). Implementation matters: a review of research on the influence of implementation on program outcomes and the factors affecting implementation. Am. J. Community Psychol. 41, 327–350. doi: 10.1007/s10464-008-9165-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Gearing, R. E., El-Bassel, N., Ghesquiere, A., Baldwin, S., Gillies, J., and Ngeow, E. (2011). Major ingredients of fidelity: a review and scientific guide to improving quality of intervention research implementation. Clin. Psychol. Rev. 31, 79–88. doi: 10.1016/j.cpr.2010.09.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Gresham, F. M. (2017). “Features of fidelity in schools and classrooms: constructs and measurement” in Treatment fidelity in studies of educational intervention. eds. G. Roberts, S. Vaughn, S. N. Beretvas, and V. Wong (New York, NY: Taylor & Francis), 22–38.

Google Scholar

Lillehoj, C. J., Griffin, K. W., and Spoth, R. (2004). Program provider and observer ratings of school-based preventive intervention implementation: agreement and relation to youth outcomes. Health Educ. Behav. 31, 242–257. doi: 10.1177/1090198103260514

PubMed Abstract | CrossRef Full Text | Google Scholar

Lorenston, M., Oh, Y. J., and LaBanca, F. (2015). “STEM21 digital academy Fidelity of implementation: valuation and assessment of program components and implementation” in Implementation fidelity in education research: Designer and evaluator considerations. eds. C. V. Meyers and W. C. Brandt (New York: Routledge).

Google Scholar

McGrew, J. H., Bond, G. R., Dietzen, L., and Salyers, M. (1994). Measuring the fidelity of implementation of a mental health program model. J. Consult. Clin. Psychol. 62, 670–678. doi: 10.1037/0022-006X.62.4.670

CrossRef Full Text | Google Scholar

Meyers, C.V., and Brandt, W.C. (2015). Implementation fidelity in education research: Designer and evaluator considerations. New York: Routledge.

Google Scholar

Mowbray, C. T., Holter, M. C., Teague, G. B., and Bybee, D. (2003). Fidelity criteria: development, measurement, and validation. Am. J. Eval. 24, 315–340. doi: 10.1177/109821400302400303

CrossRef Full Text | Google Scholar

O’Donnell, C. L. (2008). Defining, conceptualizing, and measuring Fidelity of implementation and its relationship to outcomes in K–12 curriculum intervention research. Rev. Educ. Res. 78, 33–84. doi: 10.3102/0034654307313793

CrossRef Full Text | Google Scholar

Roberts, G., Vaughn, S., Beretvas, S. N., and Wong, V. (2017). Treatment Fidelity in studies of educational intervention. New York, NY: Taylor & Francis.

Google Scholar

Schoen, R. C., Bray, W. S., Tazaz, A. M., and Buntin, C. K. (2022). "Description of the cognitively guided instruction professional development program in Florida: 2013–2020 ". (Tallahassee, FL: Florida State University).

Google Scholar

Schoen, R. C., LaVenia, M., Tazaz, A. M., Farina, K., Dixon, J. K., and Secada, W. G. (2020). "Replicating the CGI experiment in diverse environments: Effects of year 1 on student mathematics achievement ". (Tallahassee, FL: Florida State University).

Google Scholar

Teague, G. B., Bond, G. R., and Drake, R. E. (1998). Program Fidelity in assertive community treatment. Am. J. Orthopsychiatry 68, 216–232. doi: 10.1037/h0080331

CrossRef Full Text | Google Scholar