The influence of ready-made tools on students’ learning by modelling with differential equations systems

This article discusses the role played by the tool when students learn about differential equations systems (DE) by modelling. The discussion was based on a three-case sub-study of an ongoing study of group-reports from experienced mathematics teachers participating in a masters’ program in mathematics education. In the teaching sequences, setting the scene for the students’ modelling of authentic problems by DE, it was indispensable to include a variety of digital resources such as databanks and software for numerical solutions, graphical representations, and some sorts of simulations. Apps with simulations of commonly used DE models are widespread on the internet, some of them are user-friendly and elaborated to a degree that justify use of the term ready-made tools. The issue addressed in this article is whether such ready-made tools constitute shortcuts to the students’ modelling process and thereby obstacles in their learning of mathematics. For the analysis, the term direction of modelling was used to make a distinction between expressive and explorative modelling, respectively. Direction of modelling proved useful for the analysis of students’ learning not only with relation to the ready-made tool but also more generally. In line with the author’s previous research, students’ learning of mathematics by modelling was conceptualised in terms of emergent models and modelling and detected by textual analysis of students’ written reports. The study gave new insight into the students’ learning processes in the form of a variety of patterns for interplay between the tool use and the learning of mathematics. This variety seems to be pivotal for the designs of modelling sequences in general and particularly in the case of DE due to their dependence on digital resources.

1. Introduction

This article presents a study of learning by modelling. The study took place in a group of Norwegian teachers, in the following called students, in a master’s program in mathematics education. Within mathematics education, the term ‘learning by modelling’ would most often refer either to learning mathematics or to learning about/developing competence in modelling (see Blomhøj and Ärlebäck, 2018, p. 94). This article is about the first. The mathematical subject was differential equations systems (DE) which makes the use of some sort of ICT tools indispensable. The aim of the study was to enquire about the interplay between students’ learning and their use of tools in the context of modelling with DE.

The students used a variety of ICT tools in different ways, some of which were found on the web, ready-made, and especially tailored for single DE models. Since one of the goals of the students’ projects was learning about DE and DE models, the use of such ready-made tools raised concerns about whether they might restrict the learning process by shortcutting it. Other more general ICT tools, however, had the potential for creation of similar sub-routines that might play the same role as ready-made ones. Therefore, delineation of ready-made tools was difficult. Hence, the students’ written reports about the modelling projects were analysed to shed light on the research question: How does the use of tools influence on students’ learning by modelling with differential equations systems?

This study is adding new results to an ongoing meta study of learning mathematics by modelling based on 26 group reports as described beyond. The group reports constitute 26 individual cases (Cases 1 to 26), some of which have been included in prior studies by the author:

The research question ‘Does the students’ use of exploratory tools contribute to their concept formation? If so, how does it contribute?’ was inquired in Andresen (2020) based on two cases (Cases 15 and 19), where tailored, interactive tools were used for exploration as part of the students’ modelling projects. In the first case the students’ modelling process took outset from the DE models, whereas in the second case the students modelling took outset from the problem situation. In both cases, the students’ concept formation within the field of DE models were supported by their use of the tools. The study can be seen as a forerunner for the present study which include more cases and more detailed analyses regarding the tools and the tool use.

The research question ‘What are the conditions for ‘spin-off’ learning from students’ mathematical modelling in the case of modelling epidemics?’ was inquired in Andresen (2021) based on four cases (Cases 5, 13, 19, and 20). The study introduced the notion of ‘spin-off’ learning and justified the use of the term by its intertwinement with mathematical learning. ‘Spin-off’ learning comes via mathematical modelling, lending authority from the subject although it is neither coherent nor theoretically founded. The results by Andresen (2021) pointed out conditions for ‘spin-off’ learning in the form of four distinct circumstances internal to the modelling process: (a) the initial (horizontal) mathematising, (b) validation of the model (final or preliminary), (c) application of a ready-made model, and (d) interpretation of the results of a modelling sequence. The study can also be seen as a forerunner for the present study regarding the textual analysis and the notion of direction of modelling (see below).

In line with Andresen (2019, 2020, 2021), the learning of mathematics was conceptualised in the present study in terms of emergent modelling following Gravemeijer and Stephan (2002) and Gravemeijer (2020). The notions of emergent models and modelling originated in Realistic Mathematics Education (RME) (see Freudenthal, 1991). The basic principle of RME is that students have the opportunity to reinvent mathematics through horizontal and vertical mathematising. According to Gravemeijer and Stephan (2002), horizontal and vertical mathematising may be modelled by passing four levels of mental activity (situational, referential, general, and formal), where a new mathematical reality is created at each level. Raising from one level to the next is driven by reflections, which substantiate progressive mathematising. Horizontal mathematising is described as the passing from the first to the second level, and vertical mathematising as passing further up. This four-layer model was the basis for the design heuristics of emergent models aiming to support students’ processes of emergent modelling (Gravemeijer and Stephan, 2002). Later, Gravemeijer (2020) described emergent modelling as an incremental process in which models and mathematical conceptions co-evolve. Central to the emergent modelling design heuristic is the use of a series of sub-models. Together, they substantiate an overarching model which develops from a model of informal mathematical activity into a model for more formal mathematical reasoning. The overarching model is mental, with Gravemeijer (2020) mentioning, for example, the concepts of ‘distribution’ and ‘function.’ In this view, modelling is not separated from mathematics nor from ‘reality.’ In the case of differential equation models, the essential concepts encompass solution, slope field, equilibrium points, linearisation, and others.

It follows that in this view, the two goals mentioned by Niss and Blum (2020), namely modelling for the sake of mathematics and mathematics for the sake of modelling, are intertwined.

In line with Andresen (2020, 2021), the notion of ‘direction of modelling’ was applied. The direction of modelling refers to the distinction between expressive and explorative modelling. In contrast with the distinction by Niss and Blum (2020) between descriptive and prescriptive modelling, which concerns more general aims for the relations between the model and the extra-mathematical domain, this distinction between expressive and explorative modelling relies on aims internal to the process (Andresen, 2021):

i. Expressive modelling is understood as a student’s activity aiming to capture a problem through a mathematical model, be it ready-made or under creation. Expressive modelling encompasses the student’s own expression, in mathematical terms, of quantities and relations in connection with some sort of problem-solving. The important point is that the mathematical model is perceived by the students as their own novel creation.

ii. Explorative modelling is understood as an activity aiming to explore a mathematical model, be it ready-made or under creation. This includes testing the model against data to evaluate the model. Testing may imply the interpretation in an actual context of the model, parts of its mechanisms, or of its output. The important point here is that for students, the mathematical model is pre-existing, although it may be new to them.

The notion of the direction of modelling was introduced in Andresen (2020). Expressive modelling is in harmony with Niss’ description of a Danish mathematics education narrative where students have to work intellectually independently (Niss, 2020, p. 320). Creative mathematical reasoning (CMR) by Lithner (2008) is pivotal in this narrative. Expressive modelling is in harmony with the design heuristics of emergent models. Explorative modelling is, in contrast, represented, for example, by the prevailing form in school mathematics modelling tasks. Such tasks often present a model and ask for the results of providing a certain input (Berget and Bolstad, 2019, in Norwegian). In this form, explorative modelling can be linked with types of imitative reasoning by Lithner (2008), that is, with algorithmic reasoning.

Modelling is not a linear process, neither in the traditional modelling circles, for example by Blomhøj and Jensen (2003, p. 125) nor in the four-layer model by Gravemeijer and Stephan (2002). In terms of the direction of modelling, sequences of expressive modelling will normally encompass processes of explorative modelling. The modelling sequence in Blomhøj and Jensen (2003) is overall expressive: it encompasses six sub-processes, each of which requires creative non-routine activities. However, these subprocesses will include exploration and try out of (parts of) the mathematical models under construction. Andresen (2007) concluded that sequences of explorative work may serve to support students’ concept formation and at the same time prepare the students for expressive modelling. In this study, the direction (explorative vs. expressive) of modelling is detected in smaller and larger subsections of the overall modelling process described in the texts by condensation and interpretation of the meaning of the subsection.

Similarly, the process of learning by modelling is far from linear by nature. Andresen (2022) describes a case study based on students’ completion of a modelling project and concludes that the learning trajectory in terms of emergent modelling can be seen as a cluster of activities resulting from the rich learning environment. There seemed to be a paradoxical discrepancy in the case study between the messy and unstructured process documented in the students’ group report on the one hand, and the learning outcome as it was evaluated in informal conversations and in the interviews at the oral examination, on the other hand. The case study shows that the learning trajectory must not necessarily be clear and linear to be fruitful. The students’ reports displayed signs of activity at situational, referential, and general levels and, in total in the report, shifts in both directions between these levels. In addition, the students demonstrated representational literacy by shifting between plain language and wordings, formal language and formulars, and graphic representations in the report (Andresen, 2022).

The students’ learning trajectories in the form of messier or more systematic clusters of activities can develop in interplay with changes in the direction of modelling. The role of the tool would be closely related to this interplay, be it used for exploration of a ready-made or home-made model, or in connection with expressive modelling.

It is important to note that the use of the tool, though, is not built into the tool itself but depends on the user. According to the theory of instrumental genesis, an artefact like an exploratory tool does not in itself serve as a tool for anybody. The term “instrumental genesis” denotes the process in which the artefact becomes an instrument (Drijvers and Gravemeijer, 2005). The French theory of instrumental genesis is based on the idea that an artefact, for example a CAS calculator, does not in itself serve as a tool for the student. It becomes useful, and then denoted an “instrument,” only after the student’s formation of (one or more) mental utilisation scheme(s). Such utilisation schemes connect, according to the French theory, the artefact with conceptual knowledge and understanding of the way it may be used to solve a given task. Thereby, the utilisation schemes contribute to the formation of instrumented action schemes. So, an instrument consists of the tool, for example a laptop with the CAS software Derive, the student’s mental utilisation schemes and the task or problem to be solved (Drijvers, 2003). The present study’s founding on the ideas of emergent modelling and models implies a slight modification, though, of the ideas of instrumental genesis. Rather than formation of utilisation schemes and building up action schemes, mental models and mental modelling activities support the construction of a tool based on the artefact. In this view, the construction of a tool still proceeds through activities in a two-sided relationship between tool and learner as a process in which the tool in a manner of speaking shapes the thinking of the learner, but also is shaped by his thinking (Drijvers and Gravemeijer, 2005).

The theory of instrumental genesis in the original, French version as well as in this study’s modified version imply that the students’ development of mathematical conceptions (i.e., in terms of emergent models) cannot be studied if use of technology is considered separate from the student’s other activities. This view opposes the standpoint, that teaching may be performed independently of what tools the students have at their disposal. It is also in contrast to the view, that the influence of use of ICT can be overlooked as if it were just a matter of carrying out boring routines. In line with this, Jean-Baptiste Lagrange stressed (Lagrange, 2005, pp. 131–132) that ‘the traditional opposition of concepts and skills should be tempered by recognising a technical dimension in mathematical activity, which is not reducible to skills. A cause of misunderstanding is that, at certain moments, a technique can take the form of a skill.’

In the case of modelling, the dynamical systems’ view on DE (Blanchard et al., 2002) will generate a learning environment where ICT tools are needed for both expressive and explorative work. The question addressed in this article concerns the type and role of tools for both.

2. Materials and methods

2.1. Data

The students attended a masters’ program that requires 60 ECTS in mathematics and 2 years of professional practice as a mathematics teacher.¹ Data for the study is in each of the 26 cases a group report that stems from the students’ attending the one-semester, 15 ECTS course ‘Modelling in and for mathematics teaching and learning,’ between 2014 and 2022. The course encompassed a mathematics education theory part including, amongst others, sections of Niss and Blum (2020) and excerpts from Gravemeijer and Stephan (2002). The DE part of the course was based on Blanchard et al. (2002), who progressively built up DE models and examples, and balanced between qualitative, quantitative, and numerical methods. Inspired by this, groups of students (2–3 persons) under sparse supervision were asked to formulate, complete, and present a project that encompassed a simple DE model, and to report the project. The aim of the project was, according to the formal guidelines: ‘To formulate, complete and present a project that encompasses the building and/or revision of a simple differential equation model using appropriate digital tools.’ The guidelines proposed a structure of the report encompassing (i) Introduction and research question, (ii) Building or description of the model and discussion of it, (iii) Qualitative and quantitative evaluation of the model, (iv) Conclusion and discussion, and (v) Perspectives. Purposes of the project were: (1) to learn about differential equations by doing a modelling project, and (2) to get personal experiences with learning mathematics from doing a modelling project. Each group chose what DE model they wanted to study, inspired by the textbook and by examples from the lectures and from the internet.

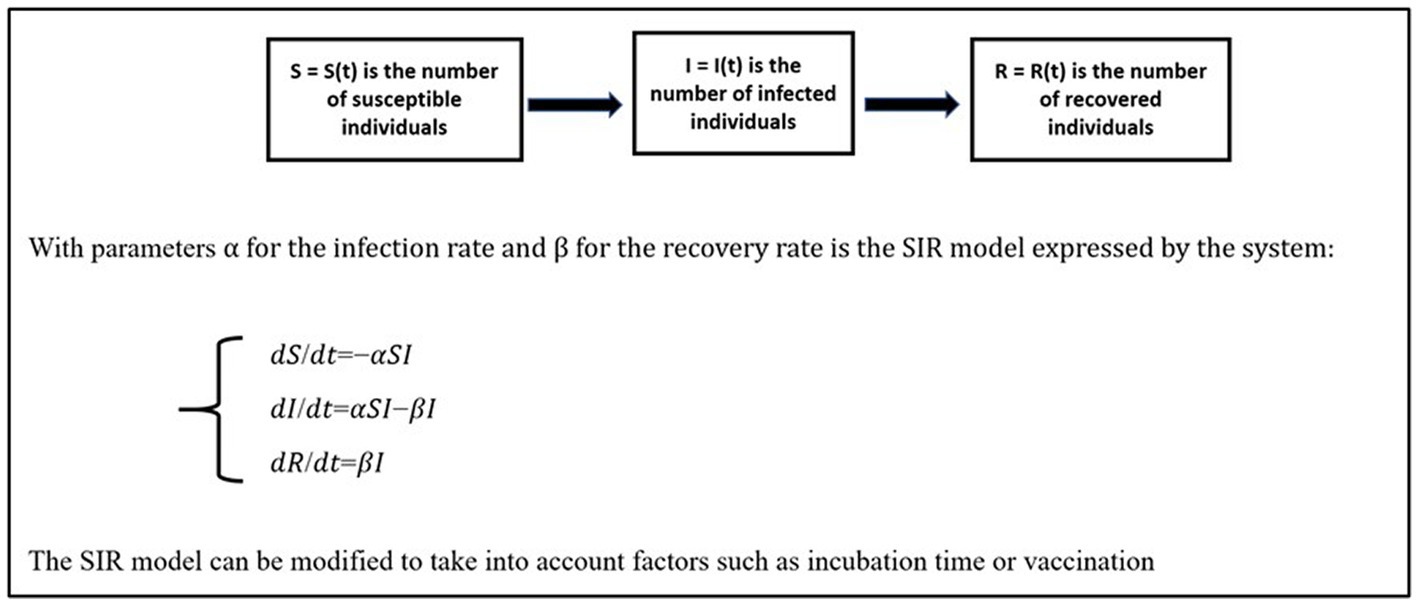
The course’s individual examination included an interview on this project (10 min). These interviews served as a means for evaluation of the students’ learning outcome, and they were not included as part of data for this study. In the modelling projects, the students were expected stepwise to establish an overarching DE-systems model in a process, contrasting with bare application of a model, that is, contrasting with picking out a ready-made model and fitting its parameters with data. However, the students would not be able to establish a stepwise model from scratch, purely based on progressive mathematising and the formation of sub-models. Therefore, they were free to involve and build on ready-made models, such as the predator–prey model and its modifications (Figure 1) or the SIR model and its modifications (Figure 2).

FIGURE 1

Figure 1. The Predator – Prey model.

FIGURE 2

Figure 2. The SIR model of epidemics.

2.2. Methods

The conceptualisation of learning in terms of emergent models and modelling was operationalised as a tool for textual analysis with reference to Cobb (2002, p. 193), who stated that the four-layer model might ‘facilitate (…) the analysis of mathematical learning in instructional situations (…). The explication of a mapping between a situation and a model might then be viewed as a description of the way that the situation became structured during modelling activity.’ Based on this, the four-layer model, in line with Andresen (2020, 2021), was operationalised in this study as a tool for textual analysis of reports to interpret students’ mathematical concept formation.

The students’ collective learning processes were documented by their own descriptions of the mathematical modelling activities and by the reflections reproduced in the reports. The descriptions and reflections were reported in a convincing way: they used a first-person perspective in their writings in the report which is mentioned as a sign of being an active learner by Ju and Kwon (2007). This impression of validity was supported by interviews conducted during the individual examinations as a basis for the evaluation. The reliability of the study’s analysis rested on the condensation of meaning from units of convincing texts, in accordance with the qualitative methodology described in Kvale (2001). The meaning of each unit was interpreted in accordance with the emergent modelling framework.

The textual analysis, presupposing that the students’ mental activities were reflected by the wording in their reports, served to stratify the mathematical learning process in terms of passing through four levels: situational, referential, general, and formal. Each appearance of a mathematical concept or its related notions in the text was assigned to a level of activity in the four-layer model (Gravemeijer and Stephan, 2002). In this way, signs of students’ activity, displayed by the wording in reports, were stratified regarding the levels. Progressive mathematisation, then, was detected as progressive variation between the levels and interpreted as steps of the students’ concept formation in the form of sub-models evolving into an emergent model. Accordingly, the mathematical learning outcome was conceptualised following Cobb (2002) as emergent models of essential mathematical concepts.

2.2.1. Tool for analysis of the learning of mathematic

Each case implied a qualitative textual analysis (Kvale, 2001; Ju and Kwon, 2007) of one report (between 13 and 30 pages in Norwegian). The overall strategy for the modelling process and all the applied tools were identified. For each mathematical concept related to DE, signs in the text were identified and interpreted (not disjunctively coded) regarding the level of activity in the terms used by Gravemeijer and Stephan (2002):

(1) Situational level with descriptions in natural language and own wordings,

(2) Referential level, where a ‘model of’ was created and enquired. A ‘model of’ was identified by the students’ use of situation related terms and half-way formalised explanations, for example, that ‘the number of sick persons will grow exponentially over time’,

(3) General level with creation and handling of a ‘model for.’ A ‘model for’ was identified by the students’ use of general expressions and terms with no visible relation to the situation, for example, that ‘We find that the graph of I(t) hits the maximum value if the parameter has a value of 0.259’,

(4) Formal level with general reasoning and considerations, which were very rare in the reports. In each case, concept formation in terms of progressive mathematisation was condensed.

The ‘direction’ of modelling was interpreted based on meaning condensation of naturally delineated subsections of the text. The delineation of subsections was not a division into disjointed classes; smaller subsections of explorative modelling could be embedded in an expressive modelling section and vice versa. The subsection’s direction was labelled (a) expressive modelling, that is, the process was driven by the problem, or (b) explorative modelling, that is, the model was the starting point.

During the present study’s analyses, the internal aims were identified, either by having them explicitly stated in the text or based on an interpretation of the textual context. The notion of directions of modelling was applied in the study’s analysis to capture the role of ready-made models. Use of the term intended to nuance the analysis and make it more fine-grained regarding the interplay between ready-made models and students’ learning trajectories. The idea was to link ready-made models with ready-made tools tailored to apply to them; for example, tools or apps made for simulation of the Predator – Prey model (Figure 1),

or for simulation of the SIR model of epidemics (Figure 2).

Expectedly, some of the students would use appropriate ready-made tools for the exploration of their chosen ready-made model. Explorations may encompass students’ producing graphs or running simulations based on various inputs and parameter adjustments. If so, the ready-made tool was linked with explorative modelling. The study aimed to enquire about students’ learning of mathematics from the combination of ready-made tools used for explorative modelling and, in addition, to juxtapose it with learning from the other combinations: Other tools used for explorative and expressive modelling, respectively, and ready-made tools used for expressive modelling. Other tools, here, are understood to be ICT tools not tailored for application on a specific DE model like, for example, the software Python, GeoGebra, Mathlab or Excel. Ready-made tools might also be tailored, not for a specific DE model, but for a specific procedure such as graphing the slope field. When working with a specific DE model, such tools are interpreted in this study to serve as ready-made tools rather than ‘other tools.’

Finally, the cases were juxtaposed; the combinations of tools, concept formation, and directions of modelling were discussed with the aim to shed light on the research question.

2.2.2. Two step analysis of data

This article’s study of modelling with DE focused on sub-models in the individual cases (reports). In each case, the overarching mental model was the mathematical idea to model some sort of interaction like, for example, interaction between populations of predator and prey or between populations of susceptible, infected, and recovered people. The analysis was carried out in two steps with the aim of finding patterns of interplay between learning and tool use in the variety of DE models, overall strategies, and tools represented in the 26 cases.

2.2.2.1. Step one

The first step was elaborated from the description in Andresen (2019). In addition to the individual textual analysis of the cases that followed in step two, the cases were initially coded according to

i. Mathematical model of interaction: Predator – prey models (PP), epidemic models (SIR), models of a harmonic oscillator (HO), exponential growth (Ex), logistic growth (Lo), and others (Ot).

ii. ICT tool: Students’ ICT competencies spanned from almost novice to expert. In the cases/reports, Excel (Ex), GeoGebra (GG), Python (Py), Mathlab (Ml), and POLYMATH (PM) were used. There are several ready-made ICT tools available on the web for the exploration and enquiry of differential equation models. Such ready-made tools were marked (RMXX), specified into (RMSIR), etc.

iii. Data source: The students found data on the web (dw), with a few exceptions who on their own got, or from the beginning had, access to suitable data in an area of interest (od). A few tables from the textbook were also used (dt).

iv. Overall strategy: The cases represent a variety of methods. In some cases, the students took one model and a seemingly corresponding dataset as their starting point (Start Mod) and made efforts to estimate the model’s parameters to fit the data. Others described a step – by step procedure with increasingly complex models (step-by-step) aiming at fitting the model to the data. The use of graphs is common for checking (uG) and some found numerical solutions (NS). Many applied analytical methods (AM), such as the Jacobi determinant and eigenvalues, are used to determine or check the model.

The 14 cases in the study by Andresen (2019) were grouped into four groups by combining the criteria (i) and (iv), suggesting a relationship between the DE model and the overall strategy. Andresen noticed (2019) that instrumental genesis took place in cases with ready-made tools as well as in cases with other tools. Instrumental genesis implies the process of incorporating the tool into one’s intellectual preparedness. It follows that ready-made tools could be used in these cases, not only for explorative modelling but also for expressive modelling when relevant. The present study of 26 cases is an elaboration of the 2019 study and encompasses its 14 ‘old’ reports.

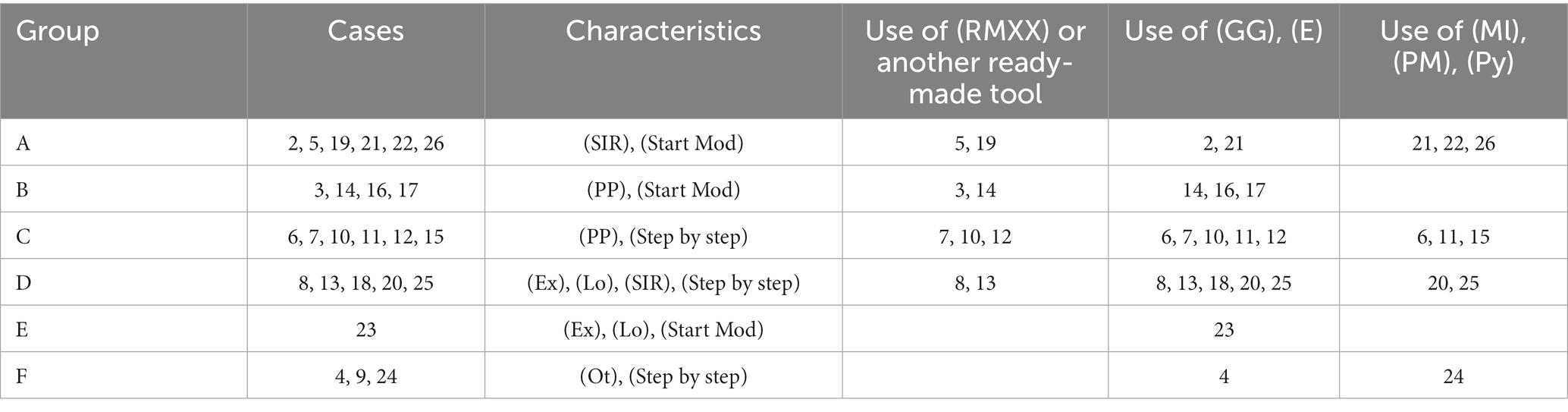
All 26 cases in the present study were coded in six groups A – F, determined by the combination of DE model and overall strategy. (For example, group A encompasses cases that concern with the SIR model combined with start-with-the-model strategy). In the search for patterns of results, the cases in each group were then sorted according to the type of tool used: (i) special tailored for one DE model (RMXX), (ii) basic tools, familiar to most students (GG) and/or (E), and (iii) more advanced mathematics-oriented tools with a higher entrance level (Ml), (PM), and/or (Py). Some cases included the use of more than one type of tool.

Step one of the analyses gave the result shown in Table 1.

TABLE 1

Table 1. Grouping of cases 2 - 24.

As it was mentioned above, the reports from some of the cases in Table 1 were analysed in earlier studies with a variety of research questions different from the present study’s research question. Hence, excerpts from case 6 was presented in Andresen (2022), excerpts from case 13 were presented in Andresen (2019), excerpts from cases 15 and 19 were presented in Andresen (2020), and excerpts from cases 5, 13, 19 and 20 were presented in Andresen (2021).

2.2.2.2. Step two

The present study’s second step offers fine-grained coding and sub-coding of the direction of modelling combined with analysis of the students’ learning, as described above and in Andresen (2021). For each of the 26 cases, a table was produced containing the smallest units of text, naturally delineated after its meaning and the direction of modelling. Each unit was marked by (a) level of activity in the four-level model, (b) direction of modelling, (c) content: mathematical concept, sub-model, notions, and comments, and (d) tool in use. In contrast with the study in Andresen (2020), the direction of modelling and tool in use are separately coded in columns (b) and (d), respectively, in this study. Andresen (2020) observed all four combinations of expressive and explorative use of both types of tools. The present study’s nuancing of the coding may serve to provide more information about this. Thereby, the analysis may serve to pinpoint not only the interplay between tool and the direction of modelling but also, via the level of mental activity, between tool and learning.

3. Results

This paragraph presents excerpts from the analyses of Cases 10, 11, and 14. These cases were selected based on the grouping of cases shown in Table 1. The cases were chosen (i) to demonstrate a variety of combinations of strategy and tool use as a basis for the related learning trajectory for the Predator – Prey DE model and (ii) to avoid repetition of data presentation from earlier publications. Cases 10, 11, and 14 was not included in any of the prior publications from the overall, ongoing study.

After a summary of common trends and discrepancies between the three cases, each case is presented through an additional, initial brief overview of the report followed by shortened (chronological) excerpts. To document and exemplify the textual analysis in Step 2, each excerpt is presented with its codes and remarks. None of the three cases displayed clear signs of activity at (level 4) formal level. Therefore, there are no excerpts with such signs in the presentation of the cases.

The excerpts were chosen to demonstrate the development/emergence of a mental model of only one mathematical concept central to DE, namely equilibrium point. The idea of emergent models and modelling implies, according to Gravemeijer (2020), that a series of sub-models substantiate an overarching mental model which develops from a model of informal mathematical activity into a model for more formal mathematical reasoning. In the case of DE as the overarching model, the essential concepts encompass the solution, slope field, equilibrium points, linearisation, and others. Among these, the concept of equilibrium points was selected for the presentation of excerpts from all three cases. Equilibrium point is a pivotal concept in DE and in addition, it is of importance for the linking of qualitative and graphical analyses of DE models (Blanchard et al., 2002). Determination and characterisation of equilibrium points was an important issue in all three cases, and it involved a variety of use of tools.

The presentation of each case ends with a short summary of the findings regarding connections between tool use and the level of activity concerning the equilibrium point. Finally, the findings from the three cases are juxtaposed and synthesised into the study’s main conclusions.

3.1. Common trends and discrepancies

3.1.1. The overall structure of the cases

The overall structure of the three case reports is similar. The starting point is presented and elaborated in the introduction, and data are filled into the expressions of the model under enquiry. Evaluation of the model under enquiry rests on how well it fits with the real world, either in the form of comparing output values or qualitatively. The reports’ conclusions contain reflections upon the process and some remarks or reflections about the concept of mathematical modelling as a technique to gain insight into authentic problems, issues, or questions about nature or society.

3.1.2. Starting points

Case 14 takes the Predator – Prey model as the starting point and as the object of enquiry. The task is then to apply the model to a relevant situation by filling in the data, adjusting the model’s parameters, evaluating the results, and elaborating the model. This procedure was repeated in a series of rounds.

Cases 10 and 11 take outsets from a situation that calls for description with the aim of predicting or controlling the future development of interaction between two populations. This choice of starting situation obviously does not leave it as an open question to create a suitable model. During their stepwise procedure, which is rather like the rounds in case 14, though, the cases include critical discussions about the models’ shortcomings related to the start situation.

3.1.3. Directions of modelling

All three cases encompass subsections of exploration of the models under enquiry, be it as part of the overall strategy, as in case 14, or after evaluation and elaboration of a preliminary model, as in all three cases. Similarly, all three cases encompass subsections of expressive modelling after evaluation of a preliminary model, for making a better fit of parameters or to better capture phenomena where the old model failed. Cases 10 and 11, in addition, set the overall goal to model the start situation.

3.1.4. Use of tools

The three cases represent the use of different tools. Case 10, in addition to the students’ own creations in Excel, only included the use of ready-made tools for generating phase portraits (pg) and null-clines. Case 11 includes the students’ own creations using GeoGebra and MathLab. Case 14 includes the use of ready-made ICT tools tailored for the Predator – Prey DE model as the only ICT tool.

3.2. The cases 10, 11 and 14

3.2.1. Case 10

The starting point is a wish to learn about mathematical modelling by doing it, and to learn about how to learn mathematics from modelling. (This is in line with the goal description of the master’s program course.) The students will model the interaction between populations of capelin and Arctic codd in The Barents Sea, and they will give good arguments for the societal and environmental importance of gaining insight into this. They started with exponential growth and fit parameters, evaluated against data using graphical tools, and elaborated the model via logistic growth into a revised Lotka-Volterra model. They find equilibrium points and linearise the system using analytical methods to determine the eigenvalues and, thereby, the types of equilibrium. They then find null-clines and graph them in GeoGebra to get an impression of how well the model fits with the data and with their expectations of the interaction between populations. In addition, they used another web tool to generate graphs of their solutions. In conclusion, they discussed a series of relevant aspects of the development of populations of codd, capelin, and other sea creatures, which could or could not be captured by a model. They especially address their high learning outcome and their troubles with finding and using relevant ICT tools (Table 2).

TABLE 2

Table 2. Case 10.

They use the tools Phaseportrait Generator from http://onlinesciencetools.com/tools/phaseportrait (pg).

The students in case 10 use the ready-made pg. tool when they try to capture a new (hypothetical) situation, i.e., for expressive modelling in sub-sections of the process (Exc. No 28, 30, 33). In Exc. No 35 they try to capture a new situation without using pg. In addition, they use the same tool (pg) for testing revised versions of their model against data by visual inspection of the graphical representation (Exc. No 29, 31). The testing was interpreted as exploration of the suggested model, that is, as explorative modelling.

The excerpts were picked out when the students tried to make their model fit with the data about populations of each of the species in the absence of the other. These situations correspond to equilibrium points. They demonstrate activity at (levels 1, 2, and 3) concerning the equilibrium point (Exc. No 37). In addition, they strive to fit the solution curves with the desired shape (elliptic) without mentioning the connection between the type of equilibrium point and the shape of the solution curves (Exc. No 27, 28, 29, 30, 31, 32, 33). In these excerpts, they use the tool (pg) to generate phase diagrams for various values of the parameters. After some rounds, they seem to give up and switch to linearisation of the system and determination of eigenvalues by analytical methods. The students did not explicitly mention equilibrium points under the enquiry of the phase diagram. The connection between the shape of the curves and the type of equilibrium is explicitly mentioned in the AM section of their enquiry.

3.2.2. Case 11

The starting point is a wish to gain insight into the dynamics of interactions between populations of predators and prey and show a graphical representation of such interactions. They choose snow rabbit as the pry and lynx as the predator, inspired by literature on the web saying that this is a classic example of the interaction, but also that there are some unexplained issues here. For example, the students wanted to include issues of stress amongst the female snow rabbits as a novel parameter that disturbs the original model. Stepwise, they start with exponential growth and graph it in GeoGebra after an initial estimation of the parameters based on guessing. Thereafter, they explored logistic growth, and the models were tested by visual inspection of graphs generated in GeoGebra. Next, they introduced terms to model the interaction between the two populations and started to use MathLab to generate phase portraits and solution curves for visual inspection. They used analytical methods to determine the types of equilibrium points via linearisation by a Jacobi matrix and finding eigenvalues. The eigenvalues are in terms of the model’s parameters, which they estimate and test by visual inspection of graphs generated by MathLab. The evaluation was repeated against the data and their initial graphical representation of the interaction. They extended the model with new terms to capture the phenomenon of stress among female rabbits and successfully tested the new model against data. They concluded that they have achieved their goals, including the learning goals, by using a combination of ICT tools, textbooks, calculations, and discussions (Table 3).

TABLE 3

Table 3. Case 11.

The students use MathLab (M) in the excerpts.

The students create preliminary models (expressive modelling) based on considerations about the situation without use of tool (exc. No 16). These considerations may be novel to the students although they may be well known to others. Therefore, they can be interpreted as creative thinking (Lithner, 2008). They explore the new model without using tool by considerations about equilibria (exc. No 18, 34) Later, they use Mathlab to explore their preliminary models (exc. No 35, 36, and 50, 51, 52, 55, 56).

Equilibrium points are discussed at (levels 1, 2, and 3) without using tools (Exc. No 18, 34). Further, equilibrium points are discussed at (level 3) without using the tool in (Exc. No 48, 49), leading to qualitative enquiry of the type of equilibrium using M (Exc. No 50, 51, 52). They include the evaluation of the model by visual inspection (Exc. No 53). Finally, the students fit the parameters once more and tested the model by visual inspection (Exc. No 54, 55, 56). In the last round, excerpts 54–56 do not explicitly mention the equilibrium points.

3.2.3. Case 14

The starting point was to investigate the interaction between small rodents and foxes using the Lotka-Volterra model. They start with the search for and estimation of data regarding the populations. They adopted the textbook’s model since it has the same cyclic periodicity as small rodents. Stepwise via exponential and logistic growth, they end up with parameters that generate maximums for the population sizes fitting with their data. The model was checked using a ready-made tool connected to the textbook. (This tool has some severe deficiencies which restrict its use. In this case and in this restricted area, however, the students managed to get proper results.) They continue by finding the equilibrium points and characterising them by linearisation of the system via the Jacobi matrix and determination of eigenvalues using analytical methods. They determine the types of equilibrium points and compare them with the phase portrait. Next, they determine the null-clines to obtain an impression of the behaviour of the solutions. Their analysis is based on a graphical representation of the phase portraits and null-clines. They concluded that their final model had strengths and weaknesses and elaborated on additional living conditions for small rodents and foxes. They noted that they did not solve differential equations (Table 4).

TABLE 4

Table 4. Case 14.

In the excerpts the students use the RMPP tool HPGSystemSolver from the textbook.

There were no signs in the text that indicated expressive modelling.

The students adopted the Lotka-Volterra model and tried to fit its parameters to the estimated data. They find that the equilibrium points (Exc. No 32) without using the ready-made tool (RMPP) and with no reference to the situation (level 3). Afterwards, they interpreted these in semi-formalised terms (level 2). Then, they determine their types by analytical methods (AM). The methods are applied without reference to the situation, that is, at (level 3) and encompass linearisation via the Jacobian matrix and determination of eigenvalues (Exc. No 34, 35, 36). In Exc. No. 37 they characterise the equilibrium point based on the eigenvalues, still at (level 3). Next, they test the model (explore it) by comparing the suggested type of equilibrium point, namely, the idea of a saddle, with a phase diagram generated by the RMPP tool. The procedure is repeated, and the results are summed up in Exc. No. 51 at the general level (level 3) and compared with the same figure generated by the RMPP tool. Finally, in Exc. No. 52, the students evaluate the results concerning equilibrium points in semi-formalised terms (level 2) and with reference to the tool generated figure(s).

3.3. Summary of the three cases

The ready-made tools in these cases served to generate phase diagrams (Case 10) and slope fields (Case 14). In case 10, it was used for explorative as well as expressive modelling, and both types of modelling took place without using the tool. In contrast, the tool in case 14 was used for explorative modelling alone. There were no signs of expressive modelling with or without using the tool in case 14. The tool in case 11 was of the type ‘more advanced’ (Table 1). Although there was both expressive and explorative modelling in case 11, the tool was not used for expressive modelling but only for exploring the preliminary models.

Signs in case 10 indicate activity at (levels 1, 2, and 3) concerning equilibrium points with the tool (Exc. No 29, 30, 31), and without the tool (Exc. No 37). Signs in case 11 indicate activity at (levels 2 and 3) concerning equilibrium points with the tool (Exc. No 36 and others) and (levels 1, 2, and 3) without tool (Exc. No 18, 34). Finally, in case 14, signs indicate activity at (level 3) and 1) concerning equilibrium points with tool (Exc. No. 52) and at (levels 2 and 3) without tool (Exc. No 33).

To form a basis for answering the research question: How does the use of tools influence on students’ learning by modelling with differential equations systems? The results of analysis of cases 10, 11 and 14 are summed up in the following. All in all, the analyses reveal that in groups working with Predator–Prey DE models and by focusing on equilibrium points:

i) It is possible to find examples of expressive modelling with use of simple ‘ready-made ITC tools’* in a group that models exploratively and expressively also without tools.

ii) It is possible to find examples of explorative modelling with the use of simple ‘ready-made ICT tools’* in a group that models exploratively also without tools.

iii) It is possible to find examples of explorative modelling with the use of ‘more advanced’* tools in a group that models exploratively and expressively also without tools.

iv) It is possible to trace a learning trajectory as a cluster of activities at and switching between (levels 1, 2 and 3) in all the three cases. Not all levels of activity involved use of tools.

v) It is possible to find examples of (level 3) activity with and without use of ICT tool of both types, that switch to (level 2) and to (level 1), directly or successively.

vi) It is possible to find examples of (level 1) activity that switch to (level 2) and (level 3), directly or successively.

* ref. Table 1.

But how does the tool influence student learning? In cases 10 and 14, the students had similar simple, ready-made tools at their disposal. The students in case 10 used it for explorative as well as expressive modelling, whereas the students in group 14 only used it explorative. Therefore, ready-made tools, apparently, did not restrict the direction of the students’ modelling process. Neither was the use of ready-made tools linked with directions of modelling that differed from directions in the rest of the modelling. Hence, ready-made tools cannot be said to strictly exclude or impose directions of modelling in the groups’ work. Still, the ready-made tools may strengthen or downplay explorative or expressive tendencies in a group’s work. Learning was detected in the form of activity at all three levels and switching between them. Switches from level three and downwards happened with as well as without both types of tools in all three cases. Tool use, therefore, cannot be said to obstacle this aspect of learning meaning that, for example, interpretation of results and evaluations of mathematical concepts in the concrete context still happens under the use of tools. Switches from level one and upwards were detected which means that the use of tool did not replace the development of the mathematical as well as the mental model from the concrete context. All in all, the tool use therefore cannot be said to obstacle the students’ learning. In contrast, the analyses reveal that the use of both types of tools serves to support the students’ learning of mathematics.

4. Discussion

The excerpts demonstrate the cases’ variety of combinations of direction and level of activity combined with the use of tools. They do not provide evidence of causality or strict connections. Rather, the excerpts should support the view that the cases document possible combinations of tool use and the development of the concept of equilibrium points as a mental model.

4.1. About textual analysis

As a method to detect learning, textual analysis of students’ written reports has obvious and more sophisticated weaknesses.

It is obvious that the author of the text is unidentified, be it a text copied or summarised from the web or from some book or report. Neither is it clear, even if the students as a group created the text on their own, whether they had delegated the writing to the members of the group. In the worst case, the individual student did not need to even read the complete report before it was delivered. This uncertainty is included when adapting the idea of groupwork as a basis for individual learning, and the learning outcome was evaluated individually at the examination and in informal talk during the master’s program course. Nevertheless, as data for enquiry into the formation of mental models, group reports might not be the strongest foundation. However, it would not be possible for any student to write explanations and interpretations of relations and concepts, not to mention results and graphs created on their own if the student had not understood them properly. Signs of mental activity at the different levels of Gravemeijer’s (2020) model should not be assigned to the individual student’s head, but rather be seen as manifests of their collective work.

This raises the question of the absence of signs: The students in case 10 used a tool from the web and switched to AM without explicitly mentioning the connection between the type of equilibrium point and shape of the curve. They might, as well, have seen the connection as if it were clear and understood, or maybe they only realised, or focused on, the connection when they started to work by AM. In general, the absence of signs alone should not be interpreted as documentation of anything in a qualitative case study context. Follow-up interviews can be inspired by unexpected content of reports or written answers in questionnaires, but this study did not include follow-up interviews or notes from the oral examinations. Therefore, the analysis of Case 10 regarding this point is not conclusive. In Case 11, the students mentioned and discussed equilibrium points with and without using tool (M). In the later excerpts, however, when they repeat their rounds of enquiry, they stop mentioning equilibrium points explicitly. This could be their choice to avoid repetition of wordings, but whatsoever it should never be interpreted as a loss of understanding of the connection between the phase portrait and shape of curves, and type of equilibrium.

4.2. The study

Furthermore, the delineation of units for the analysis depends on the object it aims to enquire about. The complete study aimed to enquire about the complexity of modelling with DE involving levels of mental activity, directions of modelling, use of tools, and groups of students. To simplify complexity, this study focused on equilibrium points in Predator Prey models in three groups of students, using one tool each. The units for analysis were primarily delineated in the cases by considering the direction of modelling and after the use of tools. Consequently, some excerpts entail coding of more than one level of activity.

This simplification implies that most of the materials in the form of the other 23 reports only indirectly contributed to the study. The author’s earlier enquiries into the material served partly as a basis for the present study, directed its design, and informed its analysis as a supplement to well-acknowledged research literature.

In Case 14, the students only used the ready-made tool from the textbook which, as mentioned above, did not work properly (the tool). This points to the issue of having an appropriate tool at disposal. In Cases 10 and 14, the students mentioned in their final discussions that they saw two main obstacles for the project to run, namely finding suitable data and finding suitable ICT tools. The textbook, obviously, was designed to use its own tool as a basis for exercises, etc. Since this did not work properly, the students were encouraged to find their own ICT tool solutions. It is important to note, hence, that the tools were not distributed to the students randomly. Their choice of ICT tool corresponds to, for example, what they used (or not used) in their daily work as teachers. The degree of familiarity or lack of familiarity with the tool would influence their work with the project. In the later years of the master’s course, however, almost all the students were familiar with Python. This serves as a strong support for them in their projects. It would have been interesting to include their reports in this study, but with few exceptions, they all model epidemics.

4.3. The results

The direction of modelling was not linked with learning in the analysis but only with tool use. The cases showed very few examples of expressive modelling and no clear signs of mental activity linked with steps of expressive modelling at all. Signs of learning, in the study’s conceptualisation of the concept, were identified in all three cases, but a clear connection between the levels of activity and the use of the tool was not established. Direction of learning may depend more on the group than on the tool. The students in case 11 were familiar with their tool and used it for testing by visual inspection of each new version of their model. Their learning outcome, reflected in the signs of activity at (levels 1, 2, and 3), could not be directly linked with each step of the cyclic procedure. Rather, the idea about clusters of activity can capture the case and offer a description of the influence of the tool. Their familiar tool allowed the students to try out their ideas about how to improve the initial model because they had the opportunity to get an immediate answer and be directed further. This interpretation, however, does not claim anything about how the students would have worked if they had not had their tool.

4.4. Perspectives

This study points to important issues in designing modelling sequences in school mathematics. Easy access to data would on the one hand support a fast and smooth start of the modelling process. On the other hand, the search for and estimation of data seem to add to the understanding of the problem and, in some cases, even cause spin-off learning (Andresen, 2021). Familiarity with a suitable tool may be more valuable than a ‘fancy’ design of tailored tools since the use of the tool seems more important than the tool itself.

In this study, the task was almost completely open. Most of the students in the master’s program course have chosen Predator Prey (PP) and Epidemic (SIR) DE models (see Table 1). This may be due to the subject but may also be partly due to the character of the task. For more expressive modelling to unfold, a careful design would possibly direct the students into more of their own creations without leading them. More expressive modelling would, assumable, be in line with Niss’s description of the mathematics education narrative.

Data availability statement

The datasets presented in this article are not readily available because all written in Danish and Norwegian language. Requests to access the datasets should be directed to TWV0dGUuQW5kcmVzZW5AdWliLm5v.

Ethics statement

Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent for participation was not required for this study in accordance with the national legislation and the institutional requirements.

Author contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This work was solely funded by the University of Bergen.

Acknowledgments

The author would like to acknowledge the hard work of the students attending the course and all the academic integrity researchers whose studies were reviewed as part of this study.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^European credit transfer and accumulation system for higher education. Sixty ECTS credits are the equivalent of a full standard academic year of study or work.

References

Andresen, M. (2007). Understandings of ‘modelling’. In Demetra Pitta-Pantazi and George Philippou (eds.): Proceedings of the fifth congress of the European society for research in mathematics education. 22–26 February 2007, CERME 5: Larnaca, Cyprus (2042–2049).

Google Scholar

Andresen, M. (2019). Role of the tool for teaching towards a modelling perspective on differential equation systems. In: Proceedings of the PME and Yandex Russian conference: technology and psychology for mathematics education. Moskov, Russia: HSE Publishing House. p. 99–106

Google Scholar

Andresen, M. (2020). To learn about differential equations by modelling. In: A. Donevska-Todorova, E. Faggiano, J. Trgalova, Z. Lavicza, R. Weinhandl, and A. Clark-Wilson, et al., (Eds.). Proceedings of the tenth ERME topic conference (ETC 10) on mathematics education in the digital age (MEDA), 16–18 September 2020 in Linz, Austrian. Johannes Kepler University: Linz, Austrian. p. 419–426

Google Scholar

Andresen, M. (2021). Spin off learning about epidemics from modelling with differential equations. Quadrante 30(2) mathematical modelling in the teaching and learning of mathematics: Part 2. Guest Editors: Susana Carreira and Werner Blum.

Google Scholar

Andresen, M. (2022). Learning trajectory as a complex cluster of activity. In J. Hodgen, E. Geraniou, G. Bolondi, and F Feretti. (Eds.). Proceedings of the twelfth congress of the European society for research in mathematics education (CERME12), 2–6 February 2022, Free University of Bozen-Bolzano, Bozen-Bolzano, Italy.

Google Scholar

Berget, I., and Bolstad, O. (2019). Perspektiv på matematisk modellering i Kunnskapsløftet og Fagfornyinga. Nordisk tidsskrift for utdanning og praksis 13, 83–97. doi: 10.23865/up.v13.1882

CrossRef Full Text | Google Scholar

Blanchard, P., Devaney, R. L., and Hall, G. R. (2002). Differential equations. Pacific Grove, CA: Brooks/Cole

Google Scholar

Blomhøj, M., and Ärlebäck, J. (2018). Theory-practice relations in research on applications and modelling. In T. Dreyfus, M. Artigue, D. Potari, and S. Prediger, &, K. Ruthven (Eds.), Developing research in mathematics education. Twenty years of communication, cooperation and collaboration in Europe (pp. 90–105). London, New York: Routledge.

Google Scholar

Blomhøj, M., and Jensen, T. H. (2003). Developing mathematical modelling competence: conceptual clarification and educational planning. Teach. Math. Appl. 22, 123–139. doi: 10.1093/teamat/22.3.123

CrossRef Full Text | Google Scholar

Cobb, P. (2002). Modelling, symbolizing and tool use in statistical data analysis. In K. Gravemeijer, R. Lehrer, B. Oersvan, and L. Verschaffel (Eds.), Symbolizing, modelling and tool use in mathematics education (pp. 171–195). Dordrecht, Netherlands: Kluwer Academic Publishers.

Google Scholar

Drijvers, P. (2003). Learning Algebra in a computer environment. Design research on the understanding of the concept of parameter. Dissertation. Utrecht: CD-Beta Press.

Google Scholar

Drijvers, P., and Gravemeijer, K. (2005). “Computer algebra as an instrument” in The didactical challenge of symbolic calculators. eds. I. D. Guin, K. Ruthven, and L. Trouche (Boston, MA: Springer), 163–196.

Google Scholar

Freudenthal, H. (1991). Revisiting mathematics education. Dordrecht: Kluwer Academic Publishers.

Google Scholar

Gravemeijer, K. (2020). Emergent modelling: an RME design heuristic elaborated in a series of examples. Educ. Design. 3.

Google Scholar

Gravemeijer, K., and Stephan, M. (2002) Emergent models as an instructional design heuristic. In K. Gravemeijer, R. Lehrer, B. Oersvan, and L. Verschaffel (Eds.) Symbolizing, modelling and tool use in mathematics education (pp. 145–169). Dordrecht: Kluwer Academic Publishers.

Google Scholar

Ju, M.-K., and Kwon, O. N. (2007). Ways of talking and ways of positioning: students’ beliefs in an inquiry-oriented differential equations class. J. Math. Behav. 26, 267–280. doi: 10.1016/j.jmathb.2007.10.002

CrossRef Full Text | Google Scholar

Kvale, S. (2001). Interview. En introduktion til det kvalitative forskningsinterview. Hans Reitzels Forlag. Copenhagen, Denmark. (In Danish)

Google Scholar

Lagrange, J.-B. (2005). “Using symbolic calculators to study mathematics” in The didactical challenge of symbolic calculators. eds. D. Guin, K. Ruthven, and L. Trouche (Boston, MA: Springer), 113–136.

Google Scholar

Lithner, J. (2008). A research framework for creative and imitative reasoning. Educ. Stud. Math. 67, 255–276. doi: 10.1007/s10649-007-9104-2

CrossRef Full Text | Google Scholar

Niss, M. (2020). “The impact of Dutch mathematics education on Danish mathematics education” in International reflections on the Netherlands didactics of mathematics. ICME-13 Monographs. ed. M. van den Heuvel-Panhuizen (Cham: Springer), 317–324.

Google Scholar

Niss, M., and Blum, W. (2020). The learning and teaching of mathematical modelling. London: Routledge.

Google Scholar