Katharina Reschke
Ricarda Steinmayr
Birgit Spinath- 1Institute for Education Studies, Heidelberg University, Heidelberg, Germany
- 2Department of Psychology, Technical University Dortmund, Dortmund, Germany
- 3Department of Psychology, Heidelberg University, Heidelberg, Germany
The present study examined to what extent teachers’ judgments of students’ aptitude and students’ perceived teachers’ judgments explain gender differences in the early development of students’ math self-concepts. A sample of N = 519 elementary school students was investigated at four measurement occasions from the end of third until the end of fourth grade. We assessed students’ self-concepts and their perceived teachers’ judgments of their aptitude in math. Teachers (N = 27) judged students’ aptitude in math and provided students’ math grades. First, we found significant gender differences in students’ math self-concepts, teachers’ judgments, and students’ perceived teachers’ judgments, but not in students’ math grades. Second, structural equation models showed that teachers’ judgments of students’ aptitude as well as students’ perceived teachers’ judgments of students’ aptitude longitudinally predicted students’ self-concepts. Mediation analyzes demonstrated that teachers’ judgments and students’ perceived teachers’ judgments contributed to gender differences in students’ math self-concepts. Implications for future research and practice are discussed.
1. Introduction
The underrepresentation of women in STEM (science, technology, engineering, and math) careers and girls in such majors in high school are persistent challenges (see Lauermann et al., 2015). Women make up only 28% of the workforce in STEM related professions (National Science Board, 2018). This underrepresentation is problematic both because women disproportionately fail to benefit from lucrative, high-status careers, and because this reduces diversity that could increase technological and scientific innovations (Hill et al., 2010). Accordingly, the question arises whether girls and women are underrepresented in the STEM sector? In addition, it would be desirable and necessary to recruit girls and women for this field in view of the shortage of skilled workers and the declining number of students in the STEM sector (Federal Statistical Office, 2023). In the current study, we focus on the math domain, because math is an important element not only for mathematicians, but in all STEM disciplines. As the roots of this underrepresentation start early (Master and Meltzoff, 2020), we focus on elementary school students in order to examine effects on the gender gap in math early during the school trajectory. Empirical evidence shows that in the early school years boys and girls do not significantly differ in their math achievement and if so, the differences were very small (e.g., Hyde et al., 1990; Herbert and Stipek, 2005; Else-Quest et al., 2010; Reilly et al., 2015; Heyder et al., 2019). Therefore, students’ math achievement cannot be the initial starting point for the gender gap in STEM. Aside from students’ actual achievement, it seems more likely that students’ beliefs about their own competencies, namely their self-concepts, might play an important role for choosing STEM majors and careers (see Lauermann et al., 2015, 2017). Indeed, there is ample evidence for gender differences in students’ math self-concepts from elementary school on, with boys showing higher self-concepts in math than girls (e.g., Else-Quest et al., 2010; Heyder et al., 2019). But how can these gender differences in students’ math self-concepts be explained? There is a strong need to bring forth insights in order to understand when and why girls develop lower math self-concepts.
The development of gender differences in students’ math self-concepts is complex with multiple causes. Expectancy-Value Theory (Eccles et al., 1983) assumes that previous achievement, socializers’ judgments (e.g., from teachers and parents) as well as students’ perceptions of these judgments have an impact among others on students’ self-concepts. Various studies have showed that students’ achievement cannot explain gender differences in students’ self-concepts (e.g., Else-Quest et al., 2010; Heyder et al., 2019). Instead, it was shown that teachers’ judgments of students’ aptitude might partially explain the relationship between gender and students’ self-concept in a cross-sectional study (Heyder et al., 2019). Beyond these prior studies, we not only examined teachers’ judgments of students’ aptitude but also students’ perceived teachers’ judgments as possible factors that might explain gender differences in students’ math self-concepts. We also extend the literature by taking a longitudinal approach focusing on the early stage of math education. Understanding the onset of gender differences in math can help to prevent them from increasing during the school trajectory. First, we analyzed mean differences in students’ math grades, teachers’ judgments of students’ aptitude in math, students’ perceived teachers’ judgments, as well as students’ math self-concepts. Second, we computed a longitudinal structural equation model with teachers’ judgments, as well as students’ math self-concepts. Third, we computed a longitudinal structural equation model with teachers’ judgments of students’ aptitude and students’ perceived teachers’ judgments as predictors of students’ math self-concepts. In this model, it was tested whether teachers’ judgments and students’ perceived teachers’ judgments predicted students’ subsequent self-concepts and whether the effects of teachers’ judgments on students’ self-concepts were mediated by students’ perceived teachers’ judgments. Finally, we checked whether gender differences in mathematical ability self-concepts were mediated by teachers’ judgments and students’ perceived teachers’ judgments. The findings of this study contribute to a better knowledge about underlying processes of gender differences in students’ math self-concepts.
2. Theoretical background
2.1. Academic self-concept: definition, development and gender differences
Academic self-concepts are defined as individuals’ evaluation or self-perceptions of their competence in certain domains (Shavelson et al., 1976; Eccles et al., 1983). Academic self-concepts are typically measured via self-report and assessed by asking students’ how good they think they are in a specific domain such as Math (Eccles et al., 1983). Therefore, the construct is domain-specifically operationalized and students’ self-concepts vary across different subjects. For the development of academic self-concepts, researchers have commonly identified three prominent comparison processes: social, temporal, and dimensional comparisons (Wolff et al., 2018). The social comparison means that students compare their own achievement with that of their classmates, whereas the temporal comparison addresses the comparison of one’s actual achievement with previous results. The dimensional comparison process refers to a comparison of one’ achievement across domains (e.g., math versus verbal achievement). Due to this dimensional comparison effects, the I/E model (Marsh, 1986) assumes that math achievement negatively relates to students’ verbal self-concepts, whereas verbal achievement has a negative effect on students’ math self-concept.
At the beginning of primary school, students have quite high, positive self-concepts, which decrease and stabilize over the school years (Jacobs et al., 2002). During this time, students are very sensitive to social comparisons, feedback and evaluations from their teachers (Spinath and Spinath, 2005a; Natale et al., 2009), which is reflected in an adjustment of the self-concept. Because students’ self-concepts develop and form in elementary school, it was important for us to examine at such an early stage what factors can predict gender differences in students’ math self-concepts. This is why findings are so important and necessary, so that negative developments can be prevented at an early stage.
Empirical evidence highlights gender differences in students’ math self-concepts in favor of boys. Studies found boys to have higher self-concepts in math compared to girls already in elementary school with effect sizes ranging from d = 0.36 to d = 0.52 (Wigfield et al., 1997; Tiedemann, 2000; Dickhäuser and Stiensmeier-Pelster, 2003; Herbert and Stipek, 2005; Chamorro-Premuzic et al., 2010; Steinmayr et al., 2019). Other studies reported correlations between students’ gender and students’ math self-concepts with r = 0.20 for elementary school students (Jacobs et al., 2002). Fredricks and Eccles (2002) as well as Jacobs et al. (2002) found in their longitudinal study gender differences in students’ math self-concepts both in elementary school and secondary school. The gender gap was larger in elementary school. Girls had a less steep decline in their self-concepts over time compared to boys which led to a convergence of girls’ and boys’ math self-concepts in secondary school (Fredricks and Eccles, 2002; Jacobs et al., 2002). Besides these primary studies, two meta-analyzes found significant differences between boys and girls in students’ math self-concept with an average effect size of d = 0.25 (Wilgenbusch and Merrell, 1999) and d = 0.33 (Else-Quest et al., 2010). Summing up, the presented results show that boys have higher math self-concepts than girls across the school years. Given these gender differences in students’ math self-concepts, it is worthwhile to look for factors that can explain why boys have significantly higher self-concepts in math compared to girls about school time. We used the Expectancy-Value-Model by Eccles et al. (1983) as theoretical basis, because this model makes assumptions about specific factors influencing students’ self-concepts.
2.2. Expectancy-value theory
Expectancy-Value-Theory (EVT) by Eccles et al. (1983) is a conceptual framework for the development of achievement motivation. The model was originally designed to explain gender differences in achievement-related motivation and behavior. EVT differentiates two motivational constructs that are hypothesized to influence students’ achievement and education-related choices (e.g., course plans in secondary school or career choices). These motivational constructs are expectancies and task values. In the present study, we only focus on academic self-concepts as expectancies, because large gender differences were found in this construct. EVT holds that students’ self-concepts are influenced by (1) students’ stable characteristics such as their aptitude and previous achievement outcomes, (2) socializers’ beliefs such as teachers’, parents’ or peers’ beliefs, and (3) students’ perception of socializers’ beliefs and expectations for them. Furthermore, the model holds that socializers’ beliefs influence students’ self-concepts indirectly through students’ perceptions of socializers’ beliefs. In the present study, we focused on teachers as socializers, because they represent a major environmental influence on children’s development and might be especially important for the formation of students’ self-concepts in elementary school as teachers are the first point of contact for feedback and information on students’ own achievement and abilities (Tiedemann, 2000; Gunderson et al., 2012). Moreover, as EVT assumes effects of teachers’ judgments and students’ perceptions of these judgments on their self-concepts but not on their motivation such as interest or utility value, we focused on students’ self-concepts as outcomes in our study.
2.3. Predicting students’ math self-concepts to explain gender differences
Based on the theoretical assumptions of EVT and the I/E model, this section will present previous results of empirical studies that examined whether students’ achievement, teachers’ judgments of students’ aptitude as socializers’ beliefs as well as students’ perceived teachers’ judgments can predict students’ math self-concepts and whether these factors play a role in explaining gender differences.
2.3.1. Students’ achievement
The relationship between students’ academic achievement and their self-concepts in a specific domain is well-established. Findings from countless studies showed the association between academic achievement and corresponding self-concepts to vary from moderate to highly positive correlations with r = 0.30–0.60 (Helmke and van Aken, 1995; Guay et al., 2003; Valentine et al., 2004; Marsh et al., 2005; Möller et al., 2009; Marsh and Martin, 2011). Furthermore, there is ample evidence that students’ previous academic achievement has an impact on students’ subsequent self-concepts (e.g., Helmke and van Aken, 1995; Skaalvik and Valås, 1999; Viljaranta et al., 2014). Moreover, the association between academic achievement and students’ self-concepts depends on students’ age. Students in elementary school often have very positive self-concepts with little variation, which leads to a weak correlation between students’ self-concepts and grades. Self-concepts become more realistic in the sense of more in line with external criteria when students grow older, leading to more interindividual variation and a stronger relationship between students’ self-concepts and grades (Jacobs et al., 2002; Spinath and Spinath, 2005a,b). Besides the positive correlations between performance and self-concept in the same domain, numerous studies as well as several meta-analyzes found support for the assumption of the I/E model, namely that students’ verbal achievement is negatively related to students’ math self-concept (Möller et al., 2009, 2020; Marsh et al., 2015). However, this research indicated that social and dimensional comparison effects of academic achievements on self-concepts are much smaller in elementary school children than secondary school students (Möller et al., 2011; Ehm et al., 2014; Lohbeck and Möller, 2017; Möller et al., 2020).
Due to these reported associations between students’ achievement and self-concepts, academic achievement can be an explaining factor for gender differences in students’ math self-concepts. In order to discuss whether students’ achievement might explain gender differences in students’ math self-concepts in more detail, the following section will shed light on gender differences in students’ math achievement. Results from two meta-analyzes showed very small gender differences in math achievement in favor of boys with effect sizes d = 0.13 (Hyde et al., 1990) and d = 0.07 (Reilly et al., 2015). The authors also identified significant moderators. In one meta-analysis (Hyde et al., 1990), gender differences in students’ math achievement depended on the mathematical content. Boys and girls did not differ in their achievement for algebra, arithmetic, and geometry, but only for calculus (d = 0.20). In the other meta-analysis (Reilly et al., 2015), students’ age turned out to be a moderator of gender differences in students’ math achievement. Whereas boys and girls did not differ in their achievement in elementary school, differences were found at the end of high school. This finding is in line with that of a study by Steinmayr and Spinath (2008) showing boys to outperform girls in math achievement in 11th and 12th grade (d = 0.19). In PISA 2018, only very small gender differences in students’ math achievement were found in favor of boys with five points across all OECD states (OECD, 2019). In contrast to these findings, other studies found no significant gender differences in students’ math achievement for students’ grades (Marsh and Yeung, 1998; Tiedemann, 2000; Dickhäuser and Stiensmeier-Pelster, 2003; Chamorro-Premuzic et al., 2010; Wach et al., 2015) and standardized test achievement (Marsh and Yeung, 1998; Herbert and Stipek, 2005; Heyder et al., 2019). A meta-analysis by Else-Quest et al. (2010) and results from the recent Trends in Math and Science Study (TIMSS; Mullis et al., 2016) reported no significant gender differences in students’ math achievement. Achievement differences between boys and girls in the verbal domain are small in elementary school, but become even greater in secondary school (Voyer and Voyer, 2014). To sum up, accumulating evidence suggests that gender differences in students’ achievement are not existent or if they exist, the differences are only small. Therefore, students’ academic achievement cannot serve as an explanation for gender differences in students’ math self-concepts. Thus, it is worthwhile to examine other factors that can possibly explain why boys have significantly higher math self-concepts compared to girls.
2.3.2. Teachers’ judgments of students’ aptitude
Teachers are important socializers for students who have certain assumptions about their students’ aptitude and expectations about students’ future performance. In the last 50 years, many studies have examined the role of teachers’ judgments in determining student outcomes. It is important to note, that teachers’ judgments can be operationalized differently, e.g., as teachers’ predictions of students’ achievement in the near future, as teachers’ estimations of students’ past or current achievement or as teachers’ estimations of students’ current aptitude in a specific subject such as mathematics (Heyder et al., 2019). In this study we focused on teachers’ judgments of students’ aptitude in math. Aptitude is defined as an individual’s capacity for learning and proficiency in a specific domain (Snow, 1992; Stemler and Sternberg, 2013). Therefore, students’ aptitude is the potential to learn and achieve. At the same time, it is a prerequisite for achievement outcomes such as school grades, but is not always reflected by actual achievement (e.g., underachievers). Teachers can not directly observe students’ aptitude in contrast to students’ actual achievement. A previous study found that teachers’ judgments of students’ aptitude predict students’ achievement development (Heyder et al., 2019). Anyhow, gender differences were not analyzed. Results of two cross-sectional studies in elementary school contexts showed small associations (r = 0.12 / r = 0.26) between teachers’ judgments of students’ aptitude in math and students’ math self-concepts (Tiedemann, 2000; Dickhäuser and Stiensmeier-Pelster, 2003). Madon et al. (2001) found in their longitudinal study that teachers’ judgments of students’ aptitude at the beginning of sixth grade predicted students’ self-concepts at the end of sixth grade (ß = 0.12). Besides those studies that examined cross-sectional and longitudinal associations between teachers’ judgments of students’ aptitude and students’ self-concepts, one study directly investigated whether teachers’ judgments explained gender differences in students’ self-concepts (Heyder et al., 2019). The authors showed that teachers’ judgments of students’ aptitude in math mediated the relationship between gender and students’ math self-concepts. In their model, teachers’ judgments explained 50% variance of the relationship between gender and students’ self-concepts. This was even true after controlling for actual competence, math grades, and parents’ estimations of their children’s math aptitude (Steinmayr et al., 2019). Nevertheless, both studies were cross-sectional and it is still unclear whether teachers’ judgments of students’ aptitude have longitudinal effects on students’ self-concepts over a longer period of time and can therefore serve as an explaining factor of gender differences in students’ self-concepts. In addition to associations between teachers’ judgments and students’ self-concepts, it is also important to look at gender differences in teachers’ judgments of students’ aptitude per se.
Overall, studies on gender differences in teachers’ judgments of students’ aptitude in math are rare and their findings are inconsistent. Whereas some study results showed that teachers judged boys and girls as equally talented in math (Dickhäuser and Stiensmeier-Pelster, 2003; Herbert and Stipek, 2005), other findings clearly demonstrated teachers to judge boys’ aptitude in math to be higher compared to girls’ aptitude with effect sizes of d = 0.46 (Heyder et al., 2019; Steinmayr et al., 2019) and d = 0.26 (Tiedemann, 2000). Jussim and Eccles (1992) showed an association between students’ gender and teachers’ judgments of students’ talent in math (ß = 0.06/0.08).
Taken together, the reported studies showed associations between teachers’ judgments of students’ aptitude and students’ self-concept supporting the assumption that teachers’ judgments of students’ aptitude have the potential to explain gender differences in students’ self-concepts. However, most of the reported studies had a cross-sectional design and could not clarify whether teachers’ judgments affect the development of students’ self-concepts. Concerning gender differences in teachers’ judgments per se, findings were inconsistent. Whereas teachers’ judged boys to be more talented in math than girls in some studies, other studies did not find significant differences in teachers’ judgments for boys and girls. Accordingly, it is worthwhile to examine gender differences in teachers’ judgments of students’ aptitude in math with another sample and to test whether these judgments can also explain gender differences in students’ math self-concepts longitudinally.
2.3.3. Students’ perceived teachers’ judgments of students’ aptitude
Even though EVT holds that socializers’ beliefs affect students’ self-concepts through students’ perception of these socializers’ beliefs (Eccles et al., 1983), this part of the model became little attention in educational-psychological research and literature so far. In a study with German elementary school students, students’ perceived teachers’ judgments significantly mediated the relationship between teachers’ judgments of students’ math aptitude and students’ math self-concepts (Dickhäuser and Stiensmeier-Pelster, 2003). Moreover, students’ perceived teachers’ judgments predicted students’ self-concepts in math more strongly (ß = 0.47) compared to students’ math grades (ß = 0.22). These findings highlight the importance of students’ perceived teachers’ judgments for their self-concepts. In this study, boys showed significantly higher perceived teachers’ judgments of students’ math aptitude than girls (d = 0.30; Dickhäuser and Stiensmeier-Pelster, 2003). As amply demonstrated, boys show higher perceived teachers’ judgments of students’ math aptitude in elementary school. These perceived teachers’ judgments are strong predictors of students’ self-concepts and mediated the relationship between teachers’ judgments of students’ aptitude and students’ self-concepts. Therefore, students’ perceived teachers’ judgments seem to be an important factor when explaining gender differences in students’ math self-concepts. To our knowledge, the reported study is the only one that examined the role of perceived teachers’ judgments for students’ self-concepts. With a cross-sectional design such as in this reported study, it remains unclear whether boys and girls significantly differ in their perceived teachers’ judgments across elementary school years. Furthermore, it is worthwhile to examine whether students perceived teachers’ judgments mediate the relationship between teachers’ judgments of students’ aptitude in math and students’ math self-concepts in a longitudinal design and can thus explain gender differences in students’ math self-concepts.
3. Research questions and hypotheses
The present study aimed at exploring the reasons underlying the reported gender differences in students’ math self-concepts. Therefore, the current study was designed to simultaneously explore whether teachers’ judgments of students’ aptitude and students’ perceived teachers’ judgments longitudinally predict students’ math self-concepts. Moreover, we tested whether the effects of teachers’ judgments on students’ self-concepts were mediated by students’ perceived teachers’ judgments.
Specifically, we addressed the following research questions and derived the following hypotheses:
1. Cross-sectional: Are there gender differences in students’ self-concepts and students’ perceived teachers’ judgments in favor of boys? We expect that boys show higher self-concepts in math and higher perceived teachers’ judgments than girls, even though there are no gender differences in students’ math grades. We also expected that teachers judge boys’ aptitude in math higher than girls’ aptitude in math.
2. Longitudinal: Do teachers’ judgments of students’ aptitude longitudinally predict students’ math self-concepts? We expect prior teachers’ judgments of students’ aptitude in math to predict students’ subsequent math self-concepts.
3. Longitudinal: Do students’ perceived teachers’ judgments of students’ aptitude longitudinally predict students’ math self-concepts? We expect prior students’ perceived teachers’ judgments to predict students’ subsequent math self-concepts.
4. Longitudinal: Are the longitudinal effects of teachers’ judgments of students’ aptitude on students’ self-concepts mediated by students’ perceived teachers’ judgments? We expect that the longitudinal effects of teachers’ judgments on students’ self-concepts are mediated by students’ perceptions of teachers’ judgments.
5. Longitudinal: Do teachers’ judgments of students’ aptitude and students’ perceived teachers’ judgments mediate the relationship between gender and students’ math self-concepts? We expect both teachers’ judgments and students’ perceived teachers’ judgments to explain gender differences in students’ self-concepts.
4. Method
4.1. Sample and procedure
The sample consisted of a total of N = 519 students (49.9% girls) and N = 27 teachers (100% women). Data were collected in 27 classes at 11 elementary schools in the German state of Baden-Württemberg across seven measurement occasions (Lohbeck and Möller, 2017; Weidinger et al., 2018; Heyder et al., 2019). In order to attract schools to participate in the study, the study director contacted the relevant school principals and personally introduced himself and the project. Elementary school in the north of Baden-Württemberg were approached. Comparing the present data with those from the Federal Statistical Office (2023) indicated that the participating children were representative for the population in the federal state where they came from in terms of gender ratio (χ2 = 0.004, df = 1, p = 0.950) and immigration background (χ2 = 0.220, df = 1, p = 0.639). Because teachers’ judgments were assessed at only four measurement occasions, we focused on these four measurement occasions, which were spaced 4 months apart (t1: at the end of third grade; t2: at the beginning of fourth grade; t3: in the middle of fourth grade; t4: at the end of fourth grade). Students mean age was 8.28 years (SD = 0.54) at t1 and 9.93 years (SD = 0.72) at t4. Participation in the study was voluntary. Parents consented to their children’s participation in the study by signing a consent form. All students answered questions about their motivation in mathematics in their classrooms on a regular school day. In order to ensure that all students worked at the same speed, a trained research assistant administered the questionnaire and read all items aloud. Overall, the assessments took about 45 min. During the same time, teachers provided information about students’ grades and indicated their judgments of students’ aptitude.
4.2. Measures
4.2.1. Students’ gender
Students gender was coded as 1 = male and 2 = female.
4.2.2. Students’ math self-concept
We assessed students’ math academic self-concepts with three items: “How good are you at math?” with a response format ranging from 1 (very good) to 5 (very bad), “How easy is it for you to learn new things in math?” ranging from 1 (very easy) to 5 (very hard), and “To which group of students do you belong in your class in math?” ranging from 1 (the best) to 5 (the worst). These items were based on a questionnaire for assessing students’ academic self-concept according to expectancy-value theory (Eccles and Wigfield, 1995) and established in previous studies (e.g., Brunner et al., 2008; Weidinger et al., 2018) that supported the construct validity of academic self-concept. The internal consistency of math self-concepts was good at all four measurement occasions (α = 0.84 to 0.85). In order to present the values of this scale more intuitively, the items were recoded so that higher values stood for higher academic self-concept.
4.2.3. Teachers’ judgments of students’ aptitude in math
We assessed teachers’ judgments of students’ aptitude in math with one item, namely, “In your opinion, how talented is the following student in math?.” Teachers’ judgments were given on a 5-point response format ranging from 1 (not talented) to 5 (very talented). Teachers’ judgments of students’ aptitude were assessed with one item only, because this construct is a very narrow construct, and additional items would be phrased in the same way. Moreover, other researchers examining teachers’ judgments of students’ aptitude and achievement have also assessed these constructs with single-item measures (Hoge and Butcher, 1984; Tiedemann, 2000; Kuklinski and Weinstein, 2001; Dickhäuser and Stiensmeier-Pelster, 2003; Fischbach et al., 2013).
4.2.4. Students’ perceived teachers’ judgments
We assessed students’ perceived teachers’ judgments with three items, namely, “My teacher believes that I am good at math,” “My teacher believes that it is easy for me to learn new things in math,” and “My teacher believes that I belong to the best group of students in math in my class” with a response format ranging from 1 (totally disagree) to 5 (totally agree). The internal consistency of students’ perceived teachers’ judgments was good at all four measurement occasions (α = 0.80 to 0.86).
4.2.5. Math grades
Teachers gave information about students’ math grades (from their report cards). In Germany, a one stands for the best grade and six for the worst. We reversed the polarity of math grades such that higher values indicated better math achievement ranging from 1 = insufficient/fail (minimum) to 6 = excellent (maximum) so that the effects of math grades on other variables in our models can be better interpreted.
4.3. Statistical analyzes
4.3.1. Variance analyzes
In order to examine mean differences between boys and girls on students’ math grades, teachers’ judgments of students’ aptitude, students’ perceived teachers’ judgments and students’ math self-concepts, multivariate analysis of variance were computed for each construct at the four measurement occasions. Post-hoc comparisons were calculated to analyze differences in a construct at one specific measurement occasion. Additionally, we computed effect sizes (Cohen’ s d) in order to interpret the magnitude of the several mean differences.
4.3.2. Structural equation models
One aim of our study was to examine whether teachers’ judgments of students’ aptitude and students’ perceived teachers’ judgments longitudinally predict students’ math self-concepts. Therefore, we computed two longitudinal cross-lagged panel models with reciprocal effects between teachers’ judgments of students’ aptitude and students’ self-concepts in the first model. The second model included reciprocal effects between students’ perceived teachers’ judgments and students’ self-concepts. As teachers’ judgments of students’ aptitude were assessed with one item only, these were modeled as manifest variables. Students’ perceived teachers’ judgments and students’ self-concepts were modeled as latent variables with three indicators each. To correct for the clustering in our data (students nested in different classes and schools) and sampling error, we used the “TYPE = COMPLEX” option in Mplus. We also included the stabilities of the several variables and intercorrelations within one measurement occasion. All structural equation models were computed using Mplus 7.11 (Muthén and Muthén, 1998/2013).
Another aim of our study was to analyze whether teachers’ judgments of students’ aptitude and students’ perceived teachers’ aptitude can explain gender differences in students’ math self-concepts. Also, we wanted to test whether effects of teachers’ judgments of students’ aptitude on students’ self-concepts are mediated through students’ perceived teachers’ judgments. For this, we computed a structural equation model with reciprocal effects between teachers’ judgments of students’ aptitude, students’ perceived teachers’ judgments and students’ math self-concepts (see Figure 1). Also, we included effects from gender on students’ math self-concepts and on the independent variables. Stabilities of the variables and intercorrelations within one measurement occasion were included as well. In order to analyze whether the effects from teachers’ judgments of students’ aptitude on students’ self-concepts are mediated through students’ perceived teachers’ judgments, we included indirect effects of teachers’ judgments over students’ perceived teachers’ judgments on students’ self-concepts in our model. Also, we included indirect effects of gender over teachers’ judgments and students’ perceived teachers’ judgments on students’ self-concepts. These indirect effects were computed using the bootstrap method. Moreover, we requested confidence intervals.
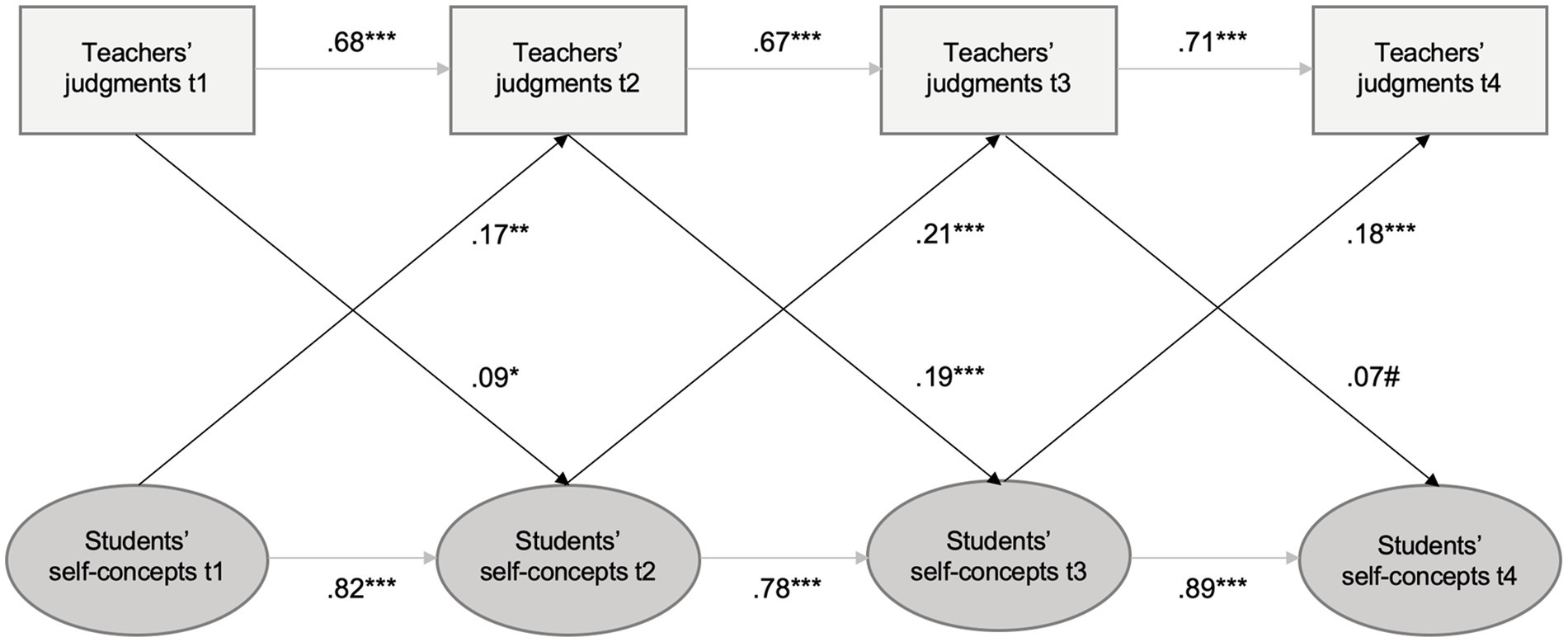
Figure 1. Cross-lagged panel model with teachers’ judgments of students’ aptitude in math and their math-specific self-concepts. For greater clarity, indicators of latent constructs (items), method factors and intercorrelations to each measurement occasion are not depicted in this figure. *** p < 0.001; ** p < 0.01, * p < 0.05, # p < 0.10.
On a related note, the word “effect” is used in the sense of a statistical prediction in a cross-lagged panel model (one prior variable predicts another subsequent variable) with different measurement occasions and is not meant to be causal.
4.3.3. Evaluation of model fit
For the model fit of the two structural equation models, we took into account the χ2 value with degrees of freedom, the Comparative Fit Index (CFI), and the Root Mean Square Error of Approximation (RMSEA). Because the χ2 value depends on the sample size and can easily become significant in large samples (Ullman, 2007), this value must be interpreted with caution. For the CFI, values higher than 0.95, and for the RMSEA, values lower than 0.05 are considered excellent. Such an excellent fit occurs when the model fits the data well. If the values for the CFI are lower than 0.90 and the values for RMSEA are higher than 0.10, then the model is not acceptable (Hu and Bentler, 1999; Marsh et al., 2004).
4.3.4. Handling missing data
As in every longitudinal study, we had to deal with missing data in the present study. The main reason for missing data was illness, whereby some students missed one or more measurement occasions. These missing data ranged from 11.4% (t1) to 19.5% (t3) for students’ math grades, from 11.4% (t2) to 24.7% (t1) for teachers’ judgments of students’ aptitude, from 9.8% (t1) to 14.1% (t4) for academic self-concept, and from 9.6% (t1) to 13.7% (t3, t4) for students’ perceived teachers’ judgments. Students with missing data did not differ from students without missing data. To handle missing data in Mplus, we used the full information maximum likelihood (FIML) method. This is an approach that typically yields less biased estimates under the missing at random assumption than traditional approaches such as listwise or pairwise deletion. Also, this method takes all information into account (i.e., cases with missing values) when estimating the model parameters and maintains statistical power at the same time (Schafer and Graham, 2002; Enders, 2010).
5. Results
5.1. Descriptive statistics and gender differences
Table 1 shows the means (M), standard deviations (SD), and internal consistencies (α) for the examined variables across our four measurement occasions for the whole sample as well as for girls and boys separated. The results from MANOVA showed no significant gender effect for math grades [F(4,340) = 1.95, p = 0.12, d = 0.3]. Post-hoc univariate analyzes showed no gender differences at each measurement occasion. Even there were no significant mean differences in students’ math grades, teachers rated students’ math aptitude significantly higher for boys [F(4,306) = 5.36, p < 0.001, d = 0.54]. This pattern was found for each measurement occasion. According to this, boys showed significantly higher perceived teachers’ judgments of their aptitude in math compared to girls [F(4,366) = 6.12, p < 0.001, d = 0.52]. Post-hoc univariate analyzes confirmed this for each measurement occasion. Also, boys showed significantly higher math self-concepts than girls among all measurement occasions [F(4,365) = 9.79, p < 0.001, d = 0.66]. The differences in teachers’ judgments for boy s and girls can be described as small effects (Cohen’s d). The effect sizes for the significant differences between boys in girls in their perceived teachers’ judgments of their aptitude and in their math self-concept varied from small to medium. Intercorrelations between all examined variables can be seen in Table 2.
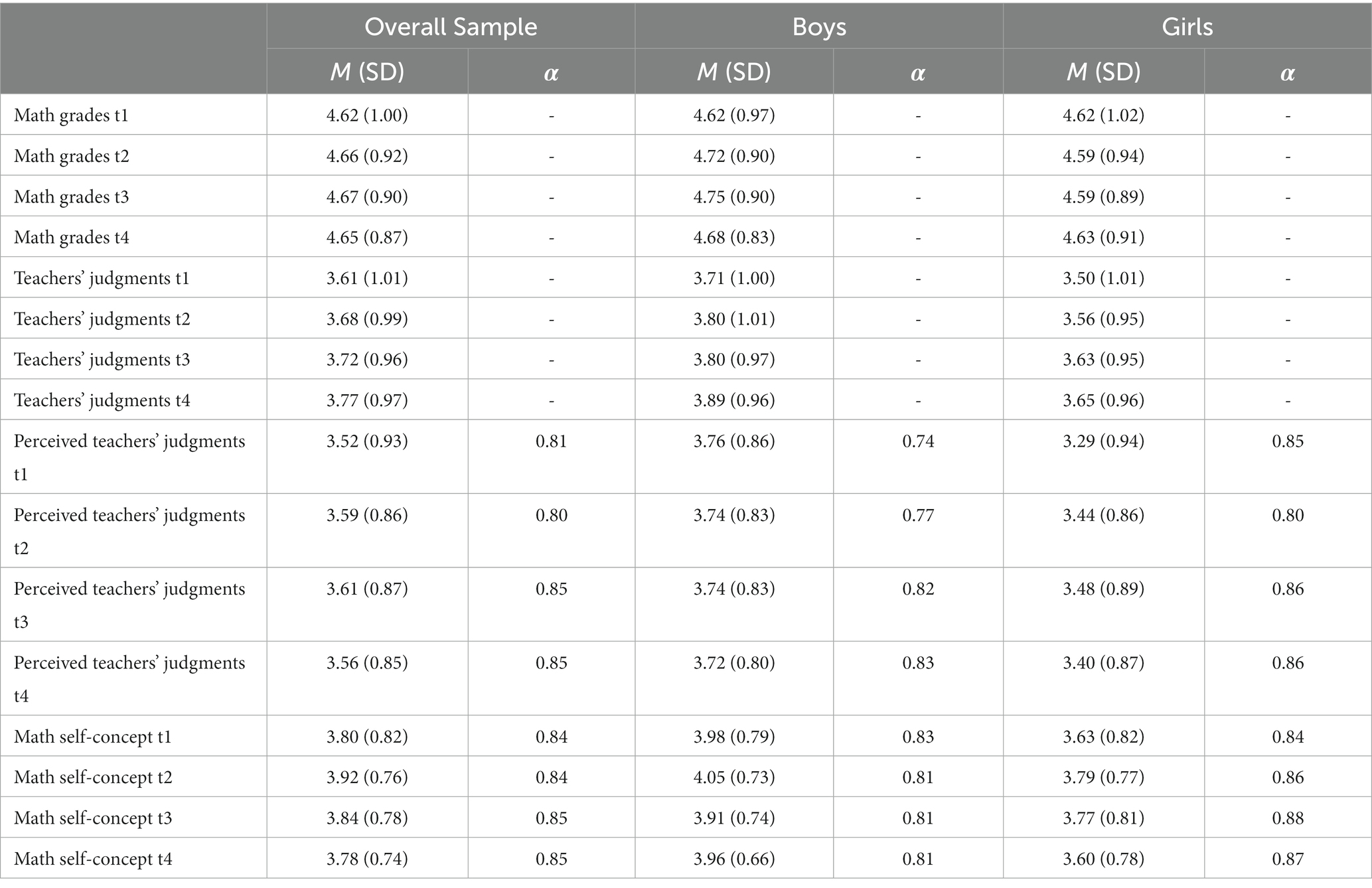
Table 1. Means (M), standard deviations (SD), and internal consistencies (α) for the whole sample as well as for boys and girls separated.
Table 2. Intercorrelations among all variables.
5.2. Longitudinal effects from teachers’ judgments and students’ perceived teachers’ judgments on students’ self-concepts
In order to analyze longitudinal effects between teachers’ judgments of students’ aptitude and students’ math self-concept as well as between students’ perceived teachers’ judgments and students’ math self-concept, two structural equation models with cross-lagged effects were computed. The first model with teachers’ judgments of students’ aptitude and students’ self-concepts (see Table 3; Figure 1) fitted the data well [χ2(81) = 123.51, p < 0.01; CFI = 0.986; TLI = 0.980; RMSEA = 0.040; SRMR = 0.029]. The high correlations within a construct at different measurement occasions, suggests a relatively high stability of the constructs over the elementary school years. On the one hand, we found significant effects from teachers’ prior judgments of students’ aptitude on students’ subsequent self-concepts (from t1 to t2 ß = 0.10, p < 0.05; from t2 to t3 ß = 0.19, p < 0.001). This indicates that teachers’ prior judgments of students’ aptitude longitudinally predict students’ subsequent self-concepts in elementary school. The effect from teachers’ judgments to t3 on students’ self-concepts to t4 was not significant. On the other hand, we found significant effects from prior self-concepts on subsequent teachers’ judgments to all measurement occasions (ß = 0.17–0.21, p < 0.001). These results provide support that not only teachers’ judgments predict students’ self-concepts, but also that students’ prior self-concepts predict subsequent teachers’ judgments of students’ aptitude.
Table 3. Standardized stability and cross-lagged effects with standard errors and confidence intervals for teachers’ judgments of students’ aptitude in math (TJ), and students’ math self-concepts (MSC).
The second model with students’ perceived teachers’ judgments of their aptitude and students’ self-concepts (see Table 4; Figure 2) also fitted the data well [χ2(231) = 565.89, p < 0.001; CFI = 0.947; TLI = 0.937; RMSEA = 0.066; SRMR = 0.040]. Again, the constructs were relatively stable over time. In this model, we found one significant path from students’ perceived teachers’ judgments of their aptitude to t3 on students’ self-concepts to t4 (ß = 0.27, p < 0.05). Also, we found one significant path from students’ self-concepts to t2 on students’ perceived teachers’ judgments of their aptitude to t3 (ß = 0.34, p < 0.05). We found little support for our hypothesis that students’ perceived teachers’ judgments of students’ aptitude longitudinally predict students’ math self-concepts.
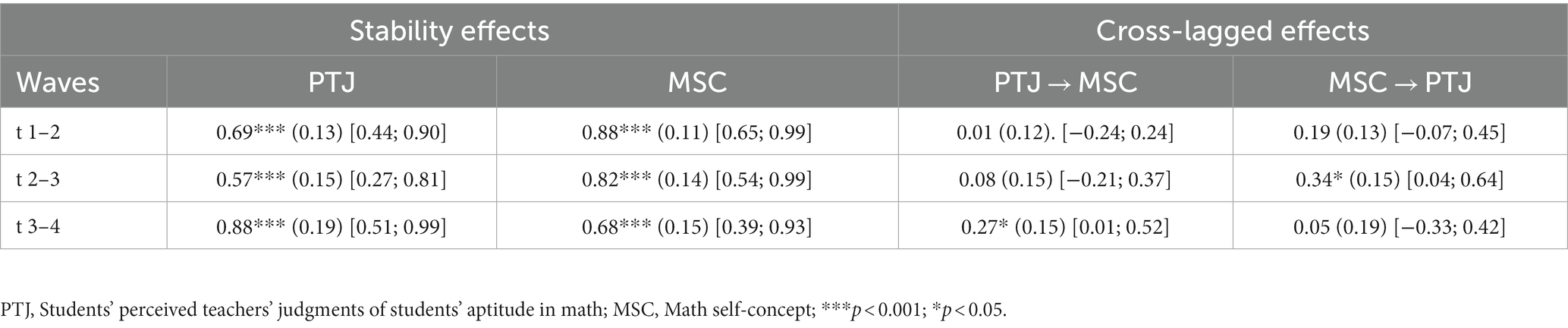
Table 4. Standardized stability and cross-lagged effects with standard errors and confidence intervals for students’ perceived teachers’ judgments of students’ aptitude in math (PTJ), and students’ math self-concepts (MSC).
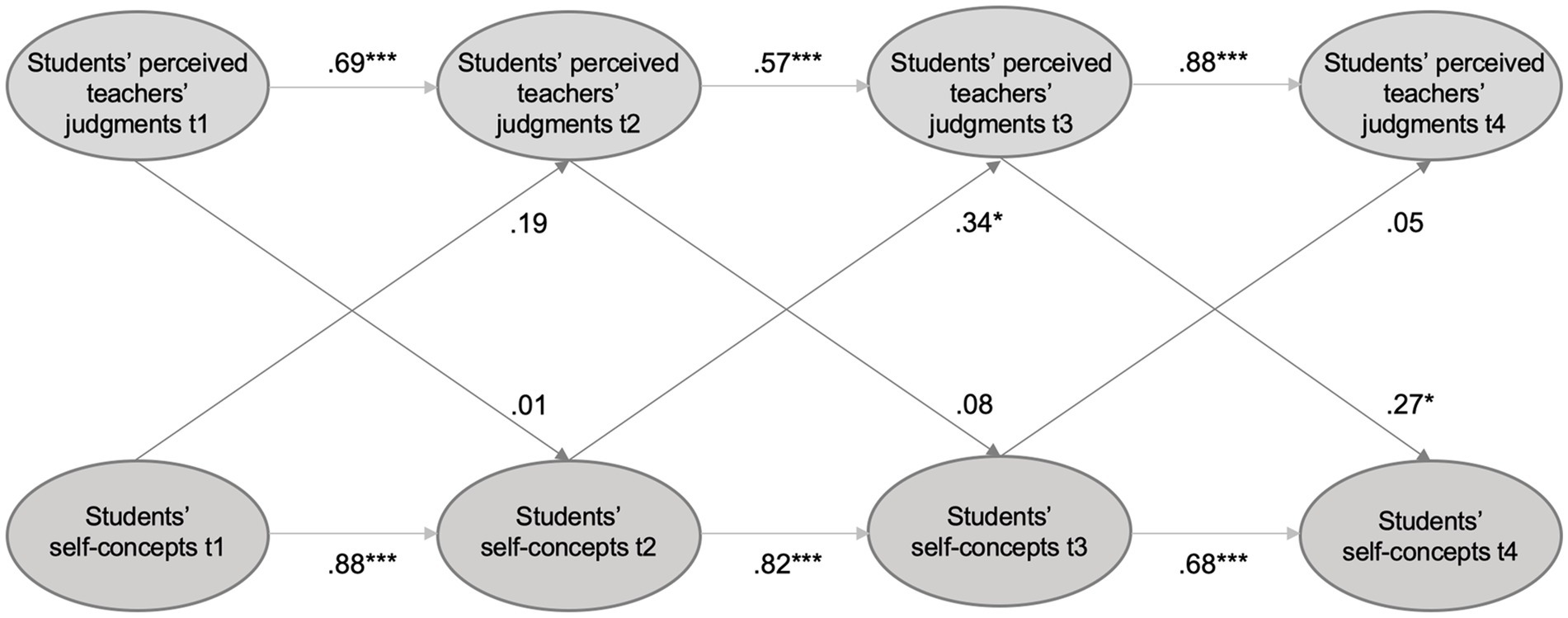
Figure 2. Cross-lagged panel model with students’ perceived teachers’ judgments and their math-specific self-concepts. For greater clarity, indicators of latent constructs (items), method factors and intercorrelations to each measurement occasion are not depicted in this figure. *** p < 0.001; * p < 0.05.
5.3. Teachers’ judgments and students’ perceived teachers’ judgments as explaining factors of gender differences in students’ academic self-concepts
In order to examine whether teachers’ judgments of students’ aptitude and students’ perceived teachers’ judgments of students’ aptitude can explain gender differences in students’ math self-concepts we computed a longitudinal structural equation model with these variables among all four measurement occasions (see Table 5; Figure 3). The model fit was acceptable with [χ2(327) = 723.70, p < 0.001; CFI = 0.947; TLI = 0.934; RMSEA = 0.059; SRMR = 0.039]. First, we found one significant direct effect from prior teachers’ judgments of students’ aptitude at t2 on students’ subsequent self-concepts at t3 (ß = 0.17, p < 0.01). Second, there were two significant direct effects from prior teachers’ judgments of students’ aptitude on students’ subsequent perceived teachers’ judgments of students’ aptitude (from t2 to t3 ß = 0.19, p < 0.001; from t3 to t4 ß = 0.14, p < 0.05). Third, we found one significant direct effect from students’ perceived teachers’ judgments of students’ aptitude at t3 on students’ subsequent self-concepts at t4 (ß = 0.26, p < 0.05). In addition to the direct effects of teachers’ judgments of students’ aptitude and students’ perceived teachers’ judgments on students’ self-concepts, we examined whether these effects are mediated through students’ perceived teachers’ judgments. We found that teachers’ judgments of students’ aptitude (t2) had an indirect effect on students’ self-concepts (t4) (ß = 0.11, p < 0.01). But contradictory to our hypothesis, this indirect effect was not mediated through students’ perceived teachers’ judgments of students’ aptitude, but through teachers’ judgments of students’ aptitude at t3. Finally, we examined the effects of gender on students’ self-concepts to all four measurement occasions. We found gender to be a significant predictor at the first measurement occasion (ß = −0.31, p < 0.001) and at the fourth measurement occasion (ß = −0.12, p < 0.001). Students’ self-concepts at t2, and t3 were not significantly predicted by gender. Moreover, gender predicted teachers’ judgments (ß = −0.11, p < 0.05) as well as students’ perceived teachers’ judgments at the first measurement occasion (ß = −0.33, p < 0.001) but was not a significant predictor at the other measurement occasions. The results of the indirect effects showed that the effect of gender on students’ self-concepts at t2 was significantly mediated by students’ self-concepts at t1. For the effect of gender on students’ self-concepts at t3, indirect effects could be found via students’ self-concepts at t2 and teachers’ judgments at t2. For the effect of gender on students’ self-concepts at t4, indirect effects could be found via prior self-concepts, teachers’ judgments as well as students’ perceived teachers’ judgments. These results suggest that gender differences in students’ self-concepts can be explained by prior teachers’ judgments of students’ aptitude, students’ perceived teachers’ judgments as well as by prior self-concepts.
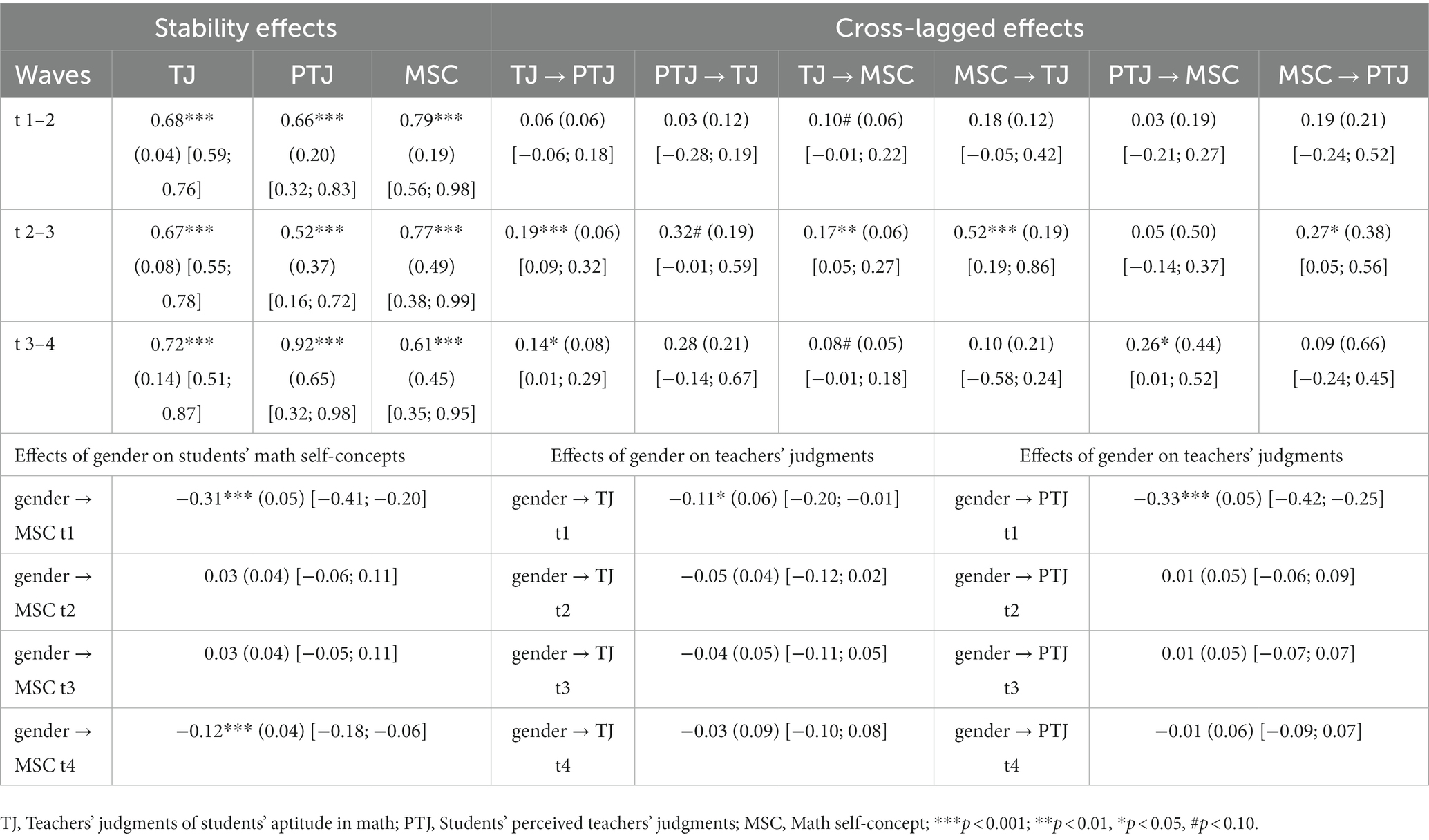
Table 5. Standardized stability and cross-lagged effects with standard errors and confidence intervals for teachers’ judgments of students’ aptitude in math (TJ), students’ perceived teachers’ judgments (PTJ), and students’ math self-concepts (MSC).
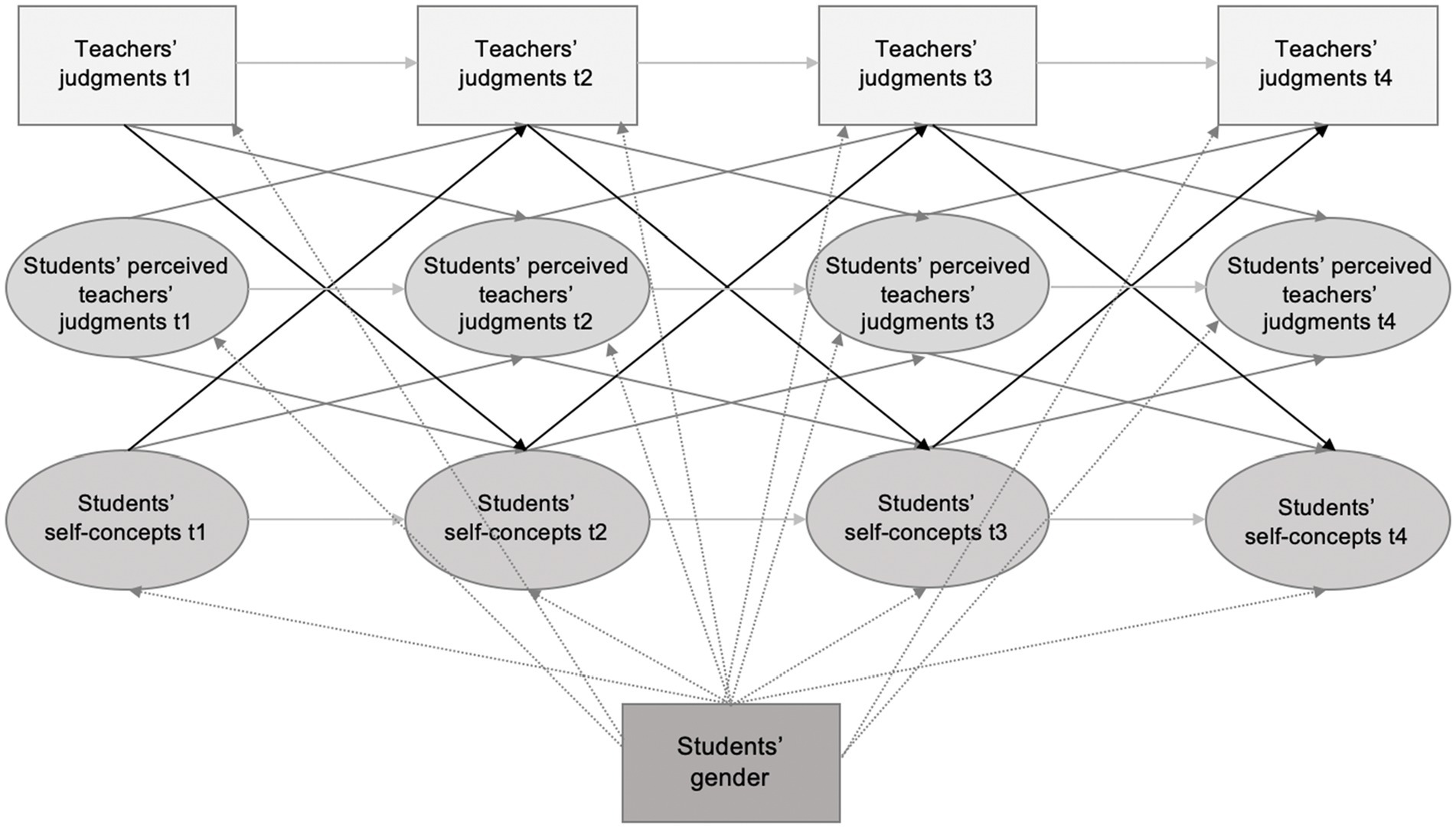
Figure 3. Cross-lagged panel model with teachers’ judgments of students’ aptitude in math, students’ perceived teachers’ judgments and their math self-concepts. For greater clarity, indicators of latent constructs (items), method factors and intercorrelations to each measurement occasion are not depicted in this figure.
6. Discussion
The present study was designed to contribute to a better understanding of the reasons behind the underrepresentation of women in STEM domains and girls in STEM-related majors. Therefore, we focused on students’ self-concept as one predictor of education-related choices. A primary purpose of this study was to analyze gender differences in students’ math self-concepts, their math grades, teachers’ judgments of students’ aptitude in math and students’ perceptions of teachers’ judgments. A second and the central purpose of this research was to explain gender differences in students’ math self-concepts. Both teachers’ judgments and students’ perceived teachers’ judgments were tested as possible explaining factors. Accordingly, a first point of discussion will refer to gender differences in the examined variables. Afterwards, we will discuss whether teachers’ judgments and students’ perceptions of these judgments can explain gender differences in students’ math self-concepts. Finally, we will discuss limitations of our study, ideas for future research and practical implications.
6.1. Gender differences in the examined variables
In line with our hypothesis, we found significant gender differences in students’ math self-concepts in favor of boys at all measurement occasions. These differences can be described as small to medium effect sizes. These empirical findings are consistent with previous reports showing boys to have higher math self-concepts in elementary school than girls (Wigfield et al., 1997; Tiedemann, 2000; Dickhäuser and Stiensmeier-Pelster, 2003; Herbert and Stipek, 2005; Chamorro-Premuzic et al., 2010; Heyder et al., 2019).
Moreover, we found no significant gender differences in students’ math grades, which is also in line with previous findings indicating that boys and girls do not differ in their math achievement (e.g., Tiedemann, 2000; Dickhäuser and Stiensmeier-Pelster, 2003; Else-Quest et al., 2010; Heyder et al., 2019). This indicates that gender differences in students’ self-concepts cannot be traced back to gender differences in students’ achievement. Consequently, there must be other factors influencing students’ self-concepts in a way that boys develop higher self-concepts in math compared to girls.
Although boys and girls in our sample did not differ in their math achievement, teachers judged boys to be significantly more talented in math than girls. At all measurement occasions, teachers’ judgments of students’ aptitude were significantly higher for boys than for girls. These results are consistent with findings from previous studies that also showed significant differences in teachers’ judgments of students’ aptitude in math, but no significant gender differences in students’ math achievement (Jussim and Eccles, 1992; Tiedemann, 2000; Heyder et al., 2019). The present results, in conjunction with those presented by other researchers, clearly indicate that teachers are subject to a math-male stereotype when they have to judge students’ aptitude in math. Based on the fact that teachers judged boys to be more talented in math, it is not surprising that boys showed significantly higher perceived teachers’ judgments of students’ aptitude in math than girls. These differences were significant at all four measurement occasions. To our knowledge, only one previous study examined gender differences in students’ perceived teachers’ judgments. This study was cross-sectional and also showed boys to have higher perceived teachers’ judgments of students’ aptitude in math than girls (Dickhäuser and Stiensmeier-Pelster, 2003). Therefore, students’ perception of teachers’ judgments might also be an important variable for the explanation of gender differences in students’ math self-concepts.
In sum, our findings show consistent gender differences in students’ math self-concepts in elementary school already. Moreover, our study provided empirical support for gender differences in teachers’ judgments of students’ aptitude and students’ perceptions of teachers’ judgments without having differences in students’ achievement. These differences might explain why boys develop higher self-concepts in math during elementary school than girls. The next section will shed light on, whether teachers’ judgments and students’ perceptions of these judgments predict students’ math self-concepts to explain gender differences.
6.2. Teachers’ judgments and students’ perceived teachers’ judgments as explaining factors of gender differences in students’ academic self-concepts
In our first longitudinal model, we found significant effects of prior teachers’ judgments on students’ subsequent self-concepts in math. These findings are in line with the assumption of EVT that socializers’ beliefs predict students’ self-concepts (Eccles et al., 1983). These effects are also consistent with findings from cross-sectional studies demonstrating significant small associations between teachers’ judgments of students’ aptitude and students’ self-concepts (Tiedemann, 2000; Madon et al., 2001; Dickhäuser and Stiensmeier-Pelster, 2003; Heyder et al., 2019).
Moreover, the results of the second longitudinal model showed one significant effect of students’ prior perceived teachers’ judgments of students’ aptitude on students’ subsequent self-concepts (t3 to t4). This finding provides little support for the assumption of EVT, namely, that perceived teachers’ judgments as perceptions of socializers’ beliefs predict students’ self-concepts (Eccles et al., 1983). Whereas only one study reported a cross-sectional association between students’ perceived teachers’ judgments and students’ self-concepts (Dickhäuser and Stiensmeier-Pelster, 2003), this study showed one longitudinal effect. Nevertheless, it is unclear, whether only one of three possible effects of students’ perceived teachers’ judgments on students’ self-concepts became significant. One explanation might be that students’ self-concepts were highly stable over time in elementary school and it might be hard for other variables to explain further variance. At this point, our results indicate that both teachers’ judgments of students’ aptitude in math and students’ perceptions of these judgments have direct effects on students’ math self-concepts over time.
In our overall model, we again found evidence for direct effects of teachers’ prior judgments of students’ aptitude and students’ perceived teachers’ judgments on students’ subsequent self-concepts. Based on these findings, it seems highly likely that students develop their self-concepts based on teachers’ judgments. Furthermore, we found significant direct effects of teachers’ prior judgments on students’ perceptions of teachers’ judgments. Teachers seem to communicate their judgments to their students in different ways such as through feedback and attributional processes as well as through emotional responses and classroom practices (Stipek et al., 2001; Georgiou et al., 2002; Upadyaya and Eccles, 2015). For example, when a teacher has high expectations for a boy in math, the teacher will challenge and encourage him more in class, for example, giving him more challenging tasks and praising him for the corresponding performance. Subsequently, the boy will transfer this information into his perceived teachers’ judgments and assumes that the teacher thinks he is gifted. In contrast, if a teacher assumes a girl to have a lower math aptitude, he or she will challenge and encourage her less in class by providing less challenging tasks and attributing good performance to effort, for example. As a result, the girl will perceive a lower judgment of her math aptitude.
Another interesting finding concerns the mediation effect of teachers’ judgments on students’ self-concepts through students’ perceived teachers’ judgments. So, teachers’ judgments had an indirect effect on students’ self-concepts, but this effect was not mediated through students’ perceived teachers’ judgments but through teachers’ judgments one measurement occasion later. This suggests that the effects of teachers’ judgments on students’ self-concepts seem to be more directly than mediated through students’ perceptions of their teachers’ judgments. This finding highlights the importance of teachers’ beliefs about students’ aptitude for students’ self-concepts. In other words, what the teacher thinks about a student’s aptitude is an important factor when students develop their self-concepts.
One final result we want to put attention to is that effects of students’ gender on students’ self-concepts in math completely disappeared at t2 and t3 and partially disappeared at t4 after including teachers’ judgments and students’ perceived teachers’ judgments as predictors of students’ self-concepts. Furthermore, we found indirect effects of gender on students’ self-concepts via teachers’ judgments and students’ perceived teachers’ judgments. These findings emphasize that teachers’ judgments of students’ aptitude and the perception of these by the students can explain gender differences in students’ self-concepts in math. Our study goes beyond the finding that teachers’ judgments explained half of the variance of the relationship between gender and self-concepts (Heyder et al., 2019), because of our longitudinal design with four measurement occasions. Students seem to develop their self-concept based on messages they receive from important socializers such as teachers. Our study provided empirical support for the idea that students in elementary school seem to have internalized their teachers’ judgments with a math-male stereotype resulting in lower math self-concepts for girls even though girls and boys do not differ in their math achievement. One can assume that the effects of teachers’ judgments on students’ perceived teachers’ judgments and students’ self-concepts are in line with self-fulfilling prophecy effects (Brophy and Good, 1970). It can be argued that based on their judgment or belief about students’ aptitude in math, teachers treat boys and girls differently in class such as providing more support, more challenging tasks and better feedback to students with higher judged aptitudes. As argued above, students perceive their teachers’ judgments based on various teacher expressions and behaviors. These student perceptions, in turn, have effects on self-concepts. This is a worrying finding because students’ self-concepts themselves have effects on students’ achievement as well as their education-related choices such as majors and careers in turn. Consequently, it is not surprising that women or girls are underrepresented in STEM domains.
Gender differences in students’ math self-concepts were not fully explained to our last measurement time point at the end of grade 4. This suggests that there must be other variables besides teachers’ judgments and students’ perceived teachers’ judgments that can explain gender differences in students’ math self-concepts. At this time, students are quite before their transfer to secondary school. Maybe beliefs from other important socializers such as their parents or peers become more important and have effects on students’ self-concepts as well. Previous research has shown that, in addition to teachers, parents also have gender-stereotypic perceptions of their children’s aptitude. In a study from Herbert and Stipek (2005), parents rated boys’ math competencies higher than girls in both third and fifth grades. Moreover, parent ratings of children’s competence were a particularly strong predictor of children’s judgments of their math skills. One difference between the study mentioned above and our study, however, is that the parents were asked to assess the competencies that the children already have. In our study, we focused on the assessment of students’ aptitude in the sense of an underlying potential that does not necessarily translate into achievement. In addition to teachers’ and parents’ judgments, the judgments of peers also seem to play a role for the development of students’ self-concepts. For example, Lorenz et al. (2020) showed with social network analyzes that ninth-grade students adapt their expectations toward the average expectations of their friends. The fact that we did not include parents’ and peers’ judgments in our study, will also be addressed in the limitation section.
Our results point to the importance of teachers’ judgments of students’ aptitude and students’ perceived teachers’ judgments for the development and explanation of gender differences in students’ math self-concepts during their time in elementary school.
6.3. Limitations and future research
The current study has a longitudinal design with four measurement occasions in order to examine whether teachers’ judgments of students’ aptitude and students’ perceived teachers’ judgments predict students’ math self-concepts over a longer period of time in elementary school. Even though we found effects from prior teachers’ judgments and students’ perceived teachers’ judgments on students’ self-concepts, these effects cannot be interpreted as causal effects. It is possible that a third variable has an influence on our examined variables. To clarify whether teachers’ judgments and students’ perceptions of these judgments have a causal influence on students’ self-concepts, future studies should compute an experiment, in which students get simulated feedback from teachers.
As reported above, we focused on the math domain as one of the STEM domains, because girls are underrepresented in these majors and careers. Indeed, we found that girls showed significantly lower math self-concepts compared to boys. Moreover, teachers’ rated girls’ aptitude in math as significantly lower as boys’ aptitude in math, although girls and boys did not significantly differ in their math achievement. This indicates that teachers might be biased by math-male stereotypes. Accordingly, it would also be interesting to examine gender differences in teachers’ judgments and students’ self-concepts in a domain, in which girls might be better such as languages.
It is unknown why teachers judged boys’ aptitude in math higher than girls’ aptitude in math even though they did not differ in their math achievement. It may help to explore and understand the underlying mechanisms. One possible explanation might be that teachers attribute boys’ achievement to their high aptitude and girls’ achievement to their high effort. In a study by Fennema et al. (1990) teachers more often named boys to be the best students in class and attributed boys’ success to aptitude and girls’ success to effort. Furthermore, Tiedemann (2000) showed that teachers attributed boys’ failures in math to a lack of effort, but girls’ failures to a lack of aptitude. Future studies should systematically examine teachers’ judgments of students’ aptitude in math, teachers’ attributions as well as students’ achievement in order to analyze gender differences in the math domain in more detail. In addition, future research is needed to explore possible opportunities to reduce this math-male stereotype, which will be discussed in the section to practical implications in detail.
In our study we focused on elementary school, because during this time students use feedback from different sources such as achievement in exams and direct feedback from their teachers in order to develop a more realistic self-concept. Teachers’ judgments can have far-reaching consequences not only for the development of students’ self-concepts but also for recommendation for secondary school. Nevertheless, future research could shed light on whether teachers’ judgments have significant effects on students’ subsequent self-concepts in secondary school and to test whether teachers’ judgments become less important over time.
One shortcoming of the present study is that all teachers in our sample were female. It is interesting that the gender differences in teachers’ judgments were highly significant even though boys and girls did not differ in their achievement. Maybe female teachers have internalized the math-male stereotype to which they were exposed in former times. Therefore, the question arises whether the gender gap in teachers’ judgments might depend on teachers’ gender. Robinson-Cimpian et al. (2014) found the gender difference in teachers’ judgments of students’ ability in math to be larger for female than for male teachers. From this perspective, future research should systematically examine whether gender differences in teachers’ judgments depend on teachers’ gender and why female teachers might be more math-male stereotyped. The mechanisms behind that phenomenon should be explored in more detail.
Moreover, we focused on teachers’ judgments as socializers’ beliefs, because teachers play an important role in students’ development. The results of our study suggested that gender differences in students’ math self-concepts at t4 could not be fully explained by teachers’ judgments and students’ perceptions of teachers’ judgments. Consequently, there must be further variables that might have an influence on students’ math self-concepts at the end of elementary school. Prior research showed that parents’ math-gender stereotypes can affect their perceptions of their own children’s math ability even in early elementary school (Gunderson et al., 2012). Furthermore, Wolff (2021) found in his recent study that gender stereotypes shared by students’ classmates can have a substantial impact on students’ math self-concepts. Therefore, it would be worthwhile to examine different socializers’ beliefs such as from teachers, parents and peers in one study in order to examine their relative importance for students’ self-concepts in order to explain these gender differences.
6.4. Practical implications
Beyond our described implications for further research, there are some important practical implications of these findings that should be mentioned in the following. In our study, teachers judged girls’ aptitude in math significantly lower than boys’ aptitude although girls and boys did not differ in their actual achievement. The underestimation of girls’ aptitude in math might be biased by a math-male stereotype and not based on objective criteria. This prevalence of math-male stereotypes can have far-reaching negative consequences for girls’ motivation (development), their achievement (in form of self-enhancement effects) and their educational choices such as majors in high school, study programs and careers. From this perspective, interventions are needed to reduce these biased judgments or these lower judgments for girls, respectively. One possibility for an intervention might be to make teachers aware of this math-male stereotype and biased judgments. Another possibility might be to provide teachers with empirical evidence showing that girls and boys do not differ in their math achievement. Teachers should also consciously make sure that they support boys and girls with the same performance in math equally. Heyder et al. (2019) proposed that these interventions can be integrated in the teacher education at university or as additional training for in-service teachers. In addition to prevention and intervention measures for teachers, offers for students should also be established. For example, girls could benefit from a workshop in which they learn to perceive their aptitude for mathematics independently of the assessments of different peers. This workshop was also intended to present female role models in the STEM sector and to make it clear that girls and women can be just as successful as boys and men. Reducing this gender bias might lead to a higher decision of girls to select a STEM career.
7. Conclusion
In conclusion, the current study provides new insights into how gender differences in students’ math self-concepts can be explained. Both teachers’ judgments of students’ aptitude in math and students’ perceived teachers’ judgments had longitudinal effects on students’ math self-concepts and can therefore explain why boys show higher math self-concepts than girls during the time of elementary school.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.
Author contributions
BS and RS have provided the data set and supervised the project and supplemented individual points in the manuscript and reviewed the manuscript. KR analyzed the data and wrote the manuscript. All authors contributed to the article and approved the submitted version.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Brophy, J. E., and Good, T. L. (1970). Teachers’ communication of differential expectations for children’s classroom performance: some behavioral data. J. Educ. Psychol. 61, 365–374. doi: 10.1037/h0029908
Brunner, M., Krauss, S., and Kunter, M. (2008). Sex differences in mathematics: does the story need to be rewritten? Intelligence 36, 403–421. doi: 10.1016/j.intell.2007.11.002
Chamorro-Premuzic, T., Harlaar, N., Greven, C. U., and Plomin, R. (2010). More than just IQ: A longitudinal examination of self-perceived abilities as predictors of academic performance in a large sample of UK twins. Intelligence 38, 385–392. doi: 10.1016/j.intell.2010.05.002
Dickhäuser, O., and Stiensmeier-Pelster, J. (2003). Wahrgenommene lehrereinschätzungen und das fähigkeitsselbstkonzept von jungen und mädchen in der grundschule. [Perceptions of teacher evaluations and the academic self-concept of boys and girls in elementary school]. Psychol. Erzieh. Unterr. 50, 182–190.
Eccles, J. S., Adler, T. F., Futterman, R., Goff, S. B., Kaczala, C. M., Meece, J. L., et al. (1983). “Expectancies, values, and academic behaviors” in Achievement and achievement motivation. ed. J. T. Spence (San Francisco, CA: W. H. Freeman), 75–146.
Eccles, J. S., and Wigfield, A. (1995). In the mind of the actor: the structure of adolescents’ task values and expectancy-related beliefs. Personal. Soc. Psychol. Bull. 21, 215–225. doi: 10.1177/0146167295213003
Ehm, J. -H., Lindberg, S., and Hasselhorn, M. (2014). Reading, writing, and math self-concept in elementary school children: influence of dimensional comparison processes. Eur. J. Psychol. Educ. 29, 277–294. doi: 10.1007/s10212-013-0198-x
Else-Quest, N. M., Hyde, J. S., and Linn, M. C. (2010). Cross-national patterns of sex differences in mathematics: A meta-analysis. Psychol. Bull. 136, 103–127. doi: 10.1037/a0018053
Federal Statistical Office. (2023). Statistisches Bundesamt. Pressemitteilung N004 vom 23. Available at: https://www.destatis.de/DE/Presse/Pressemitteilungen/2023/01/PD23_N004_213.html. (Accessed January 2023).
Fennema, E., Peterson, P. L., Carpenter, T. P., and Lubinski, C. A. (1990). Teachers’ attributions and beliefs about girls, boys, and mathematics. Educ. Stud. Math. 21, 55–69. doi: 10.1007/BF00311015
Fischbach, A., Baudson, T. G., Preckel, F., Martin, R., and Brunner, M. (2013). Do teacher judgments of student intelligence predict life outcomes? Learn. Individ. Differ. 27, 109–119. doi: 10.1016/j.lindif.2013.07.004
Fredricks, J. A., and Eccles, J. S. (2002). Children’s competence and value beliefs from childhood through adolescence: growth trajectories in two male-sex-typed domains. Dev. Psychol. 38, 519–533. doi: 10.1037/0012-1649.38.4.519
Georgiou, S., Christou, C., Stavrinides, P., and Panaoura, G. (2002). Teacher attributions of student failure and teacher behavior toward the failing student. Psychol. Sch. 39, 583–595. doi: 10.1002/pits.10049
Guay, F., Marsh, H. W., and Boivin, M. (2003). Academic self-concept and academic achievement: developmental perspectives on their causal ordering. J. Educ. Psychol. 95, 124–136. doi: 10.1037/0022-0663.95.1.124
Gunderson, E. A., Ramirez, G., Levine, S. C., and Beilock, S. L. (2012). The role of parents and teachers in the development of gender-related math attitudes. Sex Roles 66, 153–166. doi: 10.1007/s11199-011-9996-2
Helmke, A., and van Aken, M. A. G. (1995). The causal ordering of academic achievement and self-concept of ability during elementary school: A longitudinal study. J. Educ. Psychol. 87, 624–637. doi: 10.1037/0022-0663.87.4.624
Herbert, J., and Stipek, D. (2005). The emergence of sex differences in children’s perceptions of their academic competence. J. Appl. Dev. Psychol. 26, 276–295. doi: 10.1016/j.appdev.2005.02.007
Heyder, A., Steinmayr, R., and Kessels, U. (2019). Do teachers’ beliefs about math aptitude and brilliance explain sex differences in children’s math ability self-concept? Front. Educ. 4, 1–11. doi: 10.3389/feduc.2019.00034
Hill, C., Corbett, C., and St Rose, A. (2010). Why so few? Women in science, technology, engineering, and mathematics. Washington, DC: AAUW.
Hoge, R. D., and Butcher, R. (1984). Analysis of teacher judgments of pupil achievement levels. J. Educ. Psychol. 76, 777–781. doi: 10.1037/0022-0663.76.5.777
Hu, L., and Bentler, P. M. (1999). Cutoff criteria for fit indexes in covariance structure analysis: conventional criteria versus new alternatives. Struct. Equ. Model. 6, 1–55. doi: 10.1080/10705519909540118
Hyde, J. S., Fennema, E., Ryan, M., Frost, L. A., and Hopp, C. (1990). Sex comparisons of mathematics attitudes and affect: A meta-analysis. Psychol. Women Q. 14, 299–324. doi: 10.1111/j.1471-6402.1990.tb00022.x
Jacobs, J. E., Lanza, S., Osgood, D. W., Eccles, J. S., and Wigfield, A. (2002). Changes in children's self-competence and values: sex and domain differences across grades one though twelve. Child Dev. 73, 509–527. doi: 10.1111/1467-8624.00421
Jussim, L., and Eccles, J. S. (1992). Teacher expectations II: construction and reflection of student achievement. J. Pers. Soc. Psychol. 63, 947–961. doi: 10.1037/0022-3514.63.6.947
Kuklinski, M. R., and Weinstein, R. S. (2001). Classroom and developmental differences in a path model of teacher expectancy effects. Child Dev. 72, 1554–1578. doi: 10.1111/1467-8624.00365
Lauermann, F., Chow, A., and Eccles, J. S. (2015). Differential effects of adolescents’ expectancy and value beliefs about math and english on math/science-related and human-services-related career plans. Int. J. Sci. Technol. Res. 7, 205–228.
Lauermann, F., Tsai, Y.-M., and Eccles, J. S. (2017). Math-related career aspirations and choices within eccles et al.’s expectancy–value theory of achievement-related behaviors. Dev. Psychol. 53, 1540–1559. doi: 10.1037/dev0000367
Lohbeck, A., and Möller, J. (2017). Social and dimensional comparison effects on math and reading self-concepts of elementary school children. Learn. Individ. Differ. 54, 73–81. doi: 10.1016/j.lindif.2017.01.013
Lorenz, G., Boda, Z., Salikutluk, Z., and Jansen, M. (2020). Social influence or social selection? Peer effects on the development of educational expectations among adolescents in Germany. Br. J. Sociol. Educ. 41, 643–669. doi: 10.1080/01425692.2020.1763163
Madon, S., Smith, A., Jussim, L., Russell, D. W., Eccles, J., Palumbo, P., et al. (2001). Am I as you see me or do you see me as I am? Self-fulfilling prophecies and self-verification. Personal. Soc. Psychol. Bull. 27, 1214–1224. doi: 10.1177/0146167201279013
Marsh, H. W. (1986). Verbal and math self-concepts: An internal/external frame of reference model. Am. J. Educ. Res. 23, 129–149. doi: 10.2307/1163048
Marsh, H. W., Abduljabbar, A. S., Parker, P. D., Morin, A. J. S., Abdelfattah, F., Nagengast, B., et al. (2015). The internal/external frame of reference model of self- concept and achievement relations: age-cohort and cross-cultural differences. Am. Educ. Res. J. 52, 168–202. doi: 10.3102/0002831214549453
Marsh, H. W., Dowson, M., Pietsch, J., and Walker, R. (2004). Why multicollinearity matters: A reexamination of relations between self-efficacy, self-concept, and achievement. J. Educ. Psychol. 96, 518–522. doi: 10.1037/0022-0663.96.3.518
Marsh, H. W., and Martin, A. J. (2011). Academic self-concept and academic achievement: relations and causal ordering. Br. J. Educ. Psychol. 81, 59–77. doi: 10.1348/000709910X503501
Marsh, H. W., Trautwein, U., Lüdtke, O., Köller, O., and Baumert, J. (2005). Academic self-concept, interest, grades, and standardized test scores: reciprocal effects models of causal ordering. Child Dev. 76, 397–416. doi: 10.1111/j.1467-8624.2005.00853.x
Marsh, H. W., and Yeung, A. S. (1998). Longitudinal structural equation models of academic self-concept and achievement: Gender differences in the development of math and English constructs. Am. Educ. Res. J. 35, 705–738. doi: 10.2307/1163464
Master, A., and Meltzoff, A. (2020). Cultural stereotypes and sense of belonging contribute to gender gaps in STEM. International journal of gender. Sci. Technol. 12, 152–198.
Master, A., and Meltzoff, A. N. (2020). Cultural stereotypes and sense of belonging contribute to gender gaps in stem. Int. J. Sci. Technol. Res. 12, 152–198. Retrieved from: https://genderandset.open.ac.uk/index.php/genderandset/article/view/674
Möller, J., Kuska, S. K., and Zaunbauer, A. (2011). “Einflussfaktoren auf die Entwicklung des Selbstkonzepts im Grundschulalter [Influencing factors of the development of self- concept during elementary school years]” in Selbstkonzepte im Grundschulalter. eds. F. Günther and F. Hellmich (Stuttgart: Kohlhammer), 159–172.
Möller, J., Pohlmann, B., Köller, O., and Marsh, H. W. (2009). A meta-analytic path analysis of the internal/external frame of reference model of academic achievement and academic self- concept. Rev. Educ. Res. 79, 1129–1167. doi: 10.3102/0034654309337522
Möller, J., Zitzmann, S., Helm, F., Machts, N., and Wolff, F. (2020). A Meta-analysis of relations between achievement and self-concept. Rev. Educ. Res. 90, 376–419. doi: 10.3102/0034654320919354
Mullis, I. V. S., Martin, M. O., Foy, P., and Hooper, M. (2016). TIMSS 2015 international results in mathematics. Boston, MA: TIMSS and PIRLS International Study Center.
Muthén, L. K., and Muthén, B. O. (1998/2013) Mplus version 7.11 [computer software]. Los Angeles, CA: Muthén & Muthén.
Natale, K., Viljaranta, J., Lerkkanen, M.-K., Poikkeus, A.-M., and Nurmi, J.-E. (2009). Cross! Lagged associations between kindergarten teachers’ causal attributions and children’s task motivation and performance in reading. Educ. Psychol. 29, 603–619. doi: 10.1080/01443410903165912
National Science Board. (2018). Science and Engineering indicators. Available at: https://nsf.gov/statistics/2018/nsb20181/assets/nsb20181.pdf
Reilly, D., Neumann, D. L., and Andrews, G. (2015). Sex differences in mathematics and science achievement: A meta-analysis of national assessment of educational progress assessments. J. Educ. Psychol. 107, 645–662. doi: 10.1037/edu0000012
Robinson-Cimpian, J. P., Lubienski, S. T., Ganley, C. M., and Copur-Gencturk, Y. (2014). Teachers’ perceptions of students’ mathematics proficiency may exacerbate early sex gaps in achievement. Dev. Psychol. 50, 1262–1281. doi: 10.1037/a0035073
Schafer, J. L., and Graham, J. W. (2002). Missing data: our view of the state of the art. Psychol. Methods 7, 147–177. doi: 10.1037//1082-989X.7.2.147
Shavelson, R. J., Hubner, J. J., and Stanton, G. C. (1976). Self-concept: validation of construct interpretations. Rev. Educ. Res. 46, 407–441. doi: 10.3102/00346543046003407
Skaalvik, E. M., and Valås, H. (1999). Relations among achievement, self-concept and motivation in mathematics and language arts: A longitudinal study. J. Exp. Educ. 67, 135–149. doi: 10.1080/00220979909598349
Snow, R. E. (1992). Aptitude theory: yesterday, today, and tomorrow. Educ. Psychol. 27, 5–32. doi: 10.1207/s15326985ep2701_3
Spinath, B., and Spinath, F. M. (2005a). Development of self-perceived ability in elementary school: the role of parents' perceptions, teacher evaluations, and intelligence. Cogn. Dev. 20, 190–204. doi: 10.1016/j.cogdev.2005.01.001
Spinath, B., and Spinath, F. M. (2005b). Longitudinal analysis of the link between learning motivation and competence beliefs among elementary school children. Learn. Instr. 15, 87–102. doi: 10.1016/j.learninstruc.2005.04.008
Steinmayr, R., and Spinath, B. (2008). Sex differences in school achievement: what are the roles of personality and achievement motivation? Eur. J. Personal. 22, 185–209. doi: 10.1002/per.676
Steinmayr, R., Weidinger, A. F., Heyder, A., and Bergold, S. (2019). Warum schätzen Mädchen ihre mathematischen Kompetenzen geringer ein als Jungen? Z. Entwicklungspsychol. Pädagog. Psychol. 51, 71–83. doi: 10.1026/0049-8637/a000213
Stemler, S. E., and Sternberg, R. J. (2013). “The assessment of aptitude” in APA handbook of testing and assessment in psychology. Testing and assessment in school psychology and education: Vol. 3. eds. K. F. Geisinger, B. A. Bracken, J. F. Carlson, J.-I. C. Hansen, N. R. Kuncel, and S. P. Reise (Washington, DC: American Psychological Association), 281–296.
Stipek, D. J., Givvin, K. B., Salmon, J. M., and MacGyvers, V. L. (2001). Teachers’ beliefs and practices related to mathematics instruction. Teach. Teach. Educ. 17, 213–226. doi: 10.1016/S0742-051X(00)00052-4
Tiedemann, J. (2000). Sex-related beliefs of teachers in elementary school mathematics. Educ. Stud. Math. 41, 191–207. doi: 10.1023/A:1003953801526
Ullman, J. B. (2007). “Structural equation modeling” in Using multivariate statistics. eds. B. G. Tabachnick and L. S. Fidell, vol. 5 (Boston, MA: Allyn & Bacon/Pearson Education), 676–780.
Upadyaya, K., and Eccles, J. (2015). Do teachers’ perceptions of children’s math and reading related ability and effort predict children’s self-concept of ability in math and reading? Educ. Psychol. 35, 110–127. doi: 10.1080/01443410.2014.915927
Valentine, J. C., DuBois, D. L., and Cooper, H. (2004). The relation between self-beliefs and academic achievement: a meta-analytic review. Educ. Psychol. 39, 111–133. doi: 10.1207/s15326985ep3902_3
Viljaranta, J., Tolvanen, A., Aunola, K., and Nurmi, J.-E. (2014). The developmental dynamics between interest, self-concept of ability, and academic performance. Scand. J. Educ. Res. 58, 734–756. doi: 10.1080/00313831.2014.904419
Voyer, D., and Voyer, S. D. (2014). Gender differences in scholastic achievement: a meta-analysis. Psychol. Bull. 140, 1174–1204. doi: 10.1037/a0036620
Wach, F. S., Spengler, M., Gottschling, J., and Spinath, F. M. (2015). Sex differences in secondary school achievement - the contribution of self-perceived abilities and fear of failure. Learn. Instr. 36, 104–112. doi: 10.1016/j.learninstruc.2015.01.005
Weidinger, A. F., Steinmayr, R., and Spinath, B. (2018). Changes in the relation between competence beliefs and achievement in math across elementary school years. Child Dev. 89, e138–e156. doi: 10.1111/cdev.12806
Wigfield, A., Eccles, J. S., Yoon, K. S., Harold, R. D., Arbreton, A. J. A., Freedman- Doan, C., et al. (1997). Change in children’s competence beliefs and subjective task values across the elementary school years: A 3-year study. J. Educ. Psychol. 89, 451–469. doi: 10.1037/0022-0663.89.3.451
Wilgenbusch, T., and Merrell, K. W. (1999). Sex differences in self-concept among children and adolescents: a meta-analysis of multidimensional studies. Sch. Psychol. Q. 14, 101–120. doi: 10.1037/h0089000
Wolff, F. (2021). How classmates’ gender stereotypes affect students’ math self-concepts: A multilevel analysis. Front. Psychol. 12:599199. doi: 10.3389/fpsyg.2021.599199
Keywords: academic self-concept, gender differences, teachers’ judgments, math, elementary school
Citation: Reschke K, Steinmayr R and Spinath B (2023) Predicting students’ math self-concepts to explain gender differences through teachers’ judgments and students’ perceived teachers’ judgments. Front. Educ. 8:1096148. doi: 10.3389/feduc.2023.1096148
Edited by:
Yiming Cao, Beijing Normal University, ChinaReviewed by:
Xiang Hu, Renmin University of China, ChinaKatja Upadyaya, University of Helsinki, Finland
Copyright © 2023 Reschke, Steinmayr and Spinath. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Katharina Reschke, UmVzY2hrZUBpYncudW5pLWhlaWRlbGJlcmcuZGU=