- Department of Mathematics Education, IPN–Leibniz Institute for Science and Mathematics Education, Kiel, Germany
Mathematics is applied in a broad range of academic disciplines and thus takes on a paramount role for college access. However, students often take for granted the necessity of mathematics for STEM subjects but are unaware of or insufficiently informed about the role of mathematics for subjects outside of STEM. In fact, there is no in-depth empirical investigation on which mathematical prerequisites are expected by university instructors from incoming non-STEM undergraduates. The present paper addresses this research gap. We conducted a three-round Delphi study with N = 19/547/337 university instructors in Germany teaching undergraduates in non-STEM programs. Our results show that many more subjects require mathematical knowledge than is commonly assumed. We present a comprehensive catalogue of mathematical prerequisites that students are expected to have at the beginning of their studies. The prerequisites include (1) mathematical content, (2) mathematical processes, (3) views about the nature of mathematics, and (4) personal characteristics. The expected mathematical prerequisites primarily address a basic understanding and do not require formalistic or abstract mathematical knowledge and skills. The Delphi study also revealed five subject groups in which similar mathematical prerequisites are expected. Although the study’s focus is on German instructors, it provides valuable insights for an international audience as well. For example, future research can use our results to adapt instruments to explore predictors of college success. In addition, our results inform stakeholders involved in the transition from high school to college and in college education, such as teachers preparing their students for future study, college instructors making their expectations transparent to incoming students, and policymakers involved in curriculum design.
1. Introduction
The aspects that are included in mathematical education are shaped by social expectations and general social change. For example, the so-called “New Math” curricula, first in the United States and then in Western Europe, emphasized in-depth and abstract mathematical aspects in response to the Sputnik shock; in the 1970s, there was a turn toward much more basic mathematics; and in the 1980s, mathematics education focused on problem solving (e.g., Schoenfeld, 2004; Steen, 2006). With regard to the important role of mathematics in the transition from high school to college, the debate about what aspects should be included in mathematics instruction is ongoing. In college, mathematics takes on a gatekeeper role: Enrolment in middle and high school mathematics classes affects college attendance (Atanda, 1999; Byun et al., 2015; Douglas and Attewell, 2017) and mathematics performance restricts access to sought-after majors (Douglas and Attewell, 2017). The gatekeeper role is accentuated given that nearly 70% of BA/BS graduates acquire credits in statistics and applied mathematics (Douglas and Salzman, 2020) and about 60 % (resp. 33%) of college freshmen taking remedial mathematics courses at 2 year (resp. 4 year) institutions and only 50 % (resp. 58%) passing them (Chen, 2016). As a consequence, American College Testing [ACT] (2008) called for “Non-negotiable Knowledge and Skills for Eighth-Grade Students to Be on Target for College and Career Readiness”–including mathematics including basic operations, statistics, concepts and properties of numbers, equations and inequalities, graphical representations, plane figures, and measurement (p. 32f).
Indeed, mathematics is employed by a variety of academic disciplines inside and outside of mathematics departments (Steen, 2001; Mulhern and Wylie, 2006; Alcock et al., 2008; Grcar, 2011; Laging and Voßkamp, 2017), so its paramount role in college access does not come as a surprise. However, some scholars question whether the same mathematics education is fitting for all majors (Steen, 2006; Bryk and Treisman, 2010; National Center on Education and the Economy, 2013; Logue, 2016) and suggest curricula which highlight the use of mathematics by a multiplicity of disciplines (The Mathematical Association of America [MAA], 2004; Saxe and Braddy, 2015; Parker et al., 2018; Transforming Postsecondary Education - Math, 2018). Put bluntly: “The math pathway for students pursuing majors in the math-oriented disciplines is well established [i.e., from algebra to calculus],” but “many students in the social sciences, arts, and humanities, and those seeking careers in business, applied technologies, health sciences, and other fields, could be served just as well by another pathway” (Bryk and Treisman, 2010, no page). As a consequence, Grcar (2011) calls also for the involvement of university instructors who teach outside of mathematics departments in informing mathematics education: “their view of the mathematics skills needed by university students would appear to be relevant to K-12 education” (p. 712).
The role of mathematics at the transition from high school to university in Germany is the same and yet different. The high school graduation certificate “Abitur” officially attests all graduates a general readiness to study and allows them to take basically every major at a German university. To earn the Abitur, students usually have to pass 12 or 13 years of schooling, with the last 2 years characterized by a relatively great freedom in choosing classes. However, mathematics (in addition to German as native language) is compulsory from first grade throughout high school. High school graduates have thus been taught at least the fundamentals of calculus, linear algebra and statistics. Unlike in the U.S., there are no general entrance tests for college admission nor placement tests and remedial courses. Nevertheless, students often struggle with mathematics in tertiary education. Students in science, technology, engineering, and mathematics (STEM) programs, unsurprisingly, are confronted with mathematics-related challenges (Heublein et al., 2010; Dieter, 2012), yet students enrolled in disciplines outside of STEM also feel unprepared with respect to mathematics (Heublein et al., 2010; Scheller et al., 2013). Heublein et al. (2010) surveyed both students graduating from university studies as well as drop-outs. They found that up to one third of college drop-outs outside STEM assess their mathematical prior knowledge as insufficient. These numbers illustrate that mathematics takes a crucial role in college dropout and success in Germany as well, and - given that dropout typically occurs early - that mathematics is of particular importance at the transition from high school to university. Moreover, these numbers moreover highlight the importance of mathematics not only for taking up a study in the STEM disciplines, but especially also outside of the STEM field.
The importance of mathematics, however, is often hard to grasp. Although mathematics has already gained and continues to gain increasing significance in several disciplines, it is mostly invisible to non-experts - a phenomenon labeled as “relevance paradox” (Niss, 1994). Through the lens of the relevance paradox, the above numbers of students feeling unprepared for their studies might also indicate that a substantive number of students, while still in high-school, is unaware of the role of mathematics for their sought-after majors, and therefore, might possibly put too little effort in mathematics. Indeed, a discrepancy between expectations of high school graduates and what they encounter in their first years at college is observed in the U.S. as well (Venezia et al., 2004).
In sum, mathematics holds an important role in the transition from high school to mathematics, both in countries employing college entrance testing (such as the U.S.) and in countries which do not (such as Germany). It is therefore indispensable for high school students to become aware of this preeminent role of mathematics, and hence, that school mathematics education also reflects this. Given that mathematics is crucial for disciplines inside and outside STEM, school mathematics education must not only address mathematics’ relevance for studying a major inside STEM subjects, but outside STEM as well. In order to adequately convey the mathematics-related prerequisites needed for a sought-after major, it is therefore necessary to know what university instructors expect from their undergraduates, both inside and outside STEM. So far, however, mathematics at the transition from high school to university is mainly informed from the perspective of STEM majors (Schoenfeld, 2004; Steen, 2006; Xia and Watanabe, 2017; Deeken et al., 2020). The present study therefore aims at elucidating: Which mathematical prerequisites do university instructors outside STEM expect their new undergraduates to bring from school?
2. Methodology
To approach the above research question, we conducted a three round Delphi study. In Delphi studies, expert interviews are conducted iteratively and participants receive feedback after each survey round (Linstone and Turoff, 1975). A major advantage of the Delphi technique is that it reduces bias due to social pressure within the expert group (Rowe et al., 1991).
2.1. Instrument
In order to increase the willingness to participate and to reduce sample mortality, we utilized a list of given mathematical aspects to be rated by university instructors regarding their relevance as prerequisites expected from freshmen. To this end, the present study built on and extended previous work of Deeken et al. (2020), who had already identified university instructors’ expectations on mathematical prerequisites inside STEM. Deeken et al. (2020) identified 179 mathematical prerequisites addressing mathematical content (e.g., basic algebraic rules; domain and range of functions; relation between function and derived curve; vectors represented as arrows), mathematical processes (e.g., handling of standard mathematical notations and representations; plausibility checks; mathematical modeling), views about the nature of mathematics (understanding characteristics of mathematics as a scientific discipline, e.g., that proving is central to mathematical endeavor), and personal characteristics (e.g., frustration tolerance; diligence, and willingness to engage in mathematics). This catalog of prerequisites from Deeken et al. (2020) was taken as a starting point as we assumed that expectations outside STEM generally do not to extend beyond those inside STEM. Yet, we also assumed prerequisites regarding stochastics and statistics to be more differentiated outside than inside STEM, so we refined the aspects on stochastics based on current national educational standards in Germany (KMK, 2012) (Supplementary Table 1). As a result, the instrument employed in the present study included 188 prerequisites (Supplementary Table 2). Additionally, the instrument included open text boxes for participants to raise any concerns about the given aspects, to vote for additional aspects or to suggest refinements, to rule out influences due to the given list of aspects.
2.2. Sample
In order to explore the expected mathematical prerequisites for new undergraduates in the majors outside STEM, we invited university instructors who lecture classes involving mathematical content early on in the respective degrees. We assumed the sample would be responsible for the implemented curricula and its requirements, possess the necessary mathematical knowledge and skills, and be knowledgeable of mathematics related challenges students might face at university. To recruit this sample, we followed a two-step procedure.
First, we identified subjects outside STEM that require knowledge of school mathematics and for which new undergraduates therefore would be expected to bring mathematical prerequisites. As a starting point, based on information from the Federal Statistical Office (Destatis, 2018) and the German University Rectors’ Conference (Hochschulkompass, 2021), we compiled a list of all possible subjects to be studied in dual, training-integrated, vocational/practice-integrated, full-time, and part-time Bachelor degree courses at any public higher education institution in Germany.1 From this list, we excluded those subjects (e.g., biology, mathematics, and engineering), that had already been included in the previous study by Deeken et al. (2020). For the remaining subjects, we then researched course and class descriptions, and information available online and assessed whether the subjects include mathematical content beyond the very basics (that is, mathematics taught below grade 6) or not. Based on this assessment, we excluded degree courses, (a) which required no more than a basic mathematical literacy (e.g., German language and literature studies), or (b) which were interdisciplinary courses (in this case, we referred to the respective disciplinary courses; for example, economic law was referred to economics). The resulting list comprised 69 subjects to be included in the present Delphi study, comprising, for example, library science, pedagogy, home economics, medicine, and economics (Supplementary Table 3 for the full list of included subjects). These 69 subjects represented a total of 851 degree courses.
As a second step, we researched contact information of university instructors representing these subjects to be invited as experts in our Delphi study. To this end, we assigned degree courses offered by public higher education institutions to the 69 subjects identified. Some subjects (e.g., economics) were represented by a much higher number of degree courses offered in German institution than others (e.g., landscape architecture). We therefore selected at least 20 % of the identified degree courses, but did not include more than 25 degree courses (starting with institutions with the highest numbers of students and descending). We then identified classes addressing mathematical content in these degree courses. For courses including pure mathematics classes (e.g., mathematics for economists or statistics for psychologists), we selected these, for courses without designated mathematics classes, we selected the first two classes in the degree program, which according to the class descriptions include mathematical contents and must be taken up to the 6th semester (e.g., research methodologies in the social sciences or construction technology). If there were three or more in the first two semesters, these were used. We finally researched online the contact details of university instructors teaching the selected classes between 2015 and 2019 (i.e., the last 5 years when we started the sample selection in fall 2019). As a result, our expert sample included 1953 university instructors at 164 different institutions all over Germany (from a total of 356 German universities, excluding Theological Colleges and Universities of Fine Arts and Design; Statista, 2022).
2.3. Delphi study
2.3.1. Delphi round 1
As described above, a list of 188 mathematical aspects was used as a starting point for the current Delphi study, which had been identified in a previous study on prerequisites for taking up a STEM degree course and refined for stochastics. Literature showed, however, that outside STEM, mathematical prerequisites might be not as comprehensive as inside STEM, for example, less focused on calculus or abstract mathematical ideas (e.g., Steen, 2006; Bryk and Treisman, 2010; National Center on Education and the Economy, 2013). The first Delphi round therefore served to explore (a) if the instrument is appropriate for investigating the expectations of university instructors outside STEM as well, and (b) how diverse university instructors’ expectations are and if there possibly might be a consensus across so many different disciplines.
As we did not want to overburden the full sample by a too large instrument (and risk reduced willingness to participate at all), we decided to explore the above questions in only a small subsample. To this end, we selected 51 instructors (out of the 1953 identified) with a particular responsibility and experience in higher education teaching to be invited in the first round. Selected instructors thus held the position of the responsible contact for the mathematics-containing module(s) of the study program, or had many years of teaching experience in this area. The instructors covered a broad variety of subjects, federal states, and types of higher education institution, as well as degree courses with presumably differing mathematical content (e.g., mathematics for economists, statistics, statics, and stability theory, etc.). In addition, degree courses with the highest enrolment rates were represented by a larger number of instructors.
N1 = 19 university instructors participated, and rated on a three-level scale (not necessary; rather necessary; absolutely necessary) the extent to which the given mathematical aspects are necessary to successfully begin a degree course they are teaching. As we were not interested in the participants’ responses as an expression of their personal traits but rather in their expert view on the different subjects, we assigned the degree courses they were teaching to one of the subjects included in our list of 69 subjects. We then explored the data with respect to similar response patterns across different subjects. In case of ambiguity, we also drew on course and class descriptions.
We found that basically all prerequisites of the categories mathematical processes, views about the nature of mathematics and personal characteristics were rated as necessary across all subjects. Differences, and thus subject-specific patterns, however, were found with respect to mathematical content aspects. We identified three subject groups, each group demanding similar mathematical content aspects. One group included subjects, such as architecture or facility management, and was characterized by prerequisites spanning across all mathematical content areas similar to the prerequisites found necessary for the STEM subjects (we denoted this group as engineering-oriented subjects). Another group included economics, psychology and social sciences, and required less, but still substantive aspects of mathematical basics, stochastics, calculus, and linear algebra. The third group included subjects in the humanities, social sciences, and health sciences (e.g., pharmacy, social work, communication science/public relations) and was characterized by prerequisites on mathematical basics and stochastics.
2.3.2. Delphi round 2
The second round aimed at validating and refining the results in a larger sample of university instructors, so the whole sample of 1,953 instructors was invited. Based on the results of Delphi round 1, we compiled three different questionnaires corresponding to the three identified subject groups. Each participant was asked to indicate a subject he or she is teaching in and was assigned one of the three questionnaires, respectively. That is, each participant was assigned only those aspects which had been found to be rather necessary or absolutely necessary in the previous round. To avoid skewed and biased data, however, participants were able to optionally review the aspects rated as not necessary in round 1. The questionnaires additionally included open text boxes to be used for comments, adaptions, refinements, etc., (here, participants could also state aspects as important, which previously had been rated not necessary).
Again, participants were asked to rate in how far the given mathematical aspects are necessary to successfully begin a degree course they are teaching. In order to in fact assess university instructors’ expectations, we emphasized to not describe mathematical competencies currently observed among their students, but rather their expectations of the necessary minimum learning prerequisites that undergraduates should bring when transitioning from high school to university. Following the procedure of Deeken et al. (2020) for STEM subjects, participating instructors rated the aspects on mathematical content, mathematical processes, and views about the nature of mathematics using a three-point scale (not necessary; Level 1; Level 2) and on personal characteristics using a four-point Likert scale (unimportant; rather unimportant; rather important; important). Regarding mathematical content, Level 1 addressed basic knowledge of mathematical content aspects, algorithms or routines, and Level 2 addressed flexible and integrated knowledge (Deeken et al., 2020). Mathematical processes on Level 1 referred to routines, which can be reproduced in familiar situations and applied to unfamiliar situations involving simple middle school mathematics content, and on Level 2 to routines, which can additionally be performed in unfamiliar situations involving high school mathematics content. Regarding views about the nature of mathematics Level 1 referred to an abstract meta-knowledge (i.e., the learners have been told this information), and Level 2 to own experiences (i.e., by observing, reflecting or performing a mathematical activity). A detailed Level description is provided in the Supplementary Table 4.
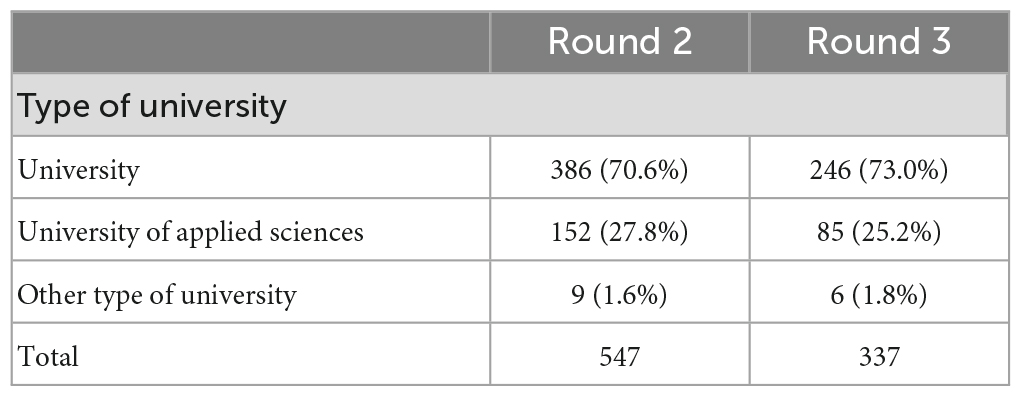
From all responding university instructors, we included those who provided valid responses on at least 25% of the given mathematical learning prerequisites to rate. As a result, 547 cases were analyzed (Table 1). About 84% of the university instructors reported having proficient teaching experience (i.e., that they had taught a course with mathematics content at least five times). See Supplementary Table 5 for a detailed sample description.
2.3.2.1. Data analysis and results of Delphi round 2
For data analysis, again, we were interested in investigating which subjects require similar mathematical prerequisites. We therefore assigned each participating university instructor to one of the 69 subjects identified, based on the classes (resp. degree courses) they had indicated to teach. For each subject, we then determined, if there is a consensus on a particular mathematical prerequisite. The consensus criteria went beyond a simple majority criterion:
- A prerequisite was considered necessary if 2/3 of all respondents in a subject considered the prerequisite necessary.
- A prerequisite was considered not necessary if 3/4 of all respondents in a subject considered the prerequisite not necessary.
- If less than 2/3 but more than 1/4 of the respondents in a subject considered a prerequisite necessary, we recorded no consensus on this prerequisite.
We decided for a 2/3 threshold, as this is a widely used criterion for the assessment of majorities (e.g., in the political context of constitutional amendments). The criterion for aspects to be considered not necessary should be even more restrictive. Labeling a learning prerequisite as not necessary for a particular study program would have greater consequences; it is less problematic if students bring along a mathematical learning prerequisite but do not need it than vice versa.
If new mathematical aspects were named by the respondents in the open text boxes, only those mentioned by at least three university teachers were included. We chose this criterion to adequately consider new aspects but not to draw heavily on individual opinions. Although some comments were made, no mentioned aspect met this criterion.
Additionally, sixty-six participants (12,1 %) rated the optionally given whole set of learning prerequisites [Group 1: 1 (2,4 %); Group 2: 24 (11,9 %); Group 3: 22 (23,5 %); Group 4: 16 (12,6 %); and Group 5: 3 (4,8 %)]. Results showed, that only a few learning prerequisites, which had been flagged as not necessary after round 1, were regarded as necessary by few instructors of specific subjects. We therefore listed them as potentially necessary for the respective subject, but not for the whole subject group in the final results.
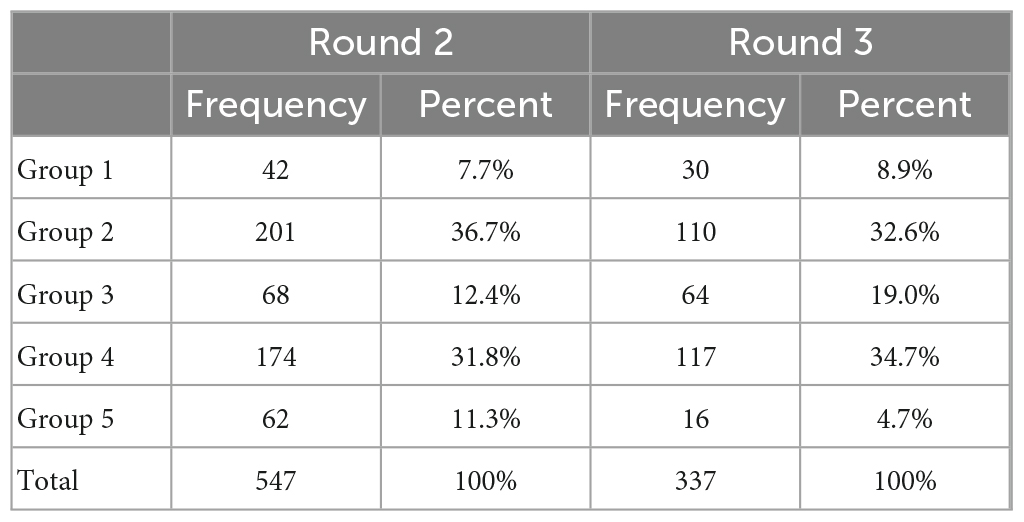
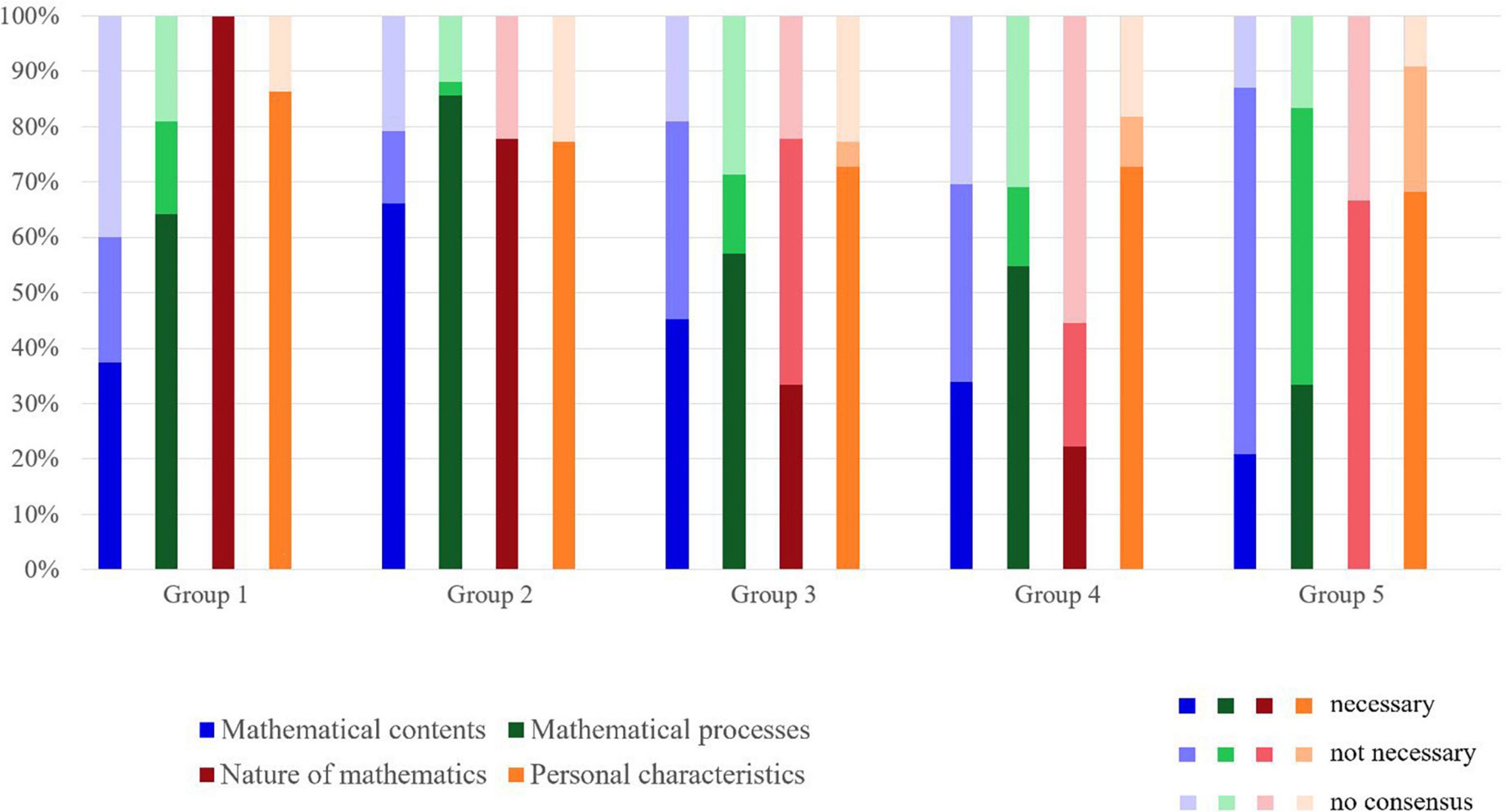
After assigning each prerequisite in each subject one of the three tags “necessary,” “not necessary” or “no consensus” (based on the above criteria), we conducted a cluster analysis (linkage between the groups, squared Euclidean distance; see Supplementary Table 6 for details). As a result, we had to refine the preliminary three subject groups from the first Delphi round into five groups (Table 2). Again, group 1 contained engineering-oriented subjects and the expected learning prerequisites mainly focused on mathematical basics and covered a broad range of mathematical processes. This group had the lowest requirements regarding stochastics/statistics but the highest regarding geometry. Group 2 included economics and psychology. Expected learning prerequisites were most extensive compared to the other groups and were closest to the expectations for the STEM studies (such as physics or mechanical engineering). Expectations regarding stochastics/statistics were even higher than for the STEM studies. Group 3 contained subjects close to the natural sciences (such as medicine, or nutritional science). Here, requirements focused on mathematical basics and stochastics/statistics. Group 4 spanned across documentation, educational, health, media, social and sports science, and required similar prerequisites as the group 2 subjects, though less extensive. Group 5 included social work, communication and administrative science and was characterized by the overall lowest level of mathematical requirements compared to the other groups. Some mathematical basics were expected as well as a substantive number of aspects on stochastics/statistics. Interestingly, all groups but group 5 required an understanding of adequate views on the nature of mathematics. Additionally, personal characteristics related to the learning of mathematics (such as frustration tolerance or openness toward mathematics in higher education) were expected by all subject groups.
Overall, that is based on all 547 participating instructors for all subjects, the consensus on which learning prerequisites are necessary for undergraduates to bring from high school, was quite low (18%). However, within each of the five groups, the consensus rate was substantially higher (Group 1: 46 %; Group 2: 71 %; Group 3: 59 %; Group 4: 56 %; and Group 5: 54 %). We considered this result as another indicator of a meaningful grouping of subjects.
2.3.3. Delphi round 3
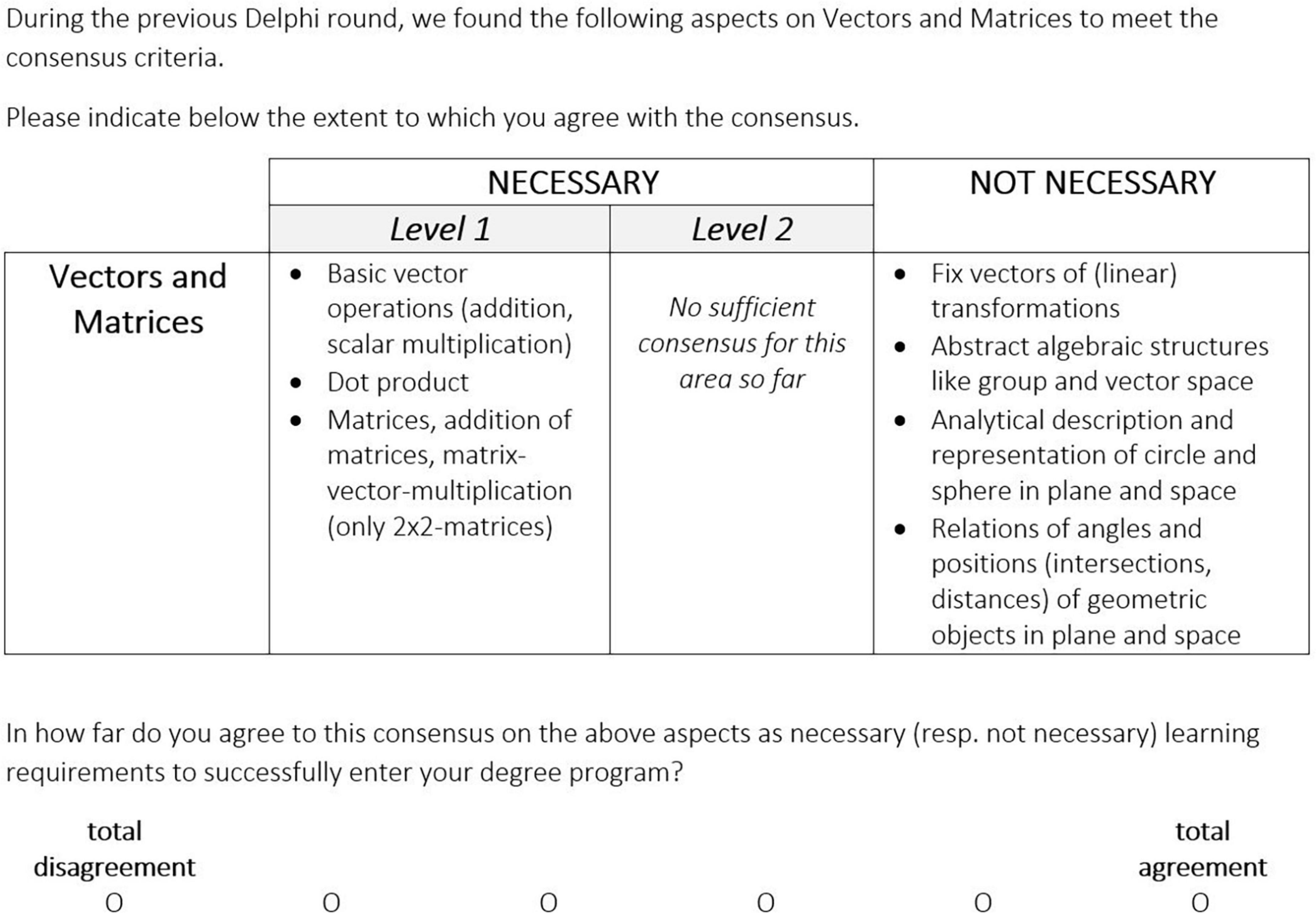
Delphi round 3 aimed to validate and consolidate the findings of round 2. To this end, we fed back the results of round 2 to the experts again. This time, we employed five questionnaires, one for each of the five subject groups identified in round 2, the structure of the questionnaires, however, was the same across groups. For learning prerequisites that already met the criteria for consensus in round 2 we asked for a final confirmation (6-point Likert scale: 1 = “total disagreement” to 6 = “total agreement”). Note that this meant to confirm both, that some learning prerequisites are necessary (at the respective level) and others are not (Figure 1).
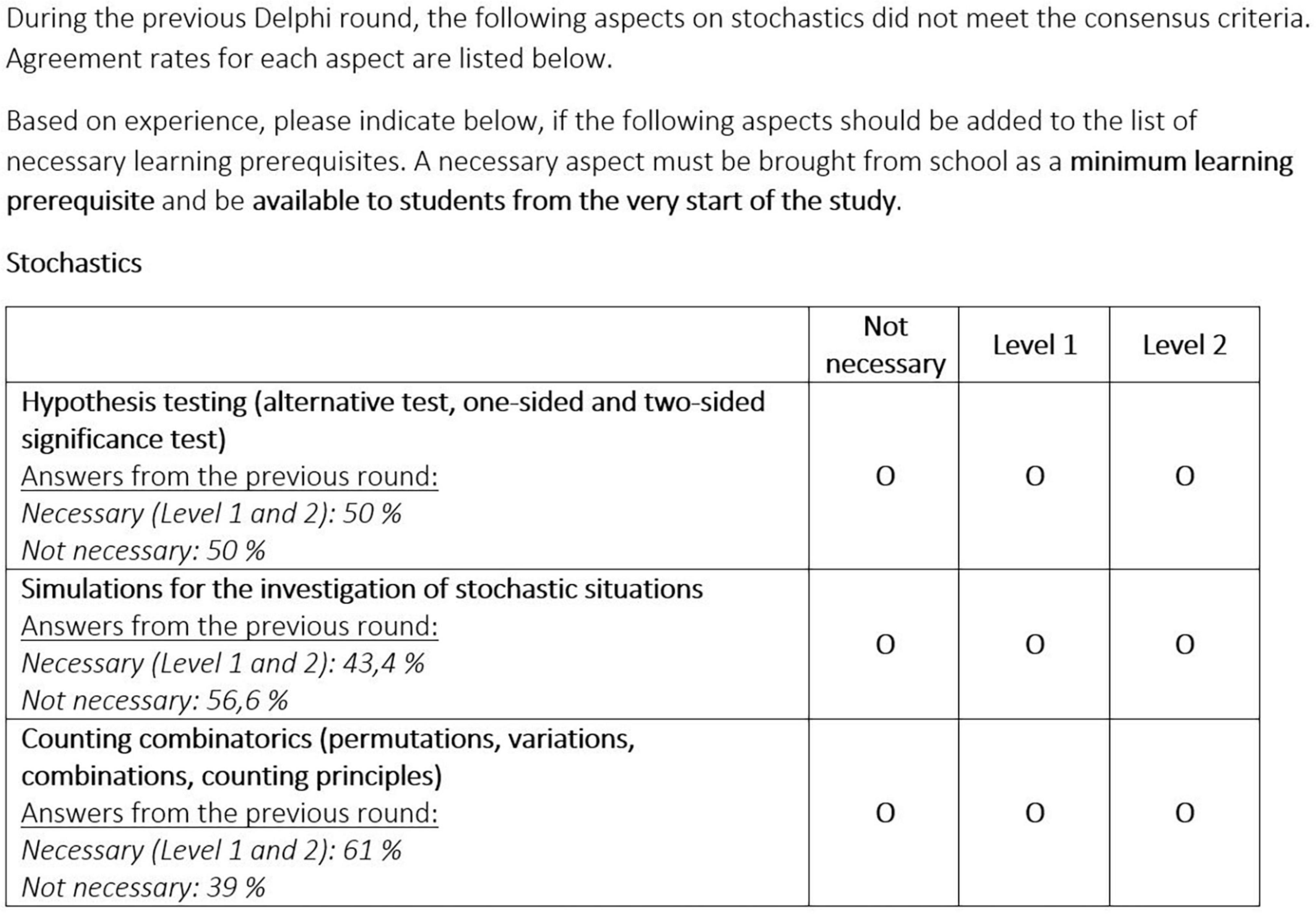
For learning prerequisites without consensus in round 2 we provided the participants with the summarized results from round 2 and asked for a new rating (Figure 2). As in round 2 we used a three-point scale for mathematical contents, mathematical processes, and views about the nature of mathematics (not necessary, necessary at Level 1 or Level 2) and a four-point scale for personal characteristics (unimportant; rather unimportant; rather important; important). Like in round 2, the round 3 questionnaires gave the opportunity to all five groups to review all learning prerequisites which were initially identified for the instrument in round 1, so that each university instructor could also consider the prerequisites outside their own group. Again, they were provided with open text boxes to indicate their concerns, make refinements or add further aspects they regarded necessary.
Note that we invited a slightly reduced sample of 1,766 university instructors to participate in this round as some experts invited to the second round were not reached or had indicated that they did not wish to participate in the study. Based on the subjects they were teaching the university instructors were assigned one of the five groups and thus one of the five questionnaires. Some university instructors viewed their expertise in another subject than the previously assigned one, so they were moved to the subject of their expertise. For the analysis, we only included those participants who provided valid responses on at least 25 learning prerequisites. As a result, 337 data sets were analyzed (Table 1). Table 3 displays a juxtaposition of participants for each of the five groups in Delphi round 2 and 3. The samples in round 2 and 3 were similarly composed by the five groups. Within each group, the subjects were represented in a similar manner across the two Delphi rounds, as well. Moreover, concerning university type and teaching experience, the round 3 sample was comparable to the round 2 sample (Table 1). See Supplementary Table 7 for a detailed sample composition by study area.
2.3.3.1. Data analysis and results of Delphi round 3
Data analysis aimed at investigating (a) in how far there was consensus on learning prerequisites which had not met the criteria in round 2, and (b) in how far the consensus on already agreed on learning prerequisites was stable across Delphi rounds. In order to investigate consensus on previously unclear learning prerequisites so far unclear (a), we applied the round 2 criteria to the subject groups:
- A prerequisite was considered necessary if 2/3 of all respondents in a subject group considered the prerequisite necessary.
- A prerequisite was considered not necessary if 3/4 of all respondents in a subject group considered the prerequisite not necessary.
- If less than 2/3 but more than 1/4 of the respondents in a subject group considered a prerequisite necessary, we recorded no consensus on this prerequisite.
Following this procedure, we found a substantial amount of learning prerequisites which had not met the criteria in round 2 to now meet the criteria for consensus (Group 1: 44; Group 2: 18; Group 3: 36; Group 4: 26; and Group 5: 59). For most of these prerequisites, the trend found in round 2 was consolidated in round 3 (i.e., a learning prerequisite, which was regarded necessary by the majority of instructors, but did not meet the 2/3 criterion in round 2, now met the 2/3 criterion). In only three cases, the trend changed: The math prerequisite did not appear to be necessary after round 2. Thus, the majority of participants in the subject group in question indicated that this mathematical learning prerequisite was not necessary. However, they now met the 2/3 criterion for necessary mathematical learning prerequisites (Group 1: 2; Group 5: 1).
In order to investigate the stability of consensus from round 2, (b) we analyzed the mean agreement on the given 6-point Likert scale (with agreement defined as a rating of 4–6). Within all five groups, the agreement rates were quite high–92.5% (Group 1), 93.2% (Group 2), 94.1% (Group 3), 88.6% (Group 4) and 92.4% (Group 5)–indicating a good stability of the round 2 results.
Finally, we analyzed the university instructors’ comments, refinements and additions given in the open text boxes. Again, we only included comments, refinements or additions made by at least three participants per subject group to not skew the data. We did not find learning prerequisites deemed necessary by instructors of multiple fields within the groups. However, single prerequisites (Group 2: 1 prerequisite; Group 3: 5 prerequisites) were marked necessary by instructors of one specific subject (e.g., medicine). As a consequence, we did not index them necessary for the whole group, but indexed them as necessary for the respective single subject.
3. Results
The overall aim of the present Delphi study was to clarify the question: Which mathematical prerequisites do university instructors outside STEM expect their new undergraduates to bring from school? Over the three Delphi rounds, we found university instructors’ expectations being very diverse across all the different subjects outside STEM, but quite coherent within the five subject groups listed in Table 2. We will therefore present the results in two steps. First, we give a summary of those learning prerequisites for which we found consensus among the whole sample of university instructors. Then, we present the specifics of the five identified subject groups. Given the magnitude of our results, we provide agreement rates on each of the 188 learning prerequisites in each of the five subject groups in the Online Resource 2, and, in this section, give an overview on trends and highlights.
3.1. Consensus across all subjects
Across all subjects, that is among all participating university instructors, consensus was found on 48 out of 188 learning prerequisites (26%). 41 prerequisites were found necessary, 7 were regarded not necessary (for a detailed listing see Online Resource 2). Among the necessary learning prerequisites, 13 addressed mathematical content with 12 of them focusing mathematical basics and one stochastics/statistics. 14 mathematical processes were agreed upon as necessary learning prerequisites, most of them addressing basics, but also control strategies, communication skills, problem solving and collecting information in mathematics text books, the internet or other sources. Another 14 personal characteristics were regarded necessary across all subject groups including openness toward mathematics as a scientific discipline and the way of learning mathematics at universities. The 7 learning prerequisites, which were viewed not necessary across all subject groups, addressed enhanced, abstract and formal aspects of mathematics. There was no overall consensus on views about the nature of mathematics, neither regarding them necessary nor not necessary.
3.2. Consensus within subject groups
Consensus within subject groups was deemed substantially higher (Group 1: 70%; Group 2: 81%; Group 3: 78%; Group 4: 70%; Group 5: 86%). Table 4 and Figure 3 show a result overview of round 3. This finding indicates, that, although there is no wide consensus across all the different subjects outside STEM, there are subjects sharing similar expected learning prerequisites.
Subject group 1 (engineering-related subjects such as architecture and landscape design) stands out, as here, university instructors expected aspects of Euclidian geometry as necessary learning prerequisites, whereas in all the other subject groups university instructors viewed these aspects either not necessary or did not reach agreement. Contrary, compared to the other subject groups, only little was expected regarding stochastics/statistics in group 1. Regarding mathematical processes, instructors of group 1 expected the second highest number of learning prerequisites (27 out of 42), including basic processes as well as more enhanced ones (such as explaining mathematical concepts based on their definition). Interestingly, instructors of this subject group expected all aspects regarding the nature of mathematics as an abstract meta-knowledge (in contrast to the other groups, in which only single or even no aspects are expected necessary). Also, instructors in this group expected the highest number of personal characteristics as necessary.
The most extensive expectations were expressed by university instructors on psychology and economics (i.e., group 2). Six prerequisites (e.g., linear and quadratic equations and functions) were considered necessary on an advanced level of understanding (i.e., Level 2). Only five mathematical processes were not agreed upon and only one was regarded not necessary (development and formulation of mathematical proofs to a given statement). Similar to group 1, university instructors of this group expected a broad view about the nature of mathematics as necessary as well as a wide range of personal characteristics. The requirements of group 2 clearly show that, in addition to comprehensive mathematical content knowledge, university instructors expect extensive mathematical competences from undergraduates that go beyond purely content-related aspects.
In subject group 3 (natural science-related subjects such as medicine or nutritional science) university instructors considered primarily aspects of mathematical basics and stochastics/statistics necessary. Most aspects of Euclidian geometry, linear algebra and analytical geometry were either regarded not necessary or did not meet the consensus criteria. In addition, group 3 instructors considered several aspects of calculus as necessary learning prerequisites, yet rather the less formal and intuitive aspects (e.g., a graphic understanding of continuity as a “solid line” and calculating differential and integral of real-valued functions was regarded necessary, whereas a concept of series as sequence of partial sums was not). Expected mathematical processes addressed mainly basic and less abstract and formalistic processes. Only three aspects of the nature of mathematics were regarded necessary (e.g., new undergraduates should view mathematics as the learning of precise and abstract thinking that goes beyond the straightforward application of standard methods to standard problems). Instructors of this group also expected a broad range of personal characteristics, but not those touching the abstract and formal nature of mathematics (e.g., the willingness to solve even challenging and abstract mathematical problems was regarded not necessary). Interestingly, the vast majority of group 3 instructors (82.3%) indicated that they were expecting school science knowledge.
Similar to group 3, university instructors of subject group 4 (including study subjects like documentation, educational, health, media, social, and sports science) primarily expected aspects of mathematical basics and stochastics/statistics. Nearly all aspects of Euclidian geometry, calculus, linear algebra, and analytical geometry were either regarded not necessary or did not meet the consensus criteria. Expected mathematical processes mainly addressed basic processes (such as the handling of basic mathematical representations) and rather the application of mathematics (e.g., solving extra-mathematical problems by means of mathematics) than more abstract and formalistic processes (e.g., understanding and evaluating given mathematical proofs was regarded not necessary). Only two aspects of the nature of mathematics were regarded necessary (e.g., new undergraduates should view mathematics as the learning of precise and abstract thinking that is much more than the straightforward application of standard methods to standard problems). Instructors of this group also expected a broad range of personal characteristics, but not those touching the abstract and formal nature of mathematics (e.g., the willingness to deduce new relations and formulae or to solve even challenging and abstract mathematical problems were regarded not necessary).
The overall least extensive expectations were expressed by instructors of group 5 (including social work, communication, and administrative science). A total of 108 out of 188 (57%) learning prerequisites were agreed on as not necessary. Necessary aspects of mathematical content addressed mathematical basics typically taught up to lower secondary as well as aspects of statistics/stochastics. Similarly, most of the mathematical processes were regarded not necessary or were not agreed upon, and those meeting the consensus criteria for necessary aspects addressed rather basic application processes (e.g., switching between standard representations, or estimating orders of magnitude). Group 5 stands out, as views on the nature of mathematics were either agreed on as not necessary (six aspects) or did not meet the consensus criteria (three aspects). Also, compared to the other groups, the lowest number of personal characteristics was regarded necessary.
4. Discussion
The present study aimed at investigating expectations university instructors outside STEM put on their new undergraduates with respect to mathematical learning prerequisites to be brought from school education. Based on the above results we can conclude the following three main findings.
First, there is a variety of subjects beyond STEM requiring mathematical knowledge and skills from incoming first-year undergraduates. This finding echoes the importance of mathematics to a broad (and growing) range of disciplines and contexts (as pointed out by, e.g., Niss, 1994; Steen, 2001; Grcar, 2011). This finding also impressively illustrates that it would be shortsighted to tailor mathematics education only for those students interested in taking up a STEM or STEM-intense major – both, with respect to secondary mathematics education and (remedial) undergraduate mathematics courses at colleges and universities. Likewise, the finding underscores the importance of (more) transparence on the part of colleges and universities. Obviously, many students lack information on the role of mathematics in the studies (e.g., Venezia et al., 2004), thus feel unprepared when entering college and university (e.g., Heublein et al., 2010; Scheller et al., 2013) and in fact lack mathematical knowledge and skills essential for the subject they wish to study (e.g., Mulhern and Wylie, 2006). Colleges and universities, as well as secondary teachers preparing future college/university students should therefore explicitly disclose that and which (school) mathematics is relevant for a broad range of degree courses at colleges and universities.
Second, university instructors generally expect different learning prerequisites for the different subjects, but there are five subject groups each sharing similar mathematical learning prerequisites. The expected requirements reflect the mathematical content aspects and procedures typically employed in the respective disciplines. For example, group 3 instructors expected incoming first-year undergraduates to have an understanding of probabilities, which is often needed in medical diagnostics (e.g., Gigerenzer et al., 2007), and group 1 instructors expected an understanding of geometry, which is foundational for architecture design (e.g., Verner and Maor, 2005). Likewise, group 2 instructors’ rather extensive expectations (including calculus) are in line with Alcock et al. (2008) finding a more comprehensive curriculum of secondary mathematics (including calculus) being predictive for students passing business courses. This group’s expectations also map mathematical aspects relevant to statistics in psychology (such as calculation or algebraic reasoning, Mulhern and Wylie, 2006). Overall, the expectations are less extensive compared to those expressed by STEM university instructors (see Deeken et al., 2020), yet one group (group 2: economics and psychology) shares a substantial number of expected mathematical prerequisites with those expected for the STEM studies. Other than in the STEM subjects, understanding stochastics/statistics seems more needed outside STEM as in four of the five groups instructors conveyed quite comprehensive understanding of respective concepts.
Third, there is consensus across all investigated subjects on 41 required mathematical learning prerequisites. These consensus prerequisites address standard lower secondary mathematical content aspects as well as fundamental mathematical processes and personal characteristics needed for the successful solving of mathematics-related exercises. This result shows, that there is consensus across all subjects, but at the same time, expectations also vary quite widely. Debates on what to target in school mathematics education, which are contrasting career paths inside vs. outside STEM (e.g., Schoenfeld, 2004; Steen, 2006), currently do not include such variance outside STEM as well. As school mathematics education cannot (and shall not) serve as a preparation for single, selected studies, it should thus rather provide students with a broad foundation of mathematics knowledge and skills and explicitly inform, that, how and which mathematical aspects are needed in a wide range of subjects and contexts (see Steen, 2001).
4.1. Limitations
As every empirical study, this study comes with limitations as well. Although we thoroughly selected subjects to be included in the study, we had to rely on publicly available information for the respective programs. If the information did not explicitly address mathematics or mathematical content aspects, the subject was not included. Our results may therefore only be interpreted for the subjects listed in the Online Resource 3. Furthermore, the study reflects the situation in Germany. Yet the need to view mathematics education from other than the STEM-related disciplines has been expressed also in other countries (e.g., Steen, 2001; Grcar, 2011) and one may assume that introductory courses (which have been the focus of this study) are rather canonical within many disciplines.
4.2. Implications
Despite the above limitations, the present study raises implications for both, future research and practice. So far, this study’s findings only reflect university instructors’ views on required mathematical learning prerequisites for studying a major outside STEM. We cannot conclude if secondary education provides high school graduates with these prerequisites, nor if having the prerequisites available is a warrant for successfully finishing the studies. Future research should thus investigate, which prerequisites are met by first-year undergraduates of the different subjects at the transition from high school to university. Additionally, studies are needed to explore, in how far the identified learning prerequisites are in fact predictive for study success. Given that recognizing the importance of mathematics is often restricted to the STEM studies (and thus, many underestimate its role for other disciplines), it is an open question, if students pursuing a major outside STEM are aware of the expectations the university instructors place on them. Also, it is unclear, in how far the mathematical aspects and processes expected by university instructors are addressed in school mathematics education beyond the standard, generally STEM-related, contexts.
With respect to educational practice, the present study helps to inform (high) school mathematics teachers. They may use the catalog of mathematical learning prerequisites expected in the different disciplines to develop teaching material, which addresses single mathematical aspects in contexts other than the standard ones. For example, derivatives could be applied in economics problems such as identifying short-run marginal costs from unit cost functions, additional to inner-mathematical problems or classical applications in physics (acceleration as the derivative of velocity). Implementing such material may help to illustrate the broad range of contexts, mathematics plays an important role in, and may promote the idea that mathematics is needed in other than the STEM subjects as well. Likewise, university instructors from the different disciplines could employ the catalog to make their expectations transparent to future students and to design respective introductory (or remedial) courses, which are better aligned with the specific needs of the different study programs. The catalog can moreover inform those instructors who are involved in the designing of entrance or placement tests. Finally, the present study calls for implications in educational policy. To smoothen the transition from high school to university, educational policy should initiate programs which bring together instructors from secondary and tertiary education to better align curricula. The catalog of identified prerequisites may guide such joint endeavor.
5. Closing remarks
In the beginning of this manuscript, we argued that there is an ongoing debate on which aspects should be included in mathematics education in school. The present study contributes one perspective to this debate, namely the expectations university instructors put on incoming first-year undergraduates’ mathematical learning prerequisites in non-STEM majors. We may not claim that mathematics education should be exclusively oriented toward this perspective only, but rather that it should also be taken into account when designing standards, learning materials or (remedial) courses. The diversity of subjects drawing on mathematics as well as the diversity of expected mathematical requirements found here emphasize the need for a broader, not only STEM-related view on mathematics education.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
The studies involving human participants were approved by the Ethics Committee of the Leibniz Institute for Science and Mathematics Education. Written informed consent to participate in this study was provided by the participants.
Author contributions
DR: analysis, design, writing, and editing. IN: writing, editing, and supervision. AH: analysis, writing, editing, and supervision. All authors contributed to the article and approved the submitted version.
Funding
This study was funded by the Leibniz Institute for Science and Mathematics Education.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2023.1089509/full#supplementary-material
Footnotes
- ^ Note that there are different types of universities in Germany: “Universities” are more focused on theory, while “Universities of Applied Sciences” focus on the practical application of knowledge. In addition, there are special “Universities of Applied Sciences” (e.g., colleges of administration for police training).
References
Alcock, J., Cockcroft, S., and Finn, F. (2008). Quantifying the advantage of secondary mathematics study for accounting and finance undergraduates. Account. Finance 32:311. doi: 10.1111/j.1467-629X.2008.00261.x
American College Testing [ACT] (2008). The Forgotten Middle: Ensuring that all students are on target for college and career readiness before high school. Iowa, IA: ACT.
Atanda, R. (1999). Do gatekeeper courses expand education options? Report No. NCES 1999-303. Washington, DC: National Center for Education Statistics.
Bryk, A., and Treisman, U. (2010). Make math a gateway, not a gatekeeper. Chronicle of higher education. Available online at: http://chronicle.com/article/Make-Math-a-Gateway-Not-a/65056/ (accessed March 31, 2023).
Byun, S.-Y., Irvin, M. J., and Bell, B. A. (2015). Advanced math course taking: Effects on math achievement and college enrollment. J. Exp. Educ. 83, 439–468. doi: 10.1080/00220973.2014.919570
Chen, X. (2016). Remedial coursetaking at U.S. public 2- and 4-year institutions: Scope, experiences, and outcomes (NCES 2016-405). Washington, DC: National Center for Education Statistics.
Deeken, C., Neumann, I., and Heinze, A. (2020). Mathematical prerequisites for STEM programs: What do university instructors expect from new STEM undergraduates? Int. J. Res. Undergrad. Math. Educ. 6, 23–41. doi: 10.1007/s40753-019-00098-1
Destatis (2018). Bildung und kultur. studierende an hochschulen. Fächersystematik. Stand: Wintersemester 2016/2017. Destatis. [Education and culture. Students in higher education institutions. Classification of subjects. Winter semester 2016/2017]. Wiesbaden: Statistisches Bundesamt.
Dieter, M. (2012). Studienabbruch und studienfachwechsel in der mathematik: Quantitative bezifferung und empirische untersuchungen von bedingungsfaktoren [Study drop-out and major change in mathematics: Quantitative description and empirical investigation of influencing factors]. Dissertation. Duisburg: University Duisburg-Essen.
Douglas, D., and Attewell, P. (2017). School mathematics as gatekeeper. Sociol. Q. 58, 648–669. doi: 10.1080/00380253.2017.1354733
Douglas, D., and Salzman, H. (2020). Math counts: Major and gender differences in college mathematics coursework. J. High. Educ. 91, 84–112. doi: 10.1080/00221546.2019.1602393
Gigerenzer, G., Gaissmaier, W., Kurz-Milcke, E., Schwartz, L. M., and Woloshin, S. (2007). Helping doctors and patients make sense of health statistics. Psychol. Sci. Public Interest 8, 53–96. doi: 10.1111/j.1539-6053.2008.00033.x
Grcar, J. F. (2011). Mathematics turned inside out: The intensive faculty versus the extensive faculty. High. Educ. 61, 693–720. doi: 10.1007/s10734-010-9358-y
Heublein, U., Hutzsch, C., Schreiber, J., Sommer, D., and Besuch, G. (2010). Ursachen des studienabbruchs in bachelor- und in herkömmlichen studiengängen [Reasons for study drop out from bachelor and other programs]. Hannover: HIS.
Hochschulkompass (2021). Hochschulkompass. ein angebot der hochschulrektorenkonferenz [College compass. An offer by the german rectors’ conference]. Available online at: https://www.hochschulkompass.de (accessed March 31, 2023).
KMK (2012). Bildungsstandards im fach mathematik für die allgemeine hochschulreife [National education standards in mathematics for the higher education entrance qualification]. Available online at: http://www.kmk.org/fileadmin/Dateien/veroeffentlichungen_beschluesse/2012/2012_10_18-Bildungsstandards-Mathe-Abi.pdf (accessed March 31, 2023).
Laging, A., and Voßkamp, R. (2017). Determinants of maths performance of first-year business administration and economics students. Int. J. Res. Undergrad. Math. Educ. 3, 108–142. doi: 10.1007/s40753-016-0048-8
Linstone, H. A., and Turoff, M. (1975). The Delphi method: Techniques and applications. Boston, MA: Addison-Wesley.
Logue, J. (2016). Pushing new math paths. Inside Higher Ed. Available online at: https://www.insidehighered.com/news/2016/04/21/tpsemath-working-reform-math-education (accessed March 31, 2023).
Mulhern, G., and Wylie, J. (2006). Mathematical Prerequisites for learning statistics in psychology: Assessing core skills of numeracy and mathematical reasoning among undergraduates. Psychol. Learn. Teach. 5, 119–132. doi: 10.2304/plat.2005.5.2.119
National Center on Education and the Economy (2013). What does it really mean to be college and work ready? The mathematics required of first year community college students. Washington, DC: National Center on Education and the Economy.
Niss, M. (1994). “Mathematics in society,” in Didactics of mathematics as a scientific discipline, eds R. Biehler, R. W. Scholz, R. Sträßer, and B. Winkelmann (Dordrecht: Kluwer Academic Publishers), 367–378.
Parker, S., Traver, A. E., and Cornick, J. (2018). Contextualizing developmental math content into introduction to sociology in community colleges. Teach. Sociol. 46, 25–33. doi: 10.1177/0092055X17714853
Rowe, G., Wright, G., and Bolger, F. (1991). Delphi: A reevaluation of research and theory. Technol. Forecast. Soc. Change 39, 235–251. doi: 10.1016/0040-1625(91)90039-I
Saxe, K., and Braddy, L. (2015). A common vision for undergraduate mathematical sciences programs in 2025. Washington, DC: Mathematics Association of America.
Scheller, P., Isleib, S., and Sommer, D. (2013). Studienanfängerinnen und studienanfänger im wintersemester 2011/12 [First-year students in winter semester 2011/12]. Hannover: HIS.
Statista (2022). Anzahl der hochschulen in deutschland in den wintersemestern 2016/2017 bis 2021/2022 nach Hochschulart [Number of universities in germany in the winter semesters 2016/2017 to 2021/2022 by type of university]. Available online at: https://de.statista.com/statistik/daten/studie/247238/umfrage/hochschulen-in-deutschland-nach-hochschulart/ (accessed March 31, 2023).
Steen, L. A. (2001). “Revolution by stealth: Redefining university mathematics,” in Teaching and learning of mathematics at the university level, ed. D. Holton (Dordrecht: Kluwer Academic Publishers), 303–312. doi: 10.1007/0-306-47231-7_27
Steen, L. A. (2006). From the 2000s: facing facts: Achieving balance in high school mathematics. Math. Teach. 100, 86–95. doi: 10.5951/MT.100.5.0086
The Mathematical Association of America [MAA] (2004). Undergraduate courses in the mathematical sciences: CUPM curriculum guide 2004. Washington, DC: Mathematical Association of America.
Transforming Postsecondary Education - Math (2018). Upper division pathways. Available online at: https://www.tpsemath.org/upper-division-pathways (accessed March 31, 2023).
Venezia, A., Kirst, M. W., and Antonio, A. L. (2004). Betraying the college dream: How disconnected K-12 and postsecondary education systems undermine student aspirations. Stanford, CA: Stanford Institute for Higher Education Research, Bridge Project.
Verner, I. M., and Maor, S. (2005). Mathematical aspects of educating architecture designers: A college study. Int. J. Math. Educ. Sci. Technol. 36, 655–671. doi: 10.1080/00207390500064098
Keywords: transition school-university, college readiness, school mathematics, university mathematics, Delphi study
Citation: Rohenroth D, Neumann I and Heinze A (2023) Mathematical prerequisites for non-STEM programs. Front. Educ. 8:1089509. doi: 10.3389/feduc.2023.1089509
Received: 04 November 2022; Accepted: 27 March 2023;
Published: 05 May 2023.
Edited by:
Timothy Fukawa-Connelly, Temple University, United StatesReviewed by:
Kris Green, St. John Fisher College, United StatesAriel Mariah Lindorff, University of Oxford, United Kingdom
Copyright © 2023 Rohenroth, Neumann and Heinze. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dunja Rohenroth, cm9oZW5yb3RoQGxlaWJuaXotaXBuLmRl
 Dunja Rohenroth
Dunja Rohenroth Irene Neumann
Irene Neumann