Conceptualizing and measuring instructional quality in mathematics education: A systematic literature review

Conceptualizing and measuring instructional quality is important to understand what can be understood as “good teaching” and develop approaches to improve instruction. There is a consensus in teaching effectiveness research that instructional quality should be considered multidimensional with at least three basic dimensions rather than a unitary construct: student support, cognitive activation, and classroom management. Many studies have used this or similar frameworks as a foundation for empirical research. The purpose of this paper is to investigate the relation between the conceptual indicators underlying the conceptual definitions of the quality dimensions in the literature, and the various operational indicators used to operationalize these factors in empirical studies. We examined (a) which conceptual indicators are used to conceptualize the basic dimensions theoretically, (b) to which extent the operational indicator in the literature cover these conceptual indicators, and (c) if which additional indicators are addressed by the measurement instruments, which are not part of the theoretical conceptualization. We conducted a systematic literature review on the conceptualization and operationalization of Instructional Quality in Primary and Secondary Mathematics Education based on PRISMA procedures. We describe the span of conceptual indicators connected to the three basic dimensions over all articles (a) and analyze to which extent the measurement instruments are in line with these conceptual indicators (b, c). For each measurement dimension, the identified quality dimensions identified are, taken together, largely representative of the conceptual indicators connected to the core factor, but also a number of critical misconceptions occurred. Our review provides a comprehensive overview of the three basic dimensions of instructional quality in mathematics based on theoretical conceptualizations and measurement instruments in the literature. Beyond this, we observed that the descriptions of a substantial amount of quality dimensions and their conceptualizations did not clearly specify if the intended measurement referred to the learning opportunities orchestrated by the teacher, or the utilization of these opportunities by students. It remains a challenge to differentiate measures of instructional quality (as orchestrated by the teacher) from (perceived) teacher competencies/knowledge, and students’ reactions to the instruction. Recommendations are made for measurement practice, as well as directions for future research.

Introduction

For almost five decades, instructional quality has remained a key topic in mathematics education research (FIAC, Schlesinger and Jentsch, 2016). The evaluation of teaching quality in mathematics has become increasingly important following international student assessment studies indicating that even in economically developed countries such as those in Europe, the USA, and Australia, approximately 20% of students lack sufficient skills in mathematics (Maass et al., 2019). Therefore, improving the quality of mathematics instruction has become a pressing issue for both researchers and practitioners (Cobb and Jackson, 2011).

Instructional quality, which is generally considered an “elusive” concept (Brown and Kurzweil, 2017, p. 3), refers to the degree to which instruction is effective, efficient, and engaging. Brophy and Good (1984) argued that research on effective teaching was largely influenced by the measurement of instructional quality. In this study, instructional quality refers to observable characteristics of classroom instruction that are orchestrated by teachers and goes along with desirable development of students’ learning outcomes in a theoretically plausible way, supported by empirical evidence. Valid measures of instructional quality are important and imperative since they provide theoretical conceptualizations of instruction that lead to students’ cognitive and affective–motivational learning progress, which have been put to an empirical test. Therefore, they have the potential to go beyond simply measuring the amount of instruction and can serve as a means of improving instruction (Boston, 2012), to provide useful feedback to guide instructional improvements (Schlesinger and Jentsch, 2016), to focus on the quality of the learning environments teachers create for students, to assist districts in monitoring and evaluating reform efforts (Learning Mathematics for Teaching Project, 2010), and to trigger conversations about equitable learning opportunities (Boston, 2012). However, researchers lack adequate knowledge of the characteristics of effective teaching in classrooms in order to establish the robust link between teaching and learning (Blömeke et al., 2016). Furthermore, there has been a long-standing debate about how these characteristics of effective teaching for successful learning in schools should be evaluated (Schlesinger and Jentsch, 2016).

All models of instructional quality differentiate between various measurement dimensions, which are assumed to describe different characteristics of effective instruction, which relate to differences in learning progresses. In this study, the term measurement dimensions refers to a single, empirically measurable dimension of instructional quality mentioned in a manuscript, which can be at different levels of granularity (Praetorius and Charalambous, 2018): for example, dimensions, sub-dimensions, indicators, coding-items, -rubrics, and single codes. A well-known German framework of Three Basic Dimensions has been developed by several studies from German-speaking countries within the TIMSS Video Study to define teaching quality as a combination of three overarching basic measurement dimensions: (a) a clear, well-structured classroom management, (b) supportive, student-oriented classroom climate, and (c) cognitive activation (Klieme, 2013).

Many studies have used this or a similar three-dimensional framework provided by Klieme et al. (2009) as a foundation for further empirical research (Schlesinger and Jentsch, 2016). In the sequel, we will refer to these three dimensions as basic dimensions. Taut and Rakoczy (2016) briefly addressed a content-specific conceptualization for an extended version. Seidel and Shavelson (2007) argued that classroom assessment is also an important additional factor of instructional quality. They further divided student orientation and added classroom assessment to the three frequently identified basic dimensions: (a) classroom management; (b) cognitive activation; (c) student orientation, consisting of the component of (c1) organizational choices on the one hand, and (c2) supportive relationships on the other; and (d) classroom assessment. Pianta and Hamre (2009) also conceptualize three global, generic dimensions that help to understand how practices and content are implemented. Similar to the three dimensions proposed by Klieme et al. (2009), they distinguish (a) classroom organization, (b) emotional support, and (c) instructional support. In their teaching and learning model, Seidel and Shavelson (2007) distinguish (a) goal clarity and orientation, (b) learning climate, (c) teacher support and guidance, (d) executing learning activities, and (e) evaluation.

The popularity of the three-dimensional framework is plagued by incoherent conceptualization. Multiple labels (e.g., classroom management/organization, classroom climate/student orientation/emotional support) are used to characterize the same nature of the classroom, which leads to misunderstandings among scholars and practitioners. Theoretically, the three-dimensional frameworks we just described were conceptualized as being generic in nature (Praetorius et al., 2018). However, the discussion as to what extent a generic perspective on instructional quality requires a subject-specific specification, extension or differentiation is subject to ongoing discussions in the field (e.g., Schlesinger and Jentsch, 2016; Jentsch et al., 2020; Lindmeier and Heinze, 2020; Praetorius et al., 2020; Dreher and Leuders, 2021; Praetorius and Gräsel, 2021). Furthermore, the conceptualization of the dimension Cognitive Activation can differ largely between studies within one subject (e.g., mathematics; Schlesinger and Jentsch, 2016).

Given this heterogeneity, it has become important to structure or systematically analyze previous studies to capture the commonalities and differences in these approaches, to clarify misconceptions, and to propose recommendations for future conceptualizations of instructional quality. For example, Praetorius and Charalambous (2018) recently reviewed 12 classroom observation frameworks used for measuring quality in mathematics instruction and reflected on the differences in the theoretical underpinnings and their operationalization related to the frameworks. This work represents one of two perspectives that may provide insights into what is actually understood under the basic dimensions: Measurement instruments applied in empirical studies to measure instructional quality, and specifically the basic dimensions, draw on compositions of observable and measurable properties of classroom instruction, called operational indicators (Figure 1, blue area). However, how a construct is operationalized using sub-scales and items and dimensions is crucially dependent on how it is conceptualized from a theoretical perspective. While Praetorius and Charalambous (2018, p. 539) already claimed that “the process of operationalization is closely associated with fundamental theoretical questions,” measurement and conceptualization were addressed independently. From this second theoretical perspective, research works usually start from conceptual definitions (Quarantelli, 1985) for each basic dimension. In the literature, these conceptual definitions often comprise essential and in principle observable properties of classroom instruction, called conceptual indicators here (Figure 1, yellow area), which define the corresponding basic dimension of instructional quality. The conceptual indicators used to define the basic dimensions in the original manuscript are presented by the red area in Figure 1.

FIGURE 1

Figure 1. Visualization of the main concepts of the study.

The primary purpose of this study is to investigate the extent to which the indicators from the two perspectives match the three basic dimensions from Klieme’s (2013) framework: To what extent do the operational indicators and conceptual indicators used in the literature overlap? Are there indications of concept underrepresentation (yellow area without blue area) or indication of construct-irrelevant measurement (blue area without yellow area)? Finally, does the original definition of the basic dimensions fall inside the overlap of conceptual and operational indicators? The second goal of the manuscript is concerned with measurement dimensions, which are discussed in the literature, but do not come under the purview of one of the three basic dimensions. The main question here is, how can they be systematized into a set of new, additional overarching quality dimensions, which may represent additional “basic dimensions” in the future? Even though initial answers to this question based on the analysis of observation tools are available, more and diverse indicators of instructional quality are discussed in the literature, beyond those found in observation tools. In the following sections, we will prepare this investigation by considering each of the two perspectives comprehensively.

Conceptualizing instructional quality in mathematics

Deciding on measurements in research involves the process of defining how a construct will be assessed, known as conceptualization. Prior attempts to measure instructional quality traditionally focused on instructional inputs or instructional outputs (Brown and Kurzweil, 2017). Output-based definitions of instructional quality focus on how student behaviors and accomplishments—such as student performance on a posttest or student affect toward learning after instruction (Merrill et al., 1979). While students’ learning progress is unquestionably a critical criterion to validate measures of instructional quality, students’ test performance does not indicate which characteristics of classroom instruction may have caused the corresponding development (Boston, 2012). To capture the relationship between instruction and students’ development, it is essential to examine all major factors influencing student achievement, which may relate to students’ prior characteristics, school- or family-related context variables, or instruction itself (Junker et al., 2005). Meanwhile, input measures for instructional quality include school infrastructure, teaching and learning materials, or characteristics of teachers or instructors (Otara and Niyirora, 2016). This research tradition reflects, for example, the assumed importance of teacher characteristics for high-quality teaching (Blömeke et al., 2016). However, this perspective again does not directly capture the effects of classroom instruction, which makes it difficult to exploit the corresponding measures as described above.

Further research focused on the teaching process, that is, teacher behavior and observable characteristics of classroom instruction instead of output or input measures. Traditionally, this research focused on what are called “surface structures” today (Köller and Baumert, 2001). These surface structures are discrete and easily observable units of teaching activity, such as whether the teacher asks questions, whether the students give correct answers, or whether the teacher reinforces students. These behaviors are measured in terms of their presence or absence of specific actions, and require limited inference by the observer. This process–product paradigm produces a diverse list of effective teaching components that the researchers choose to observe and assume to influence its quality. Following Borich (1977), classroom assessment should include both process and product measures, since we cannot assume that stable teacher behavior always produces stable pupil outcomes, or that stable pupil outcomes are always attributable to stable teacher behaviors. Glass (1974) qualifies this statement, by specifying that no characteristic of teaching should be incorporated into rating scales until research has established that it can be reliably observed and that it significantly relates to desired pupil outcomes.

Research during the past four decades has ceased to concentrate on discrete, directly observable teaching practices and teacher personality or teacher behavior in the classroom to explain learning progress (Creemers and Kyriakides, 2015). The research focus has shifted toward a more interactive Process–Mediation–Product Paradigm (Brophy and Good, 1986; Brophy, 2000, 2006). This emphasizes, models, and investigates the relationship between the teaching acts, techniques or strategies (processes) as orchestrated by the teacher, and students’ usage (mediation) of the learning opportunities entailed in this orchestration, which ultimately lead to students’ progress (product) (Praetorius et al., 2014). From this perspective, instructional quality is a construct that reflects those teachers’ instructional practices that can be connected to students’ learning processes (mediation) in a theoretically and empirically observable plausible way (Blömeke et al., 2016).

Although most studies on instructional quality are grounded in this process–mediation–product paradigm (Jentsch and Schlesinger, 2017), available empirical results are rather weak and inconsistent for those characteristics of instruction, which go beyond discrete, directly observable characteristics, and require a substantial amount of inference by the observer, teachers, or students (Krauss and Bruckmaier, 2014). For example, Johnson and Johnson (1999) argued that the traditional classroom learning group, in which students are assigned to work together and accept that they have to do so, are different from the “real” cooperative learning group in which students work together to accomplish shared goals by discussing material with each other, helping one another understand it, and encouraging each other to work hard. In this sense, indicators for instructional quality can be categorized into surface structures (e.g., grouping students), that can be observed directly, without much inference, and deep structures (e.g., encouraging cooperative learning) that require interpretations based on subject-specific or general models of teaching and learning (Schlesinger and Jentsch, 2016).

Evaluating deep structures usually requires more inference than surface structures in their evaluation, but have often provided more valid results (e.g., on the role of high-level thinking) than related surface structure measures (e.g., students’ oral participation in class) (Schlesinger and Jentsch, 2016). Praetorius et al. (2014) argue that low-inference ratings cannot adequately assess the characteristics of the deep structure of instruction, for instance, cognitive activation. Therefore, most classroom observation tools dig into the deep structure of teaching (Lanahan et al., 2005; Praetorius et al., 2014) using high-inference coding systems. The presence of aspects from surface structures and the quality of the deep structures can vary almost independently from each other (Baumert et al., 2010). Nevertheless, Schlesinger and Jentsch (2016) claimed that an instrument is necessary that contains items at any inference level, since in some cases, the indicators for the surface structure are a necessary, yet not sufficient indication for the quality at deep structure. For example, students’ mathematical high-level thinking can only occur when the lesson time is connected to the learning of mathematics (i.e., time on task).

First models, such as the basic dimension framework, exist to describe main (and hypothetically independent) factors of instructional quality at the deep structure. However, as argued above, conceptualization and operationalization of the construct in the literature nevertheless vary widely. Praetorius and Charalambous (2018) identified critical issues regarding the conceptualization of instructional quality: First, previous studies conceptualized the construct with various foci from individual learning and development to classroom discourse, from teacher knowledge over task potential to teacher classroom behavior. Second, for none of the reviewed frameworks was it entirely clear as to why certain conceptual indicators were included. Even in cases when explicit references were made to theories, these references were often rather brief “leaving the reader without a clear understanding of how the respective theory led to the conceptualization of a specific framework element” (Praetorius and Charalambous, 2018, p. 539). In short, a coherent theoretical understanding of the deep structure of instructional quality is not available. The main goal of this study is to approach this issue by reviewing how different studies conceptualize basic dimensions of instructional quality, and relate these to the way these dimensions are measured in research.

Measuring instructional quality in mathematics

The way mathematics instructional quality is measured in empirical studies might thus provide a second, additional perspective on the construct. Research on instructional quality has drawn on a range of data sources to capture how teachers orchestrate classroom instruction. Until recently, the body of research measuring instructional quality relied predominantly on data from student ratings of instruction and teacher self-reports to tap a variety of different quality aspects (Wagner et al., 2016). Student ratings are occasionally criticized as being rather global, not specific to different dimensions of teacher behavior, and easily influenced by students’ personal preferences (De Jong and Westerhof, 2001). Teacher reports are sometimes considered to be biased by self-serving strategies or perceived teaching ideals. Some scholars have used teacher surveys or teacher lesson logs to reconstruct patterns of curriculum coverage and the way this curriculum is delivered, or draw on interviews to gather information about teachers’ instructional practice (Ball and Rowan, 2004). Other studies have focused on teaching documents, such as tasks (e.g., Baumert et al., 2010) or text books to derive indicators of instructional quality (e.g., Van Den Ham and Heinze, 2018; Sievert et al., 2019, 2021a,2021b) although this method does not yield accurate information about the nature of interactions between teachers and students and interpretations of reform practices (Mayer, 1999). Likewise, analyses of student work may provide crucial information about students’ use of learning opportunities provided by the teacher and their performance. However, these documents reflect not only the quality of instruction, as orchestrated by the teacher, but also the characteristics of the group of students, for example, in terms of prior achievement or motivation.

In light of this criticism, research has turned toward more direct assessments of instructional quality, such as classroom observations. Such observation has involved either detailed field notes of teachers’ and students’ activities, videotaping, or the use of more structured checklists or codes to reduce the data into categories of construct(s) underlying consistent high-quality instruction, such as students’ opportunities to learn, their engagement in learning, and teachers’ interactions with students over instructional tasks (Ball and Rowan, 2004). Even though they are time-consuming and expensive and also prone to distortions by rater biases, they are considered to be among the most promising ways to assess instructional quality (Taut and Rakoczy, 2016). Capturing how teachers orchestrate students’ work and learning in classrooms and the process of teaching and learning, may offer an external and, in the best case, objective perspective on the quality of instruction.

Over the past decade, a wide range of observation instruments have been developed to assess the classroom environment globally or examine specific aspects of the classroom setting, which vary in the facets of instructional quality addressed and in terms of their specificity to a single subject, such as mathematics and the bandwidth of grade levels covered (Praetorius et al., 2014). The Classroom Assessment Scoring System (CLASS; Pianta et al., 2008) is a standardized observation measure that assesses global classroom quality across grades and across content areas, from preschool to high school. Hamre and Pianta (2007) proposed a latent structure for organizing meaningful patterns of teacher–child interaction, which in turn are the basis for the three dimensions of interaction—Emotional Support, Classroom Organization, and Instructional Support. Within each of its three broad domains are a set of more identifiable and scalable dimensions of classroom interactions that are presumed to be important to students’ academic and social development. For example, the domain of Emotional Support includes three dimensions: positive classroom climate, teacher sensitivity, and regard for student perspectives. Within each of these dimensions are posited a set of behavioral indicators reflective of that dimension. For instance, the positive classroom climate dimension includes observable behavioral indicators such as the frequency and quality of teacher affective communications with students (smiles, positive verbal feedback) as well as the degree to which students appear to enjoy spending time with one another. The Elementary Mathematics Classroom Observation Form (EMCOM; Thompson and Davis, 2014) was designed to observe classroom strategies and activities with a specific focus on the teaching and learning of primary mathematics, with quality dimensions such as (a) calculation and math concepts, (b) student engagement, (c) instruction, (d) technology activities, and (e) materials and manipulative activities.

In sum, there is a growing focus on observation as a useful approach to capturing the quality of classrooms. The available observation tools select different sets of quality dimensions based on their respective focus. However, some of these quality dimensions show partial overlap between observation tools, for example, instruction in EMCOM, classroom talk in the Instructional Quality Assessment (IQA; Matsumura et al., 2008), and the two talk dimensions in the Flanders Interaction Analysis Category (FIAC, Amatari, 2015). Therefore, the question arises as to what extent these observation instruments reflect a joint understanding of instructional quality, as it is, for instance, proposed by Klieme et al.’s (2009) framework. Moreover, this perspective, as well as perspectives drawing on other data sources, require that the conceptual definitions and their entailed conceptual indicators, are described in terms of operational indicators, which can be evaluated objectively, reliably, and validly by the rater (e.g., trained research staff, student, teacher) based on the available data (e.g., videos, independent classroom observation, or own experience of the lesson). This leads to the question as to what extent the operational indicators used in the literature actually reflect the conceptual definitions of basic dimensions of instructional quality.

The basic dimensions framework as a starting point toward a common conceptualization of instructional quality in mathematics

Curby et al. (2011) argued that without consistent and appropriate conceptualization of a construct, attempts to operationalize, measure, and manipulate instructional quality by professional development are doomed to failure. In the past, there was a strong emphasis on the measurement of instructional quality rather than the conceptualization of the multifaceted construct (Seidel and Shavelson, 2007). While numerous attempts have been made to conceptualize instructional quality, the corresponding frameworks vary widely.

Only the few frameworks mentioned above have explicitly justified their theoretical structure (Praetorius and Charalambous, 2018). One of them is the German framework of the Three Basic Dimensions (TBD) as mentioned above, where the three-part structure is explained referring to the three generic goals of classroom teaching and learning distinguished by Diederich and Tenorth (1997). According to Lipowsky et al. (2009), these basic dimensions are latent variables that are related but not identical to specific instructional practices. Praetorius et al. (2018) identified a few studies that conducted confirmatory or exploratory factor analyses to examine the underlying factor structure of the three-dimensional instrument (Kunter et al., 2005; Lipowsky et al., 2009; Kunter and Voss, 2013; Fauth et al., 2014; Künsting et al., 2016; Taut and Rakoczy, 2016). Lipowsky et al. (2009) found that 10 video rating dimensions of instructional quality could be subsumed under the three-factor structure. Fauth et al. (2014) found the same three-dimensional structure in elementary school students’ ratings on instructional quality. Kunter et al. (2007) combined three sources of information (student reports, teachers’ self-reports, and expert ratings of tasks given to students by teachers) to examine instructional quality and confirmed its three-dimensional structure.

While most of the identified empirical studies support the three-factorial separation of the basic dimensions, two other studies identified more than three dimensions in their analyses (Kunter et al., 2005; Taut and Rakoczy, 2016). Rakoczy (2008) found four factors in a factor analysis based on the data used by Lipowsky et al. (2009) but using a larger set of video rating dimensions. The factor called student-oriented climate was divided into one factor for organizational aspects (provision of choice, individualization) and one for social aspects (teacher–student relationship). Taut and Rakoczy (2016) further indicated that the empirical structure of the observation instrument lacks correspondence with its original normative model but mirrors a five-factor model based on recent literature, with an extension of an assessment and feedback factor, as well as two different aspects of student orientation. Furthermore, Praetorius and Charalambous’s (2018) analysis of observation instruments found operational indicators that could not be subsumed under the three basic dimensions. Therefore, the authors of this paper proposed four additional dimensions (Content Selection and Presentation, Practicing, Assessment and Cutting across Instructional Aspects aiming to maximize student learning).

In sum, the strong theoretical basis speaks for taking the three basic dimensions as a first structuring framework, when analyzing conceptual and operational indicators from the literature on instructional quality in mathematics. Most extensions proposed in the past were based on existing observation frameworks (or data generated with these frameworks), and resulted either in splitting existing dimensions into sub-dimensions, or adding further dimensions. However, a broader consideration of instructional quality in the literature, including but not limited to observation instruments and taking into account conceptual as well as operational indicators, may provide a more accurate picture of how instructional quality is conceptualized in current research on mathematics instruction.

Generic or subject-specific instructional quality

One may ask whether frameworks of instructional quality that are specific to a single subject such as mathematics are necessary. While Occam’s Razor principle calls for prioritizing generic frameworks when more specific extensions do not add to understanding, points have indeed been made that all three basic dimensions may contain subject-specific indicators in some sense (e.g., Praetorius et al., 2020). It remains unclear in many papers, however, what constitutes subject-specificity of instructional quality framework.

First, one may ask whether an indicator of instructional quality can be described and applied validly without referring to the domain (e.g., using visualizations; example adapted from Dreher and Leuders, 2021), whether it must be specified to the subject (e.g., using representations that support mathematical learning), or even to the specific learning content (e.g., using representations that appropriately represent the structure of algebraic expressions). Several authors argue that many generic indicators need to be specified in a subject- or content-specific way to be measured validly. Lipowsky et al. (2009) followed exactly this approach and could show that video-based coding of instructional quality, which was very specific to the content at hand, contributed to the explanation of student learning beyond generic dimensions of instructional quality. Therefore, from the perspective of applicability, it is an open question as to what extent indicators of instructional quality need to be specified to a single subject or content.

Second, and related to this, one may consider to what extent the same indicators of instructional quality dimensions are considered relevant by instructional quality experts from different subjects. In Praetorius et al. (2020), experts in science, physical, and history education jointly compared indicators for each dimension of the Praetorius and Charalambous (2018) framework between the three subjects. They found indicators that were only considered relevant for one or two of the three subjects for five of the seven dimensions (including classroom management, but not the dimensions related to exercises and formative assessment).

Third, another perspective connects subject-specificity of instructional quality to the extent, to which subject-specific knowledge is necessary to judge or rate (Wüsten, 2010; Dorfner et al., 2017; Heinitz and Nehring, 2020; Lindmeier and Heinze, 2020; Dreher and Leuders, 2021). Some studies have shown that at least some aspects of instructional quality are related to teachers’ subject-specific professional knowledge (e.g., Baumert et al., 2010; Jentsch et al., 2021). We do not know of any studies on the effects of raters’ subject-specific knowledge on ratings of instructional quality. Studying the necessity of subject-specific knowledge for judging or enacting certain indicators of instructional quality is a promising, but challenging desiderate for future research.

Finally, how general or specific an indicator of instructional quality is may also be judged empirically by studying if it is equally predictive for student learning in different subjects or, on a more fine-grained level, for different contents or learning goals (cf., Lindmeier and Heinze, 2020; Dreher and Leuders, 2021) provided sufficiently broad applicability of the indicator.

This review primarily aims at forming a basis for judging the relevance of different indicators for one specific subject, mathematics. This approach allows describing what is discussed in the literature for this specific subject, retaining potentially specific aspects, and preventing too early abstraction into generic dimensions. This way, one may not necessarily expect (though it is possible) to identify dimensions or indicators that are specific to a single subject. However, one may expect to find patterns of indicators and dimensions that are characterized by a specific subject and deviate from corresponding patterns for other subjects. It must be noted, however, that analyzing a single subject restricts the possibility of finding dimensions as clearly subject-specific. What can be done is to provide first insights by analyzing subject-specificity regarding applicability relevance, knowledge, or predictivity (as described above) of the different dimensions and indicators for mathematics based on the literature.

In summary, a coherent analysis of conceptual and operational indicators used to describe instructional quality in mathematics is not currently available. However, such an analysis would be of particular importance to systematize the wide range of existing conceptualizations and measurement instruments into a coherent structure, and to contrast the emerging conceptualization for mathematics with similar conceptualizations in other subjects.

The current study

How the quality of mathematics instruction as a multifaceted construct is conceptualized, measured, and how these measures are validated in terms of their content, is of considerable importance for mathematics education. In this contribution, we examine conceptualizations and measurements of instructional quality under the perspective of Klieme et al.’s (2009) basic dimensions framework. As noted above, conceptualizations of the basic dimensions in this framework vary in the literature.

Therefore, one of the goals is to systematize descriptions of the basic dimensions from the literature into a clear and concise conceptual definition (conceptualization). In this vein, our first goal is to collect, for each basic dimension, those observable characteristics of classroom instruction that are usually used to characterize the dimension in theoretical terms (conceptual indicators, yellow ellipse in Figure 1). The starting point for this is the conceptual indicators given in Klieme et al.’s (2009) framework for each basic dimension (red area in Figure 1), but other conceptual indicators may arise from the literature. A second goal is to describe which observable characteristics of classroom instruction are captured by measurement dimension that intend to assess the basic dimensions (operational indicators, blue ellipse in Figure 1). Our third goal is to compare conceptual indicators and operational indicators assigned to each of the three basic dimensions. To capture the overall state of the discussion, we disregard if the conceptual indicators and operational indicators occur in the same or in different manuscripts. Optimally, all conceptual indicators that are used in a conceptual definition of a basic dimension correspond to an operational indicator, which is assessed by some measurement dimension. Conversely, all operational indicators assessed by any measurement dimension reflect a conceptual indicator, which occurs in a conceptual definition of the basic dimension (overlap of yellow and blue region). We assume that the conceptual indicators given in the original framework (Klieme et al., 2009) fall into this region. Other indicators in the overlapping region outside the red area might be candidates for extending the original definition. We also assume that the overlap between the conceptual indicators and measurement dimensions is not perfect. This allows the study of construct-irrelevant aspects of measurement dimensions (parts of the blue ellipse outside the yellow ellipse), and construct underrepresentation in the measurement dimensions in the literature (parts of the yellow ellipse outside the blue ellipse).

Summary of research questions

Based on the distinction between conceptual definitions and measurement dimensions, and the distinction between conceptual indicators and operational indicators, the purpose of this review is to describe the commonalities and differences between the conceptualizations and the measurement of the three basic dimensions of instructional quality in mathematics. Accordingly, we conducted a systematic analysis of the literature on instructional quality in primary and secondary mathematics education, focusing on the following guiding questions:

1) Conceptual definitions and conceptual indicators for basic dimensions

a) Which conceptual indicators are used in the literature to conceptualize the three basic dimensions in instructional quality from a theoretical perspective?

b) How much variability can be found in this theoretical conceptualization of the basic dimensions in the literature?

2) Measurement dimensions and operational indicators for basic dimensions

a) To what extent is it possible to assign the measurement dimensions found in the literature to one of the three basic dimensions of Klieme et al.’s framework based on the operational indicators used to assess instructional quality?

b) To what extent do the descriptions of these operational indicators define subject-specific aspects of instructional quality?

3) How can the conceptual (from Q1) and operational indicators (from Q2) be synthesized to sharpen and extend the basic dimensions framework?

a) Which characteristics of classroom instruction occur as conceptual indicators as well as operational indicators for each basic dimension of instructional quality (overlapping area of yellow and blue ellipses)? We assume that this overlap characterizes a common understanding of the corresponding basic dimension of instructional quality.

b) To what extent are the conceptual indicators (from Q1) completely covered by the identified operational indicators (from Q2)? This question refers to construct underrepresentation, that is, “blind spots” in the empirical research on the basic dimensions (yellow, without blue part).

c) To what extent do the operational indicators (from Q2), which are used to assess the basic dimensions, correspond to conceptual indicators (from Q1) for the same basic dimension? This question refers to the content validity of the measurement dimensions found in the literature. Measurement dimensions, which are subsumed under a basic dimension in empirical research, but address conceptual indicators that are not connected to conceptual definitions of the basic dimension (blue, without yellow), run counter to the validity of the measurement dimension.

d) How can the operational indicators (from Q2) belonging to measurement dimensions, which cannot be assigned to basic dimensions, be grouped into new factors of instructional quality?

Materials and methods

Literature search

This study has been undertaken as a systematic literature review based on PRISMA guidelines (Moher et al., 2009; Figure 2). PRISMA statement consist of four steps: identification, screening, eligibility, and inclusion criteria. Identification is the process to enrich the main keywords using several steps so that a wide range of articles can be retrieved from the database. The second phase is screening, a process to include or exclude articles based on criteria decided by the authors and generated using the database. Excluding articles means eliminating unnecessary articles according to the types. The third phase is eligibility; all articles are examined by reading through the title, abstract, method, result, and discussion to ensure they meet the inclusion criteria and parallel with the current research objectives. The final phase is inclusion criteria where the articles left fulfill the requirement to be analyzed.

FIGURE 2

Figure 2. PRISMA flow diagram.

Identification

The Web of Science (all databases) was searched last mainly by one reviewer on October 25, 2020. The search strategy consisted of three groups of search terms combined with the Boolean operator “OR,” representing the following components: (1) “Mathematics AND Instructional Quality,” (2) “Mathematics AND Classroom Quality,” and (3) “Mathematics AND Teaching Quality.” Title and abstract were included as search fields. Articles in languages other than English were not included. After eliminating duplicates, n = 1,841 publications were in the initial database.

Screening

Studies with a focus on general issues relating to mathematics instruction, such as School Management, Education Policy, Text Books, New Technology, Teachers’ Professional Development, Cultural and International Comparisons (n = 413) were excluded. We also excluded studies that specialized in instruction in University, College, and Higher Education (n = 384), which focused on learners in Kindergarten, Preschool, Early Childhood, and the Head-start Program (n = 112), or on learners with disabilities and other special needs (n = 61). Finally, studies that primarily investigated teaching in Physics, Science, general STEM instruction, and other disciplines (n = 356) were not included. Studies that assessed instructional quality by Student Performance, Motivation, Competences, Interest, Self concept, Peer-Interaction or other measures that did not directly correspond to actual classroom instruction (n = 200) were also excluded. Abstracts were further selected for retrieval of the paper only if they were peer-reviewed journals and conference papers or book chapters.

Eligibility for analysis of operational indicators

The full text could not be obtained for 48 of the remaining 341 articles. Therefore, 237 articles were considered in detail for eligibility based on titles, abstract, method, result, and discussion to ensure they met the inclusion criteria. The full texts were coded independently by two reviewers, who marked each article as “included” or “excluded.” For excluded articles, a reason for the exclusion was documented. The first author selected relevant studies by judging the title, abstract, and full text against the criteria for inclusion and exclusion. In case of doubt, the second author independently judged these papers. Subsequently, two authors discussed the eligibility of these publications until consensus was reached. Accordingly, another 125 publications were excluded, leaving 112 publications (95 journal articles and 17 conference papers) from 2006 to 2020 for the analysis of operational indicators.

Eligibility for analysis of conceptual definitions

To analyze conceptualizations of the Basic Dimensions proposed by Klieme et al. (2009) used in the literature, we selected 10 of the remaining publications for each basic dimension (Classroom Management, Student Support, and Cognitive Activation). Since the keywords for the conceptual definitions of the three basic dimensions, such as Cognitive Activation, may not appear in the title or abstract, we selected those 10 articles from the existing pool of full-text articles that were included for the analysis of operational indicators. The study applied a systematic approach to collect conceptual definitions based on three inclusion criteria: (a) conceptualizing all the three basic dimensions; (b) specifying the multiple indicators that can be used to measure the basic dimensions and the different aspects of the basic dimensions; (c) citing other references to affirm the validity of the conceptual definitions.

Analysis of conceptual definitions

A qualitative content analysis was conducted to identify the conceptual indicators that constitute the conceptual definitions given in the texts selected for each basic dimension. To derive these conceptual indicators from the definitions, we applied a text mining method proposed by Kaur and Gupta (2010). Conceptual indicators were extracted by identifying the “keywords” that are a small set of words, or key phrases to comprise very crucial information about the conceptual definitions.

Accordingly, the conceptual definitions were preprocessed manually in the following steps: (a) stopword elimination—common words with no semantics and which do not aggregate relevant information to the task (e.g., “the,” “a”) were eliminated; (b) stemming: semantically similar terms, such as “Dealing with disruptions,” “Coping with disruptions,” and “Managing disruption” were considered as equivalent to each other and therefore redundant words were replaced by a single term. In this case, we only retained the verb “Deal with.” However, the semantically related words of a target educational field should be kept separate and clustered as a group of candidate indicators, such as disruption, misbehavior, and disciplinary conflict. Consequently, all the semantically similar words relative to the conceptual element were combined and counted as one indicator “Dealing with disruptions/misbehavior/disciplinary conflict.” The tedious efforts of stopword removal and semantic stemming were to convert textual data to an appropriate format and size for further qualitative analysis.

Coding of measurement dimensions

We used a qualitative method that combines deductive and inductive coding to analyze measurement dimensions carried out in empirical studies on instructional quality. From a deductive standpoint, our analysis is to test the German framework of three basic dimensions and hence anchored in classifying the measurement dimensions to the three basic dimensions. From an inductive standpoint, there are no previous frameworks comprehensive enough to code all operational indicators of the measurement dimensions. Although the findings are built on the German framework of three basic dimensions and also influenced by conceptual indicators outlined by previous researchers, the findings arise directly from the analysis of the raw data, not from a priori expectation or predefined model. The combination of these approaches allows us to (a) condense raw textual measurement dimensions into a brief, summary format; (b) establish clear links between the conceptual indicators and the summary operational indicators derived from the empirical evidence on measurement dimensions; and (c) develop a framework of the underlying operational indicators going beyond the existing German framework of Three Basic Dimensions.

To support full-text analysis, the computer-assisted qualitative data analysis software MAXQDA was used (Kuckartz and Rädiker, 2019). The code system was developed iteratively based on a subsample of the text, adding further articles after each revision. Results of reliability crossing segmenting, deductive and inductive coding phases can be found in Table 1.

TABLE 1

Table 1. Results of reliability crossing training/testing phases.

Segmenting

As units of analysis (Strijbos et al., 2006), we extracted measurement dimensions from the publications. Measurement dimensions are single, empirically measurable dimensions of instructional quality mentioned in a manuscript text under consideration. As mentioned above, measurement dimensions are structured hierarchically (Praetorius and Charalambous, 2018). At the lowest hierarchy level, single coding rubrics for one observable classroom characteristics or one questionnaire item may form a measurement dimension. In a manuscript, authors may combine or aggregate several measurement dimensions into a higher-level (parent) measurement dimension (e.g., different rubrics or items referring to higher-order thinking), and several of these higher-level measurement dimensions may again be collected into even higher-level parents (e.g., cognitive activation).

For segmenting, the names of each measurement dimension were marked in each manuscript. Moreover, the following data were marked for each measurement dimension: its operational definition, its parent measurement dimension (if there was a parent measurement dimension). Two coders initially segmented five randomly selected manuscripts to obtain a joint understanding of the measurement dimensions that would be identified as the unit of analysis. The level of agreement between the coders was calculated by Percent Agreement. According to House et al. (1981) a value of 70% is necessary, 80% is adequate, and 90% is good. During the training phase, the percentage of agreement on segmenting between two raters ranged from 84% for the first training phase of segmenting (5 manuscripts) and 86% for the second phase (10 manuscripts). Both reviewers segmented all remaining articles. Disagreements were resolved by group discussion between the authors, and by jointly reviewing the articles until consensus was reached.

Deductive coding

We assigned each measurement dimension to one of the basic dimensions proposed by Klieme et al. (2009): Student Support, Cognitive Activation, and Classroom Management. If none of them was found to fit, the measurement dimension would be labeled as Not Assignable. The decision was based on the name and operational definition of the measurement dimension. When there was still doubt, we also took into account the parent measurement dimensions to which it was assigned in the corresponding article.

Two human coders were trained in the spring of 2020, introducing them to the project, the coding manual, and unit of analysis. Any comprehension questions were resolved in this context as well. In the four coding phases, both coders coded about 30 randomly selected measurement dimensions independently. After the first two coding phases, interrater agreement was considered suboptimal, so further training and clarifying discussions were implemented. In the fourth coding phase, the two raters reached 77% agreement and a Cohen’s Kappa of 0.68, which was considered sufficient. Each of the two coders then analyzed the disjointed subsets of all articles. One more phase of double coding was conducted to check whether the two coders still achieved an acceptable level of interrater agreement.

Inductive coding

The general inductive approach was used to analyze the measurement dimensions to identify operational indicators to measure instructional quality. Since the unit of analysis (measurement dimensions) was identified, the inductive coding began with close and multiple readings of measurement dimensions and consideration of the operational indicators inherent in the dimensions.

Two coders then created a label (e.g., a word or short phrase) for an emerging indicator to which the measurement dimension was assigned. The label conveyed the core theme or essence of a measurement dimension. Emerging indicators were developed by studying the measurement dimensions repeatedly and considering corresponding conceptual indicators and how these fit with the German Framework of Three Basic Dimensions. The principles of the inductive coding included: (a) the label for the upper level of operational indicators referred to the general basic dimensions (e.g., Classroom Management, Cognitive Activation); (b) the label for the lower-level or specific indicator could be the sub-dimensions of the three-dimensional framework (see Appendix 1), if the sub-dimensions outlined from the previous works perfectly represented the underlying meaning of the operational indicators (e.g., Challenging Task and Questions, Effective Time Use/Time on Task); (c) some indicators could be combined or linked under a superordinate indicator when the underlying meanings were closely related, according to the outlined conceptual indicators. For example, Behavior Management referred to all classroom activities to identify/strengthen desirable student behaviors, to prevent disciplinary conflicts/disruptions/undesirable behaviors, and to deal with disruptions/misbehavior/disciplinary conflict; (d) If an operational indicator was closely associated with one conceptual indicator outlined before, but is not explicitly described by the conceptual definition, we gave them a label and integrated the new label into the existing framework of the basic dimensions. For example, Instructional Design and Plan was assumed to be closely associated with Lesson Structure, Lesson Procedure, and Transition between Lesson Segment. Therefore, we linked all the closely associated indicators under a superordinate indicator instructional structure. The primary purpose of the inductive approach is to allow research findings to emerge from the frequent, dominant, or significant themes inherent in raw data; (e) If the measurement dimension was not closely associated by any conceptual indicator, but appeared quite often in the empirical instruments, we assigned them to a unified label, such as Technology, Assessment, Content, and Presentation. This process led to broader operational indicators that might neither be embedded in any basic dimension of the German framework nor be described in their conceptual definitions.

In inductive coding, the coded indicators were continuously revised and refined. During the process, coders searched for new insights, including contradictory points of view, and consequently gained joint understanding of the coding system. If new codes emerged, the coding frame was changed according to the new structure. Finally, a hierarchical framework of specific operational indicators was developed inductively. We identified 27 operational indicators on the second level and 15 on the third level corresponding to one of the basic dimensions, which were deductively coded as the first level of the hierarchical framework. A complete list of these operational indicators can be found in Table 2.

TABLE 2

Table 2. Frequency table of the identified operational indicators (Inductive Coding).

Results

Conceptual definitions and conceptual indicators for basic dimensions (Q1)

We analyzed the conceptual indicators derived from the conceptual definitions given in the 10 selected texts for each basic dimension. In the section, we will present the conceptual indicators across all texts (Q1a), as well as results on the variability in conceptual definitions (Q1b).

Classroom management

According to Klieme et al. (2009, p. 141), Classroom Management requires teachers to “establish clear rules and procedures, manage transitions between lesson segments smoothly, keep track of students’ work, plan and organize their lessons well, manage minor disciplinary problems and disruptions, stop inappropriate behavior, and maintain a whole-group focus.” Going beyond the original definition, Table 3 shows the conceptual indicators identified in the conceptual definitions of the basic dimension Classroom Management. To further systematize the conceptual indicators, we divided them into a set of sub-dimensions. The same sub-dimensions of the three-dimensional framework (see Appendix 1) were found within the conceptual definitions: disruptions and discipline problems (D), effective time use/time on task (T), monitoring/withitness (M), and clear rules and routines (R). Beyond this classification, the indicator referring to planning instruction (P) emerged as an additional sub-dimension. The resulting classification for analyzing the conceptual indicators is presented in the second column of Table 3.

TABLE 3

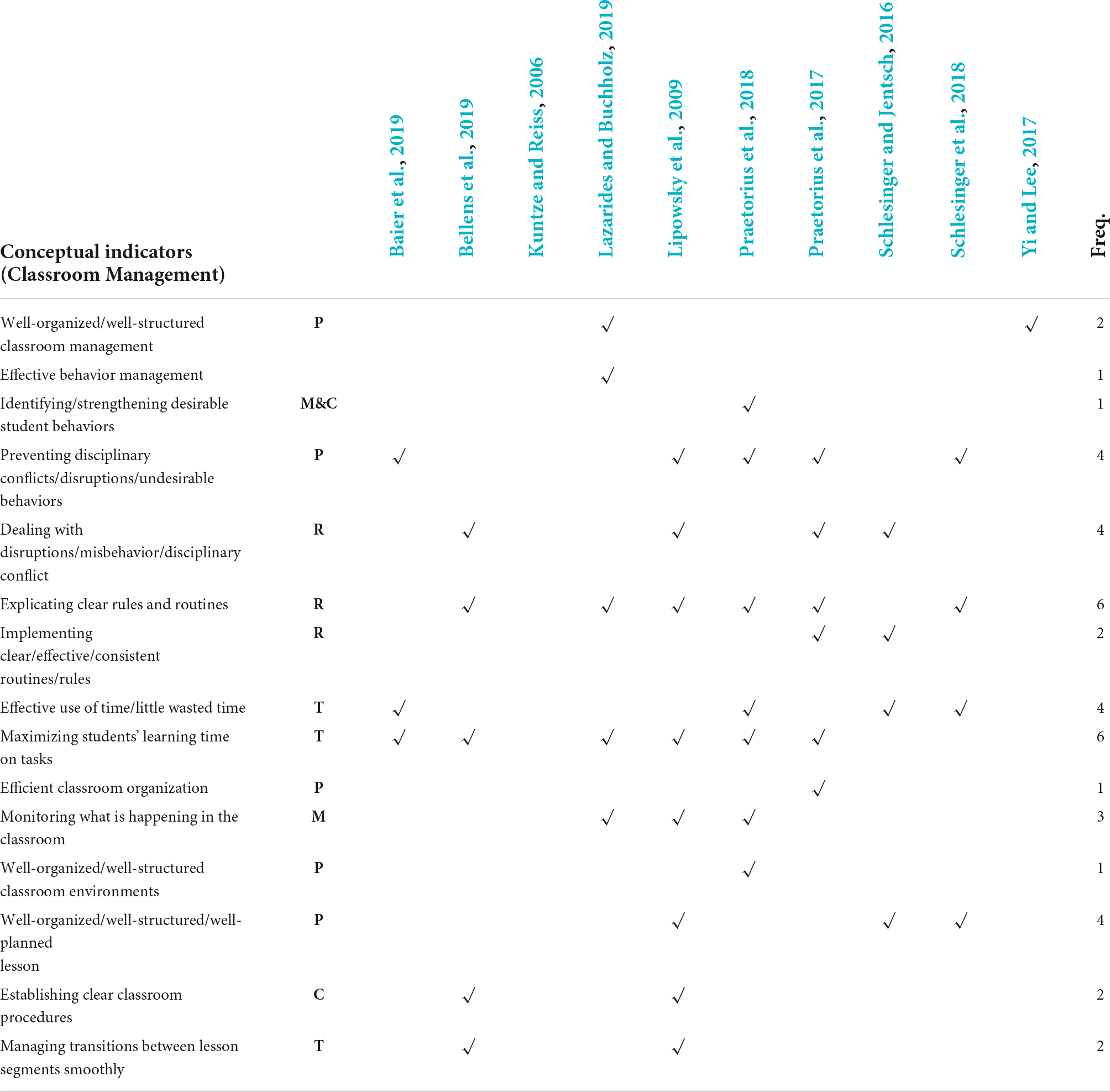
Table 3. Overview of conceptual indicators of Classroom Management described by various conceptual definitions in previous studies.

The most frequent conceptual indicators used for classroom management are explicating clear rules and routines, dealing with and preventing disruptions/misbehavior/disciplinary conflict (taken together here), and maximizing students’ learning time on task.

Some conceptual indicators are described in more abstract terms, and combine other conceptual indicators. For example, Lazarides and Buchholz (2019) conceptualized classroom management as a form of effective behavior management in class. Meanwhile, Lipowsky et al. (2009) and Praetorius et al. (2018) claimed that there are various ways to manage behavior management in the classroom: identifying and strengthening desirable student behaviors, preventing disruptions and minimizing the likelihood of disciplinary problems, and dealing with misbehavior, disruptions, and conflicts.

However, some terms are used in the conceptual definitions, which are not straightforward to compare. For example, Schlesinger et al. (2018) argued that structured and well-organized lessons are evidence-based characteristics of effective classroom management. Well-organized and well-structured classroom environments have been identified by Praetorius et al. (2018) as one of the core components of successful instruction. More abstractly, Lazarides and Buchholz (2019) mention well-organized classroom management. To what extent well-organized lessons and well-organized classroom environments should be taken as the same thing or point to different aspects of instruction is not clarified in the literature.

Prior studies have mentioned aspects of classroom management, which are specific to subjects (other than mathematics; Praetorius et al., 2020). In line with the generic nature of the three basic dimensions framework, however, the reviewed conceptual definitions of classroom management did not consider aspects that could be identified as specific to mathematics education.

Student support

The original idea behind the basic dimension is “supportive teacher–student relationships, positive and constructive teacher feedback, a positive approach to student errors and misconceptions, individual learner support and caring teacher behavior” (Klieme et al., 2009, p. 141). In line with this, the most frequently mentioned indicators of student support are: Providing constructive/positive feedback, offering individual/differentiated/personal support, positive/supportive/caring/respectful classroom climate, and supportive student–student relationships. As shown in Table 4, the sub-dimensions adopted from the general framework are support of competence experience (SC), autonomy experience (SA), and support of social relatedness experience (SS). Additionally, the sub-dimensions referring to general learning support (LS), adaptive teacher support (A), and feedback (F) emerged from the analysis.

TABLE 4

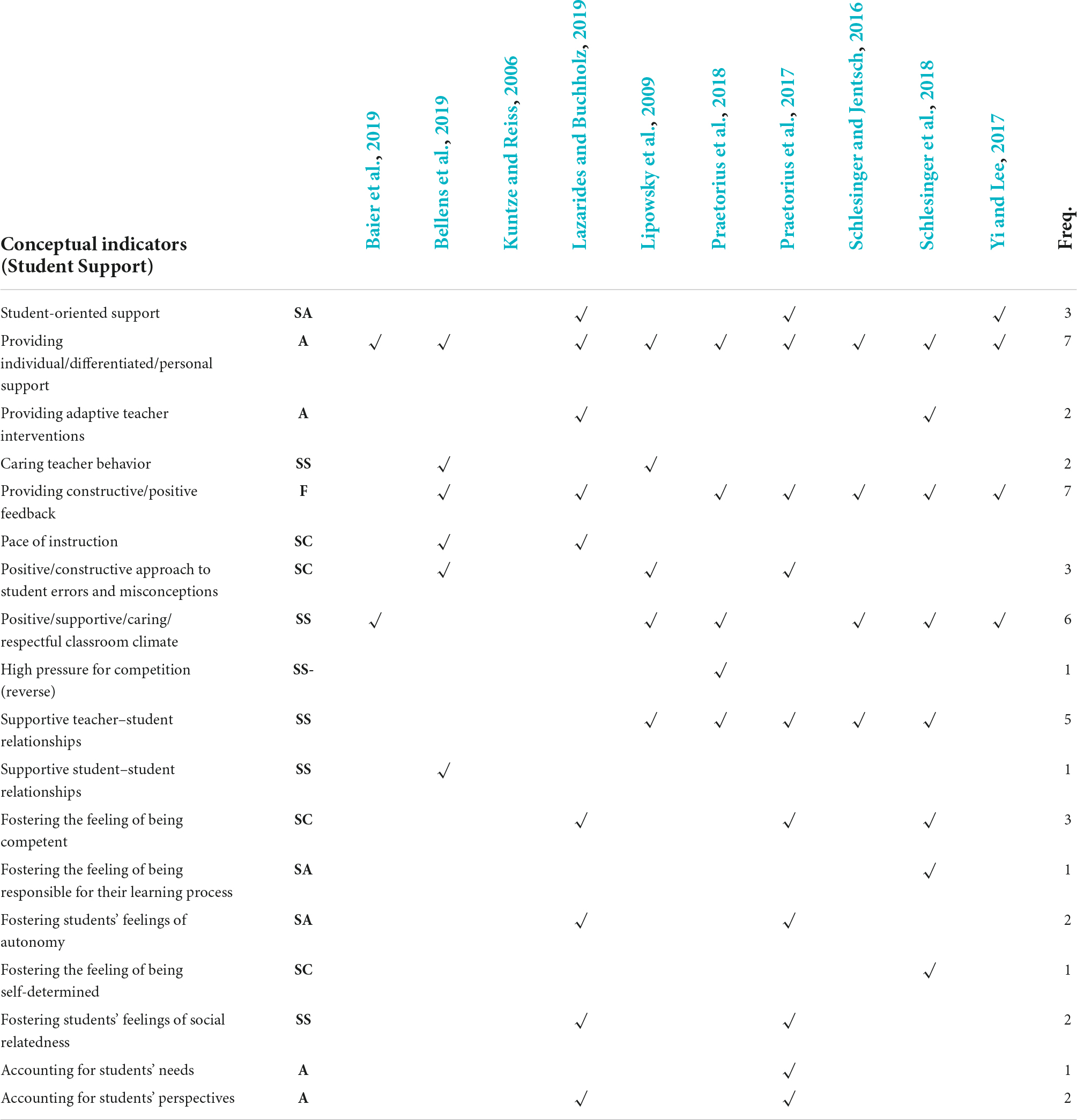
Table 4. Overview of conceptual indicators of Student Support described by various conceptual definitions in previous studies.

Confusion remains in naming the different conceptual indicators. In the conceptualization of Klieme et al. (2006), according to Lipowsky et al. (2009), the construct of supportive classroom climate covers a bunch of features of teacher behavior, which include caring teacher behavior. The indicators, however, are not clearly defined here. Averill (2012) describes a broad range of specific “caring” teacher behaviors, including involving students in classroom decision-making, using “safe” questioning practices (i.e., those that do not expose students to potential embarrassment or intimidation), creating a sense of shared endeavor, encouraging and expecting respectfulness and being respectful of students, and incorporating specific pedagogies such as collaborative work, stories and narratives, and journaling.

Student support is conceptualized as an overarching dimension of teaching behaviors in some studies, which aim to enhance students’ feelings of autonomy (Praetorius et al., 2017; Schlesinger et al., 2018). Yet present these approaches diverge in the definition of the term “autonomy.” Dickinson (1995) considers autonomy as measured in terms of three shared key concepts: learner independence, learner responsibility, and learner choice. Praetorius et al. (2017) argued that autonomy is closely aligned with and derived from self-determination theory, but they also included other basic needs, such as feeling competent, or being socially integrated, as part of teacher support. Therefore, despite a relatively simple conceptual definition, the construct of student support is connected to a wide range of varying conceptual indicators, which makes it difficult to compare results over studies.

In spite of this wide range of conceptual indicators, our review only identified a few aspects in the conceptual definitions of student support, which could be seen as subject-specific to mathematics. The most prominent aspect could be a positive and encouraging approach to errors and misconceptions, which has attracted specific attention in the field of mathematics (but may be of some, though varying importance also in other subjects). It comprises interventions by the teachers, which help students to deal with negative emotions when dealing with their own errors or misconceptions (Rach et al., 2012; Tulis, 2013; Kyaruzi et al., 2020).

Cognitive activation

Klieme et al. (2009, p. 140) integrated “these key features of mathematical instruction—challenging tasks, activating prior knowledge, content-related discourse and participation practices within the construct of cognitive activation.” The most frequently mentioned indicators of cognitive activation are: Activating prior knowledge, providing cognitively challenging tasks, promoting higher-level thinking, and supporting conceptual/deep understanding. The resulting classification thus comprises challenging tasks and questions (CT), exploring and activating prior knowledge (PK), and discursive and co-constructive learning (D). Moreover, exploration of the students’ ways of thinking/elicit student thinking (T) and supporting metacognition (M) emerged as additional sub-dimensions.

Compared with the other two basic dimensions, the underlying conceptual indicators of Cognitive Activation are more diverse in nature. This indicates that the nature of this basic dimension may be more complex and diverse than the other two.

In Table 5 it can be seen that the most frequently mentioned indicator in the conceptual definition is higher-order thinking. For example, according to Lipowsky et al. (2009), cognitive activation is an instructional practice that encourages students to engage in higher-level thinking and thereby develop an elaborated knowledge base. In cognitively activating instruction, the teacher stimulates the students to disclose, explain, share, and compare their thoughts, concepts, and solution methods by presenting them with challenging tasks, cognitive conflicts, and differing ideas, positions, interpretations, and solutions.

TABLE 5

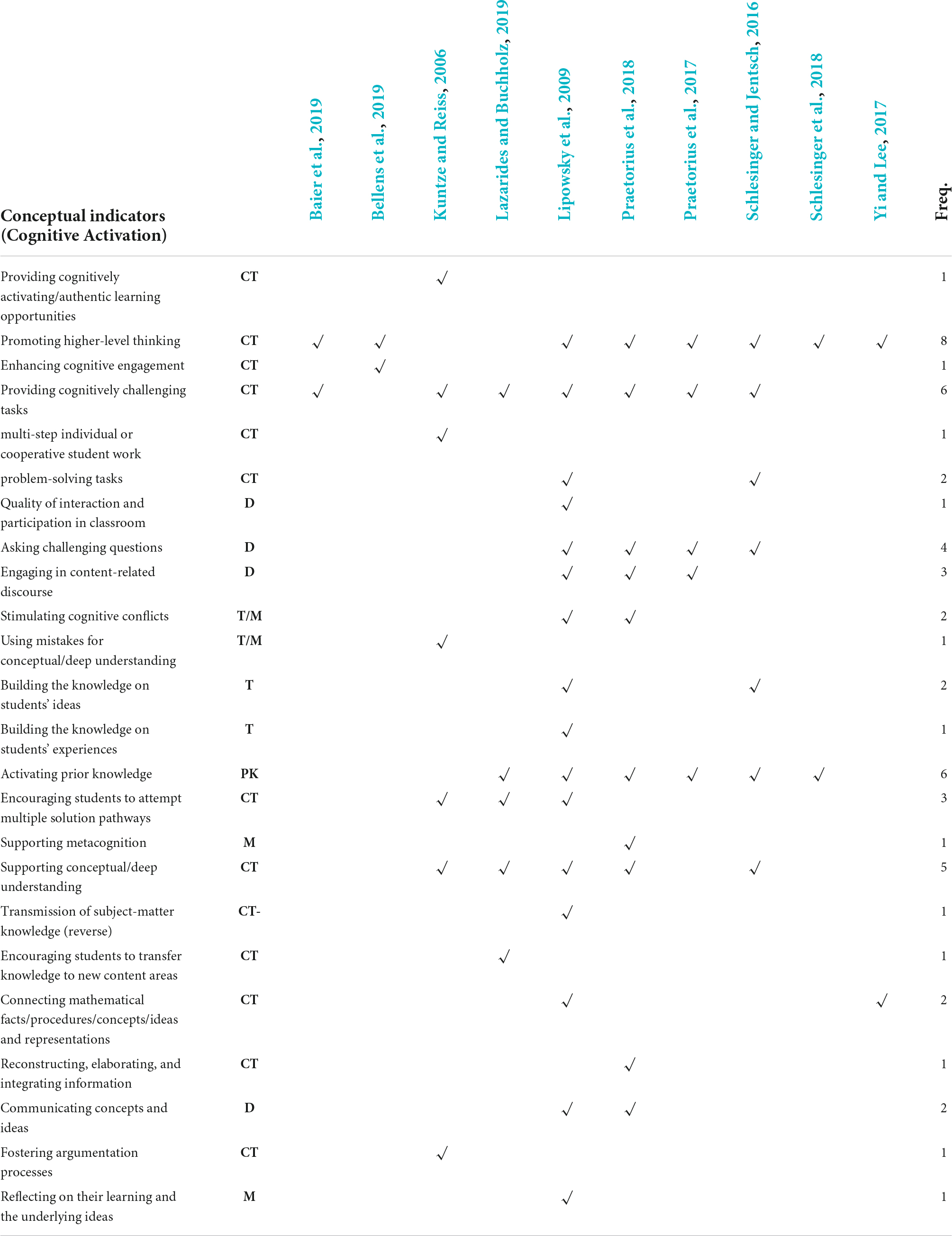
Table 5. Overview of conceptual indicators of Cognitive Activation described by various conceptual definitions in previous studies.

Divergent opinions exist with regard to facilitating higher-order thinking. An incomplete list of the instructional practices assumed to facilitate higher-order thinking include encouraging students to transfer knowledge to new content areas (Lazarides and Buchholz, 2019), connecting mathematical facts/procedures/concepts/ideas and representations (Lipowsky et al., 2009; Yi and Lee, 2017), reconstructing, elaborating, and integrating information (Praetorius et al., 2018), providing problem-solving tasks (Lipowsky et al., 2009; Schlesinger and Jentsch, 2016), fostering argumentation processes (Kuntze and Reiss, 2006), and reflecting on their learning and the underlying ideas (Lipowsky et al., 2009).

Lipowsky et al. (2009) pointed out that the quality of interaction and participation in classrooms is another important means of cognitive activation. In cognitively activating classrooms, interaction is characterized by the teachers’ use of questions to stimulate students to think critically about concepts, to use them in problem-solving, decision-making or other higher-order applications, and to engage in discourse about their own ideas about these concepts and their application (Brophy, 2000).

The qualitative content analysis used to identify the conceptual indicators was based on the conceptual definitions of three basic dimensions, which have to be considered to be geared toward a generic subject-overarching conceptualization (Charalambous and Praetorius, 2018). Therefore, it is important to mention that some of these conceptual indicators also contain aspects that are closely associated with the content to be taught or special pedagogic methods commonly used in mathematics education. Most subject-specific aspects, within the identified conceptual indicators for cognitive activation, include (a) a constructive, learning-oriented approach to student errors and misconceptions, which was specifically discussed from a mathematical perspective in several studies (Rach et al., 2012; Tulis, 2013; Heemsoth and Heinze, 2014); (b) encouraging students to attempt multiple solutions: Multiple solution methods are discussed in mathematics education to build up well-connected knowledge about mathematical concepts and procedures (Achmetli et al., 2019) and to support students’ interest and self-regulation (Schukajlow and Rakoczy, 2016). Lipowsky et al. (2009) regarded it as a reverse indicator if students are requested to solve mathematical problems and tasks in a standard manner previously demonstrated by the teacher. In Cognitive Activation in the Classroom (COACTIV, Bruckmaier et al., 2016), subject-specific PCK was measured by asking teachers to provide multiple solutions to a problem; (c) using and connecting different representations, which can further contribute to gaining a deeper understanding of the learning contents (Goldin, 1998; Duval, 2006; Große, 2014); and (d) providing adaptive teacher interventions. Supporting students’ mathematical proficiency requires teachers to continuously adapt their instruction in response to their students’ instructional needs (Gallagher et al., 2022).

Measurement dimensions and operational indicators for basic dimensions (Q2)

The second research question concerns as to what extent is it possible to assign the measurement dimensions found in the literature to one of the three basic dimensions of Klieme et al.’s framework based on the operational indicators they use to assess instructional quality. In the 112 reviewed publications, 292 coding frameworks to measure Instructional Quality were investigated either theoretically or empirically. They included 2,127 measurement dimensions, and 63.5% of the identified measurement dimensions (N = 1,351) have the associated explicit operational definitions that could be used to try to assign them to one of the three basic dimensions. In the other cases, assignments were—whenever possible—based on the name of the measurement dimensions and overarching measurement dimensions they were assigned to in the manuscript. Table 6 shows the results. While the fewest measurement dimensions (13%) referred to classroom management, cognitive activation accounted for the highest (31%). Notably, 34% of the measurement dimensions could not be assigned to one of the three basic dimensions.

TABLE 6

Table 6. Frequency table of the identified measurement dimensions crossing three basic dimensions (deductive coding).

Classroom management and student support were originally conceptualized as generic dimensions without referring to a specific subject (Klieme et al., 2009). In the current study, a number of measurement dimensions show some subject-specificity—while often on a superficial level. For instance, the subject-specific nature of Classroom Management is revealed by adding an adverbial phrase (e.g., in math lessons, it is obvious what we are or not allowed to do. In mathematics, it takes a very long time at the start of the lesson until the students settle down and start working. In mathematics, our teacher makes sure that we pay attention). The adverbial phrases do not modify in any way the fundamental meaning of the measurement dimensions. Similarly, student support can be subject-specific by emphasizing the subject of the teachers (e.g., our mathematics teacher does his/her best to respond to students’ requests as far as possible. Our mathematics teacher tells me how to do better when I make a mistake. Our mathematics teacher is concerned). In this case, mathematics, however, can be easily replaced by any other subject, such as biology or English.

Beyond these more formal references to the subject, other instruments clearly refer to the content at hand as a norm to evaluate instruction. For example, instead of capturing teacher–student communication in general, these instruments attend to the interactions through a content-related lens, examining aspects and focusing on the mathematical precision and accuracy in communication and the appropriateness of the mathematical language and notations used (Charalambous and Praetorius, 2018).

Most examples of operational indicators that are substantially associated with the specific subject could be assigned to basic dimension cognitive activation: Challenging Tasks (e.g., our mathematics teacher modifies tasks in a way that allows us to recognize what we have understood); Using Mistakes for Deep Understanding (remediating student errors and difficulties: substantially addressing students’ misconceptions and difficulties with math); Encouraging Students to Attempt Multiple Solutions (e.g., comparing or considering multiple solution strategies for a mathematical problem; our mathematics teacher provides us with tasks that do not have a clear solution and lets us explain this); Using and connecting different representations (e.g., whether manipulatives or drawn representations were used for this purpose; whether the representations were appropriate for explaining the algorithm; whether the representation was explicitly and completely mapped to the algorithm); Building the Knowledge on Students’ Ideas, Experiences, and Prior Knowledge (e.g., the teacher uses mathematical contributions: captures whether and how the teacher responds to and builds on students’ mathematical product).

Some of the operational indicators that are substantially associated with a specific subject could not be assigned to any of the generic dimensions. This refers to specific ways of assessment (e.g., in a math problem, my teacher values the procedure and not just the results), or to Content Selection and Presentation (e.g., the teacher focuses on the fundamental mathematical aspects. The teacher initiates the adequate use of mathematical language). Some measurement frameworks took into account indicators like the depth of the mathematical lesson; the Richness of the mathematics; or Mathematical focus, coherence, and accuracy. The application of technology that was specifically developed for working mathematically (e.g., spreadsheet software) or mathematics learning can be seen as further examples of subject-specific indicators (e.g., Use a wide variety of materials and resources, such as games, puzzles, riddles, and technological devices, for teaching and learning mathematics. Use computers and digital technologies as tools in teaching mathematics.).

How can the conceptual (from Q1) and operational indicators (from Q2) be synthesized to sharpen and extend the basic dimensions framework? (Q3)

In the next step, the operational definitions of the measurement dimensions in the literature were analyzed and classified. Table 2 provides an overview of the operational indicators, which were identified through inductive coding. Although not shown in the table, some measurement dimensions in the literature were too general to derive meaningful operational indicators, since they tended to address overall evaluations of Instructional Quality (N = 13), or only named general constructs, such as one of the three basic dimensions—Classroom Management (N = 44), Cognitive Activation (N = 108), and Student Support (N = 31).

One of the challenges in this assignment was that many measurement dimensions address more than one operational indicator, such as “Challenging tasks and questions,” or “Lesson structuring and assessment.” In this case, the measurement dimensions were counted for both operational indicators.

N = 52 operational indicators were found to be reverse-scored items. Among them, the most common items that are negatively worded are assigned to Higher-Order Thinking (N = 11, e.g., memorizing formulas and procedures; doing similar exercises over and over again) and Time Management (N = 7, e.g., Students do not start working for a long time after the lesson begins; A lot of time gets wasted in mathematics lessons).

In Table 2, we further examined if the identified operational indicators are corresponding to the conceptual indicators summarized above (Q1), and if the operational indicators were already described in the previous general framework outlined by Praetorius et al. (2018). This illustrative list of indicators serves to indicate both the overlaps and the differences between existing conceptual and operational definitions. Certain subtle differences, which cannot be simply attributed to inclusions (√) and deletions (–), were highlighted with question marks.

Overlapping area of the identified conceptual and operational indicators

Question 3a is concerned with the overlapping area of yellow and blue ellipses in Figure 1, that is, what characteristics of classroom instruction occur as conceptual as well as operational indicators for each basic dimension of instructional quality. In addition, we considered which of the indicators mentioned above go beyond the definitions of the basic dimensions by Klieme et al. (2009). In general, our analysis indicates that, the original German framework of three basic dimensions are covering fewer constructs, compared with the understanding of the basic dimensions in Tables 2–5. Some adjustments can be suggested to extend the three-factor general framework in light of the review conducted above.

In short, some of the operational indicators used in measurement dimensions assigned to the basic dimensions in the literature and some conceptual indicators used to characterize them go beyond the conceptual indicators described by Klieme et al. (2009). Therefore, we suggest adjustments to ensure that the new framework comprehensively reflects the conceptualization and measurement of these basic dimensions in the literature.

Moreover, some measurement dimensions used in the literature could not be classified to the three basic dimensions. Accordingly, we propose basic dimensions for an extension of Klieme et al.’s (2009) model, which reflects a broader spectrum of measurement dimensions used in the literature. In the diagrams visualizing these suggestions.

• Red circles with red area refer to the three original basic dimensions.

• Red boxes with red area describe groups of operational indicators outlined by Praetorius and Charalambous (2018).

• Dual color boxes with gray area describe groups of indicators that occur as conceptual indicators in conceptual definitions and in measurement dimensions in the literature, but not in the Klieme et al. (2009) framework.

• Blue-dotted boxes describe groups of indicators that do not occur as conceptual indicators in conceptual definitions in the literature, but occur in measurement dimensions in the literature, which can be assigned to the basic dimension.

• Blue-dotted circles with white area describe basic dimensions we suggest to be added to the framework.

• Blue boxes with white area describe those indicators irrelevant to instructional quality.

Classroom management

As shown in Figure 3, besides the four indicators that already existed in the three-dimensional framework, namely (Lack of) disruptions and discipline problems (Effective) time use/time on task, Monitoring/withitness and Clear rules and routines, Classroom Organization and Learning Environment should be considered as additional indicators to measure Classroom Management. This extension is based on the conceptual definition of the basic dimension as well as supported by empirical evidence. Similarly, an indicator at the upper level, which can be further divided into a set of sub-indicators, is assumed to be insightful to assess the instructional structure in the mathematics classroom.

FIGURE 3

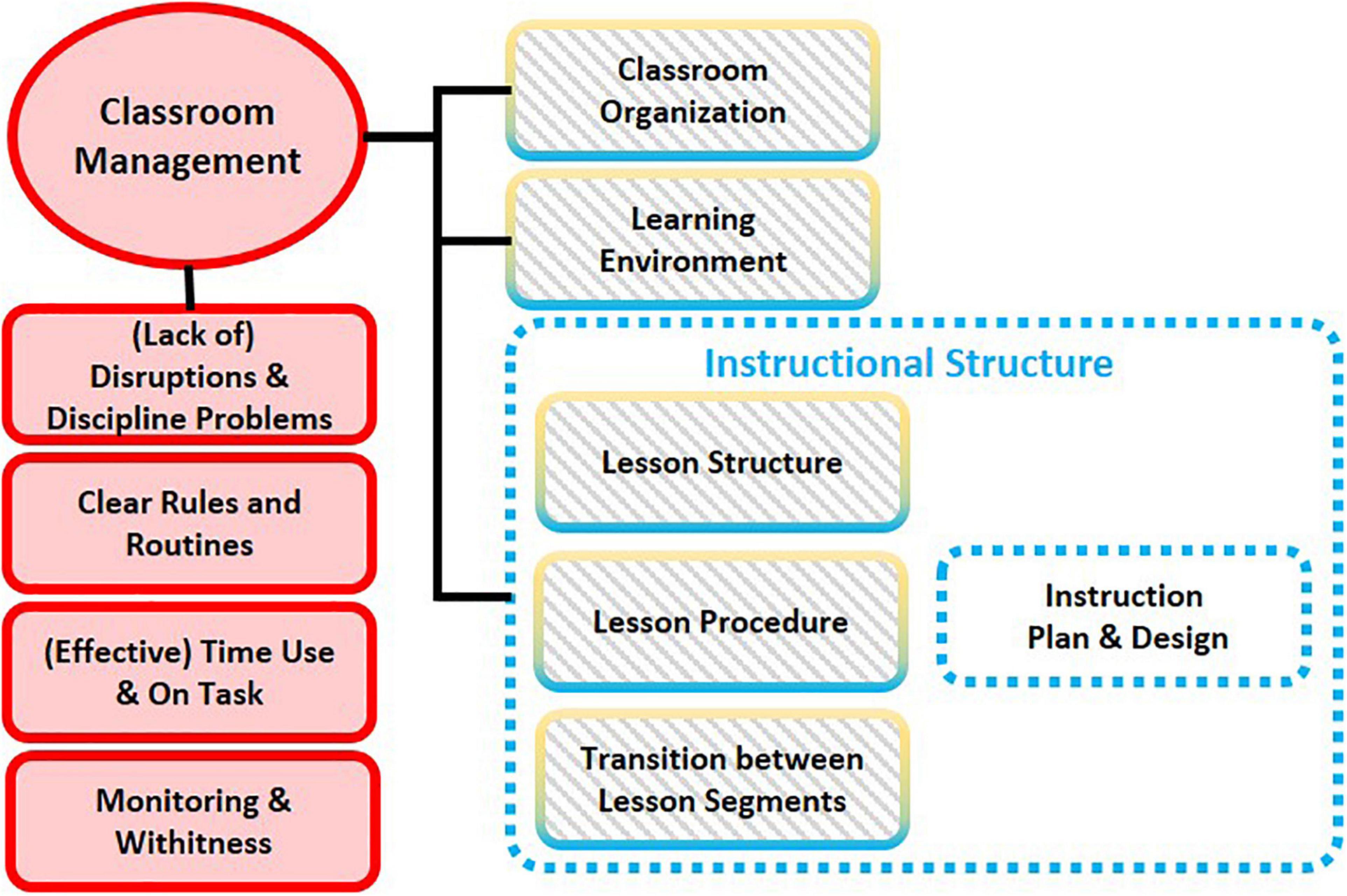
Figure 3. Suggested adjustments on the measurement framework of Classroom Management according to the comparison between conceptual indicators and empirical measurement dimensions.

Student support

In the existing three-dimensional framework (As shown in Figure 4), Student Support is assessed from three major perspectives: Support of Competence Experience, Support of Social Relatedness Experience, and Support of Autonomy Experience. In the refined framework, we suggest to add two more indicators, that is, Emotional Support and Positive Climate. The latter one is somehow opposite to the negative indicator of Support of Autonomy Experience—Performance Pressure and Competition.

FIGURE 4

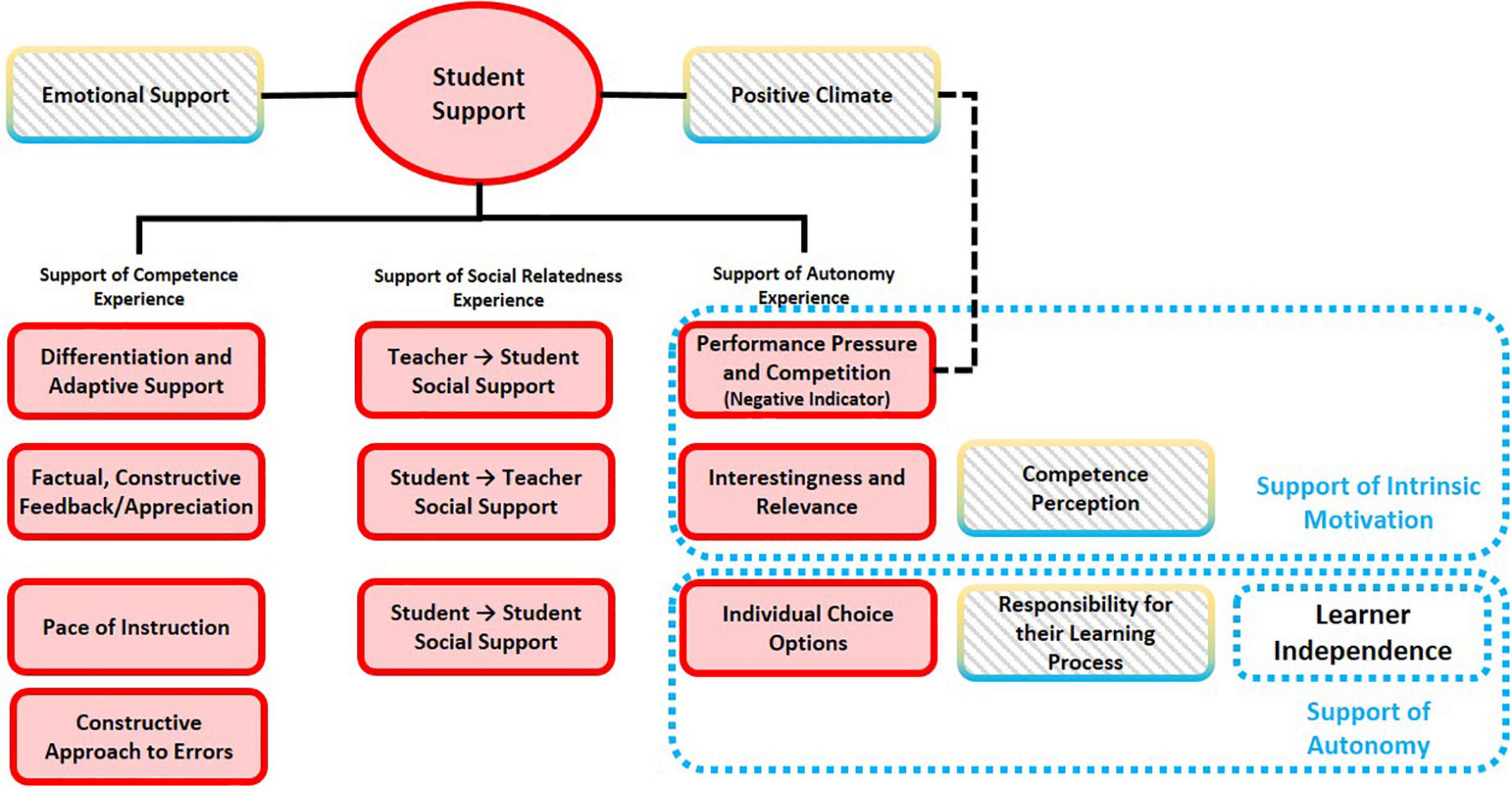
Figure 4. Suggested adjustments on the measurement framework of Student Support according to the comparison between conceptual indicators and empirical measurement dimensions.

The original three-dimensional framework presents a mixed perspective that combines different indicators to assess the sub-dimension Support of Autonomy Experience. Confusion can be caused by the indicators that obviously do not belong to the sub-dimension of Autonomy such as Interestingness and Relevance, Performance Pressure and Competition. According to the Intrinsic Motivation Inventory (IMI; Ryan, 1982; McAuley et al., 1989), interest/enjoyment is considered the self-report measure of intrinsic motivation; the perceived competence concepts are theorized to be positive predictors of intrinsic motivation, and pressure/tension is theorized to be a negative predictor of intrinsic motivation. In addition, based on the conceptual analysis of the indicators related to support motivation and autonomy, we suggest to integrate more indicators in the framework, and a reconstruction of the indications seems to be more consistent with the three shared key concepts of autonomy identified by Dickinson (1995), namely, learner independence, learner responsibility, and learner choice. Therefore, we suggest integrating more operational indicators identified from the literature and refining the structure of indicators based on the conceptual definitions of the complex constructs Intrinsic Motivation and Autonomy, which can be further regarded as the upper level of the sub-dimension of the basic dimension Student Support.

Note that in Praetorius and Charalambous (2018), the student support dimension was divided into a socio-emotional dimension capturing aspects of social relatedness, and a dimension capturing cross-cutting instructional aspects to maximize student learning, capturing most of what refers to adaptive teacher behavior (e.g., differentiation and adaptive support) and autonomy support in our categorization.

Cognitive activation

This analysis of conceptual and operational definitions leads to wide-ranging indicators, which partially reflect the conceptual definition of Cognitive Activation from the original basic dimension framework. Further operational indicators, however, suggest reorganizing the original framework, and extending it by additional conceptual indicators. As shown in Figure 5, the general idea is to differentiate Cognitive Activation into aspects of teachers’ active facilitation during instruction, the choice of challenging tasks for instruction, and students’ cognitive engagement in higher-order thinking. The current framework contains a number of indicators that can be assigned to the sub-dimension of teachers’ cognitive facilitation. Our analysis added further indicators for this sub-dimension, which are specifically discussed for mathematics classroom instruction, such as using encouraging solutions, using mistakes, stimulating cognitive conflict, or fostering argumentation.

FIGURE 5

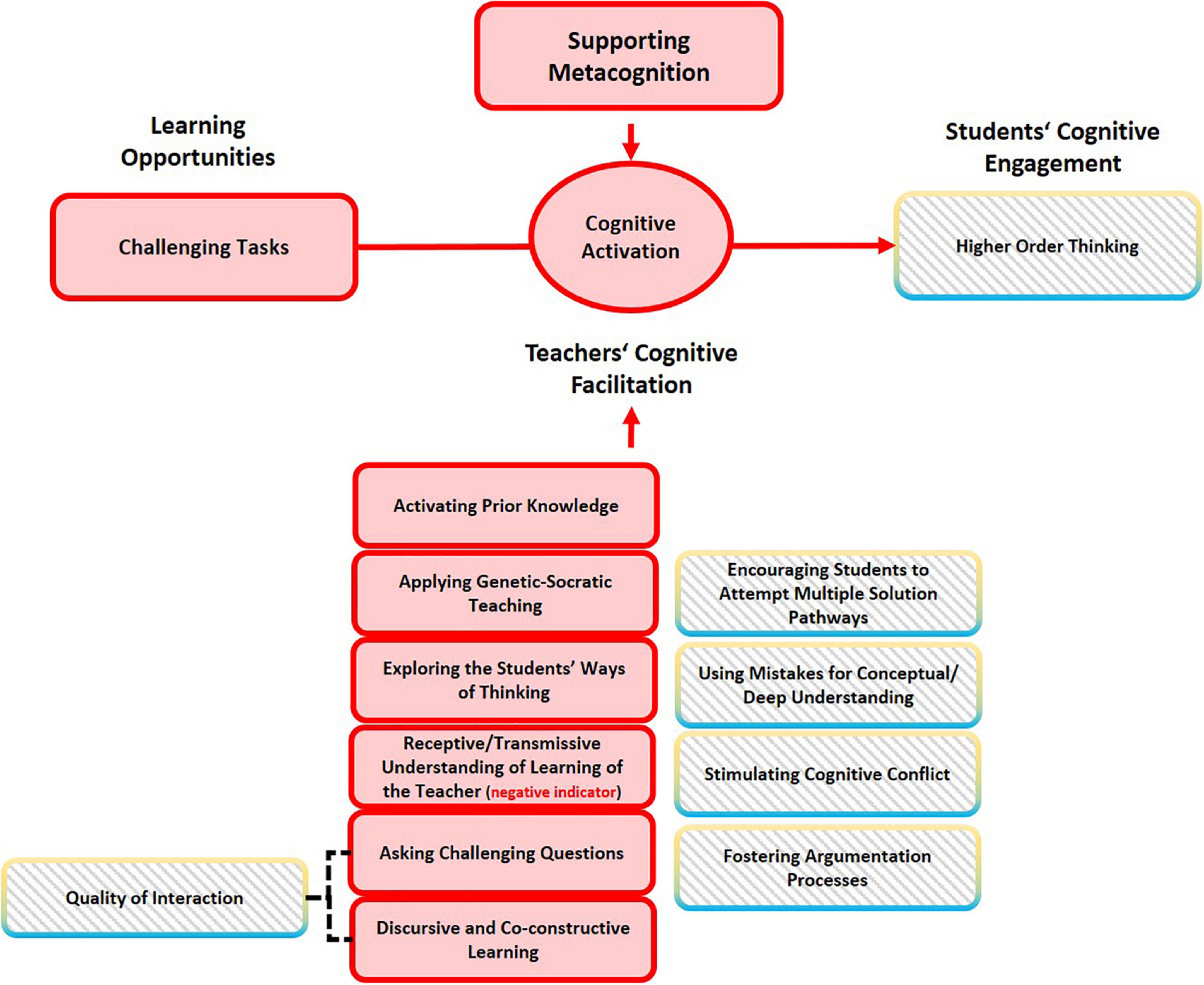
Figure 5. Suggested adjustments on the measurement framework of Cognitive Activation according to the comparison between conceptual indicators and empirical measurement dimensions.

As an aspect of mediation, students’ cognitive engagement in higher-order thinking reflects their responses to teachers’ facilitation.

Concept underrepresentation (Q3b)?

Regarding Question 3b, all the conceptual indicators identified from the conceptual definitions were operationalized to measure instructional quality in previous empirical studies. As shown in Tables 3–5, all conceptual indicators can be assigned to one major sub-dimensions defined by the original German framework of the Three Basic Dimensions. Therefore, concept underrepresentation does not seem to be a major issue. Furthermore, this perspective does indicate that “blind spots” do not exist in the empirical research on the basic dimensions. However, as we mentioned above, some conceptual indicators may not find exactly corresponding operational indictors in the literature. For example, the operational indicator Emotional support might be marginally different from the conceptual indicator Caring teacher behavior.

Construct irrelevance (Q3c)?

Regarding Question 3c, empirical evidence with respect to Construct Irrelevance was found in the analysis. A group of operational indicators used in empirical research was not covered by the definition of instructional quality: School Level Management (N = 10), Teaching Resource (N = 7), Student Characteristics (N = 12), Student Performance (N = 4), and Teacher Quality (N = 85). For example, given the widespread agreement that teachers must know teaching strategy, teacher characteristics predict teachers’ effectiveness and, in particular, how well they succeed in providing high-quality instruction that fosters student learning (Kunter et al., 2013), it is surprising that several empirical studies have conceptualized instructional quality as teacher quality (e.g., mathematical content knowledge, Mathematical pedagogical knowledge, communication skills and personal commitment). Some studies have also used student characteristics (e.g., students’ social skills, knowledge of learners), and performance (e.g., in this class, we learn a lot almost every day) as indicators of instructional quality.

How can the operational indicators (from Q2) belonging to measurement dimensions, which cannot be assigned to the three basic dimensions, be grouped into new factors of instructional quality (Q3d)?

A number of measurement dimensions could not be matched to the three basic dimensions (Q2). The corresponding operational indicators seemed to be irrelevant to instructional quality, when the perspective of the three basic dimensions framework is taken—even taking into consideration a broader perspective on the framework based on our analysis of conceptual definitions in the literature. These indicators partially related to constructs, that we did not subsume under instructional quality in our understanding, for example, measures related to Student Performance, Student Characteristics, Teacher Quality, and School Level Management (cf. boxed outside “general quality assessment” in Figure 6). In the last step of our analysis, we systematized the remaining non-assignable measurement dimensions into coherent categories. Taking the three additional overarching dimensions assessment, practice and application, and content selection and presentation from Praetorius and Charalambous (2018), as a starting point, all remaining measurement dimensions could be assigned to one overarching dimension (cf. Figure 6). For example, indicators such as Content Accuracy, Instructional Clarity, and the usage of Math Language could be subsumed under content selection and presentation.

FIGURE 6

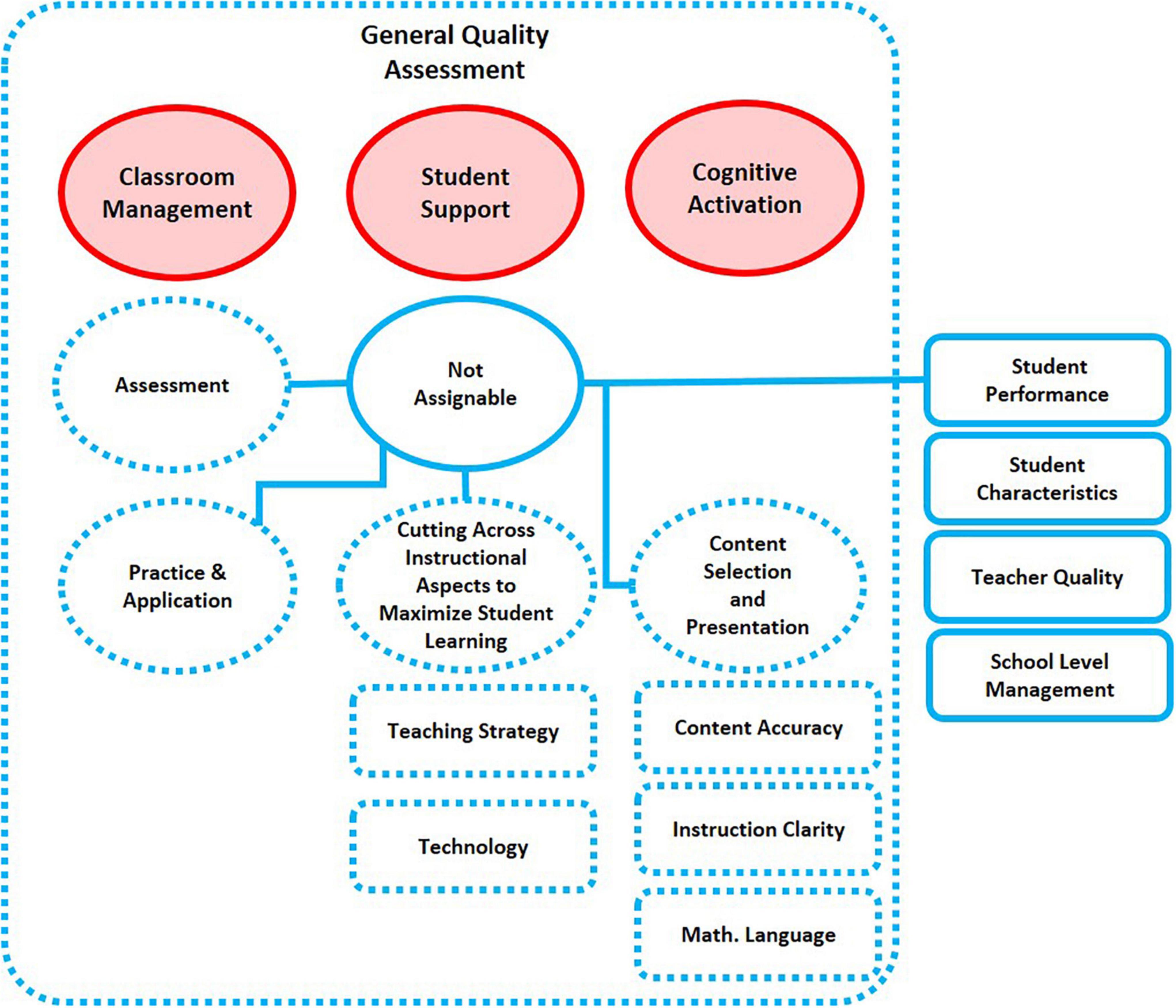
Figure 6. Suggested adjustments on the overall measurement framework according to the comparison between conceptual indicators and empirical measurement dimensions.

Different from teachers’ pedagogical knowledge, Teaching Strategy is the way teachers use different classroom practices to foster learning. This operational indicator is commonly used (N = 115) as a measurement item in the literature (e.g., Demonstrate a variety of teaching methods, Include effective strategies of conducting the class in teaching mathematics, Students work together through cooperative learning). To some extent, this indicator can be allocated to the dimension capturing cutting across instructional aspects to maximize student learning, which was proposed by Praetorius and Charalambous (2018) to cluster together instructional aspects, such as adaptation, active engagement, and creating an environment that nurtures productive habits (e.g., agency, ownership/autonomous learning). Note that in the present study, we formulate the need for a new account of cutting across instructional aspects. Another indicator of receiving increasing attention, which can be integrated under this measurement dimension is Technology. While the findings on the role of Technology are not universal in assessing instructional quality, a few experimental data have proved the necessity of this extension.

Discussion

The German framework of Three Basic Dimensions (Klieme et al., 2009) has been used as a conceptual foundation for instructional quality measurement and analysis frequently in the past. Both conceptual and operational definitions of the basic dimensions must represent and capture the diversity of indicators that characterize these dimensions, so that the complex construct can be measured reliably and validly. Inspired by reflections on instructional quality given by Praetorius et al. (2018) who summarized the differences and commonalities in the operationalization of three basic dimensions in classroom observation instruments, this review attempts to clarify the construct of instructional quality. We examined how basic dimensions for the mathematics classroom were conceptualized in the literature and how empirical studies operationalized them. The methodological novelty of this study was the introduction of the systematic review of conceptual and operational indicators and their comparative analysis to determine the convergence and divergence between the two types of indicators. As a result, we suggested a broader and more comprehensive framework for assessing instructional quality.

Regarding the conceptual definitions of the basic dimensions, we noted that a number of studies did not report a conceptual definition of the basic dimensions focused in the manuscript. A close analysis of the existing definitions in the literature revealed that, although coherent in many aspects, the details vary from manuscript to manuscript. This regards, naturally, the naming of the different conceptual indicators. Beyond this, some conceptual indicators used in the manuscripts are relatively broad, leaving much room for different interpretations, and comprising a number of more specific indicators from other manuscripts. This study suggests conceptual definitions of the basic dimensions in terms of conceptual indicators to provide a more robust frame for empirical measurement of the dimensions. It reflects more or less the union of all aspects that are subsumed under a single basic dimension. Therefore, the conceptualizations proposed in our work are definitely more explicit than the original description by Klieme et al. (2009), and at some places also broader (in terms of newly integrated indicators, e.g., instructional structure, support of autonomy, and teachers‘ cognitive facilitation).

It is perhaps not surprising that a large variety of operational indicators used to measure instructional quality exists in the literature. However, not all studies provide sufficiently detailed information on their operational definitions and the applied operational indicators to achieve a clear classification. Future studies should be more explicit in how they conceptualize and measure constructs of instructional quality.

A majority of the operational indicators found in the literature can be assigned to one of the three basic dimensions. This underpins that the basic dimensions framework captures a broad range of classroom characteristics subsumed under instructional quality. However, the relationship between the operational indicators used in these studies and the conceptual indicators drawn from the review of conceptual definitions is complex.

Almost all conceptual indicators identified in the literature for the three basic dimensions could actually be matched to operational indicators found in empirical studies. This indicates that the proposed conceptualization of basic dimensions of instructional quality is supported by corresponding instruments used in the field.

Meanwhile, some operational indicators, which were assigned to basic dimensions, could not be matched to conceptual indicators that characterized the corresponding dimension. Examples are Learner Independence for Student Support and Instruction Plan and Design for Classroom Management. Accordingly, the proposed new framework extends previous conceptual definitions for these basic dimensions.

For Cognitive Activation, contrarily, all identified operational indicators correspond to some conceptual indicator. This indicates that for Cognitive Activation, theoretical conceptualizations and empirical measurements are relatively consistent, when taking a broad perspective across a large variety of manuscripts. Nevertheless, several of the identified conceptual indicators go beyond the original conceptualization of Classroom Management as proposed by Klieme et al. (2009), for example, Quality of Interaction, Using Mistakes for Conceptual/Deep Understanding, and Stimulating Cognitive Conflict.

Therefore, we can arguably claim that there is a need for extension of the conceptualization of the basic dimensions in the original framework by Klieme et al. (2009), so that it reflects a “core understanding” (in the sense of the overlap between operational and conceptual indicators) in the current literature. A concrete proposal for this extension, based on an extensive literature review, has been made in the results section.

Moreover, attempts have been made before to extend the basic dimension framework by additional overarching dimensions of instructional quality, beyond the three from the original framework. However, these analyses (e.g., Praetorius and Charalambous, 2018) were based on a specific subset of the literature, namely classroom observation instruments. Based on a broader collection of operational indicators used to measure instructional quality in current research, a similar categorization into additional dimensions assessment, practice and application, and content selection and presentation proved sufficient in our analysis to categorize the remaining operational indicators. As noted above, the dimension student support is distributed over two different aspects (socio-emotional support and cutting across aspects aiming to maximize student learning) in Praetorius and Charalambous’s (2018) research. In our framework, this differentiation is reflected by a separate sub-dimension of student support corresponding to socio-emotional support and social relatedness in our proposed framework.

Finally, our literature search brought up a number of studies that attempt to measure instructional quality by proxy measures, which we propose to exclude from the construct. In our proposed understanding, instructional quality refers to observable characteristics of classroom instruction that are orchestrated by teachers, and go along with desirable development of students’ learning outcomes. Correspondingly, measures such as stable teacher characteristics beyond classroom behavior, general school characteristics, or student outcomes are represented outside instructional quality in Figure 6. Future research on instructional quality should focus on measures validly capturing the orchestration of learning opportunities by the teacher in the classroom, or during preparation of classroom work.

In summary, analyzing the variation and common elements of conceptual and operational definitions of instructional quality dimensions underpins the importance of working toward a joint understanding of basic dimensions of instructional quality. The proposed framework of operational definitions is in large parts compatible with existing conceptualizations of instructional quality that extend the basic dimensions framework. Importantly, however, we can provide a comprehensive and extensive description of the original basic dimensions and the proposed additional dimensions based on a large volume of literature on instructional quality in the mathematics classroom.

Our analysis is limited in the sense that it is restricted to the instructional quality of mathematics classrooms. As described above, it may form a basis for a more systematic comparison of conceptualizations of teaching quality as it was done for different subjects other than mathematics by Praetorius et al. (2020). Future research will need to analyze which indicators and dimensions of instructional quality require a subject- or even content-specific elaboration, and for which a generic, overarching conceptualization without further specification is sufficient. Currently, most of the analyzed instruments, which have been developed by researchers and practitioners, either do not consider subject-specific aspects of instructional quality as instruments that are used for different subjects, or consider the specific aspects at a superficial level by merely using terms like “mathematics” with generic instruments. Other indicators drawn from the literature, especially with respect to Cognitive Activation or Content Selection and Presentation, are primarily discussed in the field of mathematics education, as for example, considering multiple solutions and using mistakes for learning. Given that a thorough command of the subject-related content seems to be a necessary condition for the appropriate selection and implementation of mathematical tasks in the classroom, there is a great need in the instructional quality field to create or adapt measures that capture a fuller range of activities, practices, and interactions in classrooms that are more strongly and directly linked to the subject-specific aspect of mathematics education and its deep structures. We could derive a number of conceptual and operational indicators that can be seen as subject-specific for good theoretical reason. For example, using multiple representations is closely connected to the abstract nature of mathematical concepts, which can be fully grasped only by identifying and using the relationship between the different representations used to work with them (e.g., graph, table, algebraic expression for a function; Goldin, 1998; Duval, 2006). However, the results on mathematics-specific aspects of instructional quality are limited to the few works focusing on subject-specific instructional quality (e.g., Lindmeier and Heinze, 2020; Praetorius et al., 2020; Dreher and Leuders, 2021) and theoretical analyses from different perspectives on subject-specificity. The open questions can surely not be resolved by a review focusing on mathematics as a specific subject. What our review can contribute is to describe a specific profile of those aspects of instructional quality that are considered important when focusing on mathematics. Our results indicate that this specific profile is strongly determined within the basic dimension Cognitive Activation, as well as Content Selection and Presentation (cf. Praetorius and Charalambous, 2018). Future research should derive similar profiles for other subjects, to allow a comparison between subjects that parallels the one presented in Praetorius et al. (2020), based on systematic reviews of conceptual and operational definitions of instructional quality. Accordingly, identifying the general and subject-specific components of instructional quality is an ongoing endeavor (Praetorius et al., 2020).

Moreover, it must be noted that we selected the basic dimensions framework as a starting point for our analysis. In spite of its widespread use, this might be debated, and starting from other frameworks might have led to a different framework structure. Matching the overarching dimensions and the associated conceptual indicators with conceptual indicators of overarching quality dimensions from other frameworks would be an interesting effort to see how the frameworks relate to each other. However, our literature search included empirical works building on a range of different instructional quality frameworks (e.g., TRU, MQI). Therefore, the main elements of these frameworks, which have been put to empirical measurement, are likely included in our analysis.

To conclude, we propose a framework to describe the current understanding of instructional quality in mathematics classrooms in the literature. Even though the structure of the resulting framework is similar to prior work, the empirical basis of our analysis is broader than in prior works. This allowed us to extend the description of the basic dimensions and capture perspectives on the construct from a wide range of works. Moreover, being able to assign measurement dimensions and operational indicators from the literature to the new framework might allow determining a common language to describe different conceptualizations instructional quality, and related empirical results on instructional quality.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

JM, AB, and SU contributed to conception and design of the study. JM organized the database and wrote the first draft of the manuscript. JM and AB performed the statistical analysis. JM and SU contributed to manuscript revision, read, and approved the submitted version. All authors contributed to the article and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Achmetli, K., Schukajlow, S., and Rakoczy, K. (2019). Multiple solutions for real-world problems, experience of competence and students’ procedural and conceptual knowledge. Int. J. Sci. Math. Educ. 17, 1605–1625. doi: 10.1007/s10763-018-9936-5

CrossRef Full Text | Google Scholar

Amatari, V. O. (2015). The instructional process: A review of Flanders’ interaction analysis in a classroom setting. Int. J. Second. Educ. 3, 43–49. doi: 10.11648/j.ijsedu.20150305.11

CrossRef Full Text | Google Scholar

Averill, R. (2012). Caring teaching practices in multiethnic mathematics classrooms: Attending to health and well-being. Math. Educ. Res. J. 24, 105–128. doi: 10.1007/s13394-011-0028-x

CrossRef Full Text | Google Scholar

Baier, F., Decker, A. T., Voss, T., Kleickmann, T., Klusmann, U., and Kunter, M. (2019). What makes a good teacher? The relative importance of mathematics teachers’ cognitive ability, personality, knowledge, beliefs, and motivation for instructional quality. Br. J. Educ. Psychol. 89, 767–786.

Google Scholar

Ball, D. L., and Rowan, B. (2004). Introduction: Measuring instruction. Element. Sch. J. 105, 3–10. doi: 10.1086/428762

CrossRef Full Text | Google Scholar

Baumert, J., Kunter, M., Blum, W., Brunner, M., Voss, T., Jordan, A., et al. (2010). Teachers’ mathematical knowledge, cognitive activation in the classroom, and student progress. Am. Educ. Res. J. 47, 133–180. doi: 10.3102/0002831209345157

CrossRef Full Text | Google Scholar

Bellens, K. Van Damme, J. Van Den Noortgate, W., Wendt, H., and Nilsen, T. (2019). Instructional quality: Catalyst or pitfall in educational systems’ aim for high achievement and equity? An answer based on multilevel SEM analyses of TIMSS 2015 data in Flanders (Belgium), Germany, and Norway. Large Scale Assess. Educ. 7, 1–27.

Google Scholar

Blömeke, S., Olsen, R. V., and Suhl, U. (2016). Relation of student achievement to the quality of their teachers and instructional quality. Teach. Qual. Instr. Qual. Stud. Outcomes 2, 21–50. doi: 10.1007/978-3-319-41252-8_2

CrossRef Full Text | Google Scholar

Borich, G. D. (1977). Sources of invalidity in measuring classroom behavior. Instr. Sci. 6, 283–318. doi: 10.1007/BF00120659

CrossRef Full Text | Google Scholar

Boston, M. (2012). Assessing instructional quality in mathematics. Element. Sch. J. 113, 76–104. doi: 10.1086/666387

CrossRef Full Text | Google Scholar

Brophy, J. (2000). Teaching. Brussels: International Academy of Education.

Google Scholar

Brophy, J. (2006). Observational Research on Generic Aspects of Classroom Teaching. London: Routledge.

Google Scholar

Brophy, J., and Good, T. L. (1984). Teacher behavior and student achievement. Occasional Paper No. 73. East Lansing, MI.

Google Scholar

Brophy, J. E., and Good, T. L. (1986). “Teacher behavior and student achievement,” in Handbook of Research on Teaching, ed. M. C. Wittrock (London: MacMillan), 328–375.

Google Scholar

Brown, J., and Kurzweil, M. (2017). Instructional Quality, Student Outcomes, and Institutional Finances. Washington, DC: American Council on Education.

Google Scholar

Bruckmaier, G., Krauss, S., Blum, W., and Leiss, D. (2016). Measuring mathematics teachers’ professional competence by using video clips (COACTIV video). ZDM 48, 111–124. doi: 10.1007/s11858-016-0772-1

CrossRef Full Text | Google Scholar

Charalambous, C. Y., and Praetorius, A.-K. J. Z. (2018). Studying mathematics instruction through different lenses: Setting the ground for understanding instructional quality more comprehensively. ZDM 50, 355–366. doi: 10.1007/s11858-018-0914-8

CrossRef Full Text | Google Scholar

Cobb, P., and Jackson, K. (2011). Towards an empirically grounded theory of action for improving the quality of mathematics teaching at scale. Math. Teach. Educ. Dev. 13, 6–33.

Google Scholar

Creemers, B., and Kyriakides, L. (2015). Process-product research: A cornerstone in educational effectiveness research. J. Classroom Interact. 50, 107–119.

Google Scholar

Curby, T. W., Rudasill, K. M., Edwards, T., and Pérez-Edgar, K. (2011). The role of classroom quality in ameliorating the academic and social risks associated with difficult temperament. Sch. Psychol. Q. 26:175. doi: 10.1037/a0023042

CrossRef Full Text | Google Scholar

De Jong, R., and Westerhof, K. (2001). The quality of student ratings of teacher behaviour. Learn. Environ. Res. 4, 51–85. doi: 10.1023/A:1011402608575

CrossRef Full Text | Google Scholar

Dickinson, L. (1995). Autonomy and motivation a literature review. System 23, 165–174. doi: 10.1016/0346-251X(95)00005-5

CrossRef Full Text | Google Scholar

Diederich, J., and Tenorth, H.-E. (1997). Theorie der schule: Ein studienbuch zu geschichte, funktionen und gestaltung. Berlin: Cornelsen Scriptor.

Google Scholar

Dorfner, T., Förtsch, C., and Neuhaus, B. J. (2017). Die methodische und inhaltliche Ausrichtung quantitativer Videostudien zur Unterrichtsqualität im mathematisch-naturwissenschaftlichen Unterricht. Zeitschrift für Didaktik der Naturwissenschaften 23, 261–285. doi: 10.1007/s40573-017-0058-3

CrossRef Full Text | Google Scholar

Dreher, A., and Leuders, T. (2021). Fachspezifität von Unterrichtsqualität–aus der Perspektive der Mathematikdidaktik. Unterrichtswissenschaft 49, 285–292. doi: 10.1007/s42010-021-00116-9

CrossRef Full Text | Google Scholar

Duval, R. (2006). A cognitive analysis of problems of comprehension in a learning of mathematics. Educ. Stud. Math. 61, 103–131. doi: 10.1007/s10649-006-0400-z

CrossRef Full Text | Google Scholar

Fauth, B., Decristan, J., Rieser, S., Klieme, E., and Büttner, G. (2014). Grundschulunterricht aus schüler-, lehrer-und beobachterperspektive: Zusammenhänge und vorhersage von lernerfolg. Z. Pädagogische Psychol. 28, 127–137. doi: 10.1024/1010-0652/a000129

CrossRef Full Text | Google Scholar

Gallagher, M. A., Parsons, S. A., and Vaughn, M. (2022). Adaptive teaching in mathematics: A review of the literature. Educ. Rev. 74, 298–320. doi: 10.1080/00131911.2020.1722065

CrossRef Full Text | Google Scholar

Glass, G. V. (1974). “A review of three methods of determining teacher effectiveness,” in Evaluating Educational Performance, ed. H. J. Walberg (McCutcheon, MI: McCutchan), 11–32.

Google Scholar

Goldin, G. A. (1998). Representational systems, learning, and problem solving in mathematics. J. Math. Behav. 17, 137–165. doi: 10.1016/S0364-0213(99)80056-1

CrossRef Full Text | Google Scholar

Große, C. S. (2014). Mathematics learning with multiple solution methods: Effects of types of solutions and learners’ activity. Instr. Sci. 42, 715–745. doi: 10.1007/s11251-014-9312-y

CrossRef Full Text | Google Scholar

Hamre, B. K., and Pianta, R. C. (2007). “Learning opportunities in preschool and early elementary classrooms,” in School readiness and the transition to kindergarten in the era of accountability, eds R. C. Pianta, M. J. Cox, and K. LaBrie Snow (Baltimore, MD: Paul H Brookes Publishing), 49–83.

Google Scholar

Heemsoth, T., and Heinze, A. (2014). “How should students reflect upon their own errors with respect to fraction problems?,” in Proceedings of the 38th Conference of the International Group for the Psychology of Mathematics: Mathematics Education at the Edge, PME, Dublin, OH.

Google Scholar

Heinitz, B., and Nehring, A. (2020). Kriterien naturwissenschaftsdidaktischer Unterrichtsqualität–ein systematisches Review videobasierter Unterrichtsforschung. Unterrichtswissenschaft 48, 319–360. doi: 10.1007/s42010-020-00074-8

CrossRef Full Text | Google Scholar

House, A. E., House, B. J., and Campbell, M. B. (1981). Measures of interobserver agreement: Calculation formulas and distribution effects. J. Behav. Assess. 3, 37–57. doi: 10.1007/BF01321350

CrossRef Full Text | Google Scholar

Jentsch, A., Casale, G., Schlesinger, L., Kaiser, G., König, J., and Blömeke, S. (2020). Variability and generalizability of ratings for quality of math classes between and within lessons. Unterrichtswissenschaft 48, 179–197. doi: 10.1007/s42010-019-00061-8

CrossRef Full Text | Google Scholar

Jentsch, A., and Schlesinger, L. (2017). “Measuring instructional quality in mathematics education,” in Proceedings of CERME10 (Dublin: CERME), 3073–3080.

Google Scholar

Jentsch, A., Schlesinger, L., Heinrichs, H., Kaiser, G., König, J., and Blömeke, S. (2021). Erfassung der fachspezifischen Qualität von Mathematikunterricht: Faktorenstruktur und Zusammenhänge zur professionellen Kompetenz von Mathematiklehrpersonen. J. Math.-Didaktik 42, 97–121. doi: 10.1007/s13138-020-00168-x

CrossRef Full Text | Google Scholar

Johnson, D. W., and Johnson, R. T. (1999). Making cooperative learning work. Theor. Pract. 38, 67–73. doi: 10.1080/00405849909543834

CrossRef Full Text | Google Scholar

Junker, B. W., Weisberg, Y., Matsumura, L. C., Crosson, A., Wolf, M., Levison, A., et al. (2005). Overview of the Instructional Quality Assessment. Oakland, CA: Regents of the University of California. doi: 10.1037/e644942011-001

CrossRef Full Text | Google Scholar

Kaur, J., and Gupta, V. (2010). Effective approaches for extraction of keywords. Int. J. Comput. Sci. Issues 7:144.

Google Scholar

Klieme, E. (2013). “The role of large-scale assessments in research on educational effectiveness and school development,” in The Role of International Large-Scale Assessments: Perspectives from Technology, Economy, and Educational Research, eds M. von Davier, E. Gonzalez, I. Kirsch, and K. Yamamoto (Berlin: Springer), 115–147. doi: 10.1007/978-94-007-4629-9_7

CrossRef Full Text | Google Scholar

Klieme, E., Lipowsky, F., Rakoczy, K., and Ratzka, N. (2006). “Qualitätsdimensionen und wirksamkeit von mathematikunterricht,” in Untersuchungen zur bildungsqualität von schule, eds M. Prenzel and L. Allolio-Näcke (Münster: Waxmann), 127–146.

Google Scholar

Klieme, E., Pauli, C., and Reusser, K. (2009). “The Pythagoras study: Investigating effects of teaching and learning in Swiss and German mathematics classrooms,” in The Power of Video Studies in Investigating Teaching Learning in the Classroom, eds J. Tomáš and T. Seidel (Münster: Waxmann), 137–160.

Google Scholar

Köller, O., and Baumert, J. (2001). Leistungsgruppierungen in der sekundarstufe I. ihre konsequenzen für die mathematikleistung und das mathematische selbstkonzept der begabung [Ability-grouping at secondary level 1. Consequences for mathematics achievement and the self-concept of mathematical ability]. Z. Pädagogische Psychol. 15, 99–110. doi: 10.1024/1010-0652.15.2.99

CrossRef Full Text | Google Scholar

Krauss, S., and Bruckmaier, G. (2014). Das Experten-Paradigma in der Forschung zum Lehrerberuf. 241–261, Münster: Waxmann.

Google Scholar

Kuckartz, U., and Rädiker, S. (2019). Analyzing Qualitative Data with MAXQDA. Berlin: Springer. doi: 10.1007/978-3-030-15671-8

CrossRef Full Text | Google Scholar

Künsting, J., Neuber, V., and Lipowsky, F. (2016). Teacher self-efficacy as a long-term predictor of instructional quality in the classroom. Eur. J. Psychol. Educ. 31, 299–322. doi: 10.1007/s10212-015-0272-7

CrossRef Full Text | Google Scholar

Kunter, M., Baumert, J., and Köller, O. (2007). Effective classroom management and the development of subject-related interest. Learn. Instr. 17, 494–509. doi: 10.1016/j.learninstruc.2007.09.002

CrossRef Full Text | Google Scholar

Kunter, M., Brunner, M., Baumert, J., Klusmann, U., Krauss, S., Blum, W., et al. (2005). Der mathematikunterricht der PISA-schülerinnen und-schüler. Zeitschrift Erziehungswissenschaft 8, 502–520. doi: 10.1007/s11618-005-0156-8

CrossRef Full Text | Google Scholar

Kunter, M., Klusmann, U., Baumert, J., Richter, D., Voss, T., and Hachfeld, A. (2013). Professional competence of teachers: Effects on instructional quality and student development. J. Educ. Psychol. 105:805. doi: 10.1037/a0032583

CrossRef Full Text | Google Scholar

Kunter, M., and Voss, T. (2013). “The model of instructional quality in COACTIV: A multicriteria analysis,” in Cognitive Activation in the Mathematics Classroom and Professional Competence of Teachers, eds M. Kunter, J. Baumert, W. Blum, U. Klusmann, S. Krauss, and M. Neubrand (Berlin; Springer), 97–124. doi: 10.1007/978-1-4614-5149-5_6

CrossRef Full Text | Google Scholar

Kuntze, S., and Reiss, K. (2006). Profile mathematikbezogener motivationaler prädispositionen – Zusammenhänge zwischen motivation, interesse, fähigkeitsselbstkonzepten und schulleistungsentwicklung in verschiedenen lernumgebungen. Math. Didactica 29, 24–48.

Google Scholar

Kyaruzi, F., Strijbos, J.-W., and Ufer, S. (2020). Impact of a short-term professional development teacher training on students’ perceptions and use of errors in mathematics. Front. Educ. 5:559122. doi: 10.3389/feduc.2020.559122

CrossRef Full Text | Google Scholar

Lanahan, L., McGrath, D. J., McLaughlin, M., Burian-Fitzgerald, M., and Salganik, L. (2005). Fundamental Problems in the Measurement of Instructional Processes: Estimating Reasonable Effect Sizes and Conceptualizing What is Important to Measure. San Diego, CA: American Educational Research Association. doi: 10.1037/e539802012-001

CrossRef Full Text | Google Scholar

Lazarides, R., and Buchholz, J. (2019). Student-perceived teaching quality: How is it related to different achievement emotions in mathematics classrooms? Learn. Instr. 61, 45–59. doi: 10.1016/j.learninstruc.2019.01.001

CrossRef Full Text | Google Scholar

Learning Mathematics for Teaching Project (2010). Measuring the mathematical quality of instruction. J. Math. Teach. Educ. 14, 25–47. doi: 10.1007/s10857-010-9140-1

CrossRef Full Text | Google Scholar

Lindmeier, A., and Heinze, A. (2020). Die fachdidaktische Perspektive in der Unterrichtsqualitätsforschung: (bisher) ignoriert, implizit enthalten oder nicht relevant? Empirische Forschung zu Unterrichtsqualität 66, 255–268.

Google Scholar

Lipowsky, F., Rakoczy, K., Pauli, C., Drollinger-Vetter, B., Klieme, E., and Reusser, K. (2009). Quality of geometry instruction and its short-term impact on students’ understanding of the Pythagorean Theorem. Learn. Instr. 19, 527–537. doi: 10.1016/j.learninstruc.2008.11.001

CrossRef Full Text | Google Scholar

Maass, K., Geiger, V., Ariza, M. R., and Goos, M. (2019). The role of mathematics in interdisciplinary STEM education. ZDM 51, 869–884. doi: 10.1007/s11858-019-01100-5

CrossRef Full Text | Google Scholar

Matsumura, L. C., Garnier, H. E., Slater, S. C., and Boston, M. D. (2008). Toward measuring instructional interactions “at-scale”. Educ. Assess. 13, 267–300. doi: 10.1080/10627190802602541

CrossRef Full Text | Google Scholar

Mayer, D. P. (1999). Measuring instructional practice: Can policymakers trust survey data? Educ. Eval. Policy Anal. 21, 29–45. doi: 10.3102/01623737021001029

CrossRef Full Text | Google Scholar

McAuley, E., Duncan, T., and Tammen, V. V. (1989). Psychometric properties of the Intrinsic Motivation Inventory in a competitive sport setting: A confirmatory factor analysis. Res. Q. Exerc. Sport 60, 48–58. doi: 10.1080/02701367.1989.10607413

PubMed Abstract | CrossRef Full Text | Google Scholar

Merrill, M. D., Reigeluth, C. M., and Faust, C. (1979). The Instructional Quality Profile: Procedures for Instructional Systems Development. Cambridge, MA: Academic Press.

Google Scholar

Moher, D., Liberati, A., Tetzlaff, J., Altman, D. G., and Group, P. (2009). Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. Ann. Int. Med. 151, 264–269. doi: 10.7326/0003-4819-151-4-200908180-00135

PubMed Abstract | CrossRef Full Text | Google Scholar

Otara, A., and Niyirora, A. (2016). Educational inputs: A defining factor in planning for quality secondary education in Rwanda. Int. J. Dev. Sustain. 5, 120–136.

Google Scholar

Pianta, R. C., and Hamre, B. K. (2009). Conceptualization, measurement, and improvement of classroom processes: Standardized observation can leverage capacity. Educ. Res. 38, 109–119.

Google Scholar

Pianta, R. C., La Paro, K. M., and Hamre, B. K. (2008). Classroom Assessment Scoring System™: Manual K-3. Baltimore, MD: Paul H Brookes Publishing.

Google Scholar

Praetorius, A.-K., and Charalambous, C. Y. (2018). Classroom observation frameworks for studying instructional quality: Looking back and looking forward. ZDM 50, 535–553. doi: 10.1007/s11858-018-0946-0

CrossRef Full Text | Google Scholar

Praetorius, A.-K., and Gräsel, C. (2021). Noch immer auf der Suche nach dem heiligen Gral: Wie generisch oder fachspezifisch sind Dimensionen der Unterrichtsqualität? Unterrichtswissenschaft 49, 167–188. doi: 10.1007/s42010-021-00119-6

CrossRef Full Text | Google Scholar

Praetorius, A.-K., Herrmann, C., Gerlach, E., Zülsdorf-Kersting, M., Heinitz, B., and Nehring, A. (2020). Unterrichtsqualität in den Fachdidaktiken im deutschsprachigen Raum – zwischen Generik und Fachspezifik. Unterrichtswissenschaft 48, 409–446. doi: 10.1007/s42010-020-00082-8

CrossRef Full Text | Google Scholar

Praetorius, A.-K., Klieme, E., Herbert, B., and Pinger, P. (2018). Generic dimensions of teaching quality: The German framework of three basic dimensions. ZDM 50, 407–426. doi: 10.1007/s11858-018-0918-4

CrossRef Full Text | Google Scholar

Praetorius, A.-K., Lauermann, F., Klassen, R. M., Dickhäuser, O., Janke, S., and Dresel, M. (2017). Longitudinal relations between teaching-related motivations and student-reported teaching quality. Teach. Teach. Educ. 65, 241–254. doi: 10.1016/j.tate.2017.03.023

CrossRef Full Text | Google Scholar

Praetorius, A.-K., Pauli, C., Reusser, K., Rakoczy, K., and Klieme, E. (2014). One lesson is all you need? Stability of instructional quality across lessons. Learn. Instr. 31, 2–12. doi: 10.1016/j.learninstruc.2013.12.002

CrossRef Full Text | Google Scholar

Quarantelli, E. (1985). “The need for clarification in definition and conceptualization in research,’ in Disasters Mental Health-Selected Contemporary Perspectives, Ed. B. J. Sowder (Washington, DC: U.S. Department of Health and Human Services, Public Health Service, Alcohol, Drug Abuse, and Mental Health Administration, National Institute of Mental Health), 41–73.

Google Scholar

Rach, S., Ufer, S., and Heinze, A. (2012). Lernen aus Fehlern im Mathematikunterricht - kognitive und affektive Effekte zweier Interventionsmaßnahmen. Unterrichtswissenschaft 2012, 213–234.

Google Scholar

Rakoczy, K. (2008). Motivationsunterstützung im mathematikunterricht: Unterricht aus der perspektive von lernenden und beobachtern. Münster: Waxmann.

Google Scholar

Ryan, R. M. (1982). Control and information in the intrapersonal sphere: An extension of cognitive evaluation theory. J. Pers. Soc. Psychol. 43:450. doi: 10.1037/0022-3514.43.3.450

CrossRef Full Text | Google Scholar

Schlesinger, L., and Jentsch, A. (2016). Theoretical and methodological challenges in measuring instructional quality in mathematics education using classroom observations. ZDM 48, 29–40. doi: 10.1007/s11858-016-0765-0

CrossRef Full Text | Google Scholar

Schlesinger, L., Jentsch, A., Kaiser, G., König, J., and Blömeke, S. (2018). Subject-specific characteristics of instructional quality in mathematics education. ZDM 50, 475–490. doi: 10.1007/s11858-018-0917-5

CrossRef Full Text | Google Scholar

Schukajlow, S., and Rakoczy, K. (2016). The power of emotions: Can enjoyment and boredom explain the impact of individual preconditions and teaching methods on interest and performance in mathematics? Learn. Instr. 44, 117–127. doi: 10.1016/j.learninstruc.2016.05.001

CrossRef Full Text | Google Scholar

Seidel, T., and Shavelson, R. (2007). Teaching effectiveness research in the past decade: The role of theory and research design in disentangling meta-analysis results. Rev. Educ. Res. 77, 454–499. doi: 10.3102/0034654307310317

CrossRef Full Text | Google Scholar

Sievert, H., van den Ham, A.-K., and Heinze, A. (2021a). Are first graders’ arithmetic skills related to the quality of mathematics textbooks? A study on students’ use of arithmetic principles. Learn. Instr. Sci. 71:101401. doi: 10.1016/j.learninstruc.2020.101401

CrossRef Full Text | Google Scholar

Sievert, H., van den Ham, A.-K., and Heinze, A. (2021b). The role of textbook quality in first graders’ ability to solve quantitative comparisons: A multilevel analysis. ZDM 53, 1417–1431. doi: 10.1007/s11858-021-01266-x

CrossRef Full Text | Google Scholar

Sievert, H., van den Ham, A.-K., Niedermeyer, I., and Heinze, A. (2019). Effects of mathematics textbooks on the development of primary school children’s adaptive expertise in arithmetic. Learn. Individ. Differ. 74:101716. doi: 10.1016/j.lindif.2019.02.006

CrossRef Full Text | Google Scholar

Strijbos, J.-W., Martens, R. L., Prins, F. J., and Jochems, W. M. (2006). Content analysis: What are they talking about? Comput. Educ. Assess. 46, 29–48. doi: 10.1016/j.compedu.2005.04.002

CrossRef Full Text | Google Scholar

Taut, S., and Rakoczy, K. (2016). Observing instructional quality in the context of school evaluation. Learn. Instr. 46, 45–60. doi: 10.1016/j.learninstruc.2016.08.003

CrossRef Full Text | Google Scholar

Thompson, C. J., and Davis, S. B. (2014). Classroom observation data and instruction in primary mathematics education: Improving design and rigour. Math. Educ. Res. J. 26, 301–323. doi: 10.1007/s13394-013-0099-y

CrossRef Full Text | Google Scholar

Tulis, M. (2013). Error management behavior in classrooms: Teachers’ responses to student mistakes. Teach. Teach. Educ. 33, 56–68. doi: 10.1016/j.tate.2013.02.003

CrossRef Full Text | Google Scholar

Van Den Ham, A.-K., and Heinze, A. (2018). Does the textbook matter? Longitudinal effects of textbook choice on primary school students’ achievement in mathematics. Stud. Educ. Eval. 59, 133–140. doi: 10.1016/j.stueduc.2018.07.005

CrossRef Full Text | Google Scholar

Wagner, W., Göllner, R., Werth, S., Voss, T., Schmitz, B., and Trautwein, U. (2016). Student and teacher ratings of instructional quality: Consistency of ratings over time, agreement, and predictive power. J. Educ. Psychol. 108:705. doi: 10.1037/edu0000075

CrossRef Full Text | Google Scholar

Wüsten, S. (2010). Allgemeine und Fachspezifische Merkmale der Unterrichtsqualität im Fach Biologie: Eine Video-und Interventionsstudie. Berlin: Logos Verlag Berlin GmbH.

Google Scholar

Yi, H. S., and Lee, Y. (2017). A latent profile analysis and structural equation modeling of the instructional quality of mathematics classrooms based on the PISA 2012 results of Korea and Singapore. Asia Pacific Educ. Rev. 18, 23–39. doi: 10.1007/s12564-016-9455-4

CrossRef Full Text | Google Scholar

Appendix

APPENDIX 1

Appendix 1. The three generic dimension framework of assessing teaching quality (Praetorius et al., 2018).