Impact of extracurricular factors on the academic performance of university students during the COVID-19 pandemic

This article aims to study the incidence of extracurricular factors relating to (a) personal work situation and place of residence; (b) family finances; and (c) access to the virtual environment on the academic results of university students during the COVID-19 pandemic. Regression models were used to determine the impact of the different factors on academic performance in a sample of 138 students of the Primary Education Teaching Degree at a Spanish Public University. The results show that students who devote themselves wholly to studying without having to work obtain better academic results than those who have to combine study and work. Furthermore, internet access affects academic results, with students having ADSL and Wi-Fi via smartphones reporting the highest grades.

Introduction

Much of the research into school performance at different educational levels focuses on determining which factors influence and condition students’ academic performance (Quintero Quintero et al., 2013). Over time, a consensus has been reached that students’ academic performance may be affected by a variety of factors ranging from personal characteristics through to those of a socio-cultural nature. According to García-Martín and Cantón (2016), there are four blocks of socio-educational variables that affect school performance: (a) organizational factors at school level, (b) organizational factors at classroom level, (c) teacher-related factors, and (d) factors related with the family context.

The COVID-19 pandemic triggered a sudden change in teaching-learning processes due to the situations of confinement that still persist in some countries. Higher education is no exception and has also been affected. In one of the first global studies of 424 universities and other higher education institutions, the International Association of Universities (Jandrić, 2020; Marinoni et al., 2020) found that the virus had a major impact on the teaching-learning process, with two-thirds of the institutions studied suddenly having to change their face-to-face teaching model to virtual or distance learning without prior organization or experience. Authors such as Hodges et al. (2020) referred to this phenomenon as “emergency remote teaching” due to the fact that the necessary technical and organizational infrastructure for distance education was lacking at the time (Vlachopoulos and Makri, 2019; Rasheed et al., 2020; Erlam et al., 2021).

In the particular case of Spain, during the State of Alarm decreed from 14 March to 21 June 2020, the new circumstances provoked a change in the way universities prepared classes and assessed students and the general teaching processes of their teaching staff. In turn, this also brought about a sudden change for students in terms of how they were assessed and received lessons. The teaching staff had to modify the programs and syllabuses of the different subjects, in some cases altering the content, the teaching methodology and the percentages of continuous and final assessment (López-Iñesta and Sanz, 2021). Different studies have provided interesting results regarding the impact on both teachers and students. Examples include the study by Pérez-López et al. (2021), which analyses distance education from the perspective of university students, and Rapanta et al. (2020), which reflects on the reorientation of teacher presence and learning activity during and after the COVID-19 crisis.

In this new context, classrooms were hastily transferred to students’ homes and Information and Communication Technologies (ICT) and access to smart learning environments became essential tools (Huang et al., 2020). This situation highlighted the insufficient technical infrastructure, the lack of training in the use and application of educational platforms and the implications for pedagogical and teaching-learning models (Bao, 2020; Hodges et al., 2020; Mulenga and Marbán, 2020; López-Iñesta and Sanz, 2021).

The experience during the 2019/2020 academic year revealed a need for greater attention to extracurricular factors that can affect academic performance. For example, the consequences of the digital divide and the lack of equity in access to digital infrastructure need to be taken into account (Lloyd, 2020). UNESCO data¹ about the education response warn that half of the students that COVID-19 keeps out of the classroom (around 800 million students) do not have access to a computer and 43% (around 700 million students) do not even have internet access at home. In addition, roughly 56 million students live in places without mobile networks. In the same vein, authors such as Reimers and Schleicher (2020) point out that most education systems are not prepared for the world of digital learning opportunities. In quantitative terms, their study found that in OECD countries an average of 95% of students had access to a computer and 90% had internet access, yet 65% did not have sufficient bandwidth.

In light of these results, it may be concluded that the challenges of ensuring educational continuity are not resolved with the mere deployment of digital solutions for distance learning, and that care must be taken to prevent the use of technology in education from further amplifying existing inequalities and deepening the digital divide (Van Dijk, 2020). In this sense, Rodicio García et al. (2020) offer an interesting overview of the literature on the digital divide and the related causes and factors. There is general agreement that access to technology is an essential cause behind the digital divide (Van Dijk, 2020).

In addition, other factors such as economic situation or age can have a negative effect on students’ academic performance. Earlier studies such as Riggert et al. (2006) and other more recent articles such as Ruesga et al. (2014) show that there is a direct relationship between students’ age and having to combine studies with work, which has a negative impact on academic results.

Predictions of academic performance are one of the tools used to identify the most influential factors in order to better understand and address this problem. Quality education and successful students are both priority objectives for all academic institutions, and many studies have been carried out regarding prediction of academic performance using different techniques such as artificial intelligence or learning analytics (Hejazi et al., 2011; Paunonen and Ashton, 2013; Fonteyne et al., 2017; Helal et al., 2018; Sanz et al., 2020), system dynamics (Sanz et al., 2019; Vinatea, 2019) and regression models (Tanujaya et al., 2017).

Over the last 2 years there has been a proliferation of studies on the different factors affecting student performance associated with the impact of COVID-19. The main objective of the current study is to analyze the incidence of different extracurricular factors (technological, economic, and student characteristics) on the academic performance of university students during the 2019/2020 academic year by applying regression modeling (Figure 1).

FIGURE 1

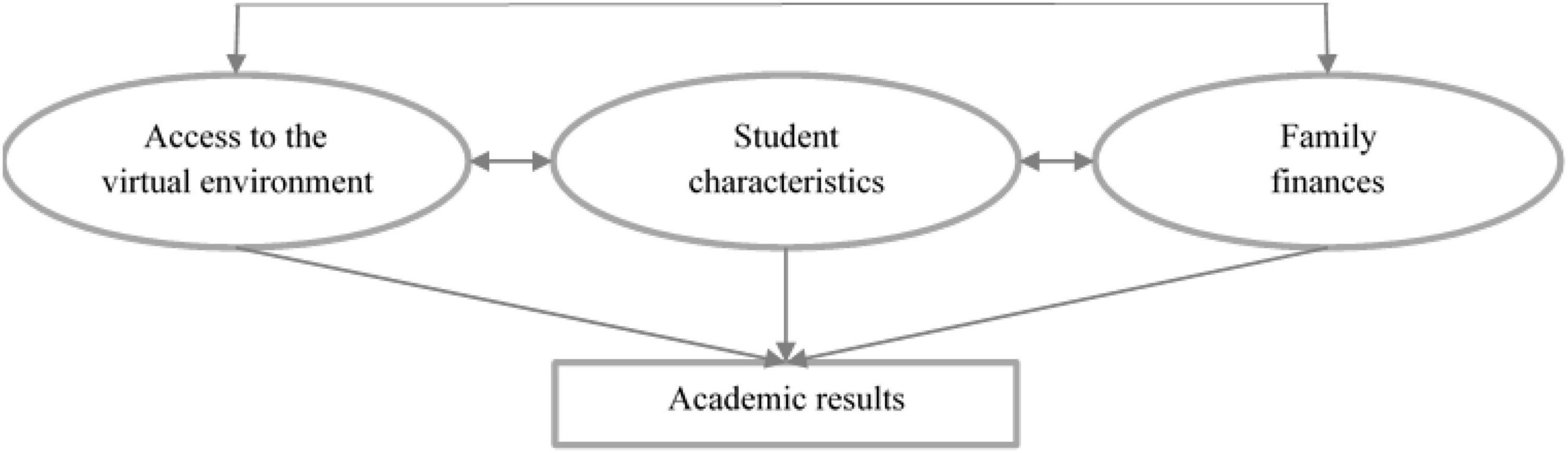
Figure 1. Causal diagram showing the relationship between variables (technological, economic, student characteristics, and academic results).

The secondary objectives of this work are as follows:

1. To study the association relationships between academic performance and factors affecting access to virtual environments, family finances and the student’s personal characteristics.

2. To design a predictive model based on the dependency relationships studied.

Based on the above, the study is divided into three sections. The first section describes the “Materials and methods” used to determine the study population and sample, along with the data collection instrument and how the data were analyzed. The second section sets out the “Results and discussion,” which is divided into three subsections: (a) a descriptive analysis offering a description of the sample; (b) an inferential analysis, which outlines the relationships between the variables studied; and (c) the predictive model use case, involving construction and validation of the regression model. Finally, the third section outlines the “Discussion and conclusion.”

Materials and methods

Population and sample

This research presents an experimental study where 138 students are involved (24 males and 114 females) in the third year of the Bachelor’s Degree in Primary Education Teaching at a Spanish public university. The average age of the sample was 21.25 ± 2.94 years. A non-probabilistic convenience sample was used. It is important to note that, there were 419 students in the third year of the aforementioned degree, then the sample was representative with a 95% confidence level and a margin error of 7%.

Instrument

In order to obtain the variables that characterize the students, a battery of questions was created on the Moodle teaching platform using the Questionnaire tool, which allows the answers to be completely anonymous. The questions refer to extracurricular factors relating to the students’ family context: (a) the economic situation in the family environment (“family finances”), (b) their place of residence, and (c) access to a virtual teaching-learning environment via the internet. Accordingly, all matters related to the aforementioned variables become relevant and they are proposed as potential influential markers of students’ academic results as suggested by Reimers and Schleicher (2020).

Given the nature of the data collected, it was decided that the process should be confidential. The students were informed that it was a research project and a protocol was established with notification to the university ethics committee. The gender variable was not included because, as shown in the results of the surveys by the National Statistics Institute²,³ on the use of information and communication technologies in households in 2019 and 2020, no inequalities in terms of internet use were observed between men and women in the group under study.

Another variable, which in the model is considered to be dependent upon the rest of the variables described, is the students’ academic results measured as the weighted average of the continuous assessment marks (40%) and the final exam mark (60%) obtained during the period of the experiment. It should be noted that the methodology upon which the teaching-learning process was based prior to declaration of the state of alarm was not modified, given that the face-to-face classes were replaced by synchronous virtual sessions and the face-to-face tutorials were replaced by video tutorials.

Details of the questions relating to the first part are shown in Figure 2.

FIGURE 2

Figure 2. Battery of questions.

The validation of the questionnaire is done about the reliability and validity of it (Lacave et al., 2015). Reliability refers to the confidence that can be had in the data obtained and was studied by first performing an internal consistency analysis measured through the Alpha Ordinal coefficient (0.591) since the variables of our study are nominal (Hoffmann and Stover, 2013). Loewenthal and Lewis (2001) warns that, in scales with less than 10 items, an internal consistency value of 0.6 can be considered acceptable.

To calculate the Alpha Ordinal coefficient, a factorial analysis was carried out following to Dominguez-Lara (2018). The factorial weights of each item were obtained, with values 0.801; 0.244; 0.360; 0.675; 0.309; and 0.313. To interpret the values, it is necessary to follow the order of the battery of questions (Figure 2).

Data collection and analysis

To achieve the first objective, we must define a system that allows us to study the association between academic performance and factors affecting access to virtual environments, family finances, and the student’s personal characteristics.

A system is defined as a set of variables that are related to a problem and allow its explanation. This system may be represented through a causal diagram (Martín, 2019) with the following elements: (a) ellipses representing the variables of the system, (b) arrows highlighting the relationships between variables or between variables and the problem, and (c) rectangles that identify the problem or objective of the system.

The procedure we follow to construct a causal diagram consists of several steps. Firstly, the direct relationships between the variables of interest and the problem to be resolved must be studied. These may be referred to as first-level variables. After that, the relationships between the variables obtained and those that have not resulted from the previous relationship are determined. These are known as second-level variables. This process continues until no more relationships are observed or until all the variables are present in the diagram. Since the aim is to obtain associations between variables, descriptive and inferential analysis must be carried out.

The predictive model will be based on the results obtained in the descriptive and inferential analysis, and therefore it will take as its basis the summary of these analyses as shown in the causal diagram. In addition, a linear least squares regression is performed for the dependent variables considered due to their numerical nature, as well as a multinomial regression for the qualitative polytomous variables.

When working with an empirical model as in our case, i.e., based on statistically significant relationships, the parameter values must be calibrated based on a sample of inputs (independent variables) and outputs (dependent variables) of the model. For this purpose, part of the sample used (84 students) was randomly selected.

After calibrating the model, the parameters must have values that make physical sense, otherwise the model may have predictive power for the data set used in the calibration, but it will have very little explanatory power and will not be widely generalizable.

Once the model has been calibrated, a different set of values to those used in the calibration phase must be used in the validation phase. In our case the 54 students not used previously were taken.

In order to determine the validity of the model, different indices are calculated to quantify the goodness of fit between the real data and the data simulated by the model:

• The most commonly used index is the coefficient of determination, which ranges from 0 to 1 and represents the percentage of variance in the observed data explained by the model.

• The Nash—Sutcliffe model efficiency coefficient (Nash and Sutcliffe, 1970) generates results less than or equal to 1. If the result is 1 the model is perfect, while if it is zero the error variance is equal to the variance of the observed data, meaning that the mean of the observed data will have a similar predictive skill to that of the model and so the model is not good. Values below zero mean that the model is poor.

• The modified index of agreement (Willmott, 1981) returns values ranging from 0 to 1, with the latter value implying a perfect model.

• The ratio of the root mean squared error to the mean absolute error (RMSE/MAE) allows us to determine to what extent the existence of outliers is affecting the model.

Results

The results are broken down into three sections: (a) a descriptive study showing the characteristics of the students, (b) an inferential study showing the association between the variables considered, which will be classified at different levels to design the causal diagram of the variables relating to access to technology and economic level that affect a student’s academic performance, and (c) construction and validation of the predictive model to simulate academic performance based on the result in the causal diagram.

Descriptive analysis

The students had academic results with a mean score of around 7 out of 10 (6.819 ± 1.387). As Table 1 shows, most students (92.9%) lived in their usual residence during the confinement and very few stayed in student flats or second residences (7.2%). With regard to internet access for virtual classes, the majority had fiber broadband (61.9%) as opposed to ADSL (16.7%), with the telephone companies being equally distributed. In addition, it should be noted that the personal work situation and family breadwinners were considered to be positive, given that 70.2% were solely devoted to studying and 50% had both parents as breadwinners.

TABLE 1

Table 1. Measures of association and difference between categories for the study variables and academic results.

Inferential analysis

This section is divided into two parts:

(a) The first part relates all the questions in the battery with the academic results. This allows us to obtain first-level variables, that is, the variables that are directly related to the variable under study.

(b) The second part relates the variables in the battery of questions to the first-level variables obtained previously. Thus, we obtain the so-called second-level variables (those that do not have a direct cause-effect relationship with the academic results but do intervene indirectly). If second-level variables are obtained, we proceed to the next level and so on until all possible relationships are exhausted.

In addition, the nature of the variables is taken into account for this study. The dependent variable (academic results) is quantitative, and the independent variables are all categorical except for age, which is also quantitative.

The strength of the relationship between a quantitative variable and another categorical variable is determined by Cohen’s index. Cohen’s F was used in our study because the categorical variables have more than two categories. An effect size of 0.2–0.5 may be considered “small,” 0.5–0.8 is a “medium” effect size, and anything over 0.8 is a “large” effect size, with Cohen’s F potentially returning values greater than 1.

Likewise, the mean and standard deviation were calculated for each of the categories and the ANOVA test was applied, given that the conditions for applicability (normal data distribution and homoscedasticity) were met in all cases. This was done to determine whether the difference between the means was statistically significant with a 95% confidence level. In the case of significant differences between variables, Tukey’s test was used to determine which categories indicate those differences. Pearson’s correlation was used in the case of relationships between two quantitative variables.

Table 2 shows the numerical analysis carried out. As can be seen, the variable that has a medium relationship with academic results is the personal work situation (Cohen = 0.653). Furthermore, there are significant differences between the academic results of the different categories (ANOVA = 10.614, p-value < 0.0001). When Tukey’s test is performed, these differences appear between those who solely study and the other two groups (Tukey: p-value 1–2 = 0.001; p-value 1–3 = 0.003), with students in the third category (who studied and worked and were dismissed due to the COVID-19 crisis) obtaining lower marks and therefore achieving the lowest level.

TABLE 2

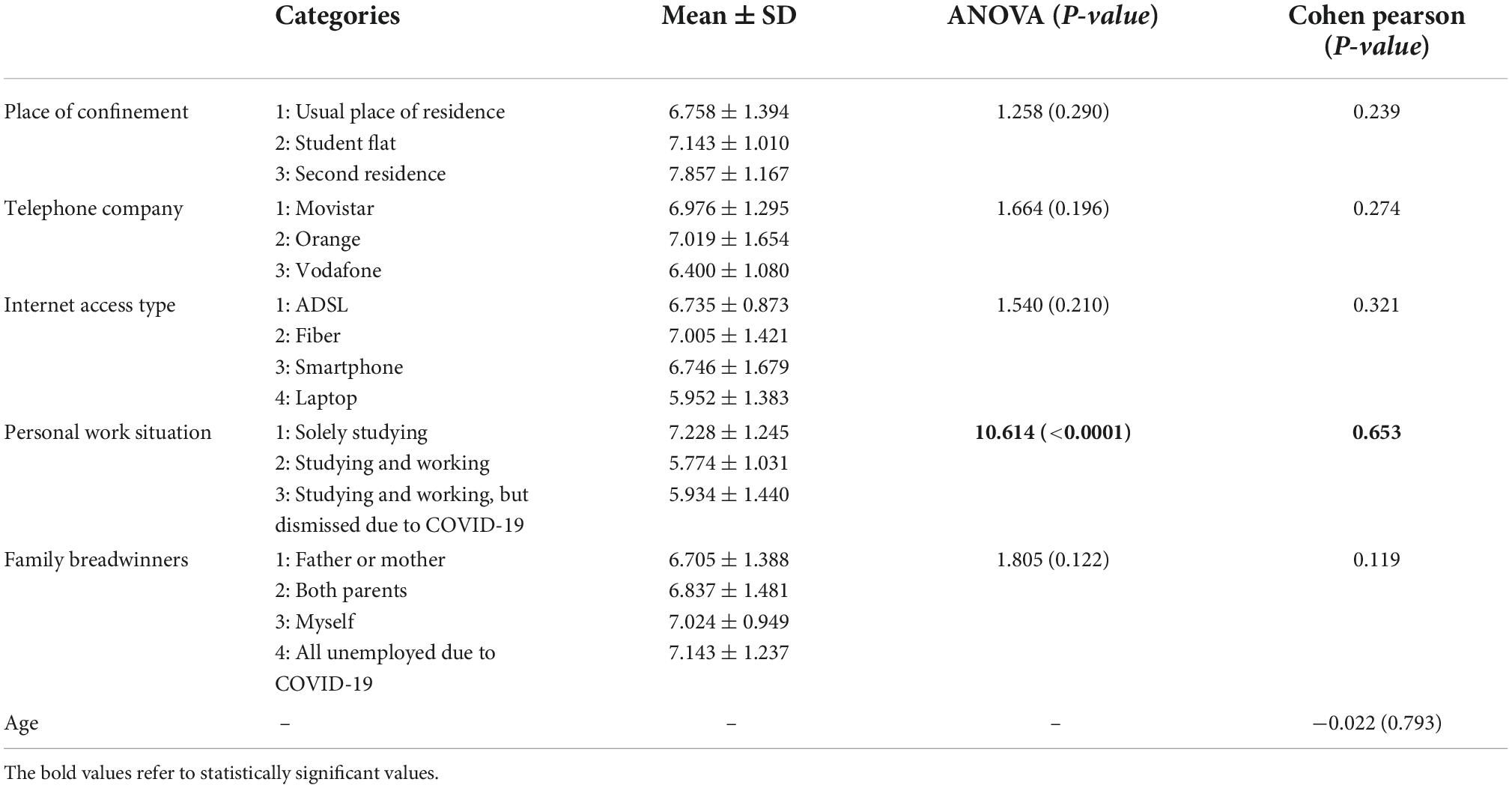
Table 2. Measures of association and difference between categories for the study variables and academic results.

It should also be noted that the variable with the next closest association is the internet access type (Cohen = 0.321). Although there were no statistically significant differences between the means of the academic results in the different categories (ANOVA = 1.540; p-value = 0.210), it may be seen that ADSL/Fiber and Smartphones are associated with higher academic results.

Accordingly, this first study identifies personal work situation as a first-level variable, although the possible associations between this variable and the rest of the variables are studied in order to eliminate from the use case (the predictive model) any possible correlated or associated variables that predict a variable.

Table 3 shows an association with age (Cohen = 0.826) and statistically significant differences between the different categories (ANOVA = 3.517; p-value = 0.034). Tukey’s test determines that there are differences between students who are solely devoted to studying and those who were also working and were dismissed during the state of alarm (Tukey: p-value 1–3 = 0.026), with the mean age being higher in the second case.

TABLE 3

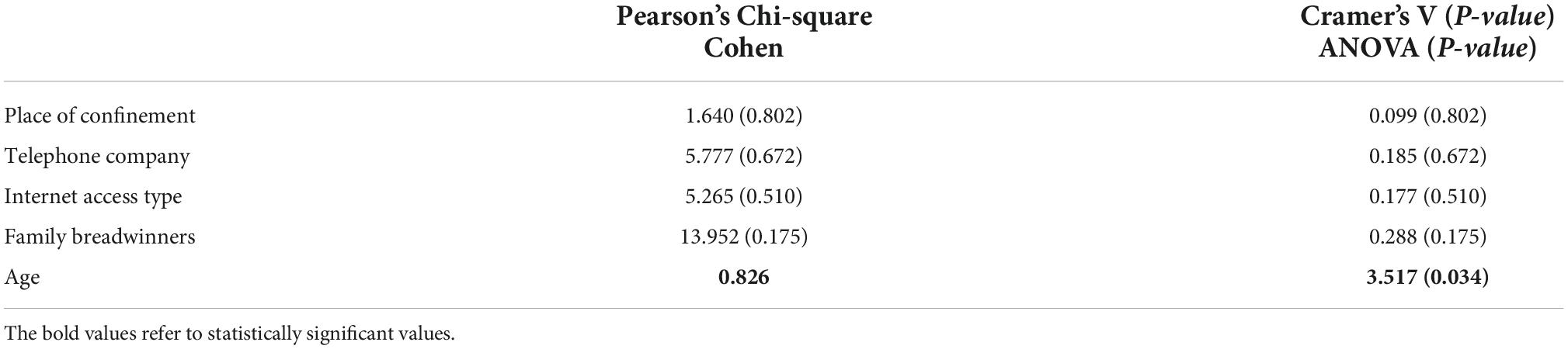
Table 3. Measures of association and difference between categories for the study variables and personal situation.

It should be noted that in addition to relating categorical variables to a quantitative variable (age), now the rest of the relationships are also established between categorical variables. Pearson’s Chi-square test and Cramer’s V were used to determine the relationship between them.

The second-level variable identified is Age, which in turn may be related with the following three variables (see details in Table 4): (a) telephone company (Cohen = 0.661); (b) internet access type (Cohen = 0.513), and (c) family breadwinners (Cohen = 1.175).

TABLE 4

Table 4. Measures of association and difference between categories for the study variables and age.

It is important to note that there are statistically significant differences between the ages of the breadwinner categories (ANOVA = 5.116; p-value = 0.003), differing from those unemployed due to COVID-19 (Tukey; p-value 1–4 = 0.009, p-value 2–4 = 0.012). These results determine addition of the first-level variables of telephone company, internet access type and family breadwinners, although they have a lesser impact on academic performance.

With respect to the telephone company, the relationship with academic performance is not significant, although this may be due to the excellent coverage of all the companies.⁴ However, although the association is not particularly high, its presence is important according to both UNESCO and OECD guidelines (Reimers and Schleicher, 2020), which state that education systems must provide the necessary resources for the teaching-learning process, including adequate internet access.

Finally, the only variable remaining to include in the causal diagram is the place of confinement, which was not introduced at the first-level given that no relationship with Age was determined. For this purpose, the relationship with the four first-level variables was analyzed (see Tables 3, 5). An association with Internet Access Type was found (V Cramer = 0.340; p-value = 0.003). In line with the findings of UNESCO (2020), there are places where there are no mobile networks or insufficient network coverage (Reimers and Schleicher, 2020).

TABLE 5

Table 5. Measures of association between place of confinement and third-level variables.

The results of the analysis are summarized in Figure 3.

FIGURE 3

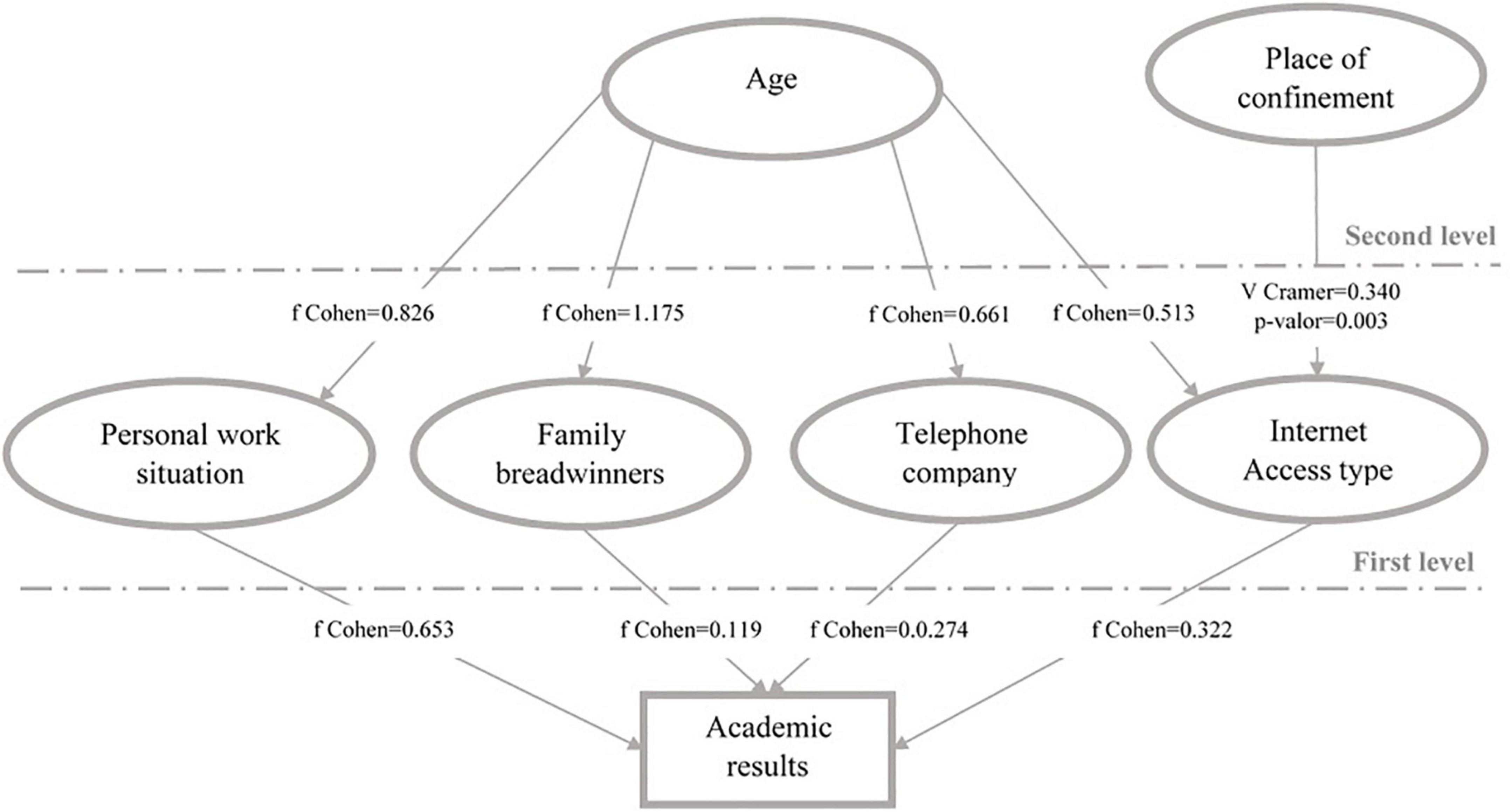
Figure 3. Causal diagram showing the relationship between academic results and student-related variables during a state of alarm in which virtual teaching is carried out.

Use case: Predictive model

Academic Results is a predictor variable according to Figure 3, which determines that there is an equation (Equation 1) with a linear combination of dummy variables (see Table 6) that predict students’ academic results.

$res\mathrm{\_}aca{d}_i=\mathrm{\hspace{0.25em}5.33}+1.184\cdot sp\mathrm{\_}1-0.272\cdot sp\mathrm{\_}2-(1)$

$0.426\cdot sf\mathrm{\_}1-0.322\cdot sf\mathrm{\_}2-0.106\cdot sf\mathrm{\_}3+0.430\cdot ct\mathrm{\_}1+$

$0.330\cdot ct\mathrm{\_}2+0.854\cdot ai\mathrm{\_}1+0.728\cdot ai\mathrm{\_}2+1.030\cdot ai\mathrm{\_}3$

TABLE 6

Table 6. Dummy variables to predict academic results.

The dummy variables are created based on the categorical variables that have an association with the dependent variable Academic Results (res_acad_i where i is the student). Accordingly, sp_1 = 1 would be a student who solely studies and sp_2 = 1 would be a student who studies and works, but if sp_1 = 0 and sp_2 = 0, it would correspond to the category of studying and working but dismissed due to COVID-19.

The coefficients of Equation 1 indicate that being in a personal work situation of solely studying increases academic results by 1.184 points. Meanwhile, students who are working and studying obtain lower marks, with a decrease of 0.272 points. For those in category 3, studying and working but dismissed due to COVID-19, the base situation does not change (5.33 points). This is in line with the results presented in the descriptive and inferential study (Table 2), where the mean was higher for the first category. With respect to family breadwinners, academic results declined in all cases. However, a relationship with Table 2 was observed, with the smallest decreases in cases where the students themselves are the family breadwinners. Telephone companies do not show a significant increase in scores, although the scores are higher for Orange. Finally, in terms of internet access, ADSL and smartphone have the highest scores, with the latter showing the greatest increase (1.030 points).

The prediction of Equation 1 has a coefficient R = 0.525 and a standard error of the estimate of 1.259 points. The equation was accepted after obtaining a model with F = 2.771, p-value = 0.006. Likewise, Table 7 shows that the personal situation variable is significant, as determined by the construction of the causal diagram (Table 2), and there is no collinearity (Tolerance > 0.1), also determined by the construction of the causal diagram.

TABLE 7

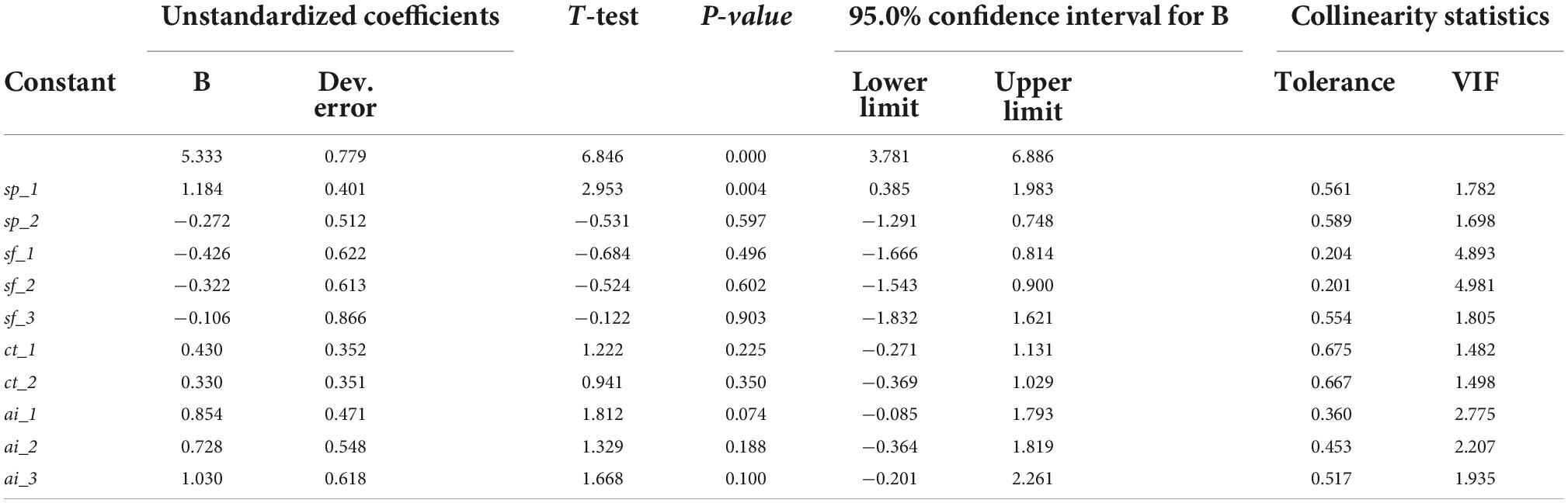
Table 7. Coefficients, significance, and collinearity of the parameters of the academic results prediction equation.

After the above, we calculated the first-level variables concerning Age. In this case, a multinomial logistic regression was applied instead of linear regression, given that the intention is to predict categorical variables with more than two categories.

Equations 2, 3 determine the model to predict the personal situation variable, indicating that for each 1-unit increase in the variable Age, the logarithm of the ratio of the two probabilities P(sp = 1)/P(sp = 3) decreases by 0.233, and the logarithm of the ratio of the two probabilities P(sp = 2)/P(sp = 3) decreases by 0.116. This indicates that the higher the age, the lower the probability of being in personal situation 1 or 2 (as already predicted in the descriptive and inferential analysis) and the lower ages are those who solely study (sp = 1).

$\log \left(\frac{P(sp=1)}{P(sp=3)}\right)=6.515-0.233\cdot Age(2)$

$\log \left(\frac{P(sp=2)}{P(sp=3)}\right)=2.469-0.116\cdot Age(3)$

Equations 4–6 determine the prediction of the family breadwinner, indicating that the higher the age, the more likely it is that the breadwinner is the student himself/herself in family situation 3.

$\log \left(\frac{P(sf=1)}{P(sf=4)}\right)=-3.125+0.245\cdot Age(4)$

$\log \left(\frac{P(sf=2)}{P(sf=4)}\right)=-10.780+0.623\cdot Age(5)$

$\log \left(\frac{P(sf=3)}{P(sf=4)}\right)=-14.927+0.703\cdot Age(6)$

In the case of the telephone company, Eqs 7, 8 show that the higher the age, the lower the probability that the telephone company is Orange or Movistar.

$\log \left(\frac{\text{P}(\text{ct}=1)}{\text{P}(\text{ct}=3)}\right)=6.550-0.304\cdot Age(7)$

$\log \left(\frac{\text{P}(\text{ct}=2)}{\text{P}(\text{ct}=3)}\right)=3044-0.134\cdot Age(8)$

Finally, the likelihood of having internet access with a smartphone or ADSL is higher the older the age.

$\log \left(\frac{\text{P}(\text{ai}=1)}{\text{P}(\text{ai}=4)}\right)=-2.417+0.199\cdot Age(9)$

$\log \left(\frac{\text{P}(\text{ai}=2)}{\text{P}(\text{ai}=4)}\right)=-0.202+0.031\cdot Age(10)$

$\log \left(\frac{\text{P}(\text{ai}=3)}{\text{P}(\text{ai}=4)}\right)=-4.980+0.237\cdot Age(11)$

Table 8 shows that these multinomial logistic regressions are poor (Mc-Fadden < 0.2) (Pando and San Martín, 2004), although the parameters obtained are in line with reality, as detailed above. This is due to the sample size, given that in all cases the dependent variable had few observed values in some categories, as shown in the observed-predicted classification matrix when using the percentage of correct classifications as a measure of prediction quality. Accordingly, only equation (Equation 1) is considered for verification of the model.

TABLE 8

Table 8. Model fitting using likelihood ratio, goodness-of-fit and Pseudo R2 tests.

After simulating the model for the sample of 54 students (Figure 4), a coefficient of R = 0.511 was obtained, indicating an efficient model with an index value of 0.256, W = 0.651 and RMSE/MAE = 1.296.

FIGURE 4

Figure 4. Graphical validation of the model for a sample of 54 students.

Discussion and conclusion

The research presented in this article aims at contributing to the state of the art of studies that analyze different factors affecting university student performance associated with the impact of COVID-19 on the academic performance of students during the 2019/2020 academic year that attended a face-to-face university. Therefore, the academic community and students had to respond in a way that combined an emergency response as stated by Hodges et al. (2020), taking decisions about methodological, educational platforms and technical options (Bao, 2020; Hodges et al., 2020; Mulenga and Marbán, 2020; López-Iñesta and Sanz, 2021), without being able to plan or ensure that all the persons involved had the minimum required technological means, the necessary digital skills and attitudes prone to change Rapanta et al. (2020) and Pérez-López et al. (2021).

In this study, the causal diagram constructed quantifies the association between students’ academic performance and personal, economic and technological access factors. These relationships allow us to predict students’ performance based on a regression model. The determinant factors were found to be a personal work situation of solely studying and access to internet with ADSL or smartphone.

Our findings suggest, through the analysis of the causal diagram and the predictive model, that the personal work situation of the students is the first-level variable with the greatest impact on academic results. Students who were solely studying obtained the best grades with a difference of almost two points compared to those who were also working or who had lost their jobs due to the COVID-19 pandemic. This is in line with the findings of Ruesga et al. (2014) which suggest that working negatively affects students’ academic performance in Spain, demonstrating that equality is lacking in this situation. However, at an international level not all studies report such a negative effect (Riggert et al., 2006).

The analysis of the data leads us to find that the second-level variable associated with personal work situation is age, with the youngest students being those who solely study. In this sense, age also has an impact on three variables that are considered to be first-level but which have a lesser effect on academic performance. Firstly, family breadwinners, with the breadwinners being the father and/or mother in the case of the youngest students and with statistically significant differences to those whose option was that the whole family had been made unemployed due to COVID-19 or that the students themselves were the family breadwinners. These results are in line with the study by Ruesga et al. (2014), who identified the age of the students as a determinant of the employment situation where academic performance is affected in the case of students who are family breadwinners. Secondly, technological access, defined according to the telephone company and internet access type, shows a medium-level association with academic results, but with no statistically significant differences between the different categories. Finally, the third second-level variable is the place of residence where students spent the confinement period, also related to the internet access type. Different studies carried out in the framework of COVID-19 indicate that this access depends on the family economy and, sometimes, on the student’s place of residence (UNESCO, 2020; Pérez-López et al., 2021), which generates situations in which inequity and dependence on digital infrastructure are exacerbated (Lloyd, 2020; Reimers and Schleicher, 2020; Van Dijk, 2020).

Future lines of research could broaden the scope of the study and address the distance learning model implemented following COVID-19 by applying a wider analysis of the students’ cognitive factors, and also taking into account the perspective of teachers. This would allow the identification of strengths and weaknesses and further develop the empirical evidence regarding the education model imposed.

Data availability statement

The dataset used and analyzed in the current study is available from the corresponding author on reasonable request.

Author contributions

MS and EL-I designed the research, collected the data, analyzed the research, searched the literature, and wrote the manuscript. Both authors contributed to the article and approved the submitted version.

Funding

This research was partially supported by the project GV/2021/110 from Generalitat Valenciana.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^ UNESCO. Education: from school closure to recovery. Available at https://www.unesco.org/en/covid-19/education-response.
2. ^ Instituto Nacional de Estadística (INE). Encuesta sobre equipamiento y uso de tecnologías de información y comunicación en los hogares 2019 (Survey on Equipment and Use of Information and Communication Technologies in Households 2019). Available at https://www.ine.es/dynt3/inebase/es/index.htm?padre=6057.
3. ^ Instituto Nacional de Estadística (INE). Encuesta sobre equipamiento y uso de tecnologías de información y comunicación en los hogares 2020 (Survey on Equipment and Use of Information and Communication Technologies in Households 2020). Available at https://www.ine.es/dynt3/inebase/es/index.htm?padre=6898.
4. ^ Organización de Consumidores y Usuarios (OCU). ¿Qué cobertura tiene tu operador móvil? (What coverage does your mobile operator have?). Available at https://www.ocu.org/tecnologia/telefono/consejos/operadores-moviles.

References

Bao, W. (2020). COVID-19 and online teaching in higher education: A case study of Peking University. Hum. Behav. Emerg. Technol. 2, 113–115. doi: 10.1002/hbe2.191

PubMed Abstract | CrossRef Full Text | Google Scholar

Dominguez-Lara, S. (2018). Fiabilidad y alfa ordinal. Actas Urológ. Español. 42, 140–141. doi: 10.1016/j.acuro.2017.07.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Erlam, G. D., Garrett, N., Gasteiger, N., Lau, K., Hoare, K., Agarwal, S., et al. (2021). What really matters: Experiences of emergency remote teaching in university teaching and learning during the COVID-19 pandemic. Front. Educ. 6:639842. doi: 10.3389/feduc.2021.639842

CrossRef Full Text | Google Scholar

Fonteyne, L., Duyck, W., and De Fruyt, F. (2017). Program-specific prediction of academic achievement on the basis of cognitive and non-cognitive factors. Learn. Indiv. Differenc. 56, 34–48. doi: 10.1016/j.lindif.2017.05.003

CrossRef Full Text | Google Scholar

García-Martín, S., and Cantón, I. (2016). “Factores que inciden en el rendimiento académico. El camino hacia el éxito escolar de todos,” in Psicología y Educación: Presente y Futuro, ed. J. L. Castejón (Virgina: ACIPE- Asociación Científica de Psicología y Educación), 2190–2197.

Google Scholar

Hejazi, E., Naghsh, Z., Sanzgari, A. A., and Tarkhan, R. A. (2011). Prediction of academic performance: the role of perception of the class structure, motivation and cognitive variables. Proc. Soc. Behav. Sci. 15, 2063–2067. doi: 10.1016/j.sbspro.2011.04.054

CrossRef Full Text | Google Scholar

Helal, S., Li, L., Liu, L., Ebrahimie, E., Dawson, S., Murray, D. J., et al. (2018). Predicting academic performance by considering student heterogeneity. Knowl.-Based Syst. 161, 134–146. doi: 10.1016/j.knosys.2018.07.042

CrossRef Full Text | Google Scholar

Hodges, C., Moore, S., Lockee, B., Trust, T., and Bond, A. (2020). The difference between emergency remote teaching and online learning. Educ. Rev. 27, 1–12.

Google Scholar

Hoffmann, A., and Stover, J. (2013). Correlaciones policóricas y tetracóricas en estudios factoriales exploratorios y confirmatorios. Cienc. Psicol. 7, 151–164.

Google Scholar

Huang, R. H., Liu, D. J., Tlili, A., Yang, J. F., and Wang, H. H. (2020). Handbook on Facilitating Flexible Learning During Educational Disruption: The Chinese Experience In Maintaining Undisrupted Learning in COVID-19 Outbreak. Beijing: Smart Learning Institute of Beijing Normal University.

Google Scholar

Jandrić, P. (2020). Postdigital research in the time of COVID-19. Postdig. Sci. Educ. 2, 233–238. doi: 10.1007/s42438-020-00113-8

CrossRef Full Text | Google Scholar

Lacave, C., Molina, A. I., Fernández, M., and Redondo, A. (2015). “Análisis de la fiabilidad y validez de un cuestionario docente,” in Actas de las XXI Jornadas de la Enseñanza Universitaria de la Informática, ed. Universitat Oberta La Salle (Andorra la Vella: Universitat Oberta La Salle), 136–143. http://hdl.handle.net/2117/76844

Google Scholar

Lloyd, M. (2020). “Desigualdades educativas y la brecha digital en tiempos de COVID-19,” in Educación y pandemia: una visión académica, ed. H. Casanova Cardiel (Ciudad de México: Universidad Nacional Autónoma de México), 115–121.

Google Scholar

Loewenthal, K., and Lewis, C. A. (2001). An Introduction to Psychological Tests and Scales, 2nd Edn. America: Psychology Press, doi: 10.4324/9781315782980

PubMed Abstract | CrossRef Full Text | Google Scholar

López-Iñesta, E., and Sanz, M. T. (2021). Estudio de dos modelos de aprendizaje semipresencial en educación superior. Latin Am. J. Phys. Educ. 15:17. http://www.lajpe.org/mar21/15_1_17.pdf.

Google Scholar

Marinoni, G., Land, H., and Jensen, T. (2020). The Impact of COVID-19 on Higher Education Around the World. Paris: International Association of Universities.

Google Scholar

Martín, J. (2019). Teoría y Ejercicios Prácticos de Dinámica de Sistemas. Madrid: Vensim.

Google Scholar

Mulenga, E., and Marbán, J. (2020). Is COVID-19 the Gateway for Digital Learning in Mathematics Education? Contemp. Educ. Technol. 12:e269. doi: 10.30935/cedtech/7949

CrossRef Full Text | Google Scholar

Nash, J. E., and Sutcliffe, J. V. (1970). River flow forecasting through conceptual models part I - A discussion of principles. J. Hydrol. 10, 282–290. doi: 10.1016/0022-1694(70)90255-6

CrossRef Full Text | Google Scholar

Pando, V., and San Martín, R. (2004). Regresión Logística Multinomial. Cuad. Soc. Esp. Cien. Forest. 18, 323–327. doi: 10.31167/csef.v0i18.9478

CrossRef Full Text | Google Scholar

Paunonen, S., and Ashton, M. (2013). On the prediction of academics performance with personality traits: A replication study. J. Res. Personal. 47, 778–781. doi: 10.1016/j.jrp.2013.08.003

CrossRef Full Text | Google Scholar

Pérez-López, E., Atochero, A., and Rivero, S. (2021). Educación a distancia en tiempos de COVID-19: Análisis desde la perspectiva de los estudiantes universitarios. Rev. Iberoameric. Educ. Dist. 24, 331–350. doi: 10.5944/ried.24.1.27855

CrossRef Full Text | Google Scholar

Quintero Quintero, M. T., Orozco Vallejo, G. M., and Patiño Giraldo, L. E. (2013). El desempeño académico: una opción para la cualificación de las instituciones educativas. Plumilla Educativa, 12, pp. 93–115.

Google Scholar

Rapanta, C., Botturi, L., Goodyear, P., Guàrdia, L., and Koole, M. (2020). Online university teaching during and after the COVID-19 crisis: Refocusing teacher presence and learning activity. Postdig. Sci. Educ. 2, 923–945. doi: 10.1007/s42438-020-00155-y

CrossRef Full Text | Google Scholar

Rasheed, R. A., Kamsin, A., and Abdullah, N. A. (2020). Challenges in the online component of blended learning: A systematic review. Comput. Educ. 144:103701. doi: 10.1016/j.compedu.2019.103701

CrossRef Full Text | Google Scholar

Reimers, F., and Schleicher, A. (2020). Un Marco Para Guiar Una Respuesta Educativa a la Pandemia del 2020 del COVID-19. Paris: OCDE.

Google Scholar

Riggert, S., Boyle, M., Petrosko, J., Ash, D., and Rude-Parkins, C. (2006). Student employment and higher education: Empiricism and contradiction. Rev. Educ. Res. 76, 63–92. doi: 10.3102/00346543076001063

CrossRef Full Text | Google Scholar

Rodicio García, M. L., Ríos-de Deus, M. P., Maria Jose, M.-G., and Maria, P. A. (2020). La brecha digital en estudiantes españoles ante la Crisis de la COVID-19. Rev. Internac. Educ. Just. Soc. 9, 103–125. doi: 10.15366/riejs2020.9.3.006

CrossRef Full Text | Google Scholar

Ruesga, S., da Silva, J., and Monsueto, S. (2014). Estudiantes universitarios, experiencia laboral y desempeño académico en España. Rev. Educ. 365, 67–95. doi: 10.4438/1988-592X-RE-2014-365-265

CrossRef Full Text | Google Scholar

Sanz, M. T., Gonzalez-Calero, J. A., Arnau, D., and Arevalillo-Herraez, M. (2019). Using reading comprehension to build a predictive model for the fourth-grade grade students’ achievement when solving word problems in an intelligent tutoring system. Rev. Educ. 384, 37–64. doi: 10.4438/1988-592X-RE-2019-384-409

CrossRef Full Text | Google Scholar

Sanz, M. T., López-Iñesta, E., Garcia-Costa, D., and Grimaldo, F. (2020). Measuring arithmetic word problem complexity through reading comprehension and learning analytics. Mathematics 8:1556. doi: 10.3390/math8091556

CrossRef Full Text | Google Scholar

Tanujaya, B., Mumu, J., and Margono, G. (2017). The relationship between higher order thinking skills and academic performance in mathematics instruction. Int. Educ. Stud. 10, 78–85. doi: 10.5539/ies.v10n11p78

CrossRef Full Text | Google Scholar

UNESCO (2020). COVID-19 y Educación Superior: De los Efectos Inmediatos al día Después. France: UNESCO.

Google Scholar

Van Dijk, J. (2020). The digital divide. New Jersey: John Wiley & Sons Inc.

Google Scholar

Vinatea, J. A. (2019). Modelo de Dinámica De Sistemas Para Predecir El Efecto De Las Tutorías En La Población De Alumnos En Riesgo De Deserción Académica De La Facultad De Ingeniería Industrial Y De Sistemas De La Universidad Nacional De Ingeniería. Ph.D. thesis, New Jersey: John Wiley & Sons Inc.

Google Scholar

Vlachopoulos, D., and Makri, A. (2019). Online communication and interaction in distance higher education: A framework study of good practice. Int. Rev. Educ. 65, 605–632. doi: 10.1007/s11159-019-09792-3

CrossRef Full Text | Google Scholar

Willmott, C. J. (1981). On the validation of models. Physical Geogr. 2, 184–194. doi: 10.1080/02723646.1981.10642213

CrossRef Full Text | Google Scholar