- Institute for Education in Science and Social Studies, University of Teacher Education Lucerne, Lucerne, Switzerland
The goal of this video study was to investigate whether the gender composition of a pair influences collaboration during the pair programming process. Pair programming is an agile software development technique in which two people share a computer and jointly develop a program. One of the programmers, the driver, operates the keyboard and mouse; the other, the navigator, reviews the code and helps without touching the keyboard or mouse. These two roles are swapped at regular intervals. Video data were collected during a half-day robotics workshop for students in Grades 5–9 (10–14 years old) and gifted students in Grades 3–6 (8–11 years old) at the University of Teacher Education Lucerne. A total of 203 pairs with different gender compositions (homogeneous female, homogeneous male, heterogeneous) were filmed during the pair programming process. Without consideration of the grade level the research results showed that there were no significant differences between the pairs based on gender composition in terms of task-solving speed, number of assistance requests, role changes, or rule violations by the navigator. In heterogeneous pairs, male and female students in the navigator role intervened equally often. These results initially appear to be consistent with several previous studies, which also found no significant differences based on gender composition. However, when only students in Grades 7–9 (12–14 years old) were considered, there were two significant differences. First, the homogeneous male pairs violated the rule that the navigator does not touch the keyboard or mouse more often than the other pairs. This suggests that homogeneous male pairs are not ideal for students in Grades 7–9 (12–14 years old). Second, as previously shown in other studies, heterogeneous pairs showed the greatest variability in task-solving speed. This may indicate compatibility issues among some heterogeneous pairs in Grades 7–9. In this study, only quantitatively measurable indicators of collaboration were considered. Further research on gender and pair programming should therefore focus on the quality of collaboration.
Introduction
Definition of pair programming and extension to a robotics workshop
Pair programming is one of the twelve practices of Extreme Programming (XP), an approach to software development established by Beck (1999). In pair programming, two people program together and take the roles of driver (also called pilot) and navigator (also called copilot or observer; Beck, 1999). The person in the driver role operates the keyboard and mouse, while the person in the navigator role watches, supervises, and supports without touching the computer. During the process, the members change roles periodically. Although only one person operates the computer, decisions about program development are made jointly. Adequate communication skills are important in this process (Werner and Denning, 2009; Hanks et al., 2011; Denner et al., 2014).
A robotics workshop differs from a typical programming experience in that a robot must be operated in addition to the computer. This requires an extension of pair programming rules. Therefore, Zhong and Wang (2021) proposed a new form of role assignment: hardware operator and software operator. One person takes care of the software (i.e., programming the robot) while the other person operates the hardware (i.e., building the robot). In a study with students in Grade 6 in China, Zhong and Wang (2021) compared the new roles (software–hardware) with the traditional ones (driver–navigator). In the traditional driver–navigator pairs in their study, one person operated the computer and the robot, while the other person supported them. They found no significant differences between the traditional driver–navigator and software–hardware pairs. However, they pointed out that the learners in their study worked with the educational mBot robot model, which required little additional design work due to its simple assembly. Therefore, learners in the hardware operator role were able to complete their tasks quickly and focus on observing and supporting, which corresponds to the traditional navigator role. To compare driver–navigator pairs with software–hardware pairs, more diverse hardware tasks are necessary.
Effects of pair programming in a school context
Pair programming is prevalent in both the workplace and education and has thus received much attention in research (Gómez et al., 2017). However, few studies have looked at pair programming in a school context. The existing studies have found the following results. Learners who engage in pair programming perform better than solo programmers (Iskrenovic-Momcilovic, 2019; Çal and Can, 2020). They acquire more programming knowledge (Denner et al., 2014) and computational thinking skills (Seo and Kim, 2016). In addition, they gain a better understanding of programming concepts, higher problem-solving skills, more confidence in programming, more positive attitudes toward programming, and more interest (Papadakis, 2018). Most learners prefer pair programming to solo programming because working with another person supports their learning, creates a positive and fun learning atmosphere, and prepares them for larger projects (Papadakis, 2018; Celepkolu et al., 2020; Çal and Can, 2020). Girls report that they gain more enjoyment of computer science as a subject by programming in pairs. They understand tasks better, learn more, and have more perseverance in solving problems. In addition, they value the socialization, communication, and support that pair programming provides (Liebenberg et al., 2012). Female learners also prefer to ask experienced peers rather than the instructor when something is not clear to them and appreciate being able to share their uncertainties with someone (Werner and Denning, 2009; Ying et al., 2019).
Factors for success of pair programming
These positive effects of pair programming can only occur if the technique is implemented correctly (Bowman et al., 2020). Program development rules and procedures must be clearly stated, communicated, and followed (Çal and Can, 2020). These rules should allow both individuals to participate and collaborate on an equal footing. To this end, researchers have formulated guidelines. Williams and Kessler’s (2000) guidelines related to professional practice are commonly used. Werner et al. (2004a) built on these guidelines and broadened the perspective to include the school setting. Williams et al. (2008) addressed the implementation of pair programming in the academic context. Zarb et al. (2013) articulated several principles for effective communication in collaborative programming. These guidelines are supported by research findings. For example, when roles are regularly reversed, this leads to a high level of commitment from both individuals (Plonka et al., 2011). It is also important that both individuals perform each role for approximately the same amount of time (McDowell et al., 2006). Individuals who hold the driver role rarely and briefly are more likely to drop out of pair programming. This can be explained by their inability to comprehend the actions of the driver (Plonka et al., 2011, 2012).
For pair programming to be effective, it is also important that the members of a pair are compatible (Hanks et al., 2011; Tunga and Tokel, 2018; Bowman et al., 2020). Pairs should be grouped based on their characteristics to speed up the task-solving process, enable knowledge transfer, improve the quality of the program they develop, and create a learning atmosphere (Williams et al., 2006; Alshehri and Benedicenti, 2014). Various characteristics of learners can influence the effectiveness of pair programming, including general academic performance, personality, and learning style. Their attitudes toward pair programming can also have an impact. The way learners are grouped can also affect their compatibility. The results of several studies suggest that communication and collaboration are enhanced when learners have similar skills (Katira et al., 2005; Salleh et al., 2011; Al-Ramahi et al., 2013; Denner et al., 2014; Bowman et al., 2019). Familiarity and friendship can impact pair programming as well (Denner et al., 2014). In interviews, most learners indicate that they interact better, are more productive, and feel more comfortable collaborating with a familiar person (Celepkolu et al., 2020). However, some learners prefer to work with non-familiar students because they collaborate more professionally (Demir and Seferoglu, 2021). If learners in a pair are not friends, a lack of interaction occurs more frequently (Campe et al., 2020).
Influence of gender on pair programming
The gender composition (homogeneous female, homogeneous male, heterogeneous) of a pair can also have an impact on their compatibility and, thus, their collaboration. In gender studies, a distinction is made between the terms sex and gender. Sex refers to biological sex, while gender refers to how it is interpreted socially (Lünenborg and Maier, 2013). Gender is a cultural and social construct created by society, which establishes gender roles and gender-typical behaviors and characteristics (Satz, 2012). Maccoby (1998) further argues that gendered aspects of behavior can be influenced by the gender of one’s counterpart. When boys are present, girls are under more pressure to maintain their gender identity by performing gender-conforming behavior, and vice versa (Maccoby, 1990; Brutsaert, 1999; Kröll, 2010; von Ow and Husfeldt, 2011; Amon et al., 2012; Flore and Wicherts, 2015; Wedl and Bartsch, 2015).
The field of computer science is often described as technology-oriented, competitive, masculine, and not very social (Werner et al., 2004b; Nosek et al., 2009; Diekman et al., 2010, 2011; Cheryan et al., 2011; Choi, 2015). This stereotypical image is incompatible with female gender roles (Eagly, 1987; Cheryan et al., 2013) and women’s preference for people-oriented and collaborative careers (Ying et al., 2019). Various studies have indicated that women have more negative attitudes than men toward computer science (Chang et al., 2012; Başer, 2013; Jarratt et al., 2019) and are less confident in their abilities in the field (Beyer et al., 2003; Maguire et al., 2014; Coto and Mora, 2019; Fraunhofer IAIS, 2019; Jarratt et al., 2019; Campe et al., 2020). However, several studies have shown that there are no gender differences in performance in computer science at either the university (Akinola, 2016) or public education (Papadakis, 2018; Iskrenovic-Momcilovic, 2019). Despite this, women are underrepresented in education and employment in science and engineering (National Center for Science and Engineering Statistics, 2019).
Pair programming can be used to show female learners that programming can also be a collaborative and social task. This can counter the stereotypical image of computer science careers as antisocial and competitive (Werner et al., 2004b; Liebenberg et al., 2012; Choi, 2015; Ying et al., 2019). However, considering that computer science and robotics are seen as typically masculine in society, girls may feel that their gender identity is threatened when working with boys and therefore hold back (Flore and Wicherts, 2015). In gender homogeneous pairs, though, gender identity may take a back seat, allowing the students to focus on developing their competence (Kessels, 2002; Faulstich-Wieland et al., 2004; von Ow and Husfeldt, 2011). This might reduce the perceived external social pressure and fear of social exclusion (Esch and Herrmann, 2008). In homogeneous female pairs, girls can also appear confident in fields that are perceived as male (Kröll, 2010; Booth and Nolen, 2012).
To date, there have been few empirical studies examining the influence of gender on pair programming (Salleh et al., 2011; Zhong et al., 2016; Gómez et al., 2017). Studies by Katira et al. (2005) and Choi (2015) have suggested that, in an academic context, heterogeneous groups are less compatible than homogeneous ones. In a survey by Choi (2015), female students in heterogeneous groups were more likely to report difficulties and conflicts, while those in homogeneous groups spoke of compatibility. Homogeneous female and male groups did not differ significantly in compatibility and communication. In contrast, a study by Demir and Seferoglu (2021) did not demonstrate significant differences between homogeneous and heterogeneous groups in terms of compatibility or the experience of flow. Results regarding productivity are also inconclusive. Some studies have failed to demonstrate a significant difference between homogeneous and heterogeneous groups (Choi, 2015; Akinola, 2016; Demir and Seferoglu, 2021). In contrast, in a study by Jarratt et al. (2019), homogeneous male groups showed the highest levels of productivity. Moreover, Gómez et al. (2017) found that gender heterogeneous groups showed the greatest variability in productivity, which could indicate compatibility issues.
In school contexts, no significant compatibility differences between homogeneous and heterogeneous groups have been demonstrated to date. However, homogeneous female groups exhibit the closest partnership. They also communicate and discuss their ideas more frequently than other compositions (Zhong et al., 2016). Therefore, they invest more time in sharing ideas about the task than male groups, while homogeneous male groups communicate more frequently about non-task-related topics (Campe et al., 2020). In a study by Tsan et al. (2016), the code quality of homogeneous female groups was significantly lower than those of other gender compositions, though only four female groups were examined. Zhong et al. (2016) found no significant differences in the performance of the different gender compositions. In a study by Underwood et al. (2000), heterogeneous groups showed less verbal interaction and less balanced keyboard use than homogeneous groups. Male students moved the cursor more frequently and made more decisions. However, in this experiment, learners did not engage in pair programming: they performed a cloze task instead of writing a program.
The results on the compatibility of homogeneous and heterogeneous groups are somewhat contradictory. It has been suggested that the duration of pair programming may be the determining factor, as this has varied widely across studies. In addition, because of the few women in computer science, often few female pairs were studied (Choi, 2015). In general, samples have tended to be small. Participants have varied in age and pair programming has been implemented differently. More research is needed, especially in the school context, on whether and to what extent assignment to homogeneous and heterogeneous pairs affects learner collaboration (Jarratt et al., 2019).
Research questions and hypotheses
The present study aims to address this research gap. In the context of a half-day robotics workshop at the learning lab at the University of Teacher Education Lucerne, the study investigates the extent to which division into homogeneous and heterogeneous pairs affected the collaboration of the learners. The robotics workshop was designed for students in Grades 5–9 (10–14 years old) and gifted students in Grades 3–6 (8–11 years old). In Switzerland, compulsory education for children begins in Grade 1 at the approximate age of 6 and ends in Grade 9 at the approximate age of 14. The research questions and hypotheses of this study are presented below.
RQ1) To what extent do homogeneous and heterogeneous pairs differ in terms of task-solving speed?
Many studies in the academic context have suggested that different gender compositions do not differ significantly in terms of code productivity (Choi, 2015; Akinola, 2016; Gómez et al., 2017; Demir and Seferoglu, 2021). In contrast, in a study by Jarratt et al. (2019), homogeneous male groups showed the highest degree of productivity. Research on this question in school contexts is rare. Zhong et al. (2016) found no significant difference in performance in their study of students in Grade 6 at a Chinese primary school. Consistent with these previous research results, we hypothesize that homogeneous and heterogeneous pairs will not differ in terms of task-solving speed.
RQ2) To what extent do homogeneous and heterogeneous pairs differ in terms of the number of assistance requests?
The stereotypically male image of computer science can have a negative impact on women. Women rate themselves as less competent in computer science, despite equal accomplishments. They are also more likely to report that they do not understand all programming concepts and have less confidence in their products (Jarratt et al., 2019). Therefore, we hypothesize that homogeneous female pairs will request assistance more often than homogeneous male and heterogeneous pairs.
RQ3) To what extent do girls and boys in heterogeneous pairs differ in terms of their adherence to previously communicated pair programming guidelines?
Learners were presented with research-derived pair programming guidelines. This study focuses on two of these rules. The first one is that the navigator must not touch the computer (Werner et al., 2004a). As previously noted, girls’ gender identity may be threatened in heterogeneous groups (Flore and Wicherts, 2015). In a study by Underwood et al. (2000) that examined gender interaction in a non-pair programming context, boys dominated computer use. Consistent with previous research, we hypothesize that girls will be more reserved, and boys will dominate in gender heterogeneous pairs. This leads to the assumption that male learners in heterogeneous pairs will be more likely to disobey pair programming rules. We hypothesize that boys will touch the keyboard or mouse more often and for longer when they are navigator than girls.
RQ4) To what extent do heterogeneous and homogeneous pairs differ in terms of their adherence to previously communicated pair programming guidelines?
As previously mentioned in homogeneous female pairs, girls can be more confident in areas that are perceived as masculine (Kröll, 2010; Booth and Nolen, 2012). Therefore, we assume that gender homogeneous pairs will better adhere to the rules of pair programming. To date, no significant difference has been demonstrated between homogeneous female and male pairs in terms of compatibility and communication (Choi, 2015). Regarding the first rule of pair programming, we hypothesize that learners in gender heterogeneous pairs will touch the keyboard or mouse when they are navigator more often and for longer than those in gender homogeneous pairs. The second pair programming rule is that the roles of navigator and driver should be swapped regularly (Williams and Kessler, 2000; Werner et al., 2004a; Williams et al., 2008). Both individuals should hold the two roles for approximately the same amount of time since this indicates a high level of commitment from both individuals (McDowell et al., 2006; Plonka et al., 2011). We hypothesize that learners will switch roles more frequently in homogeneous pairs than in heterogeneous pairs.
Materials and methods
Context and participants
To verify whether the division into homogeneous and heterogeneous pairs influenced learners’ collaboration in a robotics workshop, a video study was conducted. The videos were recorded in the learning environment “Discovering the City of the Future with Roberta®” at the University of Teacher Education Lucerne. This workshop was offered during the fall term of 2020 to students in Grades 5–9 (10–14 years old) and gifted students in Grades 3–6 (8–11 years old). Teachers in Central Switzerland could register to have their classes visit the learning environment, resulting in a non-random sample. Written consent to film the students during the workshop was obtained from their legal guardians in advance. Learners whose guardians did not provide consent experienced no disadvantages. In the learning lab, the instructor randomly selected four pairs from each class to be filmed. We chose to film the beginning of the work phase directly after the task was introduced. Approximately 50 min were filmed per pair. The students did not know the exact topic of the study.
The learning environment was developed on the basis of the principles of the Roberta® initiative by the Fraunhofer Institute for Intelligent Analysis and Information Systems (IAIS). The initiative focuses on developing robotics workshops that appeal equally to students of all genders (Fraunhofer IAIS, 2019). In the learning environment, the students were able to program the educational LEGO® Mindstorms EV3 robot model to function in a city of the future using the EV3-G graphical programming language. After a joint introduction to robotics and the EV3-G programming environment, the learners started with the first task: programming an autonomous vehicle. For this, they had to program the robot to drive autonomously along a black line.
One workshop instructor and one assistant accompanied each class in the learning environment. To ensure that learners experienced similar conditions despite the different instructors, we formulated guidelines in a workshop staff manual. For the introduction to pair programming, we gave the workshop instructors a script based on the pair programming guidelines found in the research literature (Williams and Kessler, 2000; Werner et al., 2004a; Williams et al., 2008). Learners were not required to perform any hardware tasks; they received the robot fully assembled. Therefore, we did not use the hardware–software role assignment framework proposed by Zhong and Wang (2021). Instead, we chose a combination of the hardware and navigator roles. The driver operated the computer (i.e., programmed the robot). The navigator thought along, monitored the driver, helped without touching the computer, and operated the robot. We determined that the pairs had to swap roles after each subtask. During the role swap, the students physically traded places.
We analyzed a total of 203 videos. The distribution of filmed pairs by grade level is shown in Table 1. The youngest learner on the videos was 8 years old and the oldest was 15. The mean age was 11.36 with a standard deviation of 1.3. The filmed pairs were evenly distributed among homogeneous female, homogeneous male, and heterogeneous pairs (Table 2).
Learners were divided into homogeneous female, homogeneous male, and heterogeneous pairs by their teachers before the workshop using predetermined criteria. Biological sex was used for the gender criterion. In addition, learners were grouped according to performance. Both general academic performance and prior knowledge of programming were considered. The age difference between the learners in a pair was not to exceed 1 year. In summary, the pairs were to be divided as homogeneously as possible according to performance level, prior programming knowledge, and age. To facilitate neutral collaboration, students were paired with individuals with whom they were neither particularly good friends nor enemies. This division was intended to prevent these factors from distorting the differences among gender compositions. Since, in practice, it is not possible to perfectly assign every learner in a class according to all criteria, teachers also conducted an observation assignment to collect information about the learners’ general academic performance, prior programming knowledge, relationship, and age difference. These were treated as possible confounding variables.
Measures
The video recordings and the completed observation assignments were evaluated using a codebook that contained definitions, instructions, and categories. First, we conducted a test run of the codebook with three individuals. Then we adapted it according to their feedback. Subsequently, we introduced two student assistants to the codebook in a 1-h session. To avoid bias in the results, we did not inform the assistants of the exact research objective or hypotheses of this study.
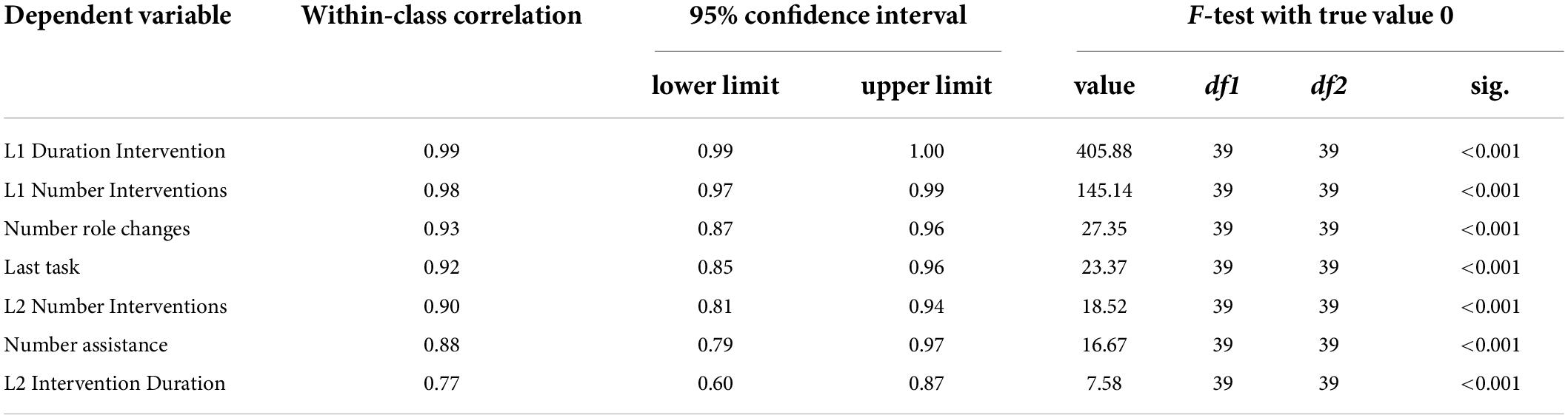
To examine intercoder reliability (i.e., the extent of agreement between the coding of the two student assistants) 20% of the videos were double coded. We selected the 40 double-coded videos randomly, with care taken to include roughly equal numbers of videos from all grade levels and gender compositions. According to the preconditions, we calculated the intraclass correlation coefficient (ICC) (3,1), two-way mixed, single measure absolute agreement. The ICC–the within-class correlation column in Table 3–was lowest for the variable L2 Intervention Duration, the average duration that Learner 2 intervened when he/she was navigator, with ICC = 0.77 and a confidence interval of [0.60, 0.87]. The variable L1 Duration Interventions had the highest coefficient with ICC = 0.99 and a confidence interval of [0.99, 1.00]. In the literature, rater agreement above a value of 0.7 is considered good (Greve and Wentura, 1997; Greguras and Robie, 1998). Since all values were above this guideline value, it can be assumed that the agreement among the coders was satisfactory. The ICC was significant for all dependent variables (see sig. column in Table 3).
The following section describes how the dependent variables were determined. To test the first research question, task-solving speed had to be calculated. Therefore, information about the last task a pair worked on was gathered and used, along with their total work time, to calculate how many tasks they worked on per hour.
The number of assistance requests, needed for the second research question, was determined based on how often learners asked for and received help (e.g., by a hand signal). Assistance could be provided by a supervisor (i.e., workshop instructor, assistant, or teacher) or other learners. Help that was not actively requested was not counted, nor was help with technical problems that the learners had not initiated themselves. The number of assistance requests was combined with the total work time to determine a pair’s average number of assistance requests per hour.
For the third and fourth research questions, the number of times the navigator intervened was determined. If the person in the navigator role touched the computer mouse or keyboard, this was counted as an intervention. For a person to intervene at all, he or she had to assume the role of navigator at least once during the independent working phase. The longer someone held this role, the higher the possible number of interventions. Therefore, the number of times an individual intervened was combined with how long they held the navigator role to determine the average number of interventions per navigator hour. To estimate the total number of times learners in a pair intervened, the interventions of the two individuals were added together.
To calculate the average intervention duration, also for the third and fourth research questions, the total duration of an individual’s interventions was divided by the number of times he or she intervened. The averages of the two individuals in a pair were then added together. The sum rather than the average of the pair was used because the average intervention duration depended on the duration of time spent in the navigator role. In many cases, the duration of navigation time was unbalanced, so an average of the two individuals in a pair would not be meaningful.
The number of times the individuals switched places was used to calculate how many times the pairs changed roles, which was needed for the fourth research question. One of the pair programming guidelines was to switch places after each subtask. If a pair was working on the third task at the end of the working period, they should have changed roles twice. Thus, the target number of role changes was the number of the last task minus one. Actual role changes were subtracted from the target value. Positive values of this variable indicated that individuals changed roles too often, while negative values indicated they did not do so often enough. A zero-value indicated that the number of role changes was equal to the target value.
Data analysis
Since only isolated normal distributions were available in the present data set, we chose non-parametric procedures for the tests for confounding variables and hypotheses. The measurements obtained for each group were compared using a Kruskal–Wallis test and a post hoc Dunn–Bonferroni pairwise comparison method. Because the groups (students in Grades 5–6, students in Grades 7–9, gifted students in Grades 3–6) differed greatly in size, we chose Cohen’s pooled standard deviation (ds) as the effect size. A Wilcoxon test was used to test whether the central tendencies of the dependent variables differed between boys and girls in heterogeneous pairs. The following sections examine whether the possible confounding variables impacted the dependent variables.
The Kruskal–Wallis test found that age difference and learner relationship had no significant effect on the dependent variables. Therefore, these variables were not included in the hypothesis tests. However, the test showed that other variables (grade level, difference in general academic performance, and difference in prior programming knowledge) had a significant influence on the dependent variables of the study.
According to the Kruskal–Wallis test, grade level had a significant effect on task-solving speed (H = 9.72, p = 0.008). The Dunn–Bonferroni test revealed that there was a significant difference between the task-solving speed of the gifted students and the students in Grades 7–9 (z = −2.59, p = 0.029, ds = 0.28), as well as the speed of the students in Grades 5–6 and the students in Grades 7–9 (z = −2.74, p = 0.018, ds = 0.37). The students in Grades 7–9 completed the tasks faster than the other students. According to Cohen (1988), this variable had a small effect in both cases.
Another significant difference based on grade level was found using the Kruskal–Wallis test. This concerned the total number of interventions by the navigator (H = 8.34, p = 0.015). The Dunn–Bonferroni test revealed that there was a significant difference between the number of interventions among the students in Grades 7–9 and the students in Grades 5–6 (z = 2.75, p = 0.018, ds = 0.45). Interventions were less frequent among the students in Grades 7–9 than the students in Grades 5–6. According to Cohen (1988), this was a weak effect.
The Kruskal–Wallis test also showed that the difference in general academic performance had a significant effect on the number of requests for assistance (H = 8.69, p = 0.034). The Dunn–Bonferroni test revealed a significant difference in the number of assistance requests by pairs with similar and equal general academic performance (z = 2.73, p = 0.038, ds = 0.37). Pairs in which learners had the same general academic performance requested more help than pairs with similar general academic performance. The effect size was small (Cohen, 1988).
The difference in prior programming knowledge also had a significant effect on the number of assistance requests, according to the Kruskal–Wallis test (H = 14.21, p = 0.001). The Dunn–Bonferroni test revealed that there was a significant difference in the number of assistance requests by groups in which both individuals had prior programming knowledge and those in which both lacked this knowledge (z = 3.67, p = 0.001, ds = 0.59). Pairs in which both learners lacked prior programming knowledge requested more help than pairs in which both individuals had prior knowledge. The effect was medium-sized, according to Cohen (1988).
To summarize, the age difference and the relationship between learners did not show a significant effect on any of the dependent variables studied. Moreover, none of the confounding variables showed a significant effect on some of the dependent variables (number of interventions by the navigator, average intervention duration, number of role changes, or sum of the average intervention durations). The significant results reported concerning confounding variables are summarized in Table 4.
Results
Task-solving speed by gender composition (RQ1)
First, we examined whether task-solving speed differed based on the gender composition of the pair. The slowest pair worked on an average of 2.80 tasks per hour; the fastest group worked on 13.54. The mean was 5.93 tasks per hour with a standard deviation of 1.43. The Kruskal–Wallis test revealed that there was no significant difference based on gender composition in terms of task-solving speed (H = 2.56, p = 0.279). Among students in Grades 7–9 (12–14 years old), the heterogeneous pairs showed the greatest variability in task-solving speed (see Figure 1).
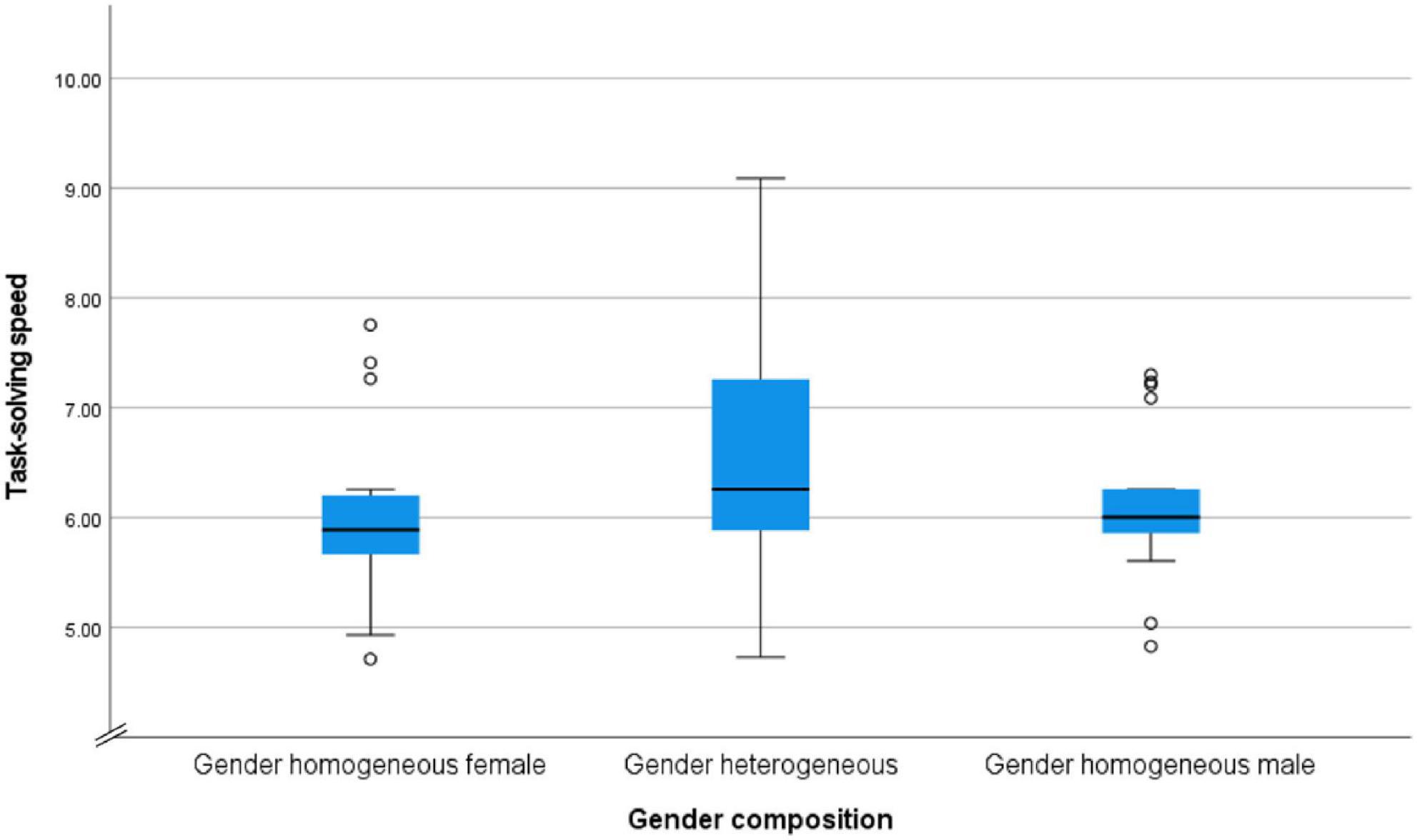
Figure 1. Box plot for task-solving speed (tasks worked on per hour) by gender composition among students in Grades 7–9 (n = 54).
Number of assistance requests by gender composition (RQ2)
Next, we calculated whether the pairs with different gender compositions requested different amounts of assistance. Since there were pairs that did not request help, the minimum value was zero. The group with the highest value requested assistance an average of 17.02 times per hour. The mean value was 4.18 with a standard deviation of 3.33. The pairs did not differ significantly in the number of assistance requests based on gender composition (H = 0.18, p = 0.916).
Adherence to pair programming guidelines of girls and boys in heterogenous pairs (RQ3)
We further investigated whether the number of interventions by the navigator differed between individuals in gender heterogeneous pairs. There were learners who were never the navigator, as well as individuals who held that role for a long time (minimum = 0 min, 0 s; maximum = 1 h, 1 min, 7 s). The mean was 23 min, 3 s, with a standard deviation of 13 min, 47 s. For most heterogeneous pairs, both learners held the role of navigator for about the same amount of time. The mean number of interventions per navigator hour was 11.40 (SD = 15.30). The Wilcoxon test was used to test whether the measures of central tendency for the number of interventions made by boys and girls in gender heterogeneous pairs differed. The number of interventions by boys (Mdn = 6.06) was not significantly different from the number of interventions by girls (Mdn = 5.59; asymptotic Wilcoxon test: z = −0.60, p = 0.546, n = 60).
Next, we examined whether the average intervention duration by the navigator differed between the individuals in heterogeneous pairs. The shortest average intervention duration was 0 min, 1 s and the longest was 2 min, 30 s. The mean was 0 min, 11 s, with a standard deviation of 0 min, 13 s. The Wilcoxon test revealed that the measures of central tendency for the average intervention duration of boys (Mdn = 0 min, 8 s) and girls (Mdn = 0 min, 7 s) in heterogeneous pairs were not significantly different (asymptotic Wilcoxon test: z = −0.72, p = 0.469, n = 35).
Adherence to pair programming guidelines by gender composition (RQ4)
We also examined whether the number of role changes differed based on the gender composition of the pairs. Almost half of the pairs (77 out of 176) changed roles the correct number of times. There were pairs that made four fewer place changes than the ideal number (minimum) and pairs that made six more that they should have (maximum). The mean was −0.44, with a standard deviation of 1.84. Thus, most pairs adhered to this specification but there was a tendency to make fewer place swaps than required. The Kruskal–Wallis test revealed that there were no significant differences in the number of role changes between the pairs based on gender composition (H = 0.93, p = 0.628).
We conducted further investigation to determine if the total number of interventions by the navigator differed by gender composition. In 8.13% of the pairs (13 of 160), neither learner intervened. The pair with the most interventions intervened a total of 137.58 times per navigator hour. The mean was 21.77 times per hour, with a standard deviation of 22.41. The Kruskal–Wallis test revealed that there was no significant difference in the number of interventions based on gender composition (H = 3.07, p = 0.215).
When only students in Grades 7–9 (12–14 years old) were considered, however, the Kruskal–Wallis test revealed that there was a significant difference between the total number of interventions based on gender composition (H = 8.61, p = 0.014). The Dunn–Bonferroni test also showed a significant difference in the total number of interventions made by the homogeneous female and the homogeneous male pairs (z = −2.52, p = 0.035, ds = 1.07), as well as the heterogeneous and the homogeneous male pairs (z = −2.62, p = 0.027, ds = 1.06). Both effect sizes were found to be high. The boxplot (Figure 2) shows that overall, students in the homogeneous male pairs in Grades 7–9 intervened more frequently than those in other pairs.
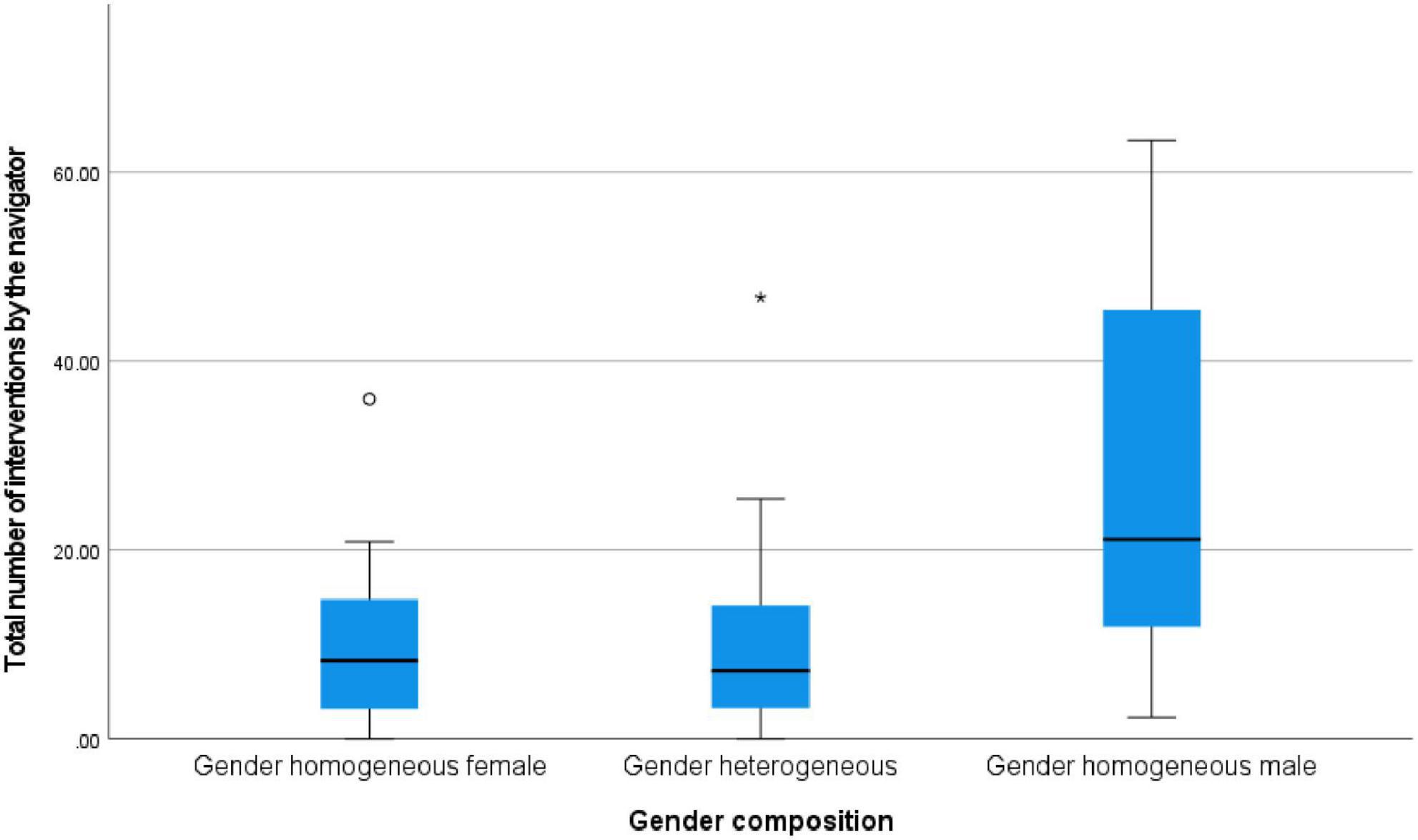
Figure 2. Boxplot of total number of interventions per navigator hour by gender composition among students in Grades 7–9 (n = 50). The * in the boxplot is a symbol for an extreme value.
In the final step, we examined whether the sum of the average intervention durations by the two individuals in a pair differed by gender composition. The lowest sum was 0 min, 2 s and the highest was 2 min, 39 s. The mean was 0 min, 23 s, with a standard deviation of 0 min, 21 s. The Kruskal–Wallis test revealed that there was no significant difference between the pairs based on gender composition in terms of the sum of the average intervention durations (H = 0.54, p = 0.765). Table 5 summarizes the results related to the research questions.
Discussion
Task-solving speed by gender composition (RQ1)
The first research question aimed to examine whether homogeneous and heterogeneous pairs differ in terms of task-solving speed. We hypothesized that gender composition would have no effect on task-solving speed. The results of this video study indicate that homogeneous and heterogeneous pairs did not differ significantly; thus, the first hypothesis can be supported. This result is consistent with the findings of previous studies that found no significant difference between homogeneous and heterogeneous pairs in terms of coding productivity (Choi, 2015; Akinola, 2016; Zhong et al., 2016; Gómez et al., 2017; Demir and Seferoglu, 2021). However, Jarratt et al.’s (2019) finding that homogeneous male pairs were the most productive could not be confirmed by the results of the present study.
The finding that heterogeneous pairs had the greatest variability in productivity, addressed by Gómez et al. (2017), was also evident among the students in Grades 7–9 (12–14 years old) in this study. This could indicate a higher likelihood of compatibility issues among heterogeneous pairs in Grades 7–9. Some researchers show that heterogeneous pairs are less compatible than homogeneous ones (Katira et al., 2005; Choi, 2015), but this has not yet been demonstrated in the school context (Zhong et al., 2016). However, in a study by Underwood et al. (2000), heterogeneous pairs showed less verbal interaction than homogeneous pairs, even in the school context. Considering that good communication, quantitatively and qualitatively, is critical for effective pair programming (Werner et al., 2004a; Hanks et al., 2011; Denner et al., 2014; Rodríguez et al., 2017), this could negatively impact the task-solving speed of these pairs. This result may indicate that not only the quantity of communication, as in Underwood et al. (2000), but also the quality of communication, as in Zarb et al. (2013), is crucial. Further qualitative analysis in this study would be needed to explore this assumption. With the background knowledge that adolescents mostly have same-sex friends, it is likely that many learners in heterogeneous pairs are not friends. Research shows that non-friend pairs perform better (Demir and Seferoglu, 2021). However, they are also more likely to experience situations in which there is no interaction at all (Campe et al., 2020). The great variability in task-solving speed is therefore consistent with observations made in other contexts.
Number of assistance requests by gender composition (RQ2)
The second research question aimed to investigate whether homogeneous and heterogeneous pairs differed in terms of the number of assistance requests. We hypothesized that homogeneous female pairs would request more help than pairs with other gender compositions. The results of this video study show that the pairs did not differ significantly in terms of the number of assistance requests based on gender composition. Therefore, the second hypothesis can be rejected. Homogeneous female pairs did not request more help than homogeneous male pairs or heterogeneous pairs.
As previously mentioned, research has suggested that the male image of computer science affects women’s confidence, interest, and attitudes, though not their abilities. Women are more likely than men to report not fully understanding programming concepts and have less confidence in their products (Jarratt et al., 2019). However, the assumption that this uncertainty among girls affects the amount of help they request cannot be confirmed.
One possible explanation is the use of pair programming. Female learners are more productive and confident when they participate in pair programming than when they program alone (Zhong et al., 2016). Pair programming can show female learners that programming can also be a collaborative task. This can, to some extent, alter the stereotypical image of computer science as an antisocial (Werner et al., 2004b; Liebenberg et al., 2012; Ying et al., 2019) and competitive (Werner et al., 2004b; Choi, 2015) working environment. Therefore, pair programming can help attract more women to computer science. In interviews about pair programming, women have mentioned that they prefer to ask experienced peers rather than the workshop instructor when they are unsure about something and appreciate being able to share their uncertainties with someone (Werner and Denning, 2009; Ying et al., 2019). These factors may explain why homogeneous female pairs were no more likely to check with the workshop instructor than the other gender composition.
Adherence to pair programming guidelines in heterogeneous pairs (RQ3)
The third research question dealt exclusively with heterogeneous pairs. It examined the extent to which girls and boys would differ in following the previously communicated pair programming guidelines. We hypothesized that boys in the role of navigator would touch the computer keyboard or mouse more often than girls and that their interventions would last longer. The results of this study show that boys did not intervene significantly more often than girls, nor were their interventions significantly longer. Both parts of the hypothesis can thus be rejected. Girls and boys in heterogeneous pairs intervened in the role of the navigator with approximately equal frequency and duration. These results contradict the assumption that girls feel that their gender identity is threatened when collaborating with boys on a robotics task and therefore hold back (Flore and Wicherts, 2015). One possible explanation is that the learning environment was designed so that girls no longer perceived the robotics task as masculine. Furthermore, the tendency of boys to dominate the keyboard (Underwood et al., 2000) was not reflected in the results of this study. Considering the Underwood et al. (2000) study did not use pair programming guidelines, the present result may be another indication of the positive effects of pair programming on collaboration.
Adherence to pair programming guidelines by gender composition (RQ4)
The fourth research question aimed to investigate the extent to which heterogeneous and homogeneous pairs would differ in their adherence to pair programming guidelines. We hypothesized that homogeneous pairs would change roles more frequently than heterogeneous pairs. Further we hypothesized that the total number of interventions by the navigator and the sum of the average intervention durations by the learners in a pair would be higher among heterogeneous pairs than homogeneous pairs. The results of this study show that homogeneous pairs did not switch roles more frequently than heterogeneous pairs. Therefore, the hypothesis can be rejected. Regarding the total number of interventions by the navigator, learners in homogeneous male pairs in Grades 7–9 intervened more frequently. This difference was significant, and the effect size can be considered high according to Cohen (1988). Among the other age groups, there were no significant differences based on gender composition. The hypothesis that learners in heterogeneous pairs would touch the computer keyboard or mouse more often than those in pairs with other gender compositions can thus be rejected.
The gender compositions also did not differ significantly in terms of the sum of the average intervention durations. The hypothesis that interventions would last longer in heterogeneous pairs than the pairs with other gender compositions can also be rejected. The research findings support studies that found no significant differences in compatibility between homogeneous female and male pairs (Choi, 2015) or between homogeneous and heterogeneous pairs (Zhong et al., 2016; Demir and Seferoglu, 2021). However, they are not consistent with studies indicating that heterogeneous pairs are less compatible than homogeneous pairs (Katira et al., 2005; Choi, 2015). Nevertheless, the results of the present video study cannot be directly compared to these findings because within the scope of this study compatibility was only measured indirectly. For example, female students in heterogeneous pairs have reported difficulties and conflicts, while those in homogeneous pairs have reported good compatibility (Choi, 2015). In contrast, learner satisfaction was not analyzed in this video study. The assumption that girls benefit most from being in a group with other girls because homogeneous female pairs have the closest partnerships and communicate and discuss more (Zhong et al., 2016) cannot be confirmed in this study. The assumptions that gender identity takes a back seat to the development of competence in homogeneous pairs (Kessels, 2002; Faulstich-Wieland et al., 2004; von Ow and Husfeldt, 2011) and that girls may be more confident in homogeneous pairs (Kröll, 2010; Booth and Nolen, 2012) are also not supported by the results of this study.
Children and adolescents tend to have same-sex friends. The findings of previous studies suggest that partners who are friends perform less and collaborate less professionally (Demir and Seferoglu, 2021). Working professionally within the context of pair programming means adhering to the rules of this practice. The close friendship between same-sex learners may explain why homogeneous male pairs in Grades 7–9 were least likely to abide by the rules.
Limitations
Teachers self-registered their classes. Among other factors, the duration of the trip to the learning workshop and the teacher’s interest in computer science could have had an influence on this decision. Since the site of the learning environment was mainly accessible to school buildings in the city and canton of Lucerne, other cantons and rural areas were underrepresented. If the teacher was interested in the topic, it is possible that these learners have already been exposed to computer science topics in class. Classes that visited the learning workshop could therefore have had above-average prior knowledge in this area. It can also be assumed that learners behave differently in an out-of-school workshop than in the classroom. In addition, the cameras were highly visible in the learning environment. Learners may have found it socially desirable to follow the pair programming guidelines. Since it was a robotics workshop, the rules of pair programming had to be extended: the person who held the role of navigator also operated the robot. Therefore, the results of this study cannot be compared to pair programming studies without robots or with different role assignment frameworks, as interaction with the robot could be a confounding factor. Students were assigned to pairs based on research-guided criteria. Therefore, the results cannot be compared with studies in which learners were allowed to choose their own partners, randomly assigned, or assigned according to other criteria. Learners were instructed to switch roles after solving each subtask. Role switching was physically accomplished by changing places, which was not the case in all previous studies.
Research outlook
The purpose of this study was to investigate whether and to what extent being assigned to homogeneous and heterogeneous pairs would influence students’ collaboration during pair programming in a robotics workshop. In general, the results of this study seem to indicate that pair programming has significant potential to make robotics more gender-neutral. The clear role specifications in pair programming promote equality. However, based on the results of this study, it is not possible to recommend a specific gender composition. Further research is needed. In this study, only quantitatively measurable indicators of collaboration were considered. A full assessment of collaboration in pair programming based on gender composition would also require qualitative considerations. For example, research shows that good communication is critical to the success of pair programming. It would be interesting to know if one partner dominates the conversation, what the pairs discuss, and which pairs best adhere to the research recommendations for communication in pair programming. In addition, it would be worthwhile to take a closer look at the groups that scored highest on the quantitative assessment. This would allow the researchers to review the quantitative ratings and identify best practices. Furthermore, future research could survey learners to determine which gender composition they are most comfortable with or ask them about compatibility problems, as in other studies. In addition, individual learners could be studied. For example, it would be interesting to see if an individual intervenes more often if they already have programming skills. Due to the camera position, neither the activities on the screen nor those on the activity-based playground mat could be studied. Therefore, with the video footage available, it was not possible to analyze the full interaction with the robot. Future research could address this gap, as there have been few studies investigating pair programming when working with robots. For example, it could be studied whether one partner touches the robot more often than the other.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.
Author contributions
JK and DB: conceptualization and methodology. JK, AS, and DB: validation and writing – review and editing. JK: formal analysis, investigation, data curation, writing – original draft preparation, and visualization. JK and AS: resources and project administration. All authors have read and agreed to the published version of the manuscript.
Funding
Project development and implementation of the learning environment were funded by the STEM-Switzerland funding program of the Swiss Academies of Arts and Sciences. The University of Teacher Education Lucerne also supported the implementation of the learning environment and the research.
Acknowledgments
The present study was allowed to be conducted in the fall semester of 2020 at the University of Teacher Education Lucerne in a learning environment entitled “Discovering the City of the Future with Roberta®.” We would therefore like to thank the participating institutions, the University of Teacher Education Lucerne and the Lucerne University of Applied Sciences, as well as the STEM-Switzerland funding program of the Swiss Academies of Arts and Sciences, which made it possible to implement the learning environment. We thank also go to all the project staff, workshop instructors, assistants, teachers, and students who attended the learning workshop.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Akinola, S. O. (2016). Computer programming skill and gender difference: An empirical study. Am. J. Sci. Ind. Res. 7, 1–9.
Al-Ramahi, M., Alazzam, I., and Alsmadi, I. (2013). The impact of using pair programming: A case study. IJTCS 4, 313–329. doi: 10.1504/IJTCS.2013.060633
Alshehri, S., and Benedicenti, L. (2014). Ranking and rules for selecting two persons in pair programming. J. Softw. 9, 2467–2473. doi: 10.4304/jsw.9.9.2467-2473
Amon, H., Bartosch, I., Lembens, A., and Wenzl, I. (2012). Gender_Diversity-Kompetenz im naturwissenschaftlichen Unterricht. Fachdidaktische Anregungen für Lehrerinnen und Lehrer. IMST Gender_Diversitäten Netzwerk. Klagenfurt: Institut für Unterrichts – und Schulentwicklung.
Başer, M. (2013). Attitude, gender and achievement in computer programming. Middle East J. Sci. Res. 14, 248–255.
Beck, K. (1999). Embracing change with extreme programming. Computer 32, 70–77. doi: 10.1109/2.796139
Beyer, S., Rynes, K., Perrault, J., Hay, K., and Haller, S. (2003). “Gender differences in computer science students,” in Proceedings of the 34th SIGCSE Technical Symposium on Computer Science Education - SIGCSE, (New York, NY: ACM Press), 49–53. doi: 10.1145/611892.611930
Booth, A. L., and Nolen, P. (2012). Gender differences in risk behaviour: Does nurture matter? Econ. J. 122, F56–F78. doi: 10.1111/j.1468-0297.2011.02480.x
Bowman, N. A., Jarratt, L., Culver, K. C., and Segre, A. M. (2019). How prior programming experience affects students’ pair programming experiences and outcomes. ITiCSE 2019, 170–175. doi: 10.1145/3304221.3319781
Bowman, N. A., Jarratt, L., Culver, K. C., and Segre, A. M. (2020). Pair programming in perspective: Effects on persistence, achievement, and equity in computer science. J. Res. Educ. Eff. 13, 731–758. doi: 10.1080/19345747.2020.1799464
Brutsaert, H. (1999). Coeducation and gender identity formation: A comparative analysis of secondary schools in Belgium. Br. J. Soc. Educ. 20, 343–353. doi: 10.1080/01425699995308
Çal, H., and Can, G. (2020). The influence of pair programming on secondary school students’ confidence and achievement in computer programming. Trakya Eðitim Dergisi 10, 221–237. doi: 10.24315/tred.575098
Campe, S., Denner, J., Green, E., and Torres, D. (2020). Pair programming in middle school: Variations in interactions and behaviors. Comput. Sci. Educ. 30, 22–46. doi: 10.1080/08993408.2019.1648119
Celepkolu, M., Galdo, A. C., Boyer, K. E., Wiebe, E. N., Mott, B. W., and Lester, J. C. (2020). “Student reflections on pair programming in middle school: A thematic analysis,” in The Interdisciplinarity of the Learning Sciences (ICLS 2020), eds M. Gresalfi and I. S. Horn (Nashville, TN: International Society of the Learning Sciences), 803–804.
Chang, S., Shieh, R. S., Liu, E. Z., and Yu, P. (2012). Factors influencing women’s attitudes towards computers in a computer literacy training program. Turk. Online J. Educ. Technol. 11, 177–187.
Cheryan, S., Plaut, V. C., Handron, C., and Hudson, L. (2013). The stereotypical computer scientist: Gendered media representations as a barrier to inclusion for women. Sex Roles 69, 58–71. doi: 10.1007/s11199-013-0296-x
Cheryan, S., Siy, J., Vichayapai, M., Drury, B., and Kim, S. (2011). Do female and male role models who embody STEM stereotypes hinder women’s anticipated success in STEM? Soc. Psychol. Pers. Sci. 2, 656–664. doi: 10.1177/1948550611405218
Choi, K. S. (2015). A comparative analysis of different gender pair combinations in pair programming. Behav. Inf. Technol. 34, 825–837. doi: 10.1080/0144929X.2014.937460
Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences. 2nd edn. Hillsdale, NJ: Lawrence Erlbaum Associates, Publishers.
Coto, M., and Mora, S. (2019). Are there any gender differences in students’ emotional reactions to programming learning activities? Interacción 2019, 1–8. doi: 10.1145/3335595.3335608
Demir, Ö, and Seferoglu, S. S. (2021). The effect of determining pair programming groups according to various individual difference variables on group compatibility, flow, and coding performance. J. Educ. Comput. Res. 59, 41–70. doi: 10.1177/0735633120949787
Denner, J., Werner, L., Campe, S., and Ortiz, E. (2014). Pair programming: Under what conditions is it advantageous for middle school students? J. Res. Technol. Educ. 46, 277–296. doi: 10.1080/15391523.2014.888272
Diekman, A. B., Brown, E. R., Johnston, A. M., and Clark, E. K. (2010). Seeking congruity between goals and roles: A new look at why women opt out of STEM careers. Psychol. Sci. 21, 1051–1057. doi: 10.1177/0956797610377342
Diekman, A. B., Clark, E. K., Johnston, A. M., Brown, E. R., and Steinberg, M. (2011). Malleability in communal goals and beliefs influences attraction to STEM careers: Evidence for a goal congruity perspective. J. Pers. Soc. Psychol. 101, 902–918. doi: 10.1037/a0025199
Eagly, A. H. (1987). Sex Differences in Social Behavior: A social-Role Interpretation. London: Psychology Press, doi: 10.4324/9780203781906
Esch, M., and Herrmann, J. (eds) (2008). Qualität Durch Chancengleichheit. Gleichstellung als Strategischer Faktor im Qualitätsmanagement Technischer Universitäten. Gütersloh: Bertelsmann.
Faulstich-Wieland, H., Weber, M., and Willems, K. (2004). Doing Gender im Heutigen Schulalltag. Empirische Studien zur Sozialen Konstruktion von Geschlecht in Schulischen Interaktionen. Suwałki: Juventa.
Flore, P. C., and Wicherts, J. (2015). Does stereotype threat influence performance of girls in stereotyped domains? A meta-analysis. J. Sch. Psychol. 53, 25–44. doi: 10.1016/j.jsp.2014.10.002
Gómez, O. S., Solari, M., Calvache, C. J. P., and Ledezma-Carrizalez, A. C. (2017). “A controlled experiment on productivity of pair programming gender combinations: Preliminary results,” in 20th Ibero-American Conference on Software Engineering, CIbSE 2017 (Argentina: CIbSE), 197–210.
Greguras, G. J., and Robie, C. (1998). A new look at within-source interrater reliability of 360-degree feedback ratings. J. Appl. Psychol. 83, 960–968. doi: 10.1037/0021-9010.83.6.960
Greve, W., and Wentura, D. (1997). Wissenschaftliche Beobachtung. Eine Einführung, 2nd edn. Weinheim: Psychologie Verlags Union.
Hanks, B., Fitzgerald, S., McCauley, R., Murphy, L., and Zander, C. (2011). Pair programming in education: A literature review. Comput. Sci. Educ. 21, 135–173. doi: 10.1080/08993408.2011.579808
Iskrenovic-Momcilovic, O. (2019). Pair programming with scratch. Educ. Inf. Technol. 24, 2943–2952. doi: 10.1007/s10639-019-09905-3
Jarratt, L., Bowman, N. A., Culver, K. C., and Segre, A. M. (2019). A large-scale experimental study of gender and pair composition in pair programming. ITiCSE 2019, 176–181. doi: 10.1145/3304221.3319782
Katira, N., Williams, L., and Osborne, J. (2005). “Towards increasing the compatibility of student pair programmers,” in Software Engineering, 2005. ICSE 2005. Proceedings. 27th International Conference on, (St. Louis: IEEE), 625–626. doi: 10.1109/ICSE.2005.1553618
Kessels, U. (2002). Undoing Gender in der Schule. Eine Empirische Studie über Koedukation und Geschlechtsidentität im Physikunterricht. Suwałki: Juventa.
Kröll, D. (ed.) (2010). ”Gender und MINT.” Schlussfolgerungen Für Unterricht, Beruf und Studium. Kassel: Kassel University Press.
Liebenberg, J., Mentz, E., and Breed, B. (2012). Pair programming and secondary school girls’ enjoyment of programming and the subject Information Technology (IT). Comput. Sci. Educ. 22, 219–236. doi: 10.1080/08993408.2012.713180
Lünenborg, M., and Maier, T. (2013). Gender Media Studies: Eine Einführung. Konstanz: UVK. doi: 10.36198/9783838538723
Maccoby, E. E. (1990). Gender and relationships: A developmental account. Am. Psychol. 45, 513–520. doi: 10.1037/0003-066X.45.4.513
Maccoby, E. E. (1998). The Two Sexes: Growing up Apart, Coming Together. Cambridge: Harvard University Press.
Maguire, P., Maguire, R., Hyland, P., and Marshall, P. (2014). Enhancing collaborative learning using pair programming: Who benefits? AISHE J. 6, 1411–14125.
McDowell, C., Werner, L., Bullock, H. E., and Fernald, J. (2006). Pair programming improves student retention, confidence, and program quality. Commun. ACM 49, 90–95. doi: 10.1145/1145287.1145293
National Center for Science and Engineering Statistics (2019). Women, Minorities, and Persons with Disabilities in Science and Engineering. Arlington: National Science Foundation.
Nosek, B. A., Smyth, F. L., Sriram, N., Lindner, N. M., Devos, T., Ayala, A., et al. (2009). National differences in gender–science stereotypes predict national sex differences in science and math achievement. PNAS 106, 10593–10597. doi: 10.1073/pnas.0809921106
Papadakis, S. (2018). Is pair programming more effective than solo programming for secondary education novice programmers? A case study. IJWLTT 13, 1–16. doi: 10.4018/IJWLTT.2018010101
Plonka, L., Segal, J., Sharp, H., and van der Linden, J. (2011). “Collaboration in pair programming: Driving and switching,” in Agile Processes in Software Engineering and Extreme Programming (XP 2011), eds A. Sillitti, O. Hazzan, E. Bache, and X. Albaladejo (Berlin: Springer), 43–59. doi: 10.1007/978-3-642-20677-1_4
Plonka, L., Segal, J., Sharp, H., and van der Linden, J. (2012). “Investigating equity of participation in pair programming,” in Agile India 2012, (Bengaluru: IEEE), 20–29. doi: 10.1109/AgileIndia.2012.16
Rodríguez, F. J., Price, K. M., and Boyer, K. E. (2017). “Exploring the pair programming process: Characteristics of effective collaboration,” in Proceedings of the 2017 ACM SIGCSE Technical Symposium on Computer Science Education, SIGCSE ’17, (New York, NY: ACM), 507–512. doi: 10.1145/3017680.3017748
Salleh, N., Mendes, E., and Grundy, J. (2011). Empirical studies of pair programming for CS/SE teaching in higher education: A systematic literature review. IEEE Trans. Softw. Eng. 37, 509–525. doi: 10.1109/TSE.2010.59
Satz, D. (2012). “Gender,” in The Oxford Handbook of Political Philosophy, ed D. Estlund doi: 10.1093/oxfordhb/9780195376692.013.0019
Seo, Y., and Kim, J. (2016). Analyzing the effects of coding education through pair programming for the computational thinking and creativity of elementary school students. Indian J. Sci. Technol. 9, 1–5. doi: 10.17485/ijst/2016/v9i46/107837
Tsan, J., Boyer, K. E., and Lynch, C. F. (2016). “How early does the CS gender gap emerge? A study of collaborative problem solving in 5th Grade Computer,” in Proceedings of the 47th ACM Technical Symposium on Computer Science Education (SIGCSE), (New York, NY: Association for Computing Machinery), 388–393. doi: 10.1145/2839509.2844605
Tunga, Y., and Tokel, T. (2018). “The use of pair programming in education: A systematic literature review,” in Paper presented at EDUCCON 2018 Education Conference, Ankara, 19–29.
Underwood, J., Underwood, G., and Wood, D. (2000). When does gender matter? Interactions during computer-based problem solving. Learn. Instr. 10, 447–462. doi: 10.1016/S0959-4752(00)00008-6
von Ow, A., and Husfeldt, V. (2011). Geschlechterdifferenzen und schulische Leistungen. Eine Übersicht zum Forschungsstand. Aarau: PH FHNW.
Wedl, J., and Bartsch, A. (2015). Teaching Gender? Zum reflektierten Umgang mit Geschlecht im Schulunterricht und in der Lehramtsausbildung. Bielefeld: Transcript Verlag, doi: 10.14361/9783839428221
Werner, L., Denner, J., and Bean, S. (2004a). “Pair programming strategies for middle school girls,” in Proceedings of the 7th IASTED International Conference on Computers and Advanced Technology in Education, Kauai, 161–166.
Werner, L., Hanks, B., and McDowell, C. (2004b). Pair-programming helps female computer science students. JERIC 4:4. doi: 10.1145/1060071.1060075
Werner, L., and Denning, J. (2009). Pair programming in middle school: What does it look like? J. Res. Technol. Educ. 42, 29–49. doi: 10.1080/15391523.2009.10782540
Williams, L., and Kessler, R. (2000). All I really need to know about pair programming I learned in kindergarten. Commun. ACM 43, 108–114. doi: 10.1145/332833.332848
Williams, L., Layman, L., Osborne, J., and Katira, N. (2006). “Examining the compatibility of student pair programmers,” in AGILE 2006, (Minneapolis: IEEE), 411–420. doi: 10.1109/AGILE.2006.25
Williams, L., McCrickard, D. S., Layman, L., and Hussein, K. (2008). “Eleven guidelines for implementing pair programming in the classroom,” in AGILE 2008, (Toronto: IEEE), 445–452. doi: 10.1109/Agile.2008.12
Ying, K. M., Pezzullo, L. G., Ahmed, M., Crompton, K., Blanchard, J., and Boyer, K. E. (2019). “In their own words: Gender differences in student perceptions of pair programming,” in Proceedings of the 50th ACM Technical Symposium on Computer Science Education (SIGCSE’19), (New York, NY: Association for Computing Machinery), 1053–1059. doi: 10.1145/3287324.3287380
Zarb, M., Hughes, J., and Richards, J. (2013). “Industry-inspired guidelines improve students’ pair programming communication,” in Proceedings of the 18th ACM Conference on Innovation and Technology in Computer Science Education 2013, New York, NY, 135–140. doi: 10.1145/2462476.2462504
Zhong, B., Wang, Q., and Chen, J. (2016). The impact of social factors on pair programming in a primary school. Comput. Hum. Behav. 64, 423–431. doi: 10.1016/j.chb.2016.07.017
Keywords: pair programming, gender composition, collaboration, educational robotics, computer sciences
Citation: Küng J, Schmid AM and Brovelli D (2022) Gender and pair programming–Effects of the gender composition of pairs on collaboration in a robotics workshop. Front. Educ. 7:973674. doi: 10.3389/feduc.2022.973674
Received: 20 June 2022; Accepted: 21 July 2022;
Published: 08 August 2022.
Edited by:
Christian Giang, Swiss Federal Institute of Technology Lausanne, SwitzerlandReviewed by:
Günther Matthias Funk, University of the Azores, PortugalAnnamaria De Santis, University of Modena and Reggio Emilia, Italy
Copyright © 2022 Küng, Schmid and Brovelli. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Janine Küng, amFuaW5lLmt1ZW5nQHBobHUuY2g=
 Janine Küng
Janine Küng Andrea M. Schmid
Andrea M. Schmid Dorothee Brovelli
Dorothee Brovelli