- Department of Curricula and Methods of Teaching Mathematics, Princess Alia University College, Al-Balqa Applied University, Al-Salt, Jordan
Aim: The present study aimed at investigating the association of the mathematical proficiency and mathematical thinking skills among female teachers of the first three grades in public schools of Amman city, Jordan.
Method: The study adopted the descriptive analytical research approach. A sample of 174 female teachers of the first three grades was recruited in the present study. To collect data, the study used a mathematical proficiency tests (39 items) covering the domains of the conceptual understanding, procedural fluency, strategic competency, adaptive reasoning, and the productive desire. In addition, the study used a mathematical thinking skills test consisted of (20) items distributed over seven mathematical thinking skills; they were: Induction skill, conclusion skill, symbolizing skill, logical thinking skill, guessing skill, demonstration skill, and modeling skill. Data were analyzed using SPSS software (v. 26).
Results: The study findings showed that female teachers of the first three grades had a moderate level of mathematical proficiency (43.60 ± 16.04), a good level of mathematical thinking skills (6.51 ± 4.628). In addition, the study found significant statistical positive correlation between mathematical proficiency and mathematical thinking skills (r = 0.681, p ≤ 0.05) among female teachers of the first three grades in Amman.
Conclusion: The study concluded that mathematical proficiency is significantly associated with mathematical thinking skills in their domains. The study recommended increasing female teachers’ competencies and skills related to mathematical proficiency and mathematical thinking throughout intensive courses and workshops.
Introduction
Mathematics is an integral part of our lives, and our students today are growing up in an environment that has changed from the past (Hwa, 2018). The technology used in homes, schools and streets is all built on mathematical knowledge (Bakker et al., 2021).
In response to these changes in society and education, a new concept of mathematics education arose - to change the previous concept that was concerned with the skill in performing arithmetic operations - called “mathematical proficiency” (Corrêa and Haslam, 2020), which aims to focus on understanding the content, along with thinking in a mathematical way to increase the individual’s ability to solve problems. In a mathematical way, and increases his ability to inference and analysis (Sudiarta and Widana, 2019).
Mathematical proficiency encompasses all aspects of expertise, competence, and knowledge of mathematics, and it is made up of five interrelated and interdependent strands that support each other and they are summarized as following: The Conceptual understanding that is defined as Understanding mathematical concepts, processes, and relationships (Phuong, 2020). A second component is the procedural fluency, which is the skill in executing procedures flexibly, accurately, and appropriately (Yulian, 2018). The third component is the strategic competence, which is the ability to formulate, represent, and solve mathematical problems. The fourth component is the adoptive reasoning, which is defined as the ability to reason logically, reflectively, explain, and justify (Phuong, 2020). Finally, the fifth component is the productive disposition that is defined as the innate tendency, desire, or tendency to view mathematics as a useful, useful, and worthy subject, along with a belief in diligence and personal competence (Yulian, 2018).
There are classroom practices that develop students’ ingenuity, such as giving students tasks that develop their mathematical skills and make them participate positively and engage in work that requires data collection, reading texts, using intuition and justification, and needs to stimulate students’ motivation and enthusiasm for learning, such as using gamification in teaching (Samawi et al., 2020), as it requires the teacher builds a blueprint for linking previous information and experiences with subsequent experiences, and asks questions that challenge students’ thinking and encourage them to work as cooperative groups in which each person supports the other and considers the success of his colleague as part of his own success (Hawari and Noor, 2020; Calabrese Barton et al., 2021).
Mathematical proficiency cannot be accomplished once, but it requires training, provision of resources, acquiring knowledge of pedagogy, and conducting a study that measures the effectiveness of conducting experimental units to develop and measure students’ mathematical proficiency (Gaillard, 2018; Hutajulu et al., 2019).
The National Council of Researches (NCR) in the United States indicated that the concept of success in mathematics is the extent to which the learner is able to comprehend mathematical concepts (Sharma, 2022), link previous concepts with modern concepts, and his ability to benefit from them in the correct and followed procedures in solving the given mathematical tasks, and its ability of recognizing the mathematical errors used, and avoiding them, and their ability to justify, explain, clarify, conclude, and evaluate, in order to give appropriate solutions, and then make a decision in choosing the optimal solution (Hokonya, 2021).
A set of classroom practices that develop mathematical proficiency were reported in literature, including: mathematical tasks, providing learning opportunities through the tasks that the teacher presents to his/her students (Glasnovic Gracin, 2018), which work on developing their abilities to use sense and justification, encourage them to collect data, and explore mathematical situations, paying attention to mathematical explanations, thoughtful planning, developing motivation, encouraging students to engage productively in mathematics lessons, encouraging students to engage in learning communities rather than individual learning, encouraging students to evaluate their performance effectively to become proficient, and developing educational materials (Fitzgerald and Palincsar, 2019; Rohid and Rusmawati, 2019).
Statement of problem and purpose
Because of the importance of developing the five components for the development of mathematics education, many studies have emphasized the focus on mathematics teachers and teachers to develop the components of their mathematical proficiency through training them on teaching practices that in turn enhance the mathematical prowess of their students, that is, in order to facilitate the understanding of mathematical learners, teachers and teachers themselves need to develop a deep understanding of for mathematics, as Niss and Højgaard (2019) indicated that mathematics teachers do not focus on developing all components of mathematical proficiency, so they show their interests to some extent in conceptual understanding with a weakness in developing procedural fluency and their interest in other components is limited, it is rare that they give students opportunities to solve mathematical problems that in turn, develop their strategic competence. However, there is a significant gap in the literature linking the mathematical proficiency and mathematical thinking among primary stage teachers, specifically in the Middle East context. Therefore, the present study sought to bridge the gap represented by the association between mathematical proficiency and tendency towards mathematics among the female teachers of the first three grades in Jordan.
Research questions
The present study sought to answer the following research questions:
1. What is the level of mathematical proficiency among female teachers of the first three grades in public schools in Jordan?
2. What is the level of mathematical thinking among female teachers of the first three grades in public schools in Jordan?
3. What is the association between mathematical proficiency and mathematical thinking among female teachers of the first three grades in public schools in Jordan?
Definitions of the study
Mathematical proficiency
Mathematical Proficiency is a large concept consisting of five interlocking elements. During the past decades, many researchers have discussed the development of a deep understanding of mathematics through the components of mathematical virtuosity, a new term that appeared at the beginning of the twenty-first century by both Kilpatrick and others (Kilpatrick, 2009), and represents one of the outcomes of learning mathematics. Which the National Research Council (2001) recommended that it be necessary to pay attention to it in teaching mathematics to students. These components are:
1. Conceptual Understanding: Understanding concepts, generalizations, and the connection between mathematical ideas.
2. Procedural Fluency: The ability to implement mathematical procedures and operations accurately, efficiently and flexibly.
3. Strategic Competence: The ability to solve and form problems.
4. Adaptive Reasoning: The ability to think logically, justify and explain.
5. Productive Disposition: It means the ability to form positive attitudes towards mathematics, belief in the importance of mathematical logic, and consolidating the idea among students that mathematics is important and meaningful in practical life.
Mathematical thinking
It is a process of searching for a meaning or an idea in a situation or experience related to a mathematical context, that is, it is thinking in the field of mathematics where the elements or components of the situation or experience are represented in numbers, symbols, shapes, concepts or generalizations, and since it is possible to model and represent many situations and problems with models And mathematical representations, so mathematical thinking is considered to be inclusive of all different forms and patterns of thinking. In addition, mathematical thinking is a pattern of thinking that a person does when exposed to a mathematical situation, which is represented in one of the following manifestations: extrapolation, deduction, generalization, expression with symbols, proof, mathematical logic, conjecture, and modeling.
Previous studies
Hasan (2018) conducted a study aimed at knowing the correlation between the mathematical proficiency of mathematics teachers and the mathematical proficiency of their students, and the researcher adopted a descriptive associative approach to answer the research questions. For the purpose of data collection, two tests of mathematical proficiency were built, the first for teachers, which was finalized by 8 test items and of the type of essays, and a test for mathematical prowess for students, which was finalized by 8 essay items as well. The sample consisted of twenty secondary school teachers and teachers from the Third Rusafa Education Directorate, and 800 male and female students. The results showed that teachers and students possess academic prowess, and female students outperform male students in the test prepared for mathematical proficiency.
In a study conducted by Awofala (2017) that aimed to assess the mathematical proficiency among Nigerian students, the researchers used the quantitative research approach to identify the level of mathematical proficiency among secondary school students in Nigeria. The results of the study showed that senior secondary school students were more mathematically proficient. However, the study found significant statistical differences between senior secondary school students in the components of the mathematical proficiency scale. The study recommended to conduct further research studies to assess mathematical proficiency levels among Nigerian students from public school.
Al-Maloohi and Al-Ahmadi (2020) conducted a study that aimed to identify the level of mathematical proficiency among sixth-grade students. To achieve the research objectives, the researchers used the descriptive approach. The study sample consisted of (390) sixth-grade students from seven schools of government schools affiliated to the Department of Education in the city of Riyadh. This research used two tools, namely: a test containing seven questions that measure the level of female students’ mathematical proficiency in four components, namely: (conceptual understanding, procedural fluency, strategic competence, and adaptive reasoning), and a scale for measuring productive desire that contains three domains. The results of the study showed that the level of the sixth grade female students is low in conceptual understanding, procedural fluency, strategic competence, and adaptive reasoning, and average in productive desire. The study concluded with some recommendations; including: the need to pay attention to mathematical proficiency and its development, and to choose all that contributes to it in terms of teaching strategies or educational programs, with a focus on balancing concepts in the content of mathematics curricula.
In a study by Qutainah and Al-Share’ (2021), the purpose was to investigate the level of mathematical proficiency among the ninth grade students and its relationship to their beliefs about learning mathematics, and the descriptive correlative approach. The study sample consisted of (306) male and female students from all Amman schools, who were chosen by random method. To achieve the purposes of the study, the researchers prepared the Mathematical Proficiency Test, developed the Beliefs Scale, and their validity and reliability were ascertained. The results showed that the level of mathematical proficiency is medium, and students’ estimates of their beliefs about learning mathematics are medium, except for teaching methods, which are high. The results showed statistically significant differences between the mean scores of students’ estimates of their beliefs in the field of teaching methods; in favor of females. In addition, the findings showed an inverse correlation between the level of students’ mathematical proficiency and their estimates of their beliefs.
Radwan et al. (2016) study aimed to investigate the effect of an educational program using mathematical proficiency in mathematical thinking and achievement. The researcher used the experimental method and quasi-experimental design, as the study population consisted of seventh grade students, and the study was applied to a sample that was chosen purposively. The study sample was divided into two groups, an experimental group that was taught using an educational program based on mathematical proficiency, and a control group that was taught in the traditional method in the first semester of the year (2015/2016). The study tool consisted of two tests, one of them is achievement in mathematics, and the other is a test of mathematical thinking. The study reached the following results: (1) There are statistically significant differences at the level of significance (0.05 ≥ α) between the mean scores of seventh grade students The primary students who studied the unit of direct proportion and inverse proportion using the traditional method (the control group), and the scores of the seventh grade students who studied using the educational program based on mathematical proficiency (the experimental group). (2) There are statistically significant differences at the level of statistical significance (α ≤ 0.05) between the mean scores of the achievement test for seventh grade students who studied the direct proportion and inverse proportion unit using the traditional method (the control group), and the scores of the seventh grade students who studied the unit of direct proportionality and inverse proportionality according to an educational program based on mathematical proficiency (the experimental group), on the total score of the post-achievement test, and the differences were in favor of the experimental group. (3) There is a statistically significant relationship between achievement and mathematical thinking among the seventh grade female students in the experimental group. The results indicated that there is a strong direct relationship between academic achievement and mathematical thinking.
Khalil and Al-Natheer (2020) conducted a study that aimed to build a model based on the integration between mathematical proficiency and twenty-first century skills, to develop an educational unit in the light of the prepared model, and to measure its effectiveness in academic achievement and learning retention for fourth graders. The quantitative approach was used through conducting an experimental study. The research used a variety of educational materials, namely: a proposed model, an educational unit, a teacher’s guide, an exercise book, and an educational software. The research used two quantitative tools: an achievement test and a deferred achievement test (equivalent). Each of them was divided into the levels approved in TIMSS international tests (knowledge, application, inference), and their validity and reliability were calculated before they were approved for application. The sample of the study was (43) students from the fourth grade of primary school in Ibn Al-Qayyim School in Al-Darb Governorate, the number of members of the experimental group was (22) students, and the number of members of the control group was (21) students. The study found that there is a statistically significant difference at the level α ≤ 0.05 between the mean scores of the students of the experimental and control groups in the post administration of the achievement test at the levels (knowledge, application, inference) and the achievement test as a whole, in favor of the experimental group. In addition, there is no statistically significant difference at α ≤ 0.05 level between the mean scores of the experimental group students in the post- and delayed administration of the achievement as a whole. It appeared that there was a statistically significant relationship at the level α ≤ 0.05 between the scores of the students in the experimental group in the post administration of the achievement test and the delayed posttest (learning retention), and the correlation coefficient value was 0.659.
Materials and methods
Research design
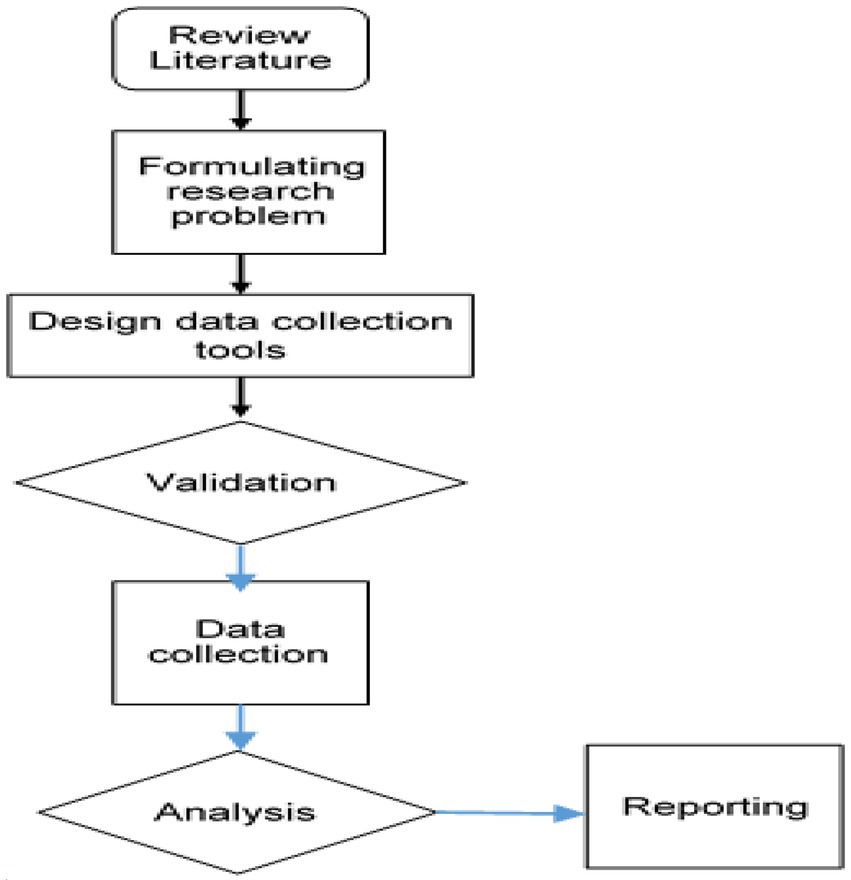
This study adopted the quantitative research approach through conducting a cross-sectional study. The cross-sectional research approach was chosen due to its appropriateness to achieve the study objectives. In addition, the cross-sectional research approach is quick, cost-effective and enable the researchers to collect quantitative data from the study participants. Figure 1 is a graphical representation of the research design steps adopted in this study.
Research population
The research population was represented by Jordanian first three grades female teachers in Amman city, Jordan. Based on the statistical data released by the Jordanian Ministry of Education, there is a total of 2,226 teachers of the first three grades (1,124 males and 1,112 females).
Research sample
The convenient sampling strategy was used to select the sample study. The sample size was calculated using G*Power 3.1.9.7, using a medium effect size (0.3), an alpha value of 0.05, a power of 0.95, the total sample size was calculated to be 134 female teachers. To overcome any technical issues, another 15% were added, and another 15% were added as well to avoid dropout problems. Therefore, the final sample size was 174 female teachers of the first three grades in Amman teachers.
Data collection tools
The study used the following data collection tools:
1. Mathematical proficiency test that consisted of four domains (Conceptual understanding, Procedural fluency, Strategic competency, and adaptive reasoning), and a scale for the fifth domain (Productive desire). This data collection tool was adopted from Al-Obaidi and Fares (2018) study. The content of the tests was as following:
• Conceptual understanding (13 statements) distributed over: Understanding basic mathematical ideas from concepts and relations (1, 2, 3), correctly merging mathematical ideas (4, 5, 6), connecting concepts to their applications (7, 8), recalling formulas from memory (9, 10, 11), representing mathematical situations as figures, drawings, or other mathematical shapes (12, 13).
• Procedural Fluency (8 items) distributed over: Have the skill to implement procedures accurately and flexibly (14, 15, 16), Understand concepts and procedures in a predictable manner (17, 18), uses the appropriate algorithm to perform the arithmetic operations (19, 29, 21).
• Strategic Competency (10 items) distributed over: formulating and plotting the mathematical problems (22, 23, 24), Uses well-known formulas to solve problems (25, 26, 27), Determines the necessary data and ignores the excess information (28, 29), Verifies that a special case has been reached that helps it as an input to solve the problem instead of the general method (30, 31).
• Adaptive Reasoning (8 items) distributed over: Seeks to think logically about the relationships between knowledge and attitudes (32, 33, 34, 35), and providing justifications and explanations (36, 37, 38, 39).
The test was administered on a pilot sample of 20 female teachers of the first three grades to ensure the clarity of the items and calculate the mean time required to complete the test. It was found that the appropriate time to complete the test was 70 min.
The test was validated through presenting the test to a group of experts and academic staff specialized in mathematics education and there was an agreement on the completeness of the mathematical proficiency test. The construct validity was performed as well to calculate the correlation of each item to the whole test score. To find the correlation between the essay items with the total test score, Pearson’s correlation coefficient was calculated and it was found to be ranging between 0.319 and 0.390. For the multiple choice items, the point biserial correlation coefficient was calculated and it was found that all correlation coefficients were statistically significant and ranging between 0.304 and 0.396.
To assess the correlation between the test items and the domain it belongs to, Pearson’s correlation coefficient was used and it was found that all correlation coefficients were statistically significant and ranging between 0.505 and 0.594 for the essay items and 0.502 to 0.597 for the multiple choice items.
To assess the reliability of the mathematical proficiency test, the Cronbach’s Alpha coefficient was used and it was found that the value of the Cronbach’s Alpha coefficient was (0.80).
– The productive desire scale: The researchers adopted the productive desire test used in Al-Obaidi and Fares (2018). The scale consisted of (22) items scored on four-point Likert scale (Strongly agree, agree, disagree, and strongly disagree) given the weights of 1 to 4, respectively. The items were covering two domains, as following: Realize the value and nature of mathematics by looking at it as realistic and useful domain (11 items) and Belief in the individual’s competence and diligence (11 items).
Therefore, the lowest score was 22 and the highest was 88. The scale was administered over a pilot sample of 20 female teachers of the first three grades and the required time to calculate the scale was found to be 15 min. The scale was validated in the original study. However, the construct validity was assessed in this study and it was found that the correlation coefficient of the items with the total scale score was ranging between 0.283 and 0.357.
In addition, the reliability of the scale was verified using the Cronbach’s Alpha coefficient that was (0.83).
2. Mathematical Thinking test: The study adopted the mathematical thinking test developed by Al-Mutairi (2021), which consisted of (20) items distributed over seven mathematical thinking skills; they were: Induction skill (items 1, 2, and 3), conclusion skill (items 4, 5 and 6), symbolizing skill (items 7, 8 and 9), logical thinking skill (items 10, 11, and 12), guessing skill (items 13, 14, and 15), demonstration skill (items 16, 17, 18, and 19), and modeling skill (item 20). Each item was given a score of 1, the participant get 1 if answer correctly and 0 if answers incorrectly.
The test was validated in the original study and it was assessed for reliability through conducting a pilot study over a sample of (20) female teachers of the first three grades. The researchers used the test–retest method to ensure the test reliability and it was found that the Pearson’s correlation coefficient value was (0.86).
Data collection procedure
The researchers approached the study participants (female teachers of the first three grades) and obtained their written consent. The data collection tools were administered in a closed hall over three rounds with an average of 69 participants in each round. The participants obtained a full clarification about the aims of the study and its significance in improving mathematics teaching for the first three grades in Jordan. After conducting the tests, the researchers collected the data and scored the tests based on the previously set scoring system.
Data analysis
The study used the Statistical Package of Social Sciences (SPSS) (v. 26, IBM Corp. Chicago, IL, USA) to analyze the gathered data. The descriptive statistics were used to describe the participants’ baseline data and their test scores. In addition, Pearson’s correlation coefficient was used to assess the association between participants’ mathematical proficiency scores and their mathematical thinking skills. A significance level of (α ≤ 0.05) was used as a statistical significance threshold in this study.
Results
A total of 174 female teachers of the first three grades participated in the present study. The mean years of experience of the enrolled female teacher of the first three grades was (9.32 ± 3.90). The participants were divided into two groups based on the median (7) of years of experience (Results not shown in tables).
The results presented in Table 1 represent the means and standard deviations for the female teachers of the first third grades scores on the mathematical proficiency test. The results showed that the enrolled females of the first three grades had a low level of conceptual understanding (10.58 ± 3.90), strategic competency (10.90 ± 3.91) and procedural fluency (12.36 ± 8.73). However, they had a high level in the adaptive reasoning domain (9.68 ± 3.61) and productive desire domain (65.04 ± 8.73). In total, the enrolled female teachers of the first three grades had a moderate level of mathematical proficiency (43.60 ± 16.04).
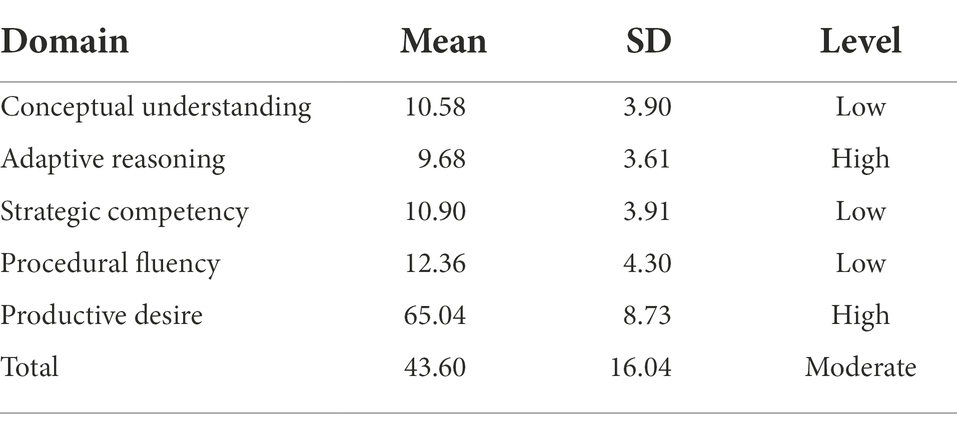
Table 1. Means and Standard Deviations of the female teachers of the first three grades scores on the mathematical proficiency test.
To assess the differences in the mathematical proficiency test based on the enrolled female teachers of the first three grades years of experience, an Independent samples t-test was used. The results in Table 2 show the independent samples t-test for the differences in the mathematical proficiency based on the participants’ years of experience. The results indicated that there was significant statistical differences between the female teachers who had less than 7 years of experience and the female teachers who had 7 years or more of experience in conceptual understanding (t = 8.6071, p = 0.000), adaptive reasoning (t = 3.5016, p = 0.000), strategic competency (t = 2.9972, p = 0.003), procedural fluency (t = 4.9537, p = 0.000), productive desire (t = 3.5330, p = 0.000) and the whole mathematical proficiency test (t = 2.9151, p = 0.004).
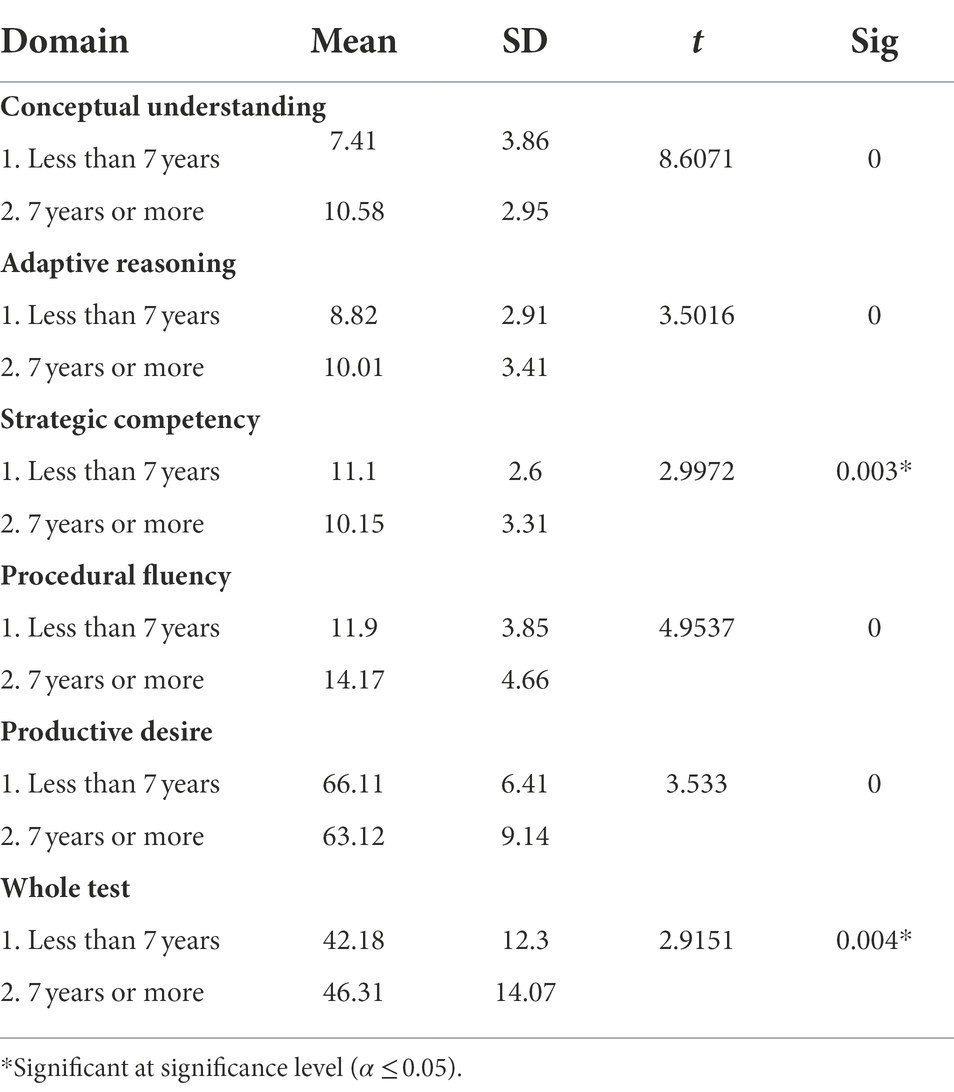
Table 2. Independent samples t-test for the differences in the mathematical proficiency based on the participants’ years of experience.
Moreover, the results presented in Table 3 represent the mean scores of the enrolled females of the first three grades scores on the mathematical thinking skills. The results showed that the enrolled female teachers of the first three grades got highest mean scores in the guessing domain (1.39 ± 0.864), followed by conclusion domain (1.30 ± 1.09). In the third rank was the demonstration skills domain (1.11 ± 1.08) followed by the induction domain in the fourth rank (0.83 ± 0.624). In the fifth and sixth rank were the logical thinking domain (0.70 ± 0.701) and the expression with symbols domain (0.69 ± 0.904). In total, the mean score of the enrolled female teachers of the first three grades in the mathematical thinking test was (6.51 ± 4.628).
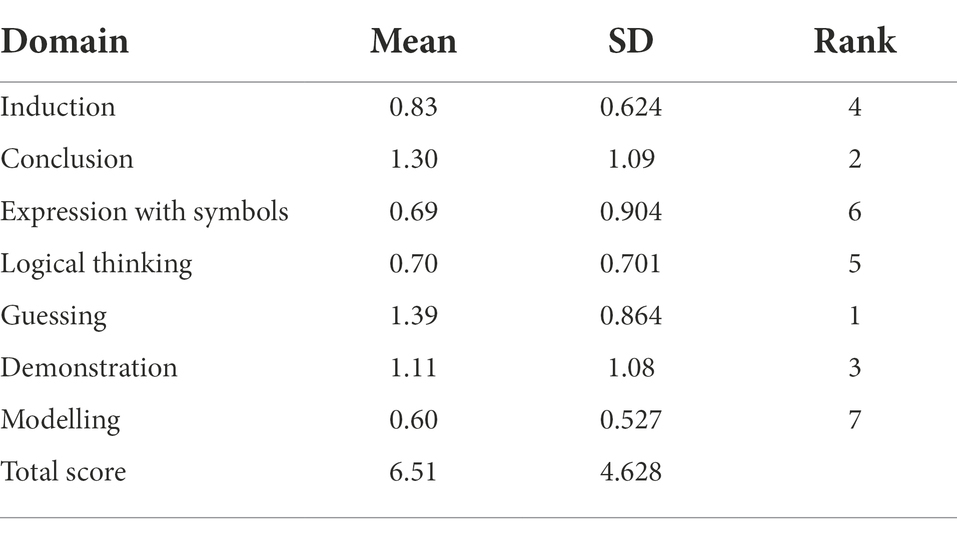
Table 3. Means and Standard Deviations of the female teachers of the first three grades scores on the mathematical thinking test.
To assess the differences in the mathematical thinking skills test based on the enrolled female teachers of the first three grades years of experience, an Independent samples t-test was used. The results in Table 4 show the independent samples t-test for the differences in the mathematical thinking skills based on the participants’ years of experience. The results showed that there was significant statistical differences between female teachers having less than 7 years of experience and those having 7 years or more of experience in Induction skills (t = 2.8990, p = 0.004), conclusion skills (t = 9.4181, p = 0.000), expression with symbols skills (t = 2.4529, p = 0.01), logical thinking skills (t = 3.5521, p = 0.000), guessing skills (t = 2.6458, p = 0.008), demonstration skills (t = 2.0018, p = 0.004), modelling skills (t = 2.2714, p = 0.02), and the whole mathematical thinking skills test (t = 3.0429, p = 0.000).
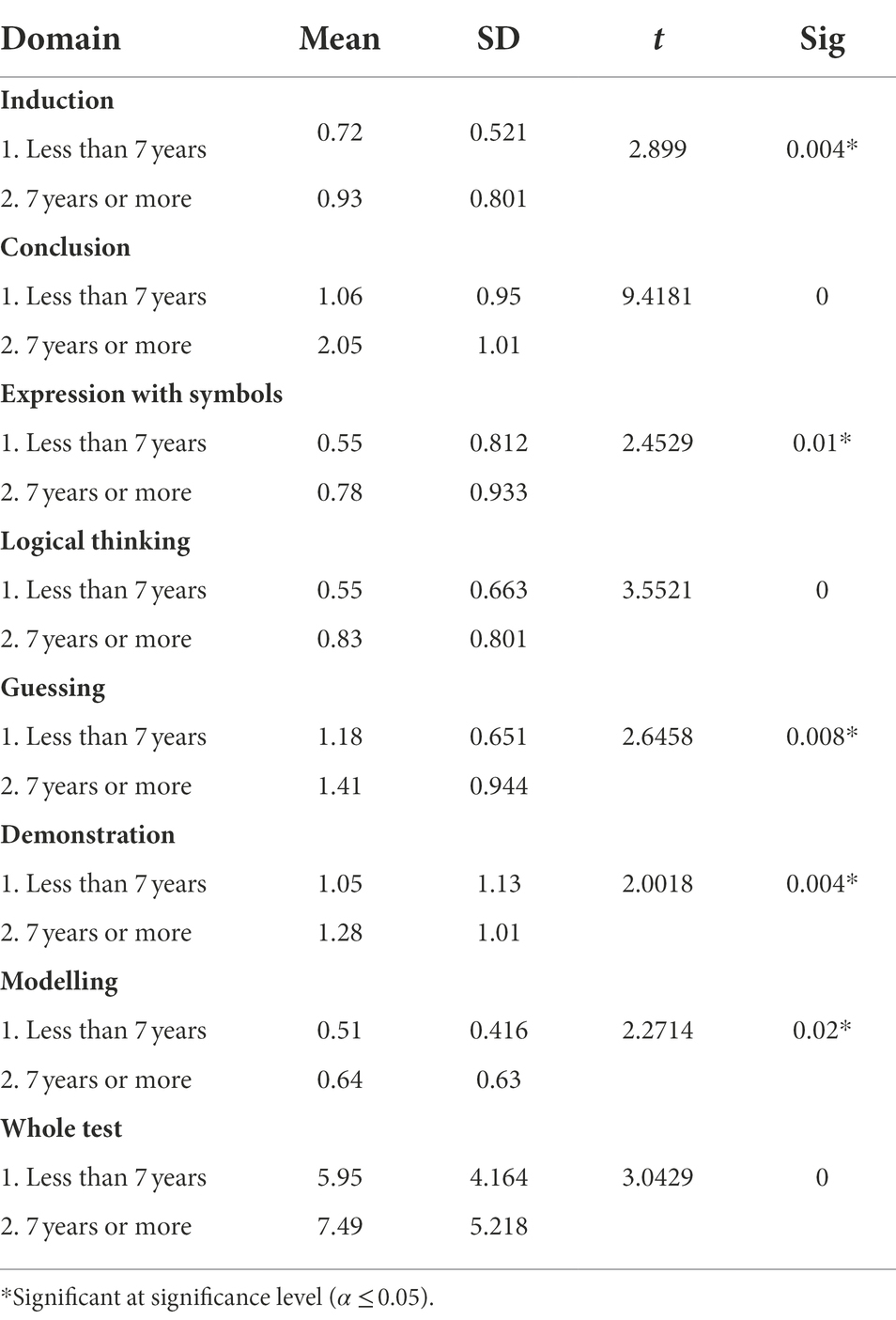
Table 4. Independent samples t-test for the differences in the mathematical thinking skills test based on the participants’ years of experience.
To assess the association between mathematical proficiency and mathematical thinking skills, Pearson’s correlation coefficient was used. The results presented in Table 5 show the Pearson’s correlation coefficient between the mathematical proficiency test and its domains on one hand and the mathematical thinking skills test and its domains on the other hand. The results showed that there was a significant statistical positive correlation between mathematical proficiency and mathematical thinking skills (r = 0.681). The results showed that a significance level of (α ≤ 0.05), there was a significant statistical positive correlation between all mathematical proficiency test domains and mathematical thinking skills domains as the Pearson correlation factor was ranging between 0.149 and 0.641.
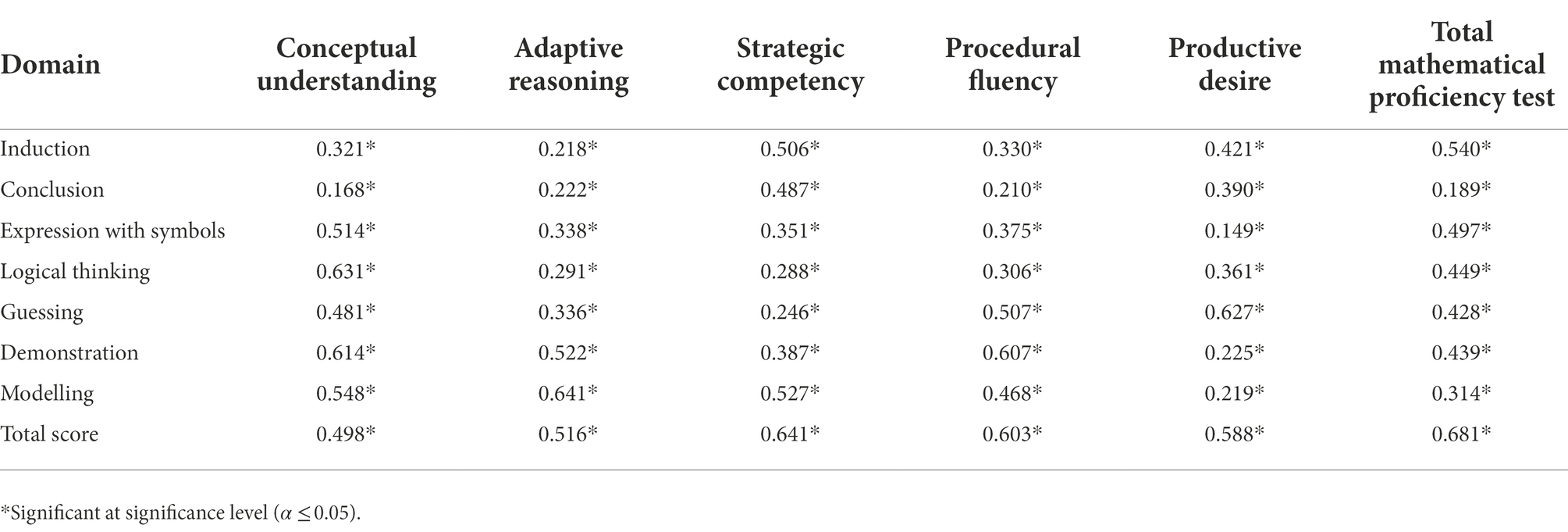
Table 5. Pearson’s correlation coefficient between mathematical proficiency and mathematical thinking skills.
Discussion
The beauty of mathematics lies in the interdependence of all its concepts through the creation of a large network of knowledge that can be applied in all aspects of life. Mathematics in order to help students until the end of their university studies in the gradual understanding of the complex problems in our current society that are required to be solved by educational and educational institutions and curricula, including mathematics curricula.
In Jordan, tremendous efforts were exerted by the official authorities in the ministry of education to equip the mathematics teachers, especially those assigned for the first grades, with the required skills that enable to effectively deliver the educational material for the students. For example, in all Jordanian universities, the professional diploma for preparing and qualifying teachers is a national professional diploma accredited by the Ministry of Education. It aims to raise the capabilities and competencies of first-grade teachers for teaching subjects in Arabic, English, mathematics and science in its branches. The diploma works to qualify those wishing to join the education sector and prepare them to lead the educational process with distinction.
The present study sought to explore the level of mathematical proficiency and mathematical thinking skills among female teachers of the first three grades in Amman, and to identify the association between these skills. A sample of 174 subjects enrolled in this study and subjected to both mathematical proficiency and mathematical thinking skills tests.
Our findings suggested that the enrolled female teachers of the first three grades had a moderate level of mathematical proficiency, which could be referred to their low scores obtained in the conceptual understanding, strategic competency, and procedural fluency domains. These low scores might be attributed to the focus on procedural teaching in teacher qualification programs, i.e., providing the procedure to reach the solution and not clarifying the concept. This finding was evidenced by the results reported by Khalil & Al-Natheer who indicated that in the sense that teaching mathematics in mathematics departments emphasizes the acquisition and development of skills more than it emphasizes teaching concepts in order to understand them, as most of the female teachers participating in this study did not give an explanation of the test items that need clarification and did not show a high ability to link these concepts to their uses in life or science other. The weakness of the female teachers participating in this study in strategic efficiency can also be attributed to their inability to identify important data and redundant information and their failure to rely on special cases to reach the solution. In addition, the researcher attributes the weakness of the female teachers participating in this study in the domain of procedural fluency to their tendency to provide one specific answer, and their inability to provide multiple answers to one problem, and that they tend to present procedures that are often incorrect because they are quick to answer and inaccuracy in following the appropriate algorithm.
The findings of the present study showed that the enrolled female teachers of the first three grades had a good level of mathematical thinking skills. This result might be referred to diversity of teaching strategies and methods adopted in teacher preparation programs, such as problem-based education, challenge-based learning, project-based learning, and the diversity of enrichment activities accompanying these strategies and the organization of ideas, had a significant impact on the development of student teachers thinking skills. In addition, this result might be attributed to the continuous professional development courses and workshops offered by the ministry of education in Jordan and focusing on improving mathematical thinking skills among primary stage teachers. This supported by the findings reported by Radwan et al. (2016) who revealed that females were superior to males in the mathematical thinking skills.
Furthermore, the study found significant statistical positive correlation between the mathematical proficiency and mathematical thinking skills among female teachers of the first three grades. This results could be attributed to that Mathematical proficiency requires understanding the meanings of procedures and how they are related to each other, accomplishing calculations and applying procedures in solving problems, as well as mastering procedural fluency, in addition to that strategic proficiency represented in the ability to form, demonstrate and solve mathematical problems, all of this makes the individual able to use The mathematical knowledge that he/she possesses and employing them in various forms, and this includes the skills of mathematical thinking. In addition, this result might be referred to that the mathematical proficiency stems from the concept of the constructivist view of mathematics as a way and a pattern of thinking, and it contains many features that make it a fertile field for training teachers of the first grades on patterns and methods of sound and logical thinking and their development, and contributing to building character and capacity for creativity and gaining deep understanding.
Conclusion
The present study concluded that Jordanian female teachers of the first three grades had a moderate level of mathematical proficiency, a good level of mathematical thinking and they varied in their levels of mathematical thinking and mathematical proficiency based on their years of experience. In addition, the study concluded that there was a significant statistical positive correlation between mathematical proficiency and mathematical thinking skills among female teachers of the first three grades in the public schools of Amman city, Jordan.
Despite the significant findings of the present study, still there are a number of limitations that might affect the generalization of the study findings. These limitations include the geographical limitations, as the present study was conducted in the educational directorate affiliated to Amman city. Therefore, the findings of the present study cannot be generalized to female teachers of the first three grades in other educational directorates. In addition, this findings of this study are limited to female teachers as the study sample did not include male participants.
Based on the findings of the present study, it is recommended to review the content of the teacher preparation programs accredited in the Jordanian university and delivered to mathematics teachers and ensure its coverage to a wide range of mathematics-related skills including mathematical proficiency and mathematical thinking skill. In addition, it is recommended to conduct intensive workshops and training courses to improve teachers’ competencies and skills related to mathematical proficiency and mathematical thinking.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
The studies involving human participants were reviewed and approved by Institutional Review Board (IRB) at Al-Balqa Applied University. The patients/participants provided their written informed consent to participate in this study.
Author contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Al-Maloohi, A., and Al-Ahmadi, S. (2020). Mathematical proficiency level of the 6th grade students in Riyadh. J. Math. Educat. 23, 192–216. doi: 10.21608/ARMIN.2020.87558
Al-Mutairi, M. S. (2021). Mathematical thinking skills for eighth grade students in the State of Kuwait. Al-Hussein Univ. J. Res. Stud. 5, 47–73.
Al-Obaidi, N., and Fares, E. (2018). Mathematical proficiency among students of the department of mathematics in the faculties of education. Master Thesis, Faculty of Education for pure sciences, Baghdad University, Baghdad, Iraq.
Awofala, A. O. (2017). Assessing senior secondary school students’ mathematical proficiency as related to gender and performance in mathematics in Nigeria. Int. J. Res. Educat. Sci. 3, 488–502. doi: 10.21890/ijres.327908
Bakker, A., Cai, J., and Zenger, L. (2021). Future themes of mathematics education research: an international survey before and during the pandemic. Educ. Stud. Math. 107, 1–24. doi: 10.1007/s10649-021-10049-w
Calabrese Barton, A. M., Schenkel, K., and Tan, E. (2021). The ingenuity of everyday practice: a framework for justice-centered identity work in engineering in the middle grades. J. Pre-College Eng. Educat. Res. 11:6. doi: 10.7771/2157-9288.1278
Corrêa, P. D., and Haslam, D. (2020). Mathematical proficiency as the basis for assessment: a literature review and its potentialities. Math. Teach. Res. J. 12, 3–20.
Fitzgerald, M. S., and Palincsar, A. S. (2019). Teaching practices that support student sensemaking across grades and disciplines: a conceptual review. Rev. Res. Educ. 43, 227–248. doi: 10.3102/0091732X18821115
Gaillard, N. D. (2018). The impact of number talks on third-grade students’ number sense development and mathematical proficiency. Doctoral dissertation. Columbia, SC: University of South Carolina.
Glasnovic Gracin, D. (2018). Requirements in mathematics textbooks: a five-dimensional analysis of textbook exercises and examples. Int. J. Math. Educ. Sci. Technol. 49, 1003–1024. doi: 10.1080/0020739X.2018.1431849
Hasan, A. (2018). The correlation between the mathematical prowess of secondary school mathematics teachers and the mathematical prowess of their students. J. Educat. Sci. 8, 21–36.
Hawari, A. D. M., and Noor, A. I. M. (2020). Project based learning pedagogical design in STEAM art education. Asian J. Univ. Educat. 16, 102–111. doi: 10.24191/ajue.v16i3.11072
Hokonya, W. M. (2021). An exploration of the mathematical learner identities of high school learners who participated in after school mathematics clubs in primary school. Unpublished PhD Thesis. Grahamstown: Rhodes University.
Hutajulu, M., Minarti, E. D., and Senjayawati, E. (2019). Improving of mathematical proficiency and disposition using multi representation approach on vocational students. J. Phys. Conf. Ser. 1315:012023. doi: 10.1088/1742-6596/1315/1/012023
Hwa, S. P. (2018). Pedagogical change in mathematics learning: harnessing the power of digital game-based learning. J. Educ. Technol. Soc. 21, 259–276.
Khalil, I., and Al-Natheer, M. (2020). The effectiveness of a developed educational unit based on the integration model between mathematical prowess and twenty-first century skills in developing academic achievement and retention of learning among fourth graders. J. Educat. Psychol. Sci. 14, 1–36.
Kilpatrick, J. (2009). The mathematics teacher and curriculum change. El profesor de Matemáticas y el cambio de currículo. Pna.
National Research Council. (2001). Educating teachers of science, mathematics, and technology: new practices for the new millennium. National Academies Press.
Niss, M., and Højgaard, T. (2019). Mathematical competencies revisited. Educ. Stud. Math. 102, 9–28. doi: 10.1007/s10649-019-09903-9
Phuong, H. T. M. (2020). Measuring conceptual understanding, procedural fluency and integrating procedural and conceptual knowledge in mathematical problem solving. Int. J. Sci. Res. Manag. 8, 212–218. doi: 10.18535/ijsrm/v8i05.el02
Qutainah, G., and Al-Share, I. (2021). Mathematical proficiency of ninth grade students in Jordan and its relation to their beliefs about learning mathematics. IUG J. Educat. Psychol. Sci. 29, 549–572.
Radwan, I., Yaseen, S., Saliha, S., and Jaber, M. (2016). The effect of an educational program based on mathematical proficiency on the achievement and mathematical thinking of seventh grade students in Qalqilya Governorate. J. Educat. Stud. 4, 215–241.
Rohid, N., and Rusmawati, R. D. (2019). Students’ mathematical communication skills (MCS) in solving mathematics problems: a case in Indonesian context. Anatol. J. Educat. 4, 19–30. doi: 10.29333/aje.2019.423a
Samawi, F. S., Alshoubaki, N. H. H., and Shaheen, H. R. A. (2020). The effectiveness of a training program based on frank Williams’ model in developing the divergent creative feeling among students in Jordan. Int. J. Learn. Teach. Educat. Res. 19, 74–94. doi: 10.26803/ijlter.19.1.5
Sharma, A. (2022). Needs assessment analysis of economics curriculum in Indian urban schools: integrating mathematics and the context.
Sudiarta, I. G. P., and Widana, I. W. (2019). Increasing mathematical proficiency and students character: lesson from the implementation of blended learning in junior high school in Bali. J. Phys. Conf. Ser. 1317:012118. doi: 10.1088/1742-6596/1317/1/012118
Keywords: mathematical proficiency, mathematical thinking, female teachers, first grades, Jordan
Citation: Alfayez MQE (2022) Mathematical proficiency among female teachers of the first three grades in Jordan and its relationship to their mathematical thinking. Front. Educ. 7:957923. doi: 10.3389/feduc.2022.957923
Edited by:
Manpreet Kaur Bagga, Partap College of Education, IndiaReviewed by:
Laura Sara Agrati, University of Bergamo, ItalyHarina Fitriyani, Universitas Ahmad Dahlan, Indonesia
Copyright © 2022 Alfayez. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mona Qutaifan Ershed Alfayez, ZHIubW9uYS5hbGZheWV6QGJhdS5lZHUuam8=
 Mona Qutaifan Ershed Alfayez
Mona Qutaifan Ershed Alfayez