Mathematical and computational awareness before and after the pandemic

Introduction

Our basic area of interest is IT education supported by mathematics. In the mathematical didactical literature, we find many learning theories, methodological support, and psychological research, which can be successfully adapted in IT because computer science grew from mathematics, so the pedagogical aspects of the two domains are common. In the early years, when mathematics teachers taught computer science, they used this well-known toolkit quite obviously and naturally. Nowadays, IT teacher training worldwide has moved away from mathematics teacher training, and the newer generations of IT teachers no longer know or apply the achievements of mathematics didactics. With our research, we would like to introduce these theories, methods, and approaches in IT methodology again.

Furthermore, we believe that problem-based teaching and learning should be preferred in both the traditional and the changed digital educational environment, which does not teach and repeatedly record cask techniques but rather shows the method and use through applications in a task-oriented manner, arousing interest as well. Word problems are clearly used for this in mathematics education.

As the educational environment changed due to the pandemic, we revived the results of our previous publications and supplemented them with the results of students participating in purely digital education. In this way, we had the opportunity to compare the effectiveness of using the same method in two types of educational environments (classroom and digital).

Some years ago, we raised a question whether initial computer programming could be taught via teaching and solving mathematical word problems because of the high correlation between mathematical and computational thinking (Bubno and Takacs, 2014). We discovered some analogies between the famous Pólya’s problem-solving model (Polya, 2014) and the way we solve a mathematical exercise by computer programming (Bubno and Takacs, 2014, 2017, 2019), so we called this method “analogy-based algorithmization.”

Our former publications discussed before:

In Bubno and Takacs (2014), we introduced our idea and presented the analogies discovered between mathematical problem-solving and computer programming based upon George Pólya’s famous problem-solving method.

Pólya’s steps are as follows:

1. “Comprehension, understanding the problem.” It is obvious that it is a common step in all types of problem-solving, including mathematical or computational.

2. “Devising a plan” means first determining the unknown variable in mathematics that corresponds to the declaration of variables in informatics. On the other hand, we create the mathematical model (plan) that solves the problem in mathematics, and it means writing the algorithm and their implementation (plan) in computer programming.

3. “Carrying the plan” usually means solving equations in mathematics or solving the problem in any kind of mathematical method, which we modeled formerly. It also means answering the question of the problem. We do the same in computer programming when compiling and running our algorithm and making the program answer to the questions of the starting problem.

4. “Looking back” means discussing the problem. We can change initial conditions, test them, or generalize the problem in mathematics. In computer science, it means debugging, looking for other (algorithmic) solution methods, and optimizing our code.

In our former publications in this topic (Bubno and Takacs, 2014, 2017, 2019), we also presented several examples and identified what kind of programming tools we could teach with the certain types of word problems. We also presented how a well-known problem-solving method from former mathematical studies, such as Pólya’s steps, could transfer into problem-solving in another domain, supporting children’s performance while studying a new material.

We have been experimenting with different study groups from primary school to secondary school until the right generation was detected. Finally, we found that we could teach with this method effectively in the 14- to 16-year-old children. They know well the mathematical word problems and have sufficient awareness to implement this knowledge in a different domain. In 2014–2019, we had the opportunity to teach in the university grammar school, where we could conduct several teaching experiments.

Since we teach novel programming, we chose a novel programming environment Blockly, a project of Google Inc (Google, 2022). We presented how we teach the elements of the novice computer programming material in a fully digital environment, and we found that “in future,” it could be used successfully as a distance-learning option for this teaching challenge (Bubno and Takacs, 2014, 2017, 2019).

This experiment was before the pandemic. At that time, we did not think that we would be able to put our suggestion to the test. But during the pandemic, we had an opportunity to test this hypothesis in the same Hungarian secondary school.

In this experience, we taught the same novice programming elements with the same programming environment (Blockly code) (Google Inc.) (Google, 2022) and with the same exercises, but fully in distance learning in two classes in the spring of 2021. We loaded the results into the former dataset we had analyzed before. In this study, we can compare the results of the students and their self-assessment before and after the period of emergency distance learning.

By comparison, we found that the performance of the children was not worse than that of our former pupils.

We placed our research in the conceptual scope of mathability. The definition of mathability was introduced in Baranyi and Gilanyi (2013). The aim of this new subject was to investigate and model human thinking during the work of the individual with infocommunication tools. Specifically, our research focused on developing secondary school students’ computational thinking aided by their prior mathematical problem-solving thinking and knowledge.

The literature distinguishes high-mathability and low-mathability teaching approaches and educational tools (Baranyi and Gilanyi, 2013; Biro and Csernoch, 2013; Chmielewska and Gilanyi, 2018; Sebestyén et al., 2022a,b). In the 2017 CogInfoCom Conference, we presented our method and Blockly code as a high-mathability approach and educational tool (Bubno and Takacs, 2017).

In Bubno and Takacs (2019), we started to examine the mathematical psychological aspects of our method. Based on the relevant learning theories (Piaget, Seymour Papert) and focusing on the main theories of mathematical psychology (…2017, 2019!), we examined our methodology and Blockly as a teaching tool as well. We nested our findings into mathability research.

However, due to the pandemic, we also had to learn and examine new, non-domain-specific psychological aspects, both for the sake of our research and for the success of our teaching.

During the pandemic, several studies investigated the effect of pandemic closure on education. Many of them dealt with the fact that closure arrived suddenly, without warning, and there was no time to plan and prepare the transition to online learning environments, and prepare online teaching materials and aids for the homeschool environment. We studied a new concept: resilience. It is the ability to adapt to the new variable world rapidly (Raghunathan et al., 2022).

Others addressed the psychological effects of the pandemic, how children’s motivation and interest decreased, and what was the impact of confinement on their social relationships with their age-group or other (e.g., verbal) abilities (Gares et al., 2020; Nilsberth et al., 2021; Sofianidis et al., 2021).

Several articles can be found on emergency remote teaching, which report on the technical and psychological difficulties experienced in the pandemic, mostly from personal accounts or surveys, from the perspective of both teachers and students (Chmielewska et al., 2020; Nilsberth et al., 2021; Sofianidis et al., 2021; Can and Bardakci, 2022; Karakose et al., 2022a,b; Lavidas et al., 2022). It is also often stated that the pandemic brought to the surface many of the problems we had already perceived in traditional education, but there was no urgency to handle (Nilsberth et al., 2021).

There are questionnaire-based research studies on the difficulties of teaching in different age-groups from the kindergarten children (Gares et al., 2020; Karakose et al., 2021; Nilsberth et al., 2021; Sofianidis et al., 2021; Lavidas et al., 2022) to university students. Some of them are about the afterlife of methods during the pandemic as well. Based on these studies, we can say that it was the most difficult to hold the attention of the youngest age-group. The teachers who taught this generation experienced the most difficulties during this period. Furthermore, involving parents in the teaching process was essential. Unfortunately, mathematics preparation often proved impossible for this age-group, or was limited to certain elements of the curriculum (e.g., spatial and temporal orientation).

Examining learning environments, Lavidas et al. (2022) showed that although excellent, easily accessible online teaching materials for the preschool age-group were already available, not many kindergarten teachers had incorporated them into distance education, and even fewer of them would like to continue using them in classroom education, unlike in primary and secondary schools and higher education.

These findings are important to us because we worked with our preferred online tool before, during, and after the pandemic. Moreover, we believe that it gives a sense of security to both instructors and students. Although the environment is changing, the tool remains the same. It is much easier to change 1 day to the next, if it is necessary. Furthermore, quarantined students can join as well.

Using a questionnaire-based research method, we tried the most to gather experience and offer practical advice on how we can be more prepared to respond to a similar situation in education in future (Chmielewska et al., 2020; Nilsberth et al., 2021; Raghunathan et al., 2022).

Chmielewska et al. (2020) stated priorities: First is the optimal education space (technically) and second is the educational content, in the sense of its form and methodology. It is of crucial importance to support relationships between students and students, and students and teachers by creating the conditions for effective collaboration work. Finally, we should strive to use open-source resources in the teaching process. We agree with the priorities mentioned here, and we tried to apply them, yet unconsciously, in our teaching process under emergency remote teaching.

Blockly code is an open and free source and environment that can be used from any device running on a web browser without identification. The codes we create can be shared (through the link generated), but there is no need to have a Google or any other account. Chmielewska et al. (2020) recommended that during pandemic teaching, we must not overwhelm children with complex and lengthy tasks because if they cannot solve them, they lose motivation. The result is either that they do not solve them or, as is often the case according to surveys, that they do solve them, but with the help of their parents, peers, or solutions found on the Internet. We should therefore strive to discuss and assign problems that can be divided into shorter portions, and we would have to use similar types of exercises to their homework.

By teaching using the “algorithm-based analogy” method, we use only mathematical word problems that children know well from their former studies, and they have already studied how to solve these problems in their previous mathematics lessons. The novelty was also to “translate” them to the language of computers.

Resilience

In this study, we do not investigate in detail but strongly agree with the statement (Sofianidis et al., 2021; Ulla and Perales, 2021; Raghunathan et al., 2022) that a teacher’s abilities, proficiency, confidence, and resilience in a pandemic environment can be crucial to children’s success. Teachers can motivate and give good or bad patterns in these skills. Digital generations, although born into technology, have difficulty using them, especially when it does not meet their interest. The responsibility of infocommunication technology teachers is enormous in this situation. Some studies (Gares et al., 2020; Anthony and Noel, 2021; Pozo et al., 2021; Sofianidis et al., 2021) have dealt with adaptation to the digital environment and measured teachers’ skills in this area according to their subject. In Pozo et al. (2021), we found a different categorization of teachers’ attitude. It investigated what type of teaching is preferred by teachers of certain subjects during the pandemic depending on the frequency and type of digital technology use.

Cognitive overload

We have already discussed the general overwhelming of children in the context of the pandemic. The topic of cognitive overload (Ambrus, 2015) focuses more on the overwhelming of the mind between the problem-solving processes. It investigates the working memory limits and tries to give solutions to how we can train our working memory to successfully solve new tasks. The most relevant suggestion from our point of view is that if schemas are built into long-term memory, learners can successfully learn analog-based elements of problem-solving. So, the schemas must be built first, after which we can continue teaching with “more serious” programming tasks, items, or languages.

According to the cognitive overload theory, which was developed and adapted by Sweller et al., in mathematical problem-solving, problem solvers must have many problem positions and schemes of solution steps in their minds, like chess players. After the problem solvers successfully recognize the already known problem positions or its sub-problems during the new problem, they can easily recall and activate these schemes (Ambrus, 2015). If students do not have an adequate schema, they resort to the trial-and-error method. Although it is a natural learning method in the evolutionary and behavioral biology and these attempts also require metacognitive abilities, Biro and Csernoch (2013) showed that they do not support the development of algorithmic skills. Another problem is that these attempts greatly overload the capacity of the working memory, which is small anyway. According to Miller’s law, the number of objects that can be stored in the working memory of an average person is 7 ± 2; recent research claims that this was an optimistic estimate; in fact, 4 ± 1 information units is closer to reality. Furthermore, if the task is not only to store information but also to process it, this capacity is no more than 2 or 3 units (Ambrus, 2015).

In Bubno and Takacs (2019), we presented that our “analogy-based algorithm” method helps pupils not to overload their working memory during problem-solving. The method is based on well-known steps that lead the problem solver during the problem-solving.

Furthermore, to avoid cognitive overload, we use a block programming editor called Blockly code for teaching. With Blockly, we can even create newer block languages or web applications (Domokos et al., 2017), but in the classroom, we used them only for simple novice programming.

Students do not learn a new language, they do not need to bother with syntax of the language, they only need to care about developing the logical structure of the algorithm, and the physical implementation is automatically generated. In case of Blockly, there are five different languages to translate, including Python.

In Bubno and Takacs (2019), we examined a Blockly code programming editor in the sense of Bruner’s representation stages, and we found that although it is a symbolic stage tool of full value, it has some lower stage elements (like colors and drag-and-drop technique) that can support avoiding cognitive overload.

Analogy-based algorithm method

The analogy-based algorithm method is based on Pólya’s problem-solving model (Polya, 2014), where each step corresponded to the steps of the computer problem-solving. In Hungarian mathematical teaching, Pólya’s steps were translated into five steps that lower grade students can easily understand and memorize: gathering data, creating a plan, counting, checking, and answering. In Bubno and Takacs (2017), we state that by recalling this well-known scheme in teaching novice computer programming, we can build a bridge between mathematical and computational problem-solving. Gathering data corresponds to input, while answering (after checking) corresponds to output. Planning and counting are the algorithm.

First, we collect data from the text of the word problem, and second, we clarify how many variables we must use. After that, we create a plan, where we have to identify what kind of programming tool we need to solve the problem (the basic programming tools we teach in novice programming are loops, lists, and conditional statements), and write the algorithm. Finally, we must build the checking part in the program (by using any of programming tool) and answer the problem depending on the result of the checking. So, answering after checking means that the program must respond to the problem anyway, but we have to ensure that it reports only the correct result or the fact that it indicates an error.

Materials and methods

Participants and their circumstances

We taught 63 students in the four study groups before the pandemic (33 girls and 30 boys) and 33 students during the pandemic (11 girls and 22 boys) in regular classes of a secondary school. We did not sample students, the experiments were carried out within subject frameworks, in the algorithm topic of the information technology courses.

In the first experiment in 2017, we had four student groups of various grades (from 8th to 11th) in a Hungarian secondary school (University of Debrecen Secondary Grammar School). In 2021, we had two 9th grade student groups in the same school. All the student groups in this school have subject orientation. In the first experiment, the orientation of our groups ranged from science, engineering (applied sciences), economics to languages, while during the pandemic, the orientation of the groups included applied sciences and economics.

In this school, computer science is taught in groups of 15–18 students. Every student has their own computer in the classroom to be able to work independently. The rooms are relatively large and spacious, and children often complain that they do not see the board well. In the groups before the pandemic, we often allowed them to come closer to the teacher’s desk for this reason, and they watched the teacher’s solution and explanation in a semicircular layout. This way the atmosphere became relaxed and unconstrained. The whole group solved the task together with the teacher, and the students could come up with questions; thus, an active discussion about the task developed. Children’s suggestions were discussed by the whole group right away. The teacher had immediate feedback on whether students had understood the task and could follow the lesson properly.

The disadvantage of this method was that they had to reproduce the previously discussed problem solution independently by going back to their own machines. Students were given practice assignments and homework, and there were informal online learning groups for all the student groups, where they could share homework and assignments with each other and the teacher or ask questions.

The pandemic teaching environment took place in the official e-learning system of the school called “E-suli.” Pupils could upload or link their solutions there, and all the necessary teaching aids that the teacher shared with them were available there. The class was held on Webex.

First, we have to clarify that during emergency remote teaching, we did not face problems that others often mentioned about pupils’ home circumstances. In this school, our students were relatively well equipped with home appliances, and their families had adequate technology at home both in quantity and quality. During the pandemic lockdown, broadband internet access was subsidized by the Hungarian government for families with children having to take part in distance education.

The school management also tried to eliminate this potential problem and supported it with appropriate lesson organization. All the groups had two computer science lessons a week by the normal timetable. During emergency remote teaching, one lesson was held online, and the other one was not compulsory for students: it could be used for more informal discussions, individual help, development, consultation, or report, which also was online.

Throughout the lessons of the emergency remote teaching, the teacher’s screen was shared with the students who could see it at close range on their own home devices, and parallelly they could perform the task step-by-step in another window as the teacher progressed. However, the activity of the children, the discussion of the task was not as vivid and relaxed as before. The pandemic group also had access to official textbook aids to facilitate independent, home-based learning of the curriculum. The textbook was processed at the beginning of the discussion of the material, and the teacher presented the relevant parts of the textbook, which was the classic curriculum about computer programming with pseudocode, block diagram, and Python codes. The teacher interpreted the sample codes from the textbook in different programming languages and solved the same problems that were found in the textbook in Blockly code as well.

As we have already highlighted, during emergency remote teaching, the teachers’ confidence was a factor of crucial importance in order to bring out the best performance from the students that we can expect from them under normal circumstances. In computer science teaching, the credibility of the teachers would have been questioned if they had not been able to respond to the sudden change with appropriate resilient behavior in the virtual online environment. On the other hand, the educational content also had to be relevant and placed immediately in an online environment. The “analogy-based algorithm” method and the chosen Blockly code programming environment proved to be fully capable of supporting it.

Task and procedures

Our study was based on the same questionnaire method we had used years ago at the first examination (Bubno and Takacs, 2019). We taught the teaching material, students wrote exams, they were given homework to be submitted, and they got their marks. Some months later, we asked them to fill out the test and the questionnaire.

In the 2020/21 academic year, we repeated the whole teaching process with two new groups during the pandemic (from November 2020 to January 2021), and we asked pupils to fill out the same test and questionnaire in June 2021 after the pandemic closure was canceled in Hungarian schools.

Although the teaching material and the whole process were online, the survey was conducted via printed test and questionnaire. The first reason was that we did not want children to test the program codes in the programming environment. On the other hand, some of the questions referred to other programming languages (pseudocode and block diagram) and not Blockly codes.

The test consisted of nine main tasks with 81 subtasks at every task. In Bubno and Takacs (2019), we detailed the whole test, and now, we just briefly outlined the main characteristics of the test.

There were four main aspects that we observed during the evaluation:

1. Generic concepts: problem-solving, analogy recognition, algorithm evaluation, code correctness, code optimization, and terminology usage.

2. Programming tools: variable, conditional statement, loop, list, and print.

3. Critical factors: data, algorithm, math (run), check, and answer.

4. Mathematical concepts: word problem, logical statement, set, discussion, equation, diagrams, linear function, and Pythagorean triples.

As for mathematical concepts, we have mentioned the facts as follows:

The test focuses heavily on problem-solving, specifically based on mathematical word problems as the essence of our algorithmic teaching method is based on which programming tools can be taught with which type of word problem (Bubno and Takacs, 2014, 2017).

Pólya’s last step was “looking back,” which means discussion of the problem, how to generalize a problem, and what to do with the plan in order to solve more general problems.

In the first task, we presented an algorithm that changes the value of two variables. In the second and third tasks, we created algorithms for certain mathematical theorems or concepts, especially Pythagorean triples and linear functions. There was a Blockly code in all the three tasks, and children had to give the answer and recognize the mathematical concepts. In the fourth task, we presented a diagram that illustrates the result of the pseudocode (not in Blockly language), and children first had to recognize the connection between the diagram and the code. Then, they had to decide what programming control tools are required to implement the code. The fifth task was a block diagram, and children had to recognize the certain programming control tools in it.

In the sixth, eighth and ninth tasks, children got implemented word problems in Blockly code. They had to decide whether the program would solve the problem or not, and what we could do to generalize the problem. Moreover, they had to decide what programming tools were required to implement the code correctly in order to solve the problem and to print the result. In the seventh task, they got a Blockly code full of mistakes, and they had to categorize all the mistakes from the code.

After filling out the test, we asked them to fill out a questionnaire as well. They had to evaluate all the tasks on a Likert scale (from 1 to 5) and describe how difficult it was to solve each one of them. We used this self-assessment as a subjective measurement of cognitive overload.

During the evaluation of children’s solutions, wrong solutions were categorized to be algorithmic, mathematical, or terminological in nature and distinguished those from the cases where there were no solutions or mistakes. We gave 1 point for a good answer and from 0 to 0.9 for the mistake depending on the category of the mistake and the significance of the error. For example, maybe we gave 0.9 if there was only a terminology usage problem in a free text answer, but we gave 0 if we were faced with a serious misconception either mathematical or computational.

Data gathering and processing

We gathered our data into a multidimensional ROLAP cubes and processed with OLAP technology. We chose the point of the solution and the point of self-assessment as the main indicators. The main dimensions of the dataset are as follows:

1. Task: the attributes of which are category (of the task and subtasks), critical factor, programming tool, and mathematical concept.

2. Pupil: the attributes of which are grade, orientation, Blockly code (whether they learned or not) and Blockly year (when they learned, including the pandemic period, as an attribute).

3. Solution: the attributes of which are the generic type of mistakes and typical mistakes.

The average points were calculated based on the points students earned in each subtask, and we presented them grouped by attributes according to our former study (Bubno and Takacs, 2019). We also compared the surveyors’ self-assessment points with the obtained results. We can say we changed the points into marks in both cases.

In this study, we describe these results (marks and points as percentages). We present these former results as percentage and based on the distribution of scores, supplemented by the results during the pandemic. It is also a novelty that we have now created a correlation table (Takacs and Bubno, 2022) from the points obtained for the same subtasks according to their categorization. We compare each attribute occurrence (value) (aspect) in pairs, drawing a cross-tabulation to see which attribute occurrences have strong or weak correlations in the results obtained.

Finally, we found a specific correlation before and during the pandemic, and we plot the multiplicity with a trend line on a scatter chart (each point represents the result achieved by a student).

In this article, we do not present all the aforementioned results in diagrams or tables, but we included the dashboard that we built based on our data cube, and those interested can study it in detail (Takacs and Bubno, 2022).

Results

Self-assessment

In Figure 1, we compared the average points and the self-assessment points that our students reached before and during the pandemic in the different programming environments we measured by the tasks.

FIGURE 1

Figure 1. Self-assessment.

Children’s self-assessment points (result distance from the examination points by tasks) were approximately normally distributed in both the experiments (before pandemic: kurtosis = 1.69, skewness = −0.29, SD = 1.32, N = 384; pandemic: kurtosis = −0.11, skewness = −0.28, SD = 1.60, N = 270) (Dinya, 2011), so we experienced that neither the psychological impact of the pandemic nor the learning environment caused a prominent underestimation or overestimation in the pandemic student groups compared with the traditional learners. Students could meet block diagrams and pseudocodes in their former studies, but we taught them only Blockly two times a week in 45-min infocommunication classes for 7–8 weeks during the experiment.

The plot diagram presents that in both groups of students, self-assessment was closest to the real score for Blockly. In the case of block diagrams, the former student group overestimates themselves, while in the case of pseudocode, the group underestimates their performance. The pandemic group is different in the sense that it overestimates the results in all the programming environments. We assume the reason could be the lack of the verbal expression used in the classroom environment during problem-solving. When the teacher and the students discuss the problem, they think together, and the teacher can rapidly reflect on the arising good and bad ideas. It was very difficult to imitate the same verbal interaction in the distance learning environment, so in the classroom environment, students did not face whether their result was not exactly right, and we can say they did not get enough response to perform a realistic self-assessment.

Before the pandemic, the average point gathered from 81 was 33.1, while after the pandemic, it was 34.9. It is an improvement of 1.7 points. Girls in the pandemic scored 13.1 points higher than their predecessors, with an average score increase from 30.0 to 42.1. Boys in the pandemic performed worse than before, with an average score drop from 36.5 to 30.7.

Psychological aspects in the sense of answered questions

Before the pandemic, we did not examine how many subtasks were answered. During the pandemic, teachers often experienced a kind of decrease in motivation and in work morale. So now, we wanted to see whether our students prove these or not.

In Figure 2, we can see the ratio of the answered and unanswered subtasks. In the left two tables, we can see the amount and the percentage distribution. In the right table and in the diagram, we can see the results by tasks and weighted by the number of subtasks for the pandemic and non-pandemic groups and for the whole sample on average.

FIGURE 2

Figure 2. Answered subtasks before and during the pandemic on average.

However, students in the pandemic answered more of the subtasks, and their result is slightly (not significantly) lower than the average of the whole sample, while students’ result before the pandemic has improved a little.

In Figure 2, we can see in detail which questions were popular and which were avoided by most. Students in the pandemic responded higher (62.9 vs. 56.1) to the first task, which was about variable value exchange, and the sixth and seventh tasks, which were the first Blockly code interpretation and the debugging tasks. A similar amount of answers was given to task 2, task 8, and task 9 (Pythagorean triples, and two Blockly code interpretations). However, significantly fewer responses were received to the third, fourth, and fifth tasks. Task 3 was about the linear function, and we experienced that they could hardly recognize the mathematical model. We believe it is more of a mathematical problem and not algorithmic; however, the effect of this fact on the correct interpretation of the algorithm is obvious. If pupils have recognized the mathematical concept, they can easily succeed solving the task, and vice versa. So, we can say that a well-known mathematical concept (stored in long-term memory) can support solving new problems because it means less cognitive load. The fourth task was the pseudocode, and the fifth was the block diagram. These were omitted by most of the students. So, we can say that neither group was comfortable with different programming environments.

Results by the main characteristics

If we study the detailed results of the main characteristics shown in Figure 3, we can notice that among the general concepts, everything besides analogy recognition is better in the pandemic group than before, although significant differences are observed only in problem-solving and terminology usage. If we look at critical factors, we notice that the score for data gathering achieved is a little lower than before the pandemic, and unfortunately, the reached points for the checking part of the problems are significantly worse. However, we can see that in the case of the algorithm, “answer and run” the results are significantly better.

FIGURE 3

Figure 3. Average results by the main characteristics.

Regarding the success of the acquisition of programming tools, we can conclude that the emergency remote teaching group result is better than the before-pandemic group result. List and loop management are particularly prominent. However, if it was not necessary to use a particular programming tool, it was less elaborate. It is an interesting fact.

Recognizing mathematical concepts showed a more differentiated picture. We are afraid that it can be the impact of mathematics teaching during the pandemic, which could be much more difficult to accomplish than teaching computer science. Diagram interpretation and knowledge about sets were significantly worse than before the pandemic, while equations, linear functions, and general word problem-solving skills proved to be significantly better. The use or recognition of other mathematical concepts was almost the same in each group.

Mistakes

In our dataverse (Takacs and Bubno, 2022), the typical mistakes are described in a table. We categorized each subtask by three types of mistakes: algorithmic, mathematical, or terminology usage. Of course, we distinguish the correct answers and the unanswered (where the error cannot be determined) questions from mistakes. We can conclude that there were similar mistake combinations in the two periods; moreover, students made the same algorithmization mistakes nearly in the similar tasks, resulting in almost the same results. A striking difference is seen mainly in the combination of mathematical and less typically articulation skills.

Summarizing the results above this finding confirms that results in pandemic and before pandemic were not very different. Furthermore, we examined the correlation between word problems and algorithm, and word problems and all the programming tools (variable, loop, list, conditional statement, and print). We found correlations between the most significantly dependent pairs of attribute occurrences (Figure 4). In addition to these, further significant dependent pairs of attribute occurrences were “data and variable,” “algorithm evaluation and analogy recognition,” “algorithm evaluation and code correctness,” and “print and answer.”

FIGURE 4

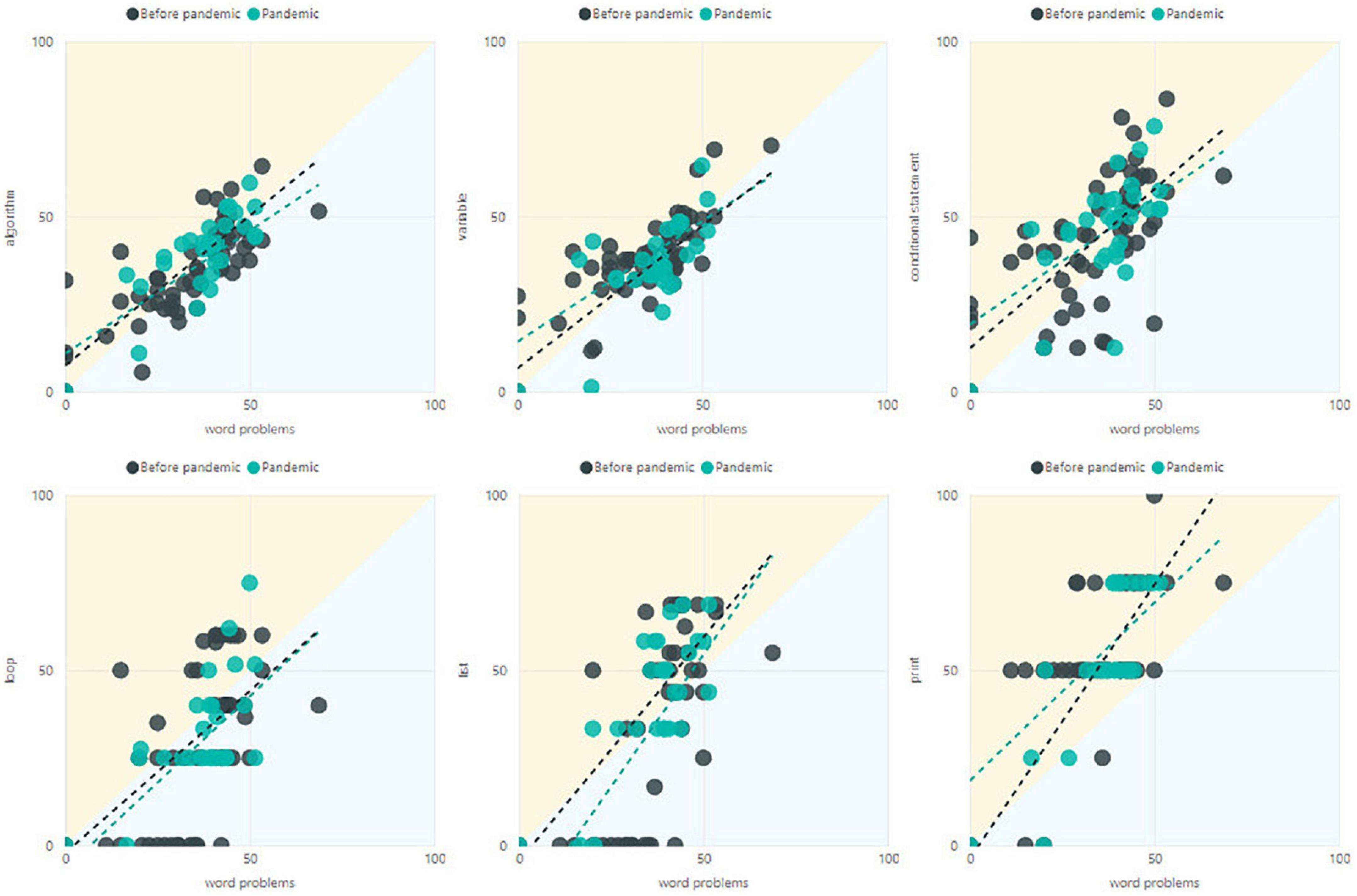
Figure 4. Correlation between word problems and algorithm, and word problems and all the programming tools.

Discussion

This study was conducted as an adaptation of a previous experiment in a changing teaching environment. At the time of the pandemic lockdown, we had the opportunity to test our previous hypothesis in Hungary that our previously developed and taught analog-based algorithmic teaching method would hold its place in distance learning and would not achieve worse results in terms of method efficiency. We also compared the results with previous ones on an empirical level. The data and statistical studies confirmed our hypothesis.

Beyond the examined hypothesis in this study, we confirmed one of our former hypotheses from Bubno and Takacs (2017, 2019), where we assumed that analogies in problem-solving from mathematics can support computational problem-solving.

During the literature review, we got acquainted with the conceptual scope of resilience, and we feel that further results could be achieved by understanding the psychological processes of teachers and students that take place in the teaching process, all of which can support students’ success in different learning environments.

The complete data are accessible in our dataverse (Takacs and Bubno, 2022).

Limitation

Our experiment was carried out in the standard study groups of a Hungarian secondary grammar school of a university. We did not sample these students for the experiment, although there was a former recruitment process before the admission, and as a grammar school, the standard of this school is higher than that of an average secondary school.

Our two experiments have differences in the number of participants as well. In this school, the classes are divided into two for the IT lessons. It means that during the pandemic, we worked with two study groups with 33 students altogether from two different classes. Their results were compared with the results of 96 students from the six former (before pandemic) study groups. The orientation of the classes (and students’ affinity for IT) was different (from humanities to engineering).

The authors of this study have been working together on this topic for many years, but only one of them taught the pupils participating in the experiments. We tried to prevent the teacher’s bias and confirm the validity of the experiment. To achieve that, the teacher-researcher corrected the test like an average school paper, while the other researcher corrected according to the indicators of the dataset we analyzed.

Conclusion

We had a hypothesis in 2014 that novice computer programming can be successfully taught with mathematical word problems. We selected a programming environment that we think is suitable, which was Google Blockly. With Blockly, we taught in an online environment in the classroom. Furthermore, we developed a standardized set of tasks and a result measurement examination. We tested the method on the students we teach. There was no prior selection, and we taught the programming module in standard school student groups according to our method, in IT lessons. According to our other hypothesis, this method and the selected environment complete each other, so it could be successful in a purely digital environment in future. We managed to prove this during the pandemic, in the spring semester of the 2020/21 academic year. We carried out the experiment in two groups of students. Their results were compared with the results of the previous participants in attendance education. According to our hypothesis, the results of the participants in digital education are not worse than those of their former peers. The hypothesis was confirmed by the results of the measurement examination.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://adattar.unideb.hu/dataset.xhtml?persistentId=doi:10.48428/ADATTAR/VHGKF7.

Ethics statement

Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.

Author contributions

KB designed the teaching and evaluation method and evaluated the test and the questionnaire. VT taught based on the method, prepared and cleaned the ROLAP cube, and visualized the result. Both authors contributed to the article and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ambrus, A. (2015). A matematika tanulás-tanítás néhány kognitív pszichológiai kérdése = Some cognitive psychological question in mathematics education. Gradus 2, 63–73.

Google Scholar

Anthony Jnr, B., and Noel, S. (2021). Examining the adoption of emergency remote teaching and virtual learning during and after COVID-19 pandemic. Int. J. Educ. Manag. 35, 1136–1150. doi: 10.1108/IJEM-08-2020-0370

CrossRef Full Text | Google Scholar

Baranyi, P., and Gilanyi, A. (2013). “Mathability: Emulating and enhancing human mathematical capabilities,” in Proceedings of the 2013 IEEE 4th International Conference on Cognitive Infocommunications (CogInfoCom), (Piscataway, NJ: IEEE Computer Society), 555–558. doi: 10.1109/CogInfoCom.2013.6719309

CrossRef Full Text | Google Scholar

Biro, P., and Csernoch, M. (2013). “Deep and surface structural metacognitive abilities of the first year students of Informatics,” in Proceedings of the 2013 IEEE 4th International Conference on Cognitive Infocommunications (CogInfoCom), (Piscataway, NJ: IEEE Computer Society), 521–526. doi: 10.1109/CogInfoCom.2013.6719303

CrossRef Full Text | Google Scholar

Bubno, K., and Takacs, V. L. (2014). “Solving word problems by computer programming,” in Problem Solving in Mathematics Education, eds A. Ambrus and E. Vásárhelyi (Budapest: ELTE), 193–208.

Google Scholar

Bubno, K., and Takacs, V. L. (2017). “The mathability of word problems as initial computer programming exercises,” in Proceedings of the 2017 8th IEEE International Conference on Cognitive Infocommunications (CogInfoCom), (Piscataway, NJ: IEEE Computer Society), 000039–000044. doi: 10.1109/CogInfoCom.2017.8268213

CrossRef Full Text | Google Scholar

Bubno, K., and Takacs, V. L. (2019). Cognitive aspects of mathematics-aided computer science teaching. Acta Polytech. Hung. 16, 73–93. doi: 10.12700/APH.16.6.2019.6.6

CrossRef Full Text | Google Scholar

Can, Y., and Bardakci, S. (2022). Teachers’ opinions on (urgent) distance education activities during the pandemic period. Adv. Mob. Learn. Educ. Res. 2, 351–374. doi: 10.25082/AMLER.2022.02.005

CrossRef Full Text | Google Scholar

Chmielewska, K., Ciskowska, W., Glazik, D., Marcinek, D., Wojciechowska, K., and Gilanyi, A. (2020). “Learnability - Are we ready for distance learning?,” in Proceedings of the 2020 11th IEEE International Conference on Cognitive Infocommunications (CogInfoCom), (Piscataway, NJ: IEEE Computer Society), 000465–000470. doi: 10.1109/CogInfoCom50765.2020.9237881

CrossRef Full Text | Google Scholar

Chmielewska, K., and Gilanyi, A. (2018). Educational context of mathability. Acta Polytech. Hung. 15, 223–237. doi: 10.12700/APH.15.5.2018.5.13

CrossRef Full Text | Google Scholar

Dinya, E. (2011). Biometria az orvosi gyakorlatban = Biometrics in Medical Practice. Budapest: Medicina.

Google Scholar

Domokos, P., Szell, M., and Takacs, V. L. (2017). “Blocklino: A graphical language for Arduino,” in Proceedings of the 2017 8th IEEE International Conference on Cognitive Infocommunications (CogInfoCom), (Piscataway, NJ: IEEE Computer Society), 000045–000050. doi: 10.1109/CogInfoCom.2017.8268214

CrossRef Full Text | Google Scholar

Gares, S. L., Kariuki, J. K., and Rempel, B. P. (2020). Community Matters: Student-Instructor Relationships Foster Student Motivation and Engagement in an Emergency Remote Teaching Environment. J. Chem. Educ. 97, 3332–3335. doi: 10.1021/acs.jchemed.0c00635

CrossRef Full Text | Google Scholar

Google (2022). Google: Blockly Code. Available online at: https://developers.google.com/blockly (accessed April 30, 2022).

Google Scholar

Karakose, T., Ozdemir, T. Y., Papadakis, S., Yirci, R., Ozkayran, S. E., and Polat, H. (2022a). Investigating the Relationships between COVID-19 Quality of Life, Loneliness, Happiness, and Internet Addiction among K-12 Teachers and School Administrators—A Structural Equation Modeling Approach. Int. J. Environ. Res. Public Health 19:1052. doi: 10.3390/ijerph19031052

PubMed Abstract | CrossRef Full Text | Google Scholar

Karakose, T., Yirci, R., and Papadakis, S. (2022b). Examining the Associations between COVID-19-Related Psychological Distress, Social Media Addiction, COVID-19-Related Burnout, and Depression among School Principals and Teachers through Structural Equation Modeling. Int. J. Environ. Res. Public Health 19:1951. doi: 10.3390/ijerph19041951

PubMed Abstract | CrossRef Full Text | Google Scholar

Karakose, T., Polat, H., and Papadakis, S. (2021). Examining Teachers’ Perspectives on School Principals’ Digital Leadership Roles and Technology Capabilities during the COVID-19 Pandemic. Sustainability 13:13448. doi: 10.3390/su132313448

CrossRef Full Text | Google Scholar

Lavidas, K., Apostolou, Z., and Papadakis, S. (2022). Challenges and opportunities of mathematics in digital times: preschool teachers. Views. Educ. Sci. 12:459. doi: 10.3390/educsci12070459

CrossRef Full Text | Google Scholar

Nilsberth, M., Liljekvist, Y., Olin-Scheller, C., Samuelsson, J., and Hallquist, C. (2021). Digital teaching as the new normal? Swedish upper secondary teachers’ experiences of emergency remote teaching during the COVID-19 crisis. Eur. Educ. Res. J. 20, 442–462. doi: 10.1177/14749041211022480

CrossRef Full Text | Google Scholar

Polya, G. (2014). How to Solve it: A New Aspect of Mathematical Method. Princeton: Princeton University Press.

Google Scholar

Pozo, J., Pérez Echeverría, M., Cabellos, B., and Sánchez, D. L. (2021). Teaching and Learning in Times of COVID-19: Uses of digital technologies during school lockdowns. Front. Psychol. 12:656776. doi: 10.3389/fpsyg.2021.656776

PubMed Abstract | CrossRef Full Text | Google Scholar

Raghunathan, S., Darshan Singh, A., and Sharma, B. (2022). Study of resilience in learning environments during the Covid-19 pandemic. Front. Educ. 6:677625. doi: 10.3389/feduc.2021.677625

CrossRef Full Text | Google Scholar

Sebestyén, K., Csapó, G., Csernoch, M., and Abari, K. (2022a). Measuring the algorithmic skills of students working with low-and high-mathability programming approaches. Acta Polytech. Hung. 19, 93–112. doi: 10.12700/APH.19.1.2022.19.7

CrossRef Full Text | Google Scholar

Sebestyén, K., Csapó, G., Csernoch, M., and Aradi, B. (2022b). Error recognition model: high-mathability end-user text management. Acta Polytech. Hung. 19, 151–170. doi: 10.12700/APH.19.1.2022.19.10

CrossRef Full Text | Google Scholar

Sofianidis, A., Meletiou-Mavrotheris, M., Konstantinou, P., Stylianidou, N., and Katzis, K. (2021). Let students talk about emergency remote teaching experience: secondary students’ perceptions on their experience during the covid-19 pandemic. Educ. Sci. 11:268. doi: 10.3390/educsci11060268

CrossRef Full Text | Google Scholar

Takacs, V. L., and Bubno, K. (2022). Data from: Blockly questionnaire and Correlation table in Block Languages Dataverse. Debrecen: ADATTAR Data Repository of University of Debrecen. doi: 10.48428/ADATTAR/VHGKF7

CrossRef Full Text | Google Scholar

Ulla, M. B., and Perales, W. F. (2021). Emergency remote teaching during covid19: The role of teachers’ online community of practice (cop) in times of crisis. J. Interact. Media Educ. 1:9. doi: 10.5334/jime.617

CrossRef Full Text | Google Scholar