Developing Preschool Teachers’ Computational Thinking Knowledge, Attitudes, Beliefs, and Teaching Self-Efficacies: A Curriculum-Based Professional Development Program

Grounded in transformative teacher development through the curriculum-based professional learning (CBPL) approach to teaching-learning, this exploratory study surveyed the computational thinking (CT) views of 25 in-service teachers before and after their CT professional development programme workshops. Multivariate outcome multilevel cross-classification analysis showed that after their workshops, these teachers changed their CT knowledge, CT attitudes, CT beliefs, and CT teaching self-efficacy. Teachers reporting greater CT knowledge than others felt greater overall CT teaching self-efficacy, including for both plugged and unplugged CT activities. Moreover, teachers who reported a school culture of sharing and teamwork or sufficient school resources for CT activities were more likely than other teachers to have greater teaching self-efficacy for plugged CT activities or CT activities overall. These results highlight the importance of school culture, school technology resources, and teachers’ reported CT knowledge to their CT teaching self-efficacy.

Introduction

As computational thinking (CT) become increasingly important to more jobs (Bull et al., 2020), more countries are incorporating CT into their school curricula often mandatory (Gretter and Yadav, 2016; Sands et al., 2018; Li et al., 2020). However, early childhood education (ECE) research on CT is still in its infancy (Angeli et al., 2016), with no consensus on the definition of CT or how to teach it in ECE. Still, educators generally agree that professional development is crucial to helping teachers teach with CT activities (Barr and Stephenson, 2011; Bower et al., 2017; Yadav et al., 2017).

Past studies show that teacher professional development programs (PDP) for CT can help teachers gain an understanding of the subject and foster favorable attitudes toward teaching with CT activities (Hestness et al., 2018; Ketelhut et al., 2020; Rich et al., 2021a), but teachers without prior CT experience acquired only superficial CT understanding (Bower et al., 2017). However, short PDPs (50 min to 6 h) did not increase teachers’ beliefs in their ability to plan and execute actions to achieve specified goals (self-efficacy, Bandura, 1977), change their negative beliefs about CT (Rich et al., 2021a), or adequately prepare teachers to teach with CT activities (Bower et al., 2017). Hence, teacher PDP to help them develop both CT knowledge and CT teaching effectiveness requires (a) alignment to their CT curriculum (Darling-Hammond and Richardson, 2009), (b) embedding into their teaching (e.g., learn-by-doing, apply CT activities into their teaching; Bayar, 2014; Darling-Hammond and Richardson, 2009 (c) peer support (Villegas-Reimers, 2003; Darling-Hammond and Richardson, 2009; Bayar, 2014), and (d) longer, intensive, ongoing, systematic training (Dori and Herscovitz, 2005; Darling-Hammond and Richardson, 2009). Furthermore, a supportive school culture for the PDP enhances its effectiveness (Avalos, 2011).

Considering these findings from past studies, we proposed, designed and implemented curriculum-based professional learning (CBPL) (Short and Hirsh, 2020), PDP to help 25 teachers integrate CT into their curriculum and teaching (not a stand-alone CT subject). This study explores the impact of this PDP on 25 participating teachers’ CT knowledge, attitudes, beliefs, and CT teaching self-efficacy.

Curriculum-Based Professional Learning Program

We begin with the theoretical framework undergirding the CBPL program. Then, we specify its implementation.

CBPL Theoretical Framework

According to the CBPL approach, high-quality curricular resources and active instruction experiences help teachers improve their knowledge, attitudes, beliefs, and teaching to improve their students’ learning outcomes (Short and Hirsh, 2020). Curriculum-driven professional development is more focused and intentional than otherwise (Wong and Tsui, 2007). Mutually supportive schools, districts, and professional development providers can further improve teachers’ teaching (Akinyemi and Nkonki, 2020).

Curriculum-based professional learning includes four design features: core, functional, structural and essential (Short and Hirsh, 2020). Following Mishra and Koehler’s (2006) technological pedagogical content knowledge (TPACK) framework for teacher knowledge, core design features (curriculum, transformative learning, equity) develop preschool teachers’ shared understanding of CT concepts and their relevance to daily life, pedagogical content teaching skills, and diverse lesson activities (both plugged and unplugged). Transformative learning experiences introduce new teaching materials (e.g., videos) that teachers use during the PDP and then with young learners in class, thereby helping teachers enhance their perceptions, beliefs, and self-efficacies. To promote equity, the PDP uses culturally and developmentally appropriate integration of CT into ECE.

Functional design features of PDP includes learning designs, reflection/feedback, beliefs, and change management. The learning designs introduce CT integrated curriculum with peer teachers, who implement and mirror pedagogical strategies with digital tools to teach CT. Reflection and feedback enhances teachers’ practical skills with these tools. As teachers’ competences grow, PDP cultivates change in their teaching beliefs. PDP also helps teachers become change agents and manage their changes to enhance their CT integrated classroom practices and scaffold student learning.

Structural design provide regularity and increase consolidation of learning. Grounded in constructionist learning theory (Csizmadia et al., 2019), teachers collaborate to plan, implement, and assess new CT teaching materials and lessons for effectiveness and sustainability. Over time, they adapt their teaching practices to their students’ needs.

Essential elements are leadership, coherence, and resources. PDP helps groups of leaders and teachers develop a shared, long-term vision for school-wide CT integration. Furthermore, they build networks with other schools implementing CT for mutual sharing and support. With sufficient resources, they can build sufficient material (e.g., Beebots) and staff capacity for CT implementation.

CBPL Implementation

The CBPL training course includes six workshops across 6 months and a summer training institute for participants to apply their workshop ideas to teaching students. The first workshop helps teachers understand the critical dimensions of Brennan and Resnick’s (2012) CT framework: key ideas (e.g., iteration, parallelism; computational concepts), computer scientist actions (e.g., debugging projects; computational practices), and computer scientist views of the world (computational perspectives). In this workshop, teachers learned about CT components via daily life problem-solving activities and a related short video. They learned terms such as “loops,” “conditionals,” and “variables” within simple computer program structures. Then, they explored links between CT components and the ECE curriculum via brainstorming and discussion. Next, they reflected on CT’s educational purposes and made recommendations for excellent CT instruction. We encouraged their use of CT within a suitable educational philosophy and ECE learning environment. The first workshop promoted open discussion around questions such as these (rather than simply giving answers):

1). Does young children’s involvement in CT activities imply that the ECE learning environment should include CT?

2). If children engage in plugged or unplugged CT-related activities, can we presume that are excited to learn more?

These teachers considered five CT uses.

1. CT to learn recent technological developments (e.g., use CT to teach technology and robotics principles, such as computer programming);

2. Integrated view of CT (e.g., use CT to consolidate understanding in other curriculum areas, such as language, digital literacy, mathematics);

3. Challenge students’ thinking (e.g., use CT to strengthen children’s capacity to solve problems and plan strategies);

4. Use CT to develop metacognition (e.g., use CT to increase children’s capacity to reflect on their learning and extend their scientific inquiry);

5. Address psychological and motivational needs (e.g., use CT as a learning environment to reduce anxiety and fear of mistakes; increase motivation and self-esteem).

The second workshop enhanced teachers’ pedagogical understanding of computational concepts, practices, and perspectives via hands-on practice. Teachers examined data practices, modeling, simulation practices, computational problem-solving practices, and systems thinking activities. To understand and apply these practices to ECE, they collaborated in groups to solve CT problems involving the programming of Beebots, Cubetto, Robo_Wunderland, and ScratchJr (artifact-based learning, Bairaktarova et al., 2012).

These teachers also developed “activities … to engage a variety of audiences with great ideas from computer science and CT, without learning coding, programming or even using a digital device” (unplugged CT, Bell and Vahrenhold, 2018, p. 497; T. Bell et al., 1998). These activities incorporate games, puzzles, stories, challenges, and rich sensory experiences (see examples at Hello Ruby; code.org; ACARA; CS Unplugged, Bell, 2021). Unplugged activities are inexpensive, accessible, and require few resources (Lee and Recker, 2018). Unplugged CT promotes its development by complementing programming, integrating it into other topics, and scaffolding teachers and students, serving as a “priming phase” before programming to increase students’ awareness of algorithmic stages (Huang and Looi, 2021). By using familiar materials and concepts, unplugged CT such as paper circuitry activities “provide multiple entry points for students less familiar with computational thinking concepts” to learn algorithmic thinking, conditional logic, debugging, etc. (Lee and Recker, 2018). Lastly, these teachers wrote reflections on how their understanding and teaching of CT changed.

The third workshop cultivates teacher beliefs to support their CT teaching via group exploration and application. As participating teachers discuss, understand, implement, and assess CT teaching practices, they appreciate their effectiveness and sustainability, which enhances their beliefs and attitudes about effective CT teaching (Bower et al., 2017; Yadav et al., 2017; Corradini et al., 2018). Notably, they increase their belief in their capacity to act and accomplish teaching goals (teaching self-efficacy, Bandura, 2000). They created a bank of design scenarios and resources for teaching and assessing the CT learning of young children. Challenged to develop suitable CT activities for ECE, these teachers created compelling practical application scenarios.

We encouraged these teachers to use a scientific approach to these activities that encourages students to identify a problem, present a hypothesis, conduct an experiment, analyze the results, discuss their perspectives, generalize the findings, and revise accordingly (Merrill, 2002). Below are examples for various age groups based on their usefulness, availability, affordability, and variety in the local market (not tied to any one robotic platform):

Pre-nursery (2–3 years): Unplugged CT.

K1 (3–4 years): Unplugged CT, and Robotics.

K2 (4–5 years): Unplugged CT, Robotics, and Digital apps.

K3 (5–6 years): Unplugged CT, Robotics, Digital apps, and ScratchJr.

Rather than prescribe best practices, our course sought to equip teachers with tools to identify best resources and practices for each plugged or unplugged activity. For example, we revised Kemp’s model of instructional design (Kemp, 1985) to highlight nine key elements in each activity’s development:

1) Determine specific learning objectives and concerns related to CT.

2) Determine the key features and needs of students to consider while planning CT learning experiences.

3) Develop a clear understanding of the CT lesson content and examine the proposed activity components for CT learning goals.

4) Specify the CT instructional objectives and expected outcomes to design suitable CT activities.

5) Logically present the CT content for each instructional element.

6) Develop CT instructional strategies that facilitate students’ attainment of learning objectives and enhance their proficiency.

7) Construct the CT instructional materials and choose the most effective delivery.

8) Develop CT instruments to assess students’ progress toward objectives.

9) Select appropriate CT resources (time, materials, and class organization for the activities) to aid in teaching and learning processes.

In the fourth and fifth workshops, groups of teachers collaborated to iteratively design shared CT curricula and lessons for ECE based on their school’s available resources and culture; and the capabilities, dispositions, and predispositions of both teachers and students (Seow et al., 2019; Kotsopoulos et al., 2021). In this iterative design, they clarified their representative modeling, CT processes and errors, and students’ errors, and then used this information to improve their lessons and curricula (Fields et al., 2019). Based on Kemp’s (1985) framework, we designed the CT integration resource bank so that its structure emphasizes the critical CT components for a lesson, including suitable in-house plugged, unplugged and web resources. Teachers in the same grade level collaboratively created lesson plans for CT integration; they identified supportive resources for the CT content, designed a lesson plan, used available materials, and presented it to other teachers (with videos, PowerPoint presentations, documents, and photographs). These complex lesson plans:

• Specified lesson topic/title and grade level of students.

• Described the background and rationale.

• Identified of the objectives and evaluation methods for CT integration.

• Specified the needed resources and timeline.

• Described the use of unplugged or plugged resources.

• Described its implementation.

The fourth and fifth sessions prepared teachers to design a CT instructional project following theoretical orientation (workshop 1), practical training (workshop 2) and exploration (workshop 3). The research team evaluated and analyzed each project, and gave the teachers feedback to help them reflect on possible improvements.

The sixth workshop focused on teacher feedback and a CT integrated curriculum. Specifically, teachers discussed key obstacles to creating and teaching an effective lesson plan. They shared CT teaching experiences, practical examples, and results for young children at various ages.

Using a bottom-up approach, teams of teacher representatives led the other participants to create a CT integrated curriculum (Lassonde and Israel, 2009) and institutionalize it. Teacher representatives developed further learning and teaching resources (plugged and unplugged) to enrich 2 to 6-year-old students’ learning activities, conduct reviews of activities associated with age-appropriate CT integration (Bers et al., 2014), shared best practices (Melasalmi and Husu, 2016), and enhanced professional development for colleagues (Kermani and Aldemir (2015). Also, they expanded their teacher networks within and across schools, and strengthened partnerships with community key players to attract support and additional resources for long-term planning (Palts and Pedaste, 2020).

As a result of these CBPL workshops, we expect teachers to improve their CT knowledge, beliefs, attitudes and self-efficacies.

Method

In this study, 25 kindergarten teachers participated in a CT PDP and completed a pre-PDP survey and post-PDP survey. We used a multivariate outcome, multilevel cross-classification to analyze their survey responses: (a) for significant differences across pre-and post-surveys, and (b) to test an explanatory model of their CT teaching self-efficacy.

Participants

We used a convenience sample. Of the eight invited kindergartens, five kindergartens consented to conduct this PDP. Due to COVID-19 delay, only two kindergartens participated in this 6-month, school-site training programme at different times (February–July 2021: 13 teachers, 1 principal, 1 curriculum coordinator; June–December 2021: 13 teachers, 1 principal, 1 curriculum coordinator). Both kindergartens served 2.2 to 6-year-old students. Figure 1 explains our participant recruitment strategy and study protocol.

FIGURE 1

Figure 1. Recruitment strategy and study protocol.

All 25 teachers are qualified and registered ECE teachers in Hong Kong (see demographics in Table 1) and consented to participate in this research.

TABLE 1

Table 1. Participant’s demographics (N = 25).

Procedure

All 25 teachers participated in six, 2-h CT PDP workshop sessions, and then taught CT to students aged two to 6 years during either a 6-week summer school or a 2-week camp. All of them wrote reflections at the end of each workshop. All participants confirmed that they did not engage in other workshops during this time. All teachers responded to pre-workshop surveys, and 21 of them completed the post-workshop survey. All teachers were interviewed after the sixth workshop.

Data

Statistical power differs across levels. For α = 0.05 and an effect size of 0.4, statistical power for 25 people is 0.52 and for 46 survey completions across time is 0.80 (Konstantopoulos, 2008). As this small sample has low statistical power, false negatives are likely, but significant results remain valid.

Survey

The pre-workshop survey included the following fourteen definitions and thirty-three knowledge altogether forty-seven items.

Teacher beliefs about Computers and Computational Thinking (Rich et al., 2021a) has three subscales: (a) value beliefs (CT belief, 2 items; e.g., All students should learn CT); (b) value beliefs for teaching coding (CT attitude, 3 items; e.g., Interest in teaching with CT/want to continually improve teaching with CT) and (c) CT self-efficacy (7 items; e.g., I am ready to teach plugged/unplugged CT activities). All items had 5 point Likert-type scales, unless indicated otherwise. CT value belief response options ranged from “1-Strongly disagree” to “5-Strongly agree.” CT self-efficacy items response options ranged from “1- extremely unconfident” to “5-extremely confident.”

The post-workshop survey was identical to the pre-workshop survey, except for these additional open-ended questions:

1. Define computational thinking in your own words.

2. Is it possible to integrate computational thinking into the ECE classroom? Yes/No.

(a) How would you incorporate computational thinking into your ECE classroom if you answered yes?

(b) If not, why is it so difficult to integrate computational thinking into the classroom?

Post is a dichotomous variable that indicates whether the data are from the post-survey (value = 1; otherwise 0 for pre-survey).

Reflections

In the last 30 min of workshops, 2, 3, 5, and 6, participants were prompted to write a short reflection (200–300 words) about their: (1) understanding of CT developed in this phase, (2) CT integration in ECE and (3) how they perceived the workshop activities as helping (or not contributing) to their understanding after that phase.

Semi-Structured Interviews

After the last workshop, each teacher individually participated in 30 min, semi-structured interviews with a project leader who asked the following questions:

1) What does CT mean to you?

2) What are your pedagogical strategies for developing ECE students’ CT?

3) What technologies can be used to develop Kindergarten students’ CT?

4) What prevents you from developing your students’ CT?

5) What could help you develop your students’ CT?

6) How did participation in these workshops change your view about integrating CT in ECE?

Analysis

Survey Analytic Issues and Statistics Strategies

Accurate analyses of these data must address issues involving outcomes and explanatory variables (see Table 2).

TABLE 2

Table 2. Statistics strategies to address each analytic difficulty.

Outcome issues include differences across teachers or across time, discrete outcomes and multiple outcomes. As completed surveys at the same time or by the same teacher likely resemble one another more than those completed at different times or by different teachers (cross-classified data), an ordinary least squares regression underestimates the standard errors, so we use a multilevel cross-classification analysis (Goldstein, 2011). For ordered discrete outcomes (e.g., ratings), ordinary least squares regressions can bias the standard errors, so we use an ordered Logit regression (Kennedy, 2008). To aid understanding of these results, we report the odds ratio of the regression coefficient, namely the percentage increase or decrease in the likelihood of the outcome (Kennedy, 2008). Multiple outcomes can have correlated residuals that underestimate standard errors, so we use multivariate outcome multilevel analysis (Hox et al., 2017).

Explanatory variable issues include omitted variable bias, indirect effects, cross-level interactions, many hypotheses’ false positives, effect size comparisons, and robustness. As unspecified, omitted explanatory variables can cause omitted variable bias (Kennedy, 2008), we use a difference-in-differences analysis of participants at different times to reduce this bias (Bertrand et al., 2004). Separate, single-level tests of indirect mediation effects on cross-classified data can bias results, so we test for simultaneous multi-level mediation effects with a multilevel M-test (MacKinnon et al., 2004).

With cross-classified data, incorrectly modeling interaction effects across levels (e.g., survey response × teacher) can bias the results, so we use a random effects model (Hox et al., 2017). If an explanatory variable’s regression coefficient (e.g., β_yvj = β_yv0 + g_yvj) differs across levels (g_yvj ≠ 0?), then we model the possible cross-level moderation with structural variables (e.g., teacher).

As testing many hypotheses can cause false positives, we reduce them via the two-stage linear step-up procedure; it outperformed 13 other methods in computer simulations (Benjamini et al., 2006). When testing whether effect sizes differ, Wald and likelihood ratio tests do not apply at boundary points, so we use Lagrange multiplier tests, which also have more statistical power for small deviations from the null hypothesis (Bertsekas, 2014).

Lastly, we test whether the results remain stable (robust) despite small data or analytic differences (Kennedy, 2008). As any mis-specified equation in a multiple outcome model can introduce errors into otherwise correct equations, we model each outcome variable separately. Then, we separately run subsets of the data.

Pre- vs. Post-workshops Differences

We model each survey response to a question with a multivariate outcome, multilevel cross-classification analysis (Hox et al., 2017).

${\mathbf{\text{Response}}}_{\text{yit}}={\mathrm{\beta }}_{\text{y}}+e_{\text{yit}}+f_{\text{yt}}+{\mathrm{\beta }}_{\text{yx}}{\mathbf{\text{Post}}}_{\text{yt}}(1)$

In the vector of variables Response, the outcome variable (response to survey question) y by teacher i at time t has a centered intercept β_y with unexplained components (residuals) at the response- and time-levels (e_yit, f_yt). Possible Response outcomes y include define CT (algorithm, analytic ability, solve as computer scientist, logical, problem solve), CT knowledge (know CT, teach CT, teach CT to children, teach unplugged CT), beliefs (all learn CT, effective teaching helps students learn CT), attitude (interest, improve, attend training), self-efficacy (overall CT teaching, plugged CT teaching, unplugged CT teaching). Then, we test whether teacher responses to questions on the pre-workshops and post-workshops surveys differ, as indicated by the significance of the regression coefficient of Post, namely β_yx (see summary statistics Table 3 and the results in Table 4).

TABLE 3

Table 3. Summary statistics (N = 46).

TABLE 4

Table 4. Multilevel cross-classification differences analysis.

CT Teaching Self-Efficacies

Next, we test whether school attributes or teacher characteristics are linked to CT_Teaching_Self-efficacy.

$\mathbf{\text{CT}}\mathrm{\_}\mathbf{\text{Teaching}}\mathrm{\_}\mathbf{\text{Self}}-{\mathbf{\text{efficacy}}}_{yit}={\mathrm{\beta }}_{\text{y}}+e_{\text{yit}}+f_{\text{yt}}(2)$

In the vector CT_Teaching_Self-efficacy, the outcome variable y (overall CT teaching self-efficacy, plugged CT teaching self-efficacy, unplugged CT teaching self-efficacy) by teacher i at time t has a centered intercept β_y with residuals at the response- and time-levels (e_yit, f_yt).

First, we add School variables: leadership, school culture of sharing and teamwork, sufficient CT resources, technology classrooms, and resources for technology training. Then, we added a time variable: Post. Next, we added teacher beliefs (T_Belief): all students should learn CT, and effective teaching helps students learn CT. Afterward, we added teacher attitudes (T_Attitude): interested in teaching with CT, continually find better ways to teach CT, want more teaching training. Then, we add teacher knowledge (T_Knowledge): know CT, know steps for teaching CT, know CT for teaching ECE, and know unplugged CT. Lastly, we added Interaction terms among significant explanatory variables.

$\mathbf{\text{CT}}\mathrm{\_}\mathbf{\text{Teaching}}\mathrm{\_}\mathbf{\text{Self}}-{\mathbf{\text{efficacy}}}_{\text{yit}}$

$={\mathrm{\beta }}_{\text{y}}+e_{\text{yit}}+f_{\text{yt}}+{\mathrm{\beta }}_{\text{yis}}{\mathbf{\text{School}}}_{\text{yit}}+{\mathrm{\beta }}_{\text{yiu}}{\mathbf{\text{Post}}}_{\text{yit}}+{\mathrm{\beta }}_{\text{yiv}}\mathbf{\text{T}}\mathrm{\_}{\mathbf{\text{Belief}}}_{\text{yit}}$

$+{\mathrm{\beta }}_{\text{yiw}}\mathbf{\text{T}}\mathrm{\_}{\mathbf{\text{Attitude}}}_{\text{yit}}+{\mathrm{\beta }}_{\text{yix}}\mathbf{\text{T}}\mathrm{\_}{\mathbf{\text{Knowledge}}}_{\text{yit}}$

$+{\mathrm{\beta }}_{\text{yiz}}{\mathbf{\text{Interaction}}}_{\text{yit}}(3)$

We use an alpha level of 0.05. We also analyze residuals for influential outliers.

Analysis of Written Reflections and Individual Interviews

We conducted thematic analysis of the written reflections, applying initial coding, axial coding and theoretical coding to identify major patterns and themes (Braun and Clarke, 2006). In the initial coding, data were coded by keywords or phrases (e.g., algorithm, if-then). In the axial coding, the data were coded into categories (e.g., beliefs) and sub-categories (all children should learn CT; only technically-inclined children should learn CT). In the theoretical coding, data were compared with pre-existing models of PDP effects on CT knowledge, beliefs, attitudes, and teaching self-efficacies (e.g., Rich et al., 2021b).

We analyzed the semi-structured interviews (Fraenkel et al., 2015) with Creswell’s (2012) six-step method. First, we anonymized and converted all interview transcripts to text. Then, the lead author read the interview transcripts several times to understand the interviewees’ ideas and tone. Initial codes were developed and then iteratively refined (Fraenkel et al., 2015). Next, the codes were evaluated, and some were merged while others were deleted. Then, themes were developed and organized into a hierarchy of codes. Tables and figures were created to illustrate the findings. Finally, findings were examined, and thick description and inter-coder reliability tested the trustworthiness of the interpretations.

Findings

The summary statistics generally showed moderate to high levels of CT knowledge, beliefs, attitudes, and teaching self-efficacies (See Table 3), especially on the post-workshop surveys (as shown in the next section). The multivariate outcome, multilevel cross-classification results below show significant differences in pre- vs. post-workshops responses, and a path analysis modeling antecedents of CT teaching self-efficacies.

Pre- vs. Post-workshops Differences

These teachers’ survey responses regarding CT definition, beliefs, attitudes, knowledge, and CT teaching self-efficacies showed vast differences before vs. after the workshops. After the workshops, these teachers were far more likely) to define CT as including algorithmic solution of a problem, analytic ability, solving problems as a computer scientist, logical problem solving, or problem solving (+47% or higher odds ratio for each, see Table 4). After the workshops, these teachers were much more likely to know what CT is (+44%), know steps to teach CT effectively (+36%), know CT enough to teach it to young children (+48%), and know unplugged CT enough to teach it (+49%). After the workshops, these teachers were also far more likely to believe that all students should learn CT (+48%) and that effective teaching helps students learn CT (+35%). Their following attitudes also vastly improved after the workshops: interest in integrating CT into their teaching (+49%), continually find better ways to teach CT (+48%), and want to attend more training about teaching practices (+33%). After the workshops, teachers reported greater overall CT teaching self-efficacy (+44%), plugged CT teaching self-efficacy (+47%), and unplugged CT teaching self-efficacy (+42%).

CT Teaching Self-Efficacy

CT teaching self-efficacy often differed more across teachers (teach with CTA overall: 62%; teach with plugged CTA: 64%; teach with unplugged CTA: 50%) than across time (overall CTA: 38%; plugged CTA: 36%; unplugged CTA: 50%; see Table 5). (See Appendix Table A1 for correlation-variance-covariance matrices). All results discussed below describe first entry into the regression, controlling for all previously included variables. Ancillary regressions and statistical tests are available upon request.

TABLE 5

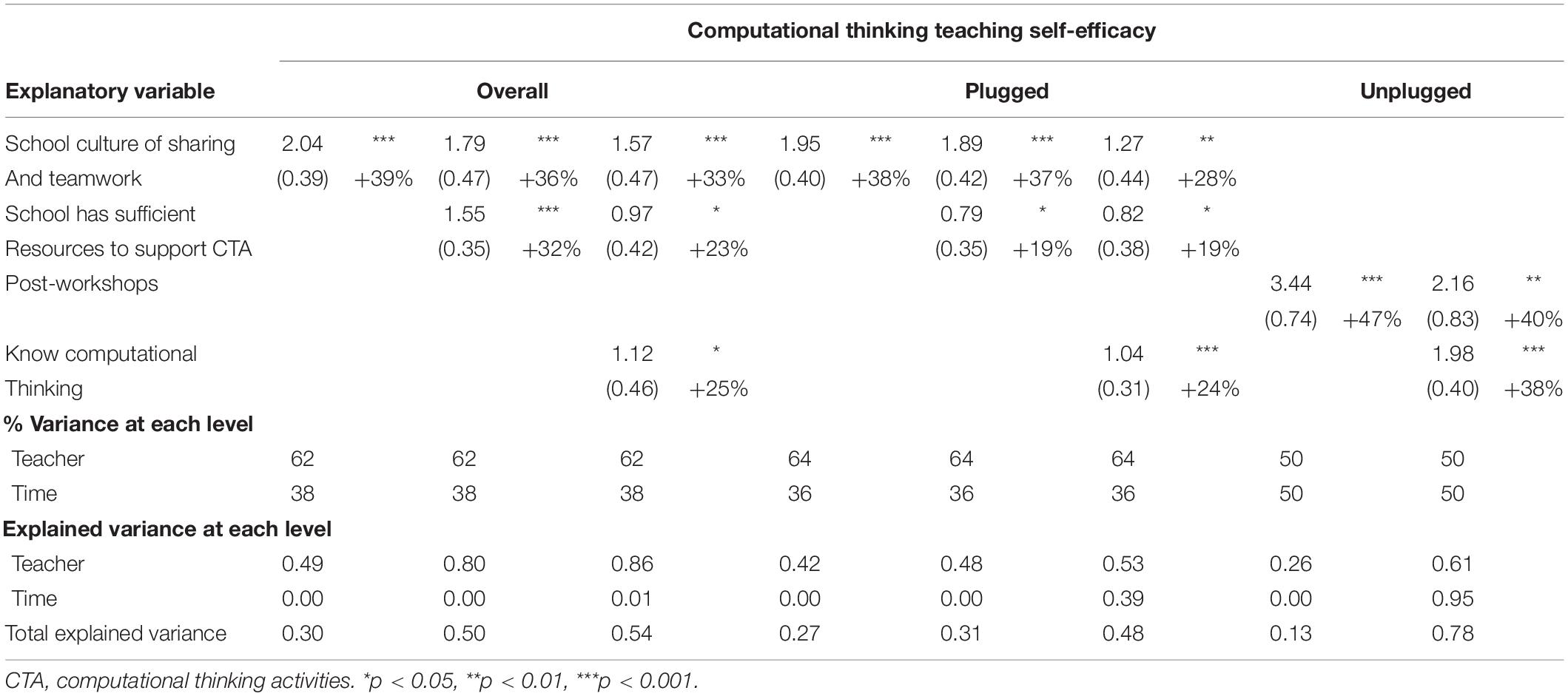
Table 5. Summary of multilevel cross-classification analyses of overall / plugged / unplugged computational thinking teaching self-efficacy.

Teachers’ Overall CT Teaching Self-Efficacy

School attributes and teachers’ perceived knowledge accounted for differences in teachers’ overall CT teaching self-efficacy (see Table 5 and Figure 2). Teachers in schools with a culture of sharing and teamwork, in schools with perceived sufficient resources to support CTA, or who viewed themselves as knowing CT were more likely than other teachers to report greater overall CT teaching self-efficacy (respectively, +39%, +32%, +25%).

FIGURE 2

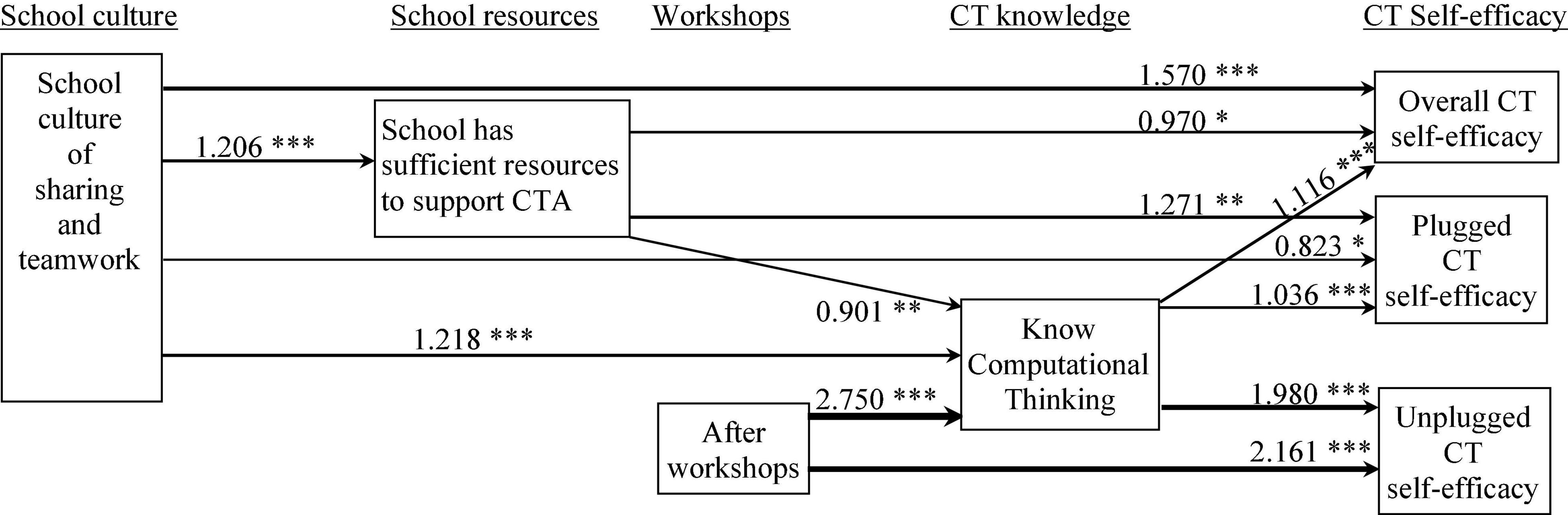
Figure 2. Path analysis of antecedents of overall / plugged / unplugged computational thinking (CT) teaching self-efficacy. Thicker arrows indicate larger effect sizes. *p < 0.05, ^**p < 0.01, ^***p < 0.001 5.2 Written Reflections and Interviews.

These results showed significant mediation effects. Teachers in the school with a culture of greater sharing and teamwork were 27% more likely than those in the other school to have sufficient resources to support CTA, which in turn was linked to 32% greater overall CT teaching self-efficacy (12% mediation; z = 3.15; p = 0.002). In the school with a culture of greater sharing and teamwork, teachers were 27% more likely than those in the other school to view themselves as knowing CT, which in turn was linked to 32% greater overall CT teaching self-efficacy (12% mediation, z = 2.11, p = 0.035). In the school with greater sufficiency of resources to support CTA, teachers were 21% more likely to view themselves as knowing CT, which in turn was linked to 25% greater overall CT teaching self-efficacy (37% mediation, z = 2.36, p = 0.018). The final explanatory model accounted for 54% of the differences in overall CT teaching self-efficacy.

Teachers’ Plugged CT Teaching Self-Efficacy

School attributes and teachers’ perceived knowledge also accounted for differences in teachers’ plugged CT teaching self-efficacy. Teachers in the school with a culture of greater sharing and teamwork or perceived sufficient resources to support CTA, or who viewed themselves as knowing CT were also more likely than other teachers to have greater plugged CT teaching self-efficacy (respectively, +38%, +19%, +24%).

These results also showed significant mediation effects. In the school with a culture of greater sharing and teamwork, teachers were 27% more likely than teachers in the other school to view themselves as knowing CT, which in turn was linked to 24% greater plugged CT teaching self-efficacy (33% mediation, z = 2.692, p = 0.007). The final explanatory model accounted for 48% of the variance in plugged CT teaching self-efficacy.

Teachers’ Unplugged CT Teaching Self-Efficacy

Lastly, workshop completion and teachers’ perceived knowledge accounted for differences in teachers’ unplugged CT teaching self-efficacy. Teachers who completed the workshops or viewed themselves as knowing CT were more likely than other teachers to have greater unplugged CT teaching self-efficacy (respectively, +47%, +38%).

These results also showed significant mediation effects. Teachers who completed the workshops were 44% more likely than other teachers to view themselves as knowing CT, and in turn were 38% more likely than other teachers to have greater unplugged CT teaching self-efficacy (37% mediation, z = 3.204, p = 0.001). The final explanatory model accounted for 78% of the variance in unplugged CT teaching self-efficacy.

All other explanatory variables and interactions were not significant. Analysis of residuals showed no substantial outliers. Robustness tests on data subsets and single outcomes showed similar results.

Our thematic analysis of participants’ written reflections and interviews identified important PDP learning components and need for further support.

Valuable PDP Components

Participants identified six valuable PDP components: (a) poor initial CT knowledge, (b) consequent importance of concrete CT experiences, (c) educational resources, (d) collaborative planning, (e) student involvement, and (f) spacing between workshops. Most of these teachers reported no formal training in computers, and many teachers shared teacher T-13’s understanding of CT.

I have never heard about the word “computational thinking” before attending these workshops.

(Teacher-13′s Reflection after the 2nd workshop, T-13-R2).

Like T13, most of these participants had no knowledge of CT.

As a result, many participants like T-17 and T-12 appreciated the informal learning activities.

Hands-on participation in these PDP workshops made me confident, aware of my own ability to decompose real-world problems. T-17-I(interview) require concrete experience to build the conceptual understanding of CT. T-12-R3.

These teachers explained how their hands-on activities and concrete experiences helped them develop their CT understanding and skills and apply them (e.g., decompose real-world problems).

These teachers’ low initial CT competence inclined them toward teaching with unplugged CT activities. For example, T-11 said I love the concept that CT can be implemented through unplugged activities and I am very confident with unplugged pedagogy of teaching CT concepts T-11-I.

I am going to apply unplugged CT in my class with 3-4-year-old students. T-12-R2.

Like many of these teachers, T-19 and T-12 enthusiastically embraced teaching CT to their young students with unplugged activities. As indicated in the above statistics, teachers reported greater CT teaching self-efficacy for using unplugged rather than plugged activities.

Hence, collaborative planning and the introduction of new education materials and technologies were critical to some teachers using them to teach their students via plugged activities. For example, T-9 said:

Collaborative planning enhanced our collective knowledge of CT and in the future, it will help us to enhance our CT practice through collaborative efforts such as planning, development of resources, assessments etc. T-9-I.

T-9 argued that the collaborative planning both improved their understanding of CT and aids their subsequent CT teaching practices. T-4 explained how she used the provided technologies to teach her students.

Happy-Map activities are very good when it comes to teaching CT concepts to my K1s, I used Happy-Map step by step guide and next week I introduced the same CT conceptual understanding to find treasure map using Beebots. Students were able to apply the understanding learned through Happy-Map. T-4-R3.

T-4 appreciated the PDP-provided teaching resources (Happy-Map) and technologies (Beebots), using them in her school lessons to help her students learn CT concepts.

T-2-I added:

The supplied and developed educational material during collaborative planning will help me use the websites etc. to develop my skills further after this training programme.

T-2 reported that the PDP educational material was not only immediately useful but also valuable for her continuing education after completing the PDP.

Like T-4, T-17 and T-24 valued the opportunities to apply their new CT knowledge and teaching skills directly to student lessons to help them learn.

This is not only to enhance their logical thinking but also to give them opportunities to develop higher-order thinking skills through CT. For example, when I asked one of my K3 students using Cubetto, what to do when we finish our command buttons. The student replied start using numbers for the commands that need to repeat so that we can reach treasure without losing command buttons. It was exactly the “loop” conceptual understanding of CT. T-17-I.

T-17 appreciated how her students developed higher-order thinking skills via CT activities with Cubetto, as illustrated via her students’ loop understanding and application.

T-24 highlighted the importance of such opportunities between workshops.

I have learned more and clarified my concepts as I get a chance to use the learned new knowledge through workshops in practice for a couple of weeks after workshops. This has given me a chance to reflect on practice and ask for clarification to consolidate my understanding before the next workshop. T-24-R6.

The long spacing between workshops offered these teachers the opportunities to apply their CT teaching to their students, reflect on the results, ask for help and consolidate their understanding before additional learning in the next workshop.

Need for Further Support

Still, these teachers highlighted the need for additional support, including time, management, resources, networking across schools, and parent understanding. T-9 highlighted the importance of time.

Time for planning and execution is the most crucial aspect as we lack experience and understanding required to execute CT. After implementation of CT integrated activities in short summer camp will help us to enhance our practice. T-9-R5.

T-9 appreciated the valuable time used for planning and implementing lessons during summer camp, especially as novices.

T-16 noted the importance of management and resources.

It is necessary to have management onboard to provide us budgetary solutions as our school lacks robots and digital devices to develop plugged CT. T-16-R6.

As T-16 notes, supportive managers can provide budget funding to buy needed CT resources such as robots and digital devices.

Also, T-2 argues for the importance of networking.

Networking support with other kindergartens integrating CT in practice will be an additional way for continues development of CT enhanced curriculum. T-2-I.

Specifically, T-2 noted that networking with other schools teaching CT can support their continuing CT development, especially of their curricula.

Outside school, T-23 pointed out the importance of parents.

Development of parental understanding alongside with teacher development is equally important. We will be bringing parents onboard for CT enhanced practices. T-23-I.

T-23 highlighted the value of parental support, and will engage them to back their CT teaching.

Discussion

This exploratory study examined the effects of a curriculum-based professional learning (CBPL) professional development program on 25 in-service teachers’ views of computational thinking (CT). After the workshops, their CT understanding, CT beliefs, CT attitudes, and CT self-efficacies improved both significantly and substantially. Among these teachers, those who reported a stronger school culture of sharing and teamwork, or sufficient school resources for CT activities showed greater CT self-efficacies. Teachers reporting greater CT knowledge had greater CT self-efficacies.

Pre- vs. Post-workshop Differences

The result suggest that these workshops changed not only these teachers’ CT knowledge and CT attitudes but also their CT beliefs and CT teaching self-efficacies.

CT Knowledge

After completing the workshops, these teachers were far more likely to define CT as including an algorithmic solution of a problem, analytic ability, solving problems as a computer scientist, logical problem solving, or general problem-solving. So, after the workshops, these teachers were much more likely to believe that they knew (a) what CT is, (b) steps for teaching CT effectively, (c) CT well enough to teach it to young children, and (d) unplugged CT well enough to teach it. These large differences support those of past studies showing that PDPs can help teachers learn about CT (e.g., Ketelhut et al., 2020; Rich et al., 2021b). Unlike past studies of shorter PDP, this study showed that after this longer PDP, these teachers were more likely than before to view themselves as having enough knowledge of CT and CT pedagogy to teach to young children. Together, these studies indicate that PDPs can effectively help teachers learn CT knowledge and pedagogy, suggesting that educators can use effective PDPs for in-service teachers’ training regarding CT knowledge.

CT Attitudes

After these workshops, these teachers reported better attitudes toward teaching than before, especially regarding CT teaching. Specifically, they reported greater interest in CT teaching, a desire to continually find better ways to teach CT, and a desire to attend training about teaching practices. These results cohere with those of past studies showing that PDPs can improve teachers’ attitudes toward CT teaching (e.g., Bower et al., 2017; Hestness et al., 2018; Rich et al., 2021b). Together, these results suggest that educators can use effective PDPs to improve teacher attitudes toward CT teaching.

CT Beliefs

After completing these workshops, these teachers were more likely to have beliefs supporting CT teaching than before. Specifically, they were more likely to believe that (a) all students should learn CT and (b) effective teaching helps students learn CT. Unlike past studies of shorter PDPs that failed to change teachers’ CT beliefs (Rich et al., 2021b), this study showed that after this longer PDP, these teachers espoused supportive beliefs of CT teaching. If future studies replicate this result, they would suggest that educators can use effective PDPs to foster supportive teacher beliefs toward CT teaching.

CT Teaching Self-Efficacies

After these workshops, these teachers reported greater CT teaching self-efficacies than before. Specifically, they reported greater overall CT teaching self-efficacy, plugged CT teaching self-efficacy, and unplugged CT teaching self-efficacy than before., this study showed that after this longer PDP, teachers reported greater CT teaching self-efficacies. If future studies support this result, they would suggest that educators can use effective PDPs to increase teachers’ CT teaching self-efficacies.

Explanatory Model of CT Teaching Self-Efficacies

School, workshop completion and teacher’s CT knowledge were all linked to CT teaching self-efficacies. In the school with a greater sharing and teamwork culture or sufficient resources to support CT teaching, teachers reported greater overall and plugged CT teaching self-efficacies. These results suggest the importance of school culture and resources for supporting CT teaching. Also, workshop completion was linked to greater unplugged CT teaching self-efficacy. Unlike past studies of shorter PDPs (Rich et al., 2021b), this longer PDP increased teachers’ unplugged CT self-efficacy. Lastly, teachers who reported greater CT knowledge reported greater overall, plugged, and unplugged CT teaching self-efficacies, cohering with past studies regarding the importance of teacher CT knowledge for CT teaching self-efficacy (Rich et al., 2021b).

Insight Into Future PDP Design Choices

These teachers shared several insights regarding effective PDP and further needs. As many of them knew little CT, they appreciated the importance of concrete activities, educational resources, collaboration, teaching CT with unplugged activities, and enough time between workshops to apply CT. First, the concrete activities, educational resources, and collaboration helped these teachers learn an alien topic, CT. The collaborative planning helped them develop and apply CT teaching activities to their own students, especially the transitional instruction of teaching CT with unplugged activities to their students before doing so with plugged activities. Suitable spacing between workshops also enabled these teachers to apply their CT, ask for help and consolidate before the next workshop. Hence, future PDPs can consider including concrete activities, educational resources, collaboration, transitional instruction, and suitable spacing between workshops.

These teachers highlighted the need for additional support regarding time, management, resources, networking, and parents. Sufficient time allowed teachers to collaboratively learn, plan, implement and assess their newly learned CT. Furthermore, management support can provide them with such time and needed resources (technology, staff) to teach CT well. Beyond their school walls, networking with other schools teaching CT (, with researchers) and with parents can build broad community support and understanding of CT and CT instruction.

Limitations and Future Research

Our study is limited by its small, unrepresentative, convenience sample of Hong Kong ECE teachers and its absence of a control group. The small sample limits our statistical power to detect smaller effect sizes. Furthermore, this study only included 2 schools, so we need studies with many more schools to determine whether these school differences are idiosyncratic or occur more broadly. Also, our unrepresentative sample of only ECE teachers in Hong Kong limits the potential of this study to generalize to the broader population of ECE teachers. Hence, future studies can include larger, representative samples of ECE teachers in more schools in more countries. Also, this study lacked a control group, which limits causal claims, so future studies can employ randomized, controlled trials to support stronger causal claims.

Conclusion

This exploratory study showed that a curriculum-based professional learning professional development program changed these in-service teachers’ views of computational thinking (CT). After the workshops, their CT understanding changed significantly. After completing the workshops, these teachers were more likely than before to define CT as including the algorithmic solution of a problem, analytic ability, solving problems as a computer scientist, logical problem solving, or general problem-solving. After these workshops, these teachers were more likely than before to believe that they knew (a) what CT is, (b) steps for teaching CT effectively, (c) CT well enough to teach it to young children, and (d) unplugged CT well enough to teach it.

These workshops also changed their CT beliefs, CT attitudes, and CT self-efficacies. After these workshops, these teachers reported better attitudes toward teaching than before: greater interest in CT teaching, greater desire to continually find better ways to teach CT, and greater desire to attend training about teaching practices. Compared to before these workshops, these teachers were more likely than before to have beliefs supporting CT teaching: (a) all students should learn CT and (b) effective teaching helps students learn CT. After these workshops, these teachers reported greater overall, plugged, and unplugged CT teaching self-efficacies.

School, workshop completion and teacher’s CT knowledge were all linked to CT teaching self-efficacies. In the school with a greater sharing and teamwork culture or sufficient resources to support CT teaching, teachers reported greater overall and plugged CT teaching self-efficacies. Also, teachers who reported greater CT knowledge reported greater overall, plugged, and unplugged CT teaching self-efficacies.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Ethics Statement

The studies involving human participants were reviewed and approved by The Education University of Hong Kong. The patients/participants provided their written informed consent to participate in this study.

Author Contributions

AS contributed to the conception and design of the study and wrote the first draft of the manuscript. MC performed the statistical analysis. Both authors organized the database, wrote sections of the manuscript, and contributed to the manuscript revision, read, and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akinyemi, A. F., and Nkonki, V. (2020). Partnership in communities of practice towards teachers’ professional development. Acad. J. Interdiscip. Stud. 9, 34–34. doi: 10.36941/ajis-2020-0109

CrossRef Full Text | Google Scholar

Angeli, C., Voogt, J., Fluck, A., Webb, M., Cox, M., Malyn-Smith, J., et al. (2016). A K-6 computational thinking curriculum framework: implications for teacher knowledge. J. Educ. Technol. Soc. 19, 47–57.

Google Scholar

Avalos, B. (2011). Teacher professional development in teaching and teacher education over ten years. Teach. Teach. Educ. 27, 10–20. doi: 10.1016/j.tate.2010.08.007

CrossRef Full Text | Google Scholar

Bairaktarova, D., Evangelou, D., Bagiati, A., and Dobbs-Oates, J. (2012). “The role of classroom artifacts in developmental engineering,” in Proceedings of 2012 ASEE Annual Conference & Exposition, (San Antonio, TX), 25–1338.

Google Scholar

Bandura, A. (1977). Self-efficacy: toward a unifying theory of behavioural change. Psychol. Rev. 84:191. doi: 10.1037//0033-295x.84.2.191

CrossRef Full Text | Google Scholar

Bandura, A. (2000). Exercise of human agency through collective efficacy. Curr. Dir. Psychol. Sci. 9, 75–78. doi: 10.1111/1467-8721.00064

CrossRef Full Text | Google Scholar

Barr, V., and Stephenson, C. (2011). Bringing computational thinking to K-12: what is involved and what is the role of the computer science education community? ACM Inroads 2, 48–54. doi: 10.1145/1929887.1929905

CrossRef Full Text | Google Scholar

Bayar, A. (2014). The components of effective professional development activities in terms of teachers’ perspective. Online Submission 6, 319–327. Google Scholar,

Google Scholar

Bell, T. (2021). CS unplugged or coding classes? Commun. ACM 64, 25–27. doi: 10.1145/3457195

CrossRef Full Text | Google Scholar

Bell, T., and Vahrenhold, J. (2018). “CS unplugged—how is it used, and does it work?,” in Adventures between Lower Bounds and Higher Altitudes, (Berlin: Springer), 497–521. doi: 10.1007/978-3-319-98355-4_29

CrossRef Full Text | Google Scholar

Bell, T., Witten, I. H., and Fellows, M. (1998). Computer Science Unplugged: Off-line Activities and Games for All Ages. Computer Science Unplugged. Available online at: https://www.csunplugged.org/en/

Google Scholar

Benjamini, Y., Krieger, A. M., and Yekutieli, D. (2006). Adaptive linear step-up procedures that control the false discovery rate. Biometrika 93, 491–507. doi: 10.1093/biomet/93.3.491

CrossRef Full Text | Google Scholar

Bers, M. U., Flannery, L., Kazakoff, E. R., and Sullivan, A. (2014). Computational thinking and tinkering: exploration of an early childhood robotics curriculum. Comput. Educ.72, 145–157. doi: 10.1016/j.compedu.2013.10.020

CrossRef Full Text | Google Scholar

Bertsekas, D. P. (2014). Constrained Optimization and Lagrange Multiplier Methods. New York, NY: Academic.

Google Scholar

Bertrand, M., Duflo, E., and Mullainathan, S. (2004). How much should we trust differences-in- differences estimates? Quart. J. Econ. 119, 249–275. doi: 10.1162/003355304772839588

CrossRef Full Text | Google Scholar

Bower, M., Wood, L. N., Lai, J. W., Highfield, K., Veal, J., Howe, C., et al. (2017). Improving the computational thinking pedagogical capabilities of school teachers. Aust. J. Teach. Educ. 42, 53–72. doi: 10.14221/ajte.2017v42n3.4

CrossRef Full Text | Google Scholar

Braun, V., and Clarke, V. (2006). Using thematic analysis in psychology. Qual. Res. Psychol. 3, 77–101. doi: 10.1191/1478088706qp063oa

PubMed Abstract | CrossRef Full Text | Google Scholar

Brennan, K., and Resnick, M. (2012). “New frameworks for studying and assessing the development of computational thinking,” in Proceedings of the 2012 Annual Meeting of the American Educational Research Association, Vol. 1, (Vancouver, BC), 25 Google Scholar.

Google Scholar

Bull, G., Garofalo, J., and Hguyen, N. R. (2020). Thinking about computational thinking: origins of computational thinking in educational computing. J. Digit. Learn. Teach. Educ. 36, 6–18.

Google Scholar

Corradini, I., Lodi, M., and Nardelli, E. (2018). “An investigation of italian primary school teachers’ views on coding and programming,” in In Proceeedings of International Conference on Informatics in Schools: Situation, Evolution, and Perspectives, (Petersburg), 228–243. doi: 10.1007/978-3-030-02750-6_18

CrossRef Full Text | Google Scholar

Creswell, J. W. (2012). Educational Research: Planning, Conducting and Evaluating Quiantitative and Qualitative Research, 4th Editio Edn. London: Pearson.

Google Scholar

Csizmadia, A., Standl, B., and Waite, J. (2019). Integrating the constructionist learning theory with computational thinking classroom activities. Inform. Educ. 18, 41–67. doi: 10.15388/infedu.2019.03

CrossRef Full Text | Google Scholar

Darling-Hammond, L., and Richardson, N. (2009). Research review/teacher learning: what matters. Educ. Leadersh. 66, 46–53. Google Scholar,

Google Scholar

Dori, Y. J., and Herscovitz, O. (2005). Case-based long-term professional development of science teachers. Int. J. Sci. Educ. 27, 1413–1446. doi: 10.1080/09500690500102946

CrossRef Full Text | Google Scholar

Fields, D. A., Lui, D., and Kafai, Y. B. (2019). “Teaching computational thinking with electronic textiles: modeling iterative practices and supporting personal projects in exploring computer science,” in Computational Thinking Education, (Berlin: Springer), 279–294. doi: 10.1007/978-981-13-6528-7

CrossRef Full Text | Google Scholar

Fraenkel, J. R., Wallen, N. E., and Hyun, H. H. (2015). “The nature of research,” in How to Design and Evaluate Research in Education, (New York, NY: McGraw-Hill Education), 1–26.

Google Scholar

Goldstein, H. (2011). Multilevel Statistical Models. Sydney: Edward Arnold.

Google Scholar

Gretter, S., and Yadav, A. (2016). Computational thinking and media & information literacy: an integrated approach to teaching twenty-first-century skills. TechTrends 60, 510–516. doi: 10.1007/s11528-016-0098-4

CrossRef Full Text | Google Scholar

Hestness, E., Ketelhut, D. J., McGinnis, J. R., and Plane, J. (2018). Professional knowledge building within an elementary teacher professional development experience on computational thinking in science education. J. Technol. Teach. Educ. 26, 411–435. doi: 10.1186/s12913-016-1423-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Hox, J. J., Moerbeek, M., and Van de Schoot, R. (2017). Multilevel Analysis: Techniques and applications. New York, NY: Routledge.

Google Scholar

Huang, W., and Looi, C. K. (2021). A critical review of literature on “unplugged” pedagogies in K-12 computer science and computational thinking education. Comput. Sci. Educ. 31, 83–111. doi: 10.1080/08993408.2020.1789411

CrossRef Full Text | Google Scholar

Kemp, J. E. (1985). The Instructional Design Process. New York, NY: Harpercollins College Division.

Google Scholar

Kennedy, P. (2008). Guide to Econometrics. New York, NY: Wiley-Blackwell.

Google Scholar

Ketelhut, D. J., Mills, K., Hestness, E., Cabrera, L., Plane, J., and McGinnis, J. R. (2020). Teacherthinking into elementary science. J. Sci.Educ. Technol. 29, 174–188. doi: 10.1007/s10956-019-09798-4

CrossRef Full Text | Google Scholar

Kermani, H., and Aldemir, J. (2015). Preparing children for success: integrating science, math, and technology in early childhood classroom. Early Child. Dev. Care 185, 1504–1527. doi: 10.1080/03004430.2015.1007371

CrossRef Full Text | Google Scholar

Konstantopoulos, S. (2008). The power of the test in three-level cluster-randomized designs. J. Res. Educ. Eff. 1, 66–88. doi: 10.1080/19345740701692522

CrossRef Full Text | Google Scholar

Kotsopoulos, D., Floyd, L., Dickson, B. A., Nelson, V., and Makosz, S. (2021). Noticing and naming computational thinking during play. Early Child. Educ. J. 50, 1–10.

Google Scholar

Lassonde, C. A., and Israel, S. E. (2009). Teacher Collaboration for Professional Learning: Facilitating Study, Research, and Inquiry Communities. New Jersey, NJ: John Wiley & Sons, doi: 10.1002/9781118269442

CrossRef Full Text | Google Scholar

Lee, V. R., and Recker, M. (2018). Paper circuits: a tangible, low threshold, low-cost entry to computational thinking. TechTrends 62, 197–203. doi: 10.1007/s11528-017-0248-3

CrossRef Full Text | Google Scholar

Li, Y., Schoenfeld, A. H., Graesser, A. C., Benson, L. C., English, L. D., and Duschl, R. A. (2020). On computational thinking and STEM education. J. STEM Educ. Res. 3, 147–166. doi: 10.1007/s41979-020-00044-w

CrossRef Full Text | Google Scholar

MacKinnon, D. P., Lockwood, C. M., and Williams, J. (2004). Confidence limits for the indirect effect: distribution of the product and resampling methods. Multivariate Behav. Res. 39, 99–128. doi: 10.1207/s15327906mbr3901_4

CrossRef Full Text | Google Scholar

Melasalmi, A., and Husu, J. (2016). The content and implementation of shared professional knowledge in early childhood education. Early Years 36, 426–439.

Google Scholar

Merrill, M. D. (2002). First principles of instruction. Educ. Tech. Res. Dev. 50, 43–59.

Google Scholar

Mishra, P., and Koehler, M. J. (2006). Technological pedagogical content knowledge: a framework for teacher knowledge. Teach. Coll. Rec. 108, 1017–1054.

Google Scholar

Palts, T., and Pedaste, M. (2020). A model for developing computational thinking skills. Inf. Educ. 19, 113–128. doi: 10.15388/infedu.2020.06

CrossRef Full Text | Google Scholar

Rich, P. J., Larsen, R. A., and Mason, S. L. (2021a). Measuring teacher beliefs about coding and computational thinking. J. Res.Technol. Educ. 53, 296–316.

Google Scholar

Rich, P. J., Mason, S. L., and O’Leary, J. (2021b). Measuring the effect of continuous professional development on elementary teachers’ self-efficacy to teach coding and computational thinking. Comput. Educ. 168:104196. doi: 10.1016/j.compedu.2021.104196

CrossRef Full Text | Google Scholar

Sands, P., Yadav, A., and Good, J. (2018). “Computational thinking in K-12,” in Service Teacher Perceptions Of Computational Thinking. In Computational Thinking in the STEM Disciplines, ed. M. S. Khine (Berlin: Springer), 151–164. Google Scholar. doi: 10.1007/978-3-319-93566-9_8

CrossRef Full Text | Google Scholar

Seow, P., Looi, C., How, M., Wadhwa, B., and Wu, L. (2019). “Educational policy and implementation of computational thinking and programming: case study of Singapore,” in Computational Thinking Education, eds S. C. Kong and H. Abelson (Singapore: Springer Open), 345–362.

Google Scholar

Short, J., and Hirsh, S. (2020). The Elements: Transforming Teaching through Curriculum-Based Professional Learning. New York, NY: Carnegie Corporation of New York. Web Copy.

Google Scholar

Villegas-Reimers, E. (2003). Teacher Professional Development: An International Review of the Literature. Paris: International Institute for Educational Planning. Google Scholar.

Google Scholar

Wong, J. L., and Tsui, A. B. (2007). How do teachers view the effects of school-based in-service learning activities? a case study in China. J. Educ. Teach. 33, 457–470. doi: 10.1080/02607470701603290

CrossRef Full Text | Google Scholar

Yadav, A., Gretter, S., Good, J., and McLean, T. (2017). “Computational thinking in teacher education,” in Emerging Research, Practice, and Policy on Computational Thinking, eds P. J. Rich and C. B. Hodges (Berlin: Springer), 205–220. doi: 10.1007/978-3-319-52691-1_13

CrossRef Full Text | Google Scholar

Appendix A: Ancillary Results

APPENDIX TABLE A1

Appendix Table A1. Correlations, variances, and covariances of outcomes and significant explanatory variables in the lower left, diagonal and upper right matrices.