- Department of Educational Sociology, Danish School of Education, Aarhus University, Aarhus, Denmark
This study investigated the role of social contexts for gender disparities in education by examining the associations between gender-stereotypical beliefs (GSB) of students, peers, and teachers and gender achievement patterns in the classroom and students’ self-concept in language and math. We applied multilevel models with school fixed effects to a unique sample of combined survey and register data from Denmark to analyze detailed learning environments within schools and their correlations with gender differences in self-concept across subject domains. Results showed a gender gap in favor of boys in mathematics, net of academic achievement that were consistent across classrooms. In language, the influence of gender varied across classrooms. Furthermore, although GSB and gender achievement patterns did not alter the gender gap in either language or mathematics, we found that they moderated the relationship between gender and self-concept in heterogeneous ways across subjects. While teachers’ GSB increased the gender gap in language by decreasing boys’ self-concept, the students’ own GSB was more important for students’ self-concept in mathematics. Moreover, girls’ mathematics self-concept was lower in classrooms, in which, female peers had a relatively higher level of mathematics achievement compared to boys, suggesting that counter-stereotypical achievement patterns in the classroom do not increase students’ self-concept in subjects with strong gender stereotypes. On the contrary, girls are most likely to compare themselves to female peers, resulting in a negative association with self-evaluations. Our results highlighted the role played by social contexts in schools in the generation of gender differences in self-concept in traditionally stereotyped subject domains, but also showed important differences in how boys and girls were affected by their learning environments across different subject domains, suggesting there are different mechanisms at play.
Introduction
Recent decades have seen considerable change in patterns of gender disparities in education. Two notable tendencies are evident and contribute to a complex pattern of vertical and horizontal gender inequality. On the one hand, women have increased their levels of participation in tertiary education and have now surpassed men in terms of educational attainment, both in the United States (DiPrete and Buchmann, 2013) and in most European countries (Vincent-Lancrin, 2008). Furthermore, studies have shown that female students outperform male students in most subject domains, particularly in language (Voyer and Voyer, 2014; Reilly et al., 2019). However, while female students a few decades ago had almost universally lower academic achievement in STEM (Science, Technology, Engineering, and Math)-related subjects compared to male students (Reilly, 2012), there has been a slight decline in the number of countries with gender achievement gaps in mathematics (Hyde et al., 2008; Else-Quest et al., 2010; OECD, 2019) and the gender gap in science now favors girls in most countries (Neuschmidt et al., 2008; Mullis et al., 2020). On the other hand, despite women’s higher levels of vertical educational attainment, strong horizontal gender segregation persists. Accordingly, women remain underrepresented in most STEM fields and particularly within math-intensive fields (UNESCO, 2017; McNally, 2020). Whether horizontal segregation constitutes a problem is open to debate. Nevertheless, research has suggested that horizontal segregation, beginning as early as in upper secondary education, is linked to subsequent inequality in the labor market, with math-intensive tracks providing the greatest advantages (Birkelund et al., 2021).
An important conclusion from prior research is that disparity in academic and educational outcomes do not reflect inherent gender differences, but are a result of culturally embedded gender beliefs in the form of stereotypes—that is, a belief or set of beliefs regarding the characteristics, attributes, or behaviors of a particular group or category of people (Hilton and Von Hippel, 1996). Empirical research has shown that gender disparities in prior academic achievement cannot alone explain gender differences in entry to STEM fields (Riegle-Crumb et al., 2012). Combined with variations in gender disparities in educational outcomes across national contexts and cohorts (Penner, 2008), these findings support sociological theories on the social nature of gender. Although gender can be perceived as a social structure with importance for educational stratification (Risman, 2004; England, 2010), gender is not a fixed category, but a social construction constituted through a multilayered system of macro-level structures and cultural beliefs, as well as micro-level contexts of personal interactions and exchanges (Correll, 2004; Ridgeway and Correll, 2004). Accordingly, it has been suggested that gender is likely to be more salient in some social interactions than in others and different social settings may activate certain stereotypes or social scripts regarding gender identity and achievement (Ridgeway, 2009). So far, research has tended to focus on a specific dimension of gender differences (e.g., boys’ lower reading scores or girls’ under-representation in STEM), thus, providing important yet narrow explanations for the existence of such differences (Legewie and DiPrete, 2014; Mann et al., 2015; Retelsdorf et al., 2015; Riegle-Crumb and Morton, 2017; Muntoni and Retelsdorf, 2018). Thus, there is a shortage of theoretical explanations covering the broad constellation of gender differences and similarities in terms of educational outcomes, as well as empirical research investigating the social construction of gender identity and inequality in social contexts (Riegle-Crumb et al., 2018). Moreover, we currently have limited knowledge of the presence and variability of cultural gender beliefs and stereotypes across different school contexts characterized by diverse achievement-related gender structures and how they may shape gender disparities in competence beliefs of male and female students.
To address this gap, this paper investigates the role of school contexts in students’ competence beliefs in traditionally gendered subjects. Previous research has shown that students’ competence beliefs – or academic self-concept – are key factors in predicting educational behavior (Wigfield and Eccles, 2000) and documented the existence of gender gaps in self-concept in different academic subjects in line with traditional gendered patterns. While boys typically hold more positive self-concepts in mathematics (Goldman and Penner, 2016) and science (Sikora and Pokropek, 2012), girls typically hold more positive self-concepts in language (Jacobs et al., 2002), net of actual achievement. Building on psychological and sociological research, we focused on two determinants of competence beliefs that potentially generate gendered patterns in attainment. First, we examined the role of gender-stereotypical beliefs (GSB). Girls generally hold lower self-concepts than boys at equal ability levels (Correll, 2001) and it has been suggested that self-concept is an expression of internalized gender beliefs (Charles and Bradley, 2009; Eccles, 2011; Breda et al., 2020). Accordingly, if a girl believes that boys are more competent in mathematics, she might view mathematical competence as inconsistent with female gender identity and thus, doubt her mathematical ability. Indeed, research has shown associations between gender stereotypes and students’ self-concept in the traditionally male-dominated subject of mathematics (Riegle-Crumb and Peng, 2021) and the traditionally female-dominated subject of reading (Retelsdorf et al., 2015; Muntoni et al., 2021). Second, we investigated whether gender-stereotypical achievement patterns in the classroom affected the competence beliefs of male (female) students in mathematics (language) and the extent to which counter-stereotypical achievement reduced gender gaps in self-concept across gender-stereotypical subject domains.
We applied multilevel models to combined survey and register data on 1,099 Danish compulsory school students and their respective language and mathematics teachers to investigate how GSB in the classroom influence students’ self-concept in language and mathematics. Our study contributes and adds to the existing body of research in three specific ways. First, unlike most previous research, which has typically focused on gender stereotypes among either students, peers, or teachers, we used a unique data set that includes all three dimensions. Combined with the fact that our data was sampled at the classroom level, we were able to investigate very rich variations in GSB within and across different social contexts in schools. Second, we expand on previous research on GSB in schools by also including information on gender-achievement patterns in classrooms. While gender beliefs are one important dimension of the classroom environment, another is the relative achievement of male/female students across different subject domains. To the best of our knowledge, research on the influence of gender-achievement patterns in the classroom on gender differences has been limited or non-existent. We believe that this is an important dimension of the social context in schools with possible implications for the construction of gender and inequality across classrooms. Third, we added to prior research on the role of peers in terms of students’ educational outcomes in general and gender differences in domain-specific self-concept, in particular, by distinguishing between male and female peers. This distinction was motivated by empirical research that has shown that STEM-related outcomes and course-taking in high school are influenced by same-gender friendships (Riegle-Crumb et al., 2006; Raabe et al., 2019).
Theoretical Perspectives
Gender Differences in Students’ Competence Beliefs
The expectancy-value theory offers a powerful framework for understanding gender differences in students’ achievement-related behavior. According to this perspective, there are two components of students’ motivation: expectancy beliefs (e.g., competence beliefs) and task value beliefs (e.g., interest and utility) (Eccles and Wigfield, 1995). Individuals holding higher expectancy and task beliefs are more likely to pursue a specific subject. There is a degree of overlap between expectancy beliefs and the terms self-efficacy and academic self-concept, and expectancy beliefs have often been operationalized as such in empirical studies (Bong and Skaalvik, 2003; Marsh et al., 2019). Academic self-concept refers to an individual’s assessment of their ability (Wigfield and Eccles, 2000) and varies across different subject domains, such as language and mathematics (Marsh et al., 2006; Jansen et al., 2014). Students’ beliefs about their competencies most likely reflect two distinct elements: a descriptive and a normative element. On the one hand, students’ academic self-concept can be expected to reflect their actual ability. On the other hand, students evaluate their ability through a subjective lens, reflecting on social and cultural norms. Previous empirical research has supported this by showing that even when performing at the same level as their male peers, girls were less confident in their math and science abilities (Else-Quest et al., 2010).
Many scholars have investigated gender differences in students’ competence beliefs across different subject domains, as well as the sources of these differences. Findings in this field have generally reflected the culturally gendered perception of subject domains, with math as a male domain and language as a female domain, in that girls have a lower academic self-concept than boys in math domains (Goldman and Penner, 2016), while boys have a lower academic self-concept than girls in language domains (Durik et al., 2006; Ireson and Hallam, 2009). Importantly, these gender differences have often remained even when controlling for achievement. In a study using data from TIMSS 2015, Mejía-Rodríguez et al. (2021) documented the existence of a gender gap in mathematics self-concept in most participating countries, usually favoring boys. This difference in self-concept across male and female students remained after controlling for academic achievement and other covariates and was evident as early as 4th grade. However, findings have been less robust about the language self-concept of male students, with some studies finding no statistically significant gender differences (Skaalvik and Skaalvik, 2004; Evans et al., 2011). Nevertheless, boys’ self-concept, rather than their innate ability, is an important predictor of their language achievement (Heyder et al., 2017). Furthermore, girls’ self-concept in math is related to their belief in math ability as innate (i.e., a fixed mindset), whereas no such relationship has been found between boys’ self-concept in language and their beliefs about innate language ability (Heyder et al., 2021), suggesting that girls may, to a larger degree, have internalized beliefs about gender and ability.
School Contexts and the Social Construction of Gender and Competence Beliefs
According to many sociological and psychological theories, students’ achievement-related outcomes are influenced by social contexts and interactions. Specifically, sociological scholarship has repeatedly documented the centrality of social influences for gender differences in achievement-related outcomes in general (Legewie and DiPrete, 2012; Salikutluk and Heyne, 2017; Raabe et al., 2019) and gender disparities in orientations toward STEM in particular (Crosnoe et al., 2008; Legewie and DiPrete, 2014; Riegle-Crumb and Morton, 2017). Such research suggests that gender is a multi-level system that is (re-)constructed through interactions and experiences in social contexts, such as schools and classrooms, and that to better understand gender inequality we need to consider variation in such contexts (Ridgeway and Correll, 2004; Risman, 2004). The production of gender roles and positions in schools is likely a consequence of the fact that images of femininity and masculinity are socially constructed in everyday student interactions with peers and teachers, who, thus, collectively functions as active agents of gender socialization. A similar perspective can be found in Eccles (1994) expectancy-value theory, which states that socializing agents, such as peers and teachers, play an important role in shaping students’ academic self-concept. In particular, peers have been found to play an important part in gender role socialization (Witt, 2000) and, perhaps, even discourage gender non-conformity through victimization (Lamb et al., 1980; Aspenlieder et al., 2009). Moreover, same-gender peers are particularly important in shaping gendered patterns in academic outcomes, by both serving to promote gender conformity in educational decisions (Riegle-Crumb et al., 2006; Rosenqvist, 2018; Raabe et al., 2019) and serving as reference points for self-evaluations that shape competence beliefs (Thijs et al., 2010).
Gender-Stereotypical Beliefs in the Classroom
Stereotypes can be defined as reflecting “general expectations about members of particular social groups” (Ellemers, 2018, p. 276). In education, different subject domains have often been shown to be gendered. In general, math and math-related domains are stereotyped as male, while language domains are stereotyped as female (Charles and Bradley, 2009; Martinot et al., 2012; Heyder and Kessels, 2013; Nowicki and Lopata, 2017). Stereotypical expectations can reflect both actual and false differences. On the one hand, descriptive expectations reflect an observed gendered pattern, such as the mathematics achievement of boys and girls in a particular classroom, and, thus, a seemingly “true” representation of gender differences. On the other hand, expectations may reflect not only students’ actual achievement but also cultural perceptions of gender and how well-suited boys and girls are for different subject domains. Importantly, even the observed gender differences rarely reflect inherent biological gender differences, but can most often be ascribed to socialization (Ellemers, 2018). Furthermore, expectations concerning an entire social group, such as girls or boys, are often imprecise when directed at a single individual, but can still have negative consequences by reinforcing the stereotype.
The students’ own stereotypical beliefs have been shown to have a negative influence on outcomes, such as achievement and self-concept (Plante et al., 2009, 2013; Heyder and Kessels, 2013), but stereotypes often stem from significant others in social contexts. The negative consequences of being exposed to stereotypical beliefs have often been framed as a stereotype threats, which describes how exposure to stereotypical beliefs can lead to stereotypes becoming self-fulfilling prophecies (Steele, 1997). Stereotype threat has been found in controlled experimental settings for both girls in math achievement (Flore and Wicherts, 2015) and boys in language achievement (Pansu et al., 2016). However, recent studies have explored the role of stereotype threat and the generally negative impact of gender-stereotypical beliefs in the context of the classroom, emphasizing the role of the gender-stereotypical beliefs of socializing agents such as teachers and peers for various student outcomes. Specifically, factorial survey studies have found evidence of teachers’ judgment of students being biased by gender stereotypes (Holder and Kessels, 2017), while the gender-stereotypical beliefs of teachers have been found to negatively affect girls’ achievement (Alan et al., 2018) and self-concept (Heyder et al., 2019) in mathematics and boys’ self-concept (Retelsdorf et al., 2015) and achievement (Muntoni and Retelsdorf, 2018) in reading. Similarly, the gender-stereotypical beliefs of peers have been found to negatively affect girls’ achievement in math (Salikutluk and Heyne, 2017) and boys’ self-concept in reading (Muntoni et al., 2021).
Gender-Stereotypical Achievement Patterns in the Classroom
In addition to culturally embedded perceptions of gender, an important aspect of social contexts in schools is the achievement pattern in the classroom; i.e., the academic performance of a student’s peers. To understand how students form academic self-concepts and the role played by social comparison in an educational setting, (Marsh, 1987) proposed the idea of the big-fish-little-pond (BFLP) effect. According to this perspective, students compare their academic ability to that of their classroom peers when forming an academic self-concept. This implies that students in higher-achieving social contexts have lower academic self-concepts than students of similar ability in lower-achieving settings. Numerous empirical studies have supported the BFLP effect (Seaton et al., 2010; Fang et al., 2018; Loyalka et al., 2018), as well as confirmed its generalizability across cultural contexts (Seaton et al., 2010; Loyalka et al., 2018). However, research has also shown that social comparison processes differ across gender and that students’ academic self-concept is mainly affected by same-gender classmates and only to a lesser extent by different-gender peers (Thijs et al., 2010). Furthermore, in the mathematics domain, gender has been shown to moderate the BFLP effect since female students tend to be more responsive than male students to the achievement of peers (Plieninger and Dickhäuser, 2015). While previous research has provided important evidence that gender is a relevant frame of reference within classrooms, as well as of heterogeneous influences of social comparison across gender, no study, to date, has investigated how classroom achievement patterns intersect with cultural perceptions of gender and how this influences students’ evaluation of their competences. In this paper, we argue that when gender is used as a frame of reference, gender identity plays an important role in the social comparison process. In contrast to the more general BFLP perspective in which students’ self-concept is negatively affected by average peer performance, students may be positively affected by high-achieving same-sex peers because such peers can function as role models and, thus, provide counter-stereotypical evidence of gender suitability within a subject domain. Accordingly, girls may hold more positive self-concepts in mathematics if surrounded by female peers that counteract the stereotype that girls have lower ability than boys within this subject domain do. Consequently, counter-stereotypical achievement patterns potentially can disrupt gender stereotypes and how they influence students’ self-concept. We defined counter-stereotypical achievement patterns as math (language) classrooms in which female (male) students have higher average achievement than male (female) students—i.e., classrooms in which girls’ (boys’) relative achievement contradicts the stereotypical expectation. Specifically, we expected that being in a classroom, in which female peers outperform male peers in mathematics achievement could increase girls’ mathematics self-concept through identification.
The Present Study
In this study, we investigated the influence of gender on students’ self-concept within and between classroom contexts in language and mathematics, which represents traditionally stereotyped subject domains. We posed three specific research questions:
1 Is there a gender gap in students’ self-concept in language and mathematics net of actual subject-specific achievement, and does the influence of gender vary across classrooms?
2 Do students, peers, and teachers’ GSB affect gender gaps in self-concept in language and mathematics?
3 Does the gender-achievement pattern in the classroom affects gender gaps in language and mathematics self-concept?
First, based on previous research on gender gaps in education, we hypothesized that there is a gender gap in self-concept in the language (Durik et al., 2006; Ireson and Hallam, 2009) and mathematics (Goldman and Penner, 2016). Specifically, we expected girls to hold a more positive self-concept in language and boys in mathematics, net of actual achievement in the respective subjects.
H1: There is a gender gap in students’ self-concept in language and mathematics, following traditional gender-stereotypical patterns:
H1a: Girls hold more positive self-concepts compared to boys in language net of actual achievement.
H1b: Boys hold more positive self-concepts compared to girls in mathematics net of actual achievement.
Second, drawing on previous research on gender stereotypes across subject domains, we hypothesized that GSB affects gender gaps in the language (Retelsdorf et al., 2015; Muntoni et al., 2021) and mathematics (Heyder et al., 2019). Contrary to most previous research, our data included information on the GSB of students themselves as well as their peers and (subject-specific) teachers. Furthermore, due to the sampling of full classrooms, we were able to distinguish between male and female peers to examine the extent to which the influence of the GSB on same- and different-gender peers differ. Specifically, we hypothesized that GSB about the language of students, peers, and teachers would be associated with a more positive language self-concept for girls and less positive for boys. By contrast, we expected that GSB about the mathematics of students, peers, and teachers would be associated with a more positive mathematics self-concept for boys and less positive for girls.
H2: GSB in the classroom context influences gender gaps in language and mathematics:
H2a: GSB, regarding language, is associated with more positive language self-concepts for girls and less positive for boys, net of actual achievement.
H2b: GSB, regarding mathematics, is associated with more positive mathematics self-concepts for boys and less positive for girls, net of actual achievement.
Third, while one dimension of the classroom gender context is GSB, another is the specific gender-achievement pattern. Does subject-specific achievement in the classroom follow traditional gender-stereotypical patterns or is there a counter-stereotypical achievement pattern with boys (girls) outperforming girls (boys) in the language (mathematics) and with what implications for students’ self-concept? Specifically, we hypothesized that counter-stereotypical achievement patterns in the classrooms could alter gender gaps in self-concept.
H3: The specific gender-achievement pattern in the classroom influences gender gaps in language and mathematics:
H3a: Counter-stereotypical achievement in mathematics classrooms (i.e., girls outperforming boys) reduces the gender gap by increasing mathematics self-concepts among female students.
H3b: Counter-stereotypical achievement in language classrooms (i.e., boys outperforming girls) reduces the gender gap by increasing language self-concepts among male students.
Materials and Methods
Data and Sample
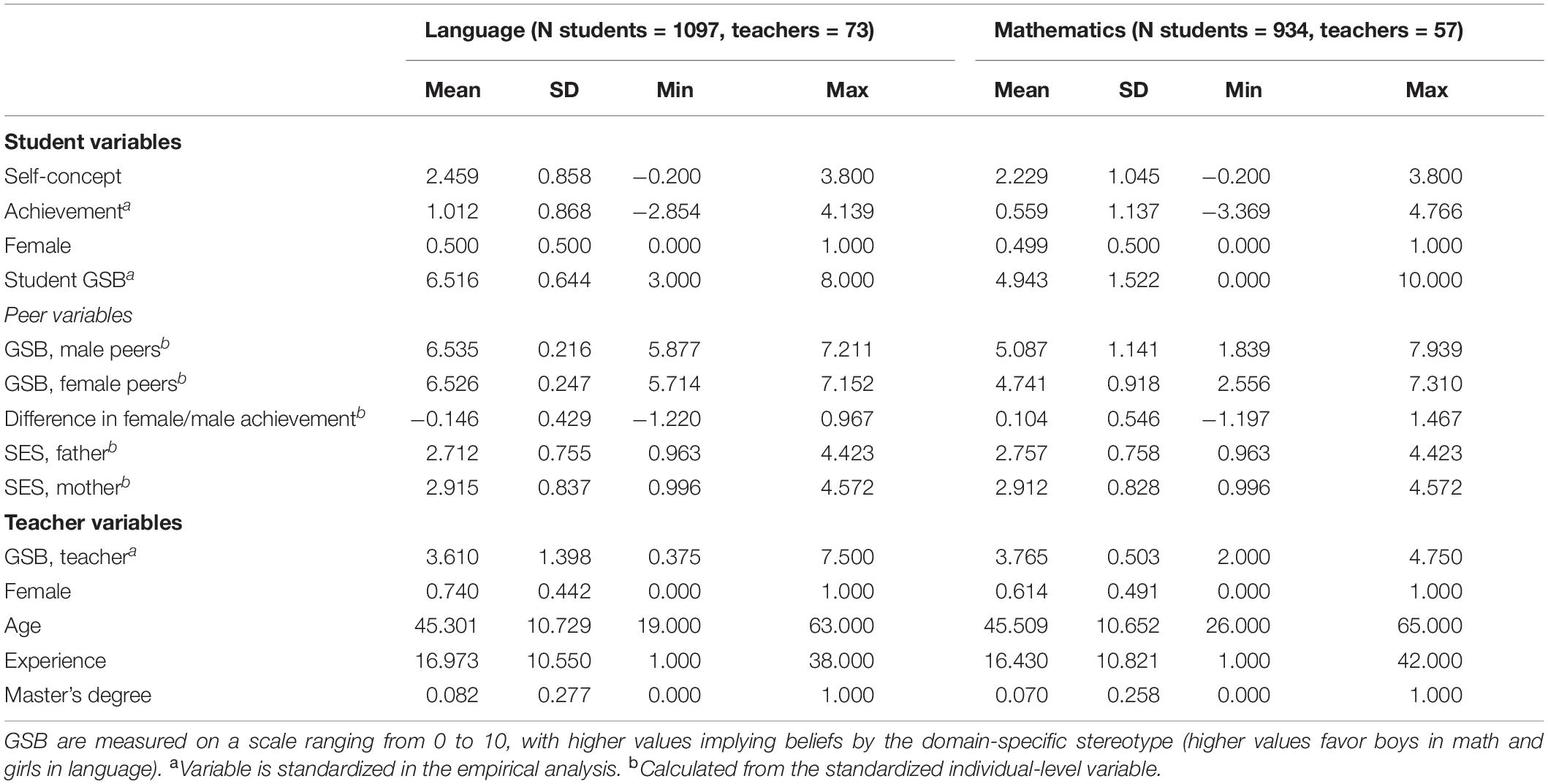
The survey was conducted in 2019 as part of the project Exploring School Culture (ESCU) at Aarhus University and included a sample of students nested in 94 classrooms at 33 Danish schools, specifically 6th (N = 1,094, response rate = 80.2%) and 9th-grade students (N = 892, response rate = 74.3%) and their teachers in Danish and mathematics (N = 143, response rate = 61.6%). Recruited schools registered their 6th and 9th-grade classrooms, and data were collected among the entire classrooms of students (for more information on recruitment and data collection, see Authors 2021). Through unique student identifiers, we were able to combine the survey data with high-quality background information on parental education, income, and occupation, as well as standardized test scores in reading and mathematics from tests conducted in the 6th and 8th grades for the 6th and 9th-grade students, respectively, from the Danish registers.
Combining survey and register data had four major advantages. First, sampling entire classrooms allowed us to analyze fine-grained gender-specific learning environments that include all students within a classroom linked to their teachers in language and mathematics, respectively, which represent two important and traditionally gender-stereotyped subject domains. Second, the data included measures of GSB at the student, classroom, and teacher levels across language and mathematics, developed from existing scales (e.g., Martinot et al., 2012) and adjusted to the Danish context, as well as detailed information on students’ achievement in the same subjects. Accordingly, contrary to most previous research on gender beliefs and stereotypes in schools, which typically focus on either students, peers, or teachers, we were able to analyze a multilevel dataset that includes all three dimensions. Third, drawing on register data allowed us to include an extensive set of control variables that were not based on students’ self-reports and were available for the entire population. Fourth, linking survey data on students’ academic self-concept to information on their actual achievement from national tests enabled us to investigate students’ self-concept in different subject domains net of actual achievement in these subjects.
Students’ Self-Concept
We measured self-concept in the language and mathematics domains based on two separate four-item scales (e.g., “I am just not good at mathematics/Danish”) answered on a five-point Likert scale. These items stemmed from the self-concept measure from the Programme for International Student Assessment 2012 (OECD, 2013), reworked to also fit the Danish language domain. The scales exhibited high internal consistency, as indicated by Cronbach’s alpha for both mathematics (9th-grade α = 0.93 and 6th-grade α = 0.90) and language (9th-grade α = 0.90 and 6th-grade α = 0.87). See Appendix Table 1 for the full list of items. In our analyses, we estimated the gender gap in self-concept as the coefficient for the gender variable in a model predicting the self-concept.
Independent Variables
Student-Level Variables
We used test scores from nationally administered mandatory high-stakes standardized tests to measure student achievement in both subjects. The tests were adaptive; i.e., items were adapted to match students’ competence level based on previous responses. For 6th-grade students, the test was taken in the spring of 2019, at the same time as the survey was conducted, while for the 9th-grade students, the test was taken the previous year when they were in 8th grade.
The measures of domain-specific GSB were based on items about perceived differences in ability and attitudes from the “mathematics as a gendered domain” scale (Leder and Forgasz, 2002). Items were translated to Danish and reworked to present general statements that respondents could connect to either boys or girls. Specifically, respondents reacted to seven statements (e.g., “The weakest students in mathematics/Danish are…”) by indicating whether this is most true for girls or boys on an 11-point scale with “primarily girls” at the one extreme (0) and “primarily boys” at the other (10), with a neutral category in the middle (5). The broad scope of the measure sought to capture beliefs that go beyond observed gender differences in achievement. The stereotype scales displayed high internal consistency, with Cronbach’s alpha for mathematics (9th grade α = 0.89 and 6th grade α = 0.85) and language (9th grade α = 0.92 and 6th grade α = 0.87). For the analyses, both GSB measures were coded, so that a higher score indicated beliefs in line with the common stereotype (i.e., favoring boys in mathematics and girls in language). See Appendix Table 2 for the full list of items.
Classroom-Level Variables
We included several explanatory variables at the classroom level based on teacher and peer measures. For teachers, we included a measure of GSB corresponding to the one described for students above. Specifically, this measure was based on seven corresponding items that were answered in the same way as for the students. The internal consistency was acceptable for mathematics (α = 0.71) and high for language (α = 0.92).
For the peer group, we included measures of GSB, mean achievement, and differences in achievement between female and male peers. The peer GSB measure was calculated as the mean of the student GSB scales at the classroom level for each subject and male and female students separately. Peer achievement was calculated as the mean achievement of students at the classroom level. The individual student was excluded when calculating peer variables, to avoid including the student in their peer group.
Finally, we calculated the gender-specific achievement pattern in the classroom using the difference between female and male achievement in mathematics (female achievement minus male achievement), meaning that a positive score on this variable indicated that the female peer group outperformed the male peer group in the classroom. For language, we did the opposite (i.e., male achievement minus female achievement), meaning that a positive score indicated that the male peer group outperformed the female peer group. Controlling for the classroom-specific gender difference in achievement also served to remove residual variance in the GSB measures that simply reflected the observed gender-achievement patterns in the classroom.
Control Variables
As previous research has indicated an association between socioeconomic status (SES) and GSB (Davis, 2007; Cotter et al., 2011; Pampel, 2011), we controlled for SES at both the individual and classroom levels. We measured the SES of the student’s father and mother individually through a composite measure of income (in quartiles), years of education, and occupation (four categories: self-employed, employed, student, and unemployed). We combined these measures by deriving polychoric factor scores (Holgado-Tello et al., 2010). For the SES of both father and mother, we aggregated at the classroom level to calculate a measure of peer SES, while excluding the individual student, as for the other peer variables.
To control for spurious associations with teacher GSB, we included controls for teacher characteristics: gender, age in years, education (a dummy indicating whether they hold a master’s degree), and teaching experience in years. Table 1 presents an overview of unstandardized variables included in the analyses. For descriptive statistics by gender, see Appendix Tables 3, 4.
Notably, teacher GSB was generally lower than student and peer GSB, suggesting that either teacher were less inclined to hold stereotypical beliefs or that teachers were more inclined to social desirability bias than were the students. Nevertheless, the GSB of teachers generally showed a statistically significant positive correlation with those of students and peers (see Appendix Tables 5, 6 in the Appendix for correlation matrices). Notably, however, female peers’ GSB and teacher GSB in language were negatively correlated, suggesting that the girls held lower GSB in language, regardless of the GSB of their teacher.
Analytical Strategy
To test our hypotheses, we analyzed data using a linear multilevel regression model consisting of two levels: students (level 1) and classrooms (level 2). The multilevel framework had several advantages in this context. First, the multilevel strategy allowed us to obtain unbiased standard errors from our hierarchical data, despite violating the principle of independent sampling of observations. Second, we were able to partition the variance in self-concept into student-level and classroom-level variance components, allowing us to determine and study the variance that can be attributed to the social context of the classroom. Third, we tested whether the effect of gender on self-concept varied across the classroom context; i.e., if the impact of gender on a student’s competence beliefs depended on the social context of the classroom. We examined this for both language and mathematics self-concept by fitting a random slope for gender and testing this more elaborate model against a simpler random intercept model using a likelihood ratio test.
Finally, while our data contained three levels (students nested in classrooms that were nested in schools), our research questions focused on the first two levels. Therefore, we treated the school level as incidental in our models by adding dummy indicators for each school. This corresponded to a school fixed effects approach, which has previously been used in similar analyses (McNeish and Wentzel, 2017). Besides being a strategy for modeling the school level, the fixed effects approach had the added benefit of significantly reducing selection bias by taking into account selection processes in schools, which may otherwise have biased our estimates. This strategy is valid under the assumption that there is the limited systematic selection of students into classrooms within schools—i.e., that classrooms are formed more or less at random (for a similar argument see Ammermueller and Pischke, 2009). Although we cannot completely rule out the selection at the school level, the strategy is realistic in the Danish context, where schools sought to create equal classrooms by “balancing” resources. This particular characteristic of the Danish compulsory school system implies very limited selection within schools and, at worst, a selection process that can be characterized as negative; i.e., “better” and more experienced teachers tend to be allocated to more disadvantaged classrooms, which would yield conservative estimates (for elaboration see Andersen and Reimer, 2019).
All models were estimated separately for each subject. For the analyses, we group-mean centered all student-level variables and grand-mean centered all classroom-level variables. All analyses were carried out using Stata version 17.
Missing values in our data occurred mainly at the teacher level due to non-response. For language, teacher non-response reduced our sample by 17% and for mathematics by 36%. Due to teacher non-response, we had no information to impute teacher variables. Therefore, we chose a listwise deletion approach to handle missing values. We also excluded classrooms with less than eight student responses. This resulted in an analytical sample of 1,097 students for language and 934 students for mathematics.
Results
We present results from our empirical analysis in three steps. First, we investigated whether or not students’ self-concept differed across classrooms and if there was a gender gap in students’ self-concept in language and mathematics net of actual academic achievement. Second, we tested whether the influence of gender on students’ self-concept varied across language and mathematics classrooms. Third, we introduced measures of gender-stereotypical beliefs and achievement patterns and their interaction with students’ gender.
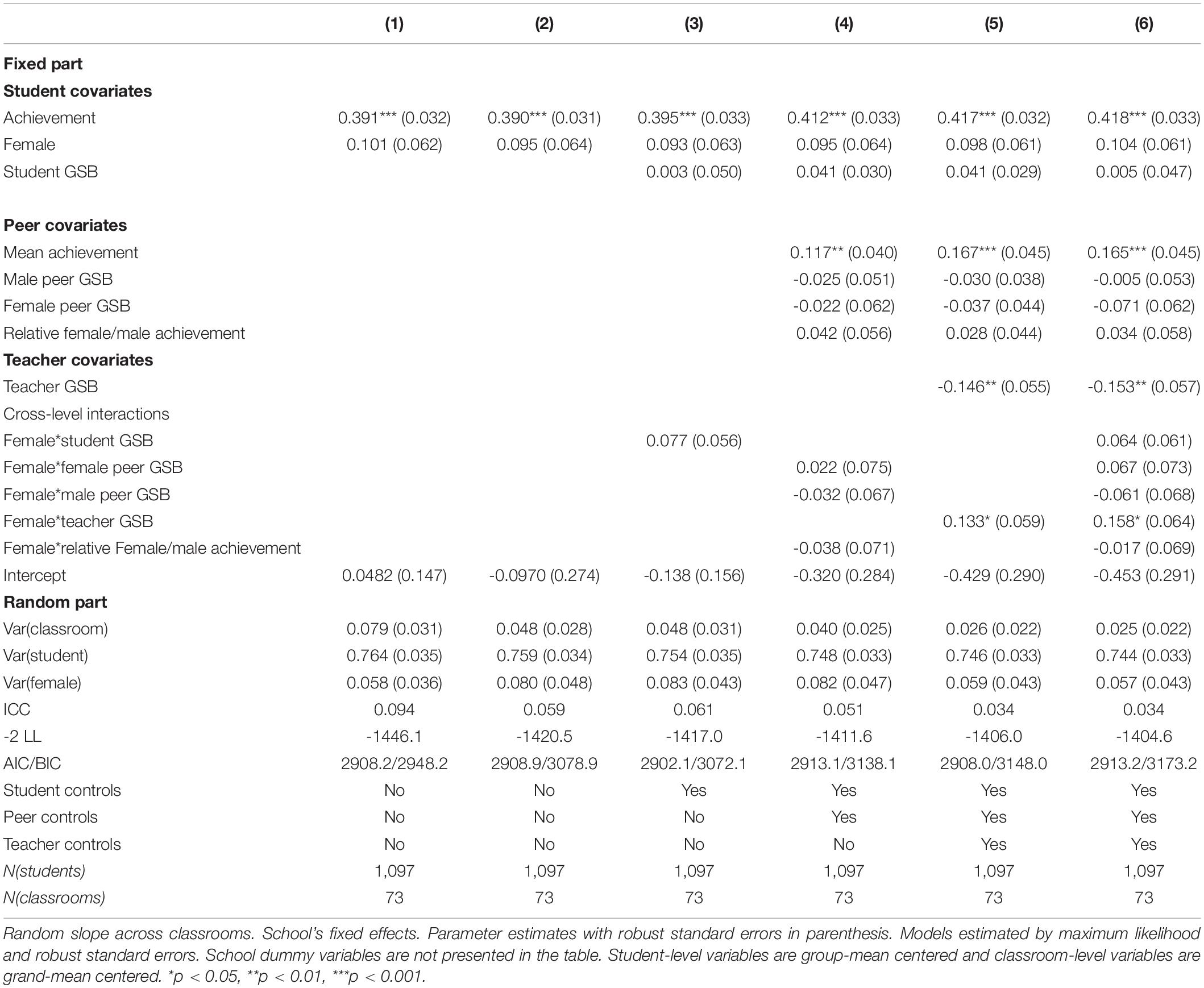
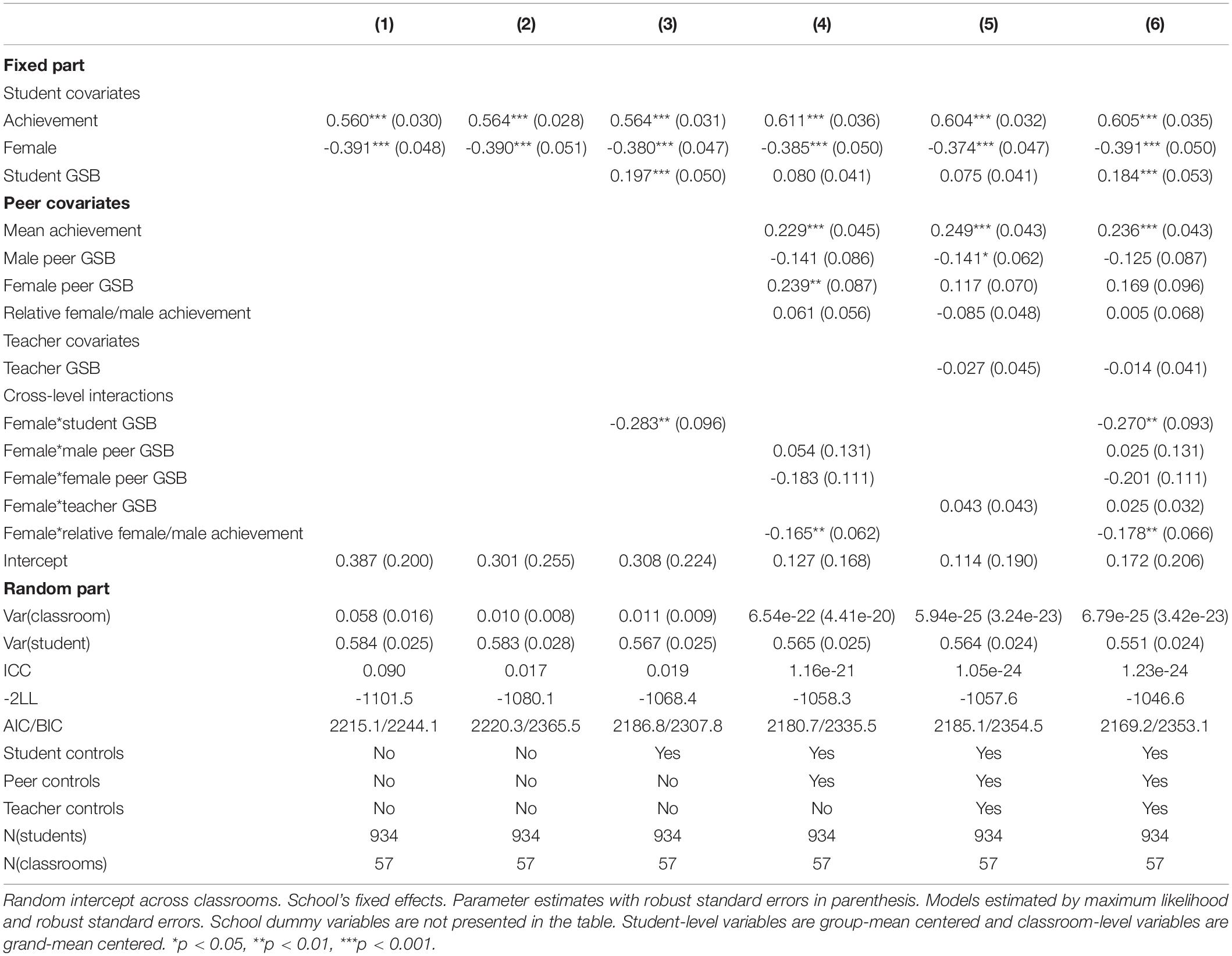
Tables 2, 3 present the impact of student, peer, and teacher covariates on students’ self-concept in language and mathematics. In Model 1, we estimated a baseline model including only students’ gender and achievement as predictors of self-concept to estimate the mean gender difference in self-concept across language and mathematics. In Model 2, we included school fixed effects to account for unobserved factors at the school level and thus, focus the analysis on within-school variation. Models 3–5 introduced covariates at the student, peer, and teacher levels, respectively, measuring gender-stereotypical beliefs and achievement patterns, as well as their interaction with students’ gender. The main influence of these factors indicated how they affected students’ self-concept on average—i.e., across both male and female students—and whether including them in the models affected the gender gap in self-concept in language/mathematics, as well as the difference in gender gaps across classrooms. We included cross-level interactions between students’ gender and measures of gender-stereotypical beliefs and achievement to assess heterogeneous effects across male and female students. Finally, Model 6 included the full model with all cross-level interactions.
Tables 2, 3 show that in both language and mathematics, the ICC was 9%. Accordingly, 9% of the variation in students’ self-concept could be attributed to factors at the classroom level. Model 2 showed that there is a gender gap in students’ self-concept in mathematics, while the gender gap in language did not reach conventional levels of statistical significance. In mathematics, there was a large gender gap of 0.39 standard deviations in favor of boys. Accordingly, on average, girls tended to evaluate their mathematics competencies as worse than boys, net of their actual academic achievement. In language, the gender gap was reversed: on average, girls evaluated themselves more positively than boys (b = 0.101), although this difference was not statistically significant.
To examine whether the influence of gender varied across classrooms, we tested a random slope of gender (i.e., whether the gender gap varied across classrooms) in both subjects using a likelihood ratio test. The results shown in Table 4 supported the presence of a random slope in the language (p = 0.06), but not in mathematics. Accordingly, the gender gap in mathematics self-concept was stable across classrooms, while the difference between male and female students in language self-concept varied across classrooms. Consequently, in our empirical analysis, we modeled mathematics self-concept using a random intercept model, while allowing a random slope for gender in language self-concept.
In Model 3 in Tables 2, 3, we added students’ GSB and the interaction of these beliefs with students’ gender. In language, we found no evidence of students’ GSB having a significant influence on their self-concept, neither on average nor across male and female students. In mathematics, by contrast, students’ GSB had a positive average influence on self-concept and a significantly negative association with gender. Consequently, female students’ GSB negatively affected their self-concept in mathematics. In Model 4 in Tables 2, 3, we included peer covariates. We distinguished between the GSB of male and female students to examine if peer influence is gender-specific. Furthermore, we added information on mean peer achievement as well as the gender-achievement pattern in the classroom to investigate how counter-stereotypical achievement patterns influenced students’ self-concept in language and mathematics. Mean peer achievement in the classroom had a positive influence on students’ self-concept in both language and mathematics. There was no significant impact of peer covariates or their interaction with gender in language. In mathematics, however, we found that the better the mathematics achievement of female peers relative to that of male peers, the lower the mathematics self-concept of girls. In Model 5 in Tables 2, 3, we examined the influence of teachers’ GSB and the interaction of these beliefs with students’ gender. We found that teachers’ stereotypical beliefs influenced students’ self-concept in language, but not in mathematics. Accordingly, boys’ language self-concept was lower when their teachers endorsed gender stereotypes concerning language ability. Model 6 in Tables 2, 3 represented the full model including all student, peer, and teacher covariates and their interactions with gender. Results from this model showed that the relationship between gender and self-concept in language was moderated by the teacher’s GSB. Meanwhile, the relationship between gender and self-concept in mathematics was moderated by students’ GSB and by counter-stereotypical achievement patterns. These moderation effects remained when taking into account all other covariates and interactions. Consequently, as illustrated in Figure 1, our empirical analysis showed that the gender gap in students’ self-concept in language increased with teachers’ GSB because there was a negative effect on male students.
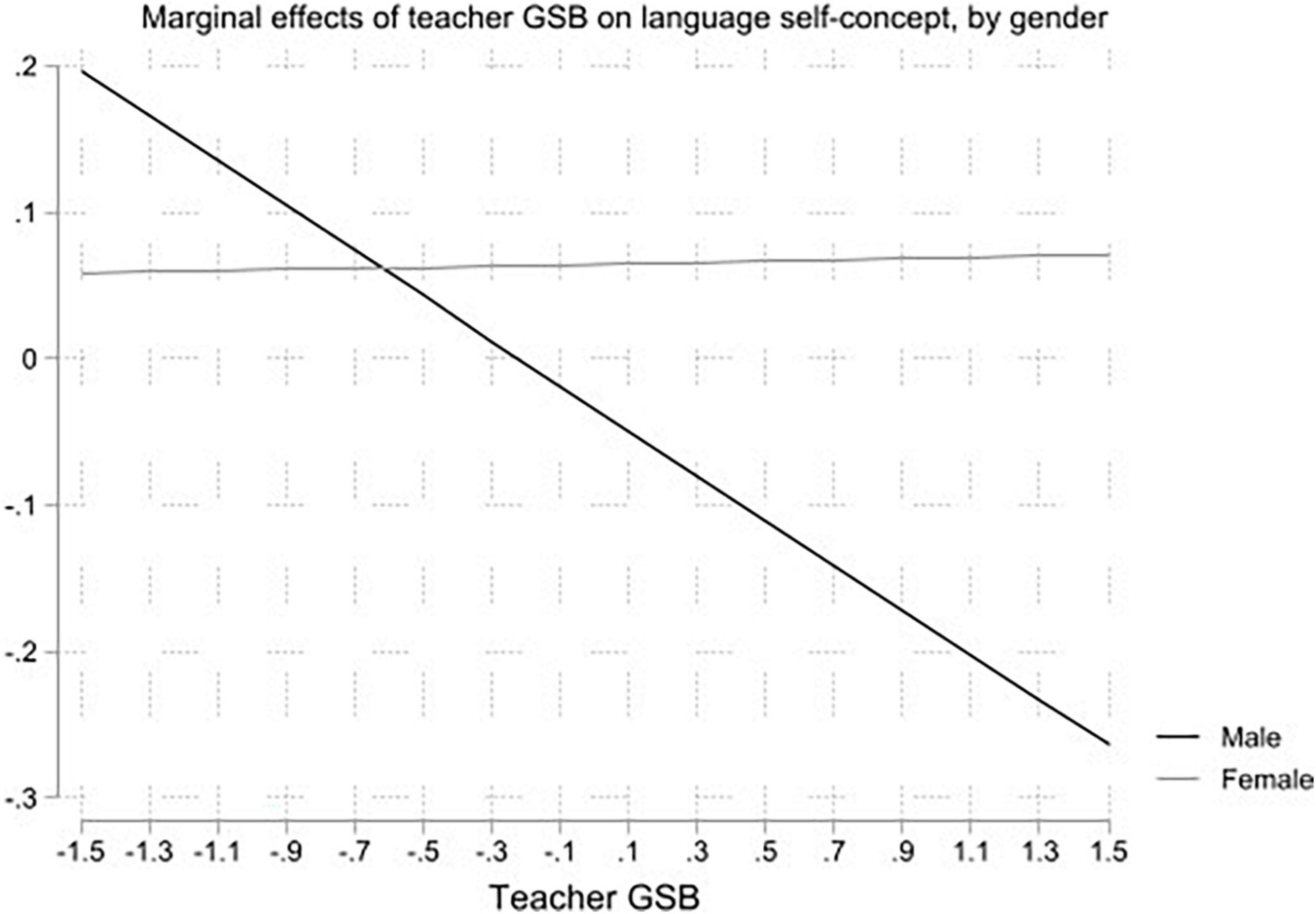
Figure 1. Teacher gender-stereotypical belief (GSB) and predicted language self-concept by gender. Marginal effects of teacher GSB on language self-concept by gender. Based on estimates from Model 6 in Table 2.
The gender gap in mathematics was unaffected by teachers’ GSB. As illustrated in Figure 2, in addition to the GSB and relative performance of female peers, gender differences in mathematics self-concept were mostly affected by students’ own GSB. Stronger GSB correlated with higher mathematics self-concept among boys and lower mathematics self-concept among girls, increasing the gender gap.
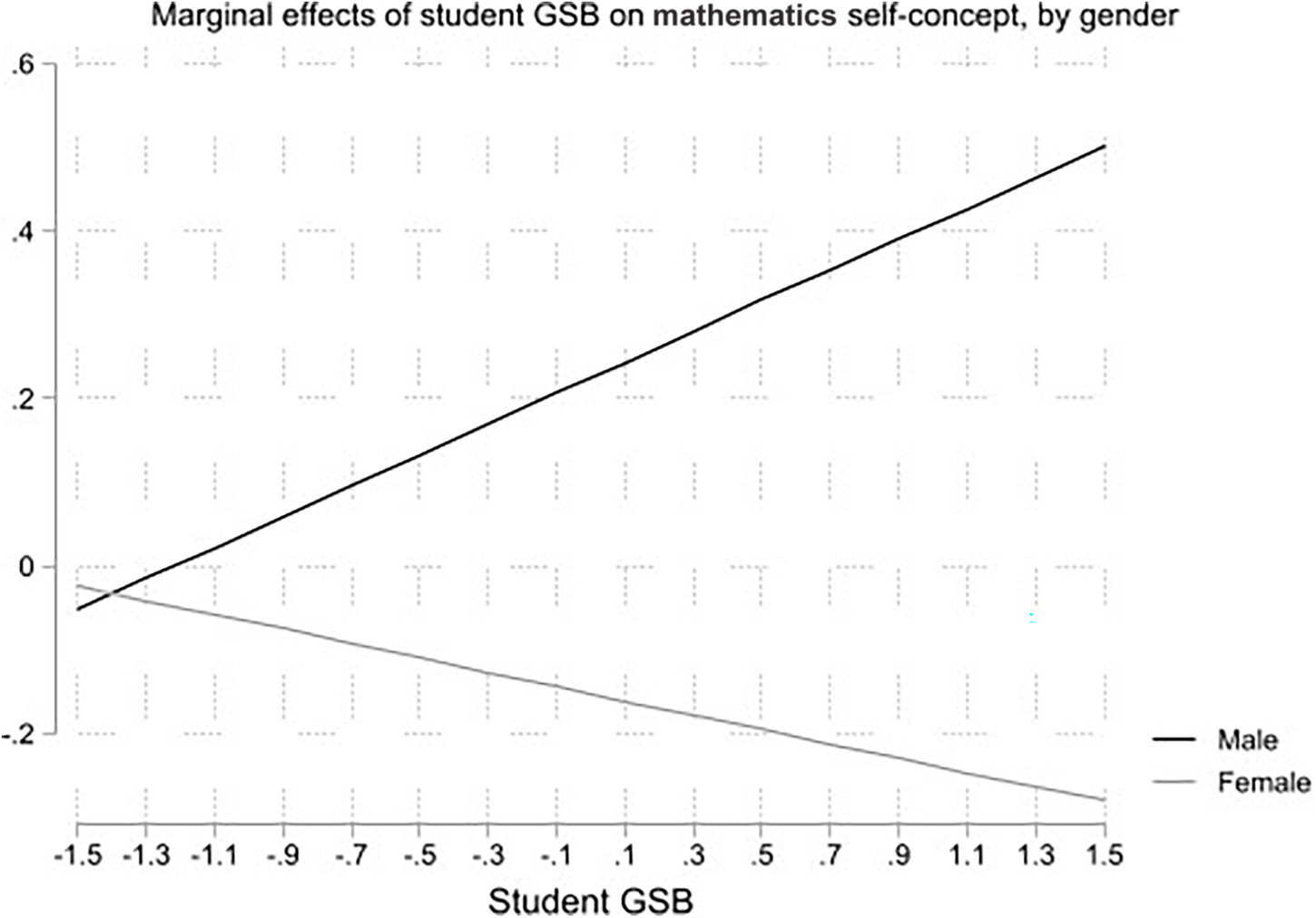
Figure 2. Students’ GSB and predicted mathematics self-concept by gender. Marginal effects of teacher GSB on mathematics self-concept by gender. Based on estimates from Model 6 in Table 3.
In addition to students’ own GSB, the relative achievement of female/male students also moderated the relationship between gender and self-concept in mathematics. Figure 3 illustrates that female students on average had lower mathematics self-concept in classrooms with “over-performing” female peers.
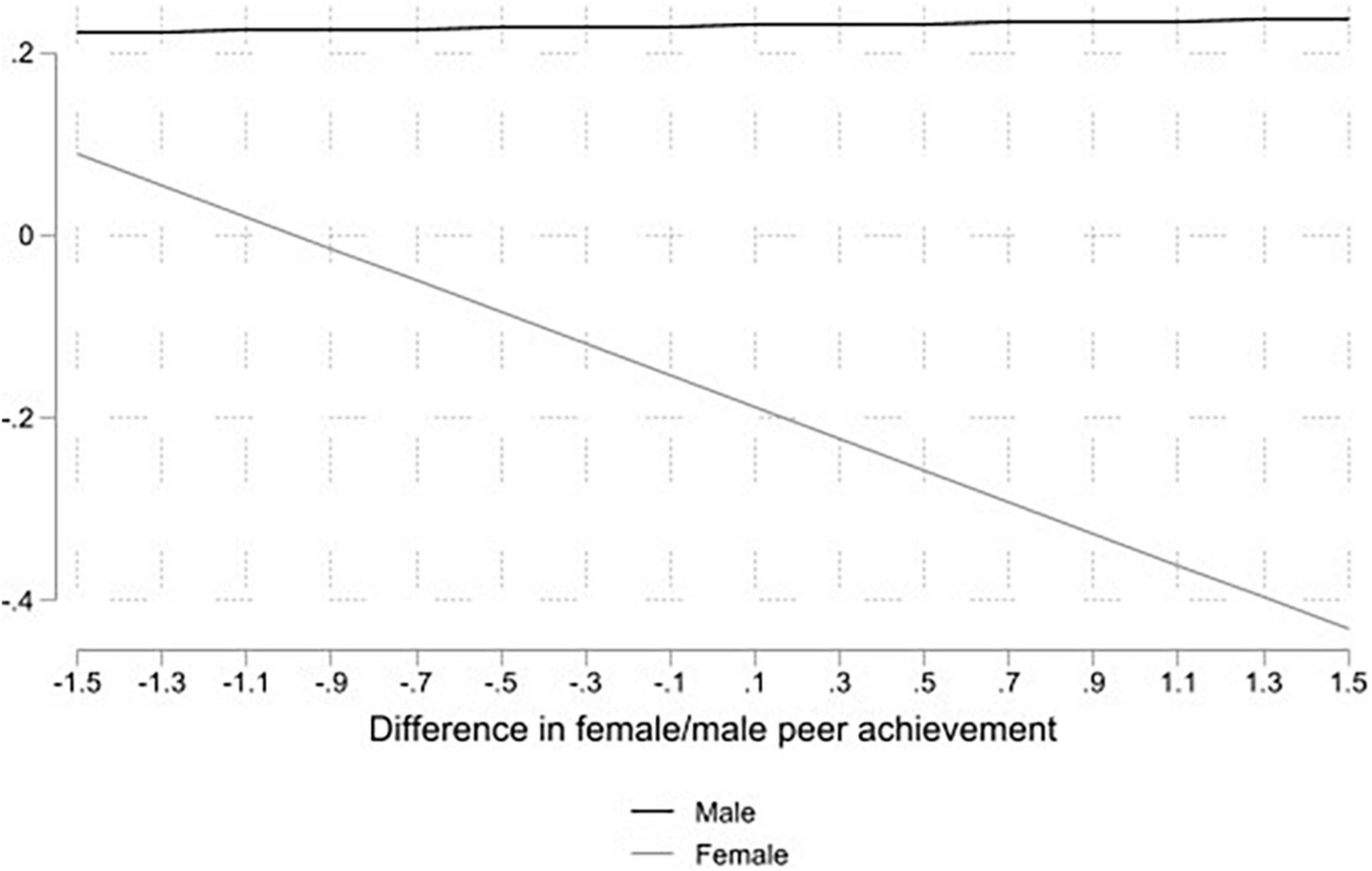
Figure 3. Difference in female/male peer achievement and predicted mathematics self-concept by gender.
Accordingly, being in a counter-stereotypical classroom in terms of stereotypical mathematics achievement did not benefit girls’ self-concept in mathematics. On the contrary, the mathematics self-concept of girls was lower when their female peers in the classroom outperformed their male peers in mathematics.
In summary, our empirical analysis showed that 9% of the variation in students’ self-concept in language and mathematics was due to variations at the classroom level. The ICC was reduced to approximately 6% in language and approximately 2% in mathematics when introducing school fixed effects to the model. Including contextual covariates further reduced the ICC in both subjects; in the full model, the ICC was close to 0 in mathematics and approximately 3% in language. Furthermore, there was a significant gender gap in students’ self-concept in mathematics, but not in language. Gender differences in students’ self-concept were unaffected by gender-stereotypical beliefs and achievement patterns since the influence of gender in both subjects was approximately equal across models. Yet, the influence of gender on self-concept varied across classrooms in language, with almost half the variation attributed to interactions between GSB and gender. The random slope of gender in language was reduced by approximately 28% when introducing teacher GSB. Finally, we found evidence of interaction effects between students’ gender and GSB, although the specific mechanism differed across subjects. While teachers’ GSB were important for the gender gap in students’ self-concept in language, they did not have an impact on gender differences in students’ mathematics self-concept. The more teachers endorsed the stereotype that language is for girls, the lower the language self-concept of boys net of actual achievement. By contrast, the influence of students’ own gender-stereotypical beliefs differed between male and female students in mathematics. The more girls endorsed the stereotype that mathematics is for boys, the lower their assessment of their mathematical ability. Moreover, girls’ self-concept was negatively affected by counter-stereotypical achievement in mathematics; i.e., when female peers in the classroom outperformed male peers.
Discussion
This paper set out to investigate gender differences in students’ competence beliefs in language and mathematics and the role of gender beliefs and gender-achievement patterns in the social context of classrooms. We analyzed combined survey and register data from Denmark, which had the advantage that it included measures of GSB at the student, (female/male) peer, and teacher levels, as well as detailed information on student and peer achievement. Furthermore, we only analyzed within-school variation, thus, taking into account selection processes in schools. Our analysis pointed to three main findings. First, consistent with our hypothesis, we found a gender gap in mathematics self-concept favoring boys, even among boys and girls with the same level of performance. This gender gap was quite large (0.39 SD) and did not vary across classrooms. By contrast, the gender gap in language varied across classrooms (p = 0.06). Second, we found that GSB influenced gender gaps in self-concept in both language and mathematics. An increase in GSB was generally associated with a larger gender gap, driven by a decrease in self-concept among students of the negatively stereotyped gender. Accordingly, GSB resulted in a lower self-concept among girls in mathematics and boys in language. Meanwhile, although the general mechanism of GSB was consistent across subject domains, how they operate differed. In language, gender differences in self-concept (which varied across classrooms) were driven by teachers’ GSB. As teachers’ GSB increased, language self-concept among boys decreased. By contrast, boys’ language self-concept was unaffected by their own and male/female peers’ GSB. In mathematics, gender differences in self-concept (which did not vary across classrooms) reflected students’ own GSB. Accordingly, the greater the extent to which individual (female) students endorsed the stereotype that math is for boys, the lower their mathematical self-concept. Third, counter-stereotypical achievement patterns in mathematics classrooms hurt girls’ self-concept. Accordingly, girls did not benefit from being surrounded by female peers that outperformed male peers. Instead, girls in such counter-stereotypical classrooms in terms of mathematics achievement assessed their competence in mathematics at a lower level than girls in classrooms characterized by more gender-stereotypical achievement patterns. This negative influence on achievement among female peers was likely due to a social comparison effect where girls compared themselves to their female classroom peers.
Theoretical and Practical Implications
While our findings support previous empirical and theoretical understandings of the importance of socializing agents (Eccles, 1994) and social contexts (Crosnoe et al., 2008; Legewie and DiPrete, 2014; Riegle-Crumb and Morton, 2017; Salikutluk and Heyne, 2017; Raabe et al., 2019) for the development of competence beliefs, we have also highlighted how these processes differ according to gender and subject domains. Until now, most research has focused on one specific subject domain (such as language or mathematics) and gender beliefs and stereotypes among students, peers, or teachers (Retelsdorf et al., 2015; Salikutluk and Heyne, 2017; Alan et al., 2018; Muntoni and Retelsdorf, 2018; Heyder et al., 2019; Muntoni et al., 2021). Our study contributes to a greater understanding of the interplay between gender-stereotypical beliefs and achievement patterns and students’ self-concept in gender-stereotypical subjects by analyzing very detailed social contexts in classrooms. Accordingly, this paper is to our knowledge the first to consider the multifaceted nature of GSB in schools. While many of our results support what we know from previous studies concerning gender differences in self-concept and the role of GSB, our study adds to this body of research by providing evidence of the complex nature of gender beliefs in schools and their consequences on student outcomes. Most importantly, our findings suggest that how GSB influences students’ self-concept are not necessarily homogeneous across gender and subject domains. While students’ GSB was associated with students’ self-concept in both language and mathematics, the gender gap in language self-concept differed across classrooms within schools. Accordingly, the social context seemed to play a different role in language classrooms than in mathematics classrooms because gender differences in self-concept were related to differences across classrooms. Combined with the finding that language self-concept among boys was most strongly influenced by teacher GSB, this finding suggests that the gender gap in the language is perhaps more malleable. If the language self-concept of male students varies across different social contexts and is influenced by the teacher, then interventions to counteract GSB among teachers might be able to reduce the gender gap in language self-concept.
In contrast to the male disadvantage in language, the gender gap in mathematics was very large and constant across classrooms. This fits well with the finding that girls’ mathematics self-concept reflected their own GSB net of their actual mathematics achievement. Accordingly, the female disadvantage in mathematics reflected strong internalized beliefs about gender and mathematics among the girls themselves. This result may be interpreted in light of cross-cultural research on gender inequality, which has argued that while (vertical) gender inequalities tend to decline in affluent Western democracies, self-expressive value systems, particularly in highly egalitarian countries, still endorse the idea that the genders are innately and fundamentally “equal but different,” and therefore continue to encourage the development and enactment of culturally masculine or feminine affinities (Charles and Bradley, 2009). Under these “post-materialist” gender regimes, gender segregation retains legitimacy because it can be understood as the result of free choices by equal, yet innately different, men and women (Thébaud and Charles, 2018). In this context, Denmark can be thought of as a prime example and girls’ (boys’) strong internalization of GSB in mathematics (language) might be understood as a way of expressing “gendered selves” through cultural gender beliefs. In addition to suggesting a very different mechanism in play than in the case of language, the role of female students’ own GSB may also point to a much more stubborn problem. While teachers’ GSB about students may be altered through targeted interventions, female students’ own internalized perceptions concerning the mathematical ability of girls are most likely harder to change. This is particularly true if such internalized perceptions are intertwined with “natural” and free expressions of gender identity (Cech, 2013) and if girls have a more fixed mindset about math ability with consequences for their competence beliefs (Heyder et al., 2021).
Finally, girls’ mathematics self-concept was also influenced by gender-stereotypical achievement patterns of female peers. Our results provided evidence of a social comparison effect, whereby girls evaluated themselves more harshly when surrounded by high-achieving female peers. This result is partly in line with previous research, which has suggested that classmates in general (Salikutluk and Heyne, 2017) and the gender stereotypes of classmates specifically (Muntoni et al., 2021) play an important role in students’ educational outcomes. However, we only found this to hold for girls. Consequently, girls may be more prone to the influence of female peers, as has also been suggested by research on gender differences in STEM (Riegle-Crumb et al., 2006; Raabe et al., 2019), which has particularly stressed that intra-gender social comparison effects are stronger than inter-gender effects (Thijs et al., 2010).
In summary, researchers, politicians, and schools should bear in mind that GSB among students, peers, and teachers has a significant and extensive influence on students’ competence beliefs and that gender gaps in self-concept in language and mathematics are important for later gender segregation and inequality. Yet, gender beliefs operate in very different ways (Correll, 2001) and need careful consideration and attention, both at the individual and classroom level. Furthermore, our study points to an important distinction between internalized GSB and the GSB of others, which calls for a context-sensitive approach to the consequences for students and the development of possible interventions.
Limitations and Future Directions
The results from this study should be interpreted in light of several limitations. First, the survey data consisted of a non-random sample of schools. During the data collection process, random samples of schools were invited to participate; however, only a fraction of the schools agreed to participate, which meant that schools to some extent self-selected into our sample (although schools could only choose to participate if they had been invited). Analyses of the representativeness of the sample revealed only minor differences between the full population and the sample in terms of parental income and education, as well as 6th-grade test scores (about 0.1 SD). No differences were found in terms of 9th-grade test scores or school size. In other words, the sample was not perfectly representative, but discrepancies in observed characteristics were small (Smith et al., 2021). Furthermore, our original sample of teachers, particularly those teaching mathematics, was significantly reduced due to non-response. We chose not to impute missing data since we did not have good imputation variables at the teacher level. If, for instance, teachers decided to participate in the survey based on certain unobserved characteristics, our results may be biased.
Second, our study aimed to investigate the role of school contexts in the generation of gender disparities in educational outcomes. Yet, we do not know if such disparities – in this case in self-concept – are consequential for later outcomes. An important task for future research is to examine whether early gender disparities translate into later gender differences and inequality in educational behavior and pathways, both within and across gender.
Third, while our explicit measure of GSB was straightforward to implement, there may have been a social desirability bias. Accordingly, we might have underestimated GSB in our sample due to respondents not providing honest answers [deliberately or because of cognitive constraints regarding introspective access to gender perceptions (Wenz et al., 2016)]. Future research should investigate GSB using techniques that have been shown to reduce social desirability bias, such as factorial surveys investigating implicit gender beliefs and their causal mechanisms. Furthermore, future studies could focus on collecting data capable of distinguishing between individual GSB and the perceived GSB of others to explore the internalization of GSB from the social context.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.
Ethics Statement
Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent for participation was not provided by the participants’ legal guardians/next of kin in accordance with the local legislation and institutional requirements.
Author Contributions
IA and ES contributed to conception and design of the study, and organized the database. IA performed the statistical analysis and wrote the first draft of the manuscript. ES wrote sections of the manuscript. All authors contributed to the article and approved the submitted version.
Funding
This research was supported by the VELUX Foundation, Denmark (Grant Number 00017032).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2022.840618/full#supplementary-material
References
Alan, S., Ertac, S., and Mumcu, I. (2018). Gender stereotypes in the classroom and effects on achievement. Rev. Econ. Statistics 100, 876–890. doi: 10.1162/rest
Ammermueller, A., and Pischke, J.-S. (2009). Peer effects in European primary schools: evidence from the progress in international reading literacy study. J. Labor Econ. 27, 315–348.
Andersen, I. G., and Reimer, D. (2019). Same-gender teacher assignment, instructional strategies, and student achievement: new evidence on the mechanisms generating same-gender teacher effects. Res. Soc. Stratification Mobility 62:100406.
Aspenlieder, L., Buchanan, C. M., McDougall, P., and Sippola, L. K. (2009). Gender nonconformity and peer victimization in pre- and early adolescence. Int. J. Dev. Sci. 3, 3–16. doi: 10.3233/DEV-2009-3103
Birkelund, J. F., Karlson, K. B., and Reimer, D. (2021). Upper secondary school tracking, labour market outcomes and intergenerational inequality in Denmark. Long. Life Course Stud. 12, 279–298.
Bong, M., and Skaalvik, E. M. (2003). Academic self-concept and self-efficacy: how different are they really? Educ. Psychol. Rev. 15, 1–40.
Breda, T., Jouini, E., Napp, C., and Thebault, G. (2020). Gender stereotypes can explain the gender-equality paradox. Proc. Natl. Acad. Sci. U S A. 117, 31063–31069. doi: 10.1073/pnas.2008704117
Cech, E. A. (2013). The self-expressive edge of occupational sex segregation. Am. J. Sociol. 119, 747–789.
Charles, M., and Bradley, K. (2009). Indulging our gendered selves? sex segregation by field of study in 44 countries. Am. J. Sociol. 114, 924–976. doi: 10.1086/595942
Correll, S. J. (2001). Gender and the career choice process: the role of biased self-assessments. Am. J. Sociol. 10, 1691–1730. doi: 10.1086/321299
Correll, S. J. (2004). Constraints into preferences: gender, status, and emerging career aspirations. Am. Sociol. Rev. 69, 93–113.
Cotter, D., Hermsen, J. M., and Vanneman, R. (2011). The end of the gender revolution? gender role attitudes from 1977 to 2008. Am. J. Sociol. 117, 259–289. doi: 10.1086/658853
Crosnoe, R., Riegle-Crumb, C., Field, S., Frank, K., and Muller, C. (2008). Peer group contexts of girls’ and boys’ academic experiences. Child Dev. 79, 139–155. doi: 10.1111/j.1467-8624.2007.01116.x
Davis, S. N. (2007). Gender ideology construction from adolescence to young adulthood. Soc. Sci. Res. 36, 1021–1041.
DiPrete, T. A., and Buchmann, C. (2013). The Rise of Women: The Growing Gender Gap in Education and what it Means for American Schools. New York, NY: Russell Sage Foundation.
Durik, A. M., Vida, M., and Eccles, J. S. (2006). Task values and ability beliefs as predictors of high school literacy choices: a developmental analysis. J. Educ. Psychol. 98:382.
Eccles, J. S. (1994). Understanding women’s educational and occupational choices: applying the Eccles, et al. model of achievement-related choices. Psychol. Women Quarterly 18, 585–609.
Eccles, J. S. (2011). Gendered educational and occupational choices: applying the Eccles, et al. model of achievement-related choices. Int. J. Behav. Dev. 35, 195–201. doi: 10.1177/0165025411398185
Eccles, J. S., and Wigfield, A. (1995). In the mind of the actor: the structure of adolescents’ achievement task values and expectancy-related beliefs. Personal. Soc. Psychol. Bull. 21, 215–225.
Else-Quest, N. M., Hyde, J. S., and Linn, M. C. (2010). Cross-national patterns of gender differences in mathematics: a meta-analysis. Psychol. Bull. 136, 103–127. doi: 10.1037/a0018053
England, P. (2010). The gender revolution: uneven and stalled. Gender Soc. 24, 149–166. doi: 10.1111/cars.12076
Evans, A. B., Copping, K. E., Rowley, S. J., and Kurtz-Costes, B. (2011). Academic self-concept in black adolescents: do race and gender stereotypes matter? Self Identity 10, 263–277. doi: 10.1080/15298868.2010.485358
Fang, J., Huang, X., Zhang, M., Huang, F., Li, Z., and Yuan, Q. (2018). The big-fish-little-pond effect on academic self-concept: a meta-analysis. Front. Psychol. 9:1569. doi: 10.3389/fpsyg.2018.01569
Flore, P. C., and Wicherts, J. M. (2015). Does stereotype threat influence performance of girls in stereotyped domains? a meta-analysis. J. School Psychol. 53, 25–44. doi: 10.1016/j.jsp.2014.10.002
Goldman, A. D., and Penner, A. M. (2016). Exploring international gender differences in mathematics self-concept. Int. J. Adolescence Youth 21, 403–418. doi: 10.1080/02673843.2013.847850
Heyder, A., and Kessels, U. (2013). Is school feminine? implicit gender stereotyping of school as a predictor of academic achievement. Sex Roles 69, 605–617. doi: 10.1007/s11199-013-0309-9
Heyder, A., Kessels, U., and Steinmayr, R. (2017). Explaining academic-track boys’ underachievement in language grades: not a lack of aptitude but students’ motivational beliefs and parents’ perceptions? Br. J. Educ. Psychol. 87, 205–223. doi: 10.1111/bjep.12145
Heyder, A., Steinmayr, R., and Kessels, U. (2019). Do teachers’ beliefs about math aptitude and brilliance explain gender differences in children’s math ability self-concept? Front. Educ. 4:34. doi: 10.3389/feduc.2019.00034
Heyder, A., Weidinger, A. F., and Steinmayr, R. (2021). Only a burden for females in math? gender and domain differences in the relation between adolescents’ fixed mindsets and motivation. J. Youth Adolescence 50, 177–188. doi: 10.1007/s10964-020-01345-4
Holder, K., and Kessels, U. (2017). Gender and ethnic stereotypes in student teachers’ judgments: a new look from a shifting standards perspective. Soc. Psychol. Educ. 20, 471–490.
Holgado-Tello, F. P., Chacón-Moscoso, S., Barbero-García, I., and Vila-Abad, E. (2010). Polychoric versus pearson correlations in exploratory and confirmatory factor analysis of ordinal variables. Qual. Quantity 44, 153–166.
Hyde, J. S., Lindberg, S. M., Linn, M. C., Ellis, A. B., and Williams, C. C. (2008). Gender similarities characterize math performance. Science 321, 494–495. doi: 10.1126/science.1160364
Ireson, J., and Hallam, S. (2009). Academic self-concepts in adolescence: relations with achievement and ability grouping in schools. Learn. Instruct. 19, 201–213.
Jacobs, J. E., Lanza, S., Osgood, D. W., Eccles, J. S., and Wigfield, A. (2002). Changes in children’s self-competence and values: gender and domain differences across grades one through twelve. Child Dev. 73, 509–527. doi: 10.1111/1467-8624.00421
Jansen, M., Schroeders, U., and Lüdtke, O. (2014). Academic self-concept in science: multidimensionality, relations to achievement measures, and gender differences. Learn. Individual Differ. 30, 11–21.
Lamb, M. E., Easterbrooks, A., and Holden, G. W. (1980). Reinforcement and punishment among preschoolers: characteristics, effects, and correlates. Child Dev. 51, 1230–1236.
Leder, G. C., and Forgasz, H. J. (2002). Two New Instruments To Probe Attitudes about Gender and Mathematics. Bundoora VIC: La Trobe University.
Legewie, J., and DiPrete, T. A. (2012). School context and the gender gap in educational achievement. Am. Sociol. Rev. 77, 463–485.
Legewie, J., and DiPrete, T. A. (2014). The high school environment and the gender gap in science and engineering. Sociol. Educ. 87, 259–280. doi: 10.1177/0038040714547770
Loyalka, P., Zakharov, A., and Kuzmina, Y. (2018). Catching the big fish in the little pond effect: evidence from 33 countries and regions. Comp. Educ. Rev. 62, 542–564.
Mann, A., Legewie, J., and DiPrete, T. A. (2015). The role of school performance in narrowing gender gaps in the formation of STEM aspirations: a cross-national study. Front. Psychol. 6:171. doi: 10.3389/fpsyg.2015.00171
Marsh, H. W. (1987). The big-fish-little-pond effect on academic self-concept. J. Educ. Psychol. 79:280.
Marsh, H. W., Craven, R. G., and Martin, A. J. (2006). What is the nature of self-esteem? unidimensional and multidimensional perspectives. Self-Esteem: Issues Answers 1, 16–25. doi: 10.1186/s12913-016-1423-5
Marsh, H. W., Pekrun, R., Parker, P. D., Murayama, K., Guo, J., Dicke, T., et al. (2019). The murky distinction between self-concept and self-efficacy: beware of lurking jingle-jangle fallacies. J. Educ. Psychol. 111:331.
Martinot, D., Bagès, C., and Désert, M. (2012). French children’s awareness of gender stereotypes about mathematics and reading: when girls improve their reputation in math. Sex Roles 66, 210–219. doi: 10.1007/s11199-011-0032-3
McNally, S. (2020). Gender Differences in Tertiary Education: What Explains STEM Participation?. London: Centre for Economic Performance. CEP Discussion Paper No. 1721.
McNeish, D., and Wentzel, K. R. (2017). Accommodating small sample sizes in three-level models when the third level is incidental. Multivariate Behav. Res. 52, 200–215. doi: 10.1080/00273171.2016.1262236
Mejía-Rodríguez, A. M., Luyten, H., and Meelissen, M. R. (2021). Gender differences in mathematics self-concept across the world: an exploration of student and parent data of TIMSS 2015. Int. J. Sci. Mathematics Educ. 19, 1229–1250.
Mullis, I. V. S., Martin, M. O., Foy, P., Kelly, D. L., and Fishbein, B. (2020). TIMSS 2019 International Results in Mathematics and Science. Chestnut Hill, MA: Boston College, TIMSS & PIRLS International Study Center.
Muntoni, F., and Retelsdorf, J. (2018). Gender-specific teacher expectations in reading—the role of teachers’ gender stereotypes. Contemporary Educ. Psychol. 54, 212–220. doi: 10.1016/j.cedpsych.2018.06.012
Muntoni, F., Wagner, J., and Retelsdorf, J. (2021). Beware of stereotypes: are classmates’ stereotypes associated with students’ reading outcomes? Child Dev. 92, 189–204. doi: 10.1111/cdev.13359
Neuschmidt, O., Barth, J., and Hastedt, D. (2008). Trends in gender differences in mathematics and science (TIMSS 1995-2003). Stud. Educ. Eval. 34, 56–72. doi: 10.1016/j.stueduc.2008.04.002
Nowicki, E. A., and Lopata, J. (2017). Children’s implicit and explicit gender stereotypes about mathematics and reading ability. Soc. Psychol. Educ. 20, 329–345. doi: 10.1007/s11218-015-9313-y
OECD (2013). Results: Ready to Learn (Volume III): Students’ Engagement, Drive and Self-Beliefs. Paris: OECD Publishing.
Pampel, F. (2011). Cohort changes in the socio-demographic determinants of gender egalitarianism. Soc. Forces 89, 961–982. doi: 10.1353/sof.2011.0011
Pansu, P., Régner, I., Max, S., Colé, P., Nezlek, J. B., and Huguet, P. (2016). A burden for the boys: evidence of stereotype threat in boys’ reading performance. J. Exp. Soc. Psychol. 65, 26–30. doi: 10.1016/j.jesp.2016.02.008
Penner, A. M. (2008). Gender differences in extreme mathematical achievement: an international perspective on biological and social factors. Am. J. Sociol. 114, S138–S170. doi: 10.1086/589252
Plante, I., De la Sablonnière, R., Aronson, J. M., and Théorêt, M. (2013). Gender stereotype endorsement and achievement-related outcomes: the role of competence beliefs and task values. Contemporary Educ. Psychol. 38, 225–235. doi: 10.1016/j.cedpsych.2013.03.004
Plante, I., Théorêt, M., and Favreau, O. E. (2009). Student gender stereotypes: contrasting the perceived maleness and femaleness of mathematics and language. Educ. Psychol. 29, 385–405. doi: 10.1080/01443410902971500
Plieninger, H., and Dickhäuser, O. (2015). The female fish is more responsive: gender moderates the BFLPE in the domain of science. Educ. Psychol. 35, 213–227.
Raabe, I. J., Boda, Z., and Stadtfeld, C. (2019). The social pipeline: how friend influence and peer exposure widen the STEM gender gap. Sociol. Educ. 92, 105–123.
Reilly, D. (2012). Gender, culture, and sex-typed cognitive abilities. PLoS One 7:e39904. doi: 10.1371/journal.pone.0039904
Reilly, D., Neumann, D. L., and Andrews, G. (2019). Gender differences in reading and writing achievement: evidence from the National Assessment of Educational Progress (NAEP). Am. Psychol. 74:445. doi: 10.1037/amp0000356
Retelsdorf, J., Schwartz, K., and Asbrock, F. (2015). “Michael can’t read!” teachers’ gender stereotypes and boys’ reading self-concept. J. Educ. Psychol. 107, 186–194. doi: 10.1037/a0037107
Ridgeway, C. L. (2009). Framed before we know it: how gender shapes social relations. Gender Soc. 23, 145–160.
Ridgeway, C. L., and Correll, S. J. (2004). Unpacking the gender system: a theoretical perspective on gender beliefs and social relations. Gender Soc. 18, 510–531. doi: 10.1177/1557988320927285
Riegle-Crumb, C., and Morton, K. (2017). Gendered expectations: examining how peers shape female students’ intent to pursue STEM fields. Front. Psychol. 8:329. doi: 10.3389/fpsyg.2017.00329
Riegle-Crumb, C., and Peng, M. (2021). Examining high school students’ gendered beliefs about math: predictors and implications for choice of STEM college majors. Sociol. Educ. 94:003804072110147.
Riegle-Crumb, C., Farkas, G., and Muller, C. (2006). The role of gender and friendship in advanced course taking. Sociol. Educ. 79, 206–228. doi: 10.1177/003804070607900302
Riegle-Crumb, C., King, B., Grodsky, E., and Muller, C. (2012). The more things change, the more they stay the same? prior achievement fails to explain gender inequality in entry into STEM college majors over time. Am. Educ. Res. J. 49, 1048–1073. doi: 10.3102/0002831211435229
Riegle-Crumb, C., Kyte, S. B., and Morton, K. (2018). “Gender and racial/ethnic differences in educational outcomes: examining patterns, explanations, and new directions for research bt - handbook of the sociology of education in the 21st Century,” in, Handbook of the Sociology of Education in the 21st Century, ed. B. Schneider (Berlin: Springer International Publishing).
Risman, B. J. (2004). Gender as a social structure: theory wrestling with activism. Gender Soc. 18, 429–450.
Rosenqvist, E. (2018). Two functions of peer influence on upper-secondary education application behavior. Sociol. Educ. 91, 72–89.
Salikutluk, Z., and Heyne, S. (2017). Do gender roles and norms affect performance in maths? the impact of adolescents’ and their peers’ gender conceptions on maths grades. Eur. Sociol. Rev. 33, 368–381.
Seaton, M., Marsh, H. W., and Craven, R. G. (2010). Big-fish-little-pond effect: generalizability and moderation—two sides of the same coin. Am. Educ. Res. J. 47, 390–433.
Sikora, J., and Pokropek, A. (2012). Gender segregation of adolescent science career plans in 50 countries. Sci. Educ. 96, 234–264. doi: 10.1002/sce.20479
Skaalvik, S., and Skaalvik, E. M. (2004). Gender differences in math and verbal self-concept, performance expectations, and motivation. Sex Roles 50, 241–252.
Smith, E., Reimer, D., Andersen, I. G., and Sortkær, B. (2021). Exploring School Culture: Technical Report for Data Collection. Danish School of Education. Available online at: https://projekter.au.dk/fileadmin/projekter/Exploring_School_Culture/Ebog_-_ESCU_technical_report.pdf (accessed December 15, 2021).
Steele, C. M. (1997). A threat in the air: how stereotypes shape intellectual identity and performance. Am. Psychol. 52:613. doi: 10.1037//0003-066x.52.6.613
Thijs, J., Verkuyten, M., and Helmond, P. (2010). A further examination of the big-fish-little-pond effect: perceived position in class, class size, and gender comparisons. Sociol. Educ. 83, 333–345.
UNESCO (2017). Cracking the Code: Girls’ and Women’s Education in Science, Technology, Engineering and Mathematics (STEM). Paris: UNESCO.
Vincent-Lancrin, S. (2008). “The reversal of gender inequalities in higher education: an on-going trend,” in Higher Education to 2030: Demography, Vol. 1 (Paris: OECD Publishing). doi: 10.1787/9789264040663-11-en
Voyer, D., and Voyer, S. D. (2014). Gender differences in scholastic achievement: a meta-analysis. Psychol. Bull. 140:1174. doi: 10.1037/a0036620
Wenz, S. E., Olczyk, M., and Lorenz, G. (2016). Measuring Teachers’ Stereotypes in the NEPS. Bamberg: Leibniz Institute for Educational Trajectories, National Educational Panel Study. NEPS Survey Paper, 3.
Wigfield, A., and Eccles, J. S. (2000). Expectancy-value theory of achievement motivation. Contemporary Educ. Psychol. 25, 68–81.
Keywords: gender differences, social contexts, gender-stereotype, self-concept, multilevel (hierarchical) regression
Citation: Andersen IG and Smith E (2022) Social Contexts and Gender Disparities in Students’ Competence Beliefs: The Role of Gender-Stereotypical Beliefs and Achievement Patterns in the Classroom for Students’ Self-Concept in Gender-Stereotypical Subjects. Front. Educ. 7:840618. doi: 10.3389/feduc.2022.840618
Received: 21 December 2021; Accepted: 28 March 2022;
Published: 16 May 2022.
Edited by:
Daniela Barni, University of Bergamo, ItalyReviewed by:
Marlene Kollmayer, University of Vienna, AustriaMalte Jansen, Institute for Educational Quality Improvement (IQB), Germany
Copyright © 2022 Andersen and Smith. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ida G. Andersen, aWRhZ3JhbkBlZHUuYXUuZGs=
 Ida G. Andersen
Ida G. Andersen Emil Smith
Emil Smith