Impact of Subgoal Labeling on Online Worked Example Learning in Mathematics for Primary School Students

The no-subgoal-worked examples and the subgoal-worked examples are “one problem and two solutions.” Previous studies have found that the effect of subgoal-worked examples learning is better than that of no-subgoal-worked examples. However, there is still ambiguity around the subgoal-worked examples learning effect and mechanism of the subgoal labeling form. To address this issue, the current study recruited a total of 130 Chinese children (M_age = 8.78 years) to mathematical online learning under different worked example forms. The results revealed that, as compared with the no-subgoal-worked example, the subgoal-worked example increased primary school students’ working memory resource depletion. However, it did not improve their scores. Moreover, as compared with the subgoal-worked example, the focused subgoal-labeled worked example did not promote primary school students’ learning effectiveness in mathematics. However, the individual choice subgoal-labeled worked example improved primary school students’ near-transfer scores. It also reduced their mental effort and working memory resource depletion. It, therefore, appears to be a more effective subgoal-labeled worked example learning approach.

Introduction

Worked Example

Knowledge is necessary for individuals’ survival and development. School education is an important way for individuals to gain systematic knowledge. The teaching materials’ design is the main objective factor influencing the effectiveness of school education. John Sweller examined instructional material design since the 1970s (Sweller, 1988, p.262). Through experimental research, he found that learning from worked examples is a more effective form of instructional material design for knowledge acquisition than problem solving (Sweller and Cooper, 1985, p.70). The worked example provides individuals with a step-by-step approach to problem solving (Atkinson et al., 2000, p.200). Based on prior knowledge, the individual reads and thinks about a worked example to understand the new knowledge of problem solving. This also involves mastering its application.

Later, Sweller (1988, p.270) proposed cognitive load theory. Cognitive load is the total amount of cognitive resources required for an individual to process a certain kind of information. Sweller and Chandler (1994, p.221) classified cognitive load into extraneous, intrinsic, and germane cognitive load. This was according to their functions. Extraneous cognitive load occurs when learning materials are poorly presented. This leads to reduced learning outcomes (Kalyuga et al., 2004, p.568). Intrinsic cognitive load is caused by the complexity of the learning material itself (Leahy and Sweller, 2019, p.8). Germane cognitive load represents students’ level of understanding of learning through effort. This contributes to the transfer of information from the short-term to long-term memory and ultimately to learning (Demetriadis et al., 2008, p.942). During learning, these three types of cognitive load can be cumulative. Together, they determine the total cognitive load elicited by the information material. If the number of cognitive resources needed to process a certain type of information exceeds the individual’s cognitive processing capacity, it will cause a cognitive overload. It will also reduce the learning effect.

Subgoal-Worked Example and Subgoal Labeling

Worked examples may improve the learning effect. However, some researchers have found that when students solve new problems after learning from worked examples, they do not solve the problems according to the rules implied in the original worked example. However, they tended to solve the problems by the similarity of the surface features between the new problems and the original worked example. Catrambone and Holyoak (1990, p.595) suggested that the main reason for this phenomenon was that students were easily attracted by the surface features presented in the worked example. They, thus, ignored the rules and principles implicit in the worked example. Therefore, to facilitate learners’ deeper processing and understanding of the worked example’s structural features, Catrambone and Holyoak (1990, p.600) proposed a subgoal-worked example. This groups the worked example’s complete steps into several meaningful step groups (or small events) that can be understood and processed separately when solving new problems. They also experimentally concluded that, when students effectively understood the subgoal elements of the worked example steps, they were able to improve their performance on the transfer test. According to cognitive load theory, subgoal-worked examples have a similar learning mechanism to that of low-component interactive material and, therefore, do not usually induce high levels of cognitive load (Gerjets et al., 2019, p.133). On this basis, subgoal-worked examples can effectively reduce learning difficulty.

Catrambone (1994, p.610) outlined a model for a subgoal-worked example: First, learners group a series of steps based on the basic structure of the worked examples. They then self-explain the reasons for the grouping. They finally summarize the basis for the grouping (i.e., subgoal labels). Catrambone (1998, p.355) argued that subgoal labels divide worked example step groups into meaningful information categories. These may improve learners’ abilities to solve additional problems. To examine whether subgoal labeling may facilitate the learning effect of a worked example, Gerjets et al. (2004, p.170) conducted an experiment with 120 university students as participants. They had knowledge of physics as experimental materials. The experiment showed that the participants performed better on the medium-transfer and far-transfer tests with the subgoal labeled. This was as compared to having no subgoal labeled. However, there was no significant difference in their performance on the near-transfer test. Subsequently, several studies have similarly found that subgoal labeling promotes learners’ attention to the structural features of the worked example. This allowed learners to organize worked example information more effectively. It, thus, improved the transfer test performance (Salden et al., 2010, p.381; Margulieux et al., 2012, pp.71–78). Previous subgoal-labeled studies were conducted in the offline paper-based form. To investigate the applicability of subgoals labeled to online teaching environments, Margulieux et al. (2013, pp.978–980) enrolled 18 elementary and middle school teachers as participants. The aim was to learn and practice computer science through the worked examples. They found that the participants in the subgoal-labeled worked examples group scored significantly higher on both the near- and far-transfer tests than the no-subgoal-labeled worked examples group. Morrison et al. (2015, pp.21–29) designed “self-generated subgoal labeling.” This allowed learners to observe and summarize the basis of the subgoal step groups. It also allowed the learner to be “given subgoal labeling.” This presented the grouping basis of the subgoal step groups to the learner directly. The results showed that in contextual transfer exercises with close links to the original questions, the participants in the given subgoal labels group performed significantly better than those in the self-generated subgoal labels group did. Conversely, the results were reversed in the isomorphic transfer exercise. Subsequently, the researchers found that, when college students engaged in online computer programming worked examples, the subgoal-labeled group’s problem-solving ability was significantly higher than that of the unlabeled group (Margulieux and Catrambone, 2016, p. 60; Margulieux and Catrambone, 2019, pp.130–134). Therefore, subgoal labeling may improve the learning of worked example subgoals for specific content to some extent.

Research Questions

In summary, previous studies found that participants learned better in the subgoal-worked examples than in the no-subgoal-worked examples. This may be because the no-subgoal-worked example presented an entire problem solution. Students needed to process more elements in their working memory. There were inadequate cognitive resources to think deeply about the structural features of the worked examples (Atkinson et al., 2000, p.213; Lusk and Atkinson, 2007, p.752). In contrast, the solution steps of the subgoal-worked example were based on small events. This would reduce the participants’ cognitive load. In addition, subgoal labeling allows learners to group the same type of learning content into meaningful structures. These enhance their understanding and memory of the worked examples content (Atkinson et al., 2003, p.762; Margulieux et al., 2020, p.8). However, the content of the two previously worked examples studies are mostly focused on college students’ knowledge learning. Conversely, the cognitive abilities of elementary and middle school students are not yet well developed. Furthermore, their mathematical knowledge is commonly taught as subgoal-worked examples. It is also taught by expanding the worked examples learning content. It may help to verify the applicability of subgoal-worked examples learning. Previous studies have found that primary school students’ abstract logic skills were not fully developed. They were also more inclined to engage in specific image thinking (Gerjets et al., 2004, p.170). Conversely, primary school students’ working memory capacity were relatively low. In addition, their information processing abilities were weak. Therefore, it is expected that concrete small-event subgoal-worked examples may have better learning effects as abstract holistic subgoal-worked examples.

Previous research has also found that subgoal labels may improve the learning effects of subgoal-worked examples. The possible reasons include: subgoal labels emphasize the worked example structure, help learners organize new information effectively, and improve self-explanation (Margulieux and Catrambone, 2016, p.69). However, most studies focus on given subgoal labels. Relatively few studies have been conducted on self-generated subgoal labels. Simultaneously, Morrison et al. (2015, pp.21–29) found that given subgoals are more suitable for simple contextual transfer. He also found that self-generated subgoal labels are more suitable for isomorphic transfer. However, some researchers posited that self-generated subgoal labels may increase a task’s difficulty. It may also increase the extraneous cognitive load. To address these phenomena, the study proposed subgoal labels with different degrees of generation. It attempts this by drawing on the results of previous studies (Chi and Wylie, 2014, p.220). It also provided the focused subgoal labeling. This is where students were asked to organize their language to answer the meaning of the corresponding subgoal-worked example steps. This was based on the questions provided. This type of subgoal labeling may result in students’ higher extraneous cognitive load because there is relatively little given content and more generative content. Therefore, the researchers expected a relatively poor learning effect for the focused subgoal labeling. The second is the individual choice subgoal labeling. This is where students were asked to select the meaning of the subgoal-worked example steps from the options provided. This occurred without organizing their own language. Therefore, a better learning effect for the individual choice subgoal labeling was expected. This would reduce the students’ extraneous cognitive load. This would be due to the relatively large amount of given content and less generative content. In addition, students’ active choice of learning content would significantly motivate them (Chen et al., 2018, p.490). Therefore, this study also measured their working memory capacity at the end of the worked examples learning. This serves to better explain the primary school students’ mathematics effect on the no-subgoal and subgoal-worked examples under the two types of subgoal labels. This is as an indicator to compare the depletion of working memory resources for each group of participants. Working memory is not a constantly finite resource. However, it is a finite resource that may be depleted. A decrease in one’s working memory capacity during worked examples learning will cause students to have insufficient working memory resources to complete subsequent tests. This would lower their subsequent test scores and produce a working memory resource depletion effect. Based on the above analysis, the study proposed two research hypotheses: (1) As compared with the no-subgoal-worked examples, the subgoal-worked examples reduced primary school students’ cognitive load and working memory resource depletion. However, it increased the transfer scores. (2) As compared with the subgoal-worked examples, the individual choice subgoal-labeled worked examples increased the primary school students’ near-transfer scores. They also reduced mental effort and working memory resource depletion. However, the focused subgoal-labeled worked examples did not differ from the transfer scores of the subgoal-worked examples.

Materials and Methods

Participants

The participants were 130 elementary school students from the fourth grade of a regular primary school. This was in a midsize Chinese town. This school has an average level of academic attainment and socio-economic status relative to the national average. The participants were entirely novices regarding the learning content. They were selected by quiz questions. All 130 students (71 girls and 59 boys; M_age = 8.78 years, SD = 0.66) completed all stages of the experiment. They strictly followed the instructions. The participants were randomly assigned to each group: the no-subgoal-worked examples (N = 33), the subgoal-worked examples (N = 33), the focused subgoal-labeled worked examples (N = 32), and the individual choice subgoal-labeled worked examples (N = 32).

Design

This experiment adopted a single-factor design. The worked example form included a no-subgoal-worked example, a subgoal-worked example, a focused subgoal-labeled worked example, and an individual choice subgoal-labeled worked example. The no-subgoal-worked example referred to a holistic solution to the encounter problem. The subgoal-worked example referred to a small-event decomposition solution to the encounter problem. The focused subgoal-labeled worked example and the individual choice subgoal-labeled worked example each presented the subgoal-worked example to the learner. They were given three clues to the subgoal solution. One of these was the correct answer. The participants’ cognitive load level, working memory capacity, near-transfer test scores, and far-transfer test scores were recorded. This occurred after the worked examples were learned.

Materials

The experimental materials included pre-test questions, working memory capacity test materials; worked example materials, cognitive load scales, and near- and far-transfer test materials (see Supplementary Appendix A for details).

Pre-test Questions

This consisted of 10 questions, eight of which were multiple-choice questions. These were on addition, subtraction, multiplication, and division. One multiple-choice question was on the concept of “a relative problem.” There was one application question on the “encounter problem.” All the questions were presented on an A4-size sheet of paper.

Worked Example Materials

The worked example materials included four no-subgoal-worked examples, four subgoal-worked examples, four focused subgoal-worked examples, and four individual choice subgoal-worked examples for the “encounter problem.” The no-subgoal-worked examples included the face of the “encounter problem” and the overall solution steps (see Figure 1). The first step in the solution procedure is to calculate the total distance traveled by multiplying the sum of the speeds of the two individuals (A and B) by the time taken. This requires participants to adopt a holistic thinking approach to learning. The subgoal-worked examples included the face of the “encounter problem” and the decomposition solution steps (see Figure 2). The first step of the solution procedure is to calculate the total distance of A (multiplying A’s speed by A’s time taken); the second step is to calculate the total distance of B (multiplying B’s speed by B’s time taken; the third step is to add A’s total distance to B’s total distance to calculate their combined total distance. Participants thus need to adopt a step-by-step approach to learning. The focused subgoal-labeled worked examples included the face of the “encounter problem” and the decomposition steps. The top-right corner of each question presented three questions related to the idea or steps of the “encounter problem” (see Figure 3). First, participants had to read the three prompting questions to help them better understand the learning content; they were then asked to use a decomposition of small events to learn the solution. The individual choice subgoal-worked examples included the problem face of the “encounter problem” and the decomposed solution steps. The top-right corner of each problem presented the three problems. It also presented the corresponding three options related to the idea or steps of the “encounter problem” (see Figure 4). Participants were first asked to choose one correct option for each question. The correct choice provided clues to help them better understand what they were learning. Then, for the focused subgoal-labeled worked examples, they used a decomposition of small events to learn the solution.

FIGURE 1

Figure 1. No subgoal-worked example.

FIGURE 2

Figure 2. Subgoal-worked example.

FIGURE 3

Figure 3. Focused subgoal-labeled worked example.

FIGURE 4

Figure 4. Individual choice subgoal-labeled worked example.

The worked example materials were presented in the form of PowerPoint, with one worked example problem per page.

Cognitive Load Scale

The scale was employed to measure the learners’ perceived cognitive load on their learning from the worked examples. It included two questions on mental effort and task difficulty. It had a nine-point illustrated rating scale. This consisted of one (very easy) to nine (very difficult). This scale was identical to that used by Paas (1992). Its reliability was found to be good by Paas (1992, p.429) and Paas et al. (1994, p.420). The Cronbach’s alpha for the current sample was 0.69.

Working Memory Capacity Test Materials

The working memory capacity test was based on that employed by Chen et al. (2018, p.492). It has been widely employed to measure the working memory capacity of primary school students (Chen et al., 2018, p.499; Leahy and Sweller, 2019, p.15). It consisted of four difficulty levels from low to high. They each consisted of three-six equations in turn. They had three trials for each difficulty level. In total, 54 equations were included. During the test, the participants were required to simultaneously complete both the processing and memorization tasks in working memory. First, the participants were presented with the first equation. They were asked to determine whether the equation’s result was correct. They had to write down the answer in the appropriate place in the answer booklet, remembering the first number of the equation. Thereafter, the second equation was presented with the same requirements until all equations were presented in one test. The participants were asked to recall and write down the first digit of each equation sequentially. The experiment began with two practice sessions. The participants were asked to listen and learn before proceeding to the formal working memory capacity test. At the end of the test, participants’ recall scores were calculated as the working memory capacity score. One digit was correctly recalled. The maximum score was 54. During the test, one equation was played on each PowerPoint slide for 6 s.

Transfer Test Materials

The transfer test was paper-based and contained near- and far-transfer tests. This indicated encounter problems with different surface features. However, they had the same structural features. The far-transfer test indicated encounter problems with different surface and structural features. The near-transfer tests and far-transfer tests each consisted of two individual choice questions and one application question. This was for a total of three questions and five points. Each individual choice question was worth one point for each correct choice. Each application question was worth three points. This included two points for the calculation steps and one point for the result. The points were allocated as follows: Zero points for the incorrect calculation steps and results, two points for the correct calculation steps and incorrect results, two points for the incomplete calculation steps and correct results, one point for directly giving the correct calculation results, and three points for both the complete calculation steps and correct results. The transfer test material was presented in PowerPoint. One question was presented on each PowerPoint slide. The participants had to write their answers under the corresponding question number in the answer booklet.

Ethics Statement

Ethical approval for this research was obtained from the Research Ethics Committee of Ludong University of China. This study of human participants has been ethically reviewed and approved in accordance with local legislation and institutional requirements. Written informed consent to participate in this study was provided by the participants’ legal guardian or next of kin.

Procedures

To ensure that elementary school students’ a priori knowledge did not adversely affect the test results, all potential participants completed a 5-min test of basic knowledge and asked to calculate the answer to each question as accurately as possible. At the end of the test, students who had sufficient basic knowledge were required to learn the encounter problem. However, they did not know that the encounter problem was intended to select participants for the formal experiment. As some of the experiments were completed by computer, selected participants were given the opportunity to practice with computer keystrokes and thereby familiarize themselves with the experimental procedures.

Worked Example Stage

To prevent external factors distracting participants, the experiment was conducted in a quiet computer room, in small groups of 10 participants each. The instruction for the no-subgoal-worked example and the worked example was “Hello, class! We will study four worked example problems of an ‘encounter problem’ in mathematics. In a moment you will see the first worked example problem. Please try to read and remember the steps of solving such problems. When the first question is completed, click the button to go to the next worked example problem until you finish studying the four worked example problems. The whole learning stage will take 10 min. When you are ready, press the space bar to start studying.” The instruction under the focused subgoal-labeled worked example was: “Hello, class! We are going to study four example problems of ‘encounter problems’ in mathematics. Next to each example problem, there are three small reflection problems. Please write the answer you think is correct in the corresponding place on the answer booklet. Please also remember the steps of solving such worked example problems. When you finish studying the first one, click the button to enter the study of the second worked example problem. Do this until you finish studying the four worked example problems.” They had 10 min to learn the worked examples. The instruction under the individual choice subgoal-labeled worked example was “Hello, class! We are going to study four worked examples of ‘encounter problems’ in mathematics. Next to each worked example, there are three small multiple-choice problems. Please choose the option you think is correct before the corresponding question number in the answer booklet. Please also remember the steps to solve these worked examples. When you complete the first one, click the button to go to the second worked example. Do this until you finish the four worked examples.” The entire study period lasted 10 min.

Cognitive Load Measurement Stage

The Paas scale was presented to the participants, and the instruction for mental effort was “Hello, class! Now, please evaluate your mental effort as accurately as possible. This is regarding learning for this type of question based on the state of learning you have just experienced. Use the following scale of one-nine representing increasing levels of effort. One indicates that it was very easy; five indicates that it required moderate effort, and nine indicates that it was very hard. Choose an appropriate number from the nine in the answer booklet to mark with a ‘√’.” The guiding phrase for the difficulty of the task was “Hello, class! How difficult do you think it is to learn the example now? The following levels of one-nine represent increasing difficulty. One indicates that it is very easy; five indicates that it is moderately difficult, and nine indicates that it is very difficult. Please choose an appropriate number from the nine numbers in the answer booklet to mark with a ‘√’.” The measurement time was 2 min.

The Working Memory Capacity Test Stage

Each group of participants was presented with the working memory capacity test material. The instruction was “Hello, classmate! The following is a memory test. PowerPoint will present three-six equations in sequence. You should mark ‘√’or ‘×’on the corresponding question number in the answer booklet. Please remember the first number of the equations. Thereafter, PowerPoint will present the second equation. You will also need to determine whether it is correct or incorrect. You must also remember the first number of the equation, and so on. This must occur until three-six equations are presented. You have to write down the first number of each equation in the appropriate place in the answer booklet.” The formal working memory capacity test began with two practice sessions. This ensured that the students had mastered the operations. The quiz took 20 min to complete.

Transfer Test Stage

Six test questions were presented to the participants in a sequence. They were instructed to answer in the corresponding positions in the answer booklet. The total test time was limited to 15 min. The participants’ cognitive load levels, working memory capacity, and transfer test scores were recorded.

Results

Comparison of the Effectiveness of Online Learning in Mathematics for Primary School Students Under the Subgoal-Worked Example and the No-Subgoal-Worked Example

Table 1 shows the participants’ cognitive load level, working memory capacity, and transfer scores in different example formats. The aim was to compare whether there were differences in the online learning effects of the primary school students under the no-subgoal-worked example and the subgoal-worked example. Independent samples t-tests were conducted on the mental effort, task difficulty, working memory capacity, and near- and far-transfer scores of the participants under the two worked example forms. The results showed that there was no statistically significant difference in the participants’ mental effort under the no-subgoal-worked example (M = 4.03, SD = 2.46) and the subgoal-worked example (M = 3.00, SD = 2.44), t₍₆₄₎ = 1.711; p = 0.092. There was no statistically significant difference in the task difficulty in the participants under the no-subgoal-worked example (M = 3.94, SD = 2.05) and the subgoal-worked example (M = 3.91, SD = 2.54), t₍₆₄₎ = 0.053; p = 0.958. This suggests that the two worked example forms did not have a significant effect on the primary school students’ cognitive load levels.

TABLE 1

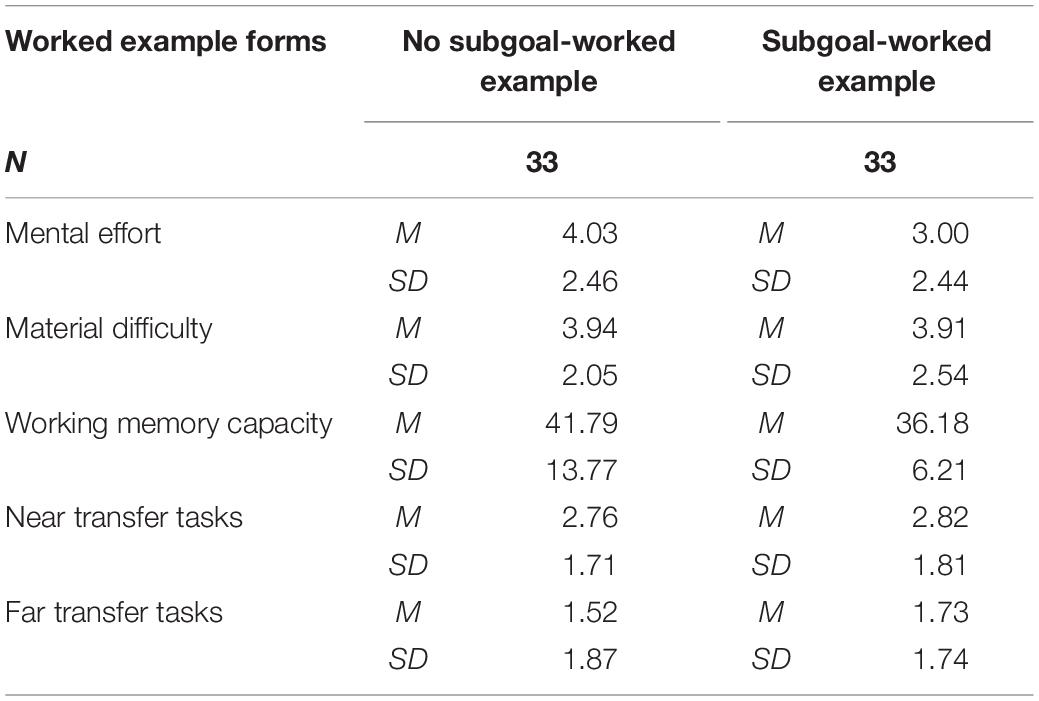
Table 1. Participants’ cognitive load level, working memory capacity and transfer scores in different example forms.

The working memory capacity of participants under the no-subgoal-worked example (M = 41.79, SD = 13.77) was significantly higher than that under the subgoal-worked example (M = 36.18, SD = 6.21), t₍₆₄₎ = 2.132, p = 0.039. This suggests that working memory resource depletion was higher for primary school students under the subgoal-worked example.

The no-subgoal-worked example (M = 2.76, SD = 1.71) and the subgoal-worked example (M = 2.82, SD = 1.81), t₍₆₄₎ = −0.140; p = 0.889 did not differ significantly in participants’ near-transfer scores. There was no significant difference in participants’ far-transfer scores under the no-subgoal-worked example (M = 1.52, SD = 1.87) and the subgoal-worked example (M = 1.73, SD = 1.74), t₍₆₄₎ = −0.477; p = 0.635. This indicates that the two worked example forms did not have a significant effect on the far- and near-transfer scores of primary school students. This showed that the subgoal-worked example increased working memory resource depletion during learning. This was as compared to the no-subgoal-worked example. However, it did not improve the transfer scores of primary school students.

The Facilitation of Subgoal Labeling on Online Learning of Worked Example Mathematics Subgoal for Primary School Students

Table 2 shows the participants’ cognitive load levels, working memory capacity, and transfer scores in the three worked example forms. The aim was to examine whether subgoal labeling could facilitate the learning efforts of subgoal-worked examples. One-way analyses of variance were conducted on the mental effort, task difficulty, working memory capacity, near-and far-transfer scores among the subgoal-worked examples, the focused subgoal-labeled worked example, and the individual choice subgoal-labeled worked example. The mental effort scores were significantly different among the three forms. The post hoc test (Tamhane) showed that the mental effort of participants employing the individual choice subgoal-labeled worked example (M = 1.78, SD = 0.83) was significantly lower than those employing the subgoal-worked example (M = 3.00, SD = 2.44, p = 0.029). It was also significantly lower than that of the focused subgoal-labeled worked example (M = 4.06, SD = 1.19, p < 0.001). The participants’ mental effort was not significantly different between the focused subgoal-labeled worked example (M = 4.06, SD = 1.19) and the subgoal-worked example (M = 3.00, SD = 2.44, p = 0.086). The task difficulty between the participants was not significantly different under the subgoal-worked example (M = 3.91, SD = 2.54), the focused subgoal-labeled worked example (M = 3.56, SD = 1.97), and the individual choice subgoal-labeled worked example (M = 3.50, SD = 2.62), F_{(2, 94)} = 0.277, MSE = 1.585, p = 0.759. This suggested that the math subgoal-worked example mental effort was lowest for primary school students under the individual choice subgoal-labeled worked example in online learning. The primary school students’ mental efforts were not significantly different between the subgoal-worked example and the focused subgoal-labeled worked example. The worked example forms did not have a significant effect on the primary school students’ task difficulty.

TABLE 2

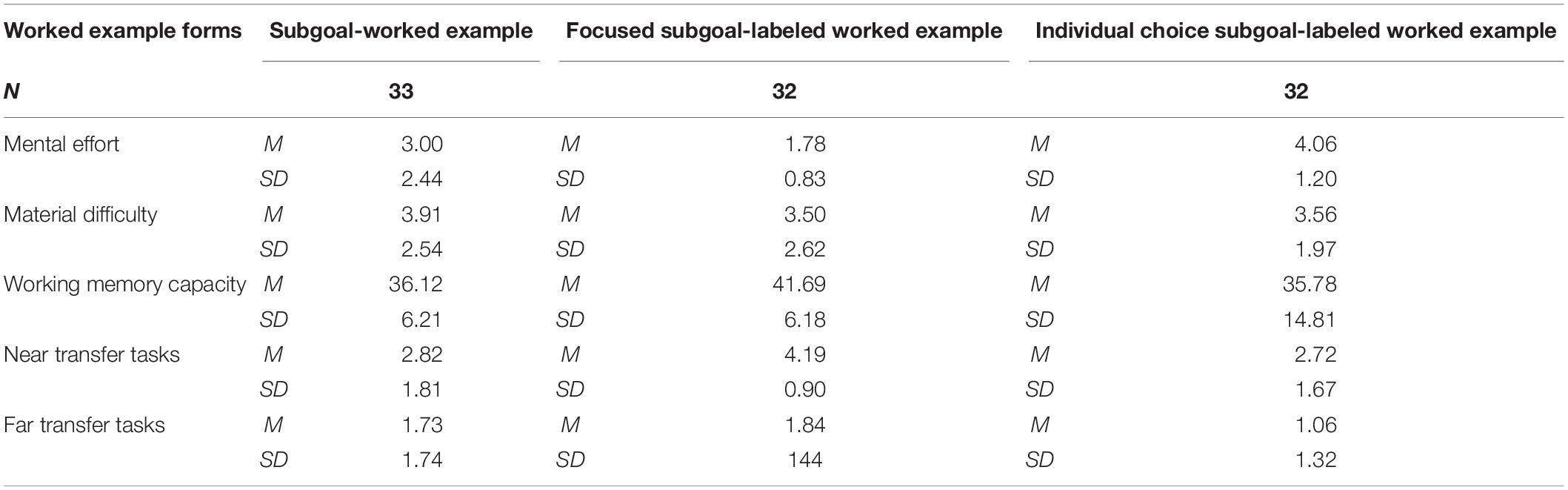
Table 2. Participants’ cognitive load level, working memory capacity and transfer scores in the three worked example forms.

According to previous studies (Chen et al., 2018, p.495; Leahy and Sweller, 2019, p.18), the working memory capacity after learning from worked examples represents the participants’ working memory resource depletion. Therefore, higher working memory capacity represents less working memory resource depletion and, in turn, the smaller the working memory capacity, the greater the working memory resource loss. The participants’ working memory capacity differed significantly between the three worked example forms, F_{(2,94) =} 3.569, MSE = 350.002, p = 0.032. The post hoc test’s (Tamhane) results showed that the working memory capacity of the participants under the individual choice subgoal-labeled worked example (M = 41.69, SD = 6.18) was significantly higher than that of the subgoal-worked example (M = 36.18, SD = 6.21, p = 0.002). However, there was no significant difference between the working memory capacity of the participants under the focused subgoal-labeled worked example (M = 35.78, SD = 14.81) and the subgoal-worked example (M = 36.18, SD = 6.21, p = 0.999). This indicates that the primary school students’ working memory resource depletion under the individual choice subgoal-labeled worked example was the lowest in the online learning of the mathematics subgoal-worked example. The subgoal-worked example and the focused subgoal-labeled worked example had no significant effect on primary school students’ cognitive resource depletion.

Participants’ near-transfer test scores were significantly different among the three worked example forms, F_(2,94) = 9.409, MSE = 21.647, p < 0.001. The post hoc test’s (Tamhane) results showed that participants employing the individual choice subgoal-labeled worked example (M = 4.19, SD = 0.90) received significantly higher scores. This was in comparison to those employing the subgoal-worked example (M = 2.82, SD = 1.81, p = 0.001) and the focused subgoal-labeled worked example (M = 1.67, SD = 0.30, p < 0.001). However, there was no significant difference between the focused subgoal-labeled worked example (M = 1.67, SD = 0.30) and the subgoal-worked example (M = 2.82, SD = 1.81, p = 0.994). This indicated that primary school students had the highest near-transfer scores under the individual choice subgoal-labeled worked example. This was in the online learning of the math subgoal-worked example. However, there was no significant difference between the subgoal-worked example and the focused subgoal-labeled worked example.

Participants’ far-transfer scores were not significantly different among the subgoal-worked example (M = 1.73, SD = 1.74), the individual choice worked example (M = 1.84, SD = 1.44), and the focused subgoal-labeled worked example (M = 1.06, SD = 1.32), F_(2,94) = 2.497, MSE = 5.701, p = 0.088). This indicates that there was no significant difference among the three worked example forms.

It is evident that the learning effect was not significantly different between the focused subgoal-labeled worked example and the subgoal-worked example. Therefore, the focused subgoal-labeled worked example did not promote the primary school students’ online learning effect. As compared to the worked example subgoal, primary school students with their individual choice subgoal-labeled, had a lower mental effort. They also had lower working memory resource depletion. Furthermore, they experienced higher near-transfer scores. Therefore, the individual choice subgoal label promoted the primary school students’ online learning effect.

Discussion

Comparison of the Effectiveness of Online Learning in Mathematics for Primary School Students Under the Subgoal-Worked Example and the No-Subgoal-Worked Example

Previous research on the no-subgoal-worked examples and subgoal-worked examples learning focused on college students solving “probability problems.” The results showed that participants in the subgoal-worked examples tended to perform better under near and far transfer than in the subgoal-worked examples (Margulieux et al., 2013, p.980; 2020, p.15; Catrambone, 2014, p.180). To verify further the effectiveness of the subgoal-worked example, this study designed a no-subgoal-worked example and a subgoal-worked example of the “encounter problem.” It was determined that there was no significant difference in the transfer scores between the two worked example forms. This was different from the results of previous studies. Gerjets et al. (2004, p.40) enrolled college students as participants, who were better at organizing and processing information. The subgoal-worked examples could help them discover the deep knowledge structure of the worked examples more easily. It could also help them form and remember knowledge blocks more quickly. Therefore, students had higher near-transfer scores in the subgoal-worked example. In the present study, there was no significant difference in the transfer scores between the no-subgoal-worked example and the subgoal-worked example. This may be because the primary school students tended to focus on the surface features of the worked example. It may also be because they ignored the structural features (Hancock-Niemic et al., 2016, p.120). They therefore did not develop mental representations for solving “encounter problems.” Conversely, as compared with college students, primary school students had a lower level of transfer ability (Zhao et al., 2019, p.33; Lin et al., 2021, p.76). Therefore, the transfer scores were poor in both the worked example forms.

The results showed that primary school students’ cognitive load was not significantly different between the no-subgoal-worked example and the subgoal-worked example. However, this was not in line with the findings of Gerjets et al. (2004, p.170). They found lower levels of cognitive load among college students in the subgoal-worked example. Gerjets et al. (2004, p.170) chose a “probability problem” with an eight-step worked example. The steps in the no-subgoal-worked example were difficult abstract formulas, numerical substitutions, and calculations. However, the steps of the subgoal-worked example were mostly small events with similar structures. These were easier to understand and remember (Catrambone, 2014, p.180). Therefore, the college students’ cognitive load level in the subgoal-worked example was lower. In this study, the experimental material was an “encounter problem.” Both the no-subgoal- and subgoal-worked examples contained the problem surface and the three steps required to solve the problem. In the worked example learning process, primary school students tended to read the same problem face first. They then learned the solution steps. However, due to the limitation of their thinking level, they may simply observe and imitate the solution steps (Qu and Zhang, 2019, p.42). They may lack in-depth thinking about the rules and principles implied in each step. In summary, in the two worked examples, their assessment of the difficulty and mental effort invested was mainly based on the number of solution steps. This was instead of the principles implied in them. Therefore, primary school students’ mental efforts and the task difficulty were not significantly different between the two examples.

Furthermore, the results showed that the working memory resources of primary school students employing the subgoal-worked example were significantly depleted. This was in comparison to those employing the no-subgoal-worked example. The no-subgoal-worked example adopts a holistic approach to solving the “encounter problem.” This caused primary school students to have a harder time understanding the arithmetic principles in the problem-solving steps. Therefore, they focused on the arithmetic steps instead. However, the four mixed operations in parentheses were simpler (Zhang and Lin, 2005, p.786). Therefore, their working memory resources were less depleted. The subgoal-worked example was a decomposition of the “encounter problem” into small events. The principles of the operations in the solution steps were relatively easy to understand. Therefore, primary school students devoted more working memory resources to learn and understand each operation step and its principles. Therefore, working memory resource depletion was higher in the subgoal-worked example.

The Facilitation of Subgoal Labeling on the Online Learning of Mathematics Subgoal-Worked Example for Primary School Students

Subgoal labeling is an important factor that affects the learning effect (Morrison et al., 2015, p.26; Margulieux et al., 2018, p.710). Combined with previous research (Renkl, 2002, p.540; Roelle and Renkl, 2020, p.131), this study designed a focused subgoal-labeled worked example. It also designed an individual choice subgoal-labeled worked example. It was found that primary school students employing the individual choice subgoal-labeled worked example had significantly higher near-transfer scores than those employing the subgoal-worked example. However, the primary school students employing the focused subgoal-labeled worked example were not significantly different from those employing the subgoal-worked example. Previous research suggests that during the worked example learning process, participants could effectively improve students’ problem-solving skills and improve their transfer test scores (Schworm and Renkl, 2007, p.285; Griffin et al., 2008, p.100). This occurred when participants were given eliciting questions. It was also when they were asked to think about and write their answers to the questions. This was while learning the worked example. Thus, the results of the individual choice subgoal-labeled worked example were consistent with the results of previous studies. The results of the focused subgoal-labeled worked example were inconsistent with those of previous studies. The individual choice subgoal label guided the primary school students to self-explain the principles of the solution steps. It also provided a scope for reflection. This prompted them to construct quickly a schema for solving the “encounter problem.” Conversely, this reduced the depletion of their working memory resources. They therefore had more working memory resources to complete the transfer test. Thus, the individual choice subgoal label facilitated primary school students’ transfer scores. In contrast, the focused subgoal labeling provided only questions. Students had to think about the answers, organize the language, and write the answers themselves. This consumed many of their working memory resources. They thus did not have enough resources to form a schema for the “encounter problem.” This affected their completion of the subsequent transfer test. Therefore, focused subgoal labeling did not facilitate transfer scores for the worked example online learning.

Furthermore, the results showed that primary school students employing the individual choice subgoal-labeled worked example implemented a significantly lower mental effort than those employing the subgoal-worked example. This may be the fact that in the individual choice subgoal-labeled worked example, they were more likely to understand the “encounter problem.” This provided primary school students with the principles of each operation step. Therefore, they would have lower mental effort levels. The results also showed that there was no significant difference between the mental effort of the primary school students in the focused subgoal-labeled worked example and the subgoal-worked example. The reason for this was that although the focused subgoal-labeled worked example provided problems, the relevant answers to the problems required the primary school students to put in the corresponding mental effort. Therefore, the focused subgoal-labeled worked example did not reduce the primary school students’ mental efforts. There was no significant difference in the assessment of task difficulty among the three worked example forms. This was probably because the assessment of the worked example learning process focused on the worked example itself rather than on the subgoal-labeled form. Therefore, the subgoal labeling did not have a significant effect on the assessment of task difficulty of the online subgoal-worked example learning in mathematics.

The results also revealed that the participants’ working memory resource depletion in the individual choice subgoal-labeled worked example was significantly lower than that in the subgoal-worked example. The individual choice subgoal-labeled worked example provided participants with solutions to the problems by presenting the problem surface with options. This resulted in less effort and lower mental effort during the learning process. The individual choice subgoal-labeled worked example reduced the working memory resource attrition of primary school students. In contrast, there was no significant difference between the working memory of participants under the focused subgoal-labeled worked example and the subgoal-labeled worked example. This was probably because the focused subgoal-labeled worked example only provided reference questions. A further reason could be that primary school students had to think about and write their answers while reading the worked example. Therefore, a lot of writing would take up their working memory resources. Thus, the focused subgoal-labeled worked example did not reduce the working memory resource depletion of primary school students.

Whether Working Memory Depletion Can Cause a Working Memory Resource Depletion Effect

Chen et al. (2018, p.500) concluded that if primary school students consumed too much working memory resources during the worked example learning process, they did not have sufficient resources to complete the subsequent tests. They therefore exhibited a working memory resource depletion effect. The results showed that as compared to the no-subgoal-worked example, the primary school students employing the subgoal-worked example had a high working memory resource depletion. However, the test scores were not different: primary school students showed no working memory depletion effect. As compared to the individual choice subgoal-labeled worked example, the primary school students employing the subgoal-worked example had high working memory resource depletion and low-test scores. They showed a working memory resource depletion effect. These two results contradict each other. There are arguments against this contradiction. We suggest that the investigation of the working memory resource depletion effect should not only focus on the relative depletion of working memory resource. However, this was also on the causes and effects of depletion. Furthermore, it was on the depletion of absolute working memory resources.

In this study, as compared to the subgoal-worked example, the no-subgoal-worked example and the individual-choice-labeled worked example both had less relative working memory resource depletion. They also had sufficient working memory resources to complete the subsequent tests. However, the test scores were still relatively lower in the no-subgoal-worked example. They were also higher in the individual choice subgoal-labeled worked example. Possible reasons were that the students employing the no-subgoal-worked example appeared to be intimidated and gave up thinking about the worked example. This was although there was less depletion of their working memory resources. However, it concurrently did not form a schema for the “encounter problem.” Therefore, even with sufficient working memory resources, the transfer test could not be completed effectively. Conversely, the individual choice subgoal-labeled worked example enhanced students’ deeper thinking about the “encounter problem.” It also provided them with directions for its interpretation. This promoted students to employ fewer working memory resources to form schemas about the “encounter problem” As a result, they had more working memory resources to complete the subsequent tests. They thus scored higher on the tests. The results indicate that there were different reasons for the low depletion of working memory resources between the two forms. Therefore, their transfer test results were different.

As compared with the individual choice subgoal-labeled worked example, the subgoal-worked example scores showed high working memory resource depletion. However, it had relatively poor transfer scores. It was speculated that the students employing the subgoal-worked example had poor transfer test scores due to the high depletion of their working memory resources. A further possible reason was the lack of sufficient resources to complete the transfer. This was because it was a resource-constrained process; the primary school students did not learn to solve the “encounter problem” at all. They therefore could not effectively complete the subsequent transfer test, even if they had sufficient resources. Moreover, the study did not further investigate participants’ working memory resource depletion over different learning intervals. Whether the working memory resources of the subjects recovered after an interval of time remains unclear. Therefore, the investigation of the working memory attrition effect should also focus on absolute working memory resource attrition. This should occur within the framework of the resource-constrained process and material-constrained process theories.

Conclusion

Four different worked example forms were designed in this study: the subgoal-worked example, the no-subgoal-worked example, the individual-choice-labeled worked example, and the focused subgoal-labeled worked example. The study investigated the mathematics worked example learning effect for primary school students in different worked example forms. Based on the experimental results, the following conclusions can be drawn: (1) as compared with the no-subgoal-worked example, the subgoal-worked example increased primary school students’ working memory resource depletion. However, it did not improve their scores. (2) As compared with the subgoal-worked example, the focused subgoal-labeled worked example did not promote the learning effectiveness of primary school students in mathematics. However, the individual choice subgoal-labeled worked example improved primary school students’ near-transfer scores. It also reduced their mental effort and working memory resource depletion. It is therefore a more effective subgoal-labeled worked example learning approach.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

The studies involving human participants were reviewed and approved by Ethics Committee audit certificate of Ludong University. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin. The animal study was reviewed and approved by Ethics Committee audit certificate of Ludong University.

Author Contributions

XG processed the data, performedthe data analysis, and produced the figures and tables. XD contributed to the writing and editing of the research methodology, results, and discussion. HL designed the research project, contributed to the design of the research instruments, and the writing and editing of the research methodology. All authors contributed to the conceptualization of the research, discussed the results, and commented on the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2022.832901/full#supplementary-material

References

Atkinson, R. K., Catrambone, R., and Merrill, M. M. (2003). Aiding transfer in statistics: examining the use of conceptually oriented equations and elaborations during subgoal learning. J. Educ. Psychol. 95, 762–773. doi: 10.1037/0022-0663.95.4.762

CrossRef Full Text | Google Scholar

Atkinson, R. K., Derry, S. J., Renkl, A., and Wortham, D. (2000). Learning from examples: instructional principles from the worked examples research. Rev. Educ. Res. 70, 181–214. doi: 10.3102/00346543070002181

CrossRef Full Text | Google Scholar

Catrambone, R. (1994). Improving examples to improve transfer to novel problems. Mem. Cognit. 22, 606–615. doi: 10.3758/BF03198399

PubMed Abstract | CrossRef Full Text | Google Scholar

Catrambone, R. (1998). The subgoal learning model: creating better examples so that students can solve novel problems. J. Exp. Psychol. Gen. 127, 355–376. doi: 10.1037/0096-3445.127.4.355

CrossRef Full Text | Google Scholar

Catrambone, R. (2014). Teaching subgoals to students improve learning. Zugriffam 12, 172–183. doi: 10.1016/j.apergo.2014.06.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Catrambone, R., and Holyoak, K. J. (1990). Learning subgoals and methods for solving probability problems. Mem. Cognit. 18, 593–603. doi: 10.3758/BF03197102

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, O., Castro-Alonso, J. C., Paas, F., and Sweller, J. (2018). Extending cognitive load theory to incorporate working memory resource depletion: evidence from the spacing effect. Educ. Psychol. Rev. 30, 483–501. doi: 10.1007/s10648-017-9426-2

CrossRef Full Text | Google Scholar

Chi, M. T. H., and Wylie, R. (2014). The ICAP framework: linking cognitive engagement to active learning outcomes. Educ. Psychol. 49, 219–243. doi: 10.1080/00461520.2014.965823

CrossRef Full Text | Google Scholar

Demetriadis, S. N., Papadopoulos, P. M., Stamelos, I. G., and Fischer, F. (2008). The effect of scaffolding students’ context-generating cognitive activity in technology-enhanced case-based learning. Comput. Educ. 51, 939–954. doi: 10.1016/j.compedu.2007.09.012

CrossRef Full Text | Google Scholar

Gerjets, P., Scheiter, K., and Catrambone, R. (2004). Designing instructional examples to reduce intrinsic cognitive load: molar versus modular presentation of solution procedures. Instr. Sci. 32, 33–58. doi: 10.1023/B:TRUC.0000021809.10236.71

CrossRef Full Text | Google Scholar

Gerjets, P., Scheiter, K., and Catrambone, R. (2019). Reducing cognitive load and fostering cognitive skill acquisition: benefits of category-a voiding instructional examples. Proc. EuroCogSci. 17, 133–138. doi: 10.4324/9781315782362-32

CrossRef Full Text | Google Scholar

Griffin, T. D., Wiley, J., and Thiede, K. W. (2008). Individual differences, rereading, and self-explanation: concurrent processing and cue validity as constraints on meta comprehension accuracy. Mem. Cogn. 36, 93–103. doi: 10.3758/MC.36.1.93

PubMed Abstract | CrossRef Full Text | Google Scholar

Hancock-Niemic, M. A., Lin, L., Atkinson, R. K., Renkl, A., and Wittwer, J. (2016). Example-based learning: exploring the use of matrices and problem variability. Educ. Technol. Res. Dev. 64, 115–136. doi: 10.1007/s11423-015-9403-8

CrossRef Full Text | Google Scholar

Kalyuga, S., Chandler, P., and Sweller, J. (2004). When redundant on-screen text in multimedia technical instruction can interfere with learning. Hum. Factors 46, 567–581. doi: 10.1518/hfes.46.3.567.50405

PubMed Abstract | CrossRef Full Text | Google Scholar

Leahy, W., and Sweller, J. (2019). Cognitive load theory, resource depletion and the delayed testing effect. Educ. Psychol. Rev. 31, 457–478. doi: 10.1007/s10648-019-09476-2

CrossRef Full Text | Google Scholar

Lin, H. X., Wang, Y. P., and Zheng, S. J. (2021). The impact of example problem pair forms on elementary students’ learning of mathematical operations. Math. Educ 30, 74–78.

Google Scholar

Lusk, M. M., and Atkinson, R. K. (2007). Animated pedagogical agents: Does their degree of embodiment impact learning from static or animated worked examples? Appl. Cognit. Psychol. 21, 747–764. doi: 10.1002/acp.1347

CrossRef Full Text | Google Scholar

Margulieux, L. E., and Catrambone, R. (2016). Improving problem solving with subgoal labels in expository text and worked examples. Learn. Instruct. 42, 58–71. doi: 10.1016/j.learninstruc.2015.12.002

CrossRef Full Text | Google Scholar

Margulieux, L. E., and Catrambone, R. (2019). Finding the best types of guidance for constructing self-explanations of subgoals in programming. J. Learn. Sci. 28, 108–151. doi: 10.1080/10508406.2018.1491852

CrossRef Full Text | Google Scholar

Margulieux, L. E., Catrambone, R., and Guzdial, M. (2013). “Subgoal labeled worked examples improve K-12 teacher performance in computer programming training,” in Proceedings of the 35th Annual Conference of the Cognitive Science Society, eds M. Knauff, M. Pauen, N. Sebanz, and I. Wachsmuth (Austin, TX: Cognitive Science Society), 978–983.

Google Scholar

Margulieux, L. E., Catrambone, R., and Schaeffer, L. M. (2018). Varying effects of subgoal labeled expository text in programming, chemistry, and statistics. Instr. Sci. 46, 707–722. doi: 10.1007/s11251-018-9451-7

CrossRef Full Text | Google Scholar

Margulieux, L. E., Guzdial, M., and Catrambone, R. (2012). “Subgoal-labeled instructional material improves performance and transfer in learning to develop mobile applications,” in Proceedings of the Ninth Annual International Conference on International computing Education Research, (New York, NY: ACM), 71–78. doi: 10.1145/2361276.2361291

CrossRef Full Text | Google Scholar

Margulieux, L. E., Morrison, B. B., and Decker, A. (2020). Reducing withdrawal and failure rates in introductory programming with subgoal labeled worked examples. Int. J. STEM Educ. 7:19. doi: 10.1186/s40594-020-00222-7

CrossRef Full Text | Google Scholar

Morrison, B. B., Margulieux, L. E., and Guzdial, M. (2015). “Subgoals, context, and worked examples in learning computing problem solving,” in Proceedings of the eleventh annual International Conference on International Computing Education Research, (New York, NY: ACM), 21–29.

Google Scholar

Paas, F. G., Van Merriënboer, J. J., and Adam, J. J. (1994). Measurement of cognitive load in instructional research. Percept. Mot. Skills 79, 419–430. doi: 10.2466/pms.1994.79.1.419

PubMed Abstract | CrossRef Full Text | Google Scholar

Paas, F. G. W. C. (1992). Training strategies for attaining transfer of problem-solving skill in statistics: a cognitive-load approach. J. Educ. Psychol. 84, 429–434. doi: 10.1037/0022-0663.84.4.429

CrossRef Full Text | Google Scholar

Qu, K. J., and Zhang, Q. (2019). Comparison of learning effect between single-content examples and double-content examples on arithmetic operation rules. Math. Educ. 28, 41–45.

Google Scholar

Renkl, A. (2002). Worked-out examples: instructional explanations support learning by self-explanations. Learn. Instr. 12, 529–556. doi: 10.1016/S0959-4752(01)00030-5

CrossRef Full Text | Google Scholar

Roelle, J., and Renkl, A. (2020). Does an option to review instructional explanations enhance example-based learning? It depends on learners’ academic self-concept. J. Educ. Psychol. 112, 131–147. doi: 10.1037/edu0000365

CrossRef Full Text | Google Scholar

Salden, R. J. C. M., Koedinger, K. R., Renkl, A., Aleven, V., and McLaren, B. M. (2010). Accounting for beneficial effects of worked examples in tutored problem solving. Educ. Psychol. Rev. 22, 379–392. doi: 10.1007/s10648-010-9143-6

CrossRef Full Text | Google Scholar

Schworm, S., and Renkl, A. (2007). Learning argumentation skills through the use of prompts for self-explaining examples. J. Educ. Psychol. 99, 285–296. doi: 10.1037/0022-0663.99.2.285

CrossRef Full Text | Google Scholar

Sweller, J. (1988). Cognitive load during problem solving: effects on learning. Cogn. Sci. 12, 257–285. doi: 10.1207/s15516709cog1202_4

CrossRef Full Text | Google Scholar

Sweller, J., and Chandler, P. (1994). Why some material is difficult to learn. Cogn. Instr. 12, 185–233.

Google Scholar

Sweller, J., and Cooper, G. A. (1985). The use of worked examples as a substitute for problem solving in learning algebra. Cogn. Instr. 2, 59–89. doi: 10.1207/s1532690xci0201_3

CrossRef Full Text | Google Scholar

Zhang, Q., and Lin, H. X. (2005). Worked example learning about the rules of the four fundamental admixture operations of arithmetic. Acta Psychol. Sin. 37, 784–790.

Google Scholar

Zhao, H. J., Li, Y., and Liu, X. Z. (2019). The influence of adult online learning motivation on learning transfer: the moderating effect of knowledge inertia. Educ. Res. 40, 33–34.

Google Scholar