
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Educ. , 28 April 2022
Sec. Assessment, Testing and Applied Measurement
Volume 7 - 2022 | https://doi.org/10.3389/feduc.2022.803040
This article is part of the Research Topic Validity, Reliability and Efficiency of Comparative Judgement to Assess Student Work View all 13 articles
Comparative judgement (CJ) is often said to be more suitable for judging exam questions inviting extended responses, as it is easier for judges to make holistic judgements on a small number of large, extended tasks than a large number of smaller tasks. On the other hand, there is evidence it may also be appropriate for judging responses to papers made up of many smaller structured tasks. We report on two CJ exercises on mathematics and science exam papers, which are constructed mainly of highly structured items. This is to explore whether judgements processed by the simplified pairs version of CJ can approximate the empirical difference in difficulty of pairs of papers. This can then be used to maintain standards between exam papers. This use of CJ, not its other use as an alternative to marking, is the focus of this paper. Within the exercises discussed, panels of experienced judges looked at pairs of scripts, from different sessions of the same test, and their judgements were processed via the simplified pairs CJ method. This produces a single figure for the estimated difference in difficulty between versions. We compared this figure to the difference obtained from traditional equating, used as a benchmark. In the mathematics study the difference derived from judgement via simplified pairs closely approximated the empirical equating difference. However, in science, the CJ outcome did not closely align with the empirical difference in difficulty. Reasons for the discrepancy may include the differences in the content of the exams or the specific judges. However, clearly, comparative judgement need not lead to an accurate impression of the relative difficulty of different exams. We discuss self-reported judge views on how they judged, including what questions they focused on, and the implications of these for the validity of CJ. Processes used when judging papers made up of highly structured tasks were varied, but judges were generally consistent enough. Some potential challenges to the validity of comparative judgement are present with judges sometimes using re-marking strategies, and sometimes focusing attention on subsets of the paper, and we explore these. A greater understanding of what judges are doing when they judge comparatively brings to the fore questions of judgement validity that remain implicit in marking and non-comparative judgement contexts.
High stakes exams in England have since 2011 used a standard maintaining approach called ‘comparable outcomes’, the aim of which is to avoid grade inflation by using statistical approaches to set grade boundaries to ensure roughly the same percentage of students get the same grade each year.1 Judgement of performance through inspection of scripts is limited to a small sample of scripts, typically between six and ten, on marks near key grade boundaries. The comparable outcomes method has been criticised for its inability to reflect any genuine change in performance year on year, while the script inspection element, due to how limited it is, has been criticised for a lack of rigour and a lack of independence from the statistical approaches. In response to these criticisms, Ofqual, the Regulator of educational qualifications for England, in 2019 invited the exam boards in the United Kingdom to discuss and investigate the possibility of using comparative judgement (CJ) evidence in maintaining exam standards (Curcin et al., 2019, p. 14) as this could allow better use of evidence based on judgements of candidate scripts.
Using CJ to maintain exam standards typically involves exam scripts from the current exam for which standards are being set and scripts from a previous exam representing the benchmark standard that is to be carried forward. Judges are presented with pairs of student exam scripts – typically one from each exam – and make decisions about which is better. Many judgements are made by many judges. A statistical model such as the Bradley-Terry model (Bradley and Terry, 1952, p. 325) is then used to convert these judgements into a measure of script quality. The measures for each script from both exams are located on the same scale allowing the mapping of scores (and boundary marks for different grades) from one exam to the other, thus allowing a boundary mark on the benchmark exam to be equated to the new exam (Bramley, 2005, p. 202). A simplified version of this method has also been developed at Cambridge University Press & Assessment, as described in Benton et al. (2020, p. 5). In this method, called simplified pairs, the mapping of scores between different tests is undertaken without the need to estimate values on a common scale by fitting a statistical model. This makes it more efficient, as scripts only need to appear in one comparison, rather than many. Note that this method can only be used as a means to find a mapping between two existing mark scales. Unlike other CJ approaches, it does not provide a fresh ranking of the exam scripts included in the study (see, Benton, 2021, for further details).
In 2019 Oxford, Cambridge and RSA Examination (OCR) – one of the exam boards which deliver high stakes exams in England, and part of Cambridge University Press & Assessment – correspondingly launched a programme of research which aimed to evaluate the effectiveness of using comparative judgement to maintain standards in exams. The programme eventually comprised 20 CJ exercises across several subjects and qualification types and overall outcomes are recorded in Benton et al. (2022). The present article, in focusing specifically on the two exercises on highly structured papers, and exploring insights in more detail, makes a contribution distinct from that work.
Comparative judgement requires that judges make holistic judgements of student work. Much previous research on the use of CJ in awarding has focused on examinations requiring essay-type responses (e.g., Gill et al., 2007, p. 5; Curcin et al., 2019, p. 10). CJ has been successfully used to “scale performances by students in creative writing essays, visual arts, philosophy, accounting and finance, and chemistry (laboratory reports)”, according to Humphry and McGrane (2015, p. 459) who assert that it is promising for maintaining standards on assessments made up of extended tasks. For this reason, initially the OCR research programme trialled assessments made of extended tasks where holistic judgements might be seen to be more appropriate, e.g., Sociology, English Language and English Literature.
However, OCR were interested in the possibility of applying the same CJ standard-setting methods across all subjects, including science, technology, engineering, and mathematics (STEM) subjects which tend not to include extended tasks. CJ has not been studied as thoroughly in relation to STEM subjects, or subjects utilising extended tasks. Consequently, exercises in both mathematics and science were set up, and are reported on here. The present article aims to answer questions about the nature of holistic judgements and whether judges can make them on highly structured papers. This will help to inform debate on the future use of CJ for maintaining standards in STEM subjects.
The insights from this paper may also be valuable for those interested in maintaining exam standards in other, non-United Kingdom, education systems that utilise high-stakes external tests where it is important to maintain standards. The procedures discussed in the present article were developed in and for the United Kingdom context, in which there is a need to equate standards of assessments from year to year. Crucially, in this context, more established statistical equating methods, such as pre-testing of items, are not available, as items are created anew for each year and are not released in advance of the exams being sat in order to preserve the confidentiality of the assessment. Note that in what follows, it is uses of CJ for standard maintaining that are discussed; the use of CJ as an alternative to marking is not a focus here. In the discussed exercises, all the scripts used had been marked – the goal is the maintenance of standards between assessments set in different years.
The paper starts with a brief literature review and a discussion of prior findings from OCR trials for non-STEM subjects (which utilised mostly more extended tasks) including surveys of judges taking part in these trials. Following that, we present the findings of two CJ exercises in STEM subjects (mathematics and science), as well as the outcomes of surveys of their judges. Our discussion and conclusions focus on the accuracy and validity of CJ for judging highly structured exam papers such as those used to assess STEM subjects in United Kingdom high stakes exams. We then consider implications for decision-making about whether CJ is a suitable way to maintain exam standards in subjects using highly structured papers.
Literature identifies features which may impact the accuracy and validity of judgements and judges’ ability to make judgements. These can relate to the processes judges use, the questions (or parts of scripts) that they attend to, and whether they are able to make holistic judgements or conversely just end up re-marking the papers and adding up the marks. This section will explore what we know currently about judgemental processes in assessment.
Work on the cognitive processes used by judges of exam scripts has been pioneered by Cambridge Assessment researchers, with a substantial series of linked research projects in the 2005–2010 period central to that (e.g., Suto and Greatorex, 2008, p. 214; Suto et al., 2008, pp. 7–8; Crisp, 2010a, p. 3). The research area is a subset of the field of judgement and decision-making, in which there has been psychological research under various paradigms. Areas such as “what information people pay attention to”, the heuristics and biases they face, and the role of the behavioural and social, were explored, as were assessments of the sequences of mental processes undertaken when making decisions. Much of this research, however, focused on marking. Through think-aloud sessions, observation and interview, the processes used in marking, such as scrutinising, elaborating and scanning, were described (e.g., Suto et al., 2008, p. 7; Crisp, 2010b). Crisp (2008) found in a marking study that most aspects of the candidate work noted by examiners related to relevant content knowledge, understanding and skills. As discussed, the present article considers the case for CJ for standard maintaining purposes, not as an alternative to marking.
Where there are several questions that must be considered in a script it is possible that judges may only pay attention to a subset (Verhavert et al., 2019). For Verhavert et al. (2019) the structure of a task impacts on both the reliability and the complexity of a CJ exercise for judges. Similarly, in a study of different CJ approaches to making grading decisions in a biology exam, Greatorex et al. (2008, pp. 4–5) report that it was clear that not all questions received equal consideration. The researchers found from analysis of which questions judges referenced as those that they focused on the most, that the same question (a long-answer question with more marks than any others on the paper) was referenced for all methods. Crucially, however, this long answer question empirically discriminated poorly, suggesting that judges are not good at determining which questions they should be focusing on due to their greater discriminatory power. They concluded that what judges across these methods focus on were “some key questions but not necessarily the most useful ones” (p. 9). Greatorex (2007, p. 9), in reviewing wider literature, highlights that “experts are good at knowing what they are looking for but they are not good at mentally combining information”.
Using CJ for maintaining standards between tests will require that judges compare performances on different tests including different questions, e.g., a response to the 2018 exam and the 2019 exam. These two exams will intend to assess the same constructs to the same standard, but the difficulty of the particular questions and therefore exams varies between years. (In the United Kingdom’s exam systems papers are not pre-tested so the difficulty of the items is not known before papers are sat). Judgements between different exam papers require that judges can take some account of these differences in their decision-making. Black (2008, p. 16) found that judges in a CJ exercise tended to suggest that comparing scripts where the candidates were answering different questions – “because the papers under comparison were different in different years” – was “fairly difficult”. Judges noted that they frequently had to remind themselves what the candidates were writing about, and that it is difficult to make like-with-like comparisons in this context.
Baird (2007, p. 142) raised the concern that “examiners cannot adequately compensate in their judgements of candidates’ work for the demands of the question papers”. The concern is that, as suggested by Good and Cresswell (1988, p. 278), subject experts will be more impressed by a candidate achieving a high score on an easy paper than by a candidate achieving a (statistically equivalent) lower score achieved on a harder paper. An experiment presented by Benton et al. (2020, p. 21) for an English literature examination appears to suggest that this concern is not always justified, as in that case the CJ method meant that judges were able to appropriately make allowances for paper difficulty. This paper extends this work to mathematics and science exams when grade boundaries are set using CJ.
Humphry and McGrane (2015, p. 452) highlight that judging between responses to different exam questions, potentially of different difficulty, across several assessment criteria, can increase cognitive load to the extent that the task becomes difficult and potentially unreliable. This therefore brings out the question of potential re-marking of each individual question – “rather than making a holistic judgement” – and then just adding up the scores (though this means the difficulty of each paper is not accounted for). Leech and Chambers (2022) found that when judging a physical education exam, judges varied in their approach. Some re-marked the scripts, only one (of six) marked purely holistically, and the others combined both approaches. The level of re-marking of each question observed suggests that judgements were only partially, if at all, holistic.
Another issue in relation to what judges attend to is the question of construct-irrelevant features. Bramley (2012, p. 18) carried out an experiment into whether manipulating features of scripts that did not alter the marks, such as quality of written response and proportion of missing to incorrect responses, changed judges’ views of script quality. The two largest effects were seen by changing the proportion of marks gained on items defined as testing “good chemistry” knowledge, (Bramley, 2012, p. 19) where scripts with a higher proportion appeared better on average, and replacing incorrect with missing responses, where scripts with missing responses appeared worse on average. The implication is that the decision on relative quality is affected by the makeup of the scripts chosen. More recent work on this (Chambers and Cunningham, 2022) found that replacing incorrect answers with missing answers affected judges’ decision-making. Scripts with missing responses, rather than zeroes, received statistically significantly lower script measures on average. If judges are looking at construct-irrelevant features, this is a threat to the validity of the CJ awarding process.2 Chambers and Cunningham found that other construct-irrelevant features of spelling, punctuation, grammar, and appearance (e.g., crossings-out and text insertions and writing outside of the designated answer area) did not impact judges’ decisions, however.
STEM subjects have been previously investigated as part of CJ exercises. For example, the accuracy of holistic judgements in history (non-STEM) and physics (STEM) was investigated by Gill and Bramley (2013, p. 310). In this study, examiners made three different kinds of judgements. These were: absolute judgements (that is, was the script worthy of the grade or not?), comparative judgements (of which script is better), and judgements of their own confidence in their other judgements. In both subjects, relative judgements were more accurate than absolute ones, and judgements the examiners were ‘very confident’ in were more accurate than other judgements. However, in physics, the further apart two scripts were in terms of overall mark the greater the likelihood of a correct relative judgement, but in history the link was weaker. This may suggest that in STEM there are more “right answers” and less scope for legitimate differences in judge professional judgement.
Jones et al. (2015, p. 172) used CJ to successfully assess mathematical problem solving. They highlighted that CJ was more useful when judging mathematics if longer, more open-ended tasks were used. In a similar manner, Humphry and McGrane (2015, p. 457) described paired CJ comparisons as “likely to be more suitable for extended tasks because they allow students to show a range of abilities in a single and coherent performance, which can be compared holistically”. However, in examinations assessing STEM subjects – at least as currently designed in the United Kingdom – there are typically not a small number of extended tasks, but many shorter answer questions. As Jones et al. (2015) indicate, this is not an intrinsic feature of STEM assessments, but is generally the case, at least in the United Kingdom. STEM assessments and highly structured exams are not synonymous. This means that it is not whether a subject is STEM or not that determines whether it is appropriate for use in CJ, but how structured the exam is. In other words, item design, not item content, is the issue at stake. This paper will therefore be discussing the issue in this way.
Initially the OCR programme looked at assessments where holistic judgements might be more straightforward, as tasks are generally extended response and fewer in number. The programme investigated, among others, Sociology, English Language and English Literature. The precision of the outcomes of these exercises was high, with standard errors (which indicate the precision of the grade boundary estimates) of between 1.5 and 2.5 on each test – i.e., typically a confidence interval of ±1.2 marks on the test (Benton et al., 2022).
Point biserial correlations3 demonstrate the association between the CJ judgement and the original marks given to each script. For exams comprising extended responses these were between 0.34 and 0.52 - encouraging figures. Further trials included exam papers with a mix of more and less structured tasks e.g., Geography, Business Studies, Enterprise and Marketing, Child Development, and Information Technologies (Benton et al., 2022). Outcomes of these CJ exercises were as accurate as with all the exercises using extended response question papers, with standard errors between 1.4 and 2.7. Consequently, we thought perhaps CJ exercises on papers made up mainly of highly structured tasks would be equally reliable.
The judges of these exercises were also asked about how they make their decisions. OCR judges differed in their views of whether it was at all straightforward to compare responses to tests from different series (i.e., those with different sets of questions, albeit likely similar in form). While many judges felt that they were able to do this, another was “not sure it was possible” and some papers were described as “apples and pears”. This corresponds to the insights of Black (2008, p. 16), mentioned earlier.
A further question of interest is that of how judges decide between scripts which each demonstrate different legitimate strengths to different degrees. Many judges in these trials suggested they had difficulty deciding between, for instance, scripts with greater technical accuracy and greater “flair”, or scripts with strengths in reading and strengths in writing, and so on. This was clearly a challenge for many judges (roughly a third in these trials).
A notable number of judges responded that they were making judgements primarily on certain long-answer questions. The validity of this approach can be challenged. On the one hand, candidates should answer the whole script, and awards are based on all responses. On the other, these questions are worth more marks and are likely therefore to contribute more to rank order determinations on marks as well as by judgement. They might be seen to demonstrate more true ability. However, most judges who said that they judged mainly on long answer questions said they did so as these questions were worth more marks, not because they were seen as intrinsically stronger determiners of quality.
Judges in these trials had not necessarily internalised an idea of “better” that is distinct from what the mark scheme says should be credited. What they were effectively asking for was some measure of standardisation. Even those judges who said that the constructs they were judging resided in their minds, not in the mark scheme, suggested that this was because of their experience of marking. This then calls into question the idea that judges can make holistic judgements separate from marks, or at least that they can be confident in what they are doing. On the other hand, other judges suggested that CJ made them more thoughtful and deep judgements of quality.
In order to assess the suitability of the simplified pairs method of comparative judgement for accurately estimating the true difference in difficulty between pairs of highly structured papers, and to investigate the nature of decisions made by judges, we defined two research questions. These were:
RQ1 (the accuracy question): “Can comparative judgement estimate the true difference in difficulty between two exam papers comprising many highly structured tasks?”
RQ2: (the validity question): “How do judges make comparative judgements of students work from exam papers comprising many highly structured tasks, and what validity implications does understanding their processes have?”
In the main, RQ1 was addressed using the results of the CJ exercises, while RQ2 is addressed via insights from follow-up surveys of the judges involved in the exercises.
The first aim of both studies reported in this paper was to assess whether the simplified pairs method of comparative judgement could accurately estimate the true difference in difficulty between two exam papers (as determined by statistical equating). If they can, this means there is the potential for the method to be used in standard maintaining exercises, where the difference in difficulty between last year’s paper and this year’s is fundamental.
In the simplified pairs method (see Benton et al., 2020, p. 5), judges undertake many paired comparisons and decide which of each pair is better, in terms of overall quality of work. For example, there might be six judges who each make 50 comparisons between pairs of scripts (one from each exam paper), with the difference in marks (from the original marking) for each pair varying between 0 and 25 marks. In about half the comparisons, the paper 1 script will have the higher mark and about half the time the paper 2 script will have the higher mark. Each script should only appear in one paired comparison, so 300 different scripts from each paper will be required.
For each paired comparison, the number of marks given to each script is recorded, as well as which script won the comparison. This is so that we can determine the relationship between the mark difference and the probability that script A (from paper 1) beats script B (from paper 2). This relationship is then used to answer the following question:
Suppose a script on paper 1 has been awarded a score of x. How many marks would a script from paper 2 need to have a 50% chance of being judged superior?
If we have many paired comparisons for each mark difference, we could take the raw percentages as probabilities of superiority and use them to answer this question. However, it is unlikely that the relationship between mark difference and probability of superiority will be a smooth progression. More likely, we will have something like the pattern evident in Table 1.
It is not clear from this whether the 50% probability of the paper 2 script being judged superior is at a mark difference of 0 marks, or between 2 (40%) and 3 marks (71%).
To overcome this issue, the simplified pairs method uses a logistic regression to generate a smoothed relationship between the mark difference and the probability of the paper 2 script being judged superior. In this type of model, for the ith pair of scripts judged by the jth judge we denote the difference between the mark awarded to the paper 2 script and that awarded to the paper 1 script as dij. We set yij = 0 if the judge selects the paper 1 script as superior and yij = 1 if they select the paper 2 script. The relationship between yij and dij is then modelled using the usual logistic regression equation:
From this equation we need to find the value of dij such that P(yij = 1) = 0.5. This will give us the mark difference associated with a probability of 0.50 that the paper 2 script will be judged superior. If we denote the estimated coefficients in the logistic regression model as and , then after some re-arranging the estimated difference in difficulty for a probability of 0.50 is:
This difference can then be compared with the empirical difference in difficulty between the two papers.
As this method only requires each script to appear in one paired comparison, it has a notable advantage over alternative CJ methods, which generally require that each script appears in many comparisons. The results of these comparisons are then combined and analysed using a statistical model, such as the Bradley-Terry model (Bradley and Terry, 1952, p. 325). Simplified pairs does not require this step, meaning that a much greater number of scripts can be included in a simplified pairs study compared to Bradley-Terry methods, without the judges having to spend any more time on making judgements.
It is also important to consider the design of CJ exercises. There are several aspects to this, including the choice of papers, the number of scripts and judges, the range of marks that the scripts will cover, and the instructions to the judges. These are outlined in the following sections.
The first step in each study involved selecting two assessments to be used for the analysis. We used GCSE (General Certificate of Secondary Education) assessments for both exercises, which are typically sat by students at the age of 16 in England.
For the mathematics exercise, we created the assessments by splitting a single 100-mark GCSE Mathematics exam component into two 50-mark examinations (“half-length assessments”). The original full-length assessment for analysis was chosen as it was taken by a large sample of students, which meant that we could undertake a formal statistical equating, to use as a comparator to the results from the simplified pairs.
Further details on the two half-length assessments are displayed in Table 2, and some example questions are listed in Appendix B (see Supplementary Material). Each half-length assessment contained 10 questions worth a total of 50 marks. The mean scores of each question were calculated based on the responses of all 16,345 candidates and are also displayed. As can be seen, the total of these mean question scores indicates that Half 2 was roughly 5 marks harder than Half 1.
For science, the exam papers we chose were the foundation tier chemistry papers from the OCR Combined Science A GCSE qualification. Two papers, named component 03 and component 04, were used. Example questions are listed in Appendix B (see Supplementary Material). As with the Mathematics paper, these papers were chosen partly because they were taken by many students. An additional reason for choosing these papers was that the mean mark was higher on component 03 by around 9% of the maximum. One aim of this research was to see if examiners could make allowances in their judgements for differences in paper difficulty, and this seemed like a reasonable level of difference (i.e., challenging, but not impossible).
Both science papers had a maximum mark of 60 and were each worth 1/6th of the whole qualification for foundation tier candidates. However, it is worth noting that the science papers did not cover the same content. This contrasts with the situation in a typical standard maintaining exercise (such as awarding), when the two papers being compared are based on mostly the same content. It also contrasts with the mathematics exercise described here and with previous trials of the simplified pairs method (e.g., Benton et al., 2020). Therefore, the examiners in this exercise may have found the task harder than a similar task undertaken to assist with awarding.
In both exercises, exam scripts were randomly selected for the simplified pairs comparison exercise, 300 from each paper (or half paper in the case of mathematics). As the exercises were independent of one another, this means 300 scripts were selected in mathematics and 300 in science; these were all different students. For mathematics, different samples of students were used to provide script images for the Half 1 assessments and for the Half 2 assessments.
In standard maintaining exercises we are interested in determining changes in difficulty across the whole mark range (or at least the mark range encompassing all the grade boundaries). Therefore, in CJ studies in this context it is important to ensure that the paired comparisons include scripts with a wide range of marks in both papers.
For each half-length assessment in mathematics, scripts with scores between 10 and 45 (out of 50) on the relevant half were selected, with an approximately uniform distribution of marks within this range. Scripts from each half were randomly assigned to pairs subject to the restriction that the raw scores of each half-script within a pair had to be within 15 marks of one another.
For science, the intention was that the spread of scripts across the mark range was the same for both components (an approximately uniform distribution from 20% to 90% of maximum marks). However, due to a small error in the code used to select the scripts, the range for component 04 was actually from 13% to 90% of the maximum mark. This contributed to the fact that the average score for the scripts selected for component 04 was around 4.5 marks lower than for component 03. This error was not picked up until after the exercise was complete. It will not have had any effect on the statistical analysis, as there were still many comparisons made across a broad range of mark differences. However, it is possible that it had a psychological impact on the examiners (who might have expected a more even distribution of mark differences).
The range of marks on the scripts was 12 to 53 on component 03 and 8 to 484 on component 04. The scripts were randomly assigned to pairs. For some pairs, the component 03 script had a higher mark and for some the component 04 script did. Some pairs had a very large difference in marks, whilst others had a difference of zero marks.
Six experienced examiners were recruited to take part in each exercise – i.e., six for mathematics and six for science. However, in the GCSE Science exercise, one judge subsequently dropped out due to other commitments. Each examiner was given 50 pairs of scripts (half-scripts for mathematics) to compare (on-screen), and they were asked to determine ‘Which script is better, based on overall quality?’.
The examiners were given additional guidance explaining that this involved making a holistic judgement of the quality of the scripts, using whatever method they wished, to choose the better one. They were also told that they should use their professional judgement to allow for differences in the relative difficulty of each test. In advance of the task, the examiners were provided with the exam papers and mark schemes and asked to re-familiarise themselves with both. Beyond this, there was intentionally no specific training provided, as the rationale of CJ is for examiners to use their professional judgement to make holistic judgements.
All judgements were made on-screen using the Cambridge Assessment Comparative Judgement Tool5. No marks or other annotations were visible to the judges on any of the scripts.
Figure 1 shows further details on the design of the science CJ task (and some of the results). Each numbered ‘point’ on the figure represents one pair of scripts, with the number indicating the examiner making the judgement. The horizontal axis shows the mark given to the script from component 03 and the vertical axis the mark given to the script from component 04. Blue indicates that the script from component 03 was judged superior, and red that the component 04 script was judged superior. The diagonal line is a line of equality between the two marks, so that points below the line indicate a pair where the script from component 03 had a higher raw mark than the component 04 script. Unsurprisingly, blue points were more likely to be below the line and red points more likely to be above the line. More detailed analysis of the relationship between assessment scores and judges’ decisions will be shown later in this article.
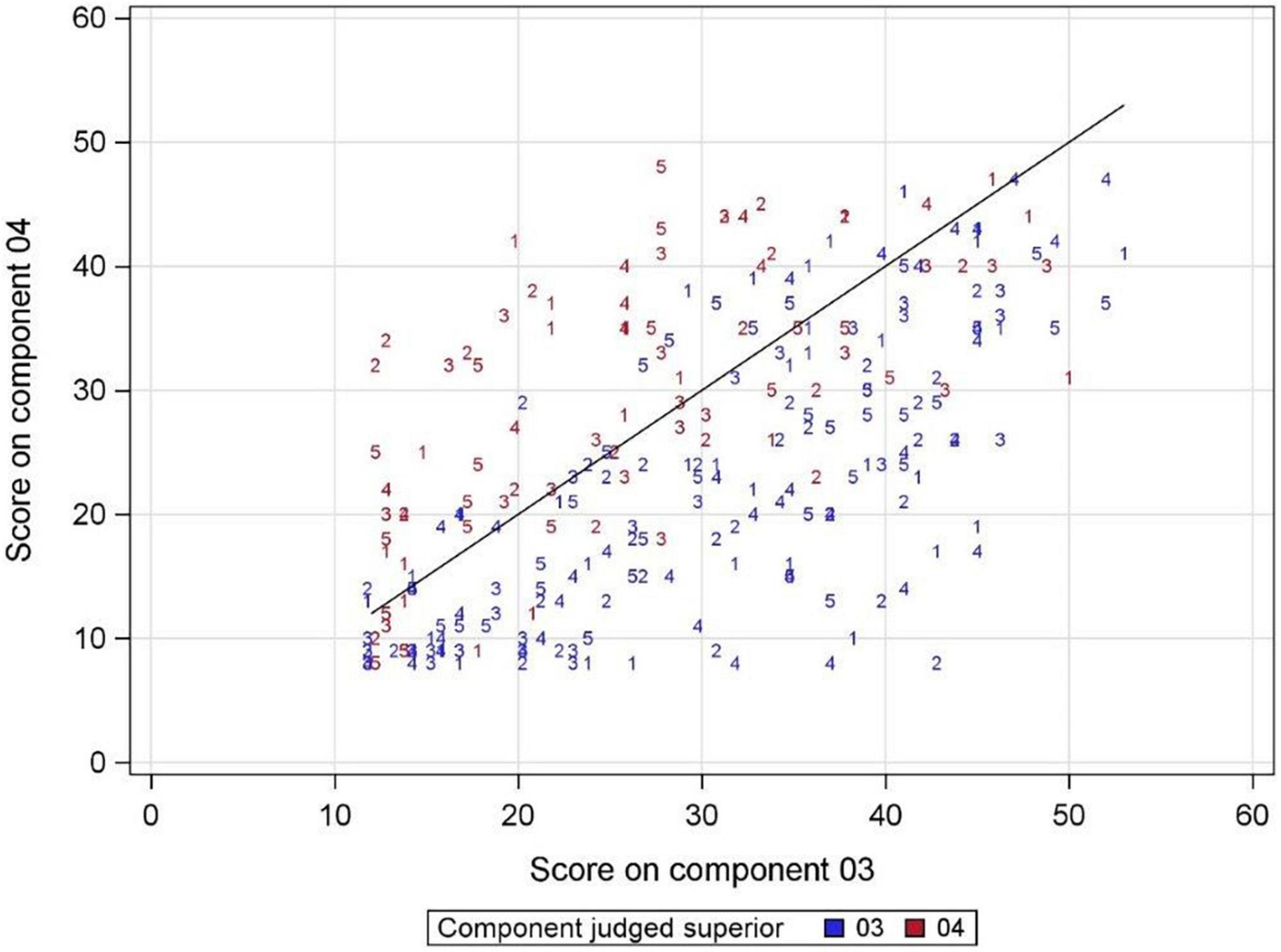
Figure 1. The design of the simplified pairs study. The locations of the points show which scores on science component 03 were paired with which scores on component 04 and the numbers indicate which examiner made the judgement. The black line is a line of equality, rather than a regression line.
The follow-up surveys provided data to address Research Question 2 – “How do judges make comparative judgements of students work from exam papers comprising many highly structured tasks, and what validity implications does understanding their processes have?” After both studies, the judges who had taken part were invited to take part in short surveys to inform the researchers about their experiences of the task and about how they thought they made their judgements. The surveys were administered to judges via SurveyMonkey™ a short time after they had finished their judgements and took approximately 10 min to complete. The two surveys were slightly different in their questions, but similar enough for answers to be compared here. Insights from the surveys, especially those that relate to the validity of the exercise, are discussed in what follows.
These surveys were developed by the researchers, based on those used in earlier exercises within the wider series of studies, with the precise wording and focus of questions being arrived at as a result of an iterative process. The questions are listed in Appendix A (see Supplementary Material), except where they are not directly related to the subject of this article. A combination of open questions and closed-response questions using five-point Likert scales were utilised. Surveys were used in order to get responses rapidly, in order that insights could be acted upon within the wider series of studies in terms of future exercise design.
Data from open questions were analysed using both a priori and inductive methods. A priori themes were predicted from previous experience and literature (on issues including approaches to judging where students had uneven performance across a paper). Inductive methods revealed new themes (such as differences in approach between mathematics judges and science judges).
Here, and in Section “Simplified Pairs Results,” we present results that answer RQ1. Firstly, the overall difference in difficulty between the two assessments in each exercise is shown. Table 3 presents the results of a mean equating between the two half-length assessments in the Mathematics GCSE, which demonstrates the empirical difference in difficulty between the two half papers. Table 4 presents the results of the equating between component 03 and component 04 in the Science GCSE. These were based on the scores of all students taking the component(s), not just those included in the CJ exercise. The tables show that for the mathematics exercise, Half 2 was about 5 marks harder than Half 1 and for science, component 04 was about 5 and a half marks harder than component 03.
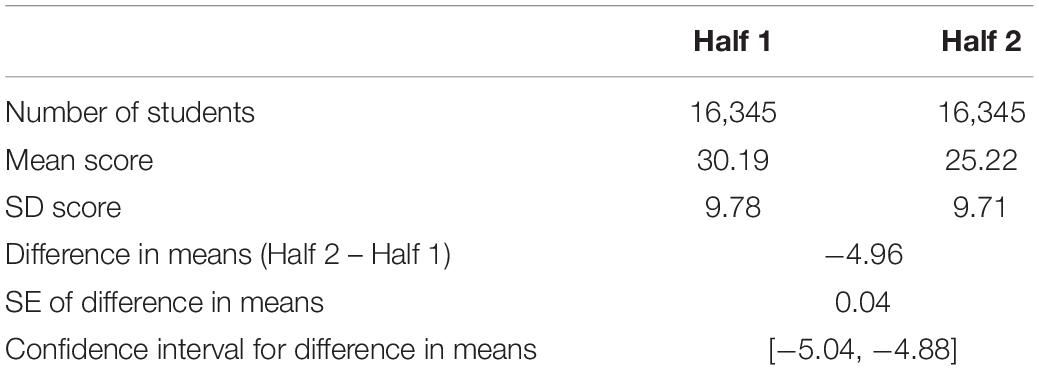
Table 3. Results from mean equating of the actual scores of pupils taking the two half papers (mathematics).

Table 4. Results from mean equating of the actual scores of pupils taking the two components (science).
Next, we present an estimate of the overall difference in difficulty between components (or half papers) using the results of the simplified pairs exercise. Figures 2, 3 plot the proportion of paired comparisons where the script from Half 2 (mathematics) or component 04 (science) was judged superior, against the mark difference between each pair of scripts. Larger points depict mark differences with more judgements made. As can be seen, the proportion of pairs where Half 2 (or component 04) is deemed superior tends to increase with the extent to which the mark on the Half 2 (or component 04) script exceeds the mark on the Half 1 (component 03) script.
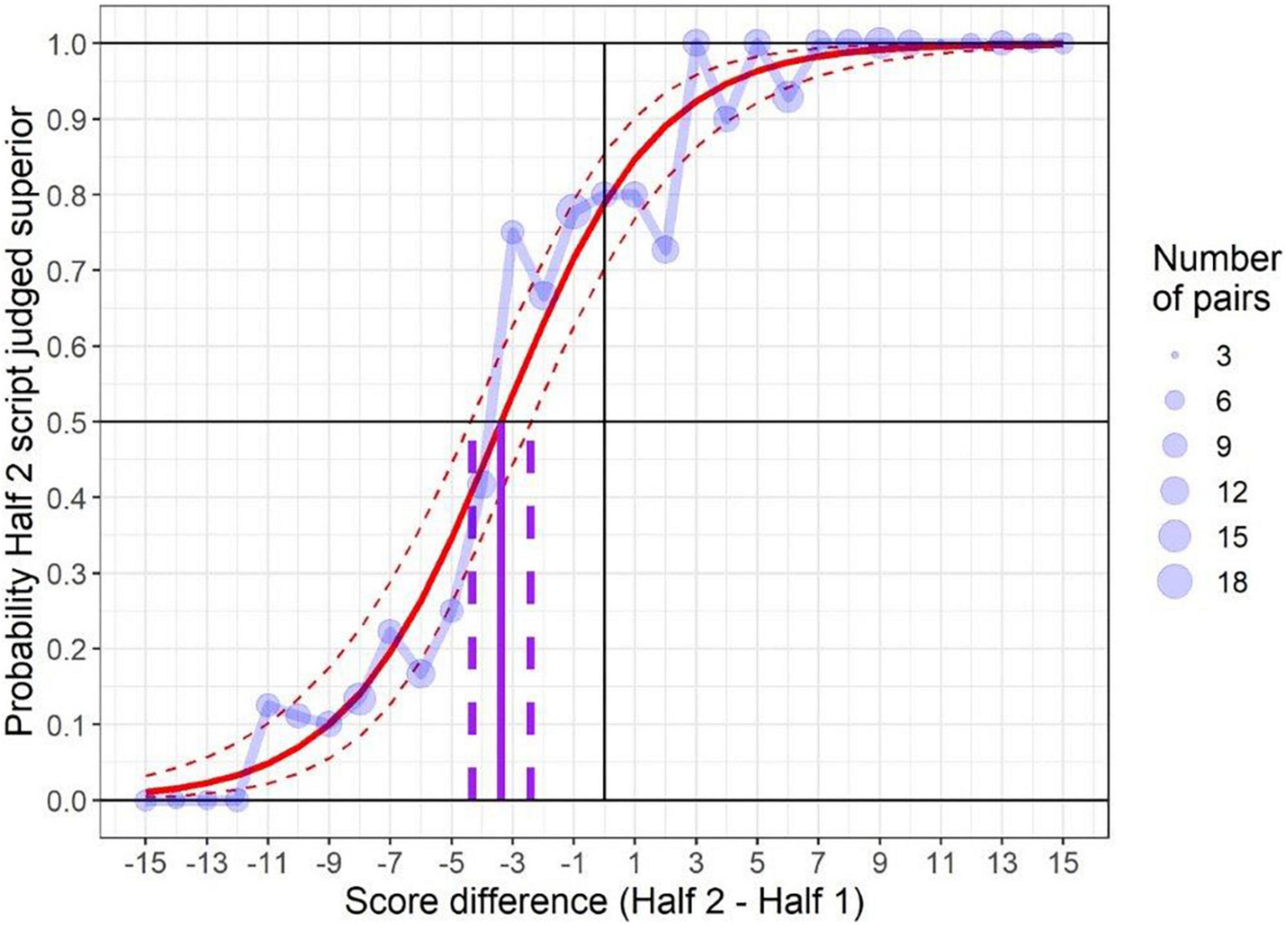
Figure 2. Graphical depiction of the results of using simplified pairs to gauge the relative difficulty of two assessment versions (mathematics).
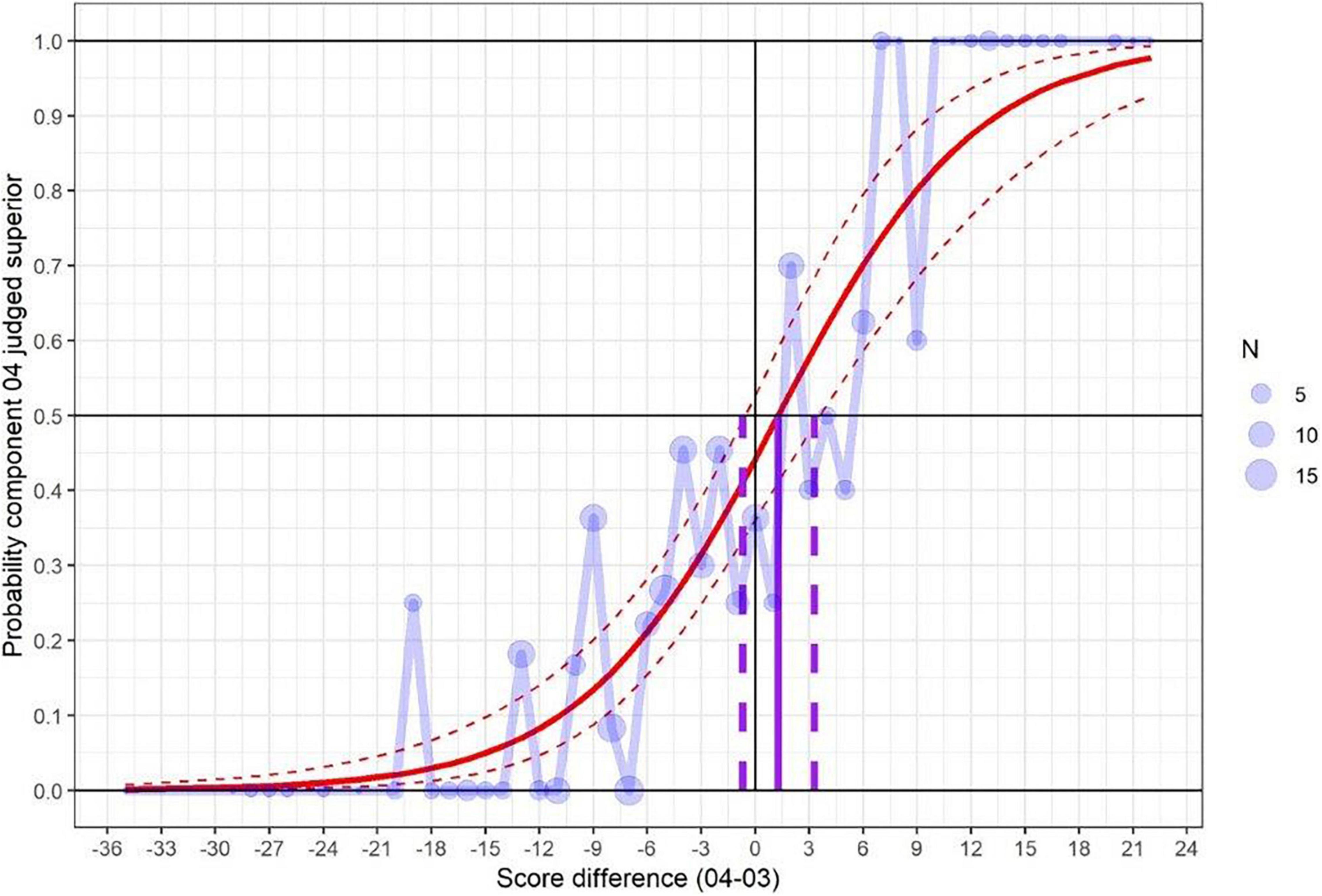
Figure 3. Graphical depiction of the results of using simplified pairs to gauge the relative difficulty of two assessment versions (science).
The formal analysis within a simplified pairs study was done using logistic regression6. This is represented by the solid red line in Figures 2, 3 which smoothly captures the relationship between mark differences and the probability of a Half 2 (or component 04) script being judged superior. The main purpose of this analysis is to identify the mark difference where this fitted curve crosses the 0.5 probability. For mathematics, this happens at a mark difference of −3.4. This implies that a Half 2 script will tend to be judged superior to a Half 1 script wherever the mark difference exceeds −3.4. In other words, based on expert judgement we infer that Half 2 was 3.4 marks harder than Half 1.
A 95 per cent confidence interval for this value (the dashed vertical lines) indicates that the judged difference in difficulty was between −2.4 and −4.3 marks. It should be noted that the size of this confidence interval, of essentially plus or minus a single mark, was very narrow compared to previous published examples of both simplified pairs (Benton et al., 2020, p. 19) or other kinds of CJ in awarding (Curcin et al., 2019, p. 11). This was because the relationship between mark differences and judges’ decisions depicted in Figure 2 was much stronger than in many previous applications, leading to increased precision.
The estimated difference based on expert judgement (via simplified pairs) fell a little short of the true difference at only 3.4 marks. Furthermore, the confidence interval for the simplified pairs estimate did not overlap with the empirical difference. This indicates that we cannot dismiss the differences in results from mean equating and simplified pairs as being purely due to sampling error. Nonetheless, the exercise correctly identified the direction of difference in difficulty and the estimate was close to the correct answer.
For science, the curve crosses the 0.5 probability at a mark difference of 1.3 marks, which indicates that, according to examiner judgement, component 04 was easier by just over 1 mark. The 95% confidence interval was between −0.7 and 3.3 marks. As this range includes zero, we cannot be sure, from judges’ decisions, that there was any difference in difficulty between the two papers.
This result contrasts with the empirical difference in difficulty according to the marks (Table 4), which revealed that component 04 was around 5.4 marks harder. This result will be discussed further in the “Discussion” section of this report.
Tables 5, 6 show some statistics on the judge fit for both exercises, and how long the judges took on average to make their judgements. A visual depiction of how the fitted logistic curves differed between judges is shown in Figures 4, 5.
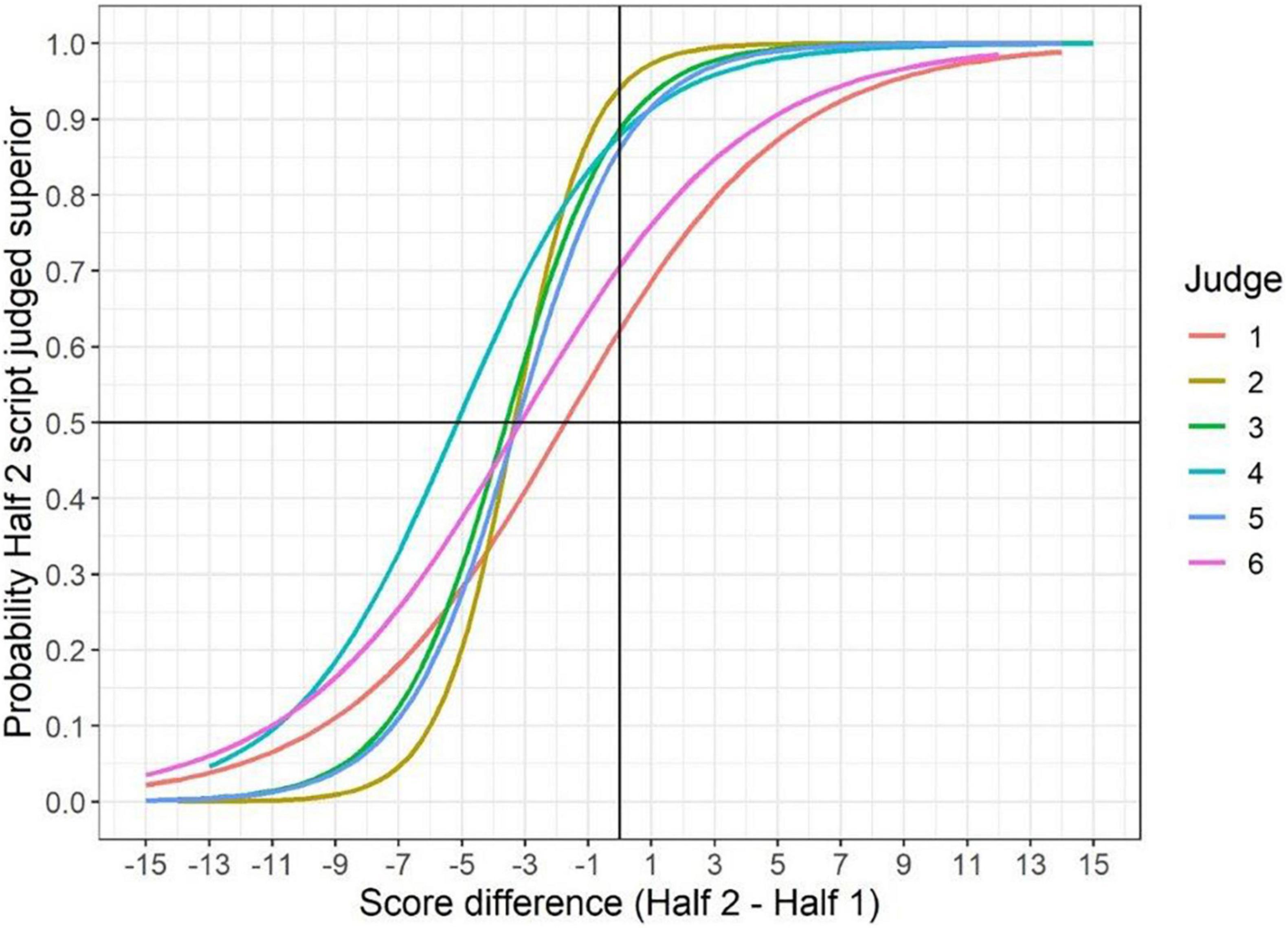
Figure 4. The relationship between differences in marks for a pair and the likelihood of selecting half 2 as superior (by judge).
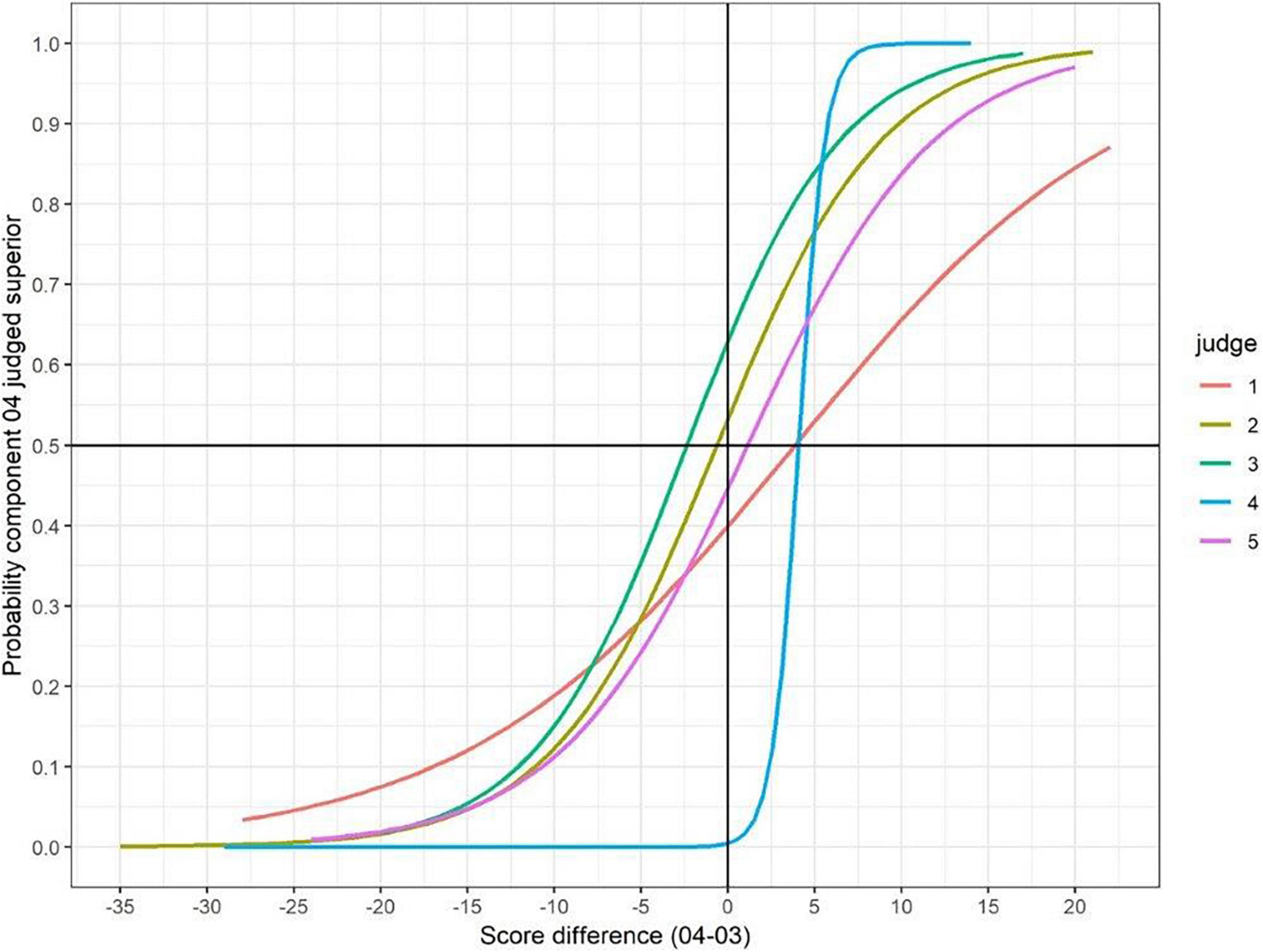
Figure 5. The relationship between differences in marks for a pair and the likelihood of selecting component 04 as superior (by judge).
In both exercises, each judge displayed strong point biserial correlations between the differences in marks for the half-scripts (or components) being compared and the decision they made about which was superior. The range of point biserials in the two exercises (between 0.63 to 0.82 in mathematics and between 0.42 and 0.67 in science) compared well with the range shown in studies of more subjectively marked subjects such as English Literature, as explored in Benton et al. (2020, p. 22), where judges’ point-biserial correlations were between 0.33 and 0.62. This reiterates the strong relationship between mark differences and judges’ decisions in both exercises considered in this article.
In the GCSE Mathematics exercise, all six judges selected Half 2 as being superior more than 50 per cent of the time and, similarly, each of the logistic curves for separate judges intersects the 0.5 probability line at mark differences below zero. This indicates a unanimous suggestion across judges that Half 2 was a harder assessment than Half 1.
In GCSE Science, the picture was more mixed. Results from judges 1, 4 and 5 would suggest that component 04 was easier (by between 1 and 4 marks), whereas for judge 3, component 03 came out as easier (by about 2.5 marks). For judge 2, there was almost no difference in difficulty. This lack of agreement about which paper was easier contrasts with previous research, where judges agreed unanimously about which paper was harder. However, the differences (in terms of paper difficulty) between judges in the current exercise were not that large and were similar to those found in the previous research.
Furthermore, although four out of the five judges had similar shaped curves, the results from judge 4 were somewhat different. This judge had a much steeper curve, pointing to a more ordered set of decisions about which script was superior. We looked more closely at the decisions of this judge and found that the relationship between mark difference and decision was almost perfect, with only one judgement out of order: the examiner judged component 04 to be superior for all mark differences of 4 or more, and judged component 03 to be superior for all mark differences of 3 or less (with one exception). This suggests that this judge was actually remarking the scripts and then basing their decision of superiority on a pre-conceived idea about the difference in difficulty between the two components. Interestingly, that pre-conception was that component 04 was easier by about 4 marks, which was very different from the empirical difference (component 04 harder by 5.5 marks).
Tables 5, 6 also show judge fit calculated using INFIT and OUTFIT7 (see Wright and Masters, 1990). For mathematics, none of the values are high enough (or low enough) to warrant serious concern over any of the judges. The highest values occur for the two judges (judges 1 and 6) with logistic curves (Figure 4) that suggest the smallest estimated difference in the difficulty of the tests. For science, Judge 4 stands out as having particularly low values of INFIT (0.50) and OUTFIT (0.33), which suggests over-fitting of the data to the model, consistent with this judges’ apparent tendency to re-mark. However, since decisions within the exercise are to some extent a matter of opinion (see Benton et al., 2020, p. 10) we tend to prioritise information from point biserials over judge “fit”.
The median time required per judgement was between 2.2 and 5.6 min for mathematics and between 4.9 and 6.7 min for science. There was quite a strong negative relationship in science between the median time and the point biserial correlation, with longer median time associated with a lower correlation. This suggests that some of the examiners may have found it a more challenging task, and this meant they were both slower and less accurate.
In Tables 3, 4 we presented the overall empirical difference in difficulty between the two components (or half papers), using mean equating. We now extend this further by equating these across the full mark range. For this we used equipercentile equating, which generated an equivalent mark on Half 2 (or component 04) for each mark on Half 1 (component 03). This was done using the R package equate (Albano, 2016). The results of the equating were then compared with the equivalent marks generated by the logistic regression results from the simplified pairs exercise.
Figure 6 (mathematics) and Figure 7 (science) present the results of this analysis, with the red lines showing the results according to the equating, and green lines the results according to the CJ exercise. The dashed lines represent 95% confidence intervals for the equivalent marks. For reference, the graph also includes a straight diagonal line of equality.
In mathematics, the results from empirical equating (the red line) confirm that Half 2 was harder than Half 1. This difference in difficulty is particularly visible for marks between 25 and 45 marks on Half 1. A similar pattern is also visible from the results of simplified pairs (the blue line) indicating a reasonable level of agreement between the two techniques.
According to the empirical equating for science, component 04 was harder than component 03 across the whole mark range, with the difference steadily increasing between marks of 0 and 20 on component 03 (up to a maximum of 6.2 marks). Above this mark, the difference fell steadily up to a mark of 45, above which there were only a few candidates so there was less certainty about the equivalent mark on component 04. No candidates achieved a mark higher than 53 on component 03. The equivalent marks according to the results of the CJ exercise were very different, varying between 0 and 1 mark easier for component 04. The confidence intervals for these marks were also substantially wider than those generated by the equating. Only at the very top of the mark range does the confidence interval for the simplified pairs method encompass the estimate from equating.
This section provides insights from the surveys, which help to answer RQ2. Results are presented here in a narrative fashion, in order to explore findings in more detail. Answers to both Likert-scale and open questions are integrated into what follows, while descriptive statistics, as they would offer little insight, are not presented in tabular form.
The judges were asked how straightforward they found the process of making a holistic judgement of script quality. One science judge responded that this was ‘very straightforward’ and three considered it ‘somewhat straightforward’. The remaining judge said they were not sure and admitted to ‘counting points’ to start with. In the mathematics survey, five out of the six judges said it was at least somewhat straightforward, with two of them believing it to be entirely straightforward. The sixth considered the process to be ‘not very straightforward’, noting that given that mathematics papers contain lots of questions of differing demand, making a holistic judgement of mathematics papers was in their view very difficult. They highlighted that it would be easier to compare two responses to the same question, or two sets of questions of the same standard. Another mathematics judge, who had difficulties making holistic judgements initially, nonetheless said that this grew easier over time.
Across the two exercises, the judges suggested different specific processes for making their judgements. When asked how they believed that they made their judgements, all science judges said that they looked at the answers to key questions. However, four out of the five judges also said that at times they needed to look at the number of correct responses in each paper. This was particularly the case for lower quality scripts, where there were often no responses to the questions with more marks. One science judge also mentioned that they ignored the responses to multiple-choice questions, an interesting finding potentially highlighting the extent to which CJ methods can be considered more applicable to longer-response items. Meanwhile, in mathematics, some judges focused on the number of answers correct, while others attempted to match questions on each half of the paper by either (a) their perceived difficulty or (b) the skills required to answer them, and then tried to determine which script was superior. Candidates’ working was considered by two mathematics judges to be a significant discriminator, while another highlighted communication. Many of the judges said that they used many of these different processes at the same time.
In both surveys, the judges were asked directly which of the two papers they were judging they believed to have the more difficult questions. Three out of the five science judges thought that the two different exam papers were of the same level of demand, whilst one thought (correctly) that component 04 was more demanding and one judge was unsure. The judge who was unsure put this uncertainty down to the fact that ‘the scripts were rarely assessing the same assessment objectives with comparably scored questions, so the level of demand varied’. Encouragingly, four out of the six mathematics judges correctly identified Half 2 as the more difficult of the two half-length assessments, while another saw the two halves as very similar in difficulty. The sixth noted only that one half was more difficult than the other but did not specify which. Here it can be seen that the outcomes of the two exercises respond to the view that examiners find it difficult to make judgements about overall paper difficulty (e.g., Good and Cresswell, 1988, p. 278) in diverse ways – that is, the mathematics judges were able to correctly approximate the empirical difference in difficulty of the two half-scripts, while the majority of the science judges could not do this.
Judges differed in their views as to whether questions worth more marks are invariably better discriminators of candidate quality. Those mathematics judges agreeing to this contention highlighted that high-tariff questions allow for problem-solving skills to be evidenced and are often of greater complexity, while those opposed noted that some high-tariff questions can be quite routine, and can be prepared for, while communication issues can be more revealing in low-tariff questions. There was also disagreement among science judges on the same theme, with two agreeing somewhat, two disagreeing somewhat and one neither agreeing nor disagreeing. One science judge who agreed said that the higher tariff questions required answers involving explaining or analysing. Of those who disagreed, one stated that the statement was not true for weaker candidates, because they achieved fewer marks on the higher tariff questions. This is an interesting response, because at first glance it sounds like a definition of a discriminating question. Perhaps they were suggesting that most low ability candidates would get zero on the higher tariff questions, meaning that it would be impossible to discriminate between them. Another judge thought that the six-mark questions test writing ability as much as chemistry ability.
There was more agreement than disagreement in both studies with the contention that certain types of questions were better discriminators than others. All science judges agreed (three ‘entirely’ and two ‘somewhat’) that some types of questions were better discriminators. Only three of the science judges expanded on their response, with general agreement that questions requiring interpretation, application or explanation responses were better discriminators. One science judge elaborated further by saying that this was the case for high performing candidates, but that for weak candidates the ‘recall’ questions were better discriminators. Mathematics judges had similar responses. An additional question asked more explicitly about what types of questions were better discriminators. The most selected responses in the science context (selected by four judges each) were ‘questions testing application of knowledge’ and ‘questions involving analysis of information and ideas’. Mathematics judges offered varied opinions in response to the same question, including multi-part questions, knowledge and understanding questions, and data analysis.
There was also no strong agreement between mathematics judges as to whether they believed they did consistently focus on particular types of questions in their judgements, some suggesting that unstructured questions might be a useful tiebreaker but others attempting to make holistic judgements based on all types of questions across the paper. Only three of the science judges said that they focused on certain question types when making their judgements, two of whom said that they focused on ‘questions testing knowledge and understanding’. The remaining science judge selected ‘other’ as their response, but their explanation suggested that they too focused on ‘questions testing application of knowledge’, alongside ‘levels of response questions’. One judge said that the reason they did not focus on certain question types was that they were asked to look at the whole script when making their judgements. Overall, though, it is reassuring that the judges were mainly focusing on the same question types when making their judgements, because it suggests a degree of consistency in their method.
Many mathematics judges described difficulties in making judgements of pairs where a candidate’s response to one half-script was better in one sense, but worse in another sense, than the other candidate’s response to the other half-script in the pair. For example, one mathematics judge noted an example where one candidate performed more strongly on trigonometry, but less well on algebra, while another indicated an example where one candidate answered every question, though not entirely correctly, while the other produced correct solutions to about half the questions. Most judges suggested that the tiebreaker for them in such cases was performance on the higher tariff, “harder” questions towards the end of the paper. One of the challenges here is that it is by no means clear what the correct tiebreaker “should” be, in this context. It is worth noting that this same issue arises even when making comparisons within the same test (Bramley, 2012, p. 24). As such we cannot expect holistic judgements of quality to match the mark scale exactly.
Finally, in their survey, two mathematics judges indicated a belief that comparative judgement methods might work less well for mathematics than subjects involving longer, more discursive answers such as English or history. This relates back to the general question that underpins this article – does CJ struggle in relation to papers comprised mainly of highly objective, short-answer questions (as mathematics and science papers typically are), because of the difficulty for judges of knowing how to sum the many different small bits of evidence of candidate quality presented in each item (taking into account the variance in item difficulty) in coming to a holistic judgement. While the outcomes in these two exercises lead to an equivocal finding in relation to this question, what is perhaps likely to be less equivocal is the attitude of judges to whether they think they can do what is required. For comparative judgement to be operationalised, the support of those intended to be used as judges would be vital.
Principally, the concern here lies in the fact that, in many mathematics assessments, achieving the right answer the most times is the main objective (it “boils down to right or wrong”, according to one judge). This was also highlighted by judges who noted that it can be difficult to avoid simply re-marking the scripts. It was suggested that the need to bear in mind many small judgements of superiority (of candidates’ performance on questions testing different skills, for example) and then combine them into one overall judgement, for example, leads to more cognitive load and a more tiring task than marking, again suggesting that it may perhaps be difficult to establish judge support for the greater use of comparative judgement in the future.
On the other hand, most of the judges had never taken part in a comparative judgement exercise before and their experiences varied. More experienced judges might have been more consistently supportive. Moreover, it should be acknowledged that the surveyed judges did mostly say that the process was straightforward (at least once they had got into it) – implying that, as is often the case with complex changes to processes, while there might be hesitation initially, eventually this would give way to acceptance and then confidence.
The information revealed in the judge surveys helps us gain a better understanding of the ways in which the judges in both studies made their judgements. It also offers some clarity as to issues around what parts of the papers the judges were attending to, such as the relative importance of higher- and lower-tariff questions to judges’ decisions and the comparative significance of diverse types of questions in demonstrating candidate quality.
However, what is perhaps most striking about the survey outcomes is that (a) there is no consistency across judges in the same survey about what they regard as important and (b) a difference in what is regarded as important between mathematics judges (considered collectively) and science judges (considered collectively) that might explain the difference in outcomes between the two studies is not evident. In other words, it is not the case that, for instance, mathematics judges thought that they were clearly much more capable than science judges at determining the difficulty of questions, or that science judges were clearly not as good at deciding which questions to focus on. This means it is not easy to explain why one of the exercises “succeeded” and the other did not, at least by reference to the judges’ processes.
The findings of the two studies discussed above offer several points for further discussion relating to the appropriateness, accuracy, and validity of the use of comparative judgement in subjects with highly structured papers. In Section “Overall Outcomes,” we discuss the overall outcomes of the exercises, in order to address RQ1. Then, in Section “How Judges Judge,” insights from the surveys are discussed to explore some of the validity issues relevant to RQ2.
Firstly, the overall outcomes of the two exercises are discussed, in order to answer RQ1. It is notable that the two studies, despite being nearly identical in structure, resulted in somewhat different outcomes. In the mathematics study, the results of the simplified pairs exercise meant that, based on expert judgement, we can infer that the Half 2 paper was 3.4 marks harder than Half 1. This was about 1.6 marks away from the empirical difference estimated from statistical equating, where Half 2 was 5 marks harder than Half 1. Judges unanimously agreed that Half 2 was a harder paper than Half 1, suggesting that it is possible for judges to make determinations of test difficulty. This appears to at least somewhat allay Baird’s (2007, p. 142) concern that examiners cannot compensate for the differing demands of question papers from year to year. In line with Benton et al. (2020, p. 21), we suggest here that our judges were able to appropriately make allowances for paper difficulty in this exercise at least.
However, in the science study there was no consistency between judges as to which component was harder. The fact that there is a distinction between the studies is a somewhat discouraging finding in terms of the consistency of CJ. This lack of consistency between judges is despite the fact that in the science study, the empirical difference between the papers, as estimated from statistical equating, was 5.4 marks, with component 04 harder than component 03. Results from three judges suggest that component 04 was easier (by between 1 and 4 marks), whereas for another judge, component 03 came out as easier (by about 2.5 marks) and for a final judge, the two papers were almost equal in difficulty. Overall, these judgements amounted to component 04 being viewed as about 1 mark easier than component 3, but this was not statistically significantly different from zero (no difference). It is important to note that, despite these differences, the variability of results from different judges in terms of their assessments of paper difficulty were not that large as a percentage of the maximum mark on the paper.
On the other hand, the range of point-biserial correlations between mark difference and the likelihood of selecting the second of the two papers as the harder was between 0.63 and 0.82 in mathematics and 0.42 and 0.67 in science. This means that the judges were both mostly consistent with each other, in terms of working out which paper was harder, and their judgements were mostly accurate. The range of point-biserials here is not far from the range demonstrated in CJ exercises concerning more subjectively marked subjects where papers are constructed from a smaller number of less structured extended tasks, such as English Literature. See, for example, Benton et al. (2020, p. 22), where the range was between 0.33 and 0.62. Both exercises – mathematics and science – therefore demonstrate a strong relationship between how far apart the papers in any pair were in terms of marks, and the judges’ likelihood of correctly determining which was superior. The fact that these ranges were similar to those evident for papers with more extended tasks is encouraging. However, if judges are not capable on the whole of correctly determining which of the papers was harder, as was the case in the GCSE Science exercise, the consistency of their judgements matters less – in other words, are they just reliably incorrect?
Judge fit (consistency) also has some value for the validity of the exercise, though this is of less significance in terms of illustrating the accuracy of the exercise (RQ1) than the point-biserial correlation between the judge’s decision and the mark difference between the papers they were judging. Moreover, few judges stood out in terms of their INFIT and OUTFIT values. On the other hand, it could be suggested in relation to RQ2, that, where judges misfit the model, this could be because there were re-marking rather than making holistic judgements. The activity of re-marking is related to the structure of the items. Re-marking is more likely in a structured question paper than a paper requiring extended responses. This highlights the need for further work to address the question about the meaning of holistic judgement in CJ and its relationship to processes such as re-marking; this conversation has also been contributed to by Leech and Chambers (2022).
Both exercises also offer interesting insights in relation to the processes that judges used to make their judgements, and how they found the exercises, which can help to answer RQ2. The fact that a majority of judges in both studies considered it at least “somewhat straightforward” to make holistic judgements is encouraging, although at least one mathematics judge offered a contrary view, arguing that given that mathematics papers contain lots of small questions of differing demand, a holistic judgement was difficult to arrive at. However, this was a minority view. These findings accord with those of earlier studies involving papers with more extended tasks (e.g., Greatorex, 2007; Black, 2008; and Jones et al., 2015), suggesting that there is nothing specific about the fact these papers had highly structured tasks that meant judges felt it was less straightforward to judge them holistically.
However, the cognitive load put on judges who have to sum up many different small pieces of evidence, while taking appropriate account of the difference in difficulty of the papers overall, is clearly substantial. This echoes the findings of Verhavert et al. (2019) who found that the structure of a task impacts the complexity of decisions made by judges. Moreover, there are significant commonalities with the work of Leech and Chambers (2022), who found that in more structured papers many judges were making judgements that were, at best, partially holistic. We can therefore see that this problem is more evident in papers made up of highly structured tasks as is typical of United Kingdom exam board papers in mathematics and science. Finally, whether judges can correctly assess and take account of the difficulty of papers (as questioned by Good and Cresswell, 1988, p. 278) is something that these studies provide only ambiguous evidence on.
The survey findings from these studies are generally similar to those relating to earlier CJ exercises (concerning papers with more extended tasks) in the insights they provide about the processes that judges use. That is, that different processes are used by judges, with many judges utilising many of the processes at the same time, but outcomes are generally consistent with one another. For example, all science judges looked at answers to key questions, as was the case in the study by Greatorex et al. (2008, pp. 4–5); and most at the number of correct responses. The fact that judges across both studies used a variety of different processes, and yet were generally consistent with one another (in the same study), suggests that the ability to make a holistic judgement of script quality is not necessarily directly related to the specific process used to make that judgement.
In one respect, this is a good thing, since it is generally acknowledged as a strength of marking that it involves processes that are relatively consistent across markers, and so the fact that outcomes (if not processes) are consistent in CJ is encouraging. However, from a public confidence viewpoint, does the variation in judgemental and discriminatory processes used by CJ judges have the potential to cause disquiet? Current marking and awarding processes value standardisation and transparency, which CJ does not in the same way. The issue of the different approaches used by different judges may be of concern, particularly in relation to the ability to maintain an audit of how decisions have been made. The work of Chambers and Cunningham (2022) on other aspects of decision-making processes in CJ is also important in this regard.
A follow-on issue from that of process is that of which items in the papers judges most frequently attended to. Judges did not agree about whether higher-tariff questions were more useful in general for their judgements; instead, which questions were more helpful depended on their type and what skills they were testing. Overall, though, it does appear that judges were generally focusing their attention on certain questions. Generally, the same kinds of questions were focused on in each study. Some subject-specific issues arose, including the key role judges saw for candidates showing their working in mathematics, and the idea of skills application and analysis in science, indicating the many different concerns at play in the assessment of candidates in different subjects.
Other causes of challenging decisions include where the writer of one script in a pair was better at one skill or in one section of the paper but the writer of the other was better at another skill or section, and each is important; a general instruction to make a holistic judgement may not be clear enough to guide judges in these cases. A variety of heuristics seemed to be used by judges on these occasions. For example, as was the case in earlier studies of papers featuring more extended tasks (e.g., Greatorex et al., 2008, pp. 4–5), there is some evidence that performance on higher-tariff questions is attended to more, particularly as tiebreakers if the two candidates in a pair are close in quality. There is a sense here of these judges identifying a hierarchy of skills. In other words, if two candidates were relatively evenly matched in performance on most elements, they would be separated by their performance on the skills tested more in these higher-tariff questions, such as problem-solving, say. This may be a good thing, as long as it is done relatively consistently by judges, but if the higher-tariff questions are not testing the same skills or knowledge as the paper as a whole, the issue of certain parts of the paper playing an outsize role in judgements is a live one.
Indeed, if it is the case, as it seems to be in these studies, that CJ judges attend more to certain questions (such as those worth more marks, or those more related to problem-solving than recall, for example) than others, what does this mean for validity? The hypothetical situation where a script which had overall received fewer marks but was judged superior due to the judge preferring its writer’s answers to problem-solving questions, for example, raises significant questions about the acceptability of comparative judgement-informed awarding processes in consistency terms. This situation is likely to be mitigated by the simplified pairs approach, which collates many judgements and regresses them against the scripts’ mark difference, but this mitigation (which reduces the impact of any individual judge’s inconsistency from the approach of others) may not be recognised by judges or other stakeholders. Furthermore, it might be seen as a good thing that judges concentrate on certain, better-discriminating, questions, if these can be seen as identifying the superior mathematician or scientist, say, more efficiently. However, there is certainly a potential tension here; ultimately, what should we be asking judges to decide their judgements on?
This issue is not unique to CJ in subjects relying on highly structured papers, but may be more pertinent in them. This is because papers using extended response tasks are likely to test the required skills in most, if not all, of their tasks, whereas highly structured papers may have one set of sections or items focusing on each required skill. In a marking schema, the sum of individual judgements of candidates’ performance on these skills thus creates an overall mark which reflects their performance appropriately across all skills tested on the paper, but with holistic comparative judgements creating this overall judgement appropriately may be more of a challenge. What is important – both in marking and CJ – is that there is clarity as to what kind of skills are being tested when and why, and if there is meant to be a hierarchy of skills.
The issue of whether judges were simply re-marking the papers in front of them in accordance with their original mark schemes, and then selecting as superior the one they awarded the most marks to (in contrast to, as was intended, making true quick holistic judgements) is an important one for the validity of CJ. Evidence from these studies suggests that, at least for some judges, reverting to re-marking was difficult to avoid. All the judges chosen for these studies were experienced markers of the relevant qualifications, and as such had been trained in performing the precise item-by-item determinations of right or wrong that are critical to how marking works in these contexts. The psychological transition to making CJ judgements is substantial. This is for two reasons. Firstly, a quick assessment being made of the overall quality of a paper, in a holistic fashion, is very different from the precise, standardised methods of marking. Secondly, an individual judge’s decision matters less in CJ, in that CJ methods bring together the judgements of many. This situation (where judges do not need to act as though their judgement alone has to be right all the time) may be difficult for judges to adjust to. It may have been the case that this latter point was not understood well by judges, who were used, as markers, to their marking being decisive in a student’s outcomes, and therefore expected to put a lot of effort into getting it right every single time.
This highlights the importance for the future, if CJ is to be rolled out in wider settings, and especially in STEM subjects and highly structured papers, of getting judge training right. CJ relies significantly on judges making their judgements in the way we want them to, but without necessarily telling them how. Judges with experience of marking need to be aided to make the transition to the CJ mindset – perhaps with training materials, testimonials from judges who have used CJ about how it works, and evidence of its appropriateness, as well as the opportunity to try the method and receive feedback. It should not be assumed that this is a trivial issue, as working under a CJ mindset may be seen by judges as a challenge to their professionalism as markers. CJ thus risks not being viewed as a desirable task, and then not getting the necessary examiner buy-in. However, evidence from these studies suggests that judges’ ease with the process increased throughout the exercises – i.e., as they gained experience and knowledge about what they were doing – implying that this transition is possible to achieve.
So, can comparative judgement accurately estimate the true difference in difficulty between two exam papers comprising many highly structured tasks (RQ1)? The mathematics study reported on here suggests that the estimated difference derived from simplified pairs could closely approximate the empirical equating difference. However, in the science exercise, the CJ outcome did not closely align with the empirical difference in difficulty between the two papers. It is difficult to explain this discrepancy, though reasons may include the differences in the content of the exams or the specific judges. Nonetheless, based on the science exercise, we now know for certain that comparative judgement need not lead to an accurate impression of the relative difficulty of different exams. More research is needed to ascertain the particular conditions (if any) under which we can be confident that CJ can accurately estimate the true difference in difficulty between two exams of highly structured tasks.
We have also addressed the question of how judges make comparative judgements of students’ work from exam papers comprising many highly structured tasks (RQ2). The processes that judges used to make decisions when judging papers made up of highly structured tasks were varied – with the same judge likely to use different processes throughout their work. However, on the whole, judges were generally consistent enough in their processes.
One strategy used by some judges working on highly structured papers was to make decisions based on a subset of the exam paper. The validity of CJ depends on judgements that are holistic because judgements made on a subset of the questions in an exam may omit some target constructs which, consequently, means that scripts may be being judged (for the purpose of assigning grades) against different criteria to those they are being marked against. This may not be acceptable as it is then unclear exactly what skills students are being assessed on. Moreover, those skills embodied in the mark schemes may be subtly different. Another strategy reported by judges was to re-mark the papers and then compare scripts based on a totting up of scores on the items in the paper. However, re-marking within a CJ exercise negates the benefit of speed. It also means that judges are not necessarily accounting for the differences in difficulty between 1 year’s paper and the next. In all these cases, a greater understanding of what judges are doing when they judge comparatively brings to the fore questions of assessment judgement validity that generally remain implicit in the marking and non-comparative judgement contexts.
The strategies used in exam marking processes are well understood (e.g., Suto et al., 2008; Crisp, 2010a). This paper adds to our understanding of processes used by CJ judges when making decisions about highly structured papers. However, this area is still not as well theorised as that of decision-making in marking. More research to further this understanding and to build knowledge of the impact of judging decisions and processes on CJ outcomes would be welcome. Further research is also required into what is meant by a holistic decision, and how to manage the cognitive load that arises when judging student work which contains many short answer questions, so that exam boards can provide fuller guidance to judges about how they should make decisions in CJ tasks and what information in the papers they should be concentrating on.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. The patients/participants provided their written informed consent to participate in this study.
TB conceptualized the simplified pairs method and designed the maths study. TL and SH organized the maths study. TG ran the science study on the same design. TL, TG, and SH wrote the first manuscript draft, with TG writing the section on study findings, TL the section on judge survey findings and the discussion, and SH the introduction and conclusion sections. All authors contributed to manuscript revision and read and approved the submitted version.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
We would like to acknowledge the contributions of colleagues in OCR, including Natalie Gawthrop, Charlotte Gow, and Stephen Furness, for supporting the operationalisation of the CJ work, and Terry Child for developing the CJ software tool.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2022.803040/full#supplementary-material
Albano, A. D. (2016). equate: an R package for observed-score linking and equating. J. Statistical Software 74, 1–36. doi: 10.18637/jss.v074.i08
Baird, J.-A. (2007). “Alternative conceptions of comparability,” in Techniques for Monitoring the Comparability of Examination Standards, eds P. E. Newton, J.-A. Baird, H. Goldstein, H. Patrick, and P. Tymms (London: Qualifications and Curriculum Authority). doi: 10.2307/j.ctv15r5769.4
Benton, T. (2021). Comparative judgement for linking two existing scales. Front. Educ. 6:775203. doi: 10.3389/feduc.2021.775203
Benton, T., Cunningham, E., Hughes, S., and Leech, T. (2020). Comparing the Simplified Pairs Method of Standard Maintaining to Statistical Equating. Cambridge: Cambridge Assessment. Cambridge Assessment Research Report.
Benton, T., Gill, T., Hughes, S., and Leech, T. (2022). A Summary of OCR’s Pilots of the use of comparative judgement in setting grade boundaries. Res. Matters Cambridge Assess. Publication 33, 10–30.
Black, B. (2008). Using an Adapted Rank-ordering Method to Investigate January versus June Awarding Standards. Cambridge: Cambridge Assessment. Cambridge Assessment Research Report.
Bradley, R. A., and Terry, M. E. (1952). Rank analysis of incomplete block designs: i. the method of paired comparisons. Biometrica 39, 324–345. doi: 10.2307/2334029
Bramley, T. (2005). A rank-ordering method for equating tests by expert judgement. J. Appl. Meas. 6, 202–223.
Bramley, T. (2012). The effect of manipulating features of examinees’ scripts on their perceived quality. Res. Matters: Cambridge Assess. Publication 13, 18–26.
Chambers, L., and Cunningham, E. (2022). Exploring the validity of comparative judgement - do judges attend to construct-irrelevant features?. Front. Educ. 6: 802392.
Crisp, V. (2008). Exploring the nature of examiner thinking during the process of examination marking. Cambridge J. Educ. 38, 247–264. doi: 10.1080/03057640802063486
Crisp, V. (2010a). Towards a model of the judgement processes involved in examination marking. Oxford Rev. Educ. 36, 1–21. doi: 10.1080/03054980903454181
Crisp, V. (2010b). Judging the grade: exploring the judgement processes involved in examination grading decisions. Eval. Res. Educ. 23, 19–35. doi: 10.1080/09500790903572925
Curcin, M., Howard, E., Sully, K., and Black, B. (2019). Improving Awarding: 2018/2019 Pilots. Ofqual report Ofqual/19/6575. Coventry: Ofqual
Gill, T., and Bramley, T. (2013). How accurate are examiners’ holistic judgements of script quality? Assess. Educ: Principles Policy Practice 20, 308–324. doi: 10.1080/0969594x.2013.779229
Gill, T., Bramley, T., and Black, B. (2007). “An investigation of standard maintaining in GCSE English using a rank ordering method,” in Paper Presented at the Annual Conference of the British Educational Research Association, (London).
Good, F. J., and Cresswell, M. J. (1988). Grade awarding judgements in differentiated examinations. Br. Educ. Res. J. 14, 263–281. doi: 10.1080/0141192880140304
Greatorex, J. (2007). “Contemporary GCSE and a-level awarding: a psychological perspective on the decision-making process used to judge the quality of candidates’ work,” in Paper Presented at the Annual Conference of the British Educational Research Association, (London).
Greatorex, J., Novakovic, N., and Suto, I. (2008). “What attracts judges’ attention? a comparison of three grading methods,” in Paper Presented at the Annual Conference of the International Association for Educational Assessment, (Cambridge).
Humphry, S., and McGrane, J. (2015). Equating a large-scale writing assessment using pairwise comparisons of performances. Australian Educ. Research. 42, 443–460. doi: 10.1007/s13384-014-0168-6
Jones, I., Swan, M., and Pollitt, A. (2015). Assessing mathematical problem-solving using comparative judgement. Int. J. Sci. Math Educ. 13, 151–177. doi: 10.1007/s10763-013-9497-6
Leech, T., and Chambers, L. (2022). How do judges in Comparative Judgement exercises make their judgements? Res. Matters Cambridge Univ. Press Assess. Pub. 33, 31–47.
Ofqual (2017). Comparable Outcomes and New A Levels. Available online at: https://ofqual.blog.gov.uk/2017/03/10/comparable-outcomes-and-new-a-levels/ (accessed 6 October 2021).
Suto, I., and Greatorex, J. (2008). What goes through an examiner’s mind? using verbal protocols to gain insights into the GCSE marking process. Br. Educ. Res. J. 34, 213–122. doi: 10.1080/01411920701492050
Suto, I., Crisp, V., and Greatorex, J. (2008). Investigating the judgemental marking process: an overview of our recent research. Res. Matters: Cambridge Assess. Publication 5, 6–9.
Verhavert, S., Bouwer, R., Donche, V., and De Maeyer, S. (2019). A meta-analysis on the reliability of comparative judgement, assessment in education: principles. Policy Practice 26, 541–562. doi: 10.1080/0969594x.2019.1602027
Keywords: comparative judgement, pairwise comparisons, standard maintaining, structured exams, educational assessment, simplified pairs
Citation: Leech T, Gill T, Hughes S and Benton T (2022) The Accuracy and Validity of the Simplified Pairs Method of Comparative Judgement in Highly Structured Papers. Front. Educ. 7:803040. doi: 10.3389/feduc.2022.803040
Received: 27 October 2021; Accepted: 06 April 2022;
Published: 28 April 2022.
Edited by:
Sven De Maeyer, University of Antwerp, BelgiumReviewed by:
Liesje Coertjens, Catholic University of Louvain, BelgiumCopyright © 2022 Leech, Gill, Hughes and Benton. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tony Leech, YW50aG9ueS5sZWVjaEBjYW1icmlkZ2Uub3Jn; Tim Gill, dGltLmdpbGxAY2FtYnJpZGdlLm9yZw==
†These authors have contributed equally to this work and share first authorship
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.