Diagnostic Classification Models for Actionable Feedback in Education: Effects of Sample Size and Assessment Length

E-learning is increasingly used to support student learning in higher education. This results in huge amounts of item response data containing valuable information about students’ strengths and weaknesses that can be used to provide effective feedback to both students and teachers. However, in current practice, feedback in e-learning is often given in the form of a simple proportion of correctly solved items rather than diagnostic, actionable feedback. Diagnostic classification models (DCMs) provide opportunities to model the item response data from formative assessments in online learning environments and to obtain diagnostic information to improve teaching and learning. This simulation study explores the demands on the data structure (i.e., assessment length, respondent sample size) to apply log-linear DCMs to empirical data. Thereby we provide guidance to educational practitioners on how many items need to be administered to how many students in order to accurately assess skills at different levels of specificity using DCMs. In addition, effects of misspecification of the dimensionality of the assessed skills on model fit indices are explored. Results show that detecting these misspecifications statistically with DCMs can be problematic. Recommendations and implications for educational practice are discussed.

1 Introduction

Feedback in education is a powerful tool to enhance student learning (Black and Wiliam, 1998; Nicol and Macfarlane-Dick, 2006). It can be conceptualized as information that is provided to students regarding aspects of understanding or performance. Following the feedback model from Hattie and Timperley (2007), this information can be focused on four different levels: task-oriented feedback (e.g., regarding correctness or completeness of the performed tasks), process-oriented feedback (i.e., focused at the learning processes that are required to understand or complete the tasks), feedback about self-regulation (i.e., supporting students to monitor, direct, and regulate actions towards learning goals), and feedback directed to the self (i.e., expressing evaluations and affect about the student, generally unrelated to the tasks). In order to obtain beneficial effects from feedback, learning goals must be properly defined, current levels of performance should be compared with desired levels of performance, and one must engage in appropriate actions to close the gap between current and desired performance (Sadler, 1989).

1.1 Actionable Feedback From e-Learning in Higher Education

In academic settings, learning goals are often defined by course-specific targets, criteria and standards. Feedback can provide information about how students’ levels of performance relate to these goals. Yet, various courses in higher education consist of large groups of students, making it intractable for teachers to provide personalized feedback to individual students. Further, it can be difficult to keep track of learning progress at group level. The emergence of computer-based learning facilities can provide support for this. The use of e-learning environments to support learning processes in higher education has emerged over the last decades and the widespread use of these new technologies led to the availability of huge amounts of student data. Although this data can be a rich source of information for personalized teaching and learning, in itself it does not lead to quality improvement of education. It must lead to actionable feedback by analyzing, describing and visualizing the data, i. e, feedback that can be acted upon. This requires the data to be transformed into meaningful information using learning analytical approaches in order to provide both students and teachers with knowledge about learning progress (Ferguson, 2012). Despite the opportunities the emerging field of learning analytics research entails and the available expertise at universities, large-scale adoption of learning analytics to improve teaching and learning in higher education is lacking (Viberg et al., 2018).

Nevertheless, some form of learning analytics to provide feedback is implemented in virtually all e-learning environments. For example, practice exercises are often provided with immediate feedback about correctness of responses. Although this fine-grained, task-oriented feedback has been found to positively affect student learning (see for example VanLehn, 2011), it does not provide insight in cognitive strengths and weaknesses to support self-monitoring. That is, if a student knows that their answer to a certain question is incorrect, this does not imply that they can infer which knowledge or skills are lacking and which materials need more practice. To address this, e-learning modules generally include short formative assessments after a sequence of lessons about a specific topic. In current practice, feedback on these online formative assessments is often given in the form of proportions of correctly solved items. These metrics are simple and intuitive, but they are oversimplified measures of proficiency and ignore factors of learners, content, and context. This can result in biased representations of students’ strengths and weaknesses, which can lead to poor learning choices. Moreover, the information these metrics provide about learning progress is not very specific and can therefore be difficult for both students and teachers to act upon. Stakeholders generally seek more detailed diagnostic information about knowledge, skills and abilities (Huff and Goodman, 2007).

Diagnostic feedback is information about how students’ current levels of performance relate to desired levels of performance. This type of feedback indicates whether or not students have mastered the skills that are required to solve certain tasks (Huff and Goodman, 2007). In the context of the feedback model from Hattie and Timperley (2007) described above, this diagnostic information provides not only task-oriented feedback, but also process-oriented feedback and feedback that can support self-regulation. It can be regarded as process-oriented feedback since it provides insight in the skills and processes that underlie task performance. In addition, it shows students’ learning progress with respect to these skills, and this detailed information about strengths and weaknesses supports self-monitoring (Schunk and Zimmerman, 2003). This can be helpful for students since poor judgment of one’s own performance and progress can result in poor learning choices, such as terminating study or skipping over important learning opportunities (e.g., Brown, 2001). Diagnostic feedback enables students to determine where they should focus their attention and effort, thus to make more effective learning choices (Bell and Kozlowski, 2002). Thereby it can support self-regulation by providing actionable information (Nicol and Macfarlane-Dick, 2006). Diagnostic information can also be helpful for teachers, because it allows them to timely undertake appropriate pedagogical actions, such as personalized interventions if a student lacks understanding of specific concepts, or if a student is falling behind and may be at risk for course dropout or failing. At group level, the information allows teachers to adjust educational strategies, for example if specific skills or topics are not mastered by many students, indicating that these require additional attention in class.

1.2 Cognitive Diagnostic Assessment

Formative assessments in e-learning provide opportunities to obtain detailed information with cognitive diagnostic assessment, which aims to measure knowledge structures and processing skills in students to provide information about their cognitive strengths and weaknesses (Leighton and Gierl, 2007b). For this end, a so-called cognitive model is specified that links understanding to performance (Norris et al., 2007). Educational domain experts define a set of skills, abilities and cognitive processes that are required to solve certain items, which are referred to as attributes. Note that this limits the scope of cognitive diagnostic assessment to well-defined domains, since specifying a cognitive model requires thorough understanding of the domain and the cognitive processes that underlie item response behavior. The objective of cognitive diagnostic assessment is to classify students based on their item responses in terms of mastery or nonmastery of each of the attributes. These classifications result in attribute profiles indicating which attributes students have mastered. For example, if one is interested in assessing the construct “solving algebraic equations”, diagnostic feedback provides information about mastery of different attributes that are involved in this construct, such as understanding the meaning of symbols, performing algebraic manipulations, and constructing graphical representations. This information can guide students in choosing learning materials they need to study to become masters of the attributes they have not yet mastered, hence this information is actionable.

Diagnostic assessment can support the analysis of student behavior at various levels of detail by defining attributes at different granularity levels. For example, for assessment of the construct “solving algebraic equations” we specified (among others) the coarsely defined attribute “performing algebraic manipulations”. Alternatively, this can be broken down into multiple attributes such as performing basic arithmetic operations, simplifying expressions, and performing factorizations. One could argue that more fine-grained assessment provides more information and is therefore superior to assessing more coarsely defined attributes, but this is not necessarily true. As Sadler (2007) states, fine-grained learning objectives and assessment in education result in the accumulation of small knowledge components and achieving short-term objectives, but feedback on such small components is not necessarily meaningful and may not result in integrated knowledge and skills. On the other hand, coarsely defined attributes may not provide sufficient details to lead to actionable diagnostic feedback. It is therefore important to carefully consider the purpose and receiver of the feedback to determine a granularity level that is valuable from an educational perspective, in the sense that it is both meaningful and actionable (see e.g., Thompson and Yonekura, 2005).

1.3 Statistical Issues

Considerations in the specification of a cognitive model extend beyond these educational concerns. In addition, statistical issues need to be considered, which are the focus of the current study. To estimate students’ attribute profiles, statistical models are used that relate students’ item responses to their skills and abilities. Well-suited models to obtain diagnostic information with respect to multiple attributes based on item response data are diagnostic classification models (DCMs; Rupp et al., 2010). These models can yield multidimensional diagnostic profiles based on assessment data. We focus on DCMs under the log-linear cognitive diagnosis modeling (LCDM) framework because of its modeling flexibility and straightforward interpretation. This is a general model specification framework that subsumes a continuum of models that can be expressed easily (more details are provided in Section 2).

To obtain good model fit and accurate estimates of diagnostic profiles, a sufficient number of items measuring the attributes must be administered to a sufficient number of students. If a set of attributes is decomposed into more fine-grained attributes, the number of attributes increases and thereby the statistical model complexity increases as well. This puts higher demands on the data structure (e.g., assessment length, respondent sample size) and it may become impossible to estimate attribute profiles, although the explicit data requirements remain unclear.

Further, determining a granularity level when defining attributes and constructing items involves careful consideration of the underlying cognitive processes that cause item response behavior and how these processes can be represented by a set of distinct skills. In practice, the granularity level of attributes is often constrained by the purpose of the assessment and practical considerations rather than completely driven by theories about how students reason and learn (Bradshaw, 2017). However, ideally cognitive models “reflect the most scientifically credible understanding of typical ways in which learners represent knowledge and develop expertise in a domain” (Pellegrino et al., 2001, p. 45), which asks for a set of distinct skills. Specifying multiple fine-grained attributes that represent similar or strongly related skills can result in high correlations between the attributes, reflecting that a multidimensional model was forced to fit a unidimensional assessment (Sessoms and Henson, 2018), resulting in subscores that have no added value (Sinharay, 2010). In some situations it can still be useful to retain highly correlated attributes as separate attributes (e.g., if each attribute is associated with a specific remedial action). However, if there are no practical reasons to split them, it may be preferable to define one composite attribute to obtain more reliable estimates of the attribute profiles (Templin and Bradshaw, 2013). On the other hand, coarse-grained attributes can also result in model misfit if the application of a specified skill varies across items measuring that skill (Rupp et al., 2010). This stresses the importance of evaluating model fit after applying DCMs to empirical data. Thus, although diagnostic measurement models offer opportunities to obtain diagnostic feedback in higher education based on data from formative assessment in e-learning, defining a cognitive model can be challenging. The attribute specification affects not only the meaningfulness and actionability of the feedback, but also the statistical model results. Model complexity, assessment length, and respondent sample size are all factors to take into account in cognitive diagnostic assessment.

1.4 Current Study

In the current study, we approach two issues in defining cognitive models from a statistical perspective to guide practitioners in specifying attribute structures and designing formative assessments to enable the application of DCMs.

Data Requirements

The first issue that is addressed in this study concerns data requirements for the statistical model that relates students’ item responses to their skills and abilities. As described, applying DCMs to empirical data requires not only educational considerations about the meaningfulness and actionability of feedback, but one also needs to consider practical issues such as the availability of sufficient data (i.e., assessment length, respondent sample size) and empirical model fit (Rupp, 2007; Rupp et al., 2010). When more complex models are estimated, the demands on the data structure are higher. Unfortunately, there is relatively little research that compares results of competing models in diagnostic measurement using real or simulated data sets; although there are exceptions, see for example Kunina-Habenicht et al. (2012) and Cai et al. (2013). Kunina-Habenicht et al. explored effects of sample size and model misspecifications on DCM results, but the levels of the variables in their study were limited. Only sample sizes of 1,000 and 10,000 respondents and 25 and 50 items were considered, whereas in online formative assessment in higher education sample sizes will generally be (much) smaller. Some research has been conducted in cognitive diagnostic assessment based on small sample sizes with simulations comparing the results of nonparametric and parametric methods, see for example Chiu et al. (2018). Generally, nonparametric methods work better with smaller sample sizes (30–50 respondents), whereas parametric methods perform better with larger sample sizes (200–500 respondents) (Ma et al., 2020). Although this shows the opportunity to apply DCMs to e-learning data in higher education, the explicit sample size requirements are not clarified. In the current study, we focus on university courses with large groups of students, hence on parametric methods. By means of a simulation study, we explore whether it is feasible to use log-linear DCMs to obtain diagnostic information about students based on e-learning data with respondent sample sizes common in this domain. We aim to gain insight in the feasibility of making statements about attribute mastery based on such data by studying how many items need to be administered to how many students in order to obtain high classification accuracy and to allow for adequate evaluation of model fit.

Attribute Granularity

The second issue that is addressed in this study concerns effects of misspecification of the dimensionality of the underlying attribute structure; more specifically of the definitional grain size of the attributes.¹ As mentioned, defining attributes requires consideration of the cognitive processes involved in item response behavior, and thus of the grain size of the true underlying skills and mechanisms that result in the item responses, since granularity misspecifications can result in model misfit. Although decisions about attribute grain size are often constrained by the purpose of the assessment and/or practical considerations, they are ideally grounded in theory about how students learn (Pellegrino et al., 2001). If limited substantive knowledge is available about the nature of the attributes, it is useful if empirical data can support these decisions, for example based on item response data from existing assessments in the domain of interest. It is important to note that such retrofitting procedures can limit both the scope of the attributes that can be measured and the number of measurements of each attribute (Gierl and Cui, 2008; de la Torre and Minchen, 2014), and that it is not assured that items with specific cognitive characteristics exist in assessments developed without a cognitive model. However, content development for any assessment is likely to involve breaking down a larger construct into subdomains, which can be considered as multiple dimensions. Therefore, although one needs to proceed with caution when retrofitting, it can be useful for learning more about the constructs of interest (Liu et al., 2018).

In the current study, we explore to what extent log-linear DCMs can be used to examine attribute grain size. For pragmatic reasons, we assume that a true dimensionality exists. We distinguish two situations: too coarse-grained assessment, in which single attributes are evaluated that in reality represent multiple distinct skills, and too fine-grained assessment, in which multiple attributes are evaluated that in reality represent the same (or highly similar) skills. In the simulation study, we explore how absolute model fit indices are affected by such misspecifications and what the power of these fit indices is to detect these. We also explore whether relative fit indices can detect the correct dimensionality of the attribute structure.

To summarize, the following research questions are addressed in the context of online formative assessment in higher education (i.e., with respondent sample sizes reasonable in this domain):

1. How many items need to be administered to how many students to obtain high classification accuracy and adequate evaluation of model fit when assessing mastery of different numbers of skills using log-linear DCMs?

2. How are model fit indices influenced by misspecification of the grain size (i.e., dimensionality) of the measured skills?

By answering these questions with a simulation study, we aim to provide guidance for assessment construction in an educational context in which it is desired to obtain diagnostic information regarding multiple skills.

2 Methods

The research questions are approached with a simulation study. This allows to generate data under certain assumptions and compare model results with the “true” generating mechanisms. In the remainder of this section, first some (technical) background about diagnostic classification models under the LCDM framework is provided, followed by a description of the study design and details of the simulation study.

2.1 The Log-Linear Cognitive Diagnosis Modeling Framework

As mentioned, diagnostic classification models aim to classify students as master or nonmaster of specified attributes. DCMs are therefore also known as restricted latent class models since they are used to classify respondents in a restricted number of latent classes (i.e., attribute profiles). Suppose an assessment with I items that measures A binary attributes. The attribute profile for latent class c is denoted by the vector α_c = [α_c1, … , α_cA], where α_ca = 1 if attribute a is mastered and α_ca = 0 if not. DCMs directly estimate the probability that a respondent meets the criteria for a given diagnosis (i.e., that a respondent falls into a particular latent diagnostic class given their item responses). The estimates depend on both expert judgment and empirical evidence. Domain experts encode which attributes are required to solve each item into a so-called Q-matrix, which is an I × A matrix indicating for each item i whether it measures each attribute a (q_ia = 1) or not (q_ia = 0). The Q-matrix in combination with data from diagnostic assessment enables estimation of parameters related to item and respondent characteristics.

As the name implies, the LCDM uses a log-linear framework to parameterize the relation between attribute mastery and item response probabilities. Specifically, the conditional probability π_ic that a respondent with attribute profile α_c responds correctly to item i is modeled as follows:

${\pi }_{ic}=P\left(X_{ic}=1\mid {\mathit{\alpha }}_c\right)=\frac{\exp \left({\lambda }_{i,0}+{\mathit{\lambda }}_i^{T}h\left({\mathit{\alpha }}_c,{\mathit{q}}_i\right)\right)}{1+\exp \left({\lambda }_{i,0}+{\mathit{\lambda }}_i^{T}h\left({\mathit{\alpha }}_c,{\mathit{q}}_i\right)\right)}(1)$

Here, X_ic represents the dichotomously scored response to item i by a respondent in latent class c, which equals 0 or 1 for an incorrect or correct response respectively. Further, q_i = [q_i1, … , q_iA] is the vector of binary Q-matrix entries for item i indicating which attributes the item measures. The intercept parameter λ_i,0 represents the logit (log-odds) of a correct response given that the none of the required attributes are mastered by a respondent. The vector λ_i of length 2^A− 1 contains the parameters representing the main effects and interaction effects for item i, and h (α_c, q_i) is a vector of length 2^A− 1 with linear combinations of α_c and q_i. More specifically, the item parameters, the attribute profiles of respondents, and the Q-matrix entries are combined in the exponent as follows:

${\lambda }_{i,0}+{\mathit{\lambda }}_i^{T}h\left({\mathit{\alpha }}_c,{\mathit{q}}_i\right)={\lambda }_{i,0}+\sum _{a=1}^A{\lambda }_{i,1,\left(a\right)}{\alpha }_{ca}{q}_{ia}+\sum _{a=1}^{A-1}\sum _{a^{\prime }=a+1}^A{\lambda }_{i,2,\left(a,a^{\prime }\right)}{\alpha }_{ca}{\alpha }_{c{a}^{\prime }}{q}_{ia}{q}_{i{a}^{\prime }}+\cdots (2)$

For item i, the exponent includes an intercept term (λ_i,0), all main effects (e.g., λ_i,1,(a) indicates the increase in the logit of a correct response given mastery of attribute a), and all possible (two-way up to A-way) interactions between attributes (e.g., λ_i,2(a,a′) represents the two-way interaction between attributes a and a′, allowing the logit of a correct response to change given mastery of both attributes). These item parameters λ_i are estimated using for example the expectation-maximization algorithm. The parameters are subject to monotonicity constraints to ensure that the probability of a correct response increases monotonically with the number of attributes mastered. The item response function is flexible in the inclusion of item and attribute effects, allowing to express differentially complex DCMs by constraining specific parameters from the vector λ_i to zero; the LCDM is the saturated version of many reduced DCMs (see for example Rupp et al., 2010, Ch. 7). The framework provides the possibility to use differential complexity for different items within an assessment, which reflects attribute behavior at the item level (e.g., whether nonmastery of a certain attribute can be compensated by mastery of another attribute).

Estimating a respondent’s attribute profile α_c given their item reponses is generally done within a Bayesian framework. Classification is then done based on posterior probabilities of the attribute profiles derived from the response pattern via the likelihood and the prior probabilities of latent class membership. Classification can be based on maximum a posteriori (MAP) estimates or expected a posteriori (EAP) estimates of the posterior distribution. The former uses latent class membership probabilities (i.e., posterior probabilities of each attribute profile) and does not provide direct probability estimates for each attribute separately. The latter is based on probabilities of attribute mastery for individual attributes. Huebner and Wang (2011) showed that for the DINA model (a special case of the LCDM), MAP results in higher proportions of respondents assigned with the correct attribute profile (i.e., higher profile classification accuracy), whereas EAP results in higher accuracy for the total of individual attributes (i.e., higher attribute-wise classification accuracy) and fewer severe misclassifications.

2.2 Study Design

The aim of the simulation study is to explore whether it is feasible to use the LCDM to obtain diagnostic information about students’ skills based on data from online formative assessments in higher education. In addition, we explore effects of misspecification of the dimensionality of the underlying attribute structure. In the simulation study, we manipulated the number of measured attributes, the number of items, and the number of respondents. Further, we chose plausible values for other parameters that are required to simulate item responses, namely marginal attribute difficulties, attribute associations, item loading structures (i.e., Q-matrix), and item parameters. By simulating realistic scenarios, results are expected to be informative for practitioners. For each condition 1,000 data sets are generated. The study design is summarized in Table 1 and will be described in more detail below.

TABLE 1

TABLE 1. Simulation study design and conditions for data generation.

Number of Attributes

The first manipulated variable is the number of attributes A. The levels of this variable are set to 3, 4, 5, and 6 attributes. This set of values encompasses levels that are generally used in simulation studies with DCMs (e.g., Rupp and Templin, 2008; Kunina-Habenicht et al., 2012; Liu et al., 2017) and reflect common dimensionalities of educational assessments (e.g., Sinharay et al., 2011). Although DCM applications with more attributes are described in the literature (see e.g., Sessoms and Henson, 2018), these applications need significantly more data and might have more stringent requirements on the Q-matrix in order to be identifiable (Gu and Xu, 2021). We aim to study the feasibility to apply DCMs to online formative assessment in higher education, where resources are limited and thus the maximum number of attributes is restricted. In this context, it is relevant to obtain detailed information about the different requirements for different number of attributes to inform practitioners. Therefore, we chose to increase the number of attributes with steps of 1 and restrict the maximum number to 6.

Number of Items

The second manipulated variable is the number of administered items I. The aim is to study the feasibility of applying DCMs to formative assessments in e-learning environments. Since (subjective) cognitive fatigue increases with increasing time-on-task (Ackerman and Kanfer, 2009), the amount of items should not be large. Keeping the assessment length short ensures that students are motivated to complete all items of low-stakes assessments. To simulate realistic assessment lengths, the levels of this variable are set to 10, 15, 20, 25, and 30 items.

Number of Respondents

The third manipulated variable is the number of respondents R. As described, previous simulations have shown that nonparametric methods are preferred for smaller sample sizes (30–50 respondents) and parametric methods such as DCMs for larger sample sizes (200–500 respondents) (Ma et al., 2020). To obtain more specific information about sample size requirements for DCMs, the levels of this variable are set to vary between 100 and 1,000, increasing with steps of 100. These varying levels provide useful information for university courses, since the amount of students who participate in these courses varies greatly across courses and universities.

Mastery Proportions and Attribute Associations

To simulate item response data, first R attribute profiles are generated for each number of attributes A, taking into consideration the marginal attribute difficulties (mastery proportions) and the attribute associations (correlations). For each respondent, a vector p of length A is sampled from a multivariate normal distribution with mean μ and correlation matrix Σ and these vectors are discretized at 0, resulting in attribute profiles α_c (i.e., α_ac = 0 if p_a < 0, and α_ac = 1 if p_a > 0). The mean vector μ and correlation matrix Σ are defined based on plausible values for the marginal mastery proportions and the correlations between the latent attribute variables respectively.

The aim is to evaluate whether the models are applicable in e-learning, which is a low-stakes practice environment. Students are likely to make assessments before thoroughly studying all the learning materials and some may grasp some attributes better than other attributes. Therefore, the marginal mastery proportions m_a are expected to vary across the attributes within an assessment. In each replication, μ is chosen such that it leads to marginal attribute proportions of approximately 0.3, 0.5 and 0.7 for the conditions with three attributes; 0.3, 0.5, 0.5 and 0.7 for four attributes; 0.3, 0.4, 0.5, 0.6 and 0.7 for five attributes; and 0.3, 0.4, 0.5, 0.5 0.6 and 0.7 for six attributes. These values were driven by similar rates in literature. For example, Kunina-Habenicht et al. (2012) studied conditions with mastery proportions varying from 0.3 to 0.7 versus equal mastery proportions of 0.5 across attributes. Results showed no substantial impact on classification accuracy, and although it would be interesting to verify whether this also holds in our situation with smaller sample sizes, we choose one realistic level for this factor to keep the simulation study manageable. For the same reason, we choose one level for the tetrachoric attribute correlations of attribute pairs. For each attribute pair, the correlation in Σ is sampled from U (0.5, 0.7), which are typical values for associations of subscores in subdomains in educational learning applications (Sinharay, 2010; Sinharay et al., 2011; Hofman et al., 2018). This reflects moderate to high correlations between the attributes, which is a realistic scenario for assessments within university courses that generally cover subjects that are by definition related to each other. In addition, it is in line with values that are used in similar simulation studies (e.g. Cui et al., 2012; Kunina-Habenicht et al., 2012; Liu et al., 2017).

Q-Matrix Specification

A Q-matrix is defined for each condition that results from crossing the number of attributes and items. For this study, we assume that the Q-matrix is correctly specified. Q-matrices can differ in their complexity, that is, in the number of items measuring each attribute, the number of attributes measured within each item, and the number of attributes that are measured jointly with other attributes on the assessment. Following the recommendations from Madison and Bradshaw (2015),² we ensure that each attribute is measured at least once in isolation, if possible more than once. This aligns with findings from Kunina-Habenicht et al. (2012), who demonstrated that items that load on more than three attributes are computationally demanding and lead to large standard errors of parameter estimates. Therefore, we include only unidimensional and two-dimensional items (i.e., items that measure one or two attributes). For each number of attributes A, Q-matrices are specified for the different assessment lengths I. Table 2 shows the numbers of unidimensional and two-dimensional items that are included in each Q-matrix. For the unidimensional items, we ensured that all attributes are measured the same number of times. The two-dimensional loading structures are sampled randomly from all possible structures in each replication.

TABLE 2

TABLE 2. Number of unidimensional (uni) and two-dimensional (two) items per condition resulting from crossing the number of attributes and items.

Item Parameters

To generate data, item parameters λ_i are sampled from uniform distribution such that they result in plausible response probabilities. For all items measuring one attribute, the intercepts λ_i,0 are sampled from U (−1.50, −0.80) and the main effects λ_i,1,(a) from U (2.20, 2.90). For all items measuring two attributes, the intercepts λ_i,0 are sampled from U (−1.50, −0.90), both main effects λ_i,1,(a) from U (0.90, 1.10), and the two-way interactions λ_i,2(a,a′) from U (0.30, 0.50). The probability of a correct response to an item can be calculated using Eqs. 1, 2. The range of the item response probabilities resulting from the sampled item parameters are shown in Table 3. These item response probabilities are plausible in the sense that guessing probabilities for complete nonmasters are relatively low, probabilities of correct responses for complete masters are relatively high, and incremental increases in probabilities for masters of individual attributes for two-dimensional items are nontrivial (see e.g., Liu et al., 2017 and Madison and Bradshaw, 2015 for simulations with similar ranges of response probabilities for data generation). By randomly sampling the item parameters, the generated item sets will include a mix of items of lower and higher quality.

TABLE 3

TABLE 3. Range of item response probabilities for data generation.

2.3 Data Generation

Data is generated using the statistical software R (R Core Team, 2019) with the saturated LCDM as the generating model. The simulated attribute profiles, Q-matrices, and item parameters are combined to compute the item response probabilities π_ic for each respondent using Eqs. 1, 2. Then, to generate response x_ic to item i for a respondent with attribute profile α_c, a random number u is drawn from a uniform distribution on the interval 0 to 1: u ∼ U (0, 1). This value is compared with the response probability π_ic. If u < π_ic then x_ic = 1, otherwise x_ic = 0.

In the first part of the study, 1,000 data sets are generated for each condition resulting from crossing the number of attributes (4 levels), number of items (5 levels), and number of respondents (10 levels). In the second part of the study we look at the effects of misspecification of the dimensionality of the attribute structure, for which we also generate 1,000 data sets per condition. In these situations, Q-matrices to generate data can have a different dimension than the Q-matrices to estimate the models. That is, we generate data assuming a certain number of underlying attributes (A_true) that result in the item responses. We estimate both the true generating models and models with a Q-matrix with an incompatible numbers of attributes (A_est ≠ A_true), i.e., assuming that a different number of attributes underlies the item response behaviour. We distinguish two situations in this regard. First, we look at situations where the attributes for the estimated model are too coarsely defined. We generate data assuming A_true = 2 and A_true = 4 true underlying attributes, and we estimate misspecified models assuming A_est = 1 and A_est = 2 underlying attributes respectively. The Q-matrix for estimation is therefore a reduced version of the Q-matrix used for generation (i.e., lower dimensionality). Second, we look at situations where the estimated model is too fine-grained. We consider situations for which data is generated assuming A_true = 1 and A_true = 2 true underlying attributes and we estimate models with A_est = 2 and A_est = 4 respectively. This is achieved by generating data for attribute pairs with correlations set to ρ = 0.98 to represent single, unseparable underlying skills (a value close to but not equal to 1 was chosen to prevent computational issues). This way, to estimate the misspecified and true models, we need the generating Q-matrices and a reduced version of this matrix (i.e., it is only required to reduce the dimensionality; not to increase). A set of Q-matrices with different dimensionalities is constructed as follows. First, the matrix with the highest dimension is specified following the procedures described in Section 2.2, and this dimensionality is reduced based on its loading structure. If two attributes are assumed to represent similar skills, the Q-matrix with reduced dimensionality combines these into one attribute. If an item loads on either one or both of the original attributes, the item also loads on the new attribute. An example of this reduction is shown in Supplementary Appendix Table A1).

2.4 Model Estimation

All models are estimated with the statistical software R (R Core Team, 2019) using the R package GDINA (Ma and de la Torre, 2020b; note that the LCDM is equivalent to the generalized deterministic inputs, noisy “and” gate model with a logit link [G-DINA; de la Torre, 2011]; the required monotonicity constraints were added). Classifications are based on the expected a posteriori (EAP) estimates. To answer the first research question about the demands on the data structure for the LCDM, the true generating model was fitted to each data set, i.e., using the correct Q-matrix and the saturated LCDM. Evaluation of classification accuracy and model fit indices provides insight in the requirements on the data in order to make statements about attribute mastery of respondents. To answer the second research question about the impact of dimensionality misspecifications on model fit indices, we misspecified the number of attributes in the Q-matrix following the procedure described in Section 2.3. Both the true and misspecified models are estimated and the behavior of model fit indices is evaluated.

2.5 Outcome Measures

Classification Accuracy

Correct classification rate is typically an important outcome when DCMs are applied to empirical data, since educational decisions are made based on these classifications. In educational practice, students’ learning choices are likely to be made based on evaluation of mastery results of individual attributes, for example deciding to practice with learning materials about a nonmastered attribute. We therefore evaluate the marginal attribute classification rate (i.e., attribute-wise classification accuracy).

Absolute Model Fit

We evaluate the behavior of two measures of absolute model fit of the estimated models. First, M₂ is calculated, which combines limited-information fit statistics across pairs of items to produce an overall index of model fit (Maydeu-Olivares and Joe, 2006). Asymptotic p-values for this statistic are accurate even when the data are sparse. Liu et al. (2016) showed that M₂ is a powerful tool to detect model misspecification and recommend the use of M₂ statistic for assessing the overall exact model fit in DCMs. However, the power of M₂ to detect misspecifications in the attribute structure seems to be rather low (Hansen et al., 2016).

In addition, we assess goodness of approximation with the bivariate root mean square error of approximation statistic (RMSEA₂), which is a transformation of the discrepancy between the fitted model and the population probabilities that adjusts for model complexity and expresses such discrepancy in the metric of the summary statistics used to assess model fit (see Maydeu-Olivares and Joe, 2014 for details). It shows a degree of misfit and can be regarded as an effect size measure. Simulation studies showed that for the RMSEA₂ the cutoff values 0.030 and 0.045 are reasonable criteria for excellent and good fit for the LCDM (Liu et al., 2016).

Relative Model Fit

To evaluate relative model fit both Akaike’s information criterion (AIC; Akaike, 1974) and the Bayesian information criterion (BIC; Schwarz, 1978) are considered, which are measures that compromise model fit and complexity. It is assessed whether these indices provide evidence in favor of the correctly specified models compared with the models with dimensionality misspecifications.

3 Results

3.1 Impact of Assessment Length and Respondent Sample Size on Model Results

To answer the first research question concerning data requirements for the LCDM, we assessed the conditions for which the generating model is consistent with the estimated model. For each condition resulting from crossing the number of attributes, items and respondents, we evaluated the marginal (attribute-wise) classification accuracy and the behavior of the fit statistics M₂ and RMSEA₂.

Classification accuracy is shown in Figure 1. The figure shows the accuracy averaged across replications with 90% error bars (vertical axes start at 0.7 for clearer presentation of the results). The accuracy is not highly influenced by respondent sample size, although smaller sample sizes expectedly result in more variation across replications as illustrated by the larger error bars, indicating that these results are less stable. The number of items seems to have more impact on the accuracy than the number of respondents. As expected, administering more items results in higher classification accuracy, since classifications are based on more information. For each number of attributes A we evaluated how many respondents R are needed to achieve accuracy of 0.9 (indicated by the horizontal dashed line) with different assessment lengths. The results are summarized in Table 4. When more attributes are assessed, the data requirements to achieve accuracy of 0.9 are obviously more demanding. In several conditions, this level of accuracy was not achieved with R ≤ 1,000. In the remaining conditions respondent sample size requirements vary between 100 and 300.

FIGURE 1

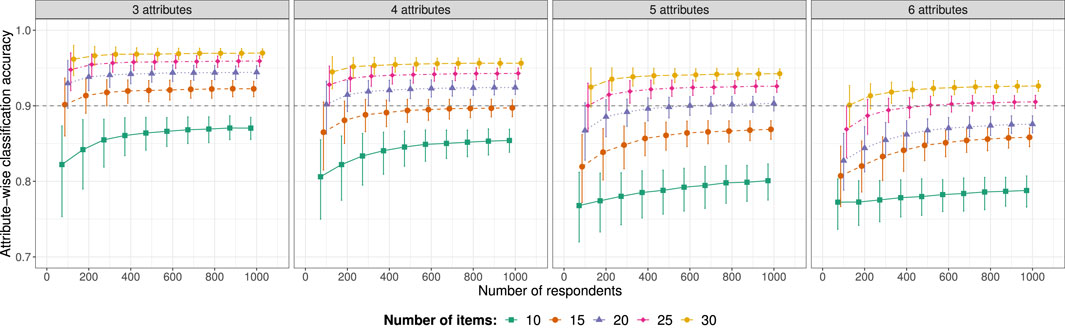
FIGURE 1. Average marginal classification accuracy (with 90% error bars) in the conditions resulting from crossing the number of attributes A, items I, and respondents R for which the generating model was consistent with the estimated model. Vertical axes start at 0.7 for clearer presentation of results and horizontal dashed lines indicate accuracy of 0.9.

TABLE 4

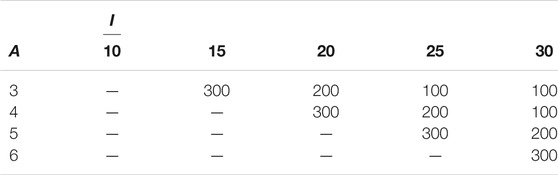
TABLE 4. Required number of respondents R to achieve a marginal classification accuracy of 0.9 when assessing A attributes with I items (“-” indicates that this level of accuracy cannot be achieved with R ≤ 1,000).

In addition to classification accuracy, we assessed the behavior of M₂. More specifically, we evaluated the rejection rates at α = 0.05. Since the estimated models correspond to the data generating mechanisms, these values represent type I error rates. All rejection rates were reasonably close to the nominal alpha level 0.05, providing no indication that this statistic is too conservative or too liberal under these circumstances (the rejection rates per condition are presented in Supplementary Appendix Table A2). Note that for the condition with 10 items and 5 or 6 attributes, the M₂ statistic could not be calculated because the degrees of freedom were too low, implying that the model was too complex for the data at hand. For a detailed description of M₂ and its degrees of freedom, we refer the reader to Maydeu-Olivares and Joe (2006) or Hansen et al. (2016).

Last, RMSEA₂ was evaluated. Note that again, for the condition with 10 items and 5 or 6 attributes, the RMSEA₂ statistic could not be calculated due to too low degrees of freedom. For the remaining conditions, Figure 2 shows the average RMSEA₂ across replications with 90% error bars. The average values are all well below the proposed cutoff value of 0.045 (Liu et al., 2016; indicated by the horizontal dashed lines), thereby indicating good model fit. For small respondent sample sizes, RMSEA₂ varied considerably across replications as illustrated by the large error bars, indicating that this statistic may not be reliable under these circumstances.

FIGURE 2

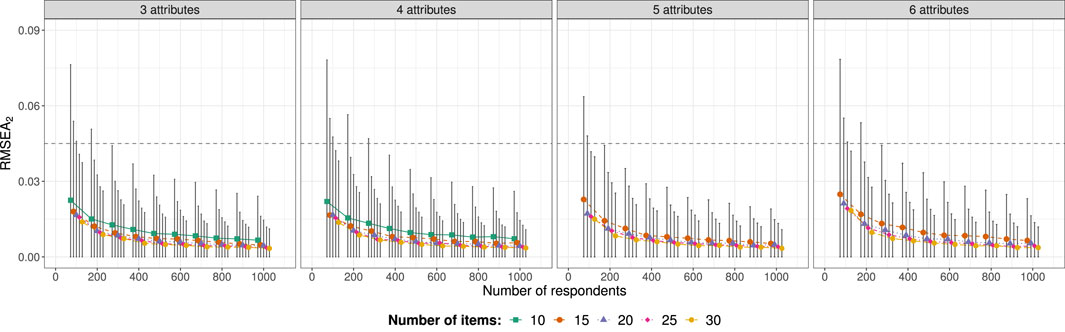
FIGURE 2. Average RMSEA₂ (with 90% error bars) in the conditions resulting from crossing the number of attributes A, items I, and respondents R for which the generating model was consistent with the estimated model. Horizontal dashed lines indicate RMSEA₂ of 0.045.

To explore the relation between RMSEA₂ and marginal classification accuracy, Figure 3 shows scatterplots of this relation for the different levels of A and I, with horizontal dashed lines indicating accuracy of 0.9 and vertical dashed lines RMSEA₂ of 0.045. We expect a negative relation between the two variables, so that a higher value of RMSEA₂ indicates lower accuracy. Although this trend is to some extent visible in the panels in Figure 3, it is evident that if many attributes are assessed with a small number of items (i.e., A = 3 and I = 10; A = 4 and I ≤ 15; A = 5 and I ≤ 20; A = 6 and I ≤ 25), the values of RMSEA₂ do not substantially increase despite the somewhat lower accuracy in these conditions. Thus, under these circumstances, RMSEA₂ fails to provide evidence of decreased model performance.³ Note that these are precisely the conditions in which 0.9 accuracy could not be achieved with R ≤ 1,000 (see Table 4), emphasizing that it is advisable to avoid these situations in cognitive diagnostic assessment with the LCDM, since one cannot adequately evaluate model performance with the RMSEA₂.

FIGURE 3

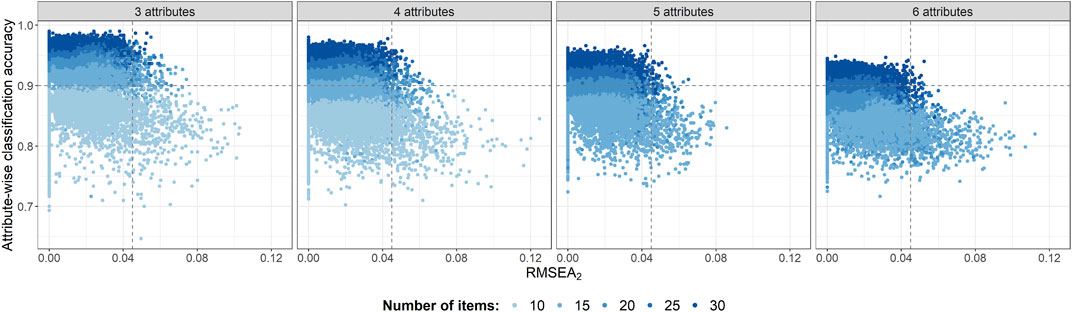
FIGURE 3. Scatterplot of marginal classification accuracy against RMSEA₂ in conditions with consistent generating and estimated models. Horizontal and vertical dashed lines indicate accuracy of 0.9 and RMSEA₂ of 0.045.

3.2 Sensitivity of Model Fit Indices to Dimensionality Misspecifications

To answer the second research question concerning dimensionality misspecifications, we assessed the conditions for which the generating model is inconsistent with the estimated model. This means the number of attributes assumed in generating the data is different from the number of attributes in the estimated model. We distinguish two situations: the attribute structure of the estimated model is too coarse-grained, or the attribute structure of the estimated model is too fine-grained. For each condition resulting from crossing the number of attributes, items and respondents, we evaluated the power of M₂ to detect misfit and the behavior of RMSEA₂. In addition, we considered the sensitivity of relative fit indices (i.e., AIC and BIC) to select the best model among models with different dimensionality.

Too Coarse-Grained Assessment

To simulate too coarse-grained assessment, models with A_est = 1 and A_est = 2 were fitted to data that was generated assuming A_true = 2 and A_true = 4 true underlying attributes respectively. The top panels in Figure 4 show the M₂ rejection rates for all conditions, which represent the power to detect this type of model misfit. Assuming a desired power of 0.8 (indicated by the horizontal dashed lines), a respondent sample size of R = 300 is required to be able to detect the misfit when I = 10. When the number of items is larger, the required number of respondents decreases. For I = 15, respondent sample sizes of R = 100 to R = 200 suffice, and when I ≥ 20 a respondent sample size of R = 100 is sufficient.

FIGURE 4

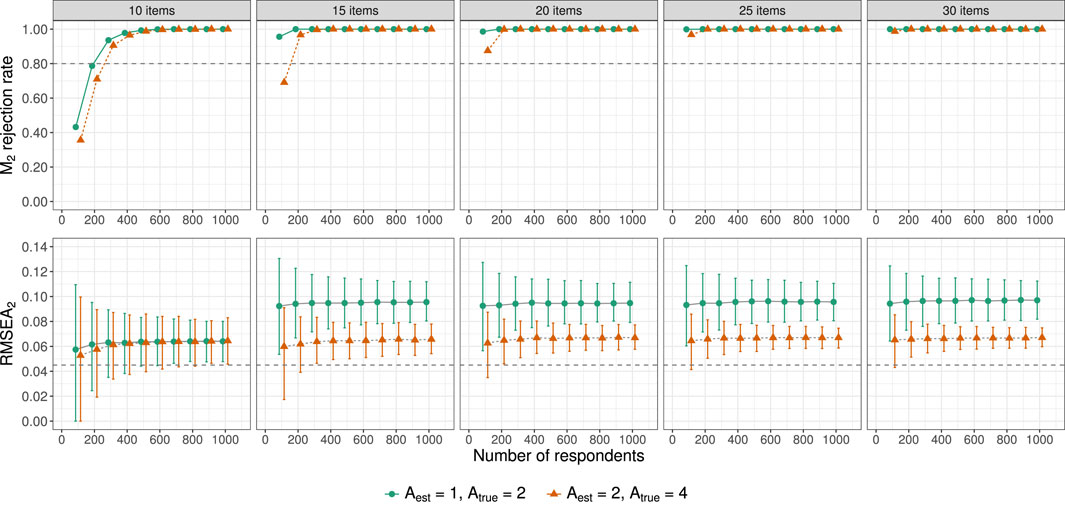
FIGURE 4. M₂ rejection rates and average RMSEA₂ (with 90% error bars) in the conditions resulting from crossing the number of items I and respondents R for which the estimated model was more coarse-grained than the generating model (A_est < A_true). Horizontal dashed lines indicate M₂ rejection rates of 0.8 (desired power) and RMSEA₂ of 0.045.

The bottom panels in Figure 4 show the average RMSEA₂ across replications with 90% error bars and horizontal dashed lines indicating the 0.045 cutoff value proposed by Liu et al. (2016). For I = 10, RMSEA₂ varies greatly across replications with averages close to the cutoff value, indicating that this statistic is not reliable under these circumstances. This lack of reliability remains an issue for small respondent sample sizes (R ≤ 200) even if the number of items increases. In the remaining conditions, RMSEA₂ correctly provides indications of model misfit.

In addition to absolute model fit indices, it is assessed whether the AIC and BIC can be used for model selection among the too coarse-grained model and the correctly specified (generating) model. Both models were estimated for each simulated data set and the model with the lowest value of each relative fit index was selected. Figure 5 shows for each condition the proportion of replications in which the true model was selected.⁴ With sufficient numbers of items and respondents (I ≥ 20, R ≥ 200) both the AIC and the BIC nearly always selected the true, more complex model. For shorter assessments and smaller respondent sample sizes, the AIC outperformed the BIC. This is in line with previous research showing that the AIC may be preferred to the BIC when candidate models are oversimplifications of more complex true models (Vrieze, 2012). However, note that when both the number of items and respondents are small (I = 10, R = 100) the AIC still selected the misspecified, less complex model a considerable amount of times. Overall, in 92.3% of all replications across all conditions both indices correctly favored the true model, in 6.9% there was disagreement between the indices with the AIC always outperforming the BIC, and in only 0.8% both indices incorrectly favored the too coarse-grained model.

FIGURE 5

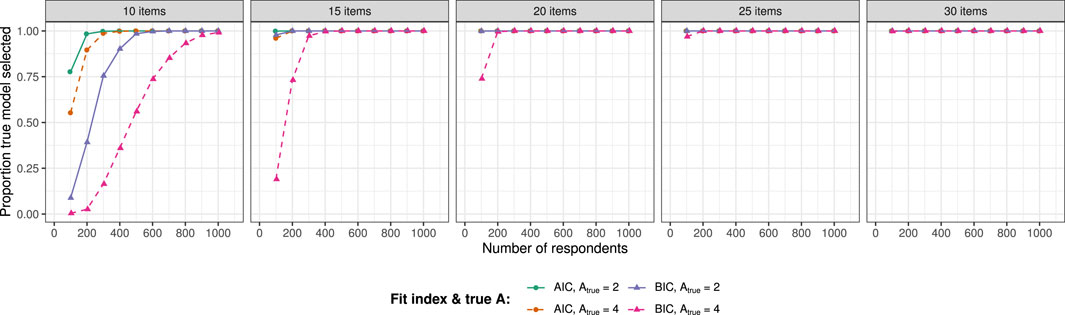
FIGURE 5. Proportion of replications where AIC and BIC preferred the true model over the too coarse-grained model. Results are displayed for the conditions with A_true = 2 and A_est = 1, 2, and with A_true = 4 and A_est = 2, 4.

Too Fine-Grained Assessment

To simulate too fine-grained assessment, models with A_est = 2 and A_est = 4 were fitted to data that was generated assuming A_true = 1 and A_true = 2 true underlying attributes respectively. Figure 6 shows the M₂ rejection rates and average RMSEA₂ with 90% error bars for all conditions. Rejection rates are low in all conditions (all $<0.1$), indicating that the power of M₂ to detect this type of misfit is low. In addition, the average RMSEA₂ values are below the cutoff value 0.045 (indicated by the horizontal dashed lines) in all conditions, thereby also failing to provide indication of misfit. Thus, whereas the absolute fit indices were able to detect too coarsely defined models (with sufficiently large numbers of items and respondents), these indices cannot be used to detect model misfit if assessment is too fine-grained.

FIGURE 6

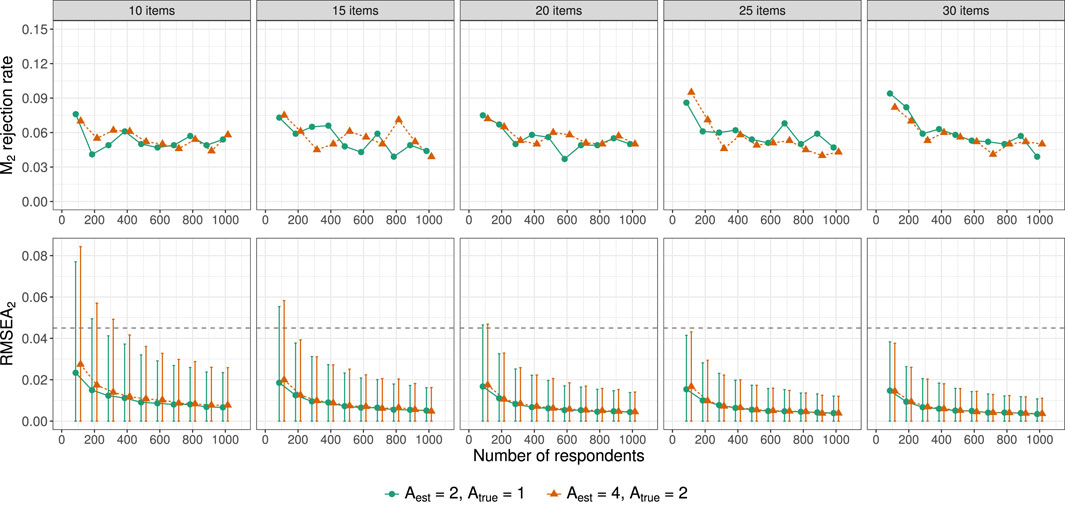
FIGURE 6. M₂ rejection rates and average RMSEA₂ (with 90% error bars)in the conditions resulting from crossing the number of items I and respondents R for which the estimated model was more fine-grained than the generating model (A_est > A_true). Horizontal dashed lines indicate RMSEA₂ of 0.045.

The too fine-grained models are more complex (i.e., include more parameters) than the models that correspond to the data generating mechanisms. More complex models are more likely to fit empirical data, explaining the low rejection rates of M₂ and the low values of RMSEA₂. To account for this, the relative fit indices AIC and BIC include penalty terms for complexity. For the AIC this penalty is 2p and for the BIC p ⋅  ln(n), where p is the number of parameters and n indicates sample size. We assessed whether the AIC and BIC provide evidence in favor of the correctly specified models compared with models with dimensionality misspecifications. Both the true generating model and the too fine-grained model were estimated for each simulated data set and the model with the lowest value of each relative fit index was selected. It was evaluated how often the true model was preferred over the misspecified model by the AIC and BIC, i.e., in what proportion of the replications the relative fit indices were lower for the true model than the misspecified model. The results are shown in Figure 7.⁵ It is evident that the BIC outperforms the AIC in all conditions. This aligns with findings from Lei and Li (2016), who found that in cognitive diagnostic modeling the AIC tends to erroneously favor more complex models. However, despite the penalty component of the BIC that increases with sample size, the performance of the BIC decreases with increasing respondent sample size for conditions with a large number of items. This suggests that, although the BIC outperforms the AIC, neither of these indices performs great in selecting the true model if competing models are more complex. In 24.4% of all replications across all conditions both indices favored the true, more parsimonious model, in 32.6% there was disagreement between the indices with the BIC always outperforming the AIC, and in 43.0% both indices incorrectly favored the too fine-grained model. The proportion of replications in which both indices favor the incorrect model increases with increasing number of items and respondents. In short, there is a continuous trend of both the AIC and the BIC favoring overly complex models. A measure with a stronger penalty for complexity may be needed with larger sample sizes.

FIGURE 7

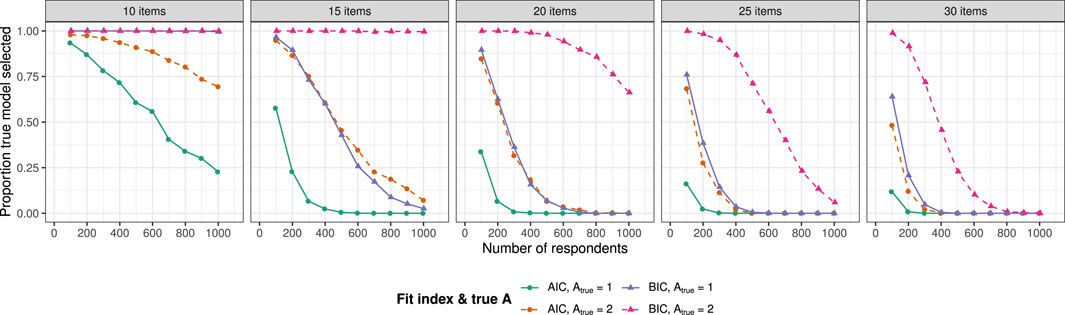
FIGURE 7. Proportion of replications where AIC and BIC preferred the true model over the too fine-grained model. Results are displayed for the conditions with A_true = 1 and A_est = 1, 2, and with A_true = 2 and A_est = 2, 4.

4 Discussion

This simulation study investigated the feasibility of applying log-linear diagnostic classification models to online formative assessments in higher education to obtain diagnostic, actionable feedback, particularly in courses with large groups of students. More specifically, we approached issues in constructing cognitive diagnostic assessments from a statistical perspective by studying data requirements of log-linear DCMs and the impact of misspecification of the grain size (i.e., dimensionality) of the measured skills on model fit indices. Regarding the data requirements, we provided minimum respondent sample sizes that are necessary to 1) obtain high accuracy in classifying students as master or nonmaster of different numbers of attributes based on assessments of different lengths, and 2) allow for adequate evaluation of model fit with the M₂ and RMSEA₂ statistics. As expected, assessing more attributes increases the demands on the data structure, with minimum respondent sample sizes varying between 100 and 300; see Table 4 for the explicit requirements. These requirements seem feasible to meet in large courses in higher education, especially since the number of items seems to have more impact on the accuracy than the number of respondents. Results showed that if attributes are assesses with a small number of items (i.e., 3, 4, 5 or 6 attributes with at most 10, 15, 20 or 25 items respectively), model fit cannot be adequately evaluated with the RMSEA₂, but if more items are administered this issue is resolved. If it is possible to include at least 20 to 30 items in formative assessments, one can accurately assess 3 to 5 attributes based on respondent sample sizes of 200 students, which is not an uncommon number in this domain.

Regarding dimensionality misspecifications, we evaluated situations where single attributes are defined that in reality represent multiple distinct skills, and situations where multiple attributes are defined that in reality represent the same (or highly similar) skills. Results showed that (with sufficient data) the absolute model fit indices M₂ and RMSEA₂ can be used to detect model misfit if attributes are too coarsely defined, but not if the definitional grain size is too fine. Moreover, the relative fit indices AIC and BIC generally provided evidence in favor of true, more fine-grained and complex models when compared with too coarsely defined models, but not in favor of true, more coarsely defined and parsimonious models when compared with too fine-grained models. Regarding too fine-grained models, we studied the extreme case with attribute correlations of 0.98, resulting in almost unseparable attributes (i.e., single dimensions). Even in this extreme case the fit indices generally preferred the incorrect, higher-dimensional models and this performance is expected to decrease further for lower attribute correlations. We recommend to be conservative if it comes to dimensionality and to give preference to parsimonious models. Results showed that the models are prone to overfitting, and that the AIC and BIC penalty terms for complexity may not be strong enough. The problem is that in practice, if dimensionality is studied empirically by fitting log-linear DCMs of different dimensionalities, it is unknown which of the two situations applies and it is thus unknown whether the results can be trusted. Since the AIC was found to perform better in one situation and the BIC in the other, it is advisable not to rely on solely one index but to evaluate their agreement to lend more support for model choice. However, even if the indices agree these results cannot be fully trusted, since there is a considerable chance of overfitting (especially with larger sample sizes). Therefore, when assessing attribute dimensionality, it is recommendable to rely on sound research in education and cognition (e.g., think-aloud studies; Leighton and Gierl, 2007a).

4.1 Implications for Educational Practice

The established data requirements provide guidance to educational practitioners for the design of online formative assessments to allow for the application of log-linear DCMs to obtain diagnostic, actionable feedback. As described, this design process starts with defining a cognitive model (i.e., specifying the attributes). Depending on the number of students that will make the assessment, the results from Table 4 can be used to determine the number of attributes and items. For example, if 300 students participate, one can choose to assess 4 attributes with 20 items. Note that if an assessment is not sufficiently long, one can consider to include covariates that provide auxiliary information to increase classification accuracy (Sun and de la Torre, 2020), such as courses taken or obtained grades (Mislevy and Sheehan, 1989). Once the number of attributes is determined, one defines the attributes at a certain granularity level. From an educational perspective, this involves consideration of the range of learning goals that are covered in the assessment and the desired specificity of feedback. In addition, the results from the simulation showed the importance of theoretical considerations regarding cognitive processes underlying item response behavior to define a set of distinct attributes, since it can be troublesome to statistically detect attribute dimensionality misspecifications.

After specifying the attribute structure, a sufficient number of items measuring these attributes are combined into an assessment. Courses that use e-learing environments generally have an item bank available with practice materials for students. Teachers can exploit these items to compose an assessment to obtain diagnostic information and specify which attribute(s) each item measures (i.e., specify the Q-matrix). Madison and Bradshaw (2015) provide guidelines for Q-matrix design that should be considered in this process. They recommend to measure each attribute a reasonable amount of times, to measure each attribute at least once in isolation (i.e., with unidimensional items), and, if two attributes are truly connected and items cannot be written to measure either attribute in isolation, to combine them into one composite attribute. More recently, Gu and Xu (2021) have provided guidelines for constructing an identified Q-matrix that should be considered. Further, in the current study it was assumed that the Q-matrix was correctly specified. Yet, the process of establishing the Q-matrix based on expert judgment is subjective in nature and may be susceptible to errors. To address this issue, the Q-matrix can be empirically validated to identify misspecified entries, for example with the general discrimination index (GDI; de la Torre and Chiu, 2016) or the stepwise Wald method (Ma and de la Torre, 2020a). These validation methods provide suggestions for modifications that improve model fit, which should be evaluated by domain experts to take a final decision about the Q-matrix to secure theoretical interpretability.

Once a formative assessment has been composed, it is provided to students in online learning environments and DCMs are estimated based on the response data. In the current study, the saturated LCDM was estimated, which corresponded to the true generating model. However, in reality the nature of attribute interactions may vary across items for complex structure items, which may call for the use of reduced DCMs. If there is no a priori theory about attribute behavior at the item level, the LCDM framework can be used to observe attribute behavior by testing for each item whether a reduced model can be estimated without a significant loss of model fit with a Wald test (de la Torre and Lee, 2013). Ma et al. (2016) found that when reduced DCMs are correctly used for different items, this can result in higher classification accuracy compared to fitting the saturated LCDM to all items, particularly when the sample size is small and items are of low quality. Once the approriate DCMs are estimated, diagnostic profiles can be obtained. This detailed diagnostic feedback can improve educational practice by allowing for better informed learning choices by both students and teachers (Nicol and Macfarlane-Dick, 2006).

In future work, we plan to implement cognitive diagnostic assessments in an online learning environment in higher education and to model item response data with log-linear DCMs. We will demonstrate with empirical data how these models can be used to provide effective feedback based on online formative assessments. To get a sense of how this can be established, we refer the reader to Jang (2008) for a framework for implementing cognitive diagnostic assessments in practice, and to Roduta Roberts and Gierl (2010) for a framework for developing score reports of cognitive diagnostic assessments. Further, for application examples see Park et al. (2020) who show the use of DCMs to report subscores in health professions education, or Gierl et al. (2010) for an implementation of cognitive diagnostic assessment in a mathematics program.

4.2 Limitations and Future Research

The current simulation study was not exhaustive with respect to conditions of model (mis)specifications, since that would not be manageable. We attempted to resemble circumstances in the domain of online learning in higher education as closely as possible by specifying plausible values in the simulation design, such as mastery proportions, attribute correlations, and item quality. Although the results of this study can be generalized beyond this specific domain, the choices for the simulation conditions were driven by this context. Note that true values may deviate from the specified values and although previous simulations have not shown substantial effects of such deviations for some of these factors (e.g., Kunina-Habenicht et al., 2012), it would be interesting to verify whether this also holds in our situation with smaller sample sizes. In addition, other types of model misspecifications may impact the results, such as underfitting or overfitting of the Q-matrix (i.e., specifying 0s where there should be 1s and vice versa) or incompleteness of the Q-matrix. Research has been conducted to explore the effects of such misspecifications in cognitive diagnostic assessment (see for example Rupp and Templin, 2008; Kunina-Habenicht et al., 2012; Lei and Li, 2016), but it would be relevant to explore these further in the context of formative assessment in higher education courses, i.e. with smaller sample sizes.

Further, we only included unidimensional and two-dimensional items. As indicated earlier, including more cross-loadings in the Q-matrix will lead to more estimation instability (Kunina-Habenicht et al., 2012). Larger sample sizes than recommended in our study may be needed if Q-matrix complexity increases and it would be interesting to extend the simulation study by including more complex items. Note that we specified our Q-matrices following guidelines from Madison and Bradshaw (2015). Q-matrix identifiability is an active research area, and more explicit requirements have recently been recommended to ensure identifiability; see Gu and Xu (2021). We evaluated our Q-matrix construction procedures, and found that in the conditions with I ≥ 3A (nearly) all our Q-matrices meet the requirements from Gu and Xu, but not in the conditions with I < 3A. Although our results did not show identification problems, it is important to take identifiability into consideration for the interpretability of the model results in practice.

Like the simulation conditions, the model fit indices used to evaluate the results were not exhaustive. Additional fit indices are available that would be interesting to explore in the context of granularity misspecifications, such as the bivariate information statistics considered by Chen et al. (2013) or by Lei and Li (2016).

Finally, we assumed a true, static attribute dimensionality. Note that the structure of skills may change over time, e.g., correlations between skills can increase and become so strongly connected that they can be viewed as a unidimensional skill (Hofman et al., 2018). Learning is a dynamic process, especially when feedback is provided, and these dynamics should be considered in diagnostic assessment too (e.g., Brinkhuis and Maris, 2019). Future studies might consider exploring highly correlated attributes and the effect of the definitional grain size on inferences about students.

4.3 Concluding Remarks

To conclude, diagnostic classification models can be a valuable tool to obtain diagnostic information based on online formative assessments in higher education. To achieve this, teachers need to specify the skills to be measured, construct assessments, and indicate for each assessment item which skill(s) it measures. The current study shows that DCMs can provide accurate diagnostic information with sufficient numbers of items and respondents, yet it stresses the importance of theoretical considerations about cognitive processes that result in item responses when specifying the skills to be measured. Note that constructing cognitive diagnostic assessments does not require statistical knowledge about data modeling, thus making it feasible for teachers in any educational domain that allows for theoretically grounded attribute specification. To enable this, e-learning platforms would need to develop user-friendly tools that enable the construction of such assessments, including instructions for teachers about the requirements concerning the numbers of skills and items and item loading structures. Constructing these assessments requires additional effort from teachers, but this is outweighed by the benefits of obtaining actionable feedback rather than (less meaningful) proportion correct scores that are generally provided in current practice.

Data Availability Statement

All R code to generate and analyze the datasets in the current study are provided in the Supplementary Materials. The R code includes detailed documentation to reproduce all presented results.

Author Contributions

All authors contributed to the planning, design and conceptualization of the study. LM performed the simulations, analyzed the results and took the lead in writing the manuscript. MB, LK and LW-dM all provided critical feedback and helped shape the research, analysis and manuscript. All authors read and approved the final manuscript.

Funding

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2022.802828/full#supplementary-material

Footnotes

¹In the current study, we refer to “misspecifications”. However, note that there are situations in which it is acceptable to retain highly correlated attributes as separate or to define composite attributes based on practical constraints (as described in Section 1.3).

²We constructed the Q-matrices following guidelines from Madison and Bradshaw (2015). More recently, Gu and Xu (2021) provided guidelines to ensure Q-matrix identifiability, which we briefly discuss in Section 4.2

³Similar patterns were found across conditions with different numbers of respondents R, see Supplementary Appendix Figure A1

⁴The analyses were repeated with model selection only if the difference in AIC or BIC was larger than 2, since smaller differences are sometimes regarded as providing no evidence for either of the models under consideration (e.g., Burnham and Anderson, 2004, p.270-271). These results were highly similar to results presented here

⁵Again, the analyses were repeated with model selection only if the difference in AIC or BIC was larger than 2, leading to highly similar results

References

Ackerman, P. L., and Kanfer, R. (2009). Test Length and Cognitive Fatigue: an Empirical Examination of Effects on Performance and Test-Taker Reactions. J. Exp. Psychol. Appl. 15, 163–181. doi:10.1037/a0015719

CrossRef Full Text | Google Scholar

Akaike, H. (1974). A New Look at the Statistical Model Identification. IEEE Trans. Automat. Contr. 19, 716–723. doi:10.1109/TAC.1974.1100705

CrossRef Full Text | Google Scholar

Bell, B. S., and Kozlowski, S. W. J. (2002). Adaptive Guidance: Enhancing Self-Regulation, Knowledge, and Performance in Technology-Based Training. Personnel Psychol. 55, 267–306. doi:10.1111/j.1744-6570.2002.tb00111.x

CrossRef Full Text | Google Scholar

Black, P., and Wiliam, D. (1998). Assessment and Classroom Learning. Assess. Educ. Principles, Pol. Pract. 5, 7–74. doi:10.1080/0969595980050102

CrossRef Full Text | Google Scholar

Bradshaw, L. (2017). “Diagnostic Classification Models,” in The Handbook of Cognition and Assessment: Frameworks, Methodologies, and Applications. Editors A. A. Rupp, and J. P. Leighton (Chicester, United Kingdom: Wiley Online Library), 297–327. doi:10.1002/9781118956588.ch13

CrossRef Full Text | Google Scholar

Brinkhuis, M. J. S., and Maris, G. (2019). “Tracking Ability: Defining Trackers for Measuring Educational Progress,” in Theoretical and Practical Advances in Computer-Based Educational Measurement Methodology of Educational Measurement and Assessment. Editors B. P. Veldkamp, and C. Sluijter (Cham: Springer International Publishing), chap. 8, 161–173. doi:10.1007/978-3-030-18480-3_8

CrossRef Full Text | Google Scholar

Brown, K. G. (2001). Using Computers to Deliver Training: Which Employees Learn and Why? Personnel Psychol. 54, 271–296. doi:10.1111/j.1744-6570.2001.tb00093.x

CrossRef Full Text | Google Scholar

Burnham, K. P., and Anderson, D. R. (2004). Multimodel Inference. Sociological Methods Res. 33, 261–304. doi:10.1177/0049124104268644

CrossRef Full Text | Google Scholar

Cai, Y., Tu, D., and Ding, S. (2013). A Simulation Study to Compare Five Cognitive Diagnostic Models. Acta Psychologica Sinica 45, 1295–1304. doi:10.3724/SP.J.1041.2013.01295

CrossRef Full Text | Google Scholar

Chen, J., de la Torre, J., and Zhang, Z. (2013). Relative and Absolute Fit Evaluation in Cognitive Diagnosis Modeling. J. Educ. Meas. 50, 123–140. doi:10.1111/j.1745-3984.2012.00185.x

CrossRef Full Text | Google Scholar

Chiu, C. Y., Sun, Y., and Bian, Y. (2018). Cognitive Diagnosis for Small Educational Programs: The General Nonparametric Classification Method. Psychometrika 83, 355–375. doi:10.1007/s11336-017-9595-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Cui, Y., Gierl, M. J., and Chang, H.-H. (2012). Estimating Classification Consistency and Accuracy for Cognitive Diagnostic Assessment. J. Educ. Meas. 49, 19–38. doi:10.1111/j.1745-3984.2011.00158.x

CrossRef Full Text | Google Scholar

de la Torre, J., and Chiu, C. Y. (2016). A General Method of Empirical Q-Matrix Validation. Psychometrika 81, 253–273. doi:10.1007/s11336-015-9467-8

PubMed Abstract | CrossRef Full Text | Google Scholar

de la Torre, J., and Lee, Y.-S. (2013). Evaluating the Wald Test for Item-Level Comparison of Saturated and Reduced Models in Cognitive Diagnosis. J. Educ. Meas. 50, 355–373. doi:10.1111/jedm.12022

CrossRef Full Text | Google Scholar

de la Torre, J., and Minchen, N. (2014). Cognitively Diagnostic Assessments and the Cognitive Diagnosis Model Framework. Psicología Educativa 20, 89–97. doi:10.1016/j.pse.2014.11.001

CrossRef Full Text | Google Scholar

de la Torre, J. (2011). The Generalized DINA Model Framework. Psychometrika 76, 179–199. doi:10.1007/S11336-011-9207-7

CrossRef Full Text | Google Scholar

Ferguson, R. (2012). Learning Analytics: Drivers, Developments and Challenges. Int. J. Technol. Enhanced Learn. 4, 304–317. doi:10.1504/IJTEL.2012.051816

CrossRef Full Text | Google Scholar

Gierl, M. J., Alves, C., and Majeau, R. T. (2010). Using the Attribute Hierarchy Method to Make Diagnostic Inferences about Examinees' Knowledge and Skills in Mathematics: An Operational Implementation of Cognitive Diagnostic Assessment. Int. J. Test. 10, 318–341. doi:10.1080/15305058.2010.509554

CrossRef Full Text | Google Scholar

Gierl, M. J., and Cui, Y. (2008). Defining Characteristics of Diagnostic Classification Models and the Problem of Retrofitting in Cognitive Diagnostic Assessment. Meas. Interdiscip. Res. Perspective 6, 263–268. doi:10.1080/15366360802497762

CrossRef Full Text | Google Scholar

Gu, Y., and Xu, G. (2021). Sufficient and Necessary Conditions for the Identifiability of the Q-Matrix. Stat. Sinica 31, 449–472. doi:10.5705/ss.202018.0410

CrossRef Full Text | Google Scholar

Hansen, M., Cai, L., Monroe, S., and Li, Z. (2016). Limited-Information Goodness-Of-Fit Testing of Diagnostic Classification Item Response Models. Br. J. Math. Stat. Psychol. 69, 225–252. doi:10.1111/bmsp.12074

CrossRef Full Text | Google Scholar

Hattie, J., and Timperley, H. (2007). The Power of Feedback. Rev. Educ. Res. 77, 81–112. doi:10.3102/003465430298487

CrossRef Full Text | Google Scholar

Hofman, A. D., Kievit, R., Stevenson, C., Molenaar, D., Visser, I., and van der Maas, H. (2018). The Dynamics of the Development of Mathematics Skills: A Comparison of Theories of Developing Intelligence. OSF Preprint. doi:10.31219/osf.io/xa2ft

CrossRef Full Text | Google Scholar

Huebner, A., and Wang, C. (2011). A Note on Comparing Examinee Classification Methods for Cognitive Diagnosis Models. Educ. Psychol. Meas. 71, 407–419. doi:10.1177/0013164410388832

CrossRef Full Text | Google Scholar

Huff, K., and Goodman, D. P. (2007). “The Demand for Cognitive Diagnostic Assessment,” in Cognitive Diagnostic Assessment for Education. Editors J. P. Leighton, and M. J. Gierl (New York: Cambridge University Press), 19–60. doi:10.1017/CBO9780511611186.002

CrossRef Full Text | Google Scholar

Jang, E. E. (2008). “A Framework for Cognitive Diagnostic Assessment,” in Towards Adaptive CALL: Natural Language Processing for Diagnostic Language Assessment. Editors C. Chapelle, Y.-R. Chung, and J. Xu (Ames, IA: Iowa State University), 117–131.

Google Scholar

Kunina-Habenicht, O., Rupp, A. A., and Wilhelm, O. (2012). The Impact of Model Misspecification on Parameter Estimation and Item-Fit Assessment in Log-Linear Diagnostic Classification Models. J. Educ. Meas. 49, 59–81. doi:10.1111/j.1745-3984.2011.00160.x

CrossRef Full Text | Google Scholar

Lei, P. W., and Li, H. (2016). Performance of Fit Indices in Choosing Correct Cognitive Diagnostic Models and Q-Matrices. Appl. Psychol. Meas. 40, 405–417. doi:10.1177/0146621616647954

PubMed Abstract | CrossRef Full Text | Google Scholar

Leighton, J. P., and Gierl, M. J. (2007a). “Verbal Reports as Data for Cognitive Diagnostic Assessment,” in Cognitive Diagnostic Assessment for Education. Editors J. P. Leighton, and M. J. Gierl (New York: Cambridge University Press), 146–172. doi:10.1017/CBO9780511611186.006

CrossRef Full Text | Google Scholar

Leighton, J. P., and Gierl, M. J. (2007b). “Why Cognitive Diagnostic Assessment,” in Cognitive Diagnostic Assessment for Education. Editors J. P. Leighton, and M. J. Gierl (New York: Cambridge University Press), 3–18. doi:10.1017/CBO9780511611186.001

CrossRef Full Text | Google Scholar

Liu, R., Huggins-Manley, A. C., and Bradshaw, L. (2017). The Impact of Q-Matrix Designs on Diagnostic Classification Accuracy in the Presence of Attribute Hierarchies. Educ. Psychol. Meas. 77, 220–240. doi:10.1177/0013164416645636

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, R., Huggins-Manley, A. C., and Bulut, O. (2018). Retrofitting Diagnostic Classification Models to Responses from IRT-Based Assessment Forms. Educ. Psychol. Meas. 78, 357–383. doi:10.1177/0013164416685599

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Y., Tian, W., and Xin, T. (2016). An Application of M2 Statistic to Evaluate the Fit of Cognitive Diagnostic Models. J. Educ. Behav. Stat. 41, 3–26. doi:10.3102/1076998615621293

CrossRef Full Text | Google Scholar

Ma, C., de la Torre, J., and Xu, G. (2020). Bridging Parametric and Nonparametric Methods in Cognitive Diagnosis. arXiv preprint arXiv:2006.15409.

Google Scholar

Ma, W., and de la Torre, J. (2020a). An Empirical Q-Matrix Validation Method for the Sequential Generalized DINA Model. Br. J. Math. Stat. Psychol. 73, 142–163. doi:10.1111/bmsp.12156

CrossRef Full Text | Google Scholar

Ma, W., Iaconangelo, C., and de la Torre, J. (2016). Model Similarity, Model Selection, and Attribute Classification. Appl. Psychol. Meas. 40, 200–217. doi:10.1177/0146621615621717

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, W., and de la Torre, J. (2020b). GDINA: An R Package for Cognitive Diagnosis Modeling. J. Stat. Soft. 93, 1–26. doi:10.18637/jss.v093.i14

CrossRef Full Text | Google Scholar

Madison, M. J., and Bradshaw, L. P. (2015). The Effects of Q-Matrix Design on Classification Accuracy in the Log-Linear Cognitive Diagnosis Model. Educ. Psychol. Meas. 75, 491–511. doi:10.1177/0013164414539162

PubMed Abstract | CrossRef Full Text | Google Scholar

Maydeu-Olivares, A., and Joe, H. (2014). Assessing Approximate Fit in Categorical Data Analysis. Multivariate Behav. Res. 49, 305–328. doi:10.1080/00273171.2014.911075

PubMed Abstract | CrossRef Full Text | Google Scholar

Maydeu-Olivares, A., and Joe, H. (2006). Limited Information Goodness-Of-Fit Testing in Multidimensional Contingency Tables. Psychometrika 71, 713–732. doi:10.1007/s11336-005-1295-9

CrossRef Full Text | Google Scholar

Mislevy, R. J., and Sheehan, K. M. (1989). The Role of Collateral Information about Examinees in Item Parameter Estimation. Psychometrika 54, 661–679. doi:10.1007/BF02296402

CrossRef Full Text | Google Scholar

Nicol, D. J., and Macfarlane‐Dick, D. (2006). Formative Assessment and Self-Regulated Learning: A Model and Seven Principles of Good Feedback Practice. Stud. Higher Educ. 31, 199–218. doi:10.1080/03075070600572090

CrossRef Full Text | Google Scholar

Norris, S. P., Macnab, J. S., and Phillips, L. M. (2007). “Cognitive Modeling of Performance on Diagnostic Achievement Tests: A Philosophical Analysis and Justification,” in Cognitive Diagnostic Assessment for Education. Editors J. P. Leighton, and M. J. Gierl (New York: Cambridge University Press), 61–84. doi:10.1017/CBO9780511611186.003

CrossRef Full Text | Google Scholar

Park, Y. S., Morales, A., Ross, L., and Paniagua, M. (2020). Reporting Subscore Profiles Using Diagnostic Classification Models in Health Professions Education. Eval. Health Prof. 43, 149–158. doi:10.1177/0163278719871090

PubMed Abstract | CrossRef Full Text | Google Scholar

Pellegrino, J. W., Chudowsky, N., and Glaser, R. (2001). Knowing what Students Know: The Science and Design of Educational Assessment. Washington (DC): National Academy Press. doi:10.17226/10019

CrossRef Full Text | Google Scholar

R Core Team (2019). R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing.

Google Scholar

Roduta Roberts, M., and Gierl, M. J. (2010). Developing Score Reports for Cognitive Diagnostic Assessments. Educ. Meas. Issues Pract. 29, 25–38. doi:10.1111/j.1745-3992.2010.00181.x

CrossRef Full Text | Google Scholar

Rupp, A. A., Templin, J., and Henson, R. A. (2010). Diagnostic Measurement: Theory, Methods, and Applications. New York: The Guilford Press.

Google Scholar

Rupp, A. A., and Templin, J. (2008). The Effects of Q-Matrix Misspecification on Parameter Estimates and Classification Accuracy in the DINA Model. Educ. Psychol. Meas. 68, 78–96. doi:10.1177/0013164407301545

CrossRef Full Text | Google Scholar

Rupp, A. A. (2007). The Answer Is in the Question: A Guide for Describing and Investigating the Conceptual Foundations and Statistical Properties of Cognitive Psychometric Models. Int. J. Test. 7, 95–125. doi:10.1080/15305050701193454

CrossRef Full Text | Google Scholar

Sadler, D. R. (1989). Formative Assessment and the Design of Instructional Systems. Instr. Sci. 18, 119–144. doi:10.1007/BF00117714

CrossRef Full Text | Google Scholar

Sadler, D. R. (2007). Perils in the Meticulous Specification of Goals and Assessment Criteria. Assess. Educ. Principles, Pol. Pract. 14, 387–392. doi:10.1080/09695940701592097

CrossRef Full Text | Google Scholar

Schunk, D. H., and Zimmerman, B. J. (2003). “Self-regulation and Learning,” in Handbook of Psychology: Volume 7 Educational Psychology. Editor I. B. Weiner (Hoboken, NJ: John Wiley & Sons), 59–78. doi:10.1002/0471264385.wei0704

CrossRef Full Text | Google Scholar

Schwarz, G. (1978). Estimating the Dimension of a Model. Ann. Statist. 6, 461–464. doi:10.1214/aos/1176344136

CrossRef Full Text | Google Scholar

Sessoms, J., and Henson, R. A. (2018). Applications of Diagnostic Classification Models: A Literature Review and Critical Commentary. Meas. Interdiscip. Res. Perspect. 16, 1–17. doi:10.1080/15366367.2018.1435104

CrossRef Full Text | Google Scholar

Sinharay, S. (2010). How Often Do Subscores Have Added Value? Results from Operational and Simulated Data. J. Educ. Meas. 47, 150–174. doi:10.1111/j.1745-3984.2010.00106.x

CrossRef Full Text | Google Scholar

Sinharay, S., Puhan, G., and Haberman, S. J. (2011). An NCME Instructional Module on Subscores. Educ. Meas. Issues Pract. 30, 29–40. doi:10.1111/j.1745-3992.2011.00208.x

CrossRef Full Text | Google Scholar

Sun, Y., and de la Torre, J. (2020). “Improving Attribute Classification Accuracy in High Dimensional Data: A Four-step Latent Regression Approach,” in Innovative Psychometric Modeling and Methods. Editors H. Jiao, and R. W. Lissitz (Charlotte, NC: Information Age Publishing), 17–44.

Google Scholar

Templin, J., and Bradshaw, L. (2013). Measuring the Reliability of Diagnostic Classification Model Examinee Estimates. J. Classif 30, 251–275. doi:10.1007/s00357-013-9129-4

CrossRef Full Text | Google Scholar

Thompson, K., and Yonekura, F. (2005). Practical Guidelines for Learning Object Granularity from One Higher Education Setting. Interdiscip. J. E-Learning Learn. Objects 1, 163–179. doi:10.28945/418

CrossRef Full Text | Google Scholar

VanLehn, K. (2011). The Relative Effectiveness of Human Tutoring, Intelligent Tutoring Systems, and Other Tutoring Systems. Educ. Psychol. 46, 197–221. doi:10.1080/00461520.2011.611369

CrossRef Full Text | Google Scholar

Viberg, O., Hatakka, M., Bälter, O., and Mavroudi, A. (2018). The Current Landscape of Learning Analytics in Higher Education. Comput. Hum. Behav. 89, 98–110. doi:10.1016/j.chb.2018.07.027

CrossRef Full Text | Google Scholar

Vrieze, S. I. (2012). Model Selection and Psychological Theory: A Discussion of the Differences between the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC). Psychol. Methods 17, 228–243. doi:10.1037/a0027127

PubMed Abstract | CrossRef Full Text | Google Scholar