- Science, Mathematics and Technology Education, Faculty of Education, University of Pretoria, Pretoria, South Africa
Formative assessment may be a useful pedagogical practice to enhance the teaching of HOTS in mathematics. This study explored the impact of a formative assessment intervention on 1) students’ achievements in HOTS mathematics tests (pre-and-post) when their teachers were supported to implement the instructional intervention and 2) Standard 4 (Grade 4) teachers’ formative assessment practices. To explore the effects of 2-day intervention for professional development teacher training, this study employed mixed methods, sequential embedded approach with single-group, pre-test, intervention (training), and post-test instruments. Data were gathered from nine primary schools involving nine teachers and 272 standard 4 students in the southern region of Botswana. Students’ tests scales were used to measure achievement in mathematical HOTS items along with classroom observations and interviewed the teachers’ experiences and reflections. Students’ achievement data were assessed for internal reliability and validity by applying the Rasch Partial Credit Model followed by descriptive analysis and Wilcoxon signed-rank testing. The observed and interviewed teacher data were analyzed by descriptive frequency counts and thematic analysis, respectively. The students’ achievement in mathematically HOTS items was found significantly improved from pre-test to post-testing. Post-intervention classroom observation showed that teachers practised the integration and implementation of some formative assessment strategies. Finally, the teachers’ experience and reflections were found to be favorably inclined to support formative assessment higher-order thinking skills as a strategy to enhance mathematics teaching.
Introduction
Formative assessment is an active and intentional learning process that partners the teacher and the students to continuously and systematically gather evidence of learning with the express goal of improving students’ learning outcomes (Moss and Brookhart, 2019). The learning process is step by step and dependent on the type of learning tasks and thinking involved in the process (Hattie and Brown, 2004). In the student’s learning process, the teacher is an inevitable stakeholder with the responsibility that goes beyond stand and delivers, but rather a teacher consciously initiates the student into collective learning achievement of every child in the classroom setting (Black and Wiliam, 2003; Moss and Brookhart, 2019).
In the 21st century, students are required to master thinking skills to deal with many situations that arise in the real world (Wilson and Narasuman, 2020). Such thinking skills more often are envisioned as Higher Order Thinking Skills (HOTS). Nooraini and Khairul (2014) define HOTS as the use of the potential of the mind to cope with new challenges. HOTS require the construction of knowledge through the use of disciplined inquiry, to produce discourse, products, or performances that have value beyond school (Brookhart, 2010; Murray, 2011). In the classroom setting, HOTS are examined in the light of three perspectives identified by Brookhart: transfer, critical thinking, and problem-solving (Brookhart, 2010; Moss and Brookhart, 2019). Thus, HOTS as transfer give students the ability to relate their learning to other elements beyond those they were taught to associate with it in more complex ways in new or different settings. HOTS as critical thinking mean students can apply wise judgment or produce a reasoned critique to reflect, reason, and make sound decisions. HOTS as problem-solving is the nonautomatic strategizing required for reaching a goal that cannot be met with a memorized solution (Brookhart, 2010; Narayanan and Adithan, 2015; Wiyaka et al., 2020).
The development of students’ HOTS is an international priority for education, Zohar and Cohen (2016), through which students can train themselves to face the demands of a modern age, the digital revolution 4.0. Thus educating the students of the 21st century who face complex real-life problems often needs a complex solution (Rajendran, 2008). Students’ HOTS can be developed through teaching and learning as well as assessment. Previous studies on the assessment transformation from summative to a more comprehensive assessment of formative in the classroom lead students to think critically and apply their knowledge in different settings that have been investigated. For instance, Babincakova et al.’s (2020) study has reported on the use of formative assessment classroom techniques (FACTs) during chemistry lessons at K7 and the results revealed a significant increase in both lower- and higher-order cognitive skills area and students’ showed a positive attitude toward the introduced method. In another study, Wilson and Narasuman (2020) sought to investigate teachers’ challenges and their strategies on integrating HOTS in School-Based Assessment (SBA), which revealed several challenges among others were workload, limited skill constructing and administering HOTS, lack of expert personnel, and ineffective teachers training faced by the respondents during the integration of HOTS in SBA instruments. In Botswana, it was also observed that the students who took part in the 2015 Trends in Mathematics and Science Study (TIMSS) study were unable to apply HOTS, such as critical thinking and problem-solving in mathematics (Masole et al., 2016). According to Masole et al. (2016), TIMSS studies have identified pedagogical issues such as availability of resources and teacher effectiveness as being among the background variables which are negative indicators of Botswana’s achievement in mathematics.
The understanding of HOTS and formative assessment are very important because teachers are the reliable person to assess student’s achievement and to understand the framework of the subject area (Mansor et al., 2013; Jerome et al., 2017; Wiyaka et al., 2020). Teachers need to be capable of deciding formative assessment approaches and constructing assessment tasks that appropriately assess the intended learning outcomes to be assessed. In this view, formative assessment is inextricably linked to teaching and learning may enhance students’ HOTS in other subjects such as mathematics and at different levels of schooling (Anderson, 2003; Jerome et al., 2019). For this reason, the aim of the current study seeks to explore the impact of a formative assessment intervention on 1) students’ achievements in HOTS mathematics tests to have changed when comparing the pre-assessment and post-assessment results upon which their teachers were supported with the instructional intervention, 2) Standard 4 teachers’ (grade 4 teachers) if their formative assessment practices in teaching HOTS have changed after an intervention, and 3) teacher’s experiences with intervention. The central assumption is that formative assessment is an integral pedagogical strategy that enhances the teaching of HOTS.
Theoretical Framework for Formative Assessment and Teaching of HOTS in Mathematics
Formative assessment is a pedagogical approach to increase student learning and enhance teacher quality. Nonetheless, effective formative assessment is not part of most classrooms, largely because teachers misunderstand what it is and don’t have the necessary skills to implement it (Moss and Brookhart, 2019). Fundamentally, formative assessment process is supported to “collect evidence of learning to inform instruction, second by second, minute by minute, hour by hour, day by day, and week by week” (Partnership for Assessment of Readiness for College and Careers; PARCC, 2010, p. 56) and anchored with three central questions: Where am I going?; Where am I now?; What strategy or strategies can help me get to where I need to go? (Hogden and Wiliam, 2006; Hattie and Timperley, 2007; Heritage, 2010; Moss and Brookhart, 2019). These central questions guide everything the teacher does, everything the student does, and everything teachers and their students do together. Moss and Brookhart (2019) affirm that formative assessment is a teacher-student learning team in using the evidence to make informed decisions about what to do next and choose strategies that have the best chance to close the learning gap and raise student achievement. Hence, formative assessment is evidence-based for student learning to make decisions about next steps is succinctly described as learning target theory of action (Moss and Brookhart, 2012; Kiplagat, 2016).
Formative assessment’s learning target theory is rooted in Vygotsky (1978) who introduced the idea of a Zone of Proximal Development between what a student can already do alone and what a student can only do with others. In this case, for instance, a child can already cycle the bicycle with training wheels but not without support. So, teachers and their students are actively and intentionally engaging in the formative assessment process when they work together to do the following: focus on learning goals; take stock of where current work is concerning the goal; take action to move closer to the goal (Brookhart, 2006; Lonka International, 2018; Moss and Brookhart, 2019). Formative assessment actively involves both teacher and students in providing feedback loops to adjust ongoing instruction and close gaps in learning, including the use of self and peer assessment (Lizzio and Wilson, 2008; Kyaruzi, 2017).
The teaching of HOTS and assessment are informed by taxonomy as the foundation for teaching and learning. Most importantly, to note at the beginning of the 21st century, Anderson and Krathwohl introduced revised Bloom’s taxonomy (Anderson et al., 2001), which replaced the original three-layer hierarchical model (Bloom et al., 1956) with two dimensions: cognitive processes and knowledge (Hattie and Brown, 2004; Brown and Hattie, 2012). Specifically, the cognitive process has six hierarchical categories: remembering, understanding, applying, analyzing, evaluating, and creating. The knowledge dimension consists of four types: factual, conceptual, procedural, and metacognitive knowledge (Radmehr and Drake, 2019). Moreover, a distinction between higher-order thinking skills (HOTS) and Low Order Thinking Skills (LOW) has been made (Zoller and Tsaparlis, 1997; Foong, 2000). LOTS items “require simple recall of information or a simple application of a known theory or knowledge to familiar situations and context.” HOTS items require “quantitative problems or qualitative conceptual questions, unfamiliar to the student, that require for their solution more than knowledge and application of known algorithms, they require analysis, synthesis, and problem-solving capabilities, the making of connections and critical evaluative thinking” (Babincakova, et al., 2020; Narayanan and Adithan, 2015; Chemeli, 2019b).
According to Mohamed and Lebar (2017) HOTS involves the individual’s ability to apply, develop, and enhance knowledge in the context of thinking. The concept of HOTS emphasizes some skills such as critical thinking, creative and innovative thinking, problem-solving, and decision-making (Ganapathy et al., 2017). For students, learning HOTS will strengthen their minds, guiding them in producing more alternatives, actions, and ideas. Learning HOTS also maintains the students’ critical thinking, helping them produce many ideas and develop problem-solving skills for their life. Hence, HOTS should be learned for completing assignments given by teachers (Wiyaka, et al., 2020; Chemeli, 2019b; Kiplagat, 2016).
In Mathematics, teachers have to be knowledgeable and skilful to select an appropriate strategy to provoke and assess students’ HOTS to prepare them for future success. Studies have revealed that a student who has acquired a higher level of thinking can do things such as analyzing the facts, categorizing them, manipulating them, putting them together, and applying them in real-life situations (Yee et al., 2011; Balakrishnan et al., 2016). HOTS involve the use of various learning processes and strategies in different complex learning situations. HOTS for an individual depends on the individual’s ability to apply, develop, and enhance knowledge in thinking. These thinking contexts include cognitive levels of analysis, synthesis and evaluation, and mastery in applying the routine things in new and different situations (Tajudin, 2015; Mohamed and Lebar, 2017).
Botswana’s Educational System and Assessment Practices
According to Fetogang (2015), Botswana has a history of emphasizing the use of examination results to judge the quality of schools and that of students. Typically, at the end of standard 4 students sit for a national examination known as the Standard 4 Attainment Test. After 7 years of primary school, students also sit for the Primary School Leaving Examination (PSLE). PSLE results provide feedback on student achievement on knowledge and skills gathered through primary education programmes but the examination is not high-stake.
Owing to the perceived teaching and learning constraints and overemphasis of external examination, Botswana Revised National Policy on Education (Government of Botswana, BOT, 1994) then advocated for Formative Assessment to be integral in the teaching and learning process and named it Continuous Assessment (CA). Ideally, CA should provide the opportunity for teachers to scaffold and discuss with students their learning difficulties experienced during their (mathematics) learning tasks. But teachers are often under pressure to prepare students for external examinations, which have to do with administrative compliance purposes and are focused on students’ learning to know and do. For instance, in the recent interview between the Botswana Guardian newspaper and the Regional Education Director, Kweneng District, the director reported that “every month the school heads must give monthly reports on the students, ensure monthly tests are written and the results are registered so that … can track the students’ performance” (Ramadubu, 2018. p.8). From the director’s interpretation of monthly tests, formative assessment is commonly erroneously labeled as administrative compliance, and it is not used to adjust initial instruction. According to Mills et al. (2017), an assessment used in the context of the director’s statement cannot deliver the promised students’ growth enabled by the formative assessment process that should occur within the daily stream of planning and instructions.
The Present Study
Botswana students have been identified as mathematically weak in HOTS such as critical thinking and problem-solving when compared with their cohort in international large-scale assessments. As noted earlier, the TIMSS 2015 study identified pedagogical issues such as teacher effectiveness as being among the background variables that are negative indicators of Botswana’s achievement in mathematics (Masole, et al., 2016). More specifically, Moyo’s (2021) baseline study showed that the participating teachers had challenges in integrating formative assessment and HOTS in the mathematics classrooms as consciously self-rated due to a lack of teacher training on assessment, time for planning, and the curriculum limitation.
It should be noted this study only reports on the main impact effects for integrating formative assessment and teaching of HOTS in Standard 4 mathematics. For a detailed description of the baseline findings of the survey, the reader is referred to Moyo (2021). Against the Moyo’s baseline survey findings, a designing intervention programme, which was named formative assessment for HOTS (FAHOTS), was implemented within the Formative Assessment theoretical framework (Accado and Kuder, 2017; Moss and Brookhart, 2019; Hattie and Timperley, 2007; Hodgen and Wiliam, 2006; Heritage, 2010; Kivunja 2015; Kyaruzi, et al., 2020), and this was linked to HOTS concepts as an attempt to address pedagogy issues. These two domains have a common characteristic that features of Formative assessment converge with the features of HOTS. The point of departure for this study was also consistent with the recent reform for Botswana Education and Training Sector Strategic Plan (Government of Botswana (BOT), 2015) in improving teaching and learning at all levels. In particular, the ETSSP emphasizes undertaking intensive teacher professional development and developing appropriate assessment patterns to organize school-based assessment and measuring skills and linking classroom assessment with a national assessment in a better way. So, this study stands out with intervention and is classified as professional development for in-service training to help teachers implement formative assessment and teach HOTS in mathematics (Accado and Kuder, 2017). The workshop-based training was plausibly designed and implemented to address the identified context of Standard 4 teachers’ offering mathematics (find brief details in the intervention section). More specifically, three research questions were investigated:
1) To what extent does the formative assessment strategies intervention enhance Standard 4 students’ HOTS academic achievement in mathematics when comparing the pre- and post-intervention?
2) To what extent does the formative assessment strategies intervention enhance Standard 4 teaching of HOTS in mathematics when comparing the pre- and post-observation?
3) What are teachers’ experiences and reflections following the formative assessment strategies intervention and mathematics teaching on the students’ learning outcomes?
Materials and Methods
Design and Participants
This study used a mixed-method, sequential embedded approach with single-group, pre-test, intervention (training), post-test design. A sample of nine teachers per school (n = 9) from Kanye schools in the southern region of Botswana was selected and exposed to the intervention. Prior to training 2-day professional training on using formative assessment and teaching of HOTS in mathematics, each participating teacher was observed teaching mathematics as per the schedule communicated to them. Students were also written the mathematics pre-test consisting of HOTS items that the researcher has extracted from Botswana Examination Council previous examinations for Standard 4 (Standard 4 is equivalent to grade 4 in other education systems).
Upon training, the teachers were given time to plan and trial the FAHOTS intervention in the classroom, and the researcher visited them (teachers), to coach on the job, and was expected to implement the FAHOTS by themselves. After 8 weeks of intervention, students took again a paper- and pencil mathematics post-test with anchor HOTS items being written. The two tests were administered according to the standardized testing procedures. The post-observation and interview were also done among the participating teachers. Figure 1 summarizes the overall research design.
FIGURE 1. Single-group pre-test-post-test design, Adapted from McMillan and Schumacher (2006).
Figure 1 summarizes the overall research design, and without a control group to compare with the experimental group leads to some important considerations that could be threats to this study’s validity. First, the measurement procedure’s possible effect on the manipulated variable’s construct validity was a very important consideration. Even the historic seminal work by Campbell (1975) affirmed that several other factors apart from the manipulated variable may contribute to the change in scores. Observed changes may be due to reactive effects, not the manipulated variable (Kerlinger and Lee, 2000). However, for this study, an intervention focused on formative assessment for HOTS (FAHOTS) as a manipulated variable and was appropriately defined based on meaningful constructs that represent the focus of the intervention effort. The intervention programme was developed by the researcher (See details in the next section) as informed by Kivunja’s assessment feedback loop (Kivunja, 2015) and the baseline survey findings. Second, history and maturation are also possible threats to the single-group pre-test-post-test design’s validity when the dependent variable is unstable, particularly because of maturational changes (Cook and Campbell, 1979; Kerlinger and Lee, 2000). Kerlinger and Lee (2000) explain that mental age increases with time, which can easily affect achievement. People can learn in any given interval, and this learning may affect dependent variables. The longer the time interval in the investigation, the greater the possibility of extraneous variables influencing dependent variable measures (Shadish, et al., 2002). However, McMillan and Schumacher (2006) suggest that if the time between the pre-test and post-test is not too long or increasing, it may no longer be a threat. They suggest that if the time between the pre-test and post-test is relatively short (at least two or 6 weeks), then maturation is not a threat. Thus, to reduce the chance of maturation, the researcher minimized the intervention time between the pre- and post-test, which was 8 weeks, and implemented all the tests between 20 May and 20 September 2019. In general, Botswana has evidence of students’ low mathematics achievement in both national examinations and international large-scale assessment (Masole et al., 2016; Botswana Examination Council, 2017); hence, history and maturation may not be a major threat in the current study. Through this study, it is envisaged to see if teacher professional development in assessment would help students to improve their learning outcome over time.
There are other possible threats apart from those mentioned above, which may affect the intervention’s implementation integrity (or “treatment fidelity”) (Hagermoser Sannetti and Kratochwill, 2005) as typically scheduled to determine whether the actual intervention was implemented as intended throughout the experiment. However, it is important to note that this study is embedded in the mixed-method approach in a complementary manner to compensate for its weakness (Gray, 2014). For this reason, a single-case intervention approach in the current study was assumed to have minimized some threats to the validity of inferences concerning the researcher’s interpretation of the effects observed and analyzed. For instance, some insights into what teachers in the schools were doing during the mathematics lessons, the baseline survey and students’ pre- and post-test was helpful to determine the level of formative assessment practices and students’ achievement, respectively. After that, the FAHOTS condition was made available to the intervention schools. Some schools were also uncertain about taking part in a study and engaging in observations, testing, and interviews as they would get disrupted in their daily delivery. However, the researcher guaranteed teachers of a minimum disruption during the project period and provided low impact intervention to be able to observe the teachers in class.
Only the matched test scores from time 1 to time 2 were used in this study, so the data of any student who was not available for both tests were rendered incomplete and subsequently dropped in the final analysis. Complete data from 272 students were obtained, that is male (n = 140, 51.5%) and female (n = 132, 48.5%). The class size was generally considered large by international standards (United Nations Educational Scientific and Cultural Organization UNESCO, 2010) and the teacher-student ratio ranged from 27 to 39 students per teacher.
All observed and interviewed teachers were women and their teaching qualifications were Primary School Teaching Certificate (2), Diploma in Primary Education (5), and Bachelor of Education (1). The teachers observed had not specialized in mathematics, rather they were specialists in languages, generals’ subjects and only one-degree holder with a physical education specialist. The teachers had 12–27 years of experience in teaching. Most of the teachers observed had only taught standard 4 for a few years, which ranged between 2 and 5 years. Only seven teachers were interviewed, whereas the other two were on sick leave during the scheduled interview week. Even during post-observation, one teacher missed due to illness and her data were eliminated from the study.
Formative Assessment for HOTS Intervention
The researcher designed a 2-day interventional programme that was extracted from the Kivunja’s Assessment Feedback Loop (2015) and linked it to HOTS, Welsh Assembly Government (2010); hence, it was named formative assessment for HOTS (FAHOTS). The researcher trained nine teachers on how to use formative assessment to enhance higher-order thinking skills (HOTS) with a particular focus on mathematics. On Day 1 of the workshop teachers were made aware of the formative assessment learning goals (LG) and Success Criteria (SC) (Kivunja, 2015; Kanjee, 2017). With the SC, teachers were made cognisant of the fact that SC was a way of linking the learning goal and indicating achievement; therefore, the SC must be shared with the students and must be related directly to the learning outcome and the HOTS task (Kivunja, 2015). The workshop was also used to discuss the value of aligning assessments to the goals with reference to HOTS derived from the Blooms’ Taxonomy and learning objectives in the Botswana Standard 4 mathematics curriculum and as well as the possibility for improvisation and creativity in the classroom.
Day 2 of the workshop focused on the effective questioning that elicits discussion and students’ higher-order thinking, as well as activating students to be instructional resources for each other (peer-assessment) and their own (self-assessment) based on focused, effective feedback strategies (Wiliam, 2011; Kanjee, 2017). The FAHOTS information was made available to selected teachers who were expected to implement FA circles weekly. Throughout the workshop topics, the researcher integrated training with videos featuring a best-practice example of the FAHOTS, followed by tasks related to those videos. To further support the teachers, they were provided with a detailed handout and PowerPoint slides with examples of lesson plans, videos, Clarke (2005)’s five strategies handouts to improve the use of questioning and some practical strategies for effective formative feedback to try out in the classroom. With this training in mind, the teachers were expected to practice FAHOTS in mathematics lessons. Additionally, the researcher created the WhatsApp social media group to reach teachers for regular supportive text messages on FA and announcement of on-site visits for classroom observation.
Instrumentation
Student Pre- and Post-tests
The students’ pre-and-post assessment was used to compare the gains attained in mathematics achievement after the intervention took place. The pre- and post-Higher-Order-Thinking Skills items were adapted from the Botswana Examination Council (BEC) tests. Having determined the pre-test results as a baseline, a post-test was also done at the end of the interventional period (8 weeks), and students were expected to answer more questions correctly based on an increase in knowledge and understanding. Ten well-functioning common items from the pre-test were retained in the post-test to ensure the similarity of the two tests, the common items linked the two tests and provided a comparison of the performance on the common scale. Each of the items consisted of open-ended questions or problems that merited partial credit when marking following the BEC’s scoring guidelines. The total number of items per question ranged from one to three, making a total of 21 pre-test items. The total composite marks for the whole paper was 40.
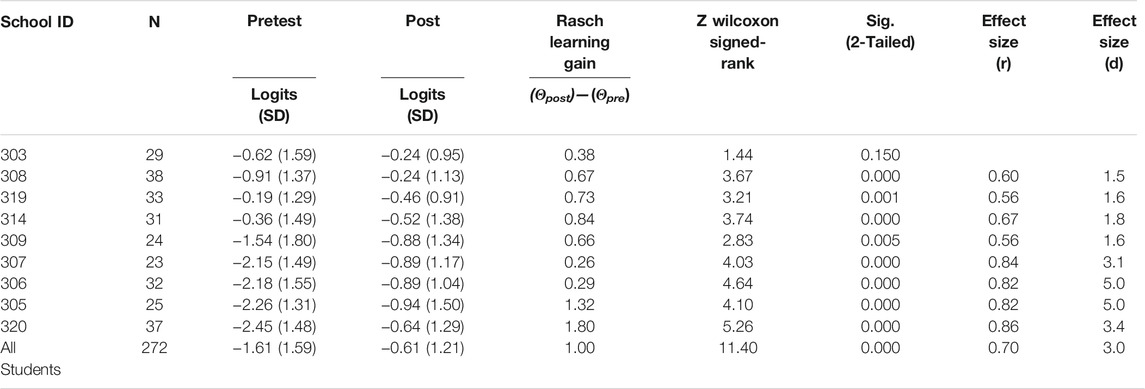
Table 1 summarizes the pre- and post-results which imply that the assessment instruments had excellent item reliability based on the Winsteps 3.75 programme (Linacre, 2016). The items (for pre-test and post-test) could be separated into nearly eight groups according to students’ responses. The scale of measure is probably low because the people are very much grouped between −3.00 and 0.00 logits, whereas the items spread from −1.6 to 2.6. On the other hand, the person’s reliability was just marginally acceptable, and the students could be separated into almost two groups by the items in both assessment instruments (See Table 1).
Teacher’s Classroom Observation and Interview
This study adapted a classroom observation rubric from Kanjee (2017), which was then customized to befit classroom observation for formative assessment practice. In classroom observation, the researcher was a non-participant and ensured that his presence in the classroom did not interfere with the teaching and learning process so that data could be collected naturally from the classroom by not coming to the class late, not interacting with students, not moving out of the class while lessons were still on and maintaining a normal facial expression (Mukherji and Albon, 2010; Kanjee and Meshack, 2014).
The adapted observational tool was termed Teacher Assessment Practice Observation Schedule (TAPOS). The observational instrument was developed by experts in the educational assessment field (Kanjee, 2017). These are researchers with extensive experience in implementing formative assessment internationally, numeracy specialists and academics based in South Africa and Tanzania who are familiar with local conditions sponsored by the University of Oxford. The tools were used in their research work over 3 years, beginning in April 2016 (McGrane et al., 2018). This study posed a similar context to employ the instrument; hence, the instrument was considered valid. The TAPOS was organized into four features, of which every level attempted to measure the components of formative assessment. Thus, from the beginning of the lesson, the teacher is expected to provide a short introduction, FA strategy that involves sharing the learning objective, success criteria, and writing it on the chalkboard: During lesson development the teacher provides a task that is focused on enhancing students’ participation, teachers’ questioning strategies and interaction which involve problem-solving as well as those questions calling for students’ HOTS, assesses the students’ HOTS exercise in their work during the lesson as individuals, pairs, and five groups before providing immediate instructional feedback and at least uses one of the feedback methods such oral feedback, students’ peer assessment and self-assessment. At the end of the lesson, the teacher completes the lesson and determines whether the learning objective has been completed, and checks whether assessment criteria have been met.
The behaviors in the TAPOS were characterized either as “Yes” and “No,” or “Seen” and “Not Seen” as well as “Often,” “Sometimes,” and “Not Seen” based on the evidence collected in the lesson observation. These behavior scores were then translated into a 2-point element scale and a 3-point element scale that quantify formative assessment practices and teaching of HOTS in mathematics. The series of lesson observations were captured at least twice per teacher in a 30-min lesson. The classroom observation was also done pre-and-post. The teachers who took part in the 2-day workshop facilitated by the researcher were expected to focus and implement their classroom lessons instruction within FAHOTS when teaching mathematics was also post-observed.
For this reason, a comparison of both findings for pre- and post-classroom observation and students’ HOTS achievement at different times was imperative to determine the level of gain and corroboration among the different findings. This approach of comparing baseline and post data is appropriate when measuring the same person to establish an indication of growth availed (Smith and Stone, 2009; Combrinck, 2018). Additionally, the observation tool was also aligned with the interview variables in systemically capturing the formative assessment strategies in the classroom. For this reason, these teachers were followed purposefully to get their viewpoints concerning the intervention through interviews.
Procedure
Upon approval of the research ethics by the University of Pretoria (ethical clearance reference number, SM18/10/02), the study was conducted based on the research clearance. All teachers and their students were informed about the study rationale and actively signed informed consent prior to their participation. There were no disturbances during the pre-test, professional development teacher training, and post-test phases that might have affected the data collection.
Analysis
Quantitative Analysis
Rasch analysis is among educational techniques used to analyze the quality characteristics of the student data responses. According to Deneen et al. (2013) “Rasch analysis is ideal for determining the extent to which items belong to a single dimension and where items sit within that dimension” (p. 446). Rasch uses a logistic model to predict the probability of responding to a specific option (Bond and Fox, 2007). Having established the common scale through Rasch using Winsteps software, the students’ mathematics achievements in HOTS from Time 1 to Time 2 were evaluated. The common scale was achieved through the anchor items (equating items), which was conducted to establish comparable scores, with equivalent meaning, on different versions of test forms of the same test (Sinharay et al., 2006). Thus, stacking of Time 1 and Time 2 in one data was employed to allow an accurate comparison of the data (Anselmi et al., 2015; Combrinck, 2018). A Wilcoxon Signed Rank Test was then computed to evaluate differences in students’ ability between pre- and post-intervention (stacked data) and the results were interpreted based on Rasch logits, including the effect size (Pallant, 2010). For observation data, it was analyzed and interpreted mostly by relative frequency counts and content analysis.
Qualitative Analysis
The interview data were from open-ended items and were analyzed qualitatively, using thick descriptions to capture respondents’ views and organize them into themes. In this case, questions were focused on formative assessment practice, strategies and their impacts on students’ learning and understanding of HOTS mathematics, techniques for students’ engagement in the classroom, strategies used to improve questioning, students’ engagement, and higher-order thinking skills. All interviews were audiotaped and transcription was done as a prerequisite to thematic data analysis by a researcher (Creswell and Plano Clark, 2017). Thematic analysis is the process of identifying patterns or themes within qualitative data. According to Maguire and Delahunt (2017), thematic analysis is not tied to a particular epistemological or theoretical perspective. This perspective makes it a very flexible method, a considerable advantage given the diversity of work in educational research; hence, it was found appropriate for the current phase of the study (Maguire and Delahunt, 2017).
Measurement Models
Rasch analysis is ideal for determining the extent to which items belong to a single dimension and where items sit within that dimension (Bond and Fox, 2007; Deneen et al., 2013). The item fit deals with whether individual items in a scale fit the Rasch model. The Rasch approach can be used to formalize conditions of invariances, leading to measurement properties (Panayides et al., 2010). Any data that deviate from the Rasch model also deviate from the requirements of the measurement (Linacre, 1996; Andrich, 2004). When the data do not fit the Rasch model, this is interpreted as an indication that the test does not have the right psychometric properties and hence needs to be revised and improved.
This study used the Winsteps 3.75 programme, which provides in-fit and outfits fit MNSQ and ZSDT (Linacre, 2016). The programme reveals where items and persons fit and where there is a misfit. All statistics are reported in terms of log-odds units and have a range of −5.00 to +5.00 with a mean set at 0.00 and a standard deviation of 1.00 (Bond and Fox, 2012; Boone et al., 2014; Linacre, 2016; Boone and Noltemeyer, 2017). According to Sharif et al. (2019), if the infit or outfit value is more than 1.40 logit, then it indicates a potentially confusing/problematic item. If the MNSQ value is less than 0.60 logit, it shows it was too easily anticipated by the respondents (Linacre, 2016). As for the internal validity of the instrument, the Rasch modeling term, unidimensional, means that all of the nonrandom variance found in the data can be accounted for by a single dimension of difficulty and ability. Thus, at least 50% of the total variance should be explained by the first latent variable/dimension; the first contrast should not have an eigenvalue >2.0 because an eigenvalue of 2.0 represents the smallest number of items that could represent a second dimension (Bond and Fox, 2012). The measure of local independence for items through correlations and according to Winsteps criteria should be below 0.70 (Linacre, 2016).
The observational instrument was developed by experts in the educational assessment field (Kanjee, 2017). These are researchers with extensive experience in implementing formative assessment internationally, numeracy specialists and academics based in South Africa and Tanzania who are familiar with local conditions sponsored by the University of Oxford. The tools were used in their research work over 3 years, beginning in April 2016 (McGrane et al., 2018). This study posed a similar context to employ the instrument; hence, the instrument was considered valid. The observation tool was also aligned with the interview variables in systemically capturing the FA strategies in the classroom.
Data Inspection and Model Fit for Student Pre- and Post-test
The response category function of all test items was evaluated. Those that did not satisfy the requirement of mean squares statistics (MNSQ) and standardized fit statistics (ZSDT) greater than 1.3 and unweighted percentages less than 10%, were identified and collapsed (Linacre, 2002, 2016).
Bond and Fox (2012) assert that for the polytomous scale, like for this current study, the acceptable MNSQ outfit value has to be in the range of 0.6–1.40. These figures suggest that any item identified below and above the range has to be removed from the analysis as it is considered a misfit. In this study, three items (Q11, 12c, and 12b) from the pre-test were found out of range, whereas the remaining items were productive measurements. As for the post-test, only two test items (Q3 and Q7) were misfits. These misfitting items were dropped from the next analysis. Even though some items were identified as a misfit, in general, the global fit statistics were not statistically significant, and this finding suggests in general that the data fitted the Rasch model. Additionally, the pre- and post-test results indicated that the mathematics assessment instrument was likely to be underpinned by a single dimension, consistent with the assessment design intent. The local independence of the test items was also independent of one another; no item for anyone answer led to an answer on another. Thus, all items’ correlation pairs were less than 0.7 (Pre-test −0.14–0.25 and post-test −0.14–0.43). The independent Rasch analysis of the anchor items was significantly and highly positively correlated with the item difficulties measured from pre-test to post-test, r = 0.913, p <0 .001. This Rasch analysis reveals that the anchor items were very stable and a productive measurement in monitoring students’ achievement.
Description of the spread of item difficulty for mathematics in stacked data results
The Wright item map is a visual summary of the relationship between item difficulties and students’ proficiencies as they emerge in the test. The items are ranked from the easiest (at the bottom) to the most difficult (at the top). The item map in Figure 2 illustrates the spread of item difficulty across the cognitive domain of mathematics constructs for the post-assessment test including the anchor items.
In Figure 2 the item threshold mean value is set at zero. The estimated students’ proficiency values in post-assessment have a negative lower mean than the item mean, which suggests that the test is targeted higher than their proficiency. Specifically, Figure 2 reveals that Q2 in pre-test means it was higher than the post Q2. Six items had higher scores in the pre-test, and 11 items had higher scores in the post-test. All the anchor items are in the same location as when selected much earlier. Many of the students are positioned in the bottom half of the map, indicating that their proficiency is low in comparison with the items and many of the students in post-mathematics assessment would still have experienced the test as a difficult one. For instance, most of the anchor items were still positioned on the top of the map, indicating overall that items are not well-targeted to the proficiency of the students and it was predictable from the pre-test.
The student’s proficiency in all nine schools was captured using a person measure from Winsteps software analysis. The use of the Rasch Measurement Model had enabled an opportunity to apply the items and threshold calibrations from the independent analysis of the baseline that is pre-test of students’ mathematics achievement to the pre-test and post-test results.
Results
Comparison of pre- and post-testing of students’ achievement findings in mathematics
Table 2 indicates participants’ counts and average logits mathematics achievement at different times. As shown in Table 2, overall the students in the pre-intervention test (n = 272) obtained a lower mean value (−1.61 logit) than when participated in the post-intervention (n = 272) test (−0.61 logit). A closer look at Table 2 reveals that all schools had slightly performed better during post-test than in pre-test.
The Wilcoxon Signed-Rank test was utilized to compare the pre-test and post-test results of students’ mathematics achievement (Table 2). The analysis shows that students’ mathematics achievement findings recorded a significantly higher gain of average achievement values from the pre-test (1.61 logit, SD = 1.59) to post-test (−0.61 logit, SD= 1.21), z = 11.40, p = 0.000, with a large effect size (d = 3.0). All the schools significantly gained from pre-test to post-test results, except for school (303), which was not significantly gained (p =0 .150). The effect sizes for all statistically significant gains in students’ achievements were so large including for the overall gain. According to Hattie (2013), “any intervention higher than the average effect (d = 0.40) is worth implementing.” For this reason, the analysis of the results for the current study shows that the effect size is large and beyond the expected average growth. This result indicates a significant large improvement in students’ performance in the post-intervention, and one can associate the improvement with the attribute of using the FA strategies. Thus, there is the likelihood that participating teachers have assimilated some formative assessment strategies well which enhanced their teaching and learning of mathematics HOTS concepts (as discussed in the next pre- and post-observation comparison section).
Classroom Observation in Pre- and Post-findings
(i) Teachers’ use of learning goals, Success Criteria, Questioning, and Learning Tasks
Frequency use of learning goal (LG) and Success Criteria (SC), questioning and interaction, learning (HOTS) tasks and feedback is considered to be effective in enhancing students’ performance. It is for the interest of this study that after the professional development, (FAHOTS), the teachers were expected to apply these elements more frequently during their lessons than before the intervention. For Table 3, the proportion of using learning goals and success criteria has to some extent changed when comparing the pre-observation to post-observation. Some teachers were seen discussing the LG and SC that were presented either orally or written at the board which is a positive practice in the formative assessment that enhances students’ understanding of lesson direction from the onset. However, the observed teachers were seen neither during the pre-observation nor during the post-observation using learning goals and success criteria on a chart or handout, which was influenced by the limitation of such resources in the classroom.

TABLE 3. Rating frequency of the use of learning goal and success criteria within the FAHOTS as observed by the researcher pre- and post-observations.
Table 4 provides an overview of the first and third quartiles, and the median scores of the observed teachers in both conditions (pre- and post-observation), regarding their use of questioning, were classified as ineffective and effective. The results of the pre-observation indicate that the teachers were inclined toward ineffective questioning (Mdn = 2.00) more than effective questioning techniques (Mdn = 1.00). This result is perhaps indicating a traditional classroom discussion in which teachers focus much of their attention on the students who raise their hands when wishing to attempt a question before them. Wilcoxon signed-rank tests show that there was no statistical significance for ineffective (z = 1.823, p = 068) and effective questioning (z = 1.414, p = 0.157) from pre-observation to post-observation, respectively (See Table 6). These results indicate that the participating teachers did not change their way of questioning, even after the FAHOTS intervention; thus, most of the teachers remained ineffective as far as questioning skills are concerned. Evidently, the descriptive value for effective questioning remained unchanged (Mdn = 1) from pre- to post-observation (See Table 4).
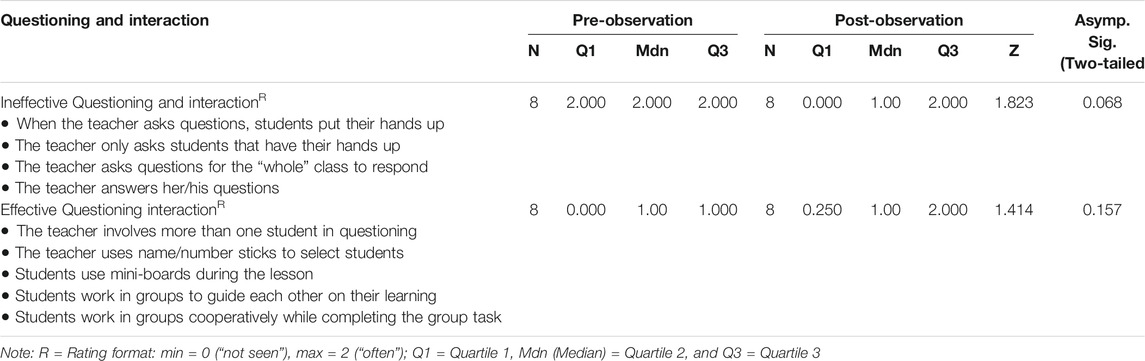
TABLE 4. Rating results for using questioning within FAHOTS as observed by the researcher during pre- and post-observations.
As for Learning tasks, Table 5 shows median pre- and post-observation scores for the observed teachers. A closer look at the results reveals that none of the teachers applied the strategy in pre-observation while only one teacher applied it during post-observation (Mdn = 1). However, participating teachers did not differ significantly in their use of learning tasks (HOTS), Z = 1.890, p =0 .059, indicating insufficient evidence for its utility in the classroom.
(ii)Peer and self-assessment pre- and post-observation

TABLE 5. Rating results for using learning tasks within FAHOTS as observed by the researcher during pre- and post-observations.
Table 6 shows (next page) the observations recorded on feedback practice provision in the observed teachers’ classrooms during pre- and post-observation. With oral feedback, an improvement was seen in post-observation. After giving students classwork, a 0.75 proportion of teachers walked around to check how students were doing compared with the pre-observation (0.00). A ratio of 0.75 of the participating teachers was also seen checking students’ responses, providing some gathered feedback or some comments when compared with the pre-observation. As for peer assessment, the participating teachers had some challenges in using the strategy (See Table 6). Nevertheless, some of the participating teachers were seen allowing students to check their partner’s work, visiting a few students to check how they conduct peer assessments and giving feedback on how the peer assessments were being conducted during post-intervention.
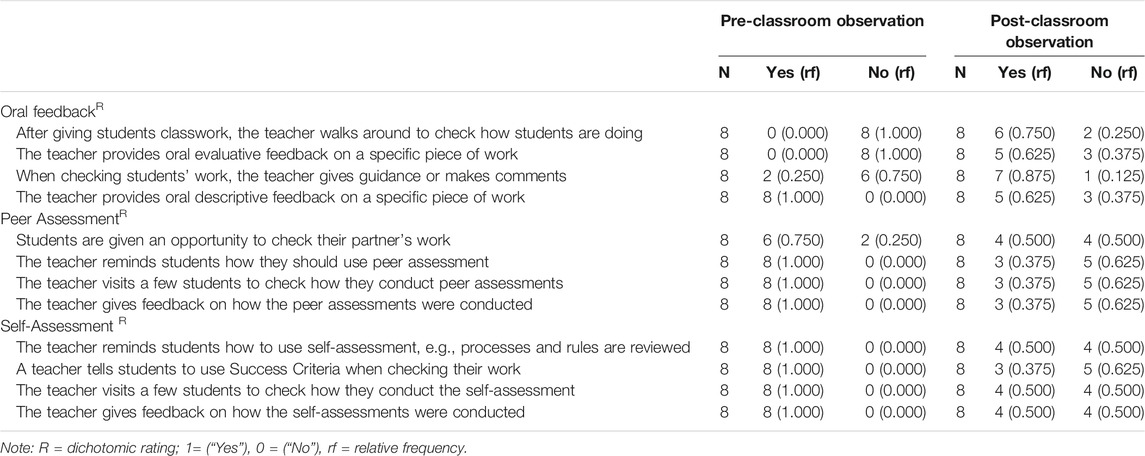
TABLE 6. The frequency and use of feedback within the FAHOTS as observed by the researcher during pre- and post-observations.
Similarly, even for self-assessment, Table 6 depicts that the proportion using the strategy ranged from 0.00 to 0.5 for pre- and post-observations, respectively. Thus, during post-observation, teachers were seen; reminding students how to use self-assessment, for instance, processes and rules reviewed; telling students to use Success Criteria when checking their work and; visited a few students to check how they conduct the self-assessment.
(iii) Mathematics Exercises and Type of Feedback for pre- and post-observation
Table 7 shows the sampled workbooks of the lower performing and higher-performing students after the lesson observations. The attempt to collect additional data from the sampling workbooks was meant to explore the level of learning tasks that involved problem-solving (HOTS) and lower-order thinking skills (LOTS) and the types of feedback given. Table 7 illustrates the data from post-observation for a small proportion of exercises (min = 10, max = 25), for LOTS (M = 18.63; SD = 5.53) to HOTS (M = 5.75; SD = 1.58). Even in pre-observation, it shows that for every 12 exercises that constitute the LOTS items (M = 31.38; SD = 8.72), only one item was for HOTS (M = 2.62; SD = 0.518). A Wilcoxon Signed Rank Test from pre-observation (M = 31.38; SD = 8.72) to post-observations (M = 18.63; SD = 5.53) for LOTS exercises was found significantly reduced (Z= 2.313, p = 0.021), with a large effect size (r= 0.818). Regarding the rate of giving HOTS, exercises had increased significantly from pre-observation to post-observation (Z= 2.388, p = 0.017), with a large effect size (r= 0.844). Most importantly, the teachers’ increase of HOTS exercises was a desirable change for classroom practice and exposed students to different problem-solving activities to activate their thinking.

TABLE 7. Rating results of students’ learning exercises during pre- and post-observation as observed by the researcher.
However, teachers’ ways of giving feedback were still worrisome as it remained mostly evaluative judgment, with no hints on what the student has done well and where she or he can improve. For example, before the intervention comments included: “Pull up your socks,” “This is poor work,” “See me.” After the intervention, feedback comments included: “Excellent work,” “Very good attempt” which is still not formative feedback.
In general, a shift of fewer LOTS, and more HOTS was observed. The acquisition of these skills will result in explanations, decisions, and products that are valid within the context of available knowledge and experience, and promote continued growth in higher-order thinking, as well as other intellectual skills. In the same vein studies that have been published are much more focused on general aspects of formative assessment in enhancing students’ achievement and learning improvement as well as indicating the effect of the intervention on generating HOTS. Hence, it is difficult for the researcher to find studies that specifically focus on the percentage of exercises needed for HOTS to be effective. However, the large effect size of HOTS exercises from pre-observation to post-observation reflects the desirable effort in the classroom practice to enhance learning HOTS among students. In addition, based on the foregoing analysis (See Table 7), types of class exercises were common to all students in this way and did not show any evidence of students’ remedial and enrichment activities respectively unless separate workbooks were used. It also appears that the majority of the teachers’ feedback is still inclined to be based on evaluative feedback.
Summary of the Relationship of Observed Teaching and Student Learning Gained
This study also explored the relationship between teaching behavior and student outcomes on the classroom level. It should be noted that one teacher was not observed for both the pre-and-post, due to absenteeism (sick leave) during classroom assessment, and even results from her students for such school (303) were low and not significant (See Table 2). It may be implied that such a teacher may have not implemented the intervention. Schools such as 320 and 305 (see Table 2) had the most improved learning outcomes, even during post-observation, there was strong evidence of formative assessment practices in those classrooms such as systematic sharing of learning goals and success criteria at the beginning of the lesson. For instance, an exemplary practice during lesson introduction included, “Which topic did we do last week?” Whole class “Money”. Teacher “Yes money, and this week we are still going to continue learning about money. Today we are still going to learn about money. How do you think money is useful in our life?” (Participant 4). In this lesson, the teacher also incorporated a range of questions and included those that promoted higher-order thinking.
The use of formative assessment during the lesson development was also observed in those classes with significantly better students’ results. Thus, the frequent use of planned questioning and interaction strategies among them were hands down, thinking time, pair and share, and exit card or whiteboard, as opposed to the traditional methods of engaging students, and task-based assessment is considered an effective way of engineering classroom discussion and enhancing students’ HOTS and academic performance. During the lesson observations, the evidence of a student’s self- and peer-assessment was also considered essential to activate students as instructional resources for each other and becoming owners of their learning as applied by teachers (Table 6). Classroom observations that were made have revealed some positive relationship between formative assessment strategies and student’s outcomes, especially in schools 320 and 305 (see Table 2).
Summary of Thematic Analysis of the Teacher Interview Data
Following the data coding process, six themes emerged from the raw data which included participants’ experience with the intervention, the impact of the strategies and the workshop, students’ reaction toward learning, barriers and support, and a general reflection on the intervention. These themes were interpreted and linked (where possible) to the constructs of the intervention conceptual framework to identify possible growth areas following the implementation of the intervention programme. Sub-themes emerged from some main themes. Under the theme impact of the strategies, it became clear that some participants who employed FA strategies did so to direct learning and effective engagement, management of the class size, and workloads. The teachers perceived the workshops as professional development and linked them to the training workshop for FA in the classroom. The majority of the participating teachers reported that the implementation of FA helped to improve students’ motivation in learning, whereas the other teachers considered FA as strategies that provide an opportunity for learning improvement. Some participants experienced some challenges during the implementation of the FA, whereas other participating teachers had support from school management.
Discussion
Pre- and Post-intervention Comparison of Mathematics Achievement
Research question 1 sought to determine the extent to which the intervention has enhanced Standard 4 students’ HOTS academic achievement in mathematics when comparing the pre- and post-intervention. The mathematics achievement findings revealed significantly different scores, which indicated how much students gained as far as learning was concerned. Note that the test in its entirety required the use of three different HOTS skills, so the gain is in the field of HOTS. The significant gain in students’ learning can be associated with the intervention. The magnitude of the effect size was beyond the expected growth, an effect size greater than Hattie’s (2013) hinge-point in the case of the intervention. This evidence corroborates the observational findings that teachers indeed did something different, and it was a sign of change in the classroom teaching and learning of mathematics.
It is important to note with the results for this study that a statistically significant gain was observed for students’ achievement in mathematics in the tests that were constituted of HOTS items. Once again, it should be noted that the finding of this study was in line with Babincakova, et al. (2020) which revealed the introduction of formative assessment classroom techniques (FACTs) in the classroom to have significantly increased both students’ lower- and higher-order cognitive skills and students showed a positive attitude toward the introduced method. More explicitly, the current results corroborate the most recent study by Chemeli (2019b), who found a positive impact of the five key FA strategies on students’ achievement in mathematics instruction.
Classroom Observations
Research question-2 investigated if Standard 4 teachers’ exposure to the FAHOTS intervention has enhanced their teaching of HOTS in mathematics when comparing the pre- and post-observation. The classroom observation results indicated that teachers employed FAHOTS to some extent. The most prominently used strategies were using learning goals, engineering effective classroom discussions on questioning, and learning tasks to elicit evidence of learning HOTS concepts. This positive development in teaching and learning is a desirable experience for the participating teachers, suggesting abandoning teaching to the test, as observed in the introduction section of this study. The workbooks also revealed significant HOTS tasks compared from pre-observations to post-observations. The findings indicate that participating teachers may have assigned some HOTS learning tasks as often as taught during the workshops.
A change in students’ exercises is a good development; however, the extent to which students were assisted with feedback to improve learning is important. The feedback findings from students’ workbooks do not seem to help the students to learn. More specifically, comments such as “pull up your socks,” and “very poor” were still noted against the incorrect solution during post-observations. Moreover, evidence of peer- and self-assessment was limited during post-observation, just like in pre-observation. These results do not support previous studies on teachers’ monitoring, scaffolding, and feedback delivery practices (Lizzio and Wilson, 2008; Kyrauzi, 2017). Despite the current study’s findings that demonstrated some limited evidence that participating teachers had on FA, the observed significant change in students’ workbooks indicates an impact on the transformation of teaching and learning of mathematics, particularly the HOTS.
Teachers’ Experiences and Reflections
Research question 3 investigated the participating teachers’ experiences following the FAHOTS intervention and mathematics teaching on the students’ learning outcomes. The participating teachers revealed some positive experiences with the FAHOTS intervention during interview findings. The participants affirmed that they had implemented at least three to five of the formative assessment strategies. Such interview findings corroborate the classroom observations and found some evidence that teachers have employed FAHOTS, particularly using learning objectives, engineering effective classroom discussions on questioning, and learning tasks to elicit evidence of learning HOTS concepts, respectively.
This positive development in teaching and learning is a desirable experience for the participating teachers to suggest abandoning the notion of teaching to the test, as observed in the introduction section of this study. Moreover, the workbooks revealed that HOTS tasks were assigned as often as taught during the workshops, which indicates possible intervention impact, though it may require long-term follow-up and support for teachers. These findings are consistent with Accado and Kuder (2017) who identified teacher training in professional development learning communities, in which the schools and the government supported and implemented the formative assessment as a way to improve students’ performance. Moreover, the study’s findings are also in line with Balan (2012), who employed a mixed-method intervention study on assessment for learning (formative assessment) in mathematics education, in which the finding was positively significant.
On the other hand, a most recent study by Chemeli (2019a) investigated the Kenyan teachers’ support for effective implementation of the FA strategies in mathematics instruction, and the findings revealed inadequate support concerning training and resources. However, the current study’s finding demonstrated some limited evidence that teacher training in FA impacted the transformation of teaching and learning of mathematics, particularly the HOTS. The participating teachers said they were in favor of the FAHOTS intervention, as revealed in the interview findings. This response may have been a socially desirable response during the interviews, but teachers did not exhibit some of these strategies during the classroom observations. However, the teacher’s support for in-service training of the FAHOTS fits well with Botswana ETSSP’s (Botswana Examination Council, 2017) proposed teacher training development in the school-based assessment.
The last part of the research question (RQ 3) investigated teachers’ reflections following the FAHOTS intervention and mathematics teaching of students’ HOTS. The results from interviewed teachers were positive toward using the FAHOTS in their classrooms. The participating teachers suggested that such professional development should be cascaded to all subjects and across different primary school levels. This result indicates that FAHOTS intervention could be used as a strategy to enhance teaching and learning of HOTS, but more evidence is needed for the long-term implementation (Black and Wiliam, 2003).
The results are in line with Melani’s (2017) findings where an in-depth case revealed that, when provided with specific information about FA through staff development, teachers became more positive toward such assessment, and their implementation skills were greatly improved. When teachers are trained, they can support the FA as a method for monitoring students. The findings support Accado and Kuder (2017), who found that mathematics teachers who received professional development (PD) training in FA provided by a university faculty with expertise in mathematics education used instructional methods to improve students’ learning. The findings in the current study were also similar to the positive factors noted by Chemeli (2019b). Chemeli found that formative assessment strategies eased the teacher’s workload, raised students’ attitudes and interests, improved students’ critical thinking, and teachers and students enjoyed using formative assessment strategies.
Even though the study systematically developed the intervention, the results should be interpreted, bearing in mind that it was only a sequential embedded approach with a single-case study, which may raise some concerns about the validity.
Limitations and Implications
First, the lack of a control group has limited findings of this study, thus, if actually, the study hit the sweet spot of students’ learning or if the intervention really worked. The findings of the current study may actually mean that it is by chance that a researcher got with really enthusiastic, smart, and motivated participants. Additionally, the tests were still too hard for participating students so the researcher is unable to confidently tell if the results would be better with better-calibrated tests. Given that participating students were not interviewed, this fact may weaken the claim as qualitative research, considering that the improvement of students’ HOTS is the main issue of this study. Having mentioned these factors, it is also imperative to note that teachers’ reflection on the experience had augmented the intervention’s impact on students’ learning of HOTS in mathematics. Second, a lack of control on the allocation and random assignment of participants and the limited number of sampled schools and teachers means that this study’s results cannot be generalized to other settings in Botswana and beyond. Moreover, the eight teachers involved were mainly from the junior position of teaching rank (only two senior teachers), experienced some challenges in teaching mathematics, and most of their students were underachievers since their school management specifically selected them to be assisted through the intervention. In addition, the test instruments used were not specifically designed with anchor items, and hence to some extent limited the test linking approach.
Conclusion
The findings showed that intervention could improve teaching and learning, as the teachers’ teaching and attitudes improved. There was evidence of patterns of change as the teachers started to use some new strategies in teaching mathematics, though written feedback remained a challenge and it was just evaluative. However, student’s achievement, pre- and post-achievement gains in mathematical HOTS items reflected to some extent the quality of instructional strategies that teachers employed in the classroom. Most importantly, it has to be considered that mathematics emphasizes students’ ability to develop and apply mathematical thinking to solve a range of problems in everyday situations, which has improved after the intervention. The participating teachers’ reflections supported findings that rolling out the formative assessment is a desirable endeavor as professional development.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Ethics Statement
The studies involving human participants were reviewed and approved by University of Pretoria, South Africa. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.
Author Contributions
All authors listed have made a substantial, Direct, and Intellectual contribution to the work and approved it for publication.
Funding
This study was funded 100% by the University of Pretoria.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
Thanks go to the teachers and students who participated and shared their thoughts about formative assessment.
References
Accado, A., and Kuder, S. J. (2017). Monitoring Student Learning in Algebra. Maths. Teach. Middle Sch. 22 (6), 352–359. doi:10.5951/mathteacmiddscho.22.6.0352
Anderson, L. W. (2003). Classroom Assessment: Enhancing the Quality of Teacher Decision Making. Mahwah, NJ: Lawrence Erlbaum Associates.
Anderson, L. W., Krathwohl, D. R., and Bloom, B. S. (2001). A Taxonomy for Learning, Teaching, and Assessing: A Revision of Bloom's Taxonomy of Educational Objectives. Boston, MA: Allyn & Bacon.
Andrich, D. (2004). Controversy and the Rasch Model: a Characteristic of Incompatible Paradigms. Med. Care 42 (1 Suppl. l), I7–I16. doi:10.1097/01.mlr.0000103528.48582.7c
Anselmi, P., Vidotto, G., Bettinardi, O., and Bertolotti, G. (2015). Measurement of Change in Health Status with Rasch Models. Health Qual. Life Outcomes 13, 16. doi:10.1186/s12955-014-0197-x
Babinčáková, M., Ganajová, M., Sotáková, I., and Bernard, P. (2020). Influence of Formative Assessment Classroom Techniques (Facts) on Student’s Outcomes in Chemistry at Secondary School. J. Baltic Sci. Edu. 19 (1), 36–49. doi:10.33225/jbse/20.19.36
Balakrishnan, M., Nadarajah, M. G., Vellasamy, S., and George, E. G. W. (2016). Enhancement of Higher Order Thinking Skills Among Teacher Trainers by Fun Game Learning Approach. World Acad. Sci. Eng. Technol. Int. J. Educ. Pedagogical Sci. 10 (12), 2954–3958.
Balan, A. (2012). Assessment for Learning: A Case Study in Mathematics Education. Malmö högskola, Fakulteten för lärande och samhälle.
Black, P., and Wiliam, D. (2003). ‘In Praise of Educational Research’: Formative Assessment. Br. Educ. Res. J. 29 (5), 623–637.
Bloom, B. S., Engelhart, M. D., Furst, E. J., Hill, W. H., and Krathwohl, D. R. (1956). Taxonomy of Educational Objectives: The Classification of Educational Goals. Handbook 1. New York, NY: Cognitive domainDavid McKay.
Bond, T. G., and Fox, C. M. (2007). Apply the Rasch Model: Fundamental Measurement in the Human Sciences. 3rd Ed. Mahwah, NJ: L. Erlbaum.
Bond, T. G., and Fox, C. M. (2012). Applying The Rasch Model: Fundamental Measurement in the Human Sciences. Second Edition 2nd Edition. New York: Routledge.
Boone, W. J., and Noltemeyer, A. (2017). Rasch Analysis: A Primer for School Psychology Researchers and Practitioners. Cogent Edu. 4, 1416898. doi:10.1080/2331186X.2017.1416898
Boone, W. J., Staver, J. R., and Yale, M. S. (2014). Rasch Analysis in the Human Sciences. London: Springer.
Botswana Examination Council. (Bec), (2017). Primary Leaving School Examination Report 2016. Gaborone.
Brookhart, S. M. (2006). Formative Assessment Strategies for Every Classroom: An ASCD Action Tool. Alexandria, VA: ASCD.
Brookhart, S. M. (2010). How to Assess Higher-Order Thinking Skills in Your Classroom. . Alexandria, VA: ASCD.
Brown, G. T. L., and Hattie, J. A. (2012). “The Benefits of Regular Standardized Assessment in Childhood Education: Guiding Improved Instruction and Learning,” in Contemporary Debates in Childhood Education and Development. Editors S. Suggate,, and E. Reese (London: Routledge), 287–292.
Campbell, D. T. (1975). III. "Degrees of Freedom" and the Case Study. Comp. Polit. Stud. 8 (2), 178–193. doi:10.1177/001041407500800204
Chemeli, J. (2019a). Impact of the Five Key Formative Assessment Strategies on Learner’s Achievement in Mathematics Instruction in Secondary Schools: A Case of Nandi County, Kenya. Int. Acad. J. Soc. Sci. Edu. 2 (1), 212–229.
Chemeli, J. (2019b). Teachers Support the Effective Implementation of the Five Key Formative Assessment Strategies in Mathematics Instruction in Secondary Schools: A Case of Nandi County, Kenya. Elixir Soc. Sci. 128, 52954–52959.
Clarke, S. (2005). Formative Assessment in Action: Weaving the Elements Together. London, Great Britain: Hodder and Stoughton.
Combrinck, C. (2018). The Use of Rasch Measurement Theory to Address Measurement and Analysis Challenges in Social Science Research. Unpublished Doctoral thesis. Pretoria: University of Pretoria.
Cook, T. D., and Campbell, D. T. (1979). “Causal Inference and the Language of Experimentation,” in Quasi-experimentation: Design & Analysis Issues for Field Settings. Editors T. D. Cook,, and D. T. Campbell (Boston, MA: Houghton Mifflin), 1–36.
Creswell, J. W., and Plano Clark, V. L. (2017). Designing and Conducting Mixed Methods Research. 3rd ed. Thousand Oaks, CA: Sage.
Deneen, C., Brown, G. T. L., Bond, T. G., and Shroff, R. (2013). Understanding Outcome-Based Education Changes in Teacher Education: Evaluation of a New Instrument with Preliminary Findings. Asia-Pacific J. Teach. Edu. 41 (4), 441–456. doi:10.1080/1359866X.2013.787392
E. V. SmithJr.,, and G. E. Stone (Editors) (2009). Applications of Rasch Measurement in Criterion-Reference Testing: Practice Analysis to Score Reporting (Maple Grove, MN: JAM Press).
Fetogang, E. B. (2015). Assessment Syllabus and the Validity of Agricultural Education. Res. J. Educ. Sci. 3 (5), 1–9.
F. N. Kerlinger,, and H. B. Lee (Editors) (2000). Foundations of Behavioral Research (Orlando, FL: Harcourt College Publishers).
Foong, P. Y. (2000). Open-ended Problems for Higher-Order Thinking in Mathematics. Teach. Learn. 20 (2), 49–57.
Ganapathy, M., Mehar Singh, M. K., Kaur, S., and Kit, L. W. (2017). Promoting Higher Order Thinking Skills via Teaching Practices. 3L 23 (1), 75–85. doi:10.17576/3l-2017-2301-06
Government of Botswana (BOT), (2015). Education & Training Sector Strategic Plan. Gaborone, Botswana: Government Printer, 23. (ETSSP 2015-2020)Retrieved from https://www.gov.bw/sites/default/files/2020-03/ElTSSP%20Final%20Document_3.pdf
Government of Botswana, BOT, (1994). The Revised National Policy on Education. Government Policy Paper. Government Paper No 2 of 1994. Gaborone: Government Printer.
Hagermoser Sanetti, L., and Kratochwill, T. R. (2005). “Treatment Integrity Assessment within a Problem-Solving Model,” in Assessment for Intervention: A Problem-Solving Approach. Editor R. Brown-Chidsey (New York: Guilford Press), 304–325.
Hattie, J. (2017). Visible Learning for Teachers: Maximizing Impact on Learning. Milton Park, Abingdon, UK: Routledge.
Hattie, J. A., and Brown, G. T. L. (2004). Cognitive Processes in asTTle: The SOLO Taxonomy (asTTle Tech. Rep. #43). Wellington, N.ZRetrieved from: https://easttle.tki.org.nz/content/download/1499/6030/version/1/file/43.+The+SOLO+taxonomy+2004.pdf.
Hattie, J., and Timperley, H. (2007). The Power of Feedback. Rev. Educ. Res. 77 (1), 81–112. doi:10.3102/003465430298487
Heritage, M. (2010). Formative Assessment: Making it Happen in the Classroom. Thousand Oaks, CA: Corwin Press.
Hogden, J., and Wiliam, D. (2006). Mathematics inside the Black Box: Assessment for Learning in the Mathematics Classroom. London, UK: Granada Learning.
Jerome, C., Lee, J. A. C., and Ting, S. H. (2017). What Students Really Need: Instructional Strategies that Enhance Higher-Order Thinking Skills (Hots) Among Unimas Undergraduates. Int. J. Business Soc. 18 (S4), 661–668.
Jerome, C., Lee, J., and Cheng, A. (2019). Undergraduate Students’ and Lecturers ’ Perceptions on Teaching Strategies that Could Enhance Higher Order Thinking Skills ( Hots ). Int. J. Edu. 40 (30), 60–70.
Kanjee, A. (2017). Assessment for Learning in Africa. Assessment For Learning Strategies Workshop Handouts And School-Based Project at Ikeleng Primary School.Winterveld from 18th February 2017 to 29th July 2017
Kanjee, A., and Meshack, M. (2014). South African Teachers' Use of National Assessment Data. South Afr. J. Child. Edu. 4, 90–113. doi:10.4102/sajce.v4i2.206
Kiplagat, P. (2016). Rethinking Primary School Mathematics Teaching: A Formative Assessment Approach. Baraton Interdiscip. Res. J. 6, 32–38.
Kivunja, C. (2015). Why Students Don't like Assessment and How to Change Their Perceptions in 21st Century Pedagogies. Ce 06, 2117–2126. doi:10.4236/ce.2015.620215
Kyaruzi, F. (2017). Formative Assessment Practices in Mathematics Education Among Secondary Schools in TanzaniaPhD Unpublished Thesis). Munich, DE): Ludwig Maximilians Universitat. Retrieved from https://edoc.ub.uni-muenchen.de/25438/7/Kyaruzi_Florence.pdf.
Kyaruzi, F., Strijbos, J.-W., and Ufer, S. (2020). Impact of a Short-Term Professional Development Teacher Training on Students' Perceptions and Use of Errors in Mathematics Learning. Front. Educ.Frontiers 5, 169. doi:10.3389/feduc.2020.559122
Linacre, J. M. (2002). What Do Infit and Outfit, Mean-Square and Standardized Mean. Rasch Meas. Trans. 16, 878.
Linacre, J. M. (2016). Winsteps® Rasch Measurement Computer Program User's Guide. Beaverton, Oregon: Winsteps.Com.
Lizzio, A., and Wilson, K. (2008). Feedback on Assessment: Students' Perceptions of Quality and Effectiveness. Assess. Eval. Higher Edu. 33 (3), 263–275. doi:10.1080/02602930701292548
Maguire, M., and Delahunt, B. (2017). Doing a Thematic Analysis: A Practical, Step-by-step Guide for Learning and Teaching Scholar. All Ireland J. Teach. Learn. Higher Edu. (Alshe-j) 8 (3), 3351
Mansor, A. N., Leng, O. H., Rasul, M. S., Raof, R. A., and Yusoff, N. (2013). The Benefits of School-Based Assessment. Asian Soc. Sci. 9 (8), 101. doi:10.5539/ass.v9n8p101
Masole, T. B., Gabalebatse, M., Guga, T., and Pharithi, M.BEC (2016). TIMSS 2015 Encyclopaedia BotswanaTIMSS & PIRLS. International Study centre. Boston College: Lynch School of Education.
McGrane, J., Hopfenbeck, T. N., Halai, A., Katunzi, N., and Sarungi, V. (2018). “Psychometric Research in a Challenging Educational Contex.” in 2nd International Conference on Educational Measurement, Evaluation and Assessment [ICEMEA 2018]. Oxford University Centre for Educational Assessment. London: University of Oxford.
McMillan, J. H., and Schumacher, S. (2006). Research in Education Evidence-Based Inquiry. 6th Ed. Boston: MA Allyn and Bacon.
Melani, B. (2017). Effective Use of Formative Assessment by High School Teachers. Pract. Assess. Res. Eval. 22 (8), 10. doi:10.7275/p86s-zc41
Mills, V. L., Strutchens, M. E., and Petit, M. (2017). “Our Evolving Understanding of Formative Assessment and the Challenges of Widespread Implementation,” in A Fresh Look at Formative Assessment in Mathematics Teaching. Reston: The National Council of Teachers of Mathematics.
Mohamed, R., and Lebar, O. (2017). Authentic Assessment in Assessing Higher Order Thinking Skills. Int. J. Acad. Res. Business Soc. Sci. 7 (2), 466–476.
Moss, C. M., and Brookhart, S. M. (2019). Advancing Formative Assessment in Every Classroom: A Guide for Instructional Leaders. Alexandria: ASCD Publisher.
Moss, C. M., and Brookhart, S. M. (2012). Learning Targets: Helping Students Aim for Understanding in Today's Lesson. Alexandria: ASCD.
Moyo, S. E. (2021). Botswana Teachers' Experiences of Formative Assessment in Standard 4 Mathematics. Unpublished PhD Thesis. Pretoria: The University of Pretoria.
Mukherji, P., and Albon, D. (2010). Research Methods in Early Childhood: An Introductory Guide. London: SAGE Publications Ltd.
Murray, E. C. (2011). Implementing Higher-Order Thinking in Middle School Mathematics Classrooms. Athens, Georgia: Doctor of Philosophy.
Narayanan, S., and Adithan, M. (2015). Analysis of Question Papers in Engineering Courses with Respect to Hots (Higher Order Thinking Skills). Am. J. Eng. Edu. (Ajee) 6. doi:10.19030/ajee.v6i1.9247
Nooraini, O., and Khairul, A. M. (2014). Thinking Skill Education and Transformational Progress in Malaysia. Int. Edu. Stud. 7 (4), 27–32.
Pallant, J. (2010). SPSS Survival Manual. A Step by Step Guide to Data Analysis Using SPSS. 4th Ed. Australia: McGraw-Hill Education.
Panayides, P., Robinson, C., and Tymms, P. (2010). The Assessment Revolution that Has Passed England by: Rasch Measurement. Br. Educ. Res. J. 36 (4), 611–626. doi:10.1080/01411920903018182
Radmehr, F., and Drake, M. (2019). Revised Bloom's Taxonomy and Major Theories and Frameworks that Influence the Teaching, Learning, and Assessment of Mathematics: a Comparison. Int. J. Math. Edu. Sci. Technol. 50 (6), 895–920. doi:10.1080/0020739x.2018.1549336
Rajendran, N. (2008). “Teaching and Acquiring Higher-Order Thinking Skills: Theory and Practice,” in Tanjong Malim Perak: Penerbit Universiti Pendidikan Sultan Idris. Perak: Penerbit University Pendidikan Sultan Idris.
Ramadubu, D. (2018). Botswana Guardian Kweneng District Headteachers Fail the Test. Retrieved from: http://www.botswanaguardian.co.bw/news/.
Shadish, W. R., Cook, T. D., and Campbell, D. T. (2002). Experimental and Quasi-Experimental Designs for Generalized Causal Inference. Boston, MA: Houghton Mifflin.
Sharif, M., Hanapi, Z., Nashir, M., Kob, C., and Abdullah, A. S. (2019). Construct Validity and Reliability of Manufacturing Industry: A Rasch Measurement Model Approaches for Pilot Study. Int. J. Acad. Res. Business Soc. Sci. 9 (3), 654–666. doi:10.6007/ijarbss/v9-i3/5733
Sinharay, S., Haberman, S., Holland, P., and Lewis, C. (2006). A Note on the Choice of an Anchor Test in Equating. ETS Res. Rep. Ser. 2012, i–9. doi:10.1002/j.2333-8504.2012.tb02296.x
Tajudin, M. (2015). “Mathematical Knowledge and Higher-Order Thinking Skills for Teaching Algebraic Problem-Solving.” in Proceedings of SOCIOINT15- 2nd International Conference on Education. Istanbul Turkey: Social Sciences and Humanities.
United Nations Educational Scientific and Cultural Organization UNESCO (2010). World Data on Education. Retrieved from: http://www.ibe.unesco.org/fileadmin/user_upload/Publications/WDE/2010/pdf-versions/Botswana.pdf?&session-id=9bef60f240054b618f9f4af6e3d00ddf (Accessed March 9, 2018)
Welsh Assembly Government (2010). Howe to Develop Thinking and Assessment for Learning in the Classroom. Retrieved from https://www.gwegogledd.cymru/wp-content/uploads/2018/04/How_to_develop_thinking_and.pdf (Accessed April 21, 2018)
Wiliam, D. (2011). Embedded Formative Assessment: Practical Strategies and Tools for K–12 Teachers. Bloomington: IN Solution Tree.
Wilson, D. M., and A/l Narasuman, S. (2020). Investigating Teachers' Implementation and Strategies on Higher Order Thinking Skills in School Based Assessment Instruments. Ajue 16 (1), 70–84. doi:10.24191/ajue.v16i1.8991
Wiyaka, W., Prastikawati, E. F., and Kusumo Adi, A. P. (2020). Higher-Order Thinking Skills (HOTS)-based Formative Assessment: A Proposed Model for Language Learning Assessment. Vjlfll 9 (2), 115. doi:10.21580/vjv9i25859
Yee, M. H., Jailani, M. Y., Widad, O., Razali, H., and Tee, T. K. (2011). “Recent Advances in Educational Technologies.” in The Effectiveness of Higher Order Thinking Skills for Generating Idea Among Technical Students
Zohar, A., and Cohen, A. (2016). Large Scale Implementation of Higher Order Thinking (HOT) in Civic Education: The Interplay of Policy, Politics, Pedagogical Leadership and Detailed Pedagogical Planning. Thinking Skills and Creativity 21, 85–96. doi:10.1016/j.tsc.2016.05.003
Keywords: formative assessement, higher order thinking skills, Rasch analysis, intervention, standard 4 mathematics teachers
Citation: Moyo SE, Combrinck C and Van Staden S (2022) Evaluating the Impact of Formative Assessment Intervention and Experiences of the Standard 4 Teachers in Teaching Higher-Order-Thinking Skills in Mathematics. Front. Educ. 7:771437. doi: 10.3389/feduc.2022.771437
Received: 30 September 2021; Accepted: 17 January 2022;
Published: 14 February 2022.
Edited by:
Chunxia Qi, Beijing Normal University, Beijing, ChinaReviewded by:
Eckhard Klieme, Leibniz Institute for Research and Information in Education (DIPF), GermanyHabiddin Habiddin, State University of Malang, Indonesia
Ilmi Zajuli Ichsan, Universitas Mohammad Husni Thamrin, Indonesia
Copyright © 2022 Moyo, Combrinck and Van Staden. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sello Editor Moyo, c2VsbG1veW9AZ21haWwuY29t, bW95b3NAdWIuYWMuYnc=
 Sello Editor Moyo
Sello Editor Moyo Celeste Combrinck
Celeste Combrinck Surette Van Staden
Surette Van Staden