- 1Department of Applied and Computational Mathematics and Statistics, University of Notre Dame, Notre Dame, IN, United States
- 2Department of Psychology, University of Notre Dame, Notre Dame, IN, United States
Introduction: Past studies have found students to perform differently between class grades and standardized test scores – two essential and complementary measures of student achievement. This study examines predictors of the relative performance between these two measures in the context of the advanced placement (AP) program, namely, we compared students’ AP exam scores to the class grade they received in the corresponding AP course. For example, if a student received a high AP class grade but a low AP exam score, what characteristics about the student or their learning context might explain such discrepancy?
Methods: We used machine learning, specifically random forests, and model interpretation methods on data collected from 381 high school students enrolled in an AP Statistics course in the 2017–2018 academic year, and additionally replicated our analyses on a separate cohort of 422 AP Statistics students from the 2018–2019 academic year.
Results: Both analyses highlighted students’ school and behavioral engagement as predictors of differential performance between AP class grades and AP exam scores.
Discussion: Associations between behavioral engagement and differential performance suggest that the ways in which a student interacts with AP course material to obtain high class grades can differ from study habits that lead to optimal performance on the AP exam. Additionally, school-level differences in relative performance pose equity concerns towards the use of AP exam scores in high-stakes decisions, such as college admissions. Implications are discussed from a pedagogical and policy perspective.
Introduction
Grades versus standardized test scores
Teacher-assigned class grades and standardized test scores are two of the most common measures of student achievement widely used in practice and research. Although both are reflective of student learning, they measure distinct constructs of graded achievement and tested achievement, respectively (Brookhart, 2015). While tested achievement more narrowly captures student mastery of key content and cognitive skills relevant to the test subject, graded achievement may encompass a broader set of learning outcomes, such as motivation, effort, participation, and other classroom- or teacher-defined goals (McMillan, 2001; Willingham et al., 2002; Bowers, 2011; Brookhart, 2015). In fact, empirical evidence has repeatedly shown grades and standardized test scores to correlate only moderately, often ranging from 0.5 to 0.6 (Brennan et al., 2001; Sadler and Tai, 2007; Bowers, 2011; Pattison et al., 2013; Brookhart, 2015). Furthermore, grades and test scores can have varying sources of construct-irrelevant variance. As most standardized tests are administered as a fixed and one-time event, daily fluctuations in students’ physical and mental health can more easily affect performance, as well as factors such as test anxiety (Haladyna and Downing, 2004; Richardson, 2015). Grades, on the other hand, can suffer from considerable variability or inconsistency in standards and practices across teachers (Brookhart, 1994). Further, grades are often assigned in reference to other students in the class, and thus students with the same ability level can receive different grades depending on the average ability level of their classmates (Calsamiglia and Loviglio, 2019; Bergold et al., 2022). In this sense, standardized test scores given by external examiners may provide a more objective and comparable measure of achievement across classrooms and schools (Calsamiglia and Loviglio, 2019). Overall, it is unsurprising that students often perform differently between grades and standardized tests, and that grades and test scores produce different rankings of students, especially when compared across classrooms and schools.
Several past studies have examined student and contextual characteristics that account for differential performance on grades and standardized tests. For example, Willingham et al. (2002) analyzed data from the National Education Longitudinal Study (NELS) and cited several sources of discrepancy between high school grade average and NELS test scores among high school seniors. These included variations in grading practices across schools, students’ scholastic engagement as defined by participation, initiative in school, and avoidance of distracting activities, and teachers’ judgments of student performance (Willingham et al., 2002). In another study, Kobrin et al. (2002) noted demographic features associated with students who had higher high school grade-point averages (GPA) relative to their SAT scores. Such characteristics included being a minority student, being female, having lower family income, speaking languages besides English, and being non-US citizens or nationals (Kobrin et al., 2002).
In a closely related line of work, researchers have separately examined the correlates of grades and those of standardized test scores and compared them to one another. Duckworth et al. (2012) found that standardized test scores were more reflective of intelligence (measured by IQ) among a sample of middle school students, whereas report card grades were more reflective of self-control, which refers to the voluntary regulation of attention, emotion, and behavior. The authors reasoned that intelligence allows students to more easily and independently acquire knowledge and skills outside of formal instruction, which may be advantageous for standardized tests if test content differs from classroom curricula. On the other hand, self-control aligns more with studying content taught in class, completing homework, and generally managing behaviors and emotions in class (Duckworth et al., 2012). Similarly, Hofer et al. (2012) found cognitive ability to be a better predictor of standardized test scores, whereas personality variables, including self-control strength and academic procrastination, were better predictors of self-reported school grades among middle school students.
Several studies have specifically investigated the differential relations between personality traits and various achievement measures. At the university level, Furnham et al. (2013) found that the big five personality traits (i.e., extraversion, agreeableness, conscientiousness, negative emotionality, and open-mindedness) accounted for more variance in coursework performance (e.g., homework, in-class assignments) than exam performance among British university students. Morris and Fritz (2015) found corroborating results, where conscientiousness and procrastination were stronger predictors of class grades than exam scores. They reasoned that contrary to the restrictive nature of exams, coursework provides much more flexibility for students’ individual traits to engage, by allowing students to choose when, where, and with whom to work (Furnham et al., 2013; Morris and Fritz, 2015). However, an important distinction to note here is that these two studies examined performance on a university course exam, rather than a standardized test. At the high school level, Meyer et al. (2019) studied the differential effects of conscientiousness and openness on grades and standardized test scores in two domains (mathematics and English). Their findings highlighted the presence of both domain- and measure-specific differences in the effects of these two traits. For example, they found that openness predicted English test scores but not math test scores, whereas conscientiousness predicted math test scores but not English test scores. They also found that conscientiousness predicted both English and math grades, and that openness had a positive effect on English grades but a negative effect on math grades (Meyer et al., 2019). This focus on conscientiousness and openness is also found in other studies examining the relationship between personality traits and achievement (e.g., Noftle and Robins, 2007; Spengler et al., 2013; Hübner et al., 2022). These studies have emphasized the ties of conscientiousness to discipline, dedication to work, and other study behaviors that are observable by teachers, thus explaining its relation to teacher-assigned grades (Spengler et al., 2013). Openness is more related to the ability to work with and apply learning strategies in novel testing formats, which is advantageous in many standardized test settings (Hübner et al., 2022).
While most studies in this line of research have made a dichotomous categorization of grades and standardized test scores, Hübner et al. (2022) recently proposed the Personality-Achievement Saturation Hypothesis (PASH), a conceptual model to distinguish between achievement measures more thoroughly by considering five features of achievement measures (standardization, relevance for student, curricular validity, instructional sensitivity, and cognitive ability saturation) along which to consider the relationship between personality traits and achievement. For example, while both the Scholastic Aptitude Test (SAT) and the Program for International Student Assessment (PISA) are standardized tests, the SAT is much more consequential and high-stakes to students than the PISA, which is mainly for monitoring purposes. Thus, the differential relations between personality traits and different achievement measures could be refined by considering not only whether a measure is a standardized test score or a grade, but along more granular features (Hübner et al., 2022).
Study goals and contributions
As grades and standardized test scores remain the basis for various high-stakes decisions in the educational system, including policy, selection, evaluation, and resource allocation decisions, studying these measures continue to be of great importance. The present study extends this line of research on the relationship between grades and standardized test scores through two main contributions.
Our first contribution is to study these measures in the context of the College Board’s Advanced Placement (AP) program. The AP program offers advanced-level coursework for high school students in over 20 different subject areas (Ewing, 2006). For each AP course, there is a corresponding standardized test given by the College Board, called the AP exam, which students take towards the end of the AP course. Satisfactory performance on AP exams grants students college credit or course exemption in relevant subjects, thus allowing them to gain a head start on college curricula while still in high school (Ewing, 2006). In our study, we compare students’ final class grade in an AP course to their performance on the corresponding AP exam. The distinctive natures of AP class grades and AP exam scores can be explored using the five features in the PASH framework (Hübner et al., 2022). Both AP class grades and AP exam scores have high curricular validity and instructional sensitivity, as the AP curriculum is designed with the intent of preparing students for the AP exam, and thus both measures are closely linked to the curriculum and coursework tasks. AP exam scores are highly relevant for students given their implications for college credit. AP class grades are also highly relevant for students, given their impact on high school grades, but perhaps to a lesser extent than AP exam scores. According to prior research indicating that cognitive ability is more strongly related to standardized test scores than grades (Hofer et al., 2012; Borghans et al., 2016), we may conceive that AP exam scores are higher on cognitive ability saturation than AP class grades. Finally, the most salient distinction between AP class grades and AP exam scores is that AP exam scores are standardized nationally, whereas AP class grades are not.
To our knowledge, this topic of differential performance between grades and standardized test scores has not been examined in an AP context but is useful for multiple reasons. First, both high school grades and AP exam scores are key factors in college admissions, an evidently high-stakes decision (Shaw et al., 2013). Therefore, it is important to understand how AP exam performance and AP coursework performance can differ in their functions as high-stakes measures, especially given the growth of AP participation nationwide over the past decade (College Board, 2019). Furthermore, there are recent shifts towards test-optional and test-flexible college admission policies, which allow applicants to withhold their SAT and ACT scores or to substitute them with alternative test scores, such as scores on AP exams or SAT II Subject Tests (Pellegrino, 2022). As such, we may expect the importance of the AP program in college admissions to grow. Second, the AP program produces grades and test scores that are aligned perfectly in terms of subject matter. With other standardized tests, such as the SAT or ACT, which have broadly defined subjects like reading and math, test content may not perfectly align with content covered in classroom curricula. This may challenge comparisons between grades and test scores or may require combining grades from multiple classes in order to make the measures comparable in content. Lastly, the AP curriculum is fairly standard at a national level, allowing for better comparisons across schools and classrooms.
The second contribution of our study is to use a machine learning approach in examining the differential performance between grades and standardized test scores. Specifically, we use random forests (Breiman, 2001). Past studies in this line of research have primarily used more traditional statistical approaches, such as multiple regression, structural equation modeling, or descriptive statistics (Brookhart et al., 2016). Although machine learning is often perceived as focused solely on making accurate predictions using a “black-box” algorithm, random forests are well-suited for exploratory data analysis and come with useful tools for interpreting model outputs (Jones and Linder, 2015). In particular, random forests do not make distributional assumptions, can handle a large number of predictors relative to observations, can easily handle continuous, nominal, and ordinal predictors without having to create dummy variables, and can learn complex interactions and nonlinear effects without explicit specification (Jones and Linder, 2015). Therefore, random forests provide a flexible tool for exploring relations among a wide range and large number of variables in a dataset and for discovering new patterns not theorized a priori. Model interpretation tools, such as individual conditional expectation (ICE) plots, partial dependence (PD) plots, and variable importance measures (VIMs), further allow for intuitive explanations and substantive conclusions of the fitted model (see Methods section for more details). Leveraging this data-driven nature of random forests, we incorporate several other predictors of achievement besides the big five personality traits, which have received substantial attention in this line of research on the differential prediction of grades and standardized test scores (Noftle and Robins, 2007; Spengler et al., 2013; Lechner et al., 2017; Meyer et al., 2019; Hübner et al., 2022). Specifically, we consider students’ engagement levels in the classroom as well as the overall school environment, students’ perceptions of teacher support, and a proxy of self-efficacy. While these student characteristics have also been examined in relation to achievement (Klem and Connell, 2004; Galyon et al., 2012; Lei et al., 2018), they have not been studied extensively in how they differentially relate to grades and standardized test scores specifically. We additionally include demographic covariates, such as age, gender, school type (public or private), and parental education. In sum, using machine learning techniques will allow us to examine whether past findings in this line of research apply in an AP context, as well as to mine the data for new patterns for which we have limited prior knowledge.
The use of machine learning for predicting student achievement is not new and has indeed become increasingly popular as research in educational data mining and learning analytics expand (Sahin and Yurdugül, 2020). The present study builds upon previous work in these areas by applying machine learning to model the differences between measures of student achievement, in addition to modeling the measures themselves. While related, the former analysis allows for an investigation and interpretation of variables that directly account for the difference in performance across assessments, whereas the latter only allows for insight into variables that predict each measure individually and to compare them.
The goal of the present study is to (1) compare the personal and contextual characteristics that predict grades vs. standardized test scores in an AP context, and to (2) investigate the predictors of differential performance between the two measures. For example, if a student receives a good final grade in an AP course but a poor AP exam score, what characteristics about the student or their learning context might explain such discrepancy? We conduct data analysis using machine learning and subsequently replicate our analysis on an additional data set to strengthen the evidence of our findings.
Materials and methods
Sample
Data were collected from 381 AP Statistics students aged 14 to 18 (M = 16.64 years, SD = 0.90) from six participating high schools in the midwestern United States during the 2017–2018 academic year. From the six schools, seven AP Statistics teachers’ class sections partook in the study. Data were collected using online self-reported surveys, with the exception of AP class grades and AP exam scores. Students received surveys at five different points throughout the academic year. Each time point included survey questions that gathered information about different student behavior and characteristics (Figure 1).
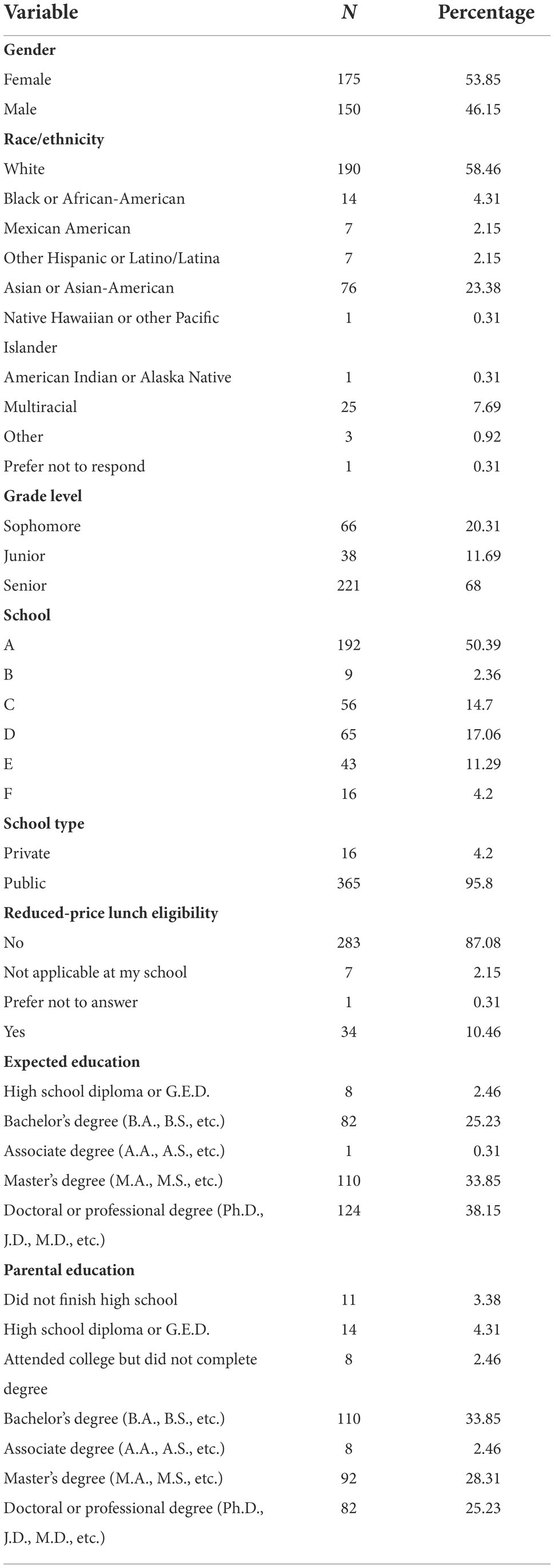
Table 1 presents the study’s sample demographics, which approximately align with available national data concerning AP Statistics students (College Board, 2018). For instance, there was an approximately equal distribution of gender in our sample (53.85% female) compared to the national pool (52.32% female; College Board, 2018). Table 1 contains information on 325 students, as it excludes 56 students who did not report demographic information, except for school and school type which were known for all students.
Measures
Personality
We used the Big Five Inventory-2 to measure five domains of personality (extraversion, agreeableness, conscientiousness, negative emotionality, and open-mindedness; Soto and John, 2017). Each personality domain has three corresponding facets with equal numbers of items per facet (see Soto and John, 2017 for more details). We obtained sum scores at the domain-level.
Procrastination
There are two types of procrastination behaviors discussed in the literature, active and passive (Chu and Choi, 2005). Active procrastinators intentionally put off their tasks, preferring to work under pressure. This type of procrastination was measured using the Active Procrastination Scale (Choi and Moran, 2009). Passive procrastinators postpone work due to reasons such as laziness, indecision, or poor prioritization. This type of procrastination was measured using the Aitken Procrastination Scale (Aitken, 1982).
Student engagement
We considered engagement at the course-specific and general levels. Micro engagement refers to a student’s engagement within a specific class, while macro engagement refers to a student’s engagement with the overall school environment (Whitney et al., 2019). Micro engagement was measured using the Scale of Student Engagement in Statistics (SSE-S; Whitney et al., 2019), which includes three subscales of engagement – affective, behavioral, and cognitive. Macro engagement was measured using the Student Engagement in Schools Questionnaire (SESQ; Hart et al., 2011), which also includes three subscales – affective, behavioral, and cognitive. For both types of engagement, a sum score was obtained separately for each of the three subscales. For micro engagement, which was surveyed at three different time points, an average sum score was obtained across the time points for each subscale.
Teacher support
A measure of students’ perception of teacher support was created by taking items from two sources, the Teacher Academic Support Scale of the Classroom Life Instrument (Johnson and Johnson, 1983) and the Experiences with Faculty dimension of the National Survey of Student Engagement (2000). The measure has been previously validated (Ober et al., 2021b).
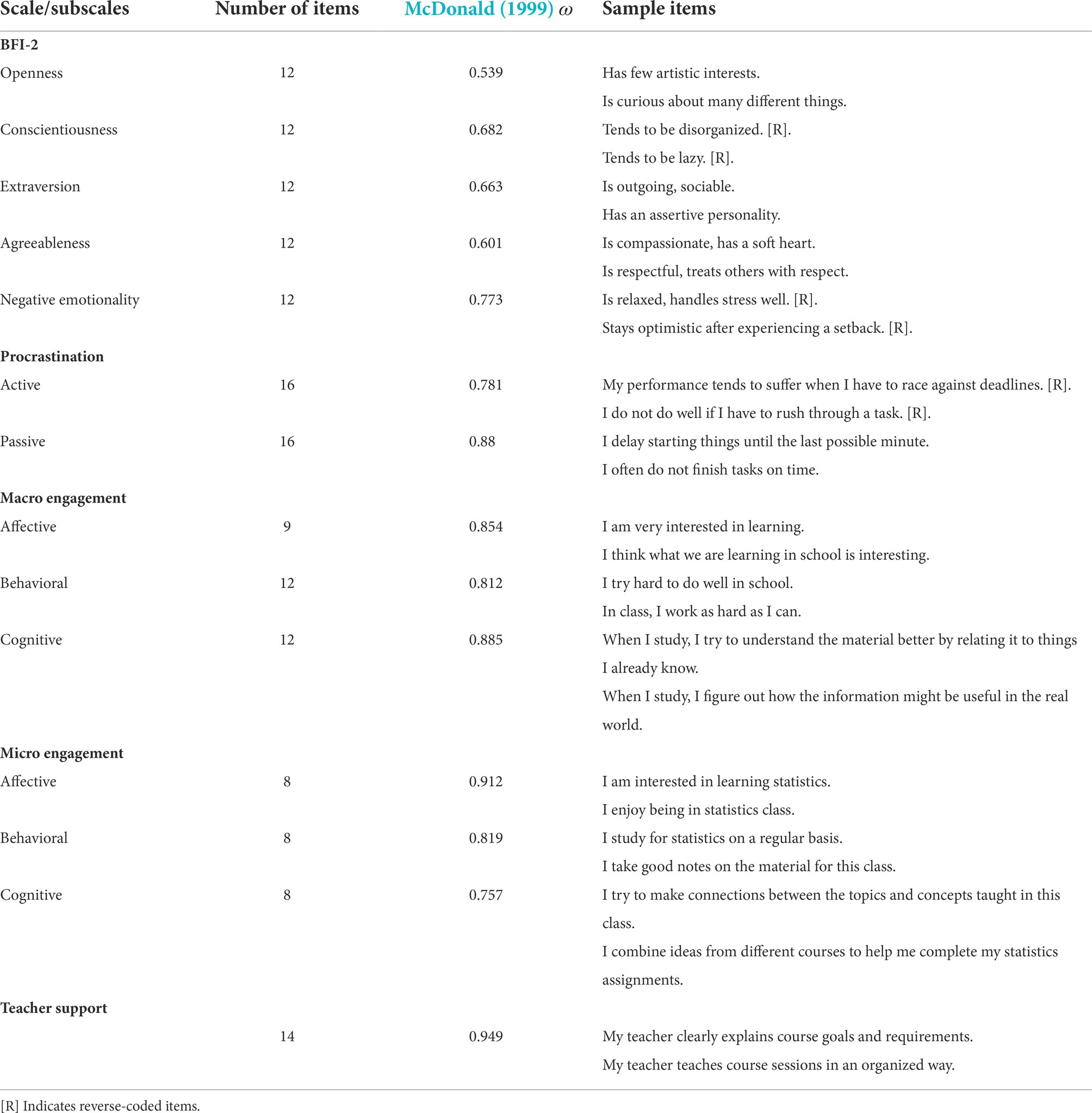
See Table 2 for details on the above self-report scales used, including the number of items, sample items, and reliability estimates of each score.
Mathematics background
We gathered information about students’ math background and interests. Specifically, students were asked for the number of previous math classes they have taken in high school and the reason they are taking AP Statistics.
Self-predicted AP exam scores
Towards the end of the academic year, students were asked whether they plan to take the AP Statistics exam and what they think they will score on the AP Statistics exam, which can be considered an indicator of self-efficacy in statistics.
Achievement measures
At the conclusion of the academic year (i.e., after time point 5 in Figure 1), we collected two measures of student achievement in the AP Statistics course: final class grades (a numerical score from 0 to 100, occasionally exceeding 100 due to extra credit points) and AP exam scores (an integer score from 1 to 5, such that 1 corresponds to ‘no recommendation’ and 5 to ‘extremely well qualified’; Mattern et al., 2009).
Difference score
A measure of differential performance between AP class grades and AP exam scores (“difference score” henceforth) was computed by converting each achievement measure into a percentile rank and then subtracting the class grade percentile rank from the AP exam score percentile rank. Therefore, a positive difference score indicates a student ranking at a higher percentile on the AP exam compared to their class grade, and a negative difference score indicates a student ranking at a higher percentile on the class grade compared to their AP exam score.
Analysis plan
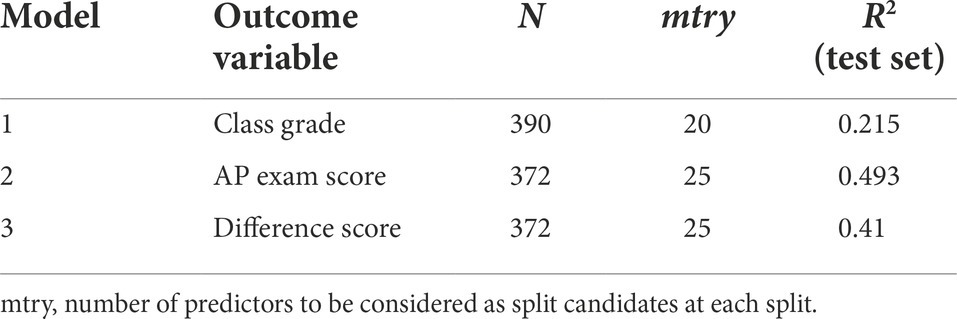
We used random forests to analyze the data. Random forests are a popular machine learning technique that build an ensemble of decision trees. Decision trees are learned by partitioning a predictor space into non-overlapping groups, such that groups are most homogenous (i.e., for continuous outcome variables, minimize the residual sum of squares) with respect to the outcome variable (James et al., 2021). Partitions are made in a top-down approach, meaning the algorithm starts with the whole predictor space, then successively splits the space on a selected predictor and a cut-off value for that predictor. At each split, two new nodes are created. This process is called recursive binary splitting and continues until a stopping criterion is met, such as a threshold for the minimum number of observations in a terminal node. Predicted values are assigned to each observation by taking the average of outcome variable values of the observations in the same terminal node (James et al., 2021). Random forests enhance the performance of single decision trees by growing B decision trees using bootstrapped samples from the data (James et al., 2021). At each split in a single tree, a random sample of mtry predictors, out of all available predictors, is chosen as split candidates. Random subsets of predictors are created in this way to prevent strong predictors from always being selected to split on, which helps to decorrelate and diversify the trees. In doing so, the trees balance out each other’s errors and obtain more accurate predictions as an ensemble. For continuous outcome variables, predictions from all trees are averaged to return one prediction per observation.
We used the randomForest package to implement the analysis in R (Liaw and Wiener, 2002). We built three random forest models in total – one for predicting class grades, one for predicting AP exam scores, and one for predicting difference scores. For each outcome, we trained the model and conducted hyperparameter tuning with a training set (66.67%) and evaluated predictive performance on a test set (33.33%). Each random forest contained B = 500 trees, and each tree was constrained to a minimum of five observations in terminal nodes, which are standard choices (Liaw and Wiener, 2002). Each model was tuned over the hyperparameter mtry, which is the number of predictors to be considered as split candidates at each split. This hyperparameter controls the strength of the randomization in the split selection process and thus plays an important role in random forests’ predictive performance (Bernard et al., 2009). Each forest was tuned across values of mtry from 5, 10, 15, 20, 25, to search for the value resulting in the lowest five-fold cross validation root mean squared error (RMSE) within the training set. Hyperparameters control the learning process and are tuned by the user (e.g., rather than estimated during model fitting) in this way to select a value that optimizes predictive performance. Because this is unique to the learning process of each model, we may obtain different hyperparameter values for each of our three models.
For each model, we examined predictive performance using and predictive features using permutation-based VIMs, ICE, and PD plots. VIMs quantify the impact of each predictor on the outcome variable. For each predictor, the VIM indicates the change in out-of-bag error (measured by the increase in mean squared error for continuous outcome variables) after permuting only that predictor, averaged over the B trees (Liaw and Wiener, 2002). Therefore, a large value indicates greater importance and contribution to the overall prediction. VIMs were scaled to vary between 0 and 100 to ease interpretation. In past research involving educational data mining, a subset of the predictors, such as 5 or 10, are usually examined (Sinharay et al., 2019). To probe the relation between the predictors and outcomes that the models learned, we used ICE and PD plots (Friedman, 2001; Goldstein et al., 2015). ICE plots describe the partial effect of a subset of predictors by displaying how predictions of the outcome change as the predictor changes, given fixed values of all other predictors, per observation. PD plots display the average of all observations’ curves in an ICE plot. Overlaying the PD plot on the ICE plot gives useful clues for both the heterogeneity in the effects among observations, as well as the average partial effect.
Results
Descriptive statistics
Class grades (M = 87.23, SD = 8.74) and AP exam scores (M = 3.73, SD = 1.20) were correlated at 0.57. Once converted to percentile ranks, the correlation was 0.58. This is consistent with other studies that found grades and standardized test scores to correlate in a similar range (Brookhart et al., 2016). Distributions of class grades, AP exam scores, and differences scores (M = 0.00, SD = 26.18) are given in Figure 2.
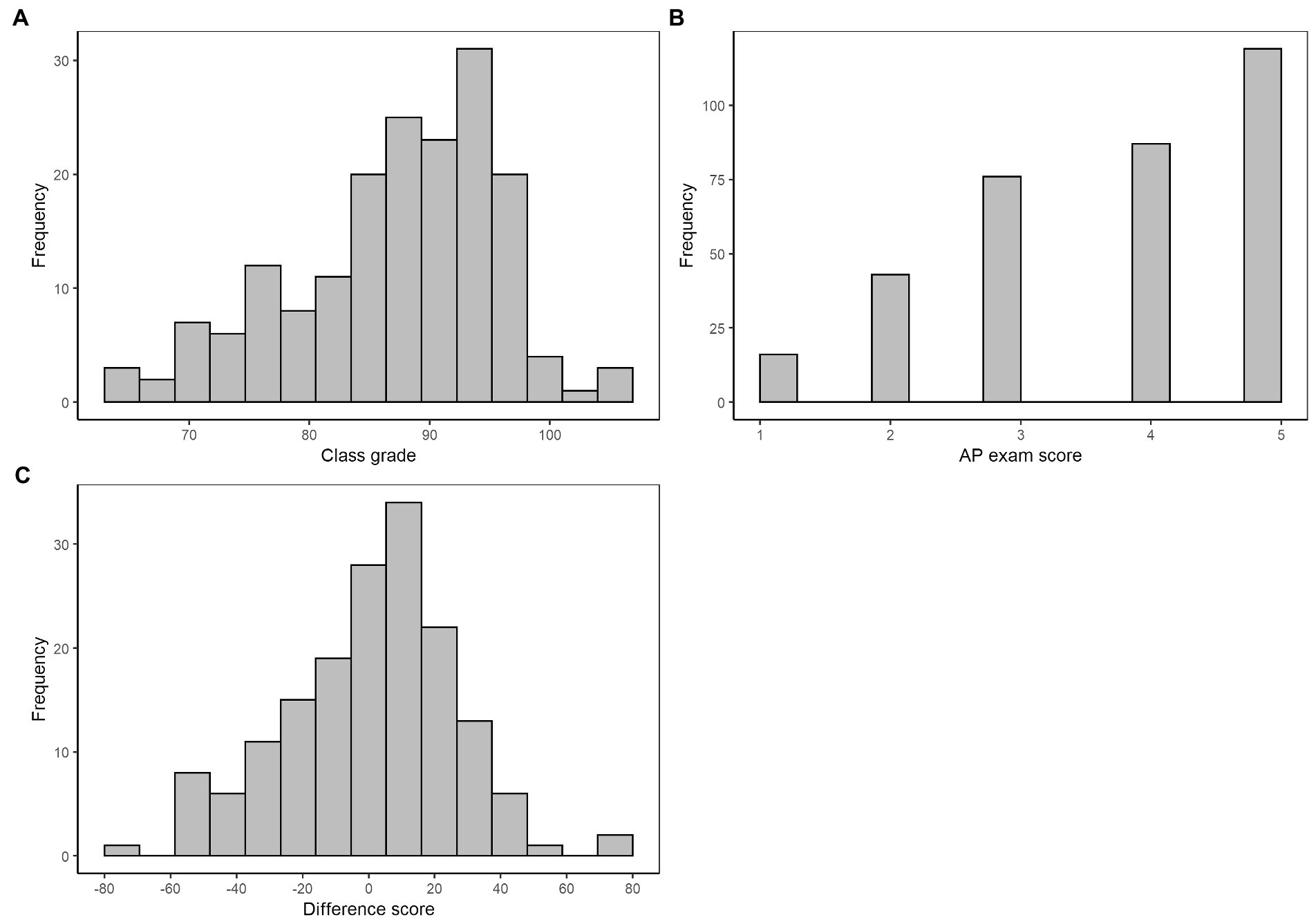
Figure 2. Distributions of class grades (Panel A), AP exam scores (Panel B), and different scores (Panel C).
Pearson correlations between the continuous and binary predictors and the three outcome variables are presented in Table 3. Class grades were most correlated with school type, affective micro engagement, teacher support, and self-predicted AP exam scores, whereas AP exam scores were most correlated with gender, a desire to learn statistics as a reason for taking AP Statistics, conscientiousness, agreeableness, affective micro engagement, active procrastination, and self-predicted AP exam scores. Correlates of difference scores included age, openness, passive procrastination, teacher support, and self-predicted AP exam scores.
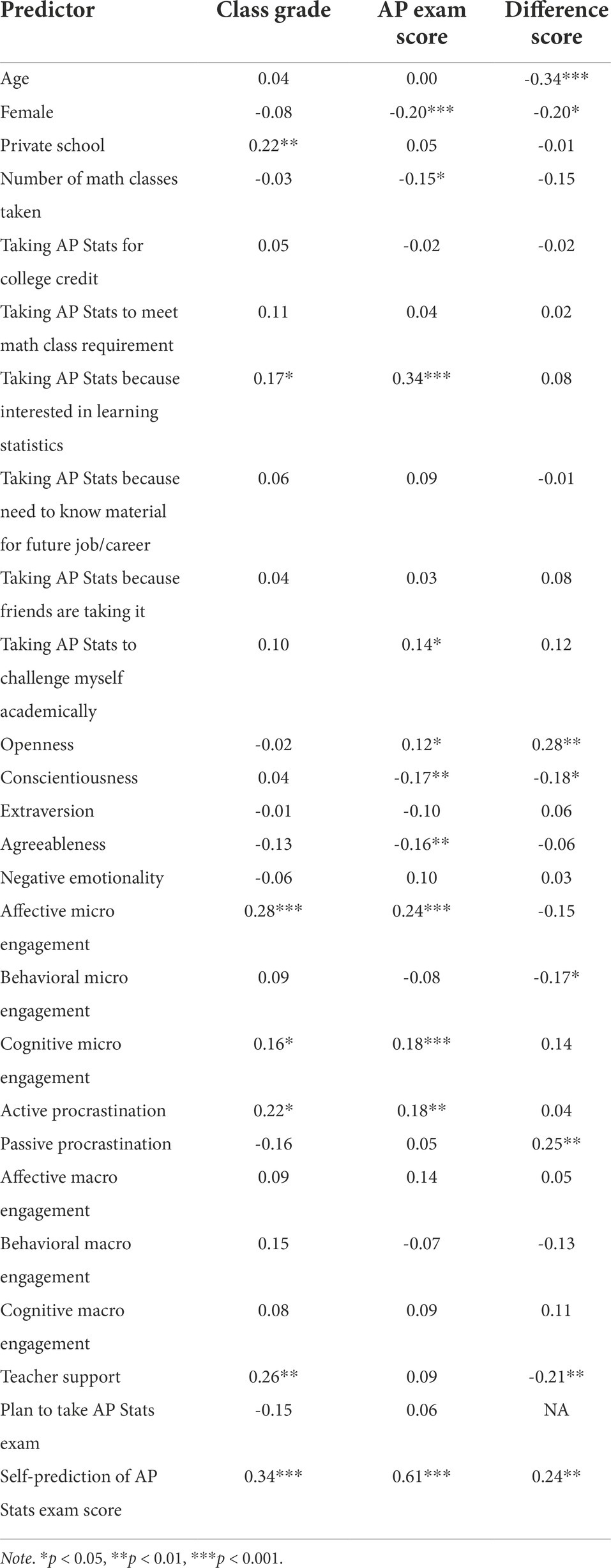
Table 3. Pearson correlations between continuous and binary predictors and the three outcome variables.
Model results
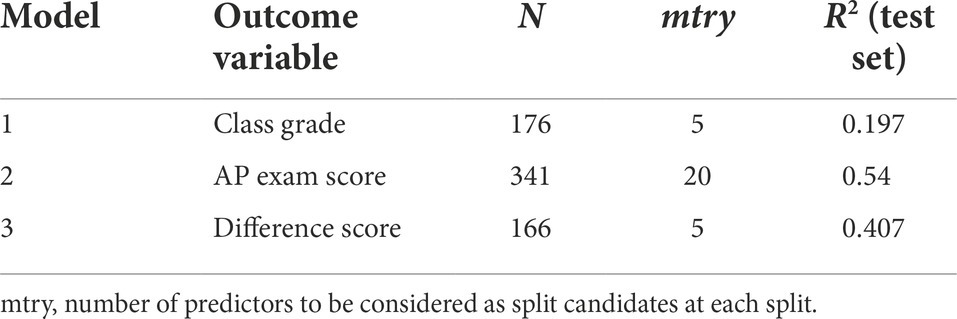
The model results, including sample size, hyperparameter values, and test set performance, of the three random forests predicting class grades, AP exam scores, and difference scores respectively, are presented in Table 4. Each model was trained and tested on a different sample size due to differences in missingness of each outcome variable. Missing predictor data (14.4% missing) were imputed using the R package and function missForest (Stekhoven, 2013), an iterative imputation method based on a random forest (Stekhoven and Buhlmann, 2012). This non-parametric method is particularly useful for mixed-type data and can handle complex interactions and non-linear relations present among predictors (Stekhoven and Buhlmann, 2012). MissForest has also been shown to perform better than other popular imputation methods, including k-nearest neighbor imputation and multivariate imputation by chained equations (MICE; Stekhoven and Buhlmann, 2012). Observations from school A were eliminated from the class grade and difference score models due to unavailability of class grade data from this school. Macro engagement was removed from the analysis due to high missingness (nearly 50%) in student responses from time point 3. This left a total of 29 predictors.
Comparing the R2 values across the three models in Table 4, the AP exam score model had the highest predictive performance, followed by the difference score model, and the class grade model had the poorest performance. This is not surprising, as the AP exam score model was built on the largest sample size, and thus the model had more information from which to learn patterns. Furthermore, the AP exam is a national standardized exam that has undergone many stages of development, calibration, and review by psychometricians. Therefore, we can expect the AP exam score to have stronger validity and reliability across all school. On the other hand, class grades have not gone through the same level of standardization as the AP exam and may contain more measurement error. When variables have a large amount of measurement error, the predictive ability of machine learning models suffers (Jacobucci and Grimm, 2020).
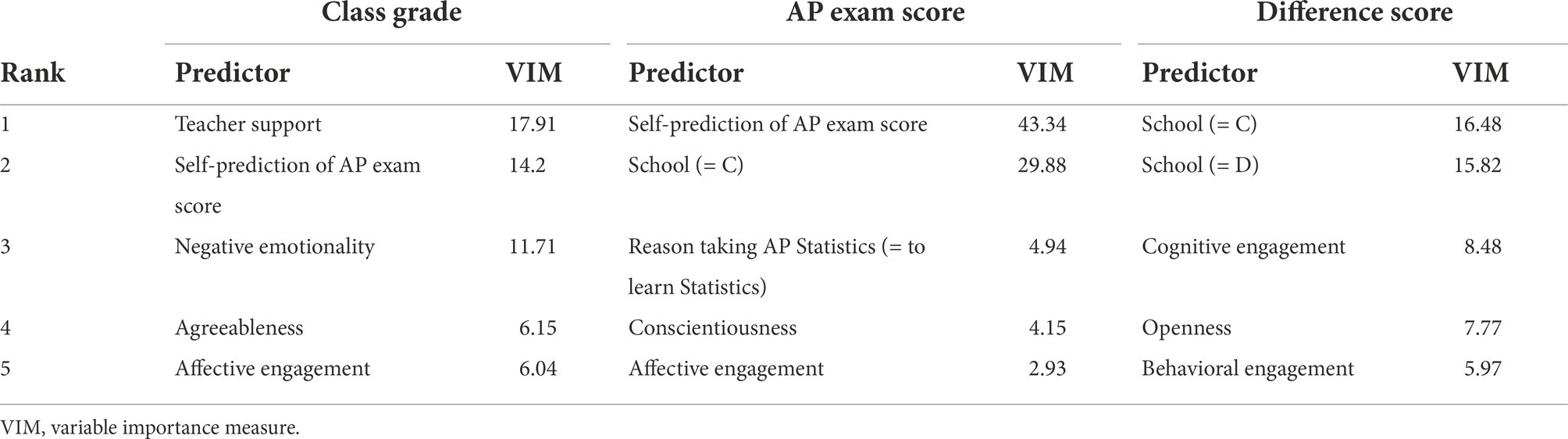
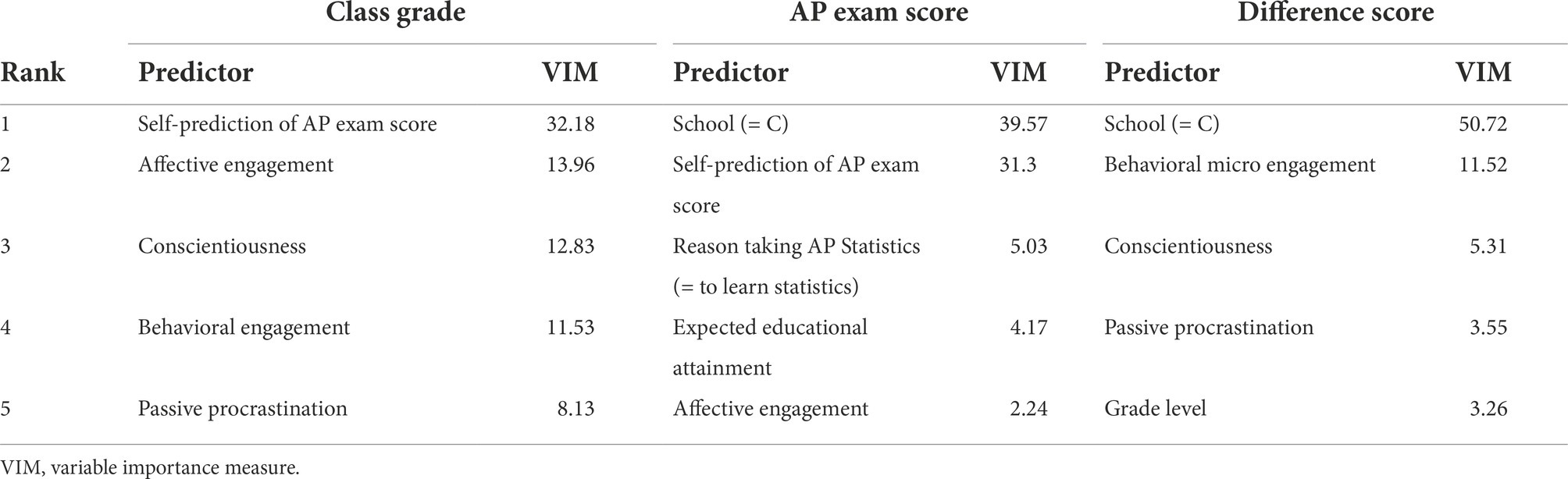
Table 5 presents VIMs from the top five most important predictors from each of the three models. Comparing the top predictors of class grades to those of AP exam scores revealed both similarities and differences. Both models included students’ self-predicted AP exam score as a top predictor, although it had a much higher relative importance in the AP exam score model than in the class grade model. Regardless, this highlights ties of students’ self-efficacy to both student achievement measures. Besides students’ self-predicted AP exam scores, another largely dominant predictor for the AP exam score model was school, highlighting the presence of school-level differences in students’ performance on the AP exam. In contrast, the class grade model did not have any largely dominant predictors and had importance measures that were more evenly split among other student-level predictors, including teacher support and negative emotionality.
Examining the VIMs of the difference score model revealed that the most influential predictors of the differential performance between class grades and AP exam scores included students’ school, engagement, and personality. Figure 3 illustrates the effects of these predictors on predicted difference scores in four ICE plots. To ease comparisons between each observation’s curve in the ICE plots, we centered the predictions at the minimum observed value (left end of plot) of the predictors to generate centered ICE plots (Goldstein et al., 2015). First, the ICE plot for school in Panel A of Figure 3 shows a general trend of lower predicted difference scores associated with school C, meaning higher performance on class grades than AP exam scores, and higher predicted difference scores associated with school D, meaning higher performance on AP exam scores than class grades. Note that school names have been arbitrarily assigned. For engagement, Panel B shows that behavioral engagement does not substantially affect predictions until it reaches above-average levels of engagement, at which point increasing behavioral engagement is associated with lowering predicted difference scores, indicating better performance on class grades relative to AP exam scores. Conversely, predicted difference scores increased with increasing levels of cognitive engagement for most observations, as shown in Panel C, indicating better performance on AP exam scores relative to class grades. Similarly, Panel D shows an increasing trend in predicted difference scores with increasing levels of openness in most observations.
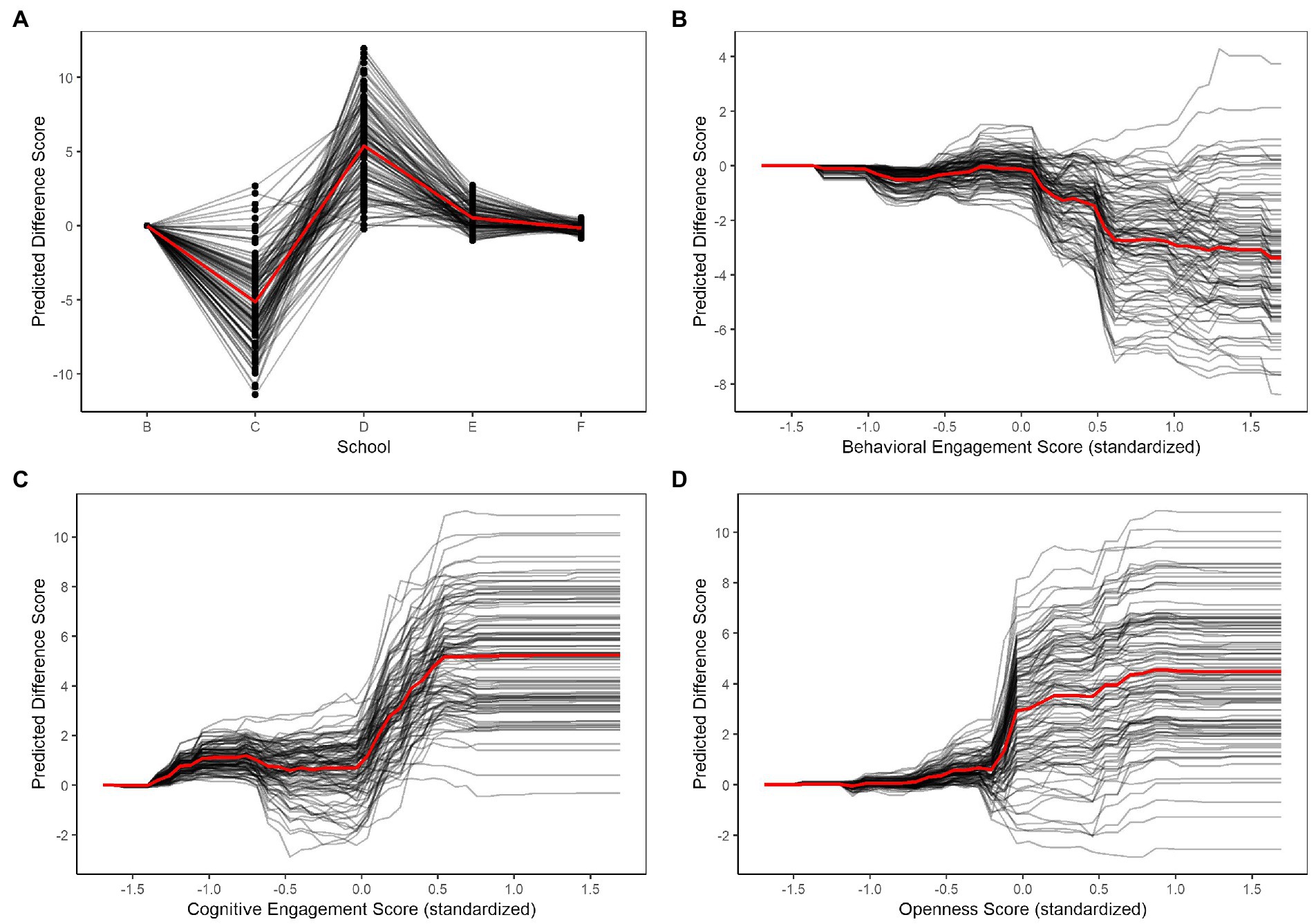
Figure 3. Centered individual conditional expectation (black line) and partial dependence (red line) plots of four important predictors of difference scores: school (Panel A), behavioral engagement (Panel B), cognitive engagement (Panel C), and openness (Panel D).
Replication study
The above analysis was replicated on additional data to investigate whether patterns remain consistent when using a new cohort of students from a similar academic environment. The data was collected in the 2018–2019 academic year from 422 AP Statistics students aged 14–18 (M = 16.80 years, SD = 0.82). These students came from the same six high schools and seven teachers’ classrooms as the data from the main study collected in the 2017–2018 academic year (see Table 6 for sample demographic information for the replication study). The data contains the same predictors and three outcomes as before.
Tables 7, 8 present model results from the replication study. Overall, the analysis on the replication study’s data produced reasonably similar results as the main study. The R2 values across the three models remained similar, with the AP exam score model having the best performance and the class grade model having the worst. As before, predictions of class grades and AP exam scores both relied dominantly on students’ self-predictions of their AP exam performance. Students’ school remained another dominant predictor for the AP exam score model. On the other hand, the class grade model had a different set of important student-level predictors, besides the self-predicted AP exam score, which now included conscientiousness, behavioral engagement, and passive procrastination. Strong predictors of the difference score model included school and behavioral engagement as before, with school C and higher behavioral engagement still being associated with lower predicted difference scores. Other predictors of the difference score model now included conscientiousness and passive procrastination.
Given a few of these differences in important predictors, we caution against over-interpreting the effects of predictors whose importance measures failed to replicate. Regardless, the replication study showed that much of the major findings from the main study can be found when using the next academic year’s data, and most dominant patterns are unchanged across different samples of students in similar academic environments.
Investigating school differences
Given that school C came up as a strong predictor in both analyses, we investigated whether there are any traits that distinguish school C from the others by comparing the breakdown of demographic variables across the six schools using the main study’s data. In general, school C had a more diverse demographic composition of students. For example, school C had a larger proportion of students who are eligible for free or reduced-price lunch programs (17.86%), whereas some other schools had none (average 8.52% for other schools). School C also had the largest proportion of multiracial students (12.50%) and a smaller proportion of white students (46.43%) compared to the other schools (average 5.23 and 63.04%, respectively). While most schools’ responses to parental education were dominated by a bachelor’s, master’s, or doctoral degree, school C’s responses were more evenly split among other responses, such as high school diploma or “did not finish high school” (23.21% for school C compared to average 4.25% for other schools). A similar observation can be made for students’ expected education and the proportion of students who answered ‘high school diploma’ (3.57% for school C compared to average 0.83% for other schools). From these observations, it appears that school C contains a more diverse student body in terms of race/ethnicity, socio-economic status, and students’ visions for their education.
Discussion
Teacher-assigned grades and standardized test scores continue to be studied as key measures of student achievement and are each employed in various high-stakes decisions in the educational system (Brennan et al., 2001). This study examined differences between these two measures in the context of an AP Statistics course. Specifically, we used machine learning to explore students’ personal and contextual characteristics as predictors of AP class grades, AP exam scores, and differential performance between the two, as defined by a difference score indicating the difference in percentile ranks. We additionally replicated the analysis on data from the following academic year.
Students’ self-predictions of their AP exam performance predicted both class grades and AP exam scores in both the main and replication studies. This provides some evidence of consistency between the two as measures of achievement in the AP Statistics course. However, compared to the AP exam score model, the class grade model had poorer predictive performance with less consistent model interpretation results between the main and replication studies. Whereas the AP exam score model had a small number of strong predictors, the class grade model had a larger number of moderate predictors, including personality and engagement characteristics. This is not surprising, based on past studies that have spoken to the multidimensionality of grades compared to standardized test scores (Bowers, 2011; Brookhart et al., 2016).
The difference score model revealed several possible contributors to the differential performance between class grades and AP exam scores. As a contextual characteristic, students’ school was a strong predictor of difference scores in both the main and replication studies. In particular, we observed that a school may collectively produce higher percentile ranks in class grades compared to AP exam scores, as school C in our study did. One explanation for this could be that a school has standards for coursework performance that differs from the national standards of the AP exam performance, and thus its students’ class grades may appear inflated relative to their AP exam scores. A related explanation is that a school lacks critical resources for its students to perform on par with the national pool of AP students in other schools. While the availability of AP coursework has expanded in less-resourced schools in recent years (Malkus, 2016), there are challenges in effectively implementing AP courses across all schools, such as variability in students’ prior exposure to inquiry-based learning as demanded in AP courses (Long et al., 2019) or qualified teachers (Burton et al., 2002). As resources often differ between schools, this presents an equity concern towards the use of AP exam scores in high-stakes decisions.
Personal characteristics also surfaced as important predictors of differential performance. In both the main and replication studies, students’ effort, attention, and participation in class, as measured by a high behavioral engagement score, predicted a higher class grade performance relative to AP exam performance. This is consistent with past literature that have found student engagement levels to account for discrepancy between grades and other standardized test scores (Willingham et al., 2002). There are several possible explanations for this. Math performance of students who have the capacity for success are more likely to be negatively affected by stressful or high-stakes situations (Beilock, 2008). In the context of our study, this means students with high behavioral engagement put in a great deal of effort into coursework and thus likely have high class grades and capacity for success. However, due to the anxiety associated with high-stakes assessments, they may not be able to perform as optimally on the AP exam. Another explanation could be that the effort put into certain aspects of obtaining a higher class grade that are not entirely relevant to the AP exam may be distracting from obtaining a higher AP exam score, as the nature of coursework and the AP exam differ. For example, a student who puts in hours working on homework problems for a higher class grade may forget that the AP exam is timed and that self-pacing is important (Osgood et al., 2017).
It is interesting to note that we did not find personality traits, particularly conscientiousness and openness, to be consistently strong predictors of AP exam scores and class grades. While multiple studies have found conscientiousness to be predictive of grades and openness to be predictive of standardized test scores (Noftle and Robins, 2007; Spengler et al., 2013; Meyer et al., 2019), there are possible explanations for why we did not consistently observe these findings in our main and replication studies. First, the tie between openness and standardized test scores due to standardized tests invoking a desire to explore and investigate new testing formats (Hübner et al., 2022) does not apply to AP exams. This is because the AP curriculum is designed to prepare students for the year-end AP exam, such that students are repeatedly exposed to the types of problems that are anticipated on the AP exam throughout the AP course (Chu, 2000). This distinguishes AP exams from other standardized tests which may have lower instructional sensitivity and curricular validity (Hübner et al., 2022). Second, we incorporated many more predictors into our models than other studies have considered, using a data-driven, machine learning approach. Given that we examined VIMs, which are compared relative to other predictors in the models, it is possible that in the presence of the other predictors, such as self-predicted AP exam scores and teacher support, these personality traits did not contribute as much to the prediction of our outcome variables.
Implications
The implications of our study findings are two-fold. First, from an equity and policy perspective, an exclusive focus on AP exam scores for evaluating achievement in AP courses for high-stakes decisions, such as college admissions, may adversely impact students in less resourced schools, which often include underrepresented minority students. Other studies have come to similar conclusions in non-AP contexts. For example, Brennan et al. (2001) cautioned against sole reliance on standardized test scores to determine educational outcomes after examining the relative equitability of test scores from the eighth-grade Massachusetts Comprehensive Assessment System to teacher-assigned grades. Geiser and Santelices (2007) also found SAT scores to correlate more with students’ socioeconomic factors compared to high school GPA and further found high school GPA to be more predictive of various college outcomes than SAT scores. However, this does not mean that an exclusive focus on AP class grades will be more fair or equitable. Grades are often viewed as being less reliable and less consistent compared to standardized test scores, as they depend on subjective judgments of teachers as well as the average ability level of other students in the class, which will also differ by school (Calsamiglia and Loviglio, 2019). Common grading practices, such as “grading on the curve” can also be problematic for making important placement decisions based on grades (Bergold et al., 2022) and additionally pose equity concerns (Bowen and Cooper, 2021). These considerations highlight the complementary strengths and limitations of both grades and standardized test scores as high-stakes measures (Brennan et al., 2001; Willingham et al., 2002), and findings from this study suggest that these nuances are relevant in an AP context as well. As such, decision makers may benefit from the consideration of both AP exam scores and AP class grades for a more holistic view of student achievement in AP courses. This should also be combined with efforts to provide more resources to schools in disadvantaged communities in order to address disparities in learning environments that give rise to equity concerns of these achievement measures in the first place.
Second, from a pedagogical perspective, this study may provide insight for students and educators in preparation for AP exams to obtain desired outcomes. In particular, we warn of the possibility that high coursework performance throughout the academic year may not guarantee or translate to high AP exam scores, depending on study habits or other behavioral characteristics such as test anxiety. Findings from the study highlight that the ways in which a student interacts with course material may sometimes differ from what is needed to perform optimally on a national, high-stakes assessment like the AP exam. Further, while our current study is retrospective, we envision possible future work that could build upon the predictive modeling nature of this study employing machine learning techniques. This could involve early detection and intervention for students who may be improperly preparing for the AP exam, given their behavioral engagement in the AP coursework throughout the year.
Limitations
There are several limitations associated with this study. First, as the number of students sampled from each school were uneven, it is likely that schools with larger sample sizes had a stronger influence on our models than schools with smaller sample sizes. This is not ideal, given that different schools contribute different characteristics (e.g., public or private, sociodemographic composition of students), all of which may not have been adequately represented in our sample. We also worked with a relatively small number of schools, with an appreciable amount of missing outcome data that led to small sample sizes. Given that we applied machine learning, which are typically used on much larger datasets, our sample sizes may not have been nearly large enough for the random forest models to stably learn and detect reliable patterns in the data (Yarkoni and Westfall, 2017). Other problems with our data included the low scale reliability for the Big Five Inventory-2, particularly the openness domain (see Ober et al., 2021a). Nevertheless, we aimed to counteract these limitations by replicating our analyses on an additional dataset to examine the consistency of our findings.
We also made some analytical choices throughout the study which could have impacted our results. For example, we only used a single machine learning algorithm for our analyses. While we chose random forests given their ease of interpretation, flexibility, and applicability, many other machine learning algorithms exist (e.g., support vector machines, gradient boosting), which could have led to better predictive performance. We further made several analytical choices within the random forest models, such as the use of permutation-based VIMs, which largely guided our interpretations of the model results. Other forms of VIMs are available, such as those that measure the total decrease in node impurities (measured by residual sum of squares for continuous outcome variables) from splitting on the predictor, averaged over all the trees in the forest (Liaw and Wiener, 2002). However, this form of VIMs is known to be biased, and permutation-based VIMs are generally preferred (Loecher, 2022). Future studies should work with larger sample sizes and examine whether similar findings are found when using other machine learning techniques and interpretation tools.
We further cannot conclude that the findings from this study are applicable to other subjects besides AP Statistics or that they are representative of the entire AP program. As different AP subjects require different skills and have varying student demographics, additional studies should confirm similarities or differences across findings in other AP participants and subject areas. Further, an inherent limitation with studying achievement in an AP context is sample selection bias. The fact that our study’s sample of AP Statistics students attend a school that offers the AP program, chose to enroll in the AP course, and took the AP exam at the end of the academic year may already be an indication of a certain level of achievement, thus reducing the amount of variability in our sample. Future studies in this line of work should focus on sampling from schools with diverse sociodemographic backgrounds with conceivably different levels of achievement to obtain more variability and representability of the general population.
Conclusion
In this study, we sought to compare the personal and contextual characteristics that predict class grades vs. standardized test scores in an AP context, and to subsequently examine variables that explain differential performance between the two. The application of machine learning provided exploratory findings into possible sources of differential performance between grades and AP exam scores in an AP Statistics course, including students’ school and engagement. Given the persisting prominence of the AP program in US high schools and its continued role in high-stakes decisions such as college admissions, this study contributes important knowledge into the relationship between grades and standardized test scores – two essential, ubiquitous, and complementary measures of student achievement.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
The studies involving human participants were reviewed and approved by University of Notre Dame Institutional Review Board. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.
Author contributions
YC and MH: study conception and design. YC: data collection and funding acquisition. HS, MH, and TO: analysis and interpretation of results, and draft manuscript preparation. All authors reviewed the results and approved the final version of the manuscript.
Funding
This project is supported by the National Science Foundation grant DRL-1350787 awarded to YC.
Acknowledgments
We would like to thank the high school teachers and students who participated in this project, as well as other members of the Learning Analytics and Measurement in Behavioral Sciences (LAMBS) Lab.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aitken, M. E. (1982). A Personality Profile Of The College Student Procrastinator (Order No. 8218139). Available from ProQuest Dissertations & Theses Global. (303242158). Available at: https://www.proquest.com/dissertations-theses/personality-profile-college-student/docview/303242158/se-2
Beilock, S. L. (2008). Math performance in stressful situations. Curr. Dir. Psychol. Sci. 17, 339–343. doi: 10.1111/j.1467-8721.2008.00602.x
Bergold, S., Weidinger, A. F., and Steinmayr, R. (2022). The “big fish” from the teacher’s perspective: a closer look at reference group effects on teacher judgments. J. Educ. Psychol. 114, 656–680. doi: 10.1037/edu0000559
Bernard, S., Heutte, L., and Adam, S. (2009). “Influence of hyperparameters on random forest accuracy” in Multiple Classifier Systems. MCS 2009. Lecture Notes in Computer Science. Vol. 59. eds. J. A. Benediktsson, J. Kittler, and F. Roli (Berlin, Heidelberg: Springer), 171–180.
Borghans, L., Golsteyn, B. H. H., Heckman, J. J., and Humphries, J. E. (2016). What grades and achievement tests measure. Proc. Natl. Acad. Sci. U. S. A. 113, 13354–13359. doi: 10.1073/pnas.1601135113
Bowen, R. S., and Cooper, M. M. (2021). Grading on a curve as a systemic issue of equity in chemistry education. J. Chem. Educ. 99, 185–194. doi: 10.1021/acs.jchemed.1c00369
Bowers, A. J. (2011). What's in a grade? The multidimensional nature of what teacher-assigned grades assess in high school. Educ. Res. Eval. 17, 141–159. doi: 10.1080/13803611.2011.597112
Brennan, R., Kim, J., Wenz-Gross, M., and Siperstein, G. (2001). The relative equitability of high-stakes testing versus teacher-assigned grades: an analysis of the Massachusetts comprehensive assessment system (MCAS). Harv. Educ. Rev. 71, 173–217. doi: 10.17763/haer.71.2.v51n6503372t4578
Brookhart, S. M. (1994). Teachers’ grading: practice and theory. Appl. Meas. Educ. 7, 279–301. doi: 10.1207/s15324818ame0704_2
Brookhart, S. M. (2015). Graded achievement, tested achievement, and validity. Educ. Assess. 20, 268–296. doi: 10.1080/10627197.2015.1093928
Brookhart, S. M., Guskey, T. R., Bowers, A. J., McMillan, J. H., Smith, J. K., Smith, L. F., et al. (2016). A century of grading research: meaning and value in the most common educational measure. Rev. Educ. Res. 86, 803–848. doi: 10.3102/0034654316672069
Burton, N. W., Whitman, N. B., Yepes-Baraya, M., Cline, F., and Kim, R. (2002). Minority student success: the role of teachers in advanced placement program® (AP®) courses. ETS Res. Rep. Series 2002, i–81. doi: 10.1002/j.2333-8504.2002.tb01884.x
Calsamiglia, C., and Loviglio, A. (2019). Grading on a curve: when having good peers is not good. Econ. Educ. Rev. 73:101916. doi: 10.1016/j.econedurev.2019.101916
Choi, J. N., and Moran, S. V. (2009). Why not procrastinate? Development and validation of a new active procrastination scale. J. Soc. Psychol. 149, 195–212. doi: 10.3200/socp.149.2.195-212
Chu, J. M. (2000). Preparing for the AP exam: the dangers of teaching to the test. Hist. Teach. 33, 511–520. doi: 10.2307/494947
Chu, A., and Choi, J. N. (2005). Rethinking procrastination: positive effects of “active” procrastination behavior on attitudes and performance. J. Soc. Psychol. 145, 245–264. doi: 10.3200/socp.145.3.245-264
College Board (2018). Program Summary Report. Available at: https://secure-media.collegeboard.org/digitalServices/pdf/research/2018/Program-Summary-Report-2018.pdf (Accessed October 23, 2022).
College Board (2019). Student Participation and Performance in Advanced Placement Rise in Tandem. Available at: https://www.collegeboard.org/releases/2018/student-participation-and-performance-in-ap-rise-in-tandem (Accessed October 23, 2022).
Duckworth, A., Quinn, P., and Tsukayama, E. (2012). What no child left behind leaves behind: the roles of IQ and self-control in predicting standardized achievement test scores and report card grades. J. Educ. Psychol. 104, 439–451. doi: 10.1037/a0026280
Ewing, M. (2006). The AP Program and Student Outcomes: A Summary of Research. College Board Research Report, No. RN-29. New York: The College Board. Available at: https://files.eric.ed.gov/fulltext/ED561027.pdf
Friedman, J. H. (2001). Greedy function approximation: a gradient boosting machine. Ann. Stat. 29, 1189–1232. doi: 10.1214/aos/1013203451
Furnham, A., Nuygards, S., and Chamorro-Premuzic, T. (2013). Personality, assessment methods and academic performance. Instr. Sci. 41, 975–987. doi: 10.1007/s11251-012-9259-9
Galyon, C. E., Blondin, C. A., Yaw, J. S., Nalls, M. L., and Williams, R. L. (2012). The relationship of academic self-efficacy to class participation and exam performance. Soc. Psychol. Educ. 15, 233–249. doi: 10.1007/s11218-011-9175-x
Geiser, S., and Santelices, M. V. (2007). Validity of High-School Grades in Predicting Student Success beyond the Freshman Year: High-School Record vs. Standardized Tests as Indicators of Four-Year College Outcomes. Research & Occasional Paper Series: CSHE. 6.07. Center for Studies in Higher Education Center for Studies in Higher Education at the University of California, Berkeley. Research & Occasional Paper Series: CSHE.6.07. Available at: https://files.eric.ed.gov/fulltext/ED502858.pdf
Goldstein, A., Kapelner, A., Bleich, J., and Pitkin, E. (2015). Peeking inside the black box: visualizing statistical learning with plots of individual conditional expectation. J. Comput. Graph. Stat. 24, 44–65. doi: 10.1080/10618600.2014.907095
Haladyna, T. M., and Downing, S. M. (2004). Construct-irrelevant variance in high-stakes testing. Educ. Meas. Issues Pract. 23, 17–27. doi: 10.1111/j.1745-3992.2004.tb00149.x
Hart, S. R., Stewart, K., and Jimerson, S. R. (2011). The student engagement in schools questionnaire (SESQ) and the teacher engagement report form-new (TERF-N): examining the preliminary evidence. Contemp. Sch. Psychol. 15, 67–79. doi: 10.1007/BF03340964
Hofer, M., Kuhnle, C., Kilian, B., and Fries, S. (2012). Cognitive ability and personality variables as predictors of school grades and test scores in adolescents. Learn. Instr. 22, 368–375. doi: 10.1016/j.learninstruc.2012.02.003
Hübner, N., Spengler, M., Nagengast, B., Borghans, L., Schils, T., and Trautwein, U. (2022). When academic achievement (also) reflects personality: using the personality-achievement saturation hypothesis (PASH) to explain differential associations between achievement measures and personality traits. J. Educ. Psychol. 114, 326–345. doi: 10.1037/edu0000571
Jacobucci, R., and Grimm, K. J. (2020). Machine learning and psychological research: the unexplored effect of measurement. Perspect. Psychol. Sci. 15, 809–816. doi: 10.1177/1745691620902467
James, G., Witten, D., Hastie, T., and Tibshirani, R. (2017). “Tree-Based Methods”, in An Introduction to Statistical Learning. Springer Texts in Statistics. Springer, New York, NY.
Johnson, D. W., and Johnson, R. (1983). Social interdependence and perceived academic and personal support in the classroom. J. Soc. Psychol. 120, 77–82. doi: 10.1080/00224545.1983.9712012
Jones, Z., and Linder, F. (2015). Exploratory Data Analysis Using Random Forests. In Prepared for the 73rd Annual MPSA Conference.
Klem, A. M., and Connell, J. P. (2004). Relationships matter: linking teacher support to student engagement and achievement. J. Sch. Health 74, 262–273. doi: 10.1111/j.1746-1561.2004.tb08283.x
Kobrin, J. L., Camara, W. J., and Milewski, G. B. (2002). Students with Discrepant High School GPA and SAT® I Scores. College Board Research Report, No. RN-15. New York: The College Board. Available at: https://files.eric.ed.gov/fulltext/ED562878.pdf
Lechner, C., Danner, D., Rammstedt, B., and Rammstedt, B. (2017). How is personality related to intelligence and achievement? A replication and extension of Borghans et al. and Salkever. Personal. Individ. Differ. 111, 86–91. doi: 10.1016/j.paid.2017.01.040
Lei, H., Cui, Y., and Zhou, W. (2018). Relationships between student engagement and academic achievement: a meta-analysis. Soc. Behav. Personal. Int. J. 46, 517–528. doi: 10.2224/sbp.7054
Loecher, M. (2022). Unbiased variable importance for random forests. Commun. Stat. Theory Methods 51, 1413–1425. doi: 10.1080/03610926.2020.1764042
Long, M. C., Conger, D., and McGhee, R. (2019). Life on the frontier of AP expansion: can schools in less-resourced communities successfully implement advanced placement science courses? Educ. Res. 48, 356–368. doi: 10.3102/0013189x19859593
Malkus, N. (2016). AP at Scale: Public School Students in Advanced Placement, 1990-2013. AEI Paper & Studies. Available at: https://www.aei.org/research-products/report/ap-at-scale-public-school-students-in-advanced-placement-1990-2013/ (Accessed October 23, 2022).
Mattern, K. D., Shaw, E. J., and Xiong, X. (2009). The Relationship between AP® Exam Performance and College Outcomes. College Board Research Report, No. 2009-4. New York: The College Board. Available at: https://files.eric.ed.gov/fulltext/ED561021.pdf
McMillan, J. H. (2001). Secondary teachers’ classroom assessment and grading practices. Educ. Meas. Issues Pract. 20, 20–32. doi: 10.1111/j.1745-3992.2001.tb00055.x
Meyer, J., Fleckenstein, J., Retelsdorf, J., and Köller, O. (2019). The relationship of personality traits and different measures of domain-specific achievement in upper secondary education. Learn. Individ. Differ. 69, 45–59. doi: 10.1016/j.lindif.2018.11.005
Morris, P., and Fritz, C. (2015). Conscientiousness and procrastination predict academic coursework marks rather than examination performance. Learn. Individ. Differ. 39, 193–198. doi: 10.1016/j.lindif.2015.03.007
National Survey of Student Engagement (2000). The NSSE Report: National Benchmarks of Effective Educational Practice. Bloomington, IN: Indiana University Center for Postsecondary Research and Planning.
Noftle, E. E., and Robins, R. W. (2007). Personality predictors of academic outcomes: big five correlates of GPA and SAT scores. J. Pers. Soc. Psychol. 93, 116–130. doi: 10.1037/0022-3514.93.1.116
Ober, T. M., Cheng, Y., Jacobucci, R., and Whitney, B. M. (2021a). Examining the factor structure of the big five Inventory-2 personality domains with an adolescent sample. Psychol. Assess. 33, 14–28. doi: 10.1037/pas0000962
Ober, T. M., Coggins, M. R., Rebouças-Ju, D., Suzuki, H., and Cheng, Y. (2021b). Effect of teacher support on students’ math attitudes: measurement invariance and moderation of students' background characteristics. Contemp. Educ. Psychol. 66:101988. doi: 10.1016/j.cedpsych.2021.101988
Osgood, J., McNally, O., and Talerico, G. (2017). The personality of a “good test taker”: self-control and mindfulness predict good time-management when taking exams. Int. J. Psychol. Educ. Stud. 4, 12–21. doi: 10.17220/ijpes.2017.03.002
Pattison, E., Grodsky, E., and Muller, C. (2013). Is the sky falling? Grade inflation and the signaling power of grades. Educ. Res. 42, 259–265. doi: 10.3102/0013189X13481382
Pellegrino, C. (2022). Test-optional policies: implementation impact on undergraduate admissions and enrollment. Coll. Univ. 97:4-6, 8-10, 12-19.
Richardson, J. (2015). Coursework versus examinations in end-of-module assessment: a literature review. Assess. Eval. High. Educ. 40, 439–455. doi: 10.1080/02602938.2014.919628
Sadler, P. M., and Tai, R. H. (2007). Accounting for advanced high school coursework in college admission decisions. Coll. Univ. 82, 7–14.
Sahin, M., and Yurdugül, H. (2020). Educational data mining and learning analytics: past, present and future. Bartin Üniversitesi Egitim Fakültesi Dergisi 9, 121–131. doi: 10.14686/buefad.606077
Shaw, E. J., Marini, J. P., and Mattern, K. D. (2013). Exploring the utility of advanced placement participation and performance in college admission decisions. Educ. Psychol. Meas. 73, 229–253. doi: 10.1177/0013164412454291
Sinharay, S., Zhang, M., and Deane, P. (2019). Prediction of essay scores from writing process and product features using data mining methods. Appl. Meas. Educ. 32, 116–137. doi: 10.1080/08957347.2019.1577245
Soto, C. J., and John, O. P. (2017). The next big five inventory (BFI-2): developing and assessing a hierarchical model with 15 facets to enhance bandwidth, fidelity, and predictive power. J. Pers. Soc. Psychol. 113, 117–143. doi: 10.1037/pspp0000096
Spengler, M., Lüdtke, O., Martin, R., and Brunner, M. (2013). Personality is related to educational outcomes in late adolescence: evidence from two large-scale achievement studies. J. Res. Pers. 47, 613–625. doi: 10.1016/j.jrp.2013.05.008
Stekhoven, D. J. (2013). missForest: Nonparametric Missing Value Imputation Using Random Forest. R package version 1.4. Available at: https://cran.r-project.org/web/packages/missForest/missForest.pdf
Stekhoven, D. J., and Buhlmann, P. (2012). MissForest—non-parametric missing value imputation for mixed-type data. Bioinformatics 28, 112–118. doi: 10.1093/bioinformatics/btr597
Whitney, B. M., Cheng, Y., Broderson, A. S., and Hong, M. R. (2019). The scale of student engagement in statistics: development and initial validation. J. Psychoeduc. Assess. 37, 553–565. doi: 10.1177/0734282918769983
Willingham, W. W., Pollack, J. M., and Lewis, C. (2002). Grades and test scores: accounting for observed differences. J. Educ. Meas. 39, 1–37. doi: 10.1111/j.1745-3984.2002.tb01133.x
Keywords: grades, standardized test scores, advanced placement, random forest, achievement measures, machine learning, replication
Citation: Suzuki H, Hong M, Ober T and Cheng Y (2022) Prediction of differential performance between advanced placement exam scores and class grades using machine learning. Front. Educ. 7:1007779. doi: 10.3389/feduc.2022.1007779
Edited by:
Xiaoming Zhai, University of Georgia, United StatesReviewed by:
Wenchao Ma, University of Alabama, United StatesJennifer Meyer, University of Kiel, Germany
Copyright © 2022 Suzuki, Hong, Ober and Cheng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ying Cheng, eWNoZW5nNEBuZC5lZHU=
 Honoka Suzuki
Honoka Suzuki Maxwell Hong2
Maxwell Hong2 Teresa Ober
Teresa Ober Ying Cheng
Ying Cheng