- 1Institute for Educational Evaluation, Associated Institute at the University of Zurich, Zurich, Switzerland
- 2Institute of Education, University of Zurich, Zurich, Switzerland
Complementing widely used explanatory models in the educational sciences that pinpoint the resources and characteristics for explaining students’ distinct educational transitions, this paper departs from methodological traditions and evaluates the predictive power of established concepts: to what extent can we actually predict school track enrollment based on a plethora of well-known explanatory factors derived from previous research? Predictive models were established using recursive partitioning adopted from machine learning. The basis for the analyses was the unique Zurich Learning Progress Study in Switzerland, a longitudinal study that followed a sample of 2000 students throughout compulsory education. This paper presents an exemplary examination of predictive modeling, and encourages educational sciences in general to explore beyond the horizon of their disciplinary methodological standards, which may help to consider the limits of an exclusive focus on explanatory approaches. The results provide an insight into the predictive capacity of well-established educational measures and concepts in predicting school track enrollment. The results show that there is quite a bit we cannot explain in educational navigation at the very end of elementary education. Yet, predictive misclassifications mainly occur between adjacent school tracks. Very few misclassifications in the future enrollment of academic-track and basic-track students, i.e., those pursuing the most- and least-prestigious tracks, respectively, occur.
1 Introduction
Historical and current practice in the educational sciences has relied considerably on explanatory modeling (Hofman et al., 2017; Yarkoni and Westfall, 2017). In the field of research on educational outcomes, this has resulted in the search for a plethora of predictors that help to explain child development (Bradley and Corwyn, 2002), students’ educational transitions and navigations (Barone, 2011; Billingham and Hunt, 2016; Doren and Grodsky, 2016; Dumont et al., 2019), or inequalities in learning progress at the institutional and the neighborhood level (Coleman, 1968; Rumberger and Palardy, 2005; Aikens and Barbarin, 2008; Ewijk and Sleegers, 2010). The research approaches are often deductive. In a theory-driven and hypothesis-testing way, explanatory relationships between enforcing and attenuating factors in educational processes and outcomes are investigated. On this basis, an elaborate understanding of moderating and mediating relationships explaining educational outcomes is built. These studies provide highly valuable insights into the interactions and mechanisms underlying disparate educational pathways. The explanatory power of predictors is depicted by the use of standardized measures (such as effect sizes, Cohen, 1988) or the proportion of variance explained (Lewis-Beck, 1980). However, how accurately explanatory concepts can actually predict educational outcomes is rarely considered. One possible reason for this omission is that predictive modeling is not in the standard methodological toolbox of educational science research. Furthermore, predictive approaches are considered an atheoretical and purely data-driven approach to knowledge generation. The strength of explanatory modeling in providing in-depth insight into underlying mechanisms is considered the downside of models set up for purely predictive purposes, where such mechanisms are treated as a “black-box” (Strobl et al., 2009b). In contrast, explanatory approaches are not concerned with the predictive capacity of the modeled concepts. Hence, the almost exclusive methodological restriction and narrowing in favor of explaining empirical observations can result in the establishment and preservation of theoretically elegant explanatory models and concepts, which may nonetheless have very limited capacity to predict actual human behavior and outcomes (Hofman et al., 2017; Yarkoni and Westfall, 2017); or at least, the preservation of theories and concepts for which we have no baseline of knowledge of their predictive capacity. We argue that when predictive modeling is applied as a complement on the basis of well-established explanatory concepts, this would enable educational research to explore the predictive power of their explanatory models. Asking how accurate empirically well-established explanations can actually predict educational outcomes means that it is possible to gauge how much is still “unknown.” Hence, the empirically founded understanding from explanatory research is put into perspective. This article explores this issue based on an exemplary study on school track enrollment in Switzerland; a well-researched topic from an explanatory angle in the educational sciences.
1.1 The School Track’s Imprint on Future Trajectories
In accordance with Germany and Austria, rigid early tracking is characteristic of the Swiss education system. In lower secondary education—starting around age 12 and lasting for 3 years—students are separated into different school tracks with differential cognitive demands. These tracks then open up disparate prospects for academic performance development and future careers.1 The academic track (Progymnasium) in lower secondary education, when followed up at the upper secondary level, allows for direct entry into universities2 and hence prepares students for academic careers. Other lower secondary education tracks (basic and extended requirements) frequently result in vocational education careers. Vocational education and training (VET) is the predominant form of upper secondary education in Switzerland. About two-thirds of youth cohorts pursue vocational education at the upper secondary level, where they enter vocational training (mainly apprenticeships) in about 230 different occupations (e.g., SERI, 2017). However, vocational education tracks are very heterogeneous in their level of cognitive demand and future job prospects (Stalder, 2011; Sacchi and Salvisberg, 2014).
Whereas the pursuit of the academic-level track in lower (and upper) secondary education mostly requires passing a competitive entry exam, access to vocational education encompasses competition in the apprenticeship market. Here, the school track pursued at the lower secondary level functions as a highly important signal and appraisal attribute, informing prospective employers on applicants’ cognitive ability, motivation, ambition and, thus, on-the-job performance potential. The school grades are often secondary in this regard (e.g., Meyer, 2008; Scharenberg et al., 2017). Empirical findings indicate that the chances of accessing cognitively demanding vocational education tracks are reduced sharply for those who conclude lower secondary education on the basic-requirements track compared with those on the extended-requirements track, even if they possess the same academic proficiency (Meyer, 2008; Buchmann et al., 2016; Meyer, 2018). As the school track pursued divides chances for academic and vocational careers as well as it determines the kinds of occupational fields in which graduates can gain access, school tracking—at an early stage—sets youths’ life courses for labor-market integration and social positioning in the long run (e.g., Meyer, 2008).
1.2 Concepts and Explanations From Previous Research: What Factors Underlie School-Track Placement?
The primary determinant for school-track placement is academic performance. In brief, the procedure is as follows: Teachers evaluate students based on their performance, which becomes manifest in students’ grades. Teachers then make recommendations as to which school track the student should enter, e.g., they may suggest that the student take the entry-level exam for the academic track. Simultaneously, parental expectations play a role. Parents counsel their children as to which school track they want them to enter. Thus, parents may not follow the teacher’s recommendations for track placement and appeal his or her decision, e.g., they may or may not enroll their child in the entry-level exam for the academic track and supportive training courses. Children also actively engage in navigating their own educational pathways on the basis of their aspirations.
There has been a lot of educational research explaining students’ distinct transitions in a tracked educational system. Although academic performance is the primary determinant for placing students on school tracks, overlap exists in students’ performance across different school tracks (e.g., Angelone et al., 2013). Hence, performance alone cannot explain tracking decisions. Socioeconomic resources are intertwined closely with how parents, teachers and children navigate educational careers (e.g., Boudon, 1974; Bourdieu and Passeron, 1977; Bourdieu, 1985; Bradley and Corwyn, 2002; Ditton and Krüsken, 2006; Maaz and Nagy, 2009; Dumont et al., 2019). Students’ ascriptive attributes and their heritage can influence school-track placement via (implicit) socially selective teacher evaluations. School grades not only mirror student performance but also encompass teachers’ expectations and attributions (Ditton and Krüsken, 2006; Neuenschwander and Malti, 2009). Students’ social behavior, presumed motivation and social integration in class have, as an example, been found to be associated with their school grades and to influence teachers’ recommendations for school-track placement (Neuenschwander and Malti, 2009; Schneider, 2011; Neuenschwander, 2012; Rottermann et al., 2015; Becherer et al., 2017). Drawing on expectancy value theory (Eccles and Wigfield, 2002), students’ own expectations and values also affect their performance as well as their career choices. How young people, for example, perceive their competence levels in school domains, and how highly they appreciate achievement in the relative domains (including perceptions on the amount of effort needed and their chances of succeeding), influences their investment, their performance, and thus their choices (Eccles and Wigfield, 2002). In this vein, expectancy value considerations (explicitly or implicitly), which are again embedded in the familial contexts in which children are raised, underlie young people’s own navigation of their educational trajectories.
While tracking takes place at the end of elementary education, the development of preconditions conducive to learning in school and predictive of future educational choices already takes place prior to entering school. Intertwined with their social backgrounds, children start school at very different levels of initial knowledge (e.g., Moser and Stamm, 2005; Moser et al., 2005), and initial knowledge has been shown to be highly predictive of subsequent performance gains (e.g., Ceci and Liker, 1986; Schneider and Björklund, 1992). Initial knowledge also encompasses competence in the language spoken in school, which is the basis for students’ active participation in class (Zöller et al., 2006). Extant literature on early childhood education (e.g., Stamm, 2010) generally highlights the importance of early stages and familial environments, where the baseline is set for future outcomes.
Against this backdrop of “established” concepts and explanatory factors underlying school-track placement, this study focuses in an exemplary fashion on how well our understanding has become by predicting school-track placement; using performance measures, socioeconomic resources, cognitive abilities and students’ adaptive functioning and competence and value-related beliefs at the following stages: 1) upon school entry; 2) during elementary education; 3) at the end of elementary education. We expect the predictions to become more accurate as we include—longitudinally—education-related measures throughout the elementary school career and up to the end of elementary education. In order to get an idea of how accurate tracking predictions may be, we drew on predictive modeling adopted from machine learning based on longitudinal data from the Zurich Learning Progress Study, Switzerland.
Although predictive modeling is not at all novel to research in educational processes, the vast majority of applications and publications comes from the field of learning analytics (e.g., Dawson et al., 2017; Leitner et al., 2017; Ranjeeth et al., 2020) and educational data mining (e.g., Romero and Ventura, 2010; Guo et al., 2015; Saa, 2016). Some of these studies have explicitly been using students’ background characteristics in their prediction (e.g., Miguéis et al., 2018) and quite a few have employed random forest classifiers for that purpose (e.g., Golino et al., 2014). To the best of our knowledge, however, there is no published study so far that has attempted to predict school tracking decisions, especially not in the context of the Swiss school system.
2 Methods
2.1 Population, Sample and Measures: The Zurich Learning Progress Study
2.1.1 Tracking in the Context of Zurich
The sample underlying the analyses in this study was drawn from the student population in the Canton of Zurich, Switzerland. In Zurich, only about 16% of students pursue the academic-level track (Langgymnasium) in the first grade of lower secondary education. Around one-half of the student population pursues the extended-requirements track in the first grade of lower secondary education (level A) compared with one-third of students who pursue the basic-requirements track, encompassing level B and, in some municipalities, level C. These rates have remained fairly stable over the past decade (e.g., BISTA, 2018a). Access to the academic track requires passing examinations in math and language at the end of elementary education. Thus, in the sixth grade of elementary education, parents can enroll their children in entry exams at grammar schools. The students’ grades in language and math from the most recent school report are also included in the final grading. Thus, teachers’ recommendations and parents’ decisions to enroll their children in entry-level exams, as well as the children’s latest school grades and performance on said entry-level exams, comprise the basis for placement on academic tracks. Each municipality in Zurich decides whether to organize their lower secondary education into two or three further divisions (A, B and, optionally, C). A is a cognitively more demanding track than B and (optionally) C.3 Placement on these tracks is based on teachers’ evaluations (school grades) in discussions with parents (see BISTA, 2018b). During the second and third years of lower secondary education, students who opt for the academic-level track for their upper secondary education (again) can enroll in entry-level exams at grammar schools.
2.1.2 Sample
The Zurich Learning Progress Study monitors learning progress of a stratified random sample of N = 2,043 students, who enrolled in 120 first-grade regular elementary school classes in the 2003/04 school year. All students within the sampled classrooms were surveyed and took part in standardized educational assessments in grade 1, 3, 6 and 9. This study focused on all students for whom school-track information at the lower secondary level exists, which is N = 1,885 students. Following elementary education, N = 247 students in the sample, corresponding to 13% of the students, pursued the academic track (Langgymnasium). N = 901 students pursued the extended-requirements track (level A), which is 48%, and N = 737 pursued the basic-requirements track (levels B/C), which corresponds to 39% of the sample.
2.1.3 Assessment Procedure and Measures
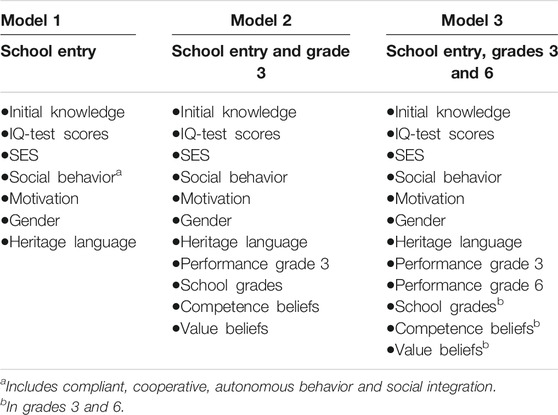
The first standardized assessment and survey [1] immediately followed school enrollment in 2003 (at the age of 6–7 years). In this first assessment, we tested the students’ initial knowledge (gained before elementary school) in terms of language (German reading skills and vocabulary) and mathematical understanding. In addition, children’s cognitive abilities were measured by the culture fair intelligence test (CFT 1; Weiss and Osterland, 1997). These initial assessments were conducted in form of oral examinations by trained, prospective, elementary-school teachers that were recruited from the Zurich University of Teacher Education. Further, additional survey data was gathered. The student’s teachers were asked to evaluate in a teacher questionnaire their students social behavior (compliant, autonomous and cooperative behavior and social integration). Also, in a playful manner (videotaped puppet interviews on school experiences), the children themselves were prompted to agree or disagree with statements on their school motivation. Sample questions included “Are you looking forward to going to school in the morning?” and “Do you sometimes dislike going to school?” Thus, the motivational measure was based on children’s self-reporting. Parents filled out a questionnaire on their socioeconomic resources. Based on this questionnaire, their social status was operationalized. Students’ social status as a composite factor was measured based on parents’ education (highest educational attainment) and cultural capital in the form of books available at home (e.g., Moser and Stamm, 2005; Moser et al., 2005). These measures operationalized the children’s preconditions for learning in school. The second assessment [2] (around age 9) occurred at the end of third grade. At this stage, academic performance in mathematics and language (German) was assessed. The third assessment [3] (around age 12) in mathematics and language occurred at the end of sixth grade, which is the last grade of elementary school and thus, the basis for school-track placement. In both, third and sixth grades, academic performance in mathematics and language (German) was assessed via standardized written tests developed to reflect the Canton of Zurich’s official school curriculum. The tests on school performance were scaled according to the probabilistic Rasch model (e.g., Bond and Fox, 2015). Drawing on expectancy value theory (Eccles and Wigfield, 2002), competence beliefs in mathematics and language, as well as subject-related value beliefs (subdomains: eagerness to learn, relevance and utility) were assessed in both third and sixth grades, and children reported their school grades. The scales on competence beliefs focused on the overarching question, “Can I do it?” and included six items for each subject, including “I have problems in mathematics” and “Language is easy”. Measurement of value-related beliefs focused on the overarching question, “Do I want it and why?” and included four items per subdomain, such as “Mathematics is unimportant to me” and “Language is useful” (Descriptive statistics of these measures are reported in the Supplementary Appendix, Table A5). The study’s target measure was the school track on which students were placed at the end of elementary education, distinguishing between 1) academic track, 2) A-levels (extended requirements) and 3) B/C-levels (basic requirements). Information on the school tracks was gathered based on official education statistics (Bildungsstatistik, BISTA; e.g., Tomasik et al., 2017), which, as a secondary database, was matched to the sample data.
2.2 Analytic Strategy
The study’s objective was to investigate how far our understanding of educational transitions goes by analyzing how well we can actually predict students’ pathways at the lower secondary level based on well-established education-related measures in a longitudinal fashion. Thus, the methodological focus is on predictive modeling. To evaluate how well placement on school tracks can be predicted based on early education-related measures, we used recursive partitioning in terms of the random-forest methodology (Breiman, 2001). Recursive partitioning methods, adopted from machine learning, have become increasingly popular in many scientific fields. In contrast to parametric classification models, such as logistic regression, these methods allow for modeling complex, non-linear relations and interactions between variables in a data-driven way and do not rely on strong model assumptions, such as the functional form of the association between predictors and outcomes. Random forests can further deal with high dimensionality, thereby allowing for the inclusion of many correlated predictors without losing prediction accuracy (Lantz, 2015; Strobl et al., 2009a).
The rationale for recursive partitioning (for more details, see Strobl et al., 2009a) is that the feature space spanned by all predictor variables is recursively split into sets of respondents with similar response patterns. Decision-tree classifiers channel observations into a final predicted class based on branching decisions, resulting in a tree-like structure (e.g., Lantz, 2015). Each node of the decision tree corresponds to a split in the data, in which the variable (and optimal cut point) that best predicts the target (in this case, school track) is selected for the next split. To select splitting variables and cut points, impurity-reduction measures, or p-value association tests, serve as split criteria to best separate/classify observations based on the target variable (e.g., school track). In each terminal node of the tree, the predicted response class corresponds to the majority in the respective node. The logic to assess prediction accuracy follows the idea of extrapolation, the objective of which is to create a classifier that allows for generalizing in new instances. The classifier is generally fit in a (randomly drawn) learning sample of the data, and prediction accuracy is tested in a (randomly drawn) test sample of the data. Single classification trees are unstable and can change in the partitioning structure due to small differences in the distribution of variables in the learning sample. Random forests are an ensemble of multiple classification trees (e.g., Breiman, 2001) and allow for higher generalizability. In random forests, trees are fitted on different learning samples, while different random subsets of predictor variables are used simultaneously, which helps avoid overfitting (e.g., Strobl et al., 2009a). The final classification in random forests is based on the majority prediction over the multiple classification trees fitted. Based on 10-fold cross-validation, we evaluated prediction accuracy. This means that we fit the models 10 times, each on 90 percent of the sample, and evaluated how well our model generalized and predicted the outcomes of the unseen 10 percent of the sample (e.g., Lantz, 2015). However, the data imbalance presented a problem, i.e., the classes (respectively, school tracks) were not represented equally in the data. The minority of students followed the academic-level track following sixth grade, and the majority of students followed the extended-requirements track. Classifiers are more sensitive to detecting the majority class and less sensitive to the minority class, resulting in higher error rates in predicting the minority class (e.g., He and Garcia, 2009; Fernandez et al., 2013; Haixiang et al., 2017). The synthetic minority oversampling technique (SMOTE) (e.g., Chawla et al., 2002) is a commonly used oversampling method in imbalanced classification (Haixiang et al., 2017). Instead of creating exact copies from the minority class through simple oversampling, it works by creating synthetic samples. The algorithm selects two or more similar instances in the minority group using a nearest-neighbor distance measure. It then synthesises a new minority instance that lies (based on the covariates) somewhere between these nearest neighbors (for an applied example, see Kunert, 2017).
In this study, random forests were implemented using the party package (Hothorn et al., 2006; Hothorn et al., 2018) in the Software R (R Core Team, 2020). Partitioning was based on the p-values of association tests (which include testing a global null hypothesis), and recursion was stopped when no further significant associations were found (e.g., Hothorn et al., 2006). The number of trees fitted for random forests defaults to 500, and the number of variables selected for each random subset is equal to the square root of all predictors included. Missing values were multiply imputed in the 10-fold cross-validation samples using predictive mean matching (Robitzsch et al., 2016), then combined into an average estimate. The oversampling technique SMOTE was applied based on the R-package smotefamily (Wacharasak, 2018) using the five nearest neighbours. For performance evaluation, we reported overall prediction accuracy and balanced prediction accuracy (mean across the true positive rates for each track), as well as precision and F-measures separately for each predicted school track (e.g., He and Garcia, 2009) and the G-mean measure for multiclass classification (e.g., Sun et al., 2006). In the Supplementary Appendix (Tables A6–A8), for comparative purposes, we additionally show the results when applying a parametric multinomial logistic regression instead of the more sophisticated combination of a SMOTE sampling approach and random forest classifier.
We followed a stepwise procedure in which we fit three predictive models, including education-related measures surveyed at these points: 1) school enrollment; 2) school enrollment and in third grade; and 3) school enrollment and in third and sixth grades. In Model 1, we included information on children’s preconditions in the form of socioeconomic resources as parental SES, the children’s scores on the initial IQ test, their initial knowledge in reading and math, their gender and migrant background (heritage language), their teachers’ initial evaluations of their social behavior, and the children’s self-reported motivation at the start of primary school. In Model 2, we included standardized academic performance measures in both language and math in third grade, students’ school grades (mirroring teachers’ evaluations) and their self-reported competence and value-related beliefs. Model 3 further complemented Model 2 by including school grades, standardized academic performance in language and math, and competence and value-related beliefs at the end of elementary education, which were the basis for placement into school tracks (see Table 1). In a stepwise procedure, running Models 1–3, we investigated how well we could predict subsequent placement into school tracks and checked how much of an increase in prediction accuracy we gained when moving from early education measures to the addition of late education-relevant measures.
3 Results
Tables 2–4 display the prediction results of random forests based on the predictor sets of Models 1–3 (see Table 1). The rows contain observed school tracks of students, while the columns display predictions based on the cross-validation samples. In the diagonal, the correct classifications by school track are displayed, while off-diagonal cells include misclassifications. The percentages in the diagonal represent the shares of correctly classified students out of all students pursuing respective school tracks (true positive rates by track, row percentages). This value is also known as the recall statistic in the extant literature (e.g., He and Garcia, 2009).4
Thus, these tables provide an idea of how accurate (approximately) we can be when predicting placement into school tracks by early and late education-related measures. Focusing on school-entry measures (Model 1, see Table 2), the total fraction of correct classifications for Model 1, which is overall prediction accuracy, is 64%. The prediction error (1-accuracy) amounts to 36%. Thus, based on education-related predictors measured upon school entry, such as students’ initial knowledge in reading and math, their scores in an IQ assessment, their familial SES, their motivation and teachers’ evaluations of their social behavior, we can build a classifier that predicts future school-track placement with about 64% accuracy. If we focus on balanced prediction accuracy, which is the mean across the true positive rates for separate tracks, then the balanced prediction accuracy reaches 65%. Focusing on the tracks separately, we can correctly classify approximately 65% of students following the academic track based on school-entry measures, compared with about 57% of those on the extended-requirements track (Level A) and 73% of those on the basic-requirements track (levels B/C). Focusing on the off-diagonal cells (misclassifications), we can see that misclassifications mainly occur between adjacent school tracks. For example, based on these early predictors, 31% of those on the academic track and 25% of those on the basic-requirements track are misclassified as pursuing the extended-requirements track. Meanwhile, 24% of those on the extended-requirements track are misclassified as following the basic-requirements track, and 20% of the extended-requirements track students are misclassified as following the academic track. Conversely, only minor misclassification exists between the most- and least-advantageous tracks, which is between students following the academic- and basic-requirements tracks. Only about 4% of those pursuing the academic track are wrongly classified as basic-track students, whereas 2% pursuing the basic track are misclassified as academic-track students. This suggests that the most advantageous and most risky tracks, with solid precision, can be separated based on education-related measures taken upon school entry.
If we also include performance measures and school grades in math and language, as well as competence and value-related beliefs, in third grade, which is in mid-elementary education, overall prediction accuracy increases to 71%. Accordingly, the prediction error is reduced to 29% (Model 2, Table 3). In addition, balanced prediction accuracy totals 71%. Including third-grade measures, we can classify approximately 70% of students following the academic track correctly, with about 69% of students on the extended-requirements track and 74% on the basic-requirements track. Again, misclassifications (off-diagonal cells) mainly occur between adjacent school tracks, whereas separation between academic- and basic-requirements tracks is possible at high accuracy.
Complementing the predictor set by school grades and performance in language and math in sixth grade and students’ competence and value-related beliefs at the end of elementary education (Model 3, Table 4), overall prediction accuracy rises to 79%, and prediction error drops to 21%. Balanced prediction accuracy across the different school tracks totals 77% (mean across correct classification rates for separate school tracks). Including sixth-grade measures, we can predict about 71% of all academic-track students correctly, compared with 79% of extended-requirements track students and 82% of students pursuing the basic-requirements track. Like before, misclassifications more commonly occurred between adjacent tracks than between the most- and least-advantageous tracks. Of those pursuing the basic-requirements track, no one was misclassified as following the academic-level track; and of those pursuing the academic-level track, about 2% were misclassified as pursuing the basic-requirements track. All in all, no perfect prediction seems possible based on education-related measures, even if they are measured at the end of elementary education and thus directly underlie placement on school tracks. Although overall prediction performance improves when including variables measured in sixth grade, the increased accuracy appears to be modest.
4 Discussion
Complementing the near-exclusive focus on explanatory models in the educational sciences, predictive modeling strategies allow exploring the predictive capacity of explanatory factors and concepts (Hofman et al., 2017; Yarkoni and Westfall, 2017). They put the explanations derived from theory-elaborative and hypothesis-testing research into perspective. In other words, they allow for testing and gauging the limits of our understanding of educational outcomes by evaluating the predictive power of our explanations.
In an exemplary fashion, this study investigated how far (institutionalized) school tracking can actually be predicted using a broad set of early and late education-related measures highlighted in previous explanatory research. Although we know about manifold factors determining track placements, we have no frame for evaluating how predictable such transitions have become in total, given our theoretical and conceptual understanding of them. If the explanatory factors, as an aggregate, lead to successful predictions of school-track placement, then this would suggest that, given these widely established educational predictors, little unpredictable mobility exists in terms of students’ performance development and educational navigation during elementary education, and that, as such, we have an established set of predictors and understanding on which we can forecast these transitions. However, if high unpredictability remains, then this would prompt future explanatory research to think further and consider what else may be in play that would lead to such unpredictable dynamics.
The exemplary results show that even if, in a longitudinal fashion, a diverse set of well-established predictors is used in combination with a random-forest model for prediction—including standardized performance measures, school grades, socioeconomic resources, individual preconditions and beliefs—predicting the placement of students on school tracks is still prone to substantive misclassifications. Approximately, the transition of one out of five students is erroneously predicted at the very end of elementary education. Thus, there is quite a bit we cannot explain in educational navigation at the very end of elementary education. Yet, predictive misclassifications mainly occur between adjacent school tracks. Very few misclassifications in the future enrollment of academic-track and basic-track students, i.e., those pursuing the most- and least-prestigious tracks, respectively, occur. In this regard, the institutionalized tracking system seems to distinguish at the lower and upper ends between what is already observed prior to starting school; implying that little unpredictable mobility seems to occur during elementary education between the margins given our theoretical understanding of factors underlying educational careers.
Though explanatory research provides us with a set of explanations, we can only grasp how well we can actually explain specific outcomes by evaluating the explanations’ predictive power in a predictive modeling framework. Predictive modeling strategies hence allow educational researcher to explore the limits of their understanding of educational outcomes and, by this, to put the knowledge gained from explanatory approaches into perspective. In other words, the predictive approach is asking about the maximum amount of variance that could be possibly explained by a set of predictors when taking into account all possible higher order and non-linear interactions between them. This approach is not bound by the limitation that we cannot understand or interpret these interactions. It rather shows the amount of information that is inherent to this set of predictors. If this amount is large, we can assume that we at least were able to identify the relevant variables correlated with the outcome. If this amount is small, this either hints to some overseen variables or to some inherent randomness of the entire process. Yet, as we lack a benchmark for the “predictability of human behavior” in general, there is no frame for evaluating whether the theoretical limit of forecasting specific outcomes has been reached (as there may be an inherent aspect of randomness), or if misclassifications may arise due to issues of measurement error, data quality, the predictive modeling approach chosen or because there are other unmeasured (or unmeasurable) factors at play (Hand, 2006; Hofman et al., 2017). One could, for instance, argue that our lean operationalization of socio-economic status (otherwise not feasible due to data protection regulations) was not sufficient enough to capture important aspects of that construct such as income or occupational activity. Still, it is difficult to decide between more conceptual reasons for misclassification (e.g., some inherent randomness in the process investigated) or methodological ones (e.g., an important predictor measured with low reliability only).
Finally, the reported findings contribute to the ongoing discussion whether tracking as such is rather beneficial or rather disadvantageous for the reproduction of social inequalities and for upward mobility of students with lower socio-economic status. Proponents of between-school tracking argue that such an educational policy better allows adjusting to the needs and abilities of all students as compared to a unity school system (Maaz et al., 2008). Furthermore, tracking is said to have beneficial effects on the academic self-concept of weaker students (Marsh et al., 2018) and studies are cited showing little if any difference in the learning progress of students at different tracks (despite, of course, differences in the overall level; e.g., Schneider et al., 2002; Schneider and Stefanek, 2004). Opponents, in turn, claim that the different learning context related to between-school tracking would exacerbate social inequalities and result in differential learning gains (Solga, 2008). They cite studies showing that by international comparison, school systems with later tracking tend to provide more equal opportunities as index by lower correlations between socio-economic status and educational attainment (e.g., Schütz and Wößmann, 2005). There is empirical evidence for both positions, depending on the context investigated or the subject domain taken into consideration (Maaz et al., 2010). Both positions, however, build on the assumption that the allocation of students according to some specified criterion works sufficiently well. Our results point to the possibility that there is a substantial amount of randomness in this allocation process. In other words, even if we would want to accept that tracking is conducted not only contingent on merit but also biased by socio-economic status, gender or language background, we would not be able to explain many of the allocation decisions made. This finding calls for future research investigating these obviously important factors and this is exactly the point where predictive modeling can and should become a starting point for investigation and explanation.
Data Availability Statement
The datasets presented in this article are not readily available because the data is confidential and contracts on data use may need be set up in agreement with the canton of Zurich. Requests to access the datasets should be directed to dXJzLm1vc2VyQGliZS51emguY2g=.
Author Contributions
LH conducted the analyses and wrote the article in close collaboration with MT. UM was responsible for data collection.
Funding
The University of Zurich funded part of the publication costs.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2021.793447/full#supplementary-material
Footnotes
1Different tracking models exist across and even within cantons in Switzerland. For the Canton of Zurich, the model of separating students in lower secondary education into different school tracks remains the dominant one in use.
2In some cantons (including Zurich), access to the academic track at the lower secondary and/or upper secondary level requires passing an exam upon completion of primary or lower secondary education.
3The vast majority of students pursue lower secondary education in tracks A and B. Only a minority of students pursue track C, as models with three divisions are not widespread in Zurich (e.g., BISTA, 2018a).
4In the table footnotes, further performance measures are reported. The precision statistic encompasses column percentages of the correctly classified students predicted to follow their respective school tracks. The F-measure combines recall and precision (e.g., He and Garcia, 2009). For a performance comparison between Models 1–3, the balanced prediction accuracy (mean across school tracks) and the multi-class G-mean statistic, according to Sun et al. (2006), are reported.
References
Aikens, N. L., and Barbarin, O. (2008). Socioeconomic Differences in reading Trajectories: The Contribution of Family, Neighborhood, and School Contexts. J. Educ. Psychol. 100, 235–251. doi:10.1037/0022-0663.100.2.235
Angelone, D., Keller, F., and Moser, U. (Editors) (2013). Entwicklung schulischer Leistungen während der obligatorischen Schulzeit. Bericht zur vierten Zürcher Lernstandserhebung zuhanden der Bildungsdirektion des Kantons Zürich. Zürich: Universität Zürich, Institut für Bildungsevaluation.
Barone, C. (2011). Some Things Never Change. Sociol. Educ. 84, 157–176. doi:10.1177/0038040711402099
Becherer, J., Köller, O., and Zimmermann, F. (2017). Sozialverhalten und Schulleistungen. Z. Erziehungswiss 20, 405–424. doi:10.1007/s11618-017-0771-1
Billingham, C. M., and Hunt, M. O. (2016). School Racial Composition and Parental Choice. Sociol. Educ. 89, 99–117. doi:10.1177/0038040716635718
BISTA (2018a). Die Schulen im Kanton Zürich 17/18. Bildungsdirektion Kanton Zürich: Volksschulamt. Available at: https://bi.zh.ch/internet/bildungsdirektion/de/themen/zahlen-fakten/veroeffentlichungen/_jcr_content/contentPar/publication_6/publicationitems/die_schulen_im_kanto_3/download.spooler.download.1532503125889.pdf/BiZH_BP_Vade18_NEU_RZ_180628.pdf (Accessed November 7, 2018).
BISTA (2018b). Neues Volksschulgesetz: Sekundarstufe. Merkblatt. Bildungsdirektion Kanton Zürich: Volksschulamt. Available at: https://vsa.zh.ch/internet/bildungsdirektion/vsa/de/schulstufen_schulen/schulstufen/sekundar/_jcr_content/contentPar/downloadlist/downloaditems/merkblatt_organisati.spooler.download.1392906115194.pdf/3375_0_merkblattsekfreltern.pdf (Accessed November 30, 2018).
Bond, T. G., and Fox, C. M. (2015). Applying the Rasch Model: Fundamental Measurement in the Human Sciences. 3rd ed. New York: Routledge.
Boudon, R. (1974). Education, Opportunity, and Social Inequality: Changing Prospects in Western Societies. New York: Wiley.
Bourdieu, P. (1985). “Das Bildungswesen ein maxwellscher Dämon,” in Praktische Vernunft. Editor P. Bourdieu (Frankfurt am Main, Germany: Suhrkamp), 36–41.
Bourdieu, P., and Passeron, J.-C. (1977). Reproduction in Education, Society, and Culture. London: Sage.
Bradley, R. H., and Corwyn, R. F. (2002). Socioeconomic Status and Child Development. Annu. Rev. Psychol. 53, 371–399. doi:10.1146/annurev.psych.53.100901.135233
Buchmann, M., Kriesi, I., Koomen, M., Imdorf, C., and Basler, A. (2016). “Differentiation in Secondary Education and Inequality in Educational Opportunities: The Case of Switzerland,” in Models of Secondary Education and Social Inequality: An International Comparison. Editors H. Blossfeld, S. Buchholz, J. Skopek, and M. Triventi (Cheltenham, UK: Edward Elgar). 111–128.
Ceci, S. J., and Liker, J. K. (1986). A Day at the Races: A Study of IQ, Expertise, and Cognitive Complexity. J. Exp. Psychol. Gen. 115, 255–266. doi:10.1037/0096-3445.115.3.255
Chawla, N. V., Bowyer, K. W., Hall, L. O., and Kegelmeyer, W. P. (2002). SMOTE: Synthetic Minority Over-sampling Technique. jair 16, 321–357. doi:10.1613/jair.953
Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences. Hillsdale, NJ: Lawrence Erlbaum.
Coleman, J. S. (1968). Equality of Educational Opportunity. Equity Excell. Educ. 6, 19–28. doi:10.1080/0020486680060504
Dawson, S., Jovanovic, J., Gašević, D., and Pardo, A. (2017). “From Prediction to Impact,” in LAK '17: Proceedings of the Seventh International Learning Analytics and Knowledge Conference, Vancouver, BC, Canada, March 13–17, 2017. Editor M. Hatala (New York: Association for Computing Machinery), 474–478. doi:10.1145/3027385.3027405
Ditton, H., and Krüsken, J. (2006). Der Übergang von der Grundschule in die Sekundarstufe I. ZfE 9, 348–372. doi:10.1007/s11618-006-0055-7
Doren, C., and Grodsky, E. (2016). What Skills Can Buy: Transmission of Advantage through Cognitive and Noncognitive Skills. Sociol. Educ. 89, 321–342. doi:10.1177/0038040716667994
Dumont, H., Klinge, D., and Maaz, K. (2019). The many (Subtle) Ways Parents Game the System: Mixed-Method Evidence on the Transition into Secondary-School Tracks in Germany. Sociol. Educ. 92, 199–228. doi:10.1177/0038040719838223
Eccles, J. S., and Wigfield, A. (2002). Motivational Beliefs, Values, and Goals. Annu. Rev. Psychol. 53, 109–132. doi:10.1146/annurev.psych.53.100901.135153
Ewijk, R. V., and Sleegers, P. (2010). The Effect of Peer Socioeconomic Status on Student Achievement: a Meta-Analysis. Educ. Res. Rev. 5, 134–150. doi:10.1016/j.edurev.2010.02.001
Fernández, A., López, V., Galar, M., Del Jesus, M. J., and Herrera, F. (2013). Analysing the Classification of Imbalanced Data-Sets with Multiple Classes: Binarization Techniques and Ad-Hoc Approaches. Knowledge-Based Syst. 42, 97–110. doi:10.1016/j.knosys.2013.01.018
Golino, H. F., Gomes, C. M. A. G., and Andrade, D. (2014). Predicting Academic Achievement of High-School Students Using Machine Learning. Psychology 5, 2046–2057. doi:10.4236/psych.2014.518207
Guo, B., Zhang, R., Xu, G., Shi, C., and Yang, L. (2015). “Predicting Students’ Performance in Educational Data Mining,” in Proceedings of the 2015 International Symposium on Educational Technology, Xi’an, China, March 21–22, 2017. Editors F. L. Wang, T. L. Wong, O. Au, Q. Liu, and S. Wu (Piscataway, NJ: Institute of Electrical and Electronics Engineers), 125–128.
Haibo He, H., and Garcia, E. A. (2009). Learning from Imbalanced Data. IEEE Trans. Knowl. Data Eng. 21, 1263–1284. doi:10.1109/tkde.2008.239
Haixiang, G., Yijing, L., Shang, J., Mingyun, G., Yuanyue, H., and Bing, G. (2017). Learning from Class-Imbalanced Data: Review of Methods and Applications. Expert Syst. Appl. 73, 220–239. doi:10.1016/j.eswa.2016.12.035
Hand, D. J. (2006). Classifier Technology and the Illusion of Progress. Stat. Sci. 21, 1–14. doi:10.1214/088342306000000060
Hofman, J. M., Sharma, A., and Watts, D. J. (2017). Prediction and Explanation in Social Systems. Science 355, 486–488. doi:10.1126/science.aal3856
Hothorn, T., Hornik, K., Strobl, C., and Zeileis, A. (2018). Package-party. A Laboratory for Recursive Partitioning. Version: 1.3-1. Available at: https://cran.r-project.org/web/packages/party/party.pdf (Accessed November 14, 2018).
Hothorn, T., Hornik, K., and Zeileis, A. (2006). Unbiased Recursive Partitioning: A Conditional Inference Framework. J. Comput. Graphical Stat. 15, 651–674. doi:10.1198/106186006X133933
Kunert, R. (2017). SMOTE Explained for Noobs – Synthetic Minority Over-sampling Technique Line by Line. Tutorial. Available at: http://rikunert.com/SMOTE_explained (Accessed February 8, 2019).
Lantz, B. (2015). “Evaluating Model Performance,” in Machine Learning with R. Editor B. Lantz (Birmingham: ProQuest Ebook Central), 311–345. Available at: http://ebookcentral.proquest.com/lib/ethz/detail.action?docID=2122139.
Leitner, P., Khalil, M., and Ebner, M. (2017). “Learning Analytics in Higher Education-A Literature Review,” in Learning Analytics: Fundaments, Applications, and Trends. Editor A. Peña-Ayala (Cham, Switzerland: Springer International Publishing), 1–23. doi:10.1007/978-3-319-52977-6_1
Lewis-Beck, M. S. (1980). Applied Regression: An Introduction [Sage University Paper Series on Quantitative Applications in the Social Sciences No. 07-022. Newbury Park, CA: Sage.
Maaz, K., Baumert, J., and Trautwein, U. (2010). Genese sozialer Ungleichheit im institutionellen Kontext der Schule: Wo entsteht und vergrößert sich soziale Ungleichheit? Z. für Erziehungswissenschaft 12, 11–46. doi:10.1007/978-3-531-92216-4_2
Maaz, K., and Nagy, G. (2009). Der Übergang von der Grundschule in die weiterführenden Schulen des Sekundarschulsystems: Definition, Spezifikation und Quantifizierung primärer und sekundärer Herkunftseffekte. Z. für Erziehungswissenschaften 12, 153–182.
Maaz, K., Trautwein, U., Ldtke, O., and Baumert, J. (2008). Educational Transitions and Differential Learning Environments: How Explicit Between-School Tracking Contributes to Social Inequality in Educational Outcomes. Child. Dev. 2, 99–106. doi:10.1111/j.1750-8606.2008.00048.x
Marsh, H. W., Pekrun, R., Murayama, K., Arens, A. K., Parker, P. D., Guo, J., et al. (2018). An Integrated Model of Academic Self-Concept Development: Academic Self-Concept, Grades, Test Scores, and Tracking over 6 Years. Dev. Psychol. 54, 263–280. doi:10.1037/dev0000393
Meyer, T. (2018). Von der Schule ins Erwachsenenleben: Ausbildungs- und Erwerbsverläufe in der Schweiz. Social Change Switzerland 13, 1–14. doi:10.22019/SC-2018-00002
Meyer, T. (2008). “Wer hat dem wird gegeben: Bildungsungleichheit in der Schweiz,” in Sozialbericht 2008. Die Schweiz vermessen und verglichen. Editors C. Suter, S. Perrenoud, R. Levy, U. Kuhn, D. Joye, and P. Gazareth (Switzerland: ZürichSeismo), 60–81.
Miguéis, V. L., Freitas, A., Garcia, P. J. V., and Silva, A. (2018). Early Segmentation of Students According to Their Academic Performance: A Predictive Modelling Approach. Decis. Support Syst. 115, 36–51. doi:10.1016/j.dss.2018.09.001
Moser, U., Berweger, S., and Stamm, M. (2005). “Lesekompetenzen bei Schuleintritt,” in Für die Schule bereit? Lesen, Wortschatz und soziale Kompetenzen beim Schuleintritt. Editors U. Moser, M. Stamm, and J. Hollenweger (Oberentfelden: Sauerländer), 37–58.
Moser, U., and Stamm, M. (2005). “Die Untersuchung im Überblick,” in Für die Schule bereit? Lesen, Wortschatz, Mathematik und soziale Kompetenzen beim Schuleintritt. Editors U. Moser, M. Stamm, and J. Hollenweger (Oberentfelden: Sauerländer), 13–26.
Neuenschwander, M. P., and Malti, T. (2009). Selektionsprozesse beim Übergang in die Sekundarstufe I und II. Z. Erziehungswiss 12, 216–232. doi:10.1007/s11618-2009-0074-2
Neuenschwander, M. (2012). “Selektionsprozesse beim Übergang in die Sekundarstufe I, die Berufsbildung und die tertiäre Ausbildung,” in Bildung-Arbeit-Erwachsenwerden. Ein interdisziplinärer Blick auf die Transition im Jugend- und jungen Erwachsenenalter. Editors M. M. Bergman, S. Hupka-Brunner, T. Meyer, and R. Samuel (Basel, Switzerland: Springer), 180–201.
R Core Team (2020). R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. Available at: https://www.R-project.org/(Accessed December 10, 2018).
Ranjeeth, S., Latchoumi, T. P., and Paul, P. V. (2020). A Survey on Predictive Models of Learning Analytics. Proced. Comp. Sci. 167, 37–46. doi:10.1016/j.procs.2020.03.180
Robitzsch, A., Pham, G., and Yanagida, T. (2016). “Fehlende Daten und Plausible Values,” in Large-scale assessment mit R: Methodische grundlagen der österreichischen Bildungsstandard-Überprüfung. Editors S. Breit, and C. Schreiner (Wien, Austria: Facultas), 259–294.
Romero, C., and Ventura, S. (2010). Educational Data Mining: A Review of the State of the Art. IEEE Trans. Syst. Man. Cybern. C 40, 601–618. doi:10.1109/tsmcc.2010.2053532
Rottermann, B., Neuenschwander, M. P., Rösselet, S., and Niederbacher, E. (2015). Bedingungen von erwartungswidrigen Schulniveauzuweisungen beim Übergang in die Sekundarstufe I. Z. für Soziologie der Erziehung Sozialisation 35, 417–433.
Rumberger, R. W., and Palardy, G. J. (2005). Does Segregation Still Matter? the Impact of Student Composition on Academic Achievement in High School. Teach. Coll. Rec. 107, 1999–2045.
Saa, A. A. (2016). Educational Data Mining and Students’ Performance Prediction. Int. Jounral Adv. Comp. Sci. Appl. 7, 212–220. doi:10.14569/IJACSA.2016.070531
Sacchi, S., and Salvisberg, A. (2014). Arbeitsmarktperspektiven von Fachkräften aus unterschiedlichen Berufen 2013. Report im Auftrag des Staatssekretariats für Bildung, Forschung und Innovation SBFI. Zurich, Switzerland: SMM.
Scharenberg, K., Wohlgemuth, K., and Hupka-Brunner, S. (2017). Does the Structural Organisation of Lower-Secondary Education in Switzerland Influence Students' Opportunities of Transition to Upper- Secondary Education? A Multilevel Analysis. Swiss J. Sociol. 43, 63–88. doi:10.1515/sjs-2017-0004
Schneider, T. (2011). Die Bedeutung der sozialen Herkunft und des Migrationshintergrundes für Lehrerurteile am Beispiel der Grundschulempfehlung. Z. Erziehungswiss 14, 371–396. doi:10.1007/s11618-011-0221-4
Schneider, W., and Bjorklund, D. F. (1992). Expertise, Aptitude, and Strategic Remembering. Child. Dev. 63, 461–473. doi:10.2307/113149210.1111/j.1467-8624.1992.tb01640.x
Schneider, W., Knopf, M., and Stefanek, J. (2002). The Development of Verbal Memory in Childhood and Adolescence: Findings from the Munich Longitudinal Study. J. Educ. Psychol. 94, 751–761. doi:10.1037/0022-0663.94.4.751
Schneider, W., and Stefanek, J. (2004). Entwicklungsveränderungen allgemeiner kognitiver Fähigkeiten und schulbezogener Fertigkeiten im Kindes- und Jugendalter. Z. für Entwicklungspsychologie Pädagogische Psychol. 36, 147–159. doi:10.1026/0049-8637.36.3.147
Schütz, G., and Wößmann, L. (2005). Chancengleichheit im Schulsystem: Internationale deskriptive Evidenz und mögliche Bestimmungsfaktoren [IFO Working Paper No. 17]. München: IFO Institute for Economic Research.
SERI (2017). Vocational And Professional Education and Training in Switzerland. Facts And Figures 2017. Bern, Switzerland: State Secretariate for Education, Research and Innovation.
Solga, H. (2008). Wie das deutsche Schulsystem Bildungsungleichheiten verursacht [WZBrief Bildung No. 1]. Berlin: Wissenschaftszentrum Berlin für Sozialforschung.
Stalder, B. (2011). The Intellectual Demands of Initial Vocational Education and Training in Switzerland. Ratings for the Period 1999‐2005. Basel: Institute of Sociology, University of Basel: TREE.
Stamm, M. (2010). Frühkindliche Bildung als Basis von Schulerfolg? Analysen zur Wirksamkeit früher Bildungsförderung. Die Deutsche Schule 3, 255–267.
Strobl, C., Malley, J., and Tutz, G. (2009b). An Introduction to Recursive Partitioning: Rationale, Application, and Characteristics of Classification and Regression Trees, Bagging, and Random Forests. Psychol. Methods 14, 323–348. doi:10.1037/a0016973
Strobl, C., Hothorn, T., and Zeileis, A. (2009a). Party on! A New, Conditional Variable-Importance Measure For Random Forests Available In The Party Package. R. J. 1, 14–17. doi:10.32614/rj-2009-013
Sun, Y., Kamel, M., and Wang, Y. (2006). “Boosting for Learning Multiple Classes with Imbalanced Class Distribution,” in Proceedings of the Sixth International Conference on Data Mining (ICDM’06), Hong Kong, China, December 18–22, 2006. doi:10.1109/ICDM.2006.29
Tomasik, M., Oostlander, J., and Moser, H. (2017). Von der Schule in den Beruf. Wege und Umwege in der nachobligatorischen Ausbildung. Zurich: Universität Zürich.
Wacharasak, S. (2018). Package‚ Smotefamily. A Collection of Oversampling Techniques for Class Imbalance Problem Based on SMOTE. (version 1.3). Available at: https://cran.r-project.org/web/packages/smotefamily/smotefamily.pdf(Accessed December 10, 2018).
Yarkoni, T., and Westfall, J. (2017). Choosing Prediction over Explanation in Psychology: Lessons from Machine Learning. Perspect. Psychol. Sci. 12, 1100–1122. doi:10.1177/1745691617693393
Zöller, I., Ross, J., and Schöler, H. (2006). “Einfluss soziokultureller Faktoren auf den Schriftspracherwerb im Grundschulalter,” in Risikofaktoren kindlicher Entwicklung: Migration, Leistungsangst und Schulübergang. Editor A. Schründer-Lenzen (Wiesbaden, Germany: VS Verlag für Sozialwissenschaften), 45–65.
Keywords: predictive modeling, educational transitions, school tracking, random forests in an applied setting, educational navigations
Citation: Helbling LA, Tomasik MJ and Moser U (2022) Putting an Explanatory Understanding into a Predictive Perspective: An Exemplary Study on School Track Enrollment. Front. Educ. 6:793447. doi: 10.3389/feduc.2021.793447
Received: 12 October 2021; Accepted: 17 December 2021;
Published: 01 February 2022.
Edited by:
Ze Wang, University of Missouri, United StatesReviewed by:
Joniada Milla, Saint Mary’s University, CanadaGil Keppens, Vrije University Brussel, Belgium
Copyright © 2022 Helbling, Tomasik and Moser. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Laura A. Helbling, bGF1cmEuaGVsYmxpbmdAaWJlLnV6aC5jaA==
 Laura A. Helbling
Laura A. Helbling Martin J. Tomasik
Martin J. Tomasik Urs Moser
Urs Moser