- 1Department of Educational Psychology and Leadership, Texas Tech University, Lubbock, TX, United States
- 2Department of Teacher Education, Texas Tech University, Lubbock, TX, United States
Teacher buy-in is a critical component for the success of any educational reform, especially one involving evaluation and compensation. We report on an instrument developed to measure teacher buy-in for district-developed designation plans associated with a state pay-for-performance (PFP) program, and teacher responses. We used modern test theory to investigate the instrument’s psychometric properties, a procedure often missing from research reports of self-designed surveys. A sample of 3,001 elementary, middle school, and high school teachers in Texas school districts participated in the survey. Our results suggest satisfactory reliability of the instrument and adequate discriminant validity in measuring distinct but related aspects of teacher buy-in. In addition, we found that teacher support for PFP as instantiated in their particular districts was generally high, but still buy-in levels varied significantly among different teacher groupings, pointing the way for future developers of pay-for-performance schemes to improve or maximize their acceptance.
Introduction
International interest in teacher performance incentive pay has fluctuated over the years, and schemes to introduce it are often met with resistance (Burgess et al., 2001; Thompson and Price, 2012). However, teacher characteristics such as experience and qualifications, the main determinants of salaries for most school districts, are poor predictors of teachers’ ability to improve student learning (Rivkin et al., 2005; Aaronson et al., 2007). Recently there have been national policy initiatives to reward teachers and schools for improvements in student learning in the United States (“Teacher Incentive Fund” in 2007 and “Race to the Top” in 2009), Australia (“Rewards for Great Teachers” in 2011), United Kingdom (“Performance-Related Pay for Teachers” in 2014), and other countries such as South Korea, India, and Chile. Pay-for-performance (PFP) and incentive plans may also take place at the state (e.g., “Ohio Teacher Incentive Fund,” 2006), or district (e.g., “ProComp” in Denver, 1999) levels, and may have many forms (Hill and Jones, 2020). The evidence for the effectiveness of PFP for teachers on student outcomes is mixed, but in general points to a small positive impact (see Pham et al., 2020 for a recent meta-analysis of 37 primary studies). Our perspective here is that no PFP program will be successful unless the teachers are in support of a PFP initiative (Kelley et al., 2002). This study, then, examines the extent to which teachers support one particular PFP program instituted across the State of Texas that provides salary increases to teachers and additional income to districts based on student performance and teacher classroom evaluations. Our focus is on that necessary first step, teacher buy-in.
In the interest of clarity, we begin by distinguishing among the different terms used in this area of education policy. “Performance pay” or PFP generally refers to programs introduced since the year 2000 that base teachers’ pay on classroom performance. Teacher performance may be measured by evaluation or professional development, or student performance indicators such as value-added test score gains, student learning objectives, or other valid and reliable estimates of student achievement. “Merit pay” was the term most often used before PFP became popular and refers to teacher compensation based either on principal evaluations or, more recently, standardized test scores. Merit pay is essentially synonymous with PFP. “Incentive pay” is a more general term for giving teachers extra compensation, often for recruitment purposes to attract teachers to a particular school or subject area. However, the term “incentive” is often used in conjunction with PFP programs as reflecting part of their rationale. PFP programs are usually motivated by one or more of four related purposes—to encourage teachers to focus on improving measurable student performance, to promote retention of highly effective teachers, to attract highly qualified candidates to the teaching profession rather than a traditionally better-paid alternative, and to incentivize low-performing teachers to improve or leave the profession.
Literature Review
Our literature review draws on research from three areas of PFP for teachers: 1) the impact of PFP policy schemes on teachers; 2) teacher support for PFP policy schemes; 3) responses to PFP policies that vary according to teacher characteristics. We see the underlying rationale for PFP as influenced by motivation theories, which explain why people make the decisions they do, and equity theory which states that a person should be concerned about the way awards are distributed in a group (Lane and Messe, 1971). Kelley et al. (2002) and Yuan et al. (2013) relied on Vroom (1964) expectancy and Locke and Bryan (1968) goal-setting theories to guide their studies of motivation among teachers involved in PFP programs. PFP schemes can be characterized as attempts to influence teacher decisions to better meet organizational goals (Reeve, 2016). Their success potentially rests upon the teachers’ motivations to support them and their perceptions that the rewards are equitable or fair (Colquitt, 2012). PFP programs may both influence teacher motivation and be affected by it.
Early studies of various types of school reform concluded that few change efforts were successful without teacher commitment to the new policies (Firestone, 1989; Fuhrman et al., 1991; Odden and Marsh, 1988). Later work by Berends and colleagues on the New American Schools whole-school reform reached the same conclusion (Berends et al., 2002). Few researchers have examined PFP reform effects on teacher performance, primarily because it is more difficult to measure teacher productivity than that of workers in many other occupations (Hill & Jones, 2020). First, calculating the value-added effects of teachers on student achievement is controversial (see the recent description by Amrein-Beardsley, 2019 of a related lawsuit for example), and not all teacher assignments are associated with value-added scores. Second, observational evaluations are difficult to conduct reliably (Ho and Kane, 2013), and widely-used observation instruments may not lend themselves to certain teaching assignments such as art, music, physical education, or advanced algebra.
Despite these hurdles, Lavy (2009) found that PFP in Israel resulted in enhanced after-school teaching and responsiveness to students’ needs. Jones (2013) found that PFP for individual teachers in Florida resulted in greater work effort. On the other hand, Fryer (2013) found no effect for PFP on teacher absence or retention in New York City, and Yuan et al. (2013) in their randomized study of three programs found no effects on instruction, work effort, job stress, or collegiality.
Regarding PFP program effect on motivation, some studies examined teachers before a PFP system was introduced, others after. Munroe (2017) surveyed music teachers randomly assigned to one of two hypothetical groups. In one group teacher effectiveness for merit pay was to be measured by portfolio, in the other standardized test scores. Higher levels of motivation were recorded among the portfolio group. A randomized study of a PFP program in Metro Nashville Public Schools by Springer et al. (2011) found that 80% of the teachers in the PFP group reported no effect on their teaching because they were already motivated to work as effectively as possible before the PFP experiment. Similar results were obtained by Kozlowski and Lauen (2019), whose interviews with teachers about performance incentives revealed they were motivated to serve their students rather than maximize income and that they were already working as hard as they could. Kelley et al. (2002) studied PFP and motivation in Kentucky and North Carolina schools. In general, they found that teachers understood the program goals, were motivated to achieve them, and were not stressed by any added pressure.
Findings are mixed on teacher support for PFP schemes. Azordegan et al. (2005), Ballou and Podgursky (1993), and Heneman and Milanowski (1999) all found that teachers were generally in favor of PFP programs. Milanowski (2007) canvassed the opinions of teacher candidates and found that they, too, were generally in favor. A study of performance-based pay bonuses for teachers in the Indian State of Andhra Pradesh found that 80% of teachers liked the idea, involvement in the program enhanced support (but it declined with age, experience, training, and base pay), and initial support was related to subsequent teacher value added (Muralidharan and Sundararaman, 2011).
On the other hand, Cornett and Gaines (1994) found that teachers prefer to be compensated for extra work rather than performance and are only positive about PFP if they participate. They concluded that perceptions of unfairness and lack of support by teachers led to the failure of PFP programs across the country. Farkas et al. (2003) determined that 60% of teachers favor financial incentives for teachers with consistently outstanding principal evaluations but only 38 percent support them when performance is tied to standardized tests. Goldhaber et al. (2011) reported that only 17 percent favored PFP policies in Washington State. In their report of a Phi Delta Kappan poll of teacher attitudes Langdon and Vesper (2000), 53% were in favor of PFP versus 90% of the general public. A set of evaluation studies of the ProComp program in Denver and the Texas Educators Excellence Grant (TEEG) found consistent support for PFP policies (Springer et al., 2011; Wiley et al., 2010). Of relevance to the question of teacher support is the position of the two national teacher unions, which have traditionally been steadfastly in opposition to incentive pay and in favor of salaries based on academic degrees, preparation, growth, and length of service (Koppich, 2010). Most K-12 teachers belong to one or other of the unions.
Teachers’ responses to PFP programs have varied according to experience, grade level, and gender. Goldhaber et al. (2011) determined that veteran teachers were less supportive of PFP programs than novice teachers. Several studies found teachers in the upper grades were more supportive of PFP policies than elementary level teachers (Ballou and Podgursky, 1993; Farkas et al., 2003; Jacob and Springer, 2007; Goldhaber et al., 2011). Ballou and Podgursky (1993), Goldhaber et al. (2011), and Hill and Jones (2020) all found gender differences in responses to PFP programs, with male teachers tending to respond more positively than females.
Related to perceptions of the policy of PFP are teachers’ opinions of the appraisal systems that are used to evaluate them. Several researchers have noted discrepancies in perceptions among teachers and between teachers and administrators on this issue (e.g., Reddy et al., 2017; Paufler and Sloat, 2020). Overall, researchers report that teachers may feel demoralized or negatively pressured by systems that have components that are difficult to understand (e.g., Bradford and Braaten, 2018), and by systems that prioritize accountability over teacher development (e.g., Deneire et al., 2014; Cuevas et al., 2018; Derrington and Martinez, 2019; Ford and Hewitt, 2020). Many researchers recommend incorporating the voices of all appraisal system stakeholders to build common understanding and ensure buy-in (Reddy et al., 2017; King and Paufler, 2020).
To buy into a PFP program, teachers need a full understanding of the impact of the scheme on themselves and other stakeholders, and on how PFP decisions are made. Teachers are also likely to have beliefs about whether the PFP system will benefit the district in terms of teacher recruitment and improved retention. Also, teachers are apt to have greater buy-in if they believe the PFP system provides a fair opportunity for them to receive additional performance-based compensation. All these factors have the potential for driving the success (or failure) of a PFP policy.
Context for the Study
In the constant quest for improved teacher quality, PFP programs continue to be instituted in the United States and elsewhere. One such state-wide scheme was introduced by the 2019 Texas legislature in House Bill 3 (HB3). PFP is not new to Texas. In 2005 the Houston Independent School District (HISD) implemented a districtwide $14.5M PFP scheme while the state meanwhile had two other programs targeting schools with predominantly poor students. HISD has been described as “the poster child for doing professional compensation wrong” (Baratz-Snowden, 2007, p. 19). HISD compared the value-added scores of HISD teachers to teachers in 40 other schools across the state in order to measure performance that would earn extra compensation. The technicalities were a mystery to the teachers and so created confusion, there were accounting errors that required some teachers to return money, and there was little perceived equity in who received rewards. The administrators of HB3 were not going to make these mistakes.
The Relevant Legislation
The Texas Education Agency (TEA) described HB3 on their website as “a sweeping and historic school finance bill … one of the most transformative Texas education bills in recent history.”1 They named it the Teacher Incentive Allotment (TIA), whose goal was to provide a realistic pathway for top-performing teachers in the state to earn a six-figure salary. Like many PFP systems, the TIA was designed to help attract highly effective teachers to the profession and incentivize them to work in the hard-to-staff schools located in rural and high-poverty areas. The mechanism for doing so involves identifying the state’s top performing teachers and differentiating financial compensation to their districts based on the degree of rurality and poverty of individual campuses within participating districts (see www.tiatexas.org for state map with compensation amounts).
The policy underlying HB3 does not rest on the “flawed assumptions” alluded to by Kozlowski and Lauen (2019), and therefore may not be doomed to the “disappointing results” that they found in their research. The motivation for HB3 is far removed from Kozlowski and Lauen’s assumptions that teachers are primarily motivated by money and currently not working hard enough. Its purpose is to identify the highest performing teachers and reward them substantially, the more so if they work in hard-to-staff or rural schools. Thus, rather than incentifying them to “work harder,” HB3 is intended to 1) attract more of the best and brightest to the profession and 2) encourage the highest quality teachers to work in the schools that most need them.
The Program
Some features of the TIA program differ from traditional PFP schemes. For example, the TIA program is unique among PFP systems in that there are state-level requirements, but school districts decide how to satisfy them. Districts must demonstrate the reliability and validity of two appraisal components—observation and student growth—and then describe the system used for identifying and designating teachers for recognition. Having received the TEA approval, districts may identify top-performing teachers and make one of three tiered “designations” (Recognized, Exemplary, or Master).
Following an initial screening of applications, school districts submit appraisal data, including designation information, for system verification (i.e., verification that the designation system did, in fact, identify teachers who are among those most effective in the state). School districts, however, have significant control over the system they use for designation, including what instruments are used for teacher observations and the methods used for calculating student growth (e.g., value-added measures, pre- and post-tests, student learning objectives, portfolios), how each component is weighted, and whether additional components like student surveys are included in designation decisions. The effect of this policy, if not its purpose, is to allow considerable flexibility among school districts in their choice of teacher observation systems and measures of student growth. It is against this backdrop that the current research took place.
The Data
The TEA made available to district administrators a number of resources intended to help prepare for participation, including a buy-in survey to gauge, prior to implementation, the extent to which there is support for 1) participation in the TIA, and 2) the district plan for making designation decisions. Results from this survey could be included by districts at the time of application to help gauge the extent of support within the local education agency, and, if necessary, make changes.
The Research
The purpose of this study is two-fold. First, we present the psychometric properties of a new survey, the Teacher Buy-in Survey (TBS), designed to measure teacher buy-in for a state PFP scheme. Specifically, the first two research questions, RQ1 and RQ2, address the reliability and validity of the instrument and its factor structure:
RQ1. Is the instrument a reliable and valid tool for measuring understanding and perceptions of the TIA program among eligible teachers?
RQ2. Is the hypothesized factor structure adequately supported in a sample of eligible teachers and subgroups?
Second, we examine whether aspects of teacher buy-in vary among different groups of teachers. The groupings we identified were grade level, teaching assignment, and campus locale. We also looked at variations according to degree of information seen to be offered by the district, and expectations that the teachers themselves would receive a designation. The following research questions, RQ3 and RQ4, address these survey outcomes:
RQ3. Do teachers generally support PFP as represented by the TIA?
RQ4. How are the aspects of teacher buy-in different among eligible teachers and subgroups?
Although it is not always standard procedure for researchers to describe the statistical properties of a survey or questionnaire they may have developed for a policy-related study, we feel that there are potential policy implications if one cannot be assured that the results described have been generated by a reliable and valid instrument. We want to be certain that any future policy decisions are based on evidence, in this case the perceptions and buy-in of participating teachers, that truly represents the concepts or factors that we, the researchers, claim to have measured. For this reason, we make some effort here to assure policymakers and school district administrators that any of our findings that may influence their future decisions regarding the introduction of PFP schemes are based on sound scientific evidence.
Method
Sample
The target population was elementary, middle school, and high school teachers in Texas school districts electing to participate in the TIA program. A convenience sample of 3,001 eligible teachers in 13 participating districts was available to take the TBS, and it is their data that form the basis for this study.
Instrument Item Generation
We derived content for the instrument from research related to teacher appraisal systems as well as from directions provided by the Agency. We define buy-in according to three related constructs: 1) the extent to which teachers understand the local designation plan (understanding), 2) the extent to which teachers support their district moving forward with the application (attitudes), and 3) reasons why teachers support the system and the decision to move forward (perceptions of fairness). We generated items for the TBS to reflect these three constructs. First, researchers drafted a set of questions. These were reviewed and edits suggested by Agency members. We prepared a second draft of questions, which was subject to further edits before being finalized. To ensure the face validity of the TBS, we also compared the final items with those in an instrument developed by Dallas Independent School District that is used as part of their Teacher Excellence Initiative (see https://tei.dallasisd.org/). No further changes resulted from this comparison. All items used a 5-point Likert scale ranging from 1 (strongly disagree) to 5 (strongly agree).
Data Collection
Teachers responded to the TBS between April 6, 2020 and June 1, 2020. The participating districts provided the names and email addresses of eligible teachers, and a link to the online survey (operated by Qualtrics®) was sent to the email addresses. Study participation was voluntary. All participants submitted their consent to participate and agreed that responses would be kept confidential to the extent permitted by law and reports presented in aggregate. An electronic copy of survey responses was exported for data analysis.
Data Analysis
Data analysis proceeded in three stages. In the first stage, we conducted exploratory factor analysis (EFA) to identify the number and the nature of latent constructs (factors) that explain the associations (i.e., correlations) among the initial pool of 31 items. In the second stage, confirmatory factor analysis (CFA) evaluated the final set of 28 items in terms of 1) item reliability, 2) alignment to the hypothesized factor structure, 3) discriminant validity, and 4) measurement equivalence between teacher subgroups. Lastly, bivariate and multivariate tests were performed to compare the scores on the TBS between various subgroups of eligible teachers.
We split the sample into two random subsamples; we utilized the data from the first subsample (n = 700) for EFA providing the basis for constructing CFA models that were fitted to the data from the second subsample (n = 703) (see Fabrigar et al., 1999). The data split was done within each district, so that the distribution of teachers across the districts was almost identical between the two subsamples. The comparisons of teacher subgroups utilized the data from the full sample (N = 1,403). We completed all analyses using R (R Core Team, 2019) and Mplus 7.0 (Muthén and Muthén, 1998–2017).
Exploratory Factor Analysis
Retention of factors was guided by parallel analysis, in addition to more conventional methods such as scree test (Cattell, 1966) and eigenvalue greater than 1 (K1) criterion (Kaiser, 1960). Parallel analysis (Horn, 1965; Hayton et al., 2004) generates several random data sets and then compares eigenvalues derived from the random data against eigenvalues from real data. Factors that produce a real eigenvalue equal to or less than an average random eigenvalue are considered to explain no more than sampling variability in the real data and thus they are discarded. Only factors that account for “meaningful” variance of the data are retained (Humphreys and Montanelli, 1975; Montanelli and Humphreys, 1976; Turner, 1998). The validity of parallel analysis has been evidenced in various studies—i.e., it consistently outperforms other retention techniques (e.g., Zwick and Velicer, 1986; Glorfeld, 1995; Thompson and Daniel, 1996; Velicer et al., 2000).
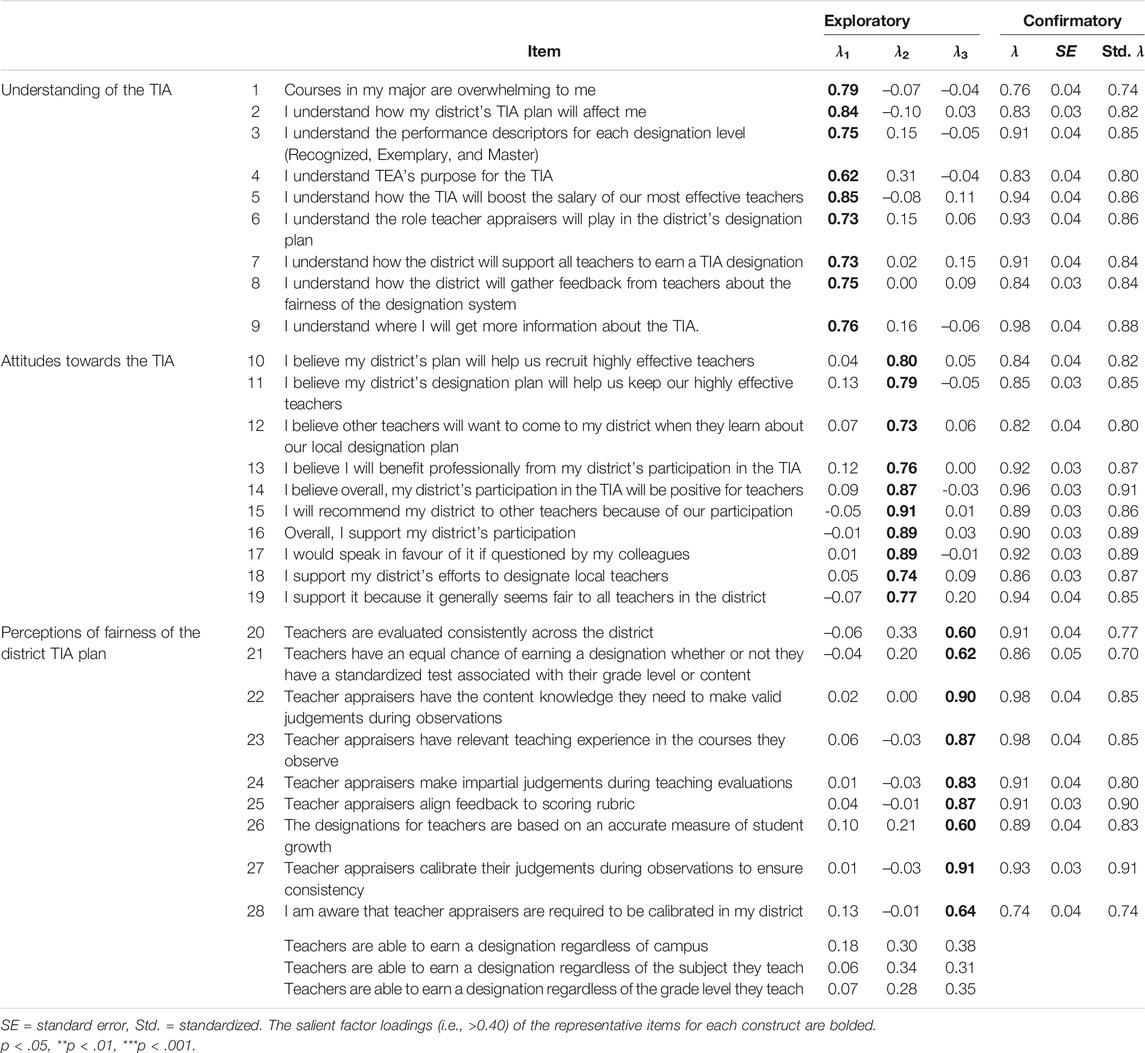
In this study, parallel analysis inspected 31 real eigenvalues (i.e., 31 items in the initial pool) in comparison to 31 average random eigenvalues from 200 random data sets. That is, the first (average) random eigenvalue was compared to the first real eigenvalue, the second random eigenvalue to the second real eigenvalue, and so on. Once we determined the number of factors for retention, we then fitted an EFA model to reveal the nature of the extracted factors and their indicators (items). Those items having a (unstandardized) factor loading equal to or greater than 0.40 were deemed representative of the factor (Hair et al., 1998; Backhaus et al., 2006).
Confirmatory Factor Analysis
We constructed a CFA model based on the findings from the preceding EFA (3 factors and their 28 indicators). The analysis proceeded as follows. First, we evaluated factor loadings as a test for item reliability. An item having a standardized loading less than 0.50 in absolute value was considered to lack reliability because 75% (= 1–0.502) or more variance of responses on that item is unique and thus unexplained by the factor (Kline, 2005). Second, we examined the discriminant validity of the instrument. Specifically, factor correlations less than 0.85 were considered to support discriminant validity for the set of factors (Kline, 2005). We also performed an empirical test by comparing the hypothesized CFA model against a series of nested models where the factor correlations were constrained to 1.00 (i.e., perfect collinearity) one by one (Anderson and Gerbing, 1988). If imposing a 1.00 correlation led to a considerable loss in model fit—∆CFI of 0.002 (Meade et al., 2008) or 0.01 (Cheung and Rensvold, 2002) and/or ∆RMSEA of 0.015 (Chen, 2007), the hypothesized model was favored over the alternative models, from which discriminant validity can be inferred. Third, we fitted a series of multiple-group mean-and-covariance-structure (MACS) models to confirm measurement equivalence of the instrument across different teacher subgroups—i.e., metric and scalar invariance (see Lee et al., 2011; Little and Lee, 2015). We conducted invariance testing by comparing a model in which specific parameters (i.e., items loadings and/or intercepts) are constrained to equality across groups and a nested model in which these parameters are freely estimated in all groups. If imposing equality constraints led to a substantial loss in fit (Cheung and Rensvold, 2002; Chen, 2007; Meade et al., 2008), the level of invariance being tested was rejected.
We evaluated the fit of all hypothesized models in terms of both absolute and comparative fit as measured by relative/normed model chi-square (χ2/df; Wheaton et al., 1977), root mean square error of approximation (RMSEA; Steiger and Lind, 1980), standardized root mean square residual (SRMR; Muthén and Muthén, 1998–2017), comparative fit index (CFI; Bentler, 1990), and Tucker-Lewis index (TLI; Tucker and Lewis, 1973). In general, acceptable χ2/df values range from 2 (Tabachnick and Fidell, 2007) to 5 (Wheaton et al., 1977) while lower values indicate good fit. An RMSEA/SRMR value equal to or less than 0.08 (Browne and Cudeck, 1992) and a CFI/TLI value equal to or greater than 0.90 (Hoyle and Panter, 1995) deem acceptable, though lower RMSEA/SRMR values (≤0.06) and higher CFI/TLI values (≥0.95) are generally preferred (Hu and Bentler, 1999).
Teacher Subgroup Comparisons
We created scale scores for each teacher by averaging his or her responses on the items within each retained factor (3 scores). On the 5-point Likert scale, scores could range from 1 to 5 with a higher value indicating a higher level of the construct—for example, a greater understanding of the TIA. We conducted analysis of variance (ANOVA) or independent-samples t-test (with Satterthwaite approximation if appropriate) depending on the number of subgroups being compared. When ANOVA indicated a significant overall group difference at 0.05 alpha level, the subgroups were pairwise compared at a Bonferroni-corrected alpha level.
Results
Sample Demographics
Of 3,001 eligible teachers in 13 participating districts, 1,403 or 46.8% completed the online survey. We found this response rate to be satisfactory, given that it was a low-stakes, voluntary survey, with no immediate incentive (such as a stipend) offered for completion. Of those 1,403 participants, the largest group (45.4%) was elementary-level teachers and the majority taught core curriculum (59.9%). More than two thirds of the participants were working at suburban campuses (71.4%) and 6.1% at charter schools.
RQ 1
Parallel analysis suggested that three factors are optimal, as the first three eigenvalues from the real data (19.70–1.46) were larger than the parallel eigenvalues derived from 200 random data sets (1.41–1.32) (see Figure 1). In addition, a stiff “cliff” between the third and fourth (real) eigenvalues (Δ = 0.48) followed by a shallow “scree” provided additional support for three factors.
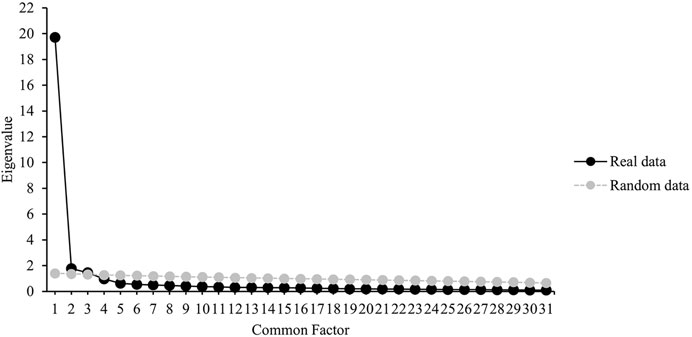
FIGURE 1. Eigenvalues from real data and random data. Note. Black dots represent eigenvalues obtained from real data, and gray dots represent eigenvalues averaged across 200 random data sets.
The 3-factor EFA solution, via maximum likelihood (ML) estimation and quartimin oblique rotation, was inspected to identify salient indicators (items) of each individual factor. Of those 31 items in the initial pool, three had a factor loading smaller than 0.40 and they were excluded from further analyses. It is possible that the low loadings were triggered by the wording “are able to” in these three items. Table 1 shows the three excluded items and the 28 reserved at this exploratory stage, which characterize the three factors: Understanding of the TIA, Attitudes towards the TIA, Perceptions of Fairness of the district’s TIA plan.
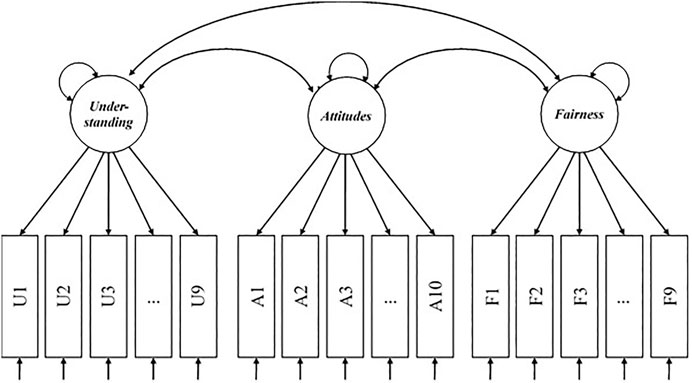
RQ 2
Figure 2 depicts the factor structure hypothesized in the CFA model. The χ2/df of 3.69 (= 1253.81/340) indicated good fit of the model. Both the RMSEA value of 0.08 and the SRMR value of 0.07 suggested close fit of the model to the data. In addition, the model’s comparative fit was satisfactory—CFI = 0.95 and TLI = 0.94.
Table 1 presents the (unstandardized and standardized) factor loadings from the 3-factor CFA solution. The factor loadings of all 28 items were significant at 0.001 alpha level. The Attitudes items produced slightly higher standardized loadings (median = 0.86, range = 0.80–0.91) and thus greater reliability at the item level, compared to the Understanding (median = 0.84, range = 0.74–0.88) and Fairness (median = 0.83, range = 0.70–0.91) items.
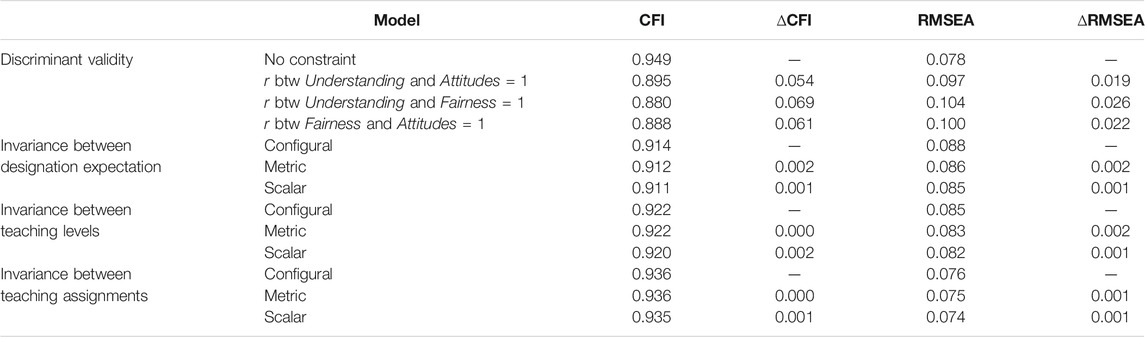
The factor correlations were significant and in the expected directions (0.76–0.83). They were all less than 0.85, suggesting adequate discriminant validity for the three factors. Further, significant results of ΔCFI and ΔRMSEA tests provided additional support for the discriminant validity of the instrument (Table 2).
Multiple-group MACS analysis, which was based on the final CFA model, was performed using 1) three teacher groups of designation expectation: teachers who expect a designation, those who do not, and those are unsure; 2) three teacher groups of grade level: elementary, middle school, and high school; and 3) two groups of teaching assignment: core curriculum and other subjects. The results of invariance testing were summarized in Table 2. Imposing equality constraints on the loadings and/or intercepts yielded a trivial loss in model fit, indicating that the items have the same unit of measurement and the same origin (i.e., scalar invariance) and therefore comparisons of item responses and factor means between different 1) designation expectations, 2) grade levels, and 3) teaching assignments are tenable (Widaman and Reise, 1997).
In summary, the CFA results supported the ability of the TBS for adequately (i.e., reliably and validly) measuring teachers’ understanding and perceptions about the TIA and their districts’ TIA plan.
RQ 3
We measured three components of buy-in or support among the teachers who responded to the TBS: Understanding, Attitudes, and perception of Fairness. Looking at each of these across the different teaching assignments, we see that responses ranged on the 5-point scale as follows: for Understanding 71.3–79.5%; for Attitudes 72.7–84.6%; and for Fairness 72.1–81.9%. This represents a high general level of buy-in or support for the TIA across all teaching assignments, comparing favorably with that reported in other studies, which ranged from a low of 17% (Goldhaber et al., 2011 to a high of 80% (Muralidharan and Sundararaman, 2010).
RQ 4
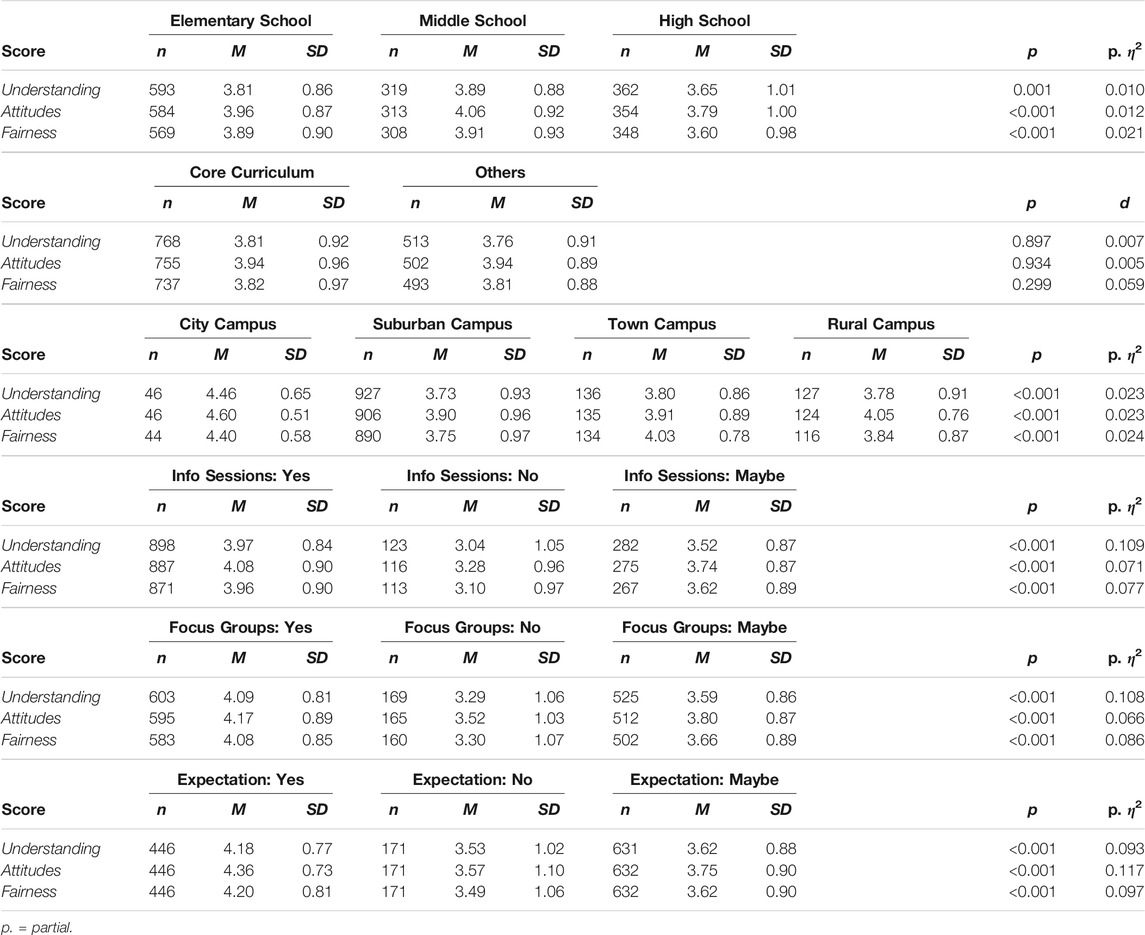
Table 3 shows the understanding, attitudes, and fairness scores for different subgroups of eligible teachers along with the results for the subgroup comparisons In general, middle-school teachers reported the highest levels on all three components. Elementary school teachers were next, followed by those in the high schools. Pairwise comparisons indicated significant differences between the elementary vs high schools (all corrected p < 0.001) and between the middle vs high schools (all corrected p < 0.001).
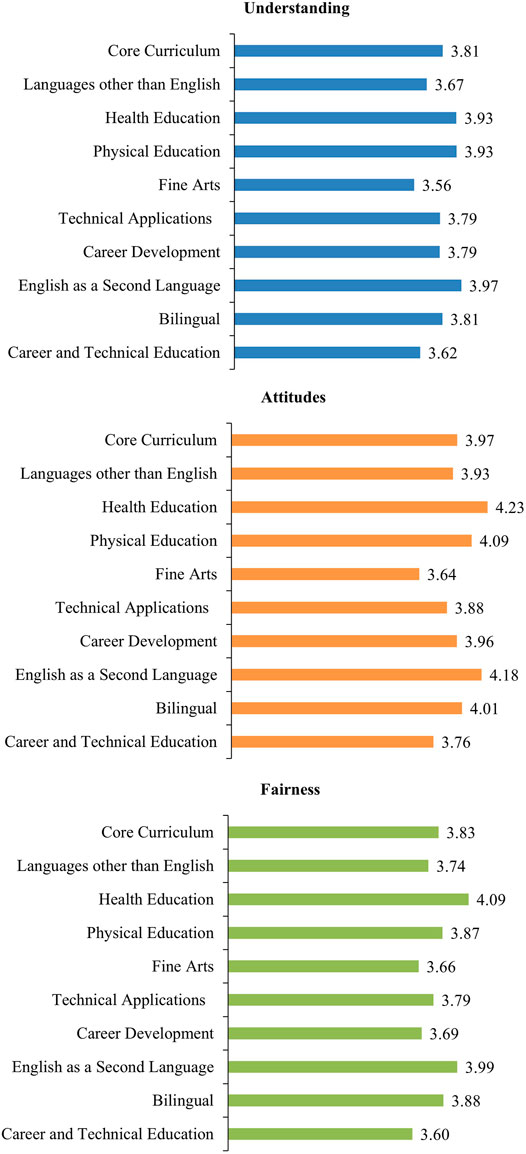
Figure 3 presents the mean scale scores by teaching assignment. Although the scores varied across individual assignments, teachers who teach the core curriculum showed similar levels of understanding, attitudes, and fairness as compared to those who teach other subjects (all p > 0.05).
As shown in Table 3, teachers in the city campuses had the highest levels of understanding, attitudes, and fairness about the district’s TIA plan. Their scores were significantly higher than the scores for teachers in the suburban campuses (all corrected p < 0.001), town campuses (all corrected p < 0.001, except for fairness), or rural campuses (all corrected p < 0.001). The scores did not differ among teachers who were working at the suburban, town, or rural campuses (all corrected p > 0.05).
Teachers who were aware of district information sessions for teachers about TIA had the highest levels of understanding, attitudes, and fairness about the district’s TIA plan, followed by those who are unsure and those who were unaware. All pairwise comparisons of these three subgroups were significant (all corrected p < 0.001). Similarly, teachers who were aware that the district held focus groups with teachers about TIA showed the highest levels of understanding, attitudes, and fairness, followed by those who are unsure or unaware (all corrected p < 0.001).
Teachers who expect to earn a designation demonstrated the highest levels of understanding, attitude, support, and fairness regarding the district’s TIA plan, followed by those who are unsure (all corrected p < 0.001) and those who did not expect a designation (all corrected p < 0.001). The scores were comparable between the latter two subgroups (all corrected p > 0.05).
Discussion
Regarding the properties of the TBS, our findings contribute to an under-developed area of policy research related to buy-in to PFP programs. We have demonstrated that the TBS provides a reliable measure for assessing teachers’ overall level of buy-in or support for the TIA, including their understanding of the designation system, how it would affect salary, and the role that appraisals would play. The TBS also enabled assessment of teachers’ beliefs about the positive outcomes that would accrue from participation, including helping the district recruit and retain effective teachers, and teachers’ willingness to speak in support of the program. The instrument was further able to reliably assess teachers’ perceptions of fairness of the designation system itself (e.g., teachers have an equal chance of earning designation regardless of campus/teaching assignment/subject) after exclusion of the three items whose wording may have suggested “capacity” rather than fairness to the respondents. Instead, observation protocols, as well as perceived fairness of appraisal, seemed to figure more prominently into the underlying subscale.
The overall levels of support represented by their responses to the TBS suggest that TEA and the participating school districts have done a good job of making the program transparent to teachers, and generally involving and engaging them in the pay reform represented by the program (Max & Koppich, 2009). The level of buy-in represented in our data matches those studies that found teachers were generally supportive of PFP programs, either in theory or in practice, and considered the method for evaluating teachers as equitable. TEA viewed the achievement of teacher buy-in as a critical condition for the TIA of reaching its goals of recruiting and retaining high quality teachers, particularly in rural and hard-to-staff schools, and raising teacher salaries.
The results comparing different teacher groupings should be interpreted with some caution, since over half the sample did not complete the survey (overall response rate = 46.8%). Those who did were differentially encouraged by their district administrators, resulting in uneven response rates among districts (4.9–90.9%). This caveat aside, it is evident that degree of teacher buy-in for the TIA among those who responded was influenced by different teacher attributes. Perhaps least surprising is the fact that those teachers who expected to be designated for incentive pay showed higher levels of buy-in than those who did not. They apparently took more trouble to find out about the program, showed positive attitudes towards it, and perceived it to be fair. Although understandable, this is not a given, and school districts should be heartened that those who feel they deserve recognition are informed and confident about the program designed to evaluate them.
A little less expected, and with no obvious explanation, is the finding that high school teachers measured significantly lower on all aspects of buy-in than both elementary and middle-school teachers, with middle-school teachers showing the highest levels of buy-in. Without further information it is difficult to develop logical hypotheses as to why high school teachers are less motivated to find out about the incentive pay scheme, are less supportive, and have lower perceptions of its fairness than teachers at the other grade levels. It is worth noting that, in contrast to our finding, Goldhaber et al. (2011) study reported that high school and middle school teachers were more likely than elementary teachers to prefer merit pay over other incentives such as smaller classes or a teacher’s aide.
Looking at the demographic differences of campuses, we see that teachers in the city campuses recorded significantly higher levels in all three constructs than teachers in the town, suburban, and rural settings. Perhaps teachers who live and teach in the cities are subject to higher costs of living and thus more likely to respond to an initiative that promises significant salary increases. This finding, in fact, bodes well for one of the policy intentions of HB3. Since salaries for designated teachers in rural districts will receive proportionately higher increases in this program, it is possible that this may draw in some high performing city teachers who are struggling with the higher costs of urban living or otherwise less motivated to move to a rural community.
Our study was limited, as we have noted, by a response rate that was depressed by the fact that the survey was voluntary, teachers were variously encouraged by district administrators to participate, and they were not offered an incentive to complete it. The convenience sampling employed may have led to a non-representative sample of the target population, which may limit the generalizability of current findings. Further, in the interests of anonymity, we had no access to gender and years of teaching experience, two factors that we have already seen may affect response to teacher incentive pay.
These limitations notwithstanding, it is apparent that, no matter the groupings identified in our study, degree of support for the incentive program and perceptions of its fairness (at least at the outset) follow the levels of understanding that teachers acknowledge. If teachers were aware of district information sessions and focus groups about the TIA, then they were significantly more likely to show higher levels of buy-in. This points unequivocally to the importance of district communication and getting the word out to all teachers about the proposed teacher incentive scheme. The more you know about it, the more you are likely to support it. This finding is in line with previous reports that teachers were opposed to PFP schemes until they became more involved and has policy implications both at the district and the state level. The state administrators my wish to add further guidelines, or even requirements, as to how districts should inform their teachers about proposed PFP programs. The additional information on the different subgroups may be of use to districts who intend to enroll in the TIA or similar PFP schemes in the future, in particular with regard to their plans for advance communications about the program, and how to target those communications towards groups who are less likely to be open to buy-in.
In summary, our findings have three main implications for policymakers. First, and in corroboration with previous research, the more thoroughly teachers are informed in advance about a PFP program, the more likely they are to show support for it. Therefore, state and district authorities should devote considerable effort into clear communication of the purpose for the PFP and mechanisms for implementing it. Second, PFP schemes will not succeed if stakeholders, particularly teachers (and, by implication, their unions) are not supportive of its goals and the mechanisms for achieving them. It is too late to wait until the program is fully established before canvassing the teachers to determine their level of buy-in. If teacher buy-in is measured early in the process, as it was done for the TIA, any evidence of early push-back may still leave the program organizers time to make necessary adaptations. Third, it cannot be assumed that all teachers will respond in the same way to PFP programs, and districts would do well to direct specific effort towards informing and convincing subgroups of teachers who are more likely to be apathetic, resistant, or even opposed to the notion of PFP. Given the generally high levels of buy-in we found among the teachers who were knowledgeable about the program, TIA program leaders should be heartened that their initiative has goals that resonate with these teachers: to reward high quality teachers in ways that improve recruitment and retention in the State’s most hard-to-staff schools.
It remains to be seen whether these goals will actually be realized, and whether the levels of buy-in we identified hold up after the first round of designations is complete and some teachers begin to receive salary increases. We note the findings of Mintrop et al. (2018), who found that charter school teachers’ responses to a teacher incentive program began with enthusiasm (“consonance”) during the adoption phase, but were then followed by a period of resistance (“dissonance”), and finally, after the power of the incentive function had dulled, reached the acceptance phase (“resonance”). We look forward to conducting further surveys with teachers in districts participating in the Texas TIA after they have received designations to see if similar or different patterns transpire, and to examine any changes that do occur in support of the PFP program in general and their district scheme in particular. We also plan in the longer term to assess whether the TIA’s policy goals of attracting the best teachers to the most needed schools are achieved.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics Statement
The studies involving human participants were reviewed and approved by Texas Tech University IRB. The patients/participants provided their written informed consent to participate in this study.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1See https://tea.texas.gov/about-tea/government-relations-and-legal/government-relations/house-bill-3.
References
Aaronson, D., Barrow, L., and Sander, W. (2007). Teachers and Student Achievement in the Chicago Public High Schools. J. labor Econ. 25 (1), 95–135. doi:10.1086/508733
Amrein-Beardsley, A. (2019). The Education Value-Added Assessment System (EVAAS) on Trial: A Precedent-Setting Lawsuit with Implications for Policy and Practice. Flagstaff: eJEP: eJournal of Education Policy. http://nau.edu/COE/eJournal/.
Anderson, J. C., and Gerbing, D. W. (1988). Structural Equation Modeling in Practice: A Review and Recommended Two-step Approach. Psychol. Bull. 103 (3), 411–423. doi:10.1037/0033-2909.103.3.411
Azordegan, J., Byrnett, P., Campbell, K., Greenman, J., and Coulter, T. (2005). Diversifying Teacher Compensation. Issue Paper. Denver: Education Commission of the States.
Backhaus, K., Erichson, B., Plinke, W., and Weiber, R. (2006). Multivariate Analysis Methods: An Application-Oriented Introduction. Berlin, Germany: Springer.
Ballou, D., and Podgursky, M. (1993). Teachers' Attitudes toward merit Pay: Examining Conventional Wisdom. ILR Rev. 47 (1), 50–61. doi:10.1177/001979399304700104
Baratz-Snowden, J. C. (2007). The Future of Teacher Compensation: Déjà Vu or Something New? Washington: Center for American Progress.
Bentler, P. M. (1990). Comparative Fit Indexes in Structural Models. Psychol. Bull. 107 (2), 238–246. doi:10.1037/0033-2909.107.2.238
Berends, M., Bodilly, S., and Kirby, S. N. (2002). Looking Back over a Decade of Whole-School Reform: The Experience of New American Schools. Phi Delta Kappan 84 (2), 168–175. doi:10.1177/003172170208400214
Bradford, C., and Braaten, M. (2018). Teacher Evaluation and the Demoralization of Teachers. Teach. Teach. Educ. 75, 49–59. doi:10.1016/j.tate.2018.05.017
Browne, M. W., and Cudeck, R. (1992). Alternative Ways of Assessing Model Fit. Sociological Methods Res. 21 (2), 230–258. doi:10.1177/0049124192021002005
Burgess, S., Croxson, B., Gregg, P., and Propper, C. (2001). The Intricacies of the Relationship between Pay and Performance of Teachers: Do Teachers Respond to Performance Related Pay Schemes? Centre for Market and Public Organisation. Bristol: University of Bristol. Working Paper, Series No. 01/35.
Cattell, R. B. (1966). The Scree Test for the Number of Factors. Multivariate Behav. Res. 1 (2), 245–276. doi:10.1207/s15327906mbr0102_10
Chen, F. F. (2007). Sensitivity of Goodness of Fit Indexes to Lack of Measurement Invariance. Struct. Equation Model. A Multidisciplinary J. 14 (3), 464–504. doi:10.1080/10705510701301834
Cheung, G. W., and Rensvold, R. B. (2002). Evaluating Goodness-Of-Fit Indexes for Testing Measurement Invariance. Struct. Equation Model. A Multidisciplinary J. 9 (2), 233–255. doi:10.1207/s15328007sem0902_5
Colquitt, J. A. (2012). “Organizational justice,” in The Oxford Handbook of Organizational Psychology. Editor S. W. J. Kozlowski (Oxford University Press), Vol. 1, 526–547. doi:10.1093/oxfordhb/9780199928309.013.0016
Cornett, L. M., and Gaines, G. F. (1994). Reflecting on Ten Years of Incentive Programs: The 1993 SREB Career Ladder Clearinghouse Survey. Southern Regional Education Board Career Ladder Clearinghouse. Atlanta, Georgia: Southern Regional Education Board.
Cuevas, R., Ntoumanis, N., Fernandez-Bustos, J. G., and Bartholomew, K. (2018). Does Teacher Evaluation Based on Student Performance Predict Motivation, Well-Being, and Ill-Being? J. Sch. Psychol. 68, 154–162. doi:10.1016/j.jsp.2018.03.005
Deneire, A., Vanhoof, J., Faddar, J., Gijbels, D., and Van Petegem, P. (2014). Characteristics of Appraisal Systems that Promote Job Satisfaction of Teachers. Educ. Res. Perspect. 41 (1), 94–114.
Derrington, M. L., and Martinez, J. A. (2019). Exploring Teachers' Evaluation Perceptions: A Snapshot. NASSP Bull. 103 (1), 32–50. doi:10.1177/0192636519830770
Fabrigar, L. R., Wegener, D. T., MacCallum, R. C., and Strahan, E. J. (1999). Evaluating the Use of Exploratory Factor Analysis in Psychological Research. Psychol. Methods 4 (3), 272–299. doi:10.1037/1082-989x.4.3.272
Farkas, S., Johnson, J., and Duffett, A. (2003). Stand by Me: What Teachers Really Think about Unions, Merit Pay, and Other Professional Matters. New York: Public Agenda Foundation.
Firestone, W. A. (1989). Educational Policy as an Ecology of Games. Educ. Res. 18 (7), 18–24. doi:10.3102/0013189x018007018
Ford, T. G., and Hewitt, K. (2020). Better Integrating Summative and Formative Goals in the Design of Next Generation Teacher Evaluation Systems. epaa 28 (63), 63. doi:10.14507/epaa.28.5024
Fryer, R. G. (2013). Teacher Incentives and Student Achievement: Evidence from New York City Public Schools. J. Labor Econ. 31 (2), 373–407. doi:10.1086/667757
Fuhrman, S., Clune, W., and Elmore, R. (1991). “Research on Education Reform: Lessons on the Implementation of Policy,” in Education Policy Implementation. Editor A. Odden (Albany: State University of New York Press).
Glorfeld, L. W. (1995). An Improvement on Horn's Parallel Analysis Methodology for Selecting the Correct Number of Factors to Retain. Educ. Psychol. Meas. 55 (3), 377–393. doi:10.1177/0013164495055003002
Goldhaber, D., DeArmond, M., and DeBurgomaster, S. (2011). Teacher Attitudes about Compensation Reform: Implications for Reform Implementation. ILR Rev. 64 (3), 441–463. doi:10.1177/001979391106400302
Hair, J. F., Anderson, R. E., Tatham, R. L., and Black, W. C. (1998). Multivariate Data Analysis. 5th ed. Upper Saddle River: Prentice-Hall.
Hayton, J. C., Allen, D. G., and Scarpello, V. (2004). Factor Retention Decisions in Exploratory Factor Analysis: A Tutorial on Parallel Analysis. Organizational Res. Methods 7 (2), 191–205. doi:10.1177/1094428104263675
Heneman III, H. G., and Milanowski, A. T. (1999). Teachers Attitudes about Teacher Bonuses under School-Based Performance Award Programs. J. Personnel Eval. Educ. 12 (4), 327–341. doi:10.1023/a:1008063827691
Hill, A. J., and Jones, D. B. (2020). The Impacts of Performance Pay on Teacher Effectiveness and Retention. J. Hum. Resour. 55 (1), 349–385. doi:10.3368/jhr.55.2.0216.7719r3
Ho, A. D., and Kane, T. J. (2013). The Reliability of Classroom Observations by School Personnel. Seattle: Bill & Melinda Gates Foundation. Research Paper. MET Project Available at: https://files.eric.ed.gov/fulltext/ED540957.pdf .
Horn, J. L. (1965). A Rationale and Test for the Number of Factors in Factor Analysis. Psychometrika 30 (2), 179–185. doi:10.1007/bf02289447
Hoyle, R. H., and Panter, A. T. (1995). “Writing about Structural Equation Models,” in Structural Equation Modeling: Concepts, Issues, and Applications. Editor R. H. Hoyle (Thousand Oaks: Sage), 158–176.
Hu, L. T., and Bentler, P. M. (1999). Cutoff Criteria for Fit Indexes in Covariance Structure Analysis: Conventional Criteria versus New Alternatives. Struct. Equation Model. A Multidisciplinary J. 6 (1), 1–55. doi:10.1080/10705519909540118
Humphreys, L. G., and Montanelli Jr., R. G. (1975). An Investigation of the Parallel Analysis Criterion for Determining the Number of Common Factors. Multivariate Behav. Res. 10 (2), 193–205. doi:10.1207/s15327906mbr1002_5
Jacob, B., and Springer, M. G. (2007). Teacher Attitudes on Pay for Performance: A Pilot Study. Nashville: National Center on Performance Incentives. Working Paper 2007-06.
Jones, M. D. (2013). Teacher Behavior under Performance Pay Incentives. Econ. Educ. Rev. 37 (1), 148–164. doi:10.1016/j.econedurev.2013.09.005
Kaiser, H. F. (1960). The Application of Electronic Computers to Factor Analysis. Educ. Psychol. Meas. 20 (1), 141–151. doi:10.1177/001316446002000116
Kelley, C., Heneman III, H., and Milanowski, A. (2002). Teacher Motivation and School-Based Performance Awards. Educ. Adm. Q. 38 (3), 372–401. doi:10.1177/00161x02038003005
King, K. M., and Paufler, N. A. (2020). Excavating Theory in Teacher Evaluation: Evaluation Frameworks as Wengerian Boundary Objects. Educ. Pol. Anal. Arch. 28 (57), 1–12. doi:10.14507/epaa.28.5020
Kline, R. B. (2005). Principles and Practice of Structural Equation Modeling. 2nd ed. New York: The Guilford Press.
Koppich, J. E. (2010). Teacher Unions and New Forms of Teacher Compensation. Phi Delta Kappan 91 (8), 22–26. doi:10.1177/003172171009100805
Kozlowski, K. P., and Lauen, D. L. (2019). Understanding Teacher Pay for Performance: Flawed Assumptions and Disappointing Results. Teach. Coll. Rec. 121 (2), 1–38.
Lane, I. M., and Messe, L. A. (1971). Equity and the Distribution of Rewards. J. Personal. Soc. Psychol. 20 (1), 1–17. doi:10.1037/h0031684
Langdon, C. A., and Vesper, N. (2000). The Sixth Phi Delta Kappa Poll of Teachers' Attitudes toward the Public Schools. The Phi Delta Kappan 81 (8), 607–611.
Lavy, V. (2009). Performance Pay and Teachers' Effort, Productivity, and Grading Ethics. Am. Econ. Rev. 99 (5), 1979–2011. doi:10.1257/aer.99.5.1979
Lee, J., Little, T. D., and Preacher, K. J. (2011). “Methodological Issues in Using Structural Equation Models for Testing Differential Item Functioning,” in Cross-cultural Data Analysis: Methods and Applications. Editors E. Davidov, P. Schmidt, and J. Billiet (New York: Routledge), 55–85.
Little, T. D., and Lee, J. (2015). “Factor Analysis: Multiple Groups,” in Wiley StatsRef: Statistics Reference Online. Editors N. Balakrishnan, B. Everitt, W. Piegorsch, and F. Ruggeri (Wiley), 1–10. doi:10.1002/9781118445112.stat06494.pub2
Locke, E. A., and Bryan, J. F. (1968). Goal-setting as a Determinant of the Effect of Knowledge of Score on Performance. Am. J. Psychol. 81 (3), 398–406. doi:10.2307/1420637
Max, J., and Koppich, J. E. (2009). Engaging Stakeholders in Teacher Pay Reform. Emerging Issues. Washington: Center for Educator Compensation Reform.
Meade, A. W., Johnson, E. C., and Braddy, P. W. (2008). Power and Sensitivity of Alternative Fit Indices in Tests of Measurement Invariance. J. Appl. Psychol. 93 (3), 568–592. doi:10.1037/0021-9010.93.3.568
Milanowski, A. (2007). Performance Pay System Preferences of Students Preparing to Be Teachers. Educ. Finance Pol. 2 (2), 111–132. doi:10.1162/edfp.2007.2.2.111
Mintrop, R., Ordenes, M., Coghlan, E., Pryor, L., and Madero, C. (2018). Teacher Evaluation, Pay for Performance, and Learning Around Instruction: between Dissonant Incentives and Resonant Procedures. Educ. Adm. Q. 54 (1), 3–46. doi:10.1177/0013161x17696558
Montanelli, R. G., and Humphreys, L. G. (1976). Latent Roots of Random Data Correlation Matrices with Squared Multiple Correlations on the diagonal: A Monte Carlo Study. Psychometrika 41 (3), 341–348. doi:10.1007/bf02293559
Munroe, A. (2017). Measuring Student Growth within a merit-pay Evaluation System: Perceived Effects on Music Teacher Motivation Career Commitment. Contrib. Music Educ. 42, 89–105.
Muralidharan, K., and Sundararaman, V. (2011). Teacher Opinions on Performance Pay: Evidence from India. Econ. Educ. Rev. 30 (3), 394–403. doi:10.1016/j.econedurev.2011.02.001
Odden, A., and Marsh, D. (1988). How Comprehensive Reform Legislation Can Improve Secondary Schools. Phi Delta Kappan 69 (8), 593–598.
Paufler, N. A., and Sloat, E. F. (2020). Using Standards to Evaluate Accountability Policy in Context: School Administrator and Teacher Perceptions of a Teacher Evaluation System. Stud. Educ. Eval. 64, 100806. doi:10.1016/j.stueduc.2019.07.007
Pham, L. D., Nguyen, T. D., and Springer, M. G. (2020). Teacher Merit Pay: A Meta-Analysis. Am. Educ. Res. J. 58, 527–566. doi:10.3102/0002831220905580
R Core Team (2019). R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing.
Reddy, L. A., Dudek, C. M., Peters, S., Alperin, A., Kettler, R. J., and Kurz, A. (2017). Teachers' and School Administrators' Attitudes and Beliefs of Teacher Evaluation: a Preliminary Investigation of High Poverty School Districts. Educ. Asse Eval. Acc. 30 (1), 47–70. doi:10.1007/s11092-017-9263-3
Reeve, J. (2016). A Grand Theory of Motivation: Why Not? Motiv. Emot. 40 (1), 31–35. doi:10.1007/s11031-015-9538-2
Rivkin, S. G., Hanushek, E. A., and Kain, J. F. (2005). Teachers, Schools, and Academic Achievement. Econometrica 73 (2), 417–458. doi:10.1111/j.1468-0262.2005.00584.x
Springer, M. G., Ballou, D., Hamilton, L., Le, V. N., Lockwood, J., McCaffrey, D. F., et al. (2011). Teacher Pay for Performance: Experimental Evidence from the Project on Incentives in Teaching (POINT). Evanston: Society for Research on Educational Effectiveness.
Steiger, J. H., and Lind, J. C. (1980). Statistically Based Tests for the Number of Common Factors Conference Presentation. Iowa City, IA: the Annual Spring Meeting of the Psychometric Society.
Tabachnick, B. G., and Fidell, L. S. (2007). Using Multivariate Statistics. 5th ed. Boston: Allyn & Bacon/Pearson Education.
Thompson, B., and Daniel, L. G. (1996). Factor Analytic Evidence for the Construct Validity of Scores: A Historical Overview and Some Guidelines. Educ. Psychol. Meas. 56 (2), 197–208. doi:10.1177/0013164496056002001
Thompson, G., and Price, A. (2012). Performance Pay for Australian Teachers: A Critical Policy Historiography. The Soc. Educator 30 (2), 3–12.
Tucker, L. R., and Lewis, C. (1973). A Reliability Coefficient for Maximum Likelihood Factor Analysis. Psychometrika 38 (1), 1–10. doi:10.1007/bf02291170
Turner, N. E. (1998). The Effect of Common Variance and Structure Pattern on Random Data Eigenvalues: Implications for the Accuracy of Parallel Analysis. Educ. Psychol. Meas. 58 (4), 541–568. doi:10.1177/0013164498058004001
Velicer, W. F., Eaton, C. A., and Fava, J. L. (2000). “Construct Explication through Factor or Component Analysis: A Review and Evaluation of Alternative Procedures for Determining the Number of Factors or Components,” in Problems and Solutions in Human Assessment: Honoring Douglas N. Jackson at Seventy. Editors R. D. Goffin, and E. Helmes (New York: Kluwer Academic/Plenum Publishers), 41–71. doi:10.1007/978-1-4615-4397-8_3
Wheaton, B., Muthén, B., Alwin, D. F., and Summers, G. F. (1977). Assessing Reliability and Stability in Panel Models. Sociological Methodol. 8, 84–136. doi:10.2307/270754
Widaman, K. F., and Reise, S. P. (1997). “Exploring the Measurement Invariance of Psychological Instruments: Applications in the Substance Use Domain,” in The Science of Prevention: Methodological Advances from Alcohol and Substance Abuse Research. Editors K. J. Bryant, M. Windle, and S. G. West (Washington: American Psychological Association), 281–324. doi:10.1037/10222-009
Yuan, K., Le, V.-N., McCaffrey, D. F., Marsh, J. A., Hamilton, L. S., Stecher, B. M., et al. (2013). Incentive Pay Programs Do Not Affect Teacher Motivation or Reported Practices. Educ. Eval. Pol. Anal. 35 (1), 3–22. doi:10.3102/0162373712462625
Keywords: teacher incentive allotment, pay-for-performance, merit pay, teacher appraisal, teacher buy-in, support, fairness
Citation: Lee J, Strong M, Hamman D and Zeng Y (2021) Measuring Teacher Buy-in for the Texas Pay-for-Performance Program. Front. Educ. 6:729821. doi: 10.3389/feduc.2021.729821
Received: 23 June 2021; Accepted: 09 August 2021;
Published: 17 August 2021.
Edited by:
Manpreet Kaur Bagga, Partap College of Education, IndiaReviewed by:
Laura Sara Agrati, University of Bergamo, ItalyMandeep Bhullar, Bhutta College Of Education, India
Copyright © 2021 Lee, Strong, Hamman and Zeng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jaehoon Lee, amFlaG9vbi5sZWVAdHR1LmVkdQ==
 Jaehoon Lee
Jaehoon Lee Michael Strong
Michael Strong Doug Hamman
Doug Hamman Yifang Zeng
Yifang Zeng