- 1Department of Education, Uppsala University, Uppsala, Sweden
- 2Department of Education, Culture and Communication, Malardalen University, Vasteras, Sweden
- 3School of Natural Sciences, Technology and Environmental Studies, Sodertorn University, Huddinge, Sweden
- 4Faculty of Education, Gothenburg University, Gothenburg, Sweden
Mathematical problem-solving constitutes an important area of mathematics instruction, and there is a need for research on instructional approaches supporting student learning in this area. This study aims to contribute to previous research by studying the effects of an instructional approach of cooperative learning on students’ mathematical problem-solving in heterogeneous classrooms in grade five, in which students with special needs are educated alongside with their peers. The intervention combined a cooperative learning approach with instruction in problem-solving strategies including mathematical models of multiplication/division, proportionality, and geometry. The teachers in the experimental group received training in cooperative learning and mathematical problem-solving, and implemented the intervention for 15 weeks. The teachers in the control group received training in mathematical problem-solving and provided instruction as they would usually. Students (269 in the intervention and 312 in the control group) participated in tests of mathematical problem-solving in the areas of multiplication/division, proportionality, and geometry before and after the intervention. The results revealed significant effects of the intervention on student performance in overall problem-solving and problem-solving in geometry. The students who received higher scores on social acceptance and friendships for the pre-test also received higher scores on the selected tests of mathematical problem-solving. Thus, the cooperative learning approach may lead to gains in mathematical problem-solving in heterogeneous classrooms, but social acceptance and friendships may also greatly impact students’ results.
Introduction
The research on instruction in mathematical problem-solving has progressed considerably during recent decades. Yet, there is still a need to advance our knowledge on how teachers can support their students in carrying out this complex activity (Lester and Cai, 2016). Results from the Program for International Student Assessment (PISA) show that only 53% of students from the participating countries could solve problems requiring more than direct inference and using representations from different information sources (OECD, 2019). In addition, OECD (2019) reported a large variation in achievement with regard to students’ diverse backgrounds. Thus, there is a need for instructional approaches to promote students’ problem-solving in mathematics, especially in heterogeneous classrooms in which students with diverse backgrounds and needs are educated together. Small group instructional approaches have been suggested as important to promote learning of low-achieving students and students with special needs (Kunsch et al., 2007). One such approach is cooperative learning (CL), which involves structured collaboration in heterogeneous groups, guided by five principles to enhance group cohesion (Johnson et al., 1993; Johnson et al., 2009; Gillies, 2016). While CL has been well-researched in whole classroom approaches (Capar and Tarim, 2015), few studies of the approach exist with regard to students with special educational needs (SEN; McMaster and Fuchs, 2002). This study contributes to previous research by studying the effects of the CL approach on students’ mathematical problem-solving in heterogeneous classrooms, in which students with special needs are educated alongside with their peers.
Group collaboration through the CL approach is structured in accordance with five principles of collaboration: positive interdependence, individual accountability, explicit instruction in social skills, promotive interaction, and group processing (Johnson et al., 1993). First, the group tasks need to be structured so that all group members feel dependent on each other in the completion of the task, thus promoting positive interdependence. Second, for individual accountability, the teacher needs to assure that each group member feels responsible for his or her share of work, by providing opportunities for individual reports or evaluations. Third, the students need explicit instruction in social skills that are necessary for collaboration. Fourth, the tasks and seat arrangements should be designed to promote interaction among group members. Fifth, time needs to be allocated to group processing, through which group members can evaluate their collaborative work to plan future actions. Using these principles for cooperation leads to gains in mathematics, according to Capar and Tarim (2015), who conducted a meta-analysis on studies of cooperative learning and mathematics, and found an increase of .59 on students’ mathematics achievement scores in general. However, the number of reviewed studies was limited, and researchers suggested a need for more research. In the current study, we focused on the effect of CL approach in a specific area of mathematics: problem-solving.
Mathematical problem-solving is a central area of mathematics instruction, constituting an important part of preparing students to function in modern society (Gravemeijer et al., 2017). In fact, problem-solving instruction creates opportunities for students to apply their knowledge of mathematical concepts, integrate and connect isolated pieces of mathematical knowledge, and attain a deeper conceptual understanding of mathematics as a subject (Lester and Cai, 2016). Some researchers suggest that mathematics itself is a science of problem-solving and of developing theories and methods for problem-solving (Hamilton, 2007; Davydov, 2008).
Problem-solving processes have been studied from different perspectives (Lesh and Zawojewski, 2007). Problem-solving heuristics Pólya, (1948) has largely influenced our perceptions of problem-solving, including four principles: understanding the problem, devising a plan, carrying out the plan, and looking back and reflecting upon the suggested solution. Schoenfield, (2016) suggested the use of specific problem-solving strategies for different types of problems, which take into consideration metacognitive processes and students’ beliefs about problem-solving. Further, models and modelling perspectives on mathematics (Lesh and Doerr, 2003; Lesh and Zawojewski, 2007) emphasize the importance of engaging students in model-eliciting activities in which problem situations are interpreted mathematically, as students make connections between problem information and knowledge of mathematical operations, patterns, and rules (Mousoulides et al., 2010; Stohlmann and Albarracín, 2016).
Not all students, however, find it easy to solve complex mathematical problems. Students may experience difficulties in identifying solution-relevant elements in a problem or visualizing appropriate solution to a problem situation. Furthermore, students may need help recognizing the underlying model in problems. For example, in two studies by Degrande et al. (2016), students in grades four to six were presented with mathematical problems in the context of proportional reasoning. The authors found that the students, when presented with a word problem, could not identify an underlying model, but rather focused on superficial characteristics of the problem. Although the students in the study showed more success when presented with a problem formulated in symbols, the authors pointed out a need for activities that help students distinguish between different proportional problem types. Furthermore, students exhibiting specific learning difficulties may need additional support in both general problem-solving strategies (Lein et al., 2020; Montague et al., 2014) and specific strategies pertaining to underlying models in problems. The CL intervention in the present study focused on supporting students in problem-solving, through instruction in problem-solving principles (Pólya, 1948), specifically applied to three models of mathematical problem-solving—multiplication/division, geometry, and proportionality.
Students’ problem-solving may be enhanced through participation in small group discussions. In a small group setting, all the students have the opportunity to explain their solutions, clarify their thinking, and enhance understanding of a problem at hand (Yackel et al., 1991; Webb and Mastergeorge, 2003). In fact, small group instruction promotes students’ learning in mathematics by providing students with opportunities to use language for reasoning and conceptual understanding (Mercer and Sams, 2006), to exchange different representations of the problem at hand (Fujita et al., 2019), and to become aware of and understand groupmates’ perspectives in thinking (Kazak et al., 2015). These opportunities for learning are created through dialogic spaces characterized by openness to each other’s perspectives and solutions to mathematical problems (Wegerif, 2011).
However, group collaboration is not only associated with positive experiences. In fact, studies show that some students may not be given equal opportunities to voice their opinions, due to academic status differences (Langer-Osuna, 2016). Indeed, problem-solvers struggling with complex tasks may experience negative emotions, leading to uncertainty of not knowing the definite answer, which places demands on peer support (Jordan and McDaniel, 2014; Hannula, 2015). Thus, especially in heterogeneous groups, students may need additional support to promote group interaction. Therefore, in this study, we used a cooperative learning approach, which, in contrast to collaborative learning approaches, puts greater focus on supporting group cohesion through instruction in social skills and time for reflection on group work (Davidson and Major, 2014).
Although cooperative learning approach is intended to promote cohesion and peer acceptance in heterogeneous groups (Rzoska and Ward, 1991), previous studies indicate that challenges in group dynamics may lead to unequal participation (Mulryan, 1992; Cohen, 1994). Peer-learning behaviours may impact students’ problem-solving (Hwang and Hu, 2013) and working in groups with peers who are seen as friends may enhance students’ motivation to learn mathematics (Deacon and Edwards, 2012). With the importance of peer support in mind, this study set out to investigate whether the results of the intervention using the CL approach are associated with students’ peer acceptance and friendships.
The Present Study
In previous research, the CL approach has shown to be a promising approach in teaching and learning mathematics (Capar and Tarim, 2015), but fewer studies have been conducted in whole-class approaches in general and students with SEN in particular (McMaster and Fuchs, 2002). This study aims to contribute to previous research by investigating the effect of CL intervention on students’ mathematical problem-solving in grade 5. With regard to the complexity of mathematical problem-solving (Lesh and Zawojewski, 2007; Degrande et al., 2016; Stohlmann and Albarracín, 2016), the CL approach in this study was combined with problem-solving principles pertaining to three underlying models of problem-solving—multiplication/division, geometry, and proportionality. Furthermore, considering the importance of peer support in problem-solving in small groups (Mulryan, 1992; Cohen, 1994; Hwang and Hu, 2013), the study investigated how peer acceptance and friendships were associated with the effect of the CL approach on students’ problem-solving abilities. The study aimed to find answers to the following research questions:
a) What is the effect of CL approach on students’ problem-solving in mathematics?
b) Are social acceptance and friendship associated with the effect of CL on students’ problem-solving in mathematics?
Methods
Participants
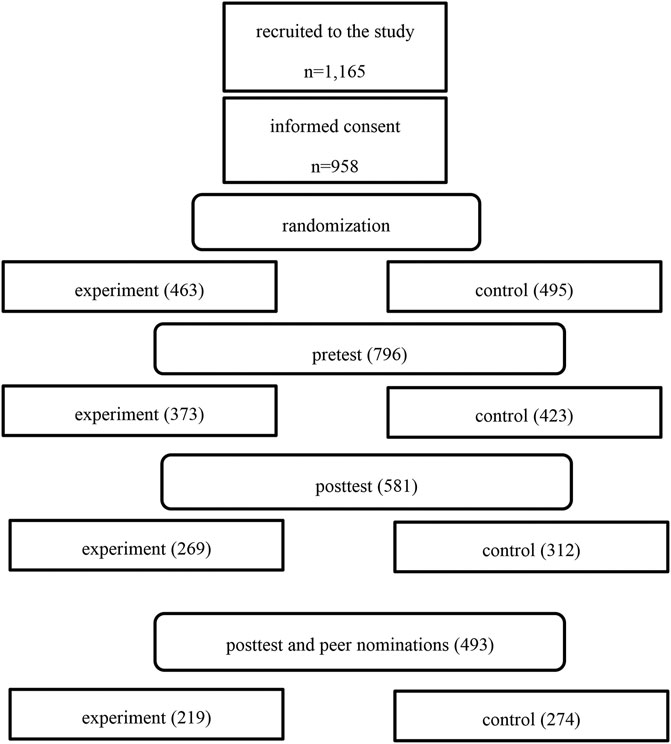
The participants were 958 students in grade 5 and their teachers. According to power analyses prior to the start of the study, 1,020 students and 51 classes were required, with an expected effect size of 0.30 and power of 80%, provided that there are 20 students per class and intraclass correlation is 0.10. An invitation to participate in the project was sent to teachers in five municipalities via e-mail. Furthermore, the information was posted on the website of Uppsala university and distributed via Facebook interest groups. As shown in Figure 1, teachers of 1,165 students agreed to participate in the study, but informed consent was obtained only for 958 students (463 in the intervention and 495 in the control group). Further attrition occurred at pre- and post-measurement, resulting in 581 students’ tests as a basis for analyses (269 in the intervention and 312 in the control group). Fewer students (n = 493) were finally included in the analyses of the association of students’ social acceptance and friendships and the effect of CL on students’ mathematical problem-solving (219 in the intervention and 274 in the control group). The reasons for attrition included teacher drop out due to sick leave or personal circumstances (two teachers in the control group and five teachers in the intervention group). Furthermore, some students were sick on the day of data collection and some teachers did not send the test results to the researchers.
As seen in Table 1, classes in both intervention and control groups included 27 students on average. For 75% of the classes, there were 33–36% of students with SEN. In Sweden, no formal medical diagnosis is required for the identification of students with SEN. It is teachers and school welfare teams who decide students’ need for extra adaptations or special support (Swedish National Educational Agency, 2014). The information on individual students’ type of SEN could not be obtained due to regulations on the protection of information about individuals (SFS 2009). Therefore, the information on the number of students with SEN on class level was obtained through teacher reports.
Intervention
The intervention using the CL approach lasted for 15 weeks and the teachers worked with the CL approach three to four lessons per week. First, the teachers participated in two-days training on the CL approach, using an especially elaborated CL manual (Klang et al., 2018). The training focused on the five principles of the CL approach (positive interdependence, individual accountability, explicit instruction in social skills, promotive interaction, and group processing). Following the training, the teachers introduced the CL approach in their classes and focused on group-building activities for 7 weeks. Then, 2 days of training were provided to teachers, in which the CL approach was embedded in activities in mathematical problem-solving and reading comprehension. Educational materials containing mathematical problems in the areas of multiplication and division, geometry, and proportionality were distributed to the teachers (Karlsson and Kilborn, 2018a). In addition to the specific problems, adapted for the CL approach, the educational materials contained guidance for the teachers, in which problem-solving principles (Pólya, 1948) were presented as steps in problem-solving. Following the training, the teachers applied the CL approach in mathematical problem-solving lessons for 8 weeks.
Solving a problem is a matter of goal-oriented reasoning, starting from the understanding of the problem to devising its solution by using known mathematical models. This presupposes that the current problem is chosen from a known context (Stillman et al., 2008; Zawojewski, 2010). This differs from the problem-solving of the textbooks, which is based on an aim to train already known formulas and procedures (Hamilton, 2007). Moreover, it is important that students learn modelling according to their current abilities and conditions (Russel, 1991).
In order to create similar conditions in the experiment group and the control group, the teachers were supposed to use the same educational material (Karlsson and Kilborn, 2018a; Karlsson and Kilborn, 2018b), written in light of the specified view of problem-solving. The educational material is divided into three areas—multiplication/division, geometry, and proportionality—and begins with a short teachers’ guide, where a view of problem solving is presented, which is based on the work of Polya (1948) and Lester and Cai (2016). The tasks are constructed in such a way that conceptual knowledge was in focus, not formulas and procedural knowledge.
Implementation of the Intervention
To ensure the implementation of the intervention, the researchers visited each teachers’ classroom twice during the two phases of the intervention period, as described above. During each visit, the researchers observed the lesson, using a checklist comprising the five principles of the CL approach. After the lesson, the researchers gave written and oral feedback to each teacher. As seen in Table 1, in 18 of the 23 classes, the teachers implemented the intervention in accordance with the principles of CL. In addition, the teachers were asked to report on the use of the CL approach in their teaching and the use of problem-solving activities embedding CL during the intervention period. As shown in Table 1, teachers in only 11 of 23 classes reported using the CL approach and problem-solving activities embedded in the CL approach at least once a week.
Control Group
The teachers in the control group received 2 days of instruction in enhancing students’ problem-solving and reading comprehension. The teachers were also supported with educational materials including mathematical problems Karlsson and Kilborn (2018b) and problem-solving principles (Pólya, 1948). However, none of the activities during training or in educational materials included the CL approach. As seen in Table 1, only 10 of 25 teachers reported devoting at least one lesson per week to mathematical problem-solving.
Measures
Tests of Mathematical Problem-Solving
Tests of mathematical problem-solving were administered before and after the intervention, which lasted for 15 weeks. The tests were focused on the models of multiplication/division, geometry, and proportionality. The three models were chosen based on the syllabus of the subject of mathematics in grades 4 to 6 in the Swedish National Curriculum (Swedish National Educational Agency, 2018). In addition, the intention was to create a variation of types of problems to solve. For each of these three models, there were two tests, a pre-test and a post-test. Each test contained three tasks with increasing difficulty (Supplementary Appendix SA).
The tests of multiplication and division (Ma1) were chosen from different contexts and began with a one-step problem, while the following two tasks were multi-step problems. Concerning multiplication, many students in grade 5 still understand multiplication as repeated addition, causing significant problems, as this conception is not applicable to multiplication beyond natural numbers (Verschaffel et al., 2007). This might be a hindrance in developing multiplicative reasoning (Barmby et al., 2009). The multi-step problems in this study were constructed to support the students in multiplicative reasoning.
Concerning the geometry tests (Ma2), it was important to consider a paradigm shift concerning geometry in education that occurred in the mid-20th century, when strict Euclidean geometry gave way to other aspects of geometry like symmetry, transformation, and patterns. van Hiele (1986) prepared a new taxonomy for geometry in five steps, from a visual to a logical level. Therefore, in the tests there was a focus on properties of quadrangles and triangles, and how to determine areas by reorganising figures into new patterns. This means that structure was more important than formulas.
The construction of tests of proportionality (M3) was more complicated. Firstly, tasks on proportionality can be found in many different contexts, such as prescriptions, scales, speeds, discounts, interest, etc. Secondly, the mathematical model is complex and requires good knowledge of rational numbers and ratios (Lesh et al., 1988). It also requires a developed view of multiplication, useful in operations with real numbers, not only as repeated addition, an operation limited to natural numbers (Lybeck, 1981; Degrande et al., 2016). A linear structure of multiplication as repeated addition leads to limitations in terms of generalization and development of the concept of multiplication. This became evident in a study carried out in a Swedish context (Karlsson and Kilborn, 2018c). Proportionality can be expressed as a/b = c/d or as a/b = k. The latter can also be expressed as a = b∙k, where k is a constant that determines the relationship between a and b. Common examples of k are speed (km/h), scale, and interest (%). An important pre-knowledge in order to deal with proportions is to master fractions as equivalence classes like 1/3 = 2/6 = 3/9 = 4/12 = 5/15 = 6/18 = 7/21 = 8/24 … (Karlsson and Kilborn, 2020). It was important to take all these aspects into account when constructing and assessing the solutions of the tasks.
The tests were graded by an experienced teacher of mathematics (4th author) and two students in their final year of teacher training. Prior to grading, acceptable levels of inter-rater reliability were achieved by independent rating of students’ solutions and discussions in which differences between the graders were resolved. Each student response was to be assigned one point when it contained a correct answer and two points when the student provided argumentation for the correct answer and elaborated on explanation of his or her solution. The assessment was thus based on quality aspects with a focus on conceptual knowledge. As each subtest contained three questions, it generated three student solutions. So, scores for each subtest ranged from 0 to 6 points and for the total scores from 0 to 18 points. To ascertain that pre- and post-tests were equivalent in degree of difficulty, the tests were administered to an additional sample of 169 students in grade 5. Test for each model was conducted separately, as students participated in pre- and post-test for each model during the same lesson. The order of tests was switched for half of the students in order to avoid the effect of the order in which the pre- and post-tests were presented. Correlation between students’ performance on pre- and post-test was .39 (p < 0.000) for tests of multiplication/division; .48 (p < 0.000) for tests of geometry; and .56 (p < 0.000) for tests of proportionality. Thus, the degree of difficulty may have differed between pre- and post-test.
Measures of Peer Acceptance and Friendships
To investigate students’ peer acceptance and friendships, peer nominations rated pre- and post-intervention were used. Students were asked to nominate peers who they preferred to work in groups with and who they preferred to be friends with. Negative peer nominations were avoided due to ethical considerations raised by teachers and parents (Child and Nind, 2013). Unlimited nominations were used, as these are considered to have high ecological validity (Cillessen and Marks, 2017). Peer nominations were used as a measure of social acceptance, and reciprocated nominations were used as a measure of friendship. The number of nominations for each student were aggregated and divided by the number of nominators to create a proportion of nominations for each student (Velásquez et al., 2013).
Statistical Analyses
Multilevel regression analyses were conducted in R, lme4 package Bates et al. (2015) to account for nestedness in the data. Students’ classroom belonging was considered as a level 2 variable. First, we used a model in which students’ results on tests of problem-solving were studied as a function of time (pre- and post) and group belonging (intervention and control group). Second, the same model was applied to subgroups of students who performed above and below median at pre-test, to explore whether the CL intervention had a differential effect on student performance. In this second model, the results for subgroups of students could not be obtained for geometry tests for subgroup below median and for tests of proportionality for subgroup above median. A possible reason for this must have been the skewed distribution of the students in these subgroups. Therefore, another model was applied that investigated students’ performances in math at both pre- and post-test as a function of group belonging. Third, the students’ scores on social acceptance and friendships were added as an interaction term to the first model. In our previous study, students’ social acceptance changed as a result of the same CL intervention (Klang et al., 2020).
The assumptions for the multilevel regression were assured during the analyses (Snijders and Bosker, 2012). The assumption of normality of residuals were met, as controlled by visual inspection of quantile-quantile plots. For subgroups, however, the plotted residuals deviated somewhat from the straight line. The number of outliers, which had a studentized residual value greater than ±3, varied from 0 to 5, but none of the outliers had a Cook’s distance value larger than 1. The assumption of multicollinearity was met, as the variance inflation factors (VIF) did not exceed a value of 10. Before the analyses, the cases with missing data were deleted listwise.
Results
What Is the Effect of the CL Approach on Students’ Problem-Solving in Mathematics?
As seen in the regression coefficients in Table 2, the CL intervention had a significant effect on students’ mathematical problem-solving total scores and students’ scores in problem solving in geometry (Ma2). Judging by mean values, students in the intervention group appeared to have low scores on problem-solving in geometry but reached the levels of problem-solving of the control group by the end of the intervention. The intervention did not have a significant effect on students’ performance in problem-solving related to models of multiplication/division and proportionality.
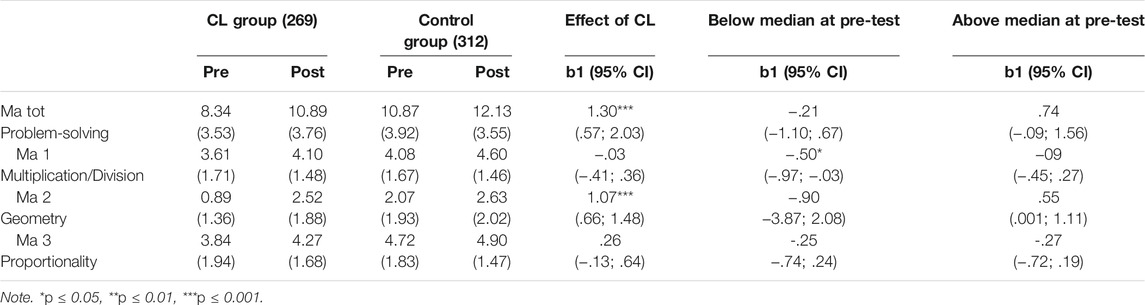
TABLE 2. Mean scores (standard deviation in parentheses) and unstandardized multilevel regression estimates for tests of mathematical problem-solving.
The question is, however, whether CL intervention affected students with different pre-test scores differently. Table 2 includes the regression coefficients for subgroups of students who performed below and above median at pre-test. As seen in the table, the CL approach did not have a significant effect on students’ problem-solving, when the sample was divided into these subgroups. A small negative effect was found for intervention group in comparison to control group, but confidence intervals (CI) for the effect indicate that it was not significant.
Is Social Acceptance and Friendships Associated With the Effect of CL on Students’ Problem-Solving in Mathematics?
As seen in Table 3, students’ peer acceptance and friendship at pre-test were significantly associated with the effect of the CL approach on students’ mathematical problem-solving scores. Changes in students’ peer acceptance and friendships were not significantly associated with the effect of the CL approach on students’ mathematical problem-solving. Consequently, it can be concluded that being nominated by one’s peers and having friends at the start of the intervention may be an important factor when participation in group work, structured in accordance with the CL approach, leads to gains in mathematical problem-solving.
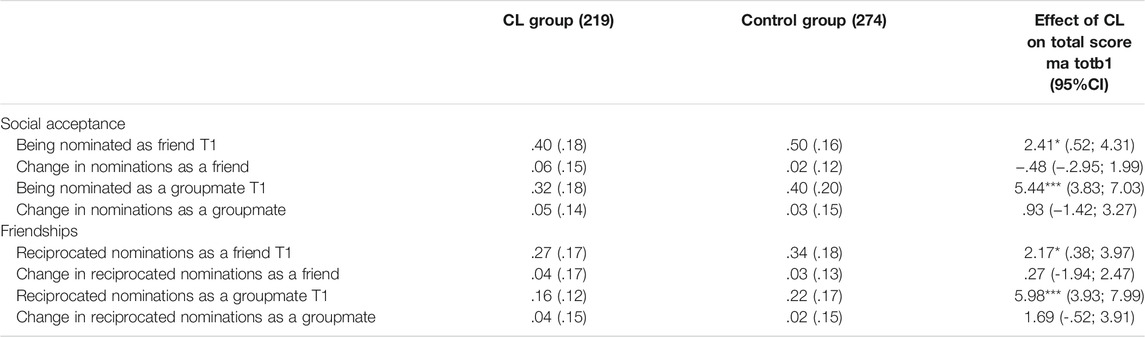
TABLE 3. Mean scores (standard deviation in parentheses) and unstandardized multilevel regression estimates for tests of mathematical problem-solving, including scores of social acceptance and friendship in the model.
Discussion
In light of the limited number of studies on the effects of CL on students’ problem-solving in whole classrooms (Capar and Tarim, 2015), and for students with SEN in particular (McMaster and Fuchs, 2002), this study sought to investigate whether the CL approach embedded in problem-solving activities has an effect on students’ problem-solving in heterogeneous classrooms. The need for the study was justified by the challenge of providing equitable mathematics instruction to heterogeneous student populations (OECD, 2019). Small group instructional approaches as CL are considered as promising approaches in this regard (Kunsch et al., 2007). The results showed a significant effect of the CL approach on students’ problem-solving in geometry and total problem-solving scores. In addition, with regard to the importance of peer support in problem-solving (Deacon and Edwards, 2012; Hwang and Hu, 2013), the study explored whether the effect of CL on students’ problem-solving was associated with students’ social acceptance and friendships. The results showed that students’ peer acceptance and friendships at pre-test were significantly associated with the effect of the CL approach, while change in students’ peer acceptance and friendships from pre- to post-test was not.
The results of the study confirm previous research on the effect of the CL approach on students’ mathematical achievement (Capar and Tarim, 2015). The specific contribution of the study is that it was conducted in classrooms, 75% of which were composed of 33–36% of students with SEN. Thus, while a previous review revealed inconclusive findings on the effects of CL on student achievement (McMaster and Fuchs, 2002), the current study adds to the evidence of the effect of the CL approach in heterogeneous classrooms, in which students with special needs are educated alongside with their peers. In a small group setting, the students have opportunities to discuss their ideas of solutions to the problem at hand, providing explanations and clarifications, thus enhancing their understanding of problem-solving (Yackel et al., 1991; Webb and Mastergeorge, 2003).
In this study, in accordance with previous research on mathematical problem-solving (Lesh and Zawojewski, 2007; Degrande et al., 2016; Stohlmann and Albarracín, 2016), the CL approach was combined with training in problem-solving principles Pólya (1948) and educational materials, providing support in instruction in underlying mathematical models. The intention of the study was to provide evidence for the effectiveness of the CL approach above instruction in problem-solving, as problem-solving materials were accessible to teachers of both the intervention and control groups. However, due to implementation challenges, not all teachers in the intervention and control groups reported using educational materials and training as expected. Thus, it is not possible to draw conclusions of the effectiveness of the CL approach alone. However, in everyday classroom instruction it may be difficult to separate the content of instruction from the activities that are used to mediate this content (Doerr and Tripp, 1999; Gravemeijer, 1999).
Furthermore, for successful instruction in mathematical problem-solving, scaffolding for content needs to be combined with scaffolding for dialogue (Kazak et al., 2015). From a dialogical perspective (Wegerif, 2011), students may need scaffolding in new ways of thinking, involving questioning their understandings and providing arguments for their solutions, in order to create dialogic spaces in which different solutions are voiced and negotiated. In this study, small group instruction through CL approach aimed to support discussions in small groups, but the study relies solely on quantitative measures of students’ mathematical performance. Video-recordings of students’ discussions may have yielded important insights into the dialogic relationships that arose in group discussions.
Despite the positive findings of the CL approach on students’ problem-solving, it is important to note that the intervention did not have an effect on students’ problem-solving pertaining to models of multiplication/division and proportionality. Although CL is assumed to be a promising instructional approach, the number of studies on its effect on students’ mathematical achievement is still limited (Capar and Tarim, 2015). Thus, further research is needed on how CL intervention can be designed to promote students’ problem-solving in other areas of mathematics.
The results of this study show that the effect of the CL intervention on students’ problem-solving was associated with students’ initial scores of social acceptance and friendships. Thus, it is possible to assume that students who were popular among their classmates and had friends at the start of the intervention also made greater gains in mathematical problem-solving as a result of the CL intervention. This finding is in line with Deacon and Edwards’ study of the importance of friendships for students’ motivation to learn mathematics in small groups (Deacon and Edwards, 2012). However, the effect of the CL intervention was not associated with change in students’ social acceptance and friendship scores. These results indicate that students who were nominated by a greater number of students and who received a greater number of friends did not benefit to a great extent from the CL intervention. With regard to previously reported inequalities in cooperation in heterogeneous groups (Cohen, 1994; Mulryan, 1992; Langer Osuna, 2016) and the importance of peer behaviours for problem-solving (Hwang and Hu, 2013), teachers should consider creating inclusive norms and supportive peer relationships when using the CL approach. The demands of solving complex problems may create negative emotions and uncertainty (Hannula, 2015; Jordan and McDaniel, 2014), and peer support may be essential in such situations.
Limitations
The conclusions from the study must be interpreted with caution, due to a number of limitations. First, due to the regulation of protection of individuals (SFS 2009), the researchers could not get information on type of SEN for individual students, which limited the possibilities of the study for investigating the effects of the CL approach for these students. Second, not all teachers in the intervention group implemented the CL approach embedded in problem-solving activities and not all teachers in the control group reported using educational materials on problem-solving. The insufficient levels of implementation pose a significant challenge to the internal validity of the study. Third, the additional investigation to explore the equivalence in difficulty between pre- and post-test, including 169 students, revealed weak to moderate correlation in students’ performance scores, which may indicate challenges to the internal validity of the study.
Implications
The results of the study have some implications for practice. Based on the results of the significant effect of the CL intervention on students’ problem-solving, the CL approach appears to be a promising instructional approach in promoting students’ problem-solving. However, as the results of the CL approach were not significant for all subtests of problem-solving, and due to insufficient levels of implementation, it is not possible to conclude on the importance of the CL intervention for students’ problem-solving. Furthermore, it appears to be important to create opportunities for peer contacts and friendships when the CL approach is used in mathematical problem-solving activities.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics Statement
The studies involving human participants were reviewed and approved by the Uppsala Ethical Regional Committee, Dnr. 2017/372. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.
Author Contributions
NiK was responsible for the project, and participated in data collection and data analyses. NaK and WK were responsible for intervention with special focus on the educational materials and tests in mathematical problem-solving. PE participated in the planning of the study and the data analyses, including coordinating analyses of students’ tests. MK participated in the designing and planning the study as well as data collection and data analyses.
Funding
The project was funded by the Swedish Research Council under Grant 2016-04,679.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We would like to express our gratitude to teachers who participated in the project.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2021.710296/full#supplementary-material
References
Barmby, P., Harries, T., Higgins, S., and Suggate, J. (2009). The array representation and primary children's understanding and reasoning in multiplication. Educ. Stud. Math. 70 (3), 217–241. doi:10.1007/s10649-008-914510.1007/s10649-008-9145-1
Bates, D., Mächler, M., Bolker, B., and Walker, S. (2015). Fitting Linear Mixed-Effects Models Usinglme4. J. Stat. Soft. 67 (1), 1–48. doi:10.18637/jss.v067.i01
Capar, G., and Tarim, K. (2015). Efficacy of the cooperative learning method on mathematics achievement and attitude: A meta-analysis research. Educ. Sci-theor Pract. 15 (2), 553–559. doi:10.12738/estp.2015.2.2098
Child, S., and Nind, M. (2013). Sociometric methods and difference: A force for good - or yet more harm. Disabil. Soc. 28 (7), 1012–1023. doi:10.1080/09687599.2012.741517
Cillessen, A. H. N., and Marks, P. E. L. (2017). Methodological choices in peer nomination research. New Dir. Child Adolesc. Dev. 2017, 21–44. doi:10.1002/cad.20206
Clarke, B., Cheeseman, J., and Clarke, D. (2006). The mathematical knowledge and understanding young children bring to school. Math. Ed. Res. J. 18 (1), 78–102. doi:10.1007/bf03217430
Cohen, E. G. (1994). Restructuring the classroom: Conditions for productive small groups. Rev. Educ. Res. 64 (1), 1–35. doi:10.3102/00346543064001001
Davidson, N., and Major, C. H. (2014). Boundary crossings: Cooperative learning, collaborative learning, and problem-based learning. J. Excell. Coll. Teach. 25 (3-4), 7.
Davydov, V. V. (2008). Problems of developmental instructions. A Theoretical and experimental psychological study. New York: Nova Science Publishers, Inc.
Deacon, D., and Edwards, J. (2012). Influences of friendship groupings on motivation for mathematics learning in secondary classrooms. Proc. Br. Soc. Res. into Learn. Math. 32 (2), 22–27.
Degrande, T., Verschaffel, L., and van Dooren, W. (2016). “Proportional word problem solving through a modeling lens: a half-empty or half-full glass?,” in Posing and Solving Mathematical Problems, Research in Mathematics Education. Editor P. Felmer.
Doerr, H. M., and Tripp, J. S. (1999). Understanding how students develop mathematical models. Math. Thinking Learn. 1 (3), 231–254. doi:10.1207/s15327833mtl0103_3
Fujita, T., Doney, J., and Wegerif, R. (2019). Students' collaborative decision-making processes in defining and classifying quadrilaterals: a semiotic/dialogic approach. Educ. Stud. Math. 101 (3), 341–356. doi:10.1007/s10649-019-09892-9
Gillies, R. (2016). Cooperative learning: Review of research and practice. Ajte 41 (3), 39–54. doi:10.14221/ajte.2016v41n3.3
Gravemeijer, K. (1999). How Emergent Models May Foster the Constitution of Formal Mathematics. Math. Thinking Learn. 1 (2), 155–177. doi:10.1207/s15327833mtl0102_4
Gravemeijer, K., Stephan, M., Julie, C., Lin, F.-L., and Ohtani, M. (2017). What mathematics education may prepare students for the society of the future? Int. J. Sci. Math. Educ. 15 (S1), 105–123. doi:10.1007/s10763-017-9814-6
Hamilton, E. (2007). “What changes are needed in the kind of problem-solving situations where mathematical thinking is needed beyond school?,” in Foundations for the Future in Mathematics Education. Editors R. Lesh, E. Hamilton, and Kaput (Mahwah, NJ: Lawrence Erlbaum), 1–6.
Hannula, M. S. (2015). “Emotions in problem solving,” in Selected Regular Lectures from the 12thInternational Congress on Mathematical Education. Editor S. J. Cho. doi:10.1007/978-3-319-17187-6_16
Hwang, W.-Y., and Hu, S.-S. (2013). Analysis of peer learning behaviors using multiple representations in virtual reality and their impacts on geometry problem solving. Comput. Edu. 62, 308–319. doi:10.1016/j.compedu.2012.10.005
Johnson, D. W., Johnson, R. T., and Johnson Holubec, E. (2009). Circle of Learning: Cooperation in the Classroom. Gurgaon: Interaction Book Company.
Johnson, D. W., Johnson, R. T., and Johnson Holubec, E. (1993). Cooperation in the Classroom. Gurgaon: Interaction Book Company.
Jordan, M. E., and McDaniel, R. R. (2014). Managing uncertainty during collaborative problem solving in elementary school teams: The role of peer influence in robotics engineering activity. J. Learn. Sci. 23 (4), 490–536. doi:10.1080/10508406.2014.896254
Karlsson, N., and Kilborn, W. (2018a). Inclusion through learning in group: tasks for problem-solving. [Inkludering genom lärande i grupp: uppgifter för problemlösning]. Uppsala: Uppsala University.
Karlsson, N., and Kilborn, W. (2018c). It's enough if they understand it. A study of teachers 'and students' perceptions of multiplication and the multiplication table [Det räcker om de förstår den. En studie av lärares och elevers uppfattningar om multiplikation och multiplikationstabellen]. Södertörn Stud. Higher Educ., 175.
Karlsson, N., and Kilborn, W. (2018b). Tasks for problem-solving in mathematics. [Uppgifter för problemlösning i matematik]. Uppsala: Uppsala University.
Karlsson, N., and Kilborn, W. (2020). “Teacher’s and student’s perception of rational numbers,” in Interim Proceedings of the 44thConference of the International Group for the Psychology of Mathematics Education, Interim Vol., Research Reports. Editors M. Inprasitha, N. Changsri, and N. Boonsena (Khon Kaen, Thailand: PME), 291–297.
Kazak, S., Wegerif, R., and Fujita, T. (2015). Combining scaffolding for content and scaffolding for dialogue to support conceptual breakthroughs in understanding probability. ZDM Math. Edu. 47 (7), 1269–1283. doi:10.1007/s11858-015-0720-5
Klang, N., Olsson, I., Wilder, J., Lindqvist, G., Fohlin, N., and Nilholm, C. (2020). A cooperative learning intervention to promote social inclusion in heterogeneous classrooms. Front. Psychol. 11, 586489. doi:10.3389/fpsyg.2020.586489
Klang, N., Fohlin, N., and Stoddard, M. (2018). Inclusion through learning in group: cooperative learning [Inkludering genom lärande i grupp: kooperativt lärande]. Uppsala: Uppsala University.
Kunsch, C. A., Jitendra, A. K., and Sood, S. (2007). The effects of peer-mediated instruction in mathematics for students with learning problems: A research synthesis. Learn. Disabil Res Pract 22 (1), 1–12. doi:10.1111/j.1540-5826.2007.00226.x
Langer-Osuna, J. M. (2016). The social construction of authority among peers and its implications for collaborative mathematics problem solving. Math. Thinking Learn. 18 (2), 107–124. doi:10.1080/10986065.2016.1148529
Lein, A. E., Jitendra, A. K., and Harwell, M. R. (2020). Effectiveness of mathematical word problem solving interventions for students with learning disabilities and/or mathematics difficulties: A meta-analysis. J. Educ. Psychol. 112 (7), 1388–1408. doi:10.1037/edu0000453
Lesh, R., and Doerr, H. (2003). Beyond Constructivism: Models and Modeling Perspectives on Mathematics Problem Solving, Learning and Teaching. Mahwah, NJ: Erlbaum.
Lesh, R., Post, T., and Behr, M. (1988). “Proportional reasoning,” in Number Concepts and Operations in the Middle Grades. Editors J. Hiebert, and M. Behr (Hillsdale, N.J.: Lawrence Erlbaum Associates), 93–118.
Lesh, R., and Zawojewski, (2007). “Problem solving and modeling,” in Second Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics. Editor L. F. K. Lester (Charlotte, NC: Information Age Pub), vol. 2.
Lester, F. K., and Cai, J. (2016). “Can mathematical problem solving be taught? Preliminary answers from 30 years of research,” in Posing and Solving Mathematical Problems. Research in Mathematics Education.
Lybeck, L. (1981). “Archimedes in the classroom. [Arkimedes i klassen],” in Göteborg Studies in Educational Sciences (Göteborg: Acta Universitatis Gotoburgensis), 37.
McMaster, K. N., and Fuchs, D. (2002). Effects of Cooperative Learning on the Academic Achievement of Students with Learning Disabilities: An Update of Tateyama-Sniezek's Review. Learn. Disabil Res Pract 17 (2), 107–117. doi:10.1111/1540-5826.00037
Mercer, N., and Sams, C. (2006). Teaching children how to use language to solve maths problems. Lang. Edu. 20 (6), 507–528. doi:10.2167/le678.0
Montague, M., Krawec, J., Enders, C., and Dietz, S. (2014). The effects of cognitive strategy instruction on math problem solving of middle-school students of varying ability. J. Educ. Psychol. 106 (2), 469–481. doi:10.1037/a0035176
Mousoulides, N., Pittalis, M., Christou, C., and Stiraman, B. (2010). “Tracing students’ modeling processes in school,” in Modeling Students’ Mathematical Modeling Competencies. Editor R. Lesh (Berlin, Germany: Springer Science+Business Media). doi:10.1007/978-1-4419-0561-1_10
Mulryan, C. M. (1992). Student passivity during cooperative small groups in mathematics. J. Educ. Res. 85 (5), 261–273. doi:10.1080/00220671.1992.9941126
OECD (2019). PISA 2018 Results (Volume I): What Students Know and Can Do. Paris: OECD Publishing. doi:10.1787/5f07c754-en
Pólya, G. (1948). How to Solve it: A New Aspect of Mathematical Method. Princeton, N.J.: Princeton University Press.
Russel, S. J. (1991). “Counting noses and scary things: Children construct their ideas about data,” in Proceedings of the Third International Conference on the Teaching of Statistics. Editor I. D. Vere-Jones (Dunedin, NZ: University of Otago), 141–164., s.
Rzoska, K. M., and Ward, C. (1991). The effects of cooperative and competitive learning methods on the mathematics achievement, attitudes toward school, self-concepts and friendship choices of Maori, Pakeha and Samoan Children. New Zealand J. Psychol. 20 (1), 17–24.
Schoenfeld, A. H. (2016). Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics (reprint). J. Edu. 196 (2), 1–38. doi:10.1177/002205741619600202
SFS 2009:400. Offentlighets- och sekretesslag. [Law on Publicity and confidentiality]. Retrieved from https://www.riksdagen.se/sv/dokument-lagar/dokument/svensk-forfattningssamling/offentlighets--och-sekretesslag-2009400_sfs-2009-400 on the 14th of October.
Snijders, T. A. B., and Bosker, R. J. (2012). Multilevel Analysis. An Introduction to Basic and Advanced Multilevel Modeling. 2nd Ed. London: SAGE.
Stillman, G., Brown, J., and Galbraith, P. (2008). Research into the teaching and learning of applications and modelling in Australasia. In H. Forgasz, A. Barkatas, A. Bishop, B. Clarke, S. Keast, W. Seah, and P. Sullivan (red.), Research in Mathematics Education in Australasiae, 2004-2007, p.141–164. Rotterdam: Sense Publishers.doi:10.1163/9789087905019_009
Stohlmann, M. S., and Albarracín, L. (2016). What is known about elementary grades mathematical modelling. Edu. Res. Int. 2016, 1–9. doi:10.1155/2016/5240683
Swedish National Educational Agency (2014). Support measures in education – on leadership and incentives, extra adaptations and special support [Stödinsatser I utbildningen – om ledning och stimulans, extra anpassningar och särskilt stöd]. Stockholm: Swedish National Agency of Education.
Swedish National Educational Agency (2018). Syllabus for the subject of mathematics in compulsory school. Retrieved from https://www.skolverket.se/undervisning/grundskolan/laroplan-och-kursplaner-for-grundskolan/laroplan-lgr11-for-grundskolan-samt-for-forskoleklassen-och-fritidshemmet?url=-996270488%2Fcompulsorycw%2Fjsp%2Fsubject.htm%3FsubjectCode%3DGRGRMAT01%26tos%3Dgr&sv.url=12.5dfee44715d35a5cdfa219f ( on the 32nd of July, 2021).
van Hiele, P. (1986). Structure and Insight. A Theory of Mathematics Education. London: Academic Press.
Velásquez, A. M., Bukowski, W. M., and Saldarriaga, L. M. (2013). Adjusting for Group Size Effects in Peer Nomination Data. Soc. Dev. 22 (4), a–n. doi:10.1111/sode.12029
Verschaffel, L., Greer, B., and De Corte, E. (2007). “Whole number concepts and operations,” in Second Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics. Editor F. K. Lester (Charlotte, NC: Information Age Pub), 557–628.
Webb, N. M., and Mastergeorge, A. (2003). Promoting effective helping behavior in peer-directed groups. Int. J. Educ. Res. 39 (1), 73–97. doi:10.1016/S0883-0355(03)00074-0
Wegerif, R. (2011). “Theories of Learning and Studies of Instructional Practice,” in Theories of learning and studies of instructional Practice. Explorations in the learning sciences, instructional systems and Performance technologies. Editor T. Koschmann (Berlin, Germany: Springer). doi:10.1007/978-1-4419-7582-9
Yackel, E., Cobb, P., and Wood, T. (1991). Small-group interactions as a source of learning opportunities in second-grade mathematics. J. Res. Math. Edu. 22 (5), 390–408. doi:10.2307/749187
Keywords: cooperative learning, mathematical problem-solving, intervention, heterogeneous classrooms, hierarchical linear regression analysis
Citation: Klang N, Karlsson N, Kilborn W, Eriksson P and Karlberg M (2021) Mathematical Problem-Solving Through Cooperative Learning—The Importance of Peer Acceptance and Friendships. Front. Educ. 6:710296. doi: 10.3389/feduc.2021.710296
Received: 15 May 2021; Accepted: 09 August 2021;
Published: 24 August 2021.
Edited by:
Dor Abrahamson, University of California, Berkeley, United StatesReviewed by:
Kathryn Holmes, Western Sydney University, AustraliaTaro Fujita, University of Exeter, United Kingdom
Copyright © 2021 Klang, Karlsson, Kilborn, Eriksson and Karlberg. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nina Klang, bmluYS5rbGFuZ0BlZHUudXUuc2U=
 Nina Klang
Nina Klang Natalia Karlsson
Natalia Karlsson Wiggo Kilborn4
Wiggo Kilborn4 Martin Karlberg
Martin Karlberg