Minimization of a Short Computer-Based Test in Reading

Introduction

This article addresses the minimization process of a computer-based formative test in sentence comprehension with both fixed and random item order. Formative assessment is an umbrella term which is used by different test frameworks that focus on multiple components of learning (e.g., teacher outcomes and student outcomes) working together to facilitate learning (Bennett, 2011). The main goal of formative assessments is seen as a support for academic learning, a secondary goal being an assessment of learning (Bloom, 1969; Black and Wiliam, 2003; Bennett, 2011). Research shows promising positive effects of formative assessments for students with special educational needs (SEN) in Algebra (Foegen, 2008; Genareo et al., 2021). But it also shows the need for more specific evaluation of concepts and applications as well as terms of test quality (Stecker et al., 2005; Kingston and Nash, 2011; Wilbert and Linnemann, 2011; Shapiro, 2013; Hattie et al., 2015; Brown, 2019). The concept more precisely means the formative use of assessment information (Good, 2011). Stated this way the composition from a component of measurement and a component of pedagogical application is stressed more firmly. In this paper, we address the component of measurement. In more detail, we analyze the length of an instrument designed for learning progress monitoring. We understand the monitoring of learning progress as a central part of a formative assessment.

The length of tests is introduced as one of the main properties of a test’s usability in practice (Wright, 1992). It is argued that digital tests offer substantial advantages due to simplified test-parallelization by random item selection. We demonstrate the principle of test minimization by assessing the statistical properties of a web-based test for sentence reading comprehension.

Background

With no change in item quality, longer tests are more likely to support decisions at the individual level (Sijtsma, 2012). If you collect more information about the person, you can reduce the standard error of measurement. But the relationship between questionnaire length, reliability and statistical power is complex (Bell and Lumsden, 1980; Sijtsma and Emons, 2011) and has to be addressed in consideration of the goal of the test. The length of a test is part of the secondary quality criteria of psychological and educational tests because the length touches the criteria of utility and economy. A test should take as little time as necessary, use as little material as possible and be easy to administer. The German Data Forum on Social Science Survey Research (RatSWD, 2015) even pointed out, that the economic efficiency of a measurement instrument is determined on the basis of the time it takes to administer and its ease of handling. This economic efficiency of a test is to be evaluated in comparison to other tests (Kubinger, 2009).

Learning progress monitoring and curriculum-based measurement provide data that can be used in instructional decision-making processes (Fuchs, 2004; Gebhardt et al., 2015). The tests have to give a reasonable reliable measure of change within students as well as an option to compare growth measures between specific groups of students. The standard errors have therefore to be addressed on the growth level. Instruments of learning progress monitoring complements educational diagnostics in the classroom and reinforces the view of individual development. Therefore, diagnostic tests for current status and screening instruments are not replaced but complemented. The goal is to get the best possible assessment of whether the student can achieve his or her learning goals. The results and data are discussed in the team of teachers to decide pedagogical measures (Blumenthal et al., 2021). Student learning should be closely monitored to evaluate the effectiveness of educational interventions and to provide formative feedback to learners and teachers. As with other tests, learning progress monitoring instruments need to address main quality criteria of tests: objectivity, reliability and validity (Good and Jefferson, 1998). Those substantiate the bridging of a theoretical construct to the mechanisms of measurement and scoring (e.g., American Educational Research Association, American Psychological Association and National Council on Measurement in Education, 2014). Criteria that relate to the practical application of tests of learning progress assessment have to be considered, too. One of the characteristics of instruments of learning progress monitoring that relate to the main quality criteria of tests as well as criteria that relate to the practical application in classrooms is its length. Compared to status tests in pre-post designs, tests with multiple measurement points or latent growth are more reliable in measuring change (Cronbach and Furby, 1970; Vaughn, et al., 2003) but in total they take more learning time away from students. Therefore, in addition to the classical quality criteria, instruments of learning progress must be practical and easy to use in the classroom, and they must be as short as possible to allow reliable measurement.

Tests that are meant to be used by practitioners repeatedly have to be practical and usable. They have to be easy to teach and time efficient (Deno, 2003a). Fuchs and Fuchs (1992) suggested that digital test administration (i.e., computer-based or web-based tests) reduces the teachers’ workload and rises the classroom usability of formative tests. More recently, multiple digital test systems were developed for repeated measurements in classrooms (Nelson et al., 2017; Mühling et al., 2019). Moreover, formative tests have to provide multiple parallel forms with homogenous unidimensional difficulty (i.e., Embretson, 1996) for repeated measurement. Additionally, the tests and their parallel forms have to be fair for different groups of test takers (e.g., students with SEN). The fairness of a test depends on its purpose and target population (American Educational Research Association, American Psychological Association and National Council on Measurement in Education, 2014). It has to be ensured that the test in question is sensitive enough to detect (eventually small and slow) change within a specific domain such as reading fluency or reading comprehension (i.e., Kazdin, 2011; Klauer, 2014). The usability, homogeneity, test fairness and sensitivity are interdependent. These criteria are necessary conditions to reach the potential of tests in learning progress monitoring. Statistical models based upon the Item-Response-Theory (IRT) are particularly suitable for evaluating the quality of tests for multiple parameters that can be evaluated (e.g., Sternberg and Grigorenko, 2002; Gebhardt et al., 2015; Anderson et al., 2017). Wilbert and Linnemann (2011) argue that the use of IRT modeling is essential for deriving formative information. Therefore, a good progress monitoring test should first check the dimensions, then the invariance and at the end consider how to shorten the test for practical use. Further steps would then be to consider how to improve and simplify the graphs, index scores and feedback for teachers.

The minimal and maximal length of a test relates directly to the usability, because a short test is deemed to be more usable. It also affects the homogeneity, fairness and sensitivity, for a short test is more delimited in the width of its representational capabilities, the item calibration and the detection of precise-enough inferences (Wright, 1992). Here, the use of IRT models is particularly advantageous. It is possible to explicitly test the homogeneity of the discrimination of the items. In the IRT models it is not only assumed that the discriminatory power of the items may differ (relaxation of τ-equivalence), but the items are constructed to address different skill levels of the same proficiency by differing item difficulty. The correlation between the latent person score and the item difficulty of the single items (not the test) is assumed to be monotonically increasing and most often modeled as a logistic function. This allows for a more precise evaluation of the test items and therefore the test itself. A person's parameter can be derived from this at an interval scale level, both within the response categories of an item and between the response categories of different items (Rost, 1999). This linkage is why IRT models are particularly useful for the construction of learning process tests (Sternberg and Grigorenko, 2002). Because of this, the items are seen as independent measures of the construct in question and are more interchangeable than in applications of the classical test theory. This way item characteristics may be seen as robust across time. Structural Equation Modeling (SEM; e.g., Kline, 2015) could be a middle way between classical and IRT methods. Here, the homogeneity assumptions between the items can also be relaxed, but the models have a more confirmatory character on the sample level and are less suitable for item calibration and the deduction of person parameters. In summary, it can be stated that IRT has advantageous measurement-theoretical properties (Lord, 1980), especially for learning progress measurements (Wilbert and Linnemann, 2011).

Item elimination when the discrimination of an item is (seemingly) lacking is routinly done in test construction (Masters, 1988). Smith et al. (2000) adressed problems concerning the reduction of items from a test mostly adressing the tranferability of the validity argument of the test and the relaxation of statistical assumptions. Yet there are good examples of successful strategies for techniques in item reduction. In the first place the predictive validity of test scores, which are based upon the reliability, have to be understood as a function of the test length (Bell and Lumsden, 1980). Zijlmans et al. (2019) evaluated the item-score reliability to evaluate an appropiate length of a test. Stewart et al. (1988) adressed change in reliability to evaluate a short-form health measure. But in our understanding the question of wether a test is long enough for the desired purpose is still not routinly asked.

Research Question

The formative use of assessment information can address students with SEN and give data-based evidence for practitioners, if specific quality criteria are met (Good, 2011). But the used tests need to address the criterion of usability. To address the usability easy-to-understand measures and quickly applicable tests are needed.

In the area of formative assessment recurring short tests of a few minutes are better suited to measure the ability of this group of people and are promising for students with SEN (Deno, 2003a). Likewise, short tests can be used more easily in open teaching concepts and in free work phases in the classroom using tablet or computer (Fuchs, 2004). For our study, the deduced and leading question is: How can the length of instruments be minimized while making sure that the estimated or calculated parameters still hold meaning and are sufficiently reliable to be used in educational decision making?

Methods

The sample and procedure are the same ones as described in Jungjohann et al. (2018) and were used to establish the psychometric properties of a reading comprehension test at sentence level (SinnL-Levumi; Jungjohann and Gebhardt, 2019) which is administered via the web-based platform www.levumi.de (Gebhardt et al., 2016).

Sample and Procedure

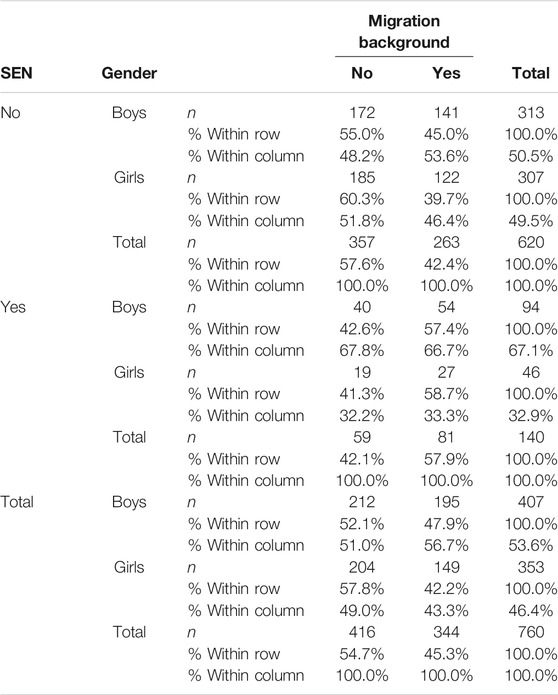
Participants were third grade students attending regular elementary schools in the northwest of Germany (N = 761). The students were distributed across 40 classrooms. The mean number of students by classroom is 19.03; in one of those classrooms there was only a single child allowed to take part. Approximately half of the participants were female (46.5%). The participants’ teachers were asked about the migration background (n = 344) and SEN (n = 140). 37 students were classified as having learning difficulties and 40 students did show a difficulty in the language of the test (i.e., German). 63 times the teachers have indicated that there is another need. Those special needs were not specified in more detail in the process of data collection. The relative and absolute frequencies are given in Table 1. There is missing background data on SEN and Migration Background for a single case.

TABLE 1

TABLE 1. Contingency table of background variables.

Trained research assistants (i.e., university students) contacted local elementary school administrators and then teachers to recruit participants with the parents’ consent. Participation was voluntary and supervised by school staff. The research assistants tested participants individually but in groups in the regular classroom. Every student did the SinnL-Levumi tests two times (t1 and t2) between autumn and Christmas holidays in 2017 on an individual tablet computer. The correct and incorrect answers and processing time is tracked by the web-based platform. After the first measurement, researchers returned three weeks later to collect the data for the second measurement. 94 students did not participate in t2 due to absence or illness. In this case, their data for the second measurement was treated as missing. During both measurements, research assistants followed the same scripted procedure including an example item. Cases that showed successive processing times under 2 s were excluded from the analysis.

Instrument

The SinnL-Levumi test (Jungjohann and Gebhardt, 2019) is programmed for a web-based application. It runs on all major browsers via a German online platform for CBM monitoring called Levumi (www.levumi.de). On the platform, teachers can use and download test materials, teacher handbooks (i.e., information and support regarding to technical operation of the platform, tests’ implementation during lessons, data interpretation, data-based decision-making) and support materials for reading instruction. All this is published with a creative commons license, meaning that it is free of charge for teachers and researchers. All students do the tests on the screen and, for both individual and group test administration, the test can be administered across multiple devices (e.g., computers or tablets) simultaneously. An interactive example is shown at the beginning of each test.

The item pool contains 60 items (Jungjohann et al., 2018) and the creation of the SinnL-Levumi reading comprehension tests followed the principles of curriculum-based measurement maze tests (Deno, 1985; Deno, 2003b). The maze is a procedure widely used within schools for evaluating students' comprehension with high correlation between maze scores and reading comprehension achievement tests (Ardoin et al., 2004; Tzivinikou et al., 2020). There is evidence that the maze technique adresses sentence-level comprehension performance rather than text-level comprehension performance (January and Ardoin, 2012) and that the maze score relied more on code-related than on language comprehension skills (Muijselaar et al., 2017).

The test measures reading comprehension on a sentence-by-sentence basis by showing students individual sentences one at a time without backspacing. All items have a similar sentence structure in the active voice and with age-appropriate syntactic structures (i.e., avoiding sentences with multiple clauses). In each sentence, one word is deleted. Three categories of items (i.e., sentences) model different syntactic and semantic structures and the items are classified by the lexical deletion pattern. Following the hierarchical construction-integration model of reading text comprehension (Kintsch and Rawson 2015), the item categories were created to cover important cognitive processes during reading comprehension. The first category includes the deletion pattern of both subjects and objects. The second category includes verbs and adjectives and the third category includes conjunctions and prepositions. In every task, the students chose from four options. For the gap, students are given one correct word and three distractors in a random order. The students’ task is to complete as many items as correctly as they can in the test time. When the time limit runs out, the students can finish the current item, and then the test closes. The following example illustrates an item of each category (translation from German):

(Category 1–Item 4) A llama has four legs/books/thumbs/camels(Category 2–Item 21) The lemonade is sweet/quiet/rich/sandy (Category 3–Item 48) I brush my teeth, before/after/soon/from I go to bed.

Previous research has tested the psychometric quality of the SinnL-Levumi reading comprehension tests according to the IRT. The SinnL-Levumi fits well with the Rasch model (RM; Rasch, 1980; see Jungjohann, Schurig and Gebhardt 2021). The test is able to track significant performance changes over time within a period of three weeks (Jungjohann et al., 2018). Within an intervention study with second graders (Anderson et al., 2020), the sum score raw values of SinnL-Levumi test correlates positive with the total score (r = 0.75), the score of the subtest at word level (r = 0.67), and with the score of the subtest at sentence level (r = 0.81) of the standardized German reading comprehension test (ELFE II; Lenhard et al., 2017). Because the ELFE II is a paper and pencil test we interpret these correlations as promising evidence that, despite different modes, the convergent validity of the test could be realized when compared to an established procedure.

Data Analysis

For the analysis a binary logistic test model (RM; Rasch, 1980) was applied. It formalizes the response probabilities of a person for correct answers by the item parameters (σ, item difficulty) and a person parameter (θ, person ability). The RM holds different desirable parsimonious properties. In the first place, it is possible to obtain θ independent from the items in use and σ independent from the sample (e.g., Scheiblechner, 2009). This translates into the main assumption of random item models (De Boeck, 2008). Here the σ are considered to be fixed parameters obtained from a calibration sample and only the θ are deemed random. So the σ have not to be estimated for every single (possibly small) sample, but can be estimated from comparable data available. This means that the items are interchangeable, though they have to be tested for model conformity nonetheless (Kubinger, 2009). The orders of the magnitude of the raw scores will be similar to the order of the ability estimates of the RM and the correlation between raw scores and scores obtained from the RM will be high. So that the usage of Rasch-ability estimates holds no additional merit after the model has been established successfully in this application. So the RM is used to evaluate the appropriateness of the usage of raw scores, evaluate the underlying dimensionality assumption and the item-fit, while practitioner feedback may be given as raw scores, making them easy to understand.

Following the theoretical principle of RM, each time items are calibrated small differences may be expected so that the stability of item calibration can be modeled as a standard error. As the number of items (or the sample) decreases in number, the differences are expected to become larger. In the first step of the analysis, σ are estimated by the pooled sample of t1 and t2 establishing an item calibration baseline. The item calibration was done as a power scoring, so that not reached items were viewed as missing (Kubinger, 2009) and the item difficulties are not confounded with the speed component of the test. The test is designed as a simple speed test, so all missing values were coded as wrong answers for the calculation of the person parameters. Specific model checks were conducted for t1 and t2. In the following step, the processing time as well as the number of items in use are evaluated to establish baseline parameters for the item reduction. Next a range of number of items and a range of test durations that still meet reasonable reliable estimates of θ are determined by eliminating items from the test and estimating the decrease in reliability of the test.

To calculate σ and θ a pairwise comparison approach (Choppin, 1968; see; Heine and Tarnai, 2015) with the pairwise R Package (Heine, 2021) was applied in R (R Core Team, 2020). In contrast to more common ways of parameter estimation like the conditional or marginal maximum likelihood, the pairwise approach delivers consistent parameters especially for small datasets with dichotomous data (Zwinderman, 1995).

With respect to the item order, the three sets of item categories always follow each other, so that all categories are touched relatively evenly when they are shortened.

Results

In the first step, item parameters were calculated with the pooled items from t1 and t2 with a dichotomous RM (Rasch, 1980). The sorted σ of the remaining 60 items are plotted in Figure 1 indicating sufficient spread of difficulties and confidence intervals roughly within the range of 1 logit $\overline{SE}=0.11$. This can be interpreted as a sufficiently small measure of random deviation (Wright and Stone, 1979).

FIGURE 1

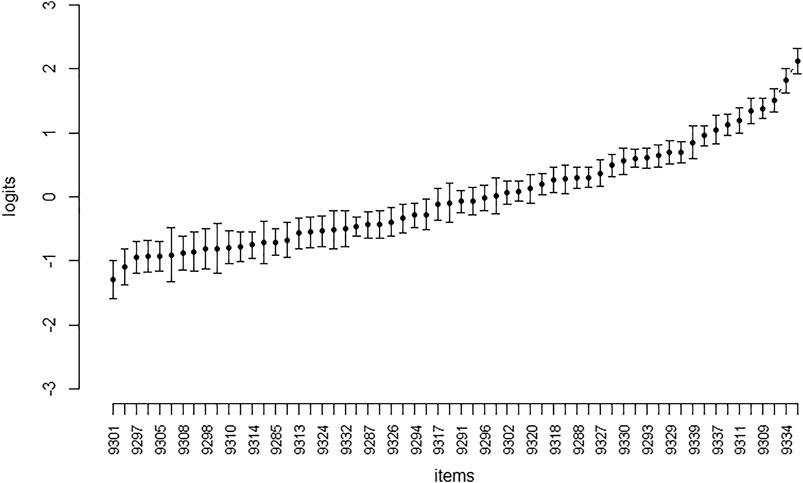
FIGURE 1. Item Parameters (60 items; sorted by σ). Note. On the Y-Axis the σ of the Items (in Logits) are given.

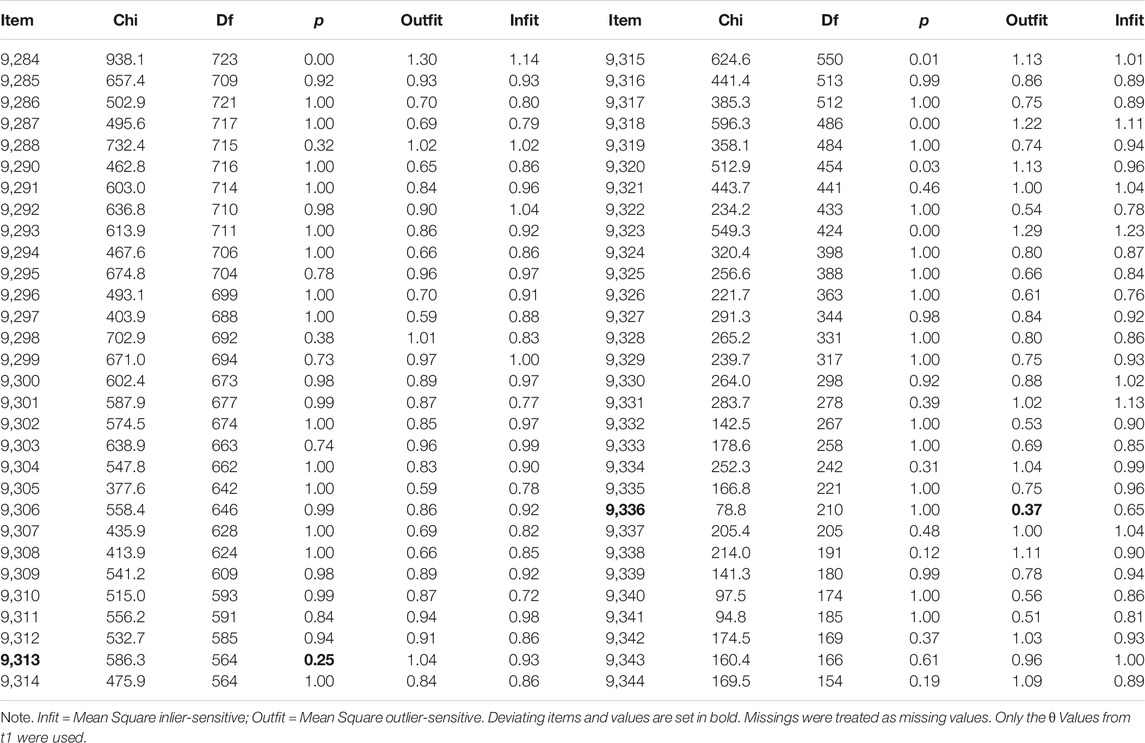
In a second step, person parameters were calculated by applying the item parameters within t1 and t2. The item fit was evaluated for every one of the 60 items by mean square statistics (Wright and Masters, 1990). All but one items reach reasonable values between 0.5 and 1.5 in Infit and Outfit. The item shows low Outfit, but acceptable Infit statistics, which can be interpreted as items that are less productive for measurement but not degrading (Linacre, 2002). The mean square values are given in Table 2. Differential item functioning was evaluated with graphical model checks (Figure 2) by a random item split and splits by gender, SEN and Migration Background. These are visualizations of Andersen’s Likelihood Ratio Tests (Andersen, 1973).

TABLE 2

TABLE 2. Infit and Outfit Statistics of the Items (t1; with missingness).

FIGURE 2

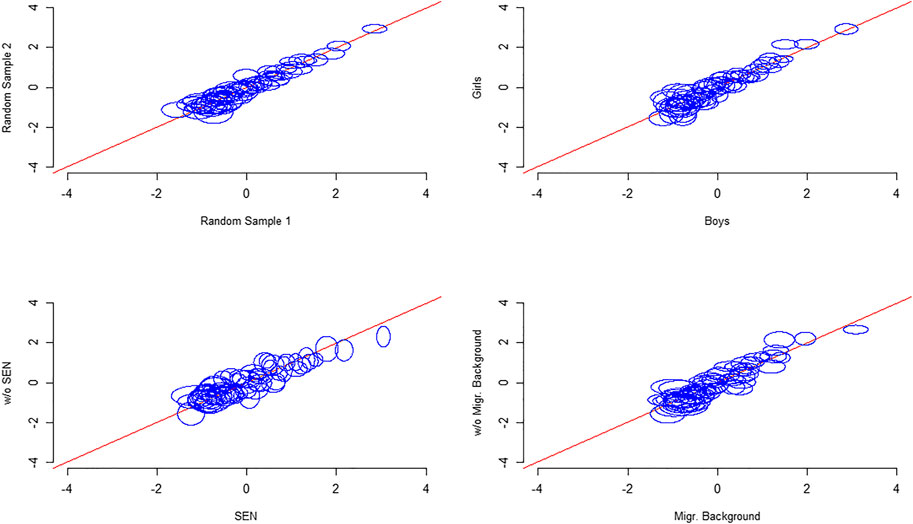
FIGURE 2. Graphical Model Check by different split criteria (60 items). Note. The blue ellipsoid represents the items’ standard errors computed by repeated subsampling (k = 30). The centers of the ellipsoids are given by the item parameters in both groups. An intersection of the ellipsoid and the bisecting angle indicates that there is no difference between the splits.

Though singular items do deviate slightly it is assumed that this effect is random after item inspection.

In the next step, the fit of the model and the estimates were evaluated by model tests and the reliability of the θ estimates. The Q3 Statistics reach mean values of Q3_t1 = −0.014 and Q3_t2 = −0.013 as can be expected under the assumption of local independence (e.g., Christensen et al., 2017).

Though not used frequently the reliability of the weighted likelihood estimation θ (WLE; Warm, 1989) can be estimated more precisely for IRT models than in a context of the classical test theory for all parameters are available (Walter and Rost, 2011) and indicate a measurement design effect or in other words the reduction of the uncertainty of the estimation of the student´s ability. It is defined as the fraction of the mean posterior variances as nominator and the ability variance as denominator (Adams, 2005).

$R=1-\frac{{\overline{\sigma }}_p^2}{{\sigma }^2}$

The reliabilities of the person ability scores within t1 (n = 761; WLE-Reliability_t1 = 0.936) and t2 (n = 631; WLE-Reliability_t2 = 0.933) underline the assumption of a precise measure of the test design on a population level even in an environment with sparse data (Adams, 2005). Finally, the item maps (Figure 3) are presented to allow for an evaluation of the homogeneity of the items and the conditional difficulty for t1 and t2. The differences are attributed to the randomization and the learning that happened between t1 and t2.

FIGURE 3

FIGURE 3. Item Maps.

After establishing reasonable model fits, the descriptive values of the sum scores for both t are calculated. As expected the scores of the students in t1 (M_t1 = 32.00, SD_t1 = 14.30) are lower than in t2 (M_t2 = 36.73, SD_t2 = 17.78), t (612) = 14.78, p < 0.001; d = 0.31. Roughly 50–60% of the items have been solved successfully indicating an appropriate item difficulty taking into account the speed component.

To check how many items have been processed the numbers of valid values per case were taken into account and plotted in Figure 4: Number of valid values per case (left hand) and processing time per item (right hand). The means range around 40 to 45 processed items (M_t1 = 39.04, SD_t1 = 13.89; M_t2 = 44.75, SD_t2 = 13.51). It can be seen that a great number of students reached the end of the test (60 items) before the 8 min ran out, indicating a surplus on time. At all t1 87 and in t2 144 students processed all 60 items. The 75% quantile reached a threshold of 50 items in t1 and even 58 items in t2. Wright and Stone (1979) report that a number of 30 (perfectly fitting) items is sufficient and the precision if the estimation of person parameters is not getting better any more when adding items. Even though it is not assumed that the items are perfect by any means this is taken as an indication of a surplus of valid values per case so that the test may be minimized at all. The processing times (Figure 4) can therefore be deemed homogenous between t1 and t2. It showed that the students roughly took about 12–15 s for a single item, though there were multiple outliers.

FIGURE 4

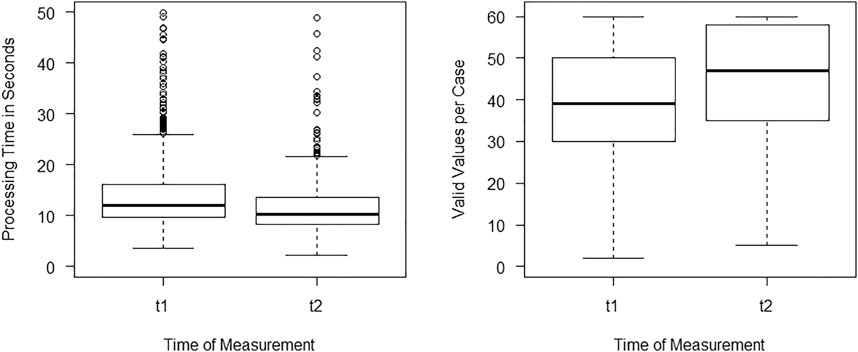
FIGURE 4. Distributions of processing time and valid values per case. Note. Number of valid values per case (right hand) and processing time per item in seconds (left hand).

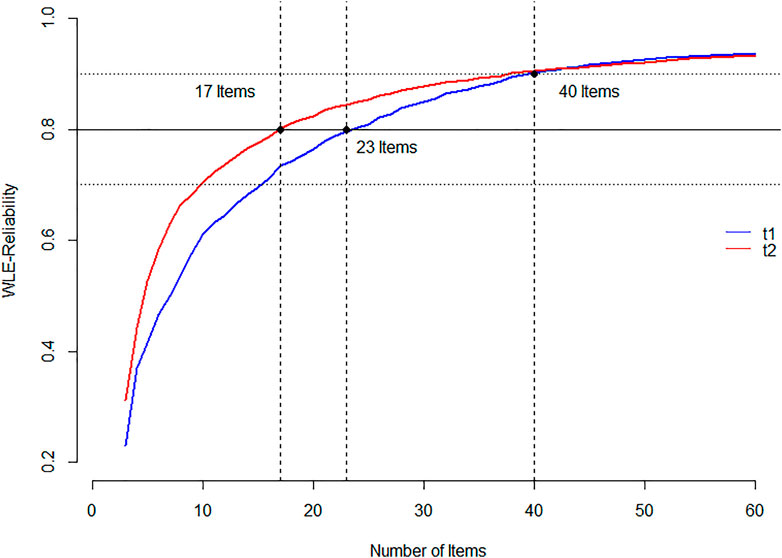
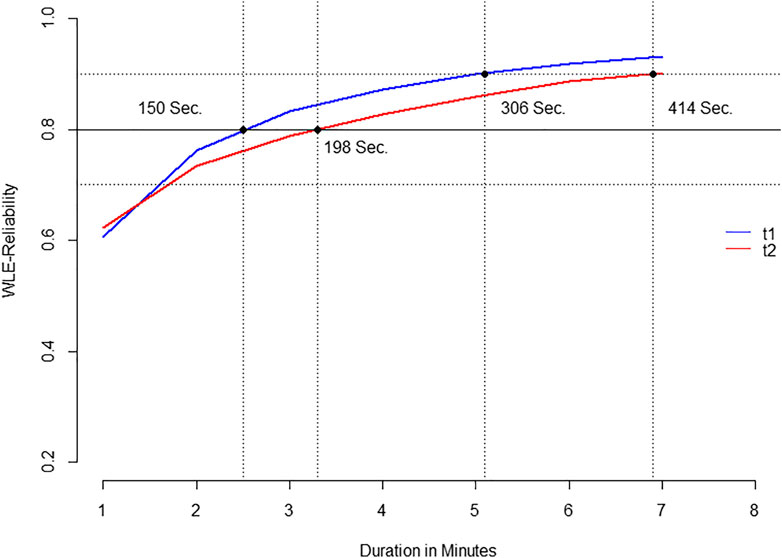
To determine reasonable cut-off values the reliability of the WLE is determined conditional to artificial margins of sparse data. On this behalf multiple models are estimated conditional to the number of items (Figure 5) and conditional to maximal processing times in minutes (Figure 6). For a better understanding, auxiliary lines are added to the plot with an intercept of 0.9, 0.8 and 0.7, indicating cut-off values between excellent, good and acceptable consistency (e.g., Kline, 2000). The number of items or time was given, when the curve crosses the threshold of 0.8 and 0.9. In the flat curve at the right hand of the figures it shows that there is a margin of test-time that does not affect the bias obtained when less items are available. The drop-off at the left hand shows the instability within the parameter estimates when there is insufficient information. It shows that roughly 40 items have to be given to reach a design effect of 0.9, though even about 20 may suffice, taking greater errors and uncertainty into account (Figure 6). More importantly about 6 min are needed to reach design effects of at least 0.9 in both samples and two to 3 min are needed to give sufficient information for at least 0.8. After establishing homogeneity, it was decided to balance the usability and the sensitivity and define a test length of 5 min.

FIGURE 5

FIGURE 5. WLE Reliability by number of items of the test.

FIGURE 6

FIGURE 6. WLE Reliability by duration of the test.

Discussion

It could be shown that the test will work sufficiently with fewer items, though it has to be taken into account that the reduction of items does imply a narrowing of the proficiency level in question. Ceiling effects will become more common indicating the need of connectable tests.

Most descriptions for test construction are for measurements at a single measurement point. These tests use many items over usually one school hour to measure a broad or multidimensional proficiency concept, covering the proficiencies of most students. Such (often) summative tests do serve well to identify students at risk of failing or with SEN, but are limited in measuring learning development over time. Those tests hold little to no relevance for everyday classroom situations or students at risk of failing or with SEN.

Since formative tests must be short, the methods described and listed here are a promising way to foster the design of tests for later use in progress monitoring. This shortness may be of particular interest for children with special needs, as it can be assumed that they often have short attention spans. In terms of quick usability, a reduction from eight to 5 min can be understood as a rather minor change. In terms of classroom use and in terms of the short concentration time of students with learning difficulties, this change can be understood as a step forward. In single-case research designs (Kazdin, 2011), where six or significantly more measurement time points must be used per student to reliably observe change, and in full classroom deployments as screening, these minutes add up quickly. These minutes can be better used for other instructions, a break or other didactic methods, since they do only improve the precision test slightly. Especially, when not the scores are interpreted, but the growth over the scores. In summary, to shorten the test, the following steps can be summarized.

• The test should be developed in a version and tested on a calibration sample according to psychometric criteria, which in any case has a sufficient length to cover the criteria to be observed (e.g. Sijtsma, 2012).

• This includes tests of item quality, fairness as well as of the test (American Educational Research Association, American Psychological Association and National Council on Measurement in Education, 2014). The even distribution of difficulty-generating characteristics on the test should be ensured.

• It should be determined what level of precision is needed to achieve the desired precision for the target population or desired measure in question (e.g. growth).

• The number of items that can be realistically achieved by the target population in what time must be examined to estimate the ratio of time and items.

• Then the item difficulties of a one or possibly higher parameter logistic model (IRT) model from the calibration sample can be used to make a stepwise reduction in the test time/item number. The rank order of the person parameters of the models should not differ between the longer and the shorter version. Criteria for the detailed analysis of IRT tests in learning progress monitoring are given in more detail by Wilbert and Linnemann (2011). A classic from which the assumptions can be derived is Lord (1980). A more general introduction to IRT modeling in contrast to classical test theory is given by Embretson (1996). Examples for the application of IRT in the context of learning progress assessment are given by Voß and Blumenthal (2020) for item pool calibration and Anderson et al. (2017) for dimensionality analysis. Also Sternberg and Grigorenko (2002) elaborate on the use of IRT in progress monitoring.

• In the case where the normative (e.g., 5 min) or the empirical criterion (e.g., receiver operating characteristic; ROC) is reached, the reduction is terminated. After that, the test should be tested on another sample. For instruments of learning process diagnostics, it is then necessary to map a learning process in order to ensure the sensitivity of the test.

A process of minimizing the test time necessary for a digital test for sentence comprehension was sketched. It was shown that the RM held true after reduction in test length by making use of the calibration of pooled item banks for a fixed and a randomized order alike. This is where the advantages of the item response modeling become apparent, since not only a single test statistic, but also item statistics and person statistics can be considered and evaluated separately (e.g., Kubinger, 2009). The successful implementation of a one parameter logistic models substantiate the use of raw scores in teacher’s feedbacks and therefore address the interpretability of the results and the time-efficiency of the test-taking alike. The execution of the test is thus possible in analog and digital form while the quality control of the test is more comprehensive than in approaches of classical test theory. Though item calibration is sample dependent it is assumed that the characteristics of the items are generalizable. So the characteristics of the learners (e.g., age-groups) in question have to be considered when establishing the sample for the calibration of the item parameters for random item IRM (De Boeck, 2008) and thus the rigorous testing of the statistical models parameters. There was no single ideal cut-off value and we did not expect that there should be one. The decision on the correct cut-off value remains qualitative under consideration of the practical needs of the test in question. There are no clear and single values when determining the minimal test-time but ranges of reasonably adequate tests times (i.e., the range of test-times with reasonable item and test-fit statistics) can be identified. Three minutes may not seem much, but in our understanding those minutes quickly sum up in classroom situations. Student-Teacher time is a valuable resource and we believe that tests have to care about this.

Additional problems remain. In the present study, only the first two measurement time points of a test to measure learning progress were available. Although these are sufficient to test the psychometric criteria of the test in the cross-section and in the follow-up, the test was not tested as a high-frequent progress diagnostic yet. Jungjohann et al. (2021) evaluated the test on another sample for four measurement time points with regard to change sensitivity over one school year. Further testing with more measurement time points and shorter time intervals is needed to examine the crucial sensitivity for change. Although, like in any other statistical analysis, the estimates of a sparse RM have bigger standard errors so the estimates are less robust. Therefore, the added value of a usable instrument may be outweighed by a loss in sensitivity (Wright, 1992). Though the number of items at hand is unlimited in theory, they still have to be created and tested. How much is enough? It is a difficult task to determine a margin for items to be repeated in randomized item selection. This is additionally complicated by the combinatory limitations but researchers should mind the number of items available within single tests and aim to minimize the risk of item repetition. Here it has to be stressed that the samples within our study are not independent. One important consequence might be that researchers might (un-)willingly design their test for a narrow skill level by deleting items indiscriminately. It is nonetheless possible to delete more difficult or easier items by design to address a specific group of test takers, following some principles of dynamic testing (Sternberg, and Grigorenko, 2002).

The selection of an appropriate difficulty level of a test for a sub-group still is a problem. A shorter test is less sensitive (Wright, 1992) because the error margins of the estimators necessarily rise. So different difficulty levels are an obvious solution. If comparable tests on different levels are developed, students can be given an appropriately challenging test. But which level to start with? By now baseline-testing (and possibly frustrating test-takers) or the intimate knowledge of teachers about their students and the test’s functioning is the only applicable way to solve this problem. The application of principles of computer-based assessments might pose a valuable addition to instruments of learning process monitoring. It may link the longitudinal results of students and the decision on appropriate difficulty levels on behalf of preceding results. It may provide a smooth transition between different difficulty levels and make differing tests obsolete. Though mode effects might still pose a challenge for tests that are meant to function both on paper and computer-based. The processing speed of the test-takers may also be addressed more intense than in this application, possibly adding additional parameters for the processing time in models to address additional difficulty parameters (e.g., by the Linear Logistic Test Model; Fischer, 1972).

To make it easier for teachers to incorporate tests in the classroom it is more effective to address the application design as well as the illustration and the presentation of results of the instruments of learning progress monitoring than the proficiency as a test administrator (Espin et al., 2017). The digitalization of diagnostic instruments may foster the practicability further due to simplified applications and evaluation alike. Especially in times of the recent pandemic it would have been possible to administer the tests via video communication. We are very much looking forward on further investigations on this matter.

Many assumptions in progress monitoring are made during test construction, but are not always empirically tested individually. Assumptions about dimensionality, invariance, and simple economical application in the classroom sometimes contradict each other. Therefore, a test can only conditionally meet all the requirements of different groups with different learning paces. This paper shows a methodological way to observe the complex assumptions in progress monitoring on test time reduction. Depending on the requirements of the target group, this approach needs to be adapted. Therefore, we need more open research in the field of progress monitoring with freely available tests, their analyses and syntax, so that the construction and mode of action can be understood individually.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://osf.io/hnbs8/.

Ethics Statement

The studies involving human participants were reviewed and approved by Faculty of Rehabilitation Science, Technical University of Dortmund. Following the requirements of the ministry of education of the federal state North Rhine-Westphalia (Schulgesetz für das Land Nordrhein-Westfalen, 2018), school administrators decided in co-ordination with their teachers about participation in this scientific study. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.

Author Contributions

MS served as primary author and data analyst. MG provided writing oversight, theoretical expertise, feedback, data, and initial study design. JJ provided theoretical expertise on reading assessment and data and served as secondary author.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Adams, R. J. (2005). Reliability as a Measurement Design Effect. Stud. Educ. Eval. 31 (2), 162–172. doi:10.1016/j.stueduc.2005.05.008

CrossRef Full Text | Google Scholar

American Educational Research Association, American Psychological Association and National Council on Measurement in Education (Editors) (2014). Standards for Educational and Psychological Testing (Washington, D.C.: AERA).

Google Scholar

Andersen, E. B. (1973). A Goodness of Fit Test for the Rasch Model. Psychometrika 38 (1), 123–140. doi:10.1007/BF02291180

CrossRef Full Text | Google Scholar

Anderson, D., Kahn, J. D., and Tindal, G. (2017). Exploring the Robustness of a Unidimensional Item Response Theory Model with Empirically Multidimensional Data. Appl. Meas. Educ. 30, 163–177. doi:10.1080/08957347.2017.1316277

CrossRef Full Text | Google Scholar

Anderson, S., Jungjohann, J., and Gebhardt, M. (2020). Effects of Using Curriculum-Based Measurement (CBM) for Progress Monitoring in reading and an Additive reading Instruction in Second Classes. ZfG 13 (1), 151–166. doi:10.1007/s42278-019-00072-5

CrossRef Full Text | Google Scholar

Ardoin, S. P., Witt, J. C., Suldo, S. M., Connell, J. E., Koenig, J. L., Resetar, J. L., et al. (2004). Examining the Incremental Benefits of Administering a Maze and Three versus One Curriculum-Based Measurement reading Probes when Conducting Universal Screening. Sch. Psychol. Rev. 33 (2), 218–233. doi:10.1080/02796015.2004.12086244

CrossRef Full Text | Google Scholar

Bell, R., and Lumsden, J. (1980). Test Length and Validity. Appl. Psychol. Meas. 4 (2), 165–170. doi:10.1177/014662168000400203

CrossRef Full Text | Google Scholar

Bennett, R. E. (2011). Formative Assessment: a Critical Review. Assess. Educ. Principles, Pol. Pract. 18, 5–25. doi:10.1080/0969594X.2010.513678

CrossRef Full Text | Google Scholar

Black, P., and Wiliam, D. (2003). 'In Praise of Educational Research': Formative Assessment. Br. Educ. Res. J. 29, 623–637. doi:10.1080/0141192032000133721

CrossRef Full Text | Google Scholar

Bloom, B. S. (1969). Some Theoretical Issues Relating to Educational Evaluation2 in Educational Evaluation: New Roles, New Means. Editor R. W. Tyler (Chicago, IL: Univ. of Chicago Press), 69, 26–50.

Google Scholar

Blumenthal, S., Blumenthal, Y., Lembke, E. S., Powell, S. R., Schultze-Petzold, P., and Thomas, E. R. (2021). Educator Perspectives on Data-Based Decision Making in Germany and the United States. J. Learn. Disabil. doi:10.1177/0022219420986120

CrossRef Full Text | Google Scholar

Brown, G. T. L. (2019). Is Assessment for Learning Really Assessment? Front. Educ. 4 (64). doi:10.3389/feduc.2019.00064

CrossRef Full Text | Google Scholar

Choppin, B. (1968). Item Bank Using Sample-free Calibration. Nature 219 (5156), 870–872. doi:10.1038/219870a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Christensen, K. B., Makransky, G., and Horton, M. (2017). Critical Values for Yen's Q3: Identification of Local Dependence in the Rasch Model Using Residual Correlations. Appl. Psychol. Meas. 41 (3), 178–194. doi:10.1177/0146621616677520

PubMed Abstract | CrossRef Full Text | Google Scholar

Cronbach, L. J., and Furby, L. (1970). How We Should Measure "change": Or Should We? Psychol. Bull. 74 (1), 68–80. doi:10.1037/h0029382

CrossRef Full Text | Google Scholar

De Boeck, P. (2008). Random Item IRT Models. Psychometrika 73, 533–559. doi:10.1007/s11336-008-9092-x

CrossRef Full Text | Google Scholar

Deno, S. L. (1985). Curriculum-based Measurement: The Emerging Alternative. Exceptional Child. 52 (3), 219–232. doi:10.1177/001440298505200303

PubMed Abstract | CrossRef Full Text | Google Scholar

Deno, S. L. (2003b). Curriculum-based Measures: Development and Perspectives. Assess. Eff. Intervention 28 (3-4), 3–12. doi:10.1177/073724770302800302

CrossRef Full Text | Google Scholar

Deno, S. L. (2003a). Developments in Curriculum-Based Measurement. J. Spec. Educ. 37 (3), 184–192. doi:10.1177/00224669030370030801

CrossRef Full Text | Google Scholar

Embretson, S. E. (1996). The New Rules of Measurement. Psychol. Assess. 8 (4), 341–349. doi:10.1037/1040-3590.8.4.341

CrossRef Full Text | Google Scholar

Espin, C. A., Wayman, M. M., Deno, S. L., McMaster, K. L., and de Rooij, M. (2017). Data-Based Decision-Making: Developing a Method for Capturing Teachers' Understanding of CBM Graphs. Learn. Disabilities Res. Pract. 32 (1), 8–21. doi:10.1111/ldrp.12123

CrossRef Full Text | Google Scholar

Fischer, G. H. (1972). Conditional Maximum-Likelihood Estimations of Item Parameters for a Linear Logistic Test Model. Vienna: University of Vienna.

Foegen, A. (2008). Algebra Progress Monitoring and Interventions for Students with Learning Disabilities. Learn. Disabil. Q. 31, 65–78. doi:10.2307/20528818

CrossRef Full Text | Google Scholar

Fuchs, L. S., and Fuchs, D. (1992). Identifying a Measure for Monitoring Student Reading Progress. Sch. Psychol. Rev. 21 (1), 45–58. doi:10.1080/02796015.1992.12085594

CrossRef Full Text | Google Scholar

Fuchs, L. S. (2004). The Past, Present, and Future of Curriculum-Based Measurement Research. Sch. Psychol. Rev. 33, 188–192. doi:10.1080/02796015.2004.12086241

CrossRef Full Text | Google Scholar

Gebhardt, M., Diehl, K., and Mühling, A. (2016). Online Lernverlaufsmessung für alle SchülerInnen in inklusiven Klassen. Z. für Heilpädagogik 67 (10), 444–454.

Google Scholar

Gebhardt, M., Heine, J.-H., Zeuch, N., and Förster, N. (2015). Lernverlaufsdiagnostik im Mathematikunterricht der zweiten Klasse: Raschanalysen und Empfehlungen zur Adaptation eines Testverfahrens für den Einsatz in inklusiven Klassen. [Learning progress monitoring in mathematic in second grade: Rasch analysis and recommendations for adaptation of a test instrument for inclusive classrooms]. Empirische Sonderpädagogik 7, 206–222.

Google Scholar

Genareo, V. R., Foegen, A., Dougherty, B. J., DeLeeuw, W. W., Olson, J., and Karaman Dundar, R. (2021). Technical Adequacy of Procedural and Conceptual Algebra Screening Measures in High School Algebra. Assess. Eff. Intervention 46 (2), 121–131. doi:10.1177/1534508419862025

CrossRef Full Text | Google Scholar

Good, R. (2011). Formative Use of Assessment Information: It’s a Process, So Let’s Say What We Mean. Pract. Assess. Res. Eval. 16 (3).

Google Scholar

Good, R., and Jefferson, G. (1998). Contemporary Perspectives on Curriculum-Based Measurement Validity in Advanced Applications of Curriculum-Based Measurement. Editor M. R. Shinn (New York, NY: Guilford Press), 61–88.

Google Scholar

Hattie, J., Masters, D., and Birch, K. (2015). Visible Learning into Action. London: Routledge. doi:10.4324/9781315722603

CrossRef Full Text

Heine, J.-H. (2021). Pairwise: Rasch Model Parameters by Pairwise Algorithm. R package version 0.4.4-5.1. Retrieved on 30.04.2021. https://CRAN.R-project.org/package=pairwise (Accessed May 1, 2021).

Google Scholar

Heine, J.-H., and Tarnai, C. (2015). Pairwise Rasch Model Item Parameter Recovery under Sparse Data Conditions. Psychol. Test Assess. Model. 57 (1), 3–36.

Google Scholar

January, S.-A. A., and Ardoin, S. P. (2012). The Impact of Context and Word Type on Students' Maze Task Accuracy. Sch. Psychol. Rev. 41 (3), 262–271. doi:10.1080/02796015.2012.12087508

CrossRef Full Text | Google Scholar

Jungjohann, J., DeVries, J. M., Mühling, A., and Gebhardt, M. (2018). Using Theory-Based Test Construction to Develop a New Curriculum-Based Measurement for Sentence reading Comprehension. Front. Educ. 3. doi:10.3389/feduc.2018.00115

CrossRef Full Text | Google Scholar

Jungjohann, J., and Gebhardt, M. (2019). SinnL-Levumi. "Sinnkonstruierendes Satzlesen" der Onlineplattform. in Leibniz-Zentrum für Psychologische Information und Dokumentation (ZPID) (Trier: Electronic Test Archive. Trier: ZPID). [Sentences Reading Comprehension Measure on www.levumi.de] (Accessed December 1, 2020). doi:10.23668/psycharchives.2463

CrossRef Full Text | Google Scholar

Jungjohann, J., Schurig, M., and Gebhardt, M. (2021). Fachbeitrag: Pilotierung von Leseflüssigkeits- und Leseverständnistests zur Entwicklung von Instrumenten der Lernverlaufsdiagnostik. Ergebnisse einer Längsschnittstudie in der 3ten und 4ten Jahrgangsstufe. Vhn 90. doi:10.2378/vhn2021.art12d

CrossRef Full Text | Google Scholar

Kazdin, A. E. (2011). Single-case Research Designs: Methods for Clinical and Applied Settings. New York: Oxford Univ. Press.

Kingston, N., and Nash, B. (2011). Formative Assessment: A Meta-Analysis and a Call for Research. Educ. Meas. Issues Pract. 30, 28–37. doi:10.1111/j.1745-3992.2011.00220.x

CrossRef Full Text | Google Scholar

Kintsch, W., and Rawson, K. A. (2015). “Comprehension,” in The Science of reading. A Handbook (Blackwell Handbooks of Developmental Psychology. Editors M. Snowling, and C. Hulme (Malden, Mass: Blackwell Publishers), 209–226.

Google Scholar

Klauer, K. J. (2014). Formative Leistungsdiagnostik: Historischer Hintergrund und Weiterentwicklung zur Lernverlaufsdiagnostik in Formative Performance monitoring Lernverlaufsdiagnostik [Learning Progress Monitoring]. Editors M. Hasselhorn, W. Schneider, and U. Trautwein (Göttingen: Hogrefe), 1–18.

Google Scholar

Kline, P. (2000). The Handbook of Psychological Testing. 2nd ed. London: Routledge.

Kline, R. B. (2015). Principles and Practice of Structural Equation Modeling. 4th ed. New York: Guilford Press.

Kubinger, K. D. (2005). Psychological Test Calibration Using the Rasch Model-Some Critical Suggestions on Traditional Approaches. Int. J. Test. 5, 377–394. doi:10.1207/s15327574ijt0504_3

CrossRef Full Text | Google Scholar

Lenhard, W., Lenhard, A., and Schneider, W. (2017). ELFE II - ein Leseverständnistest für Erst- bis Siebtklässler. Version II. Göttingen: Hogrefe Schultests. doi:10.1007/978-3-658-17983-0

CrossRef Full Text | Google Scholar

Linacre, J. M. (2002). What Do Infit and Outfit, Mean-Square and Standardized Mean? Rasch Measurement Trans. 16 (2), 878.

Google Scholar

Lord, F. M. (1980). Applications of Item Response Theory to Practical Testing Problems. New York: Routledge. Reprint 2008.

Masters, G. N. (1988). Item Discrimination: When More Is Worse. J. Educ. Meas. 25 (1), 15–29. doi:10.1111/j.1745-3984.1988.tb00288.x

CrossRef Full Text | Google Scholar

Mühling, A., Jungjohann, J., and Gebhardt, M. (2019). Progress Monitoring in Primary Education Using Levumi: A Case Study, in Proceedings of the 11th International Conference on Computer Supported Education (CSEDU). Editors H. Lane, S. Zvacek, and J. Uhomoihi, Heraklion, Greece, 2–4 March 2019 (SCITEPRESS - Science and Technology Publications), 137–144.

Google Scholar

Muijselaar, M. M. L., Kendeou, P., de Jong, P. F., and van den Broek, P. W. (2017). What Does the CBM-Maze Test Measure? Scientific Stud. Reading 21 (2), 120–132. doi:10.1080/10888438.2016.1263994

CrossRef Full Text | Google Scholar

Nelson, P. M., Van Norman, E. R., Klingbeil, D. A., and Parker, D. C. (2017). Progress Monitoring with Computer Adaptive Assessments: the Impact of Data Collection Schedule on Growth Estimates. Psychol. Schs. 54 (5), 463–471. doi:10.1002/pits.22015

CrossRef Full Text | Google Scholar

R Core Team (2020). R: A Language and Environment for Statistical Computing. Zugriff am 30.04.2021. R Foundation for Statistical ComputingVerfügbar unter: https://www.R-project.org/ (Accessed June 6, 2021).

Google Scholar

Rasch, G. (1980). Probabilistic Models for Some Intelligence and Attainment Tests. Chicago, Ill: Univ. of Chicago Press.

RatSWD, (2015). Quality Standards for theDevelopment, Application, and Evaluation of Measurement Instruments in Social Science Survey Research in RATSWD Working Paper Series (Berlin: German Data Forum (RatSWD)), 245.

Google Scholar

Rost, J. (1999). Was ist aus dem Rasch-Modell geworden? Psychologische Rundschau 50, 140–156. doi:10.1026//0033-3042.50.3.140

CrossRef Full Text | Google Scholar

Scheiblechner, H. H. (2009). Rasch and Pseudo-Rasch Models: Suitableness for Practical Test Applications. Psychol. Sci. Q. 51, 181–194.

Google Scholar

Shapiro, E. S. (2013). Commentary on Progress Monitoring with CBM-R and Decision Making: Problems Found and Looking for Solutions. J. Sch. Psychol. 51, 59–66. doi:10.1016/j.jsp.2012.11.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Sijtsma, K., and Emons, W. H. M. (2011). Advice on Total-Score Reliability Issues in Psychosomatic Measurement. J. Psychosomatic Res. 70 (6), 565–572. doi:10.1016/j.jpsychores.2010.11.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Sijtsma, K. (2012). Future of Psychometrics: Ask What Psychometrics Can Do for Psychology. Psychometrika 77, 4–20. doi:10.1007/s11336-011-9242-4

CrossRef Full Text | Google Scholar

Smith, G. T., McCarthy, D. M., and Anderson, K. G. (2000). On the Sins of Short-form Development. Psychol. Assess. 12 (1), 102–111. doi:10.1037/1040-3590.12.1.102

PubMed Abstract | CrossRef Full Text | Google Scholar

Stecker, P. M., Fuchs, L. S., and Fuchs, D. (2005). Using Curriculum-Based Measurement to Improve Student Achievement: Review of Research. Psychol. Schs. 42, 795–819. doi:10.1002/pits.20113

CrossRef Full Text | Google Scholar

Sternberg, R. J., and Grigorenko, E. L. (2002). Dynamic Testing: The Nature and Measurement of Learning Potential. Cambridge, UK: Cambridge University Press.

Stewart, A. L., Hays, R. D., and Ware, J. E. (1988). The MOS Short-form General Health Survey. Med. Care 26, 724–735. doi:10.1097/00005650-198807000-00007

PubMed Abstract | CrossRef Full Text | Google Scholar

Tzivinikou, S., Tsolis, A., Kagkara, D., and Theodosiou, S. (2020). Curriculum Based Measurement Maze: A Review. Psych 11 (10), 1592–1611. doi:10.4236/psych.2020.1110101

CrossRef Full Text | Google Scholar

Vaughn, S., Linan-Thompson, S., and Hickman, P. (2003). Response to Instruction as a Means of Identifying Students with Reading/Learning Disabilities. Exceptional Child. 69 (4), 391–409. doi:10.1177/001440290306900401

CrossRef Full Text | Google Scholar

Voß, S., and Blumenthal, Y. (2020). Assessing the Word Recognition Skills of German Elementary Students in Silent Reading-Psychometric Properties of an Item Pool to Generate Curriculum-Based Measurements. Educ. Sci. 10 (2), 35. doi:10.3390/educsci10020035

CrossRef Full Text | Google Scholar

Walter, O., and Rost, J. (2011). Psychometrische Grundlagen von Large Scale Assessments: Methoden der psychologischen Diagnostik - Enzyklopädie der Psychologie [Psychometric Foundations of Large-Scale-Assessment – Encyclopedia of Psychology. Göttingen: Hogrefe, 87–149.

Warm, T. A. (1989). Weighted Likelihood Estimation of Ability in Item Response Theory. Psychometrika 54, 427–450. doi:10.1007/BF02294627

CrossRef Full Text | Google Scholar

Wilbert, J., and Linnemann, M. (2011). Kriterien zur Analyse eines Tests zur Lernverlaufsdiagnostik. [Criteria for analyzing a test measuring learning progress]. Empirische Sonderpädagogik 3, 225–245.

Google Scholar

Wright, B. D., and Masters, G. N. (1990). Computation of OUTFIT and INFIT Statistics. Rasch Meas. Trans. 3 (4), 84–85.

Google Scholar

Wright, B. D., and Stone, M. H. (1979). Best Test Design. Chicago, Il: Mesa Press.

Wright, B. D. (1992). What Is the "Right" Test Length. Rasch Meas. Trans. 6 (1), 205.

Google Scholar

Zijlmans, E. A. O., Tijmstra, J., van der Ark, L. A., and Sijtsma, K. (2019). Item-Score Reliability as a Selection Tool in Test Construction. Front. Psychol. 9, 2298. doi:10.3389/fpsyg.2018.02298

PubMed Abstract | CrossRef Full Text | Google Scholar

Zwinderman, A. H. (1995). Pairwise Parameter Estimation in Rasch Models. Appl. Psychol. Meas. 19 (4), 369–375. doi:10.1177/014662169501900406

CrossRef Full Text | Google Scholar