Factors Influencing Success in Advanced Engineering Mathematics Courses: A Case Study

Several studies have been conducted to understand the predictors of academic performance of various levels of high school and undergraduate students as quantified by the grade point average. This study focuses specifically on engineering students as they differ from other undergraduate students in their background and expectations. We focus on quantifying essential predictors of the performance of engineering students in an advanced mathematics course. We collected data from 72 participants recruited from engineering students enrolled in the advanced engineering mathematics (AEM) course in a research university. We chose this course to represent a standard engineering mathematics course covering several essential topics. We consider several factors in our analysis, such as cellphone usage and the academic background, e.g., the academic year, number of minors, and majors, performance in prerequisite courses. We perform several regression analyses to understand the effects of cellphone usage, course schedule, and academic background on performance in the AEM course and its prerequisites. In particular, we use the stepwise regression technique using forward selection and backward elimination procedures. We discovered a few interesting findings in this case study. Firstly, for the participants in this study, we find that the daily average “screen time” on their cellphones is not a statistically significant predictor of student performance. This finding contradicts some prior studies on this participant and may indicate adaption and integration of the technology by the new generation of students in recent years. We also found that the lecturing schedule was not an influential factor for their academic performance. These findings are especially relevant during the COVID-19 pandemic, as they suggest that advanced engineering students have adapted to the use of technology and are flexible concerning lecture schedules. Another unexpected finding is that this study brings new evidence that the number of minors taken by the participants is a negative predictor of their grade in the AEM course. This observation may indicate that course-work from non-major classes may adversely impact their performance in mathematical engineering courses.

1 Introduction

This paper aims to find and quantify the factors affecting academic success in an undergraduate-level course in advanced engineering mathematics (AEM). Our focus in this work is on factors available to the instructors to improve the quality of the course. In this cross-sectional case study (Yin, 1994), we enlist 72 students enrolled in the “Advanced Engineering Course” in a private university in the United States.

Numerous studies have elaborated on various factors behind academic success. Some of the factors that have been shown to impact academic success are socioeconomic status (SES), self-efficacy, course load, duration and frequency of lectures, and prior academic performance. In recent years mobile technology has become universally accessible, with several researchers studying the impact of cellphones on academic achievements. Since this topic is vast, the above list is by no means an exhaustive one. We first review the literature on this topic and then elaborate on the rationale behind our research choices in this study. The relation between SES and academic success is well-established in the literature. A meta-analysis of 200 studies (White, 1982) showed that socioeconomic status and academic achievements are positively correlated. A replica of the study (Sirin, 2005) across 128 school districts showed a medium to strong SES–achievement relation.

Bandura (2010) defines “self-efficacy” as believing in their ability to influence events affecting their lives. Motlagh et al. (2011) show that self-efficacy is highly correlated with high school students’ academic achievement. Komarraju and Nadler (2013), de Fátima Goulão (2014) use multiple regression analysis to show that self-efficacy results in higher academic achievement in undergraduate students. Attewell and Monaghan (2016) study the rate of completion and time to degree completion and find that students who attempt 15 rather than 12 credits in their first-year graduate at significantly higher rates within 6 years of initial enrollment. Ann Clovis and Chang (2019) show that the number of credits earned in the first year is a positive indicator of attainment of degree who begin college at a 2-year institution. A study of a sample of first-year students by Szafran (2001) shows that students who register for more credits tend to earn higher GPAs.

To investigate if the lecture frequency matters for academic success, Henebry (1997) analyzes student performance in classes scheduled 1 day a week, 2 days a week, and 3 days a week. The results indicate that students have a better chance of passing the course when a class schedule meets more than once a week. Gallo and Odu (2009) examine the academic performance of students enrolled in a college algebra course. Similar to the studies by Henebry (1997), Gallo and Odu (2009) study three different lecture schedules: once per week, twice per week, and three times per week. Henebry (1997) uses regression analysis to show that the students with only one lecture per week performed significantly worse than the other two groups. We note that the academic performance between students who had two lectures per week and students who had three lectures per week was not statistically different in both these studies. However, these findings are contradicted by a recent study by Trout (2018), in which accounting students in the 1-day-a-week class performed significantly better than students in the two lectures per week. McKenzie and Schweitzer (2001) identify previous academic performance as one of the factors predicting academic success. Newman-Ford et al. (2009) find that prior educational attainment is one of the significant predictors of academic achievements. De Winter and Dodou (2011) show that high school exam scores in the natural sciences and mathematics are the strongest predictors of first-year GPA and engineering degree completion, whereas the language factor has no significant predictive value. These findings are further supported by Anderton et al. (2017) and Hine et al. (2015) for health science students. Although several studies have shown that students’ prior mathematics skills are a good predictor of undergraduate success, considering the overall high school GPA may not be effective. Indeed, Noble and Sawyer (2002) show that a high school GPA is “not” an effective predictor of the first-year GPA.

There have been several studies conducted concerning the impact of cellphone usage on learning. Lepp et al. (2014) demonstrate that cellphone usage was significantly and negatively related to actual college GPA. Duncan et al. (2012) report that in-class use of cellphones leads to lower grades. Lepp et al. (2015) also showed that college students who use cellphones more than 10 h a day experienced significantly more leisure distress than the other groups. In a 2015 study, Barr et al., 2015 show that cognitive ability was associated with less smartphone use and less time spend using online search engines. In Samaha and Hawi (2016) and Hawi and Samaha (2016), the researchers show that a smartphone addiction risk was negatively related to academic performance. Although numerous studies show cellphones impact academic achievement negatively, some studies fail to confirm this conclusion. For example, Lee (2015) does not find evidence that cellphone use impacted academic performance negatively. A correlation analysis by Winskel et al. (2019) did show significant association between cellphone use and academic performance of university students. Olufadi (2015) conclude in their work that no single mobile phone use behavior was sufficient to influence academic performance.

1.1 Rationale Behind the Selection of Factors in the Study

We design this study to help instructors and advisers to make appropriate decisions regarding engineering students taking advanced mathematics courses. We make our research choices with this goal in mind. Although socioeconomic status is a significant predictor of academic success, we did not consider it for this study for two reasons. Firstly, the students in our case study are from a private research university in the United States enrolled in a single course, a single semester. Thus, there is a lack of diversity in the SES of participants of this study. Secondly, an instructor is unlikely to have access to the SES of their students in the class. Hence, while SES may be a vital tool (White, 1982; Sirin, 2005) for administrators while making policies, it is of limited practical use to an instructor. Moreover, in most cases, the instructors do not have access to the SES of the students. Hence, we do not study the impact of SES on academic success in our work. Similarly, self-efficacy is a relevant indicator of student success (Bandura, 2010; Motlagh et al., 2011; Komarraju and Nadler, 2013; de Fátima Goulão, 2014). However, the methodology of self-efficacy measurement varies (Mamaril et al., 2016)). Since measuring self-efficacy is not a viable option for most instructors, we do not include it as a factor in our analysis.

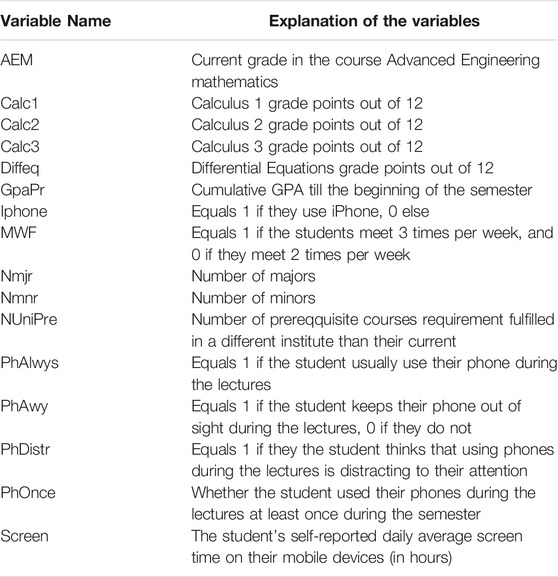
While the connection between the course load and academic achievement is well-studied (Szafran, 2001; Attewell and Monaghan, 2016; Ann Clovis and Chang, 2019), the link between the number of “minor degrees” pursued and academic success is not well-understood. To this effect, we include the “number of minors degrees sought” (Nmnr) as one of the study factors. We include the number of majors (Nmjr) as a control factor in the study. While all students were from a similar background, the academic year was not necessarily the same for all the participants. Thus we added GradYr as one of the control variables. Whether students succeed better in a course with two lectures per week or three lectures per week is a pertinent question for advisers and departments when scheduling classes. In light of Trout (2018), the issue is not settled. Since the same instructor was teaching the AEM course with two different schedules, we decided to study the effect of schedules on student success. The variable MWF serves this purpose. The variable MWF equals 1 if the student has a 50-min lecture on Monday, Wednesday, and Friday, and it is 0 if they have a 75-min lecture on Mondays and Wednesdays.

While most studies depicted a negative relationship between cellphone usage and academic performance, the lack of consensus in different studies necessitates further research. To understand the influence of screen time on grades [c.f. Samaha and Hawi (2016) and Hawi and Samaha (2016)], we include the average amount of time in hours that the participants spend on their cellphones per day (screen) in our study. Sarraf et al. (2014) found a significant difference in the survey completion rate of iPhone users and Android users. Thus, we incorporate the variable iPhone, which equals 1 if the participant uses iPhone®and 0 if they do not. Mendoza et al. (2018) show that participants who kept their cellphones with them performed worse on a quiz than those without cellphones. To take this phenomenon into account, we include a variable PhAwy which is equal to 1 if the student keeps their phone out-of-sight during the lectures and 0 if they do not. We also wanted to understand whether the students’ personal opinion about the cellphone being a distraction influences their grades or not. To this effect, we include the variable PhDistr, which equals 1 if the student thinks that using phones during the lectures is distracting to their attention.

Lastly, Simonsmeier et al. (2018), Wade and Kidd (2019), and numerous other studies have shown a strong relationship between prior knowledge and learning. We decided to add the prior knowledge as a control for this study. Instead of including the prior GPA in the study, we consider the participants’ performance in the prerequisite courses as prior knowledge. This design choice allows us to examine the role of the prerequisites courses individually. The prerequisites for the AEM course are Calculus III and Elementary Differential Equations. Thus, we include grades in Calculus III (Calc3) and Elementary Differential Equations (Diffeq) as explanatory variables for the model. Moreover, Calculus I and Calculus II are prerequisites for Calculus III. Hence we also include Calculus I grades (Calc1) and Calculus II grades (Calc2) in our models.

1.2 Choice of the Course for the Case Study

Engineering students significantly differ from liberal arts students. To this effect (Liu and Liang, 2020), find neurocognitive evidence for differences in verbal, numerical, and spatial problem-solving processes between engineering and liberal arts students (Scott and Sedlacek, 1975). use discriminant analysis techniques to show that physical scientists are different from engineers along an introspection-intellectual vs. social conventional dimension. The engineering curriculum also emphasizes applications and requires various mathematics courses such as calculus, differential equations, and numerical algebra. For example, the criteria published by the Accreditation Board for Engineering and Technology, Inc (ABET) for accrediting Mechanical Engineering Programs (Accreditation Board for Engineering and Technology, Inc., 2019, p. 30) states that the program curriculum.

“…must require students to apply principles of engineering, basic science, and mathematics (including multivariate calculus and differential equations); to model, analyze, design, and realize physical systems, components, or processes; and prepare students to work professionally in either thermal or mechanical systems while requiring topics in each area.”

Most mathematics courses, such as the Calculus sequence, are open for students of all majors. However, the course “AEM” is specifically designed for engineering students. Hence, we recruit participants from students enrolled in the AEM course, isolating only the engineering students from other majors. The course typically consists of the following topics and their applications: 1) probability and statistics, 2) linear algebra, 3) ordinary and partial differential equations.

1.3 Research Questions and Hypotheses

Given the rationale detailed in section Rationale Behind the Selection of Factors in the Study we are interested in the following research questions related to a typical engineering course:

(1). Is the amount of cellphone usage related to their grades?

(2). Does the number of minor degrees influence their grades?

(3). Is there a relation between lecturing schedule and academic performance?

To investigate the research questions formulated above, we begin with the following research hypotheses for a typical engineering undergraduate student:

(1). Academic performance in an AEM course is negatively and significantly related to their daily cellphone usage.

(2). Academic performance in an AEM course is unrelated to the number of minors taken by the students.

(3). Academic performance in an AEM course is related to the length and frequency of the lecture meetings per week.

In the following section Methodology, we describe our sample, data acquisition, preprocessing of the data. In section Analytical Approach we describe our analytical approach to obtain linear models for predicting grades in AEM, Calculus III, Calculus II, and Elementary Differential Equations. We describe the results obtained from the analysis in section Results. In section Discussion we discuss the results and their implications.

2 Methodology

2.1 Description of the Sample

The subjects for this study are engineering students from a private research institute in the northeast region of the United States. The course is intended for Mechanical and Aeronautical Engineering majors. The course covered topics such as applications of linear algebra, differential equations, and statistics. The prerequisites for the course were calculus III and differential equations. Most students in the course were junior and senior engineering students. Participants were informed that the survey would not be available to the researchers before the grades were posted.

2.2 Data Acquisition

Questionnaires were distributed to all students enrolled in the course “AEM” in Fall 2018. Out of all the students who received the questionnaire, 72 students participated in the study. The responses were stored in the department office until after the grades were posted. In the questionnaires, the students reported their grades from their courses: Calculus I, Calculus II, Calculus III, and Elementary Differential Equations. They were also requested to report the “current” AEM grade. There were two sections of this course. One section met three times per week (Monday, Wednesday, and Friday) for 50 min sessions, whereas the other met two times per week for 75-min sessions. Both sections had all the exams simultaneously and had the same homework due online, at the same time every week. They were also requested to report the “current” AEM grade, which was available to the students in the Learning Management System used by the university. In the survey, we requested the students for miscellaneous information such as their current academic year, the number of majors, minors, number of prerequisites for the course taken at a different institute, i.e., either at high school or other colleges before attending their current institute. Questions related to their cellphone usage included the type of phone (i.e., iPhone, Android, or other) the students use, the amount of screen time per day, whether they think that using a cellphone during the lecture is a distraction, or not. The screen time in this study refers to the average amount of time spent on their cellphones during a typical 24-h day. The survey asked the students if they keep their cellphone out of sight during the lectures. See Table 1 for precise definitions of all the variables. We note that the use of cellphones during the AEM course was discouraged. However, there were no academic consequences if the students used their cellphones during lectures.

TABLE 1

TABLE 1. Explanation of the variable names.

2.3 Preprocessing the Data

We have 72 observations with 16 variables in the data collected. Some of the variables had missing values and outliers. One way to deal with this issue is to remove observations with missing values or outliers altogether. However, since we collected 16 variables for each observation, removing one observation due to a missing value or an outlier would remove the other 15 variables. This approach can seriously degrade the quality of the data set. Moreover (Quintano et al., 2010), show that the presence of outliers can produce a deviation from the actual data pattern. Since we have a relatively small number of participants, we replace the missing values and outliers with imputations generated by “multiple imputations by chained equations” (Van Buuren et al., 1999; Van Buuren et al., 2006). To this effect, we used the “MICE” package in R. We identify the outliers using the “boxplot.stats” function in R (McGill et al., 1978, p. 16). Removal of the outliers rendered the variables NMjr, PhOnce, and PhAlways as redundant, and thus we removed these variables from further analysis.

2.4 Coding Language and Libraries Used

For our coding, we used R language (version 4.0.0) on a Mac Operating System [x86_64-apple-darwin17.0 (64-bit)]. We used the following libraries in our coding: readxl, stats, mice, Hmisc, MASS, dplyr, ggpubr, car, pwr, corrplot, ggplot2, qqplotr, mctest, plot3D.

2.5 Analytical Approach

2.5.1 Descriptive Analysis

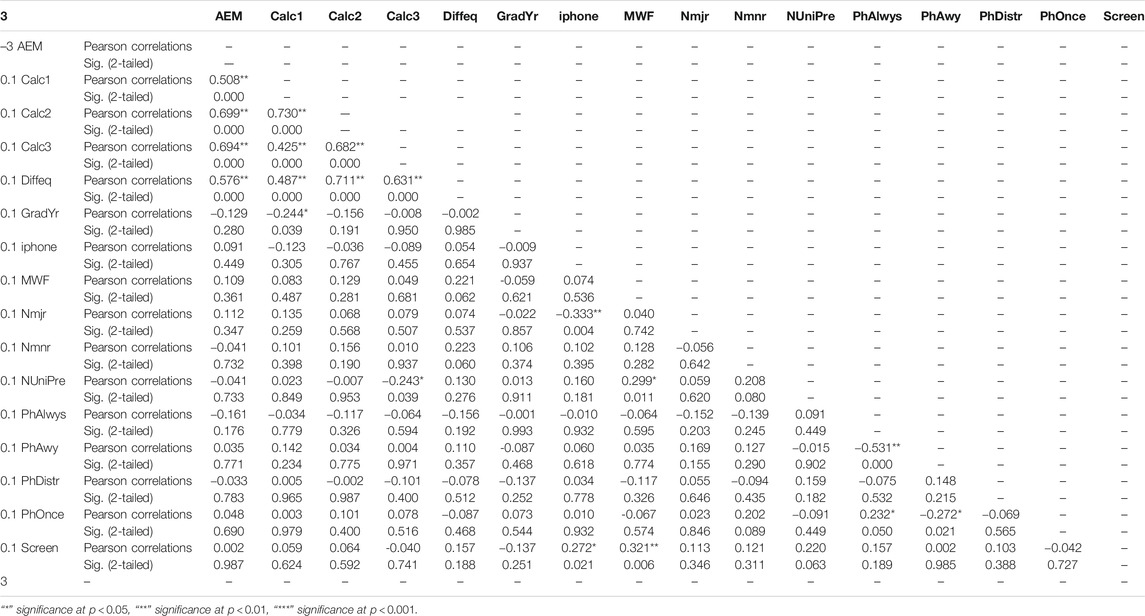
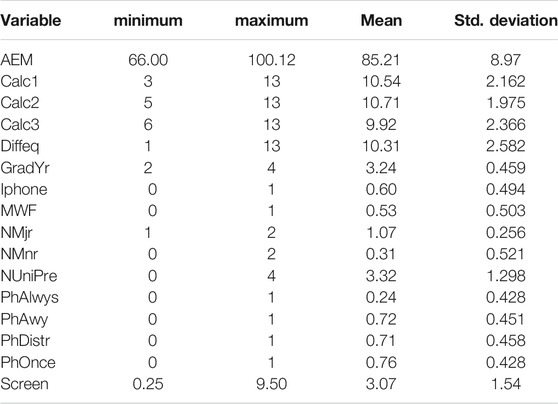
We begin with the study of the descriptive statistics of the data (see Table 1), and Pearson correlations (see Table 2) between all variables.

TABLE 2

TABLE 2. Pearson correlations between variables used in the study and their significance levels.

2.5.2 Constructing Linear Models With Grades in Advanced Engineering Mathematics as a Response Variable

We aim to construct a linear model with grades in advanced engineering mathematics as the response variable. We begin with a model that includes all possible explanatory variables, and we refer to it as the preliminary model ${\text{M}}_{\text{AEM}}^0$. We begin with Calc1, Calc2, Calc3, Diffeq, GradYr, iphone, MWF, NMnr, NUniPre, PhAwy, PhDistr, and screen as the explanatory variables with the grades in Advanced Engineering Mathematics i.e., AEM as the response variable.

2.5.3 Constructing Linear Models With Grades in Advanced Engineering Mathematics as a Response Variable Using Stepwise Regression Technique

The selection of appropriate variables is essential while constructing a linear model with multiple variables. Including more number of explanatory variables increases the coefficient of determination ($R^2$) indefinitely, leading to overfitting (Neter et al., 1996). Thus, a better approach (Theil, 1961) is to choose only those variables that maximize the adjusted coefficient of determination ($R_{adj}^2$). To this effect, we apply the forward selection algorithm Efroymson (1960) of the stepwise regression technique. We verify the resulting model with the backward elimination algorithm Beale et al. (1967). We choose the model that produces the least $R_{adj}^2$. We refer to the final model as ${\text{M}}_{\text{AEM}}^1$.

2.5.4 Constructing Linear Models With Grades in Prerequisite Courses as Response Variables

We repeat the process of constructing linear model ${\text{M}}_{\text{Calc}3}^0$ with Calculus III grades, i.e., Calc3 as a response variable. Since Calculus I and Calculus II are the only prerequisites for the Calculus III course. For our preliminary model we begin with Calc2 and Calc1 as explanatory variables. O’Dea (2020) show that the smartphone replacement cycle is about 2.88 years. Thus, we assumed that the students did not change their smartphones since they took Calculus I. Consequently, we include and iphone in our preliminary model. Since cellphone usage can vary from semester to semester, we decided not to include cellphone usage information in this model. Moreover, we can not ascertain that the students have the same academic background information in the term they took Calculus III. Hence, we do not include variables related to the academic background in this model. We apply the backward elimination algorithm and forward selection algorithms of the stepwise regression techniques. We choose the model with the largest value of $R_{adj}^2$ as the final model denoted by ${\text{M}}_{\text{Calc}3}^1$. We carried out similar regression analyses for grades in Calculus II and Elementary differential equations.

3 Results

3.1 Descriptive Statistics and Correlations

In Table 3 we describe the descriptive statistics for the variables used in this study. Table 2 shows the details of Pearson correlations between all variables and their 2-tailed significance levels. We can readily see the positive and statistically significant correlation between the variables representing the grades, i.e., AEM, Calc1, Calc2, Calc3, and Diffeq.

TABLE 3

TABLE 3. Descriptive Statistics for the variables used in this study (n = 72).

3.2 Linear Models for With Grades in Advanced Engineering Mathematics as a Response Variable

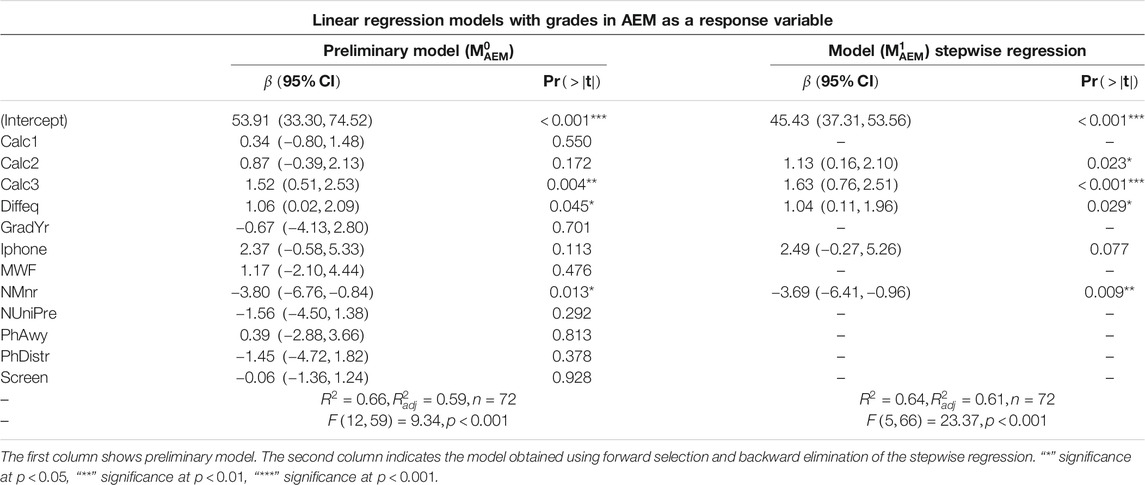
The preliminary linear model (${\text{M}}_{\text{AEM}}^0$) is shown in Table 4. It shows that Calc3 is the most important variable in this model. This model accounts for $66\text{\%}$ ($R^2=0.66,R_{adj}^2=0.59,F\left(\mathrm{12,59}\right)=9.34,p<0.001$) of the variability in grades obtained in the course. The backward elimination and forward selection algorithms both produced the same model, ${\text{M}}_{\text{AEM}}^1$. Only the variables Calc3, NMnr, Calc2, Diffeq, and iphone are retained in the stepwise regression model. This model is able to account for $64\text{\%}$ ($R^2=0.64,R_{adj}^2=0.61,F\left(\mathrm{5,66}\right)=23.37,p<0.001$) of the variance in AEM grades. Note that $R_{adj}^2$ is increased from 0.59 in model ${\text{M}}_{\text{AEM}}^0$ to 0.61 in the model ${\text{M}}_{\text{AEM}}^1$. The details of the linear model (${\text{M}}_{\text{AEM}}^1$) are seen in Table 4. As seen in Table 4, grades in Calculus III, Calculus II, and Elementary Differential Equations positively and significantly predict the AEM course grade. However, for the subjects in this study, the number of minor degrees pursued negatively ($\beta =-3.69,p=0.0087$) predicts the grades in the AEM course. As per Elliott and Woodward (2007, p. 25) normality tests are not recommended for a sample size of more than 50. We have a sample size of 72. Thus, for checking the normality of the residuals we rely on visual inspection [see Ghasemi and Zahediasl (2012) and Field (2018, p. 444)]. From the histogram in Figure 1A, and the QQ plot in Figure 1B, we see that the residuals are approximately normally distributed. We use the power calculations to verify whether the sample of 72 participants is adequate. For small effect size of 0.2 (Cohen, 2013) we need only 70 observations to achieve 80% power of the model ${\text{M}}_{\text{AEM}}^1$ at $5\text{\%}$ significance level.

TABLE 4

TABLE 4. Linear models with grades in Advanced Engineering Mathematics as response variables.

FIGURE 1

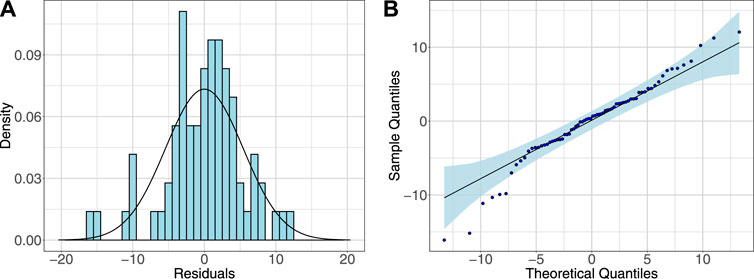
FIGURE 1. (A) Histogram of the residuals for the model (${\text{M}}_{\text{AEM}}^1$), with fitted normal curve (B) A QQ plot of the residuals.

3.3 Linear Models for Grades in the Prerequisite Courses as Response Variables

The linear model ${\text{M}}_{\text{Calc}3}^0$ accounts for $46\text{\%}$ ($R^2=0.46,R_{adj}^2=0.43,F\left(\mathrm{3,68}\right)=19.13,p<0.001$) of the variability in the Calculus III grades. See Table 5 (model ${\text{M}}_{\text{Calc}3}^0$) for more details. Using the backward elimination algorithm and forward selection algorithms of the stepwise regression techniques, we could eliminate the variables Calc1 and iphone to construct a new model ${\text{M}}_{\text{Calc}3}^1$ ($R^2=0.46,R_{adj}^2=0.45,F\left(\mathrm{1,70}\right)=58.5,p<0.001$). Note that elimination of the variables Calc1 and iphone increases the $R_{adj}^2$ from 0.43 to 0.45. As seen in Table 5 (model ${\text{M}}_{\text{Calc}3}^1$) we find that Calculus II grades positively and significantly ($\beta =0.79,p<0.001$) predict the grade in Calculus III. The details of the preliminary and final regression models for Calculus II grades (${\text{M}}_{\text{Calc}2}^0$ and ${\text{M}}_{\text{Calc}2}^1$) as well as those for grades in the course Elementary Differential Equations Grades are depicted (${\text{M}}_{\text{Diffeq}}^0$ and ${\text{M}}_{\text{Diffeq}}^1$) in Table 5. From the histogram and the QQ plots provided in the Supplementary Material, we see that the residuals for the models ${\text{M}}_{\text{AEM}}^1$, ${\text{M}}_{\text{Calc}3}^1$, ${\text{M}}_{\text{Calc}2}^1$, and ${\text{M}}_{\text{Diffeq}}^1$ are approximately normally distributed (Ghasemi and Zahediasl, 2012). Since the number of observations and predictors are the same in models ${\text{M}}_{\text{Calc}3}^1$, ${\text{M}}_{\text{Calc}2}^1$, and ${\text{M}}_{\text{Diffeq}}^1$, the power test indicates that we need only 42 observations to achieve 80% power for a small effect size of 0.2 (Cohen, 2013) at $\alpha =.05$. Hence we deem the sample size of 72 in our study to be adequate.

TABLE 5

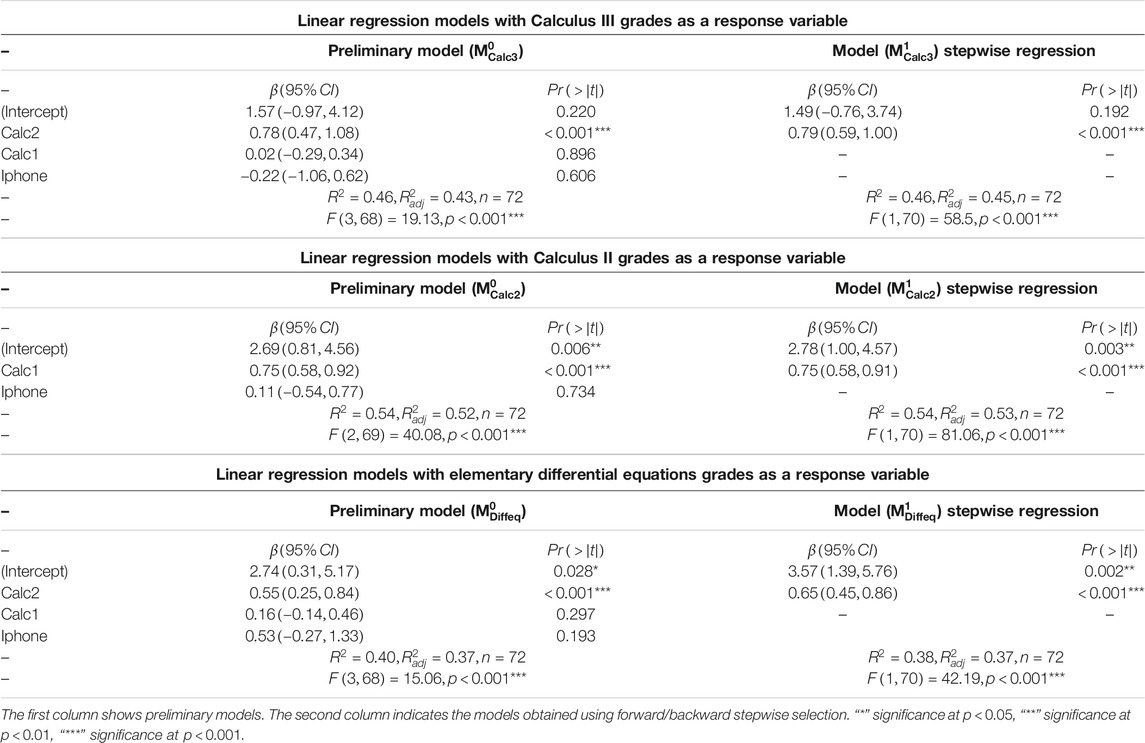
TABLE 5. Linear models with grades in Calculus II, Calculus III, and Elementary Differential Equations as response variables.

4 Discussion

One of the findings of this study is that the amount of time on a cellphone, i.e., screen time (screen) was not a statistically significant predictor of grades in the AEM course in the preliminary (${\text{M}}_{\text{AEM}}^0$) as well as the modified linear model (${\text{M}}_{\text{AEM}}^1$). Neither the backward elimination nor the forward selection algorithm of the stepwise regression resulted in screen time as one of the predictors. Moreover, the Pearson correlation between AEM and screen was not statistically significant. This conclusion is contrary to some previous work, c.f. Lepp et al. (2014), Lepp et al. (2015). However, this is in agreement with the findings by Lee (2015), Olufadi (2015), Winskel et al. (2019), where the relation between cellphone usage and academic performance was not found. The lack of evidence of the relation between screen time and academic performance could be attributed to the fact that engineering students may be adapting to the integration of technology into their academic lives. Another reason for this finding could be the rapid increase in the expansion in today’s mobile technology capabilities, enabling the users to use their devices more productively. Moreover, while Samaha and Hawi (2016), as well as Hawi and Samaha (2016), studied the negative impact of cellphone addiction, it is unclear whether smartphone addiction could be measured solely by the amount of time spent on their devices.

This study found no statistically significant difference between students’ academic performance with three lectures per week and students with two lectures per week. Recall that Henebry (1997), and Gallo and Odu (2009) showed that academic performance for students with two or three lectures per week was better than those with only one lecture per week. However, they did not find a significant difference in academic performance between students with two lectures per week and students with three lectures per week. Our findings confirm their conclusion. The models ${\text{M}}_{\text{Calc}3}^1$, ${\text{M}}_{\text{Calc}2}^1$, and ${\text{M}}_{\text{Diffeq}}^1$ also demonstrate that the performance in prerequisites is a strong predictor of performance in the current course.

Finally, our finding suggests that for the students in our study, the number of minors taken by the students is a negative predictor of the academic performance in the AEM course. This phenomenon could be due to the “mathematics avoidance behavior” (D’Ailly and Bergering, 1992). The students may be opting to spend more time studying for non-engineering courses than the AEM course. However, an investigation into this phenomenon was beyond the scope of this study.

4.1 Practical Implications and Future Work

The lack of evidence between screen time and academic performance in the AEM course indicates that the students are better at balancing cellphone usage and work. Olufadi (2015) has suggested that the “hours of study” is a better predictor of academic success than screen time. Indeed, measuring only the screen time does not provide us with the correct understanding of how the participants use the cell phones. The students may be using their devices for educational purposes. Indeed, Borba et al., (2016) conclude that mobile technology is transforming the classroom, and it can be effectively used in mathematics education. Regarding the effect of scheduling, multiple studies [c.f. Henebry (1997); Gallo and Odu (2009)] have failed to find evidence that three lectures per week are better than two lectures per week. Our study confirms this perspective. A practical implication of this finding could be to use two lectures per week for advanced courses. The use of two lectures per week can open more time for research activities for the faculty and students alike. The number of minor degrees pursued has a negative impact on participants’ academic performance in the AEM course. This finding suggests that care should be taken by academic advisors while offering additional minor degrees to students.

4.2 Limitations

In the survey, we asked for the average daily screen time. However, the data concerning the participants’ use of their cell phones for educational purposes was not collected. We made this choice for practicality; however, Olufadi (2015) points out that a single variable describing the cell phone use behavior is not enough to understand the academic performance.

One other limitation of our work is that this is a cross-sectional study. We recruited the participants from a single course in one academic semester. This design led to small sample size and lack of diversity in the subjects. Thus, readers should note this while generalizing the conclusions. We have begun collecting data from multiple years, and intend to expand upon this work for a larger sample size in a longitudinal study.

5 Conclusion

In this cross-sectional study, we aimed to understand the factors that influence the academic performance of engineering students in a typical engineering mathematics course. One of our goals was to understand the relation between screen time on cellphones and grades in such a course. We also aimed to understand how the academic background, such as the number of minor degrees pursued and lecturing schedule, are related to grades in a typical engineering mathematics course. To this effect, we recruited students from the course “AEM” from a private research university. We gathered information regarding their cellphone usage, academic background, class schedule via a survey. We formulated linear models with the AEM course grades as a response variable using stepwise regression techniques. Contrary to some prior work, we found that the amount of time spent on cell phones was not a significant predictor of success in the course. One of the reasons behind this finding could be that this study’s participants have successfully integrated mobile technology and their academic pursuits. Recall that both sections were taught by the same instructor, with the same course content, including assignments and exams. The only difference between the two sections was the schedule. However, we observed no significant difference in the academic success between sections meeting twice a week and three times a week. This observation is in line with findings by Henebry (1997) and Gallo and Odu (2009), where they found no significant difference in the academic performance of students with two lecture meetings per week and three lecture meetings per week. Another interesting finding was that the number of minor degrees pursued by the participants was a negative predictor of the course grades. One of the limitations of the study is its cross-sectional nature, which we hope to eliminate in the future by conducting a large-scale longitudinal research.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without unduereservation in the Github repository at github.com/prashantva/stem_ed_fall2018.

Ethics Statement

The studies involving human participants were reviewed and approved by Institutional Review Board, Clarkson University. The patients/participants provided their written informed consent to participate in this study.

Author Contributions

All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2021.662380/full#supplementary-material

References

Accreditation Board for Engineering and Technology, Inc (2019). Criteria for Accrediting Engineering Programs, 2020 – 2021. Tech. rep (Accessed 10 04, 2020).

Anderton, R., Hine, G., and Joyce, C. (2017). Secondary School Mathematics and Science Matters: Predicting Academic success for Secondary Students Transitioning into university Allied Health and Science Courses. Int. J. Innovation Sci. Math. Edu. (formerly CAL-laborate International) 25.

Google Scholar

Ann Clovis, M., and Chang, M. (2019). Effects of Academic Momentum on Degree Attainment for Students Beginning College at 2-year Institutions. J. Coll. Student Retention: Res. Theor. Pract. 1521025119826245.

Google Scholar

Attewell, P., and Monaghan, D. (2016). How many Credits Should an Undergraduate Take? Res. High. Educ. 57, 682–713. doi:10.1007/s11162-015-9401-z

CrossRef Full Text | Google Scholar

Bandura, A. (2010). Self-efficacy. Corsini encyclopedia Psychol. 1–3. doi:10.1002/9780470479216.corpsy0836

Google Scholar

Barr, N., Pennycook, G., Stolz, J. A., and Fugelsang, J. A. (2015). The Brain in Your Pocket: Evidence that Smartphones Are Used to Supplant Thinking. Comput. Hum. Behav. 48, 473–480. doi:10.1016/j.chb.2015.02.029

CrossRef Full Text | Google Scholar

Beale, E. M., Kendall, M. G., and Mann, D. W. (1967). The Discarding of Variables in Multivariate Analysis. Biometrika 54, 357–366. doi:10.2307/2335028

PubMed Abstract | CrossRef Full Text | Google Scholar

Borba, M. C., Askar, P., Engelbrecht, J., Gadanidis, G., Llinares, S., and Aguilar, M. S. (2016). Blended Learning, E-Learning and mobile Learning in Mathematics Education. ZDM Math. Edu. 48, 589–610. doi:10.1007/s11858-016-0798-4

CrossRef Full Text | Google Scholar

Cohen, J. (2013). Statistical Power Analysis for the Behavioral Sciences. Academic Press.

D’Ailly, H., and Bergering, A. J. (1992). Mathematics Anxiety and Mathematics Avoidance Behavior: A Validation Study of Two mars Factor-Derived Scales. Educ. Psychol. Meas. 52, 369–377.

Google Scholar

de Fátima Goulão, M. (2014). The Relationship between Self-Efficacy and Academic Achievement in Adults' Learners. Aje 1, 237–246. doi:10.30958/aje.1-3-4

CrossRef Full Text | Google Scholar

De Winter, J., and Dodou, D. (2011). Predicting Academic Performance in Engineering Using High School Exam Scores. Int. J. Eng. Edu. 27, 1343.

Google Scholar

Duncan, D. K., Hoekstra, A. R., and Wilcox, B. R. (2012). Digital Devices, Distraction, and Student Performance: Does In-Class Cell Phone Use Reduce Learning? Astron. Educ. Rev. 11 (1). doi:10.3847/AER2012011

Google Scholar

Efroymson, M. (1960). Multiple Regression Analysis. Math. Methods digital Comput. 191–203.

Google Scholar

Elliott, A. C., and Woodward, W. A. (2007). Statistical Analysis Quick Reference Guidebook: With SPSS Examples. Sage.

Field, A. (2018). Discovering Statistics Using IBM SPSS Statistics. 5th edn. Sage publications.

Gallo, M. A., and Odu, M. (2009). Examining the Relationship between Class Scheduling and Student Achievement in College Algebra. Community Coll. Rev. 36, 299–325. doi:10.1177/0091552108330902

CrossRef Full Text | Google Scholar

Ghasemi, A., and Zahediasl, S. (2012). Normality Tests for Statistical Analysis: a Guide for Non-statisticians. Int. J. Endocrinol. Metab. 10, 486–489. doi:10.5812/ijem.3505

PubMed Abstract | CrossRef Full Text | Google Scholar

Hawi, N. S., and Samaha, M. (2016). To excel or Not to excel: Strong Evidence on the Adverse Effect of Smartphone Addiction on Academic Performance. Comput. Edu. 98, 81–89. doi:10.1016/j.compedu.2016.03.007

CrossRef Full Text | Google Scholar

Henebry, K. (1997). The Impact of Class Schedule on Student Performance in a Financial Management Course. J. Edu. Business 73, 114–120. doi:10.1080/08832329709601627

CrossRef Full Text | Google Scholar

Hine, G., Anderton, R., and Joyce, C. (2015). Mathematics: A Good Predictor for success in a Health Science Degree. In Proceedings of The Australian Conference on Science and Mathematics Education (formerly UniServe Science Conference). 114–117.

Google Scholar

Komarraju, M., and Nadler, D. (2013). Self-efficacy and Academic Achievement: Why Do Implicit Beliefs, Goals, and Effort Regulation Matter? Learn. individual differences 25, 67–72. doi:10.1016/j.lindif.2013.01.005

CrossRef Full Text | Google Scholar

Lee, E. B. (2015). Too Much Information. J. Black Stud. 46, 44–61. doi:10.1177/0021934714557034

CrossRef Full Text | Google Scholar

Lepp, A., Barkley, J. E., and Karpinski, A. C. (2014). The Relationship between Cell Phone Use, Academic Performance, Anxiety, and Satisfaction with Life in College Students. Comput. Hum. Behav. 31, 343–350. doi:10.1016/j.chb.2013.10.049

CrossRef Full Text | Google Scholar

Lepp, A., Li, J., Barkley, J. E., and Salehi-Esfahani, S. (2015). Exploring the Relationships between College Students' Cell Phone Use, Personality and Leisure. Comput. Hum. Behav. 43, 210–219. doi:10.1016/j.chb.2014.11.006

CrossRef Full Text | Google Scholar

Liu, Y.-C., and Liang, C. (2020). Neurocognitive Evidence for Different Problem-Solving Processes between Engineering and liberal Arts Students. Ijep 9, 104–131. doi:10.17583/ijep.2020.3940

CrossRef Full Text | Google Scholar

Mamaril, N. A., Usher, E. L., Li, C. R., Economy, D. R., and Kennedy, M. S. (2016). Measuring Undergraduate Students' Engineering Self-Efficacy: A Validation Study. J. Eng. Educ. 105, 366–395. doi:10.1002/jee.20121

CrossRef Full Text | Google Scholar

McGill, R., Tukey, J. W., and Larsen, W. A. (1978). Variations of Box Plots. The Am. Statistician 32, 12–16. doi:10.1080/00031305.1978.10479236

CrossRef Full Text | Google Scholar

McKenzie, K., and Schweitzer, R. (2001). Who Succeeds at university? Factors Predicting Academic Performance in First Year Australian university Students. Higher Edu. Res. Dev. 20, 21–33. doi:10.1080/07924360120043621

CrossRef Full Text | Google Scholar

Mendoza, J. S., Pody, B. C., Lee, S., Kim, M., and McDonough, I. M. (2018). The Effect of Cellphones on Attention and Learning: The Influences of Time, Distraction, and Nomophobia. Comput. Hum. Behav. 86, 52–60. doi:10.1016/j.chb.2018.04.027

CrossRef Full Text | Google Scholar

Motlagh, S. E., Amrai, K., Yazdani, M. J., Abderahim, H. a., and Souri, H. (2011). The Relationship between Self-Efficacy and Academic Achievement in High School Students. Proced. - Soc. Behav. Sci. 15, 765–768. doi:10.1016/j.sbspro.2011.03.180

CrossRef Full Text | Google Scholar

Neter, J., Kutner, M. H., Nachtsheim, C. J., and Wasserman, W. (1996). Applied Linear Statistical Models.

Newman-Ford, L., Lloyd, S., and Thomas, S. (2009). An Investigation into the Effects of Gender, Prior Academic Achievement, Place of Residence, Age and Attendance on First Year Undergraduate Attainment. J. Appl. Res. Higher Edu. 1(1), 14–28. doi:10.1108/17581184200800002

Google Scholar

Noble, J., and Sawyer, R. (2002). Predicting Different Levels of Academic success in College Using High School GPA and ACT Composite Score (ACT Research Report Series No. 2002-4). Iowa City, IA: ACT.

O’Dea, S. (2020). Average Lifespan (Replacement Cycle Length) of Smartphones in the United States from 2014 to 2023 (In Years)*. Tech. rep (Accessed 20 05, 2020).

Olufadi, Y. (2015). A Configurational Approach to the Investigation of the Multiple Paths to success of Students through mobile Phone Use Behaviors. Comput. Edu. 86, 84–104. doi:10.1016/j.compedu.2015.03.005

CrossRef Full Text | Google Scholar

Quintano, C., Castellano, R., and Rocca, A. (2010). Influence of Outliers on Some Multiple Imputation Methods. Metodoloski zvezki 7, 1.

Google Scholar

Samaha, M., and Hawi, N. S. (2016). Relationships Among Smartphone Addiction, Stress, Academic Performance, and Satisfaction with Life. Comput. Hum. Behav. 57, 321–325. doi:10.1016/j.chb.2015.12.045

CrossRef Full Text | Google Scholar

Sarraf, S., Brooks, J., and Cole, J. (2014). Taking Surveys with Smartphones: A Look at Usage Among College Students (American Association for Public Opinion Research Annual Conference).

Scott, N. A., and Sedlacek, W. E. (1975). Personality Differentiation and Prediction of Persistence in Physical Science and Engineering. J. Vocational Behav. 6, 205–216. doi:10.1016/0001-8791(75)90047-0

CrossRef Full Text | Google Scholar

Simonsmeier, B. A., Flaig, M., Deiglmayr, A., Schalk, L., and Schneider, M. (2018). Domain-specific Prior Knowledge and Learning: A Meta-analysisResearch Synthesis 2018. Trier, Germany.

Sirin, S. R. (2005). Socioeconomic Status and Academic Achievement: A Meta-Analytic Review of Research. Rev. Educ. Res. 75, 417–453. doi:10.3102/00346543075003417

CrossRef Full Text | Google Scholar

Szafran, R. F. (2001). The Effect of Academic Load on success for New College Students: Is Lighter Better? Res. Higher Edu. 42, 27–50. doi:10.1023/a:1018712527023

CrossRef Full Text | Google Scholar

Theil, H. (1961). Economic Forecasts and Policy.

Trout, B. (2018). The Effect of Class Session Length on Student Performance, Homework, and Instructor Evaluations in an Introductory Accounting Course. J. Edu. Business 93, 16–22. doi:10.1080/08832323.2017.1415196

CrossRef Full Text | Google Scholar

Van Buuren, S., Boshuizen, H. C., and Knook, D. L. (1999). Multiple Imputation of Missing Blood Pressure Covariates in Survival Analysis. Stat. Med. 18, 681–694. doi:10.1002/(sici)1097-0258(19990330)18:6<681::aid-sim71>3.0.co;2-r

PubMed Abstract | CrossRef Full Text | Google Scholar

Van Buuren, S., Brand, J. P. L., Groothuis-Oudshoorn, C. G. M., and Rubin, D. B. (2006). Fully Conditional Specification in Multivariate Imputation. J. Stat. Comput. simulation 76, 1049–1064. doi:10.1080/10629360600810434

CrossRef Full Text | Google Scholar

Wade, S., and Kidd, C. (2019). The Role of Prior Knowledge and Curiosity in Learning. Psychon. Bull. Rev. 26, 1377–1387. doi:10.3758/s13423-019-01598-6

PubMed Abstract | CrossRef Full Text | Google Scholar

White, K. R. (1982). The Relation between Socioeconomic Status and Academic Achievement. Psychol. Bull. 91, 461–481. doi:10.1037/0033-2909.91.3.461

CrossRef Full Text | Google Scholar

Winskel, H., Kim, T. H., Kardash, L., and Belic, I. (2019). Smartphone Use and Study Behavior: A Korean and Australian Comparison. Heliyon 5, e02158. doi:10.1016/j.heliyon.2019.e02158

PubMed Abstract | CrossRef Full Text | Google Scholar

Yin, R. K. (1994). Case Study Research: Design and Methods, Applied Social Research. Methods Ser. 5.

Google Scholar