- 1Faculty of Arts, Macquarie University, Sydney, NSW, Australia
- 2School of Education, Faculty of Social Sciences, University of Wollongong, Wollongong, NSW, Australia
- 3School of Education and Professional Studies, Faculty of Arts, Education and Law, Griffith University, Southport, QLD, Australia
The accurate measurement of the cognitive load a learner encounters in a given task is critical to the understanding and application of Cognitive Load Theory (CLT). However, as a covert psychological construct, cognitive load represents a challenging measurement issue. To date, this challenge has been met mostly by subjective self-reports of cognitive load experienced in a learning situation. In this paper, we find that a valid and reliable index of cognitive load can be obtained through item response modeling of student performance. Specifically, estimates derived from item response modeling of relative difficulty (i.e., the difference between item difficulty and person ability locations) can function as a linear measure that combines the key components of cognitive load (i.e., mental load, mental effort, and performance). This index of cognitive load (relative difficulty) was tested for criterion (concurrent) validity in Year 2 learners (N = 91) performance on standardized educational numeracy and literacy assessments. Learners’ working memory (WM) capacity significantly predicted our proposed cognitive load (relative difficulty) index across both numeracy and literacy domains. That is, higher levels of WM were related to lower levels of cognitive load (relative difficulty), in line with fundamental predictions of CLT. These results illustrate the validity, utility and potential of this objective item response modeling approach to capturing individual differences in cognitive load across discrete learning tasks.
Introduction
The core goal of cognitive load theory (CLT) is the creation of learning environments that make optimal use of learners’ cognitive resources and reduce any demands extraneous to learning in order to optimize learning success (Paas et al., 2003, 2004). In addition to the inherent complexity of information that is to be learned, the method of presenting information to learners also affects the cognitive load learners experience when acquiring knowledge and skills. However, the understanding and application of CLT requires methods to appraise cognitive load, which could be expected to differ across tasks, contexts and learners. To-date, this has been indexed mostly by subjective self-reports of cognitive load experienced in a learning situation. In this study, we evaluated a more objective and sensitive approach to indexing cognitive load experienced by learners.
Cognitive Load: Definition, Sources and Measurement
Cognitive load is considered to be a complex multidimensional construct that consists of: (1) causal factors relating to the task, the learner and their interactive components; and (2) assessment factors such as mental load (ML), mental effort (ME), and performance (e.g., Paas and van Merriënboer, 1994). The cognitive resources needed for a certain task comprise ML, which is a result of a task’s content, presentation, structure, complexity and difficulty (Paas, 1992). On the other hand, the cognitive resources that are devoted to a task comprise ME (Paas, 1992; Paas et al., 2003). ME is intrinsic to the learner, and constitutes the degree to which cognitive resources are mobilized to enable processing and completion in complex tasks (Paas and van Merriënboer, 1994). The causal factor of cognitive load relates to aspects such as the novelty of the task and environmental conditions, while factors relating to the learner involve aspects like working memory (WM) capacity and expertise. These task and learner factors interact to further influence performance through their influence on, for example, motivation.
Cognitive load can be understood within three broad categories – intrinsic, extraneous, and germane (Sweller et al., 2019). Intrinsic cognitive load has to do with the complexity of the information which is being processed and subsumes the idea of “element interactivity” (Sweller et al., 2019). Element interactivity depends on the nature of the information and the prior knowledge of the learner processing the information. For example, complex tasks which require the processing of multiple interconnected elements are considered to have high element interactivity. By contrast, extraneous cognitive load has to do with how information is presented and the instructional procedures involved in the task. Manipulations of the presentation of instructional procedures can affect the level of element interactivity. Finally, germane cognitive load refers “[…] to the WM resources available to deal with the element interactivity associated with intrinsic cognitive load” (Sweller, 2010, p. 126). Therefore, germane cognitive load is both linked to intrinsic and extraneous cognitive load. Germane cognitive load resources can only be utilized if extraneous cognitive load is not depleting WM resources. Moreover, germane cognitive load can redistribute WM resources to process complex tasks with high element interactivity (Sweller et al., 2019).
As a covert psychological construct, which can be expected to vary across tasks, contexts and learners, cognitive load constitutes a serious challenge in terms of its accurate measurement. Without precision in its capture, application of CLT is limited to the identification of conditions under which learning is superior or inferior, without the ability to accurately tailor these principles to the specific tasks, conditions and learners involved in a particular learning situation. For instance, the split attention effect would suggest that when learners are novice, essential information should be well integrated; however, this might not be expected at higher levels of expertise. Application of this principle to optimize learning outcomes amongst diverse tasks (e.g., in reading, numeracy, and science), diverse learners (e.g., in expertise and WM capacity), and in different contexts to which the research was conducted, is complicated without the ability to carefully appraise changes in cognitive load as conditions change.
When cognitive load is measured it is most often done through the use of a subjective ranking using a Likert scale asking for invested ME (e.g., Marcus et al., 1996; Tindall-Ford et al., 1997; Salden et al., 2004; Halabi et al., 2005). A primary reason is that this method is straightforward, simple to apply, shows evidence of reliability, construct validity, and does not interfere with learning (Paas et al., 1994; Sweller et al., 1998). For instance, Paas (1992) used a one-dimensional 9-point symmetrical category rating scale (Likert-type scale) for assessing learners’ ME in different phases of learning and performance. The scale ranged from 1 (very low mental effort) to 9 (very high mental effort), on which learners rank their ME during a learning and performance task. Paas et al. (1994) tested this subjective scale for its measurement properties and found that it had good reliability (e.g., Cronbach α = 0.82) and was sensitive to variation in small levels of cognitive load. Such evidence is taken to suggest that learners are capable of introspecting their cognitive processes and use this to quantify their ME.
However, this scale has been interpreted by some cognitive load researchers by substituting “mental effort” with “task difficulty” (e.g., Ayres, 2006; Cierniak et al., 2009). By itself, asking learners to rank difficulty of learning tasks as a measure of ME is problematic. While ME and task difficulty are no doubt related, as a consequence of factors such as prior knowledge, they are not identical (van Gog and Paas, 2008). For instance, when tasks are very difficult for learners, research shows they are often not stimulated to put in the required ME (Wright, 1984; Wright et al., 1986) and, as a result, may not be reflective of the task’s cognitive load. Despite this, Sweller et al.(2011, p. 74) state that the subjective ME scale has “[…] been shown to be the most sensitive measure available to differentiate the cognitive load imposed by different instructional procedures.”
From these scales, ME (cognitive load) is indexed through a combination of the learning result and learners’ ME. That is, a learning experience is considered more optimal if it has a higher average performance than an alternative condition. Yet when two instructional conditions record the same average performance the learning condition that requires less ME has higher instructional efficiency. Accordingly, the learning condition that needs more ME is considered to be less efficient than the one that requires learners to exert less ME. Using a cognitive load framework, Paas and van Merriënboer (1993) suggested a method for quantifying this instructional efficiency. Their formula, reconciles: (E), the relative efficiency of the instructional condition; (P), the standardized z-scores for test performance scores; and (R), the standardized z-scores for the ratings of cognitive load related to the task. Based on this formula, a learning condition would be more efficient when lower subjective ratings of cognitive load correspond with higher performance scores. These scores are calculated per learner and per task, and interpreted relative to an ideal slope of 1, where instructional efficiency = 0 (or performance is equal to ME). Proximity above or below this slope denotes high or low mental efficiency, respectively. This mental efficiency model has since been expanded to include factors such as motivation (Hummel et al., 2004).
However, Hoffman and Schraw (2010) have pointed out fundamental measurement concerns with Paas and van Merriënboer’s (1993) cognitive load efficiency model beyond the well-documented issues of using self-report measures, such as measurement error arising from rater bias and over-confidence (e.g., Stone, 2000; Burson et al., 2006). Hoffman and Schraw note that task performance scores and ME scores are not commensurable and do not share a common unit of measurement. Calculations derived from incommensurable variables are problematic for interpretative and computational reasons (see Hoffman and Schraw, 2010).
Recently, studies have attempted to measure the different aspects of cognitive load (e.g., Leppink et al., 2013; Klepsch et al., 2017; Krell, 2017). For example, Krell (2017) developed a seven-point Likert scale to measure self-reported levels of cognitive load. In this study, Krell used an item response theory (IRT) approach to test the linear functioning of the self-report scale. This scale consists of 12 items, half of which measure ML (i.e., the cognitive capacity to process tasks) and the other half to measure ME (the investment of cognitive capacity by persons to process tasks). Krell tested the scale on a large sample of high school students on the performance of a standardized science test. Krell found evidence that ML and ME were different dimensions and some evidence which suggest a causal role between ML and performance but not ME and performance.
Whereas the majority of cognitive load researchers have used subjective self-report, a range of objective cognitive load measurement techniques have also been explored by cognitive load researchers (for overviews see Paas et al., 2003; Paas et al., 2008). Whereas subjective techniques are normally used to get an estimate of overall cognitive load, that is, experienced load based on the whole task procedure, continuous objective techniques can be used to determine the dynamics of cognitive load through fluctuations in cognitive load from the beginning to the end of the task (Xie and Salvendy, 2000; Paas et al., 2003). Such approaches include neuroscience (e.g., Antonenko et al., 2010; Howard et al., 2015), physiological measurements such as heart rate (e.g., Paas and van Merriënboer, 1994), pupil dilation (van Gerven et al., 2004), and blood glucose levels (e.g., Scholey et al., 2001).
Other objective cognitive load measurement techniques involve the use of secondary tasks. Secondary-task techniques are based on the assumption that performance on a secondary task can be used to reflect the level of cognitive load imposed by a primary task, and have been used successfully by several cognitive load researchers (e.g., Chandler and Sweller, 1996; Marcus et al., 1996). A recent and promising example of this technique is the rhythm method (Park and Brünken, 2015; Korbach et al., 2018). With this technique participants have to execute a previously practiced rhythm continuously by foot tapping (secondary task) while learning (primary task). Eye-tracking analysis is another objective technique to measure cognitive load. These studies investigate fixation time and number of fixations on visual stimuli as indications of ME and cognitive load (see Korbach et al., 2017; Krejtz et al., 2018).
In summary, cognitive load has been measured primarily through the use of subjective self-report scales. Less common objective measures of cognitive load have been attained through brain imaging, the monitoring of physiological processes, the use of secondary tasks, and eye tracking. While such studies (e.g., neuroscientific (fMRI) approaches to cognitive load measurement) have shown great potential (Whelan, 2007) they are cumbersome, intrusive, require considerable technical expertise beyond the capability of most CLT researchers, and are unclear about which type of cognitive load is being measured. Moreover, such measurement approaches lack ecological validity and occur within laboratory settings outside of the typical classroom learning environment. An ideal measure of cognitive load would be objective, unobtrusive, and measurable within a typical classroom environment.
A Measure of Cognitive Load Through Rasch Modeling
Self-report Likert scale ratings do not constitute measures in so far as, technically, they are observations and, as such, do not meet the basic requirements of measurement (Wright, 1997). Likert scale raw scores provide ordinal data, which means that: (1) the scale is finite or limited to a small number of observations (e.g., 5-, 7-, or 9-point); and (2) that differences between observations (i.e., ratings) are not equidistant from each other, as in an interval or ratio level scale. For a scale to qualify as a linear measure it needs to be boundless, or not limited to a finite set of observations and, critically, needs to consist of equally divisible units. Hence, a serious problem of measurement error arises when Likert scales are used as substitute measures in parametric analyses, such as analyses of variance (ANOVA) (Wright, 1997). Ideally, a behavioral measure of ME would be derived through an objective procedure that fulfills the measurement principles of a linear continuum with interval-level units. Item response modeling presents such an opportunity, while using some of the same data (e.g., performance) as CLT efficiency indices.
The Rasch Model
The Rasch (1960) model, or the one parameter logistic model (1PL), is a commonly used model in IRT. The Rasch model is a mathematical model of probability predicated on a hierarchy of item difficulties. This hierarchy of item difficulty is determined by conformity to a Guttman scalar pattern. The model depicts the probability of getting an item correct/incorrect as a logistic function of the distance between a person’s location (ability) and an item’s location (difficulty). These location estimates are situated on the same linear scale (i.e., logit scale). This relationship is expressed below in mathematical form for dichotomous data (e.g., correct/incorrect test answers):
Where P = probability of X at person n for item i and where x represents either a correct (x = 1) or an incorrect (x = 0) response. Person locations are denoted as βn and item locations as δi (Andrich et al., 2010).
According to this model, an item’s difficulty is defined as being equal to the level of ability at which 50% of persons respond successfully to that item. When the difficulty of any given item exceeds the ability of any given group of persons, a smaller percentage of persons respond successfully. A major strength of this model is that an analysis on raw data provide reliable and valid independent (stand-alone) measures of a person’s ability and the difficulty of items. These reliable person ability and item difficulty parameters, attained through a person-item interaction, potentiates an objective measure of cognitive load. That is, the difference between item difficulty δ and person ability β or (δ –β) provides an objective and performance-derived estimate of relative difficulty (or cognitive load experiences by the learner as a function of the learning task). The more the difficulty of an item exceeds the ability of the person, the greater the relative difficulty of that item for that person and, hence the greater cognitive load involved in correctly solving the item.
This approach reflects the interaction between measurable elements of cognitive load (i.e., ML, ME, and performance) and calibrates them within a single scalable trait/dimension. ML is captured through the transformation of raw performance data into reliable estimates of item/task difficulty. ME is estimated through the transformation of raw performance data into ability measures (and degree to which variation occurs with respect to difficulty estimates). This relative difficulty of items is analogous to ME as a measure of the amount of cognitive load involved in correctly responding to the task/item. This provides a summary interval level measurement of cognitive load derived by an objective mathematical procedure. It is important to note that this proposed cognitive load measure involves intrinsic cognitive load only and does not encompass extraneous cognitive load. The proposed measure deals solely with the complexity of the tasks and or difficulty of the test questions (element interactivity) and the background knowledge of the learners (e.g., their numeracy and literacy abilities).
By contrast with Paas and van Merriënboer’s (1993) efficiency model, which stem from calculations involving incommensurable variables, this IRT approach provides a psychometrically sound alternative. For example, Paas and van Merriënboer’s (1993) efficiency model uses two distinct scales to derive a measure of cognitive efficiency/cognitive load and calculates the difference between z score performance and z score effort as an efficiency measure. By contrast, a probabilistic IRT analysis transforms the raw data of a single performance measure and derives item difficulty and person ability parameters from this measurement scale (i.e., test or task scores). IRT probabilistic transformation of raw performance scores into these two parameter estimates are located on a single logit scale in interval level units. Hence, the subtraction of the ability estimates from the difficulty estimates per person item interaction is psychometrically sound as these estimates share a common logit scale.
The Present Study
We understand the concept of test validity as defined by Kane (2013) who presents an argument-based approach. In this approach “…to validate an interpretation or use of test scores is to evaluate the plausibility of the claims based on the test scores” (p. 1). This validity framework consists of (1) stating the proposed interpretation and use of the test scores and (2) evaluating the plausibility of such proposals (Kane, 2013).
In the current study, and following from Kane’s (2013) argument-based approach, we specifically propose that IRT derived statistics from standardized numeracy and literacy test scores can provide proxy measures to determine variance in learners’ intrinsic cognitive load. In order to evaluate the plausibility of this proposal we demonstrate two types of validity evidence: construct validity and concurrent criterion validity. Evidence of construct validity is demonstrated through an IRT analysis on the National Assessment Program – Literacy and Numeracy (NAPLAN) standardized test data (e.g., correct item functioning, reliability testing, and fit to the Rasch model). Moreover, we evaluate the plausibility of this proposal by attaining concurrent criterion validity evidence. Our hypothesis (H1) for criterion validity was that WM should inversely predict the relative difficulty/cognitive load requirement of learners. That is, concordant with CLT theory, higher WM capacity would decrease the experience of cognitive load and give preliminary support for the utility of this index to measure learners’ cognitive load.
Materials and Methods
Participants
Ninety-one primary school primary school-aged learners in Grade 2 (aged 7–8 years) participated in this study. Learners were recruited across three regional (n = 29) and two metropolitan schools (n = 62), with a balanced gender ratio of boys (n = 42), and girls (n = 49). All learners spoke English as their first language and had no known developmental delay or disorder.
Measures
Learning Assessment
An out-of-circulation version of Australia’s National Assessment Program – Literacy and Numeracy (NAPLAN) test was administered as the learning task (ACARA, 2011). Specifically, a numeracy test (35 multiple-choice questions) and a language conventions test which consists of a spelling subtest (25 multiple-choice questions) and a grammar subtest (25 multiple-choice questions) of NAPLAN were selected to provide raw performance data. These assessments were administered in a group setting within the students’ classrooms, which followed the protocols of the NAPLAN test.
Working Memory
Phonological and visual-spatial WM was measured by respective “Not This” and “Mr Ant” tasks from the Early Years Toolbox (EYT; Howard and Melhuish, 2017). These tasks are administered via iPad to collect scores and timing measures.
Phonological WM
The iPad-based EYT “Not This” task (Howard and Melhuish, 2017) involves the presentation of an auditory instruction, against a blank screen, to find a stimulus that does not have certain characteristics of color, shape, or size (or a combination of these; e.g., ‘Point to a shape that is not red and not a circle). After a brief retention interval, participants are then shown a stimulus array from which to identify a stimulus that satisfies the auditory instruction. The task increases in complexity from level 1 (one feature to recall) to level eight (eight features to recall). Each level consists of five trials and at least three successful responses are required to proceed to the next level. The task ends if participants fail to achieve three or more successful trials within a level, or the completion of level eight. WM capacity is estimated using a point score, calculated as: one point for each successive level, starting at the first, in which at least three trials are performed correctly and then 1/5 of a point for each successful trial thereafter.
Visual-Spatial WM
The iPad-based EYT “Mr Ant” task (Howard and Melhuish, 2017) involves recall of an increasing number of stickers placed on various locations of a cartoon ant. The task increases in complexity from level one (recalling the placement of one sticker) to level eight (recalling the placement of eight stickers). The task consists of three trials per level and failure on all trials at a given level (or completion of level eight) ends the task. In test trials, a cartoon ant with sticker/s is presented for 5 s, followed by a blank screen for 4 s, before the return of the cartoon ant without any stickers. Participants respond by tapping on the location of the missing sticker/s. WM capacity is estimated by a point score, calculated as: 1 point for each successive level, starting at the first, in which at least two trials are performed correctly and then 1/3 of a point for each successful trial thereafter.
Procedure
NAPAN tests were administered in two group sessions within students’ classrooms, across 2 days, starting with language conventions. This order and spacing is consistent with NAPLAN administration (Board of Studies Teaching and Educational Standards NSW (BOSTESNSW), 2015). Absent students completed the missed test on the day of their return to school. After completion of the NAPLAN assessments, the WM tasks were administered in a single session individually and in a quiet room. The tasks were administered in a fixed random order, as follows: RSPM; Mr Ant; and Not This. The classroom teacher was present throughout the testing phase and was on hand to assist students who had questions.
Results
Rasch Analyses
The proposed indices of cognitive load were derived from Rasch modeling analyses of the NAPLAN test performances (numeracy and language conventions). These data were analyzed using the dichotomous Rasch model, run on Rasch Unidimensional Measurement Modeling (RUMM) 2030 software (Andrich et al., 2010; for a complete interpretation of Rasch analysis, see Tennant and Conaghan, 2007). Overall fit of the data to the Rasch model indicated good model fit for both tests (chi-square all p > 0.05) (see Table 1 for summary of fit statistics). The Person Separation Index (PSI), a reliability index on the transformed logistic data, indicated very good reliability for all three tests (0.85–0.86), as did the Cronbach alpha reliability indices (0.86–0.94).
The individual fit of items to the Rasch model are identified by fit residuals outside the acceptable ranges (≤2.50 and >2.50). Residuals constitute the difference between the observed values and the theoretical Rasch estimates. Individual item misfit can also be detected by significant chi-square and F statistics, where an insignificant p value (>0.05) indicates good fit to the Rasch model. Misfit can also be detected by examination of an item’s item characteristic curve (ICC). ICCs plot the observed values against the theoretical Rasch-derived estimates represented as an s-shaped curve; the closer the proximity between the observed values and the theoretical curve the better the fit and vice versa.
One item in the language conventions test (item 48) was found to misfit the model (χ2 = 0.72, p < 0.001) at Bonferroni adjusted alpha = 0.001 and was removed from the analysis. Also, Item 25 in the language conventions test had an extreme score (defined as all responses correct or incorrect) and was not used in the analysis. Otherwise, individual item fit was acceptable for all items of each test. Overall, all tests showed evidence of good reliability and construct validity (as good fit to the unidimensional Rasch model and correct functioning of items). The spread of items relative to the ability of the learners in the numeracy and language conventions tests are depicted in Figures 1, 2, respectively.

Figure 1. Wright map of the spread of learner ability and item difficulty on the NAPLAN numeracy test (in logits). Learner abilities (on the left) range from the least able on the bottom to the most able on the top of the graph. Item difficulties (on the right) range from the least difficult on the bottom to the most difficult on the top. The map indicates that the test was difficult with the majority of learners indicating their ability levels were lower than the difficulty of the majority of items.

Figure 2. Wright Map of the spread of learner ability and item difficulty on the NAPLAN language conventions test (in logits). Learner abilities (on the left) range from the least able on the bottom to the most able on the top of the graph. Item difficulties (on the right) range from the least difficult on the bottom to the most difficult on the top. The map indicates that the test was very difficult for 20 learners’ whose ability fell below the easiest item (item 26). Overall, the majority of items fell above the ability of the majority of learners indicating a difficult test.
The high reliability indices and well-functioning of items according to the Rasch model constitutes significant evidence of the precision of the test score data which we will use to formulate our proposed intrinsic cognitive load measure. Following Kane’s (2013) validity argument approach, such evidence of the precision of our test score data will support the plausibility and generalizability of our proposed measure.
Relative Difficulty/Cognitive Load Measures
Essentially, our proposed cognitive load index is a measure of the relative difficulty of test items. This relative difficulty measure was calculated from the subsequent IRT analysis on the NAPLAN numeracy and language conventions test data. These relative difficulty/cognitive load measures were calculated for each test dimension by subtracting the IRT derived person ability estimates from the item difficulty estimates for each person-item interaction. The descriptives for these measures are depicted in Table 2 as logits and depict the mean relative difficulty/cognitive load for each person-item interaction across the two test domains.
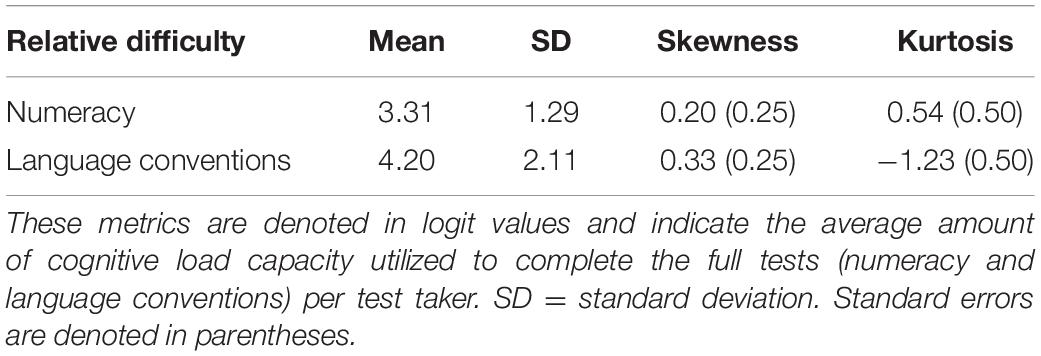
Table 2. Descriptive statistics for item response derived measures of relative difficulty/cognitive load for the numeracy and language conventions tests.
Multiple Regression Analyses
The results of the multiple regression for Model 1 (numeracy relative difficulty/cognitive load) indicated that the two WM predictors significantly explained 20% of the variance [R2 = 0.20, F(2,87) = 10.63, p < 0.001]. Phonological WM made the strongest contribution to explaining numeracy relative difficulty/cognitive load and accounted for 9% unique variance while visual-spatial WM was found to contribute 6% unique variance. It was found that as phonological WM increased by one standard deviation the relative difficulty/cognitive load index decreased by 0.31 standard deviations (β = −0.31, p < 0.01), as did visual spatial WM, which decreased by 0.26 standard deviations (β = −0.26, p < 0.05). Model 2 (language conventions relative difficulty/cognitive load) indicated that the predictors explained 7% of the variance (R2 = 0.07, F(2,87) = 0 3.18, p < 0.05). However, only phonological WM significantly contributed to unique variance (6%). As phonological WM increased by 1 standard deviation the relative difficulty/cognitive load index decreased by 0.26 standard deviations (β = −0.26, p < 0.05). Correlations of these variables are listed in Table 3 and results of the regression models are summarized in Table 4.
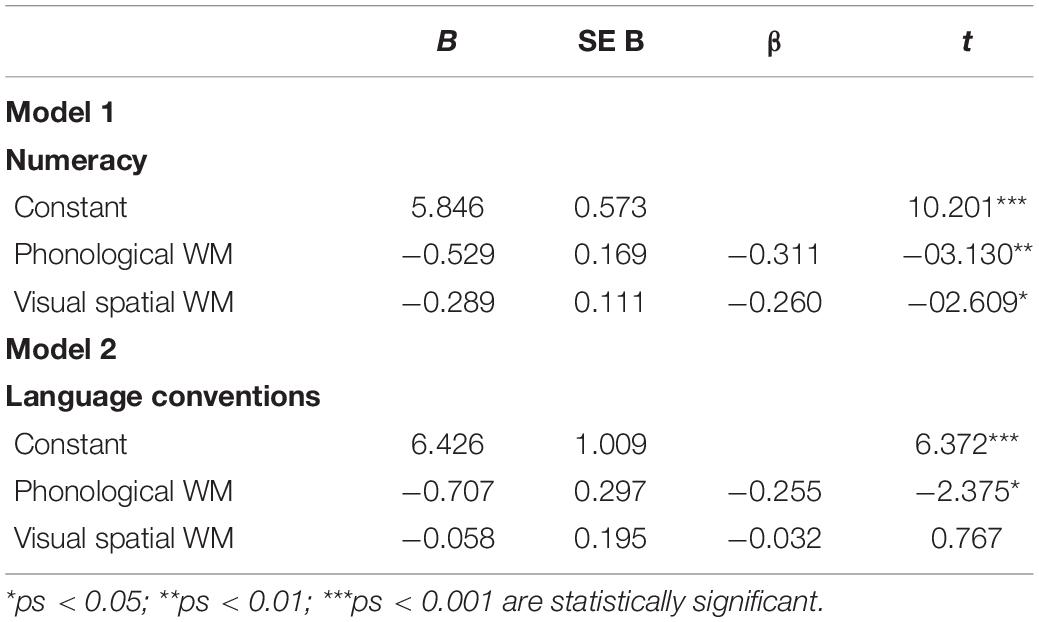
Table 4. Multiple regression results for working memory predicting relative difficulty/cognitive load measures.
Discussion
The aim of the current study was to evaluate the potential of item response modeling to generate an objective measure of intrinsic cognitive load. Results indicated that valid and reliable indices of intrinsic cognitive load can be attained by item response modeling of raw test data (or other series of complex tasks/problems within a single domain) at an interval scale level. The interaction of the two parameter estimates (item difficulty and person ability) combine into a single scalable measure, in logits, subsuming critical elements of the measurable aspects of cognitive load: ML (i.e., task difficulty) and ME (performance measures transposed into ability logits). In support of our hypothesis (H1), resulting relative difficulty indices–that is, subtraction of the person ability estimates from the item difficulty estimates–were related to cognitive resources, in the expected direction, functions as an estimate of cognitive load. This IRT approach to estimating intrinsic cognitive load is superior to subjective self-report measures as it meets the requirements of objective measurement (Andrich, 2004).
Our findings provide clear validity evidence for the plausibility of our interpretations and utility of our IRT-based measure to indicate a learner’s intrinsic cognitive load capacity. This evidence was demonstrated through a concurrent criterion validity approach in that a learner’s WM capacity was found to significantly predict our proposed cognitive load index within both numeracy and literacy domains. We found both phonological and visual spatial WM scores significantly accounted for 20% of the variance of cognitive load in the numeracy domain. This finding is consistent with prior research which has found that phonological and visual spatial WM are important predictors of numeracy processing (Alloway and Alloway, 2010; Alloway and Passolunghi, 2011). While phonological WM significantly captured 7% of the variance of our novel cognitive load index in the language conventions domain (combined spelling and grammar tasks), visual-spatial WM played no significant role.
A possible explanation for these results, that is, the small amount of variance captured by phonological WM and lack of predictive role of visual-spatial WM on our cognitive load measure may have to do with the nature of the language convention spelling and grammar tasks. In the language conventions sections of the NAPLAN tests, the spelling items consist of identification of misspelt words. The mental resources needed for this type of processing do not require deliberate thought and essentially require retrieval from long-term memory if the word is known and guessing in the case of an unknown word (though in some cases the application of spelling rules may apply). Similarly, in the grammatical section of the language conventions test the format consists of short cloze activities where a sentence is presented, and students choose the correct missing grammatical form. Here, knowledge of the correct conjugation or form of the verb or auxiliary is all that is needed to successfully complete the task. The degree to which deliberate thought is needed to control the processing of information is minimal and hence the ME and WM capacities on these tasks would not be optimal. According to Paas and van Merriënboer’s (1994) cognitive load model, the automatic processing of information bypasses the requirement of drawing on ME resources and feeds directly into performance. Hence, this type of automatic processing may have sufficiently limited the cognitive capacity requirements in the language conventions domain.
Our findings may also simply be reflective of the reduced role of visual spatial WM in language processing. For example, it is well established that visual spatial WM is important for early numeracy processing (McKenzie et al., 2003; Bull et al., 2008). Moreover, in the year three NAPLAN numeracy tests many questions comprise visual “patterns” (or similar) and consequently involve visual processing along the lines of what was assessed by the visual spatial WM tasks. By contrast, such item types requiring visual processing were not present in the language conventions test used. Therefore, this may explain the lesser role of visual spatial WM processing as a predictor of our proposed cognitive load index.
Overall, however, our findings indicated that higher levels of cognitive resources were related to lower levels of cognitive load requirements and vice versa. This is consistent with fundamental underpinnings of CLT (Sweller et al., 2019), which suggest that: cognitive load and WM capacity share an inverse relationship, such that deficiency in one aspect can be rectified by reduction in the other; and that a reduction in cognitive load can facilitate learning and performance.
Our proposed IRT modeling approach to cognitive load measurement provides a relatively simple and straightforward procedure to attain reliable and valid estimates of intrinsic cognitive load. While IRT modeling and Rasch analysis has been available to social scientists and psychologists for many decades now few have taken advantage of its superior measurement capabilities. Moreover, the creative potential of IRT modeling and its applications to cognitive load research, as well as educational and psychological research in general, has yet to be actualized.
As we have shown in this study, IRT modeling can provide an objective measure of intrinsic cognitive load outside of subjective self-report. This is particularly pertinent given the difficulty in attaining reliable self-report measures on cognitive processing of younger children (i.e., less than 7 years) (Conjin et al., 2020). The ability to ascertain reliable and valid measures of intrinsic cognitive load through a performance-based objective mathematical procedure is highly beneficial, especially for cognitive load researchers interested in measuring younger learners’ cognitive load. Moreover, this objective IRT modeling approach has ecological validity in that the performance data (i.e., tasks, problems, and questions) are collected within the classroom learning environment and are unobtrusive. The innovation of IRT and Rasch modeling into the cognitive load research paradigm offers exciting measurement opportunities beyond subjective self-report approaches.
Limitations
We wish to acknowledge several limitations of this study. First, while our study has demonstrated the utility and validity of IRT modeling to quantify intrinsic cognitive load it is important to note that IRT analysis requires large sample sizes. In the case of the current study sample size was not such an issue because we used standardized tests which have already been validated with large (nationwide) samples using IRT analyses (ACARA, 2020). Normally, a reliable IRT analysis requires (N = 200) or so (Linacre, 1994). Hence, IRT analysis may be beyond the scope of typical smaller experimental classroom-based cognitive load investigations. Second, our sample of learners were younger than the target age of the tests and this was reflected somewhat in the IRT analysis, in that many learners found the test difficult.
Future Directions
The current study has shown that our relative difficulty/cognitive load index varies with WM in relation to intrinsic cognitive load. Further validation of this measure would benefit from evaluation of the index to determine whether it varies according to the learner task following CLT principles (e.g., extraneous and germane load) and through construct (i.e., convergent) validity testing to establish the measure’s relationship with other cognitive load scales (e.g., Paas, 1992; Leppink et al., 2013; Krell, 2017). Such research is needed to show that our proposed cognitive load index varies with theoretical variations in cognitive load. Additionally, it would be desirable to investigate the performance of our proposed cognitive load index with learners at varying stages of age and development. Finally, our proposed cognitive load index may be a useful measure for those undertaking intervention research where the index can be used to assess shifts in relative difficulty (cognitive load) scores across stages of learner development.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics Statement
The studies involving human participants were reviewed and approved by University of Wollongong. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
ACARA (2011). NAPLAN. Australian Curriculum Assessment and Reporting Authority (ACARA). Available online at: http://www.nap.edu.au/naplan/naplan.html (accessed January 2, 2020).
ACARA (2020). Reliability and Validity of NAPLAN. Australian Curriculum Assessment and Reporting Authority. Available online at: https://www.nap.edu.au/resources (accessed January 2, 2020).
Alloway, T. P., and Alloway, R. G. (2010). Investigating the predictive roles of working memory and IQ in academic attainment. J. Exp. Child Psychol. 106, 20–29. doi: 10.1016/j.jecp.2009.11.003
Alloway, T. P., and Passolunghi, M. C. (2011). The relationship between working memory, IQ, and mathematical skills in children. Learn. Individ. Dif. 21, 133–137. doi: 10.1016/j.lindif.2010.09.013
Andrich, D. (2004). Controversy and the Rasch model: a characteristic of incompatible paradigms? Med. Care 42(Suppl. 1), 1–7. doi: 10.1097/01.mlr.0000103528.48582.7c
Andrich, D., Sheridan, B., and Luo, G. (2010). RUMM2030: A Windows Program for the Rasch Unidimensional Measurement Model (User Manual: Part 1 Dichotomous Data). Perth, WA: RUMM Laboratory.
Antonenko, P., Paas, F., Grabner, R., and van Gog, T. (2010). Using electroencephalography to measure cognitive load. Educ. Psychol. Rev. 22, 425–438. doi: 10.1007/s10648-010-9130-y
Ayres, P. (2006). Impact of reducing intrinsic cognitive load on learning in a mathematical domain. Appl. Cogn. Psychol. 20, 287–298. doi: 10.1002/acp.1245
Board of Studies Teaching and Educational Standards NSW (BOSTESNSW) (2015). NAPLAN. Available online at: http://www.boardofstudies.nsw.edu.au/naplan/ (accessed May 31, 2016).
Bull, R., Espy, K. A., and Wiebe, S. A. (2008). Short-term memory, working memory, and executive functioning in preschoolers: longitudinal predictors of mathematical achievement at age 7 years. Dev. Neuropsychol. 33, 205–228. doi: 10.1080/87565640801982312
Burson, K. A., Larrick, R. P., and Klayman, J. (2006). Skilled or unskilled, but still unaware of it: perceptions of difficulty drive miscalibration in relative comparisons. J. Pers. Soc. Psychol. 90, 60–77. doi: 10.1037/0022-3514.90.1.60
Chandler, P., and Sweller, J. (1996). Cognitive load while learning to use a computer program. Appl. Cogn. Psychol. 10, 151–170. doi: 10.1002/(sici)1099-0720(199604)10:2<151::aid-acp380>3.0.co;2-u
Cierniak, G., Scheiter, K., and Gerjets, P. (2009). Explaining the split attention effect: is the reduction of extraneous cognitive load accompanied by an increase in germane cognitive load? Comput. Hum. Behav. 25, 315–324. doi: 10.1016/j.chb.2008.12.020
Conjin, J. M., Smits, N., and Hartman, E. E. (2020). Determining at what age children provide sound self-reports: an illustration of the validity-index approach. Assessment 27, 1604–1618. doi: 10.1177/1073191119832655
Halabi, A. K., Tuovinen, J. E., and Farley, A. A. (2005). Empirical evidence on the relative efficiency of worked examples versus problem-solving exercises in accounting principles instruction. Issues Account. Educ. 20, 21–32. doi: 10.2308/iace.2005.20.1.21
Hoffman, B., and Schraw, G. (2010). Conceptions of efficiency: applications in learning and problem solving. Educ. Psychol. 45, 1–14. doi: 10.1080/00461520903213618
Howard, S., Burianova, H., Ehrich, J., Kervin, L., Calleia, A., Barkus, E., et al. (2015). Behavioural and fMRI evidence of the differing cognitive load of domain-specific assessments. Neuroscience 297, 38–46. doi: 10.1016/j.neuroscience.2015.03.047
Howard, S. J., and Melhuish, E. C. (2017). An early years toolbox (EYT) for assessing early executive function, language, self-regulation, and social development: validity, reliability, and preliminary norms. J. Psychoeduc. Assess. 35, 255–275. doi: 10.1177/0734282916633009
Hummel, H. G. K., Paas, F., and Koper, E. J. R. (2004). Cueing for transfer in multimedia programmes: process worksheets vs. worked-out examples. J. Comput. Assist. Learn. 20, 387–397. doi: 10.1111/j.1365-2729.2004.00098.x
Kane, M. T. (2013). Validating the interpretations and uses of test scores. J. Educ. Meas. 50, 1–73. doi: 10.1111/jedm.12000
Klepsch, M., Schmitz, F., and Seufert, T. (2017). Development and validation of two instruments measuring intrinsic, extraneous, and germane cognitive load. Front. Psychol. 8:1997. doi: 10.3389/fpsyg.2017.01997
Korbach, A., Brünken, R., and Park, B. (2017). Measurement of cognitive load in multimedia learning: a comparison of different objective measures. Instr. Sci. 45, 515–536. doi: 10.1007/s11251-017-9413-5
Korbach, A., Brünken, R., and Park, B. (2018). Differentiating different types of cognitive load: a comparison of different measures. Educ. Psychol. Rev. 30, 503–529. doi: 10.1007/s10648-017-9404-8
Krejtz, K., Duchowski, A. T., Niedzielska, A., Biele, C., and Krejtz, I. (2018). Eye tracking cognitive load using pupil diameter and microsaccades with fixed gaze. PLoS One 13:e0203629. doi: 10.1371/journal.pone.0203629
Krell, M. (2017). Evaluating an instrument to measure mental load and mental effort considering different sources of validity evidence. Cogent Educ. 4:1280256. doi: 10.1080/2331186X.2017.1280256
Leppink, J., Paas, F., Vander Vleuten, C. P. M., van Gog, T., and van Merriënboer, J. J. G. (2013). Development of an instrument for measuring different types of cognitive load. Behav. Res. Methods 45, 1058–1072. doi: 10.3758/s13428-013-0334-1
Marcus, N., Cooper, M., and Sweller, J. (1996). Understanding instructions. J. Educ. Psychol. 88, 49–63.
McKenzie, B., Bull, R., and Gray, C. (2003). The effects of phonological and visual-spatial interference on children’s arithmetical performance. Educ. Child Psychol. 20, 93–108.
Paas, F. G. W. C. (1992). Training strategies for attaining transfer of problem-solving skill in statistics: a cognitive-load approach. J. Educ. Psychol. 84, 429–434. doi: 10.1037/0022-0663.84.4.429
Paas, F. G. W. C., Ayres, P., and Pachman, M. (2008). “Assessment of cognitive load in multimedia learning environments: theory, methods, and applications,” in Recent Innovations in Educational Technology that Facilitate Student Learning, eds D. H. Robinson and G. J. Schraw (Charlotte, NC: Information Age), 11–35.
Paas, F. G. W. C., Renkl, A., and Sweller, J. (2004). Cognitive load theory: instructional implications of the interaction between information structures and cognitive architecture. Instr. Sci. 32, 1–8. doi: 10.1023/b:truc.0000021806.17516.d0
Paas, F. G. W. C., Tuovinen, J., Tabbers, H., and van Gerven, P. (2003). Cognitive load measurement as a means to advance cognitive load theory. Educ. Psychol. 38, 63–71. doi: 10.1207/s15326985ep3801_8
Paas, F. G. W. C., and van Merriënboer, J. J. G. (1993). The efficiency of instructional conditions: an approach to combine mental effort and performance measures. Hum. Factors 35, 737–743. doi: 10.1177/001872089303500412
Paas, F. G. W. C., and van Merriënboer, J. J. G. (1994). Instructional control of cognitive load in the training of complex cognitive tasks. Educ. Psychol. Rev. 6, 351–371. doi: 10.1007/bf02213420
Paas, F. G. W. C., van Merriënboer, J. J. G., and Adam, J. J. (1994). Measurement of cognitive load in instructional research. Percept. Mot. Skills 79, 419–430. doi: 10.2466/pms.1994.79.1.419
Park, B., and Brünken, R. (2015). The rhythm method: a new method for measuring cognitive load—an experimental dual−task study. Appl. Cogn. Psychol. 29, 232–243. doi: 10.1002/acp.3100
Rasch, G. (1960). Probabilistic Models for Some Intelligence and Attainment Tests. Chicago, IL: University of Chicago Press.
Salden, R. J. C. M., Paas, F. G. W. C., Broers, N. J., and van Merriënboer, J. J. G. (2004). Mental effort and performance as determinants for the dynamic selection of learning tasks in air traffic control training. Instr. Sci. 32, 153–172. doi: 10.1023/b:truc.0000021814.03996.ff
Scholey, A. B., Harper, S., and Kennedy, D. O. (2001). Cognitive demand and blood glucose. Physiol. Behav. 73, 585–592. doi: 10.1016/s0031-9384(01)00476-0
Stone, N. J. (2000). Exploring the relationship between calibration and self-regulated learning. Educ. Psychol. Rev. 12, 437–476.
Sweller, J. (2010). Element interactivity and intrinsic, extraneous, and germane cognitive load. Educ. Psychol. Rev. 22, 123–138. doi: 10.1007/s10648-010-9128-5
Sweller, J., van Merriënboer, J. J. G., and Paas, F. G. W. C. (1998). Cognitive architecture and instructional design. Educ. Psychol. Rev. 10, 251–296.
Sweller, J., van Merriënboer, J. J. G., and Paas, F. G. W. C. (2019). Cognitive architecture and instructional design: 20 years later. Educ. Psychol. Rev. 31, 261–292. doi: 10.1007/s10648-019-09465-5
Tennant, A., and Conaghan, P. G. (2007). The Rasch measurement model in rheumatology: what is it and why use it? When should it be applied, and what should one look for in a Rasch paper? Arthritis Care Res. 57, 1358–1362. doi: 10.1002/art.23108
Tindall-Ford, S., Chandler, P., and Sweller, J. (1997). When two sensory modes are better than one. J. Exp. Psychol. Appl. 3, 257–287. doi: 10.1037/1076-898x.3.4.257
van Gerven, P. W. M., Paas, F. G. W. C., van Merriënboer, J. J. G., and Schmidt, H. G. (2004). Memory load and the cognitive pupillary response in aging. Psychophysiology 41, 167–174. doi: 10.1111/j.1469-8986.2003.00148.x
van Gog, T., and Paas, F. G. W. C. (2008). Instructional efficiency: revisiting the original construct in educational research. Educ. Psychol. 43, 16–26. doi: 10.1080/00461520701756248
Whelan, R. R. (2007). Neuroimaging of cognitive load in instructional multimedia. Educ. Res. Rev. 2, 1–12. doi: 10.1016/j.edurev.2006.11.001
Wright, R. (1984). Motivation, anxiety, and the difficulty of avoidance control. J. Pers. Soc. Psychol. 46, 1376–1388. doi: 10.1037/0022-3514.46.6.1376
Wright, R., Contrada, R., and Patane, M. (1986). Task difficulty, cardiovascular response, and the magnitude of goal valence. J. Pers. Soc. Psychol. 51, 837–843. doi: 10.1037/0022-3514.51.4.837
Keywords: cognitive load, item response theory, mental effort, working memory, standardized test
Citation: Ehrich JF, Howard SJ, Bokosmaty S and Woodcock S (2021) An Item Response Modeling Approach to Cognitive Load Measurement. Front. Educ. 6:648324. doi: 10.3389/feduc.2021.648324
Received: 31 December 2020; Accepted: 22 March 2021;
Published: 22 April 2021.
Edited by:
Kate M. Xu, Open University of the Netherlands, NetherlandsReviewed by:
Andrew J. Martin, University of New South Wales, AustraliaMelina Klepsch, Abt. Lehr-Lernforschung, Universität Ulm, Germany
Copyright © 2021 Ehrich, Howard, Bokosmaty and Woodcock. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: John Fitzgerald Ehrich, am9obi5laHJpY2hAbXEuZWR1LmF1
 John Fitzgerald Ehrich
John Fitzgerald Ehrich Steven J. Howard
Steven J. Howard Sahar Bokosmaty
Sahar Bokosmaty Stuart Woodcock
Stuart Woodcock