- 1Institute of Educational Research, School of Education, University of Wuppertal, Wuppertal, Germany
- 2Akademie Wort + Zahl. Internationales Institut für Interkulturelle Bildung, Cologne, Germany
Recent studies have shown that children’s proficiency in writing numbers as part of the so-called transcoding correlates with math skills. Typically, children learn to write numbers up to 10,000 between Grade 1 and 4. Transcoding errors can be categorized in lexical and syntactical errors. Number writing is thus considered a central aspect of place value understanding. Children’s place value understanding can be structured by a hierarchical model that distinguishes five levels. The current study investigates to what extent a profound understanding of the place value system can explain individual differences in number writing. N = 266 s and third graders (126 girls) participated in the study. The children wrote down 28 verbal given numbers up to 10,000 and completed a place value test based on a hierarchical model to assess number writing skills and place value understanding. Second graders made more number writing errors than third graders and transcoding errors were mostly syntactical errors. In both grades, transcoding performance and place value understanding correlated substantially. In particular complex numbers were more often solved correctly by children with a more elaborated place value understanding. The effect of place value understanding on error rate was smaller regarding lexical errors than syntactical errors. This effect was also comparably small regarding inversion-related errors. The results underpin that writing numbers is an integral part of early place value understanding. Writing numbers can be assumed to be mostly based on the identification of the place values. However, variance in transcoding skills cannot totally be explained by place value understanding, because children with an elaborated place value understanding differed in transcoding performance, too. The differences between the grades indicate that children’s development of writing numbers is also driven by instruction in school. Thus, writing numbers and place value understanding overlap but exceed each other. We discuss how an understanding of the place value relations can be integrated in existing frameworks of place value processing. Since writing numbers is a basic skill in place value understanding, it might serve as an efficient screening method for children, who struggle severely with understanding the decimal place value system.
Introduction
When someone tells us his or her phone number, when we write down a friend’s new address, or when we make a note to take the right bus line whose number a helpful stranger told us: Many every-day contexts require to write a number from verbal information. In research, the skill to write down numbers given verbally is often referred to as transcoding (Barrouillet et al., 2004; Gilmore et al., 2018). Transcoding, as the term indicates interrelates several codes of numbers, i.e., representations, in which numbers can appear.
Dehaene (1992) proposed three codes for number representations in the frequently cited Triple Code Model. The model consists of three codes of numbers that are interrelated: 1) a verbal system, which mostly refers to number words, but also verbally stored arithmetic facts in the log-term memory (e.g., multiplication table); 2) the visual system including Arabic numerals; and 3) a quantity system covering nonverbal number representations, such as sets of dots or positions on a number line (Dehaene, 1992; Dehaene and Cohen, 1995). Thus, a number can be represented in these three codes as well as transcoded between them.
The importance of transcoding abilities for mathematical learning is emphasized by its relation to mathematical performance. Empirical studies have shown that transcoding correlates with arithmetic performance (Geary et al., 1999; Moeller et al., 2011a; Göbel et al., 2014b). Moreover, number line estimation accuracy also correlates with transcoding (Dietrich et al., 2016). In line with these results, persistent transcoding difficulties are typical for children with mathematical learning difficulties (Geary et al., 1999; Moura et al., 2013; Moura et al., 2015). Especially numbers of higher complexity challenge children with mathematical learning difficulties even at the end of primary school, when their typical developing peers have mastered transcoding (Mark and Dowker, 2015; Moura et al., 2015; Houdement and Tempier, 2019).
Transcoding abilities usually develop during primary school. While many children at the beginning of primary school show difficulties with reading or writing numbers, most of them master transcoding by end of Grade 4 (Byrge et al., 2014; Moura et al., 2015). The difficulty of number reading and writing depends–among others–on the complexity of the numbers. Single-digit numbers are only slightly affected by transcoding errors, which appear mostly in multi-digit numbers (Zuber et al., 2009; Moura et al., 2015). Moura et al. (2015) have shown that children’s transcoding proficiency regarding numbers of different complexity develops parallelly during the course of primary school: For example, first graders showed similar difficulties with numbers of low difficulty (e.g., 190) as second graders showed with numbers of moderate difficulty (e.g., 109).
The difficulty of number reading and writing is also affected by the number word system of a language. Number words vary in their transparency in different languages. For example, 35 (thirty-five) is read “sān shí wǔ” (“three ten five”) in Chinese, which is more transparent than English as the tens are given in a decomposition (three ten) and not a new word (thirty). In German, it is “fünfunddreissig” (“five and thirty”), which is even less transparent than English due to the inversion of tens and units (Zuber et al., 2009; Göbel et al., 2014a). Comparative studies between different languages have shown that transcoding is easier in terms of accuracy and reaction time in more transparent languages (Miller et al., 1995; Pixner et al., 2011; Dowker and Nuerk, 2016).
In particular the tens-units-inversion that is found for example in German and Dutch is a major challenge in transcoding (Pixner et al., 2011; Klein et al., 2013). In a comparison study regarding the influence of different characteristics of numbers (e.g., number size, pronunciation of number words, or difference between digits) on transcoding, van der Ven et al., (2017) showed that inversion was a significant predictor for transcoding difficulty. Imbo et al. (2014) compared French (non-inverted) and Dutch (inverted) speaking second-graders. Although overall transcoding performance did not differ significantly between the language groups, the Dutch speaking children had a nearly six times higher inversion error rate than their French peers.
Empirical evidence suggests that working memory is involved in transcoding difficulties in inverted languages (Camos, 2008; Zuber et al., 2009; Pixner et al., 2011). Zuber et al. (2009) have shown that transcoding correlates with visual-spatial working memory and central executive, but not with phonological working memory in first graders. However, the central executive was only involved in inversion-related transcoding errors (e.g., 53 for 35), which indicates that coordinating number word parts for tens and units is a main difficulty during transcoding in languages with tens-units inversion. In line with that, Poncin et al., (2020) recently compared transcoding performance in inverted (“five and thirty”) and non-inverted (“thirty-five”) number words at the end of primary school. The French-speaking children could solve the transcoding task given in the non-inverted (usual in French) condition in significant shorter time than the inverted (unusual in French) condition. However, German speaking children were as fast in transcoding when presented inverted number words (usual in German) as when presented non-inverted number words (unusual in German). Obviously, the tens-units-inversion leads to increased reaction times in transcoding even in children who are used to it. This result highlights the cognitive cost of inverted number words. Lopes-Silva et al., (2014) investigated the role of verbal skills beyond working memory regarding transcoding processes in non-inverted number words. In their study, phonemic awareness outran working memory capacities regarding the prediction of transcoding performance.
Transcoding Processes
Transcoding numbers from verbal to Arabic code requires an understanding of the decimal rules of number word structures (Deloche and Seron, 1982; Pixner et al., 2011): The parts of the number words (e.g., nine hundred fifty-one) have to be mapped to corresponding numerals (900, 50, 1), which need to be composed according to certain, language-specific rules (951). Barrouillet et al. (2004) proposed an often adopted asemantic, developmental, and procedural model for transcoding (ADAPT model) to specify the processes involved in transcoding. The ADAPT model focuses on procedural rules on the one hand and on the other hand on the construction of a “lexicon” for multi-digit numbers. According to the ADAPT model, transcoding does not involve eliciting details such as the meaning of the digits, given that a corresponding entry in the numerical lexicon is available. If there is no entry, procedural rules have to be employed. In this process, the number word forms a digit string that contains information about the digit value and the positional value.
Within the ADAPT model, four types of procedural transcoding rules are differentiated. Some numbers (e.g., 11) or digits (e.g., 9 in 951) are derived from long-term memory (P1 rules). When the digit strings have to be assembled, their length has to be derived from the number words as indicated by keywords such as “hundred” or “thousand” (P2 and P3 rules). P1 and P2/P3 rules are combined, when the digit value is derived from long-term memory and the position from the keyword, as in “nine hundred” (“nine” = P1, “hundred” = P2). The structure of many number words in triplets (e.g., three hundred thirty-nine thousand two hundred eleven) facilitates transcoding up to one million with just two of these rules (P2 for three-digit and P3 for four-digit numbers) (Barrouillet et al., 2004; Van de Walle et al., 2016). Finally, the written number has to be checked for completeness. If there are gaps in the digit string, they have to be filled up with zeros (P4 rules).
Two main error types in transcoding are distinguished: lexical and syntactical errors. While errors in mapping the corresponding number to a digit (e.g., 941 for 951) are considered lexical errors, wrong compositions of the numerals (e.g., 90,051 for 951) are called syntactical errors (Barrouillet et al., 2004; Deloche and Seron, 1982). After comparing lexical and syntactical transcoding errors in children with and without mathematical learning difficulties in early and middle primary school, Moura et al. (2013) reported three main effects: First, syntactical error rates were higher than lexical error rates in all children. Second, children at the beginning of primary school made more transcoding errors than children in middle primary school. And third, typical developing children showed lower transcoding error rates than children with mathematical learning difficulties. In particular, lexical error rates were very low in typical developing children both in early and middle primary school. However, first-graders with mathematical learning difficulties showed considerably higher lexical error rates. In contrast to lexical errors, syntactical errors were generally found in both groups and both stages of primary school, accounting for the three main effects. Syntactical errors mostly affected three- and four-digit numbers, while single- and two-digit numbers challenged only very few children (Moura et al., 2013).
As proposed in the ADAPT model, employing transcoding rules strongly draws on procedural knowledge such as identifying place values. Procedural knowledge refers to how rules and procedures (e.g., the rules of the ADAPT model) are carried out. In contrast to procedural knowledge, conceptual knowledge covers the understanding of why these rules and procedures apply and which structures underly them (Hiebert and Lefevre, 1986). Procedural and conceptual knowledge can be applied regarding place value understanding, too. While procedural place value understanding refers to knowledge of the place values and how they can be composed to multi-digit numbers, conceptual place value understanding can be identified with the iterative relation of the bundling units (i.e., hundreds, tens, units, etc.): ten units can be unitized to one ten and so on (Houdement and Tempier, 2019; Van de Walle et al., 2016). Rittle-Johnson and Schneider (2015) emphasize that procedural and conceptual mathematical knowledge are intertwined. The interrelation between procedural and conceptual knowledge implies that procedural skills may have a conceptual basis on which they are acquired and employed. In the case of transcoding, there is little known about its conceptual foundations.
Place Value Understanding
Against the background of the ADAPT model, transcoding implies specific knowledge of place value understanding. For the reliable employment of the procedural rules of the ADAPT model, children need to recognize the decimal unit a digit represents. According to Nuerk et al. (2014), place value information is processed in three ways: First, place value identification refers to the correct finding and naming of digit positions in a multi-digit number. Therefore, this aspect can be identified primarily with transcoding services. Second, place value activation refers to the employment–consciously or unconsciously–of the numerical information of a decimal unit, for example in number comparison tasks. Third, place value computation describes the integration of place value information in arithmetic tasks. This taxonomy is particularly used in (neuro-) psychological studies on number processing (Nuerk et al., 2014; Bahnmueller et al., 2018).
Naturally, place value understanding has been addressed by researchers from (mathematical) education, too. Based on the notion that transcoding is mostly based on a conceptual understanding of the place value system, procedural and asemantic models such as the ADPAT models have been criticized (e.g., Geary, 2004; Desoete and Grégoire, 2006). However, a profound understanding of the decimal place value system covers both procedural and conceptual aspects such as writing and reading numbers and insight in the iterative relation of the bundling units (Fuson et al., 1997a; Van de Walle et al., 2016; Herzog et al., 2019; Houdement and Tempier, 2019).
To structure the development of place value understanding, Herzog et al. (2019) proposed a developmental model of place value understanding that distinguishes five levels. The levels build up on each other hierarchically. That means that the level hierarchy implies a relation of dependence and inclusion between the levels: First, children need the knowledge of lower levels to develop successive levels (dependence). Second, children who have developed a certain level are supposed to have developed the prior levels, too (inclusion) (Battista, 2011). The levels of the model are not distinct classes of place value understanding that suddenly change. Rather, higher levels are elaborations and advancements of lower levels (Clements and Sarama, 2004). By interacting with tasks and materials based on the place value system (e.g., multi-digit arithmetic, base-ten blocks, standard algorithms), children develop a more elaborated understanding of how numbers are composed of place values and how decimal bundling units are related. As children’s place value understanding does not change suddenly, but gradually over time, the levels are interrelated in form of overlapping waves (Siegler and Alibali, 2005; Clements and Sarama, 2014). Each level can be described by typical ideas of the place value system, strategies used to solve tasks, and errors made by the children at the respective level. The gradual development of children along the levels implies that a child can be located at a certain level of which the child can solve most items; however, this child might also be able to solve single items of higher levels (e.g., by applying a specific strategy) and, vice versa, make single errors on items of lower levels (e.g., due to careless mistakes).
The model is theoretically based on a broad literature review and content analysis. The most relevant literature for the construction of the model are earlier models on place value understanding (Cobb and Wheatley, 1988; Ross, 1989; Fuson, et al., 1997b). The influence of the earlier models gets visible in the description of the levels below. However, the earlier models cover only two-digit numbers, in contrast to the model by Herzog et al. (2019). The significance of the relation between bigger bundling units such as hundreds and thousands is highlighted in the literature (Scherer and Moser Opitz, 2010; Houdement and Tempier, 2019). While the earlier models are based on classroom observations, single cases and empirical studies, there is little a posteriori evidence for their validity (Chan et al., 2014). To the best of our knowledge there are no longitudinal studies supporting the validity of the earlier models for describing learning trajectories. Longitudinal studies are especially necessary for developmental models that describe children’s typical learning trajectories (Reiss and Obersteiner, 2019). The content analysis of the place value system during the construction of the model stressed the relevance of both the identification of the place values (Nuerk et al., 2015) and the relation of the bundling units (Houdement and Tempier, 2019).
The model construction followed a four-step circle as suggested by Battista (2011). The first step was the literature review and content analysis described above. The second step was the construction of a provisory model and designing items corresponding to the levels of the provisory level. In a third step, the model was tested empirically in several piloting studies. Step four was the evaluation of the provisory model and the empirical results. In the few cases where the provisory model and the empirical findings of the piloting studies did not match, the model was slightly revised and tested again. The adaptation process of the model involved only few items that were carefully adapted to the revised models.
The final model was validated in a cross-sectional and a longitudinal study in Germany employing a one-dimensional Rasch-Analysis with a new sample (Herzog and Fritz, 2019). In the cross-sectional study, the item difficulties of the Rasch-Analysis followed the predictions of the level hierarchy in two ways: First, items operationalizing the same level showed similar difficulties; second, items of lower levels were systematically easier than items of higher levels. In the longitudinal study, students from Grade 3 and 4 showed significant increase in place value understanding as described by the model over the course of 1 year. A cross-sectional study in a different cultural and educational environment (South Africa) provides similar empirical evidence in support of the model validity (Herzog et al., 2017).
Pre-decadic Level: Initially, children perceive multi-digit numbers as entities without any decimal structure (Cobb and Wheatley, 1988; Ross, 1989; Fuson et al., 1997a). Children might be able to decompose numbers in general (e.g., 24 into 12 and 12). However, canonical decompositions into tens and units (e.g., 2 tens and 4 units) have no specific base-ten related quality to these children. The canonical decomposition as fundamental construction principle of numbers within the decimal place value system is only one of many possible decompositions and children are unlikely to recognize tens and units in this decomposition at the Pre-decadic Level.
Place Values (Level I): At first, children understand that the digits in numbers can be mapped to decimal bundling units such as units, tens, etc. (Cobb and Wheatley, 1988; Ross, 1989; Fuson, et al., 1997b). Based on this place value understanding, children at this level can map digits to corresponding bundling units. However, they do not yet understand, how the bundling units are related. That means that children at Level I can handle canonical decompositions (e.g., 2 tens and 4 units) based on the place value understanding of this level, but struggle with so-called non-canonical decompositions (e.g., 1 ten and 14 units).
Tens-Units Relation with Visual Support (Level II): At Level II, children develop an understanding of the relation of tens and units that is based on visual support (Cobb and Wheatley, 1988; Steffe, 1992). They can bundle and unbundle tens and units, but rely on counting processes to verify the equivalence of ten units and one ten. It takes decimally structured material such as base-ten blocks for them to reliably employ these counting processes (Fuson, et al., 1997a; Nührenbörger and Steinbring, 2008). Non-canonical representations that are given abstractly cannot be handled based on this place value understanding. Therefore, children might identify “ten” rather with the corresponding visualization (e.g., a tens stick, Van de Walle et al., 2016) than with a composition of ten units. Children at this level understand the relation of the bundling units only for units and tens, while bigger bundling units (e.g., hundreds) are not yet integrated (Scherer and Moser Opitz, 2010).
Tens-Units Relations without Visual Support (Level III): Level III is characterized by two developmental changes in place value understanding. First, children detach from visual representations for two-digit numbers which enables them to handle non-canonical representations of tens and units. Based on an interiorized understanding of the tens-units relation, they do not necessarily need counting routines to verify that ten units make up one ten. Second, children extend the representation-based understanding of the relation between the bundling units onto bigger units such as hundreds, thousands, etc. Like on Level II for two-digit numbers, children need decimally structured material to employ the iterative bundling principle for multi-digit numbers in general. Scherer and Moser Opitz, (2010) emphasize the necessity of bundling tens to hundreds to understand the iterative bundling principle.
General Bundling Units Relations (Level IV): At the fourth and final level of the model, children have successfully established an abstract concept of the relation between the bundling units. Similar to the transition from Level II to Level III for the relation between tens and units, children now detach from concrete representations for multi-digit numbers. As children established a profound understanding of the positional principle as well as the iterative bundling principle with this learning step, their place value understanding development is considered completed.
The Current Study
According to the ADAPT model, the rules employed during transcoding are asemantic, procedural, and developmental. The asemantic characteristic means that transcoding processes are not necessarily bound to the numerical meaning of the number words. The procedural characteristic refers to the transcoding rules. As children follow algorithms during transcoding processes, they may not actually understand the structure behind the processes. The developmental characteristic highlights that children actively develop the numerical lexicon for number words. With increasing experience, children gain routine in employing the transcoding rules. Thus, their increasing transcoding proficiency in primary school is an outcome of learning processes (Barrouillet et al., 2004; Moura et al., 2015).
Research mostly focused on working memory and phonological awareness as influencing factors on transcoding. However, given the interrelation of procedural and conceptual knowledge, the assumptions of the ADAPT model also rise questions regarding the conceptual fundaments of transcoding processes (Rittle-Johnson and Schneider, 2015). As the process of transcoding itself is asemantic, the numerical meaning of a number is not activated during transcoding. However, there has to be some kind of meaning that numbers have to children. It is unclear, to what extent children’s understanding of numbers and decimal bundling units–although not activated during transcoding–are related to their transcoding skills. Transcoding is also procedural, which means that the transcoding rules are employed by routine. Thus, the ADAPT model makes no predictions on the influence of children’s conceptual understanding on transcoding. As procedural and conceptual knowledge are interrelated, we cannot exclude an influence of conceptual place value understanding on transcoding. Finally, the ADAPT model describes transcoding as developmental. This implies that children gain knowledge that is relevant for transcoding during primary school. What knowledge is relevant for transcoding, and in particular the role of conceptual knowledge in this regard, is not finally investigated. To sum up, this study aims at investigating the role of conceptual place value understanding for transcoding skills to better understand the cognitive prerequisites of transcoding processes.
To address these questions at least partially, we investigated transcoding abilities in relation with place value understanding as described by the Herzog et al. (2019) model in German second and third graders. As place value understanding usually develops in Grades 3 to 5 (Herzog et al., 2019; Houdement and Tempier, 2019), and transcoding abilities substantially improve during Grades 1 to 3 (Moura et al., 2015), children in Grade 2 and 3 are of particular interest regarding this research question. The model allows assessing and localizing children’s individual status of place value understanding within the developmental level sequence. This approach facilitates to investigate differences in transcoding performance between children with more or less elaborated place value understanding. As the model provides qualitative descriptions of children’s place value understanding, differences in transcoding abilities might not only be explained in terms of task performance, but also in terms of children’s ideas of the place value system. The qualitative description of children’s place value understanding based on the model by Herzog et al. (2019) in relation to transcoding abilities might give insights into the conceptual underpinnings of transcoding.
Besides variance in error rates across children at different levels of place value understanding, we expect variance in error types to provide substantial information on conceptual underpinnings of transcoding. At least two aspects are highlighted in research. First, lexical and syntactical errors might differ in the way they are related to place value understanding. As lexical errors are mostly mapping errors between digits and numbers, they might be less related to place value understanding than syntactical errors (Zuber et al., 2009; 215; Moura et al., 2013). Second, the German sample allows investigating inversion related errors. Regarding the cognitive foundation of inversion errors, two competing approaches can be found in the literature. While mathematics education research considers inversion related errors as an indicator for low place value understanding (e.g., Schulz, 2014), (neuro-) psychological studies stress the influence of working memory on inversion related errors (Bahnmueller et al., 2015; Pixner et al., 2016). This study aims at contributing to this debate by investigating the influence of place value understanding and inversion related errors.
Two main research questions (RQ) will structure the investigation of cognitive underpinnings of transcoding of this study. The qualitative level description of the model of place value understanding allows making testable predictions regarding the differences in transcoding performance between children at different levels.
RQ1: To what extent does transcoding performance vary between children at different levels of place value understanding as described by the model by Herzog et al. (2019)? We expect that children at higher levels of place value do fewer transcoding errors in general. More specifically, the concept described in Level I (identification of place values) is supposed to support transcoding processes (Bahnmueller et al., 2018; Herzog et al., 2019). Thus, especially children at the Pre-decadic Level are expected to show lower transcoding performance, while children at higher levels are expected to differ only slightly regarding transcoding performance.
RQ2: How are different transcoding error categories such as lexical and syntactical as well as inversion related errors interrelated with place value understanding? Based on the underlying processes in transcoding as described in the ADAPT model, we hypothesize that syntactical errors are negatively associated with place value understanding, while lexical errors may not or only slightly be associated with place value understanding. In particular children, who do not have a conceptual basis for the identification of place values (Pre-decadic Level) are expected to make syntactical errors. The study design allows to investigate the effect of place value understanding on inversion related errors, which might contribute to the debate on the cognitive foundation of inversion-related errors.
Materials and Methods
Sample
In total 266 students participated in the study. Of the total sample, 135 students (69 female, Mage = 91.4 months, SDage = 5.7 months) were in Grade 2 and 131 (57 female, Mage = 104.3 months, SDage = 6.4 months) were in Grade 3. In both grades, data was collected during the first 3 months of the school year. Children were acquired from three schools of which one was located in an upper-class, one in a middle-class, and one in a lower-middle-class suburb. Written consent to participate in the study was acquired in advance from the parents. The study was approved by the local ethics committee of the authors’ university.
The sample was selected based on the contents of the mathematics curriculum. In Grade 1, mathematics classes cover the number range up to 20, in Grade 2 up to 100, and in Grade 3 up to 1,000. Thus, children, who just entered Grade 2 or Grade 3 are appropriate for the aims of this study. As no inclusion criteria were applied, all second- and third-graders from the selected schools participated in the study, if consent was obtained.
Instruments
Transcoding
Transcoding performance was assessed by a writing-numbers-test. Children were given 28 single-to four-digit numbers verbally. The stimuli were identical with Moura et al. (2015) and can be found in Figure 1. Transcoding errors were categorized similar to Moura et al. (2015). Incorrect mappings of numbers and digits (e.g., 961 for 951) were coded as lexical errors. Errors violating the procedural rules (e.g., 90051 for 951) were coded as syntactical errors. As a specific type of syntactical errors, inverted tens and units (e.g., 915 for 951) were coded as inversion-related errors. Based on the rules of the ADAPT model involved in the transcoding process, the numbers were categorized in numbers with null, low, medium, and high complexity (Moura et al., 2015).
Place value Understanding
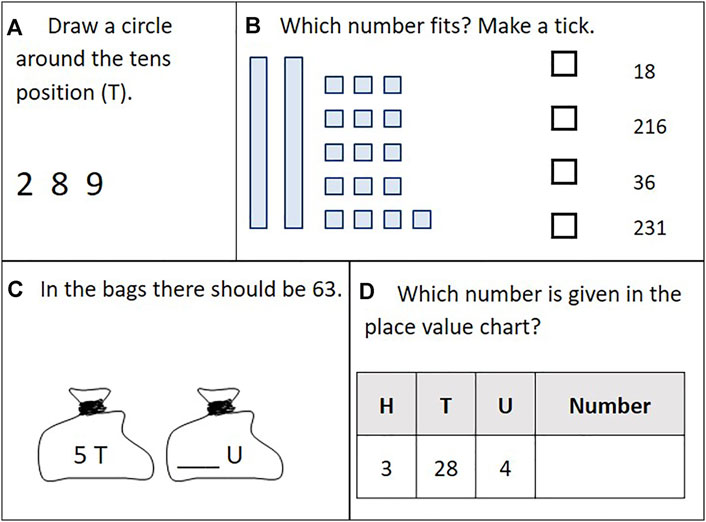
Based on the model by Herzog et al. (2019), two item collections were used to assess children’s place value understanding. Because children in Grade 2 are not yet introduced to numbers bigger than hundred and nearly no child had developed the concept of Level IV in a piloting study, we omitted Level IV items in Grade 2. The items for both Grades were based on the item collection which had been used in another study to validate the model in Germany. A one-dimensional Rasch analysis confirmed that the item difficulties were coherent with the assumptions of the theoretical model (Herzog and Fritz, 2019). Example items from the place value understanding assessment are presented in Figure 1. The full item collections are available by request to the corresponding author.
In Grade 2, 40 items aligned to the Levels I to III were employed. 16 items were aligned to Level I, while 12 items corresponded to the Levels II and III each. As items were presented in random order, more items on the first level were included in the assessment to prevent frustration and tiring in the children. 20 items (Level I: 6, Level II: 8, Level III: 6) were original items of the validation study and all additional items were variations of these items. The internal consistency of the 40 items was good (Crombach’s α =0.934).
The item collection for Grade 3 contained 48 items. Of the 48 items, 16 were aligned to Level I, 12 items were aligned to Level II and III, and 8 items were aligned to Level IV. Lower levels were overrepresented for the same reasons as in Grade 2.30 items (Level I: 7, Level II: 8, Level III: 7, Level IV: 8) were identical with the version of the validation study. The additional items on Levels I to III were identical to those included in the assessments for Grade 2. Internal consistency for the Grade 3 item collection was good (Crombach’s α =0.947).
Children’s individual level of place value development was assessed based on percentage of correct answers per level. If children solved at least 75% of the items of a level, they were assigned to the corresponding level. The highest achieved level was recorded as the current conceptual level of place value understanding (for similar approaches see Lee and Sarnecka, 2009; Ricken et al., 2013; Fritz et al., 2017; Balt et al., 2020). To address lucky guesses and mistakes, children did not have to solve all items of a level to be considered having developed the concept of the level. Determining individual level achievement by a criterion of 75% also visualizes the assumption of the levels as overlapping waves, as the development of place value understanding is not considered disruptive (i.e., replacing prior knowledge at once), but as a progressive elaboration (Siegler and Alibali, 2005; Clements and Sarama, 2014). The internal hierarchy of the levels showed in this analysis, too. In all cases, children also fulfilled the 75% criterion for lower levels than the achieved level. For example, a child that solved 75% of the items at Level III also met this benchmark for Levels I and II.
Data Collection
The data collection was conducted in the classrooms during usual lesson hours. Teachers were informed and received place value training material as an incentive for participation. Two trained undergraduate students helped with the data collection. Both received an intensive training on data collection beforehand and were supervised by the authors.
Besides the presented instruments, number line estimation and early arithmetic concepts were also assessed (but not included in this study). To minimize cognitive load, the tests were split into two sections. The tests analyzed in this study—transcoding and place value understanding—were in the same section and thus assessed on the same day. In all assessments, transcoding was assessed first, as children needed to write down numbers synchronously. The item order in the transcoding test was aligned to Moura et al. (2013; see also Figure 2). Place value understanding was assessed subsequently, because children could solve these tasks individually and in their own speed. All children had enough time to finish the place value assessment. The order of the items in the place value test were randomized across the levels. Thus, easier and more difficult items alternated. The items from the place value assessment were arranged into two sets to avoid position effects.
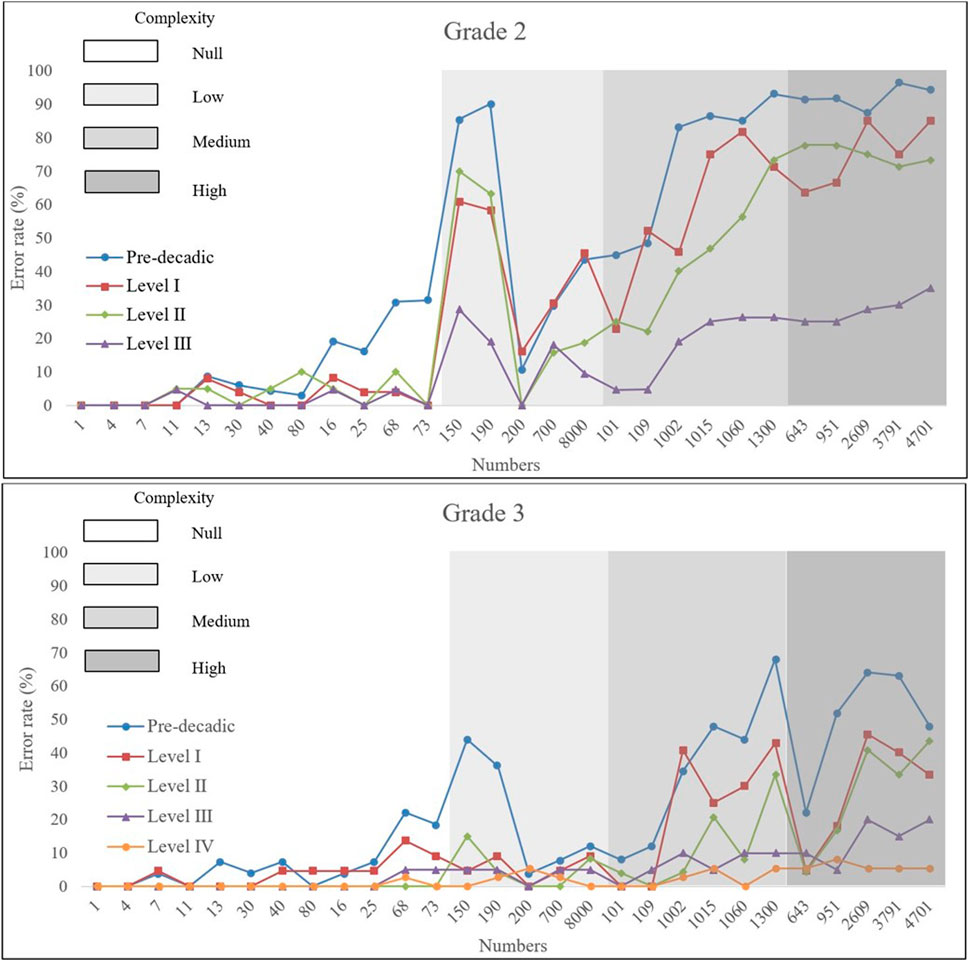
FIGURE 2. Error rates for children at different levels of place value understanding in Grade 2 and Grade 3 for the stimuli of the transcoding tasks. Numbers ordered by level of complexity (background shades).
Results
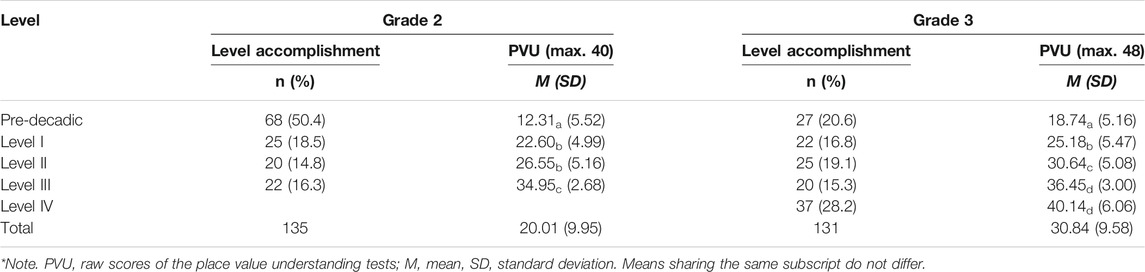
In Grade 2, half of the children were assessed at the Pre-decadic Level. The other half of the second-graders and all third-graders were nearly equally distributed across the levels of place value understanding. One-factorial ANOVAs validated the differences in place value performance between the children at different place value levels in Grade 2 (F(3, 131) = 132.064, p<.001, η2 = 0.752) and Grade 3 (F(4, 126) = 77.839, p<.001, η2 = 0.712). With two exceptions—Level I vs. II in Grade 2 (p = 0.058) and Level III vs. IV in Grade 3 (p=.112)—Bonferroni-corrected post-hoc tests showed significant differences in place value understanding between the level-subgroups in both grades. Thus, the classification of the participating children appears appropriate. The distribution of children to the levels and the corresponding descriptive statistics are summarized in Table 1.
As expected, transcoding performance was positively associated with place value understanding in both grades (RQ1). Raw scores of correct answers in transcoding tasks and place value understanding tasks correlated substantially in Grade 2 (r = 0.638, p < 0.001) and Grade 3 (r=.585, p < 0.001). Table 2 shows mean correct answers in the transcoding test for children at different levels. A one-way ANOVA confirmed that the group differences were significant in Grade 2 (F(3, 130) = 25.223, p<.001, η2 = 0.368) and Grade 3 (F(4, 125) = 12.476, p < 0.001, η2 = 0.285). Post-hoc tests (Bonferroni) revealed consistent significant lower performance only in children at the Pre-decadic Level (p < 0.019 for all comparisons).
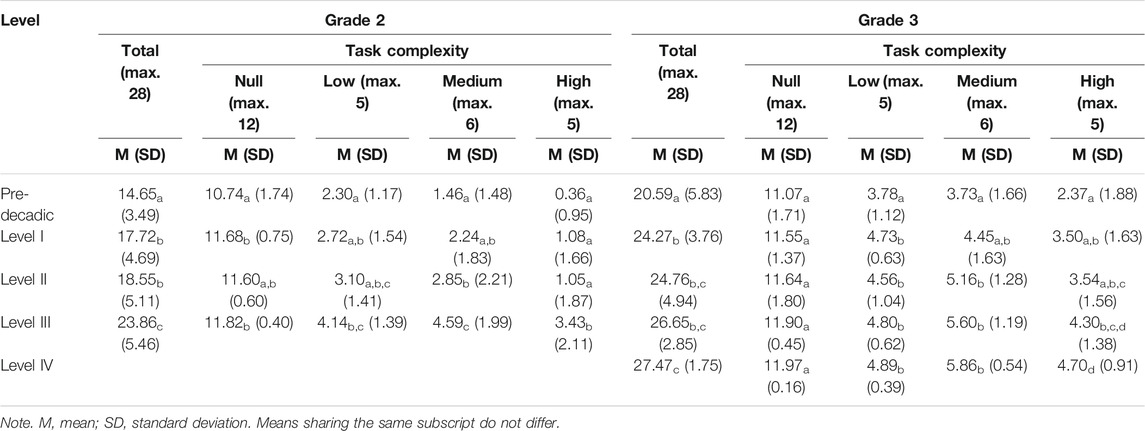
TABLE 2. Means and standard deviations of transcoding performance in children at different levels in Grade 2 and 3.
An analysis of the performance regarding numbers of different complexity provides deeper insights in the associations of transcoding and place value understanding. Transcoding complexity of stimuli was determined by the number of procedural rules in terms of the ADAPT model that have to be applied to the particular number as described by Moura et al. (2015). Regarding the numbers with the lowest complexity (Null), there were no significant differences between children at different levels (I to III or IV) of place value understanding. We found ceiling effects in all subgroups of place value understanding for the least complex numbers. With increasing number complexity, differences between the children with different place value understanding got bigger in Grade 2. In Grade 3, transcoding performance in children at the Pre-decadic Level dropped with increasing complexity of numbers. However, ceiling effects were found in children at Levels I to IV for numbers of null, low, and medium complexity. Children at Levels III and IV showed ceiling effects even for the most complex numbers. In summary, the effect of place value understanding on transcoding applied primarily for complex numbers and children at the Pre-decadic Level.
In line with Moura et al. (2015), children in Grade 3 performed better in the transcoding tasks than the second graders, even when they were at the same level of place value understanding. As for place value understanding, the effect of the Grade increases with number complexity. Within the Grade-specific subgroups, no significant correlation of chronological age and transcoding performance was found (Grade 2: r = −0.071, p = 421; Grade 3: r = −0.055, p = 0.533). We therefore conclude that, besides place value understanding, transcoding is influenced by schooling, as children in Grade 3 have been introduced to three-digit numbers.
A comparison of the error rates regarding the 28 numbers used in the transcoding tasks across children at different levels of place value understanding (Figure 2) with a comparable analysis regarding children in different grades (Moura et al., 2015) reveals similar patterns. Different Grade-levels and levels of place value understanding have nearly identical effects on the error rates. The similarities can even be found regarding the individual stimuli used in the transcoding tasks.
In line with previous research, children made substantially more syntactical errors than lexical errors (Moura et al., 2015). An analysis of the error types revealed the same significant effects of grade and place value understanding for all error types (RQ2). As comprised in Table 3, individual error rates decreased with increasing level of place value understanding, and children in Grade 3 made less errors than second graders. However, these effects did not apply to all error types to the same extent. The individual rates of syntactical errors were stronger affected by place value understanding and Grade level than lexical error rates. Different sensitivity to place value understanding is visualized by effect sizes of one-way ANOVAs, which were higher for syntactical errors (Grade 2: η2 = 0.233, Grade 3: η2 = 0.198) than for lexical errors (Grade 2: η2 = 0.097, Grade 3: η2 = 0.137).
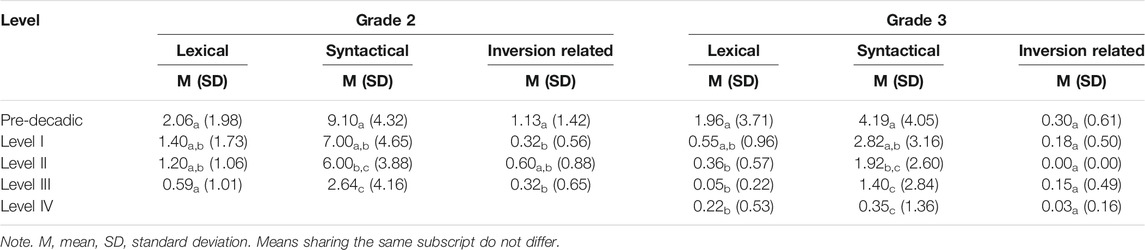
TABLE 3. Means and standard deviations of lexical, syntactical and inversion related errors in children at different levels in Grade 2 and 3.
Inversion related errors are a specific subtype of syntactical errors found in German. Pure inversion related errors only made up a small percentage (Grade 2: 10.7%, Grade 3: 6.1%) of the syntactical errors. Most syntactical errors were not inversion related, but were related to incorrect integration of hundreds (e.g., 90051) or thousands (e.g., 10002 for 1002). As for lexical errors, the effect of place value understanding on inversion related errors was rather low (Grade 2: η2 = 0.103, Grade 3: η2 = 0.073). This finding indicates that inversion related transcoding errors are only partially dependent on missing place value understanding. In contrast to place value understanding, Grade level had a bigger effect on inversion related errors, as the rate for inversion related errors in Grade 3 was only one sixth of the rate in Grade 2 for the whole sample. Only in children at the Pre-decadic Level there was no effect of the grade level.
Discussion
The results of this study show that transcoding abilities are associated with place value understanding in general (RQ1). This association was slightly stronger for second graders than for third graders and for more complex numbers. However, the differences between second- and third-graders were not significant. Especially children who have not yet developed a conceptual basis for identifying place values (Pre-decadic Level) showed lower transcoding performance than children at higher levels. The association between place value understanding and transcoding did not apply to all types of errors in the same way (RQ2). The biggest effect of place value understanding was found regarding syntactical errors. In contrast to findings reported in the literature, inversion related errors occurred only rarely (Zuber et al., 2009; van der Ven et al., 2017). As well as inversion related errors, lexical errors were only little affected by differences in place value understanding. Children at the Pre-decadic Level showed a smaller difference in error rates between Grade 2 and Grade 3. At the same time, these children performed significantly lower in the transcoding tasks than children at higher levels. We suspect that this group might be most likely to develop persistent difficulties with transcoding and even mathematical learning difficulties.
Cognitive Foundations of Transcoding
Independently from the level of place value understanding, children in Grade 3 showed higher transcoding proficiency than children in Grade 2. Thus, place value understanding may explain transcoding performance only partially. Experience with writing numbers due to exposure and formal instruction in school have to be considered another basis for children’s development of transcoding abilities, too. As age did not correlate with transcoding proficiency, transcoding abilities appear not as a result of maturing, but rather a result of education. These findings indicate that transcoding abilities are supported by, but not completely bound to an elaborated place value understanding.
Based on the data gained in this study, we can only speculate which learning contents of formal schooling promote transcoding during Grades 2 and 3. Informed by the curriculum, decimal arithmetic strategies such as break-down (27 + 15 = 20 + 10 + 7 + 5 = 30 + 12 = 42) or decompositions (27 + 15 = 27 + 3+ 12 = 30 + 12 = 42) seem reasonable contents that support children’s transcoding abilities. It is also likely that children gain experience during primary school when asked to write, read, and compare numbers. The better transcoding performance regarding more complex numbers in third graders supports this suggestion, as they have been introduced to three-digit numbers in school. More insight in schooling effects might be obtained by targeted intervention studies in Grade 2 in which the different contents can be taught separately. In addition, longitudinal single case studies over a longer time period can align the development of transcoding abilities to the development of place value understanding on the one hand and formal schooling contents on the other hand.
The findings of this study regarding the error types can be brought in line with the ADAPT model. First, the association of place value understanding and transcoding was dominantly caused by syntactical errors. Syntactical errors occur when children incorrectly apply the procedural rules of the ADAPT model. Knowledge of these rules partially corresponds with place value understanding as described by the Herzog et al. (2019) model. For instance, the knowledge of the place values (Level I) can be identified as conceptual underpinning of the P2/P3-rules. Second, lexical errors were less associated with place value understanding. Lexical errors are supposed to stem from incorrect mappings of number words and Arabic symbol. Mapping errors—may they be due to falsely learned number words or mistakes when deriving from the long-term memory—are based rather on access difficulties to the numerical lexicon than on the procedural rules described in the ADAPT model. Third, a possible reason for inversion errors highlighted in research are working memory capacities (Zuber et al., 2009): When presented an inverted two-digit number word (e.g., five-and-twenty [25 in German]), children have to keep the units part (five) in mind while waiting for and writing down the tens part (twenty). Thus, the ten-unit-inversion draws on the verbal working memory and the central executive (storage of the unit), inhibition (not writing the unit) and visual-spatial working memory (coordinating left and right when writing down the digits). The small association of place value understanding and inversion errors suggests that inversion errors are mostly bound to working memory, but only slightly on place value understanding (Bahnmueller et al., 2015; Pixner et al., 2016). Further studies in which the influence of place value understanding and working memory can be compared directly, for example in a multiple regression model, are needed in this regard.
In both grades and all levels of place value understanding, more complex numbers had higher error rates. However, the effect of number complexity did not apply to all numbers in the same way. For instance, the numbers 200, 700, and 8000 (so-called X00 and X000 numbers; Zuber et al., 2009) were not affected by the number complexity effect. These number words are directly composed by a single digit number word (e.g., seven) and the decimal bundling unit word (e.g., hundred). Obviously, children struggled less with X00 and X000 numbers than with other numbers in the same number range and the same level of complexity. This is especially interesting, as error rates rise very fast for the first numbers of low complexity (150 and 190, so-called XX0 numbers; Zuber et al., 2009). It seems as if X00 and X000 number words are more intuitive to children. The unexpected low error rate on these numbers even in children at the Pre-decadic Level—who do not have any understanding of the decimal place value system yet—underpins this explanation. In terms of the ADAPT model, the different error rates for XX0 numbers and X00/X000 numbers partially contradict the assumption that a number like 700 is transcoded by applying the rules P1 (seven: fact retrieval), P2 (hundred: open three-digit frame), and P4 (end of number word: fill in the empty slots with zeros). Given the error rates in this study, X00/X000 number words are likely to be retrieved from long-term memory just as one- and two-digit numbers in children in Grade 2 and 3. Comparable findings from Moura et al. (2015) support this hypothesis.
Transcoding is a Part of Place Value Understanding
While children at the lower levels of place value understanding performed lower in the transcoding tasks in general, 32.4% of the third graders up to Level II solved all transcoding tasks correctly. Although lacking a profound conceptual understanding of the place value system, these children did not struggle even with the most complex transcoding tasks. In Grade 3, children up to Level II showed ceiling effects except for the most complex numbers. Moura et al. (2015) reported that the vast majority of the children at the end of Grade 4 can perform transcoding tasks even when numbers are complex, while Herzog et al. (2019) showed that about half of the children at this age have not yet developed the concepts of Level III and IV. Obviously, a profound understanding of the place value system includes transcoding abilities. But against the background of the findings listed up above, we suggest that place value understanding covers more knowledge than transcoding alone. Especially an automatized understanding of the relation of the bundling units (Level III and IV) goes beyond transcoding.
Place value understanding can be differentiated into procedural and conceptual aspects (Rittle-Johnson and Schneider, 2015; Van de Walle et al., 2016; Herzog et al., 2019): While procedural place value understanding refers to the knowledge how the elements of the place value system interact, conceptual place value understanding covers the knowledge why they interact. Following the models of transcoding and place value understanding that formed the basis of this study, transcoding has to be considered a rather procedural aspect of place value understanding. This notion of transcoding is in line with the ADAPT model being a procedural model. But procedural aspects usually have a conceptual underpinning, too. Knowledge of the bundling units (Level I) appears as a reasonable conceptual basis for transcoding by theoretical considerations and the empirical results of this study. This idea was also the hypothesis for both research questions. The results of this study support this assumption partially. Children at the Pre-decadic Level performed significantly lower in the transcoding tasks than children at higher levels. At the same time, transcoding performance increased with higher level of place value understanding. Comparable group differences were found in regard to the error types. Thus, knowledge of Level I coincides with better transcoding performance as hypothesized, but the association of place value understanding with transcoding performance is not limited to the knowledge of Level I.
Research has given examples, how children can solve tasks procedurally without having a profound conceptual foundation (Selter, 2001). This might explain that 18.5% of the third graders at the Pre-decadic Level could solve all transcoding tasks in this study. These results of the study underpin the notion of transcoding as a rather procedural aspect of the model of place value understanding. An analysis of procedural and conceptual aspects of place value understanding supports the claim that place value understanding covers skills and knowledge beyond transcoding, while transcoding is an integral part but not totally incremented in place value understanding (Herzog et al., 2019).
As transcoding is a basal component of place value understanding, difficulties with transcoding tasks may be an easy to use screening tool to identify children who struggle severely with developing a profound place value understanding (Moura et al., 2015). Especially complex numbers can be helpful to find children at-risk for difficulties with place value understanding. Keeping in mind the effect of formal schooling, transcoding seems to be most useful in early primary school. Given the low prevalence of children who lack transcoding abilities, transcoding tasks may only identify children with severe difficulties within the range of mathematical learning difficulties. However, transcoding appears not as a useful screening for children with mild math difficulties which are limited to distinct aspects of mathematics.
The Role of Place Value Relations in Place Value Processing
The proposed notion of place value understanding and transcoding as overlapping domains of knowledge that are neither included nor disjunct has implications for the taxonomy of place value processing (Nuerk et al., 2015). If, as the results of this study suggest, transcoding conceptually relies both on place value identification (Level I) and an understanding of the relations between the bundling units (Levels II-IV), the latter might be added to the Nuerk et al. (2015) taxonomy. Place value relations could specify the conceptually grounded knowledge, how decimal bundling units are related and how they can be traded. This level of place value processing would especially cover the handling of non-canonical number representations with and without visualizations.
Place value relations can be distinguished from the three other levels (place value identification, place value activation, and place value computation). Place value identification can be identified with Level I (Nuerk et al., 2015; Herzog et al., 2019). The hierarchy of the developmental model of place value understanding shows that place value relations exceed place value identification (Herzog and Fritz, 2019). Place value activation refers to the numerical value of the positions in multi-digit numbers. The automatic activation of the numerical information of place values gets visible for example in number comparison (Nuerk et al., 2015). Nuerk et al., (2001) have shown that numerical information is activated separately for tens and units. The compatibility effect in number comparison, which leads to higher reaction times in comparing incongruent number pairs (e.g., 72 and 58) than congruent pairs (e.g., 72 and 61) visualizes this automatic information: The (unnecessary) information regarding the units is activated automatically and independently from the information of the tens. As place value activation affects the decimal bundling units separately, it is unlikely that this level of place value processing can be identified with place value relations. Place value computation specifies the processing of place value information when solving arithmetic tasks. Studies have shown that tasks involving carries (e.g., 27 + 18) are more difficult than tasks without carries (Imbo et al., 2007; Klein et al., 2010; Moeller et al., 2011b). In particular children with mathematical learning difficulties struggle with tasks involving carries (Lambert and Moeller, 2019). As carry tasks require to coordinate tens and units while computing, one might suspect that place value computation could be identified with place value relations. However, results from the validation studies in Germany and South Africa of the Herzog et al. (2019) model show that solving addition and subtraction tasks with carries does not necessarily imply a profound and abstract understanding of the relation of the bundling units (Herzog et al., 2017; Herzog and Fritz, 2019).
While place value relations as described here are not precisely covered by the existing levels of place value identification, there are possible interactions. As underpinned by the model hierarchy, place value identification (Level I) is a basis for place value relations. Place value computation correlates with general mathematical skills which include place value relations (Lambert and Moeller, 2019; Herzog and Fritz, 2020). These findings rise the question, how place value relations can be conceptualized within the framework of place value processing (Nuerk et al., 2015). At least two conceptualizations seem reasonable (see Figure 3): First, place value relations might be an additional fourth level of number processing. In this case, variance in place value relations would lead to different proficiency for example when handling non-canonical number representations, but not interact with effects associated with place value identification, activation, or computation. Second, place value relations could be a cross-sectional level that interacts with place value identification, activation, and computation to some extent. Such a conceptualization would imply that place value relations cannot completely be disentangled from the other levels of place value processing. Empirical research might provide evidence to decide which conceptualization is more accurate.

FIGURE 3. Possible conceptualizations of place value relations within the framework of levels of place value processing (Nuerk et al., 2015).
Limitations and Future Perspectives
At least three limitations of this study have to be considered. Each of them might inform future research on the association of place value understanding and transcoding. First, this study included no cognitive or mathematical control variables. Given the body of research on the relation between transcoding and working memory, the above made hypotheses on error types and their varying foundation on place value understanding on the one hand and working memory on the other hand deserve more detailed investigation. While transcoding and place value understanding individually predict later arithmetic performance (Moeller et al., 2011a; Herzog and Fritz, 2020), their interaction remains unclear. Based on the claim that place value understanding covers and exceeds transcoding, one might speculate that place value understanding mediates the influence of transcoding on arithmetic performance to some extent.
Second, the ADAPT model and the Herzog et al. (2019) model are supposed to be developmental. That means that children show substantial progress over time in the skills described in these models (e.g., Herzog and Fritz, 2019). The interaction of developmental trajectories in place value understanding and transcoding skills can only be evaluated validly in a longitudinal study. Results from such a longitudinal study could provide valuable insights in the development of transcoding abilities. While the ADAPT model gives a clear description on the cognitive processes in transcoding, the trajectories children follow while learning how to apply these processes remain vague. For example, the structure of the Herzog et al. (2019) model suggests that P2 (two-digit numbers) and P3 (three-digit numbers) rules are learned successively. A developmental progression of transcoding that could be derived from a longitudinal study could answer this question. Additionally, such a developmental progression would help to structure transcoding instruction for children struggling with writing numbers (Clements and Sarama, 2004).
Third, in this study transcoding was only operationalized in form of writing numbers. Against the theoretical background of the ADAPT model (reading numbers) and the Triple Code Model (magnitude representations), substantial transcoding paths have not yet been investigated regarding their association with place value understanding. For reading numbers, similar effects as found in this study seem likely, as transcoding processes specified in the ADAPT model hold for both directions. Predictions on the conceptual basis of magnitude representations such as number line estimation appear more difficult and require further research.
Data Availability Statement
The raw data supporting the conclusion of this article are available by the authors on request.
Ethics Statement
The studies involving human participants were reviewed and approved by the local ethics committee of the University of Wuppertal. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.
Author Contributions
Study design: MH and AF; Data collection: MH; Analyses: MH; Manuscript edition: MH and AF.
Funding
The publication of this article was funded by the publication fonds of the University of Wuppertal (funding number: GoldOA-PUBL20201116).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bahnmueller, J., Moeller, K., Mann, A., and Nuerk, H. C. (2015). On the Limits of Language Influences on Numerical Cognition - No Inversion Effects in Three-Digit Number Magnitude Processing in Adults. Front. Psychol. 6, 1216. doi:10.3389/fpsyg.2015.01216
Bahnmueller, J., Nuerk, H. C., and Moeller, K. (2018). A Taxonomy Proposal for Types of Interactions of Language and Place-Value Processing in Multi-Digit Numbers. Front. Psychol. 9, 1024. doi:10.3389/fpsyg.2018.01024
Balt, M., Fritz, A., and Ehlert, A. (2020). Insights into First Grade Students' Development of Conceptual Numerical Understanding as Drawn from Progression-Based Assessments. Front. Educ. 5, 80. doi:10.3389/feduc.2020.00080
Barrouillet, P., Camos, V., Perruchet, P., and Seron, X. (2004). ADAPT: A Developmental, Asemantic, and Procedural Model for Transcoding from Verbal to Arabic Numerals. Psychol. Rev. 111 (2), 368–394. doi:10.1037/0033-295X.111.2.368
Battista, M. T. (2011). Conceptualizations and Issues Related to Learning Progressions, Learning Trajectories, and Levels of Sophistication. The Maths. Enthusiast 8 (3), 507–570. doi:10.54870/1551-3440.1228
Byrge, L., Smith, L. B., and Mix, K. S. (2014). Beginnings of Place Value: How Preschoolers Write Three-Digit Numbers. Child. Dev. 85 (2), 437–443. doi:10.1111/cdev.12162
Camos, V. (2008). Low Working Memory Capacity Impedes Both Efficiency and Learning of Number Transcoding in Children. J. Exp. Child. Psychol. 99 (1), 37–57. doi:10.1016/j.jecp.2007.06.006
Chan, W. W. L., Au, T. K., and Tang, J. (2014). Strategic Counting: A Novel Assessment of Place-Value Understanding. Learn. Instruction 29, 78–94. doi:10.1016/j.learninstruc.2013.09.001
Clements, D. H., and Sarama, J. (2004). Learning Trajectories in Mathematics Education. Math. Thinking Learn. 6 (2), 81–89. doi:10.1207/s15327833mtl0602_1
Clements, D. H., and Sarama, J. (2014). “Learning Trajectories: Foundations for Effective, Research-Based Education,” in Learning over Time: Learning Trajectories in Mathematics Education (Charlotte, NC, US: IAP Information Age Publishing), 1–30.
Cobb, P., and Wheatley, G. (1988). Children’s Initial Understandings of Ten. Focus Learn. Probl. Maths. 10 (3), 1–26. doi:10.2307/30035059
Dehaene, S. (1992). Varieties of Numerical Abilities. Cognition 44 (1–2), 1–42. doi:10.1016/0010-0277(92)90049-n
Dehaene, S., and Cohen, L. (1995). Towards an Anatomical and Functional Model of Number Processing. Math. Cogn. 1 (1), 83–120.
Deloche, G., and Seron, X. (1982). From One to 1: An Analysis of a Transcoding Process by Means of Neuropsychological Data. Cognition 12 (2), 119–149. doi:10.1016/0010-0277(82)90009-9
Desoete, A., and Grégoire, J. (2006). Numerical Competence in Young Children and in Children with Mathematics Learning Disabilities. Learn. Individual Differences 16 (4), 351–367. doi:10.1016/j.lindif.2006.12.006
Dietrich, J. F., Huber, S., Dackermann, T., Moeller, K., and Fischer, U. (2016). Place-value Understanding in Number Line Estimation Predicts Future Arithmetic Performance. Br. J. Dev. Psychol. 34 (4), 502–517. doi:10.1111/bjdp.12146
Dowker, A., and Nuerk, H. C. (2016). Editorial: Linguistic Influences on Mathematics. Front. Psychol. 7, 1035. doi:10.3389/fpsyg.2016.01035
Fritz, A., Ehlert, A., Ricken, G., and Balzer, L. (2017). Mathematik und Rechenkonzepte im ersten Schuljahr–Diagnose (MARKO-D1). Göttingen: Hogrefe.
Fuson, K. C., Smith, S. T., and Lo Cicero, A. M. (1997a). Supporting Latino First Graders' Ten-Structured Thinking in Urban Classrooms. J. Res. Maths. Edu. 28 (6), 738–766. doi:10.5951/jresematheduc.28.6.0738
Fuson, K. C., Wearne, D., Hiebert, J. C., Murray, H. G., Human, P. G., Olivier, A. I., et al. (1997b). Children's Conceptual Structures for Multidigit Numbers and Methods of Multidigit Addition and Subtraction. J. Res. Maths. Edu. 28 (2), 130–162. doi:10.5951/jresematheduc.28.2.0130
Geary, D. C., Hoard, M. K., and Hamson, C. O. (1999). Numerical and Arithmetical Cognition: Patterns of Functions and Deficits in Children at Risk for a Mathematical Disability. J. Exp. Child. Psychol. 74 (3), 213–239. doi:10.1006/jecp.1999.2515
Geary, D. C. (2004). Mathematics and Learning Disabilities. J. Learn. Disabil. 37, 4–15. doi:10.1177/00222194040370010201
Gilmore, C., Göbel, S. M., and Inglis, M. (2018). An Introduction to Mathematical Cognition. London ; New York: Routledge,Taylor and Francis Group.
Göbel, S. M., Moeller, K., Pixner, S., Kaufmann, L., and Nuerk, H. C. (2014a). Language Affects Symbolic Arithmetic in Children: The Case of Number Word Inversion. J. Exp. Child. Psychol. 119, 17–25. doi:10.1016/j.jecp.2013.10.001
Göbel, S. M., Watson, S. E., Lervåg, A., and Hulme, C. (2014b). Children's Arithmetic Development: it Is Number Knowledge, Not the Approximate Number Sense, that Counts. Psychol. Sci. 25 (3), 789–798. doi:10.1177/0956797613516471
Herzog, M., Ehlert, A., and Fritz, A. (2017). A Competency Model of Place Value Understanding in South African Primary School Pupils. Afr. J. Res. Math. Sci. Tech. Edu. 21 (1), 37–48. doi:10.1080/18117295.2017.1279453
Herzog, M., Ehlert, A., and Fritz, A. (2019). “Development of a Sustainable Place Value Understanding,” in International Handbook of Mathematical Learning Difficulties. Editors A. Fritz, V. G. Haase, and P. Räsänen (Cham: Springer International Publishing), 561–579. doi:10.1007/978-3-319-97148-3_33
Herzog, M., and Fritz, A. (2020). “Konzeptuelles Stellenwertverständnis als Prädiktor für Rechenfertigkeiten,” in Beiträge Zum Mathematikunterricht 2020. Editors H.-S. Siller, W. Weigel, and J. F. Wörler (Münster: WTM-Verlag), 421–424.
Herzog, M., and Fritz, A. (20192019). “Validation of a Developmental Model of Place Value Concepts,”. Proceedings of the 43rd Conference of the International Group for the Psychology of Mathematics Education. Editors M. Graven, H. Venkat, A. Essien, and P. Vale (Pretoria, South Africa: PME), Vol. 2, 352–359.
Hiebert, J., and Lefevre, P. (1986). “Procedural and Conceptual Knowledge,” in Conceptual and Procedural Knowledge: The Case of Mathematics (New York, 1–27.
Houdement, C., and Tempier, F. (2019). Understanding Place Value with Numeration Units. ZDM Maths. Edu. 51 (1), 25–37. doi:10.1007/s11858-018-0985-6
Imbo, I., Vanden Bulcke, C., De Brauwer, J., and Fias, W. (2014). Sixty-four or Four-And-Sixty? the Influence of Language and Working Memory on Children's Number Transcoding. Front. Psychol. 5, 313. doi:10.3389/fpsyg.2014.00313
Imbo, I., Vandierendonck, A., and Vergauwe, E. (2007). The Role of Working Memory in Carrying and Borrowing. Psychol. Res. 71 (4), 467–483. doi:10.1007/s00426-006-0044-8
Klein, E., Bahnmueller, J., Mann, A., Pixner, S., Kaufmann, L., Nuerk, H. C., et al. (2013). Language Influences on Numerical Development-Inversion Effects on Multi-Digit Number Processing. Front. Psychol. 4, 480. doi:10.3389/fpsyg.2013.00480
Klein, E., Moeller, K., Dressel, K., Domahs, F., Wood, G., Willmes, K., et al. (2010). To Carry or Not to Carry-Iis This the Question? Disentangling the Carry Effect in Multi-Digit Addition. Acta Psychol. (Amst) 135 (1), 67–76. doi:10.1016/j.actpsy.2010.06.002
Lambert, K., and Moeller, K. (2019). Place-value Computation in Children with Mathematics Difficulties. J. Exp. Child. Psychol. 178, 214–225. doi:10.1016/j.jecp.2018.09.008
Lee, M. D., and Sarnecka, B. W. (2009). A Model of Knower-Level Behavior in Number-Concept Development. Cogn. Sci. 34 (1), 51–67. doi:10.1111/j.1551-6709.2009.01063.x
Lopes-Silva, J. B., Moura, R., Júlio-Costa, A., Haase, V. G., and Wood, G. (2014). Phonemic Awareness as a Pathway to Number Transcoding. Front. Psychol. 5, 13. doi:10.3389/fpsyg.2014.00013
Mark, W., and Dowker, A. (2015). Linguistic Influence on Mathematical Development Is Specific rather Than Pervasive: Revisiting the Chinese Number Advantage in Chinese and English Children. Front. Psychol. 6, 203. doi:10.3389/fpsyg.2015.00203
Miller, K. F., Smith, C. M., Zhu, J., and Zhang, H. (1995). Preschool Origins of Cross-National Differences in Mathematical Competence: The Role of Number-Naming Systems. Psychol. Sci. 6 (1), 56–60. doi:10.1111/j.1467-9280.1995.tb00305.x
Moeller, K., Klein, E., and Nuerk, H. C. (2011b). Three Processes Underlying the Carry Effect in Addition-Eevidence from Eye Tracking. Br. J Psychol 102 (3), 623–645. doi:10.1111/j.2044-8295.2011.02034.x
Moeller, K., Pixner, S., Zuber, J., Kaufmann, L., and Nuerk, H. C. (2011a). Early Place-Value Understanding as a Precursor for Later Arithmetic Performance-Aa Longitudinal Study on Numerical Development. Res. Dev. Disabil. 32 (5), 1837–1851. doi:10.1016/j.ridd.2011.03.012
Moura, R., Lopes-Silva, J. B., Vieira, L. R., Paiva, G. M., Prado, A. C., Wood, G., et al. (2015). From “Five” to 5 for 5 minutes: Arabic Number Transcoding as a Short, Specific, and Sensitive Screening Tool for Mathematics Learning Difficulties. Arch. Clin. Neuropsychol. 30 (1), 88–98. doi:10.1093/arclin/acu071
Moura, R., Wood, G., Pinheiro-Chagas, P., Lonnemann, J., Krinzinger, H., Willmes, K., et al. (2013). Transcoding Abilities in Typical and Atypical Mathematics Achievers: The Role of Working Memory and Procedural and Lexical Competencies. J. Exp. Child. Psychol. 116 (3), 707–727. doi:10.1016/j.jecp.2013.07.008
Nuerk, H. C., Weger, U., and Willmes, K. (2001). Decade Breaks in the Mental Number Line? Putting the Tens and Units Back in Different Bins. Cognition 82 (1), B25–B33. doi:10.1016/S0010-0277(01)00142-1
Nuerk, H.-C., Moeller, K., and Willmes, K. (2014). Multi-digit Number Processing. Editors R. Cohen Kadosh, and A. Dowker (Oxford University Press), Vol. 1. doi:10.1093/oxfordhb/9780199642342.013.021
Nührenbörger, M., and Steinbring, H. (2008). “Manipulatives as Tools in Teacher Education,”. International Handbook of Mathematics Teacher Education. Editors S. Llinares, and O. Chapman (Leiden, Netherlands: Brill | Sense), 2, 157–181. doi:10.1163/9789087905460_009
Pixner, S., Zuber, J., Heřmanová, V., Kaufmann, L., Nuerk, H. C., and Moeller, K. (2011). One Language, Two Number-word Systems and many Problems: Numerical Cognition in the Czech Language. Res. Dev. Disabil. 32 (6), 2683–2689. doi:10.1016/j.ridd.2011.06.004
Pixner, S., Nuerk, H.-C., and Moeller, K. (2016). Einflüsse der Inversion auf die Verarbeitung mehrstelliger Zahlen bei deutschsprachigen Kindern - ein Überblick. Lernen und Lernstörungen 5 (3), 173–188. doi:10.1024/2235-0977/a000021
Poncin, A., Van Rinsveld, A., and Schiltz, C. (2020). Units-first or Tens-First: Does Language Matter when Processing Visually Presented Two-Digit Numbers? Q. J. Exp. Psychol. (Hove) 73 (5), 726–738. doi:10.1177/1747021819892165
Reiss, K., and Obersteiner, A. (2019). “Competence Models as a Basis for Defining, Understanding, and Diagnosing Students' Mathematical Competences,” in International Handbook of Mathematical Learning Difficulties. Editors A. Fritz, V. G. Haase, and P. Räsänen (Cham: Springer International Publishing), 43–56. doi:10.1007/978-3-319-97148-3_4
Ricken, G., Fritz, A., and Balzer, L. (2013). MARKO-D: Mathematik-und Rechenkonzepte im Vorschulalter-Daignose: Mit Ergänzungstest Konventions-und Regelwissen. Hogrefe.
Rittle-Johnson, B., and Schneider, M. (2015). Developing Conceptual and Procedural Knowledge of Mathematics. Oxford Handbook of Numerical Cognition, 1118–1134.
Ross, S. H. (1989). Parts, Wholes, and Place Value: A Developmental View. Arithmetic Teach. 36 (6), 47–51. doi:10.5951/at.36.6.0047
Scherer, P., and Moser Opitz, E. (2010). Fördern im Mathematikunterricht der Primarstufe. Heidelberg: Spektrum Akademischer Verlag.
Schulz, A. (2014). Fachdidaktisches Wissen von Grundschullehrkräften. Wiesbaden: Springer Fachmedien Wiesbaden. doi:10.1007/978-3-658-08693-0
Selter, C. (2001). Addition and Subtraction of Three-Digit Numbers: German Elementary Children’s Success, Methods and Strategies. Educ. Stud. Maths. 47 (2), 145–173. doi:10.1023/a:1014521221809
Siegler, R. S., and Alibali, M. W. (2005). Children’s Thinking. 4th ed. Upper Saddle River, N.J: Pearson Education/Prentice Hall.
Steffe, L. P. (1992). Schemes of Action and Operation Involving Composite Units. Learn. Individual Differences 4 (3), 259–309. doi:10.1016/1041-6080(92)90005-Y
Van de Walle, J., Karp, K., and Bay-Williams, J. (2016). in Elementary and Middle School Mathematics: Teaching Developmentally. Editor M. Fossel. Ninth (USA: Pearson Education).
van der Ven, S. H. G., Klaiber, J. D., and van der Maas, H. L. J. (2017). Four And Twenty Blackbirds: How Transcoding Ability Mediates the Relationship between Visuospatial Working Memory and Math in a Language with Inversion. Educ. Psychol. 37 (4), 487–505. doi:10.1080/01443410.2016.1150421
Keywords: place value understanding, transcoding, numerical development, numerical cognition, number writing
Citation: Herzog M and Fritz A (2022) Place Value Understanding Explains Individual Differences in Writing Numbers in Second and Third Graders But Goes Beyond. Front. Educ. 6:642153. doi: 10.3389/feduc.2021.642153
Received: 15 December 2020; Accepted: 13 December 2021;
Published: 18 January 2022.
Edited by:
Ricardo Moura, University of Brasilia, BrazilReviewed by:
Ren Liu, University of California, Merced, United StatesRicardo Garcia, Federal University of Paraíba, Brazil
Copyright © 2022 Herzog and Fritz. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Moritz Herzog, bWhlcnpvZ0B1bmktd3VwcGVydGFsLmRl
 Moritz Herzog
Moritz Herzog Annemarie Fritz
Annemarie Fritz