Disentangling the Effects of SFON (Spontaneous Focusing on Numerosity) and Symbolic Number Skills on the Mathematical Achievement of First Graders. A Longitudinal Study

Introduction

Spontaneous Focusing on Numerosity (SFON) and symbolic number skills have both been identified as important predictors of mathematical achievement gain (e.g., Hannula-Sormunen et al., 2015; Gallit et al., 2018). Hannula et al. (2005) were the first to investigate SFON. SFON is defined as a “process of spontaneously […] focusing attention on the exact number of a set of items or incidents” (Hannula et al., 2010, p. 395). Young children pay attention to quantitative aspects of their environment: They count steps when climbing the stairs, compare the number of cookies they would like to eat or the number of objects in a storybook. The term “spontaneous” means that the process of focusing on numbers is self-initiated and not guided by others. “This attentional process is needed for triggering exact number recognition processes and using the recognized exact number in action because exact number recognition is not a totally automatic process that would take place every time a person faces something to enumerate” (Hannula et al., 2010, p. 395). Hannula-Sormunen et al. (2020) emphasize that this process of focusing attention on the exact number of objects in their surroundings is a skill that children have to learn. It enables them to efficiently utilize the innate mechanisms of subitizing for active quantification processes. A child’s SFON performance reflects their tendency to focus on the numerical, so discussions of SFON often refer to SFON tendencies, but in this paper we use the term SFON on its own.

SFON seems to be important for later mathematical achievement. Empirical findings reveal a relationship between children’s SFON and their early mathematical skills (e.g., Hannula et al., 2005; Hannula and Lehtinen, 2005; Hannula et al., 2007; Edens and Potter, 2013). There is also evidence that a child’s SFON is related to their subsequent mathematical achievement in primary school (e.g., Hannula et al., 2010; Hannula-Sormunen et al., 2015; McMullen et al., 2015). But some studies suggest number skills acquired before starting school are also important predictors of mathematical achievement in primary school (e.g., Jordan et al., 2007; Krajewski and Schneider, 2009; Conoyer et al., 2016; Gallit et al., 2018). These skills–variously termed “early numeracy” (Conoyer et al., 2016), “number sense” [Jordan et al. (2007), or “early quantity-number competencies” (Krajewski and Schneider, 2009)–include the ability to count out loud, compare numbers and magnitudes, link small magnitudes and numbers, and do simple calculations. Number skills can be divided into symbolic and non-symbolic categories. Symbolic skills (e.g., linking numbers and magnitudes, reading numbers] have been shown to be especially important for the development of further mathematical skills (e.g., Kolkman et al., 2013; Göbel et al., 2014). So both SFON and symbolic number skills are important for mathematical learning although little is known about the relationship between them, or whether one has a greater effect on subsequent mathematical achievement than the other. This study investigates how a child’s SFON and symbolic number skills at the beginning of Grade 1 may relate to mathematical achievement at the end of Grade 1.

Measuring SFON

There are a variety of tasks designed to measure SFON, and studies show that the type of task can have an influence on measured SFON (Batchelor et al., 2015; Rathé et al., 2016; Nanu et al., 2020). According to Hannula (2005), the following criteria are important when assessing SFON. In order to avoid “numerical hints,” only tasks which are new to the children and tasks without mathematical context should be used. Furthermore, the use of mathematical vocabulary (e.g., count, number word) should be avoided both before and during the test. SFON tasks should include small numbers of objects that are easy to enumerate. Finally, SFON tasks should not exceed the children’s working memory capacity or visuo-motor or verbal comprehension skills (ibid.).

Hannula et al. (e.g., Hannula et al., 2005; Hannula and Lehtinen, 2005) developed different types of action-based tasks: The imitation task, the model task, the finding task, and the selection task. In the imitation task, children are instructed to imitate the action of a test administrator (e.g., posting a certain number of blue and red envelopes into a mailbox). In the model task, the children have to carefully observe the activity of a test administrator (e.g., depicting a dinosaur with stamps) and copy the dinosaur as precisely as possible. In the finding task, the test administrator hides a toy (e.g., a gold ingot) under one of three objects (e.g., wooden hats). The children have to remember where the toy was hidden and lift the correct cover. In the selection task, the children are told to give a certain number of objects to a creature (e.g., “This creature has a problem. The creature’s legs feel terribly cold. Fortunately, there are boxes of socks under the cloth. Give this creature its own box of socks.” Hannula et al., 2005, p. 70). These tasks all have some limitations. The imitation task and the model task could, possibly, be successfully completed using imitation alone, without any numerical reasoning, especially when conducted with small quantities of objects. Also, the children have to focus on the specific activity presented by the administrator and their attention has to be drawn to this activity from the very beginning of the task. Therefore, the result might be affected by the children’s attention capacity and/or working memory. This is not the case for the selection task, which requires numerical thinking when comparing quantities.

A different type of SFON task is the picture task, which was developed by Batchelor et al. (2015). In the picture task, the children are shown a picture with different objects in varying numbers (e.g., a river with three boats, four ducks and two trees). The children are asked to describe what they see. Contrary to the action-based task, here the focus can be on different dimensions. Children may not only focus on the number of objects (e.g., “two girls”) but also on the colors of the objects (e.g., “a red shirt”) or other aspects like emotions (e.g., “the girls look happy”). In addition, the picture task is quick and easy to handle, and no specific material is required. Furthermore, the scoring is simple, and no additional analyses are necessary (ibid.). The picture task, however, also has limitations. It requires active language skills like vocabulary and number words and may be challenging for second language learners or children with language impairment (ibid.). In addition, a child’s answers might be affected by his or her interests. While some children are more interested in numbers, others might focus on colors or shapes, or the vocabulary (e.g., “I forgot what duck means in Spanish.”).

A Literature Review of SFON

Existing studies have examined SFON in different age groups. The findings of longitudinal studies reported high stability of children’s SFON across time (e.g., Hannula and Lehtinen, 2005; Bojorque et al., 2017). In the study by Hannula and Lehtinen (2005), SFON was measured at ages 4, 5 and 6 using different action-based SFON tasks. In spite of the 2-years time period and the different contexts of the tasks, there was reasonable stability in the children’s SFON.

A cross-sectional study by Kucian et al. (2012) demonstrated that children with mathematical learning disabilities aged 7–11 had significantly lower SFON, as measured by two action-based tasks, than children without disabilities. These findings could not be explained by IQ, age or gender. It remains unclear, however, whether a lower SFON leads to low mathematical skills or whether mathematical difficulties lead to a lower SFON. Gray and Reeve (2016) identified preschoolers’ math ability profiles and examined how number-specific markers like SFON (measured using three action-based tasks) and dot enumeration, as well as general markers (working memory, response inhibition, attention, and vocabulary), were associated with profiles. Results showed that the numerical markers were significantly associated with the math ability profiles, whereas the association between the other markers was either not significant or only marginally so.

Findings of cross-sectional studies provide empirical evidence that a child’s SFON, measured using action-based tasks, is positively correlated with number sense and early mathematical skills (e.g., Hannula and Lehtinen, 2005; Edens and Potter, 2013). Hannula and Lehtinen (2005) investigated SFON and early mathematical skills in preschoolers. Results showed that the children’s SFON correlated with number sequence elaboration, counting of objects, and basic arithmetic skills such as addition and subtraction. These relationships remained significant after controlling for nonverbal IQ and the comprehension of verbal instructions. Edens and Potter (2013) found that 4-year old children who spontaneously focused on numerosity had better counting skills.

Longitudinal studies have also provided insight into SFON and its relationship with mathematical skills. A study by Hannula et al. (2007) investigated how SFON, measured using action-based tasks, is related to subitizing-based enumeration and verbal and object counting skills in four and five-year-old children. Results showed that SFON was directly related to verbal counting skills even when subitizing-based enumeration was entered in the model. The association between SFON and object counting skills was mediated by subitizing-based enumeration. Further, empirical evidence shows that children’s SFON is also related to subsequent mathematical achievement in primary school (e.g., Hannula et al., 2010; Hannula-Sormunen et al., 2015; McMullen et al., 2015). Hannula et al. (2010) showed that children’s SFON in kindergarten, measured using an action-based task, accounted for a domain-specific and significant, but small, variance (2%) at the end of Grade 2. Children’s SFON was a significant predictor of arithmetic skills at the end of Grade 2, but not of reading skills. The domain specificity of SFON is also supported by the findings of Nanu et al. (2018). In their study, SFON measured at age five with action-based tasks predicted arithmetic fluency and number line estimation in fifth grade, but not rational number knowledge or mathematical achievement. Hannula-Sormunen et al. (2015) analyzed the effect of children’s SFON, again measured with action-based tasks, subitizing, and counting skills on their mathematical achievement at age of 12. Subitizing-enumeration skills were tested at age five. SFON and counting skills were then assessed a year later, at age six. Their results showed that children’s SFON and counting skills were both predictors of mathematical achievement at age 12. However, after controlling for nonverbal IQ, only SFON predicted mathematical achievement. The association between subitizing and mathematical achievement was mediated by SFON and counting skills. McMullen et al. (2015) followed a sample cohort to investigate how children’s SFON and counting skills as measured at age six related to their rational number conceptual knowledge 6 years later. These results suggest that SFON, measured using action-based tasks, and counting skills predict rational number conceptual knowledge, thus lending support to the hypothesis that SFON is a predictor of a child’s future mathematical achievement. But it should be noted that the sample in that longitudinal study was very small (N = 36).

Chan and Mazzocco (2017) investigated children’s and adults’ attention to numbers, which is a concept related to SFON. The aim of the study was “to address the ‘spontaneity’ and the malleability of SFON […] under varying conditions” (p. 77). The attention to numbers was measured using a picture-matching task, where the participants had to choose one of four pictures that matched a target picture. Results demonstrated that only 8–10% of children’s best matches were number based, while 21% of adults’ were number based. Children’s attention to number did not increase when prompted to search for other matches. In addition, children’s attention to number was affected by competing features (e.g., color, shape, position, or quantity).

Hannula et al. (2005) investigated the possibility of increasing SFON with an intervention. The results demonstrated that SFON, measured using action-based tasks, can be enhanced with a guided intervention in preschool that focused on numerical activities. However, this was only the case for children with high SFON at the first measurement point. Children with no or low SFON at the beginning of the study did not respond to the intervention. Another intervention study by Hannula-Sormunen et al. (2020) tested the effects of two early numeracy intervention programs on SFON and early numerical skills. The intervention programs were integrated into daily day care routines and included activities such as noticing numbers and number recognition that were aimed at developing the subitizing mechanism and paying attention to numerical aspects of everyday activities. The results showed that the intervention programs had a positive effect on children’s SFON as measured by action-based tasks, from pretest to posttest and a long-term effect on cardinality-related skills from posttest to delayed posttest.

Braham et al. (2018) investigated whether SFON measured with action-based tasks could be enhanced through guided parent-child interactions in a children’s museum. Children whose parents had received the numerical intervention program showed higher SFON scores than children whose parents had not. These findings suggest that parents can foster children’s SFON using numerical prompts in informal play settings.

In conclusion, this research overview shows that SFON is related to a variety of other mathematical skills, in both the short and long term. Other research, presented below, emphasizes the significance of the construct of number skills, especially symbolic number skills, for mathematical achievement gain.

Symbolic Number Skills and Its Significance for Mathematical Competence

Research also shows that early number skills such as number knowledge, verbal counting, object counting, and non-symbolic or numerical magnitude comparison are strong predictors for later mathematical achievement in primary school (e.g., Jordan et al., 2007; Krajewski and Schneider, 2009; Conoyer et al., 2016; Toll et al., 2016; Gallit et al., 2018). The process of acquiring number skills includes the innate ability to recognize a small number of items without counting called “subitizing” (e.g., Wynn, 1995), as well as skills that must be acquired through social mediation and education, like counting competence or writing numbers (Dehaene, 2001; Dowker, 2005; Kolkman et al., 2013; Hannula-Sormunen et al., 2020). Frydman (1995) and Simon and Vaishnavi (1996) stress that the process of subitizing contains non-numerical knowledge and therefore differs from other mathematical learning processes like counting. The mediation of numerical skills begins in early childhood when children mimic number sequences used by their parents or siblings (e.g., Fuson, 1988).

Krajewski (2003) found that early numerical skills, as measured 6 months before the start of school, made the greatest contribution to the prediction of arithmetic performance in first grade. Results of this study revealed that poor early numerical skills could predict mathematical difficulties at the end of first and second grade much better than measures of intelligence. Jordan et al. (2007) investigated number sense and its development as predictors for formal math achievement in first grade. They reported that number sense performance in kindergarten and number sense growth accounted for 66% of the variance in math achievement in first grade. Dornheim (2008) found that the early numerical skills in kindergarten were the main predictor of arithmetic achievement in first and second grade. This was also confirmed by the study of Gallit et al. (2018).

There is, however, empirical evidence that some aspects of number skills might be more important than others. According to Krajewski and Schneider (2009), the linkage of quantities and numbers represents the most important concept for successful mathematical learning in primary school. More recent research provides evidence that the differentiation between non-symbolic number skills (e.g. comparing magnitudes) and symbolic number skills (e.g. numerical tasks like counting and Arabic symbols) (e.g., Kolkman et al., 2013) seems to be crucial (e.g., Missall et al., 2012; Kolkman et al., 2013; Göbel et al., 2014; Toll et al., 2016; Caviola et al., 2020). Kolkman et al. (2013) investigated the role of non-symbolic and symbolic skills in early numerical development with children at age 4, 5 and 6. Their results provided evidence for the predominant role of symbolic skills as compared to non-symbolic skills in the development of mapping skills (linkage of number symbols and their corresponding quantities). According to Missall et al. (2012), symbolic skills (comparing numbers, inserting a missing number in a number sequence) are the most robust factors for predicting later math performance. They examined predictive relationships from kindergarten through third grade. Göbel et al. (2014) analysed the impact of symbolic knowledge of the Arabic numeral system and magnitude comparison on arithmetical skills 11 months later in a sample of first graders. Path models revealed that knowledge of the Arabic numeral system predicted an increase in arithmetic skills, whereas magnitude comparison skills had no impact. Caviola et al. (2020) reported similar results from a sample of second graders. Non-symbolic magnitude comparison had no association with mathematical performance. Toll et al. (2016) found that symbolic number skills (which they term number sense) measured at the end of the first year of kindergarten (M_age = 4.96) are the strongest predictors of mathematical performance (math facts and math problems) in first grade. Non-symbolic number sense (dot comparison) was only a predictor of problem solving ability. The importance of symbolic number skills for later arithmetic skills was confirmed in a review paper by Szkudlarek and Brannon (2017). Symbolic numerical competence also plays an important role in interventions aiming to improve SFON. According to Hannula-Sormunen et al. (2020) and Braham et al. (2018), symbolic numerical activities resulted in SFON achievement gains.

Non-numerical Predictors of Mathematical Competence

SFON and number skills, as well as mathematical achievement gain, are influenced by first language, gender, working memory and nonverbal IQ. Anders et al. (2012) found that the first language of the parents had an impact on the number skills of young children and their achievement gain. Also, studies by Kuratli Geeler (2019) and Sale et al. (2018) revealed that having language of classroom education as a first language had a significant influence on the numerical competence of children in kindergarten. In addition, controlling for first language is crucial when a picture-based task is used to assess SFON. The relationship between gender and numerical competence is still unclear. Some studies found no differences in numerical competence between boys and girls (e.g., Dornheim, 2008; Niklas and Schneider, 2012; Sale et al., 2018), while the research of Kuratli Geeler (2019) revealed higher numerical competences for boys in kindergarten, especially in tasks which required symbolic representation. Anders et al. (2012), on the other hand, showed that girls have a higher numerical competence in preschool. For Grade 1, the picture is more consistent, and several researchers reported higher achievement levels for boys (Krajewski, 2003; Niklas and Schneider, 2012; Sale et al., 2018; Kuratli Geeler, 2019). There is also evidence that working memory is significantly related to mathematical achievement (e.g., De Smedt et al., 2009) and therefore important to control for. Batchelor et al. (2015) found no significant correlation between SFON and working memory. Furthermore, previous study results reveal that nonverbal IQ has an impact on number skills and mathematical achievement (e.g., Krajewski and Schneider, 2009; Kuratli Geeler, 2019), whereas there was no relationship between nonverbal IQ and SFON measured with an imitation task (Hannula et al., 2010).

A review of the literature reveals that existing studies highlight the significance of SFON and identify SFON as a predictor of subsequent mathematical performance. Nevertheless, there are some research gaps. First, there is empirical evidence that symbolic number skills are also important predictors of mathematical achievement. Researchers have examined the relationship between SFON and certain aspects of mathematical competence, such as counting or subitizing, and the effect of SFON and counting competence on later mathematical achievement, but they have not yet looked at whether or how SFON and a range of symbolic numerical competences present at the beginning of school career can affect later mathematical achievement gain. Second, longitudinal studies analyzing the effect of SFON on mathematical achievement have often been conducted using small study samples. Third, the research overview shows that most studies have investigated the effect of children’s SFON on mathematical achievement using action-based tasks (e.g., Hannula and Lehtinen, 2005; Hannula et al., 2007; McMullen et al., 2015; Nanu et al., 2018). The picture task has only been used in a few instances (e.g., Batchelor et al., 2015; Rathé et al., 2019). Finally, even if most studies on SFON included non-mathematical predictors, studies that have a broad range of control variables are rare. This study aims to close these research gaps by investigating the effect of SFON and symbolic number skills on mathematical achievement gain using a verbally-based SFON task and a large sample of 1,279 first graders. First language, gender, nonverbal IQ, and working memory are included as control variables.

The following research questions are addressed:

1) To what extent do children spontaneously focus on numerosity at the beginning of Grade 1? Results from previous studies (e.g. Hannula and Lehtinen, 2005; Hannula et al., 2010) indicate that there will be a large variance in children’s SFON.

2) Is there a relationship between SFON and symbolic number skills? Research by Hannula and Lehtinen (2005), and Edens and Potter (2013), suggest there will be a moderately significant correlation.

3) Do SFON and symbolic number skills have an effect on mathematical achievement at the end of Grade 1, controlling for first language, gender, working memory and nonverbal IQ? On the basis of previous research, it is hypothesized that SFON and symbolic number skills both have an effect on mathematical achievement at the end of Grade 1.

4) Is SFON or symbolic number skills more important for mathematical achievement at the end of Grade 1? It is assumed that symbolic number skills have a greater effect on mathematical achievement gain at the end of Grade 1 than does SFON.

First language, gender, nonverbal IQ, and working memory are included as control variables. SFON is assessed with a picture task that is verbally-based. Therefore, it is likely that first language might influence a child’s SFON. Results from the studies presented in the literature review suggest that gender–boys performing better, on average–and nonverbal IQ explain variance in SFON, number skills and mathematical achievement at the end of Grade 1. It is expected that first language and working memory will also influence symbolic number skills and mathematical achievement at the end of Grade 1.

Materials and Methods

Participants and Context of the Study

In the Swiss education system, 1 year of kindergarten is compulsory and kindergarten is free of charge. Therefore, all children attend at least 1 year in kindergarten. Numerical instruction following a compulsory curriculum begins in kindergarten (Deutschschweizer Erziehungsdirektoren-Konferenz (D-EDK), 2016). This numerical instruction focuses on oral counting up to 20, counting backwards and forwards from every possible number up to 10, object counting, comparing numbers, and using number words like “bigger”, “smaller”, “more” or “less” (ibid.).

Participants were 1,279 first graders (49.1% girls, M_age = 6.82, SD = 0.38) from 77 primary schools in German-speaking Switzerland (Table 1). Invitation letters were sent to several schools via the school authorities. Teachers decided voluntarily whether they wished to participate. All parents gave written consent for the participation of their children in the study. 578 children (46.2%) had German as a first language, 316 children (25.3%) were bilingual and 232 children (18.5%) had another first language (Missing n = 125; Table 1).

TABLE 1

TABLE 1. Descriptive characteristics of the sample.

Data was collected over one school year. At the beginning of Grade 1 (t1), SFON, working memory and nonverbal IQ were assessed, with the children working individually with a test administrator in a quiet room at the children’s school. The symbolic number skills test was conducted with groups of 8–12 children at the beginning of Grade 1 (t1), after the SFON test. The test to measure mathematical achievement in Grade 1 (t2) was carried out with the whole class at the end of the school year. The teachers completed a questionnaire on children’s first language, gender, and age at the beginning of the school year.

Instruments

SFON

So that their SFON could be assessed, the children completed a picture task. The picture task was used because compared to an action-based task, it is quick and easy to handle, the scoring is simple, and no additional analyses are necessary. The pictures used in this study were variations of those used by Batchelor et al. (2015). Three pictures (Figure 1) were presented one after the other on a screen (13’’–15’’), in the same order for each child.

FIGURE 1

FIGURE 1. The pictures used in the verbally-based SFON task, drawn by Luisa Leliuc.

The test administrator introduced the SFON task as follows: “I am going to show you different pictures. We are interested in what children will tell us about these pictures. This is the first picture. What do you see in this picture?” Each single statement (e.g., yellow ducks, a pond, a pond with ducks, two girls, a T-Shirt with a flower) was scored as numerical or non-numerical. For efficiency, given the size of the sample, only the first four statements per child were written down. Each numerical answer (e.g., two ducks, three boys) was scored with 1, regardless of whether the number was correct. Answers like “some ducks” or “both girls” were scored 0. Because the German word for “a” is the same as the word for one (“a tree”), these answers were excluded. The children could achieve a maximum score of 12. Confirmatory factor analysis confirmed that the scale was unidimensional and Cronbach’s alpha was 0.87.

Symbolic Number Skills

The symbolic number skills assessment involved 22 items that covered the following topics: counting objects (7 apples, 11 dots, 23 dots) and linking the result with the correct number (3 items), comparing numbers up to 20 (5 items), writing selected numbers of the number sequence up to 20 (11 items), and writing the matching mathematical term for a picture (e.g., 2 + 3 to a picture with two red and three blue balloons; 3 items). Test instructions were given by the test administrator. Some of the tasks were explained with an example. In the number comparison task, two numbers (e.g., 3 and 1) were each written in a box in the booklet. The box with the bigger number was checked. “Here are two numbers in a box, 1 and 3. 3 is more than 1, therefore, this box is checked. Here are two other numbers, each in a box (numbers 6 and 2). You have to check the box with the bigger number.” Cronbach’s alpha was 0.88.

Mathematical Achievement at the End of Grade 1

Mathematical achievement was tested at the end of Grade 1 using an author developed test prepared for publication. The test included 27 items. The following topics were assessed: counting by steps (completing the number sequence 3, 5, 7 … 15 and 12, 14, 16, … 24; 2 items), number decomposition (e.g., 20 = __ + __ + __; 3 items), doubling the numbers 4, 7, 12 (3 items), halving the numbers 16, 18, 22 (3 items), addition (7 + __ = 13, 11 + __ = 19, 18 + __ = 23, 80 +__ = 100; 4 items), subtraction (9–3, 18–8, 17–12, 14–7; 4 items), and word problems (picture of a toy with a price tag: picture with a Swiss bill: you pay with the bill; how much change do you get? 8 items). Most of the test instruction was given using tables and pictures and the test administrator was allowed to read out the short instructions. The counting by steps task was presented in the following way: 3, 5, 7, __, __, __, 15. “Look at these numbers: 3, 5, 7. The numbers continue in the same way. Which numbers fit into the gaps? Write the correct number in the gaps.” Rasch analyses were conducted to assess the quality of the test. Weighted likelihood estimate (WLE) of reliability was 0.79. The item fit was acceptable (0.89–1.27) (Wilson, 2005). The variable was z-standardized.

Nonverbal IQ

Nonverbal IQ was measured using two subtests of CFT 1-R (Weiß and Osterland, 2013): similarities (15 items) and matrices (15 items). Cronbach’s alpha for 30 items was 0.85.

Working Memory

To measure children’s working memory, the corsi blocks (10 items) and number sequence backward (10 items) subtests of a working memory test battery for children aged 5–12 (AGTB 5–12) (Hasselhorn et al., 2012) was used. Cronbach’s alpha for 20 items was 0.72.

First Language

First language was assessed with a teacher questionnaire. Teachers were asked to indicate which language the children speak at home on a 3-point Likert-scale (1 = only German, 2 = bilingual; German and other language, 3 = other languages). Two different variables were calculated: A dichotomous variable with the groups German speaking only/bilingual and other language, and a second variable with the groups German speaking only and bilingual/other language. The analyses were carried out with both variables, but no difference in the results was found. Therefore, results for the groups German only and bilingual and other language are reported.

Statistical Analyses

To test whether a child’s SFON and symbolic number skills have an effect on mathematical achievement at the end of Grade 1, a structural equation model was set up using the lavaan package (Rosseel, 2012) on R software version 3.5.2. SFON and symbolic number skills, as well as the non-specific variables, namely, first language, gender, working memory and nonverbal IQ, were included as predictors (Figure 2). Based on the results of previous studies on the relationships between SFON, symbolic number skills and mathematical achievement, it was assumed that SFON and symbolic number skills both had a direct effect on mathematical achievement at the end of Grade 1. Further, a correlation between SFON and symbolic number skills was assumed. In addition, the non-specific variables first language, gender, working memory and IQ were expected to predict SFON, symbolic number skills and mathematical achievement. As SFON was measured using the picture task, a child’s SFON would not be affected by working memory. Finally, a correlation between working memory and nonverbal IQ was assumed.

FIGURE 2

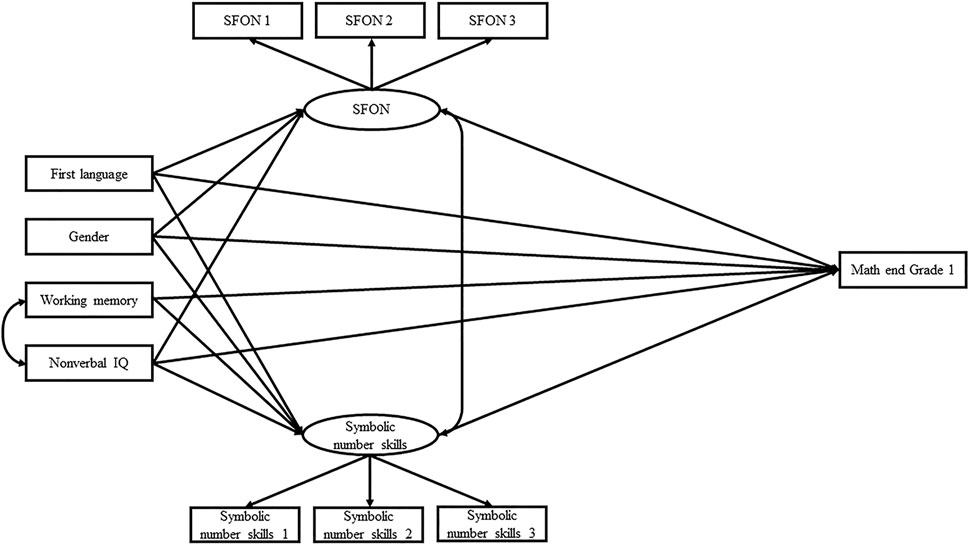
FIGURE 2. Hypothesized Model. SFON and symbolic number skills will predict mathematical achievement at the end of Grade 1 when data are controlled for non-specific predictors (first language, gender, working memory, nonverbal IQ). The oval symbols are latent variables that represent the variance shared by multiple indicators. The square symbols represent manifest variables.

In the hypothesized model, SFON and symbolic number skills were included as latent variables and parcels were built. Parcels help to reduce the complexity of models. Additionally, structural equation models based on parceled data lead to more stable estimates and fit the data better (Matsunaga, 2008). Due to the unidimensionality of the SFON construct, the parcels were allocated to the task. Homogenous or heterogenous parceling strategies can be used to build parcels of multidimensional constructs. In homogenous parceling strategies, similar items are placed in the same parcel, while “in heterogenous parceling strategies, items that share a source of systematic variation are distributed across different parcels either randomly or systematically” (Marsh et al., 2013, p. 260). Because homogenous parcels lead to bad factor loadings, heterogenous parceling strategies were used for the construct of symbolic number skills. The latent variables were z-standardized.

It is assumed that SFON and symbolic number skills measured at the beginning of Grade 1 is something that takes place at the within level. The between level does not seem to be of importance when answering the research questions because the children came into each Grade 1 class from multiple kindergarten groups, reducing the influence of class at the first measurement point. Therefore, a single-level model with cluster-robust standard errors was estimated. In addition, a single-level model was also used for empirical reasons such as a low interclass correlation (ICC = 0.025–0.045) for the SFON indicators. Model fit was evaluated using multiple fit indices. CFI values >0.95, RMSEA values <0.06, SRMR values <0.08 (Weiber and Mühlhaus, 2014) and χ²/df < 3 (Homburg and Giering, 1996) indicate a good model fit.

Results

Descriptive Statistics and Correlations

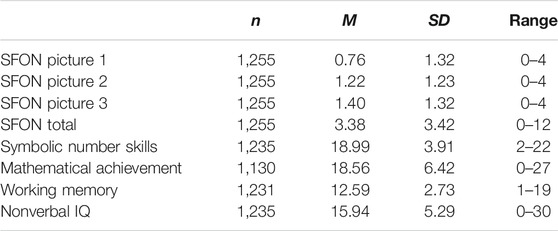
Table 2 presents the descriptive statistics for all measures which highlights the large variance between the children.

TABLE 2

TABLE 2. Descriptive Statistics for all measures.

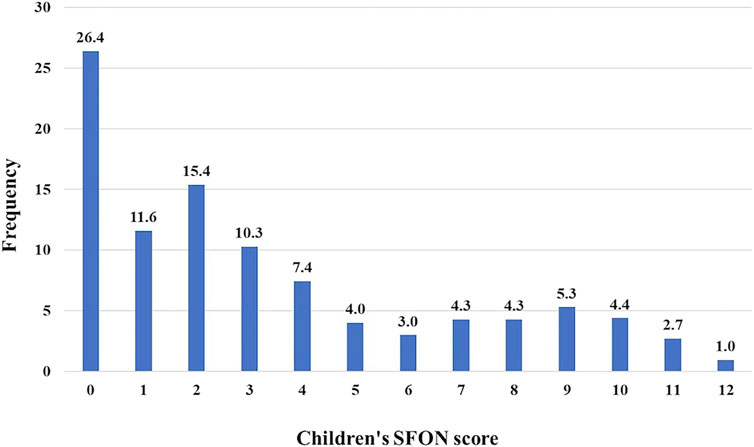
In Figure 3, the results demonstrate that SFON is heterogeneous. 26.4% of the children never gave a numerical answer. Only 1% of the children achieved the maximum SFON score. Also, the mean of 3.38 (SD = 3.42) indicates that children seem to pay little attention to the numerical aspects of the pictures at the beginning of Grade 1. To test whether the children gave more numerical answers to any one of the three SFON pictures, an ANOVA with repeated measures was conducted. The result showed significant differences in the mean values of the three SFON pictures [F(1.91, 2,395.40) = 245.00, p < 0.001, η_p² = 0.16]. A post-hoc test showed significant differences between all items (p < 0.001), with an increase of SFON-answers from picture 1 to picture 3.

FIGURE 3

FIGURE 3. Frequencies of children’s SFON.

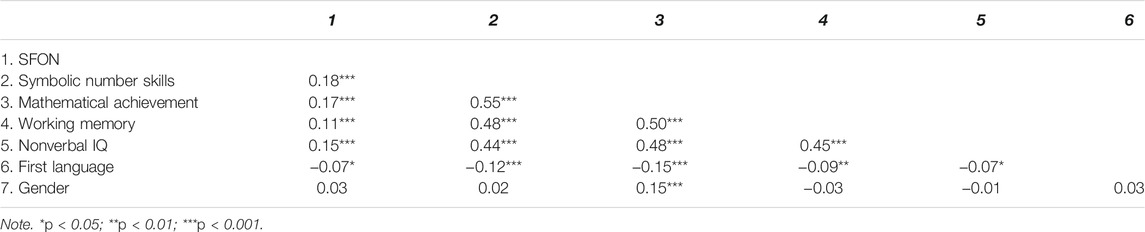
Correlation analyses (Table 3) indicate a significant, but very weak association (r < 0.2) between SFON tendency and symbolic number skills (r = 0.18, p = 0.000), mathematical achievement at the end of Grade 1 (r = 0.17, p = 0.000), working memory (r = 0.11, p = 0.000), nonverbal IQ (r = 0.15, p = 0.000) and first language (r = −0.07, p = 0.024). The strongest correlation was found between symbolic number skills and the mathematical achievement at the end of Grade 1 (r = 0.55, p = 0.000). Symbolic number skills are moderately correlated with working memory (r = 0.48, p = 0.000) and nonverbal IQ (r = 0.44, p = 0.000). Mathematical achievement at the end of Grade 1 was also significantly correlated with working memory (r = 0.50, p = 0.000) and nonverbal IQ (r = 0.48, p = 0.000). The correlation between working memory and nonverbal IQ was moderate with r = 0.45 (p = 0.000) (Cohen, 1992). All other correlations were weak.

TABLE 3

TABLE 3. Correlations between all variables.

Structural Equation Model

The model with SFON and symbolic number skills as latent variables fitted the data well, χ²(34) = 68.37, p < 0.05, CFI = 0.99, RMSEA = 0.03, SRMR = 0.03. The estimated parameters are presented in Figure 4. SFON and symbolic number skills were significant predictors of mathematical achievement at the end of Grade 1 when first language, gender, working memory and nonverbal IQ were controlled for. The effect of symbolic number skills (β = 0.32, p = 0.000) was higher than the effect of SFON (β = 0.06, p = 0.020). The correlation between SFON and symbolic number skills was weak (r = 0.11, p = 0.001). First language (β = −0.06, p = 0.130) and gender (β = 0.04, p = 0.233) did not predict SFON. But nonverbal IQ did have an effect on SFON (β = 0.12, p = 0.000). Furthermore, gender did not predict symbolic number skills. First language, working memory and nonverbal IQ were significant predictors of symbolic number skills. Children who had German as a first language had a significantly higher score for symbolic number skills. In addition, gender, working memory and nonverbal IQ predicted mathematical achievement. Boys reached higher mathematical achievement than girls at the end of Grade 1. Working memory was correlated with nonverbal IQ (r = 0.41, p = 0.000).

FIGURE 4

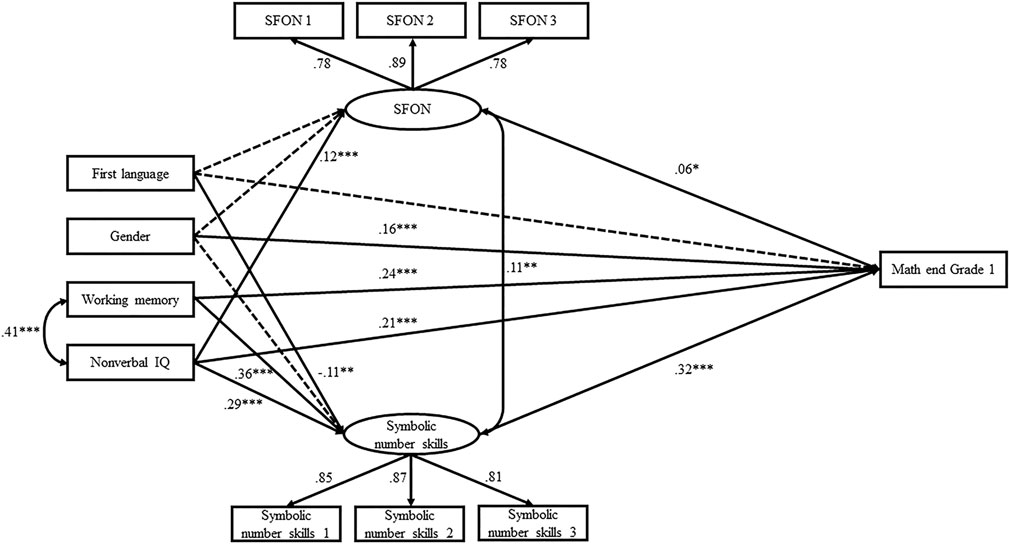
FIGURE 4. Structural equation model of the final model, containing all hypothesized paths and covariances. Solid arrows represent the hypothesized significant paths. Dashed arrows depict paths that were not significant. Standardized estimates are provided with their levels of significance. *p < 0.05, **p < 0.01, ***p < 0.001.

A comparative model was constructed to test whether the effect of SFON on mathematical achievement at the end of Grade 1 differs significantly from that of symbolic number skills. In the comparative model, the paths between SFON and mathematical achievement, and symbolic number skills and mathematical achievement, were constrained to be equal and compared with the original model. In order to assess significant model differences, the two chi-square values were compared. The difference of ∆χ² = 27.67 (∆df = 1, p = 0.000) (Urban and Mayerl, 2014) suggests that the original model leads to an improvement of the model fit. The effect of symbolic number skills on mathematical achievement is therefore higher than the effect of SFON.

To test the stability of the model with SFON and symbolic number skills as latent variables, an alternative model was run with SFON and symbolic number skills as manifest variables. A single-level model with cluster-robust standard errors was evaluated. The modified model also fitted the data well, χ²(6) = 15.35, p < 0.05, CFI = 0.99, RMSEA = 0.04, SRMR = 0.03. The effects were identical to those of the original model.

Discussion

This study investigated how a child’s SFON and symbolic number skills, measured at the beginning of Grade 1, might predict their mathematical achievement at the end of Grade 1, controlling for nonverbal IQ, working memory, gender and first language. This relationship between SFON and symbolic number skills is interesting because while SFON focuses on the spontaneous recognition of small numbers, symbolic numerical knowledge (number words, exact numeration) can be improved through education.

The study also examined the extent to which children spontaneously focus on numerosity at the beginning of Grade 1.

Previous research had demonstrated that SFON is related to early numerical skills and subsequent mathematical achievement (e.g., Hannula and Lehtinen, 2005; Hannula-Sormunen et al., 2015; Nanu et al., 2018). But symbolic number skills, including skills such as counting, object counting, linking small magnitudes and numbers, are also significant predictors of mathematical achievement (e.g., Conoyer et al., 2016; Gallit et al., 2018). Symbolic skills have been shown to be crucial for later mathematical skills (e.g., Kolkman et al., 2013; Göbel et al., 2014).

In our study, we found that the SFON scores of the sample were relatively low at the beginning of Grade 1. About a quarter of the children did not focus spontaneously on the numerical aspects of the pictures and only a few achieved the maximum SFON score.

Correlation analyses indicated a significant, but weak relationship between SFON and symbolic number skills (r = 0.18, p = 0.000). The correlation based on the structural equation model was r = 0.11 (p = 0.001). These correlations are lower than in other studies (e.g., Hannula and Lehtinen, 2005; Edens and Potter, 2013). Hannula and Lehtinen (2005) identified a significant correlation between children’s SFON and their number sequence skills (r = 0.42, p < 0.01) and object counting skills (r = 0.35, p < 0.01). Edens and Potter (2013), found that the correlation between SFON and counting skills was r = 0.71 (p < 0.01).

A couple of key reasons could account for the lower SFON scores and poor correlations found by us compared to the results reported by other SFON studies. In this study the assessment took place at the beginning of Grade 1, while in most other studies SFON was measured earlier, before school entry. Hannula and Lehtinen (2005) showed that SFON is a stable construct, so reasons other than age could account for the low SFON scores. It is likely that structured numerical instruction, which begins at age 4 in Switzerland with a compulsory kindergarten curriculum, may have influenced the result. Children begin first grade with a rather high level of symbolic skills so spontaneous focusing on small sets of items might be less important. Also, most of the studies that reported higher SFON scores used action-based tasks (e.g., Hannula and Lehtinen, 2005; Hannula et al., 2010; Nanu et al., 2018). Therefore, the outcome could have been influenced by the selection of a verbally-based picture task and its concomitant limitations. For future studies, it would be important to use both action- and verbally-based tasks and examine whether a different format of task results in different outcomes.

Results based on the structural equation model showed that both SFON and symbolic number skills significantly predicted mathematical achievement at the end of Grade 1. But the effect of number skills on mathematical achievement at the end of Grade 1 was much higher (β = 0.32, p = 0.000) than the effect of SFON (β = 0.06, p = 0.020). As in many other studies (e.g., Missall et al., 2012; Kolkman et al., 2013; Göbel et al., 2014; Toll et al., 2016; Caviola et al., 2020), the findings support the hypothesis that symbolic number skills are a very important predictor for subsequent mathematical achievement.

The finding of a small effect of SFON on mathematical achievement at the end of Grade 1 agrees with the findings of Hannula et al. (2010), but not with the findings of Hannula-Sormunen et al. (2015). This difference might be because the later study assessed fewer control variables. Other reasons that may explain the differences between the results of the Hannula-Sormunen et al. (2015) and the present study are: First, different tasks were used to measure SFON (verbally-vs. action-based). Second, in the Hannula-Sormunen et al. (2015) study only counting skills and subitizing were assessed to determine number skills, whereas in the present study, symbolic number skills were assessed using multiple tasks (e.g. counting objects and linking the result with the correct number, comparing numbers up to 20, number sequences up to 20, addition and subtraction). Third, the sample size in the Hannula-Sormunen et al. (2015) study was very small (N = 36). And finally, working memory, which might be crucial when carrying out an action-based SFON task, was not assessed.

The influence of the control variables on SFON and symbolic number skills confirms findings reported by other researchers. Nonverbal IQ and working memory affect symbolic number skills and mathematical achievement at the end of Grade 1 (e.g., De Smedt et al., 2009; Krajewski and Schneider, 2009). IQ also predicts SFON. Boys outperformed girls in mathematical achievement at the end of Grade 1, but not in SFON and symbolic number skills measured at the beginning of Grade 1. This corresponds with the findings of other studies (e.g., Niklas and Schneider, 2012; Sale et al., 2018) that the relationship between gender and mathematical performance in young children remains unclear. In addition, the picture task requires language competence therefore, first language was included as a control variable. But no effect of the children’s first language on SFON was found and it can be assumed that language competence did not affect the result. However, it would be important, to assess language competence with more differentiated measures, such as vocabulary or the knowledge of number words in future studies. The influence of first language on other numerical and mathematical constructs is harder to unpick. Number skills were predicted by first language, and bilingual children and children with German as a first language had higher symbolic number skills scores. But this was not the case for mathematical achievement at the end of Grade 1. Language requirements were low in this test, and it may be that the children with a first language other than German improved their language skills during the first year of school.

The study had some limitations. First, SFON was measured using the picture task, which is a verbally-based task. According to Batchelor et al. (2015), SFON scores are affected by the type of task used during assessments. Therefore, it is possible that an action-based task, like a selection task, could have produced different results. As Hannula and Lehtinen (2005) emphasize, it is important to use varied SFON measures to get a reliable indicator of children’s SFON. In addition, symbolic number skills were measured with a battery of sub-tests with multiple items. Therefore, to compare the effect of SFON on mathematical achievement gain, it would have been useful to also measure SFON with multiple items. Unfortunately, due to time and funding constraints, this was not possible in this study. Second, this type of SFON task requires language skills and a knowledge of number words and other vocabulary, which could influence the responses, especially those of second language learners or children with a language impairment. To deal with this problem, language competence was included in the model. The study was unable to use a more sensitive measure of language competence because of constraints. Third, the test instruction “This is the first picture” includes numerical information, which might have steered children to focus on the numerical aspects of the picture. However, the rate of numerical answers provided to the first item was very low, and it seems that the hint did not affect the children’s answers. Fourth, the third picture shows a typical numerical board game situation, which again might have caused the children to focus on numbers. This picture did have the highest number of numerical responses. There was, however, also an increase in such statements between picture 1 and picture 2. Therefore, the increase could simply be due to a habituation effect. Nevertheless, the validity of the SFON measurement could be improved. Further studies with more, revised, SFON tasks are necessary. Fifth, SFON and symbolic number skills were measured at the beginning of Grade 1, a later point than that used by most other studies. It could be that this relationship would be different at the beginning of kindergarten. Finally, on a methodological level, homogenous parceling was not possible for the symbolic number skills construct.

Given these limitations, taking into account that SFON also requires symbolic numerical skills like exact numeration, more research is needed to disentangle the complex relationship between SFON and other mathematical skills and its impact on the mathematical learning process.

Implications and Further Research

To the best of our knowledge, this is the first longitudinal study to use a large sample of more than 1,000 first graders to investigate how the relationship between SFON and a broad range of symbolic number skills influences mathematical achievement gains. The study confirms previous research findings. Both SFON and symbolic number skills predict mathematical achievement at the end of Grade 1, although symbolic number skills have a much stronger effect. These results have implications for mathematical education in kindergarten. They highlight the importance of using measures to foster symbolic number skills in general and the important role of mathematical education programs. Structured programs (e.g., Krajewski et al., 2008; Ennemoser et al., 2015) and play-based interventions (e.g., Hauser et al., 2014; Jörns et al., 2014) have been proven to be successful. There is also evidence that children’s SFON can be enhanced with guided interventions during everyday situations in day care settings too (Hannula et al., 2005; Braham et al., 2018; Hannula-Sormunen et al., 2020).

In future studies, it would also be interesting to examine if, and if so, how, the pre-school context influences how SFON and symbolic number effect mathematical achievement gain. For example, research by Kuratli Geeler (2019) has shown that children in Switzerland, which starts formal mathematical education in kindergarten, developed more symbolic numerical skills than children in kindergartens in Germany, where a child-oriented approach to early education dominates (Gasteiger et al., 2021). In addition, the present study has shown that more research into how SFON should be measured is required.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

The studies involving human participants were reviewed and approved by the University of Zurich, Faculty of Arts and Social Sciences, Ethics Committee. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.

Author Contributions

NG, DL and EMO conceptualized the research. NG and DL were responsible for the data collection. NG performed the statistical analyses, wrote the first draft, and finalized the manuscript. DL contributed substantially to the section on number skills. EMO supervised the analyses and helped to finalize the manuscript. All authors approved the submitted version.

Funding

Data collection was conducted within the project “Learning mathematics and student cooperation in grade 1 and 2”, with financial support by the swiss universities “Development of Subject-Specific Education” programme (P-9).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anders, Y., Rossbach, H.-G., Weinert, S., Ebert, S., Kuger, S., Lehrl, S., et al. (2012). Home and Preschool Learning Environments and Their Relations to the Development of Early Numeracy Skills. Early Child. Res. Q. 27 (2), 231–244. doi:10.1016/j.ecresq.2011.08.003

CrossRef Full Text | Google Scholar

Batchelor, S., Inglis, M., and Gilmore, C. (2015). Spontaneous Focusing on Numerosity and the Arithmetic Advantage. Learn. Instruction 40, 79–88. doi:10.1016/j.learninstruc.2015.09.005

CrossRef Full Text | Google Scholar

Bojorque, G., Torbeyns, J., Hannula-Sormunen, M., Van Nijlen, D., and Verschaffel, L. (2017). Development of SFON in Ecuadorian Kindergartners. Eur. J. Psychol. Educ. 32 (3), 449–462. doi:10.1007/s10212-016-0306-9

CrossRef Full Text | Google Scholar

Braham, E. J., Libertus, M. E., and McCrink, K. (2018). Children's Spontaneous Focus on Number before and after Guided Parent-Child Interactions in a Children's Museum. Dev. Psychol. 54 (8), 1492–1498. doi:10.1037/dev0000534

PubMed Abstract | CrossRef Full Text | Google Scholar

Caviola, S., Colling, L. J., Mammarella, I. C., and Szűcs, D. (2020). Predictors of Mathematics in Primary School: Magnitude Comparison, Verbal and Spatial Working Memory Measures. Dev. Sci. 23, e12957. doi:10.1111/desc.12957

PubMed Abstract | CrossRef Full Text | Google Scholar

Chan, J. Y., and Mazzocco, M. M. (2017). Competing Features Influence Children's Attention to Number. J. Exp. Child. Psychol. 156, 62–81. doi:10.1016/j.jecp.2016.11.008

CrossRef Full Text | Google Scholar

Cohen, J. (1992). A Power Primer. Psychol. Bull 112 (1), 155–159. doi:10.1037//0033-2909.112.1.155

PubMed Abstract | CrossRef Full Text | Google Scholar

Conoyer, S. J., Foegen, A., and Lembke, E. S. (2016). Early Numeracy Indicators. Remedial Spec. Educ. 37 (3), 159–171. doi:10.1177/0741932515619758

CrossRef Full Text | Google Scholar

De Smedt, B., Janssen, R., Bouwens, K., Verschaffel, L., Boets, B., and Ghesquière, P. (2009). Working Memory and Individual Differences in Mathematics Achievement: A Longitudinal Study from First Grade to Second Grade. J. Exp. Child. Psychol. 103 (2), 186–201. doi:10.1016/j.jecp.2009.01.004

CrossRef Full Text | Google Scholar

Dehaene, S. (2001). Precis of the Number Sense. Mind Lang. 16 (1), 16–36. doi:10.1111/1468-0017.00154

CrossRef Full Text | Google Scholar

Deutschschweizer Erziehungsdirektoren-Konferenz (D-EDK) (2016). Lehrplan 21. Mathematik. Kompetenzaufbau 1. Zyklus [Curriculum 21. Mathematics. Development of competence. First cycle]. Available at: https://v-fe.lehrplan.ch/lehrplan_printout.php?k=1&z=1&ekalias=0&fb_id=5 (Accessed November 12, 2020).

Google Scholar

Dornheim, D. (2008). Prädiktion von Rechenleistung und Rechenschwäche: der Beitrag von Zahlen-Vorwissen und allgemein-kognitiven Fähigkeiten [Prediction of arithmetical achievement and learning difficulties in mathematics: The contribution of numerical knowledge and cognitive ability]. Berlin: Logos-Verlag.

Dowker, A. (2005). Individual Differences in Arithmetic: Implications for Psychology, Neuroscience, and Education. New York: Psychology Press.

Edens, K. M., and Potter, E. F. (2013). An Exploratory Look at the Relationships Among Math Skills, Motivational Factors and Activity Choice. Early Child. Educ J 41 (3), 235–243. doi:10.1007/s10643-012-0540-y

CrossRef Full Text | Google Scholar

Ennemoser, M., Sinner, D., and Krajewski, K. (2015). Kurz- und langfristige Effekte einer entwicklungsorientierten Mathematikförderung bei Erstklässlern mit drohender Rechenschwäche. Lernen und Lernstörungen 4 (1), 43–59. doi:10.1024/2235-0977/a000091

CrossRef Full Text | Google Scholar

Frydman, O. (1995). The Concept of Number and the Acquisition of Number Concepts: The ‘when’, the ‘how’, and the ‘what’ of it. Cah. Psychol. Cogn. 14 (6), 653–684.

Google Scholar

Fuson, K. (1988). Children’s Counting and Number Concept. New York: Springer.

Gallit, F., Wyschkon, A., Poltz, N., Moraske, S., Kucian, K., von Aster, M., et al. (2018). Henne oder Ei: Reziprozität mathematischer Vorläufer und Vorhersage des Rechnens [Chicken or egg: Reciprocity of mathematical precursor skills and the prediction of mathematics school achievement]. Lernen und Lernstörungen 7 (2), 81–92. doi:10.1024/2235-0977/a000205

CrossRef Full Text | Google Scholar

Gasteiger, H., Brunner, E., and Chen, C.-S. (2021). Basic Conditions of Early Mathematics Education-A Comparison between Germany, Taiwan and Switzerland. Int. J. Sci. Math. Educ. 19, 111–127. doi:10.1007/s10763-019-10044-x

CrossRef Full Text | Google Scholar

Göbel, S. M., Watson, S. E., Lervåg, A., and Hulme, C. (2014). Children's Arithmetic Development: It Is Number Knowledge, Not the Approximate Number Sense, that Counts. Psychol. Sci. 25 (3), 789–798. doi:10.1177/0956797613516471

PubMed Abstract | CrossRef Full Text | Google Scholar

Gray, S. A., and Reeve, R. A. (2016). Number-Specific and General Cognitive Markers of Preschoolers' Math Ability Profiles. J. Exp. Child. Psychol. 147, 1–21. doi:10.1016/j.jecp.2016.02.004

CrossRef Full Text | Google Scholar

Hannula, M. M., Lepola, J., and Lehtinen, E. (2010). Spontaneous Focusing on Numerosity as a Domain-Specific Predictor of Arithmetical Skills. J. Exp. Child. Psychol. 107 (4), 394–406. doi:10.1016/j.jecp.2010.06.004

CrossRef Full Text | Google Scholar

Hannula, M. M., and Lehtinen, E. (2005). Spontaneous Focusing on Numerosity and Mathematical Skills of Young Children. Learn. Instruction 15 (3), 237–256. doi:10.1016/j.learninstruc.2005.04.005

CrossRef Full Text | Google Scholar

Hannula, M. M., Mattinen, A., and Lehtinen, E. (2005). ““Does Social Interaction Influence 3-Year-Old Children’s Tendency to Focus on Numerosity? A Quasi-Experimental Study in Day Care,” in Powerful Learning Environments for Promoting Deep Conceptual and Strategic Learning. Editors L. Verschaffel, E. De Corte, G. Kanselaar, and M. Valcke (Leuven: Leuven University Press), 63–80.

Google Scholar

Hannula, M. M., Räsänen, P., and Lehtinen, E. (2007). Development of Counting Skills: Role of Spontaneous Focusing on Numerosity and Subitizing-Based Enumeration. Math. Thinking Learn. 9 (1), 51–57. doi:10.1207/s15327833mtl0901_4

CrossRef Full Text | Google Scholar

Hannula, M. M. (2005). Spontaneous Focusing on Numerosity in the Development of Early Mathematical Skills. [dissertation thesis]. Finland, Turku: University of Turku. Available at: https://www.utupub.fi/handle/10024/102190 (Accessed November 12, 2020).

Google Scholar

Hannula-Sormunen, M. M., Lehtinen, E., and Räsänen, P. (2015). Preschool Children's Spontaneous Focusing on Numerosity, Subitizing, and Counting Skills as Predictors of Their Mathematical Performance Seven Years Later at School. Math. Thinking Learn. 17 (2–3), 155–177. doi:10.1080/10986065.2015.1016814

CrossRef Full Text | Google Scholar

Hannula-Sormunen, M., Nanu, C., Luomaniemi, K., Heinonen, M., Sorariutta, A., Södervik, I., et al. (2020). Promoting Spontaneous Focusing on Numerosity and Cardinality-Related Skills at Day Care with One, Two, How many and Count, How many Programs. Math. Thinking Learn. 22 (4), 312–331. doi:10.1080/10986065.2020.1818470

CrossRef Full Text | Google Scholar

Hasselhorn, M., Schumann-Hengsteler, R., Gronauer, J., Grube, D., Mähler, C., Schmid, , et al. (2012). AGTB 5-12. Arbeitsgedächtnistestbatterie für Kinder von 5 bis 12 Jahren [AGTB 5-12. Working memory test battery for children from the age of 5 to 12 years]. Göttingen: Hogrefe.

Hauser, B., Vogt, F., Stebler, R., and Rechsteiner, K. (2014). Förderung Früher Mathematischer Kompetenzen. Frühe Bildung 3 (3), 139–145. doi:10.1026/2191-9186/a000144

CrossRef Full Text | Google Scholar

Hornburg, C., and Giering, A. (1996). Konzeptualisierung und Operationalisierung komplexer Konstrukte. Ein Leitfaden für die Marketingforschung. Marketing (Münch.) 18 (1), 5–24. doi:10.15358/0344-1369-1996-1-5

CrossRef Full Text | Google Scholar

Jordan, N. C., Kaplan, D., Locuniak, M. N., and Ramineni, C. (2007). Predicting First-Grade Math Achievement from Developmental Number Sense Trajectories. Learn. Disabil Res Pract 22 (1), 36–46. doi:10.1111/j.1540-5826.2007.00229.x

CrossRef Full Text | Google Scholar

Jörns, C., Schuchardt, K., Grube, D., and Mähler, C. (2014). Spielorientierte Förderung numerischer Kompetenzen im Vorschulalter und deren Eignung zur Prävention von Rechenschwierigkeiten [Playful training of numerical skills in kindergarten for prevention of mathematical disability]. Empir. Sonderpädag. 3, 243–259. doi:10.25656/01:9933

CrossRef Full Text | Google Scholar

Kolkman, M. E., Kroesbergen, E. H., and Leseman, P. P. M. (2013). Early Numerical Development and the Role of Non-symbolic and Symbolic Skills. Learn. Instruction 25, 95–103. doi:10.1016/j.learninstruc.2012.12.001

CrossRef Full Text | Google Scholar

Krajewski, K., Nieding, G., and Schneider, W. (2008). Kurz- und langfristige Effekte mathematischer Frühförderung im Kindergarten durch das Programm „Mengen, zählen, Zahlen". Z. für Entwicklungspsychologie Pädagogische Psychol. 40, 135–146. doi:10.1026/0049-8637.40.3.135

CrossRef Full Text | Google Scholar

Krajewski, K., and Schneider, W. (2009). Early Development of Quantity to Number-Word Linkage as a Precursor of Mathematical School Achievement and Mathematical Difficulties: Findings from a Four-Year Longitudinal Study. Learn. Instruction 19 (6), 513–526. doi:10.1016/j.learninstruc.2008.10.002

CrossRef Full Text | Google Scholar

Krajewski, K. (2003). Vorhersage von Rechenschwäche in der Grundschule [Disabilities in mathematics in primary school]. Hamburg: Verlag Dr. Kovač.

Kucian, K., Kohn, J., Hannula-Sormunen, M. M., Richtmann, V., Grond, U., Käser, T., et al. (2012). Kinder mit Dyskalkulie fokussieren spontan weniger auf Anzahligkeit [Children with developmental dyscalculia spontaneously focus less on numerosity]. Lern. Lernstör. 1 (4), 241–253. doi:10.1024/2235-0977/a000024

CrossRef Full Text | Google Scholar

Kuratli Geeler, S. (2019). Mathematische Kompetenzen von Kindergartenkindern: Überprüfung eines Testinstrumentes und Analyse von Unterschieden in der numerischen Leistungsentwicklung [Mathematical skills of kindergarteners: Examining a test and analyzing the differences in numerical achievement gain of kindergarten children]. [dissertation thesis]. Zurich, Switzerland: University of Zurich. doi:10.5167/uzh-171088

CrossRef Full Text | Google Scholar

Marsh, H. W., Lüdtke, O., Nagengast, B., Morin, A. J., and Von Davier, M. (2013). Why Item Parcels Are (Almost) Never Appropriate: Two Wrongs Do Not Make a Right-Ccamouflaging Misspecification with Item Parcels in CFA Models. Psychol. Methods 18 (3), 257–284. doi:10.1037/a0032773

PubMed Abstract | CrossRef Full Text | Google Scholar

Matsunaga, M. (2008). Item Parceling in Structural Equation Modeling: A Primer. Commun. Methods Measures 2 (4), 260–293. doi:10.1080/19312450802458935

CrossRef Full Text | Google Scholar

McMullen, J., Hannula-Sormunen, M. M., and Lehtinen, E. (2015). Preschool Spontaneous Focusing on Numerosity Predicts Rational Number Conceptual Knowledge 6 Years Later. ZDM Maths. Educ. 47 (5), 813–824. doi:10.1007/s11858-015-0669-4

CrossRef Full Text | Google Scholar

Missall, K. N., Mercer, S. H., Martínez, R. S., and Casebeer, D. (2012). Concurrent and Longitudinal Patterns and Trends in Performance on Early Numeracy Curriculum-Based Measures in Kindergarten through Third Grade. Assess. Eff. Intervention 37 (2), 95–106. doi:10.1177/1534508411430322

CrossRef Full Text | Google Scholar

Nanu, C. E., McMullen, J., Munck, P., Group, P. S., and Hannula-Sormunen, M. M. (2018). Spontaneous Focusing on Numerosity in Preschool as a Predictor of Mathematical Skills and Knowledge in the Fifth Grade. J. Exp. Child. Psychol. 169, 42–58. doi:10.1016/j.jecp.2017.12.011

CrossRef Full Text | Google Scholar

Nanu, C., Laakkonen, E., and Hannula-Sormunen, M. (2020). The Effect of First School Years on Mathematical Skill Profiles. FLR 8 (1), 56–75. doi:10.14786/flr.v8i1.485

CrossRef Full Text | Google Scholar

Niklas, F., and Schneider, W. (2012). Die Anfänge geschlechtsspezifischer Leistungsunterschiede in mathematischen und schriftsprachlichen Kompetenzen [The beginning of gender-based performance differences in mathematics and linguistic competencies]. Z. Entwicklungspsychol. Pädagog. Psychol. 44 (3), 123–138. doi:10.1026/0049-8637/a000064

CrossRef Full Text | Google Scholar

Rathé, S., Torbeyns, J., De Smedt, B., and Verschaffel, L. (2019). Spontaneous Focusing on Arabic Number Symbols and its Association with Early Mathematical Competencies. Early Child. Res. Q. 48 (3), 111–121. doi:10.1016/j.ecresq.2019.01.011

CrossRef Full Text | Google Scholar

Rathé, S., Torbeyns, J., Hannula-Sormunen, M. M., and Verschaffel, L. (2016). Kindergartners’ Spontaneous Focusing on Numerosity in Relation to Their Number-Related Utterances during Numerical Picture Book reading. Math. Think. Learn. 18 (2), 125–141. doi:10.1080/10986065.2016.1148531

CrossRef Full Text | Google Scholar

Rosseel, Y. (2012). Lavaan: An R Package for Structural Equation Modeling. J. Stat. Softw. 48 (2), 1–36. doi:10.18637/jss.v048.i02

CrossRef Full Text | Google Scholar

Sale, A., Schell, A., Koglin, U., and Hillenbrand, C. (2018). Einflussfaktoren mathematischer Kompetenzen vor Schuleintritt [Factors influencing mathematical competences before school entry]. Empir. Sonderpädag. 4, 370–387. doi:10.25656/01:16781

CrossRef Full Text | Google Scholar

Simon, T. J., and Vaishnavi, S. (1996). Subitizing and Counting Depend on Different Attentional Mechanisms: Evidence from Visual Enumeration in Afterimages. Percept. Psychophys. 58 (6), 915–926. doi:10.3758/BF03205493

PubMed Abstract | CrossRef Full Text | Google Scholar

Szkudlarek, E., and Brannon, E. M. (2017). Does the Approximate Number System Serve as a Foundation for Symbolic Mathematics? Lang. Learn. Dev. 13 (2), 171–190. doi:10.1080/15475441.2016.1263573

PubMed Abstract | CrossRef Full Text | Google Scholar

Toll, S. W. M., Kroesbergen, E. H., and van Luit, J. E. H. (2016). Visual Working Memory and Number Sense: Testing the Double Deficit Hypothesis in Mathematics. Br. J. Educ. Psychol. 86 (3), 429–445. doi:10.1111/bjep.12116

CrossRef Full Text | Google Scholar

Urban, D., and Mayerl, J. (2014). Strukturgleichungsmodellierung. Ein Ratgeber für die Praxis [Structural equation modeling. A practical guide]. Wiesbaden: Springer.

Weiber, R., and Mühlhaus, D. (2014). Strukturgleichungsmodellierung. Eine anwendungsorientierte Einführung in die Kausalanalyse mit Hilfe von AMOS, SmartPLS und SPSS [Structural equation modeling. An application-oriented introduction to causal analyses using AMOS, SmartPLS and SPSS]. Berlin: Springer Gabler.

Weiß, R. H., and Osterland, J. (2013). CFT 1-R: Grundintelligenztest Skala 1 [CFT 1-R: Culture Fair Intelligence Tests - Scale 1]. Göttingen: Hogrefe.

Wilson, M. (2005). Constructing Measures. An Item Response Modeling Approach. Mahwah, N.J.: Lawrence Erlbaum Associates.

Wynn, K. (1995). Origins of Numerical Knowledge. Math. Cognit. 1, 35–60.

Google Scholar