- 1Department of Mathematics and Computer Science, University of Education of Ludwigsburg, Ludwigsburg, Germany
- 2Hamburg Center for University Teaching and Learning, University of Hamburg, Hamburg, Germany
The problem-solving performance of primary school students depend on their attitudes and beliefs. As it is not easy to change attitudes, we aimed to change the relationship between problem-solving performance and attitudes with a training program. The training was based on the assumption that self-generated external representations support the problem-solving process. Furthermore, we assumed that students who are encouraged to generate representations will be successful, especially when they analyze and reflect on their products. A paper-pencil test of attitudes and beliefs was used to measure the constructs of willingness, perseverance, and self-confidence. We predicted that participation in the training program would attenuate the relationship between attitudes and problem-solving performance and that non-participation would not affect the relationship. The results indicate that students’ attitudes had a positive effect on their problem-solving performance only for students who did not participate in the training.
Introduction
Mathematical problem solving is considered to be one of the most difficult tasks primary students have to deal with (Verschaffel et al., 1999) since it requires them to apply multiple skills (De Corte et al., 2000). It is decisive in this respect that “difficulty should be an intellectual impasse rather than a computational one” (Schoenfeld, 1985, p. 74). When solving problems, it is not enough to retrieve procedural knowledge and reproduce a known solution approach. Rather, problem-solving tasks require students to come up with new ways of thinking (Bransford and Stein, 1993). Problem-solvers must activate their existing knowledge network and adapt it to the respective problem situation (van Dijk and Kintsch, 1983). They have to succeed in generating an adequate representation of the problem situation (e.g., Mayer and Hegarty, 1996). This requires conceptual knowledge, which novice problem-solvers have to acquire (Bransford et al., 2000). As problem solving is the foundation for learning mathematics, an important goal of primary school mathematics teaching is to strengthen students’ problem-solving performance. One central problem is that problem-solving performance is highly influenced by students’ attitudes towards problem solving (Reiss et al., 2002; Schoenfeld, 1985; Verschaffel et al., 2000).
Attitudes and beliefs are considered quite stable once they are developed (Hannula, 2002; Goldin, 2003). However, students who are novices in a particular content area are still in the process of development, as are their attitudes and beliefs. It can therefore be assumed that their attitudes change over time (Hannula, 2002). However, such a change does not take place quickly (Higgins, 1997; Mason and Scrivani, 2004). Nevertheless, in a shorter period of time, it might be possible to reduce the influence of attitudes on problem-solving performance (Hannula et al., 2019). In this paper, we present a training program for primary school students, which aims to do exactly that.
Problem-Solving Performance
Successful problem solving can be observed on two levels: problem-solving success and problem-solving skills. Many studies measure the problem-solving performance of students on the basis of correctly or incorrectly solved problem-solving tasks, that is, the product (e.g., Boonen et al., 2013; de Corte et al., 1992; Hegarty et al., 1992; Verschaffel et al., 1999). In this case, only problem-solving success, that is, specifically whether the numerically obtained result is correct or incorrect, is evaluated. This is a strict assessment measure, since the problem-solving process is not taken into account. As a result, the problem-solving performance is only considered from a single, product-oriented perspective. For instance students’ performance is assessed as unsuccessful when they apply an essentially correct procedure or strategy but achieve the wrong result, or it is considered successful when students achieve the right result even though they have misunderstood the problem (Lester and Kroll, 1990). An advantage of this operationalization, however, is that student performance tends to be underestimated rather than overestimated.
A more differentiated view of successful problem solving includes the solver’s problem-solving process (Lester and Kroll, 1990; cf. Adibnia and Putt, 1998). In this way, sub-skills such as understanding the problem, adequately representing the situation, applying strategies, or achieving partial solutions are taken into account. These are then incorporated into the evaluation of performance and, thus, of problem-solving skills (Charles et al., 1987; cf. Sturm, 2019). The advantage of this operationalization option is that it also takes into account smaller advances by the solver, although they may not yet lead to the correct result. It is therefore less likely to underestimate students’ performance. In order to assess and evaluate the problem-solving skills of students in the best way and, thus, avoid over- and under-estimating their skills, direct observation and questioning should be implemented (e.g., Lester and Kroll, 1990). An analysis of written work should not be the only means of assessment (Lester and Kroll, 1990).
Attitudes and Beliefs
Attitudes are dispositions to like or dislike objects, persons, institutions, or events (Ajzen, 2005). They influence behavior (Ajzen, 1991). Therefore, it is not surprising that attitudes–which are sometimes also synonymously referred to as beliefs–are a central construct in psychology (Ajzen, 2005).
Individual attitudes to word problems influence, albeit rather unconsciously, approaches to such problems and willingness to learn mathematics and solve problems (Grigutsch et al., 1998; Awofala, 2014). Research on attitudes of primary students to word problems is scarce. Most research focuses on students with well-established attitudes. However, the importance of the attitudes of younger children is undisputed (Di Martino, 2019). Di Martino (2019) conducted a study on kindergarten children as well as on first-, third-, and fifth-graders and found that, with increasing age, students’ perceived competence in problem solving decreases, and negative emotions towards mathematical problems increase. Whether a solver can overcome problem barriers when dealing with word problems depends not only on his or her previous knowledge, abilities, and skills, but also on his or her attitudes and beliefs (Schoenfeld, 1985; Verschaffel et al., 2000; Reiss et al., 2002). It has been shown many times that attitudes towards problem solving are influencing factors on performance and learning success which should not be underestimated (Charles et al., 1987; Lester et al., 1989; Lester & Kroll, 1990; De Corte et al., 2002; Goldin et al., 2009; Awofala, 2014). Learners associate a specific feeling with an object, in this case with a word problem, triggering a specific emotional state (Grigutsch et al., 1998). The feelings and states generated are subjective and can therefore vary between individuals (Goldin et al., 2009).
Attitudes towards problem solving can be divided into willingness, perseverance, and self-confidence (Charles et al., 1987; Lester et al., 1989). This distinction comes from the Mathematical Problem-Solving Project, in which Webb, Moses, and Kerr (1977) found that willingness to solve problems, perseverance in attempting to find a solution, and self-confidence in the ability to solve problems are the most important influences on problem-solving performance. When students are willing to work on a variety of mathematics tasks and persevere with tasks until they find a solution, they are more task oriented and easier to motivate (Reyes, 1984). Perseverance is defined as the willing pursuit of a goal-oriented behavior even if this involves overcoming obstacles, difficulties, and disappointments (Peterson and Seligman, 2004). Confidence is an individual’s belief in his or her ability to succeed in solving even challenging problems as well as an individual’s belief in his or her own competence with respect to his or her peers (Lester et al., 1989). Students’ lack of confidence in themselves as problem-solvers or their beliefs about mathematics can considerably undermine their ability to solve or even approach problems in a productive way (Shaughnessy, 1985). The division of attitudes into these three sub-categories can also be found in current studies (Zakaria and Yusoff, 2009; Zakaria and Ngah, 2011).
Reducing the Influence of Attitudes and Beliefs
As it seems impossible to change attitudes within a short time frame, we developed a training program to reduce the influence of attitudes on problem solving, on the one hand, and to foster the problem-solving performance of primary-school students, on the other hand.
The training program was an integral part of regular math classes and focused on teaching students to generate and use external representations (Sturm, 2019; Sturm et al., 2016; Sturm and Rasch, 2015; see also Supplementary Appendix A). Such a program that concentrates on the strengths and weaknesses of novices and on their individually generated external representations can be a benefit for primary-school students in two ways. The class discusses how the structure described in the problem can be adequately represented so that the solution can be found, working out multiple approaches based on different student representations. The students are thus exposed to ideas about how a problem can be solved in different ways. Such a training program fulfils, albeit rather implicitly, another essential component. By respectfully considering their individual thoughts and difficulties, the students are made aware of their strengths and their creativity and of the fact that there is not a single correct approach or solution that everyone has to find (Lester and Cai, 2016; Di Martino, 2019). This can counteract fears of failure and lack of self-confidence, and generate positive attitudes (Lester and Cai, 2016; Di Martino, 2019). The teacher pays attention to the solution process rather than to the numerical result in order to reduce the influence of attitudes on performance (Di Martino, 2019). In the same way, experiencing success and perceiving increasing flexibility and agility can reduce the influence of attitudes. As a result, we expected attitudes and beliefs to have a smaller effect on problem-solving performance.
Hypothesis
Based on previous research, our goal was to reduce the influence of attitudes on the problem-solving performance of students (see Figure 1). To this end, the hypothesis was derived that participation in the training program would minimize the effect of attitudes and beliefs on problem-solving success, so that students would succeed at the end of the training despite initial negative attitudes and beliefs.
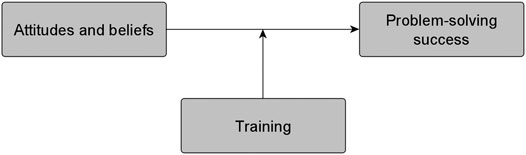
FIGURE 1. The moderation model with the single moderator variable training influencing the effect of attitudes and beliefs on problem-solving success.
Methods
Participants
In total 335 students from 20 Grade 3 classes from eight different primary schools in the German state of Rhineland-Palatinate took part in the intervention study (172 boys and 163 girls). Nineteen students dropped out because of illness during the intervention. The age of the participants ranged between seven and ten years (M = 8.10, SD = 0.47).
Procedure
This investigation was part of a large interdisciplinary project1. A central focus of the project was to investigate whether representation training has a demonstrable effect on the performance of third-graders (cf. Sturm, 2019). For this reason, we implemented a pretest-posttest control group design. The intervention took place between Measurement Points 1 and 2. We measured the problem-solving performance of the students with a word-problem-solving test (WPST) at Measurement Points 1 and 2. All other variables were measured at Measurement Point 1 only (factors to establish comparable experimental conditions: intelligence, text comprehension, and mathematical abilities; co-variates for the mediation model: metacognitive skills, mathematical abilities).
In the intervention, third-grade students worked on challenging word problems for one regular mathematics lesson a week. The intervention was based on six task types with different structures (Sturm and Rasch, 2015): 1) comparison tasks, 2) motion tasks, 3) tasks involving comparisons and balancing items or money, 4) tasks involving combinatorics, 5) tasks in which structure reflects the proportion of spaces and limitations, and 6) tasks with complex information. Two word problems were included for each task type and were presented to all classes in the same random sequence. Each task had to be completed in a maximum of one lesson.
The training was implemented for half of the classes and was conducted by the first author; the other half worked on the tasks with their regular mathematics teacher. They were not informed on the purpose of the intervention and not given any instructions on how to process the tasks. In the lessons for students doing the training, the students were explicitly cognitively stimulated to generate external representations and to use them to develop solutions. They were repeatedly encouraged to persevere and not to give up. The diverse external representations generated by the students were analyzed, discussed, and compared by the class during the training. They jointly identified the characteristics of representations that enabled them to specifically solve the tasks and identified different approaches (for more details about the study, see Sturm and Rasch, 2015). With the goal of reducing the influence of attitudes on performance, the class worked directly on the students’ own representations instead of on prefabricated representations. The aim was that students realized that it was worthwhile investing effort into creating representations and that they were able to solve problem tasks independently.
Thus, the study was composed of two experimental conditions: training program (n = 176; 47% boys) (hereinafter abbreviated to T+) and no training program (n = 159; 58% boys) (hereinafter abbreviated to T-). In order to control potential interindividual differences, the 20 classes were assigned to the experimental conditions by applying parallelization at class level (Breaugh and Arnold, 2007; Myers and Hansen, 2012). The classes were grouped into homogeneous blocks using the R package blockTools Version 0.6-3 and then randomly assigned to the experimental conditions (Greevy et al., 2004; Moore, 2012; see also Supplementary Appendix B for more information).
Measures
Word-Problem-Solving Test
Before the intervention and immediately after it, the students worked on a WPST, which we created. It consisted in each case of three challenging word problems with an open answer format. Each of the three tasks represented a different type of problem. The word problems from the WPST at Measurement Point 1 and the word problems from the WPST at Measurement Point 2 had the same structure. We implemented two parallel versions; only the context was changed by exchanging single words (see Supplementary Appendix C). An example of an item from the test is a task with complex information (Sturm, 2018): Classes 3a and 3b go to the computer room. Some students have to work at a computer in pairs. In total there are 25 computers, but 40 students. How many students work alone at a computer? How many students work at a computer in pairs? Direct observation and questioning could not be conducted due to the large number of participants in the project; only the students’ written work was available for analysis. The problem-solving process of the students could therefore only be assessed indirectly. For this reason, the performance of students in the two tests was evaluated based on problem-solving success, ruling out overestimation of performance.
Problem-Solving Success
The success of the solution was measured dichotomously in two forms: 1) correct solution and (0) incorrect solution. Only the correctness of the result achieved was evaluated. This dependent variable acted as a strict criterion that could be quantified with high observer agreement (κ = 0.97; κmin = 0.93, κmax = 1.00). A confirmatory factor analysis using the R package lavaan version 0.6-7 confirmed that the WPST measured the one-dimensional construct problem-solving success. The one-dimensional model exhibited a good model fit (Nussbeck et al., 2006; Hair et al., 2009): χ2 (27) = 36.613, p = 0.103; χ2/df = 1.356, CFI = 0.985, TLI = 0.981, SRMR = 0.032, RMSEA = 0.033 (p = 0.854). The reliability coefficients at Measurement Point 1 were classified as low (Cronbach’s α = 0.39) because the test consisted of only three items (Eid et al., 2011) and a homogeneous sample was required at this measurement point (Lienert and Raatz, 1998). The Cronbach’s alpha for the second measurement point (α = 0.60) was considered to be sufficient (Hair et al., 2009). The test score represented the mean value of all three task scores.
Attitudes and Beliefs About Problem Solving
The attitudes and beliefs of the learners were recorded with the Attitudes Inventory Items (Webb et al., 1977; Charles et al., 1987). The original questionnaire comprises 20 items, which are measured dichotomously (“I agree” and “I disagree”). The Attitudes Inventory measures the three categories of attitudes and beliefs related to problem solving: a) willingness (six items), b) perseverance (six items), and c) self-confidence (eight items). An example of an item for willingness is: “I will try to solve almost any problem.” An example of an item for perseverance is: “When I do not get the right answer right away, I give up.” An example of an item for self-confidence is: “I am sure I can solve most problems.”
Because the reported reliabilities were only satisfactory to some extent (α = 0.79, mean = 0.64) (Webb et al., 1977), the Attitudes Inventory was initially tested on a smaller sample (n = 74; M = 8.6 years old; 59% girls). A satisfactory Cronbach’s α = 0.86 was achieved (mean α = 0.73). The number of items was reduced to 13 (four items for willingness, four items for perseverance, five items for self-confidence), which had only a minor influence on reliability (α = 0.83). For economic reasons, the shortened questionnaire was used in the study. The three-factor structure of the questionnaire was confirmed with a confirmatory factor analysis using the R package lavaan version 0.6–7. As the fit indices show, the three-factor model had a good model fit: χ2 (62) = 134.856, p < 0.001; χ2/df = 2.175, CFI = 0.948, TLI = 0.935, RMSEA = 0.062 (p = 0.086) (Hair et al., 2009; Brown, 2015). The three-factor model had a better fit than the single-factor model (p = 0.0014): χ2 (65) = 152.121, p < 0.001; χ2/df = 2.340, CFI = 0.938, TLI = 0.926, SRMR = 0.061, RMSEA = 0.066 (p = 0.028). The students were grouped into three groups (M–1 SD; M; M +1SD). The responses were coded in such a way that high scores (M +1SD) indicated positive attitudes and beliefs, and low scores (M–1 SD) indicated negative attitudes and beliefs.
Additional Influencing Factors
In order to ensure the internal validity of the investigation, we collected student-related factors that influence the solution of word problems from a theoretical and empirical point of view. It has been shown that the mathematical abilities and metacognitive skills of students significantly influence their performance (Sturm et al., 2015).
Mathematical Abilities
The basic mathematical abilities were determined using a standardized German-language test as a group test (Heidelberger Rechentest HRT 1–4, Haffner et al., 2005). The test consists of eleven subtests, from which three scale values were determined: calculation operations, numerical-logical and spatial-visual skills as well as the overall performance for all eleven subtests. The reliability was only satisfactory (Cronbach’s α = 0.74). Total performance was included in the study.
Metacognitive Skills
The metacognitive skills of the students were measured using a paper-pencil version of EPA2000, a test to measure metacognitive skills before and/or after the solving of tasks (Clercq et al., 2000). The prediction skills and evaluation skills of the students were collected for all three word problems of the WPST using a 4-point rating scale: 1) “absolutely sure, it’s wrong,” 2) “sure, it’s wrong,” 3) “sure, it’s right,” and 4) “absolutely sure, it’s right” (Clercq et al., 2000). If the students’ assessments of “absolutely sure” matched their solution, they were awarded 2 points. If they agreed with “sure,” they received 1 point. No match was scored with 0 points (Desoete et al., 2003). The reliabilities were only satisfactory (Cronbach’s αtotal=0.74, αprediction=0.56, αevaluation = 0.73). A confirmatory factor analysis revealed that prediction skills and evaluation skills represent a single factor (χ2 (9) = 16.652, p < 0.001; χ2/df = 1.850, CFI = 0.952, TLI = 0.919, RMSEA = 0.053 (p = 0.396)). The aggregated factor was used as a control variable in the moderator analysis.
In addition to the variables considered in this paper, text comprehension and intelligence were also surveyed in the project. However, they are not the focus of this paper; additional information can be found in Sturm et al. (2015).
Results
Descriptive Statistics and Correlations Between the Measures
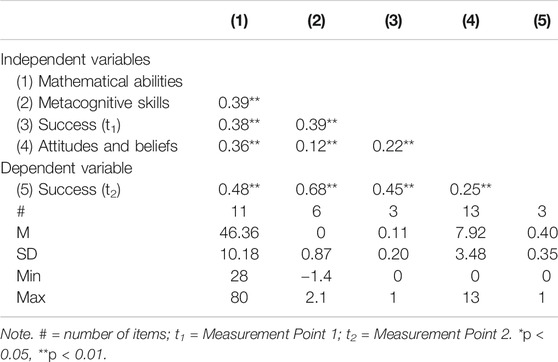
The descriptive statistics and correlations of all scales are presented in Table 1 (see Supplementary Appendix D for a separate overview for each of the experimental conditions). The signs for all correlations were as expected. The variable training program is not listed because it is the dichotomous moderator variable (T+ and T−).
Moderated Regression Analyses
The hypothesis was tested with a moderated regression analysis using product terms from mean-centered predictor variables (Hayes, 2018). This model imposed the constraint that any effect of attitudes and beliefs was independent of all other variables in the model. This was achieved by controlling for mathematical abilities, metacognitive skills, and problem-solving performance at Measurement Point 1. The estimated main effects and interaction terms are presented in Table 2.
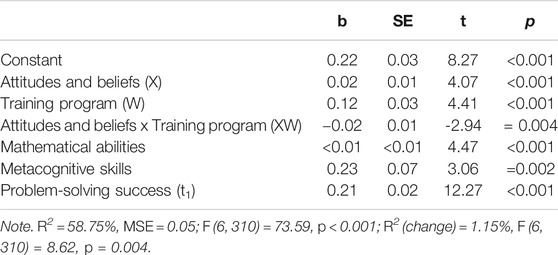
TABLE 2. Results from the regression analysis examining the moderation of the effect of attitudes and beliefs on problem-solving success (t2) by participation in the training program, controlling for mathematical abilities, metacognitive skills, and problem-solving success from the pretest.
When testing the hypothesis, we found a significant main effect of attitudes and beliefs, a significant main effect of the training program, and a significant moderator effect of the training on attitudes and beliefs as a predictor of problem-solving success. The main effect of the training program indicated that students who participated in the training performed better in the second WPST. The main effect of attitudes and beliefs showed that students with more positive attitudes and beliefs were more successful than students with negative attitudes and beliefs.
To further explore the interaction between attitudes and beliefs and the training program, we analyzed simple slopes at values of 1 SD above and 1SD below the means of attitudes and beliefs (Hayes, 2018). As can be seen from the conditional expectations in Figure 2, attitudes and beliefs did not affect the problem-solving success of students who participated in the training program. Attitudes and beliefs only had a positive effect on the problem-solving success of students who did not participate in the training.
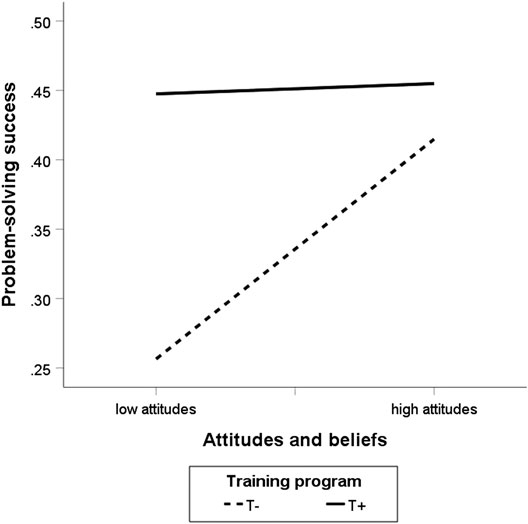
FIGURE 2. Moderator effect of the training program on problem-solving success at Measurement Point 2.
Discussion
Our results confirm previous findings that the attitudes and beliefs of students correlate with their problem-solving performance. They indicate that this correlation can be moderated by student participation in a training program. Negative attitudes and beliefs did not affect the performance of students who participated in a problem-solving training program over several weeks. Whether the training program also causes a change in the attitudes and beliefs of the students over time has to be investigated in a follow-up study, which is planned with a longer intervention period with at least two measurements of attitudes and beliefs. A longer intervention period would have the advantage that attitudes develop depending on the individual experiences of a person (Hannula, 2002; Lim and Chapman, 2015), for instance, when new experience is gathered or new knowledge is acquired (e.g., Ajzen, 2005).
Some limitations need to be considered when interpreting the results of the study. For example, the mitigating processes need to be investigated further. It is also unclear as to which components of the training are ultimately responsible for counteracting the effect of attitudes and beliefs. Although the study did not provide results in this regard, we assume that the following factors might have an effect: generating external representations, reflecting on the representations together as a group, and fostering an appreciative and constructive approach to mistakes. Further studies are needed to show whether and to what extent these factors actually attenuate the effect of attitudes and beliefs.
Furthermore, the measurement instruments for the control variables mathematical abilities and metacognitive skills were rather limited. If researchers are interested in understanding further effects of metacognitive skills, more aspects should be included. Furthermore, according to Lester et al. (1987), investigating attitudes and beliefs using a questionnaire is associated with disadvantages. How accurately students answer the questions depends on how objectively and accurately they can reflect on and assess their own attitudes. Misinterpretations and errors cannot be ruled out. The most serious disadvantage, however, is that data collection using an inventory can easily be assumed to have unjustified validity and reliability. For a deeper insight into the attitudes and beliefs of primary school students, qualitative interviews have to be implemented.
However, for the purpose of this study, it seems sufficient to consider the two control variables mathematical abilities and metacognitive abilities. We were able to ensure that the correlation between attitudes and beliefs and the mathematical performance of students was not influenced by these factors.
Regardless of the limitations, our study has some practical implications. Participation in the training program, independently of the mathematical abilities and text comprehension of students, reduced the influence of attitudes and beliefs on their performance. Thus, for teaching practice, it can be concluded that it is important not only to implement regular problem-solving activities in mathematics lessons, but also to encourage students to externalize and find their own solutions. The aim is to establish a teaching culture that promotes a variety of approaches and procedures, allows mistakes to be made, and makes mistakes a subject for learning. Reflecting on different possible solutions and also on mistakes helps students to progress. Thus, students develop a repertoire of external representations from which they can profit in the long term when solving problems.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Ethics Statement
The studies involving human participants were reviewed and approved by the Ethics Committee of the Department of Psychology, University of Koblenz and Landau, Germany. Written informed consent to participate in this study was provided by the participants' legal guardian. This study was also carried out in accordance with the guidelines for scientific studies in schools in the German state Rhineland-Palatinate (Wissenschaftliche Untersuchungen an Schulen in Rheinland-Pfalz), Aufsichts- und Dienstleistungsdirektion Trier. The protocol was approved by the Aufsichts- und Dienstleistungsdirektion Trier.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
The project was funded by grants from the Deutsche Forschungsgemeinschaft (DFG, grant number GK1561/1).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2021.525923/full#supplementary-material
Footnotes
1This project was part of the first author’s PhD thesis
References
Adibnia, A., and Putt, I. J. (1998). Teaching problem solving to year 6 students: A new approach. Math. Educ. Res. J. 10 (3), 42–58. doi:10.1007/BF03217057
Ajzen, I. (2005). Attitudes, personality and behavior. Maidenhead, United Kingdom: Open University Press.
Ajzen, I. (1998). The theory of planned behavior. Organizational Behavior and Human Decision Proc. 50 (2), 179–211. doi:10.1016/0749-5978(91)90020-T
Amarel, S. (1966). On the mechanization of creative processes. IEEE Spectr. 3 (4), 112–114. doi:10.1109/MSPEC.1966.5216589
Awofala, A. O. A. (2014). Examining personalisation of instruction, attitudes toward and achievement in mathematics word problems among nigerian senior secondary school students. Ijemst 2 (4), 273–288. doi:10.18404/ijemst.91464
Boonen, A. J. H., van der Schoot, M., van Wesel, F., de Vries, M. H., and Jolles, J. (2013). What underlies successful word problem solving? A path analysis in sixth grade students. Contemporary Educ. psychol. 38 (3), 271–279. doi:10.1016/j.cedpsych.2013.05.001
Bransford, J. D., Brown, A. L., and Cocking, R. R. (2000). How people learn: brain, mind, experience, and school. Washington, DC: National Academy Press.
Bransford, J. D., and Stein, B. S. (1993). The ideal problem solver: a guide for improving thinking, learning, and creativity. 2nd Edn. New York, NY: W. H. Freeman.
Breaugh, J. A., and Arnold, J. (2007). Controlling nuisance variables by using a matched-groups design. Organ. Res. Methods 10 (3), 523–541. doi:10.1177/1094428106292895
Brown, T. A. (2015). Confirmatory factor analysis for applied research. 2nd Edn. New York, NY: Guilford Press.
Charles, R. I., Lester, F. K., and O’Daffer, P. G. (1987). How to evaluate progress in problem solving. Reston, VA: National Council of Teachers of Mathematics.
Clercq, A. D., Desoete, A., and Roeyers, H. (2000). Epa2000: a multilingual, programmable computer assessment of off-line metacognition in children with mathematical-learning disabilities. Behav. Res. Methods Instrum. Comput. 32 (2), 304–311. doi:10.3758/BF03207799
Cox, R., and Brna, P. (1995). Supporting the use of external representation in problem solving: the need for flexible learning environments. J. Artif. Intell. Educ. 6 (2–3), 239–302. .
Cox, R. (1999). Representation construction, externalised cognition and individual differences. Learn. InStruct. 9 (4), 343–363. doi:10.1016/S0959-4752(98)00051-6
De Corte, E., Op t Eynde, P., and Verschaffel, L. (2002). ““Knowing what to believe”: the relevance of students’ mathematical beliefs for mathematics education,” in Personal epistemology: the psychology of beliefs about knowledge and knowing. Editors B. K. Hofer, and P. R. Pintrich (New Jersey, United States: Lawrence Erlbaum Associates Publishers), 297–320. doi:10.4324/9780203424964
De Corte, E., Verschaffel, L., and Op’t Eynde, P. (2000). “Self-regulation: a characteristic and a goal of mathematics education,” in Handbook of self-regulation. Editors P. R. Pintrich, M. Boekaerts, and M. Zeidner (Cambridge, MA: Academic Press), 687–726.
de Corte, E., Verschaffel, L., and Pauwels, A. (1992). Solving compare problems: An eye movement test of Lewis and Mayer’s consistency hypothesis. J. Educ. Psychol. 84 (1), 85–94. doi:10.1037/0022-0663.84.1.85
Desoete, A., Roeyers, H., and De Clercq, A. (2003). Can offline metacognition enhance mathematical problem solving?. J. Educ. Psychol. 95 (1), 188–200. doi:10.1037/0022-0663.95.1.188
Di Martino, P. (2019). Pupils’ view of problems: the evolution from kindergarten to the end of primary school. Educ. Stud. Math. 100 (3), 291–307. doi:10.1007/s10649-018-9850-3
Duval, R. (1999). “Representation, vision, and visualization: cognitive functions in mathematical thinking. Basic issues for learning (ED466379),” in Proceedings of the twenty-first annual meeting of the north American chapter of the international group for the psychology of mathematics education XXI, Cuernavaca, Mexico, October 23–26, 1999. Editors F. Hitt, and M. Santos (ERIC), 1, 3–26.
Eid, M., Gollwitzer, M., and Schmitt, M. (2011). Statistik und Forschungsmethoden: lehrbuch. [Statistics and research methods]. 2nd Edn. Weinheim, Germany: Beltz.
Goldin, G. A. (2003). “Affect, meta-affect, and mathematical belief structures,” in Beliefs: a hidden variable in mathematics education?. Editors G. C. Leder, E. Pehkonen, and G. Törner (Amsterdam, Netherlands: Kluwer Academic Publishers), 31, 59–72. doi:10.1007/0-306-47958-3_4
Goldin, G. A., Rösken, B., and Törner, G. (2009). “Beliefs—No longer a hidden variable in mathematical teaching and learning processes,” in Beliefs and attitudes in mathematics education. Editors J. Maasz, and W. Schloeglmann (Rotterdam, Netherlands; Sense Publishers), 1–18.
Greevy, R., Lu, B., Silber, J. H., and Rosenbaum, P. (2004). Optimal multivariate matching before randomization. Biostatistics 5 (2), 263–275. doi:10.1093/biostatistics/5.2.263
Grigutsch, S., Raatz, U., and Törner, G. (1998). Einstellungen gegenüber Mathematik bei Mathematiklehrern. Jmd 19 (1), 3–45. doi:10.1007/BF03338859
Haffner, J., Baro, K., Parzer, P., and Resch, F. (2005). Heidelberger Rechentest (HRT 1-4): erfassung mathematischer Basiskompetenzen im Grundschulalter [Heidelberger Rechentest (HRT 1-4): assessment of basic mathematical skills at primary school age]. Göttingen, Germany: Hogrefe.
Hair, J. F., Black, W. C., Babin, B. J., and Anderson, R. E. (2009). Multivariate data analysis. 7th Edn. London, United Kingdom: Pearson.
Hannula, M. S. (2002). Attitude towards mathematics: emotions, expectations and values. Educ. Stud. Math. 49 (1), 25–46. doi:10.1023/A:1016048823497
Hayes, A. F. (2018). Introduction to mediation, moderation, and conditional process analysis: a regression-based approach. 2nd Edn. New York, NY: Guilford Press.
Hegarty, M., Mayer, R. E., and Green, C. E. (1992). Comprehension of arithmetic word problems: Evidence from students' eye fixations. J. Educ. Psychol. 84 (1), 76–84. doi:10.1037/0022-0663.84.1.76
Higgins, K. M. (1997). The effect of year-long instruction in mathematical problem solving on middle-school students’ attitudes, beliefs, and abilities. J. Exp. Educ. 66 (1), 5–28. doi:10.1080/00220979709601392
Kirsh, D. (2010). Thinking with external representations. AI Soc. 25 (4), 441–454. doi:10.1007/s00146-010-0272-8
Lester, F. K., and Cai, J. (2016). “Can mathematical problem solving be taught? Preliminary answers from 30 years of research,” in Posing and solving mathematical problems. Editors P. Felmer, E. Pehkonen, and J. Kilpatrick (Washington, DC: Springer), 117–135. doi:10.1007/978-3-319-28023-3_8
Lester, F. K., Garofalo, J., and Kroll, D. L. (1989). “Self-confidence, interest, beliefs, and metacognition: key influences on problem-solving behavior,” in Affect and mathematical problem solving. Editors D. B. McLeod, and V. M. Adams (Berlin, Germany: Springer-Verlag), 75–88. doi:10.1007/978-1-4612-3614-6_6
Lester, F. K., and Kroll, D. L. (1990). “Assessing student growth in mathematical problem solving,” in Assessing higher order thinking in mathematics. Editor G. Kulm (Washington, DC: AAAS Publication), 53–70.
Lester, F. K. (1985). “Methodological considerations in research on mathematical problem-solving instruction,” in Teaching and learning mathematical problem solving: multiple research perspectives. Editor E. A. Silver (Mahwah NJ: Erlbaum), 41–69.
Lienert, G. A., and Raatz, U. (1998). Testaufbau und Testanalyse [Test construction and test analysis]. 6th Edn. Weinheim, Germany: Beltz.
Lim, S. Y., and Chapman, E. (2015). Effects of using history as a tool to teach mathematics on students' attitudes, anxiety, motivation and achievement in grade 11 classrooms. Educ. Stud. Math. 90 (2), 189–212. doi:10.1007/s10649-015-9620-4
Mason, L., and Scrivani, L. (2004). Enhancing students' mathematical beliefs: an intervention study. Learn. InStruct. 14 (2), 153–176. doi:10.1016/j.learninstruc.2004.01.002
Mayer, R. E., and Hegarty, M. (1996). “The process of understanding mathematical problems,” in The nature of mathematical thinking. Editors R. J. Sternberg, and T. Ben-Zeev (Mahwah NJ: Lawrence Erlbaum), 29–54.
Moore, R. T. (2012). Multivariate continuous blocking to improve political science experiments. Polit. Anal. 20 (4), 460–479. doi:10.1093/pan/mps025
M. S. Hannula, G. C. Leder, F. Morselli, M. Vollstedt, and Q. Zhang (Editors) (2019). Affect and mathematics education: fresh perspectives on motivation, engagement, and identity. New York, NY: Springer International Publishing. doi:10.1007/978-3-030-13761-8
Norman, D. A. (1993). Things that make us smart: defending human attributes in the age of the machine. New York, NY: Perseus Books.
Nussbeck, F. W., Eid, M., and Lischetzke, T. (2006). Analysing multitrait-multimethod data with structural equation models for ordinal variables applying the WLSMV estimator: what sample size is needed for valid results?. Br. J. Math. Stat. Psychol. 59 (1), 195–213. doi:10.1348/000711005X67490
Peterson, C., and Seligman, M. E. P. (2004). Character strengths and virtues: a handbook and classification. Oxford, United Kingdom: Oxford University Press.
Rasch, R. (2008). 42 Denk- und Sachaufgaben. Wie Kinder mathematische Aufgaben lösen und diskutieren [42 thinking and problem solving tasks. How children solve and discuss mathematical tasks]. 3rd Edn. Seelze-Velber, Germany: Kallmeyer.
Reisberg, D. (1987). “External representations and the advantages of externalizing one’s thought,” in The ninth annual conference of the cognitive science society, Seattle, WA, July 1, 1987 (Hove, United Kingdom: Psychology Press), 281–293.
Reiss, K., Hellmich, F., and Thomas, J. (2002). “Individuelle und schulische Bedingungsfaktoren für Argumentationen und Beweise im Mathematikunterricht [Individual and educational conditioning factors for argumentation and evidence in mathematics teaching],” in Bildungsqualität von Schule: schulische und außerschulische Bedingungen mathematischer, naturwissenschaftlicher und überfachlicher Kompetenzen. Editors M. Prenzel, and J. Doll (Weinheim, Germany: Beltz), 51–64.
Reyes, L. H. (1984). Affective variables and mathematics education. Elem. Sch. J. 84 (5), 558–581. doi:10.1086/461384
Schnotz, W., Baadte, C., Müller, A., and Rasch, R. (2010). “Creative thinking and problem solving with depictive and descriptive representations,” in Use of representations in reasoning and problem solving: analysis and improvement. Editors L. Verschaffel, E. de Corte, T. de Jong, and J. Elen (Abingdon, United Kingdom: Routledge), 11–35.
Shaughnessy, J. M. (1985). Problem-solving derailers: The influence of misconceptions on problem-solving performance. In E. A. Silver (Hrsg.), Teaching and learning mathematical problem solving: Multiple research perspectives (S. 399 -415). Lawrence Erlbaum.
Stuart, E. A., and Rubin, D. B. (2008). “Best practices in quasi-experimental designs: matching methods for causal inference,” in Best practices in quantitative methods. Editor J. W. Osborne (Thousand Oaks, CA: SAGE), 155–176.
Sturm, N. (2018). Problemhaltige Textaufgaben lösen: einfluss eines Repräsentationstrainings auf den Lösungsprozess von Drittklässlern [Solving word problems: influence of representation training on the problem-solving process of third-graders. Berlin, Germany: Springer. | Google Scholar
Sturm, N., and Rasch, R. (2015). “Forms of representation for solving mathematical word problems – development of an intervention study,” in Multidisciplinary research on teaching and learning. Editors W. Schnotz, A. Kauertz, H. Ludwig, A. Müller, and J. Pretsch (London, United Kingdom: Palgrave Macmillan), 201–223.
Sturm, N., Rasch, R., and Schnotz, W. (2016). Cracking word problems with sketches, tables, calculations and reasoning: do all primary students benefit equally from using them? Pers. Indiv. Differ. 101, 519. doi:10.1016/j.paid.2016.05.317
Sturm, N. (2019). “Self-generated representations as heuristic tools for solving word problems,” in Implementation research on problem solving in school settings. Proceedings of the 2018 joint conference of ProMath and the GDM working group on problem solving. Editors A. Kuzle, I. Gebel, and B. Rott (Münster, Germany: WTM-Verlag), 173–192.
Sturm, N., Wahle, C. V., Rasch, R., and Schnotz, W. (2015). “Self-generated representations are the key: the importance of external representations in predicting problem-solving success,” in Proceedings of the 39th conference of the international group for the psychology of mathematics education. Editors K. Beswick, T. Muir, and J. Wells (Basingstoke, United Kingdom: PME), 4, 209–216.
Sweller, J. (1994). Cognitive load theory, learning difficulty, and instructional design. Learn. InStruct. 4 (4), 295–312. doi:10.1016/0959-4752(94)90003-5
van Dijk, T. A., and Kintsch, W. (1983). Strategies of discourse comprehension. Cambridge, MA: Acadamic Press.
Verschaffel, L., De Corte, E., Lasure, S., Van Vaerenbergh, G., Bogaerts, H., and Ratinckx, E. (1999). Learning to solve mathematical application problems: a design experiment with fifth graders. Math. Think. Learn. 1 (3), 195–229. doi:10.1207/s15327833mtl0103_2
Verschaffel, L., Greer, B., and de Corte, E. (2000). Making sense of word problems. Netherlands: Swets and Zeitlinger.
Webb, N. L., Moses, B. E., and Kerr, D. R. (1977). Mathematical problem solving project technical report IV: developmental acctivities related to summative evaluation (1975–1976): Mathematics Education Development Center. Bloomington, IN: Indiana University.
Zakaria, E., and Ngah, N. (2011). A preliminary analysis of students’ problem-posing ability and its relationship to attitudes towards problem solving. Res. J. Appl. Sci. Eng. Technol. 3 (9), 866–870.
Keywords: attitudes and beliefs, word problem, training program design, problem-solving, problem-solving success, primary school, moderation effect analysis
Citation: Sturm N and Bohndick C (2021) The Influence of Attitudes and Beliefs on the Problem-Solving Performance. Front. Educ. 6:525923. doi: 10.3389/feduc.2021.525923
Received: 21 May 2020; Accepted: 18 January 2021;
Published: 17 February 2021.
Edited by:
Katharina Loibl, University of Education Freiburg, GermanyReviewed by:
Künsting Josef, University of Education Freiburg, GermanyBenjamin Rott, University of Cologne, Germany
Copyright © 2021 Sturm and Bohndick. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nina Sturm, bmluYS5zdHVybUBwaC1sdWR3aWdzYnVyZy5kZQ==
 Nina Sturm
Nina Sturm Carla Bohndick
Carla Bohndick