- Department of Learning and Leadership, University College London, London, United Kingdom
There is very little research on cognitive outcomes and challenges for children with Apert syndrome. This paper describes the findings of a 2½-year longitudinal exploration of the development of arithmetic skills in 10 children with Apert syndrome, who were aged between 4 and 9 years at the beginning of the study. There is evidence to suggest that children with Apert syndrome underachieve in mathematics, especially in areas requiring competence and confidence arithmetic. This study explored the changing strategies the children used as they developed their arithmetic problem solving skills. Of particular interest were the roles of finger gnosis and finger mobility in supporting the development of these skills. A case study approach was adopted in order to explore the children's problem solving strategies in depth. Children with Apert syndrome are born with their fingers fused and undergo several operations with the aim of ensuring that they have as many functioning fingers as possible. Finger gnosis and finger mobility were both seen to support arithmetic problem solving strategies and skills and reduce the reliance on mental strategies alone. This study found that children with Apert syndrome are disadvantaged if they are not supported to develop their finger gnosis and finger mobility skills. The findings have implications for children with Apert syndrome, but also add to the literature on the role of finger gnosis and finger mobility in the development of skills in early number and arithmetic.
Introduction
The study discussed here focused on the development of early number and arithmetic skills in 10 children with Apert syndrome. This is the first study to focus in such depth on an area of cognitive development in children with Apert syndrome.
Apert syndrome is very rare and has a birth prevalence of ~1 in 65,000, in North America and Europe. Apert syndrome is equally present in boys and girls (Cohen et al., 1992; Tolarova et al., 1997). The syndrome was first described by Wheaton in 1894 and was investigated further by Apert in 1906 (Patton et al., 1988). Advances in medical treatment of Apert syndrome have resulted in better outcomes for children and as a result the number of children with Apert syndrome in mainstream schools is likely to increase.
In Apert syndrome, children are born with some of the sutures in their skull fused (craniosynostosis) and with their fingers and toes fused (syndactyly). Apert syndrome is caused by a mutation of the fibroblast growth factor receptor 2 (FGFR2) gene (Wilkie et al., 1995). The two mutations, S252W and P253R account for 98% of those born with the syndrome (Stark et al., 2015).
In general, the literature to date has tended to focus on the management of the syndrome from a clinical perspective; much less is known about the cognitive and social development of children with Apert syndrome (Hilton, 2017).
As a result of the premature fusion in the skull and fingers, children with Apert syndrome often undergo several surgical procedures during their early years. The surgery may include vault expansions (to make room for the brain to grow) and separation of the fingers. Children with Apert syndrome often have hearing and/or visual impairments which also need to be addressed.
Children with Apert syndrome are diverse and complex, so it is hard to generalize in terms of outcomes. Much of the literature on children with Apert syndrome highlights significant variation in cognitive development and a wide range of IQ scores (Lefebvre et al., 1986; Patton et al., 1988; Renier et al., 1996). More recently, many of the assumptions about cognitive outcomes for children with Apert syndrome have been questioned, as researchers have begun to reflect on issues such as the role of the family (Yacubian-Fernandes et al., 2004) and speech and language development, visual impairments, hearing impairments and difficulties with fine motor skills (Shipster et al., 2002).
Hand Anomalies and Outcomes for Children With Apert Syndrome
Children with Apert syndrome are always born with varying degrees of fusion of the fingers. There are three types of hand in Apert syndrome, which are described below. For the purpose of this description, all digits are referred to as “fingers.” These are numbered from 1 to 5, with 1 being the thumb:
• Type I has boney or cartilaginous fusion of the three middle fingers (fingers 2–4).
• Type II has complex boney fusion of all the fingers (fingers 2–5), with the thumb joined with skin but no boney fusion.
• Type III has complex boney fusion of all five fingers.
In the UK, hand surgery is usually performed in stages before a child reaches 4 or 5 years of age. Depending on the severity and complexity of the fusion, children usually have either three or four fingers and a thumb following surgery. Due to their unusual joints, people with Apert syndrome often have stiff knuckle joints and fingers that do not bend (with the exception of the final joint in the little finger in some cases). The thumb is usually short and bent. This makes it very difficult for children to have a “normal” pinch grip, even after surgery (Taghinia et al., 2019).
Finger Representation in Apert Syndrome
There is limited research on the representation of fingers in people with Apert syndrome, either before or after surgery to release the fingers. The only study found discusses the case of an adult with Apert syndrome (Mogilner et al., 1993). In this study, the authors report that prior to surgical separation of the fingers, the fingers were represented in the brain as one single digit. Within a week after surgery, the hand area in the brain had increased and the fingers had more distinct cortical representation locations. This change was still present 6 weeks later. However, “the resulting hand area was smaller than normal and the organization was non-somatotopic” (Mogilner et al., 1993, p. 3597). This is important, as it suggests that the representation of the hand in people with Apert syndrome after surgery, is not like that of a typically-developing hand.
The Development of Arithmetic Skills in Children With Apert Syndrome
Children with Apert syndrome have a complex profile, due to the range of difficulties such as visible difference (or disfigurement), limited finger mobility, hearing impairment, and visual impairment (Hilton, 2017). Most of the literature on Apert syndrome focuses on surgical management and what literature there is on cognitive development tends to be drawn from quantitative data, based on standardized assessments.
There are very few studies on Apert syndrome that mention progress in any aspect of mathematics. In a study by Sarimski (1997), seven out of the nine children for whom there were results, scored lower in tests of arithmetic and short-term memory than they did in tests investigating perceptual and verbal skills. When asking parents about their children's academic achievements, Fearon and Podner (2013) found that many parents reported that their children with Apert syndrome had more difficulty with mathematics when compared to their verbal and reading skills.
This suggests that mathematics, particularly in the area of arithmetic, may be more challenging for children with Apert syndrome, but there is a need for a more in-depth understanding of what the difficulties might be and how they might be addressed.
Learning to Use Numbers
The Language of Number
From a very young age, children learn about counting and the language of counting from watching and copying the adults around them. The need to count, though is not instinctive, it is a human creation (Dehaene, 2011); so how does our use of number affect our development of counting and concepts of numerosity? There are two distinct ways of establishing the numerosity of a set of objects and these work independently of each other. The first of these is subitizing and the second counting. These strategies are both used to help solve arithmetic problems, but they have different roots and follow separate developmental trajectories (Clements et al., 2017).
Subitizing
The ability to subitize refers to the skill of being able to enumerate groups of visual or auditory observable objects without counting (Butterworth, 1999). This ability is shared with many other animals and is believed to be instinctive (Dehaene, 2011).
By the age of 3 years, children can usually subitize up to three objects (Fuson, 1988). For adults, the maximum number is usually four (Hughes, 1986). This form of subitizing is sometimes called “perceptual” subtitizing, as it is the ability to recognize “a number without consciously using other mental or mathematical processes and then naming it” (Sarama and Clements, 2009, p. 44). This needs to be distinguished from “conceptual” subitizing—i.e., the ability to recognize a number of objects without counting because of the way the objects are organized. Examples of conceptual subitizing can be found in dominoes, dice and finger patterns (Steffe and Cobb, 1988). Conceptual subitizing is linked to perceptual subitizing in the ways that the patterns are presented. For example, the dice pattern for six is presented as two rows/columns of three, and three is a number that can be easily perceptually subitized.
It has been argued that subitizing is a precursor to counting and, significantly, that it is a language-independent skill (Clements et al., 2017).
Learning to Count
Learning to count is no trivial task (Gelman and Gallistel, 1978; Steffe et al., 1983; Fuson, 1988) and it underpins the learning of arithmetic in school. The most commonly used model for identifying the key elements of successful counting is that proposed by Gelman and Gallistel (1978). Gelman and Gallistel (1978) proposed five counting principles that include three “how to count” principles and two “what to count” principles.
The “how to count” principles are:
1. The one-one principle (each object is counted once and once only)
2. The stable-order principle (the number words are said in a stable order, even if a child cannot remember all the words—e.g., one, two, three, five, and six)
3. The cardinal principle (the last word in the count indicates the numerosity of the set)
The “what to count” principles are:
4. The abstraction principle (any group of objects can be counted)
5. The order-irrelevance principle (objects can be counted in any order and the answer will always be the same).
It is with practice that children learn that counting is used to enumerate a set of objects and that unequal counts provide information about relative numerosities (Fuson and Hall, 1983). Children's counting strategies, however, vary and change over time, so the task of assessing their counting skills comes with many challenges.
Addition and Subtraction
Children begin to engage with tasks involving addition and subtraction with small numbers of objects before they start formal education. Hughes (1986) noticed that when 3–5 years old children were presented with a closed box containing a few cubes (for example, two or three), if a change was made (by either adding or taking away one or two cubes), the children could work out how many cubes were left in the box. Hughes (1986) also explored what happened when children had to imagine the boxes and he found that the children continued to be successful if the situations were similar to those they had experienced. In order to model the calculations, children would use their fingers, by putting up the right number of fingers and then adding or removing fingers, depending on the problem being solved.
The development of the more abstract concepts of addition and subtraction is less easy to observe. Firstly, children usually begin to understand how “one more and one less” are related to our number system (e.g., that four is three and one more and three is one less than four). Being able to do this with confidence requires knowledge of the number words, the ability to count forwards and backwards and the ability to count on from any point in the number sequence (Steffe et al., 1983).
Carpenter and Moser (1984), in a longitudinal study of 88 children aged 6–9 years, observed the changes in strategy used when children added and subtracted numbers. For addition, they identified five different strategies:
• Count all (e.g., for 3 + 4, counting out 3 objects, then counting out 4 objects and finally counting all the objects to get a total of 7)
• Count on from first number (e.g., for 3 + 4, counting on from 3 to get a total of 7)
• Count on from the larger number (e.g., for 3 + 4, counting on from 4 to get a total of 7)
• Use known number facts (retrieving a known fact from memory)
• Use derived facts (use a known fact to work out a solution—e.g., if 3 + 3 = 6, then 3 + 4 = 7 because 4 is 1 more than 3 and 3 + 4 is equivalent to 3 + 3 + 1).
For children to move on from the count all strategy, they need to be able to count on from any number in the number sequence. For children to be able to count on from the larger number, they have to able to quickly identify the larger of two numbers. These skills are all underpinned by knowledge and understanding of the counting system. These skills are also required for successful use of known and, more especially, derived facts, as illustrated above.
For subtraction, Carpenter and Moser (1984) again observed five different strategies:
• Separating from (e.g., for 5 – 2, count out 5 objects and take 2 away to leave 3)
• Adding on (e.g., for 5 – 2, count out 2 objects and then add on objects until 5 objects have been produced. Count out the 3 objects that have been added)
• Matching (e.g., for 5 – 2, line up the 5 objects and the 2 objects so that they are matched one to one. Count the remaining 3 objects in the unmatched group)
• Counting down from (e.g., for 5 – 2, count back 2 from 5, keeping track of the counting words, to get the answer 3)
• Counting up from given (e.g., for 5 – 2, count up from 2 to 5, keeping track of the number of counting words used, to get the answer 3).
It is interesting to note that for subtraction, no use of known facts was observed. This suggests that the children were not aware of the complement principle (for example, if you know that 2 + 3 = 5, you also know that 5 – 2 = 3). However, the children did demonstrate a range of interpretations that go beyond the understanding of subtraction as “taking away.” All the methods involved some form of counting, whether this was the counting of real objects, or keeping track of number words in the counting sequence.
Both during the interviews and over time, Carpenter and Moser (1984) found that there was wide variation in the choice of strategies. The main variability could be explained in terms of resources. They observed that when practical apparatus was made available, the children preferred to use this rather than using more abstract strategies.
Carpenter and Moser (1982) and Fuson (1982) observed that young children tended to use a count all strategy when they could see the objects being counted (first addend and second addend), but used a counting on strategy when the objects being used for the first addend were hidden but the objects for the second addend could be seen. It is possible though that although the children were not counting out loud they were counting silently to themselves until they reached the count of the hidden objects.
The Role of Fingers in Early Number and Arithmetic
Whenever a counting technique, worthy of the name, exists at all, finger counting has been found either to precede it or accompany it
(Dantzig, 2007, p. 9)
What it is about human fingers (where “fingers” are taken to include thumbs) that makes them so special? In much of the literature on the learning of number, fingers are identified as playing an important role in supporting understanding of our number system (Gelman and Gallistel, 1978; Hughes, 1986; Fuson, 1988; Jordan et al., 1992; Anghileri, 2006). Fingers can help children keep track of items in a count (Fuson, 1982) and they can be used to represent both cardinality and ordinality (Domahs et al., 2008). As children begin to manipulate numbers, fingers can represent objects in calculations, thereby helping children to understand that numbers can exist as abstract entities in their own right (Hughes, 1986; Anghileri, 2006).
Given that most people possess 10 fingers, it is probably no coincidence that most cultures use a base-10 number system (Hughes, 1986). Nevertheless, the use of fingers is a learned, and not a spontaneous, activity (Crollen et al., 2011). Children as young as 3 years of age use their fingers to model problem-solving (Hughes, 1986), but how does finger use change and develop over time to support numerical and arithmetic understanding?
Developing Finger Use
Finger-counting/montring activities, especially if practiced at an early age, can contribute to a fast and deep understanding of number concepts, which has an impact during the entire cycle of life by providing the sensory-motor roots onto which the number concept grows.
(Di Luca and Pesenti, 2011, p. 3)
The term “finger-montring” is the capacity to show particular numerosities with the correct number of fingers, all at once and without counting. While this seems to be common practice, there are cultural differences in the ways that children learn and are taught to use their fingers (Domahs et al., 2010; Di Luca and Pesenti, 2011).
If fingers are used as a tool to support numerical calculations, it is useful to explore how this finger use develops.
Using Fingers and Counting in Arithmetic Calculations
This use of fingers as a concrete referent, Hughes (1986) suggests, is something that children often learn from home, and is therefore a cultural artifact. Fingers are initially used to represent real objects and later to represent numbers, when the more abstract language of arithmetic is introduced (for example when asked to work out calculations such as “three add four”). Hughes (1986, p. 51) argues that fingers “play a crucial role in linking the abstract and the concrete, because they can be both representations of objects and objects in their own right.” Hughes (1986) argues that as children begin to use their fingers more efficiently, they support the understanding of one-to-one correspondence.
Jordan et al. (1992), in a study of kindergarten children who had received no formal education, identified finger counting as the strategy that distinguished the higher achieving middle-income children from their lower achieving lower-income peers. Finger counting was associated with higher performance levels on verbal calculation tasks.
In a later study, Jordan et al. (2008) found that as the children from middle-income families were beginning to use their fingers less, children from low-income fingers continued to depend on their fingers for performing calculations. This suggests that it takes a considerable amount of time (in the region of 2–3 years) for children to move on from relying on fingers to help with arithmetic calculations to confidently using known facts and other strategies to support work with numbers. Based on their findings, Jordan et al. (2008) suggest that finger use should be actively encouraged and supported in early childhood education.
Fuson (1982) observed that once children are able to count on with calculations involving numbers <10, they use several different strategies. When adding two one-digit numbers, Fuson (1982) noticed that the children could usually count on one or two mentally (e.g., 4 + 1, or 6 + 2) using their knowledge of the counting sequence. However, once the second addend was greater than two, the children usually used some sort of strategy for keeping track. Fuson (1982) noticed that these strategies usually involved fingers, where for example, three fingers may be held up in order to calculate a problem such as 4 + 3 (Fuson, 1982). Other less common strategies often involved a form of double counting, where the second addend was counted (e.g., “five is one, six is two and seven is three”). This finding is supported by research which suggests that “finger gnosia may serve as a mechanism to offload working memory demands, helping children to accurately represent quantities above the subitizing range, which in turn support arithmetic processing” (Costa et al., 2011, p. 9).
Thompson (1995), in a study of children aged between 6 and 8 years, exploring the role of counting in children's mental calculation strategies, found that counting strategies often existed, alongside the use of known facts and derived strategy use. The children observed often used their fingers to aid them with their counting. Children used their fingers to help with “counting-on” for addition, “counting-out” for subtraction (counting the minuend and then taking away the subtrahend), “counting-down-from” for subtraction (the most common strategy for subtraction) and “counting-up-from” for subtraction (the least common strategy). When children did not have enough fingers, they often used other objects around them such as their own legs, to create numbers >10. For counting-down-from, children had a number of strategies that involved keeping track of the count. For example:
Richard found 7-3 by saying:
“7……….6.5.4.”
Whilst putting up three fingers, and Rebecca correctly worked 23-9 by counting backwards starting from 22 and tallying the count on nine of her fingers.
(Thompson, 1995, p. 13)
Thompson (1995, p. 15) argued that counting “comprises a variety of sub-skills… in that it is often combined with existing skills and knowledge to generate other new skills and knowledge.” Although Thompson (1995) observed children using their fingers, he did not suggest that their use per se, was of significance. However, their role in counting and aiding keeping track was clearly significant.
Fuson and Secada (1986) investigated the role of fingers as a means of keeping track in arithmetic tasks. They explored the use of two interventions for counting on with mixed attaining children in Grade 3 and low attaining children in Grade 4. One intervention with 107 children, explored counting on using dots. The other one with 106 children involved the use of finger patterns for counting on.
For finger counting, children were taught a one-handed method of counting up to nine, which was based on the strategies they believed children spontaneously use their fingers to keep track (Fuson and Secada, 1986). The method required the children to touch each successive finger on the table, as they counted on. Fuson and Secada (1986) found that the finger counting strategy was effective for all children and that “most children spontaneously related counting on with finger patterns to their schemas of addition and thus counted on with finger patterns to solve addition word problems” (Fuson and Secada, 1986, p. 256). The children used their fingers as abstract representations to support them to count on. The children also learned how to use their fingers to count on for subtraction.
The children who received the dots intervention did not internalize their strategy in the same way. Following the dots intervention, the children were not more likely to draw diagrams to help with counting on for problems such as 5 + 4. However, the children who had learned finger counting, could easily use their fingers to count on from five to nine using the learned finger patterns to help. It therefore seems that fingers provide more than just a body-anchored tool, since when an alternative tool was demonstrated and practiced, it did not have the same long-term benefits, in terms of linking mathematical concepts and strategies.
Marton and Neuman (1990) studied the methods used by 7 years old children to solve arithmetic problems, prior to starting school. They noticed the use of “finger numbers,” where children were able to subitize finger combinations and patterns, in order to solve numerical problems. In this way, the authors argue, the children were able to develop their problem-solving strategies along a path, “first in a concrete way, later in a visualized—or rather ‘body-anchored'—and finally just in a ‘known' or ‘felt' way” (1990, p. 72). In other words, once children “know” their fingers, they no longer need to be able to see them.
Developing Understanding of Numbers and Arithmetic From a Neuroscientific Perspective
Finger Gnosis
Finger gnosis (or finger awareness) is concerned with knowing ones fingers and, for example, being able to identify one's own fingers in response to touch. In typically developing children, finger gnosis develops quickly up to the age of 6 years and then continues to develop at a slower rate up to the age of 12 years, at which point it should be fully developed (Strauss et al., 2006). Strauss et al. (2006) found that children with higher IQs have more well-developed finger gnosis.
Research by Kinsbourne and Warrington (1962) on 12 people with finger agnosia (lack of finger gnosis), identified the apparent lack of differentiation of individual fingers, in terms of touch and spatial relationship to each other. The fingers were described as representing an “undifferentiated mass” (Kinsbourne and Warrington, 1962, p. 56), as if they were a single digit. This is significant in relation to children with Apert syndrome, who, until their fingers are surgically separated, have a finger representation of a single digit (for the fingers that are fused) (Mogilner et al., 1993).
Numbers, Fingers and the Developing Brain
In recent years, there has been growing interest in the role of fingers to support children to understand number and arithmetic from a neuroscientific perspective. According to Butterworth (1999, p. 249–250) “without the ability to attach number representations to the neural representations of fingers and hands in their normal location, the numbers themselves will never have a normal representation in the brain.”
Kaufmann et al. (2008) used brain imaging techniques to explore the areas of the brain that are recruited when performing simple tasks involving number in a study involving 8-year-old children and adults. In tasks involving non-symbolic representations of number, they found that although the children and the adults were able to complete the tasks successfully, children took longer. When this was investigated further, it was discovered that when making numerical comparisons using images of hands showing differing numbers of fingers, the children (but not the adults) recruited additional areas of the brain normally used for fingers. The authors use this evidence to suggest that fingers are an important stepping stone in the development of an abstract understanding of number and that finger use should be encouraged to help develop fluency and competence in activities involving number.
Finger gnosis and fine motor skills have also been implicated in supporting the development of arithmetic skills (Noël, 2005; Gracia-Bafalluy and Noël, 2008). Noël (2005) carried out assessments of finger gnosis with 41 6–7 years old children and compared this with an assessment of their skills in arithmetic 1 year later. A correlation was found between the children's level of finger gnosis and their achievements in tasks involving number identification and simple arithmetic 1 year later. In fact, the relationship between finger gnosis and achievement in mathematics was stronger than the relationship between tests of general cognitive ability and achievement in mathematics. This was followed up with an intervention study in which children were provided with a finger-differentiation intervention, twice a week for a period of 8 weeks. The children's finger gnosis and their numerical skills both improved, when compared to a control group (Gracia-Bafalluy and Noël, 2008).
Even when children do use their fingers for solving arithmetic problems, some problems are more prone to error than others. For example, when working with 6–8 years old children, Domahs et al. (2008) found that children made “split-five” errors when doing numerical calculations that required keeping track of whole hands during a calculation (e.g., 7 + 8). The issue, the authors argue, is with working memory capacity and remembering how many “complete” hands are needed for a calculation.
In a study of children aged 8–11 years, exploring finger gnosis in children with mathematical learning difficulties, a relationship was found between finger gnosis and the children's performance when solving word problems requiring manipulation of numbers between 1 and 10 (Costa et al., 2011), but not with numbers above 10. There were no differences in other skills, such as working memory, when compared with their typically developing peers. This provides additional evidence to support the notion that good finger gnosis (for all 10 fingers) aids arithmetic problem solving.
There have been a few studies, such as that done by Long et al. (2016), that have tried to illustrate that there is no (or at best a weak) relationship between finger gnosis and skills in arithmetic. In Long et al.'s (2016) study, involving children aged 6–7 years, however, the mathematics test used had been standardized on children aged 7–11 years. As a result, raw scores were used rather than standard scores. This brings into question the validity of the findings.
It seems highly likely then, that whether we take a neuroscientific, psychological or educational perspective, finger use in early number activities can be a very important feature to support understanding of number and arithmetic.
The Current Study
Due to the gap in the literature on mathematical learning in children with Apert syndrome, there is a need to establish how these children engage with the mathematics curriculum at school. The review of the literature on Apert syndrome and on the acquisition of early number skills, led to the development of the following research questions:
a) What strategies do children with Apert syndrome use to help them solve numerical problems involving arithmetic operations?
b) Do the children's hand anomalies impact the range of strategies available to them?
Methods
The study took place over 2½ years with 10 children who lived in the UK. The children were initially visited at home with their parents; all subsequent visits took place in school. Given the complex nature of the children, and the small population of children with Apert syndrome, a qualitative (or interpretivist) approach was used. The interpretivist paradigm is useful for studies that are small-scale, concerned with understanding meanings and actions, investigating aspects of behavior that are taken for granted and where the researcher is a part of the research process (Cohen et al., 2007). Due to the complexity of children with Apert syndrome and children with other forms of complex craniosynostoses, this approach has also been recommended for clinical management. This is due to the nature of the syndromes and the impact of “third variables” such as visual impairments, hearing impairments, low expectations, and teasing (Hayward et al., 2016).
In order to understand each individual child's situation a case study approach was adopted. This allowed for flexibility with the data collection, and provided opportunities to explore the similarities and differences across the whole group of children. The case study approach provided an opportunity to identify the fine-grained detail in each child's development during the 2½ years of the study.
Yin (2009) highlights the importance of developing a solid theoretical understanding of the issues, prior to starting any case study. The case study approach may not provide evidence from which to make generalizations based on probabilities, but it does provide evidence from which theoretical propositions and analytical generalizations can be made (Yin, 2009). Case studies can also provide insights that are less likely to be obtained through experimental approaches, as they are often incidental rather than planned (Yin, 2009).
When working one-to-one with the children in school, clinical interviews were used in order to gain insight into the cognitive processes and strategies the children used (Ginsburg, 1981). The notion of the “clinical method” (or “clinical interview”) was introduced by Piaget (1929) as a method for assessing children's understanding. This method is useful for providing insight into a child's thinking. The clinical method is based on the methods used in psychology, where questions are used in order to explore personal situations and, thereby, bring about deeper understanding. Piaget (1929) proposed that this method of individualized and focused questioning can support children to explain and articulate their thinking in ways that are not possible in a standardized test. The clinical interview enables an exploration of three areas involved in mathematical thinking: discovering the cognitive processes children use; identifying and describing these processes; and assessing competence (Ginsburg, 1981). While standardized assessments and naturalistic observation have their uses, Ginsburg (1981) argues that the clinical interview can do more than any of these methods can ever hope to achieve alone.
Finally, a broad range of measures was adopted, in order to provide a flexible approach to data collection. The interview data were coded and analyzed using thematic analysis (Braun and Clarke, 2006).
Procedures
When the children were visited in school, the researcher was usually in school for the whole day, in order to maximize the opportunities to spend time with the children and staff during lessons and at break times. If possible, on each visit, one-to-one clinical interviews were carried out. The duration of the one-to-one interviews varied—some lasted for 20 min, while others lasted for over an hour. These depended on factors, such as: the age of the child; what the routines of the school/class were; how much time was available on each visit for the child to be taken out of class; how well the child was coping (e.g., if the child was getting tired or bored, or if the child wanted to return to class, the interview was ended). To ensure reliability during the one-to-one interviews, the questions used were based on existing assessments that had been reported in the literature. These assessments focused on number system knowledge, skills in arithmetic and strategies used for solving problems. The interviews were audio recorded and later transcribed. The children's finger gnosis was also assessed as often as possible. During some of the one-to-one interviews, the children's teaching/support assistants were also present.
In total there were between two and seven school visits for each child. Data were collected using a range of measures and processes. The data discussed here focus on strategy use during arithmetic problem solving, finger gnosis, and finger use.
Participants
The children in the study were all English-speaking and attended either mainstream or special provisions in UK schools. As Apert syndrome is such a rare condition, the UK charity Headlines Craniofacial Support (a charity which supports individuals and families affected by craniosynostosis) was identified as the most effective means of making contact with potential participants. Letters were sent to all the families on the Headlines Craniofacial Support mailing list where there was a family member with Apert syndrome. From the responses, 10 children were identified whose ages ranged from 4 to 9 years. The results presented are for the seven children who were visited most often. These children were visited five or six times in school. Most of the visits took place once in every school term (i.e., once every 3–6 months). Details of the children's ages at the beginning of the study, the number of fingers on each hand and the type of school attended are provided in Table 1.
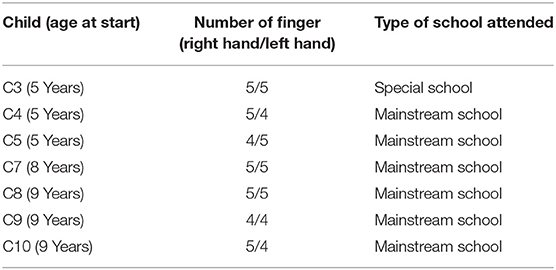
Table 1. Age of children at the beginning of the study, number of fingers, and type of school attended.
Ethical Issues
The study was approved by the Ethics Research Committee of the Institute of Education, University of London. Written and informed consent was obtained from the parents/legal guardians of all the children. The children also assented to participate. Permission was given for one-to-one interviews with the children to be audio-recorded. Informed consent was also obtained from head teachers. The analysis was pseudonymized. Confidential information and parents' or schools' contact details were only accessed by the researcher. The data collected was kept in password-protected files on the university's computer system and in locked cabinets in the researcher's office.
Materials
For the clinical interviews, questions were used to cover skills in number and arithmetic. For the purpose of reliability, the questions were based on assessments referred to in the literature, but the assessments were not scored. This allowed the focus to be on “how” and “why” the children used particular approaches, rather than on the number of questions they could answer correctly. Decisions about which questions to use depended on the developmental stage of the child and the amount of time available for the one-to-one interview. Some of the questions were repeated during several visits, in order to observe changes in strategic approaches to solving the problems.
The questions used during the one-to-one interviews to explore numerical and arithmetic skills and understanding focused on:
• Counting skills and early arithmetic—using activities adapted from Gelman and Gallistel's (1978) counting principles and Hughes (1986) box task. Children's counting skills were explored to check for evidence of Gelman and Gallistel's five counting principles (the one-one principle, the stable order principle, the cardinal principle, the abstraction principle, and the order-irrelevance principle). Hughes' box task was adapted using a bag and counters, instead of a box and cubes. A small number of counters was put into the bag and then one or two counters were added or taken out. This was repeated and the number of counters removed or added varied depending on each child's success in the activity
• “Number sense”—using activities adapted from Jordan et al.'s (2008) number sense screening tool. These questions were particularly appropriate for those children who were at the very early stages of number knowledge. This assessment focuses on counting and number recognition. Activities include: reciting the number sequence; counting a group of five objects; identifying correct counts and miscounts; reading numbers with up to 3-digits. The activities also involve number comparisons and the use of a combination of seen and hidden objects in order to calculate questions such as 2 + 1. Contextualized word problems are presented (e.g., Jose has three biscuits. Sarah gives him two more. How many does Jose have now?); and finally questions using the formal language of mathematics (e.g., how much is two and one?).
• “Number knowledge”—using activities adapted from the “Number Knowledge Test” (Griffin and Case, 1997). This assessment is designed for use with children aged 3–10 years. The questions focus on knowledge of numbers, the number system and arithmetic. The first set of questions explores knowledge of the counting numbers from 1 to 10 and addition and subtraction using both concrete objects and symbolic representations. Later questions explore similar ideas as those explored previously, but this time with 2-digit numbers. Finally, 3-digit and 4-digit numbers are introduced and questions involving bridging through 99 and 999.
Finger gnosis was assessed using a method based on Gracia-Bafalluy and Noël (2008). Each hand was assessed separately. When testing a child's finger gnosis, the child was asked to place her hand palm down on the table and her hand was covered, so that she could not see it. One finger was touched and then the cover was removed, so that the child could point to the finger that had been touched. This was repeated until each finger had been tested at least twice. This same procedure was carried out on the other hand. If the child could correctly identify most of the single finger touches, the test was repeated, but this time with two fingers being touched at the same time. These assessments were not scored, as the children had different numbers of fingers. However, it was important to know whether there were some fingers that were more difficult to identify than others, so any such instances were noted.
Analysis
The case study approach allowed for an in-depth analysis of each child. The process of analysis was on-going over the 2½ year period of the study. Much analysis took place during the data collection period as decisions about what to assess and how to assess were contingent on many factors, such as how much could be achieved during each interview. This allowed for an iterative process, which enabled each child's mathematical learning journey to be explored in depth. Reflexive thematic analysis, based on Braun and Clarke framework 2006, was used in order to identify patterns and relationships that existed both within each child and across all the children. This method provided the flexibility required and allowed for both inductive and deductive approaches to data analysis to enable the development of rich and complex understandings of the data. Once all the data had been collected, it was coded to provide an initial mapping of codes and themes and then refined further to identify the final themes.
The first three themes relate to the first research question exploring the strategies the children used and the final two themes relate to the second research question focusing on the impact of the children's' hand anomalies and how they could be supported. The themes were:
• Subitizing and comparison
• Knowledge of counting
• Strategies for solving arithmetic problems
• Different ways of using fingers
• Changes in finger gnosis.
Results
At the beginning of the study, all the parents expressed concerns about their children's progress in mathematics. They all felt that their children were doing less well in mathematics than in other curriculum subjects. This was echoed by the teachers in the first visits to the schools. School staff often said that they did not encourage children to use their fingers because the children found it physically challenging.
What follows is an analysis of the findings from the clinical interviews for the children identified in Table 1. In the extracts, the interviewer is identified by “I” and the children are identified by codes C1-C10. All the children are referred to as female, in order to maximize anonymity.
Subitizing and Comparison
All the children were able to perceptually subitize up to three, when counters were randomly presented. Conceptual subitizing was more variable and depended on the children's experiences of playing games, whether at home or at school. From the start, all the children could say which of two piles of counters of the same color were bigger (e.g., two vs. six and eight vs. three). All the children could say which numbers were bigger/smaller when spoken or presented symbolically (e.g., “Which is bigger: 5 or 4?” and “Which is smaller: 5 or 7?”). The children's knowledge of the number system was a strength, but their abilities to use this knowledge was more variable.
Knowledge of Counting
From the beginning of the study, all the children could count forwards. The differences were in how far the children could count and whether they could transcode between the spoken and written number words (presented symbolically). As the children became more confident and more practiced, their knowledge of numbers and how to read and write them developed.
Counting backwards was more problematic for some of the children at the beginning of the study. For example C8 (9 years old):
I: Can you just start counting as far as you can? [C8 appears to be counting in her head]
I: Not in your head [giggling]. I need to be able to hear you C8 [we both giggle]. Count starting from one
C8 and I: One, two, three
C8: Four, five, six, seven, eight, nine, ten, eleven, twelve, thirteen, fourteen, fifteen, sixteen, seventeen, eighteen [continues correctly up to thirty and stops]
I: Fantastic. Can you count backwards from ten?
C8: Ten, fifteen
I: Backwards from ten. So what comes before ten? [long pause]
I: What about counting backwards from five? [long pause]
I: No?
C8: No
However, 5 months later (then 10 years old), C8 was able to count back from 30.
The only other child that could count forwards, but not backwards at the beginning of the study was C3. However, during the last year of the study, C3 was observed counting backwards from 10. All the other children could count forwards and backwards (within their personal limits) from the beginning of the study. The ability to count on and backwards from a given starting number influenced the strategies that the children were able to use when performing arithmetic calculations. This was an important skill to assess, given its role in supporting counting on and counting back in addition and subtraction (Steffe et al., 1983).
Strategies for Solving Arithmetic Problems
The interviews highlighted the importance of counting in early arithmetic, as identified by Steffe et al. (1983), but also the capacity of children to perform arithmetic tasks without the use of symbolic and arithmetic language or notation (Hughes, 1986). C3, at 5 years of age provides a good example of this. The activity described below is based on Hughes (1986) box task.
I: Now if I put the four…how many are here? [pointing to the four counters]
C3: One, two, three, four [raises voice] [touches the counters as she counts]
I: Now if I put the four counters into the bag
C3: Yes
I: How many have I just put into the bag?
C3: One, two, three, four [raises voice]
I: If I put one more in [putting one counter into the bag]
C3: Yes
I: How many have I got in my bag now?
C3: One, two, three, four, five [raises voice]
This could be an example of “counting all” (Carpenter and Moser, 1984), with imagined cubes, or it could be an example of the need to repeat the number sequence from one, because of lack of familiarity with the number sequence (i.e., Fuson, 1988 “unbreakable list”). Alternatively, it could be that because she was unable to represent the problem physically, C3 needed to count.
Observing the children trying to solve numerical problems highlighted a number of challenges. The extract below with C4, aged 5 years, illustrates the impact of relying on mental strategies alone. The questions asked are all common for children of this age in English maintained schools.
I: How much is three and two?
C4: Five
I: Well done…how much is four and three?
[12 second pause]
C4: Four and three?
I: Yes four and three
C4: Seven
I: And how much is two and four?
[23 second pause]
I: Should we leave that one?
C4: Yeah
To try to understand the strategies C4 was using it is useful to look at some of the responses to the task based on Hughes (1986) box task.
I: If I put these three into this envelope [puts in three counters]
C4: Yeah
I: And I put one more in [puts one more counter into the envelope]. How many will there be in the envelope now?
C4: [pause] four
I: How did you know that?
C4: I counted in my head
C4 could also do this successfully when two counters were added. With subtraction, C4 could quickly subtract one, but could not subtract two or more by counting back. In these examples, C4 was relying on mental strategies (counting on and back) to help her calculate the answers. Once she had reached her maximum capacity to count on mentally (i.e., to add on three, or subtract one), she was unable to complete the task.
These responses are reminiscent of Fuson (1982) who found that when children could not do calculations mentally, they needed another strategy to help them keep track of the counts. For Fuson (1982), this usually involved fingers. As C4 did not use her fingers and did not opt to use any other strategy, she could not solve the problems if she was unable to “count in her head.” C4 did not use her fingers in the “intuitive” way suggested by Fuson (1982).
This example is typical of all the children apart from C10, aged 9 years at the beginning of the study (and sometimes C7, aged 8 years at the beginning of the study) who, from the start, had experience of using their fingers to help with calculations. When the other children could not count on or back mentally, they had no other strategies to fall back on and did not model the problems on their fingers or with any other concrete resources. These children only tried to solve problems with concrete materials such as counters, when prompted. For this reason, subtraction was usually done by counting back, rather than by removing the subtrahend from the minuend. When questions were presented with images (e.g., ducks on a pond), the children were more likely to use the images to help them to solve the problems.
The example below from C7, aged 8 years, highlights the difference that was made when finger use was used as an intuitive strategy. C7 had five fingers on both hands.
I: Sally has four crayons. If Stan gives her three more, how many does Sally have now?
C7: Seven
I: Good girl. How did you work that out?
C7: Ummmm I just counted in my head
I: And how did you do the counting in your head?
C7: I just counted in my head and used my fingers
I: And did you start from one, or did you start from one of the other numbers?
C7: I started from…did you say four crayons?
I: I did
C7: I started from four
Later, C7 was asked a question involving subtraction.
I: Kisha has six pennies. Peter takes away four of her pennies. How many pennies does Kisha have left? [C7 takes time]
C7: Two
I: How did you work that one out?
C7: I just used my fingers and counted back
I: OK…from?
C7: Did you say six?
I: I did say six…that's very good
C7: Yeah, I counted back from six
C7 touched her fingers as she counted and silently counted on and back. The use of fingers to keep track in problems involving addition and subtraction are similar to those described by Thompson (1995) and Fuson (1982).
As so few of the children had experience of using their fingers, parents and teachers were provided with information about the literature on the role of finger gnosis in the development of early number and arithmetic. This gave parents and schools the opportunity to engage the children in activities that encouraged finger use. Some parents and schools created their own activities, while others tried the activities described in the literature (these are discussed in more detail later). The impact of this was that most of the children began to use their fingers more to help with arithmetic problem solving. The following vignettes provide examples of the finger-based strategies the children used in arithmetic problem solving, following the interventions.
At 7 years of age, C4 was being encouraged to use her fingers both at home and at school. The extract below is between C4 and her teaching assistant (TA), after about 3 months of finger activities.
TA: How would you work out twelve plus fifty-four?…How do we work it out?
C4: I don't know
TA: Which number would you work out first…which number do we normally pick when we're adding?
C4: Twelve?
TA: C4, which number do we normally start with the bigger number or the smaller number?
C4: Big
TA: So which number are you going to start with?
C4: Fifty-four
TA: And then what will be your next step if you have fifty-four
C4: Fifty-five, fifty-six, fifty-seven [continues to count correctly to sixty-six, using all the fingers on her right hand and using her left hand to keep track of the tens]
The strategy used demonstrates understanding of the base-10 number system, with fingers being used to demonstrate one-to-one correspondence and to keep track of the tens. This was a novel strategy and enabled C4 to easily work with numbers beyond 10.
C5 provides an example of the use of fingers as a complementary strategy, using known and derived facts. The extract below is between 8-year-old C5 and the interviewer (I), following six months of finger gnosis training.
I: Can you work out thirteen add thirty-nine? You can write it down if it helps.thirteen….add…thirty-nine [spoken slowly as C5 writes 13+39] [pause]
I: Do you know what it will be?
C5: No…. I don't know what the answer is because…. The trouble is the twelve….and I've got to add another ten on
I: Yeah….so what do you think this might be? [pointing to the calculation that C5 has written down] [pause] What's the strategy you could use to work it out?
C5: Umm….nine and three….nine, ten, eleven, twelve [using fingers]. Now…fifty add two is fifty two [writes = 52]
I: How did you get the fifty C5? Where did you get the fifty from?
C5: The tens
I: The tens. Can you explain to me how you got it from the tens?
C5: Ermm…like.like…thirty and ten is forty. Then I added another ten on from the twelve
The examples from C4 and C5 described above, both highlight the point that counting can be used together with existing knowledge and skills (Thompson, 1995). In this way, finger counting can help to support new learning and understanding. By using their fingers, the children were able to demonstrate how they “knew” their fingers and could use them flexibly in calculations without relying on finger montring and its associated visual representations of numerosities. In fact, for children with Apert syndrome, finger montring is a particular challenge, due to the limited mobility in all the finger joints, including the knuckles. Unlike the children in Marton and Neuman (1990) study, the children used one-to-one correspondence and keeping track, rather than recognizing finger patterns that made different combinations for number bonds within 10.
The children in the study had different starting points in terms of the methods they used for calculations, whether the problems were presented with concrete objects or using the abstract language of mathematics (e.g., “What is three add four?”). If the objects could be seen, the children who were at earlier stages of mathematical development, would use a “count all” strategy, but would generally count on when some of the objects were hidden as in Hughes (1986) box task. Counting on from the first number and then counting on from the higher number were skills that the children learned as they gained more experience (as has already been seen). There was some use of known and derived facts, especially in problems involving addition, but not subtraction, as described by Carpenter and Moser (1984). Subtraction tended to be done by counting back, unless the question was supported by an image, or the children were prompted.
Different Ways of Using Fingers
Each child in the study had between eight and 10 fingers, so for some of the children there was a challenge when trying to “make 10.” The children were often creative in the ways they used their fingers to do this. Some of the strategies that the children used are explored below. In the descriptions of the strategies, the fingers are numbered from one to four or five on each hand, where number one is the thumb and the rest of the fingers are numbered in canonical order.
C3, who was 5 years old at the beginning of the study and had five fingers on both hands, was able to use finger montring by holding down the fingers that were not needed to show numbers less than five. For numbers above five this was not possible. This made it much harder for her to engage in activities where finger montring was required for numbers above five. This was evident in C3's engagement in whole class activities (such as number songs), where the children were expected to join in by showing the different numbers on their fingers. C3 did not use her fingers in any numerical calculations.
C4, who was 5 years old at the beginning of the study and had five fingers on her right hand and four on her left, did not use her fingers for mathematics at the beginning of the study. She was a non-identical twin and at age 5 years, her twin sibling was using her fingers to solve numerical problems. At the age of 7 years, C4 was using her fingers by counting on both hands for numbers up to 10 (adding on the missing “10” when she had counted all her fingers). For numbers larger than 10, she would count on her right hand and keep track of the 10s on her left hand, so that she could continue counting. As she counted, C4 would touch her fingers with the index finger of the hand that was not being counted.
C5 was 5 years old at the beginning of the study and did not use her fingers for numerical activities in mathematics. By the age of 7 years, she was using her fingers confidently. C5 had four fingers on her right hand and five on her left. When C5 started to use her fingers, she was already aware of the importance of 10. To ensure that her right hand could represent “five,” C5 counted both sides of finger number 3. When C5 counted on her fingers, she touched her fingers with the index finger of the hand that was not being counted.
C7 was 8 years old at the beginning of the study and had five fingers on each hand. She was confident about using her fingers from the start. She was able to quickly count on, touching her fingers as she counted (either with her finger or on another surface, such as a table or her leg).
C8 was 9 years old at the beginning of the study and had five fingers on each hand. She did not use her fingers at the beginning of the study. When she started to use her fingers, aged 10 years, she would place her fingers on the table in front of her and count out the number of fingers she needed to add on (e.g., in a calculation such as 8+6, C8 would “put eight in her head” and count out the six fingers to add on). She would leave the fingers on the table and move them as she counted. At 10 years of age, C8 knew the finger patterns for the numbers up to five, but struggled with numbers above five. She knew the finger patterns for 1, 2, 3, 4, 5, 8 (by making four and four with two hands), and 10.
C9, was 9 years old at the beginning of the study and did not use her fingers for activities in mathematics. She had four fingers on each hand. By the time she was 11 years old, C9 was using her fingers and was creating 10 by counting from one to four on her right hand and then continuing on her left hand, double counting fingers 3 and 4 on her left hand to make nine and 10. C9 touched her fingers on the table in canonical order, to keep track of the counts. This table tapping strategy is similar to that described by Fuson and Secada (1986).
C10, who was 9 years old at the beginning of the study and had five fingers on her right hand and four on her left, had developed a very complicated and quick method for doing numerical calculations using both hands. She had done this independently just before the study had started. The method involved touching fingers as she performed the calculations.
Changes in Finger Gnosis and Finger Gnosis Training
Some parents and some schools did the finger gnosis training as described by Gracia-Bafalluy and Noël (2008), while others encouraged the children to use their fingers in different ways. This was not always done consistently, but it always seemed to make a difference.
The intervention activities devised by Gracia-Bafalluy and Noël (2008) were designed to develop finger differentiation and motility. During the activities, children put colored stickers on their fingernails to match the colors in the activities. When engaging with the activities, it is advised to use the dominant hand first. The activities start with the use of two fingers and slowly progress to five. The first activity is a maze activity in which several paths have to be followed, one at a time. The activities become more complicated as the child becomes more practiced. Gracia-Bafalluy and Noël (2008) found that if children engaged with their finger-differentiation intervention, twice a week for a period of 8 weeks, their finger gnosis improved, and so did their performance in arithmetic tasks.
C5 experienced the intervention proposed by Gracia-Bafalluy and Noël (2008), so it is interesting to observe the development of her finger gnosis. At 6 years of age, with single finger touches, C5 was able to identify fingers 1, 2 and 5 on her left hand (with five fingers) and could correctly identify all four fingers on her right hand (with four fingers). On her left hand, C5 consistently mixed up fingers 3 and 4. With two finger touches, C5 could only identify the correct fingers when fingers 1 and 5 were touched on her left hand and on her right hand could only identify finger 1, when touched in combination with other fingers. Five months later, it was not possible to test C5's finger gnosis, but her teacher agreed to try the finger gnosis intervention at school. This intervention was carried out at least three times a week. Three months later, the finger gnosis assessment revealed very little change. However, after the next 3 months there was significant change. This time C5 could identify all her fingers on single finger touches and only occasionally mixed up fingers 3 and 4 on her left hand. With two finger touches, C5 was correct with all trials on both hands. C5's teacher said that C5 was now using her fingers in arithmetic problems and that this was helping her to “visualize” numbers and had improved her “sense of numbers.”
C8 illustrates the importance of continuing with finger gnosis activities until finger awareness has been fully developed. At 10 years of age, C8 (who had five fingers on each hand) could correctly identify all the fingers on her right hand with single finger touches. On her left hand, C8 was correct with all the single finger touches apart from the index finger, which she identified as either finger 3 or 4. When two finger were touched, C8 was always able to identify one of the fingers correctly and then chose one of the neighboring fingers for the second one. C8 then began the Gracia-Bafalluy and Noël (2008) finger gnosis intervention. After 4 months there were improvements in the finger gnosis assessment. C8 could reliably identify single finger touches and could correctly identify fingers 1 and 5 on both hands when two fingers were touched. At this point, C8 was beginning to use her fingers confidently to help with arithmetic tasks. After this point, C8 stopped the finger gnosis intervention and 7 months later, there was no change in her finger gnosis. She was able to identify number patterns for 1, 2, 3, 4, 5, 8, and 10 with her fingers and could use her fingers for keeping track of counts up to five in addition and subtraction problems.
C3 (who had five fingers on both hands) provides useful information with regard to finger gnosis development in Apert syndrome. At 5 years of age, C3 could not identify any finger touches and pointed to her whole hand every time a finger was touched during the finger gnosis assessment. Six months later, when C3 was 6 years old, she was able to identify her index finger on both hands. After another 4 months, C3 could correctly identify all single finger touches, but could not correctly identify any fingers correctly with two finger touches. Throughout this time, C3's teacher had actively encouraged the children to engage with finger exercises, both for mathematics and at other times. C3 could use her fingers to model different numbers below five, but did not use her fingers in any calculations.
C10 (who had five fingers on her left hand and four on her left) had started to use her fingers independently 3–4 months before the study started. The first time her finger gnosis was assessed, she was able to correctly identify all nine fingers when one finger was touched and made errors with two finger touches only with fingers 4 and 5 on her right hand and fingers 3 and 4 on her left.
All seven children engaged in some form of finger exercises, either formally or informally. C10 spontaneously started to use her fingers at 9 years of age and over the next 2 years, she made 4 years of academic progress in mathematics, in English national curriculum tests. C10 used her fingers very confidently to help with numerical calculations.
If, as suggested by Berteletti and Booth (2015), when finger gnosis improves, the somatosensory activation becomes more fine-grained and specific to each finger, it is not surprising that as the children practiced using their fingers, their finger gnosis improved and their ability and confidence to use their fingers successfully to help them solve arithmetic problems also increased. With practice, the children became quicker at recognizing (or perhaps subitizing) different finger patterns and finger combinations, as described by Marton and Neuman (1990). With all the children, when using fingers to perform an arithmetic calculation involving keeping track, some form of touch was always used, whether it was tapping the table or touching one finger with another. This suggests that individual finger gnosis plays a significant role, over and above visual pattern recognition.
Discussion
The current study is the first longitudinal study to explore aspects of mathematical development in children with Apert syndrome. It is also the first study to suggest that the hand anomalies of children with Apert syndrome may impact their ability to engage with mathematics in the classroom, especially in work involving aspects of number and arithmetic. Importantly, the findings discussed here provide additional insights that relate to the role of fingers in the development of skills in arithmetic more generally and the process of developing finger gnosis itself.
The children's development of early number and arithmetic skills followed similar trajectories. In terms of strategies, the children initially relied mostly on their mental calculation skills and number fact knowledge. School staff did not tend to encourage the children to use their fingers in numerical tasks, as they believed that the children would find this physically challenging. The children who did not initially use their fingers were limited in their arithmetic problem solving by their capacity to calculate mentally. The children used counters or other concrete resources when prompted, but did not use them spontaneously.
This study suggests that engaging in some form of finger gnosis and finger mobility activities or training has significant benefits for the children's ability to access arithmetic tasks. The use of fingers provided the children with the possibility to use strategies that did not rely totally on mental calculation and enabled them to offload some of the tasks involved in arithmetic problem solving. Further, unlike the use of concrete objects, the children, once trained, used their fingers spontaneously to support calculation. For the six children who did some form of finger awareness training, there was a distinct difference in how they were able to access the numerical tasks they were doing when they could confidently use their fingers to help. The children were all at different stages of development, but finger use did allow them to use a wide range of strategies when engaging on arithmetic problem solving. The embodied actions also provided the children with a better “feel” for number, as they could quickly find a representation to match the task.
Due to their hand anomalies and limited finger mobility, the children often had to create their own finger montring strategies and their own ways of “making 10” with their fingers. Once children had learned these skills, they were able to use their personalized strategies flexibly and with confidence.
It has already been shown that the hand surgery children with Apert syndrome undergo, has a very immediate impact on how the brain “sees” (or represents) the fingers. However, as suggested by the examples of C5 and C8, there are several different stages that the children need to progress through, in order to support effective finger gnosis and finger use. The children in the present study needed months of finger gnosis training for finger gnosis to reach the point where they could reliably identify two finger touches for all their fingers. This provides additional evidence to support the view that it takes time and practice for finger gnosis to fully develop and it adds strength to the suggestion that due to its need for fine-tuned awareness, finger gnosis has a separate developmental trajectory than the rest of the body Rusconi et al. (2014).
The study is the first longitudinal study to illustrate finger gnosis development in a population that undergoes repeated surgery to release fingers due to syndactyly. The findings provide some initial data on the length of time that is required for children with Apert syndrome to develop finger gnosis and the need for specific activities that support this. The results suggest that children with Apert syndrome can benefit from early interventions to develop finger gnosis and fine motor skills, in order to ensure that they are better able to access the curriculum and develop their skills and confidence in number and early arithmetic.
The findings add to the literature on the role of finger gnosis and finger mobility in the development of skills and understanding in early number and arithmetic. The findings also highlight the difficulties children are likely to have with developing arithmetic understanding if finger use is a challenge or is not encouraged.
Limitations
There are a number of limitations to the study. The study was limited in numbers due to the small population of children with Apert syndrome in the UK. As stated earlier, there are two variants of Apert syndrome that have some differences in terms of how the syndrome is expressed. This study did not explore any differences between the two variants. Many aspects of school life impacted the time spent with the children, both in terms of quantity and quality. This led to some inconsistencies, but it would be hard to control for these due to the nature of a study of this type. The children had different numbers of fingers and had been treated at different hospitals with different protocols for the treatment of hand anomalies in Apert syndrome.
A particular weakness of the study was due to the lack of consistency of the finger gnosis and finger training interventions. As this study seems to have identified a significant role for fingers in supporting skills in arithmetic, any future studies should include explicit interventions.
Conclusion
The discussion above provides strong evidence to suggest that hand anomalies in children with Apert syndrome put them at risk for being delayed in the development of their early arithmetic skills. The evidence presented provides support for the proposal that if these children are provided with some form of activity to help them develop their finger gnosis and fine motor skills, they are more likely to be able to use their fingers appropriately to support them in the development of their arithmetic skills. Given that finger gnosis develops quite rapidly in the first 6 years in typically developing children, it would be appropriate to begin to explore how children with Apert syndrome can be supported as early as possible to develop their finger use. This question is of great importance, as it could impact the timing of surgery and follow-up care following hand surgery.
In addition, it is possible that when children with Apert syndrome have their fingers separated there is a mismatch between their body representation structure for fingers and their visuo-spatial finger schema. Without focused activities to develop this fine-tuned finger awareness, this mismatch could provide a disincentive to engage with individual finger use, in activities such as finger counting, as the process could cause confusion and distress.
Finally, the results provide strong evidence to support the exploration of finger gnosis in children that appear to be underachieving in their early arithmetic skills. It seems that fingers do matter in the development of arithmetic skills and that we should not underestimate the potential for apparently simple interventions to have a significant impact.
Ethics Statement
The study was carried out in accordance with the recommendations of the British Educational Research Association and was approved by the Institute of Education, University of London Ethics Committee.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
I would like to thank the children, their families, and the school staff who all made it possible for this study to be undertaken.
References
Anghileri, J. (2006). Teaching Number Sense, 2nd Edn. London: Continuum International Publishing Group.
Berteletti, I., and Booth, J. R. (2015). Perceiving fingers in single-digit arithmetic problems. Front. Psychol. 6:226. doi: 10.3389/fpsyg.2015.00226
Braun, V., and Clarke, V. (2006). Using thematic analysis in psychology. Qual. Res. Psychol. 3, 77–101. doi: 10.1191/1478088706qp063oa
Carpenter, T. P., and Moser, J. M. (1982). “The development of addition and subtraction problem-solving skills,” in Addition and Subtraction: A Cognitive Perspective, eds T. P. Carpenter, J. M. Moser, and T. A. Romberg (Hillsdale, NJ: Lawrence Erlbaum Associates), 67–81.
Carpenter, T. P., and Moser, J. M. (1984). The acquisition of addition and subtraction concepts in Grades one through three. J. Res. Math. Educ. 15, 179–202. doi: 10.2307/748348
Clements, D. H., Sarama, J., and Mac Donald, B. L. (2017). “Subitizing: the neglected quantifier,” in Constructing Number: Merging Perspectives From Psychology and Mathematics Education, eds N. Anderson and M. W. Alibali (Gateway East: Springer), 13–45.
Cohen, L., Manion, L., and Morrison, K. (2007). Research Methods in Education, 6th Edn. London: Routledge.
Cohen, M. M. Jr., Kreiborg, S., Lammer, E. J., Cordero, J. F., Mastroiacovo, P., Erickson, J. D., et al. (1992). Birth prevalence study of the Apert syndrome. Am. J. Med. Genet. 42, 655–659. doi: 10.1002/ajmg.1320420505
Costa, A. J., Silva, J. B. L., Pinheiro-Chagas, P., Krinzinger, H., Lonnemann, J., Willmes, K., et al. (2011). A hand full of numbers: a role for offloading in arithmetics learning?. Front. Psychol. 2:368. doi: 10.3389/fpsyg.2011.00368
Crollen, V., Seron, X., and Noël, M. P. (2011). Is finger-counting necessary for the development of arithmetic abilities? Front. Psychol. 2:242. doi: 10.3389/fpsyg.2011.00242
Dehaene, S. (2011). The Number Sense: How the Mind Creates Mathematics, 2nd Edn. Oxford: Oxford University Press.
Di Luca, S., and Pesenti, M. (2011). Finger numeral representations: more than just another symbolic code. Front. Psychol. 2:272. doi: 10.3389/fpsyg.2011.00272
Domahs, F., Krinzinger, H., and Willmes, K. (2008). Mind the gap between both hands: evidence for internal finger-based number representations in children's mental calculation. Cortex 44, 359–367. doi: 10.1016/j.cortex.2007.08.001
Domahs, F., Moeller, K., Huber, S., Willmes, K., and Nuerk, H.-C. (2010). Embodied numerosity: Implicit hand-based representations influence symbolic number processing across cultures. Cognition 116, 251–266. doi: 10.1016/j.cognition.2010.05.007
Fearon, J. A., and Podner, C. (2013). Apert syndrome: evaluation of a treatment algorithm. Plast. Reconstruct. Surg. 131, 132–142. doi: 10.1097/PRS.0b013e3182729f42
Fuson, K. C. (1982). “An analysis of the counting-on solution procedure in addition,” in Addition and Subtraction: A Cognitive Perspective, eds T. P. Carpenter, J. M. Moser, and T. A. Romberg (Hillsdale, NJ: Lawrence Erlbaum Associates, 67–81.
Fuson, K. C., and Hall, J. (1983). “The acquisition of early number word meanings: a conceptual analysis and review,” in The Development of Mathematical Thinking, ed H. P. Ginsburg (New York, NY: Academic Press), 49–107.
Fuson, K. C., and Secada, W. G. (1986). Teaching children to add by counting-on with one-handed finger patterns. Cogn. Instr. 3, 229–260. doi: 10.1207/s1532690xci0303_5
Gelman, R., and Gallistel, C. R. (1978). The Child's Understanding of Number. Cambridge: Harvard University Press.
Ginsburg, H. (1981). The clinical interview in psychological research on mathematical thinking: aims, rationales, techniques. Learn. Math. 1, 4–11.
Gracia-Bafalluy, M., and Noël, M. P. (2008). Does finger training increase young children's numerical performance? Cortex 44, 368–375. doi: 10.1016/j.cortex.2007.08.020
Griffin, S., and Case, R. (1997). Re-thinking the primary school math curriculum: an approach based on cognitive science. Issues Educ. 3, 1–49.
Hayward, R., Britto, J., Dunaway, D., and Jeelani, O. (2016). Connecting raised intracranial pressure and cognitive delay in craniosynostosis: many assumptions, little evidence. J. Neurosurg. Pediatrics 18, 1–9. doi: 10.3171/2015.6.PEDS15144
Hilton, C. (2017). An exploration of the cognitive, physical and psychosocial development of children with Apert syndrome. Int. J. Disabil. Dev. Educ. 64, 198–210. doi: 10.1080/1034912X.2016.1194379
Hughes, M. (1986). Children and Number: Difficulties in Learning Mathematics. Oxford: Wiley-Blackwell.
Jordan, N. C., Glutting, J., and Ramineni, C. (2008). “A number sense assessment tool for identifying children at risk for mathematical difficulties,” in Mathematical Difficulties: Psychology and Intervention, ed A. Dowker (San Diego, CA: Academic Press), 45–58.
Jordan, N. C., Huttenlocher, J., and Levine, S. C. (1992). Differential calculation abilities in young children from middle-and low-income families. Dev. Psychol. 28:644. doi: 10.1037/0012-1649.28.4.644
Kaufmann, L., Vogel, S. E., Wood, G., Kremser, C., Schocke, M., Zimmerhackl, L. B., et al. (2008). A developmental fMRI study of nonsymbolic numerical and spatial processing. Cortex 44, 376–385. doi: 10.1016/j.cortex.2007.08.003
Kinsbourne, M., and Warrington, E. K. (1962). A study of finger agnosia. Brain 85, 47–66. doi: 10.1093/brain/85.1.47
Lefebvre, A., Travis, F., Arndt, E. M., and Munro, I. R. (1986). A psychiatric profile before and after reconstructive surgery in children with Apert's syndrome. Br. J. Plast. Surg. 39, 510–513. doi: 10.1016/0007-1226(86)90122-0
Long, I., Malone, S. A., Tolan, A., Burgoyne, K., Heron-Delaney, M., Witteveen, K., et al. (2016). The cognitive foundations of early arithmetic skills: it is counting and number judgment, but not finger gnosis, that count. J. Exp. Child Psychol. 152, 327–334. doi: 10.1016/j.jecp.2016.08.005
Marton, F., and Neuman, D. (1990). “Constructivism, phenomenology, and the origin of arithmetic skills,” in Transforming Young Children's Mathematics Education, eds L. P. Steffe and T. Wood (Dordrecht: International Perspectives, Kluwer, 62–75.
Mogilner, A., Grossman, J. A., Ribary, U., Joliot, M., Volkmann, J., Rapaport, D., et al. (1993). Somatosensory cortical plasticity in adult humans revealed by magnetoencephalography. Proc. Natl. Acad. Sci. U.S.A. 90, 3593–3597. doi: 10.1073/pnas.90.8.3593
Noël, M. P. (2005). Finger gnosia: a predictor of numerical abilities in children? Child Neuropsychol. 11, 413–430. doi: 10.1080/09297040590951550
Patton, M. A., Goodship, J., Hayward, R., and Lansdown, R. (1988). Intellectual development in Apert's syndrome: a long term follow up of 29 patients. J. Med. Genet. 25, 164–167. doi: 10.1136/jmg.25.3.164
Renier, D., Arnaud, E., Cinalli, G., Sebag, G., Zerah, M., and Marchac, D. (1996). Prognosis for mental function in Apert's syndrome. J. Neurosurg. 85, 66–72. doi: 10.3171/jns.1996.85.1.0066
Rusconi, E., Tame, L., Furlan, M., Haggard, P., Demarchi, G., Adriani, M., et al. (2014). Neural correlates of finger gnosis. J. Neurosci. 34, 9012–9023. doi: 10.1523/JNEUROSCI.3119-13.2014
Sarama, J., and Clements, D. H. (2009). Early Childhood Mathematics Education Research: Learning Trajectories for Young Children. London: Routledge.
Sarimski, K. (1997). Cognitive functioning of young children with Apert's syndrome. Genet Counsel. 8, 317–322.
Shipster, C., Hearst, D., Dockrell, J. E., Kilby, E., and Hayward, R. (2002). Speech and language skills and cognitive functioning in children with Apert syndrome: a pilot study. Int. J. Lang. Commun. Disord. 37, 325–343. doi: 10.1080/13682820210138816
Stark, Z., McGillivray, G., Sampson, A., Palma-Dias, R., Edwards, A., Said, J. M., et al. (2015). Apert syndrome: temporal lobe abnormalities on fetal brain imaging. Prenat. Diagn. 35, 179–182. doi: 10.1002/pd.4515
Steffe, L., and Cobb, P. (1988). Construction of Arithmetical Meanings and Strategies. New York, NY: Springer.
Steffe, L., von Glasersfeld, E., Richards, J., and Cobb, P. (1983). Children's Counting Types: Philosophy, Theory, and Application. New York, NY: Praeger.
Strauss, E., Sherman, E. M., and Spreen, O. (2006). A Compendium of Neuropsychological Tests: Administration, Norms, and Commentary. New York, NY: Oxford University Press.
Taghinia, A. H., Yorlets, R. R., Doyle, M., Labow, B. I., and Upton, J. (2019). Long-term functional upper-extremity outcomes in adults with Apert syndrome. Plast. Reconstr. Surg. 143, 1136–1145. doi: 10.1097/PRS.0000000000005479
Thompson, I. (1995). The role of counting in the idiosyncratic mental calculation algorithms of young children. Eur. Early Childh. Educ. Res. J. 3, 5–16. doi: 10.1080/13502939585207651
Tolarova, M. M., Harris, J. A., Ordway, D. E., and Vargervik, K. (1997). Birth prevalence, mutation rate, sex ratio, parents' age, and ethnicity in Apert syndrome. Am. J. Med. Genet. 72, 394–398. doi: 10.1002/(SICI)1096-8628(19971112)72:4<394::AID-AJMG4>3.0.CO;2-R
Upton, J. (1991). Apert syndrome. Classification and pathologic anatomy of limb anomalies. Clin. Plast. Surg. 18, 321–355.
Wilkie, A. O., Slaney, S. F., Oldridge, M., Poole, M. D., Ashworth, G. J., Hockley, A. D., et al. (1995). Apert syndrome results from localized mutations of FGFR2 and is allelic with Crouzon syndrome. Nat. Genet. 9, 165–172. doi: 10.1038/ng0295-165
Yacubian-Fernandes, A., Palhares, A., Giglio, A., Gabarra, R. C., Zanini, S., Portela, L., et al. (2004). Apert syndrome: analysis of associated brain malformations and conformational changes determined by surgical treatment. J. Neuroradiol. 31, 116–122. doi: 10.1016/S0150-9861(04)96978-7
Keywords: Apert syndrome, arithmetic, early number, finger gnosis, syndactyly, finger mobility
Citation: Hilton C (2019) Fingers Matter: The Development of Strategies for Solving Arithmetic Problems in Children With Apert Syndrome. Front. Educ. 4:131. doi: 10.3389/feduc.2019.00131
Received: 04 December 2018; Accepted: 25 October 2019;
Published: 26 November 2019.
Edited by:
Susana Castro-Kemp, University of Roehampton London, United KingdomReviewed by:
Lulu Healy, King's College London, United KingdomArif Mahmud, University of Roehampton London, United Kingdom
Copyright © 2019 Hilton. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Caroline Hilton, Y2Fyb2xpbmUuaGlsdG9uJiN4MDAwNDA7dWNsLmFjLnVr
 Caroline Hilton
Caroline Hilton