
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Educ. , 04 June 2019
Sec. Educational Psychology
Volume 4 - 2019 | https://doi.org/10.3389/feduc.2019.00049
This article is part of the Research Topic Process Data in Educational and Psychological Measurement View all 29 articles
 Sarah L. Toton*
Sarah L. Toton* Dennis D. Maynes
Dennis D. MaynesThe detection of examinees who have previously accessed proprietary test content is a primary concern in the context of test security. Researchers have proposed using item response times to detect examinee pre-knowledge, but progress in this area has been limited by a lack of real data containing credible information about pre-knowledge and by strict statistical assumptions. In this work, an innovative, but simple, method is proposed for detecting examinees with pre-knowledge. The proposed method represents a conditional scaling that assesses an examinee's response time to a particular item, compared to a group of examinees who did not have pre-knowledge, conditioned on whether or not the item was answered correctly. The proposed method was investigated in empirical data from 93 undergraduate students, who were randomly assigned to have pre-knowledge or not. Participants took a computerized GRE Quantitative Reasoning test and were given no items, half the items, or half the items with correct answers to study before the test, depending on their condition. Exploratory analysis techniques were used to investigate the resulting values at both the item and person-level, including factor analyses and cluster analyses. The proposed method achieved impressive accuracy of separation between disclosed and undisclosed items and examinees with and without pre-knowledge (96 and 97% accuracy for cluster analyses, respectively), demonstrating detection power for item disclosure and examinee pre-knowledge. The methodology requires minimal assumptions about the data and can be used for a variety of modern test designs that preclude other types of data forensic analyses.
Greater access to technology and the rise of standardized testing have led to an increase in threats of cheating on tests. Pre-knowledge of exam content occurs when exam items, options, and/or answers (presumed or actual) are harvested and shared with future examinees. Examinees may memorize or record exam content and divulge that information to future examinees via conversations, forums or online groups, review courses, shared files, or even by selling exam content online. The result is examinees who have accessed exam content prior to testing, gaining an unfair advantage through pre-knowledge of the content. When items are disclosed and pre-knowledge is gained, test security is violated and the validity of test scores should be questioned. In this paper, a new method for analyzing response time data is proposed that makes minimal assumptions about the nature of the data and provides meaningful information about extreme response times, aiding in the detection of disclosed items and examinees with pre-knowledge.
There are several known cases in which widespread pre-knowledge was observed after exam content was disclosed. In one case, the certifications of 139 physicians were suspended for soliciting or sharing exam content through exam preparation courses (American Board of Internal Medicine, 2010). In another case, more than 250 examinees who allegedly accessed or shared exam content on social media sites were identified and penalized (Federation of State Boards of Physical Therapy, 2015). In yet another case, the average GRE score for several countries increased by 50–100 points on test sections with scaled scores ranging from 200 to 800 (Kyle, 2002). It was discovered that exam content was being posted and widely accessed by examinees in these countries. Information on the prevalence of pre-knowledge is understandably difficult to obtain, but cases like these can provide information about the potential magnitude of the issue when the stakes for exams are high.
Pre-knowledge is difficult to detect because there are not usually external signs of this type of cheating (Bliss, 2012). Typically, examinees with pre-knowledge have accessed and memorized exam content before testing. These factors mean that the detection of pre-knowledge must be accomplished through data forensics analyses rather than through surveillance by test proctors or video cameras.
Examinees with pre-knowledge presumably do not answer test questions by conventional independent and intellectual means. Given that standardized tests have many respondents providing predictable and valid response patterns, examinees with pre-knowledge likely have different, identifiable response patterns in their data. In order to detect examinee pre-knowledge, it is important to understand how pre-knowledge influences data patterns. Differences are likely to manifest in both the item scores and the response time patterns. Additionally, examinees with pre-knowledge are likely respond to disclosed and undisclosed items differently, even after item difficulty and complexity are taken into account.
Examinees with pre-knowledge are likely to receive a higher score than they would have given their own ability, although their exact score depends on: the accuracy of the source of the pre-knowledge, their capability to memorize and recall the test content, and their ability level prior to obtaining pre-knowledge. Thus, score is not likely to be a powerful predictor of pre-knowledge unless it is analyzed in combination with other variables, such as item response times (RTs) or latencies.
There are many possible patterns that could represent pre-knowledge, but at a basic level, examinees with pre-knowledge are expected to:
• score higher on disclosed items than other items, because they likely accessed answers to these items while preparing for the exam (van der Linden and van Krimpen-Stoop, 2003; Belov, 2016a; Toton et al., in preparation);
• avoid or neglect studying for the test, thus receiving lower scores on undisclosed items than other items; and
• respond more quickly to disclosed items than to other items, because they were previously exposed to these items, and thus may spend less time reading the item content and selecting a response (van der Linden and van Krimpen-Stoop, 2003; Toton et al., in preparation).
Although we have separated items into disclosed and undisclosed for the purpose of this research, it is very common that the status of a group of items is unknown. Thus, it is important to note that detecting an item as undisclosed does not necessarily indicate that the item has not been disclosed. In addition, different subsets of examinees may have pre-knowledge of different items.
The above patterns in item scores and response times are generally expected to be true when pre-knowledge is present, although variability in these patterns is to be expected. The statistical methods to detect pre-knowledge use some or all of these patterns in order to identify examinees who are suspected of having pre-knowledge and/or items that may have been disclosed.
A wide variety of statistical approaches for detecting pre-knowledge have been explored in the literature and it is beyond the scope of this paper to review all of them. We will briefly describe categories of methods to detect pre-knowledge and a few methods to represent each category. For more comprehensive reviews on the wide variety of statistics used to detect pre-knowledge, see Bliss (2012), Eckerly (2017), or Scott (2018). Categories of methods to detect pre-knowledge include analyses of person-fit, similarity, score differences, and response times. Some methods may span multiple categories. For example, the method proposed in this paper applies the logic of person-fit and score-differencing statistics to response time data.
Person-fit statistics only require item scores to compute and are a part of a typical psychometric analysis. Thus, computing person-fit statistics to detect pre-knowledge is a standard approach for psychometricians. Examinees without pre-knowledge are expected to respond to test items in Guttman patterns, such that examinees are expected to answer easier test items correctly up until a specific difficulty level and then answer all test items harder than that level incorrectly (Guttman, 1944). Person-fit statistics quantify the degree of misfit between an examinee's responses and the expected Guttman pattern.
One person-fit statistic that is a common baseline for detecting pre-knowledge is lz (Drasgow et al., 1985). This statistic is the standardized log likelihood of a test response, based on an Item Response Theory (IRT) model. It is assumed that lz is normally distributed, but that is often not the case in live data. Karabatsos (2003) assessed the performance of 36 person-fit indices in detecting unusual response patterns (e.g., a high ability examinee answering easy items incorrectly, but difficult items correctly), including lz. The best statistic, Ht (Sijtsma and Meijer, 1992), was a non-parametric statistic that compared an examinee's response pattern to the response patterns of all other examinees. Generally, non-parametric (i.e., those not based on IRT models) person-fit indices performed better than parametric indices. Another study, which applied IRT models to simulated data to detect cheating found that the lco difference (Ferrando, 2007), a sum of squared, standardized residuals across items, performed better than other methods, including Ht (Clark et al., 2014). All of the tested person-fit methods performed poorly on data with low rates of cheating.
The main limitations of using person-fit statistics to detect pre-knowledge are that they have relatively lower power than other statistics (Belov, 2016a) and that all types of misfit to the model is identified and flagged, so drawing inferences about what may have caused the misfit to the model (e.g., examinee pre-knowledge) is extremely difficult. Additionally, if pre-knowledge is widespread, it may be that examinees without pre-knowledge exhibit misfit.
Similarity statistics quantify the agreement between examinees' responses. Answer-copying statistics are a type of similarity statistics that are typically computed for a single pair of examinees. Similarity statistics are a broader category than answer-copying statistics since they do not require labeling of source and copier examinees and are generally designed to detect groups larger than two who may have shared a source of pre-knowledge.
Angoff (1974) developed and researched the performance of eight answer-copying statistics. The two best statistics were those that (1) identified anomalously large numbers of identical incorrect responses in a pair of examinees, compared to other pairs of examinees with similar products of incorrect and identical incorrect responses, and (2) represented the maximum identical incorrect responses, or omitted responses, in a string of identical responses, compared to other pairs of examinees with similar scores. Similarly, Frary et al. (1977) developed the g2 statistic to compare the number of identical responses in a pair to the expected number of identical responses. To compute the expected number of identical responses, a source and a copier are labeled in the pair and then the probability that the copier selected the same response as the source is calculated and these probabilities are summed over all items. This difference between the expected identical responses and observed identical incorrect responses is then standardized. This statistic is based in classical test theory (CTT). Wollack (1997) expanded on this work, developing the omega (ω) statistic, which is computed in a similar manner, but is based in the framework of IRT and uses the nominal response model (Bock, 1972) to obtain the probabilities that each examinee will select a particular response option.
van der Linden and Sotaridona (2006) and Maynes (2017) also used the nominal response model to estimate probabilities of an examinee selecting a particular response. The generalized binomial test developed by van der Linden and Sotaridona (2006) counts the total identical answers between examinees and compares it to the expected number. The M4 similarity statistic compares the observed identical incorrect, identical correct, and non-matching responses to the expected counts, based on the examinees' scores, using a generalized trinomial distribution (Maynes, 2017). Both of these methods provide a way to assess mismatch between the expected level of similarity between examinees and the observed level of similarity.
The main limitation of using similarity statistics to detect pre-knowledge is that their performance is known to be affected by the examinees' scores. High-scoring examinees should have strong agreement in their responses, since they provide mostly correct responses. Additionally, similarity statistics were developed for use on fixed form tests, where all examinees receive the same items, but often cannot achieve sufficient power in modern test designs such as computerized adaptive testing (CAT) or linear-on-the-fly testing (LOFT) because the number of items in common across examinees is typically very small. Thus, similarity analyses are powerful but often cannot be conducted with confidence in data obtained from modern test designs, due to the small number of common items.
If information about the items is known, different subsets of items can be scored and then the scores compared across subsets. For example, if a subset of items is known to be undisclosed (e.g., a group of new items is added to an exam), scores on the undisclosed items can be compared to scores on the remainder of the items. Examinees with much lower scores on the undisclosed subset and much higher scores on the remainder of the items should be detected as anomalous. These analyses are often referred to as score-differencing or differential person functioning analyses.
The Deterministic, Gated Item Response Theory Model proposed by Shu et al. (2013) detects examinees with pre-knowledge by separating probably disclosed items and probably undisclosed items. Score differences between the two item types are computed and examinees are split into those suspected of having pre-knowledge and those who are not based on those differences. Depending on the classification of the examinee and the item type, the ability level on the measured construct and the ability level due to cheating are both estimated. In this way, the model can identify a “true” ability level, untainted by the influence of probably disclosed items. Eckerly et al. (2015) expanded on this work, proposing a process of purifying the scale of item and person parameters by removing detected examinees from the computation of item difficulty parameters and then using the purified item parameters to re-estimate ability estimates. This modification reduced false-positives, while maintaining detection power.
Belov (2017) developed the posterior shift statistic, which is a Bayesian analysis that compares posterior distributions of ability between subsets of items. For example, comparing known disclosed items to remaining items, or known undisclosed items to the remaining items. An expansion of this work injects a posterior shift statistic into a specially organized Markov Chain Monte Carlo to simultaneously detect disclosed items and examinees with pre-knowledge in a situation where a subset of undisclosed items is known (Belov, 2016b). The results suggest that the method performs well, even when the known undisclosed subset actually contains up to 15% disclosed items, but not when the known undisclosed subset contains 30% disclosed items. Thus, the method is robust to some error in specifying the undisclosed subset, but requires that the majority of the items in the undisclosed subset be accurately identified.
The main limitation of score-differencing statistics is that the additional information on items they require to compute is often unavailable or inaccurate. This can limit the application of score-differencing statistics to live data.
Flawed key analyses are a subset of score-differencing statistics, although they are also strongly related to similarity analyses. Items are often disclosed without official answer keys and examinees who create their own keys often make errors. If a disclosed answer key contains errors and is known, a flawed key analysis can provide valuable information about pre-knowledge. Flawed keys are commonly discovered online or by finding keys used by rogue review courses, who sometimes create practice tests out of live items and provide an answer key to score the test. To conduct a flawed key analysis when the disclosed key is known, each test is scored using the actual key and the disclosed key, and examinees with significantly higher scores on the disclosed keys are identified (Scott, 2018).
Some research has focused on estimating latent sources, which includes flawed keys, from response data. To estimate a flawed key, similarity statistics can be utilized. Scott (2018) proposed a method of estimating disclosed keys that involved computing (Wollack, 1997) omega for all possible pairs of examinees. Four methods were compared to estimate the disclosed key, selecting each item's key as the response from the (1) source in the most source-copier pairs that exceeded a threshold of omega, (2) source in the source-copier pair with the largest omega value, (3) examinee's response pattern that was in the most source-copier pairs where omega exceeded a threshold, and (4) the source that was associated with the most copiers with maximum omega values. The results showed that the fourth method performed with very high accuracy in live data and the third performed best in simulated data, indicating that the estimation of flawed keys may require different methods in different contexts.
Maynes and Thomas (2017) analyzed clusters of examinees to estimate disclosed keys. This analysis assumes that a similar cluster of examinees has been detected using the Wollack and Maynes (2016) method, which is similar to nearest neighbors clustering. In the Wollack and Maynes (2016) method, pairwise similarity is computed for all examinees. Then, similarity values and test responses are plotted against each other in a dense graph of edges. Edges that fall below a selected threshold are removed and then clusters are created by labeling the groups of connected edges. Maynes and Thomas (2017) analyzed such clusters to extract the disclosed key using four methods, selecting each item's key as the response that (1) was most commonly chosen, (2) maximized the corrected item-total correlation, (3) contributed most to a chi-square, comparing the expected responses from the nominal response model to the actual responses, and (4) had the highest Kullback-Leibler divergence (Kullback and Leibler, 1951). Simulations varying the latent ability of the disclosed key and the amount of answer copying were performed. The results showed that the method that maximized the corrected-item total correlation was the best at accurately estimating the disclosed key, particularly with high amounts of answer-copying or large cluster sizes.
Haberman and Lee (2017) expanded this research to identify multiple disclosed keys, which were estimated using multidimensional IRT models. Once the multiple disclosed keys were estimated, examinees whose responses were identical or nearly identical to those disclosed keys were identified. This method appears to have good power and low false-positive rates, but it was tested on live data, so it is impossible to determine the power of the method by comparing the detected examinees to the examinees who actually used disclosed keys.
The main limitation of flawed key analyses is that they require additional information about disclosed keys to be known or estimated. However, once disclosed keys are obtained, a flawed key analysis can provide very powerful and compelling evidence that an examinee had pre-knowledge.
The change from paper-and-pencil based testing to computer-based testing allowed the automatic collection of RT data, which inspired researchers to develop a variety of methodologies to detect pre-knowledge using RTs. van der Linden and van Krimpen-Stoop (2003) noted that due to the continuous nature of RTs, they contain more information, variability, and granularity than item score data.
van der Linden and van Krimpen-Stoop (2003) proposed a model to identify unusual RTs, particularly those resulting from pre-knowledge and item harvesting, on computerized adaptive tests. Item scores were analyzed using a three-parameter logistic IRT model (Birnbaum, 1968) and the RTs were modeled using a log-normal model. The log-normal RT model, originally published by Thissen (1983), estimates the time required for an item, the speed of the examinee, and the average RT for the population. The model by van der Linden and van Krimpen-Stoop (2003) assumes that the model for item scores is independent of the model for response times. Expected RTs for each item were estimated, using both maximum likelihood and Bayesian estimates. Extremely unusual RTs were detected by investigating the residual differences between the expected RTs and the observed RTs. The Bayesian residuals had better detection rates than the others, but also had higher false-positive rates. This method assumes that RTs have the same variance across items and examinees and that IRT model parameters for the data are accurate and consistent with known parameters. van der Linden and Guo (2008) expanded upon this research, proposing a combination of the RT and IRT models, allowing the examinees' RTs to be adjusted for their speed to investigate the correspondence of their RT patterns with the estimated time required for each item.
Meijer and Sotaridona (2006) introduced the effective response time, which is an estimate of the time necessary to respond to an item correctly. Like van der Linden and van Krimpen-Stoop (2003), they proposed a three-parameter logistic model with a log-normal model for the RTs, estimating the speed of the examinee, the time required for each item, and the average RT for the population. However, only RTs of examinees with correct responses and with probabilities of answering correctly greater than the estimated pseudo-guessing parameter were used in the computation of the effective response time. This eliminated the effects of RTs caused by random guesses and other test taker behaviors that may yield uninformative RTs. This method has reasonable Type I error rates and has been used to detect pre-knowledge in K-12 data (Liu et al., 2013).
These methods require strict assumptions be met to model the RT data. They assume that each examinee has a constant working speed, the majority of examinees do not have pre-knowledge, item parameters are known, and that difficult items take longer than easier items. Additionally, item complexity, which can be described as the number of steps that must be completed to respond to an item, appears to be largely ignored. It is possible to have a very easy item that requires a large number of steps. It is possible that the difficulty of the item could be low, while the complexity of the item is high, which should affect the RTs of the item. Most of the available models for RTs ignore important factors that influence the data and require strict assumptions about the nature of the data.
In this paper, a simple, but innovative, method for using response times to detect disclosed items and examinees with pre-knowledge is proposed that makes minimal assumptions about the data and is appropriate for a wide variety of test designs.
We propose a measure of the extremeness of a response time that compares the RT for each person on each item to a group of examinees without pre-knowledge who received the same score on that item. Comparing a sample of data tainted by pre-knowledge to another tainted sample and expecting to detect extreme examinees is unlikely to yield the desired results. In the proposed method, the group of examinees without pre-knowledge (i.e., the uncontaminated comparison group) was the control condition of an experiment on pre-knowledge. However, in practice there is often no such group. Data from pilot testing or from the first day of testing for a particular exam form could be used and assumed to be uncontaminated by pre-knowledge, since exams are unlikely to be compromised prior to the first day of administrations (barring the help of a program insider or hacking the server).
The RTs for each examinee on each item can be transformed using the natural log transformation to approximate normality. After computing means and standard deviations of the log RTs for each item for the uncontaminated comparison group, the individual log RTs can be converted into conditional zRTs, so named because the log RTs are conditioned on item score, compared to the uncontaminated comparison group, and the statistics of interest are computed as z-scores. The conditional zRT for person j on item i with an item score of s can be computed using Equation (1).
In Equation (1), RTijs represents the log-transformed response time for person j on item i with an item score of s (0 or 1), represents the average log RT for the uncontaminated comparison group on item i with an item score of s, and σCis represents the standard deviation of the log RTs for the uncontaminated comparison group on item i with an item score of s. Thus, conditional zRTs can be computed by taking the difference between an examinee's RT on an item and the average RT on that item for an uncontaminated comparison group with the same item score, divided by the standard deviation of the RTs on the item for the uncontaminated comparison group with the same item score.
After they are computed, conditional zRTs can be analyzed using exploratory grouping techniques, such as cluster analysis, to identify groups of items (disclosed and undisclosed) and examinees (with and without pre-knowledge). In the following sections, each particular component of the conditional zRTs that captures important information is discussed.
Very fast response times can be produced by fast examinees, by testing strategies such as rapid guessing, or by examinees with pre-knowledge. To distinguish between these response patterns, item score should be taken into account. Response time data are messy and depend upon item difficulty, item complexity, personal testing style, testing strategies, and the speededness of a test. RTs can encompass a huge range and still be representative of normal test-taking behavior. Underlying multidimensionality coupled with high variability makes it difficult to determine which RTs should be considered extreme. However, conditioning RTs based on item score can help to distinguish between the potential behavioral causes for extreme RTs. For example, random guesses may yield fast RTs with mostly incorrect responses, but responses made with pre-knowledge may yield fast RTs with mostly correct responses.
Examinees with pre-knowledge who attempt to mask their response patterns would also likely be detected by the proposed method, as their pattern of conditional zRTs is likely to differ from examinees without pre-knowledge. For example, an examinee with pre-knowledge may complete the test quickly and then spend a large amount of time on a single item to lengthen the test time, but conditional zRTs should indicate that the examinee was anomalously fast and responded correctly on a large number of items, then anomalously slow on a single item.
With data contaminated by cheating, it can be difficult to find meaningful separation in groups of items or persons, especially when information about the categories is unknown. One risk when analyzing contaminated data is that the results may not actually represent pre-knowledge. Thus, inferences made from contaminated data may penalize examinees with potentially life-changing consequences. Because many normal test-taking behaviors and strategies are not well-understood, model bias is a distinct possibility. It is important that examinees are not detected simply because they have employed a different test-taking strategy or exhibited an unusual test-taking style.
When computing conditional zRTs, the log RT for each examinee on each item is compared to the log RTs for that item obtained from an uncontaminated comparison group. If the uncontaminated comparison group is sufficiently large, it can be assumed to include a wide variety of test-taking strategies and other normal variation in test-taking behaviors.
Pre-knowledge is difficult to study because high-quality data are scarce. Data containing pre-knowledge are generally gathered from one of three sources: simulations, using measures that approximate pre-knowledge in real data, or experiments that empirically manipulate pre-knowledge. Each of these methods has strengths and weaknesses, which are comprehensively discussed in Thomas and Maynes (2018).
Simulations are often used to test methodologies for detecting pre-knowledge, but they do not contribute to understanding the natural patterns caused by pre-knowledge and are unlikely to capture the full variability of normal test-taking behaviors and strategies used by real examinees. Using simulated data that is too clean and does not capture the noise of normal test-taking may artificially inflate the performance of detection methods that are tested on such data.
In real data, the examinees with pre-knowledge are typically unknown. Examinees who are suspected of having pre-knowledge may be identified, but the credibility of this information varies widely between testing programs and exams. Thus, using this information as a dependent variable can introduce a significant element of uncertainty.
Using experiments to manipulate pre-knowledge allows for the creation of known examinees with pre-knowledge for a known subset of items. Tiemann et al. (2014) conducted an experimental study of pre-knowledge by asking 20 participants to write down test content they remembered after taking a test. The participants were told the next participant would be able to use this content while taking the test. Some participants were informed they would be asked to remember the content after the test and some were not. The results showed that many participants remembered imprecise information about the test content, but few remembered specific information. Ten participants who were informed in advance that they would be asked to remember test content demonstrated poor recall of the content, with only seven items and two answers remembered specifically and correctly. Surprisingly, 10 participants who were not informed they would be asked to remember test content in advance demonstrated better recall of the content, with nine items and 11 answers remembered specifically and correctly. The next part of the study investigated if access to the test content provided by previous examinees prior to testing raised scores. Two cheat sheets were created, one based on content remembered by participants who were informed they would be asked to recall test content in advance and one from those who were not. Students were randomly assigned to receive one of these cheat sheets to study and then took the test. The results showed no significant differences in test scores between students who received cheat sheets and students who did not.
A major advantage of laboratory experiments is that the data encompass the complexity of test-taking behavior and the identities of examinees with pre-knowledge can be known. However, previous studies attempting to mimic pre-knowledge in the laboratory have shown null results (Tiemann et al., 2014), possibly because participants were unmotivated or because the pre-knowledge provided was too weak to find effects. In the current study, experimental data were analyzed because of the benefits of having known groups of items and examinees while capturing normal test-taking variability.
The data utilized in this study were collected with a 3 (Pre-Knowledge: Control vs. ItemOnly vs. Item+Answer) × 2 (Item Disclosure: Disclosed vs. Undisclosed) within and between-subjects design. All participants took a computerized GRE Quantitative Reasoning test. Pre-knowledge was manipulated by allowing some participants access to some test items (with or without accompanying answers) prior to the test. In the control condition, participants took the test but were not exposed to any of the test items in advance. In the experimental conditions, participants were allowed to study 12 of the 25 test items for 20 min before the test. In the ItemOnly condition, only the items themselves were provided to the participants (without their corresponding answers). In the Item+Answer condition, both the items and the correct answers were provided to the participants.
The design of this study was different from previous experimental studies in a few key ways. First, perfectly accurate disclosed test items (and answers in the Item+Answer condition) were provided to participants, rather than attempting to have potentially unmotivated participants harvest the items themselves. Second, the effect of the examinees' motivation to harvest items or cheat was removed by simply assigning some examinees to study provided disclosed materials and some not to. The task was not identified as relevant to cheating in any way, as the researchers who conducted the study simply requested that examinees study the materials. The conditions only differed in whether or not they received test content in advance, and, if they did, the nature of that test content. Thus, pre-knowledge was investigated regardless of the examinees' ability to harvest items or motivation to cheat.
It was expected that participants in the study who were in the experimental conditions and given pre-knowledge of some items would select more correct answers on disclosed items than undisclosed items and respond more quickly to disclosed items than undisclosed items, as discussed in the Expected Patterns of Examinees with Pre-Knowledge section of this paper.
The goal of the current study is to implement the proposed method of computing conditional zRTs, described above, in experimental data to create datapoints that capture complex information about the response patterns of the examinees. Particular attention will be paid to the feasibility of calculating the conditional zRTs and the assessing which components of the statistic provide the most important information. The conditional zRTs will then be analyzed using exploratory grouping methods, such as cluster and factor analyses, to attempt to identify groups of items and groups of examinees. The performance of the method in identifying groups of items (disclosed and undisclosed) and examinees (with and without pre-knowledge) will be assessed using the known groups contained in the experimental data. The purpose of the study is to assess a new method for detecting examinees with pre-knowledge and disclosed items in experimental data. If the method performs well, it may be able to be used to detect disclosed items and examinee pre-knowledge in a variety of live testing data, including those with modern test designs that preclude many data forensics analyses.
Participants were 93 undergraduate psychology students (28 men, 64 women, and one gender non-conforming) at the University of Virginia. The sample was composed of primarily first year students (61% first year, 18% second year, 17% third year, 3% fifth year, and 1% exchange students). Participants took part in a 90 min laboratory session through the psychology department participant pool and were compensated with 1.5 h credit.
This study was conducted according to the recommendations of, and was approved by, the Institutional Review Board for Social and Behavioral Sciences at the University of Virginia. All subjects gave written informed consent in accordance with the Declaration of Helsinki.
Participants were randomly assigned to condition immediately after signing up for a timeslot to participate in the study. When participants arrived at the lab, they were asked to leave their belongings with the researcher and enter a small room with a desk and computer. All participants were given a yellow sheet of laminated paper that they could put under the door if they wanted to ask questions or contact the researcher. This prevented the participants from discovering that other participants were receiving different treatment than they were (i.e., studying test items in advance) and completing the test more quickly. After gathering informed consent and giving participants instructions, the researcher left the participant alone.
Participants in the experimental conditions were first given a packet of materials that they were told to study for 20 min before taking the test. The packet contained instructions on how to use the study materials, a test form with 12 of the 25 test items, and two pieces of scratch paper. The 12 test items in the ItemOnly condition contained only the test items and possible answer choices; the same 12 items were provided in the Item+Answer condition, including red circles indicating the correct answers.
After the pre-knowledge stage, participants in the experimental conditions took a computerized Qualtrics version of an out-of-circulation, paper-and-pencil GRE Quantitative Reasoning test (Educational Testing Service, 2017) that the researchers were granted permission to use. Computerizing the test allowed for the collection of response time data for each item.
Participants in the control condition proceeded immediately to the computerized test, without first completing the pre-knowledge stage. All participants were given 40 min to complete the test. Participants who finished any stage of the experiment in less than the allotted time could notify the researchers by slipping a yellow paper under the door (to avoid participants from overhearing others) and advance to the next stage of the experiment.
After the test, participants were given 20 min to complete a battery of individual difference measures to assess factors that might impact their performance on the test or their general willingness to cheat. This battery included self-reported effort and time spent studying the packet of 12 items (for experimental conditions only), information about the testing experience of the participant during the study, math proficiency, previous exposure to GRE study materials, demographics, test anxiety (Westside Test Anxiety Scale, Driscoll, 2007), the Big Five personality traits (TIPI, Gosling et al., 2003), Moral Foundations (MFQ30, Graham et al., 2011), and religiosity/spiritualism. The order of the scales after demographics was randomized across participants.
For more comprehensive information about the study design, participants, or measures, see Toton et al. (in preparation).
The data used in this paper was obtained by disclosing a perfectly accurate key of 12 of the 25 items to a subset of the examinees. Examinees with pre-knowledge exhibited higher scores and faster RTs on disclosed items than examinees without pre-knowledge (Toton et al., in preparation). In contrast, the examinees with and without pre-knowledge did not differ significantly in item scores or log RTs for undisclosed items. Log RTs for each item for participants in all conditions are presented in Figure 1. For more information about how the three conditions differed from one another on all measures, see Toton et al. (in preparation).
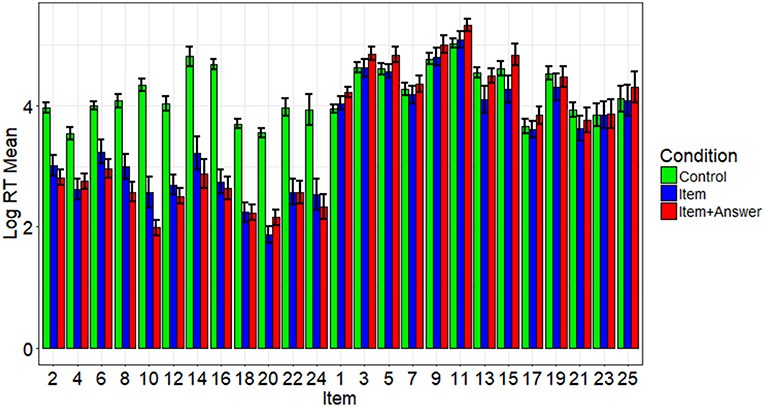
Figure 1. Average log RTs by item and condition. This figure shows the average log RT by condition (see color) and item (see x-axis). Even-numbered items were disclosed and odd-numbered items were not. The error bars represent the standard errors.
Three different transformations for approximating normality in the RT data were investigated: the square root, logistic, and inverse transformations. The logistic, or natural log transformation, was the best transformation for achieving an approximately normal distribution for the majority of the items (14/25) in the data, as assessed by the Shapiro-Wilk test (Shapiro and Wilk, 1965). The results suggested that the square root transformation could also have been used as it was the best transformation for approximating normality for 10 of the 25 items.
Descriptive statistics for each condition are presented in Table 1. Figures 2, 3 show the response patterns of item scores and log RTs for an example examinee with and without pre-knowledge. These response patterns are a graphical representation of the information that is captured in the conditional zRTs. The examinees whose data are shown in Figures 2, 3 were selected because their data mimicked patterns that were expected based on theoretical ideas of taking the test with and without pre-knowledge. However, there is large variability in the patterns for examinees, particularly in the patterns of examinees who appear to be guessing for much of the test or examinees who appear to be very high in ability on the tested construct. The selected data shown in Figures 2, 3 demonstrate support for the theoretical ideas concerning the response patterns exhibited by examinees who took the test with and without pre-knowledge.
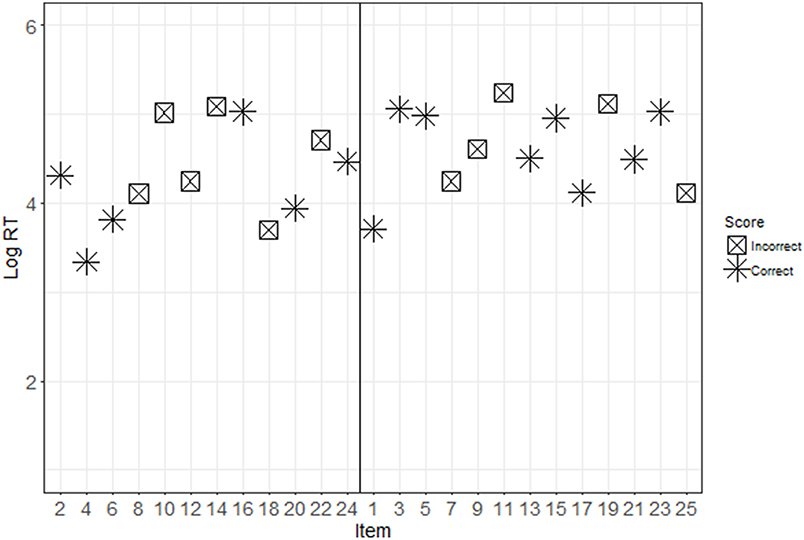
Figure 2. Response patterns for a control participant. This figure shows the item scores (see marker shape) and log RTs (y-axis) for disclosed (even, presented on the left) and undisclosed (odd, presented on the right) items. Note that for this control participant, there is no discernable difference between the response patterns for the disclosed and undisclosed items.
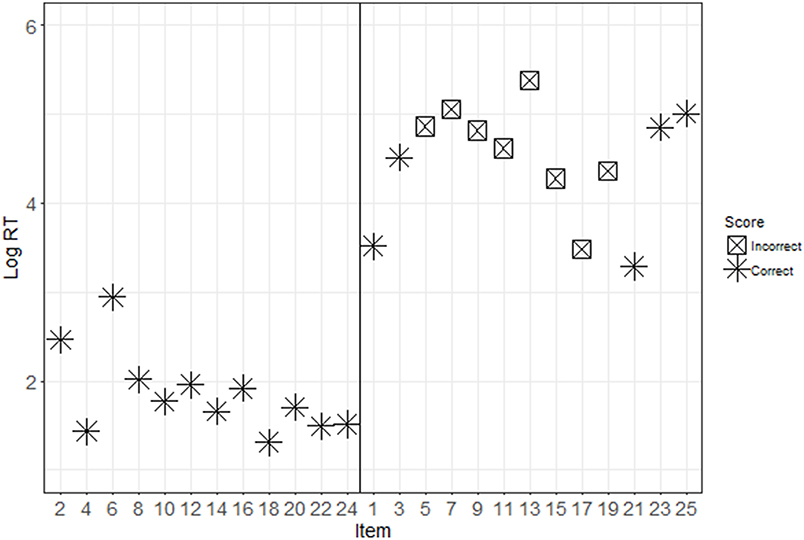
Figure 3. Response patterns for an ItemOnly participant. This figure shows the item scores (see marker shape) and log RTs (y-axis) for disclosed (even, presented on the left) and undisclosed (odd, presented on the right) items. Note that for this ItemOnly participant, there is a discernable difference between the response patterns for the disclosed and undisclosed items, such that disclosed items are more likely to be answered correctly and quickly.
To compute the conditional zRTs, the means and standard deviations of the log RTs for each item were computed for control participants (N = 33) for both correct and incorrect responses. The conditional zRTs for each person on each item were computed using Equation (1). No conditional zRTs were computed for incorrect responses to Item 4 because no examinees responded to this item incorrectly in the control or other conditions. No conditional zRTs were computed for incorrect responses to Item 1, because there was only one participant in the control condition who responded to the item incorrectly, so the standard deviation could not be computed. Conditional zRTs were not necessary in this case because no participants in the experimental conditions had incorrect responses to this item that needed to be compared to the control group. Information on the sample size, mean, and standard deviations of the log RTs for the control condition that were used to compute the conditional zRTs are presented in Table 2.
The computation of conditional zRTs based on item score and using an uncontaminated comparison group of examinees without pre-knowledge were decisions based in theoretical considerations. To test if these factors impacted the performance of the conditional zRTs, zRTs were also computed:
• without conditioning on score, using the full sample as a comparison group,
• conditioning on score, using the full sample as a comparison group, and
• without conditioning on score, using the control condition as a comparison group.
The comparison groups were used to compute the means and standard deviations in Equation (1). Note that in the current data, the majority of the participants had item pre-knowledge, so using the full sample as the comparison group should be dramatically different from using just the control condition. There were 60 examinees with pre-knowledge of 12 items, which means that there were 720 total responses of examinees with pre-knowledge to disclosed items (ignoring the possibility of missing data and assuming examinees with pre-knowledge display the expected patterns consistently). If all of these were answered anomalously quickly, then one would expect approximately 720 extremely fast zRTs. When the full sample was used as a comparison group, 69 zRTs were detected when the zRTs were not conditioned on score and 57 were detected when the zRTs were conditioned on score (see Table 3). However, when the control condition was used as the comparison group, more than 500 zRTs were detected; 504 when the zRTs were not conditioned on score and 521 when zRTs were conditioned on score.
The zRTs computed using the full sample were very different than those computed using the control participants as the comparison group, particularly for participants in the ItemOnly and Item+Answer conditions (see Figure 4). Participants in the control condition had similar zRTs no matter which computation was used, but participants in the ItemOnly or Item+Answer conditions were much more likely to have extreme zRTs detected when the control condition was used as a comparison group.
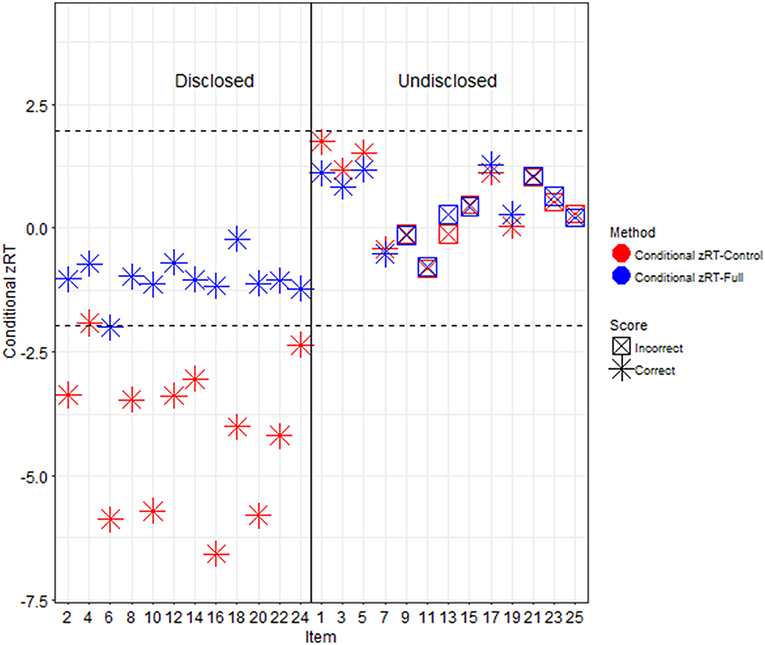
Figure 4. Conditional zRTs computed with different comparison groups. The conditional zRTs for one Item+Answer participant computed with all participants as the comparison group are presented in blue and with only control participants as the comparison group in red. The dashed lines represent z-scores of ±1.96; it is expected that 95% of the distribution of conditional zRTs will fall in between these lines. When all participants were used as the comparison group, the disclosed and undisclosed items appeared similar in terms of conditional zRTs, but when only control participants were used as the comparison group, the disclosed items for this participant appeared to be much more extreme.
The goal of the item-level analyses was to use exploratory data techniques to create groups of items and then to assess those groups to investigate if they represented disclosed and undisclosed items. Cluster and factor analyses were conducted and are presented below. Note that correlations and Kolmogorov-Smirnov tests were also investigated, and achieved good separation of item groups, but are not presented here for the sake of brevity.
K-means cluster analysis is an exploratory data analysis technique used to group datapoints into a number of clusters, where the number of clusters to create is specified by the researcher (Lloyd, 1957). First, k number of cluster center are randomly placed among the data. Second, the points closest to each center are assigned to that cluster. Third, the mean of the points assigned to each cluster is computed and the center is moved to this point. The second and third steps continue until a stable solution is obtained. If group memberships of the data are known, the estimated group memberships obtained in the cluster analysis can be compared with the known group memberships. Cluster solutions were obtained using the “kmeans” function in the “stats” package of R (R Core Team, 2016), using the Hartigan and Wong (1979) algorithm. This algorithm is an efficient k-means analysis that prevents re-analysis of data points that were not assigned to a different cluster in the last step. Comparisons of each datapoint to the cluster centers were based on Euclidean distance and iterations continued until the total within sum of squares was minimized. Cases with missing conditional zRTs were omitted from these analyses, leaving 70 complete cases for analysis. There were nine control participants with missing data, eight ItemOnly participants, and six Item+Answer participants. Two and three-cluster solutions were computed to investigate grouping accuracy for disclosed and undisclosed items and the robustness of the grouping accuracy when different numbers of clusters were specified.
The two-cluster solution grouped the items into two groups containing 14 and 11 items, respectively (see Figure 5). The group of 14 items contained all 13 undisclosed items as well as one disclosed item that was incorrectly grouped (Item 24). The group of 11 items contained all of the remaining disclosed items. Overall, 24 of the 25 items were grouped correctly into disclosed or undisclosed items. Thus, this cluster analysis produced groupings that were 96% accurate in separating disclosed and undisclosed items.
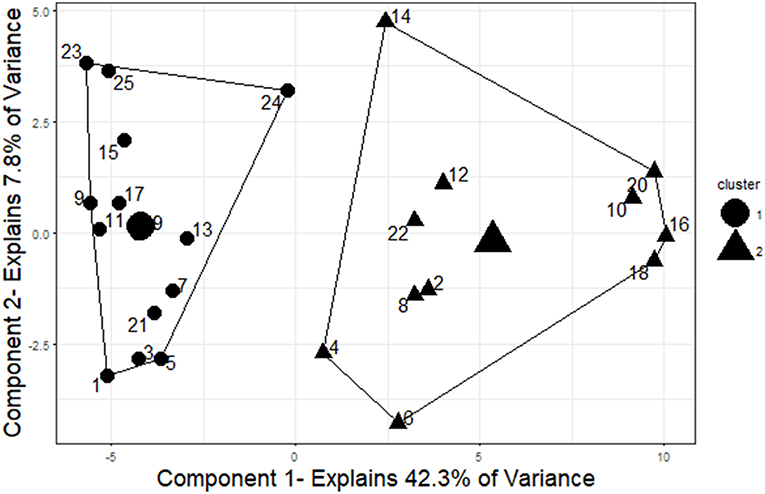
Figure 5. Two-cluster solution for items. The two clusters represent good separation between disclosed (even-numbered) and undisclosed (odd-numbered) items. The cluster centers and cluster membership are indicated by shape (triangles represent the cluster of size 11 and circles represent the cluster of size 14). To visualize the cluster results, components were obtained using principal component analysis, and the clusters are plotted on those components. This plot was created using the “fviz_cluster” function in the “factoextra” package of R (Kassambara and Mundt, 2017).
The three-cluster solution closely mirrored the two-factor solution, again grouping all of the disclosed items except item 24 into a cluster of size 11. The cluster of size 14 observed in the two-cluster solution was split into two clusters in the three-cluster solution, one of size eight and one of size six. The cluster of size eight included only undisclosed items and the cluster of size six included five undisclosed items and one disclosed item (Item 24). This cluster solution was as accurate as the two-cluster solution in grouping items based on their disclosure status.
Three sets of data were analyzed by factor analysis to explore latent components that underly similarities in data: conditional zRTs, item scores, and item log RTs. Factor solutions were assessed for the three sets of data using the “fa” function in the “psych” package of R, excluding missing data in a pairwise fashion (Revelle, 2016). The factor analyses were conducted using principal axis factoring and promax, or oblique, rotations to allow correlations between the factors. For the purposes of this analysis, factor loadings of <0.30 were considered low. One and two-factor solutions were computed to analyze differences in grouping accuracy for disclosed and undisclosed items.
The one-factor solution for conditional zRTs explained 26% of the variance and showed that the 12 disclosed items had factor loadings that were positive and strong on the factor, as well as three undisclosed items (see Table 4). The remaining undisclosed items had weak loadings on the factor, ranging from λ = −0.12 to λ = 0.25. Thus, 22 of the 25 items were grouped with items of the same disclosure status (88% accuracy).
The two-factor results for the conditional zRTs explained 42% of the variance and showed good simple structure, with all 12 disclosed items loading strongly on the first factor and 12 of the 13 undisclosed items loading strongly on the second factor (see Table 4). There were no items with cross-loadings of 0.30 or greater. One undisclosed item, Item 1, did not load strongly onto either factor, but had a negative loading on factor one and a positive loading on factor two. Thus, 24 of the 25 items were grouped with items of the same disclosure status (96% accuracy). When all cases with missing data were excluded, leaving 70 examinees for analysis, the one and two-factor solutions exhibited perfect simple structure with clear separation between disclosed and undisclosed items and no cross loadings of 0.30 or greater.
The factor analyses for item scores excluded item four, since no participants responded to that item incorrectly. The one-factor solution for item scores explained 16% of the variance and showed that 10 disclosed items and seven undisclosed items had factor loadings of 0.30 or greater on the factor. The remaining one disclosed item and six undisclosed items had factor loadings of <0.30 on the factor. Thus, 16 of the 25 items were grouped with items of the same disclosure status (64% accuracy).
The two-factor solution for item scores explained 22% of the variance and showed that nine disclosed items had factor loadings of 0.30 or greater on the first factor and that seven undisclosed items and one disclosed item had factor loadings of 0.30 or greater on the second factor, with no cross loadings of 0.30 or greater. The remaining one disclosed item and six undisclosed items did not load strongly onto either factor. Thus, 16 of the 25 items were grouped with items of the same disclosure status (64% accuracy).
The one-factor solution for log RTs explained 26% of the variance and showed that 12 disclosed items and six undisclosed items had factor loadings of 0.30 or greater on the factor. The remaining seven undisclosed items had factor loadings of <0.30 on the factor. Thus, 19 of the 25 items were grouped with items of the same disclosure status (76% accuracy).
The two-factor solution for log RTs explained 40% of the variance and showed that all 12 disclosed items had factor loadings of 0.30 or greater on the first factor and that 12 of the 13 undisclosed items had factor loadings of 0.30 or greater on the second factor, with no cross loadings of 0.30 or greater. The one remaining undisclosed item did not load strongly onto either factor but had a negative loading on factor one and a positive loading on factor two. Thus, 24 of the 25 items were grouped with items of the same disclosure status (96% accuracy).
The goal of the person-level analyses was to use cluster analyses to create groups of examinees. Cluster solutions were obtained using the “kmeans” function in the “stats” package of R (R Core Team, 2016). Cases with missing conditional zRTs were omitted from these analyses, leaving 70 complete cases for analysis. Two and three-cluster solutions were computed to investigate grouping accuracy for examinees with and without pre-knowledge, the robustness of the grouping accuracy when different numbers of clusters were specified, and to investigate if the three-cluster solution distinguished between control, Item, and Item+Answer participants. Correlational results were also investigated, and showed separation of examinees with and without pre-knowledge, but are not presented here for the sake of brevity.
The two-cluster solution grouped the examinees into two groups containing 26 and 44 participants, respectively (see Figure 6). The group of 26 examinees contained 24 control participants, one ItemOnly participant, and one Item+Answer participant. The group of 44 examinees contained 22 ItemOnly participants and 23 Item+Answer participants. Overall, 68 of the 70 examinees with no missing conditional zRTs were grouped correctly into examinees with or without pre-knowledge (97% accuracy).
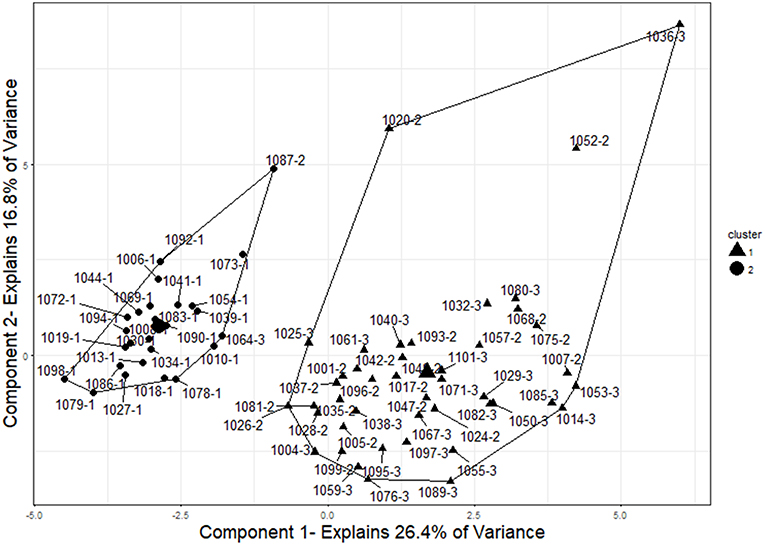
Figure 6. Two-cluster solution for examinees. The two clusters represent good separation between control (IDs that end in−1), ItemOnly (IDs that end in−2), and Item+Answer (IDs that end in−3) participants. Two examinees were grouped incorrectly by this analysis (1064-3 and 1087-2). The cluster centers and cluster membership are indicated by shape (circles represent the cluster of size 26 and triangles represent the cluster of size 44). To visualize the cluster results, components were obtained using principal component analysis, and the clusters are plotted on those components. This plot was created using the “fviz_cluster” function in the “factoextra” package of R (Kassambara and Mundt, 2017).
The three-cluster solution grouped the items into groups containing 26, 27, and 17 examinees, respectively (see Figure 7). The results closely mirrored those obtained in the two-factor solution, as the cluster of size 26 contained the same examinees as in the two-cluster analysis (24 control, one Item, and one Item+Answer). The cluster of 27 examinees contained only examinees with pre-knowledge, 15 ItemOnly participants and 12 Item+Answer participants. Similarly, the cluster of size 17 contained only examinees with pre-knowledge, six ItemOnly participants, and 11 Item+Answer participants. This cluster solution was as accurate as the two-cluster solution in grouping examinees based on whether or not they had pre-knowledge.
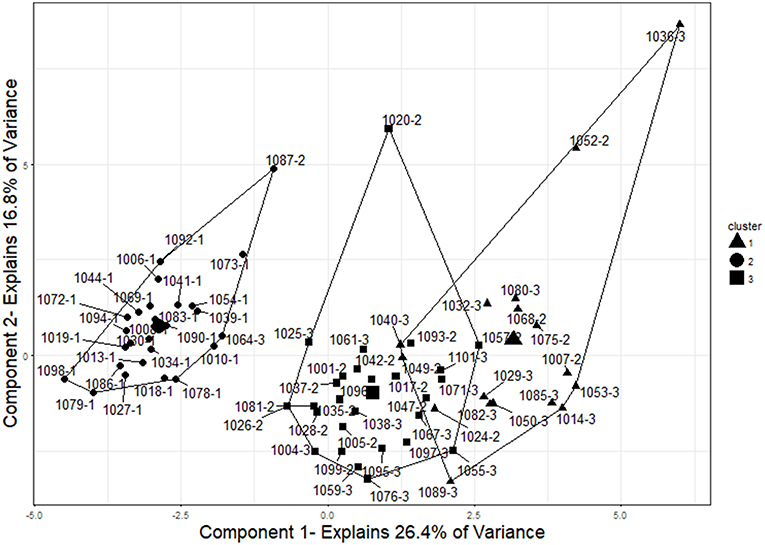
Figure 7. Three-cluster solution for examinees. The three clusters represent good separation between control (IDs that end in−1), ItemOnly (IDs that end in−2), and Item+Answer (IDs that end in−3) participants. The cluster centers and cluster membership are indicated by shape (circles represent the cluster of size 26, squares represent the cluster of size 27, and triangles represent the cluster of size 17). Two examinees were grouped incorrectly by this analysis (1064-3 and 1087-2). To visualize the cluster results, components were obtained using principal component analysis, and the clusters are plotted on those components. This plot was created using the “fviz_cluster” function in the “factoextra” package of R (Kassambara and Mundt, 2017).
Response times were transformed with the logistic transformation, conditioned on item score, and compared to log RTs from a group of examinees without pre-knowledge to compute conditional zRTs. There were two item score combinations that conditional zRTs could not be computed for. Item 1 had one incorrect response and Item 4 had no incorrect responses, so the control condition means and/or standard deviations could not be computed. The participant who responded to Item 1 incorrectly was a control condition participant. Thus, conditional zRTs would not have been computed for these item score combinations even if the mean and standard deviation for the control group had been available, because there were no response times for these item and score combinations from the experimental conditions that needed to be compared to the control condition.
Computing the zRTs using the control condition as the comparison yielded more extremely fast zRTs than using the full sample as the comparison group. Given that there were 60 examinees with pre-knowledge of 12 items, we expected around 720 extremely fast responses, assuming no missing data and that examinees with pre-knowledge consistently exhibit expected patterns. Thus, the detection of around 500 zRTs using the control sample as a comparison is much more consistent with the expectation of around 720 than the detection of 57–69 zRTs when using the full sample as the comparison group. Conditioning on score appeared to be less important to the performance of the conditional zRTs, than the choice of comparison group. The number of extremely fast zRTs computed using the same comparison groups were similar, with and without conditioning on score (for the full sample comparison group 57 and 69 and for the control condition comparison group 521 and 504, respectively). However, the number of extremely fast zRTs computed using different comparison groups were very different, even when they were matched by if they were conditioned on score (for those conditioned on score 57 and 521 and for those not conditioned on score 69 and 504, respectively). Thus, the use of a comparison group without compromise appears to be a key element in obtaining useful information from conditional zRTs.
Cluster and factor analyses found distinct groups of items, which showed very good correspondence to the disclosed and undisclosed item groups. Person-level analyses of correlations and cluster analyses identified separations between examinees with and without pre-knowledge. The cluster analyses were 96% accurate when grouping items (24 of 25 correctly grouped) and 97% accurate when grouping examinees (68 of 70 correctly grouped). The one item that was incorrectly grouped was second to last in the disclosed materials that participants received and thus may have exhibited a weaker effect of pre-knowledge than some of the other items.
Factor analyses of item scores showed poor performance in separating disclosed and undisclosed items, but factor analyses on the log RTs were about as effective at grouping items as the conditional zRTs. The two-factor solutions separated items better than the one-factor solutions. Thus, if two factors are observed in the conditional zRTs or log RTs in what was expected to be unidimensional data, item disclosure and pre-knowledge may be present. These findings indicate that disclosed items can be identified in strongly contaminated data simply by performing factor analyses on the log RTs. However, it is possible that this result is due to the large proportion of examinees with pre-knowledge in the current data and that factor analysis of conditional zRTs would outperform factor analysis of log RTs if lower rates of item disclosure or pre-knowledge were present.
The two and three-cluster solutions for grouping examinees resulted in the same accuracy. There were three conditions in the experimental study representing examinees with no pre-knowledge, examinees with pre-knowledge of items, and examinees with pre-knowledge of items and answers. The results for both cluster solutions indicate that examinees were grouped by whether they had any pre-knowledge rather than the nature of that pre-knowledge, such that examinees with pre-knowledge of items and examinees with pre-knowledge of items and answers were identified as a single group. These findings suggest that it does not matter if answers were provided, as examinees with pre-knowledge of the items exhibited similar patterns to examinees with pre-knowledge of the items and answers. It is possible that participants in the ItemOnly condition were able to solve the items they had pre-knowledge of, creating their own answer key, and thus obtaining a similar amount of pre-knowledge to those who had the answer key provided.
Many techniques for analyzing potential pre-knowledge require that examinees are administered the same items or forms, limiting their utility in practice. Conditional zRTs were developed and selected for research because they can be applied to tests administered using fixed-forms and to tests administered using other modern test designs, such as CAT, LOFT, or multi-stage adaptive testing (MSAT). This is a very important advantage of using the proposed method.
Conditional zRTs are easy to compute, analyze, and explain to exam stakeholders. The computation of conditional zRTs only requires item scores, response times, and a group of examinees to serve as an uncontaminated comparison group. Strict assumptions regarding the nature of the data are not required. The assumptions of z-scores are that the distribution is normal, hence the logistic transformation of RTs. The computation of the conditional zRTs assumes that the comparison group means and standard deviations are representative of the population of examinees without pre-knowledge who received the same score on the item. The statistical methodology is intuitive and interpreting the results does not require formidable statistical expertise. Conditional zRTs are datapoints that take into account an examinee's score on an item and the amount of time a typical examinee without pre-knowledge would take to complete the item to achieve that same score. These values could be used by testing programs of all sizes and can be used in MSAT, CAT, and LOFT test designs. These factors indicate that conditional zRTs may provide a useful method to conduct data forensics for non-traditional test designs. Thus, the main strength of conditional zRTs is the flexibility they offer for detecting item disclosure and examinee pre-knowledge across a wide variety of situations and sample sizes.
In the current study, the majority of the participants had pre-knowledge. Thus, it is possible that analyses of the conditional zRTs were able to separate disclosed from undisclosed items and examinees with pre-knowledge from those without because of the high rates of item disclosure (48%) and examinee pre-knowledge (65%) in the data. The computation of conditional zRTs should not be influenced by the proportion of item compromise or pre-knowledge, as each examinee's RTs are directly compared to a control sample of RTs with the same item scores. However, the performance of the grouping techniques, such as cluster analysis, in detecting groups of items and/or persons may be impacted by the proportion of compromise and pre-knowledge. Presumably, accuracy would decrease with smaller proportions of item compromise and examinee pre-knowledge. If the approximate baseline rates of item compromise or examinee pre-knowledge are known, the cluster analyses can be weighted with this information. If such information is unknown, other grouping techniques may perform better. We hope this research will serve to inspire future research on conditional zRTs in data with various rates of item disclosure and pre-knowledge. Additional research should compare conditional zRTs to other methods, such as the IRT-based lz person-fit statistic, score-differencing statistics, and similarity analyses. Investigating conditional zRTs in a broader range of data will illuminate when this method is most appropriate and effective as well as identifying best practices for analyzing them.
One issue that may limit the utility of the proposed method is obtaining a sufficient sample size of RTs uncontaminated by pre-knowledge for comparison. Ideally, the uncontaminated comparison group would be composed of 30 or more examinees for each possible item score. In practice, the feasibility of such a sample size is likely dependent on the characteristics of a test, such as the design. For example, it may be more difficult to achieve sample sizes of 30 or more for a CAT exam where not every examinee receives the same items, because of low administration rates for some items. Additionally, an easy item should yield a sufficient sample size for comparison of examinees with an item score of one, but may not yield a sufficient sample size of examinees with an item score of zero. In the current research, the naturally occurring available sample size was used for comparison, but future research may benefit from investigating methods for improving such comparisons with small sample sizes.
Although it is expected that examinees with pre-knowledge have identifiable response patterns, it is important to note that disclosed test content varies in accuracy and may be utilized imperfectly because of human error or other factors. The scores of examinees with pre-knowledge depend on the accuracy of the disclosed test items or key. Even in a case where the correct answer for every item on a test is disclosed, examinees may have different abilities or tendencies to memorize and recall that information accurately. Some examinees with pre-knowledge may intentionally use disclosed content imperfectly; for example, by only accessing difficult items or answering some disclosed test items incorrectly to avoid detection. Some examinees may be aware that their RTs are being monitored by testing companies and engage in behaviors to make their test-taking behaviors look less suspicious. Thus, although it is expected that examinees with pre-knowledge will display distinct response patterns in comparison to examinees without pre-knowledge, there may be considerable individual variability. It is also likely that examinees with pre-knowledge will invent novel ways of responding to avoid detection, which makes the detection of pre-knowledge an evolving problem.
Future research on conditional zRTs should attempt to improve the quality of information in the uncontaminated comparison group of log RTs. The purpose of the comparison group is to accurately capture typical response times of examinees who do not have pre-knowledge and who put an appropriate level of effort into responding to the items. In the current study, all log RTs for the examinees in the control group were used to compute the log RT means and standard deviations. Extreme outliers or rapid guesses were not excluded when computing these comparison group statistics because of the small sample size of the control condition and because such data are typical in testing data. However, the information provided by conditional zRTs could be improved by identifying and removing rapid guesses and other extreme data points prior to the computation of the comparison group statistics. This should cause increased separation in conditional zRTs between normal responses and rapid guesses or responses of examinees with pre-knowledge.
Another possible way to improve the quality of the information in the comparison group would be to use a statistic other than the mean in the calculation of the conditional zRTs. Z-scores use the mean and standard deviation to scale data and are thus most appropriate for normal distributions with sufficient sample sizes. In the current study, log transformations of response times were used to approximate normality, but it is possible that some item RT distributions remained skewed after the transformation and the mean did not accurately represent the center of the distribution because of the presence of outliers. In such cases, the median is more appropriate as an indicator of the center of the distribution. Using the median would prevent the skewness of the distribution from causing some log RTs to appear more or less extreme than they should, based on the comparison group. With sufficient sample size, it may also be possible to compute conditional zRTs matching examinees with a comparison group of examinees without pre-knowledge with a similar ability level. Although examinees with pre-knowledge likely have inflated ability estimates, this matching would compare their log RTs to the log RTs of examinees without pre-knowledge with a similar ability level. Such a comparison would likely detect the log RTs of the examinees with pre-knowledge as anomalous, even when the examinees have high ability levels. These adjustments could improve the quality of information in the comparison group, leading to improved separation of extreme log RTs from typical log RTs.
One potentially fruitful future direction for the use of conditional zRTs would be to identify groups of examinees based on their patterns. Latent profile analysis, or similar grouping methods could be used to distinguish types of responding. For example, differentiating high ability examinees from examinees with pre-knowledge or low ability examinees from random guessers. This would advance the ultimate goal of this type of research, which is to develop statistical models to identify likely examinee behaviors. Investigating how the examinee behavior patterns for an exam shift over time may provide valuable information, such as when test content may have been disclosed or the population of examinees has changed.
In this study, a new method was proposed for analyzing response times to detect pre-knowledge, computing a conditional scaling by comparing each examinee's response time on each item to a sample of response times on the same item from examinees who did not have pre-knowledge and who received the same score on that item. The comparisons were conducted using logistically transformed response times and computed as z-scores, hence the name of the resulting values, conditional zRTs. These conditional zRTs were computed and analyzed in an experimental data set obtained by randomly selecting some examinees to have pre-knowledge of half of the test items. Some examinees received only test items and some also received correct answers. The results showed that the computation of conditional zRTs was feasible, even with a small uncontaminated comparison group, and that using an uncontaminated comparison group was more important to the performance of the zRTs than conditioning on score. Exploratory analyses of the conditional zRTs found strong separation between disclosed and undisclosed items and between examinees with and without pre-knowledge.
This study was conducted according to the recommendations of, and was approved by, the Institutional Review Board for Social and Behavioral Sciences at the University of Virginia. All subjects gave written informed consent in accordance with the Declaration of Helsinki.
ST and DM developed the idea for the proposed method, both contributing critical pieces. ST provided the experimental data and drafted the manuscript. DM provided critical revisions.
ST and DM were employed by Caveon, a company that conducts data forensics analyses for a variety of clients, at the time this research was conducted.
The authors would like to thank Karen Schmidt and Yasmeen Nabhani for helping to design and conduct the experiment that yielded the data analyzed in this research. Also, thanks to Marsha Line and David Silverman for volunteering their time to administer the experiment to participants.
American Board of Internal Medicine (2010, June 9). Unprecedented action reflects ongoing commitment to protect the integrity of the medical board certification process. Available online at: https://www.abim.org/news/abim-sanctions-physicians-for-ethical-violations.aspx (accessed November 19, 2018).,
Angoff, W. (1974). The development of statistical indices for detecting cheaters. J. Am. Stat. Assoc. 69, 44–49. doi: 10.1080/01621459.1974.10480126
Belov, D. I. (2016a). Comparing the performance of eight item preknowledge detection statistics. Appl. Psychol. Meas. 40, 83–97. doi: 10.1177/0146621615603327
Belov, D. I. (2016b). A New Approach to Detecting Cluster Aberrancy. LSAC Research Report (16-05), Newtown, PA.
Belov, D. I. (2017). On the optimality of the detection of examinees with aberrant answer changes. Appl. Psychol. Meas. 41, 338–352. doi: 10.1177/0146621617692077
Birnbaum, A. (1968). “Some latent trait models and their use in inferring an examinee's ability, in Statistical Theories of Mental Test Scores (Chapters 17–20), eds F. M. Lord and M. R. Novick (Reading, MA: Addison-Wesley), 397–479.
Bliss, T. J. (2012). Statistical Methods to Detect Cheating on Tests: A Review of the Literature (Unpublished doctoral dissertation). Brigham Young University, Provo, UT.
Bock, R. D. (1972). Estimating item parameters and latent ability when responses are scored in two or more nominal categories. Psychometrika 46, 443–459. doi: 10.1007/BF02293801
Clark, M., Skorupski, W., Jirka, S., McBride, M., Wang, C., and Murphy, S. (2014). An Investigation into Statistical Methods to Identify Aberrant Response Patterns. Available online at: http://researchnetwork.pearson.com/wp-content/uploads/Data-Forensics-RD-Research-Report-Person-Fit.pdf (accessed August 8, 2018).
Drasgow, F., Levine, M. V., and Williams, E. A. (1985). Appropriateness measurement with polychotomous item response models and standardized indices. Br. J. Math. Stat. Psychol. 38, 67–86. doi: 10.1111/j.2044-8317.1985.tb00817.x
Driscoll, R. (2007). Westside Test Anxiety Scale Validation. American Test Anxiety Association. Available online at: https://files.eric.ed.gov/fulltext/ED495968.pdf
Eckerly, C. A. (2017). “Detecting preknowledge and item compromise: understanding the status quo,” in Handbook of Quantitative Methods for Detecting Cheating on Tests, eds G. J. Cizek and J. A. Wollack (New York, NY: Routledge), 101–123.
Eckerly, C. A., Babcock, B. G., and Wollack, J. A. (2015). “Preknowledge detection using a scale-purified deterministic gated IRT model,” Paper Presented at the Annual Meeting of the National Council of Measurement in Education (Chicago, IL).
Educational Testing Service (2017). Practice Book for the Paper-based GRE ® revised General Test (2nd ed.). Princeton, NJ. Retrieved from: https://www.ets.org/s/gre/pdf/practice_book_GRE_pb_revised_general_test.pdf
Federation of State Boards of Physical Therapy (2015, August 7). PEAT Investigation [Press release]. Available online at: https://www.fsbpt.org/NewsEvents/News/PEATInvestigation.aspx.,
Ferrando, P. J. (2007). Factor-analytic procedures for assessing response pattern scalability. Multivariate Behav. Res. 42, 481–507. doi: 10.1080/00273170701382583
Frary, R. B., Tideman, T. N., and Watts, T. M. (1977). Indices of cheating on multiple choice tests. J. Educ. Stat. 2, 235–256. doi: 10.3102/10769986002004235
Gosling, S. D., Rentfrow, P. J., and Swann, W. B. Jr. (2003). A very brief measure of the big five personality domains. J. Res. Pers. 37, 504–528. doi: 10.1016/S0092-6566(03)00046-1
Graham, J., Nosek, B. A., Haidt, J., Iyer, R., Koleva, S., and Ditto, P. H. (2011). Mapping the moral domain. J. Pers. Soc. Psychol. 101, 366–385. doi: 10.1037/a0021847
Guttman, L. A. (1944). A basis for scaling qualitative data. Am. Sociol. Rev. 91, 139–150. doi: 10.2307/2086306
Haberman, S. J., and Lee, Y.-H. (2017). A Statistical Procedure for Testing Unusually Frequent Exactly Matching Responses and Nearly Matching Responses. Research Report No. RR-17-23,Educational Testing Service, Princeton, NJ.
Hartigan, J. A., and Wong, M. A. (1979). Algorithm AS 136: a K-means clustering algorithm. Appl. Stat. 28, 100–108. doi: 10.2307/2346830
Karabatsos, G. (2003). Comparing the aberrant response detection performance of thirty-six person-fit statistics. Appl. Meas. Educ. 16, 277–298. doi: 10.1207/S15324818AME1604_2
Kassambara, A., and Mundt, F. (2017). factoextra: Extract and Visualize the Results of Multivariate Data Analyses. R package version 1.0.5. Available online at: https://CRAN.R-project.org/package=factoextra
Kullback, S., and Leibler, R. A. (1951). On information and sufficiency. Ann. Math. Stat. 22, 79–86. doi: 10.1214/aoms/1177729694
Kyle, T. (2002). Cheating Scandal Rocks GRE, ETS. Retrieved from http://www.thedartmouth.com/article/2002/08/cheating-scandal-rocks-gre-ets/ (accessed November 1, 2018).
Liu, X. L., Primoli, V., and Plackner, C. (2013). “Utilization of response time in data forensics of K-12 computer-based assessment,” Presented at the Conference on the Statistical Detection of Test Fraud (Madison, WI).
Lloyd, S. P. (1957). Least squares quantization in PCM. IEEE Trans. Information Theor. 2, 129–137. doi: 10.1109/TIT.1982.1056489
Maynes, D. D. (2017). “Detecting potential collusion among individual examines using similarity analysis,” in Handbook of Quantitative Methods for Detecting Cheating on Tests, eds G. J. Cizek and J.A. Wollack (New York, NY: Routledge), 47–69.
Maynes, D. D., and Thomas, S. L. (2017). “A method for estimating the latent source used by answer copiers,” Paper Presented at the Meeting of the National Council on Measurement in Education (New York, NY).
Meijer, R. R., and Sotaridona, L. (2006). Detection of Advance Item Knowledge Using Response Times in Computer Adaptive Testing. LSAC research report series; No. CT 03-03, Law School Admission Council, Newton, PA.
R Core Team (2016). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. Available online at: https://www.R-project.org/
Revelle, W. (2016). psych: Procedures for Personality and Psychological Research. Evanston, IL: Northwestern University. Available online at : http://CRAN.R-project.org/package=psych Version = 1.6.4.
Scott, M. W. (2018). A Series of Papers on Detecting Examinees Who Used a Flawed Answer Key (Unpublished doctoral dissertation). Utah State University, Logan, UT.
Shapiro, S. S., and Wilk, M. B. (1965). An analysis of variance test for normality (complete samples). Biometrika 52, 591–611. doi: 10.1093/biomet/52.3-4.591
Shu, Z., Henson, R., and Luecht, R. (2013). Using deterministic, gated item response theory model to detect test cheating due to item compromise. Psychometrika 78, 481–497. doi: 10.1007/s11336-012-9311-3
Sijtsma, K., and Meijer, R. R. (1992). A method for investigating the intersection of item response functions in Mokken's non-parametric IRT model. Appl. Psychol. Meas. 16, 149–157. doi: 10.1177/014662169201600204
Thissen, D. (1983). “Timed testing: an approach using item response theory,” in New Horizons in Testing: Latent Trait Test Theory and Computerized Adaptive Testing, ed D. J. Weiss (New York, NY: Academic Press), 179–203.
Thomas, S. L., and Maynes, D. D. (2018). “The use of data mining techniques to detect cheating,” in Data Analytics and Psychometrics: Informing Assessment Practices, eds H. Jiao, R.W. Lissitz, and A. Van Wie (Charlotte, NC: Information Age Publishing), 77–108.
Tiemann, G. C., Miller, H. L., Kingston, N. M., and Foster, D. (2014). “Protecting item content via the discrete-option multiple-choice item type,” Presented at the Conference on Test Security.
van der Linden, W. J., and Guo, F. (2008). Bayesian procedures for identifying aberrant response-time patterns in adaptive testing. Psychometrika 73, 365–384. doi: 10.1007/s11336-007-9046-8
van der Linden, W. J., and Sotaridona, L. (2006). Detecting answer copying when the regular response process follows a known response model. J. Educ. Behav. Stat. 31, 283–304. doi: 10.3102/10769986031003283
van der Linden, W. J., and van Krimpen-Stoop, E. M. L. A. (2003). Using response times to detect aberrant responses in computerized adaptive testing. Psychometrika 68, 251–265. doi: 10.1007/BF02294800
Wollack, J. A. (1997). A nominal response model approach for detecting answer copying. Appl. Psychol. Meas. 21, 307–320. doi: 10.1177/01466216970214002
Keywords: test security, latencies, cheating, pre-knowledge, data forensics, response times, experiment
Citation: Toton SL and Maynes DD (2019) Detecting Examinees With Pre-knowledge in Experimental Data Using Conditional Scaling of Response Times. Front. Educ. 4:49. doi: 10.3389/feduc.2019.00049
Received: 01 September 2018; Accepted: 16 May 2019;
Published: 04 June 2019.
Edited by:
Douglas F. Kauffman, Medical University of the Americas – Nevis, United StatesReviewed by:
Kathy Ellen Green, University of Denver, United StatesCopyright © 2019 Toton and Maynes. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sarah L. Toton, c2FyYWgudG90b25AY2F2ZW9uLmNvbQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.