Validity Evidence for Progress Monitoring With Star Reading: Slope Estimates, Administration Frequency, and Number of Data Points

The increasing use of computerized adaptive tests (CATs) to collect information about students' academic growth or their response to academic interventions has led to a number of questions pertaining to the use of these measures for the purpose of progress monitoring. Star Reading is an example of a CAT-based assessment with considerable validity evidence to support its use for progress monitoring. However, additional validity evidence could be gathered to strengthen the use and interpretation of Star Reading data for progress monitoring. Thus, the purpose of the current study was to focus on three aspects of progress monitoring that will benefit Star Reading users. The specific research questions to be answered are: (a) how robust are the estimation methods in producing meaningful progress monitoring slopes in the presence of outliers; (b) what is the length of the time interval needed to use Star Reading for the purpose of progress monitoring; and (c) how many data points are needed to use Star Reading for the purpose of progress monitoring? The first research question was examined using a Monte Carlo simulation study. The second and third research questions were examined using real data from 6,396,145 students who took the Star Reading assessment during the 2014–2015 school year. Results suggest that the Theil-Sen estimator is the most robust estimator of student growth when using Star Reading. In addition, it appears that five data points and a progress monitoring window of approximately 20 weeks appear to be the minimum parameters for Star Reading to be used for the purpose of progress monitoring. Implications for practice include adapting the parameters for progress monitoring according to a student's current grade-level performance in reading.

Introduction

Progress monitoring involves the regular (e.g., weekly, bi-weekly, or monthly) collection of educational data to make decisions about instruction or the need for additional instructional supports. The primary purpose of gathering data with progress monitoring measures is to evaluate student growth in key curricular areas (e.g., reading, mathematics, and writing) or to assess specific sub-skills contributing to student achievement in these areas. Progress monitoring is, consequently, often used to identify students who are at-risk for academic difficulty or to evaluate students' response to an academic intervention. In fact, Stecker et al. (2008) described progress monitoring as one of the most critical features of successful response to intervention (RTI) implementation. To date, many measures have been developed to monitor student growth in response to instruction or academic intervention (e.g., Star Reading, aimsweb, and Dynamic Indicators of Basic Early Literacy Skills [DIBELS]). Star Reading (Renaissance, 2015) is a computerized adaptive test (CAT) that was developed to provide periodic assessment information to educators in response to reading instruction, with a focus on examining growth over time. The three specific purposes of Star Reading are to: (a) assess students' reading comprehension; (b) produce a norm-referenced measure of students' performance in reading; and (c) generate data that represents student growth in reading over the course of the academic year (Renaissance, 2015).

Over the last three decades, a considerable amount of time and effort has been put into refining the progress monitoring measures to increase their reliability, as well as gather evidence of validity related to use and interpretation (e.g., VanDerHeyden et al., 2001; Deno, 2003). The importance of establishing strong evidence of validity that aligns with a measure's intended purpose cannot be overstated—not only is this requirement emphasized in professional standards (e.g., American Educational Research Association American, 2014), but it is also fundamental to ensuring that appropriate decisions are made with regard to students' educational programming. The process of gathering validity evidence for a measure based on its intended use is an ongoing process (Messick, 1995). In other words, there is no universal criterion that establishes a sufficient end point for the collection of validity evidence (American Educational Research Association American, 2014). Extensive, strong validity evidence including evidence of concurrent, retrospective, predictive, and construct validity, are well documented in the Star Reading technical manual (Renaissance, 2015). In addition, an independent review by the National Center on Response to Intervention (NCRTI) rated Star Reading as having convincing evidence in the categories of classification accuracy, generalizability, reliability, and validity (National Center on Response to Intervention, 2018). However, in keeping with the aforementioned conceptualization of validity, additional validity evidence for Star Reading should continue to be gathered. In particular, it would be beneficial to test users to generate additional empirical support for the use of Star Reading for the purpose of progress monitoring.

The existing literature pertaining to CAT-based progress monitoring was reviewed to identify areas where additional empirical evidence is needed to strengthen the validity argument to support the use of Star Reading for progress monitoring. Unfortunately, to date, only a few empirical studies have evaluated the technical adequacy of CATs for the purpose of progress monitoring (e.g., Shapiro et al., 2015; Nelson et al., 2017b; Van Norman et al., 2017). Therefore, a review of the broader progress monitoring literature helped to identify the primary characteristics of progress monitoring practices that contribute to strong, valid decision-making about student growth. Due to the extensive amount of literature that has accumulated on the topic of curriculum-based measurement (CBM) over the past 30 years (see Ardoin et al., 2013 for a comprehensive review of CBM development implications informed from the existing literature), we limited the scope of our review to the following focal areas relevant to extending the validity evidence supporting the use of Star Reading for the purpose of progress monitoring. These key areas are: (a) identifying a robust slope estimate; (b) determining the length of the progress monitoring interval; and (c) determining the number of data points needs to accurately represent student growth in reading.

Identification of a Robust Slope Estimate

Data-driven decision making is an integral part of an educational decision-making process (Ysseldyke et al., 2006). In the case of progress monitoring, a slope is usually generated from assessment data to make a decision about instructional progress or lack thereof. The slope is meant to represent the best estimate of the growth over time. Generating an accurate slope to represent student growth over time is challenging, given the variable nature of progress monitoring data (i.e., observed deviations of individual data points from the slope; Klingbeil et al., 2017; Nelson et al., 2017a). Regardless, in most cases, using a linear slope appears to be an appropriate practice (Van Norman and Parker, 2016a,b). The most important issue, however, when examining trends in individual students' progress monitoring slopes, was highlighted by Van Norman et al. (2013) who suggested that “outliers may drastically change the line of best fit for progress-monitoring data” (p. 296). Thus, it is important to generate a slope estimate that accurately represents an individual student's progress over time and is able to remain robust when outliers are present.

A number of statistical methods exist for calculating slopes from progress monitoring data. Most of the literature has focused on hand-fit trend lines (e.g., based on visual estimations) and linear regression methods, such as ordinary lest-squares (OLS) regression (Ardoin et al., 2013). More recently, the performance of various robust estimators, such as Huber M-estimator, Tukey's bisquare, and SMDM-estimation (i.e., an initial S-estimate, followed by an M-estimate, a Design Adaptive Scale estimate, and a final M-step; see Koller and Stahel, 2011 for more details), has been investigated in the context of CBM and progress monitoring measures (e.g., Mercer et al., 2014). Another robust estimation method, the Theil-Sen estimator, has been proposed to obtain more robust slope estimates from progress monitoring data (e.g., Vannest et al., 2012). The Theil-Sen regression, which was named after Theil (1950) and Sen (1968), yields a Theil-Sen slope estimate. This method was also referred to as Sen's slope estimator (Gilbert, 1987), the single median method (Massart et al., 1997), and the Kendall-Theil robust line (Granato, 2006) in the literature.

Unlike the other robust estimators (e.g., Huber M-estimator), the Theil-Sen estimator is similar to the OLS estimator in terms of its asymptotic efficiency (Wilcox, 1998, 2010; Wang, 2005). The main advantage of the Theil-Sen estimator over the OLS estimator is that the Theil-Sen estimator is generated from a non-parametric method, which means it makes no assumption about the underlying distribution of the data (i.e., distribution-free). In addition, the Theil-Sen estimator is a median-based estimator, and thus it may be more robust against outliers—an aforementioned common characteristic of progress monitoring data—when compared to the OLS estimator. This method appears to be more robust in producing a linear representation of the trend in progress monitoring data and has a “successful track record outside of education is in high-stakes decision arenas” (Vannest et al., 2012, p. 277). Thus, the Theil-Sen estimator appears to be a viable option for modeling progress monitoring data and, ultimately, data-driven decision making.

Additional Considerations for Strong Progress Monitoring Practices

In addition to selecting a robust estimator to calculate progress monitoring slopes, there are also other important considerations when attempting to develop strong progress monitoring practices. Significant effort has been put into identifying the amount of error associated with curriculum-based progress monitoring tools using traditional CBM probes scored for fluency and accuracy of reading performance (e.g., Poncy et al., 2005; Christ, 2006; Christ and Silberglitt, 2007; Ardoin and Christ, 2009). From a practical standpoint, assessment practices need to be efficient, to minimize the time that students are not receiving instruction. Much of the literature reports that more data points and longer data collection periods tend to lead to better decision making (Christ et al., 2012, 2013; Thornblad and Christ, 2014). Thus, it is evident that the amount of time that data are collected and the amount of data points to collect are integral to the development of sound progress monitoring practices.

Progress Monitoring Schedules

Time between testing (i.e., the progress monitoring schedule) appears to have a significant influence on the reliability and validity of growth estimates from progress monitoring measures (Christ et al., 2013). However, another important consideration in determining an appropriate progress monitoring schedule is the rate at which students acquire the skill or knowledge that is being taught (i.e., the rate of improvement). Norm-based rates of improvement in core academic areas tend to be estimated from Fall, Winter and Spring data collections (see Shapiro, 2011, for more information). However, when progress monitoring is used to assess response to academic interventions, the level of direct instruction that a student receives is more intensive than it is during regular classroom instruction (see Burns, 2010). Therefore, the expected rates of improvement are determined on a case-by-case basis depending on a number of student characteristics (e.g., grade level, the skill or subskill that is the focus of the intervention). It is, therefore, difficult to identify an optimal progress monitoring schedule that would allow align with each student's rate unique rate of acquisition for a particular skill. Regardless, some evidence suggests that less frequent data collection and longer time intervals between assessments (i.e., a less intensive schedule) may in fact be more beneficial than more frequent data collection within a shorter time span between assessments (Christ et al., 2013). For Star Reading, the ideal length of progress monitoring intervals remains an empirical problem requiring further attention from researchers.

Number of Progress Monitoring Data Points

Individual data points collected with progress monitoring measures are necessary to produce an observable trend of a student's growth over time. This trend is meant to be representative of their growth that is made in response to instruction or intervention. A greater number of data points tends to reduce the error associated with the prediction, with individual data points collected weekly for at least 14 weeks being the requirement to make relatively accurate predictions of student performance (Christ et al., 2012). This is not surprising, considering that more data can typically provide more information on student performance and growth.

Progress Monitoring With Star Reading

As an operational CAT designed for measuring growth in reading, Star Reading is one of the most widely used reading assessments in the United States (Education Market Research, 2013). Star Reading allows teachers to assess students' reading comprehension levels, reading achievement relative to peers, and individual growth in reading over time. The item formats in the Star Reading item bank include (a) vocabulary-in-context items where the student selects the word that best completes a single-context sentence with a missing word; and (b) authentic text passage items where the student responds to the item based on his or her general understanding of an authentic text passage. The vocabulary-in-context test items require the student to apply their vocabulary knowledge and use active strategies to construct meaning from a given sentence. The authentic text passage items require the student to complete a sentence with the appropriate word that suits both the semantics and the syntax of the sentence, and the context of the passage (Renaissance, 2015). As the grade level increases, maximum sentence length in the vocabulary items and average sentence length of the paragraphs in the passage items also increase gradually.

The length of a Star Reading administration is 25 items, which is typically completed in 10 min or less depending on the grade level (Renaissance, 2015). Because Star Reading is an adaptive test, each student responds to a different set of items with varying difficulty, depending on his or her responses. Students' responses to the Star Reading items are scored dichotomously (i.e., correct or incorrect) and the final score is estimated based on the Rasch model within the Item Response Theory (IRT) framework. Because the estimated Rasch scores from Star Reading are based on a logistic scale (typically ranging from −5 to 5 for Star Reading), these scores are transformed into the Unified Scaled Scores (USS) for easier interpretation. The USS scores are positive integers that typically range from 0 to 1400.

Star Reading is often administered on a regular basis (e.g., quarterly or monthly) or more frequently (e.g., weekly or bi-weekly) to help the teacher monitor his or her students' progress closely. The teacher can determine the number and frequency of Star Reading assessments on a student-by-student basis. Therefore, a Star Reading administration can be completed at different times for different students and at different frequencies. Once the test administration is complete, results are immediately reported to the teacher so the teacher can review the student's progress quickly and make appropriate changes to instructional practices. Furthermore, the Star Reading Growth Report provides the teacher with information about each student's absolute and relative growth in reading over a certain period of time (Renaissance, 2015).

Current Study

Star Reading is a widely-used, computerized-adaptive assessment tool for monitoring students' progress in reading. The accuracy of the decisions being made about students' progress based on Star Reading is an important aspect of Star Reading's validity evidence. As summarized earlier, the length of progress monitoring intervals and the number of progress monitoring data points are two important factors contributing to the validity of progress monitoring measures. Therefore, the primary goal of the present study is to determine the length of the time interval and the number of data points (i.e., the number of Star Reading administrations) needed to be able to make valid decisions based on the Star Reading results.

In addition to the length of the time interval and the number of data points, our preliminary analysis of the Star Reading results from the 2014 to 2015 school year indicated that the presence of outliers could be another important concern in the interpretation of progress monitoring data. Figure 1 shows a sample of students who were administered Star Reading during the 2014–2015 school year. Each line in Figure 1 represents a particular student's scaled scores in Star Reading (the y-axis) over a number of days (the x-axis). Although most students' scaled scores showed a linearly increasing trend (see Figure 1A), some students' scaled scores indicated large fluctuations either in the middle (see Figure 1B) or at the beginning (or end) of the progress monitoring process (see Figure 1C). This finding implies that the identification of a robust slope estimate is an important step in the interpretation of Star Reading results. Slope estimates from Star Reading that are more robust to influential outliers in the data can yield more accurate results about students' progress in reading. Furthermore, obtaining accurate slope estimates is essential to the investigation of other elements of progress monitoring with Star Reading, such as the length of the time interval and the number of data points.

FIGURE 1

Figure 1. Different patterns of outliers (A: no outlier, B: outlier in the middle, or C: outlier at the beginning/end) in the progress monitoring data from Star Reading.

In the present study, we have identified three research questions to address the over-arching needs outlined above: (1) How robust are the slope estimation methods in the presence of outliers in Star Reading? (2) What is the length of the time interval needed to use Star Reading for the purpose of progress monitoring? (3) How many data points are needed to use Star Reading for the purpose of progress monitoring? To address these research questions, two separate studies were conducted. The first study is a Monte Carlo simulation study that investigates the first research question by comparing the precision of the slope estimates from the four estimation methods (OLS, Maximum Likelihood, Theil-Sen, and Huber M-estimator) in the context of progress monitoring with Star Reading. The second study is an empirical study that focuses on the second and third research questions of this study. The real data from the Star Reading assessment (Renaissance, 2015) were analyzed to investigate the length of the time interval and the number of data points needed to use a CAT for progress monitoring. At the onset, we obtained the permission of Renaissance Learning Incorporated to use the anonymized assessment data from Star Reading. Further ethical review was not needed as per institutional guidelines and national regulations because this study involved the secondary use of data collected by Renaissance Learning.

Study 1: Monte Carlo Simulation Study

Method

The purpose of the Monte Carlo simulation study was to compare the performances of the OLS, Maximum Likelihood, Theil-Sen, and Huber M-estimator methods in estimating slopes for progress monitoring data under a hypothetical scenario where students are assumed to take Star Reading several times at a given point in the school year. For each student, the data were generated based on the following general linear model:

$\begin{array}{ll}Y=b_0+b_1\left(NumberofDays\right)+\epsilon ,& (1)\end{array}$

where Y is the student's scaled scores in Star Reading, b₀ is the intercept (i.e., the student's starting scaled score), which was set to 600, b₁ is the slope (i.e., growth per day in the scaled score unit), which was set to 0.8, the number of days is the time between the test administrations, and ε is the error in the growth (i.e., random deviations from the linear growth trend). The selected intercept and slope values are similar to those from the Star Reading assessment. The number of days was determined based on the number of data points (i.e., the number of test administrations). A 10-day interval was assumed between the consecutive test administrations (e.g., for five data points, the number of days would be 10, 20, 30, 40, and 50 for a given student).

The general linear model in Equation 1 creates a positive, linear growth line for each student based on the number of days. To examine the performance of the four estimation methods in the presence of outliers, several factors were modified in the simulation study. These factors included the number of data points (5–12 data points), the outlier magnitude (0, 50, 100, 150, or 200 scaled score points), and the position of the outlier (in the middle data point or in the last data point), resulting in 80 crossed factors. After data following a linear trend were generated based on Equation 1, the selected outlier magnitude was added to either the middle data point or the last data point. For example, if a student takes 10 assessments per year and the outlier magnitude is 100, then 100 points are added to the student's 5 or 10th score to create an outlier either in the middle or at the end of the linear growth line. When the outlier magnitude is 0, then the original linear data remain unchanged without any outliers.

The process summarized above was repeated 10,000 times for each crossed factor to produce 10,000 hypothetical students in the simulated data set. Next, for each student, a simple linear regression model was fitted to the simulated data where the scaled score was the dependent variable and the number of days was the predictor. The same regression model was estimated using the OLS, Maximum Likelihood, Theil-Sen, and Huber M-estimator methods. We included OLS as the most widely used method for estimating progress monitoring slopes. Maximum Likelihood is another widely used estimator, although it has not been examined in the context of progress monitoring. Theil-Sen and Huber-M are the two slope estimators that are robust to the presence of outliers (e.g., Mercer et al., 2014). We excluded the other robust estimators—SMDM and Tukey's bisquare—from the simulation study because Mercer's, Lyons, Johnston and Millhoff (2014) study has already indicated that Huber-M can outperform the SMDM and Tukey's bisquare estimators when outliers are present in the progress monitoring data. The following section provides a brief description of the four estimation methods used in the Monte Carlo simulation study.

Slope Estimation Methods

Ordinary least squares (OLS) is a well-known statistical method that involves the estimation of the best-fitting growth line by minimizing the sum of the squares of the residuals (i.e., differences between the observed scores and predicted scores) in the progress monitoring data. Although the OLS slope estimates are highly accurate under most data conditions (e.g., Christ et al., 2012), extreme values (i.e., outliers) in the data may lead to biased slope estimates in the direction of the outliers (Cohen et al., 2003). In this study, the OLS slope estimates were calculated using the lm function in R (R Core Team, 2018).

The Theil-Sen estimator is a robust method for finding the slope of a regression model by choosing the median of the slopes of all lines through pairs of points. The first step in calculating the Theil-Sen slope for a particular student is to generate the number of all possible slopes using the following formula:

$\begin{array}{ll}{N}_{slopes}=\frac{N_{datapoints}x(N_{datapoints}-1)}{2},& (2)\end{array}$

where N_{data points} is the number of data points (i.e., the number of assessments administered to the student) and N_slopes is the number of possible slope estimates for the student. For example, if 10 progress monitoring data points were collected for a given student, (10 × 9)/2 = 45 slope estimates would be calculated for the student. The slopes for each of the time points are then calculated using the following formula:

$\begin{array}{ll}Slope=\frac{[Scale Scor{e}_{Time 2}- Scale Scor{e}_{Time 1}]}{[Dat{e}_{Time 2}- Dat{e}_{Time 1}]},& (3)\end{array}$

where Scale Score_{Time 1} and Scale Score_{Time 2} are the scaled scores from two test administrations, Date_{Time 1} and Date_{Time 2} are the dates that the two test administrations occurred, and Slope is the growth estimated based on the change between the two scaled scores. Once all possible slopes are calculated, the median value of the estimated slopes is then used to represent the best estimate of the overall slope value for a specific set of progress monitoring data. In this study, Theil-Sen slopes were calculated using the mblm function of the mblm package (Komsta, 2013) in R (R Core Team, 2018).

The Maximum Likelihood (ML) estimator (also known as MLE) determines the slope of a linear regression model by searching for the best slope value that would maximize the likelihood function returned from the regression model. That is, the ML estimator finds the slope estimate that is the most probable given the observed progress monitoring data. In this study, the ML estimation was performed by optimizing the natural logarithm of the likelihood function, called the log-likelihood, with the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm from the optim function in R (R Core Team, 2018).

As a generalized form of the ML estimator, the Huber M-estimator (Huber, 1964, 1973) is a robust estimator that incorporates a set of weights for the residuals to reduce the impact of residuals from outliers on the likelihood function. The weights are determined based on the contribution of each residual to the objective function (see Hampel et al., 2005, for a more detailed discussion). In this study, the slope estimates for Huber M-estimator were calculated using the rlm function from the MASS package (Venables and Ripley, 2002) in R (R Core Team, 2018).

Simulation Evaluation Criteria

Once the slopes were estimated for each student using the OLS, ML, Theil-Sen, and Huber M-estimator methods, they were compared with the true slope value of 0.8 based on the bias and root mean square error (RMSE) indices:

$\begin{array}{ll}Bias=\frac{{\displaystyle {\sum }_{i=1}^K}\left({\widehat{b}}_i-b_i\right)}{K},and& (4)\end{array}$

$\begin{array}{ll}RMSE=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^K}{\left({\widehat{b}}_i-b_i\right)}^2}{K}},& (5)\end{array}$

where K is the number of replications (i.e., 10,000), ${\widehat{b}}_i$ is the estimated slope for student i (i = 1, 2, …, K), and b_i is the true slope for student i. The average bias and RMSE values over 10,000 replications were reported for each crossed factor.

Results and Discussion

The results of the Monte Carlo simulation study showed that when there was no outlier in the progress monitoring data, the slopes for the OLS, Theil-Sen, and Huber M-estimator methods were very similar based on bias and RMSE values (see Figure 2). Although bias for the ML method was similar to bias from the other three methods, RMSE for the ML method was much higher, even though there were no outliers in the data.

FIGURE 2

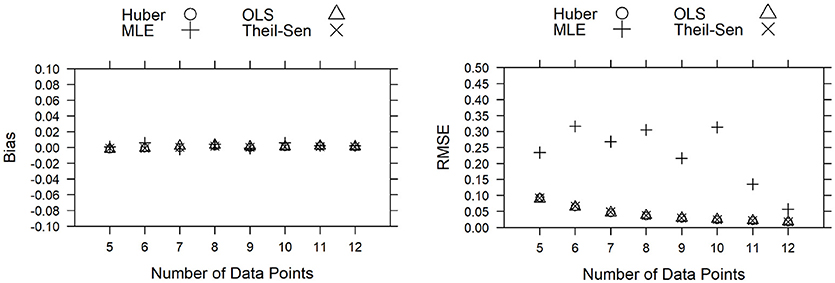
Figure 2. Bias and RMSE for the estimated slopes when no outlier is present in the progress monitoring data. (Note that the data for the OLS, Huber M-estimator, and Theil-Sen methods are almost overlapping for most data points).

Figures 3, 4 demonstrate bias and RMSE for the three estimation methods. Note that the ML method consistently performed worse than the three other estimators. Therefore, the bias and RMSE results for the ML method were not presented in Figures 2, 3 to facilitate the visual interpretation of the findings. Results show that adding outliers to the middle position did not have a significant impact on the performance of the three estimators. The OLS estimator indicated negative bias and higher RMSE values when the outlier magnitude was large (e.g., 150 or 200 scaled score points) and the number of data points was small (e.g., five or six data points). The Theil-Sen and Huber M-estimator methods performed very similarly when the outlier was added to the middle position in the data. Both estimators yielded low bias and RMSE values.

FIGURE 3

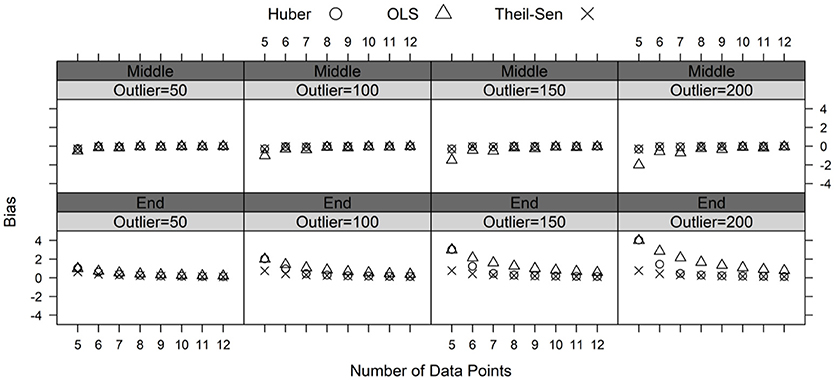
Figure 3. Bias for the estimated slopes by the magnitude of the outlier (50, 100, 150, and 200 points) and the position of the outlier (middle and end) in the progress monitoring data.

FIGURE 4

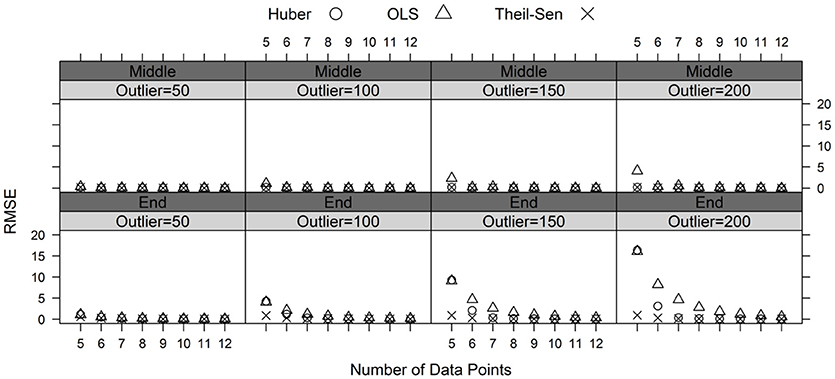
Figure 4. RMSE for the estimated slopes by the magnitude of the outlier (50, 100, 150, and 200 points) and the position of the outlier (middle and end) in the progress monitoring data.

Adding outliers to the end of the simulated progress monitoring data resulted in a more distinct effect on the slope estimates. As the outlier magnitude increased, bias and RMSE increased for the slopes generated from the OLS method, whereas bias and RMSE remained relatively stable for the slopes generated from the Theil-Sen and Huber M-estimator methods. Compared to Huber M-estimator, the Theil-Sen estimator yielded much smaller bias and RMSE when the number of data points was small (e.g., five to seven data points). In fact, bias and RMSE always remained very low for the Theil-Sen method because the median of all possible slopes in the Theil-Sen method was not influenced by the outliers in the data. The performances of the Theil-Sen and Huber M-estimator methods were similar when the number of data points was eight or more. In conclusion, the superiority of the Theil-Sen method over the OLS and Huber M-estimator methods was evident when outliers were present, especially if very few data points were being collected.

Despite the OLS estimator being the most commonly used method, a number of researchers have examined the potential of viable alternatives to produce more robust growth estimates in the context of progress monitoring. Currently, robust slope estimators, such as the Huber M-estimator and the Theil-Sen estimator, have been suggested as appropriate for progress monitoring data. Mercer et al. (2014) compared a number of slope estimators and found that the Huber M-estimator produced “negligible decreases in efficiency when no extreme values were present, but substantial increases in efficiency in the presence of extreme values” (Mercer et al., 2014, p. 180). However, the authors also noted that “evidence regarding the performance of robust estimators is very limited for the small number of observations commonly used in progress monitoring slope calculation for individual student CBM data.” (Mercer et al., 2014, p. 177). This important consideration suggests that a comparison of robust slope estimators should focus on their performance with very few observations and within a timeframe that is typical of progress monitoring schedules. The results of this study showed that the Theil-Sen estimator is more accurate than the Huber M-estimator when the number of data points is small (i.e., <8 data points) and outliers are present in the progress monitoring data. Under the ideal conditions (e.g., more data points and no outliers), both estimators performed very similarly.

A potential condition that was not modified in the Monte Carlo simulation study was the magnitude of slope as we only used a slope of 0.8 in the simulations. One can argue that the effect of outliers could vary depending on the magnitude of slope. However, our initial simulations with different slope values, which were not presented in the current study, yielded very similar RMSE and bias values. This finding suggests that the magnitude of slope does not directly interact with the magnitude of outliers in the estimation process.

Study 2: Empirical Progress Monitoring Study

Method

Sample

In this empirical study, a large sample of students who completed the Star Reading test during the 2014–2015 school year was used. Some students were excluded from the original Star Reading dataset that was provided to the researchers by Renaissance. First, only students with 12 or fewer Star Reading administrations were included because students with more than 12 administrations received Star Reading on a daily or weekly basis and demonstrated very little variability in their scaled score values, which may skew the data when examining potential progress monitoring trends. Second, the original data set included students from a variety of countries, with the majority of the data (n ≈ 99%) coming from American students. To avoid any potential confounds related to country of origin, such as differences in English language development or cultural differences, only American students were included in the datasets. The final sample of this study included 6,396,145 students.

Data Analysis

The following variables were used in the empirical data analysis: (1) grade level; (2) Star Reading Unified Scaled Score (USS) values; (3) the conditional Standard Error of Measurement (cSEM) values for each test administered; and (4) the date the Star Reading test was taken. In the context of CATs, the cSEM value represents measurement precision of an adaptive test at a given ability level. The smaller cSEM, the more accurate the test results become. Compared to fixed-length conventional tests, CATs are capable of maintaining the cSEM level across a wide range of abilities, resulting in more accurate and efficient measurement (Weiss, 2011). This feature of CATs was also observed in Star Reading so that the cSEM value was similar for most students within each grade level as well as across different grade levels.

Amount of time

The amount of time (in days and weeks) needed for progress monitoring was determined by calculating the amount of time required for a student to show growth, based on the Theil-Sen slope, beyond the median cSEM value. The value produced from this procedure will generate a minimum time interval required to observe growth that is not likely due to measurement error. In other words, the value that is produced will represent the minimum time interval required for the interpretation of progress monitoring data generated from Star Reading.

Number of data points

The optimal number of data points for adequate progress monitoring will be determined from grade-level data. The recommended number of data points will be established by observed decreases in the cSEM, while remaining within the typical progress monitoring duration. The length and duration of academic interventions is typically three to five times per week for about 30 min each session, for 10 to 20 weeks (Burns et al., 2012). In some cases, however, interventions are administered over the course of an entire school year (Burns et al., 2003). These parameters will be considered as the data are reviewed.

Results and Discussion

Expected Level of Growth for Progress Monitoring

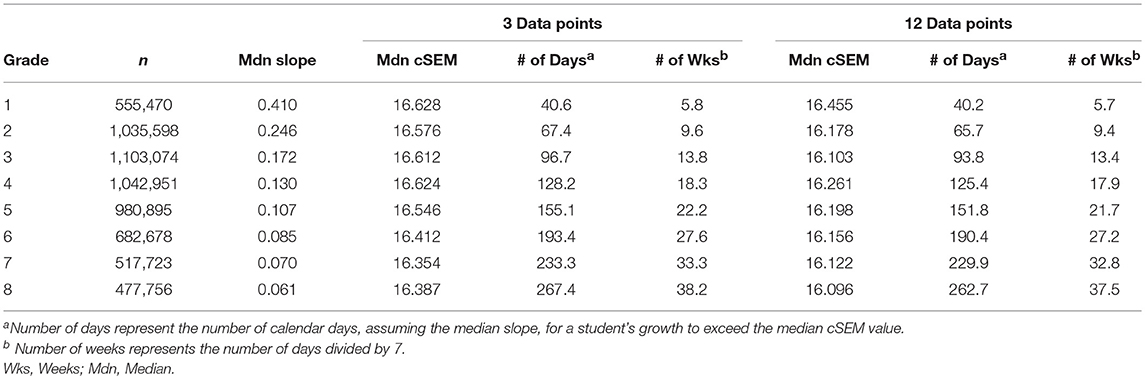
Generating median slope values by grade using the Theil-Sen method with a large sample of student data from Star Reading showed that slope values were the highest for lower grades and declined steadily as grade level increased (see Table 1). This is consistent with trends in oral reading rate across grades (Fuchs et al., 1993; Shapiro, 2010). Further, this trend makes sense intuitively, as most students are likely to make the greatest gains in reading in earlier grades. By generating this normative slope information for Star Reading, we are able to determine the amount of time and the number of data points necessary to obtain meaningful progress monitoring data using Star Reading.

TABLE 1

Table 1. Summary of normative refence point statistics.

Amount of Time

To be able to use Star Reading for progress monitoring purposes, we need to ensure that the measure is sensitive enough to growth over a relatively brief period of time (i.e., 10–20 weeks) and that observed score differences are indicative of actual growth—not measurement error. To determine if it was feasible to use Star Reading for progress monitoring purposes, we used the normative slope values that we generated to calculate the number of weeks that would be required for a student to demonstrate a score increase that would be beyond the median cSEM value for that grade level.

As seen in Table 1, the decreasing slope values contribute to a longer progress monitoring duration as grade level increases. In other words, a longer progress monitoring period is required at higher grade levels to obtain meaningful results for instructional decision making. The results suggest that only grades 1 through 4, inclusively, met the typical maximum progress monitoring period of 20 weeks for meaningful growth to be observed. It should be noted, however, that the cSEM values are relatively stable across grade levels and for the range of data points evaluated because Star Reading is a CAT-based measure. This finding suggests that the measurement error associated with the data used for progress monitoring does not vary based on the number of administrations of Star Reading. It appears that a cSEM value of approximately 16 USS points can be assumed for data collected using Star Reading.

Number of Data Points

The number of data points to be collected is an important consideration for progress monitoring purposes, as the amount of data that is collected for each student has shown to have significant implications on the decision-making process (Christ et al., 2013). The typical approach is to collect data weekly (Stecker et al., 2008), although the quality of the dataset and the length of the data collection period interact, with longer data collection periods requiring fewer data points (Christ et al., 2013). These findings, however, are based on traditional CBM that employs the use of probes to gather information on a student's level of performance. Thus, we sought to determine the number of data points that were necessary when using a CAT for the purpose of progress monitoring.

The results from the analyses are quite different from the results that were expected based on the CBM literature. It appears that relatively few data points are needed to generate a representative, psychometrically sound estimate of student growth (i.e., trend line). This was determined from the stability of the cSEM regardless of the number of data points collected and the accuracy of the Theil-Sen slope values in the simulation study result. A conservative approach would be to administer Star Reading every 2 weeks, assuming a typical progress monitoring duration of 15–20 weeks, for a total of seven to 10 data points. However, it is possible that the assessment interval could range from 2 to 4 weeks. In other words, the minimum number of Star Reading administrations could be as few as five (i.e., every 4 weeks over a 20-week intervention period).

Progress Monitoring Schedules

The question of how long and how often data should be collected for CAT-based progress monitoring measures was raised by Van Norman et al. (2017). In a related study, Nelson et al. (2017b) examined the influences of data collection schedules on estimations of progress monitoring slopes. Although their sample was smaller than the one used in the current study and only limited to grades 4 and 5, the results were similar—this provides some convergent evidence suggesting that progress monitoring slopes generated from Star Reading data do not vary as a function of data collection schedule. The results from the current study extend previous findings by demonstrating that this effect (i.e., lack of variability in the quality of slopes generated from different progress monitoring schedules) is relatively stable across grades 1 through 8. When considering individual student slopes, however, Nelson and colleagues reported that a data collection schedule that included at least 5 data points seemed to be significantly better than using only 2 or 3 data points over the course of a semester. This result also converges with our finding that bias and RMSE values for slope estimates tend to decrease as the number of data points increases. However, it is possible that some of the variability observed by Nelson et al. (2017b) when evaluating student-level OLS slope estimates could be explained by the effect of outliers in their sample. Regardless, based on the results of the current study, if the Theil-Sen estimator is used for estimating growth slopes, 6–8 data points appear to generate highly robust slope estimates, even when extreme outliers are present in the data.

Taking into consideration the aforementioned findings, to achieve a minimum of 6 total data points to generate strong progress monitoring slope estimates, data could be collected once every 2 weeks for an intervention lasting 14 weeks or once every 3 weeks for an intervention lasting 18 weeks. It appears that less frequent data collection schedules appear to be a benefit of CAT-based progress monitoring when compared to traditional CBM approaches that appear to benefit from the daily progress monitoring schedules (Thornblad and Christ, 2014). To even consider a bi-weekly progress monitoring schedule may be a significant deviation from the norm for many educators who have been trained to administer progress monitoring measures on a daily or weekly basis. However, it appears to be an accepted practice to administer progress monitoring measures on a monthly basis (Stecker et al., 2008).

General Discussion

The conceptualization of validity as an evolving property that is closely related to the use and interpretation of test scores, as opposed to being a property of the test itself (Messick, 1995), fits well within an empirical framework to support best assessment practices. In particular, advancements in assessment formats (e.g., CATs) and methods (e.g., Theil-Sen estimator) should be evaluated to ensure that the most accurate approaches are used in practice. As an example of a well-established reading assessment, considerable evidence has been produced in support of using Star Reading scores to progress monitor students' growth in reading. However, despite Star Reading receiving favorable reviews for its use as a progress monitoring measure (National Center for Intensive Intervention, 2018), additional empirical evidence that further examines the use of the scores produced from this CAT-based assessment in practice would be beneficial to test users (e.g., educators, teachers, and school psychologists).

Implications for Practice

CAT assessments, such as Star Reading, have the potential to be used for progress monitoring, given that, like CBMs, they are general outcome measures, meant to represent a student's overall achievement in a particular curricular area (e.g., reading or math). The results of this study demonstrate that it is possible to use Star Reading for the purpose of progress monitoring. A few preliminary guidelines were generated from the results. First, it appears that at least five data points should be collected, preferably in equal intervals (e.g., every 2 weeks), over the course of the implementation of an intervention. Second, the minimum number of weeks that the intervention be administered should be consistent with the number of weeks listed in Table 1 (based on the student's current grade-based reading level), to ensure meaningful growth is being interpreted. Finally, measurement error should be considered within this process to ensure that error is taken into account when interpreting Star Reading progress monitoring data. Specifically, if the median cSEM of the progress monitoring data for a particular student exceeds the value of 16 USS points (see Table 1), the student should be retested or testing should continue until median cSEM values for the data collected are below this criterion.

Future Directions

Christ et al. (2013) argued that “rate-based measures, such as CBM-R, are often more sensitive to variations in performances—as compared to measures based on frequency (e.g., the number of instances of a behavior) or accuracy (e.g., the percentage of items correct)” (p. 21). Despite Star Reading not being a rate-based measure, it appears that it is possible to use its results for the purpose of progress monitoring. Furthermore, a CAT approach to progress monitoring allows the test user to avoid the potential sources of measurement variability that are likely to appear in CBM-R measures, such as examiner characteristics, setting, delivery of directions, and alternate forms (see Christ et al., 2013, for a review).

Despite the normative and inclusive nature of the sample data obtained from the 2014 to 2015 administration of Star Reading, the suggested reference points may not apply to students with unexpected growth trajectories due to unusual or unexpected changes in USS over test administrations or high cSEM values from Star Reading as a result of irregular or inconsistent response patterns during the Star Reading administration. Therefore, a series of simulation studies could be conducted to evaluate the generalizability of the normative reference points across a variety of dataset quality conditions (e.g., unified scaled score change, cSEM, number of CAT administrations, various ability distributions). To our knowledge, Christ's, Zopluoglu, Monaghen and Van Norman (2013) simulation-based evaluation of schedule, duration, and dataset quality on progress monitoring outcomes is among the first to apply simulation methods to systematically evaluate progress monitoring procedures. Similar simulation-based procedures can be implemented to further evaluate the generalizability and stability of Theil-Sen slope estimates and corresponding grade-level growth estimates in the future.

The use of an exceptionally large sample of extant student data allowed for the generation of what are likely to be robust estimates of typical student growth for Star Reading across the grade levels. However, additional work is necessary to test the validity of the decisions that are made from the preliminary findings from the current study. This may include an analysis of the percentage of false positive and false negatives that are identified using various rates of improvement at different grade levels. It would also be beneficial to determine if the decisions of adequate vs. inadequate growth are predictive of later student performance.

There are clearly a number of possible studies that could be conducted to determine the consequences of applying the aforementioned guidelines in practice. Of course, instructional decisions should be made within the context of multiple data sources. Future research may want to consider other sources of information and how they could be used in conjunction with Star Reading progress monitoring data. In summary, despite this study making a significant contribution in demonstrating that it is possible to use Star Reading for the purpose of progress monitoring, there are a number of additional studies that could be completed prior to further support valid decisions being made in practice.

Limitations

Based on the available data, it appears that Star Reading is most useful when a student's reading level is between grades 1 and 4, inclusively. This is not a significant limitation, given that students struggling with word identification and passage reading fluency who require academic interventions and, consequently, progress monitoring are likely to be reading at a level that is within this grade range (Fuchs and Fuchs, 2001). In other words, expectations for growth are not necessarily grade-specific, but rather are associated with a given student's current grade-based level of performance in reading. For example, if a 5th grade student is reading at a 2nd grade level, a goal line based on grade 2 normative data would likely be a reasonable goal for this student. That is, the normative growth represents skill acquisition, as opposed to an innate ability for the acquisition of academic content. Regardless, as progress monitoring practices are developed, it is important to remember that one of the fundamental characteristics of measures used for this purpose is that they need to be sensitive to student growth over a relatively short period of time. As noted by Christ et al. (2013), “if the scenario requires 20 or more weeks of data, then the utility of progress monitoring and reality of inductive hypothesis testing are seriously threatened” (p. 55).

Extensive demographic data were not included in the analyses, given that a significant portion of the data did not have demographic information available. Therefore, it is unclear whether the progress monitoring slope estimates presented herein would be consistent across gender, ethnic, or socioeconomic groups. Future research may want to investigate the effects of these variables, as some evidence exists to suggest that response to instruction may be different between these groups (e.g., Sirin, 2005; Logan and Johnston, 2010; Scheiber et al., 2015).

Author Contributions

OB and DC jointly developed the framework for the validity evidence on Star Reading. OB completed most of the data analysis, while DC prepared the background and literature review of the manuscript. OB and DC completed the rest of the manuscript write-up together.

Conflict of Interest Statement

OB and DC were paid consultants for Renaissance Learning, Inc.

References

American Educational Research Association American Psychological Association, and National Council on Measurement in Education. (2014). Standards for Educational and Psychological Testing, 2nd Edn. Washington, DC: American Psychological Association.

Ardoin, S. P., and Christ, T. J. (2009). Curriculum-based measurement of oral reading: Standard errors associated with progress monitoring outcomes from DIBELS, AIMSweb, and an experimental passage set. Schl. Psychol. Rev. 38, 266–283.

Ardoin, S. P., Christ, T. J., Morena, L. S., Cormier, D. C., and Klingbeil, D. A. (2013). A systematic review and summarization of the recommendations and research surrounding curriculum-based measurement of oral reading fluency (CBM-R) decision rules. J. Sch. Psychol. 51, 1–18. doi: 10.1016/j.jsp.2012.09.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Burns, M. K. (2010). Response-to-intervention Research: is the sum of the parts as great as the whole? Perspect. Lang. literacy 36:13.

Burns, M. K., Riley-Tillman, T. C., and VanDerHeyden, A. M. (2012). RTI Applications, Vol. 1: Academic and Behavioral Interventions. New York, NY: The Guilford Press.

Burns, M. K., Senesac, B. V., and Symington, T. (2003). The effectiveness of the hosts program in improving the reading achievement of children at-risk for reading failure. Lit. Res. Instr. 43, 87–103. doi: 10.1080/19388070409558406

CrossRef Full Text | Google Scholar

Christ, T. J. (2006). Short-term estimates of growth using curriculum-based measurement of oral reading fluency: estimating standard error of the slope to construct confidence intervals. Sch. Psychol. Rev. 35, 128–133.

Christ, T. J., and Silberglitt, B. (2007). Estimates of the standard error of measurement for curriculum-based measures of oral reading fluency. Sch. Psychol. Rev. 36, 130–146.

Christ, T. J., Zopluoglu, C., Long, J. D., and Monaghen, B. D. (2012). Curriculum-based measurement of oral reading: quality of progress monitoring outcomes. Except. Child. 78, 356–373. doi: 10.1177/001440291207800306

CrossRef Full Text | Google Scholar

Christ, T. J., Zopluoglu, C., Monaghen, B. D., and Van Norman, E. R. (2013). Curriculum-based measurement of oral reading: multi-study evaluation of schedule, duration, and dataset quality on progress monitoring outcomes. J. Sch. Psychol. 51, 19–57. doi: 10.1016/j.jsp.2012.11.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Cohen, J., Cohen, P., West, S. G., and Aiken, L. S. (2003). Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences, 3rd Edn. Mahwah, NJ: Lawrence Erlbaum.

Deno, S. L. (2003). Developments in curriculum-based measurement. J. Spec. Educ. 37, 184–192. doi: 10.1177/00224669030370030801

CrossRef Full Text | Google Scholar

Education Market Research (2013). The Complete K-12 Report: Market Facts & Segment Analyses, (2013). Rockaway Park, NY: Simba Information.

Fuchs, L. S., and Fuchs, D. (2001). What Is Scientifically-Based Research on Progress Monitoring? Washington, DC: National Center on Student Progress Monitoring.

Fuchs, L. S., Fuchs, D., Hamlett, C. L., Walz, L., and Germann, G. (1993). Formative evaluation of academic progress: how much growth can we expect? Sch. Psychol. Rev. 22, 27–27.

Gilbert, R. O. (1987). Statistical Methods for Environmental Pollution Monitoring. New York, NY: Van Nostrand Reinhold.

Granato, G. E. (2006). Kendall-Theil Robust Line (KTRLine-Version 1.0)-A Visual Basic Program for Calculating and Graphing Robust Nonparametric Estimates of Linear-Regression Coefficients Between Two Continuous Variables. Techniques and Methods of the U.S. Geological Survey, Book 4, Chapter. A7, U.S. Geological Survey. with CD–ROM. 31.

Hampel, F. R., Ronchetti, E. M., Rousseeuw, P. J., and Stahel, W. A. (2005). Robust Statistics: The Approach Based on Influence Functions. New York, NY: Wiley.

Huber, P. J. (1964). Robust estimation of a location parameter. Ann. Math. Stat. 35, 73–101. doi: 10.1214/aoms/1177703732

CrossRef Full Text | Google Scholar

Huber, P. J. (1973). Robust regression: asymptotics, conjectures and Monte Carlo. Ann. Stat. 1, 799–821. doi: 10.1214/aos/1176342503

CrossRef Full Text | Google Scholar

Klingbeil, D. A., Nelson, P. M., and Van Norman, E. R. (2017). Diagnostic accuracy of multivariate universal screening procedures for reading in upper elementary grades. Remed. Spec. Educ. 35, 308–320. doi: 10.1177/0741932517697446

CrossRef Full Text | Google Scholar

Koller, M., and Stahel, W. A. (2011). Sharpening Wald-type inference in robust regression for small samples. Comput. Stat. Data Anal. 55, 2504–2515. doi: 10.1016/j.csda.2011.02.014

CrossRef Full Text | Google Scholar

Komsta, L. (2013). mblm: Median-Based Linear Models. R Package Version 0.12. Available online at: https://CRAN.R-project.org/package=mblm.

Logan, S., and Johnston, R. (2010). Investigating gender differences in reading. Educ. Rev. 62, 175–187. doi: 10.1080/00131911003637006

CrossRef Full Text | Google Scholar

Massart, D. L., Vandeginste, B. G. M., Buydens, L. M. C., De Jong, S., Lewi, P. J., and Smeyers-Verbeke, J. (1997). “12.1.5.1 single median method,” in Data Handling in Science and Technology, Vol. 20, Part A, eds D. L. Massart, B. G. M. Vandeginste, L. M. C. Buydens, S. De Jong, P. J. Lewi, and J. Smeyers-Verbeke (New York, NY: Elsevier), 355–356.

Mercer, S. H., Lyons, A. F., Johnston, L. E., and Millhoff, C. L. (2014). Robust regression for slope estimation in curriculum-based measurement progress monitoring. Assess. Eff. Interv. 40, 176–183. doi: 10.1177/1534508414555705

CrossRef Full Text | Google Scholar

Messick, S. (1995). Validity of psychological assessment: validation of inferences from persons' responses and performances as scientific inquiry into score meaning. Am. Psychol. 50, 741–749.

National Center for Intensive Intervention (2018). Progress Monitoring Tools Chart. Available online at: http://www.intensiveintervention.org/chart/progress-monitoring

National Center on Response to Intervention (2018). The Screening Tools Chart. Available online at: https://www.rti4success.org/resources/tools-charts/screening-tools-chart

Nelson, P. M., Van Norman, E. R., and Christ, T. J. (2017a). Visual analysis among novices: training and trend lines as graphic aids. Contemp. Sch. Psychol. 21, 93–102. doi: 10.1007/s40688-016-0107-9

CrossRef Full Text | Google Scholar

Nelson, P. M., Van Norman, E. R., Klingbeil, D. A., and Parker, D. C. (2017b). Progress monitoring with computer adaptive assessments: the impact of data collection schedule on growth estimates. Psychol. Sch. 54, 463–471. doi: 10.1002/pits.22015

CrossRef Full Text | Google Scholar

Poncy, B. C., Skinner, C. H., and Axtell, P. K. (2005). An investigation of the reliability and standard error of measurement of words read correctly per minute using curriculum-based measurement. J. Psychoeduc. Assess. 23, 326–338. doi: 10.1177/073428290502300403

CrossRef Full Text | Google Scholar

R Core Team (2018). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.

Renaissance (2015). Star Reading Technical Manual. Wisconsin Rapids, WI: Renaissance.

Scheiber, C., Reynolds, M. R., Hajovsky, D. B., and Kaufman, A. S. (2015). Gender differences in achievement in a large, nationally representative sample of children and adolescents. Psychol. Sch. 52, 335–348. doi: 10.1002/pits.21827

CrossRef Full Text | Google Scholar

Sen, P. K. (1968). Estimates of the regression coefficient based on Kendall's tau. J. Am. Stat. Assoc. 63, 1379–1389. doi: 10.1080/01621459.1968.10480934

CrossRef Full Text | Google Scholar

Shapiro, E. S. (2010). Academic Skills Problems, 4th Edn. Workbook. New York, NY: Guilford Press.

Shapiro, E. S. (2011). Academic Skills Problems: Direct Assessment and Intervention. New York, NY: Guilford Press.

Shapiro, E. S., Dennis, M. S., and Fu, Q. (2015). Comparing computer adaptive and curriculum-based measures of math in progress monitoring. Sch. Psychol. Q. 30, 470–487. doi: 10.1037/spq0000116

PubMed Abstract | CrossRef Full Text | Google Scholar

Sirin, S. R. (2005). Socioeconomic status and academic achievement: a meta-analytic review of research. Rev. Educ. Res. 75, 417–453. doi: 10.3102/00346543075003417

CrossRef Full Text | Google Scholar

Stecker, P. M., Fuchs, D., and Fuchs, L. S. (2008). Progress monitoring as essential practice within response to intervention. Rural Spec. Educ. Q. 27, 10–17. doi: 10.1177/875687050802700403

CrossRef Full Text | Google Scholar

Theil, H. (1950). A rank-invariant method of linear and polynomial regression analysis. I, II, III. Nederl. Akad. Wetensch. Nederl. Akad. Wetensch. Proc. 53, 1397–1412.

Thornblad, S. C., and Christ, T. J. (2014). Curriculum-based measurement of reading: is 6 weeks of daily progress monitoring enough? Sch. Psychol. Rev. 43, 19–29.

Van Norman, E. R., Nelson, P. M., and Parker, D. C. (2017). Technical adequacy of growth estimates from a computer adaptive test: implications for progress monitoring. Sch. Psychol. Q. 32, 379–391. doi: 10.1037/spq0000175

PubMed Abstract | CrossRef Full Text | Google Scholar

Van Norman, E. R., Nelson, P. M., Shin, J., and Christ, T. J. (2013). An evaluation of the effects of graphic aids in improving decision accuracy in a continuous treatment design. J. Behav. Educ. 22, 283–301. doi: 10.1007/s10864-013-9176-2

CrossRef Full Text | Google Scholar

Van Norman, E. R., and Parker, D. C. (2016a). “My progress monitoring data are nonlinear; Now what?” in Poster Presented at the Annual Convention of the National Association of School Psychologists (New Orleans, LA).

Van Norman, E. R., and Parker, D. C. (2016b). An evaluation of the linearity of curriculum-based measurement of oral reading (CBM-R) progress monitoring data: idiographic considerations. Learn. Disabil. Res. Pract. 31, 199–207. doi: 10.1111/ldrp.12108

CrossRef Full Text | Google Scholar

VanDerHeyden, A. M., Witt, J. C., Naquin, G., and Noell, G. (2001). The reliability and validity of curriculum-based measurement readiness probes for kindergarten students. Sch. Psychol. Rev. 30, 363–382.

Vannest, K. J., Parker, R. I., Davis, J. L., Soares, D. A., and Smith, S. L. (2012). The Theil-Sen slope for high-stakes decisions from progress monitoring. Behav. Disord. 37, 271–280. doi: 10.1177/019874291203700406

CrossRef Full Text | Google Scholar

Venables, W. N., and Ripley, B. D. (2002). Modern Applied Statistics with S, 4th Edn. New York, NY: Springer.

Wang, X. (2005). Asymptotics of the Theil–Sen estimator in the simple linear regression model with a random covariate. J. Nonparametric Stat. 17, 107–120. doi: 10.1080/1048525042000267743

CrossRef Full Text | Google Scholar

Weiss, D. J. (2011). Better data from better measurements using computerized adaptive testing. J. Methods Meas. Soc. Sci. 2, 1–27. doi: 10.2458/jmm.v2i1.12351

CrossRef Full Text | Google Scholar

Wilcox, R. R. (1998). Simulations on the Theil–Sen regression estimator with right-censored data. Stat. Prob. Lett. 39, 43–47.

Wilcox, R. R. (2010). Fundamentals of Modern Statistical Methods: Substantially Improving Power and Accuracy 2nd Edn. New York, NY: Springer.

Ysseldyke, J., Burns, M., Dawson, P., Kelley, B., Morrison, D., Ortiz, S., et al. (2006). School Psychology: A Blueprint for Training and Practice III. Bethesda, MD: National Association of School Psychologists.