Comparative analysis and application of rockburst prediction model based on secretary bird optimization algorithm

The accurate rockburst prediction is crucial for ensuring the safety of underground engineering construction. Among the various methods, machine learning-based rockburst prediction can better solve the nonlinear relationship between rockbursts and influencing factors and thus has great potential for engineering applications. However, current research often faces certain challenges related to the feature selection of prediction indices and poor model optimization performance. This study compiled 342 rockburst cases from domestic and international sources to construct an initial database. In order to determine the relevant prediction indicators, a feature selection method based on the ReliefF-Kendall model was proposed. The initial database was equalized and visualized using the Adasyn and t-SNE algorithms. Five rockburst prediction models [support vector machine (SVM), least-squares support vector machine (LSSVM), kernel extreme learning machine (KELM), Random Forest (RF), and XGBoost] were established by employing the Secretary Bird Optimization (SBO) algorithm and 5-fold cross-validation to optimize performance. The optimal model was selected based on a comprehensive assessment of generalization ability (accuracy, kappa, precision, recall, and F1-score) and stability (average accuracy). The reliability of the proposed feature selection, model optimization, and data balancing methods was verified by comparing the optimal model with other methods. The results indicate that the PSO-SVM model demonstrated superior prediction accuracy and generalization performance; the accuracy can reach 81.4% (optimal) and 80.1% (average). The main factors affecting the occurrence of rockburst are W_et, maximum tangential stress (MTS), D, and uniaxial compressive strength (UCS). Finally, the model was applied to the domestic rockburst engineering cases, achieving a prediction accuracy of 90% and verifying its engineering applicability.

1 Introduction

Rockburst is a dynamic instability disaster occurring in deep underground engineering under high ground stress, caused by the release of elastic strain energy within the surrounding rock during excavation and unloading (Xia et al., 2022; Xue et al., 2022; Ma et al., 2024). The random suddenness and the strong destructiveness characterize it. It can delay the construction period and cause substantial economic losses, posing a severe threat to construction personnel and equipment safety. Suppose the potential rockburst risk can be effectively predicted and evaluated (Esmatkhah Irani et al., 2022) in advance in the early stage of underground engineering. In that case, the risk of a rockburst disaster can be reduced by reasonable site selection and strengthening support measures. A significant issue in the risk control management of deep underground engineering construction is the reasonable and accurate rockburst prediction.

The current methods for predicting rockburst can be classified into three primary categories: 1) the single-criterion methods based on rockburst mechanisms, 2) the comprehensive prediction methods considering various factors influencing rockburst, and 3) the rockburst prediction methods reliant on field monitoring. Most single-criterion methods have poor engineering applicability and prediction accuracy, often failing to meet the requirements. Despite their effectiveness, methods such as microseismic monitoring have high operational costs, limiting their widespread application. The comprehensive rockburst prediction methods using mathematical theory or machine learning are widely adopted owing to their simplicity, convenience, and high engineering practicality.

The first category is based on the uncertainty theory. It includes methods such as the fuzzy mathematics method (Wang et al., 2019), grey theory method (Gao, 2008), attribute recognition theory method (Qu et al., 2022), set pair analysis method (Wang et al., 2020), efficacy coefficient method (Qiu et al., 2013), matter-element extension method (Xue et al., 2019), evidence theory method (Zhang F. et al., 2024) target closeness method (Liu et al., 2015), fuzzy matter-element theory method (Wang et al., 2015), cloud model method (Sun et al., 2024a), catastrophe progression method (Xing et al., 2024), unascertained measure theory method (Hu et al., 2023), projection pursuit method (Xu and Xu, 2010), and approximation ideal point method based on distance sorting theory (Xu et al., 2018a). The second category is based on machine learning. It involves neural networks (Zhang Q. et al., 2024), deep neural networks (Zhang et al., 2023), support vector machine (Pu et al., 2018b) naive Bayes (Zhang S. et al., 2024), logistic regression (Li and Jimenez, 2018), K nearest neighbor (Kamran et al., 2022), extreme learning machine (Li et al., 2023b), random forest (Yang, 2024), gradient boosting decision tree (Liang et al., 2020) extreme gradient boosting tree (Qiu and Zhou, 2023a), light gradient boosting machine (Qiu and Zhou, 2023b), extreme tree (Li et al., 2022), and adaptive boosting (Wang et al., 2023). The first category relies on mathematical theory and requires the determination of rockburst level thresholds and index weights, which are affected by human subjectivity. The second category, which is based on machine learning, is entirely data-driven, less subjectively affected, and can continuously update sample libraries. It can be well explained to deal with the nonlinear action relationship between rockbursts and influencing factors.

Tan et al. (2022) established a fusion method combining the diversity and accuracy weights of Stacking and Voting for the rockburst intensity classification prediction, effectively improving the performance compared to ordinary machine learning algorithms. Liu et al. (2022) proposed three Stacking ensemble algorithms considering multiple rockburst prediction indices, successfully predicting the rockburst in the vertical shaft of Zhongnanshan Tunnel. Li et al. (2021) utilized six machine learning algorithms with cross-validation for rockburst prediction models, compared the prediction accuracies to select the optimal model and predicted the rockburst in the Jinping II hydropower station diversion tunnel. Tang and Xu (2020) established nine rockburst prediction models after preprocessing the original dataset, achieving better results than the traditional theoretical criteria. Tan et al. (2021) proposed a data preprocessing method combining the LOF and improved SMOTE algorithms and established six machine learning models based on the processed dataset, significantly improving the prediction accuracy. These studies have demonstrated that machine-learning-based rockburst prediction has broad engineering application prospects. However, this method currently has three main areas for improvement: the algorithm model optimization, the prediction input index selection, and the insufficient data quality. Intelligent optimization algorithms are primarily integrated with prediction algorithms to address or avoid the issue of models becoming trapped in local optima. The commonly used optimization algorithms include the particle swarm optimization algorithm (Yuan et al., 2023), the genetic algorithm (Wei et al., 2020), the sparrow search algorithm (Xu et al., 2022), the grey wolf optimization algorithm (Kamran et al., 2024), the African vulture optimization algorithm (Qiu and Zhou, 2024), the differential evolution optimization algorithm (Deng et al., 2024)and the improved multi-verse optimization algorithm (Xie et al., 2021). Existing optimization algorithms (e.g., PSO) and others have several areas for improvement, including a tendency toward locally optimal solutions, slow convergence, and sensitivity to parameter settings. Therefore, developing an algorithmic model with exploration ability, greater adaptability, and higher efficiency is essential to improve the model’s generalization ability and predictive performance.

The accuracy of the model predictions is largely contingent upon the reliability of the input indicators. An insufficient or excessive number of prediction indicators affects the model’s performance, and there is no uniform standard for input indicators in current prediction models. Most indicators are selected through the qualitative analysis of factors influencing rockbursts or trial-and-error methods with various feature combinations, often resulting in solid subjectivity or increased computational complexity. The existing prediction index determination methods make it challenging to ensure the efficiency and objectivity of the prediction model index selection. The data-driven feature selection method based on real rockburst cases needs further study. The feature selection, an essential step in the machine learning data preprocessing phase, aims to extract the most relevant features for object recognition and classification. There are fewer studies related to data-driven feature selection for rockburst prediction metrics. Kidega et al. (2022) developed a gradient boosting (GBM) prediction model based on decision uncertainty to analyze combinations of factors affecting rock bursts. The model, combined with a 3-fold cross-validation optimization approach, found that the most important factor affecting rock bursts is the maximum tangential stress. Sun et al. (2024b) selected the microseismic characteristics of underground mines based on the correlation feature selection (CFS) algorithm and proposed the OFS-Bayes-WPS model for short-term rockburst intensity prediction. The feature selection methods can be categorized into filtering, wrappers, and embedded (Zhang et al., 2020). The ReliefF algorithm is a straightforward and effective filtering method for feature selection. In this study, we selected the optimal features for the rockburst prediction model by integrating the ReliefF algorithm with the correlation analysis to ensure the objectivity and rationality of the choice of indicators for predictive characterization. The major data quality issue is the imbalance of the data categories. In machine learning, the imbalanced datasets lead models to overemphasize the majority samples while neglecting the minority samples, thereby reducing the generalization performance. Selecting an appropriate data balancing method is crucial for improving the predictive accuracy of the models.

Based on the shortcomings of previous research, this study initially selected the rockburst prediction index set through literature reviews and analyses of the rockburst influencing factors. A total of 342 groups of rockburst engineering cases were collected from domestic and international sources. The prediction indices were determined using the established ReliefF-Kendall feature selection method. The initial database was balanced and visualized using the Adasyn oversampling and t-SNE algorithms. An optimization method combining the Secretary Bird Optimization (SBO) algorithm and 5-fold cross-validation was proposed, establishing five rockburst prediction models. The optimal prediction model was selected based on its generalization ability and stability. The reliability of feature selection, the SBO algorithm, and the Adasyn data processing algorithm were compared and analyzed using the optimal model and other methods. Finally, the engineering applicability of the model was verified through rockburst engineering cases in China.

2 Methodology

2.1 SBO algorithm

The SBO algorithm is a swarm intelligence optimization method inspired by the survival behavior of the secretary bird in nature, which involves constant hunting and predator evasion. The algorithm consists of three primary stages: initialization, exploration (hunting behavior), and development (escape behavior). During the exploration stage, the algorithm simulates the secretary bird hunting snakes (Fu et al., 2024). In the developmental stage, it mimics the bird escaping predators and finding the safest route to a haven. These stages are iteratively repeated until the model attains the maximum number of iterations, ultimately identifying the optimal solution to the optimization problem. When applied to model optimization, it shows excellent global search ability and adaptability, effectively alleviates the risk of converging to the local optimum, and the calculation efficiency is more efficient, which improves the overall optimization performance.

2.1.1 Initialization stage

This stage involves constructing and randomly initializing the positions of the secretary birds within the population space (Fu et al., 2024). Each bird’s position in the search space corresponds to the value of the decision variable. The initial positions are generated randomly according to Equation 1.

$\left\{\begin{array}{l}{x}_{ij}=l{b}_j+r\times \left(u{b}_j-l{b}_j\right),i=1,2,\dots ,N,j=1,2,\dots ,M\\ X=\left(x_{ij}\right)={\left[\begin{array}{cccccc}{x}_{11}& x_{12}& \cdots & x_{1j}& \cdots & x_{1M}\\ x_{21}& x_{22}& \cdots & x_{2j}& \cdots & x_{2M}\\ ⋮& ⋮& \ddots & ⋮& \ddots & ⋮\\ x_{i1}& x_{i2}& \cdots & x_{ij}& \cdots & x_{iM}\\ ⋮& ⋮& \ddots & ⋮& \ddots & ⋮\\ x_{N1}& x_{N2}& \cdots & x_{Nj}& \cdots & x_{NM}\end{array}\right]}_{N\times M}\end{array}\right.(1)$

where ub_j and lb_j are the upper and lower bounds; r denotes a random number between 0 and 1; X denotes the population of the secretary bird; x_i denotes the ith secretary bird; x_ij denotes the jth problem variable value of the ith secretary bird; N denotes the number of individuals in the population; and m denotes the dimension of the problem variable (Fu et al., 2024).

2.1.2 Exploration stage

The hunting behavior of secretary birds is generally categorized into three stages: searching for prey, consuming prey, and attacking prey (Fu et al., 2024). The time intervals define these stages: the first stage (t < 1/3 T), the second stage (1/3 T < t < 2/3 T), and the third stage (2/3 T < t < T).

2.1.2.1 Searching for prey

This stage employs the difference between individuals and uses the differential evolution strategy to iteratively update the position of the secretary bird through Equation 2.

$x_{ij}^{new{P}_1}=x_{ij}+\left(x_{random\_1}-x_{random\_2}\right)\times R_1,t<\frac{1}{3}T(2)$

Where x_ij^newP1 denotes the value of dimension j; t denotes the current number of iterations; T denotes the maximum number of iterations; x_{random_1} and x_{random_2} denote the randomly generated candidate solutions during the initial iteration phase; R₁ is the array of 1 × M randomly generated in the interval [0,1]; and M is the dimension of the solution space.

2.1.2.2 Consuming prey

The secretary bird delays its attack upon detecting prey, opting to observe the snake’s movements closely instead. By circling and jumping, the bird aims to deplete its snake stamina. Consequently, the snake’s random motion trajectory was simulated using Brownian motion during this phase, as shown in Equation 3. The position of the secretary bird in the Consuming Prey stage can be updated using Equation 4.

$RB=randn\left(1,M\right)(3)$

$x_{ij}^{newP1}=x_{best}+\mathit{exp}\left({\left(t/T\right)}^4\right)\times \left(RB-0.5\right)\times \left(x_{best}-x_{ij}\right),\frac{1}{3}T<t<\frac{2}{3}T(4)$

Where randn (1,M) denotes an array of dimensions 1 × M generated randomly from the standard normal distribution; and x_best denotes the current optimal value.

2.1.2.3 Attacking prey

Once the prey is exhausted, the secretary bird discerns the optimal moment to initiate an attack. At this stage, the location of the secretary bird is updated using the Lévy flight strategy, as shown in Equation 5.

$\begin{array}{l}\left\{\begin{array}{l}{x}_{ij}^{newP1}=x_{best}+\left({\left(1-\frac{t}{T}\right)}^{2\times \frac{t}{T}}\right)\times x_{ij}\times RL,t>\frac{2}{3}T\\ RL=0.5\times L\text{evy}\left(M\right)\end{array}\right.\end{array}(5)$

Where ${\left(1-\frac{t}{T}\right)}^{2\times \frac{t}{T}}$ denotes nonlinear perturbation factor; and RL denotes the weighted Levy flight coefficient.

Levy (M) denotes the Levy flight distribution function, it is calculated as Equation 6.

$Levy\left(M\right)=s\times \frac{u\times \sigma }{{\left|\nu \right|}^{-1}}(6)$

Where s is a constant valued at 0.01; n is a constant equal to 1.5; and u and v are random numbers in the interval [0,1].

2.1.3 Development stage

When a secretary bird encounters danger, it employs two escape strategies: camouflage (C1) and flight (C2). It is assumed that both strategies occur with equal probabilities. Upon detecting a threat, the bird initially seeks an appropriate environment for camouflage. Without nearby safe concealment, it resorts to flight or rapid movement to evade the danger. The individual positions corresponding to these two escape strategies are expressed in Equation 7.

$x_{ij}^{new,P2}=\left\{\begin{array}{l}{C}_1:x_{best}+\left(2\times RB-1\right)\times {\left(1-\frac{t}{T}\right)}^2\times x_{ij},r<r_i\\ \begin{array}{l}{C}_2:x_{ij}+R_2\times \left(x_{random}-K\times x_{ij}\right),else\\ K=round\left(1+rand\left(1,1\right)\right)\end{array}\end{array}\right.(7)$

Where r = 0.5, R₂ denotes an array with a dimension of (1 × M) randomly generated from the normal distribution; x_random denotes the random candidate solution for the current iteration; and k denotes a randomly selected integer, either 1 or 2.

Figure 1 shows the optimization search process based on the SBO algorithm.

Figure 1

Figure 1. Flowchart of Secretary Bird Optimization algorithm.

2.2 Machine learning algorithms

2.2.1 Support vector machine

The support vector machine (SVM) is a supervised machine learning algorithm recognized for its strong generalization ability with minor-to-medium data samples and in addressing nonlinear and high-dimensional classification problems. The fundamental concept involves the application of a kernel function to execute a nonlinear transformation, thereby mapping the original data space into a higher-dimensional space to elucidate the nonlinear relationships between inputs and outputs. This process facilitates the identification of the optimal classification surface. Given the complex nonlinear relationship between influencing factors and rockbursts, this study employed a nonlinear SVM classification model based on the Gaussian radial basis kernel function. The principle of SVM algorithm is shown in Figure 2A. The optimal classification decision function of the SVM is expressed as Equation 8.

$f\left(x\right)=\text{sgn}\left[{\displaystyle \sum _{i=1}^n}{a_i}^{*}{y}_{i}K\left(x_i\cdot x\right)+b^{*}\right](8)$

Where sgn [ ] is the sign function; a_i^* is the optimal solution; and b^* is the classification threshold.

Figure 2

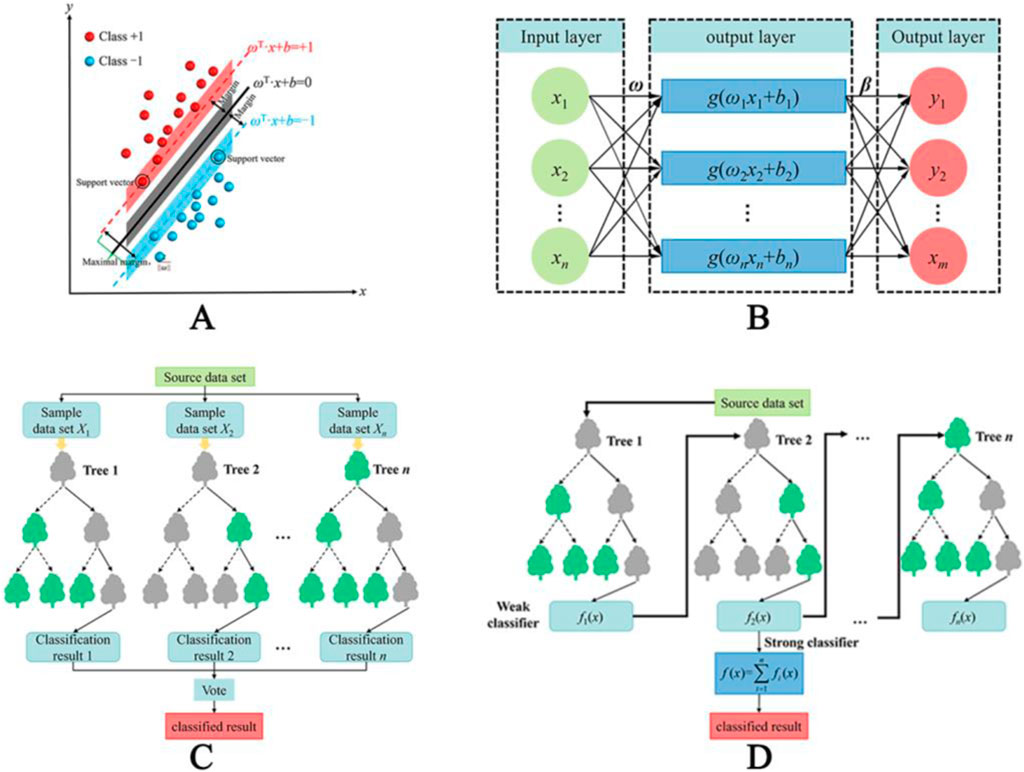
Figure 2. The principle of commonly used machine learning classification prediction algorithm: (A) SVM; (B) ELM; (C) RF; (D) XGBoost.

2.2.2 Least squares support vector machine

The least-squares support vector machine (LSSVM) is an improved SVM algorithm that substitutes the inequality constraint in the original SVM loss function with a linear least-squares criterion. This adjustment transforms the parameter optimization problem from a convex quadratic programming problem into a linear one. Consequently, the computational complexity is significantly reduced while the accuracy is preserved, enhancing the model’s generalization ability.

2.2.3 Kernel based extreme learning machine

The kernel extreme learning machine (KELM) enhances the extreme learning machine (ELM) algorithm by using a kernel function instead of random mapping. The principle of ELM algorithm is shown in Figure 2B. This improvement involves generating connection weights and bias terms from the input layer to the hidden layer randomly and then applying the kernel function to map the input sample’s low-dimensional data to a high-dimensional feature space. The model was trained by solving the weights of the output layer. This approach provides increased robustness and generalization capabilities for nonlinear classification and regression problems. The optimization function of the KELM algorithm is as Equation 9.

$F\left(x\right)=\left[\begin{array}{l}K\left(x,x_1\right)\\ ⋮\\ K\left(x,x_n\right)\end{array}\right]{\left(\frac{\mathrm{I}}{C}+{\mathrm{\Omega }}_{\text{EIM}}\right)}^{-1}L(9)$

Where K is the kernel function; (x₁, x₂, x_n) denotes the given training samples; n is the number of samples; and C represents the regularization coefficient.

2.2.4 Random forest algorithm

Random Forest (RF) is an ensemble learning algorithm that is founded on decision tree methodologies. It creates multiple training sets through random sampling and constructs the decision trees by randomly splitting node features. The final classification result is obtained by aggregating the outcomes of all terminal nodes of the decision trees through a voting mechanism. The principle of RF algorithm is shown in Figure 2C. RF is known for its strong generalization ability and adaptability to various data types. The classification function is as Equation 10.

$f\left(x_m\right)=p{\left\{h_i\left(x_m\right)\right\}}_{i=1}^{NT}(10)$

Where p is the majority vote; and NT is the number of trees in a random forest.

2.2.5 Extreme gradient boosting

Gradient Boosting Decision Tree (XGBoost) is an ensemble algorithm that employs the regression trees as the base learners. It iteratively optimizes each base learner using a gradient-boosting approach. Compared with the traditional boosting methods, XGBoost integrates regularization terms into the objective function to reduce overfitting and employs the second-order Taylor expansion of the loss function to improve both model efficiency and accuracy. The principle of XGBoost algorithm is shown in Figure 2D. The XGBoost objective function is as Equation 11.

${\widehat{y}}_i=\varphi \left(x_i\right)={\displaystyle \sum _{k=1}^K}{f}_k\left(x_i\right)\left(f_k\in F\right)(11)$

Where y_i is the output result; f_k is the kth base model classifier, with each f_k is related to an independent tree structure q and leaf fraction w; and F is the space of the classification and regression tree.

2.3 Feature selection

ReliefF is a multi-class filtering feature selection method that assesses the correlation between features and categories by evaluating the capacity of each feature to distinguish between similar samples. The process involves the following steps: First, a sample (R_i) is randomly selected from the training set (Zhang et al., 2022). Then, the k-nearest neighbour samples of the same class [denoted as (P_j)] and of different classes [denoted as (Q_j)] are identified within the training set. Finally, the weight for each feature was updated iteratively using the weight update (Tian et al., 2022) Equation 12 over n iterations, resulting in the final feature weights after processing all samples.

$\begin{array}{l}\hfill {\omega }_l^1={\omega }^i\left(A_l\right)-{\displaystyle \sum _{j=1}^k}\frac{\text{diff}\left(A_l,R_i,P_j\right)}{nk}\\ \hfill & +{\displaystyle \sum _{C\notin class\left(Ri\right)}}\frac{\left[\frac{P\left(C\right)}{1-P\left(\text{class}\left(R_i\right)\right)}·{\displaystyle \sum _{j=1}^k}\text{diff}\left(A_l,R_i,Q_j\left(C\right)\right)\right]}{nk}\hfill \end{array}(12)$

Where ωⁱ (A_l) is the weight of the lth feature A in the ith sample; P_j (j = 1, 2, …, k) is the jth sample of the k nearest neighbors of the same class as (R_i); P(C) is the proportion of samples belonging to category C in the training samples; P [class (R_i)) is the ratio of samples with the same type of R_i to the total sample; class (R_i) is the label category of R_i; Q_j(C) (j = 1, 2, … , k) is the jth sample of k nearest neighbor samples of different classes with R_i (label category is C); and n is the number of cycles (Tian et al., 2022; Zhang et al., 2022).

The Kendall correlation coefficient τ evaluates the correlation between the features and categories. Let the feature set be represented as X = {x₁, x₂, …, x_M}, and the corresponding category set as Y = {y₁, y₂, …, y_M}. The combination of each feature sequence X and its corresponding category sequence Y is denoted as Z. The calculation formula is as Equation 13.

$\left\{\begin{array}{l}\tau =\frac{C-D}{\sqrt{\left(M_0-M_1\right)\left(M_0-M_2\right)}}\\ M_0=\left[M\left(M-1\right)\right]/2\\ M_1={\displaystyle \sum _{i=1}^{{\mathrm{s}}_1}}\frac{1}{2}{U}_i\left(U_i-1\right)\\ M_2={\displaystyle \sum _{i=1}^{{\mathrm{s}}_2}}\frac{1}{2}{V}_i\left(V_i-1\right)\end{array}\right.(13)$

Where C and D denote the number of consistent element pairs and inconsistent element pairs in set Z, respectively; M represents the total number of samples; s₁ and s₂ denote the number of recurring element types in X and Y, respectively; and U_i and V_i denote the number of elements in the ith set composed of the same elements in X and Y.

The obtained correlation coefficient τ is calculated using Equation 14 to obtain the index weight ω²_l:

${\omega }_l^2=\frac{\left|{\tau }_l\right|}{{\displaystyle \sum _{l=1}^o}\left|{\tau }_l\right|}(14)$

Where τ_l is the correlation coefficient of the nth index; and o is the number of indexes.

3 Indices and data

3.1 Rockburst classification

The first step in predicting rockbursts is to classify their levels. Based on Chinese standards (Ministry of Housing and Urban-Rural Development of the People’s Republic of China, 2015), rockbursts are categorized according to the degree of damage and acoustic deformation resulting from surrounding rock ruptures. The classifications were as follows: no rockburst (None, N), light rockburst (Light, L), moderate rockburst (Moderate, M), and strong rockburst (Strong, S).

3.2 Selection of prediction indices

Owing to the complex mechanism underlying rockburst, which involves multiple influencing factors, their causes can be classified into internal and external aspects. The internal causes refer to the lithological characteristics of the surrounding rock, whereas the external causes include factors such as the project’s burial depth, excavation size and shape, and construction methods. Although excavation parameters and methods can influence the rockburst occurrences, they are not essential prerequisites owing to the project variability. Engineering practices indicate that the rockburst typically occurs in the intact brittle surrounding rocks under high-ground stress conditions. The primary conditions for rockbursts are the lithology of the surrounding rock and stress conditions. The hard, brittle rock stores elastic strain energy, whereas high-stress environments supply sufficient energy. This study selected the prediction indices based on two aspects: the lithology of the surrounding rock (including strength, brittleness, and energy storage) and stress conditions. This study summarized the rockburst prediction indices based on machine learning from the literature. Table 1 presents the selected indices from various sources, and Figure 3 shows the frequency of use for each index.

Table 1

Table 1. Part of the rockburst prediction model based on machine learning.

Figure 3

Figure 3. Number of times the rockburst prediction indices used.

As shown in Figure 3, the prediction indices include burial depth D, maximum tangential stress σ_θ, maximum principal stress σ₁, uniaxial compressive strength σ_c, uniaxial tensile strength σ_t, stress concentration coefficient σ_θ/σ_c, strength-to-stress ratio σ_c/σ₁, brittleness coefficients σ_c/σ_t and σ_c-σ_t/σ_c + σ_t, elastic energy index W_et, and surrounding rock integrity coefficient K_v. Among these, σ₁, σ_c/σ₁, K_v, σ_c-σ_t/σ_c + σ_t, and D are predicted to be used less frequently. In order to avoid the redundancy of specific indices, such as σ_θ and σ₁ representing the ground stress levels, σ_θ/σ_c and σ_c/σ₁ indicating the ratio of strength to stress, and σ_c/σ_t and σ_c-σ_t/σ_c + σ_t reflecting the rock brittleness, the indices with similar meanings were consolidated. Obtaining the integrity coefficient K_v can be challenging in practical engineering applications. Therefore, the following indices were selected as the predictive indicators for rockbursts, including maximum tangential stress σ_θ (MTS), uniaxial compressive strength σ_c (UCS), uniaxial tensile strength σ_t (UTS), stress concentration coefficient σ_θ/σ_c (SCF), brittleness coefficient σ_c/σ_t (B), elastic energy index (W_et), and burial depth (D).

3.3 Data sources and analysis

The data from typical rockburst engineering cases, both domestic and international, were collected through a literature investigation (Pu et al., 2019b; Xue et al., 2022). After excluding the missing and duplicate samples, a rockburst dataset comprising 342 samples was compiled. The scatter matrix for this dataset is shown in Figure 4. The dataset consisted of 50 samples with no rockburst (14.6%), 97 samples with light rockburst (28.4%), 122 samples with moderate rockburst (35.7%), and 73 samples with strong rockburst (21.3%). The statistical characteristics of the data are presented in Table 2. Based on the analysis of the median and mean values, it is evident that the MTS, SCF, and W_et exhibit a gradual increase corresponding to the escalation of rockburst grades. In contrast, the rest of the statistical indicators have noticeable change rules. Furthermore, the standard deviation and coefficient of variation indicate a higher degree of data dispersion. Although most machine-learning-based rockburst prediction studies exclude outliers, this study included the abnormal data in the rockburst database to account for the variability in actual rockburst projects for training and prediction purposes.

Figure 4

Figure 4. Scatter matrix diagram of rockburst prediction indices.

Table 2

Table 2. Statistical parameters of indices of rockburst data.

A single index criterion was employed to evaluate the accuracy of the original dataset, and the grading criteria and accuracy for the index are detailed in Table 3 (Kidybiński, 1981; Xu and Wang, 1999; Zhang et al., 2010). Table 3 demonstrates that the prediction accuracy of rockbursts using a single index was generally low, with the W_et criterion achieving the highest prediction accuracy at 52%.

Table 3

Table 3. Classification standard and accuracy of rockburst prediction indexs.

4 Establishment of prediction model

4.1 Model feature selection

To determine the input indices for the model more effectively, this study implemented the ReliefF-Kendall model to identify the feature set for the input indices (Figure 5). The process involved the following steps.

Step 1: The weights of the feature indexes relative to the rockburst level were calculated using the ReliefF algorithm and Kendall correlation coefficient.

Step 2: These weights were averaged to obtain the combined weight.

Step 3: A weight threshold was established to exclude the indices with weights below this threshold.

Step 4: The Spearman correlation coefficient was applied to retain the indices with the highest correlation to the rockburst level.

Figure 5

Figure 5. Feature selection flowchart.

The calculation parameters for the ReliefF algorithm included the number of nearest neighbor samples set to 10 with 50 datasets used in each iteration and the weighted mean calculated after 20 repetitions. The weights of the rockburst prediction indices are shown in Figure 6 in the following order: W_et (0.26) > MTS (0.18) > D (0.16) > SCF (0.15) > UCS (0.13) > UTS (0.10) > B (0.04). With a feature selection weight threshold of 0.10, the UTS and B indexes were excluded. Figure 7 presents the Spearman correlation coefficients for the prediction indices, which revealed a strong correlation between MTS and SCF, leading to the retention of the MTS index. Consequently, the final selected rockburst prediction indices were W_et, MTS, D, and UCS.

Figure 6

Figure 6. Weight of rockburst prediction indices.

Figure 7

Figure 7. Spearman correlation coefficient of rockburst prediction indices.

4.2 Data balancing and visualization

Most current machine learning-based rockburst prediction models effectively address the data category imbalance using the Synthetic Minority Over-sampling Technique (SMOTE). This method generates the additional samples for the minority categories through linear interpolation, often without considering the distribution characteristics between sample categories, which may result in category overlap. The adaptive synthetic sampling (Adasyn) algorithm designed to address the data imbalance adaptively can calculate the density distribution characteristics based on the “complexity” of each minority class sample. This information guides the synthesis of new samples and updates the class boundaries, gradually reducing the class imbalance. The core concept of Adasyn is to dynamically generate synthetic samples based on the distribution of samples within each category. For each minority class sample, the proportion of majority class samples among its nearest neighbours is first calculated (a higher proportion indicates more incredible difficulty in classifying the sample, leading to a more significant number of synthesized samples). New samples are then generated through linear interpolation between the minority class samples and their nearest neighbours. This study applied the Adasyn adaptive oversampling algorithm to expand the original dataset from 342 to 485 samples. The dataset consists of 121 samples of no, light, strong, and 122 moderate rockbursts. To better understand the rockburst data distribution, the t-SNE algorithm was employed for dimensionality reduction of the balanced dataset, as illustrated in Figure 8.

Figure 8

Figure 8. Data distribution after t-SNE dimensionality reduction.

4.3 Dataset partitioning and algorithm selection

This study established five rockburst prediction models using MATLAB 2021b, divided into two categories: conventional algorithms (SVM, LSSVM, and KELM) and ensemble algorithms (RF and XGBoost). To ensure the consistent model performance between the training and test sets, the balanced rockburst dataset was randomly divided into a training set comprising 340 samples and a test set comprising 145 samples, adhering to a 7:3 ratio. The proportion of samples in each category of the two data sets is consistent with the total data set.

4.4 Hyperparameter optimization

In order to improve the model’s generalization ability and performance while preventing overfitting, this study used a combination of the SBO algorithm and 5-fold cross-validation to identify the optimal model parameters. The training set was divided into five equal parts, with four parts used for training based on a specific combination of sampled parameters and the remaining part serving as the validation set. This process was repeated five times, ensuring that each data point was validated once. The parameters that achieved the highest prediction accuracy were selected as optimal. Table 4 lists the parameters and their respective ranges for optimization across different machine learning classification models. The basic parameters of the SBO algorithm were set as follows: population size set as 20; maximum number of iterations set as 100.

Table 4

Table 4. Optimized hyperparameters and corresponding sampling ranges required by different models.

4.5 Model performance evaluation

To assess the generalization ability of the established classification prediction model, precision (PRE), recall (REC), and F1-score (F1) were used to evaluate local classification performance. Additionally, the accuracy (ACC) and Kappa coefficient were employed to assess the global classification performance. Table 5 includes the calculation formulas and significance of the performance evaluation metrics. The total number of samples in the test set is represented by Q, where NN, LL, MM, and SS denote the number of correctly predicted samples and the remaining values denote the number of incorrectly predicted samples. Figure 9 illustrates the rockburst level prediction process using the machine learning model established in this study.

Table 5

Table 5. The calculation formula and significance of performance evaluation metrics.

Figure 9

Figure 9. Flowchart of rockburst prediction based on the machine learning model.

5 Model classification performance analysis

Table 6 displays the optimal hyperparameter combinations for the model, determined using the SBO algorithm and 5-fold cross-validation. Figure 10A presents the confusion matrix for the model predictions, with green, orange, and red indicating the precision, recall, and accuracy, respectively, for the different types of rockburst predictions. Figures 10B, C presents the comparison of the performance evaluation of the model. The prediction accuracies of the different models were ranked as follows: RF (82.8%) > LSSVM (82.1%) > SVM (81.4%) > KELM (80.7%) > XGBoost (67.3%). These results were notably higher than the 70.0% prediction accuracy reported by Li (2023). However, the poor prediction performance of the XGBoost model resulted in a significant difference in accuracy compared to RF, LSSVM, SVM, and KELM. The prediction accuracies of the five models that were not optimized using the SBO algorithm are shown in Table 7, from which it can be seen that the prediction accuracies were increased by 1.6%–4.0% after optimization using SBO, thus verifying the optimization effect of SBO.

Table 6

Table 6. Hyperparameter optimization results of different models based on the SBO algorithm.

Figure 10

Figure 10. Comparison of performance evaluation indices of different models based on the SBO algorithm: (A) Best prediction confusion matrix diagram of different models; (B) Local evaluation; (C) Global evaluation.

Table 7

Table 7. Optimization results of different algorithms.

Figures 10B, C demonstrates that the RF model excelled across all evaluation metrics. However, the performance accuracy of the RF, LSSVM, SVM, and KELM models was relatively similar, with the accuracy rates ranging from 80.9% to 84.0%, the recall rates from 80.7% to 82.7%, the F1 scores from 80.8% to 83.4%, and the Kappa values from 74.3% to 77.1%. The analysis of the F1 index indicated that the LSSVM achieved the highest prediction accuracy for mild and medium rockburst classifications, whereas RF was superior in predicting the strong rockburst, with an accuracy exceeding 80%. Account for the randomness in the model training and test data. Each model was trained ten times to reduce variability. Figure 11 illustrates the prediction accuracy of the test set across the various models.

Figure 11

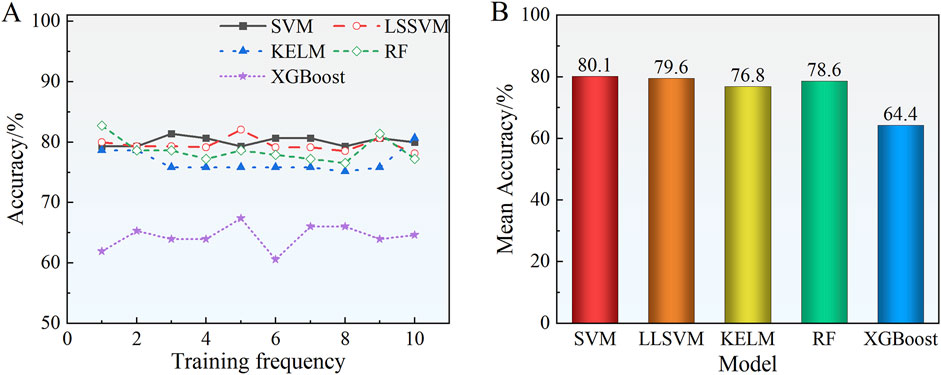
Figure 11. Prediction accuracy of different models based on the SBO algorithm: (A) Prediction accuracy of each training test set; (B) Average accuracy.

Figure 11 shows that the prediction accuracy of the different models ranged from 60.5% to 82.8%. The average prediction accuracy was ranked as follows: SVM (80.1%) > LSSVM (79.6%) > RF (78.6%) > KELM (76.8%) > XGBoost (64.4%). Although the RF model achieved a slightly higher prediction accuracy than the SVM model, the SVM model exhibited superior classification stability. Additionally, the average computation time for the SVM model was 90.77 s less than that of the RF model, which took 262.21 s. Considering the models’ generalization performance, stability, and optimization time, the SVM was selected as the preferred rockburst prediction model.

In order to verify the possibility of the SBO algorithm, the PSO, MFO, DBO, SSA, WOA, and GridSearch (GS) algorithms were adopted to optimize the SVM with the same dataset. All the models were set to the maximum of 100 iterations, with the classification prediction error rate of the model test set as the optimization objective function. Figure 12 illustrates the optimization iteration process for the different algorithms, and Table 8 presents the optimization results. The analysis of Figure 12; Table 8 revealed that the SBO, WOA, and MFO algorithms achieved superior optimization effects on the prediction accuracy, with the accuracy rates reaching or exceeding 80%. Notably, the SBO and WOA algorithms avoided the local optima and achieved the global optima in the fifth and third generations. In contrast, the MFO algorithm encountered the local optima multiple times, reaching the global optimum only in the 35th generation. Moreover, the SBO algorithm demonstrated a slightly better optimization speed than the MFO algorithm. These results confirmed the feasibility of using the SBO algorithm for the parameter optimization in the SVM model.

Figure 12

Figure 12. Fitness iterative curves.

Table 8

Table 8. Prediction results of different optimization algorithms based on the SVM model.

The SHAP method was employed to prove the validity of the feature selection approach proposed in this study. This method assigns contributions based on the marginal impact of each feature on the overall model performance. Specifically, a member’s benefits were equal to the average marginal benefits provided by the group to which they belonged. One feature was removed from the original dataset, while the remaining six were retained for prediction. The prediction results for each reduced feature set were compared with those obtained using all the features. The difference between these outcomes reflected the marginal contribution of the removed features, with a larger difference indicating a more significant influence on the prediction results. All feature sets were denoted as FS, with the feature sets with the first to seventh indicators removed labeled FS1 through FS7, respectively. In order to minimize the variability, each feature set was trained 50 times, and the average prediction accuracy was calculated for analysis. The prediction accuracy of the model is shown in Figure 13.

Figure 13

Figure 13. Prediction accuracy of different feature sets.

Table 9 lists the average prediction accuracy for different feature sets. The difference in accuracy between FS1 and FS7 and FS was denoted as Diff. A positive Diff indicated an improvement in the prediction accuracy after removing the feature index, suggesting that the index was a redundant disturbance variable in rockburst prediction. Conversely, a negative Diff indicated a decrease in the prediction accuracy after removing the feature index, implying that the index was a crucial correlating variable for rockburst prediction. Furthermore, the larger value of Diff signified the greater importance of the index for rockburst prediction. The analysis of Table 9 revealed the importance of rockburst prediction indicators in the following order: W_et, MTS, D, SCF, UCS, UTS, and B. W_et, MTS, D, and UCS were identified as the influential correlating variables, while SCF, UTS, and B were categorized as the redundant disturbance variables. This ranking of rockburst prediction indicators was consistent with the results obtained from the feature selection method established in this study.

Table 9

Table 9. Comparison of average prediction accuracy of different feature sets.

In order to verify the reliability of the Adasyn algorithm for data balancing, the comparative analysis was performed using three datasets: the original dataset (103 groups), the SMOTE-balanced dataset (146 groups), and the Adasyn-balanced dataset (145 groups), with the SBO-SVM model. Table 10 presents the prediction accuracy for each dataset. The analysis indicated that the Adasyn-based dataset achieved the highest prediction accuracy, surpassing the original and SMOTE-balanced datasets by 5.7% and 3.2%, respectively. Compared to the original dataset, Adasyn has improved the classification and prediction accuracy for the non-rockburst and slight rockburst categories.

Table 10

Table 10. Prediction accuracy of different datasets based on the SBO-SVM model.

6 Engineering verification

In order to assess the applicability of the model, the optimized SBO-SVM model was used to predict the rockburst events in domestic projects, including the Jiangbian Hydropower Station. Table 11 presents the predicted indices and actual rockburst levels, and Figure 14 illustrates the rockburst prediction results. Figure 14 shows that the predicted grades for the 12th and 13th sample groups were lower than the actual grades, likely owing to issues with the reliability of the extracted characteristic index data. Despite this, the model achieved a prediction accuracy of 90%, demonstrating the feasibility of applying the SBO-SVM model for rockburst prediction.

Table 11

Table 11. Cases of rockburst engineering.

Figure 14

Figure 14. Comparison of prediction results of rockburst SBO-SVM model.

7 Conclusion

Rockburst is a dynamic disaster in underground engineering. If it can be reasonably and accurately predicted in advance, corresponding measures can be taken to reduce the risk of loss. In this study, a data-driven feature selection method and a meta-heuristic optimization algorithm are proposed and combined with five basic algorithms (SVM, LSSVM, KELM, RF and XGBoost) for underground engineering rockburst prediction. The rationality of the proposed method is verified by comparing it with other methods. The main conclusions are as follows:

(1) Based on existing research and a literature review of rockburst influencing factors, the following indices were selected as predictors: maximum tangential stress (MTS), uniaxial compressive strength (UCS), uniaxial tensile strength (UTS), stress concentration coefficient (SCF), brittleness coefficient (B), elastic energy index (W_et), and burial depth (D). These indices were selected considering the surrounding rock lithology and in situ stress. The feature selection using the ReliefF-Kendall model and correlation analysis yielded W_et, MTS, D, and UCS as the final feature set. The model can remove the redundant features of rockburst, identify the most significant features that affect rockburst, enhance the interpretability of the model, reduce the risk of over-fitting in model prediction, and make hyperparameter tuning more efficient. The rationality of the selected indicators was validated using the SHAP method.

(2) 342 rockburst datasets were collected, balanced, and visualized using the Adasyn oversampling technique and the t-SNE algorithm. Five rockburst prediction models, SVM, LSSVM, KELM, RF, and XGBoost, were developed using the SBO algorithm and 5-fold cross-validation. The results indicated that RF achieved the highest prediction accuracy, with the RF, LSSVM, SVM, and KELM models exceeding 80% accuracy. However, only the SVM model achieved an average prediction accuracy exceeding 80%. Considering the prediction accuracy and stability, SVM was selected as the preferred rockburst prediction algorithm.

(3) Compared to six other algorithms used to optimize the SVM model, the SBO-SVM model demonstrated superior prediction accuracy and optimization speed, indicating robust generalization capability. Predictions were made using the original SMOTE-processed and Adasyn-processed datasets to verify the reliability of the Adasyn algorithm for data balancing. The prediction accuracies of the Adasyn dataset were 5.7% and 3.2% higher than those of the original and SMOTE datasets, respectively. Furthermore, the comprehensive prediction accuracy for rockbursts using machine learning (75.7%) was significantly higher than that of single-index predictions (52.0%).

(4) The established SBO-SVM model was applied to domestic rockburst projects, such as the Sangzhuling Tunnel, achieving a prediction accuracy of 90%. This result demonstrated the strong applicability of the model in engineering contexts.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://doi.org/10.24425/AMS.2019.128683.

Author contributions

TY: Conceptualization, Methodology, Software, Writing–original draft, Writing–review and editing. XG: Conceptualization, Methodology, Resources, Writing–review and editing. LW: Funding acquisition, Project administration, Resources, Writing–review and editing. YX: Investigation, Writing–review and editing. HF: Methodology, Writing–review and editing. ZZ: Supervision, Writing–review and editing. JZ: Resources, Writing–review and editing. BD: Methodology, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was supported by the China Railway Construction Co Ltd 2019 Annual Science and Technology Major Project (Grant No. 2019-A05) and the Natural Science Foundation of Hebei (Grant No. E202310057). China Railway 18th Bureau Group Limited Science and Technology Development Project (Grant No. G21-13). The authors declare that this study received funding from China Railway Construction Co., Ltd. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

Authors YX and JZ were employed by China Railway 18th Bureau Group Corporation Limited.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bai, Y., Deng, J., Dong, L., and Li, X. (2009). Fisher discriminant analysis model of rock burst prediction and its application in deep hard rock engineering. J. Cent. South Univ. Sci. Tech. 40 (5), 1417–1422.

Google Scholar

Chen, H., Li, N., Nie, D., and Shang, Y. (2002). A model for prediction of rockburst by artificial neural network. Chin. J. Geotech. Eng. 24 (2), 229–232. doi:10.3321/j.issn:1000-4548.2002.02.023

CrossRef Full Text | Google Scholar

Deng, L.-C., Zhang, W., Deng, L., Shi, Y.-H., Zi, J.-J., He, X., et al. (2024). Forecasting and early warning of shield tunnelling-induced ground collapse in rock-soil interface mixed ground using multivariate data fusion and Catastrophe Theory. Eng. Geol. 335, 107548. doi:10.1016/j.enggeo.2024.107548

CrossRef Full Text | Google Scholar

Dong, L.-j., Li, X.-b., and Kang, P. (2013). Prediction of rockburst classification using Random Forest. Trans. Nonferrous Met. Soc. China. 23 (2), 472–477. doi:10.1016/s1003-6326(13)62487-5

CrossRef Full Text | Google Scholar

Esmatkhah Irani, A., Azadi, A., Nikbakht, M., Azarafza, M., Hajialilue Bonab, M., and Behrooz Sarand, F. (2022). GIS-Based settlement risk assessment and its effect on surface structures: a case study for the Tabriz Metro—line 1. Geotech. Geol. Eng. 40 (10), 5081–5102. doi:10.1007/s10706-022-02201-x

CrossRef Full Text | Google Scholar

Fu, Y., Liu, D., Chen, J., and He, L. (2024). Secretary bird optimization algorithm: a new metaheuristic for solving global optimization problems. Artif. Intell. Rev. 57 (5), 123–102. doi:10.1007/s10462-024-10729-y

CrossRef Full Text | Google Scholar

Gao, W. (2008). Non-linear dynamic model of rock burst based on evolutionary neural network. Int. J. Mod. Phys. B 22 (09n11), 1518–1523. doi:10.1142/s0217979208047018

CrossRef Full Text | Google Scholar

Gao, W. (2015). Forecasting of rockbursts in deep underground engineering based on abstraction ant colony clustering algorithm. Nat. Hazards. 76, 1625–1649. doi:10.1007/s11069-014-1561-1

CrossRef Full Text | Google Scholar

Ge, Q., and Feng, X. (2008). Classification and prediction of rockburst using AdaBoost combination learning method. Rock Soil Mech. 29 (4), 943–948. doi:10.16285/j.rsm.2008.04.031

CrossRef Full Text | Google Scholar

Gong, F., Li, X., and Zhang, W. (2010). Rockburst prediction of underground engineering based on Bayes discriminant analysis method. Rock Soil Mech. 31 (1), 370–377. doi:10.16285/j.rsm.2010.s1.018

CrossRef Full Text | Google Scholar

Hu, X., Huang, L., Chen, J., Li, X., and Zhang, H. (2023). Rockburst prediction based on optimization of unascertained measure theory with normal cloud. Complex Intell. Syst. 9 (6), 7321–7336. doi:10.1007/s40747-023-01127-y

CrossRef Full Text | Google Scholar

Jia, Y., Lu, Q., and Shang, Y. (2013). Rockburst prediction using particle swarm optimization algorithm and general regression neural network. Chin. J. Rock Mech. Eng. 32 (2), 343–348. doi:10.3969/j.issn.1000-6915.2013.02.016

CrossRef Full Text | Google Scholar

Kamran, M., Chaudhry, W., Taiwo, B. O., Hosseini, S., and Rehman, H. (2024). Decision Intelligence-based predictive modelling of hard rock pillar stability using K-nearest neighbour coupled with grey wolf optimization algorithm. Processes 12 (4), 783. doi:10.3390/pr12040783

CrossRef Full Text | Google Scholar

Kamran, M., Ullah, B., Ahmad, M., and Sabri, M. M. S. (2022). Application of KNN-based isometric mapping and fuzzy c-means algorithm to predict short-term rockburst risk in deep underground projects. Front. Public Health 10, 1023890. doi:10.3389/fpubh.2022.1023890

PubMed Abstract | CrossRef Full Text | Google Scholar

Kidega, R., Ondiaka, M. N., Maina, D., Jonah, K. A. T., and Kamran, M. (2022). Decision based uncertainty model to predict rockburst in underground engineering structures using gradient boosting algorithms. Geomech. Eng. 30 (3), 259–272. doi:10.12989/gae.2022.30.3.259

CrossRef Full Text | Google Scholar

Kidybiński, A. (1981). Bursting liability indices of coal. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 18 (4), 295–304. doi:10.1016/0148-9062(81)91194-3

CrossRef Full Text | Google Scholar

Lan, M., Liu, Z., and Feng, F. (2014). Attempt to study the applicability of the online sequential extreme learning machine to the rock burst forecast. J. Saf. Environ. 14 (2), 90–93. doi:10.13637/j.issn.1009-6094.2014.02.020

CrossRef Full Text | Google Scholar

Li, D., Liu, Z., Armaghani, D. J., Xiao, P., and Zhou, J. (2022). Novel ensemble intelligence methodologies for rockburst assessment in complex and variable environments. Sci. Rep. 12 (1), 1844. doi:10.1038/s41598-022-05594-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J. (2023). Research on mechanism and comprehensive prediction of rockburst regarding deep buried tunnel in tectonic active area. Changsha, China: Central south university. PhD thesis. doi:10.27661/d.cnki.gzhnu.2023.000465

CrossRef Full Text | Google Scholar

Li, K., Wu, Y., Du, F., zhang, X., and Wang, Y. (2023a). Prediction of rockburst intensity grade based on convolutional neural network. Coal Geol. Expl. 51 (10), 94–103. doi:10.12363/issn.1001-1986.23.01.0018

CrossRef Full Text | Google Scholar

Li, M., Li, K., and Qin, Q. (2023b). A rockburst prediction model based on extreme learning machine with improved Harris Hawks optimization and its application. Tunn. Undergr. Space Technol. 134, 104978. doi:10.1016/j.tust.2022.104978

CrossRef Full Text | Google Scholar

Li, M., Li, K., Qin, Q., Wu, S., Liu, Y., and Liu, B. (2021). Discussion and selection of machine learning algorithm model for rockburst intensity grade prediction. Chin. J. Rock Mech. Eng. 40, 2806–2816. doi:10.13722/j.cnki.jrme.2020.1088

CrossRef Full Text | Google Scholar

Li, N., Feng, X., and Jimenez, R. (2017). Predicting rock burst hazard with incomplete data using Bayesian networks. Tunn. Undergr. Space Technol. 61, 61–70. doi:10.1016/j.tust.2016.09.010

CrossRef Full Text | Google Scholar

Li, N., and Jimenez, R. (2018). A logistic regression classifier for long-term probabilistic prediction of rock burst hazard. Nat. Hazards. 90, 197–215. doi:10.1007/s11069-017-3044-7

CrossRef Full Text | Google Scholar

Liang, W., Sari, A., Zhao, G., McKinnon, S. D., and Wu, H. (2020). Short-term rockburst risk prediction using ensemble learning methods. Nat. Hazards. 104, 1923–1946. doi:10.1007/s11069-020-04255-7

CrossRef Full Text | Google Scholar

Liu, D., Dai, Q., Zuo, J., Shang, Q., Chen, G., and Guo, Y. (2022). Research on rockburst grade prediction based on stacking integrated algorithm. Chin. J. Rock Mech. Eng. 41 (S1), 2915–2926. doi:10.13722/j.cnki.jrme.2021.0831

CrossRef Full Text | Google Scholar

Liu, L., Zhang, S., Wang, X., and Hao, Z. (2015). Application of target approaching with variable weight in prediction of rockburst intensity. Explos. Shock Waves 35 (1), 43–50. doi:10.13722/j.cnki.jrme.2021.0831

CrossRef Full Text | Google Scholar

Liu, Z., Zheng, B., Liu, J., and Lan, M. (2019). Rockburst prediction with GA-ELM model for deep mining of metal mines. Min. Metall. Eng. 39 (3), 1–4. doi:10.3969/j.issn.0253-6099.2019.03.001

CrossRef Full Text | Google Scholar

Ma, K., Peng, Y., Liao, Z., and Wang, Z. (2024). Dynamic responses and failure characteristics of the tunnel caused by rockburst: an entire process modelling from incubation to occurrence phases. Comput. Geosci. 171, 106340. doi:10.1016/j.compgeo.2024.106340

CrossRef Full Text | Google Scholar

Ministry of Housing and Urban-Rural Development of the People's Republic of China (2015). GB/T 50218-2014 Standard for engineering classification of rock mass. Beijing: China Planning Publishing House.

Google Scholar

Pu, Y., Apel, D. B., and Lingga, B. (2018a). Rockburst prediction in kimberlite using decision tree with incomplete data. J. Sustain. Min. 17 (3), 158–165. doi:10.1016/j.jsm.2018.07.004

CrossRef Full Text | Google Scholar

Pu, Y., Apel, D. B., Pourrahimian, Y., and Chen, J. (2019a). Evaluation of rockburst potential in kimberlite using fruit fly optimization algorithm and generalized regression neural networks. Arch. Min. Sci. 64 (2), 279–296. doi:10.24425/AMS.2019.128683

CrossRef Full Text | Google Scholar

Pu, Y., Apel, D. B., Wang, C., and Wilson, B. (2018b). Evaluation of burst liability in kimberlite using support vector machine. Acta geophys. 66, 973–982. doi:10.1007/s11600-018-0178-2

CrossRef Full Text | Google Scholar

Pu, Y., Apel, D. B., and Xu, H. (2019b). Rockburst prediction in kimberlite with unsupervised learning method and support vector classifier. Tunn. Undergr. Space Technol. 90, 12–18. doi:10.1016/j.tust.2019.04.019

CrossRef Full Text | Google Scholar

Qiu, D. H., Li, S. C., and Zhang, L. W. (2013). Study on rockburst intensity prediction based on efficacy coefficient method. Appl. Mech. Mater. 353, 1277–1280. doi:10.4028/www.scientific.net/amm.353-356.1277

CrossRef Full Text | Google Scholar

Qiu, Y., and Zhou, J. (2023a). Short-term rockburst damage assessment in burst-prone mines: an explainable XGBOOST hybrid model with SCSO algorithm. Rock Mech. Rock Eng. 56 (12), 8745–8770. doi:10.1007/s00603-023-03522-w

CrossRef Full Text | Google Scholar

Qiu, Y., and Zhou, J. (2023b). Short-term rockburst prediction in underground project: insights from an explainable and interpretable ensemble learning model. Acta Geotech. 18 (12), 6655–6685. doi:10.1007/s11440-023-01988-0

CrossRef Full Text | Google Scholar

Qiu, Y., and Zhou, J. (2024). Novel rockburst prediction criterion with enhanced explainability employing CatBoost and nature-inspired metaheuristic technique. Underg. Space. 19, 101–118. doi:10.1016/j.undsp.2024.03.003

CrossRef Full Text | Google Scholar

Qu, H., Yang, L., Zhu, J., Chen, S., Li, B., and Li, B. (2022). A multi-index evaluation method for rockburst proneness of deep underground rock openings with attribute recognition model and its application. Int. J. Rock Mech. Min. Sci. 159, 105225. doi:10.1016/j.ijrmms.2022.105225

CrossRef Full Text | Google Scholar

Shao, L., and Zhou, Y. (2018). MIV-MA-KELM model based prediction of rockburst intensity grade. China Saf. Sci. J. 28 (2), 34–39. doi:10.16265/j.cnki.issn1003-3033.2018.02.006

CrossRef Full Text | Google Scholar

Sun, J., Wang, W., and Xie, L. (2024a). Predicting Short-Term rockburst using RF-CRITIC and improved cloud model. Nat. Resour. Res. 33 (1), 471–494. doi:10.1007/s11053-023-10275-4

CrossRef Full Text | Google Scholar

Sun, J., Wang, W., and Xie, L. (2024b). Predicting short-term rockburst intensity using a weighted probability stacking model with optimal feature selection and Bayesian hidden layer. Tunn. Undergr. Space Technol. 153, 106021. doi:10.1016/j.tust.2024.106021

CrossRef Full Text | Google Scholar

Tan, W., Hu, N., Ye, Y., Wu, M., Huang, Z., and Wang, X. (2022). Rockburst intensity classification prediction based on four ensemble learning. Chin. J. Rock Mech. Eng. 41, 3250–3259. doi:10.13722/j.cnki.jrme.2022.0026

CrossRef Full Text | Google Scholar

Tan, W., Ye, Y., Hu, N., Wu, M., and Huang, Z. (2021). Severe rock burst prediction based on the combination of LOF and improved SMOTE algorithm. Chin. J. Rock Mech. Eng. 40 (6), 1186–1194. doi:10.13722/j.cnki.jrme.2020.1035

CrossRef Full Text | Google Scholar

Tang, Z., and Xu, Q. (2020). Rockburst prediction based on nine machine learning algorithms. Chin. J. Rock Mech. Eng. 39 (4), 773–781. doi:10.13722/j.cnki.jrme.2019.0686

CrossRef Full Text | Google Scholar

Tian, R., Meng, H., Chen, S., Wang, C., and Zhang, F. (2020). Prediction of intensity classification of rockburst based on deepneural network. J. China Coal Soc. 45 (S1), 191–201. doi:10.13225/j.cnki.jccs.2019.1763

CrossRef Full Text | Google Scholar

Tian, Y., Zhang, J., Chen, Q., and Liu, Z. (2022). A novel selective ensemble learning method for smartphone sensor-based human activity recognition based on hybrid diversity enhancement and improved binary glowworm swarm optimization. IEEE Access 10, 125027–125041. doi:10.1109/access.2022.3225652

CrossRef Full Text | Google Scholar

Wang, C., Wu, A., Lu, H., Bao, T., and Liu, X. (2015). Predicting rockburst tendency based on fuzzy matter–element model. J. Rock Mech. Min. Sci. 75, 224–232. doi:10.1016/j.ijrmms.2015.02.004

CrossRef Full Text | Google Scholar

Wang, M., Liu, Q., Wang, X., Shen, F., and Jin, J. (2020). Prediction of rockburst based on multidimensional connection cloud model and set pair analysis. Int. J. Geomech. 20 (1), 04019147. doi:10.1061/(asce)gm.1943-5622.0001546

CrossRef Full Text | Google Scholar

Wang, R., Chen, S., Li, X., Tian, G., and Zhao, T. (2023). AdaBoost-driven multi-parameter real-time warning of rock burst risk in coal mines. Eng. Appl. Artif. Intell. 125, 106591. doi:10.1016/j.engappai.2023.106591

CrossRef Full Text | Google Scholar

Wang, X., Li, S., Xu, Z., Xue, Y., Hu, J., Li, Z., et al. (2019). An interval fuzzy comprehensive assessment method for rock burst in underground caverns and its engineering application. Bull. Eng. Geol. Environ. 78, 5161–5176. doi:10.1007/s10064-018-01453-3

CrossRef Full Text | Google Scholar

Wei, M., Wang, E., and Liu, X. (2020). Assessment of gas emission hazard associated with rockburst in coal containing methane. Process Saf. Environ. Prot. 135, 257–264. doi:10.1016/j.psep.2020.01.017

CrossRef Full Text | Google Scholar

Wu, S., Wu, Z., and Zhang, C. (2019a). Rock burst prediction probability model based on case analysis. Tunn. Undergr. Space Technol. 93, 103069. doi:10.1016/j.tust.2019.103069

CrossRef Full Text | Google Scholar

Wu, S., Zhang, C., and Cheng, Z. (2019b). Prediction of intensity classification of rockburst based on PCA-PNN principle. J. China Coal Soc. 44 (9), 2767–2776. doi:10.13225/j.cnki.jccs.2018.1519

CrossRef Full Text | Google Scholar

Xia, Z., Mao, J., and He, Y. (2022). Rockburst intensity prediction in underground buildings based on improved spectral clustering algorithm. Front. Earth Sci. 10, 948626. doi:10.3389/feart.2022.948626

CrossRef Full Text | Google Scholar

Xie, C., Nguyen, H., Bui, X.-N., Nguyen, V.-T., and Zhou, J. (2021). Predicting roof displacement of roadways in underground coal mines using adaptive neuro-fuzzy inference system optimized by various physics-based optimization algorithms. J. Rock Mech. Geotech. Eng. 13 (6), 1452–1465. doi:10.1016/j.jrmge.2021.07.005

CrossRef Full Text | Google Scholar

Xie, X., Li, D., Kong, L., Ye, Y., and Gao, S. (2020). Rockburst propensity prediction model based on CRITIC-XGB algorithm. Chin. J. Rock Mech. Eng. 39 (10), 1975–1982. doi:10.13722/j.cnki.jrme.2019.1049

CrossRef Full Text | Google Scholar

Xing, W., Wang, H., Fan, J., Wang, W., and Yu, X. (2024). Rockburst risk assessment model based on improved catastrophe progression method and its application. Stoch. Environ. Res. Risk Assess. 38 (3), 981–992. doi:10.1007/s00477-023-02609-8

CrossRef Full Text | Google Scholar

Xu, C., Liu, X., Wang, E., Zheng, Y., and Wang, S. (2018a). Rockburst prediction and classification based on the ideal-point method of information theory. Tunn. Undergr. Space Technol. 81, 382–390. doi:10.1016/j.tust.2018.07.014

CrossRef Full Text | Google Scholar

Xu, F., and Xu, W. (2010). Projection pursuit model based on particle swarm optimization for rock burst prediction. Chin. J. Geotech. Eng. 32 (5), 718–723.

Google Scholar

Xu, G., Li, K., Li, M., Qin, Q., and Yue, R. (2022). Rockburst intensity level prediction method based on FA-SSA-PNN model. Energies 15 (14), 5016. doi:10.3390/en15145016

CrossRef Full Text | Google Scholar

Xu, J., Chen, J., Liu, C., Wang, J., Long, G., and Li, C. (2018b). Application research of DHNN model in prediction of classification of rockburst intensity. Ind. Mine Autom. 44 (1), 84–88. doi:10.13272/j.issn.1671-251x.2017050027

CrossRef Full Text | Google Scholar

Xu, L., and Wang, L. (1999). Study on the laws of rockburst and its forecasting in the tunnel of Erlang Mountain road. Chin. J. Geotech. Eng. (5), 569–572. doi:10.3321/j.issn:1000-4548.1999.05.009

CrossRef Full Text | Google Scholar

Xue, Y., Li, G., Li, Z., Wang, P., Gong, H., and Kong, F. (2022). Intelligent prediction of rockburst based on Copula-MC oversampling architecture. Bull. Eng. Geol. Environt. 81 (5), 209. doi:10.1007/s10064-022-02659-2

CrossRef Full Text | Google Scholar

Xue, Y., Li, Z., Li, S., Qiu, D., Tao, Y., Wang, L., et al. (2019). Prediction of rock burst in underground caverns based on rough set and extensible comprehensive evaluation. Bull. Eng. Geol. Environ. 78, 417–429. doi:10.1007/s10064-017-1117-1

CrossRef Full Text | Google Scholar

Yang, T. (2024). Recognition and prediction of precursory feature signals of coal mine rock burst based on random forest and MK trend test. Front. Comput. Intell. Syst. 8 (3), 1–5. doi:10.54097/5xwgxa77

CrossRef Full Text | Google Scholar

Yuan, H., Ji, S., Liu, G., Xiong, L., Li, H., Cao, Z., et al. (2023). Investigation on intelligent early warning of rock burst disasters using the PCA-PSO-ELM model. Appl. Sci. 13 (15), 8796. doi:10.3390/app13158796

CrossRef Full Text | Google Scholar

Zhang, F., Zhang, L., Liu, Z., Meng, F., Wang, X., Wen, J., et al. (2024). An improved dempster–shafer evidence theory based on the Chebyshev distance and its application in rock burst prewarnings. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 10 (1), 04023055. doi:10.1061/ajrua6.rueng-1201

CrossRef Full Text | Google Scholar

Zhang, L., Zhang, D., Li, S., and Qiu, D. (2012). Application of RBF neural network to rockburst prediction based on rough set theory. Rock Soil Mech. 33 (S1), 270–276. doi:10.16285/j.rsm.2012.s1.008

CrossRef Full Text | Google Scholar

Zhang, L., Zhang, D., and Qiu, D. (2010). Application of extension evaluation method in rockburst prediction based on rough set theory. J. China Coal Soc. 35 (9), 1461–1465. doi:10.13225/j.cnki.jccs.2010.09.031

CrossRef Full Text | Google Scholar

Zhang, L., Zhang, X., Wu, J., Zhao, D., and Fu, H. (2020). Rockburst prediction model based on comprehensive weight and extension methods and its engineering application. Bull. Eng. Geol. Environ. 79, 4891–4903. doi:10.1007/s10064-020-01861-4

CrossRef Full Text | Google Scholar

Zhang, Q., Zheng, T., Yuan, L., Li, X., Li, W., and Wang, X. (2024). A semi-Naïve Bayesian rock burst intensity prediction model based on average one-dependent estimator and incremental learning. Tunn. Undergr. Space Technol. 146, 105666. doi:10.1016/j.tust.2024.105666

CrossRef Full Text | Google Scholar

Zhang, S., Mu, C., Feng, X., Ma, K., Guo, X., and Zhang, X. (2024). Intelligent dynamic warning method of rockburst risk and level based on recurrent neural network. Rock Mech. Rock Eng. 57 (5), 3509–3529. doi:10.1007/s00603-023-03715-3

CrossRef Full Text | Google Scholar

Zhang, W., Lu, H., Zhang, Y., Li, Z., Wang, Y., Zhou, J., et al. (2022). A fault diagnosis scheme for gearbox based on improved entropy and optimized regularized extreme learning machine. Mathematics 10 (23), 4585. doi:10.3390/math10234585

CrossRef Full Text | Google Scholar

Zhang, Y., Zhang, M., Li, J., and Chen, G. (2023). Rockburst intensity grade prediction model based on batch gradient descent and multi-scale residual deep neural network. Comput. Syst. Sci. Eng. 47 (2), 1987–2006. doi:10.32604/csse.2023.040381

CrossRef Full Text | Google Scholar

Zhao, G., Liu, L., Wang, J., Liu, H., Zhao, J., and Fan, Z. (2019). PCA-OPF model for rock burst prediction. Min. Metall. Eng. 39 (4), 1–5. doi:10.3969/j.issn.0253-6099.2019.04.001

CrossRef Full Text | Google Scholar

Zhao, H. (2005). Classification of rockburst using support vector machine. Rock Soil Mech. 26 (4), 642–644. doi:10.16285/j.rsm.2005.04.029

CrossRef Full Text | Google Scholar

Zhou, J., Guo, H., Koopialipoor, M., Jahed Armaghani, D., and Tahir, M. (2021). Investigating the effective parameters on the risk levels of rockburst phenomena by developing a hybrid heuristic algorithm. Eng. Comput. 37, 1679–1694. doi:10.1007/s00366-019-00908-9

CrossRef Full Text | Google Scholar

Zhou, J., Li, X., and Shi, X. (2012). Long-term prediction model of rockburst in underground openings using heuristic algorithms and support vector machines. Saf. Sci. 50 (4), 629–644. doi:10.1016/j.ssci.2011.08.065

CrossRef Full Text | Google Scholar

Zhu, Y., Liu, X., and Zhou, J. (2008). Rockburst prediction analysis based on v-SVR algorithm. J. China Coal Soc. 33 (3), 277–281. doi:10.3321/j.issn:0253-9993.2008.03.009

CrossRef Full Text | Google Scholar