Optimal statistical method selection for landslide susceptibility assessment and its scale effect

Accurate landslide susceptibility assessment is vital for disaster prevention, but current mapping lacks systematic analysis of the underlying mechanisms between multi-scale factors and model performance. Taking Zhenxiong County as an example, this paper combines the IV, WOE, LR models, and PCA to reveal the impact of methodological differences and scale selection on mapping results, and quantitatively evaluates them using ROC curves and landslide density statistics. Results show that: 1) The scale effect of influencing factors is significant. Natural factors such as topography, geological conditions, and rainfall play dominant roles at the regional scale, while the impacts of human activities, geological features, and soil erosion intensity are more pronounced at local and moderate scales. 2) The landslide susceptibility mapping results of the three models at different spatial scales show similar spatial distribution trends. As the spatial scale increases, high/very high susceptibility areas and low/very low susceptibility areas spread outward, while the spatial distribution of medium susceptibility areas shows a fragmented expansion outward first and then agglomeration and contraction inward. 3) Scale selection significantly affects the accuracy of landslide susceptibility mapping, and expanding the spatial scale appropriately improves mapping precision. The IV and WOE models show the highest AUC at the 600-m buffer, while the LR model peaks at 400 m. In terms of landslide identification accuracy, the IV model performs best at 400-m buffer, WOE at 600-m buffer, and LR at 100 -meter buffer. 4) Different methods have different mapping performances. Overall, the IV model performs best, followed by the WOE model, with the LR model lagging behind. In terms of high-risk area recognition, the LR model excels, followed by the IV model, while the WOE model performs relatively poorly. 5) Scale and method selection significantly impact landslide susceptibility mapping outcomes. The IV model excelled in global prediction at the 600-m buffer, whereas the LR model was effective in pinpointing high-risk areas at the 100-m buffer. This paper proposes a landslide susceptibility evaluation method that integrates model performance and scale effects, enhancing disaster assessment and prevention capabilities.

1 Introduction

Landslides are one of the most common and destructive geological disasters in the world, causing a large number of casualties and huge economic losses every year (Di Napoli et al., 2021). As an important tool for landslide hazard research, landslide susceptibility mapping (LSM) can effectively identify the spatial distribution areas of potential landslides, provide a scientific basis for early warning, risk assessment, and disaster prevention and mitigation decisions of landslide disasters, and is of great significance to reducing the impact of landslide disasters.

With the advancement of GIS and remote sensing technologies, landslide susceptibility mapping using statistical and machine learning models has become widespread. Traditional statistical models such as IV (Guo et al., 2023), WOE (Thiery et al., 2007), and LR (Zhao et al., 2019) have achieved good predictive results by analyzing the statistical relationship between landslides and influencing factors, establishing a mathematical model between landslide occurrence probability and influencing factors (Guzzetti et al., 2006). It has the advantages of high computational efficiency, relatively low data requirements, and strong model interpretability (Lima et al., 2021). However, there are limitations in dealing with complex nonlinear relationships, which greatly affect the accuracy of landslide susceptibility mapping. In contrast, machine learning models such as Support Vector Machines (SVM) (Huang and Zhao, 2018), Random Forests (RF) (Dou et al., 2019), and Artificial Neural Networks (ANN) (Conforti et al., 2014; Nanehkaran et al., 2023) have significantly improved the accuracy of landslide susceptibility mapping due to their powerful non-linear fitting and classification capabilities (Dou et al., 2021; Feng et al., 2022)。 In addition, some studies have attempted to integrate different machine learning models, such as AdaBoost, Bagging, etc., to further improve prediction accuracy (Binh Thai et al., 2017; Chen and Li, 2020; Wu et al., 2020)。 Although machine learning models perform well in landslide susceptibility mapping, they have some inherent limitations, such as high requirements for data quality and quantity, complex models, and poor interpretability (Huang et al., 2020; Zhang et al., 2024)。 To address these issues, some studies have proposed methods to optimize data quality (Sun et al., 2023; Yang et al., 2023), Or enhance the interpretability of the model by introducing fuzzy logic based multi decision methods (Mallick et al., 2018; Nanehkaran et al., 2021)。 However, in situations where data is limited and in-depth exploration of landslide mechanisms is needed, statistical models still have certain advantages (Merghadi et al., 2020).

In view of the data characteristics and research objectives, this paper selects statistical models and focuses on the impact of the scale effect of influencing factors on landslide susceptibility mapping. However, through the analysis of existing statistical model studies, we found that the following two aspects seriously affect the accuracy and reliability of landslide susceptibility mapping. First, the choice of mapping method directly affects the accuracy of the results, that is, different models perform differently when dealing with complex geological conditions (Pourghasemi and Rahmati, 2018). Second, the choice of spatial scale also significantly affects the mapping results, and there are significant differences in mapping results at different spatial scales (Lin et al., 2021). Therefore, it is urgent to carry out multi-model and multi-scale landslide susceptibility mapping research, quantitatively analyze the relationship between model performance and scale, and select the optimal model and scale combination to improve the accuracy and reliability of landslide prediction.

Situated in the Wumeng Mountains of the northeastern region of Yunnan Province, Zhenxiong County exhibits varied topography and intricate geological characteristics, rendering it prone to precarious geological hazards like landslides. A major landslide catastrophe occurred in Liangshui Village in Tangfang Town on 22 January 2024. The landslide volume was estimated to be 50,000 cubic meters, resulting in the loss of 44 lives and causing substantial casualties and property damage. This tragic event highlights the urgent need to improve landslide susceptibility mapping and implement effective risk prevention measures.

In view of the shortcomings of existing studies in multi-scale analysis and scale effects of influencing factors, this paper takes Zhenxiong County, Yunnan Province as the research area, uses principal component analysis to quantitatively analyze the scale effects of influencing factors, and combines three statistical models, namely, information content (IV), weight of evidence (WOE) and logistic regression (LR), to explore the performance of landslide susceptibility mapping of different models at different scales. The models are evaluated by ROC curve and landslide density statistical indicators, and finally the optimal model and scale combination is proposed. The multi-model and multi-scale analysis framework developed in this study provides new insights for optimizing landslide susceptibility mapping and serves as a scientific basis for improving the precision and effectiveness of landslide disaster prevention and mitigation.

2 Materials and methods

2.1 Materials

2.1.1 Study area

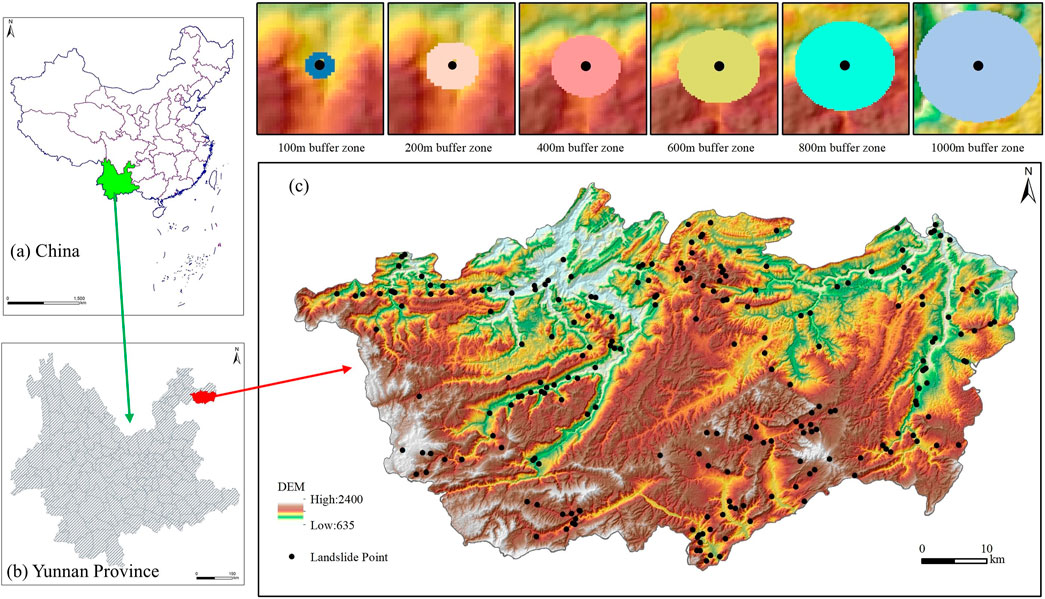
Zhenxiong County, administered by Zhaotong City in Yunnan Province, is located in the northeastern part of Yunnan, where the borders of Yunnan, Guizhou, and Sichuan provinces converge (Figure 1). The county spans geographical coordinates from approximately 104°18′E to 105°19′E longitude and 27°17′N to 27°50′N latitude, covering a total area of 3,696 square kilometers. The county is located on the mountainous slopes of the northern foothills of the Wumeng Mountains, at the northern edge of the Yunnan-Guizhou Plateau. Positioned within the source region of the Chishui River, Zhenxiong County is characterized by multiple plateau canyon-type rivers. The area boasts relatively complete strata and welldeveloped geological structures, with mountains and rivers following structural lines and stratigraphic trends. Zhenxiong County experiences a subtropical plateau monsoon climate. Its topography facilitates the entry of cold air but hampers its dissipation, resulting in persistent fog and mist throughout the year. The climate is characterized by moderate temperatures, infrequent clear skies, significant temperature fluctuations, frequent frosts, and distinct dry and wet seasons. Zhenxiong County showcases distinctive vertical climate zones due to significant elevation differences, frequently facing cold waves during winter and spring as a result of its unique 'three-dimensional climate. With an average yearly temperature of 13.7°C and average annual rainfall of 935 mm, the area’s climatic characteristics are notable.

Figure 1

Figure 1. Research location map (A): China, (B): Yunnan Province, (C): Zhenxiong County.

2.1.2 Data source

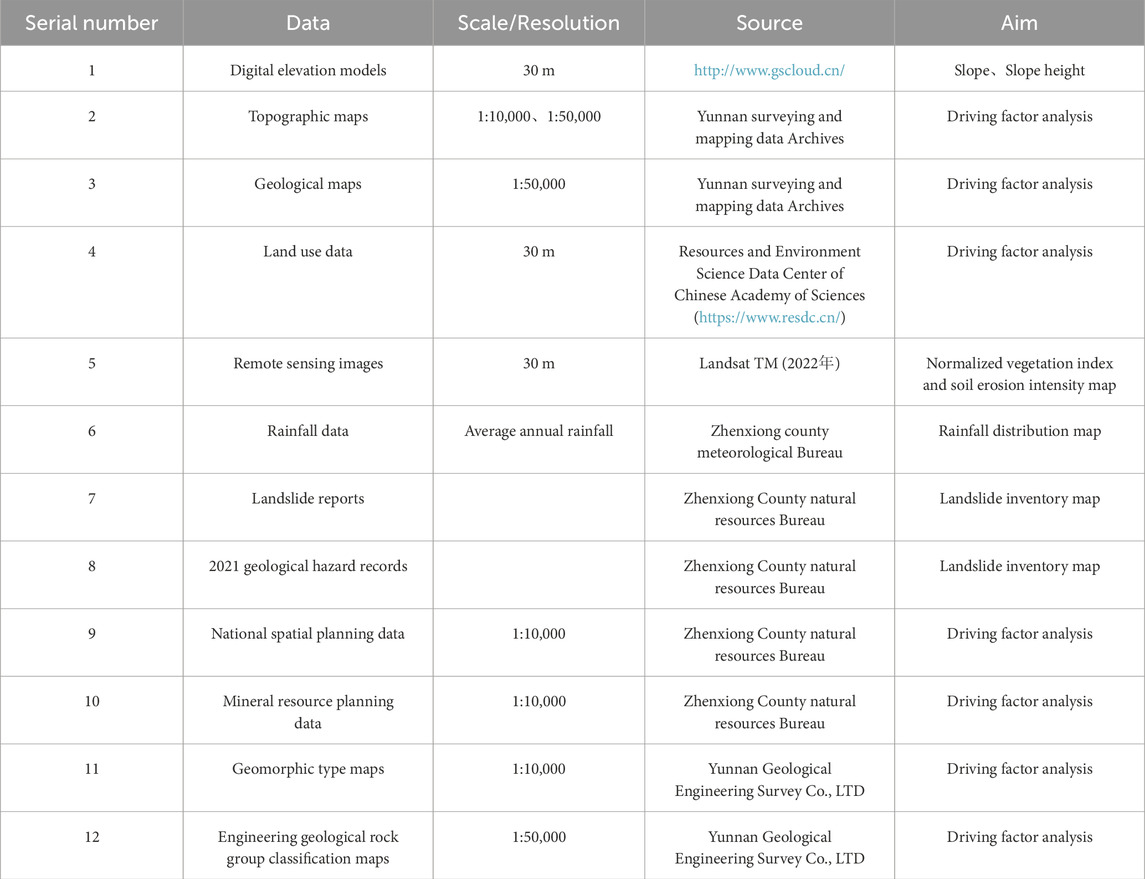
This study utilizes a wide array of data sources, including digital elevation models, topographic maps, geological maps, land use data, remote sensing imagery, rainfall data, landslide reports, geological hazard records, national spatial planning data, mineral resource planning data, geomorphological maps, and engineering geological rock group classification maps. Detailed information is provided in Table 1.

Table 1

Table 1. Data sources used in this study.

2.1.3 Landslide inventory mapping

Through on-site investigations, verification of statistical data from Zhenxiong County, remote sensing interpretation, and newly identified landslide-prone points during the survey process, a total of 217 landslides were identified in Zhenxiong County as of July 2022. The analysis of Figure 1 indicates that landslides predominantly occur in close proximity to valley areas and at the entrances of mountain gullies. Based on the investigation data and collected information, landslides in Zhenxiong County can be classified into two categories: natural landslides (caused by rainfall, earthquakes, river erosion, and other natural factors) and engineering landslides (resulting from cutting slopes and other human engineering activities). Among the 217 landslides, 156 (71.82%) were triggered by natural factors, while 61 (28.18%) were triggered by a combination of natural and human factors. No landslides were solely attributed to human factors.

2.1.4 Determination of landslide influence area

This study provides a comprehensive assessment of landslide impact by incorporating key factors such as landslide scale, thickness, and the potentially affected area. Using statistical analysis of landslides in Zhenxiong County, the buffer zone method was employed to determine the extent of landslide influence, following the approach of Dagdelenler et al. (2016). Previous studies have shown that the extent of landslide influence is often related to their size and type. Small, shallow landslides generally affect areas ranging from tens of meters to over a hundred meters, while large, shallow landslides can impact areas extending from several hundred meters to over a kilometer (Meier et al., 2020). Given that landslides in Zhenxiong County are predominantly small to medium in size and mostly shallow, a buffer distance of 100 m is chosen as the standard. This distance not only covers the direct impact range of most landslides but also strikes a balance between computational efficiency and result interpretability. To further explore the effects of various influencing factors across different spatial scales, this study also uses a multi-scale analysis by establishing buffer zones around individual landslide points at intervals of 200 m, 400 m, 600 m, 800 m, and 1,000 m. This approach allows for a more nuanced understanding of landslide dynamics across varying distances, following the methodology of similar studies (Wei et al., 2024), which have shown that using multiple buffer distances can better capture the variations in landslide influencing factors from local to regional scales.

2.1.5 Pretreatment of landslide influencing factors

The selection of influencing factors is crucial in the process of mapping landslide susceptibility. Both domestic and international research have extensively discussed various influencing factors. While some factors, such as slope angle and lithology, are widely accepted, others—like aspect, land use, soil types, and the topographic wetness index—remain subjects of debate (Segoni et al., 2012; Shu et al., 2019; Arabameri et al., 2020). The effectiveness of landslide susceptibility models is influenced by several factors, including data availability and the geological characteristics of the study area (Van Westen et al., 2006; Pereira et al., 2012; Catani et al., 2013). Therefore, the contribution of individual factors to landslides can vary across different study locations. Despite these variations, we selected factors that are commonly discussed and supported in the literature. Additionally, after a comprehensive evaluation of different factors, this study introduces an innovative factor—slope height (represented as the product of slope length and slope gradient)—to more comprehensively and accurately characterize the terrain.

Utilizing findings from both domestic and international research, as well as taking into account the specific conditions within the research field, this study has identified 15 key factors for developing a comprehensive index system for mapping landslide susceptibility, and thematic layers for these factors generated in ArcGIS. Given that the selected factors consist of both discrete and continuous variables, it is imperative to categorize the continuous variables into distinct categories with fixed intervals when utilizing a statistical model. Currently, there is no consistent criterion for determining the quantity of classification intervals for continuous variables. Considering that using too many or too few intervals can lead to model complexity issues, and referring to the 4-9 intervals commonly used in existing studies, this paper divides all continuous factors into 4-9 intervals (Chen et al., 2017; Huang et al., 2017; Park et al., 2018). The selected impact factors and their classification results are shown in Figure 2.

Figure 2

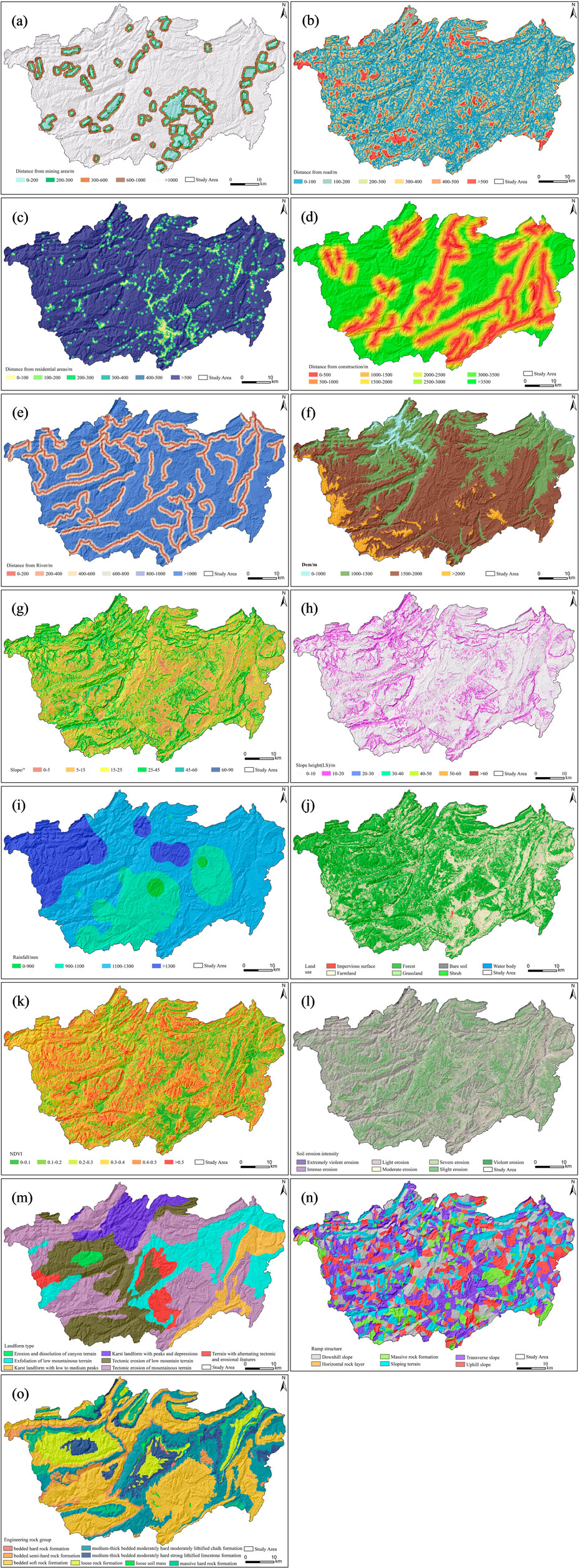
Figure 2. Drivers used in landslide susceptibility modeling (A) Distance from mining areas, (B) Distance from roads, (C) Distance from settlements, (D) Distance from structures, (E) Distance from rivers, (F) Digital elevation models (DEM), (G) Slope, (H) Slope height, (I) Rainfall, (J) Land use, (K) Normalized vegetation index (NDVI), (L) Soil erosion intensity (SEI), (M) Landform type, (N) Slope structure factor, (O) Engineering rock group.).

2.2 Methodology

2.2.1 Principal component analysis

Principal component analysis (PCA) is a dimensionality reduction technique widely used in multivariate data analysis. It transforms a set of possibly correlated variables into a set of linearly uncorrelated variables through linear transformation (Sabokbar et al., 2014). In landslide susceptibility research, PCA is often used to reduce the redundancy and correlation between influencing factors, while evaluating the contribution of each factor to landslide susceptibility. Its main steps are as follows:

The initial dataset (X) can be represented in matrix form by Equation 3:

$X=\left[\begin{array}{l}{x}_{11}{x}_{11}\cdot \cdot \cdot x_{1m}\\ \cdot \cdot \cdot \cdot \cdot \cdot \\ \cdot \cdot \cdot \cdot \cdot \cdot \\ x_{n1}{x}_{n1}\cdot \cdot \cdot x_{nm}\end{array}\right](1)$

where m is the number of causal factors, n is the landslide number, and xij (i = 1, 2, … , n; j = 1, 2, … , m) is the jth factor of the ith landslide. The mean and standard deviation of these factors can be calculated as follows:

$\overline{x_j}=\frac{1}{n}{\displaystyle \sum _{i=1}^n}{x}_{ij}(2)$

$S_j=\sqrt{\frac{1}{n-1}{\displaystyle \sum _{i=1}^n}{\left(x_{ij}-\overline{x_j}\right)}^2}\left(j=1,2,...,m\right)(3)$

Where $\overline{x_j}$ and Sj are the mean and standard deviation of factor j, respectively. These two parameters can be used to normalize the original data X and obtain the correlation matrix R = (rjk)m × m:

$y_{ij}=\frac{x_{ij}-\overline{x_j}}{S_j}\left(i=1,2,...,n;j=1,2,...,m\right)(4)$

$r_{jk}=\frac{1}{n-1}{\displaystyle \sum _{i=1}^n}\frac{\left(x_{ij}-\overline{x_j}\right)}{S_j}\frac{\left(x_{ik}-\overline{x_k}\right)}{S_k}\left(j=1,2,...,m;k=1,2,...,m\right)(5)$

The eigenvalue and eigenvector of matrix R can be determined by Equation 8:

$\left(R-{\lambda }_{i}I\right)l_i=0(6)$

where λi (i = 1, 2, … , m) and li (i = 1, 2, … , m) are the eigenvalues and eigenvectors of matrix R, respectively, li corresponds to the principal components, and λi corresponds to the variance obtained from each principal component. The effect of each eigenvalue is given by the contribution rate. A larger contribution rate indicates a larger eigenvalue. The largest eigenvalues represent the principal components regarding most of the variability in the observed data. The cumulative contribution rate α for a specific eigenvalue λk (i = 1, 2, … , m) can be obtained as follows:

$\alpha =\frac{{\lambda }_1+{\lambda }_2+...+{\lambda }_k}{{\lambda }_1+{\lambda }_2+...+{\lambda }_m}\times 100\%(7)$

If the value of α is equal to or more than 90%, k principal components are considered to contain sufficient information to represent the complex original data array. The matrix (Fij)n × k, composed of k principal components, can be expressed by:

$F_{ij}={\displaystyle \sum _{i=1}^m}{y}_{it}{l}_{tj}\left(i=1,2,...,n;j=1,2,...,k;t=1,2,...,m\right)(8)$

In this matrix, the largest contribution rate is given by the first principal component, followed by the other components, which have gradually decreasing contribution rates.

2.2.2 Susceptibility modelling for landslide

This study utilized IV, LR, and WOE models for landslide susceptibility analysis. The main steps of the modeling process are as follows.

(1) The landslide inventory map is prepared, which includes historical landslide points;

(2) We Generat thematic layers of landslide influencing factors using GIS;

(3) PCA is used to calculate the weight of each factor, and conduct subsequent analysis based on these weights.

(4) We calculate the IV, LR, and WOE indices for each factor category and summarize the values across all categories (per unit area). According to relevant research (Lee et al., 2004; Huang et al., 2020a), the landslide susceptibility index (LSI) for each unit in GIS is as follows:

$\mathit{L}\mathit{S}\mathit{I}={\displaystyle \sum _{\mathit{i}=\mathbf{1}}^{\mathit{n}}}{\mathit{w}}_{\mathit{i}}*{\mathit{s}}_{\mathit{i}\mathit{j}}(9)$

Where w_i represents the weight of the ith factor, s_ij denotes the statistical index value obtained from the three models, and j refers to the jth class of the ith factor in the given cell. Subsequently, landslide susceptibility indices (LSIs) were calculated to create susceptibility maps, and the GIS-based natural breakpoint method was applied to categorize the mapping results into five susceptibility levels ranging from extremely high to extremely low.

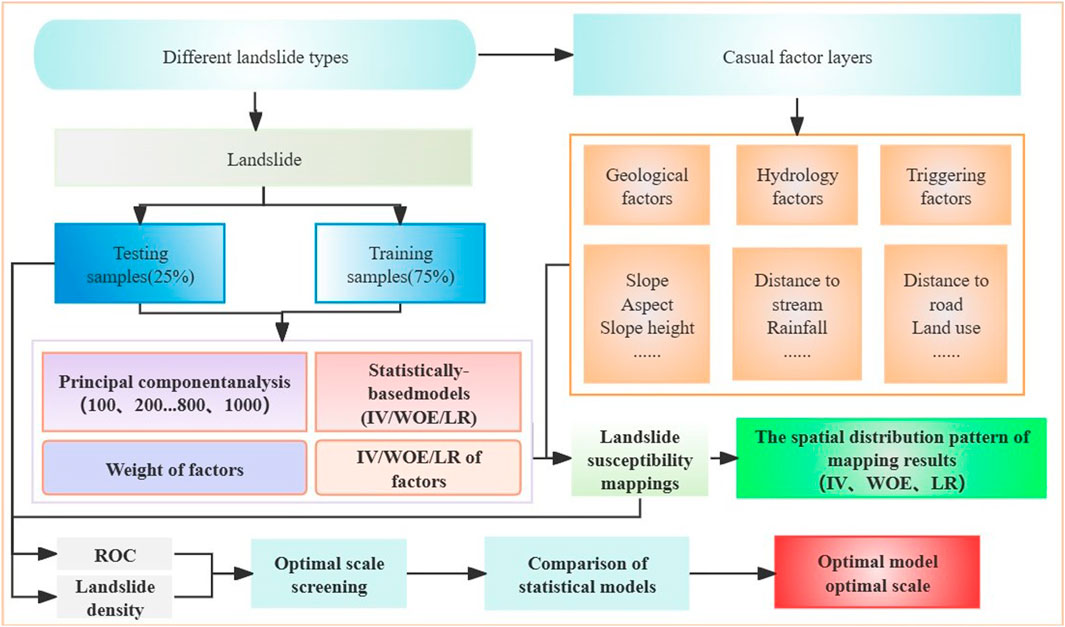
(5) Result validation and accuracy comparison analysis are conducted. Based on historical landslide data, 75% of the samples are selected as training data, while the remaining 25% are reserved for validation purposes. The training samples provide the model with information on past landslide occurrences, while the validation samples are used to verify accuracy (Erener et al., 2017; Sameen et al., 2020). To ensure the randomness of selecting training and validation samples, this study utilized the random selection tools available in ArcGIS. The specific workflow of this study is illustrated in Figure 3.

Figure 3

Figure 3. Technical flow chart.

2.2.3 Information value model

The information value model, a statistical evaluation technique rooted in information theory, was introduced by American information theorist Claude Shannon (Xu et al., 2013). Within susceptibility research, this method proves useful in pinpointing crucial factors influencing susceptibility and assessing the impact of various factors on susceptibility (Yang et al., 2020). The formula for this method is outlined as follows:

${\mathit{I}}_{\mathit{i}}=\mathbf{ln}\frac{{\mathit{N}}_{\mathit{i}}/\mathit{N}}{{\mathit{A}}_{\mathit{i}}/\mathit{A}}(10)$

Where N represents the total number of landslides that have occurred in the study area, N_i represents the number of landslides that occurred within the index X_i. A represents the total area of the study area. Ai represents the area occupied by X_i.

2.2.4 Weight of evidence model

The WOE model is a binary statistical method based on Bayesian probability statistics. It is characterized by its intuitive form, transparent modeling process, and ease of understanding. These advantages align well with the analytical approach needed for geological problem-solving, making it widely applied in landslide susceptibility assessment (Guo et al., 2021). The calculation formula is as follows:

${\mathit{W}}_{\mathit{i}}^{+}=\mathbf{ln}\left(\frac{\mathit{P}\left\{\mathit{B}|\mathit{L}\right\}}{\left.\left.\mathit{P}\{\mathit{B}\right|\overline{\mathit{L}}\right\}}\right)(11)$

${\mathit{W}}_{\mathit{i}}^{-}=\mathbf{ln}\left(\frac{\mathit{P}\{\overline{\mathit{B}}\left|\left.\mathit{L}\right\}\right.}{\mathit{P}\left\{\overline{\mathit{B}}|\overline{\mathit{L}}\right\}}\right)(12)$

$\mathit{W}={\mathit{W}}_{\mathit{i}}^{+}+{\mathit{W}}_{\mathit{i}}^{-}(13)$

Where $W_i^{+}$ represents the probability of landslide occurring within the current impact factor level, $W_i^{-}$ represents the probability of landslide occurring in parts other than the impact factor level, P is the probability of landslide, B is the landslide area under this level after classification, and L refers to the total area of the study area. , $\overline{L}$ is the total area covered by landslides in the study area, and W is the final weight.

2.2.5 Logistic regression model

The logistic regression model is a widely used statistical tool that falls under the category of generalized linear models, specifically designed to analyze binomial categorical variables (Shirzadi et al., 2012). In the context of landslide susceptibility research, this model is particularly useful because it directly relates the influencing factors to the binary outcome of landslide occurrence (whether a landslide occurs or not) (Cemiloglu et al., 2023). Due to its ability to effectively model this binary response, the logistic regression model has been extensively applied in landslide susceptibility mapping. The specific formula is as follows:

$\mathit{Y}={\mathit{a}}_{\mathbf{0}}+{\mathit{a}}_{\mathbf{1}}{\mathit{X}}_{\mathbf{1}\mathit{j}}+{\mathit{a}}_{\mathbf{2}}{\mathit{X}}_{\mathbf{2}\mathit{j}}+\dots +{\mathit{a}}_{\mathit{n}}{\mathit{X}}_{\mathit{n}\mathit{j}}(14)$

$\mathit{P}=\frac{\mathbf{exp}\left(\mathit{Y}\right)}{\mathbf{1}+\mathbf{exp}\left(\mathit{Y}\right)}(15)$

where Y is the landslide event, P is the probability of the event, a_i (i = 0,1,.n) represents the regression coefficient of the explanatory variable, X_ij (i = 0, 1, 2. n) represents the jth class of the ith explanatory variable.

2.2.6 Accuracy analysis

The Receiver Operating Characteristic (ROC) curve is a commonly used method in landslide susceptibility studies to evaluate the accuracy of models. It provides a simple and intuitive way to analyze the relationship between specificity and sensitivity fairly accurately (Pradhan, 2013; Corsini and Mulas, 2017). In this study, the Area Under the ROC Curve (AUC) is used to compare and analyze the accuracy of the models. The specific formula is as follows:

$\mathit{A}\mathit{U}\mathit{C}={\int }_{\mathbf{0}}^{\mathbf{1}}\frac{\mathbf{exp}\left(\mathit{a}/\left(\mathbf{1}-\mathit{b}\right)\right)\left({\mathit{x}/\left(\mathbf{1}-\mathit{x}\right)}^{\left(\mathbf{1}+\mathit{b}\right)/\left(\mathbf{1}-\mathit{b}\right)}\right)}{\mathbf{1}+\mathbf{exp}\left(\frac{\mathit{a}}{\mathbf{1}-\mathit{b}}\right)/{\left(\mathit{x}\left(\mathbf{1}-\mathit{x}\right)\right)}^{\left(\mathbf{1}+\mathit{b}\right)/\left(\mathbf{1}-\mathit{b}\right)}}(16)$

Where the coefficients a and b represent the dependence of test accuracy on the threshold; x is the value of ROC.

However, in actual landslide susceptibility assessment, more attention is paid to the model’s ability to identify highly landslide-prone areas, because these areas often mean greater disaster risks, and the AUC value cannot fully reflect the model’s performance in this regard. In order to more comprehensively evaluate the assessment accuracy of the model, the landslide density index (Tang et al., 2020) was introduced in this paper to conduct a comparative analysis of the model recognition ability. The formula for landslide density is as follows:

${\mathit{D}}_{\mathit{L}}={\mathit{P}}_{\mathit{S}\mathit{L}}/{\mathit{P}}_{\mathit{T}\mathit{L}}(17)$

Where D_L is the proportion of landslides within a specific susceptibility level, P_SL is the number of pixels that have landslides within that level, and P_TL is the total number of pixels that have landslides within the entire area.

3 Results

3.1 Selection and analysis of influencing factors

Landslides are complex geological hazards influenced by a combination of natural and human factors. Accurate identification and quantification of these factors are essential for landslide susceptibility mapping, which enhances the accuracy of risk assessment and improves our understanding of the driving mechanisms behind landslides. Different methods may yield varying results when quantifying these factors, due in part to the methods themselves and in part to the spatial scale effect—where the influence and mechanism of the same factor may vary across different scales. To better understand these variations and improve mapping accuracy, this section first uses principal component analysis (PCA) to explore the weight changes of each factor at different scales, revealing the multi-scale effect. Subsequently, the IV, WOE, and LR methods are applied to quantitatively assess the contribution of each factor to landslide susceptibility and analyze the mechanisms underlying these internal differences.

3.1.1 Scale effect of influencing factors

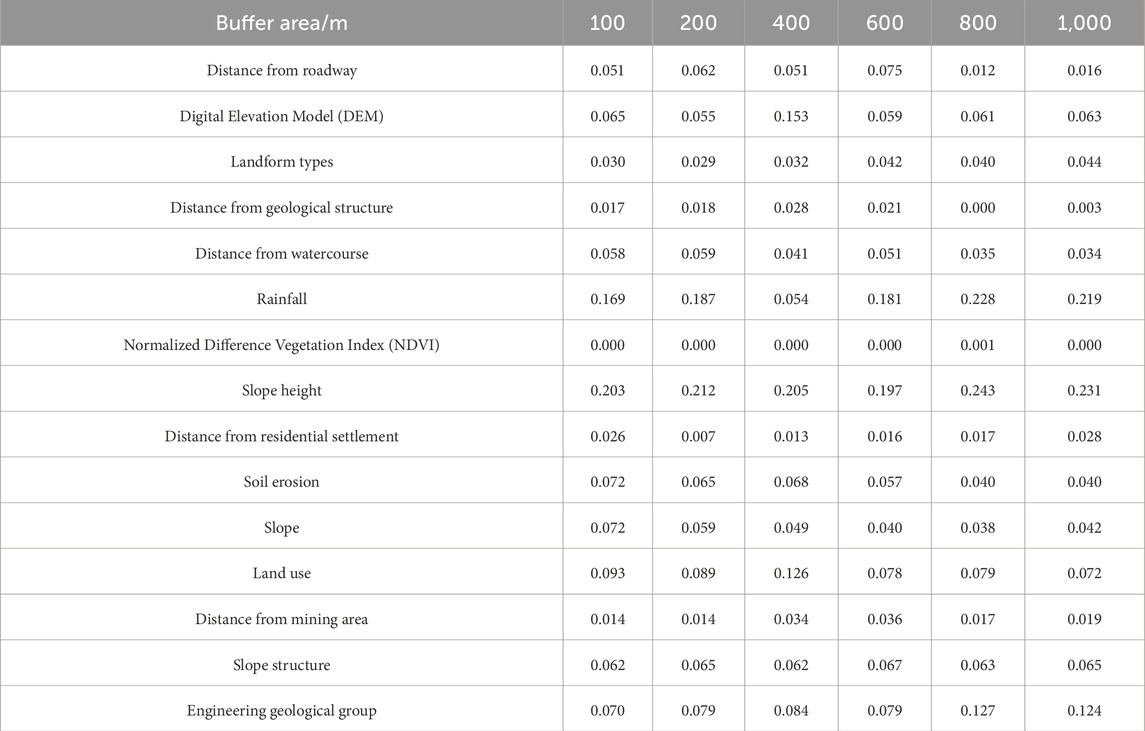
To further explore the influence of various factors on landslides at different scales, this study uses PCA (Equations 1–8) to calculate the weights of 15 factors at different scales and analyze the weights. The results show (Table 2) that the weights of the 15 factors at different scales are quite different, and some factors have obvious scale effects. The weights of slope height, rainfall, landform type and engineering rock group increase with the increase of buffer zone, suggesting that these factors play a more significant role in landslide occurrence at broader scales. Specifically, high and steep slopes provide greater gravitational potential energy, promoting landslide occurrence; different landform types reflect regional topographic characteristics, influencing the spatial distribution of landslides; the properties of engineering rock groups determine rock mass strength and stability, affecting landslide development; rainfall infiltration leads to soil saturation and increased pore water pressure, reducing slope shear strength and triggering landslides. The weights of DEM, land use type, distance from structure, distance from road, and distance from mining area at medium scale (400–600 m) are higher than those at other scales. This indicates that human activities and geological characteristics influence landslide development at medium scales by altering slope structure, stress conditions, and rock fragmentation. Specifically, DEM reflects regional topographic variations, with landslide susceptibility differing across elevation ranges; changes in land use (e.g., vegetation removal, road construction) can destabilize slopes and increase landslide risk; the distribution of structures, roads, and mining areas controls rock fragmentation and stress conditions, thereby influencing landslide development. The distance to the river, soil erosion, and slope have high weights at the local scale (100–200 m), and then decrease with the increase of the buffer zone, indicating that these factors directly act on the slope surface in a small range and significantly affect the movement and stability of the sliding body. Specifically, river erosion can weaken slope support, increasing landslide susceptibility near riverbanks; soil erosion alters slope roughness and permeability, impacting slope stability; and slope, as a key topographic factor, directly controls the movement of the sliding mass at the local scale. Notably, the weight of vegetation cover (NDVI) remains low across all buffer zones, indicating it has a relatively minor impact on landslides. This may be due to the fact that the vegetation coverage in the study area is generally good, the impact on landslides is relatively uniform, and the differences at different scales are not obvious.

Table 2

Table 2. Weight of landslide influence factors at different scales.

3.1.2 IV, WOE, LR coefficient determination

To improve the accuracy of landslide susceptibility mapping, the intrinsic driving mechanisms of landslides were thoroughly examined. Each driving factor was divided into four to nine categories, and the IV, WOE, and LR were calculated by Equations 10–15 for each category of the 15 influencing factors (Table 3).

Table 3

Table 3. IV、WOE and LR coefficient index of each landslide interval.

The results indicate that IV and WOE exhibit strong consistency in quantifying the classification information and predictive power of variables. However, the regression coefficient does not always align with IV and WOE in certain cases. For example, in the category where the distance to the mining area is less than 200 m, the RC (Regression coefficient) is 1.25, significantly higher than the IV of 0.55 and the WOE of 0.5. This suggests that proximity to the mining area has a clear and substantial influence on the assessment of landslide risk. Furthermore, the IV and WOE values for distances from the mining area in different intervals (such as 300m–600m and 600m–1000 m) show a decreasing trend, indicating that as the distance increases, the predictive efficacy diminishes. In contrast, the RC shows an increasing trend in these intervals, indicating that the logistic regression model captures more complex relationships. This may be because logistic regression, based on maximum likelihood estimation, can flexibly adjust parameters to account for nonlinear relationships or interaction effects in the data. These findings highlight the complexity of selecting appropriate methods for landslide susceptibility mapping. Relying solely on one model may introduce significant bias in the results. Therefore, a comprehensive comparison of multiple models’ performance is necessary during the modeling process. To enhance the accuracy and reliability of the mapping, model selection should be based on the specific context and characteristics of the study area.

3.2 Landslide susceptibility mapping and comparative analysis of performance

The above analysis deeply explores the mechanism of action and scale effect of landslide influencing factors. On this basis, this section will focus on the landslide susceptibility mapping effect and prediction performance of different models at different scales. By comparing and analyzing the spatial distribution pattern, ROC curve and landslide density evaluation indicators of the IV, WOE and LR at multiple scales, we can comprehensively evaluate the advantages and disadvantages of each model and select the optimal model and scale combination to provide a scientific basis for landslide risk assessment and disaster prevention and mitigation.

3.2.1 Spatial distribution patterns of susceptibility mapping from various models at multiple scales

To obtain the susceptibility results of landslides at different scales, multiply and sum the IV, WOE, and LR coefficients of the internal subcategories of influencing factors determined by PCA. The levels of susceptibility to landslides are classified into five categories: extremely low, low, moderate, high, and extremely high through the application of the natural breakpoint technique. The calculated susceptibility results for landslides are shown in Figures 4–6.

According to Figure 4, at the 100-m scale, high/extremely high prone areas are mainly concentrated in the narrow river valley areas in the north, southwest, and east of the study area, as well as the lowland areas in the southeast. Areas with low and extremely low susceptibility are mainly distributed in the lowlands and flat regions in the central, southwest, and west. Medium-susceptibility areas are mainly found in the transition zones between high/extremely high and low/extremely low susceptibility areas, showing a cross-distribution pattern with these levels. As the spatial scale increases to 200 m, the high and extremely high susceptibility areas begin to expand outward, gradually encroaching on some of the medium-susceptibility areas. However, the spatial distribution of low and extremely low susceptibility areas remains largely unchanged. At a 400-m scale, the high/extremely high and low/extremely low susceptibility areas continue to expand outward, displaying a clear trend of forming contiguous patches. Meanwhile, the medium-susceptibility areas start to occupy parts of the space originally classified as high/extremely high and low/extremely low susceptibility, leading to a certain degree of spatial contraction and fragmentation in these two levels. At scales beyond 400 m, as the spatial scale continues to increase, the outward expansion of high/extremely high and low/extremely low susceptibility areas persists, further forming more continuous patches. Although medium-susceptibility areas experience noticeable spatial contraction, they also exhibit a clear tendency to form contiguous patches.

Figure 4

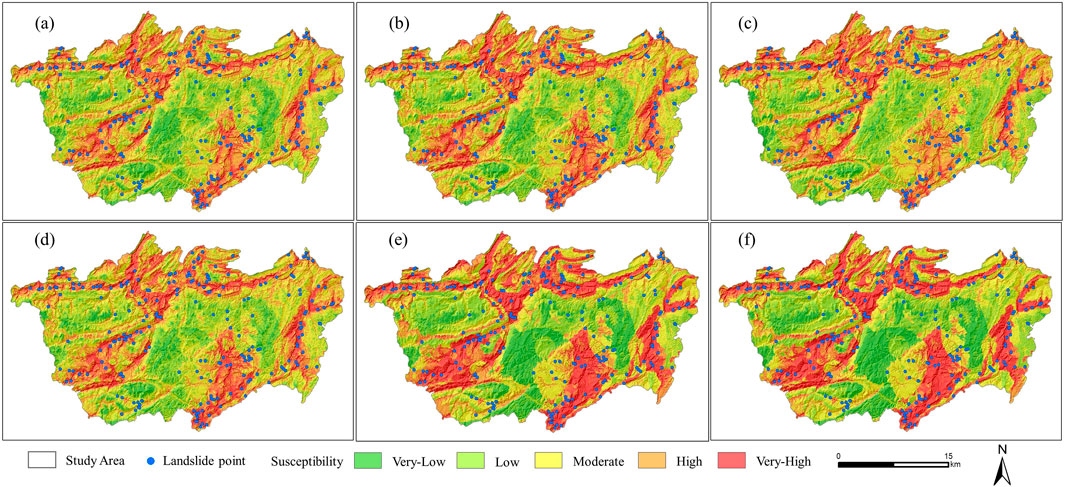
Figure 4. Landslide susceptibility maps at different scales based on the IV model (A) 100-m buffer zone, (B) 200-m buffer zone, (C) 400-m buffer zone, (D) 600-m buffer zone, (E) 800-m buffer zone, (F) 1000 m buffer).

As can be seen from Figures 5, 6, in the multi-scale modeling results of the WOE model and the LR model, the trend of the spatial distribution of low-susceptibility areas, extremely low-susceptibility areas, high-susceptibility areas, and extremely high-susceptibility areas with scale changes is consistent with the modeling results of the IV model. Specifically, with the increase of spatial scale, the spatial distribution of low/extremely low-susceptibility areas and high/extremely high-susceptibility areas shows a trend of spreading outward, while the spatial distribution of medium-susceptibility areas shows the characteristics of first spreading and then contracting.

Figure 5

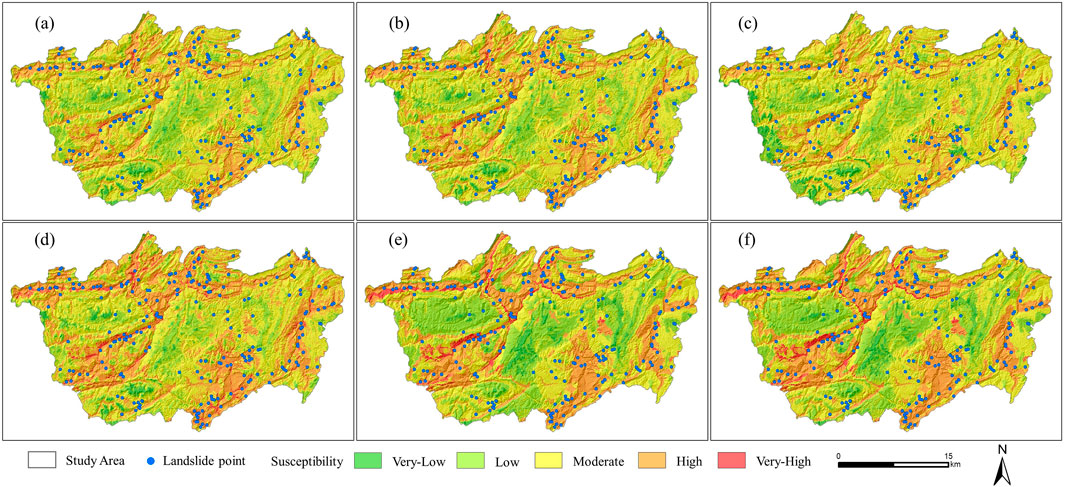
Figure 5. Landslide susceptibility map at different scales based on the WOE model (A) 100-m buffer zone, (B) 200-m buffer zone, (C) 400-m buffer zone, (D) 600-m buffer zone, (E) 800-m buffer zone, (F) 1000 m buffer).

Figure 6

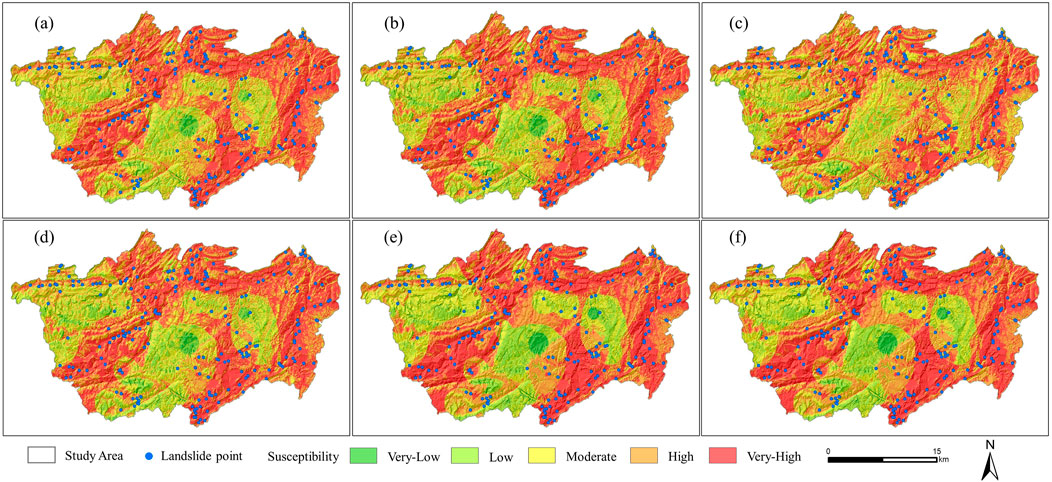
Figure 6. Landslide susceptibility map at different scales based on the LR model (A) 100-m buffer zone, (B) 200-m buffer zone, (C) 400-m buffer zone, (D) 600-m buffer zone, (E) 800-m buffer zone, (F) 1000 m buffer.

3.2.2 Comparative analysis of performance of susceptibility mapping of different models at multiple scales

3.2.2.1 Performance comparison analysis based on ROC

The above analysis reveals significant variations in susceptibility mapping across different scales and methods. To quantitatively assess these differences and validate the accuracy of the landslide susceptibility maps at various scales, 25% of the landslide data is used as test samples. The model’s performance is evaluated using the AUC value as a metric (Equation 16).

Based on Figure 7A, he AUC value initially increases and then decreases as the buffer scale expands. The highest value of 0.828 is achieved at the 600-m scale, indicating an optimal scale for landslide susceptibility modeling. The 600-m buffer scale emerges as the most suitable modeling scale for landslide susceptibility mapping using the IV model. A comparative analysis with the benchmark 100-m scale shows that moderately increasing the buffer scale can enhance mapping accuracy. However, an excessively large scale reduces accuracy, likely due to the smoothing of local geological and topographic features, which limits the model’s ability to capture micro-environmental factors critical to landslide occurrence. Figure 7B shows a similar trend for the WOE model, where the AUC value rises, falls, and then rises again as the buffer scale increases. The AUC reaches its highest value of 0.811 at the 600-m scale, suggesting this as the optimal scale for susceptibility mapping. As with the IV model, an appropriate scale enlargement improves mapping accuracy, but overly large scales result in decreased accuracy. This similarity may be due to the shared weight calculation mechanisms between the WOE and IV models, leading to comparable responses to scale changes. Figure 7C illustrates that the AUC value fluctuates with increasing buffer scale in the LR model, peaking at 0.771 at the 400-m scale. This indicates that the 400-m buffer is the most suitable scale for landslide susceptibility mapping using the LR model. Comparing this with the benchmark scale, the LR model shows improved mapping accuracy with larger buffer scales, except at the 200-m scale. This may be related to the principle of LR. The logistic regression model relies on parameter estimation and the distribution characteristics of sample data. An appropriate buffer zone scale can help the model better capture the environmental variables of landslide occurrence. However, an excessively large scale may lead to over-smoothing of environmental variables, making it difficult for the model to capture local geological differences, thus affecting the model’s predictive performance.

Figure 7

Figure 7. ROC curves and AUC values of susceptibility mapping for three models at different scales (A): IV, (B): WOE, (C): LR).

In addition to the significant differences in ROC curves caused by the difference in scale, the choice of model also has a significant impact on the ROC curve. As shown by the AUC values of each model in Figure, the IV model achieves the highest AUC values, ranging from 0.804 to 0.828, indicating the best overall performance in landslide susceptibility mapping and accurate identification of landslide-prone areas. The WOE model’s AUC values range from 0.791 to 0.811, ranking second. Although slightly lower than the IV model, the WOE model still performs well in identifying most landslide-prone areas. The LR model has the lowest AUC values, ranging from 0.742 to 0.771, suggesting weaker performance in landslide susceptibility mapping, with potentially missed or misclassified landslide-prone areas. Based on these AUC values, the IV model demonstrates the best overall mapping accuracy, followed by the WOE model, while the LR model shows the weakest performance.

3.2.2.2 Performance comparison analysis based on landslide density

The AUC is a crucial metric for assessing a model’s overall mapping performance, providing insight into its ability to differentiate between positive and negative samples. However, in the realm of assessment of landslide susceptibility, greater emphasis is placed on the model’s capacity to pinpoint highly landslide-prone areas, which pose higher disaster risks. The AUC value may not fully capture the model’s effectiveness in this specific aspect. To offer a more comprehensive assessment of the model’s mapping accuracy, this paper introduces the landslide density index (Equation 17) for a more in-depth analysis of the model’s identification capabilities.

Among the statistical indicators of landslide density, the proportion of high/extremely high prone areas reflects the accuracy of the model. As shown in Figure 8A, the accuracy of the IV model increases initially and then decreases with scale. The highest accuracy, 78.21%, occurs at the 400-m scale, indicating that this is the optimal mapping scale for the IV model. Compared to the benchmark scale, the accuracy at all scales, except for the 1000-m scale, is higher, suggesting that moderate scale increases can improve the IV model’s prediction accuracy. However, excessively large scales may reduce performance. This may be because moderate scaling helps capture regional geological characteristics, enhancing prediction accuracy, while overly large scales introduce too much heterogeneity, reducing performance. Figure 8B shows a similar trend for the WOE model, where accuracy fluctuates, increasing first and then decreasing. The highest accuracy, 74.52%, is achieved at the 600-m scale, identifying it as the optimal scale for the WOE model. Most scales show higher accuracy compared to the benchmark, further confirming that considering scale can improve landslide susceptibility mapping accuracy. The WOE model’s response to scale changes is similar to that of the IV model, suggesting both models might be influenced by similar scale effects. In contrast, Figure 8C shows that the LR model’s accuracy decreases as scale increases, with the highest accuracy at the 100-m scale. This indicates that the 100-m scale is the optimal mapping scale for the LR model. Notably, the LR model performs better at smaller scales (100 and 200 m), while larger scales (800 and 1,000 m) result in lower accuracy. This suggests that smaller scales are more suitable for landslide susceptibility mapping using the LR model, whereas larger scales may degrade accuracy. The reason for this difference may be related to the characteristics of the LR model. As a parametric statistical model, the LR model can better fit the nonlinear relationship between high-risk areas and environmental factors at a smaller scale. However, at a larger scale, this complex nonlinear relationship may be oversimplified, resulting in a decrease in the model’s predictive performance.

Figure 8

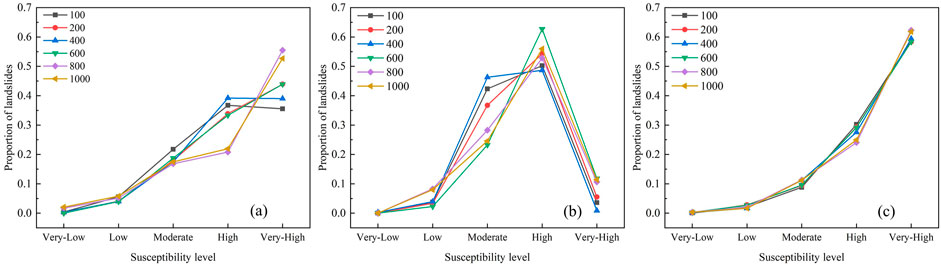
Figure 8. Statistical values of landslide density in susceptibility mapping of three models at different scales (A): IV, (B): WOE, (C): LR).

Further analysis, as shown in Figure 8A, reveals that across the six scales of the IV model, less than 10% of landslides are categorized as having low or very low susceptibility. This indicates that only a small fraction of landslides are mistakenly classified in lower susceptibility categories. In contrast, over 70% of landslides are classified as having high or very high susceptibility, suggesting that the majority of landslide assessments are accurate. In conjunction with Figure 8B, the results from the six-scale WOE model reveal that less than 10% of landslides are categorized as having low or very low susceptibility, while the proportion of those classified as high or very high susceptibility exceeds 50%, with the highest value reaching 74.52%. This indicates that the majority of landslide assessments are accurate, and the model’s predictive performance is acceptable. Similarly, Figure 9C shows that the LR model, using six scales, classifies less than 5% of landslides as having low or very low susceptibility, while over 87% are classified as having high or very high susceptibility. This underscores the LR model’s high success rate in landslide identification and demonstrates its accuracy. Overall, the LR model exhibits the highest assessment accuracy, followed by the IV model and the WOE model. Additionally, the mapping results from the LR model, displayed in Figure 9C, further validate its effectiveness in predicting high-risk areas, as evidenced by the proportion of landslide-prone zones: extremely high vulnerability zone > high vulnerability zone > medium vulnerability zone > low vulnerability zone > very low vulnerability zone.

Figure 9

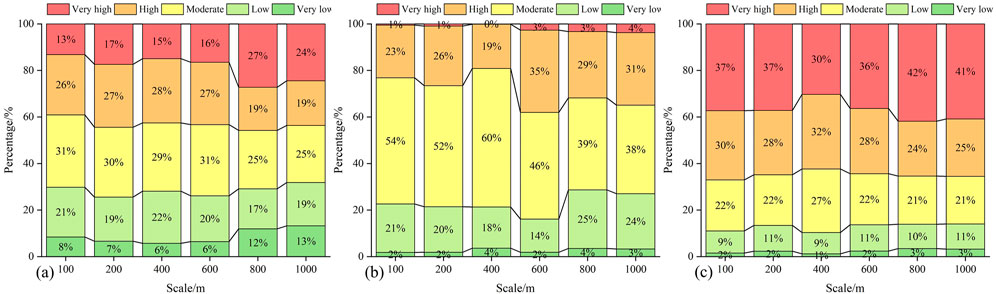
Figure 9. The proportion of each prone area in the results of susceptibility mapping with different methods and different scales (A): IV, (B): WOE, (C): LR.

3.2.2.3 Optimal selection of different models and scale combinations

By analyzing two evaluation indicators, the AUC and landslide density, we comprehensively assess the mapping performance of various models at different scales. In terms of overall assessment performance, the IV model demonstrates the greatest effectiveness, followed by the WOE model. Conversely, the LR model shows relatively weaker predictive capabilities. In terms of the optimal scale, the IV model and WOE model exhibit superior assessment accuracy at the 600-m buffer scale, whereas the LR model excels at the 400-m buffer scale. To achieve the best overall assessment accuracy, selecting the 600-m buffer scale for the IV model is advisable.

In terms of identifying high-risk landslide areas, the LR model demonstrates the superior performance, followed by the IV model, with the WOE model showing relatively weaker performance. In terms of optimal scale selection, the IV model demonstrates the highest recognition effect at the 400-m buffer scale, while the WOE model shows the best recognition effect at the 600-m buffer scale, and the LR model excels at the 100-m buffer scale. To improve the identification of landslide hazard areas, using a 100-m buffer scale in the LR model is recommended.

In practical applications, it is essential to consider the assessment performance of various models and scales comprehensively. The optimal combination should be chosen depending on the research objectives and particular requirements for reducing and averting disasters. To enhance both the overall assessment accuracy and the ability to identify highly susceptible areas, consider utilizing the 600-m buffer scale of the IV model. This scale not only improves the overall assessment accuracy but also enhances the detection of zones that are highly susceptible to landslides. The choice of specific combination should be carefully considered in light of factors such as the study area’s characteristics, data accessibility, and computing resources.

4 Discussion

4.1 Scale effect of influencing factors

This paper demonstrates that the weights of landslide influencing factors exhibit significant variations as the spatial scale changes through multi-scale analysis. The study concluded that topography, geology, and rainfall are the primary factors influencing landslides at a regional scale ranging from 800 to 1,000 m. This finding aligns with the research by Guzzetti et al. (Guzzetti et al., 1999), which indicates that geological and hydrological factors play a significant role in the occurrence of landslides at the basin scale. There is also a certain similarity with the view of Yang (Yang Yang et al., 2019) and others that “topography is the main factor in landslides on a regional scale”. At the buffer zone scale of 400–600 m, human activities and geological features exert the most significant influence on landslides. This finding is consistent with Carrara et al.'s research conclusion (Carrara et al., 1995), which asserts that at smaller scales, human activities and geological features notably impact the occurrence of landslides. When the analysis range is narrowed down to a small local area (100–200 m), the impact of erosion intensity and topographic factors on landslides becomes more pronounced. When focusing on a smaller local area (100–200 m), the influence of erosion intensity and topographic factors on landslides becomes more significant. This is a degree of correlation with Van et al.'s (Van Westen et al., 2008) conclusion that topographic factors are suitable for modeling geological hazards in local areas.

It is worth noting that the vegetation cover (NDVI) within each buffer zone has a low weight, suggesting a limited impact on landslide occurrences. This finding contrasts with the results of HU et al.'s study in a forested area of eastern Mongolia, Yunnan, China, where they concluded that NDVI is a significant predictor of landslide susceptibility (Hu et al., 2024). There are several possible reasons for this difference: (1) Significant differences in topography, geology, climate, and other natural conditions between the study area and the eastern Mongolian forest area in Yunnan Province may lead to varying degrees of influence of vegetation cover on landslides. (2) The protective effect of vegetation on landslides can be influenced by factors such as vegetation type, growth status, and the development of vegetation root systems in various areas. It is important to consider that the vegetation types and growth conditions in the study area of this article may differ from those in the Mengdong forest area of Yunnan. (3) The research methods, data types, and accuracy employed in this study might differ from those utilized in HU et al.'s study, potentially impacting the comparability of the research findings. (4) Landslide occurrences are impacted by a variety of factors, with varying weights in different regions. In the research area discussed in this paper, factors such as topography and precipitation may have a more significant impact on landslides, potentially overshadowing the role of vegetation coverage.

4.2 Performance of different statistical models in landslide susceptibility evaluation

The research employs three frequently utilized statistical models (IV, WOE, LR) to assess landslide susceptibility. It then conducts a comparative analysis of their evaluation performance. From the overall evaluation performance, the IV model shows better effectiveness than the WOE model, whereas the WOE model performs better than the LR model. Sweta et al. confirms this view (Sweta et al., 2022). In terms of evaluation effectiveness in high-risk areas, the LR model demonstrates the best performance, with the IV model coming in second place, while the WOE model shows relatively weaker evaluation results. This conclusion is consistent with Tang et al.'s study on the Loess Plateau in Shanxi Province, which found that the LR model’s forecasting accuracy exceeds that of the IV and WOE models (Tang et al., 2020). However, some studies have reached different conclusions. For instance, Khanna et al. conducted a study in India and discovered that the WOE model demonstrated superior assessment accuracy compared to the IV and LR models (Khanna et al., 2021). There are several possible reasons for this difference: (1) The geological environmental conditions vary in different study areas, leading to different dominant factors influencing the occurrence of landslides. (2) Various studies utilize different numbers and types of influencing factors, potentially impacting the assessment accuracy of the model. (3) Variations in the quantity, distribution, and quality of landslide data across different studies can impact the model’s performance.

In this research, both the IV model and the LR model demonstrated superior performance. This may be because the IV model excels in accurately evaluating the contribution of a factor to a landslide by quantifying the information in each factor class, whereas the LR model is adept at capturing intricate relationships in the data through maximum likelihood estimation. In contrast, the WOE model primarily relies on Bayesian theory and assumes that variables are unrelated to one another, which might not completely align with real-world scenarios, leading to slightly lower predictive accuracy. Nevertheless, each of the three models comes with its own set of strengths and weaknesses, and can be selected according to particular requirements and the data situation in real-world applications. For instance, the WOE model may be more suitable when dealing with small amounts of data and few influencing factors, while the IV and LR models may be more advantageous in scenarios with large amounts of data, numerous influencing factors, and complex nonlinear relationships. At the same time, it is also possible to consider the integration of different models, using their complementarity to improve the robustness of the evaluation.

4.3 The significance of selecting the optimal model and scale

This study compares methods in terms of overall assessment performance and the identification of high-risk areas, ultimately selecting the optimal scale. The research shows that the highest overall assessment accuracy is achieved by the IV model at the scale of a 600-m buffer, whereas at a 100-m buffer scale, the LR model exhibits the most successful identification of high-risk regions. This result has important theoretical and practical significance. Theoretically, this finding suggests that there exists an optimal combination of models and scales for evaluating landslide susceptibility. Traditional research often employs a single model and fixed scale for analysis, overlooking the influence of model and scale selection on assessment outcomes. This study, through systematic comparative analysis, demonstrates that the selection of model and scale greatly affects assessment accuracy, with notable variations in assessment performance among different model and scale combinations. These findings contribute to enhancing the theoretical framework of landslide susceptibility evaluation and offer novel insights for future research. In practice, utilizing the optimal model and scale combination when assessing landslide susceptibility can greatly enhance the accuracy and reliability of assessments. Compared to analyzing a single model and scale, the optimal combination can more accurately depict the spatial distribution patterns of landslides, identify high-risk areas, and offer a more solid foundation for landslide risk management and disaster prevention decisions. This has crucial implications for land use planning, project construction site selection, and emergency plan development in areas prone to landslides.

The 600-m buffer zone scale of the IV model and the 100-m buffer zone scale of the LR model, as determined in this study, can be effectively utilized for landslide risk asessment and prevention measures in the research area. For application in different regions, one can consider the concepts and methodologies presented in this article, conduct analogous analyses depending on regional circumstances and data accessibility, and choose the most suitable model and scale combination for the area. This empirical approach is deemed more scientifically sound and dependable compared to solely relying on a specific model or scale.

4.4 Limitations and future prospects of the study

While this study yielded significant results, there are limitations that still exist. The study area has a limited scope, uses a small number of influencing factors, and requires improved accuracy in field verification data. These limitations could impact the applicability and reliability of the study results. In the future, incorporating more high-precision impact factor data on a larger scale, along with high-resolution remote sensing images and field investigations, can enhance the evaluation method of landslide susceptibility. Furthermore, the potential for utilizing emerging technologies like artificial intelligence in conjunction with conventional statistical approaches should be investigated to improve assessment precision.

5 Conclusion

This paper focuses on landslides in Zhenxiong County as the research subject and employs principal component analysis (PCA) to reveal the scale effect of influencing factors. Additionally, three statistical models—IV, WOE, and LR—are combined to map landslide susceptibility. ROC curves and landslide density metrics are used to quantitatively assess the impact of method and scale selection on the accuracy of landslide susceptibility mapping. The main conclusions are as follows.

(1) The weight of landslide influencing factors shows obvious difference with the change of spatial scale. The factors of topography, geology, and rainfall have a more significant influence on landslides at a regional scale. Human activities and geological features have the most pronounced impact on landslides at a medium scale, whereas erosion intensity and topographic factors are notably more significant at a smaller, localized level.

(2) The prediction results of landslide susceptibility by the three models at different spatial scales show similar spatial distribution trends. As the spatial scale increases, the spatial distribution of high/very high susceptibility areas and low/very low susceptibility areas both show a trend of spreading outward and gradually connecting into pieces, while the spatial distribution of medium susceptibility areas first experiences a stage of fragmentation and outward expansion, and then gradually gathers and shrinks inward into pieces.

(3) The choice of scale affects the accuracy of mapping. Appropriately expanding the spatial scale can help improve the accuracy of landslide susceptibility mapping, but too large a scale may smooth the geological and topographic features, resulting in a decrease in accuracy, especially for the LR model, where a small scale performs better.

(4) Mapping accuracy is closely related to scale selection. Considering the overall assessment performance and scale effect: the IV model and WOE model exhibit the best overall assessment performance at the 600 m scale, while the LR model shows the best performance at the 400 m scale. Considering the identification of high-risk areas and scale effect: the LR model shows the best mapping effect at the 100 m buffer zone, the IV model exhibits the best mapping effect at the 400 m buffer zone, and the WOE model demonstrates the best mapping effect at the 600 m buffer zone.

(5) The choice of method and scale influences the effectiveness of landslide susceptibility mapping. The IV model demonstrated superior global assessment performance at the 600-m buffer scale, whereas the LR model excelled in identifying high-risk areas at the 100-m buffer scale.

Data availability statement

The datasets presented in this article are not readily available because some of the data is classified. Requests to access the datasets should be directed to 2669172543@qq.com.

Author contributions

YY: Conceptualization, Methodology, Software, Writing–original draft, Writing–review and editing. XWe: Conceptualization, Writing–review and editing. XWa: Investigation, Writing–review and editing. BH: Data curation, Writing–review and editing. SP: Conceptualization, Funding acquisition, Supervision, Writing–review and editing. ZL: Supervision, Writing–review and editing. JZ: Formal Analysis, Writing–review and editing. XL: Visualization, Writing–review and editing. LG: Resources, Writing–review and editing. MC: Resources, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study was supported by the National Natural Science Foundation of China (42061074, 42261073, 41971369, and 42261037), Science and Technology Talent and Platform Plan (202405AD350057) Yunnan Province Reserve Talent Program for Young and Middle aged Academic and Technical Leaders (202305AC160083 and 202205AC160014), Yunnan Provincial Basic Research Project (202401AT070103, 202201AS070024, and 202001AS070032) Yunnan Normal University Graduate Research Innovation Fund (YJSJJ23-B91, YJJJ23-B92, and YJSJ23-B95).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2024.1464775/full#supplementary-material

References

Arabameri, A., Saha, S., Roy, J., Chen, W., Blaschke, T., and Tien Bui, D. (2020). Landslide susceptibility evaluation and management using different machine learning methods in the Gallicash River Watershed, Iran. Remote Sens. 12, 475. doi:10.3390/rs12030475

CrossRef Full Text | Google Scholar

Binh Thai, P., Dieu Tien, B., Prakash, I., and Dholakia, M. B. (2017). Hybrid integration of Multilayer Perceptron Neural Networks and machine learning ensembles for landslide susceptibility assessment at Himalayan area (India) using GIS. CATENA 149, 52–63. doi:10.1016/j.catena.2016.09.007

CrossRef Full Text | Google Scholar

Carrara, A., Cardinali, M., Guzzetti, F., and Reichenbach, P. (1995). “GIS technology in mapping landslide hazard,” in Geographical information systems in assessing natural hazards (Springer), 135–175.

CrossRef Full Text | Google Scholar

Catani, F., Lagomarsino, D., Segoni, S., and Tofani, V. (2013). Landslide susceptibility estimation by random forests technique: sensitivity and scaling issues. Nat. Hazards Earth Syst. Sci. 13, 2815–2831. doi:10.5194/nhess-13-2815-2013

CrossRef Full Text | Google Scholar

Cemiloglu, A., Zhu, L., Mohammednour, A. B., Azarafza, M., and Nanehkaran, Y. A. (2023). Landslide susceptibility assessment for Maragheh County, Iran, using the logistic regression algorithm. Land 12, 1397. doi:10.3390/land12071397

CrossRef Full Text | Google Scholar

Chen, W., and Li, Y. (2020). GIS-based evaluation of landslide susceptibility using hybrid computational intelligence models. CATENA 195, 104777. doi:10.1016/j.catena.2020.104777

CrossRef Full Text | Google Scholar

Chen, W., Xie, X., Wang, J., Pradhan, B., Hong, H., Bui, D. T., et al. (2017). A comparative study of logistic model tree, random forest, and classification and regression tree models for spatial prediction of landslide susceptibility. Catena 151, 147–160. doi:10.1016/j.catena.2016.11.032

CrossRef Full Text | Google Scholar

Conforti, M., Pascale, S., Robustelli, G., and Sdao, F. (2014). Evaluation of prediction capability of the artificial neural networks for mapping landslide susceptibility in the Turbolo River catchment (northern Calabria, Italy). CATENA 113, 236–250. doi:10.1016/j.catena.2013.08.006

CrossRef Full Text | Google Scholar

Corsini, A., and Mulas, M. (2017). Use of ROC curves for early warning of landslide displacement rates in response to precipitation (Piagneto landslide, Northern Apennines, Italy). Landslides 14, 1241–1252. doi:10.1007/s10346-016-0781-8

CrossRef Full Text | Google Scholar

Dagdelenler, G., Nefeslioglu, H. A., and Gokceoglu, C. (2016). Modification of seed cell sampling strategy for landslide susceptibility mapping: an application from the Eastern part of the Gallipoli Peninsula (Canakkale, Turkey). Bull. Eng. Geol. Environ. 75, 575–590. doi:10.1007/s10064-015-0759-0

CrossRef Full Text | Google Scholar

Di Napoli, M., Di Martire, D., Bausilio, G., Calcaterra, D., Confuorto, P., Firpo, M., et al. (2021). Rainfall-induced shallow landslide detachment, transit and runout susceptibility mapping by integrating machine learning techniques and GIS-based approaches. Water 13, 488. doi:10.3390/w13040488

CrossRef Full Text | Google Scholar

Dou, J., Yunus, A. P., Bui, D. T., Merghadi, A., Sahana, M., Zhu, Z. F., et al. (2019). Assessment of advanced random forest and decision tree algorithms for modeling rainfall-induced landslide susceptibility in the Izu-Oshima Volcanic Island, Japan. Sci. TOTAL Environ. 662, 332–346. doi:10.1016/j.scitotenv.2019.01.221

PubMed Abstract | CrossRef Full Text | Google Scholar

Dou, J., Yunus, A. P., Merghadi, A., Wang, X.-K., and Yamagishi, H. (2021). “A comparative study of deep learning and conventional neural network for evaluating landslide susceptibility using landslide initiation zones,” in Understanding and reducing landslide disaster risk: volume 2 from mapping to hazard and risk zonation 5th, 215–223.

CrossRef Full Text | Google Scholar

Erener, A., Sivas, A. A., Selcuk-Kestel, A. S., and Düzgün, H. S. (2017). Analysis of training sample selection strategies for regression-based quantitative landslide susceptibility mapping methods. Comput. and Geosciences 104, 62–74. doi:10.1016/j.cageo.2017.03.022

CrossRef Full Text | Google Scholar

Feng, H. X., Miao, Z. L., and Hu, Q. W. (2022). Study on the uncertainty of machine learning model for earthquake-induced landslide susceptibility assessment. REMOTE Sens. 14, 2968. doi:10.3390/rs14132968

CrossRef Full Text | Google Scholar

Guo, Z. Z., Shi, Y., Huang, F. M., Fan, X. M., and Huang, J. S. (2021). Landslide susceptibility zonation method based on C5.0 decision tree and K-means cluster algorithms to improve the efficiency of risk management. Geosci. Front. 12, 101249. doi:10.1016/j.gsf.2021.101249

CrossRef Full Text | Google Scholar

Guo, Z. Z., Tian, B. X., Li, G. M., Huang, D., Zeng, T. R., He, J., et al. (2023). Landslide susceptibility mapping in the Loess Plateau of northwest China using three data-driven techniques-a case study from middle Yellow River catchment. Front. EARTH Sci. 10. doi:10.3389/feart.2022.1033085

CrossRef Full Text | Google Scholar

Guzzetti, F., Carrara, A., Cardinali, M., and Reichenbach, P. (1999). Landslide hazard evaluation: a review of current techniques and their application in a multi-scale study, Central Italy. Geomorphology 31, 181–216. doi:10.1016/s0169-555x(99)00078-1

CrossRef Full Text | Google Scholar

Guzzetti, F., Reichenbach, P., Ardizzone, F., Cardinali, M., and Galli, M. (2006). Estimating the quality of landslide susceptibility models. GEOMORPHOLOGY 81, 166–184. doi:10.1016/j.geomorph.2006.04.007

CrossRef Full Text | Google Scholar

Hu, B. L., Su, L. J., Zhang, C. L., Zhao, B., and Xie, Q. J. (2024). Mobility characteristics of rainfall-triggered shallow landslides in a forest area in Mengdong, China. LANDSLIDES 21, 2101–2117. doi:10.1007/s10346-024-02267-z

CrossRef Full Text | Google Scholar

Huang, F., Cao, Z., Guo, J., Jiang, S.-H., Li, S., and Guo, Z. (2020). Comparisons of heuristic, general statistical and machine learning models for landslide susceptibility prediction and mapping. Catena 191, 104580. doi:10.1016/j.catena.2020.104580

CrossRef Full Text | Google Scholar

Huang, F., Yin, K., Huang, J., Gui, L., and Wang, P. (2017). Landslide susceptibility mapping based on self-organizing-map network and extreme learning machine. Eng. Geol. 223, 11–22. doi:10.1016/j.enggeo.2017.04.013

CrossRef Full Text | Google Scholar

Huang, Y., and Zhao, L. (2018). Review on landslide susceptibility mapping using support vector machines. CATENA 165, 520–529. doi:10.1016/j.catena.2018.03.003

CrossRef Full Text | Google Scholar

Khanna, K., Martha, T. R., Roy, P., and Kumar, K. V. (2021). Effect of time and space partitioning strategies of samples on regional landslide susceptibility modelling. Landslides 18, 2281–2294. doi:10.1007/s10346-021-01627-3

CrossRef Full Text | Google Scholar

Lee, S., Ryu, J.-H., Won, J.-S., and Park, H.-J. (2004). Determination and application of the weights for landslide susceptibility mapping using an artificial neural network. Eng. Geol. 71, 289–302. doi:10.1016/s0013-7952(03)00142-x

CrossRef Full Text | Google Scholar

Lima, P., Steger, S., and Glade, T. (2021). Counteracting flawed landslide data in statistically based landslide susceptibility modelling for very large areas: a national-scale assessment for Austria. Landslides 18, 3531–3546. doi:10.1007/s10346-021-01693-7

CrossRef Full Text | Google Scholar

Lin, Q., Lima, P., Steger, S., Glade, T., Jiang, T., Zhang, J., et al. (2021). National-scale data-driven rainfall induced landslide susceptibility mapping for China by accounting for incomplete landslide data. Geosci. Front. 12, 101248. doi:10.1016/j.gsf.2021.101248

CrossRef Full Text | Google Scholar

Mallick, J., Singh, R. K., Alawadh, M. A., Islam, S., Khan, R. A., and Qureshi, M. N. (2018). GIS-based landslide susceptibility evaluation using fuzzy-AHP multi-criteria decision-making techniques in the Abha Watershed, Saudi Arabia. Environ. Earth Sci. 77, 1–25. doi:10.1007/s12665-018-7451-1

CrossRef Full Text | Google Scholar

Meier, C., Jaboyedoff, M., Derron, M.-H., and Gerber, C. (2020). A method to assess the probability of thickness and volume estimates of small and shallow initial landslide ruptures based on surface area. Landslides 17, 975–982. doi:10.1007/s10346-020-01347-0

CrossRef Full Text | Google Scholar

Merghadi, A., Yunus, A. P., Dou, J., Whiteley, J., Thaipham, B., Bui, D. T., et al. (2020). Machine learning methods for landslide susceptibility studies: a comparative overview of algorithm performance. Earth-Science Rev. 207, 103225. doi:10.1016/j.earscirev.2020.103225

CrossRef Full Text | Google Scholar

Nanehkaran, Y. A., Chen, B., Cemiloglu, A., Chen, J., Anwar, S., Azarafza, M., et al. (2023). Riverside landslide susceptibility overview: leveraging artificial neural networks and machine learning in accordance with the United Nations (UN) sustainable development goals. Water 15, 2707. doi:10.3390/w15152707

CrossRef Full Text | Google Scholar

Nanehkaran, Y. A., Mao, Y., Azarafza, M., Kockar, M. K., and Zhu, H.-H. (2021). Fuzzy-based multiple decision method for landslide susceptibility and hazard assessment: a case study of Tabriz, Iran. Geomechanics Eng. 24, 407–418. doi:10.12989/gae.2021.24.5.407

CrossRef Full Text | Google Scholar

Park, S.-J., Lee, C.-W., Lee, S., and Lee, M.-J. (2018). Landslide susceptibility mapping and comparison using decision tree models: a Case Study of Jumunjin Area, Korea. Remote Sens. 10, 1545. doi:10.3390/rs10101545

CrossRef Full Text | Google Scholar

Pereira, S., Zêzere, J. L., and Bateira, C. (2012). Technical Note: assessing predictive capacity and conditional independence of landslide predisposing factors for shallow landslide susceptibility models. Nat. Hazards Earth Syst. Sci. 12, 979–988. doi:10.5194/nhess-12-979-2012

CrossRef Full Text | Google Scholar

Pourghasemi, H. R., and Rahmati, O. (2018). Prediction of the landslide susceptibility: which algorithm, which precision? Catena 162, 177–192. doi:10.1016/j.catena.2017.11.022

CrossRef Full Text | Google Scholar

Pradhan, B. (2013). A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using GIS. Comput. and Geosciences 51, 350–365. doi:10.1016/j.cageo.2012.08.023

CrossRef Full Text | Google Scholar

Sabokbar, H. F., Roodposhti, M. S., and Tazik, E. (2014). Landslide susceptibility mapping using geographically-weighted principal component analysis. Geomorphology 226, 15–24. doi:10.1016/j.geomorph.2014.07.026

CrossRef Full Text | Google Scholar

Sameen, M. I., Pradhan, B., Bui, D. T., and Alamri, A. M. (2020). Systematic sample subdividing strategy for training landslide susceptibility models. Catena 187, 104358. doi:10.1016/j.catena.2019.104358

CrossRef Full Text | Google Scholar

Segoni, S., Rossi, G., and Catani, F. (2012). Improving basin scale shallow landslide modelling using reliable soil thickness maps. Nat. hazards 61, 85–101. doi:10.1007/s11069-011-9770-3

CrossRef Full Text | Google Scholar

Shirzadi, A., Saro, L., Hyun Joo, O., and Chapi, K. (2012). A GIS-based logistic regression model in rock-fall susceptibility mapping along a mountainous road: salavat Abad case study, Kurdistan, Iran. Nat. hazards 64, 1639–1656. doi:10.1007/s11069-012-0321-3

CrossRef Full Text | Google Scholar

Shu, H., Hürlimann, M., Molowny-Horas, R., González, M., Pinyol, J., Abancó, C., et al. (2019). Relation between land cover and landslide susceptibility in Val d'Aran, Pyrenees (Spain): historical aspects, present situation and forward prediction. Sci. total Environ. 693, 133557. doi:10.1016/j.scitotenv.2019.07.363

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, D., Gu, Q., Wen, H., Xu, J., Zhang, Y., Shi, S., et al. (2023). Assessment of landslide susceptibility along mountain highways based on different machine learning algorithms and mapping units by hybrid factors screening and sample optimization. Gondwana Res. 123, 89–106. doi:10.1016/j.gr.2022.07.013

CrossRef Full Text | Google Scholar

Sweta, K., Goswami, A., Nath, R. R., and Bahuguna, I. (2022). Performance assessment for three statistical models of landslide susceptibility zonation mapping: a case study for Dharamshala Region, Himachal Pradesh, India. J. Earth Syst. Sci. 131, 143. doi:10.1007/s12040-022-01881-6

CrossRef Full Text | Google Scholar

Tang, Y., Feng, F., Guo, Z., Feng, W., Li, Z., Wang, J., et al. (2020). Integrating principal component analysis with statistically-based models for analysis of causal factors and landslide susceptibility mapping: a comparative study from the loess plateau area in Shanxi (China). J. Clean. Prod. 277, 124159. doi:10.1016/j.jclepro.2020.124159

CrossRef Full Text | Google Scholar

Thiery, Y., Malet, J. P., Sterlacchini, S., Puissant, A., and Maquaire, O. (2007). Landslide susceptibility assessment by bivariate methods at large scales: application to a complex mountainous environment. GEOMORPHOLOGY 92, 38–59. doi:10.1016/j.geomorph.2007.02.020

CrossRef Full Text | Google Scholar

Van Westen, C., Van Asch, T. W., and Soeters, R. (2006). Landslide hazard and risk zonation—why is it still so difficult? Bull. Eng. Geol. Environ. 65, 167–184. doi:10.1007/s10064-005-0023-0

CrossRef Full Text | Google Scholar

Van Westen, C. J., Castellanos, E., and Kuriakose, S. L. (2008). Spatial data for landslide susceptibility, hazard, and vulnerability assessment: an overview. Eng. Geol. 102, 112–131. doi:10.1016/j.enggeo.2008.03.010

CrossRef Full Text | Google Scholar

Wei, X., Gardoni, P., Zhang, L., Tan, L., Liu, D., Du, C., et al. (2024). Improving pixel-based regional landslide susceptibility mapping. Geosci. Front. 101782. doi:10.1016/j.gsf.2024.101782

CrossRef Full Text | Google Scholar

Wu, Y., Ke, Y., Chen, Z., Liang, S., Zhao, H., and Hong, H. (2020). Application of alternating decision tree with AdaBoost and bagging ensembles for landslide susceptibility mapping. CATENA 187, 104396. doi:10.1016/j.catena.2019.104396

CrossRef Full Text | Google Scholar

Xu, W., Yu, W., Jing, S., Zhang, G., and Huang, J. (2013). Debris flow susceptibility assessment by GIS and information value model in a large-scale region, Sichuan Province (China). Nat. hazards 65, 1379–1392. doi:10.1007/s11069-012-0414-z

CrossRef Full Text | Google Scholar

Yang, C., Liu, L.-L., Huang, F., Huang, L., and Wang, X.-M. (2023). Machine learning-based landslide susceptibility assessment with optimized ratio of landslide to non-landslide samples. Gondwana Res. 123, 198–216. doi:10.1016/j.gr.2022.05.012

CrossRef Full Text | Google Scholar

Yang, P., Wang, N., Guo, Y., and Ma, X. (2020). Assessment of landslide susceptibility in lintong district using weighted information value model. J. Yangtze River Sci. Res. Inst. 37, 50–56. doi:10.11988/ckyyb.20190726

CrossRef Full Text | Google Scholar

Yang Yang, Y. Y., Yang Jintao, Y. J., Xu Chengdong, X. C., Xu Chong, X. C., and Song Chao, S. C. (2019). Local-scale landslide susceptibility mapping using the B-GeoSVC model. Landslides 16, 1301–1312. doi:10.1007/s10346-019-01174-y

CrossRef Full Text | Google Scholar

Zhang, R., Zhang, L., Fang, Z., Oguchi, T., Merghadi, A., Fu, Z., et al. (2024). Interferometric synthetic aperture Radar (InSAR)-based absence sampling for machine-learning-based landslide susceptibility mapping: the Three Gorges Reservoir area, China. Remote Sens. 16, 2394. doi:10.3390/rs16132394

CrossRef Full Text | Google Scholar

Zhao, Y., Wang, R., Jiang, Y. J., Liu, H. J., and Wei, Z. L. (2019). GIS-based logistic regression for rainfall-induced landslide susceptibility mapping under different grid sizes in Yueqing, Southeastern China. Eng. Geol. 259, 105147. doi:10.1016/j.enggeo.2019.105147

CrossRef Full Text | Google Scholar