Grid-search method for short-term over long-term average parameter tuning: an application to Stromboli explosion quakes

The collection of a significant catalogue of seismo-volcanic data involves the selection of relevant parts of raw signals, which can be automatised by using the short-term over long-term average (STA/LTA) method. The STA/LTA method employs the “Characteristic Function” to describe a section of a seismic record in terms of trace amplitude and first-time difference. This function is calculated in a short-term and long-term window; the ratio between the two windows defines a quantity that is controlled through threshold values, i.e., trigger on and trigger off. These threshold values indicate whether there is an increase in the energy in the seismic signal compared to the background noise. The common approach to the selection of the STA/LTA values is the adoption of literature-suggested ones. This could be a limitation as there may be cases in which a choice adapted to a specific raw signal may significantly help in the extraction of the relevant parts. To overcome the possible drawbacks of a non-adaptive choice imposed by such standard literature values, in this study, we propose a methodology for the automatic selection of STA/LTA values that can optimise the extraction of explosion quakes (EQs) from a seismo-volcanic raw signal. The values are obtained through a grid search over an index named quality–numerosity index (QNI) that measures the accordance in the automatic cuts and the consequent number of triggered seismo-volcanic events with the ones suggested by a human expert. The method was applied in the volcano domain for the specific application of the explosion quake signal extraction at Stromboli volcano. The experiments were conducted by selecting a subset of the dataset as training where to search for the best values, which were subsequently adopted in a test set. The results prove that the values suggested by our approach significantly improve the quality of the relevant part compared to the one extracted by adopting the values indicated in the literature. The methodology presented in this study can be applied to a wider typology of signals of volcanic, seismic, and other origin, potentially becoming a widely used approach in parameter optimisation processes.

1 Introduction

The issue of detecting seismo-volcanic events and their waveform extraction from raw seismic signals is a key problem of volcanic seismology (Sosa et al., 2024; Journeau et al., 2020; Soubestre et al., 2018). With the continuous growth of available data over time, due to the expansion of seismic networks, meeting this request with the help of a human operator can be laborious and time-consuming. Thus, computational methods need to be adopted, such as machine learning methods, for near real-time event detection and waveform extraction, especially for rapid risk assessment related to potential destructive events (Makus et al., 2024; Konstantinou, 2023; Lara et al., 2020). Machine learning methodologies also emerge in managing post-event intervention (Cannioto et al., 2017). The scientific community is focused on identifying and analysing the seismic signals generated by volcanic activity, for characterising potential precursors that may serve as early indicators of eruptions. This is especially crucial for the Stromboli volcano, where paroxysms—sudden and intense eruptions—pose the greatest danger to populations living in the surrounding areas (Andronico et al., 2021; Metrich et al., 2021; Giudicepietro et al., 2020). The Stromboli volcano (926 m) is part of the Aeolian archipelago in the Tyrrhenian Sea (Italy) and is renowned for its persistent explosive activity, often referred to as “Strombolian eruptions” (Giudicepietro et al., 2020). This volcanic behaviour is characterised by rhythmic bursts of gas and pyroclasts, driven by the degassing of magma (Chouet, 1996). The study of Stromboli’s volcanic signals, including seismic activity, ground deformation, and gas emissions, provides crucial insights into the underlying magmatic processes and potential eruption forecasts. Seismic activity signals, such as volcanic tremors and explosions, are particularly significant as they reflect the movement of magma and gas within the volcanic conduit. Ground deformation, monitored through techniques such as GPS and InSAR, offers valuable data on the magma’s movement beneath the surface (Schaefer et al., 2019). Gas emissions, especially the flux of sulphur dioxide $(S{O}_2)$, serve as key indicators of volcanic activity and magma ascent (Aiuppa et al., 2010). Together, these indicators constitute a comprehensive framework for understanding the Stromboli volcano’s dynamic nature and assessing the associated risks. Stromboli is an open-conduit volcano, with three summit craters (Figure 1), with persistent Strombolian activity. The explosions occur every 15–20 min. Generally, its volcanic activity is classified as follows: normal activity (specifically “explosion”), major explosion, and paroxysm (Chouet, 1996; Wassermann, 2012; Ripepe et al., 2021b). To distinguish them, the variation of frequency and energy of activity must be calculated (Calvari et al., 2021). The permanent seismic network of Istituto Nazionale di Geofisica e Vulcanologia (INGV) records seismic signals of volcanic nature, which are as follows: very long period (VLP), landslides, tornillos, explosion quakes (EQs), and many others (Wassermann, 2012). EQs along a seismic signal are generally clearly visible to the human eye. Their features are based on the variation in amplitude and frequency content, whose range is approximately 10–25 Hz. Another characteristic is that the EQs are preceded by VLPs, which are important for identifying the earthquakes themselves (Legrand and Perton, 2021; Giudicepietro et al., 2019). This feature allows for the description of the phenomena that occur in the plumbing system. Specifically, the mechanism that activates the VLP and subsequently EQs is a progressive degassing magma on the conduit. When the intensity increases, the conduit goes into resonance with the wall and produces seismic waves. After the magma starts migrating from the vent to the crater, it begins to produce resonant events such as VLPs (Konstantinou, 2023; Ripepe et al., 2021a; Liang et al., 2020; Ripepe et al., 2017; Ripepe and Harris, 2008; Chouet et al., 2003). As soon as it reaches the crater, Strombolian activity begins. Seismic stations record the EQs and produce raw signals that can be analysed. Stromboli’s volcanic system is characterised by two magma reservoirs: a shallow reservoir located 3–4 km below the surface and a deeper reservoir located approximately 11 km below the surface (Petrone et al., 2022; Mattia et al., 2008; Harris and Ripepe, 2007).

Figure 1

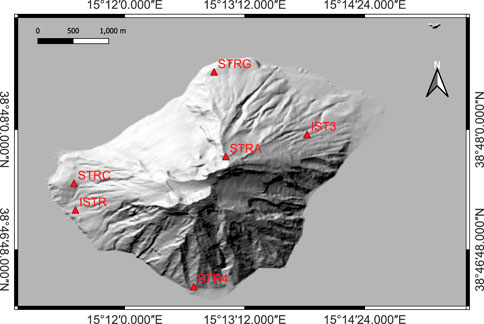
Figure 1. Permanent seismic network of Istituto Nazionale di Geofisica e Vulcanologia (INGV) on Stromboli. Map created using QGIS Development Team (2024).

The analysis of seismological data is crucial for understanding and monitoring the volcanic activity, and the short-term average/long-term average (STA/LTA) method is one of the most widely used techniques for detecting seismic events within continuous waveform data. STA/LTA is a ratio-based approach that compares the average signal amplitude over a short time window with the one over a longer time window. When a seismic event occurs, the short-term window will capture the strong amplitudes associated with the event, causing a significant increase in the STA/LTA ratio. This increase serves as a detection threshold, and when the ratio exceeds this threshold, it triggers an event detection. This method is particularly effective in identifying the onset of seismic events, such as volcanic tremors, explosions, and microseismicity, by highlighting abrupt changes in the amplitude, which indicate the start of an event (Allen, 1978). In volcanic environments, where seismic signals are often complex and embedded within noisy data, STA/LTA provides a robust mechanism for real-time event detection. The sensitivity of the STA/LTA algorithm can be adjusted by tuning the window lengths, making it adaptable to different types of seismic signals and noise levels (Withers et al., 1999). This adaptability is crucial for monitoring diverse volcanic phenomena, where the nature of seismic signals can vary significantly depending on the type of volcanic activity. Selecting STA/LTA window lengths can be an iterative process and ought to be based on real data analysis. This optimisation process may be time-consuming for human operators. The application of STA/LTA in the context of volcanic seismology has proven invaluable for the early detection of eruptive activity, allowing for timely alerts and the implementation of mitigation strategies. Furthermore, the integration of STA/LTA with other signal processing techniques enhances the overall reliability of volcanic monitoring systems (Hagerty et al., 2000). Automatic picking and cutting techniques for seismograms are essential tools in seismic data analysis, particularly in monitoring volcanic activity. These methods involve the automatic detection of seismic phases, such as P-waves and S-waves, and the precise segmentation of relevant seismic events from continuous waveform data. The automation of these processes is crucial in volcanology, where the rapid analysis of large datasets is necessary for timely eruption forecasts and hazard assessments (Beyreuther et al., 2010). Advanced algorithms, such as those based on machine learning and neural networks, have significantly improved the accuracy and efficiency of phase picking, even in the presence of noise, which is common in volcanic environments (Ross et al., 2018). Additionally, the development of techniques for automatic cutting or windowing of seismograms enables researchers to isolate specific seismic events, such as volcanic tremors or explosions, facilitating a detailed analysis of their characteristics (Hammer et al., 2012). These automated processes not only enhance the speed and reliability of seismic monitoring but also reduce the potential for human error in interpreting complex seismic signals, thereby improving the overall understanding of volcanic processes and aiding in the mitigation of volcanic risks.

In this work, we have implemented a system to perform the automatic detection and waveform extraction of a seismo-volcanic event from raw seismic signals such as EQs, using the STA/LTA method. The data were provided by the Osservatorio Vesuviano (OV)-INGV. The time range selected for the analysis is from 01 June 2019 to 14 June 2019, before the occurrence of the double paroxysm of the Stromboli volcano (Andronico et al., 2021). We have chosen the first days of the dataset as the learning set on which to perform the training of our method, owing to the large number of EQs detected.

This study is divided into four main sections:

$•$ Methodology for parameter selection: it provides a description of the method and the measures designed to evaluate the extraction of the EQs.

$•$ Experiments and results: it shows the training phase to search for the optimum parameter’s combination of STA/LTA and the testing phase where the results of the training were applied on a test set.

$•$ Discussion: it shows the interpretation of results.

$•$ Conclusions and future improvements.

2 Methodology for parameter selection

STA/LTA is based on the analysis of the ratio between short-term and long-term averages of the seismic signal amplitude. This method provides an efficient way to discriminate between seismic events and background noise in seismogram data. With the STA/LTA method, short-term window and long-term window lengths are defined to compute the average amplitudes of seismic signals. The short-term window typically spans a few seconds, capturing the immediate variations in the signal caused by seismic waves. The long-term window, on the other hand, is usually several times longer, capturing the overall background noise level. The STA/LTA ratio is calculated by dividing the average amplitude of the short-term window by the average amplitude of the long-term window. Thus, the STA/LTA is a parametric approach where two basic parameters are STA and LTA window lengths. The ratio between the two windows defines a quantity that is controlled through two other parameters, i.e., trigger on and trigger off. Selection of these parameters can be an iterative process based on real data analysis, where one must remember to continuously monitor the performance of our detection system and make the necessary updates to adapt it to the evolution of the observed phenomenon. We conducted an exploratory research to find the combination of parameters of the STA/LTA method that automatically cut at best EQs, compared to the cuts made by the expert operator. We used our tool developed for our active learning approach (D’Alessandro et al., 2022, see Section 2) to manually cut the EQs. As an example of events present in the dataset, Figure 2A shows the case of two EQs in raw signals, with a zoom on the last one (Figure 2B). To extract the spectrogram, a short-time Fourier transform was calculated using 0.5-s sliding time windows with 90% time overlapping. Figure 3 shows the STA/LTA ratio (bottom) calculated on the zoomed EQ of Figure 2 and the triggers on the signal (top): the red bar consists of trigger on threshold and the blue bar consists of trigger off threshold. When the slope of the curve exceeds the value of the trigger threshold, both for trigger on and trigger off, the red and blue bars are applied on the plot, respectively.

Figure 2

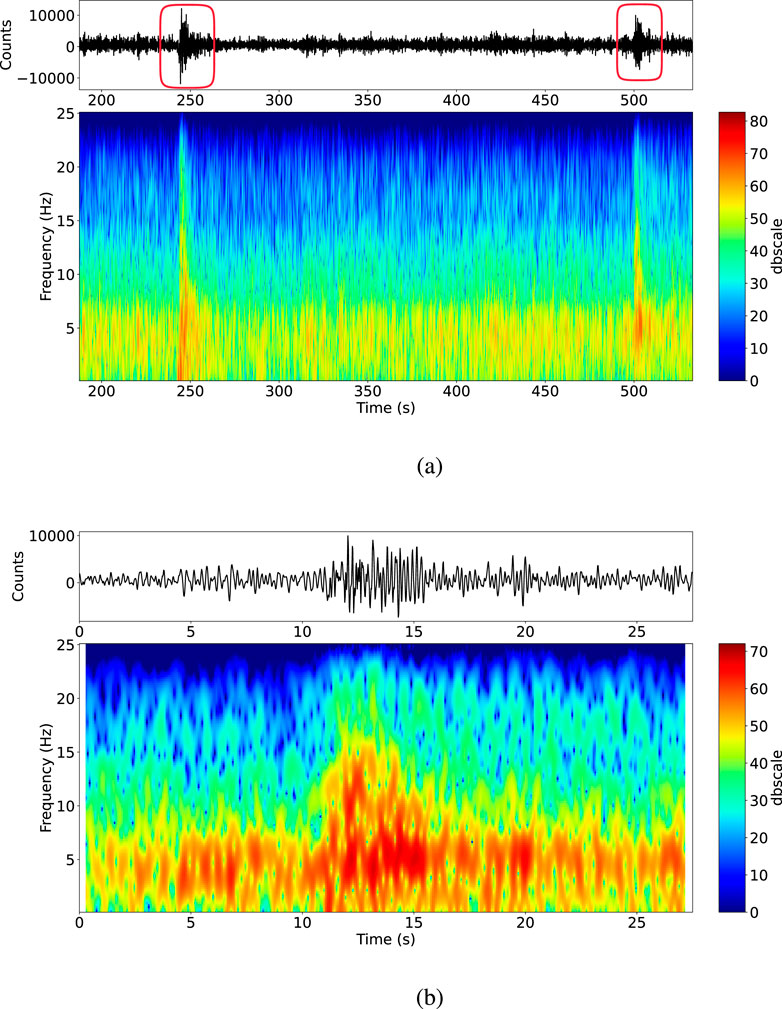
Figure 2. This figure presents a representative case of explosion quakes observed in raw seismo-volcanic signals. Each subfigure consists of two components: the raw signal displayed at the top and the corresponding spectrogram at the bottom. The raw signal is plotted with time on the x-axis, while the spectrogram illustrates the representation of this raw signal in the frequency–time domain. The side colour bar indicates frequency values in decibels. In subfigure (A), multiple explosion quakes from the Stromboli volcano’s signal are marked with red circles. In subfigure (B), a detailed view of the second explosion quake is provided.

Figure 3

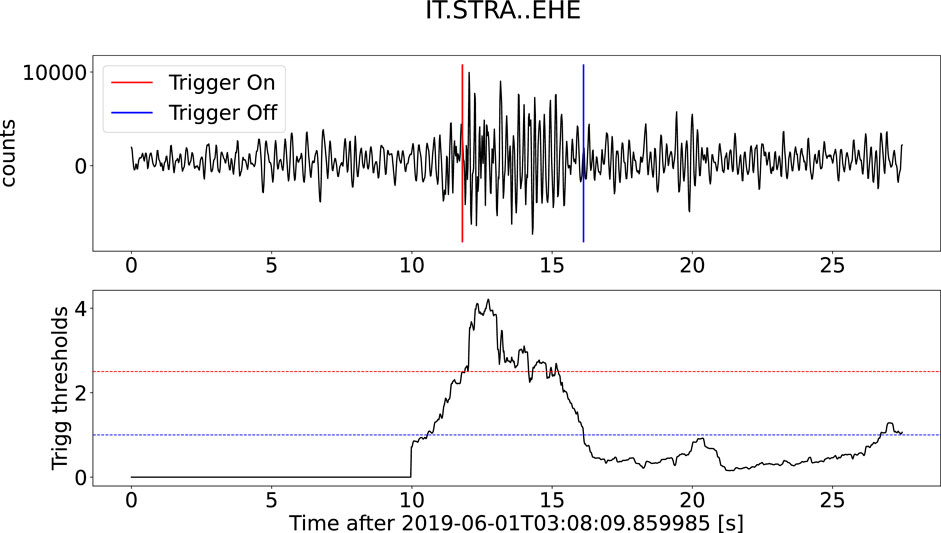
Figure 3. STA/LTA performed on the zoomed EQ of Figure 2. Red bar is trigger on and blue bar is trigger off. The figure above illustrates the raw seismo-volcanic signal, while the figure below represents time along the x-axis and trigger threshold values along the y-axis. In this example case, the chosen values of the parameters for this example were STA 1 s, LTA 10 s, trigger on 2.5, and trigger off 1.

The concept underlying our approach is based on the start and end of the time interval when the event occurs. The start and end times suggested by our approach can be compared with the selections performed by an expert operator by defining a specific measure. In particular, we have proposed two measures: the quality index and the numerosity index. The product of these two is used to define an overall measure called quality–numerosity index (QNI). As a first approach, the characteristic function (CF) $E_k$ [classic one from Allen (1978)] is used for STA/LTA and is defined as follows:

$E_k=x_k^2+{\left(x_k^{\prime }\right)}^2+C_k,(1)$

where $x_k$ is the seismic trace, $x_k^{\prime }$ its derivative, and $C_k$ (Equation 2) is an empirical weighting constant described as follows:

$C_k=\frac{{\sum }_{j=1}^k|x_j|}{{\sum }_{j=1}^k|x_j-x_{j-1}|},(2)$

to underline the importance of the amplitude and derivative.

For each raw signal considered, the STA/LTA method outputs a list of triggered events, characterised by start time and end time. Those values are compared individually with the ones chosen by the operator. For this comparison, the absolute deviation in terms of the temporal distance is computed. If this value does not exceed a certain residual value $k$, both for the start time and the end time of the event, then the cut is deemed correct. This comparison enables the assessment of the quality of the cut and the numerosity of the triggered events (see Section 2.1 for details on the quality and numerosity indices). The combination of the two indices is used to obtain an overall index of the triggered events. A list of triggered events can be generated by varying the combination of the following four parameters: STA window size (in seconds), LTA window size (in seconds), trigger on threshold, and trigger off threshold. From now on, the four parameters will be indicated with the term “quadruple.” A grid search is performed on a quadruple set, by considering the overall index computed on the related triggered events.

2.1 Evaluation measures

The quality index of a cut is designated as $qi$ and numerosity index of a cut as $ni$. These measures were designed to analyse different phenomena represented by time series; in this case, they are used for EQs. The qi measures the degree of greater temporally precise cut performed by the STA/LTA compared to one performed by the human operator. Let $m$ be the mean of all the temporal deviations computed between the STA/LTA cuts and the operator cuts and $k$ be the residual value as threshold in seconds. The qi is defined as follows:

$qi=1-\left(m/k\right).(3)$

$k$ is an arbitrarily defined constant, dependent on the reference dataset. In this case, a constant has been empirically set with a value of 10 (preset value. Reported on the repository published on GitHub, see Section 5), based on the average duration of the events (in this case, EQs). This constant falls within the definition of a finite space of values, which in this case are the local events. Therefore, it can also be included if the reference dataset is composed of local seismic events. If, however, regional, teleseismic, anthropic, and landslide (or other types of) events are also included in the dataset, the parameter changes as the finite space in which these events fall varies. Every time STA/LTA outputs a list of triggers, a check is performed to see whether the start time (also indicated as $t_{on}$, trigger on) and end time (also indicated as $t_{\mathit{off}}$, trigger off) of every trigger are temporally close to the start and end times of the EQs extracted by the expert. When a match is found (correct cut), the absolute value of the temporal distance is calculated either with the two start times and end times being within $k$ or that trigger is not considered, but it is simply taken into account when counting the triggers for the $ni$. If no match is found, the trigger is not considered but is still accounted for when counting triggers for $ni$. Figure 4 shows a representation of this process.

Figure 4

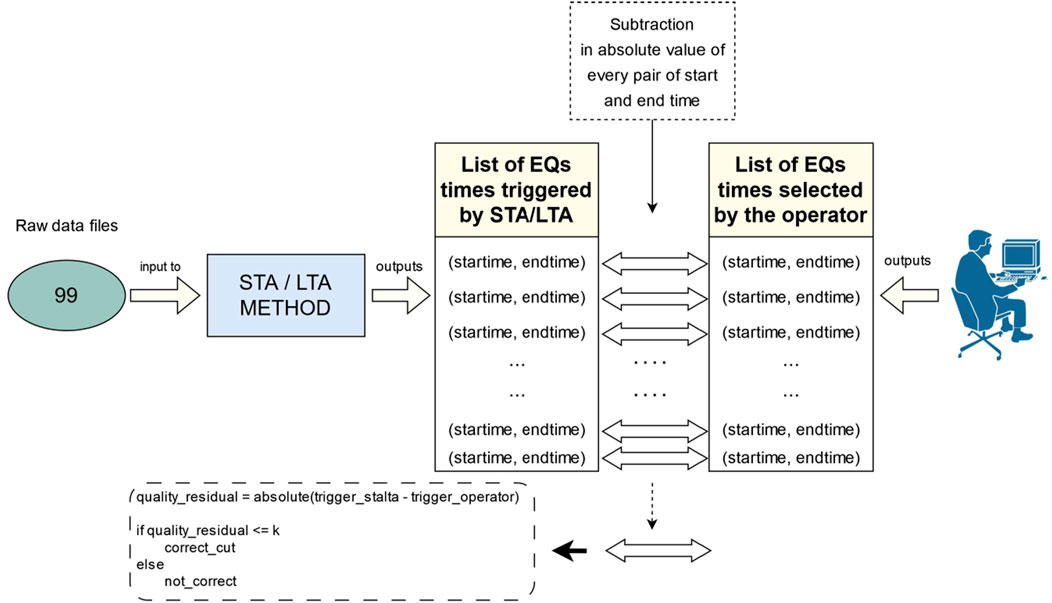
Figure 4. Selection of the trigger’s start time and end time temporally close to the times of the EQs.

All the computed deviations are stored in a list, and the mean deviation $m$ is computed and then normalised by $k$. The $qi$ is finally computed as the complement of the ratio $m/k$ so that it is defined in a range between 0 and 1, where 1 means perfect agreement among the automatic cuts and the expert cuts.

The ni measures the agreement between the number of events triggered by the automatic approach and the number of cuts selected by the human operator.

Let $enq$ be the Experimental EQs, namely, the cardinality of the set of event trigger list produced by the STA/LTA method, and $tnq$ be the Theoretical EQs, i.e., the number of the cuts performed by the human operator. The ni is thus defined:

$ni=\left\{\begin{array}{cc}enq/tnq,\hfill & \text{if\hspace{0.17em}}enq<tnq\hfill \\ \frac{tnq-mod\left(enq,tnq\right)}{tnq},\hfill & \text{if\hspace{0.17em}}tnq\le enq<2\ast tnq\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}\right.(4)$

The $ni$ takes into account the discrepancy between $enq$ and $tnq$. If $enq$ is lower than $tnq$, or $enq$ is between $tnq$ and twice $tnq$, then the $ni$ will result in a number in the range [0, 1]. Otherwise, it is set to 0. This latter case occurs when $enq$ exceeds $tnq$ by at least twice its value, resulting in an $enq$’s value being out of range. The choice of twice the value is justified by limiting the number of false events triggered by STA/LTA with the quadruple considered.

Finally, the combination of the number of events and their temporal precision selected by the automatic process, compared to human experts, makes the QNI the overall measure. This overall measure determines the effectiveness of the cut made by STA/LTA and is defined as follows (Equation 5):

$qni=qi*ni.(5)$

The $qni$ ranges between 0 and 1 and can be converted into percentages. These measures are mainly dependent on the results of the STA/LTA method (based on its few parameters) and the expertise of the operator because of the manual cut. The range of window values from STA and LTA and the threshold values for trigger on and trigger off can be determined based on the type of event one wants to detect and, therefore, cut. For instance, if one wants to detect teleseismic events compared to local ones, a wide range of STA and LTA window values must be set to ensure the expansion of the grid and improve the search for the optimum. In the beginning of Section 3.2, an in-depth analysis was conducted in this regard. On the other hand, Jones and Baan (2015) used an STA/LTA adaptive method based on the hidden Markov model. This method is independent from data, meaning that it requires only minimal configuration by the user. The goal of this methodology is to determine the probability that a term y(t) is an outlier compared to the noise population. The term y(t) corresponds to the CF of a data point from the seismogram x. STA and LTA windows are composed with these probability levels. Thus, by using this model, the objective of this work is to detect and select a seismic event. Even though this method is adaptive, it is necessary to determine values for STA and LTA window length and threshold adjustment in the initial state.

2.2 Grid-search technique

Grid search is a widely used technique in machine learning and algorithm parameter optimisation. It is used to search for the optimal combination of parameters for a model or algorithm while varying multiple parameters simultaneously. In the present case, a grid search enables an exhaustive search of the quadruples that correspond to the optimum QNI values. Figure 5 shows an example of a representative scheme of the search.

Figure 5

Figure 5. Grid-search technique for QNI values.

The grid is composed of STA window sizes represented in rows and LTA window sizes represented in columns. Every cell is also a grid, where in abscissa the $t_{on}$ and in ordinate the $t_{\mathit{off}}$ are shown. QNI values are expressed as a percentage and represented as coloured circles: the darker the colour, the higher the value. We started from a basic grid (grid on the left) with a few quadruples (STA window size (in seconds), LTA window size (in seconds), $t_{on}$, and $t_{\mathit{off}}$) and gradually expanded to a grid (grid on the right) still containing the previous grid. The cardinality of the grid is determined by the variation of the quadruples by one unit based on their order of magnitude. As an increase in the value of QNI is measured, the grid is expanded until the optimum is found. The process is repeated until the QNI values do not improve further and reach a maximum value. To formalise this concept, a recursive exploratory grid-search algorithm is proposed (Algorithm 1). Choosing to use a recursive algorithm is based on experimenting with all the possible combinations of the quadruples (STA, LTA, $t_{on}$, and $t_{\mathit{off}}$) until the best result of QNI is found. As input, the algorithm requires the range of values to construct all possible quadruples ($get\text{\_}combinations$ function), including a $step$ value for each parameter (only one is needed for both trigger thresholds). The $step$ determines the numerical distance between one value and its next value. After all possible combinations of quadruples have been calculated, the value of the QNI is determined for each of them through the $compute$ function; if this value is greater than the previously calculated QNI, then it is classified as the $best\text{\_}qni$ value (the quadruple associated with $best\text{\_}qni$ is also stored). The algorithm ends when the $best\text{\_}qni$ found in lines 5–16 exceeds the threshold value; in this case, the $best\text{\_}quintuple$ list is returned. Otherwise, the algorithm is called recursively by subtracting and adding the $step\text{\_}parameter$ ($step\text{\_}sta$, for instance) associated with the individual parameter quantities. A series of checks are performed for each parameter to verify that the lower bound of each one is respected. The lower bound is determined by the minimum size of the windows used for the detection, which are usually approximately 1 s for STA and 5 s for LTA. The upper bound for STA and LTA is determined for the search for local and regional events. This limit can, however, be varied based on one’s needs (types of events sought) (Küperkoch et al., 2010; Gentili and Michelini, 2006; Earle and Shearer, 1994). If no QNI value exceeds the threshold value, the programme returns the best value of the QNI. In our experiments, 20 iterations were set as thresholds by trial and error.

Algorithm 1. Pseudocode for recursive exploratory grid-search algorithm.

1: procedure grid_search($min\text{\_}sta$, $max\text{\_}sta$, $step\text{\_}sta$,$min\text{\_}lta$, $max\text{\_}lta$, $step\text{\_}lta,min\text{\_}trig\text{\_}on$,$max\text{\_}trig\text{\_}on$, $step\text{\_}trig\text{\_}on$, $min\text{\_}trig\text{\_}off$,$max\text{\_}trig\text{\_}off$, $step\text{\_}trig\text{\_}off$, $num\text{\_}iterations$)

2:  $quadruples\leftarrow \mathit{g}\mathit{e}\mathit{t}\text{\_}\mathit{combinations}$,($min\text{\_}sta,max\text{\_}sta,step\text{\_}sta$,$min\text{\_}lta,max\text{\_}lta,step\text{\_}lta$,$min\text{\_}trig\text{\_}on,max\text{\_}trig\text{\_}on$,$min\text{\_}trig\text{\_}off,max\text{\_}trig\text{\_}off$, $step\text{\_}trig$)

3:  $max\leftarrow 0$

4:  $best\text{\_}quintuple\leftarrow []$

5:  for all $quadruple\in quadruples$ do

6:   $qni\leftarrow \mathit{c}\mathit{o}\mathit{m}\mathit{p}\mathit{u}\mathit{t}\mathit{e}(quadruple)$    QNIcalculation value

7:   if $qni>max$ then

8:      $max\leftarrow qni$

9:      $best\text{\_}sta\leftarrow sta$

10:     $best\text{\_}lta\leftarrow lta$

11:     $best\text{\_}trig\text{\_}on\leftarrow trig\text{\_}on$

12:     $best\text{\_}trig\text{\_}off\leftarrow trig\text{\_}off$

13:     $best\text{\_}qni\leftarrow qni$

14:     $best\text{\_}quintuple\leftarrow$, $best\text{\_}sta,best\text{\_}lta$,$best\text{\_}trig\text{\_}on,best\text{\_}trig\text{\_}off,best\text{\_}qni$

15:   end if

16:  end for

17:  if $best\text{\_}qni>thresholdornum\text{\_}iterations>20$ then    For instance: threshold=80

18:   return $best\text{\_}quintuple$

19:  else

20:   $min\text{\_}sta\leftarrow min\text{\_}sta-step\text{\_}sta$

21:   if $min\text{\_}sta<1$ then

22:    $min\text{\_}sta\leftarrow 1$

23:   end if

24:   $max\text{\_}sta\leftarrow max\text{\_}sta+step\text{\_}sta$

25:   if $max\text{\_}sta>16$ then

26:    $max\text{\_}sta\leftarrow 16$

27:   end if

28:   $min\text{\_}lta\leftarrow min\text{\_}lta-step\text{\_}lta$

29:   if $min\text{\_}lta<5$ then

30:    $min\text{\_}lta\leftarrow 5$

31:   end if

32:   $max\text{\_}lta\leftarrow max\text{\_}lta+step\text{\_}lta$

33:   if $max\text{\_}lta>220$ then

34:    $max\text{\_}lta\leftarrow 220$

35:   end if

36:   $min\text{\_}trig\text{\_}on\leftarrow min\text{\_}trig\text{\_}on-step\text{\_}trig$

37:   if $min\text{\_}trig\text{\_}on<0.5$ then

38:    $min\text{\_}trig\text{\_}on\leftarrow 0.5$

39:   end if

40:   $min\text{\_}trig\text{\_}off\leftarrow min\text{\_}trig\text{\_}off-step\text{\_}trig$

41:   if $min\text{\_}trig\text{\_}off<1$ then

42:    $min\text{\_}trig\text{\_}off\leftarrow 1$

43:   end if

44:   return grid_search($min\text{\_}sta$, $max\text{\_}sta+step\text{\_}sta$,$step\text{\_}sta$, $min\text{\_}lta$, $max\text{\_}lta+step\text{\_}lta$,$step\text{\_}lta$,$min\text{\_}trig\text{\_}on$, $max\text{\_}trig\text{\_}on+step\text{\_}trig$,$min\text{\_}trig\text{\_}off$, $max\text{\_}trig\text{\_}off+step\text{\_}trig$,$step\text{\_}trig$,$num\text{\_}iterations+1$)

45:  end if

46: end procedure

3 Experiments and results

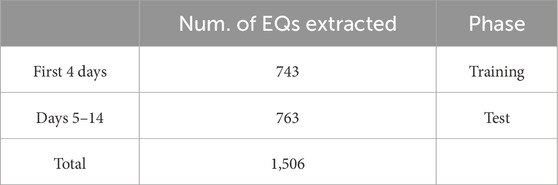
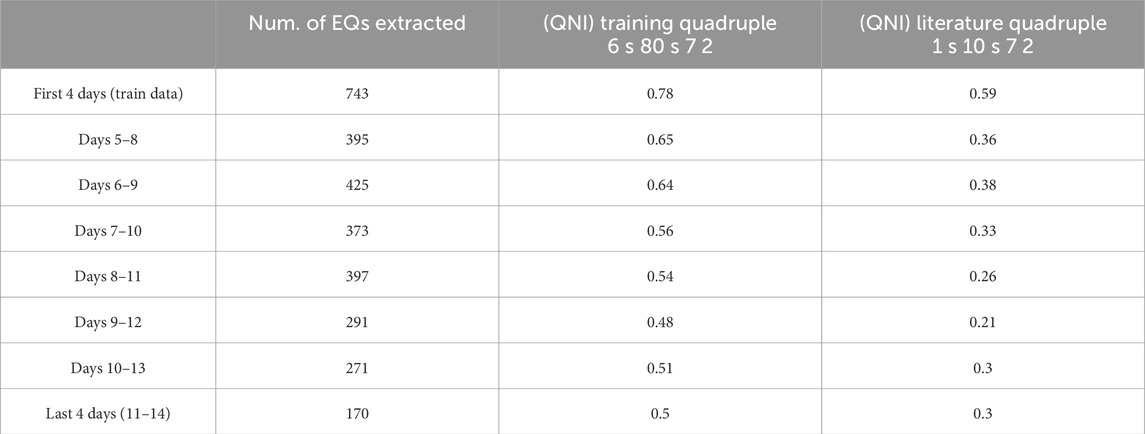
Starting from 14 days of raw data, our recently developed tool was used (D’Alessandro et al., 2022) to extract the EQ dataset thanks to the expertise of our operator. The entire dataset extracted contains 1,506 EQs. The most significant number of EQs are in the first 4 days of July, i.e., 743 EQs. This set was used as a training set. The subdivision of the training and test datasets is described in Table 1.

Table 1

Table 1. Dataset subdivision for training and test.

3.1 Training phase

A large grid was explored to better view the distribution of the QNI values. We found the densest grid in the training phase with the highest QNI values by combining a range of window values of STA and LTA, respectively, from 2 s to 16 s and 20 s to 220 s, in steps of 2 s for STA and 20 s for LTA. The same representation of the parameter values as in Figure 5 was used. For each combination of windows, $t_{on}$ and $t_{\mathit{off}}$ threshold values were combined, respectively, from 1 to 7, in steps of 0.5 for both. Every cell is a $12x12$ matrix. Figure 6 shows a screenshot of the terminal grid (8 × 11) or the result of this experiment. At the beginning, the grid was 5 × 5 and step values for STA and LTA were 2 s and 20 s, respectively. After six iterations, an 8 × 11 grid was obtained, according to the STA, LTA, and lower and upper bounds defined in Algorithm 1.

Figure 6

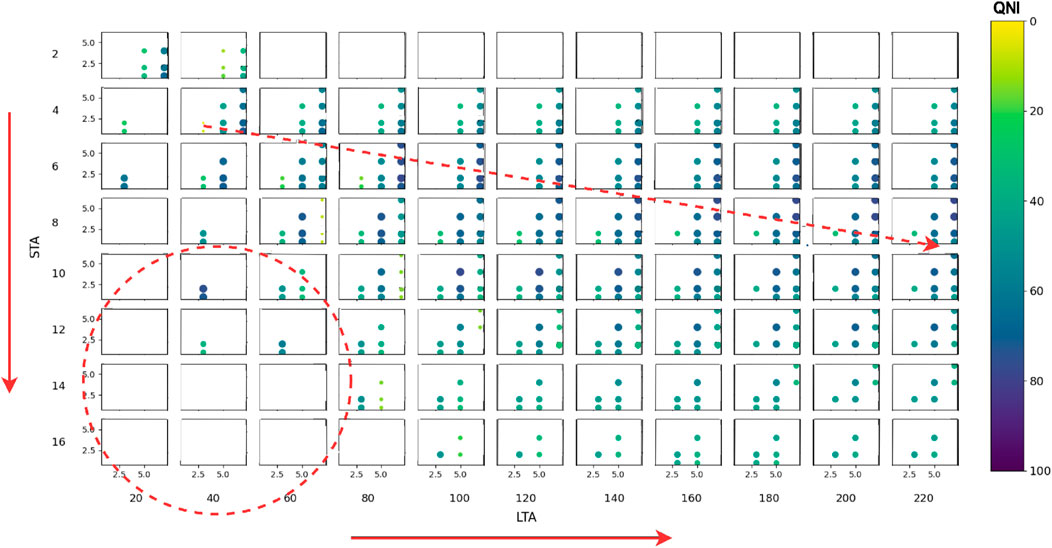
Figure 6. Grid-search exploration for STA windows (rows) and LTA windows (columns), represented by the red rows. Both STA and LTA windows are expressed in seconds. Trigger on/off thresholds, respectively, in abscissa and ordinate, are shown in every cell of the matrix. The red circle shows a region where most of the QNI values are 0. The red dashed line indicates a direction where the QNI values are increasing.

In the lower-left region (highlighted by a red circle), where STA is between 12 s and 16 s and LTA is between 20 s and 60 s, most of the QNI are 0 (no visible circles), and only a few QNI values are approximately 20, which means that this parameter’s combination is not suitable for detecting the EQs efficiently. A dashed red line was outlined to show a direction where the QNI values are increasing. The highest values of QNI are found in the central region from left to right, where STA is between 6 s and 10 s, LTA between 60 s and 220 s, $t_{on}$ between 5 and 7, and $t_{\mathit{off}}$ between 2 and 5. Neither QNI, in the first and last rows of the grid, shows an improvement, while the continuous shift toward the right region shows a saturation of the values. This means that increasing the LTA values does not improve the search for local events.

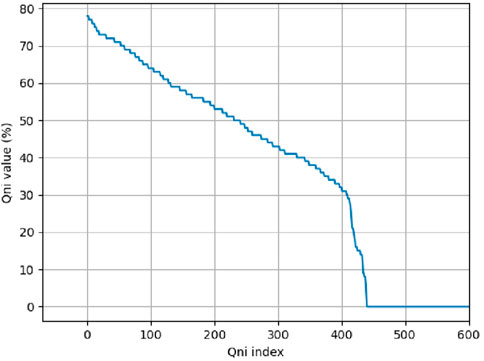
From the training phase, we extracted the list of the QNI values in descending order and generated a plot, shown in Figure 7. An index identifying the value of the QNI is indicated on the abscissa, while the value of the QNI is indicated on the ordinate. The QNI decreases with a moderate slope up to the value 30 and then rapidly decreases to 0. As a consequence, we decided to extract the quadruple associated with the highest QNI value to carry out the test phase, i.e., the one with value 0.78 resulting from the quadruple: 6, 80, 7, and 2. As can be seen, the quadruple is positioned exactly in the distribution indicated by the dashed red line in Figure 6. The selected $t_{on}$ and $t_{\mathit{off}}$ define a good balance between the quality index and numerosity index (see Equations 3, 4) of the detected EQs. This is because a lower $t_{on}$ than 7 can increase the number of false positives, and higher $t_{\mathit{off}}$ can worsen the time’s precision of the extraction.

Figure 7

Figure 7. QNI value distribution.

3.2 Testing phase

The common approach to the selection of the STA/LTA values is the adoption of literature-suggested ones. Specifically, these values are STA 1 s and LTA 10 s. Regarding the $t_{on}$ and $t_{\mathit{off}}$ values, they were set at 7 and 2, respectively, such as the ones found through the training phase. The QNI computed is indicated using these values as the literature quadruple. The test results are shown in Table 2. In particular, every row corresponds to a range of days in which a certain number of EQs have occurred. This number is indicated in the “Num. EQs extracted” column; in the other columns, the QNI values are reported after an experiment with the associated days was performed with the corresponding quadruples: training quadruple (third column, our quadruple) and literature quadruple (fourth column, quadruple extracted from the literature). An overlap of the days for testing purposes was carried out. In the first row, the testing result is shown using the same dataset used in the training phase. This first comparison was made to show our result compared to the use of the literature quadruple.

Table 2

Table 2. Testing results.

4 Discussion

The literature has shown that there is no one single strategy to search the STA and LTA moving windows to select events based on triggers (Earle and Shearer, 1994). The lengths for the STA and LTA windows depend on the frequency content of the seismogram. Long-period records require larger averaging windows than short-period records, which require shorter averaging windows. Among different approaches, we have chosen the work by Küperkoch et al. (2010) as the base case comparison owing to the completeness of this work, focussing on P-phase arrival time, where several CFs for STA/LTA were used to compare their method. They have implemented an algorithm based on higher-order statistics (HOS) for automatic P-phase arrival time determination for local and regional seismic events. The algorithm was applied to a large dataset with very heterogeneous qualities of P-onsets. They calculated several CFs by evaluating higher-order statistical moments, like skewness, kurtosis, mean, and variance. In our case, we decided to use the CF reported in Equation 1, which is the base case determined by Allen (1978). When choosing a “literature quadruple,” there is no clear standard choice for the types of events analysed, yet Küperkoch et al. (2010) values can provide a useful comparison. The results presented in the previous paragraph indicate that, as we move further away from the training set, the QNI appears to vary over time. This is due to the rapid evolution of the volcanological phenomenon, and therefore the EQs generated by it. As is well known (Andronico et al., 2021), the duration, amplitude, and frequency content of the EQs can vary rapidly as the volcanic process evolves. The results show that on average, our training quadruple produced a QNI 0.24 higher than the literature quadruple. Another strength of our approach is the tuning of the evaluation measures: for instance, $qi$ is one of the measures that can be adapted based on the data and objectives one wants to obtain; in this case (where we look for EQs in the raw data), we use the mean of the deviations to evaluate the quality of the cut, but one can consider using different evaluations such as median, mode, or kurtosis. This possibility can lead to extending the research to the general volcano domain and also in the seismic domain in tectonic areas.

Certainly, the main limitation of our study is the low cardinality of the dataset. Based on the time-consuming process of extracting the seismo-volcanic events from real raw data, future improvements will mainly concern the variability of the dataset; extending not only to other types of seismo-volcanic events, such as the following: VLP, landslides, volcanic tremors, and others (Wassermann, 2012), but also to local, regional, and teleseismic events. To achieve this, we aim to replace the human operator by automating the validation process through the use of multiple seismic stations recording the same signal within the same area. This approach replicates the current method used by operators but will be enhanced by deploying seismic stations positioned at approximately equal distances around the crater (Fenner et al., 2022), ensuring more uniform coverage and reducing potential sources of error. Another limitation is specific to the grid-search technique. In general, grid search is a powerful technique for optimising algorithm parameters, but it ought to be used judiciously as it may be time-consuming when there are many parameter combinations to evaluate. Other techniques such as random search or Bayesian optimisation may be more efficient alternatives in some cases. The choice depends on the specific problem domain and available resources. Stromboli remains a case study, but the method is applicable to any type of seismo-volcanic signal and can therefore be used on other volcanoes as well. For instance, it is also suitable for earthquakes in non-volcanic areas.

5 Conclusion and future improvements

In this scientific study, we have explored the potential of using a grid-search method to study the STA/LTA parameters to select seismo-volcanic events, starting from raw signals, with a particular focus on the volcanic activity of Stromboli. Through this application, we have proved the ability to efficiently detect local events, such as explosion quakes. The results showed a more accurate choice of parameters, compared to what was proposed in the literature (Küperkoch et al., 2010), for searching local events, such as EQs. As a first example for the approach, we exploited the constant presence of EQs before the occurrence of the double paroxysms of Stromboli volcano (Andronico et al., 2021).

With this method, one can collect seismo-volcanic events that can be used from the machine learning perspective, such as classification or regression problems, where a certain amount of data is needed for the dataset (Zhu and Beroza, 2018; Mousavi et al., 2020). We decided to use, among possible characteristic functions for STA/LTA, the classic one by Allen (1978) as the first approach. It is also possible to test other CFs as Küperkoch et al. (2010) did for their method. To compare our quadruple, we referred to the work by Küperkoch et al. (2010) to find the baseline quadruple in the literature for the detection of local events (classifying the explosion quakes as local events).

In summary, the integration of our approach is a compelling way to simplify the acquisition of labelled data in seismic–volcanic and more generally of seismic research. By synergising active learning (D’Alessandro et al., 2022) with robust deep learning algorithms and a large dataset, a path towards greater accuracy, effectiveness, and a comprehensive analysis of seismic–volcanic phenomena can be achieved.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository and accession number(s) can be found at: https://github.com/Andry92/grid-search-sta-lta.

Author contributions

ADB: conceptualization, data curation, formal analysis, investigation, methodology, project administration, software, supervision, validation, visualization, writing–original draft, and writing–review and editing. AF: data curation, formal analysis, investigation, resources, software, writing–original draft, and writing–review and editing. AD’A: conceptualization, formal analysis, investigation, methodology, supervision, validation, visualization, writing–original draft, and writing–review and editing. GLB: conceptualization, formal analysis, investigation, methodology, software, supervision, validation, visualization, writing–original draft, and writing–review and editing.

Funding

The authors declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The authors would like to acknowledge Dario Delle Donne from Istituto Nazionale di Geofisica e Vulcanologica—Osservatorio Vesuviano (INGV-OV), for helping us to extract the data from STRA seismic station.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aiuppa, A., Bertagnini, A., Métrich, N., Moretti, R., Di Muro, A., Liuzzo, M., et al. (2010). A model of degassing for stromboli volcano. Earth Planet. Sci. Lett. 295, 195–204. doi:10.1016/j.epsl.2010.03.040

CrossRef Full Text | Google Scholar

Allen, R. V. (1978). Automatic earthquake recognition and timing from single traces. Bull. Seismol. Soc. Am. 68, 1521–1532. doi:10.1785/BSSA0680051521

CrossRef Full Text | Google Scholar

Andronico, D., Del Bello, E., D’Oriano, C., Landi, P., Pardini, F., Scarlato, P., et al. (2021). Uncovering the eruptive patterns of the 2019 double paroxysm eruption crisis of stromboli volcano. Nat. Commun. 12, 4213. doi:10.1038/s41467-021-24420-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Beyreuther, M., Barsch, R., Krischer, L., Megies, T., Behr, Y., and Wassermann, J. (2010). ObsPy: a Python toolbox for seismology. Seismol. Res. Lett. 81, 530–533. doi:10.1785/gssrl.81.3.530

CrossRef Full Text | Google Scholar

Calvari, S., Giudicepietro, F., Di Traglia, F., Bonaccorso, A., Macedonio, G., and Casagli, N. (2021). Variable magnitude and intensity of strombolian explosions: focus on the eruptive processes for a first classification scheme for stromboli volcano (Italy). Remote Sens. 13, 944. doi:10.3390/rs13050944

CrossRef Full Text | Google Scholar

Cannioto, M., D’Alessandro, A., Lo Bosco, G., Scudero, S., and Vitale, G. (2017). Brief communication: vehicle routing problem and uav application in the post-earthquake scenario. Nat. Hazards Earth Syst. Sci. 17, 1939–1946. doi:10.5194/nhess-17-1939-2017

CrossRef Full Text | Google Scholar

Chouet, B. (1996). Long-period volcano seismicity: its source and use in eruption forecasting. Nature 380, 309–316. doi:10.1038/380309a0

CrossRef Full Text | Google Scholar

Chouet, B., Dawson, P., Ohminato, T., Martini, M., Saccorotti, G., Giudicepietro, F., et al. (2003). Source mechanisms of explosions at stromboli volcano, Italy, determined from moment-tensor inversions of very-long-period data. J. Geophys. Res. Solid Earth 108. doi:10.1029/2002jb001919

CrossRef Full Text | Google Scholar

D’Alessandro, A., Di Benedetto, A., Lo Bosco, G., and Figlioli, A. (2022). “An active learning approach for classifying explosion quakes,” in 2022 IEEE International Conference on Evolving and Adaptive Intelligent Systems (EAIS), Larnaca, Cyprus, May 25–26, 2022 (IEEE), 1–6. doi:10.1109/EAIS51927.2022.978751910

CrossRef Full Text | Google Scholar

Earle, P. S., and Shearer, P. M. (1994). Characterization of global seismograms using an automatic-picking algorithm. Bull. Seismol. Soc. Am. 84, 366–376. doi:10.1785/BSSA0840020366

CrossRef Full Text | Google Scholar

Fenner, D., Rümpker, G., Li, W., Chakraborty, M., Faber, J., Köhler, J., et al. (2022). Automated seismo-volcanic event detection applied to stromboli (Italy). Front. Earth Sci. 10. doi:10.3389/feart.2022.809037

CrossRef Full Text | Google Scholar

Gentili, S., and Michelini, A. (2006). Automatic picking of P and S phases using a neural tree. J. Seismol. 10, 39–63. doi:10.1007/s10950-006-2296-6

CrossRef Full Text | Google Scholar

Giudicepietro, F., Calvari, S., Alparone, S., Bianco, F., Bonaccorso, A., Bruno, V., et al. (2019). Integration of ground-based remote-sensing and in situ multidisciplinary monitoring data to analyze the eruptive activity of stromboli volcano in 2017–2018. Remote Sens. 11, 1813. doi:10.3390/rs11151813rs11151813

CrossRef Full Text | Google Scholar

Giudicepietro, F., López, C., Macedonio, G., Alparone, S., Bianco, F., Calvari, S., et al. (2020). Geophysical precursors of the July-August 2019 paroxysmal eruptive phase and their implications for Stromboli volcano (Italy) monitoring. Sci. Rep. 10, 10296. doi:10.1038/s41598-020-67220-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Hagerty, M., Schwartz, S., Garcés, M., and Protti, M. (2000). Analysis of seismic and acoustic observations at arenal volcano, Costa Rica, 1995–1997. J. Volcanol. Geotherm. Res. 101, 27–65. doi:10.1016/s0377-0273(00)00162-11016/S0377-0273(00)00162-1

CrossRef Full Text | Google Scholar

Hammer, C., Beyreuther, M., and Ohrnberger, M. (2012). A seismic-event spotting system for volcano fast-response systems. Bull. Seismol. Soc. Am. 102, 948–960. doi:10.1785/0120110167

CrossRef Full Text | Google Scholar

Harris, A., and Ripepe, M. (2007). Synergy of multiple geophysical approaches to unravel explosive eruption conduit and source dynamics – a case study from Stromboli. Chem. Erode - Geochem. 67, 1–35. doi:10.1016/j.chemer.2007.01.0032007.01.003

CrossRef Full Text | Google Scholar

Jones, J., and Baan, M. (2015). Adaptive sta–lta with outlier statistics. Bull. Seismol. Soc. Am. 105, 1606–1618. doi:10.1785/0120140203

CrossRef Full Text | Google Scholar

Journeau, C., Shapiro, N., Seydoux, L., Soubestre, J., Ferrazzini, v., and Peltier, A. (2020). Detection, classification, and location of seismovolcanic signals with multi-component seismic data, example from the piton de la fournaise volcano (la reunion, france). doi:10.1002/essoar.10501605.2

CrossRef Full Text | Google Scholar

Konstantinou, K. (2023). A review of the source characteristics and physical mechanisms of very long period (vlp) seismic signals at active volcanoes. Surv. Geophys. 45, 117–149. doi:10.1007/s10712-023-09800-0

CrossRef Full Text | Google Scholar

Küperkoch, L., Meier, T., Lee, J., Friederich, W., and Group, E. (2010). Automated determination of p-phase arrival times at regional and local distances using higher order statistics. Geophys. J. Int. 181, 1159–1170. doi:10.1111/j.1365-246X.2010.04570.x

CrossRef Full Text | Google Scholar

Lara, F., Lara-Cueva, R., Larco, J., Carrera, E., and Leon, R. (2020). A deep learning approach for automatic recognition of seismo-volcanic events at the Cotopaxi volcano. J. Volcanol. Geotherm. Res. 409, 107142. doi:10.1016/j.jvolgeores.2020.1071421016/j.jvolgeores.2020.107142

CrossRef Full Text | Google Scholar

Legrand, D., and Perton, M. (2021). What are vlp signals at stromboli volcano? J. Volcanol. Geotherm. Res. 421, 107438. doi:10.1016/j.jvolgeores.2021.107438

CrossRef Full Text | Google Scholar

Liang, C., Karlstrom, L., and Dunham, E. (2020). Magma oscillations in a conduit-reservoir system, application to very long period (vlp) seismicity at basaltic volcanoes: 1. theory. J. Geophys. Res. Solid Earth 125. doi:10.1029/2019JB017437

CrossRef Full Text | Google Scholar

Makus, P., Denolle, M., Sens-Schönfelder, C., Kopfli, M., and Tilmann, F. (2024). Analyzing volcanic, tectonic, and environmental influences on the seismic velocity from 25 years of data at Mount St. Helens. Seismol. Res. Lett. 95, 2674–2688. doi:10.1785/0220240088

CrossRef Full Text | Google Scholar

Mattia, M., Aloisi, M., Di Grazia, G., Gambino, S., Palano, M., and Bruno, V. (2008). Geophysical investigations of the plumbing system of Stromboli volcano (Aeolian islands, Italy). J. Volcanol. Geotherm. Res. 176, 529–540. doi:10.1016/j.jvolgeores.2008.04.022

CrossRef Full Text | Google Scholar

Metrich, N., Bertagnini, A., and Pistolesi, M. (2021). Paroxysms at Stromboli volcano (Italy): source, genesis and dynamics. Front. Earth Sci. 9, 593339. doi:10.3389/feart.2021.593339feart.2021.593339

CrossRef Full Text | Google Scholar

Mousavi, S., Ellsworth, W., Weiqiang, Z., Chuang, L., and Beroza, G. (2020). Earthquake transformer—an attentive deep-learning model for simultaneous earthquake detection and phase picking. Nat. Commun. 11, 3952. doi:10.1038/s41467-020-17591-w1038/s41467-020-17591-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Petrone, C., Mollo, S., Gertisser, R., Buret, Y., Scarlato, P., Del Bello, E., et al. (2022). Magma recharge and mush rejuvenation drive paroxysmal activity at Stromboli volcano. Nat. Commun. 13, 7717. doi:10.1038/s41467-022-35405-z

PubMed Abstract | CrossRef Full Text | Google Scholar

QGIS Development Team (2024). Qgis geographic information system

Google Scholar

Ripepe, M., Delle Donne, D., Legrand, D., Valade, S., and Lacanna, G. (2021a). Magma pressure discharge induces very long period seismicity. Sci. Rep. 11, 20065. doi:10.1038/s41598-021-99513-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Ripepe, M., and Harris, A. (2008). Dynamics of the 5 April 2003 explosive paroxysm observed at stromboli by a near-vent thermal, seismic and infrasonic array. Geophys. Res. Lett. 35. doi:10.1029/2007gl0325332007GL032533

CrossRef Full Text | Google Scholar

Ripepe, M., Lacanna, G., Pistolesi, M., Silengo, M., Aiuppa, A., Laiolo, M., et al. (2021b). Ground deformation reveals the scale-invariant conduit dynamics driving explosive basaltic eruptions. Nat. Commun. 12, 1683. doi:10.1038/s41467-021-21722-2s41467-021-21722-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Ripepe, M., Pistolesi, M., Coppola, D., Delle Donne, D., Genco, R., Lacanna, G., et al. (2017). Forecasting effusive dynamics and decompression rates by magmastatic model at open-vent volcanoes. Sci. Rep. 7, 3885. doi:10.1038/s41598-017-03833-3s41598-017-03833-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Ross, Z. E., Meier, M., Hauksson, E., and Heaton, T. H. (2018). Generalized seismic phase detection with deep learning. Bull. Seismol. Soc. Am. 108, 2894–2901. doi:10.1785/0120180080

CrossRef Full Text | Google Scholar

Schaefer, L. N., Di Traglia, F., Chaussard, E., Lu, Z., Nolesini, T., and Casagli, N. (2019). Monitoring volcano slope instability with synthetic aperture radar: a review and new data from Pacaya (Guatemala) and Stromboli (Italy) volcanoes. Earth-Science Rev. 192, 236–257. doi:10.1016/j.earscirev.2019.03.009

CrossRef Full Text | Google Scholar

Sosa, Y. M., Molina, R. S., Spagnotto, S., Melchor, I., Nuñez Manquez, A., Crespo, M. L., et al. (2024). Seismic event detection in the copahue volcano based on machine learning: towards an on-the-edge implementation. Electronics 13, 622. doi:10.3390/electronics13030622

CrossRef Full Text | Google Scholar

Soubestre, J., Shapiro, N., Seydoux, L., de Rosny, J., Droznin, D., Droznina, S., et al. (2018). Network-based detection and classification of seismovolcanic tremors: example from the klyuchevskoy volcanic group in kamchatka. J. Geophys. Res. Solid Earth 123, 564–582. doi:10.1002/2017JB014726

CrossRef Full Text | Google Scholar

Wassermann, J. (2012). Volcano seismology, IASPEI new manual of seismological observatory practice 2 (NMSOP-2). Potsdam: Deutsches GeoForschungsZentrum GFZ, 1–77.

Google Scholar

Withers, M., Aster, R., and Young, C. (1999). An automated local and regional seismic event detection and location system using waveform correlation. Bull. Seismol. Soc. Am. 89, 657–669. doi:10.1785/bssa0890030657BSSA0890030657

CrossRef Full Text | Google Scholar

Zhu, W., and Beroza, G. C. (2018). PhaseNet: a deep-neural-network-based seismic arrival-time picking method. Geophys. J. Int. 216, 261–273. doi:10.1093/gji/ggy423

CrossRef Full Text | Google Scholar