Permeability evolution of fractured coal subject to confining stress and true triaxial stress loading: experiment and mathematical model

The accurate elucidation and prediction of coal permeability evolution under stress loading conditions are crucial for coalbed methane production. In this study, flow experiments were conducted on six cylindrical coal samples and four cubic coal samples under both confining and true triaxial stress loading conditions, respectively. The structure and characteristic parameters of the fractures inside each coal sample were obtained using the computed tomography scanning system and image processing technologies. The coal permeability under both types of loading processes was calculated through the transient pulse method. A mathematical model was developed to assess the evolution of coal permeability under true triaxial loading based on the current true triaxial permeability model and fractal theory. The results revealed that during the confining pressure loading, the coal permeability decreased exponentially with effective stress and was effectively described using the SD model. Additionally, the coal permeability initially rapidly decreased, followed by a gradual decrease, and eventually stabilized at a constant value. Particularly, during the first three loading steps, the fracture aperture and corresponding permeability of the six cylindrical coal samples decreased by ∼51.79%–57.83% and ∼38.06%–42.12%, respectively. However, during the final three loading steps, the fracture aperture and corresponding permeability of the six coal samples decreased by ∼18.26%–23.08% and ∼22.15%–26.93%, respectively. Moreover, owing to the various crossing angles of complex fracture networks with each principal stress, the effect of each principal stress on the coal permeability evolution was highly anisotropic during triaxial stress loading. Particularly, the permeability of the ST1 sample decreased by 43.08%, 14.84%, and 42.08% during the loading of each principal stress. Similarly, the permeability of the ST2 sample decreased by ∼65.74%, 14.29%, and 19.97%. The permeability reductions for the ST3 sample were ∼34.03%, 55.85%, and 10.12%, while those for the ST4 sample were ∼35.97%, 46.51%, and 17.52%. The SD model failed to describe these anisotropic effects. Compared with the SD model, the improved model, based on the current true triaxial permeability model and fractal theory, effectively described the anisotropic effect of each principal stress on the permeability of coal samples with complex fracture networks under triaxial stress conditions.

1 Introduction

In recent years, coalbed methane (CBM), a clean energy source, has gained significant global attention (Wu et al., 2017; Zhou et al., 2021; Li et al., 2022). The development of CBM can effectively alleviate energy crises and improve mining conditions. The accurate elucidation and prediction of coal permeability evolutions during the extraction process are crucial for determining CBM production rates, optimizing extraction methods, and mitigating environmental impacts associated with CBM production.

Compared with conventional gas reservoirs, coal typically exhibits dual-porosity characteristics with complex and heterogeneous pores and fractures. These features contribute to the significantly more complex geomechanical responses observed in CBM reservoirs (Thararoop et al., 2012; Chen et al., 2014). In the dual-porosity structure of coal, the pores mainly serve as storage media and have a weak capacity for flow. The flow and exchange of methane mainly occur within the fracture network of coal, making it the primary determinant of coal permeability. Additionally, the fracture structure of coal is prone to alteration under stress, leading to stress-sensitive permeability of coal (Wang, et al., 2022; Li et al., 2023; 2024). Therefore, elucidating and predicting the evolution of coal permeability under stress is crucial for the efficient extraction of CBM (Xu et al., 2016; Du et al., 2022).

Numerous researchers have conducted various experimental and theoretical studies to explore the evolution of coal permeability under stress. For example, Meng et al. (2015) conducted experiments to measure the porosity and permeability of anthracite coal under different confining stresses and investigate the correlations between porosity, permeability, and effective stress. The results revealed that both the porosity and permeability of the coal decreased exponentially with increasing effective stress. Additionally, Xue et al. (2017) conducted a series of gas-permeability tests to investigate the evolution of coal permeability under different loading and unloading confining stress paths. The results indicated that coal permeability decreased with increasing confining stress, and the reduction rate was higher for coal samples with higher initial permeability. Moreover, with increasing axial strain, the coal permeability first decreased and then rapidly increased. Furthermore, Shi et al. (2018) conducted flow experiments on coal samples under both constant confining stress and effective stress conditions, respectively. Additionally, a mathematical model was developed to describe the observed permeability evolution of coal under stress loading. The results revealed that permeability in both constant confining and constant effective stress tests was primarily determined by the fracture structure. Moreover, Chao et al. (2019) investigated the permeability evolution of coal fracture under different axial stress conditions, temperature, moisture content, and pore stresses using a self-designed experimental device. The results revealed that both permeability and porosity are negative exponential functions of axial stress. Wang et al. (2019) conducted permeability measurement tests for coal samples under varying confining stress, axial stress, and gas stress conditions to examine the effect of cleat and bedding structures on coal permeability. The results revealed that the presence of cleat and bedding structures within the coal samples led to anisotropic permeability. Du et al. (2021) performed laboratory experiments to investigate the evolution of porosity–permeability in confined coal during the relief of axial and confining stresses. The results indicated that the application and removal of stress significantly affected the inter-particle stress, porosity, and permeability of confined coal. Yang et al. (2021) experimentally investigated the permeability and damage characteristics of raw coal under tiered cyclic loading and unloading confining stresses. The results revealed that the coal permeability decreased with increasing confining stress and numbers of loading and unloading cycles. Zhao et al. (2021) used laboratory experiments and numerical modeling to examine the evolution of coal permeability under different confining stress and gas stress. The results indicated that the coal permeability decreased with increasing gas stress, while the effective stress remained constant. Li et al. (2021) conducted gas seepage experiments under triaxial loading to investigate the combined effects of confining and axial stresses, moisture content, and gas stress on the evolution of coal permeability. The results revealed that the effect of confining stress on the permeability of gas-containing coal samples was more significant compared with axial stress. Xiao et al. (2021) developed a modified permeability model and conducted permeability tests under different confining stresses to systematically evaluate the anisotropic evolution of the stress sensitivity for permeability. The results revealed that the natural fracture system of coal exhibited complex heterogeneity, leading to varying compressibility of the fractures in various directions and significant anisotropic permeability.

These studies have focused on investigating the evolution of the pore-fracture structure and the associated flow and mechanical behavior of coal under confining stress loading. Although these studies have provided valuable insights into enhancing the efficient and sustainable extraction of CBM, they have not addressed the complex geological conditions in underground coal mines. The data from coal production and laboratory experiments indicated that the underground coal was subjected to in situ true triaxial stress conditions, which significantly influenced the behavior and properties of flow and mechanics in coal (Chen et al., 2018; Liu et al., 2019a). However, to date, reports on the permeability evolution of coal rock under true triaxial stress loading are relatively few. Relevant research has mainly focused on experimental measurements, and theoretical mathematic models for describing permeability evolution are also rare. For example, Liu et al. (2018) conducted a series of permeability measurements on cubic coal samples with anisotropic flow channels under true triaxial stress loading and investigated the permeability evolution during the loading. The results revealed that anisotropic permeability data measured under true triaxial loading were well represented by an exponential equation containing different mean cleat compressibility and stress terms. Liu et al. (2019b) investigated the directional permeability evolution of intact and fractured coal during triaxial and true triaxial loading under both dry and water-saturated conditions. The results indicated that the fractured coal exhibited significantly higher permeability anisotropy than the unfractured coal, and permeability reduction was more significant in the direction perpendicular to the maximum principal stress. Therefore, further research is still required to investigate the effect of stress on the flow behavior of fluids during true triaxial loading and associated underlying mechanisms.

In this study, flow experiments were conducted on six cylindrical coal samples with single fractures and four cubic coal samples with complex fracture networks under both confining stress and true triaxial stress loading conditions, respectively. The interior fracture structure of the coal samples was detected using the CT scanning system. Regarding the collected CT images, the characteristic parameters of fracture were obtained through image processing and analysis technology. Moreover, the evolution of coal permeability under the two types of loading processes was calculated through the transient pulse method. Additionally, a mathematical model was developed based on fractal theory to assess the evolution of coal permeability under true triaxial stress loading. Finally, the accuracy and applicability of the developed mathematical model were confirmed through comparison with the experimental results and an SD model.

2 Materials and methods

2.1 Materials

Flow experiments were conducted on six cylindrical coal samples with single fractures and four cubic coal samples with complex fracture networks under both confining and true triaxial stress loading conditions, respectively. These samples were obtained from the Xichenzhuang coal mine in Jincheng City, Shanxi Province, China. The results of the industrial analysis for the coal samples are shown in Table 1. The mineralogical compositions of the coal sample were detected via X-ray diffraction (D8 Advance, State Key Laboratory of Coal Mine Disaster Dynamics and Control, Chongqing University). The results revealed that the selected coal samples mainly consisted of 64.96% kaolinite, 16.22% illite, 9.11% quartz, 5.71% dolomite, and 4% pyrite and calcite. Additionally, the selected coal sample exhibited a density of 1.31 g/cm³.

Table 1

Table 1. The results of industrial analysis for the given samples.

All cylindrical coal samples were cut from a single coal block without macro fractures and had a volume of π × 25 × 25 × 50 mm³. Moreover, all cubic coal samples were cut from the same coal block and had a volume of 50 × 50 × 100 mm³ (Figure 1). The Brazilian split method was used to generate single fractures in all cylindrical coal samples. The surfaces of all samples were carefully polished to minimize the surface roughness (<0.01 mm), which helps to reduce the end effects. Furthermore, all samples were dried for 24 h at 78°C to prevent any residual liquid from influencing the flow experiments.

Figure 1

Figure 1. The selected cylindrical and cubic coal samples, in which the single fracture in all cylindrical coal samples is generated by the Brazilian split method.

2.2 Experimental apparatus and procedures

The flow experiments were conducted using the experimental system (RTX-3000, GCTS Company, the USA) for high-temperature and high-stress rock mechanics under both confining and true triaxial stress loading conditions (Figure 2). The system was mainly used to assess the mechanical properties and flow characteristics of rock, concrete, and coal under complex stress conditions. The testing system exhibited a maximum axial stress capacity of 3000 kN, a maximum horizontal stress capacity of 200 MPa, a maximum confining stress capacity of 200 MPa, a maximum pore fluid pressure of 200 MPa, and a maximum temperature of 200°C. Further details about the experimental apparatus are available in other sources (Peng et al., 2019; 2020).

Figure 2

Figure 2. RTX-3000 experimental system of high-temperature and high-stress rock mechanics. Note that the yellow, red, and blue arrows represent the loading directions of the three principal stresses of σ₁, σ₂, and σ₃ during the true triaxial flow experiments.

Before the flow test, the surfaces of both cubic and cylindrical coal samples were uniformly coated with silicone rubber and then wrapped with heat shrink tubing. Subsequently, the coal sample was installed into the loading cell, and the silicone oil was injected into the loading cell. Afterward, the initial stress condition was sequentially loaded onto the coal samples. For flow experiments conducted under true triaxial stress loading, the initial values for the three principal stresses (σ₁, σ₂, and σ₃) and confining stress (σ_c) were set at 9, 6, 8, and 4 MPa, respectively. For flow experiments conducted under confining stress loading, the initial confining stress (σ_c) was set at 1.5 MPa. Finally, the flow experiments conducted under different stress conditions were conducted, and the loading paths of confining stress and true triaxial stress are shown in Figures 3A, B, respectively. During all flow experiments, the pore pressure was carefully maintained at a level lower than the confining stress to prevent the leakage of N₂ from the contact area between the coal sample and heat shrink tubing.

Figure 3

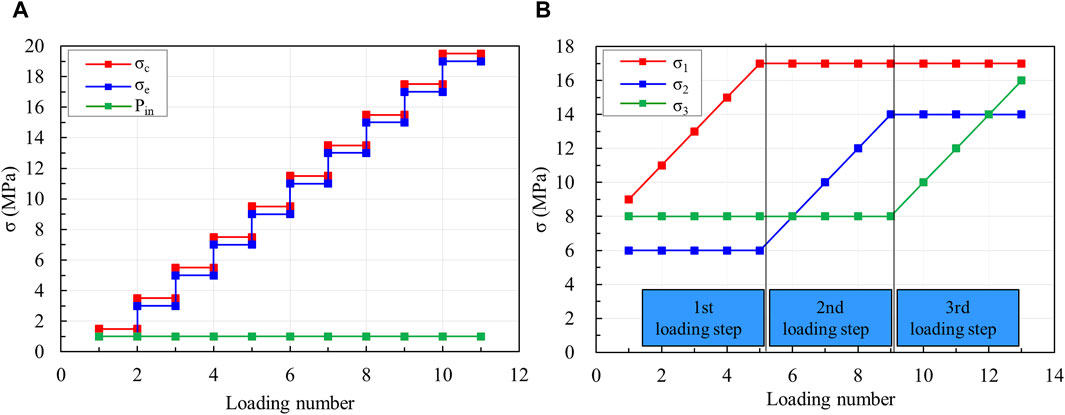
Figure 3. Stress loading path. (A) The loading path for confining stress, (B) the loading path for true triaxial stress.

The detailed experimental steps for confining stress loading are as follows: 1) N₂ was injected into the coal sample until the pressure at both the inlet and outlet of the experimental setup reached 1 MPa. 2) The outlet valve was opened to reduce the pressure at the outlet to 0 MPa. Subsequently, the outlet valve was closed to allow N₂ flow through the coal sample, and the change in the pressure difference between the inlet and outlet of the apparatus was recorded under the initial stress condition. 3) The confining stress was increased (Figure 3A), and steps a) and b) were repeated to record the change in pressure difference between the inlet and outlet under different stress conditions.

The detailed experimental steps for true triaxial loading are as follows: 1) To explore the influence of principal stress σ₁ on the permeability of the coal samples, a) N₂ was injected into the coal sample until the pressure at both the inlet and outlet of the experimental setup reached 3 MPa. b) The flow experiment was conducted, and the change in pressure difference between the inlet and outlet was recorded under the initial stress condition before achieving equilibrium. c) The σ₂ and σ₃ values were set at 6 and 8 MPa, respectively. The σ₁ was then gradually increased in intervals of 2–17 MPa, and steps a) and b) were repeated for each increment. 2) To explore the influence of principal stress σ₂ on the permeability of fractured coal samples, a) σ₁ and σ₃ were maintained at 17 and 8 MPa, respectively. b) σ₂ was gradually increased in intervals of 2–14 MPa. The flow experiment was conducted, and the change in the pressure difference between the inlet and outlet of the experimental setup was recorded under each stress condition. 3) To explore the influence of principal stress σ₃ on the permeability of fractured coal samples, a) σ₁ and σ₂ were maintained at 17 and 14 MPa, respectively. b) σ₃ was increased in an interval of 2–16 MPa. The flow experiment was conducted, and the change in the pressure difference between the inlet and outlet of the experimental setup was recorded under each stress condition.

In the experiment, the flow was assumed to be isothermal and adhered to Darcy’s law. The transient pulse method was used to measure the coal permeability under different loading conditions. The coal permeability was calculated based on the pressure difference between the inlet and outlet of the experimental setup under a specific stress condition, as Eq. 1 (Lin and Kovscek, 2014; Zhou et al., 2020).

$k=\mu \varsigma V\ln \left(\Delta P_i/\Delta P_f\right)/\left(2\Delta tA/L\right)(1)$

where k represents the permeability of the coal sample, μ denotes the viscosity of N₂, ϛ indicates the volume compressibility of N₂, and V signifies the reference volume (0.0025 m³). ΔP_i and ΔP_f represent the initial and final pressure differences between the inlet and outlet, respectively. Δt denotes the duration of the N₂ flow, A indicates the crossing area of the coal sample (0.025 m²), and L denotes the length of the coal sample (0.1 m).

2.3 Fracture structure characteristics

The internal images of all coal samples were obtained using the medical X-ray computerized tomography scanning system (SOMATOM Scope). The internal fractures were reconstructed using image processing technology such as a non-local means filter (Buades et al., 2008) and watershed segmentation (Jones et al., 2007) (Figure 4). The Avizo image processing tool was used to measure crucial fracture structure parameters, such as porosity ϕ_f, fracture aperture a, the azimuth and dip angle of fracture θ₁ and θ₂, and the maximum length of fracture branch (l^max), from the reconstructed coal sample fractures. During the flow experiments, the coal sample was oriented to align the flow direction parallel to the fracture surface. Therefore, the azimuth angle of fracture θ₁ was 0°. The tortuosity of fracture τ, the fractal dimension of fracture D_f, tortuosity fractal dimension of fracture D_Tf are defined as follows.

Figure 4

Figure 4. The reconstructed fracture. (A) The results for the coal sample with single fracture, and (B) the results for the coal sample with complex fracture networks.

The tortuosity of fracture τ is defined as the ratio of the fracture actual length L_t to the cell unit length L₀ (Ghanbarian et al., 2013).

$\tau =L_t/L_0(2)$

Yu and Cheng and Miao et al. concluded that the cumulative number N of fractures in natural rock, with a fracture length L greater than or equal to ≥l, follows the fractal scale relationship of Eq. 3 (Yu and Cheng, 2002; Miao et al., 2015a):

$N\left(L\ge l\right)={\left(l^{\max }/l\right)}^{D_f}(3)$

where D_f represents the fractal dimension of fracture, with 1 < D_f < 2 in two dimensions and 2 < D_f < 3 in three dimensions. Differentiating Eq. 2 with respect to l yields the following Eq. 4.

$dN\left(l\right)=-D_f{\left(l^{\max }\right)}^{D_f}{l}^{-\left(D_f+1\right)}dl(4)$

As the ratio of minimum to maximum fracture length (l^min/l^{max r}) in natural rock was less than 0.01, the relationship between fractal dimension D_f, l^min/l^max, and porosity ϕ can be described using the fractal theory of Eq. 5 (Yu and Li, 2001).

${\varphi }_f={\left(l^{\min }/l^{\max }\right)}^{dE-D_f}(5)$

where dE represents the number of dimensions of the Euclidean space, with dE = 2 for two dimensions and dE = 3 for three dimensions.

Liu et al. (2016) and Li B. et al. (2016) indicated a relationship between the characteristic length of fracture L₀, actual length L_t, fracture aperture a, and tortuosity fractal dimension D_Tf, expressed as follows:

$L_t=a^{1-D_{Tf}}{L}_{t0}^{D_{Tf}}={\left(\frac{L_0}{\cos {\theta }_2}\right)}^{D_{Tf}}{a}^{1-D_{Tf}}(6)$

where a = βlⁿ, β represents the proportionality coefficient, and its value generally ranges from 10^–4 to 10^–1. For self-similar fracture structures, n is equal to 1 (Klimczak et al., 2010; Torabi and Berg, 2011).

The characteristic parameters of single fractures and complex fracture networks are shown in Table 2. These parameters were used to predict the coal permeability.

Table 2

Table 2. Characteristic parameters of fracture inside the coal selected in the flow experiments.

3 Results and discussion

3.1 Permeability evolution under confining stress loading

The permeability evolution of single-fractured coal under different effective confining stresses is shown in Figure 5A. The findings indicated a negative power relationship (i.e., SD model) between fracture permeability and effective confining stress, and the fitting parameters are shown in Table 3. This suggests that the SD model effectively described the permeability evolution of single-fractured coal under confining stress loading. At low confining stress levels, the fracture underwent minimal compression, resulting in its highest permeability. As the confining stress increased, the fracture underwent further compression, leading to a gradual increase in the fluid flow resistance and a corresponding decrease in fracture permeability.

Figure 5

Figure 5. The evolution of permeability and aperture for single fracture coal. (A) Confining stress dependent permeability, in which the cube is experiment results and the dotted line is fitting results, (B) confining stress dependent fracture aperture.

Table 3

Table 3. The fitting function between permeability and effective confining stress.

According to the cubic law, which approximates the fluid flow inside a single fracture as a flow between two plates, the fracture aperture can be calculated, as illustrated in Figure 5B. The results revealed that during the first three loading steps, the fracture aperture decreased by ∼54.63%, 51.79%, 53.72%, 52.19%, 57.20%, and 57.83% of the total closure for SC1, SC2, SC3, SC4, SC5, and SC6 samples, respectively. Correspondingly, the permeability decreased by ∼43.49%, 38.06%, 45.80%, 39.52%, 40.81%, and 42.12% for samples SC1, SC2, SC3, SC4, SC5, and SC6, respectively. However, during the final three loading steps, the fracture aperture decreased by ∼19.26%, 20%, 22.49%, 23.08%, 18.26%, and 19.72% of the total closure for SC1, SC2, SC3, SC4, SC5, and SC6 samples, respectively. Moreover, permeability decreased by ∼22.91%, 22.15%, 24.29%, 26.93%, 23.93%, and 25.49% for samples SC1, SC2, SC3, SC4, SC5, and SC6, respectively. The results indicated that as the effective stress increased, fracture closure initially occurred more rapidly, slowed down, and then eventually tended to stabilize. This pattern suggests that with increasing confining stress, the permeability first rapidly decreased, followed by a gradual decrease, and eventually reached a constant value. Therefore, this phenomenon elucidates why the fractured coal exhibited a higher sensitivity to stress in permeability compared with intact coal.

3.2 Permeability evolution under true triaxial loading

Figure 6 illustrates the correlation between true triaxial stresses and the permeability of fractured coal. The findings indicated a consistent decrease in the permeability of fractured coal rock with increasing principal stresses (σ₁, σ₂, and σ₃) across the three loading steps. Additionally, the loading of each principal stress σ₁, σ₂, and σ₃ had different effects on fracture permeability. Particularly, the permeability of the ST1 sample decreased by ∼43.08%, 14.84%, and 42.08% during the entire loading process. Throughout the entire loading process, the permeability of the ST2 sample decreased by ∼65.74%, 14.29%, and 19.97%. Similarly, the permeability reductions for the ST3 sample were ∼34.03%, 55.85%, and 10.12%, while those for the ST4 sample were ∼35.97%, 46.51%, and 17.52% during the entire loading process. The permeability of ST1 was significantly sensitive to σ₁ and σ₃, while the permeability of ST2 was mainly sensitive to σ₁. However, the permeability of ST3 and ST4 was influenced by both σ₁ and σ₂.

Figure 6

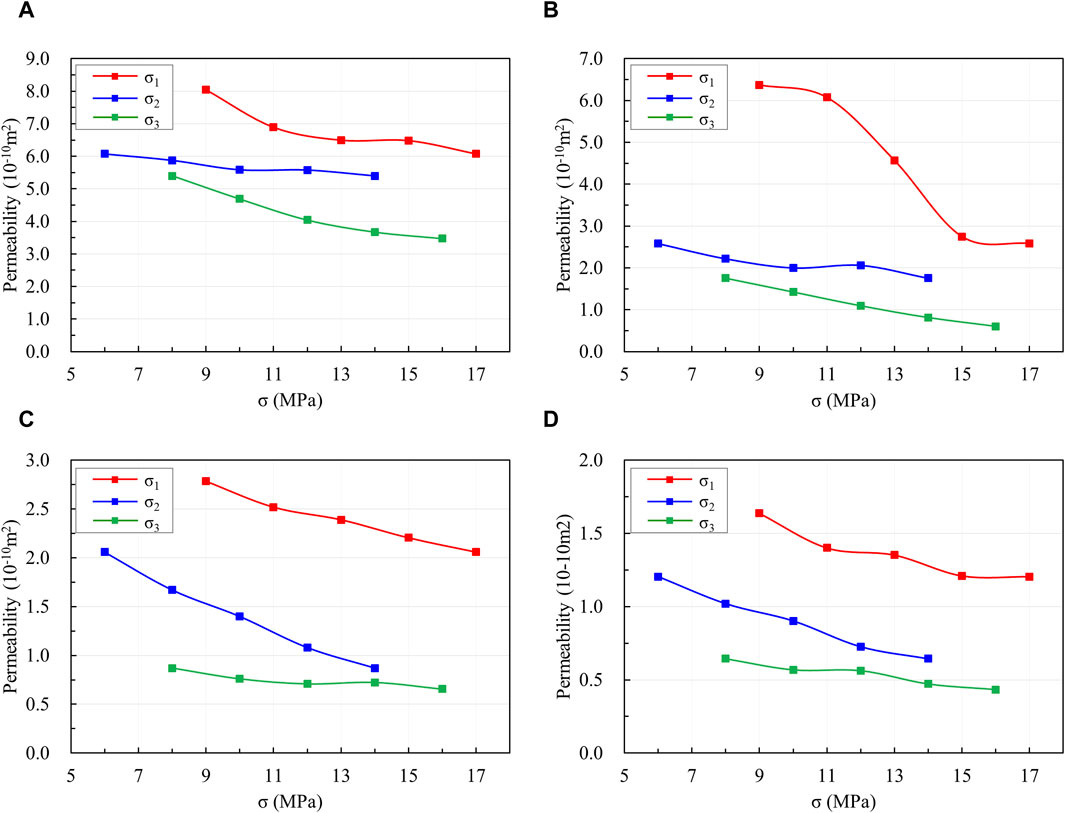
Figure 6. The evolution of permeability under true triaxial stress loading. (A) The results of ST1, (B) the results of ST2, (C) the results of ST3, (D) the results of ST4.

This sensitivity can be attributed to the complex fracture networks within the cubic sample, which exhibited varying crossing angles with each principal stress (Figure 7). The macro fractures within the ST1 sample exhibited a crossing angle of 0° with σ₂, while the crossing angle between the fracture surface and σ₁ and σ₃ was equal. As σ₁ or σ₃ increased, the macro fractures within ST1 underwent compression, leading to a decrease in the permeability of the coal sample. Similar mechanisms were applied to elucidate the permeability evolution of TS2, TS3, and TS4 during the true triaxial stress loading (Figures 7B–D). Thus, the interaction between the dip and azimuth angles of the fractures and the true triaxial stress influenced the permeability of the fractured coal, resulting in anisotropic fluid flow within the coal. This suggests that the dip and azimuth angles of the fracture surfaces should be considered when developing a permeability model for coal rock with complex fracture networks.

Figure 7

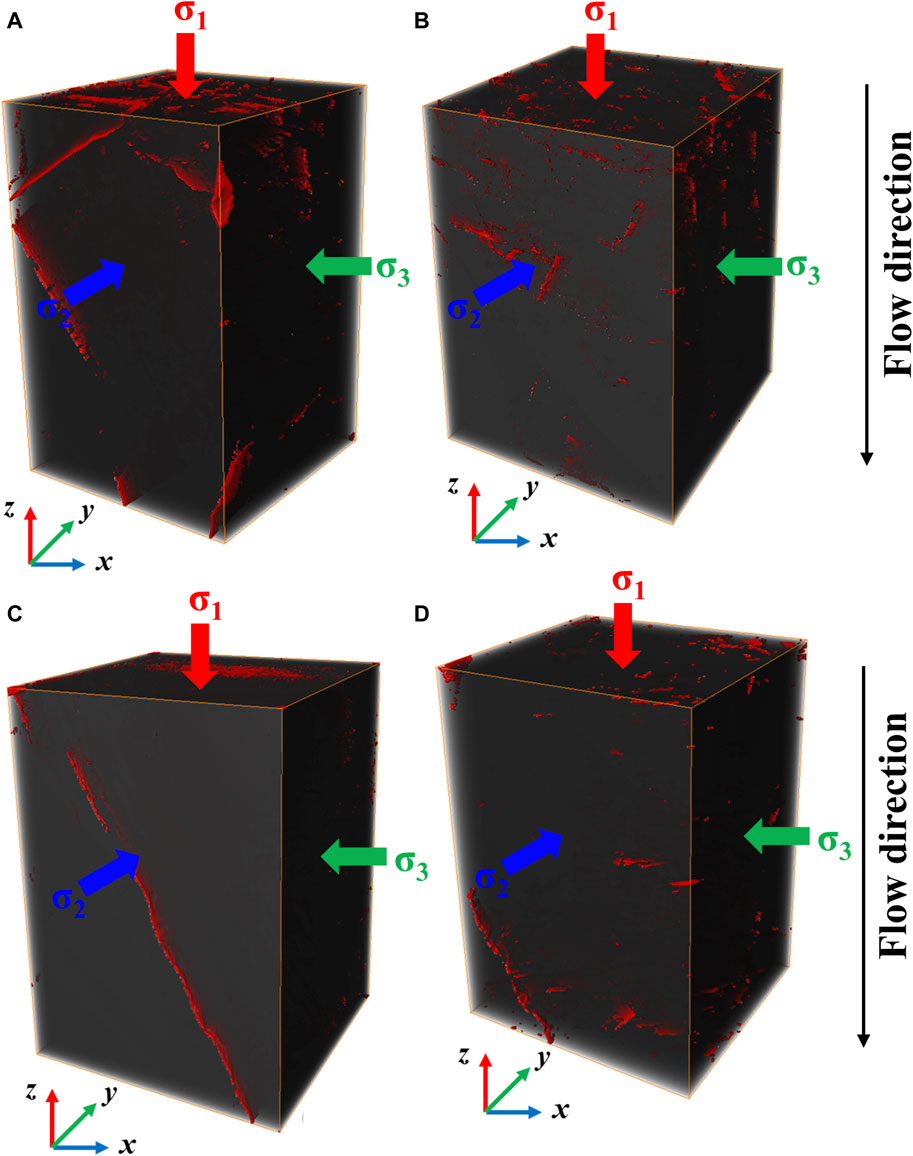
Figure 7. The relationship between macro fracture distribution and true triaxial stress loading. (A) The result for ST1 sample, (B) the result for ST2 sample, (C) the result for ST3 sample, and (D) the result for ST4 sample.

3.3 Prediction of coal permeability

3.3.1 Initial permeability model

The complex fracture networks within coal rock are formed by the interconnection of single fractures. Therefore, elucidating the flow behavior within single-fracture samples is crucial for evaluating the flow properties in coal rock with complex fracture networks. The laminar flow between smooth platers (Figure 8A, with a dip angle of θ₂ = 0°) followed cubic law of Eq. 7 (Nazridoust et al., 2006).

$q\left(l\right)=\frac{a^{3}l}{12\mu }\frac{\Delta P}{L_t}(7)$

where a represents the fracture aperture, μ denotes the fluid viscosity, ΔP signifies the stress difference between the inlet and outlet of fluid flow, and l and L_t indicate the trace length and actual length of the fracture, respectively.

Figure 8

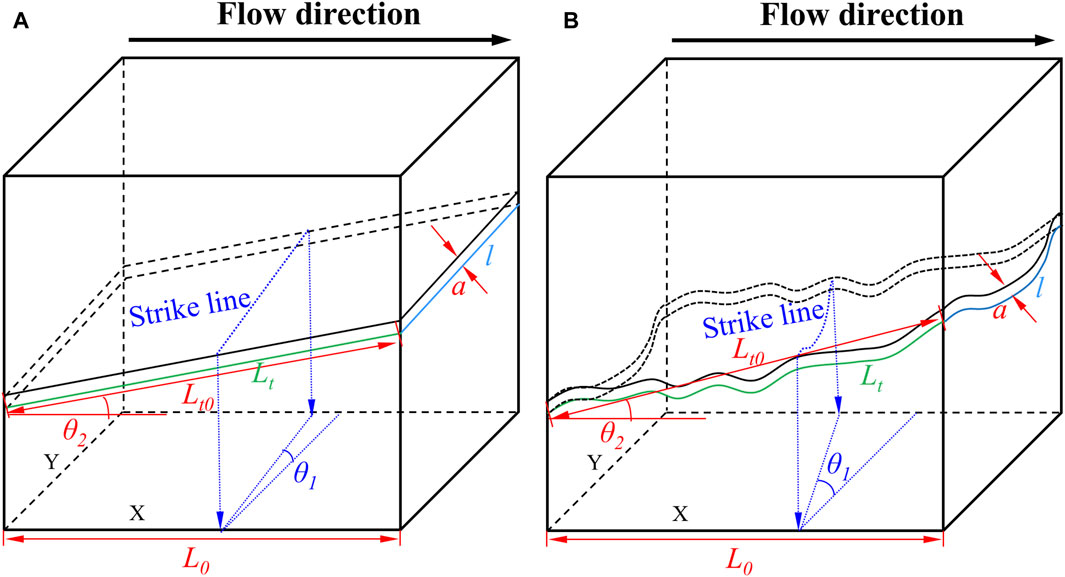
Figure 8. Schematic of a unit cell with single fracture. (A) The flat fracture, and (B) the curved fracture. In which, L₀ is the length of cell unit, L_t0 is the straight-line length of the fracture, L_t is actual length of the fracture, a is the aperture of the fracture, and l is the trace length of fracture. And θ₁ and θ₂ are the azimuth and dip angle of the fracture, respectively.

The cubic law can be rewritten to account for the orientations of fractures, as follows (Miao et al., 2015b):

$q\left(l\right)=\frac{a^{3}l\left(1-{\cos }^2{\theta }_1{\sin }^2{\theta }_2\right)}{12\mu }\frac{\Delta P}{L_t}(8)$

where θ₁ and θ₂ represent the azimuth and dip angles of the fracture, respectively. However, natural fractures in coal exhibited a rough and curved shape (Figure 8B). The relationship between straight-line length L_t0 and the actual length L_t of the curved fracture is defined by Eq. 6. The flow rate for the curved fracture (Figure 8B) can be expressed by substituting Eq. 6 into Eq. 8, as shown below.

$q\left(l\right)=\frac{a^{2+D_{Tf}}l\left(1-{\cos }^2{\theta }_1{\sin }^2{\theta }_2\right)\Delta P{\left(\cos {\theta }_2\right)}^{D_{Tf}}}{12L_0^{D_{Tf}}\mu }(9)$

The Newtonian fluid flow in porous media was described by Darcy’s law. Compared with the flow rate through the fractures, the flow rate within the coal matrix can be disregarded. Thus, the flow rate through the coal rock with single curved fractures can be calculated as follows:

$q\left(l\right)=\frac{k_{f}A}{\mu }\frac{\Delta P}{L_0}(10)$

Through a comparison of Eqs 9, 10, the permeability of coal with single curved fractures is expressed as follows:

$k_f=\frac{{L_0}^{1-D_{Tf}}{a}^{2+D_{Tf}}l\left(1-{\cos }^2{\theta }_1{\sin }^2{\theta }_2\right){\left(\cos {\theta }_2\right)}^{D_{Tf}}}{12A}(11)$

hrough the substitution of a = βl into Eq. 11, the permeability of coal with single curved fractures is expressed as follows:

$k_f=\frac{{L_0}^{1-D_{Tf}}{a}^{3+D_{Tf}}\left(1-{\cos }^2{\theta }_1{\sin }^2{\theta }_2\right){\left(\cos {\theta }_2\right)}^{D_{Tf}}}{12A\beta }(12)$

At a flow direction parallel to the single-fracture surface (Figure 8), the dip and azimuth angles of fracture were set to 0°. In the flow experiments under confining stress loading, the characteristic parameters of the coal fractures were selected, and the permeability of the single-fractured coal was predicted using Eq. 12 (Figure 9). The results revealed that the predicted permeability of single-fractured coal by Eq. 12 was consistent with the experiment data under a confining stress of 2 MPa. Additionally, the predictive permeability model for single-fractured coal samples provided a good basis for estimating the permeability of coal samples with fracture networks.

Figure 9

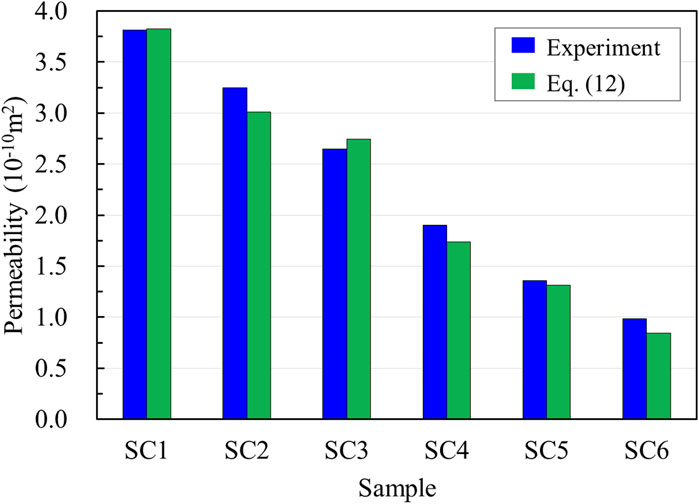
Figure 9. Comparison between the predicted value by Eq. 12 and the measured value of permeability for single-fractured coal under confining stress of 2 MPa.

According to the fractal geometry theory, the total flow rate through the complex fracture network can be calculated by integrating Eq. 9 across a range of minimum to maximum fracture length [l_min, l_max] (Xia et al., 2021).

$\begin{array}{ll}\hfill Q=& {\int }_{l^{\min }}^{l^{\max }}q\left(l\right)dN\left(l\right)=\frac{{\beta }^{2+D_{Tf}}{D}_f\left(1-{\cos }^2{\theta }_1{\sin }^2{\theta }_2\right)L_0^{1-D_{Tf}}\Delta P{\left(\cos {\theta }_2\right)}^{D_{Tf}}}{12\left(3+D_{Tf}-D_f\right)\mu L_0}\hfill \\ \hfill & {\left(l^{\max }\right)}^{3+D_{Tf}}\left[1-{\left(\frac{l^{\min }}{l^{\max }}\right)}^{3+D_{Tf}-D_f}\right]\hfill \end{array}(13)$

Generally, for fracture networks in natural coal, with l^min/l^max<<1, Eq. 13 be simplified as Eq. 14:

$Q=\frac{{\beta }^{2+D_{Tf}}{D}_f\left(1-{\cos }^2{\theta }_1{\sin }^2{\theta }_2\right)L_0^{1-D_{Tf}}\Delta P{\left(\cos {\theta }_2\right)}^{D_{Tf}}}{12\left(3+D_{Tf}-D_f\right)\mu L_0}{\left(l^{\max }\right)}^{3+D_{Tf}}(14)$

The Newtonian fluid flow in porous media was elucidated through comparison with Darcy’s law (Eq. (10)). From this comparison, the permeability of the fracture network can be calculated as follows:

$k_f=\frac{{\beta }^{2+D_{Tf}}{D}_f\left(1-{\cos }^2{\theta }_1{\sin }^2{\theta }_2\right)L_0^{1-D_{Tf}}{\left(\cos {\theta }_2\right)}^{D_{Tf}}}{12\left(3+D_{Tf}-D_f\right)A}{\left(l^{\max }\right)}^{3+D_{Tf}}(15)$

3.3.2 Permeability model under true triaxial loading

To quantitatively analyze the evolution of coal permeability during CBM extraction, numerous researchers have conducted various experiments and developed multiple predictive models to evaluate coal permeability under stress loading conditions. Among these models, the SD model (Eqs 16, 17, developed by Shi and Durucan (2004; 2005), emerged as the most classic and widely used approach. The permeability model assumes that the coal underwent linear elastic deformation upon exposure to triaxial stress loading, with compressibility mainly attributed to fractures.

$k=k_{f0}{\mathrm{e}}^{-3C_f\left(\sigma -{\sigma }_0\right)}(16)$

$C_f=\frac{C_{f0}}{\alpha \left(\sigma -{\sigma }_0\right)}\left(1-e^{-\alpha \left(\sigma -{\sigma }_0\right)}\right)(17)$

where k_f0 represents the initial permeability of the fractured coal, C_f denotes the compression coefficient of fracture, C_f0 represents the initial compression coefficient of fracture, and α represents the rate at which fracture compressibility decreases with increasing stress. In the SD model, σ represents the effective stress, while σ₀ denotes the initial effective stress.

The SD model was widely used for both laboratory tests and field predictions. The experimental results of the single-fractured coal sample under confining stress loading in this study indicated a negative exponential correlation between coal permeability and effective stress. This correlation was consistent with the behavior predicted by the SD model. However, the SD model alone cannot capture the effect of each principal stress on rock permeability under true triaxial loading conditions. To address this limitation, Li et al. (2016) extended the SD model by developing a comprehensive model to assess rock permeability under true triaxial loading conditions, as Eqs 18–21:

$k=k_{f0}{\mathrm{e}}^{-\left[C_{f1}\left({\sigma }_1-{\sigma }_{10}\right)+C_{f2}\left({\sigma }_2-{\sigma }_{20}\right)+C_{f3}\left({\sigma }_3-{\sigma }_{30}\right)\right]}(18)$

$C_{f1}=\frac{C_{f10}}{{\alpha }_1\left({\sigma }_1-{\sigma }_{10}\right)}\left(1-e^{-{\alpha }_1\left({\sigma }_1-{\sigma }_{10}\right)}\right)(19)$

$C_{f2}=\frac{C_{f20}}{{\alpha }_2\left({\sigma }_2-{\sigma }_{20}\right)}\left(1-e^{-{\alpha }_2\left({\sigma }_2-{\sigma }_{20}\right)}\right)(20)$

$C_{f3}=\frac{C_{f30}}{{\alpha }_3\left({\sigma }_3-{\sigma }_{30}\right)}\left(1-e^{-{\alpha }_3\left({\sigma }_3-{\sigma }_{30}\right)}\right)(21)$

where σ₁, σ₂, and σ₃ represent the principal stresses; σ₁₀, σ₂₀, and σ₃₀ denote the initial principal stresses; C_f1, C_f2, and C_f2 indicate the corresponding fracture compressibilities; C_f10, C_f20, and C_f20 signify the corresponding initial fracture compressibilities; α₁, α₂, and α₃ represent the rates at which fracture compressibility decreases with increasing principal stress.

The coal permeability under true triaxial loading was determined by substituting Eq. 15 into Eq. 18.

$\begin{array}{ll}\hfill k=& \frac{{\beta }^{2+D_{Tf}}{D}_f\left(1-{\cos }^2{\theta }_1{\sin }^2{\theta }_2\right)L_0^{1-D_{Tf}}{\left(\cos {\theta }_2\right)}^{D_{Tf}}}{12\left(3+D_{Tf}-D_f\right)A}{\left(l^{\max }\right)}^{3+D_{Tf}}\hfill \\ \hfill & \left\{{\mathrm{e}}^{-\left[C_{f1}\left({\sigma }_1-{\sigma }_{10}\right)+C_{f2}\left({\sigma }_2-{\sigma }_{20}\right)+C_{f3}\left({\sigma }_3-{\sigma }_{30}\right)\right]}\right\}\hfill \end{array}(22)$

The permeability test results obtained under true triaxial loading conditions in this study were used to validate the improved permeability model for fractured coal rocks exposed to true triaxial stress conditions. To streamline the calculation, it was assumed that the corresponding fracture compressibility remained constant for each loading process of principal stress. These values were calculated by substituting the data from the true triaxial loading flow experiment into Eqs 16, 17. The results are shown in Table 4. Moreover, the coal permeability evolution under true triaxial loading was predicted using the improved model (Eq. (22)) (Figure 10). The results indicated that the improved permeability model successfully predicted the coal permeability evolution under true triaxial stress loading conditions. Additionally, compared with the SD model, the permeability changes predicted by the improved model were consistent with the loading process of each principal stress. This suggests that the improved model can accurately capture the anisotropic impact of each principal stress on coal permeability under true triaxial stress loading conditions.

Table 4

Table 4. Fracture compressibilities.

Figure 10

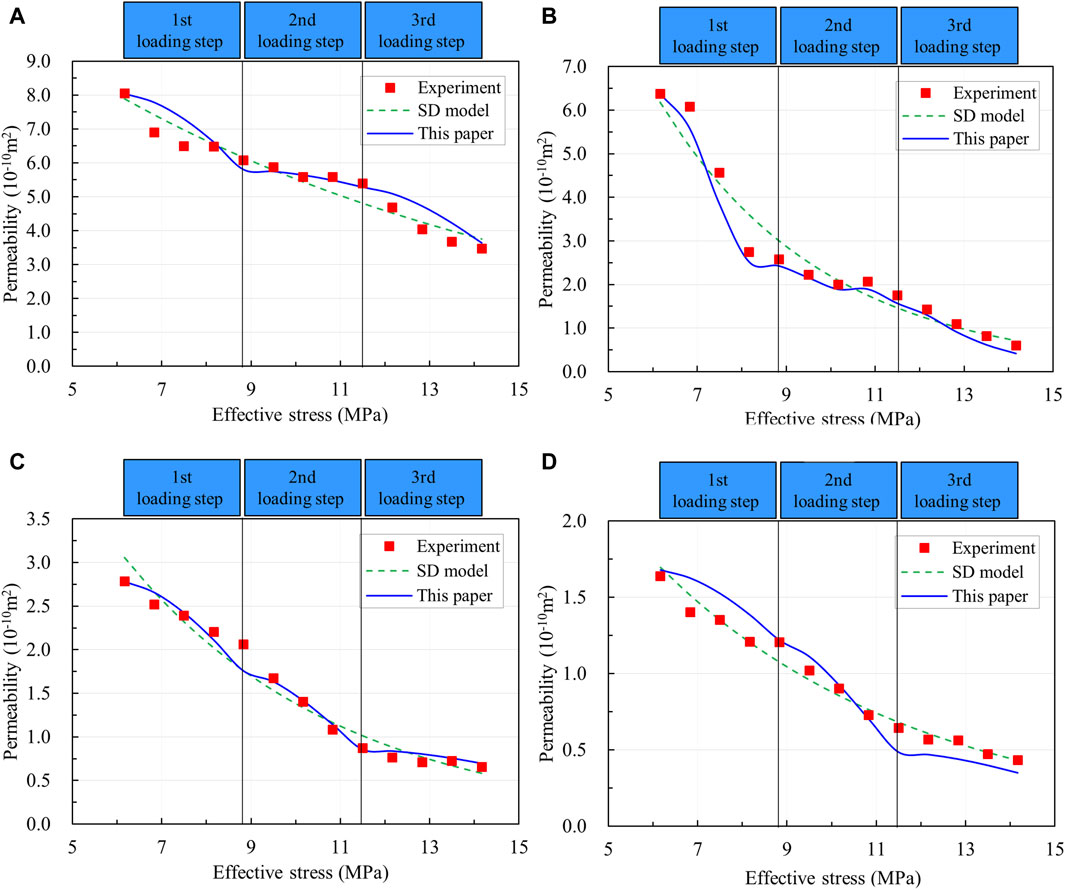
Figure 10. The permeability versus the effective stress under true triaxial stress loading. (A) Results for ST1, (B) results for ST2, (C) results for ST3, (D) results for ST4. Here, red cubes, green dashed lines, and blue lines represent the experiment results, prediction by the SD model, and prediction by the improved permeability model in this paper, respectively. Note that effective stress is equal to the average principal stress minus the pore pressure.

4 Conclusion

We conducted flow experiments on six cylindrical coal samples and four cubic coal samples under confining stress and true triaxial stress loading conditions, respectively. The evolution of coal permeability during the loading of confining stress and true triaxial stress was analyzed. According to the current true triaxial permeability model and fractal theory, an improved model was developed to elucidate the anisotropic effect of each principal stress on the permeability of coal samples with complex fracture networks. The following conclusions can be drawn.

(1) During confining pressure loading, the permeability evolution of the coal sample with a single fracture decreased exponentially with increasing effective stress and was effectively described by the SD model. Additionally, under confining pressure loading, the coal permeability first rapidly decreased, followed by a gradual decrease, and eventually reached a constant value. During the first three loading steps, the fracture aperture and corresponding permeability of the six cylindrical coal samples decreased by ∼51.79%–57.83% and ∼38.06%–42.12%, respectively. However, during the final three loading steps, the fracture aperture and corresponding permeability of the six cylindrical coal samples decreased by ∼18.26%–23.08% and ∼22.15%–26.93%, respectively.

(2) Owing to the varying crossing angles of the complex fracture networks with each principal stress, the effect of each principal stress on the permeability evolution of coal with complex fracture networks was highly anisotropic during the true triaxial stress loading. During the loading of each principal stress, the permeability of the ST1 sample decreased by ∼43.08%, 14.84%, and 42.08% for σ₁, σ₂, and σ₃, respectively. Similarly, the permeability of the ST2 sample decreased by 65.74%, 14.29%, and 19.97%. During the entire true triaxial loading, the permeability reductions for the ST3 sample were ∼34.03%, 55.85%, and 10.12%, while those for the ST4 sample were ∼35.97%, 46.51%, and 17.52%. The SD model failed to describe these anisotropic effects.

(3) The increase in principal stress parallel to the fracture surface had a minimal impact on coal permeability owing to the limited compression of the fracture. However, as the principal stress intersected the fracture surface at a specific angle, the subsequent increase in this stress significantly reduced the permeability of coal with complex fracture networks. Therefore, the dip and azimuth angle of the fracture surface should be incorporated into the permeability model for evaluating coal samples with complex fracture networks.

(4) Compared with the SD model, the improved model, based on the current true triaxial permeability model and fractal theory, effectively described the anisotropic effect of each principal stress on the permeability of coal samples with complex fracture networks.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

XH: Conceptualization, Methodology, Validation, Visualization, Writing–original draft, Writing–review and editing. YL: Conceptualization, Funding acquisition, Investigation, Supervision, Writing–review and editing. BX: Conceptualization, Funding acquisition, Investigation, Methodology, Supervision, Writing–review and editing. YL: Conceptualization, Data curation, Formal Analysis, Validation, Visualization, Writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study was jointly supported by the National Natural Science Foundation of China (grant number U19B2009 and 51974042).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Buades, A., Coll, B., and Morel, J. M. (2008). Nonlocal image and movie denoising. Int. J. Comput. Vis. 76 (2), 123–139. doi:10.1007/s11263-007-0052-1

CrossRef Full Text | Google Scholar

Chao, J. K., Yu, M. G., Chu, T. X., Han, X. F., Teng, F., and Li, P. (2019). Evolution of broken coal permeability under the condition of stress, temperature, moisture content, and pore pressure. Rock Mech. Rock Eng. 52 (8), 2803–2814. doi:10.1007/s00603-019-01873-x

CrossRef Full Text | Google Scholar

Chen, D., Shi, J. Q., Durucan, S., and Korre, A. (2014). Gas and water relative permeability in different coals: model match and new insights. Int. J. Coal Geol. 122, 37–49. doi:10.1016/j.coal.2013.12.002

CrossRef Full Text | Google Scholar

Chen, S. D., Tang, D. Z., Tao, S., Xu, H., Zhao, J. L., Fu, H. J., et al. (2018). In-situ stress, stress-dependent permeability, pore pressure and gas-bearing system in multiple coal seams in the Panguan area, western Guizhou, China. J. Nat. Gas Sci. Eng. 49, 110–122. doi:10.1016/j.jngse.2017.10.009

CrossRef Full Text | Google Scholar

Du, Z. G., Huang, Q., Sun, S. C., Guo, J. J., and Gao, F. Q. (2021). The coal inter-particle stress and porosity-permeability evolution characteristics of the confined coal by the applied loading relief effects. Arabian J. Of Geosciences 14 (11), 1040–1112. doi:10.1007/s12517-021-07452-1

CrossRef Full Text | Google Scholar

Du, Z. G., Tao, Y. W., Zhang, X. D., Ding, W. X., and Huang, Q. (2022). CBM exploration: permeability of coal owing to cleat and connected fracture. Energy Explor. Exploitation 40 (1), 38–56. doi:10.1177/01445987211057195

CrossRef Full Text | Google Scholar

Ghanbarian, B., Hunt, A. G., Ewing, R. P., and Sahimi, M. (2013). Tortuosity in porous media: a critical review. Soil Sci. Soc. Am. J. 77 (5), 1461–1477. doi:10.2136/sssaj2012.0435

CrossRef Full Text | Google Scholar

Jones, A. C., Arns, C. H., Sheppard, A. P., Hutmacher, D. W., Milthorpe, B. K., and Knackstedt, M. A. (2007). Assessment of bone ingrowth into porous biomaterials using MICRO-CT. Biomaterials 28 (15), 2491–2504. doi:10.1016/j.biomaterials.2007.01.046

PubMed Abstract | CrossRef Full Text | Google Scholar

Klimczak, C., Schultz, R. A., Parashar, R., and Reeves, D. M. (2010). Cubic law with aperture-length correlation: implications for network scale fluid flow. Hydrogeology J. 18 (4), 851–862. doi:10.1007/s10040-009-0572-6

CrossRef Full Text | Google Scholar

Li, B., Liu, R. C., and Jiang, Y. J. (2016a). A multiple fractal model for estimating permeability of dual-porosity media. J. Hydrology 540, 659–669. doi:10.1016/j.jhydrol.2016.06.059

CrossRef Full Text | Google Scholar

Li, G. F., Wang, Y., Wang, J. H., Zhang, H. W., Shen, W. B., and Jiang, H. (2021). Coupled effects of stress, moisture content and gas pressure on the permeability evolution of coal samples: a case study of the coking coal resourced from tunlan coalmine. Water 13 (12), 1653–1665. doi:10.3390/w13121653

CrossRef Full Text | Google Scholar

Li, J. H., Li, B. B., Cheng, Q. Y., and Gao, Z. (2022). Characterization of anisotropic coal permeability with the effect of sorption-induced deformation and stress. Fuel 309, 122089. doi:10.1016/j.fuel.2021.122089

CrossRef Full Text | Google Scholar

Li, M. H., Yi, G. Z., Xu, J., Cao, J., and Song, Z. L. (2016b). Permeability evolution of shale under anisotropic true triaxial stress conditions. Int. J. Coal Geol. 165, 142–148. doi:10.1016/j.coal.2016.08.017

CrossRef Full Text | Google Scholar

Li, Q., Wang, F. L., Wang, Y. L., Bai, B. J., Zhang, J. Y., Cao, L. L., et al. (2023). Adsorption behavior and mechanism analysis of siloxane thickener for CO2 fracturing fluid on shallow shale soil. J. Mol. Liq. 376, 121394. doi:10.1016/j.molliq.2023.121394

CrossRef Full Text | Google Scholar

Li, Q. C., Liu, J., Wang, S. M., Guo, Y., Han, X. Y., Li, Q., et al. (2024). Numerical insights into factors affecting collapse behavior of horizontal wellbore in clayey silt hydrate-bearing sediments and the accompanying control strategy. Ocean. Eng. 297, 117029. doi:10.1016/j.oceaneng.2024.117029

CrossRef Full Text | Google Scholar

Lin, W. J., and Kovscek, A. R. (2014). Gas sorption and the consequent volumetric and permeability change of coal I: experimental. Transp. Porous Media 105, 371–389. doi:10.1007/s11242-014-0373-9

CrossRef Full Text | Google Scholar

Liu, R. C., Li, B., and Jiang, Y. J. (2016). Critical hydraulic gradient for nonlinear flow through rock fracture networks: the roles of aperture, surface roughness, and number of intersections. Adv. Water Resour. 88, 53–65. doi:10.1016/j.advwatres.2015.12.002

CrossRef Full Text | Google Scholar

Liu, Y. B., Li, M. H., Yin, G. Z., Zhang, D. M., and Deng, B. Z. (2018). Permeability evolution of anthracite coal considering true triaxial stress conditions and structural anisotropy. J. Nat. gas Sci. Eng. 52, 492–506. doi:10.1016/j.jngse.2018.02.014

CrossRef Full Text | Google Scholar

Liu, Y. B., Yin, G. Z., Li, M. H., Zhang, D. M., Deng, B. Z., Liu, C., et al. (2019a). Anisotropic mechanical properties and the permeability evolution of cubic coal under true triaxial stress paths. Rock Mech. Rock Eng. 52, 2505–2521. doi:10.1007/s00603-019-01748-1

CrossRef Full Text | Google Scholar

Liu, Y. B., Yin, G. Z., Zhang, D. M., Li, M. H., Deng, B. Z., Liu, C., et al. (2019b). Directional permeability evolution in intact and fractured coal subjected to true-triaxial stresses under dry and water-saturated conditions. Int. J. Rock Mech. Min. Sci. 119, 22–34. doi:10.1016/j.ijrmms.2019.04.007

CrossRef Full Text | Google Scholar

Meng, Y., Li, Z. P., and Lai, F. P. (2015). Experimental study on porosity and permeability of anthracite coal under different stresses. J. Petroleum Sci. Eng. 133, 810–817. doi:10.1016/j.petrol.2015.04.012

CrossRef Full Text | Google Scholar

Miao, T. J., Yang, S. S., Long, Z. C., and Yu, B. M. (2015a). Fractal analysis of permeability of dual-porosity media embedded with random fractures. Int. J. Heat Mass Transf. 88, 814–821. doi:10.1016/j.ijheatmasstransfer.2015.05.004

CrossRef Full Text | Google Scholar

Miao, T. J., Yu, B. M., Duan, Y. Y., and Fang, Q. T. (2015b). A fractal analysis of permeability for fractured rocks. Int. J. Heat Mass Transf. 81, 75–80. doi:10.1016/j.ijheatmasstransfer.2014.10.010

CrossRef Full Text | Google Scholar

Nazridoust, K., Ahmadi, G., and Smith, D. H. (2006). A new friction factor correlation for laminar, single-phase flows through rock fractures. J. Hydrology 329 (1-2), 315–328. doi:10.1016/j.jhydrol.2006.02.032

CrossRef Full Text | Google Scholar

Peng, K., Zhou, J. Q., Zou, Q. L., and Song, X. (2020). Effect of loading frequency on the deformation behaviours of sandstones subjected to cyclic loads and its underlying mechanism. Int. J. Fatigue 131, 105349. doi:10.1016/j.ijfatigue.2019.105349

CrossRef Full Text | Google Scholar

Peng, K., Zhou, J. Q., Zou, Q. L., Zhang, J., and Wu, F. (2019). Effects of stress lower limit during cyclic loading and unloading on deformation characteristics of sandstones. Constr. Build. Mater. 217, 202–215. doi:10.1016/j.conbuildmat.2019.04.183

CrossRef Full Text | Google Scholar

Shi, J. Q., and Durucan, S. (2004). Drawdown induced changes in permeability of coalbeds: a new interpretation of the reservoir response to primary recovery. Transp. Porous Media 56 (1), 1–16. doi:10.1023/B:TIPM.0000018398.19928.5a

CrossRef Full Text | Google Scholar

Shi, J. Q., and Durucan, S. (2005). A model for changes in coalbed permeability during primary and enhanced methane recovery. SPE Reserv. Eval. Eng. 8 (4), 291–299. doi:10.2118/87230-PA

CrossRef Full Text | Google Scholar

Shi, R., Liu, J. S., Wei, M. Y., Elsworth, D., and Wang, X. M. (2018). Mechanistic analysis of coal permeability evolution data under stress-controlled conditions. Int. J. Rock Mech. Minings Sci. 110, 36–47. doi:10.1016/j.ijrmms.2018.07.003

CrossRef Full Text | Google Scholar

Thararoop, P., Karpyn, Z. T., and Ertekin, T. (2012). Development of a multi-mechanistic, dual-porosity, dual-permeability, numerical flow model for coalbed methane reservoirs. J. Nat. Gas Sci. Eng. 8, 121–131. doi:10.1016/j.jngse.2012.01.004

CrossRef Full Text | Google Scholar

Torabi, A., and Berg, S. S. (2011). Scaling of fault attributes: a review. Mar. Petroleum Geol. 28 (8), 1444–1460. doi:10.1016/j.marpetgeo.2011.04.003

CrossRef Full Text | Google Scholar

Wang, F. L., Xiao, Z. X., Liu, X., Ren, J. W., Xing, T., Li, Z., et al. (2022). Strategic design of cellulose nanofibers@zeolitic imidazolate frameworks derived mesoporous carbon-supported nanoscale CoFe2O4/CoFe hybrid composition as trifunctional electrocatalyst for Zn-air battery and self-powered overall water-splitting. J. Power Sources 521, 230925. doi:10.1016/j.jpowsour.2021.230925

CrossRef Full Text | Google Scholar

Wang, H., Yue, G. W., Yue, J. W., Li, M. M., and Zheng, X. J. (2019). Permeability of coal associated with cleat and bedding structure: measurement and modeling. Energy Sources, Part A Recovery, Util. Environ. Eff. 2019, 7363–7375. doi:10.1080/15567036.2019.1675813

CrossRef Full Text | Google Scholar

Wu, Y. T., Pan, Z. J., Zhang, D. Y., Down, D., Lu, Z. H., and Connell, L. D. (2017). Experimental study of permeability behaviour for proppant supported coal fracture. J. Nat. Gas Sci. Eng. 51, 18–26. doi:10.1016/j.jngse.2017.12.023

CrossRef Full Text | Google Scholar

Xia, B. W., Luo, Y. F., Hu, H. R., and Wu, M. Y. (2021). Fractal permeability model for a complex tortuous fracture network. Phys. Fluids 33 (9), 096605. doi:10.1063/5.0063354

CrossRef Full Text | Google Scholar

Xiao, K., Zhang, Z. T., Zhang, R., Gao, M. Z., Xie, J., Zhang, A. L., et al. (2021). Anisotropy of the effective porosity and stress sensitivity of coal permeability considering natural fractures. Energy Rep. 7 (3), 3898–3910. doi:10.1016/j.egyr.2021.06.067

CrossRef Full Text | Google Scholar

Xu, X. M., Sarmadivaleh, M., Li, C. W., Xie, B. J., and Iglauer, S. (2016). Experimental study on physical structure properties and anisotropic cleat permeability estimation on coal cores from China. J. Nat. Gas Sci. Eng. 35, 131–143. doi:10.1016/j.jngse.2016.08.050

CrossRef Full Text | Google Scholar

Xue, Y., Ranjith, P. G., Gao, F., Zhang, D. C., Cheng, H. M., Chong, Z. H., et al. (2017). Mechanical behaviour and permeability evolution of gas-containing coal from unloading confining pressure tests. J. Of Nat. Gas Sci. Eng. 40, 336–346. doi:10.1016/j.jngse.2017.02.030

CrossRef Full Text | Google Scholar

Yang, Y., Jiang, C. B., Guo, X. W., Peng, S. J., Zhao, J. J., and Yan, F. Z. (2021). Experimental investigation on the permeability and damage characteristics of raw coal under tiered cyclic unloading and loading confining pressure. Powder Technol. 389, 416–429. doi:10.1016/j.powtec.2021.05.062

CrossRef Full Text | Google Scholar

Yu, B., and Cheng, P. (2002). A fractal permeability model for bi-dispersed porous media. Int. J. Heat Mass Transf. 45 (14), 2983–2993. doi:10.1016/S0017-9310(02)00014-5

CrossRef Full Text | Google Scholar

Yu, B., and Li, J. H. (2001). Some fractal characters of porous media. Fractals 09 (03), 365–372. doi:10.1142/S0218348X01000804

CrossRef Full Text | Google Scholar

Zhao, Y. Y., Cui, D. X., Liu, J. S., Wei, M. Y., and Liu, Y. K. (2021). Evolution of coal permeability under constant effective stresses: direct measurements and numerical modeling. Energy and Fuels 35 (19), 15489–15501. doi:10.1021/acs.energyfuels.1c01425

CrossRef Full Text | Google Scholar

Zhou, D., Zhao, Z. H., Li, B., Chen, Y. D., and Ding, W. Q. (2020). Permeability evolution of grout infilled fractures subjected to triaxial compression with low confining pressure. Tunn. Undergr. Space Technol. 104, 103539. doi:10.1016/j.tust.2020.103539

CrossRef Full Text | Google Scholar

Zhou, Y. B., Li, H. S., Huang, J. L., Zhang, R. L., Wang, S. J., Hong, Y. D., et al. (2021). Influence of coal deformation on the Knudsen number of gas flow in coal seams. Energy 233, 121161. doi:10.1016/j.energy.2021.121161

CrossRef Full Text | Google Scholar