A coal bursting liability evaluation model based on fuzzy set theory and analysis of three influencing factors

The classification of coal bursting liability is of great significance for the prevention and control of rock burst. To address the shortcomings in existing bursting liability classification methods, a comprehensive evaluation model for bursting liability based on a combination of weighted-fuzzy set theory and three influencing factor analyses is proposed. The model selects four evaluation indicators: dynamic failure time (DT), elastic energy index (W_ET), bursting energy index (K_E), and uniaxial compressive strength (R_C). Two types of membership functions, trapezoidal fuzzy numbers (TFN) and Gaussian fuzzy numbers (GFN), are used to quantitatively describe the fuzziness between indicator levels. The Delphi method and a random forest feature identification method are combined to obtain a subjective and objective combined weighting, determining the optimal combination weight of the four indicators. Based on Zadeh operator (ZO), maximum-minimum operator (MMO), weighted-average operator (WAO), and all-around restrictive operator (ARO), calculations are carried out for the synthesis of indicator weights and memberships. Maximal membership principle (MMP) and Credible identification principle (CIP) are utilized as evaluation principle to assess the bursting liability level, constructing 16 fuzzy comprehensive evaluation models. The impact of membership functions, fuzzy operators, and evaluation principle on evaluation results are systematically analyzed based on the discrimination results of 127 sample sets. The results show that the optimal fuzzy comprehensive evaluation model is constructed using the trapezoidal fuzzy numbers, weighted average operator, and maximal membership principle (TFN-WAO-MMP), with a classification accuracy of 97.64%. Finally, the optimal model is applied to 10 engineering instances, and the evaluation results are consistent with the actual situation, verifying the reliability and effectiveness of the model. Overall, these findings contribute to the development of a more sophisticated and accurate method for assessing the rock burst tendency of coal specimens. By leveraging the theory of fuzzy sets, this approach provides a more nuanced and nuanced evaluation of rock burst tendency, and thus offers the potential to improve workplace safety and efficiency in the coal mining industry.

1 Introduction

As mining operations and underground excavation increase in scale and depth, elevated stress and excavation disturbances inevitably cause brittle fracturing of deep rock masses, leading to more frequent occurrences of complex geological disasters, such as rock bursts, which pose a serious threat to the safe and efficient development of deep mineral resources (Li et al., 2021; Ling hu et al., 2021; Dong et al., 2022; Wang et al., 2022; Fu et al., 2022; Zhao J. et al., 2022; Wang C. et al., 2024; He et al., 2023; Qiu et al., 2023; Zhao et al., 2024). Rock burst, a phenomenon of coal ejection occurring during the coal seam mining process, entails the release of kinetic energy accompanied by sound, vibration, air blasts, or shock waves. In severe cases, it can lead to the destruction of the roof and floor, or even demolish the mine drifts, potentially resulting in casualties. It represents one of the typical geological disasters in mining engineering (Wang, 2012; Patynska, 2013; Du, 2022; Tahmasebinia et al., 2023). The bursting liability of coal refers to the ability and inherent property of coal to generate impact damage, which is the internal cause and critical condition for rock burst occurrence (Wang, 2012; Wang et al., 2017a; Zhang et al., 2022). According to existing research statistics (Ju et al., 2021), coal seams with strong bursting liability account for 59.04% in the rock burst mines in China, while those with weak bursting liability account for 39.76% and mines with coal seams without bursting liability make up only 1.2% of rock burst incidents. Apart from China, over 450 rock bursts have been detected in the Ostrava-Karvina coalfield since the last century (Ptacek et al., 2017). On 22 February 2020, a rock burst accident occurred at the Longgu mine of Shandong Xinjulong Coal Industry Co., Ltd., resulting in four fatalities. The direct cause was the weak bursting liability of the coal seam and its roof and floor strata in the accident area. Under the influence of large-scale structural stress adjustment and mining disturbance on the working face, the rock burst accident was triggered. Figure 1 shows the damage of the on-site tunnel (Rock-Burst Research Center, 2020).

Figure 1

Figure 1. Damage situation of the roadway at Longgu Mine from 24 m to 40 m on the upper entrance of Sanlian Tunnel.

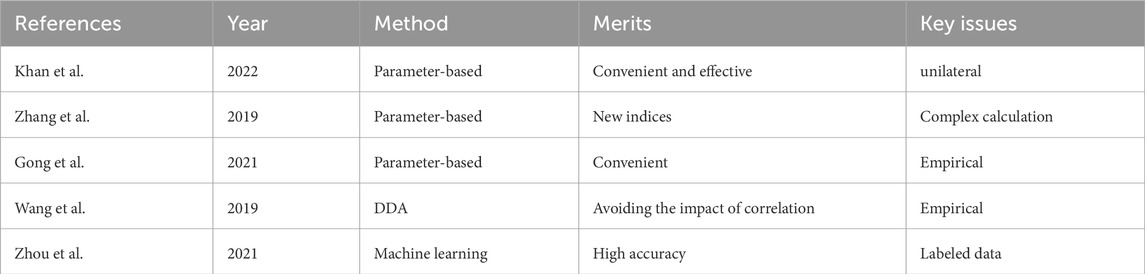
The classification of coal bursting liability is the basic work to prevent rock burst, and also the main basis to evaluate the risk degree of rock burst (Bieniawski, 1967; Kidybiński, 1981; Tan, 1988; Michel et al., 1994; Zhu et al., 2022; Konicek et al., 2013; Zhao et al., 2023; Wang et al., 2019a). The current national standard in China, “Classification and laboratory test method on bursting liability of coal” (GB/T 25217.2-2010) (Standards Press of China, 2010), uses four evaluation indicators: dynamic failure time (DT), elastic energy index (W_ET), bursting energy index (K_E), and uniaxial compressive strength (R_C). Based on the fuzzy comprehensive evaluation method, 73 combinations of evaluation results are given, but there are still 8 combinations that are difficult to determine clearly. In recent years, many scholars have conducted in-depth research on the classification of coal’s bursting liability levels and proposed various classification indicators and methods. Khan et al. (2022) proposed the elastic modulus damage index (EMDI) based on the energy evolution characteristics under different load rates, and used it as a discriminant indicator for coal’s bursting liability; Zhang et al. (2019) comprehensively considered the elastic and damage effects of coal and rock masses, proposed a modified bursting energy index (K_ED), and verified its rationality through PFC2D simulation; Gong et al. (2021) proposed the residual elastic energy index based on the linear energy storage law of rock materials; Wang et al. (2019b) introduced the distance discriminant analysis (DDA) method to evaluate the bursting liability of coal samples, avoiding the impact of correlation between evaluation indicators on the discrimination results; Zhou et al. (2021) used the AHP-entropy weight method to determine the weight of evaluation indicators and proposed an improved classification model for bursting liability of coal samples based on the theory of unascertained measures (Model comparison is shown in Table 1).

Table 1

Table 1. Model comparison of the bursting liability evaluation.

In summary, while there have been many achievements in the research of coal bursting liability classification, the following shortcomings still urgently need to be addressed:

(1) Bursting liability is influenced by various factors, and accurate determination is difficult using only a single classification indicator, while the discrimination results of different indicators sometimes contradict each other. Although GB/T 25217.2-2010 provides discrimination results under 73 different indicator combinations, the boundaries between different levels are not “clear-cut” and the transition between adjacent levels has a certain fuzziness, resulting in difficulty in determining coal sample bursting liability in 8 combinations.

(2) Due to the high degree of dispersion in coal sample test data, there is a problem of evaluation indicator weight offset between different coal bursting liabilities. Existing bursting liability assessment methods often overlook this issue, which affects the accuracy and reliability of evaluation results to a certain extent. Current weight determination methods can be mainly divided into two categories: the subjective weighting method, which is greatly influenced by the subjective intentions of decision-makers and experts, has a high degree of subjectivity and is difficult to optimize based on engineering data; and the objective weighting method, which is entirely determined by objective data, neglects expert subjective opinions, and is prone to be influenced by data fluctuations.

To address the limitations of existing methods for assessing the bursting liability of coal samples, this paper introduced fuzzy set theory to describe the fuzziness between data and levels. The Delphi random forest combined weighting method was used to determine the weights of evaluation indicators in order to reduce the interference of data fluctuations on weights and make the indicator weights more reasonable. Considering the three influencing factors of membership function, fuzzy operator and evaluation principle comprehensively, 16 fuzzy comprehensive evaluation models for bursting liability were established. Performance comparison and analysis of the above models were conducted using 127 sample sets, and the best model was selected for engineering application.

2 Principle

2.1 Fuzzy set theory

The theory of fuzzy sets, first proposed by L.A. Zadeh in 1965, employs membership degree as a means of expressing transitional states between concepts, which are often ambiguous or uncertain in nature. As such, this approach is particularly well-suited to ad-dressing problems characterized by uncertainty or indeterminate boundaries. In recent years, fuzzy set theory has found widespread application in many areas of engineering science (Şebnem, 2019; AI et al., 2023).

Given a domain of discourse U, its fuzzy set (Eq. 1) is defined as:

$U_A:U\to \left[0,1\right]\left(x\in U,U_{A\left(x\right)}\in \left[0,1\right]\right)(1)$

Where: A is a fuzzy set defined on the domain U; U_A(x) is the degree of membership of element x in A; U_A is the membership function defined on the domain U.

2.2 Fuzzy comprehensive evaluation method

Fuzzy comprehensive evaluation uses fuzzy set theory to describe the fuzziness between evaluation indicators and levels of the evaluation objects, and comprehensively evaluate based on this (Zadeh, 1965; Tabbussum et al., 2021). Firstly, two domains are determined: the factor set U= {u₁, u₂, ⋯, um} contains m indicators, where u_i (i=1,2, ⋯, m) are factors that affect the evaluation objects; V= {v₁, v₂, ⋯,v_n} is the evaluation set, where v_j (j=1,2,⋯,n) are possible status levels, and the indicators and levels are subjectively determined according to engineering practical situations. Based on the membership function, a single-factor evaluation is performed on u_i of the factor set U, and the degree of membership of each level in the corresponding evaluation set of u_i is determined, constructing a fuzzy matrix R. The weight set W is constructed according to the weight of each indicator, and then the comprehensive evaluation set B is obtained through fuzzy operation B=W∘R, and finally, the fuzzy comprehensive evaluation result is obtained based on evaluation principle.

3 Establishment of fuzzy comprehensive evaluation model

3.1 Research route and content

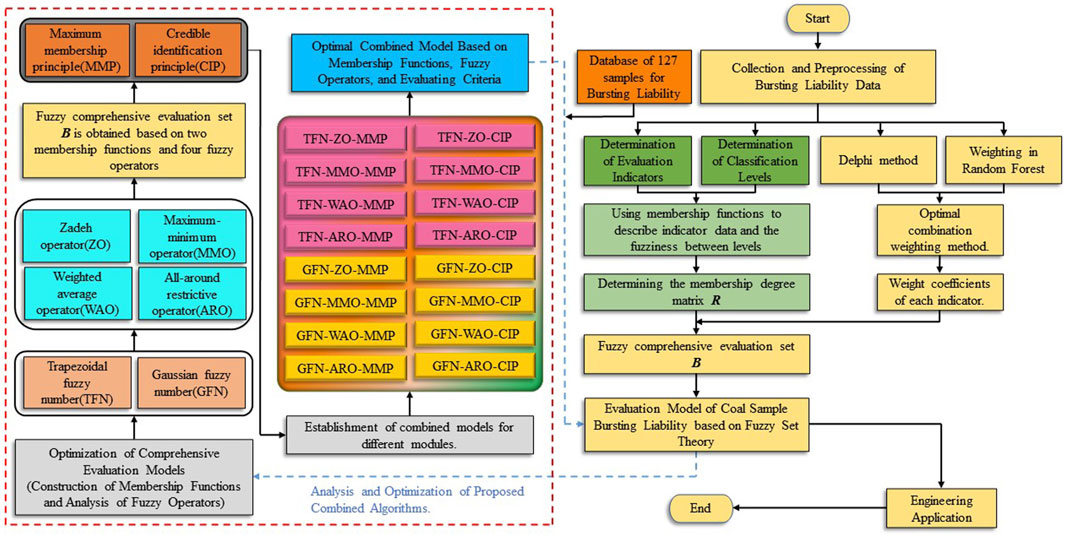
This paper proposes a comprehensive evaluation model for the bursting liability of coal based on fuzzy set theory and discusses the impact of main modeling factors such as membership function, fuzzy operator and evaluation principle on evaluation results, and selects the best comprehensive evaluation model. Figure 2 shows the basic process of con-structing and selecting the best model for the fuzzy evaluation of coal bursting liability. The main research content of this paper is:

(1) Construct an indicator system for classifying the bursting liability of coal.

(2) Based on fuzzy set theory, use trapezoidal fuzzy numbers (TFN) and Gaussian fuzzy numbers (GFN) to describe the fuzziness between indicator data and levels from both linear and nonlinear perspectives.

(3) Adopt the Delphi method-Random Forest combined weighting approach to obtain the optimal combination weights for each evaluation criterion.

(4) Synthesize the weights of indicators and membership degrees using Zadeh operator (ZO), maximum-minimum operator (MMO), weighted-average operator (WAO), and all-around restrictive operator (ARO) to obtain the fuzzy evaluation set B.

(5) Use the maximum membership principle (MMP) and credible identification principle (CIP) to determine the priority of each evaluated object.

(6) Based on fuzzy set theory and three influencing factors, construct 16 models for evaluating the bursting liability of coal samples, and select the optimal model through comparative analysis.

Figure 2

Figure 2. Fuzzy evaluation model for coal bursting liability.

3.2 Establishment of metrics system and sample index

Scientific selection of indicators is crucial to ensure accurate determination of bursting liability. Determining the bursting liability of coal primarily involves identifying the accumulated elastic energy within the coal prior to impact damage and the release rate and proportion of energy during the damage process. Therefore, this study selects dynamic failure time (DT), elastic energy index (W_ET), bursting energy index (K_E), and uniaxial compressive strength (R_C) as the evaluation indicators based on strength theory, energy theory, and related research results (GB/T 25217.2-2010). There are three reasons for selecting these four indicators: 1) They can effectively reflect the energy changes of coal during the processes of energy storage and energy consumption (damage); 2) Each indicator is easy to obtain and interpret; 3) They have been extensively tested through experiments and engineering examples and are the most commonly used evaluation indicators in determining bursting liability.

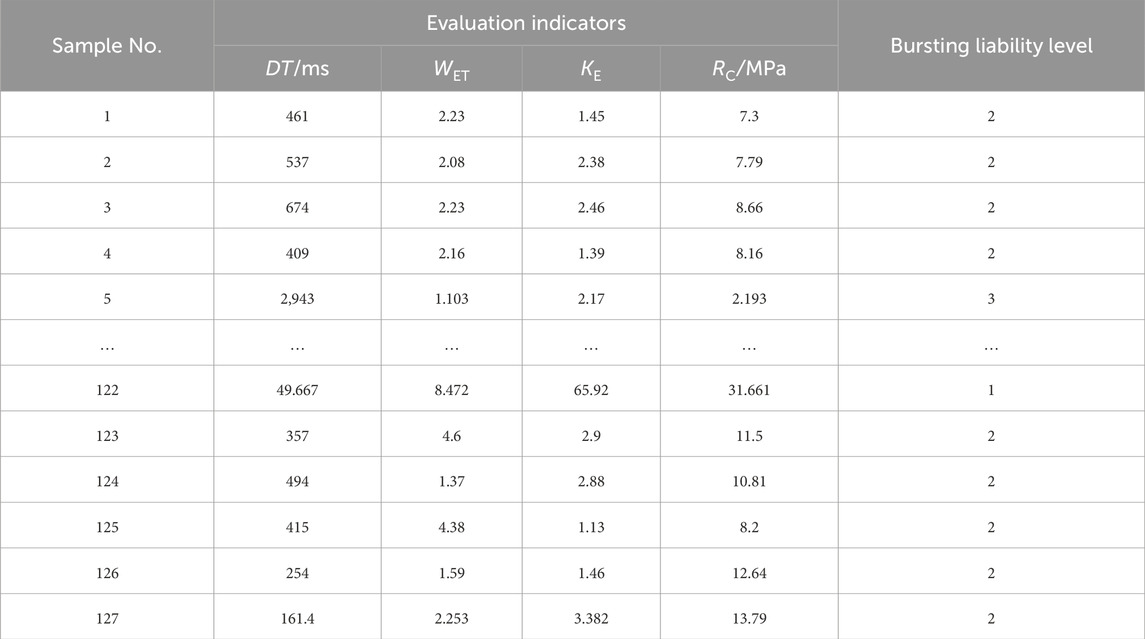
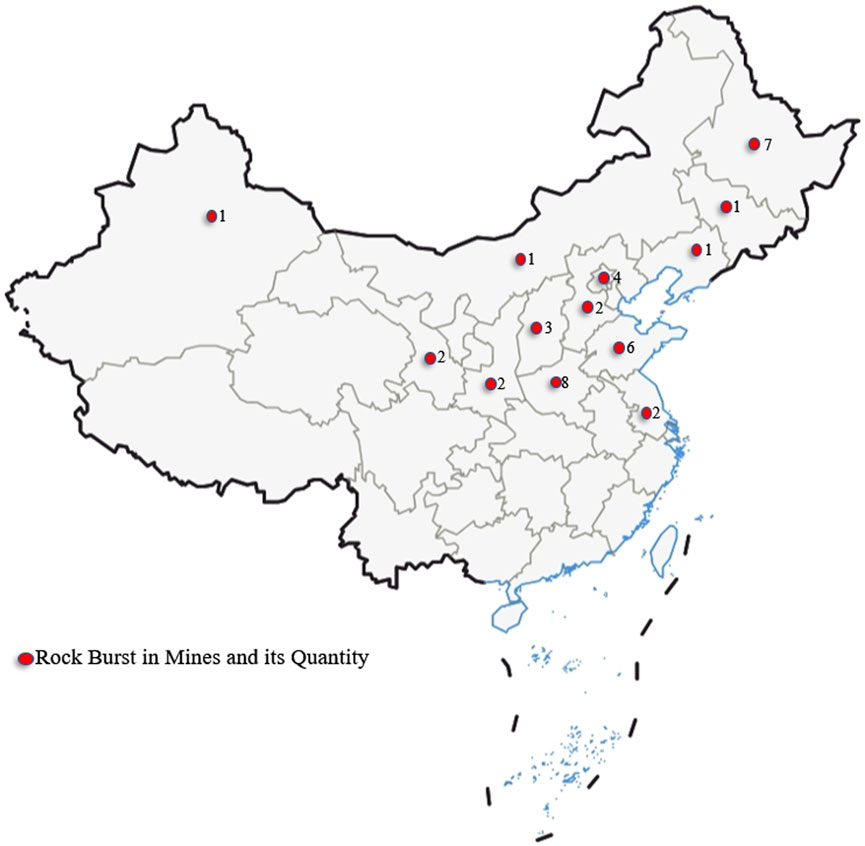
Based on the established metrics system, a sample database was constructed by collecting 127 sets of typical bursting liability samples. (Yan et al., 2011; Song et al., 2012; Li et al., 2014; Wan et al., 2014; Dong et al., 2015; Chen et al., 2016; He et al., 2016; Wang et al., 2017b; Deng et al., 2017; Li et al., 2021) (Partial sample data is shown in Table 2, full data is available in Supplementary Appendix SA). The samples were collected from 40 coal mines in 12 provinces in China, with specific distribution shown in Figure 3.

Table 2

Table 2. Partial bursting liability data.

Figure 3

Figure 3. Distribution of rock burst in mines in the sample data.

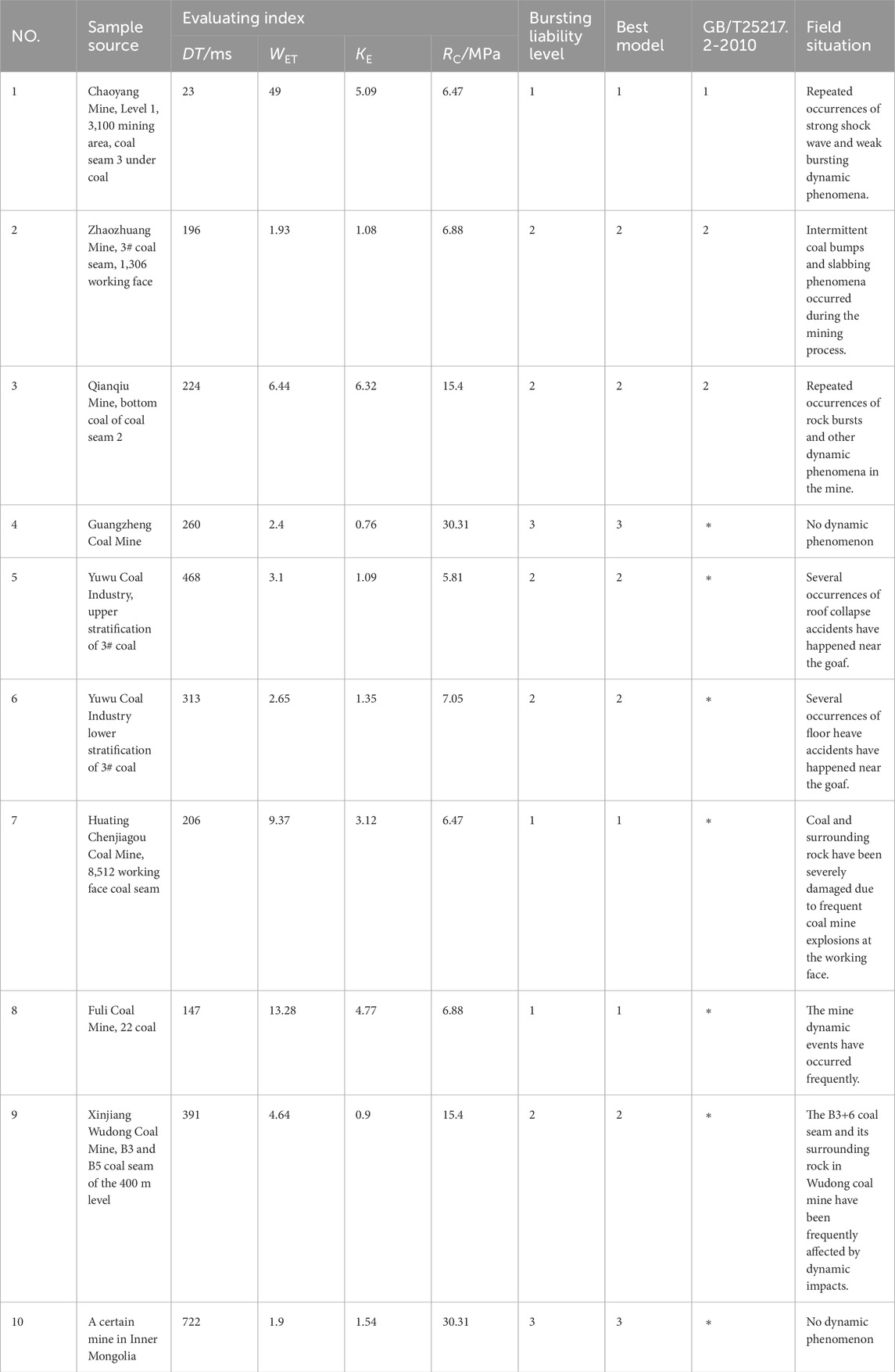
The box plots and Spearman correlation coefficients for the four evaluation indicators selected in this study are shown in Figure 4. Figure 4A–D indicate that the selected data distributions are uniform, and some abnormal values present in the test samples have been taken into account in consideration of realistic field conditions. This can validate the applicability and reliability of the proposed model in engineering applications. Figure 4E shows the correlation between the four indicators, indicating that the correlation between the indicators is weak or non-existent. This suggests that the selected indicators in this study are scientifically and reasonably chosen.

Figure 4

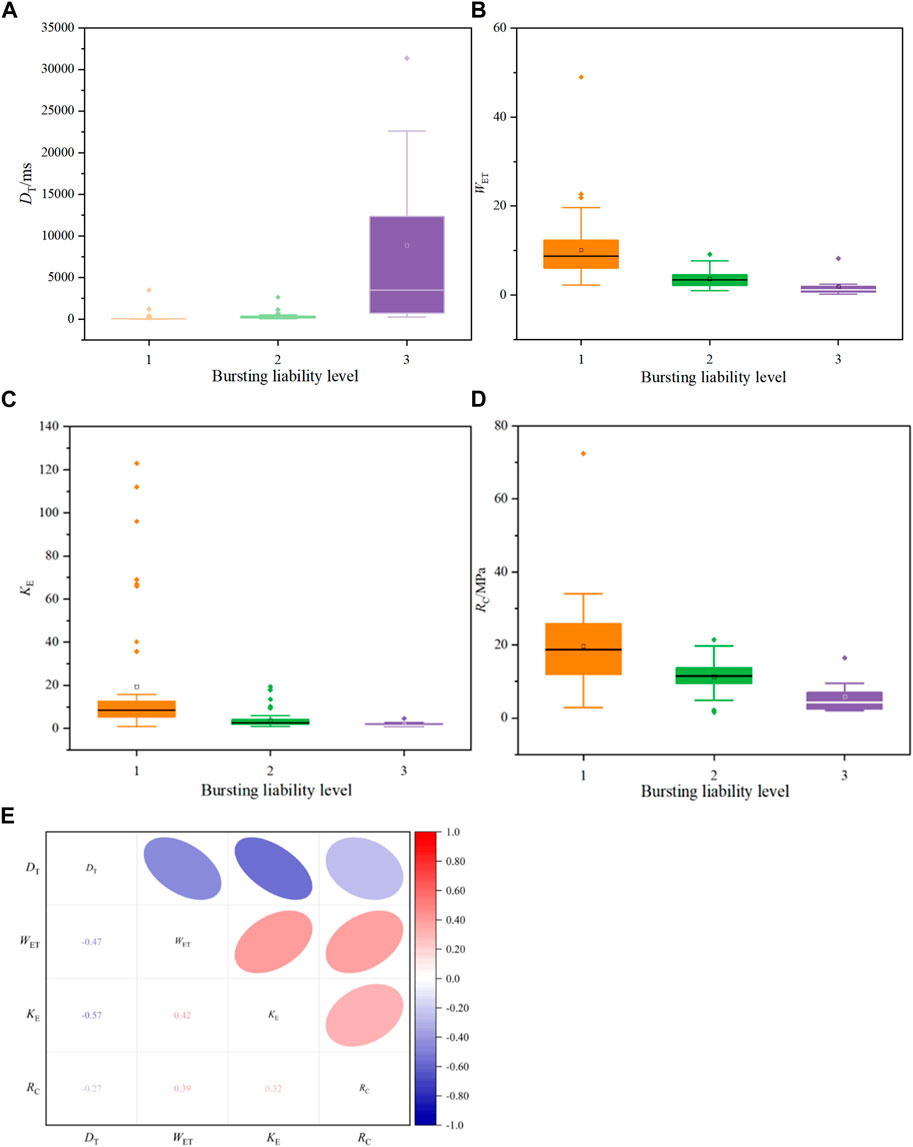
Figure 4. Box plots and correlation coefficients of different evaluation indices in sample data. (A) DT; (B) W_ET; (C) K_E; (D) R_C; (E) Correlation coefficients of different evaluation indices.

According to GB/T 25217.2-2010, Table 3 shows the classification criteria for bursting liability, which divides it into three levels: strong bursting liability (Class 1), weak bursting liability (Class 2), and no bursting liability (Class 3). As shown in Table 1, the sample database contains 53, 67, and 7 samples with strong, weak, and no bursting liability, respectively. The bursting liability evaluation index also has a corresponding quantitative grading, and there is a determined quantification range for a specific set of samples.

Table 3

Table 3. Classification criteria for bursting liability.

3.3 Determine index weights

Due to the discreteness of coal sample data in various parts of the coal seam, it is difficult to conduct specific coal seam discrimination analysis using the commonly used fixed national standard weights. So it can only be used for coal sample bursting liability discrimination at the laboratory scale, which cannot meet the needs of engineering applications and cannot supplement the problem of difficult determination of indicator weights caused by the discreteness of coal sample properties. Therefore, this article adopts the Delphi random forest subjective and objective combination weighting method to determine the weight of bursting liability indicators. It can integrate the advantages of expert engineering skills and coal seam physical and mechanical data driving, and can solve the problem of discrete coal sample properties in indicator weight determination.

3.3.1 Method for determining weights of bursting liability index based on delphi method

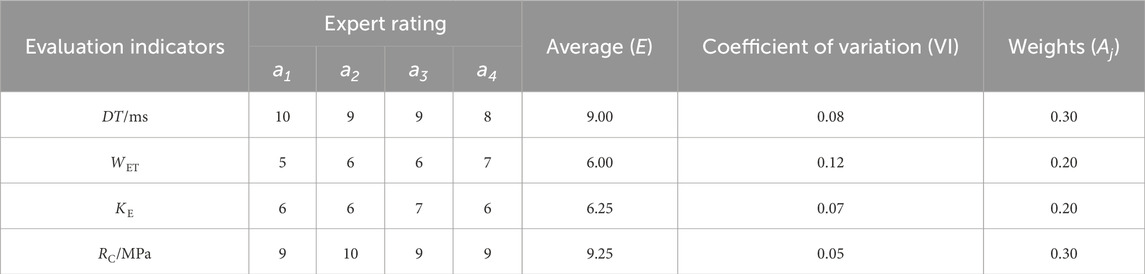
The Delphi method, also known as expert opinion method or expert inquiry survey method (Borch-Johnsen et al., 2023), is essentially a feedback anonymous inquiry method. Its principle is to use an ordered and anonymous continuous individual inquiry plan, and through controlled in-formation feedback to respondents, to clarify and select the judgments given by the expert group for a certain issue when accurate information is difficult to obtain. The steps of the Delphi method are: ①Selecting members of the expert group; ②Designing evaluation inquiry forms; ③Expert inquiry and feedback; ④Determining weights (Eq. 2) and processing results (Eq. 3). The formula for calculation is as follows:

$E={\displaystyle \sum _{w=1}^s}{a}_w/s(2)$

$V_I=D_i/E_i(3)$

Where, E is the mean value of index evaluation importance; aw represents the evaluation score of the w-th expert, with a range of 1–10 points, where 1 represents extremely unimportant and 10 represents extremely important; s is the number of expert consultations; V_I is the coefficient of variation of index importance evaluation, which represents the degree of dispersion of evaluation scores for the same index by different experts; D_i is the standard deviation of index importance evaluation; and E_i is the mean value of importance evaluation for the i-th index.

Then, the weights of each evaluation indicator are normalized (Eq. 4)

$A_j=E_i/{\displaystyle \sum _{i=1}^g}{E}_i(4)$

Where, g is the number of evaluation indicators for bursting liability.

Based on the Delphi method and expert consultations, the data obtained was normalized, and the weights of each evaluation indicator were calculated. The results, shown in Table 4, indicate that the opinions of the four experts on each evaluation indicator are relatively consistent, with coefficient of variation less than 0.25, indicating the reasonability of the subjective weights obtained. Therefore, the weights of the four indicators determined by the Delphi method are 0.30, 0.20, 0.20, and 0.30, respectively.

Table 4

Table 4. Calculation results of indicator weights using the Delphi method.

3.3.2 Method for determining weights of bursting liability index based on delphi method

The Random forest (RF) algorithm is a supervised tree ensemble model consisting of multiple classification trees (Khan et al., 2023). It can perform feature selection at each internal node of the tree, and by comparing the feature importance values of each evaluation index, it can obtain the importance ranking of the indices in the evaluation of Bursting Liability. Mean square error (MSE) or out-of-bag (OOB) error rate is usually used as the evaluation index for measuring the feature importance. In this paper, MSE is used as the cost function to determine the importance of each index parameter. The specific steps are as follows:

(1) Calculate mean square error S_ME (Eq. 5)

$S_{ME}=\frac{{\displaystyle \sum _{i=1}^n}{\left(v_j-\overline{v}\right)}^2}{n}(5)$

Where, n represents the sample size, v_j represents the bursting liability level of each indicator parameter in the sample, and $\overline{v}$ represents the average value of the total bursting liability level in the sample.

(2) Calculate the mean squared error of the node S_ME,ω (Eq. 6)

$S_{ME,\omega }=\frac{n_l·S_{ME,1}+n_r·S_{ME,r}}{n_m}(6)$

Where, n_l represents the number of nodes on the left, S_ME,l is the S_ME of the left node, n_r represents the number of nodes on the right, S_ME,r is the S_ME of the right node, and n_m represents the number of parent nodes.

(3) Calculate the importance score V_IM,im (Eq. 7) of a certain index u_i at node m

$V_{IM,im}=S_{ME,m}-S_{ME,\omega lj}-S_{ME,\omega rj}(7)$

Where, S_ME,m is the S_ME of node m, S_{ME, ωlj} is the S_ME,ω of the left node after branching; and S_{ME, ωrj} is the S_ME,ω of the right node after branching.

(4) Calculate the importance V_IM,ij (Eq. 8) of a certain index u_i in decision tree t

$V_{IM,ti}={\displaystyle \sum _{m\in M}}{V}_{IM,im}(8)$

Where, M is the set of nodes in decision tree t where the j-th bursting liability evaluation index appears.

(5) Calculate the overall importance score V_IM,i (Eq. 9) of a certain index u_i

$V_{IM,i}={\displaystyle \sum _{m\in M}}{V}_{IM,im}(9)$

(6) Obtain the feature importance I_F,I (Eq. 10) for a certain index u_i

$I_{F,i}=\frac{V_{IM,i}}{{\displaystyle \sum _{i=1}^c}{V}_{IM,t}}(10)$

Where, ${\displaystyle \sum _{i=1}^c}{V}_{IM,i}$ is the sum of the overall importance score for all indices, c is the number of indices.

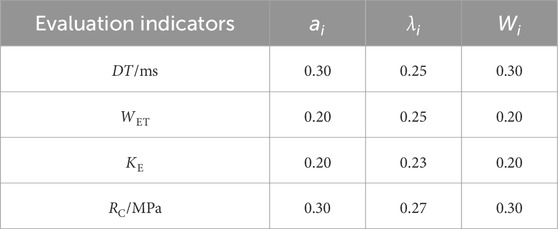
Based on the random forest feature recognition method, after calculating and normalizing the feature importance through the above steps, the weight of the four indices are 0.25, 0.25, 0.23, and 0.27 respectively.

3.3.3 Weight determination based on comprehensive weighting method

The combined weight (Eq. 11) is obtained by using the multiplication synthesis normalization method (Xu et al., 2022) to integrate the subjective weight (obtained by Delphi method) and objective weight (obtained by random forest feature recognition method) calculations mentioned above. The formula for the multiplication synthesis normalization method is:

$W_i=\frac{a_i{\lambda }_i}{\sum a_i{\lambda }_i}(11)$

Where, W_i represents the combined weight, a_i represents the subjective weight obtained through the Delphi method, and λ_i represents the objective weight obtained through the random forest feature recognition method.

The calculated combined weights are shown in Table 5 as follows:

Table 5

Table 5. Combination weight calculation results.

3.4 Establishing membership functions

Membership functions are the basis of fuzzy set theory, which are qualitative descriptions of the intermediate transitions in objective things and directly related to the discrimination results (Bonab et al., 2022). Because the objects studied in fuzzy set theory have fuzziness, there are differences in the understanding and interpretation of the same fuzzy concept by different people, making the determination of membership functions subjective. When using fuzzy mathematics to represent fuzzy phenomena, suitable membership functions should be selected based on the characteristics of the objects to match experimental facts (Adoko et al., 2013; Biasetton et al., 2022; Abdolrasol et al., 2023). In order to select the appropriate membership functions for the classification of bursting liability, this paper establishes indicator membership functions from linear and nonlinear perspectives to describe the fuzziness between indicator data and levels.

3.4.1 Weight determination based on comprehensive weighting method

Trapezoidal fuzzy number are a type of linear membership function that has the advantages of low construction difficulty and strong engineering practicality. Compared with other linear membership functions such as triangular fuzzy numbers, which are difficult to characterize properties with wide peaks, the most likely interval of trapezoidal fuzzy numbers makes up for the above shortcomings. Moreover, the most likely value of triangular fuzzy numbers is usually replaced by the mean, which is not suitable for situations with large discreteness, and large discreteness is an essential characteristic of coal sample data (Mastalerz et al., 1999; Biasetton et al., 2022). Referring to the studies of Khairuddin et al. (2021) and Thangavel et al. (2022), trapezoidal fuzzy numbers are constructed for the evaluation of the level of bursting liability.

First, the corresponding membership function distribution is determined based on the indicator type. For indicators with smaller values being better (i.e., the smaller the value, the stronger the bursting liability), the distribution function of level v₁ adopts a decreasing half-trapezoid distribution function (Eq. (12)) of slightly smaller, the distribution function of level v₂ adopts a middle-type trapezoid distribution function (Eq. (13)), and the distribution function of level v₃ adopts an increasing half-trapezoid distribution function (Eq. (14)) of slightly larger. For indicators with larger values being better (i.e., the larger the value, the stronger the bursting liability), the distribution function of level v₁ adopts an increasing half-trapezoid distribution function (Eq. (14)) of slightly larger, the distribution function of level v₂ still adopts a middle-type trapezoid distribution function (Eq. (13)), and the distribution function of level v₃ adopts a decreasing half-trapezoid distribution function (Eq. (12)) of slightly smaller. Then, according to the classification criteria for bursting liability and expert experience, the parameters a, b, c, and d included in the distribution corresponding to different levels are determined, and the membership degree is calculated by substituting the data into the corresponding membership function. The trapezoidal fuzzy number graph is shown in Figure 5.

(1) Expression for the decreasing half-trapezoid distribution function of slightly smaller

$v_j\left(u_i\right)=\left\{\begin{array}{ll}1,& u_i<a\\ \frac{b-u_i}{b-a},& a\le u_i\le b\\ 0,& b<u_i\end{array}\right.(12)$

(2) Expression for the middle-type trapezoid distribution function

$v_j\left(u_i\right)=\left\{\begin{array}{ll}\frac{u_i-a}{b-a},& a\le u_i<b\\ 1,& b<u_i<c\\ \frac{d-u_i}{d-c},& c\le u_i\le d\\ 0,& x<a\text{\hspace{0.17em}or\hspace{0.17em}}d<x\end{array}\right.(13)$

(3) Expression for the increasing half-trapezoid distribution function of slightly larger

$v_j\left(u_i\right)=\left\{\begin{array}{ll}0,& u_i<a\\ \frac{u_i-a}{b-a},& a\le u_i\le b\\ 1,& b<u_i\end{array}\right.(14)$

Figure 5

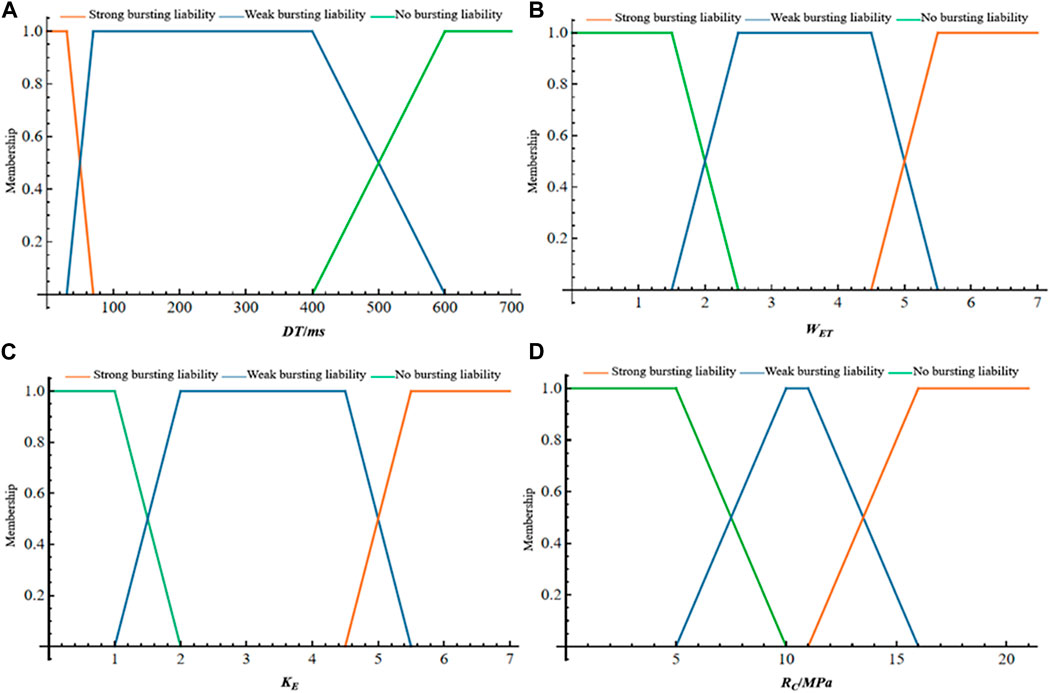
Figure 5. Trapezoidal fuzzy number evaluation index membership function. (A) DT; (B) W_ET; (C) K_E; (D) R_C.

3.4.2 Weight determination based on comprehensive weighting method

Gaussian fuzzy number is used to construct nonlinear fuzzy relationship membership functions (Dombi, 1990). Based on the research of Reddy et al. (2009), Gaussian fuzzy numbers can be constructed (half-Gaussian fuzzy numbers are used when near the extreme value), and the membership function is shown in Figure 6.

Figure 6

Figure 6. Membership function of evaluation index based on Gaussian fuzzy number. (A) DT; (B) W_ET; (C) K_E; (D) R_C.

According to the unbiased estimation theory, any u_i follows a normal distribution with u_i ∼N (μ_i, σ2 i), and the sample mean m_ij (Eq. 15) and sample standard deviation S_i (Eq. 16) of u_i are unbiased estimators of u_i and σ2 i, respectively. The m_ij and S_i of the i-th type of evaluation index for the j-th bursting liability can be expressed as:

$m_{ij}=\frac{1}{n}{\displaystyle \sum _{i=1}^n}{u}_i(15)$

$S_i=\sqrt{\frac{1}{n-1}{{\displaystyle \sum _{i=1}^n}\left(u_i-m_{ij}\right)}^2}(16)$

Based on this, Gaussian fuzzy numbers (Eq. 17) can be constructed (Yazdanpanah et al., 2022):

$v_j\left(u_i\right)=\left\{\begin{array}{ll}0,& u_i<a\\ \frac{u_i-a}{b-a},& a\le u_i\le b\\ 1,& b<u_i\end{array}\right.(17)$

When x_i=m_ij, μ_j (u_i)=1, m_ij (Eq. 18) can be taken as the average of the upper and lower boundary values of evaluation index u_i in the j-level interval. That is:

$m_{ij}=\frac{1}{n}{\displaystyle \sum _{i=1}^n}{u}_i=\frac{u_{ij}^{+}+u_{ij}^{-}}{2}(18)$

Where, $u_{\mathrm{i}}^{+}$ and $u_{\mathrm{i}\mathrm{j}}^{-}$ represent the upper and lower bounds of evaluation index u_i in the j-level interval.

Additionally, the boundary values between each index level should correspond to the same membership degree for two levels. Therefore, the calculation formula for S_i is (Eqs 19, 20):

$\exp \left[-\frac{{\left(u_i-m_{ij}\right)}^2}{2S_i^2}\right]=0.5(19)$

$S_i=\frac{u_{ij}^{+}-u_{ij}^{-}}{\sqrt{-\ln \left(0.5\right)}}(20)$

3.5 Determination of fuzzy comprehensive evaluation set

After quantifying the evaluation index values based on the membership function, the membership degree matrix R is constructed. Each element in R corresponds to a single-factor evaluation value of an indicator, and each calculation unit corresponds to a specific judgment matrix. The membership degree values of each indicator are obtained by using the membership degree function. The fuzzy comprehensive evaluation set of bursting liability category is (Eq. 21a):

$B=W\circ R=\left(w_1,w_2,\cdots ,w_m\right)\circ \left(\begin{array}{cccc}{r}_{11}& r_{12}& \cdots & r_{1n}\\ r_{21}& r_{22}& \cdots & r_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ r_{m1}& r_{m2}& \cdots & r_{mn}\end{array}\right)=\left(b_1,b_2,\cdots ,b_n\right)(\mathrm{21a})$

Where, “∘” is the fuzzy operator.

Different fuzzy operators will change the fuzzy reasoning method and affect the inference results, leading to inaccurate and unreasonable evaluation results of fuzzy evaluation models (Thangavel et al., 2022). Therefore, it is necessary to choose the appropriate fuzzy operator according to the characteristics of the project. Currently, there are four commonly used fuzzy operators, as shown in Table 6.

Table 6

Table 6. Commonly used fuzzy operators.

3.6 Comprehensive evaluation

After obtaining the fuzzy comprehensive evaluation set B, the evaluation result vector needs to be processed in order to obtain the final evaluation result. This method of determining the evaluation result is called the evaluation principle (Zhou et al., 2022). In this paper, the maximum membership principle (He et al., 2021) and the confidence principle (Lovett et al., 2005) are used for evaluation and comparative analysis is carried out.

3.6.1 Maximal membership principle (MMP)

If b_j=max (b₁,b₂,⋯,b_n) after obtaining the fuzzy evaluation set B, the evaluation level of the evaluated object is considered to be at level j.

3.6.2 Credible identification principle (CIP)

Suppose (C₁,C₂,…,C_K) is an ordered evaluation set of property space F, λ is the belief degree, and 0.5<λ≤1, generally taking 0.6–0.7 (Lovett et al., 2005), this paper takes 0.6.

When $C_1>C_2>\dots >C_K$, if it satisfies (Eq. 21b):

$k_0=\mathit{min}\left\{k:{\displaystyle \sum _{l=1}^k}{\mu }_{xl}\ge \lambda ,1\le k\le K\right\}(\mathrm{21b})$

Then the evaluation level of the evaluated object is considered to be at level C_k0.

4 Results and discussion

4.1 Model validation and evaluation

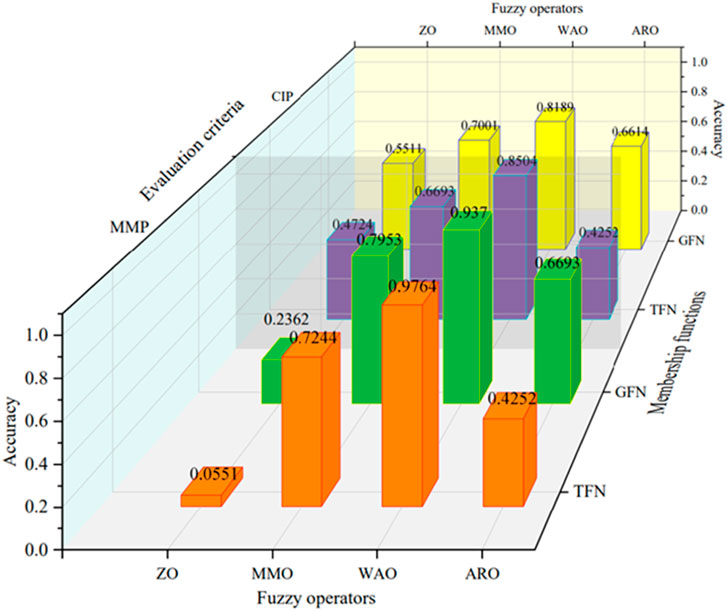
In order to validate the correctness and effectiveness of the comprehensive evaluation model constructed in this paper for classifying bursting liability levels, the effects of membership functions, fuzzy operators, and evaluation principle on the improved model evaluation results were analyzed separately. The 16 comprehensive evaluation models constructed were applied to 127 sets of test data, and the accuracy was used to evaluate the performance of the classification model. The accuracy of each evaluation model is shown in Figure 7. (The evaluation results of each model level can be found in Supplementary Appendix SA, SB).

Figure 7

Figure 7. Comparison of accuracy for different fuzzy comprehensive evaluation models.

4.2 Impact analysis of membership functions on the model

Life Science Identifiers (LSIDs) for ZOOBANK registered names or nomenclatural acts should be listed in the manuscript before the keywords with the following format:

In existing research, scholars generally focus on the application methods of evaluation models themselves and rarely systematically analyze the matching between mathematical factors in the modeling process and the evaluated objects and their impact on the evaluation results. This paper constructs a comprehensive evaluation model based on fuzzy set theory through theoretical analysis and calculations.

As shown in Figure 7, membership functions have different effects on the model evaluation results. The average accuracy of the model using trapezoidal fuzzy numbers and Gaussian fuzzy numbers are 57.48% and 67.42%, respectively. Although the model established using Gaussian fuzzy numbers has a higher average accuracy, the Trapezoidal fuzzy number- Weighted average operator- Maximal membership principle (TFN-WAO-MMP) model based on trapezoidal fuzzy numbers has the highest accuracy among the 16 models, reaching 97.64%.

From the evaluation results, trapezoidal fuzzy numbers (TFN) are suitable for evaluation indicators with wide peak intervals (such as D_T, R_C), and their most likely interval can better characterize the discreteness of coal sample data. They are good at dealing with “outlier” problems that some evaluation methods and machine learning models find difficult to solve. However, their linear expression method also leads to the loss of some intermediate information in the evaluation process. Gaussian fuzzy numbers have strong universality in nonlinear representation of fuzzy features and are almost applicable to all random variable distributions. They can better preserve some intermediate information and overall improve the accuracy of the model, but it is difficult to apply to special cases with wide indicator ranges and large changes.

4.3 Impact analysis of membership functions on the model

As shown in Figure 7, different fuzzy operators have a significant impact on the evaluation results of the model. The average accuracy of the model using Zadeh operator, maximum-minimum operator, weighted average operator, and all-around restrictive operator (ARO) are 26.38%, 69.69%, 91.34%, and 42.52%, respectively. It can be seen that the accuracy of the model using the weighted average operator is significantly higher than the other three operators, while the accuracy of the model using the Zadeh operator is the worst. The accuracy of the evaluation model using the maximum membership principle under different operators fluctuates greatly, with the highest difference reaching 92.13% and the lowest being 25.20%. The evaluation model using the weighted average operator has the highest accuracy under both evaluation principle (maximum membership principle, credible identification principle), which can better represent the fuzzy relationship between the evaluation indicators and the bursting liability category.

From the analysis of the evaluation process, the weights of the four indicators in the bursting liability discrimination are relatively balanced, making it difficult to distinguish between importance. The characteristic of the Zadeh operator is that the main factor plays a decisive role, and it is not sensitive to weights and ignores the impact of intermediate factors on bursting liability, resulting in inaccurate evaluation. The maximum-minimum operator is an improvement based on the Zadeh operator. Although it weakens the role of the main factor, it is essentially a main factor prominent type. From the results, the number of samples that are difficult to distinguish is reduced significantly compared to the Zadeh operator. The all-around restrictive operator is the opposite of the Zadeh operator, focusing on the impact of secondary factors on the evaluation result, which leads to a large number of samples that are difficult to distinguish under both evaluation principle. The weighted average operator considers the impact of all factors, and its weight function has a significant effect, providing clear discrimination results for all samples.

4.4 Impact analysis of evaluation principle on the model

As shown in Figure 7, evaluation principles have different impacts on the accuracy of the model, with average accuracies of 54.53% and 60.43% for models based on the maximum membership principle and the credible identification principle, respectively. The credible identification principle performs better in models with a large number of difficult-to-distinguish samples, with a higher average accuracy than the model based on the maximum membership principle. However, the model using the maximum membership principle has a higher maximum accuracy, and the model using the weighted average operator based on the maximum membership principle has an accuracy as high as 97.64%.

From the evaluation results, although the credible identification principle can comprehensively consider intermediate information and solve unclear grading evaluation situations, it overemphasizes intermediate factors, ignores the impact of main or secondary factors on the evaluation result, and as a result, the maximum accuracy of the model is not high enough, and it is difficult to fully consider all factors. The maximum membership principle can comprehensively consider the impact of all factors, but it is also prone to overemphasize the extreme values and lead to unreasonable evaluations. Therefore, it needs to be used in conjunction with the weighted average operator for model construction.

4.5 Model selection

Based on the analysis of the research above, combined with the accuracy comparison of various comprehensive evaluation models in Figure 7, the best model selected in this paper is the TFN-WAO-MMP combined model.

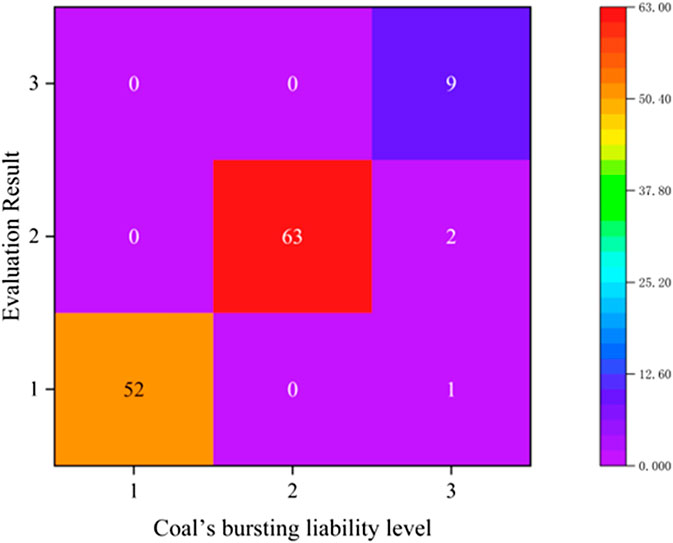
Confusion matrix is a standard visualization tool used to describe model classification performance (Kardani et al., 2021). In this paper, the determination of bursting liability is a three-class classification problem. Therefore, we can use the confusion matrix to visually describe the performance of the TFN-WAO-MMP combined model, as shown in Figure 8. The numbers on the diagonal from the upper right corner to the lower left corner in the figure indicate the number of samples where the evaluation values and actual values are consistent. The other positions indicate the number of samples where the evaluation values and actual values do not match. It can be seen that the TFN-WAO-MMP combined model has good performance in determining the bursting liability.

Figure 8

Figure 8. Confusion matrix of the TFN-WAO-MMP combined model.

5 Engineering application

In order to further verify the effectiveness and practicality of the best model, the Trapezoidal fuzzy number- Weighted average operator- Maximal membership principle (TFN-WAO-MMP) combined model selected in this paper was used to determine the bursting liability of 10 engineering examples in Table 7, and the results were compared with the results given by the national standard GB/T 25217.2-2010. As shown in Table 7, the best model in this study produced consistent results with the standard for example, 1 to Example 3 but the national standard cannot determine the bursting liability levels of Example 4 to Example 10. However, the results obtained by the best model are in line with the actual engineering situations.

Table 7

Table 7. Engineering examples and determination results.

Figure 9 presents a comparison of the evaluation results of the combined weighting method proposed in this study with those of the entropy weighting method, CRITIC method, and coefficient of variation method applied to the optimization model. Figure 9A shows the evaluation results of the optimal combined weighting method proposed in this study, which is consistent with the actual engineering situation, and its accuracy is significantly higher than that of the objective weighting method. Figure 9B–9D show that when the indicator data fluctuates, the weights determined by the objective weighting method are unreasonable and bias towards a certain indicator, making it difficult to comprehensively consider various indicators. This indicates that the accuracy of the coal bursting liability evaluation model based on the combined weighting-fuzzy set theory is high and verifies the feasibility and effectiveness of the model in coal bursting liability evaluation.

Figure 9

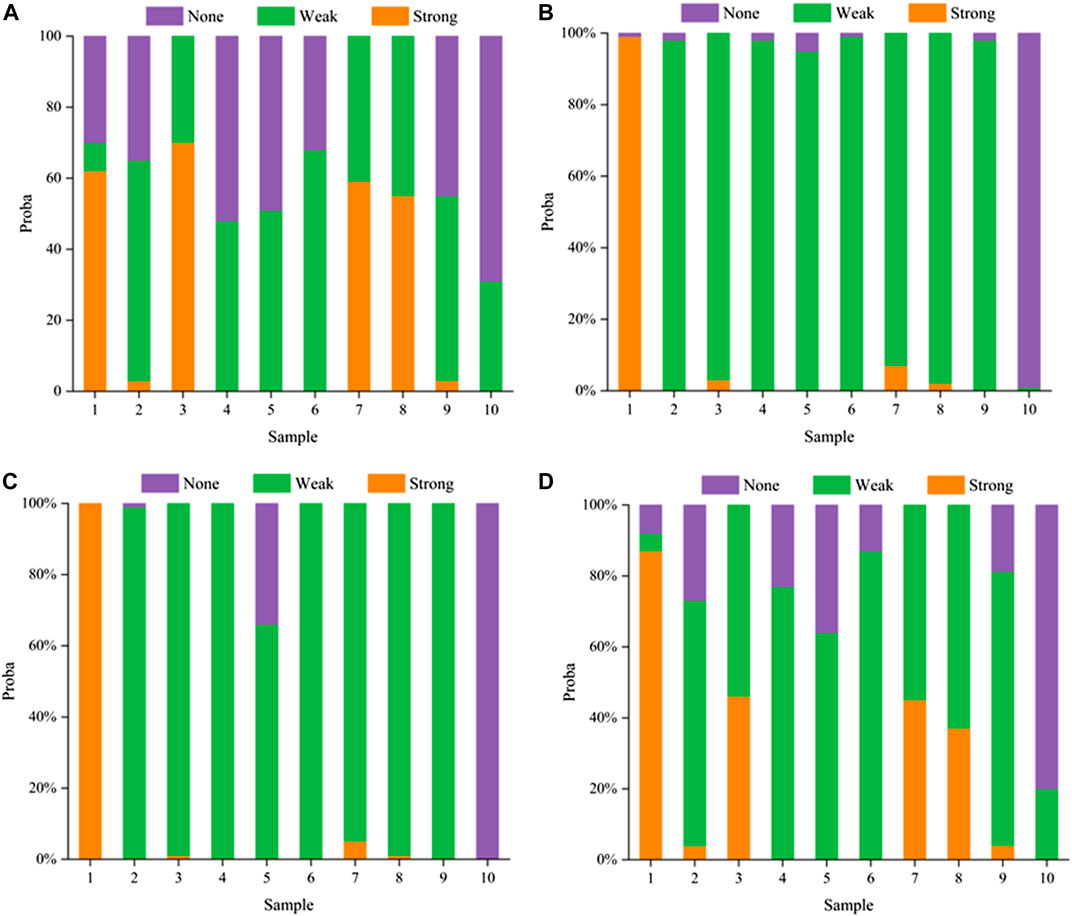
Figure 9. Comparison of evaluation results using four weighting methods. (A) Optimal combination weighting method; (B) Entropy weighting method; (C) CRITIC method; (D) Coefficient of variation method.

In this study, specific analysis was conducted with Example 7. During the excavation of the 8512-working face in the Chenjiagou coal mine in Huating, the mining pressure was apparent, and “coal explosion” sounds occurred. The surrounding rock of the roadway deformed significantly, and local support bodies had been damaged. The specific occurrence of mining pressure was that there was a total of 17 recorded “explosion sounds” in the return airway of the 8512-working face. According to incomplete statistics, 1,558 anchor rods and cables were broken due to the pressure. There were 14 recorded “explosion sounds” in the transportation return airway of the 8512-working face. According to incomplete statistics, 1980 anchor rods and cables were broken due to pressure. During the coal bursting liability identification test, individual coal samples under their natural state experienced sudden explosive dynamic destruction, pulverized into debris, and were ejected at a relatively high speed. This indicates that the coal sample’s bursting liability is strong under its natural state. It can be seen that the discriminant result of the optimal model constructed in this study is consistent with the engineering field situation, and other models make false judgments.

To sum up, the combination model TFN-WAO-MMP constructed based on the combined weighting-fuzzy set theory can accurately determine the level of coal bursting liability level. The main advantages include: 1) Compared with traditional fuzzy evaluation methods, TFN-WAO-MMP better retains the fuzzy information of the data, makes full use of engineering data to accurately evaluate the level of bursting liability. When constructing the membership function, it considers more comprehensively (such as normalization, non-negativity, and additivity of the membership degree), which can solve the problem of eight samples that are difficult to distinguish in the current national standard. 2) Compared with existing comprehensive evaluation methods and machine learning methods, TFN-WAO-MMP is not restricted by sample data and can obtain related parameters only by expert evaluation method based on the index grading criteria. Moreover, the model is simple and practical, which can evaluate the bursting liability level of underground engineering without sample data and has strong applicability. 3) The Delphi-random forest combination weighting method proposed in this study can solve the problem of objectivity weighting method being greatly affected by data fluctuations and improve the shortcomings of the subjective weighting method being limited by the discreteness of coal sample data and the difficulty in updating weights at all stages, thus improving the rationality and reliability of indicator weights.

6 Conclusion

(1) To address the deficiencies in the current discrimination methods, this study conducted a comprehensive evaluation of coal impact tendency using the combined weighting-fuzzy set theory. The Delphi method and random forest weighting method were used to determine the weights of each evaluation index. The optimal combination weighting method was determined using multiplication synthesis method. Based on two membership functions, four fuzzy operators, and two evaluation principle, 16 fuzzy mathematical comprehensive evaluation models were established.

(2) Based on 127 sets of sample discrimination results, the impact of membership functions, fuzzy operators, and evaluation principle on the model evaluation results was systematically analyzed. The Trapezoidal fuzzy number- Weighted average operator- Maximal membership principle (TFN-WAO-MMP) combined model was selected as the optimal fuzzy comprehensive evaluation model, with an accuracy of 97.64%.

(3) The Delphi method and random forest-optimal combined model were applied to 10 engineering examples, and the discrimination results were completely consistent with the actual situation. Compared with other evaluation methods, this method improved the efficiency of evaluation and avoided the effect of data fluctuations on weight determination. It also improved the rationality and reliability of indicator weights and effectively solved the problem of the eight samples that are difficult to distinguish in the national standard. This study is a beneficial supplement and improvement to the national standard and existing evaluation methods.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

CW: Writing–review and editing, Conceptualization, Funding acquisition, Methodology, Software, Supervision. ZJ: Writing–review and editing, Writing–original draft. XL: Project administration, Supervision, Writing–review and editing. TW: Investigation, Software, Writing–review and editing. YL: Writing–review and editing. SZ: Formal Analysis, Writing–review and editing. QW: Investigation, Methodology, Validation, Visualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was supported by the National Natural Science Foundation of China (42,367,024), the Key Laboratory of Safety and High-efficiency Coal Mining, Ministry of Education (Anhui University of Science and Technology) (JYBSYS202307), the Major Science and Technology Special Project of Yunnan Province (202202AG050014).

Acknowledgments

The authors are very grateful to the reviewers for carefully reading the manuscript and providing valuable suggestions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2024.1378956/full#supplementary-material

References

Abdolrasol, M., Ayob, A., Mutlag, A., and Ustun, T. (2023). Optimal fuzzy logic controller based PSO for photovoltaic system. Energy Rep. 9, 427–434. doi:10.1016/j.egyr.2022.11.039

CrossRef Full Text | Google Scholar

Adoko, A., Gokceoglu, C., Wu, L., and Zuo, Q. (2013). Knowledge-based and data-driven fuzzy modeling for rockburst prediction. Int. J. Rock Mech. Min. Sci. 61, 86–95. doi:10.1016/j.ijrmms.2013.02.010

CrossRef Full Text | Google Scholar

Al, F., Petrovic, D., and Doctor, F. (2023). A Non-Iterative reasoning algorithm for fuzzy cognitive maps based on Type 2 Fuzzy Sets. Inf. Sci. 622, 319–336. doi:10.1016/j.ins.2022.11.152

CrossRef Full Text | Google Scholar

Biasetton, N., Disegna, M., Barzizza, E., and Salmaso, L. (2022). A new adaptive membership function with CUB uncertainty with application to cluster analysis of Likert-type data. Expert Syst. Appl. 213, 118893. doi:10.1016/j.eswa.2022.118893

CrossRef Full Text | Google Scholar

Bieniawski, Z. (1967). Mechanism of brittle fracture of rocks. Int. J. Rock Mech. Min. Sci. 4 (4), 395–430. doi:10.1016/0148-9062(67)90030-7

CrossRef Full Text | Google Scholar

Bonab, S., Ghoushchi, S., Deveci, M., and Haseli, G. (2022). Logistic autonomous vehicles assessment using decision support model under spherical fuzzy set integrated Choquet Integral approach. Expert Syst. Appl. 214, 119205. doi:10.1016/j.eswa.2022.119205

CrossRef Full Text | Google Scholar

Borch-Johnsen, L., Andres-Jensen, L., Folke, F., Espersen, M., Amstrup, S., Frederiksen, M., et al. (2023). Development of video tutorials to help parents manage children with acute illnesses using a modified Delphi method. Acta Paediatr. 112 (7), 1574–1585. doi:10.1111/apa.16805

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, J. (2016). Study on theory of disaster induced by rock burst of roadway floor with wide coal pillar and the prevention techniques. Beijing: China University of Mining and Technology.

Google Scholar

Deng, Q. (2017). Study on underground pressure control in fully mechanized caving face of burst coal seam in Chenjiagou Mine. Xi'an, China: Xi'an University of Science and Technology.

Google Scholar

Dombi, J. (1990). Membership function as an evaluation. Fuzzy Set. Syst. 35, 1–21. doi:10.1016/0165-0114(90)90014-W

CrossRef Full Text | Google Scholar

Dong, L., Tao, Q., Hu, Q., Deng, Y., Chen, Y., Luo, Q., et al. (2022). Acoustic emission source location method and experimental verification for structures containing unknown empty areas. Int. J. Min. Sci. Technol. 32 (3), 487–497. doi:10.1016/j.ijmst.2022.01.002

CrossRef Full Text | Google Scholar

Dong, Y. (2015). Research on rock burst risk of working face in the zhaozhuang mine. Anshan, China: Liaoning Technical University.

Google Scholar

Du, F., Ma, J., Guo, X., Wang, T., Dong, X., Li, J., et al. (2022). Rockburst mechanism and the law of energy accumulation and release in mining roadway: a case study. Int. J. Coal Sci. Technol. 9 (1), 67. doi:10.1007/s40789-022-00521-0

CrossRef Full Text | Google Scholar

Gong, F., Wang, Y., Wang, Z., Pan, J., and Luo, S. (2021). A new criterion of coal burst proneness based on the residual elastic energy index. Int. J. Min. Sci. Technol. 31 (4), 553–563. doi:10.1016/j.ijmst.2021.04.001

CrossRef Full Text | Google Scholar

He, S., Shen, F., Chen, T., Chen, B., Mitri, H., Ren, T., et al. (2023). Study on the seismic damage and dynamic support of roadway surrounding rock based on reconstructive transverse and longitudinal waves. Adv. Geo-Energy Res. 9 (3), 156–171. doi:10.46690/ager.2023.09.04

CrossRef Full Text | Google Scholar

He, S., Song, D., Mitri, H., He, X., Chen, J., Li, Z., et al. (2021). Integrated rockburst early warning model based on fuzzy comprehensive evaluation method. Int. J. Rock Mech. Min. Sci. 142, 104767. doi:10.1016/j.ijrmms.2021.104767

CrossRef Full Text | Google Scholar

He, Y. (2016). Study on rock burst of wudong near-vertical coal seams and impact protection with constant resistance and large deformation supporting. Beijing: China University of Mining and Technology.

Google Scholar

Ju, W., Lu, Z., Gao, F., Zhao, Y., Li, W., Sun, Z., et al. (2021). Research progress and comprehensive quantitative evaluation index of coal rock bursting liability. Chin. J. Rock Mech. Eng. 40 (9), 1839–1856. doi:10.13722/j.cnki.jrme.2021.0485

CrossRef Full Text | Google Scholar

Kardani, N., Zhou, A., Nazem, M., and Shen, S. (2021). Improved prediction of slope stability using a hybrid stacking ensemble method based on finite element analysis and field data. J. Rock Mech. Geotech. Eng. 13 (1), 188–201. doi:10.1016/j.jrmge.2020.05.011

CrossRef Full Text | Google Scholar

Khairuddin, S., Hasan, M., Hashmani, M., and Azam, M. (2021). Generating clustering-based interval fuzzy type-2 triangular and trapezoidal membership functions: a structured literature review. Symmetry-Basel. 13 (2), 239. doi:10.3390/sym13020239

CrossRef Full Text | Google Scholar

Khan, A., Kim, B., Rizwan, A., Ahmad, R., Iqbal, N., Kim, K., et al. (2023). A new method for determination of optimal borehole drilling location considering drilling cost minimization and sustainable groundwater management. ACS Omega 8 (12), 10806–10821. doi:10.1021/acsomega.2c06854

PubMed Abstract | CrossRef Full Text | Google Scholar

Khan, N., Ahmad, M., Cao, K., Ali, I., Liu, W., Rehman, H., et al. (2022). Developing a new bursting liability index based on energy evolution for coal under different loading rates. Sustainability 14 (3), 1572. doi:10.3390/su14031572

CrossRef Full Text | Google Scholar

Kidybiński, A. (1981). Bursting liability indices of coal. Int. J. Rock Mech. Min. Sci. 18 (4), 295–304. doi:10.1016/0148-9062(81)91194-3

CrossRef Full Text | Google Scholar

Konicek, P., Soucek, K., Stas, L., and Singh, R. (2013). Long-hole destress blasting for rockburst control during deep underground coal mining. Int. J. Rock Mech. Min. Sci. 61, 141–153. doi:10.1016/j.ijrmms.2013.02.001

CrossRef Full Text | Google Scholar

Li, B. (2014). Study on induced mechanism of roadway floor rock burst under super-thick conglomerate stratum. Luoyang, China: Henan University of Technology.

Google Scholar

Li, Y. (2021). Study on mechanism and prevention method of coal bump controlled by large geological body. Beijing, China: Graduate School of China Coal Research Institute.

Google Scholar

Li, Y., Wang, C., and Liu, Y. (2023). Classification of coal bursting liability based on support vector machine and imbalanced sample set. Minerals 13 (1), 15. doi:10.3390/min13010015

CrossRef Full Text | Google Scholar

Li, Y., Wang, C., Xu, J., Zhou, Z., Xu, J., and Cheng, J. (2021). Rockburst prediction based on the KPCA-APSO-SVM model and its engineering application. Shock Vib. 2021, 1–12. doi:10.1155/2021/7968730

CrossRef Full Text | Google Scholar

Linghu, J., Zhao, W., Zhou, J., Yan, Z., Wang, K., Xu, C., et al. (2021). Influence of deep magma-induced thermal effects on the regional gas outburst risk of coal seams. Int. J. Coal Sci. Technol. 8 (6), 1411–1422. doi:10.1007/s40789-021-00452-2

CrossRef Full Text | Google Scholar

Lovett, T., Ponci, F., and Monti, A. (2005). A polynomial chaos approach to measurement uncertainty. IEEE Trans. Instrum. Meas. 55, 729–736. doi:10.1109/AMUEM.2005.1594600

CrossRef Full Text | Google Scholar

Mastalerz, M., and Padgett, P. (1999). From in situ coal to the final coal product: a case study of the Danville Coal Member (Indiana). Int. J. Coal Geol. 41 (1-2), 107–123. doi:10.1016/S0166-5162(99)00013-0

CrossRef Full Text | Google Scholar

Michel, A., Denis, E., and Richard, S. (1994). “On the use of the Brittleness Index Modified (BIM) to estimate the Post-Peak behavior of rocks,” in The first north American rock mech, austin, America, 1–3.

Google Scholar

Patynska, R. (2013). The consequences of the rock burst hazard in the Silesian companies in Poland. Acta Geodyn. Geomater. 10 (2), 227–235. doi:10.13168/AGG.2013.0023

CrossRef Full Text | Google Scholar

Ptacek, J. (2017). Rock burst in ostrava-karvina coalfield. Procedia Eng. 191, 1144–1151. doi:10.1016/j.proeng.2017.05.289

CrossRef Full Text | Google Scholar

Qiu, L., Zhu, Y., Liu, Q., Guo, M., Song, D., and Wang, A. (2023). Response law and indicator selection of seismic wave velocity for coal seam outburst risk. Adv. Geo-Energy Res. 9 (3), 198–210. doi:10.46690/ager.2023.09.07

CrossRef Full Text | Google Scholar

Reddy, C., and Raju, K. (2009). An improved fuzzy approach for COCOMO’s effort estimation using Gaussian membership function. J. Softw. 4 (5), 452–459. doi:10.4304/jsw.4.5.452-459

CrossRef Full Text | Google Scholar

Ren, F., Zhu, C., He, M., Shang, J., Feng, G., and Bai, J. (2023a). Characteristics and precursor of static and dynamic triggered rockburst: insight from multifractal. Rock Mech. Rock Eng. 56 (3), 1945–1967. doi:10.1007/s00603-022-03173-3

CrossRef Full Text | Google Scholar

Ren, F., Zhu, C., Yuan, Z., Karakus, M., Tang, S., and He, M. (2023b). Recognition of shear and tension signals based on acoustic emission parameters and wave form using machine learning methods. Int. J. Rock Mech. Min. Sci. 171, 105578. doi:10.1016/j.ijrmms.2023.105578

CrossRef Full Text | Google Scholar

Rock-Burst Research Center (2020). Investigation report on 2.22 Rock burst accident of Shandong. Shandong, China: New Julong Energy Co Ltd. Available at: https://burst.cumt.edu.cn/zxgk/zzjg.htm (Accessed April 21, 2020).

Google Scholar

Şebnem, Y. (2019). Decision-making for biomass-based production chains. 1. London, England: Academic Press, 113–142.

Google Scholar

Song, D. (2012). Research on rock burst evolutionary process and energy dissipation characteristics. Xuzhou, China: China University of Mining and Technology.

Google Scholar

Tabbussum, R., and Dar, A. (2021). Performance evaluation of artificial intelligence paradigms-artificial neural networks, fuzzy logic, and adaptive neuro-fuzzy inference system for flood prediction. Environ. Sci. Pollut. Res. 28 (20), 25265–25282. doi:10.1007/s11356-021-12410-1

CrossRef Full Text | Google Scholar

Tahmasebinia, F., Adam, Y., Feghali, P., and Skrzypkowski, K. (2023). A Numerical investigation to calculate ultimate limit state capacity of cable bolts subjected to impact loading. Appl. Sci-Basel. 13 (1), 15. doi:10.3390/app13010015

CrossRef Full Text | Google Scholar

Thangavel, K., Seerengasamy, U., Palaniappan, S., and Sekar, R. (2022). Prediction of factors for controlling of green house farming with fuzzy based multiclass Support Vector Machine. Alex Eng. J. 62, 279–289. doi:10.1016/j.aej.2022.07.016

CrossRef Full Text | Google Scholar

The Professional Standards Compilation Group of People's Republic of China (2010). GT/T25217.2-2010 Classification and laboratory test method on bursting liability of coal. Beijing: Standards Press of China.

Google Scholar

Wan, C. (2014). Prediction on rock burst and prevention research in the No.3 district of dongtan coalmine. Anshan, China: Liaoning Technical University.

Google Scholar

Wang, C. (2017a). Study of coal seam rock burst tendency index under effectively impact energy rate. J. Min. Strat. Control Eng. 22 (5), 9–12. (in Chinese). doi:10.13532/j.cnki.cn11-3677/td.2017.05.003

CrossRef Full Text | Google Scholar

Wang, C., Li, Y., Zhang, C., Liu, L., and Huang, X. (2019a). Study on influence of indicator dimensionless on classification model of coal's bursting liability. China Saf. Sci. J. 29 (11), 20–25. doi:10.16265/j.cnki.issn1003-3033.2019.11.004

CrossRef Full Text | Google Scholar

Wang, C., Liu, Y., Song, D., Xu, J., Wang, Q., and Zhang, S. (2024a). Evaluation of bedding effect on the bursting liability of coal and coal-rock combination under different bedding dip angles. Adv. Geo-Energy Res. 11 (1), 29–40. doi:10.46690/ager.2024.01.04

CrossRef Full Text | Google Scholar

Wang, C., Song, D., Zhang, C., Liu, L., Zhou, Z., and Huang, X. (2019b). Research on the classification model of coal’s bursting liability based on database with large samples. Arab. J. Geosci. 12 (13), 411. doi:10.1007/s12517-019-4562-2

CrossRef Full Text | Google Scholar

Wang, C., Wang, E., and Liu, X. (2012). Classification of rock burst tendency of coal seam based on entropy and ideal point method. J. Liaoning Tech. Univ. Nat. Sci. Ed. 31 (6), 838–841. (in Chinese). doi:10.4028/www.scientific.net/amr.962-965.375

CrossRef Full Text | Google Scholar

Wang, K., Zhang, G., Wang, Y., Zhang, X., Li, K., Guo, W., et al. (2022). A numerical investigation of hydraulic fracturing on coal seam permeability based on PFC-COMSOL coupling method. Int. J. Coal Sci. Technol. 9 (1), 10. doi:10.1007/s40789-022-00484-2

CrossRef Full Text | Google Scholar

Wang, L. (2017b). Study on danger area categorization of rock outburst of mining stope affected by faults. China coal. 43 (02), 108–113. doi:10.3969/j.issn.1006-530X.2017.02.024

CrossRef Full Text | Google Scholar

Wang, Q., Wang, C., Liu, Y., Xu, J., Wang, T., Li, Y., et al. (2024b). Exploration and improvement of fuzzy evaluation model for rockburst. Min. Metallurgy Explor. 41, 559–587. doi:10.1007/s42461-024-00933-3

CrossRef Full Text | Google Scholar

Xu, C., Zhang, Y., Zhang, W., Zu, H., Zhang, Y., and He, W. (2022). An ensemble learning method based on an evidential reasoning rule considering combination weighting. Comput. Intell. Neurosci. 42, 1–17. doi:10.1155/2022/1156748

CrossRef Full Text | Google Scholar

Yan, R. (2011). Research on the mechanism and Technology of rock burst control in datong coal mining area. Taiyuan, China: Taiyuan University of Technology.

Google Scholar

Yazdanpanah, S., Chaeikar, S., and Jolfaei, A. (2022). Monitoring the security of audio biomedical signals communications in wearable IoT healthcare. Digit. Commun. Netw. 9 (2), 393–399. doi:10.1016/j.dcan.2022.11.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Yin, H., Li, Z., Wang, E., Niu, Y., Tian, He, Li, X., et al. (2024b). The infrared thermal effect of coal failure with different impact types and its relationship with bursting liability. Infrared Phys. Technol. 2024, 105263. doi:10.1016/j.infrared.2024.105263

CrossRef Full Text | Google Scholar

Zadeh, L. (1965). Fuzzy sets. Inf. Control. 8 (3), 338–353. doi:10.1016/S0019-9958(65)90241-X

CrossRef Full Text | Google Scholar

Zhang, D., Guo, W., Zang, C., Gong, X., Li, Z., Qiu, Y., et al. (2019). A new burst evaluation index of coal-rock combination specimen considering rebound and damage effects of rock. Geomat. Nat. Hazards Risk 11 (1), 984–999. doi:10.1080/19475705.2020.1760945

CrossRef Full Text | Google Scholar

Zhang, W., Guo, W., and Wang, Z. (2022). Influence of lateral pressure on mechanical behavior of different rock types under biaxial compression. J. Central South Univ. 29 (11), 3695–3705. doi:10.1007/s11771-022-5196-1

CrossRef Full Text | Google Scholar

Zhao, J., Duan, S., Chen, B., Li, L., He, B., Li, P., et al. (2024). Failure mechanism of rock masses with complex geological conditions in a large underground cavern: a case study. Soil Dyn. Earthq. Eng. 177, 108439. doi:10.1016/j.soildyn.2023.108439

CrossRef Full Text | Google Scholar

Zhao, J., Jiang, Q., Lu, J., Chen, B., Pei, S., and Wang, Z. (2022a). Rock fracturing observation based on microseismic monitoring and borehole imaging: in situ investigation in a large underground cavern under high geostress. Tunn. Undergr. Space Technol. 126, 104549. doi:10.1016/j.tust.2022.104549

CrossRef Full Text | Google Scholar

Zhao, T., Zhang, P., Guo, W., Gong, X., Wang, C., and Chen, Y. (2022b). Controlling roof with potential rock burst risk through different pre-crack length: mechanism and effect research. J. Central South Univ. 29 (11), 3706–3719. doi:10.1007/s11771-022-5190-7

CrossRef Full Text | Google Scholar

Zhou, H., Liu, J., Ou, S. F., Shi, Y. J., Gao, C., Shi, L., et al. (2022). A multi-criteria analysis framework for water transfers to improve the water environments under strong artificial interventions in highly urbanized areas. Environ. Res. 220, 115244. doi:10.1016/j.envres.2023.115244

CrossRef Full Text | Google Scholar

Zhou, J., Chen, C., Wang, M., and Khandelwal, M. (2021). Proposing a novel comprehensive evaluation model for the coal burst liability in underground coal mines considering uncertainty factors. Int. J. Min. Sci. Technol. 31 (5), 799–812. doi:10.1016/j.ijmst.2021.07.011

CrossRef Full Text | Google Scholar