- 1College of Geophysics, Chengdu University of Technology, Chengdu, China
- 2Chengdu University of Technology Academic Journal Center, Chengdu, China
- 3Key Laboratory of Geomathematics of Sichuan Province, Chengdu University of Technology, Chengdu, China
- 4Southwest Oil and Gas Company, SINOPEC, Chengdu, China
- 5College of Energy, Chengdu University of Technology, Chengdu, China
- 6PipeChina Oil and Gas Control Center, Beijing, China
Deep tight gas reservoirs are one of the important unconventional gas reservoirs. Deep burial, tight reservoirs have many characteristics, including diverse accumulation patterns, multiple accumulation regulations, low natural energy generation, complex gas–water relationship, and intricate seepage mechanism. These features of gas reservoirs put forward the requirement for new methods for a reasonable production allocation of horizontal wells and optimization of such allocations from the perspective of stress sensitivity. While CO2 huff-and-puff-based models, numerical simulation models, and thermos-hydrodynamic models have been built to solve these issues, there is still a lack of theoretical guidance for reasonable production allocation, especially with the edge-water problem. Here, we present a new one-dimensional mathematical and physical model to capture the stable movement of the gas–water interface in deep tight edge-water gas reservoirs. Our results show that there is a starting pressure in deep tight gas reservoirs. The starting pressure gradient increases with the growth of water saturation, which is far greater than the starting pressure gradient of medium, shallow gas reservoirs under the same water saturation. In addition, by considering the stable movement of the gas–water interface under the starting pressure, we found that the gas well has a larger upper limit of production differential pressure, a smaller seepage velocity, and a lower upper limit of production allocation. Finally, we make a comparison between our model results and production characteristics of real gas wells and find a consistency between the model results with real data. Our model provides a theoretical framework for reasonable production allocation of gas wells in deep tight gas reservoirs with the edge water.
1 Introduction
Reasonable production allocation is critical for the policy and project design of gas reservoir development (Li et al., 2006) and plays an important role in maintaining stable production of gas reservoirs and extending the product life cycle of gas wells. It is important to increase gas reservoir recovery (Selemenev et al., 2008; Li et al., 2021) and achieve efficient gas reservoir development (Khan et al., 2014; Sergeychev et al., 2020), which has been a focus of recent research (Li et al., 2018; Li et al., 2020). For conventional gas reservoirs, the frequently used methods for reasonable production allocation of gas wells include empirical method, nodal systems analysis, gas recovery curve method, profit analysis of production, reasonable drawdown pressure, and critical liquid-carrying flow rate (Liu et al., 1999; Li et al., 2008; Liu et al., 2013; Chen et al., 2016; Liu et al., 2022). Among these methods, empirical method, nodal systems analysis, gas recovery curve method, and profit analysis of production are commonly used in guiding production allocation based on pressure-depletion drive, while the remaining two are basically used to make reasonable regulations for gas wells of the water-producing and water-drive gas reservoirs. Often, a combination of these methods is applied to guide the efficient development of conventional gas reservoirs.
However, with the exploitation of gas reservoirs, conventional gas reservoirs are gradually exhausted, and unconventional gas reservoirs become increasingly important as a replacement resource. Deep tight gas reservoirs, as an important type of unconventional gas reservoirs, have the characteristics of deep burial, tight reservoirs, diverse accumulation patterns, multiple accumulation regulations, low natural energy generation, complex gas–water relationship, and intricate seepage mechanism (Buijs et al., 2020). These special gas reservoir characteristics put forward new requirements for reasonable production allocation. There are many recent studies focused on tight gas reservoirs, such as 3D modeling (Gonzalez et al., 2014), an integrated approach with detailed static and dynamic reservoir modeling (Weijermans et al., 2016), and cross-plot multiple regression analysis (Gai et al., 2015).
Considering gas reservoirs with the edge-water issue, there are several approaches designed to enhance oil recovery, optimize CO2 huff-n-puff by multiple horizon wells, and solve complex reservoir issues. Hao et al. (2017) utilized CO2 huff-and-puff to reduce CO2 emissions and enhance oil recovery in an edge-water flock-block reservoir. Hong (1990) proposed a numerical simulation model to elucidate recovery mechanisms and find optimum operating strategies for a steeply dipping, heavy oil reservoir. Evgenii et al. (2015) discussed the results of thermos-hydrodynamic modeling performed on the sector models and selected the most effective option for the further development of the edge area of the reservoir. Wang et al. (2019) devised a physical and numerical conceptional model of a fault-block reservoir to improve CO2 sweeping efficiency by multiple horizontal wells. Anthony et al. (2015) developed a single-well numerical simulation model to detect aquifer water encroachment into an oil reservoir.
Referring to starting pressure problems, Wang et al. (2017) introduced a factor called starting pressure gradient (SPG) and proposed three methods to characterize the SPG in tight sandstone oil reservoir numerical simulation. Liu et al. (2011) carried out laboratory tests to study the gas slippage and quasi starting pressure in water-bearing gas reservoirs of low permeability and found that the relationship between the quasi SPG and the ratio of core coefficient and water saturation was a power function. Yang et al. (2016) considered the influence of stress sensitivity on the working system of the gas well and used numerical simulation to analyze the impact of stress sensitivity on the ultimate recovery of the gas well under different production distribution conditions.
Lv et al. (2017) established a new reasonable production allocation method for horizontal wells with different production capacities and different single-well control reserves through statistical analysis. Lin et al. (2022) conducted a detailed gas reservoir analysis in the Anyue gas field of the Sichuan Basin and determined the diversities of pressure system, gas–water interface, bitumen content, and charging time.
Based on their results, they provided suggestions for the optimization of gas well production allocation. However, there is still a lack of theoretical framework for the reasonable production allocation of gas wells for deep tight gas reservoirs with the edge-water problem. This might lead to potential issues, such as premature flooding of most gas wells and restriction of the high-quality development and resource utilization of deep tight gas reservoirs. Therefore, we present a new simplified model through the fluid seepage theory to provide a theoretical basis for optimizing the working system of deep tight gas reservoirs. Compared with the previous studies, we consider the influence of the starting pressure gradient on the fluid flow, which provides a theoretical basis for reasonable production allocation of complex hydrocarbon reservoirs.
2 Differential equations of natural gas motion in deep tight gas reservoirs with the edge water
A large number of studies have found that compared with conventional gas reservoirs, tight gas reservoirs commonly have a starting pressure due to the characteristics of reservoir densification and low abundance (Lv et al., 2002; Wang et al., 2013; Zhan et al., 2022; Zholobov et al., 2022). Taking a deep tight gas reservoir in western Sichuan as an example, core analysis experiments show that the starting pressure gradient increases with the growth of water saturation. When the water saturation rises from 40% to 60%, the starting pressure gradient rises from 0.0277 MPa/m to 0.0339 MPa/m, which is about five times that of a medium, shallow gas reservoir under the same water saturation condition (Figures 1, 2). This is because the deep tight gas reservoir is buried deeper, resulting in a stronger compaction and larger starting pressure gradient than medium, shallow gas reservoirs. It can be seen that the starting pressure gradient of underground seepage initiation of natural gas in deep tight gas reservoirs cannot be ignored. Thus, without considering other forces, the differential equation of the underground seepage motion of natural gas is
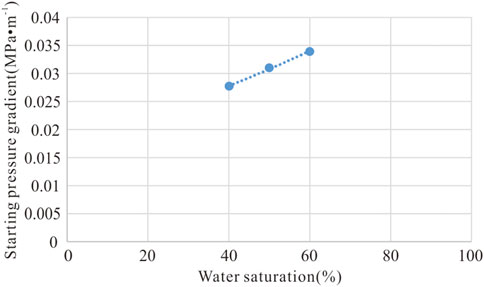
FIGURE 1. Starting pressure of typical deep tight gas reservoirs in western Sichuan under different water saturation conditions.
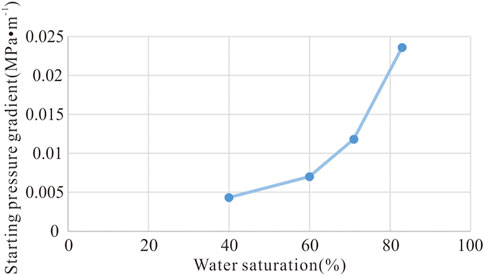
FIGURE 2. Starting pressure of typical medium, shallow gas reservoirs in western Sichuan under different water saturation conditions (Zhan et al., 2022).
3 Establishment of a reasonable production allocation model of gas wells for deep tight gas reservoirs with the edge water
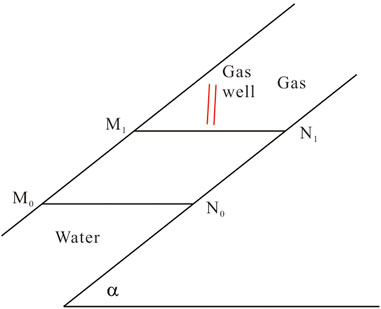
We assume that the dip of a gas reservoir with the edge water is
Formation water seepage is satisfied as
Since the pressure gradient is equal at the gas–moisture interface, that is,
In addition, the difference in seepage velocity of the two-phase fluid on the gas–moisture interface M1N1 is
According to the previous research results (Li et al., 2008; Li et al., 2001; Liu et al., 1998), only when
Equation 7 is the condition that should be met for the stable promotion of natural gas seepage velocity at the gas–water interface of deep tight gas reservoirs with the edge water. We set that the seepage cross-sectional area of the gas well is A, the distance between the gas well and the gas–water interface is L, the pressure at the gas–water boundary is pe, and the flow pressure at the bottom of the well is pwf. According to Eq. (2), the gas phase stabilizes the seepage velocity, that is,
and
Equations 8, 9 are integrated by the separated variable method:
Using Eqs 8, 10, we obtain stable seepage velocity in the gas phase:
Using Eqs 7, 11, the production pressure difference in stable motion at the gas–water interface is obtained as
Using Eqs 10, 12, we have the reasonable yield of stable motion at the gas–water interface as
When there is no starting pressure, that is,
and
According to Eqs 14–16, that is, when there is no starting pressure, the seepage velocity, reasonable pressure difference, and reasonable yield of the boundary of the side water reservoir meet the critical conditions of conventional side water and gas reservoir proposed by Li et al. (2008). Due to the existence of starting pressure, a larger production pressure difference and smaller gas well production are required to make the gas–water interface evenly promoted to achieve stable and normal production of gas wells due to the existence of starting pressure. This provides a theoretical basis for a reasonable production allocation of deep dense edge-water and gas reservoirs.
4 Model application
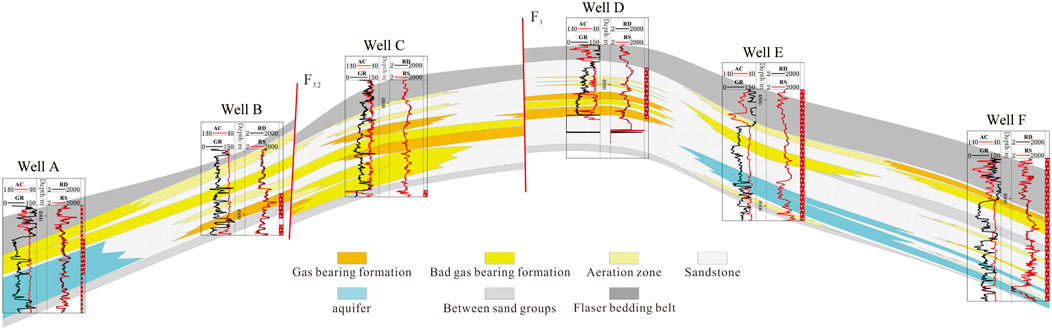
Next, we apply our theoretical model to a real deep tight gas reservoir in western Sichuan as an example. This is a typical deep tight gas reservoir, with an average buried depth of 4,500 m, average porosity of 4%, and average permeability of pressure recovery interpretation of 0.49 md. The comprehensive logging, testing, and dynamic monitoring study shows that this reservoir is a water and gas reservoir on one side (Figures 4, 5). Using the comprehensive research results from geology and gas reservoir engineering, we use equations (12), (13), (15), and (16), respectively, to calculate the reasonable pressure difference and the upper limit of reasonable production of the gas well while considering with or without a starting pressure, as in Table 1.
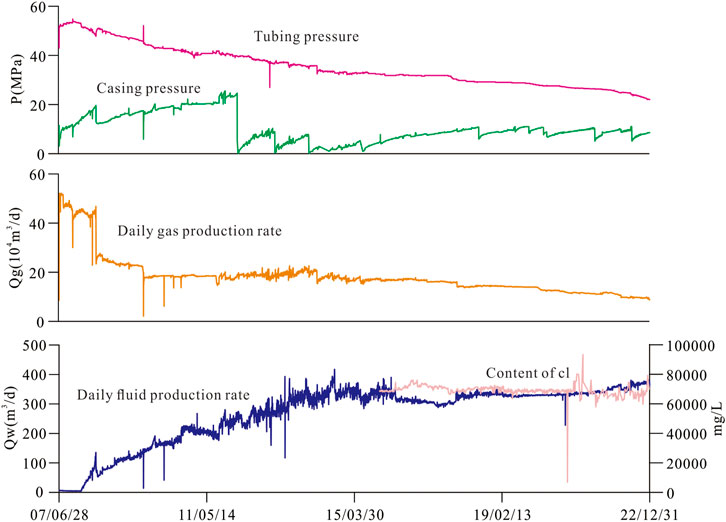
From the production curve of the gas well, we can see that the well was put into production in 2007 and mined by using the fixed production and pressure reduction method. The initial production was more than 40 × 104 m3 d-1, which was much greater than the upper limit of the stable movement of the gas–water boundary (21 × 104 m3 d-1 or 35 × 104 m3 d-1), resulting in a waterless production period of only about 1 year for the gas well. The water production rose rapidly afterward, with a rapid advancement of edge water under high-production conditions. In June 2008, the work system was adjusted to about 25 × 104 m3, and the rise rate of gas well water production slowed down. The work system was further adjusted to about 20 × 104 m3 d-1, and the gas well production was stable. The overall performance was characterized by double stability of gas production and water production, which was close to the upper limit of the stable movement of the gas–water boundary under the condition of starting pressure. All these results indicate that our model has good reliability and applicability (Figure 6).
5 Conclusion
Core experimental analysis shows that there is a starting pressure in the deep tight gas reservoir, and the starting pressure increases rapidly when the water saturation rises. The starting pressure gradient of the deep tight gas reservoir is five times that of the medium, shallow tight gas reservoir. We built a new theoretical framework to capture all these dynamics in the deep tight gas reservoir. More specifically, we established an upper limit quantitative model to consider the seepage velocity with water stable movement, production pressure, and reasonable production of the deep tight gas reservoir with the edge water of the gas–water interface. Compared with the previous research results, the existence of the starting pressure leads to a lower seepage rate and lower production upper limit in the gas well but expands the upper limit of the production pressure difference. We further applied our model to a real example of a deep tight gas reservoir. The reasonable upper limit calculated using our theoretical work is consistent with the actual production characteristics of the gas well. This demonstrates the reliability and applicability of our model, which can function as a theoretical basis for the formulation of the stable production and reasonable output of deep tight gas reservoir wells with edge water.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
WH contributed to conceptualization, methodology, analysis, and writing; NN and YS contributed to the experiment design; YX contributed to data collection; ZZ contributed to investigation, supervision, and writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Conflict of interest
ZZ and NN were employed by Southwest Oil and Gas Company, SINOPEC. YS was employed by PipeChina Oil and Gas Control Center.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer WY declared a shared affiliation with the author YS to the handling editor at the time of review.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abbreviations
References
Anthony, O. B. (4 Aug 2015). Detection of water encroachment into a marginal field oil reservoir for ultimate recovery. Lagos, Nigeria, Proceedings of the SPE Nigeria Annual International Conference and Exhibition: SPE-178375-MS. 2015: doi:10.2118/178375-MS
Buijs, H., Guerra, C., and Sonwa, Roger, 2020, Building multifrac completion strategies in tight gas reservoirs: A north sea case. Abu Dhabi, UAE, Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference: SPE-202713-MS. 9–12 Nov 2020: doi:10.2118/202713-MS
Chen, D. C., Yao, Y., Han, H., Fu, G., Song, T. J., and Xie, S. X. (2016). A new prediction model for critical liquid-carrying flow rate of directional gas wells. Natur. Gas. Ind. 36 (6), 40–44.
Gai, S. H., Liu, H. Q., He, S. L., Mo, S. Y., Lei, G., and Huang, X., (8–11 Mar 2015) . Reinterpreting the low-resistivity reservoir by using new logging model: A case study from a block in sulige tight gas field. Manama, Bahrain, Proceedings of the SPE Middle East Oil & Gas Show and Conference: SPE-172823-MS. 2015: doi:10.2118/172823-MS
Gonzalez, L., NasreldinG., , Rivero, J., Welsh, P., and Aguilera, R. (2014). 3D modeling of multistage hydraulic fractures and two-way-coupling geomechanics/fluid-flow simulation of a horizontal well in the nikanassin tight gas formation, Western Canada sedimentary basin. SPE Reserv. Eval. Eng. 17 (2), 257–270. doi:10.2118/159765-pa
Hao, H. D., Hou, J. R., Zhao, F. L., Wang, Z. X., Fu, Z. F., and Li, W. F., (17-20 Jul 2017). Synergetic CO2 huff-n-puff for edge-water fault-block reservoir: Experimental and numerical simulation. Texas, USA, Proceedings of the Carbon Management Technology Conference: CMTC-484985-MS. : doi:10.7122/484985-MS
Hong, K. C. (4–6 Apr 1990). Effects of gas cap and edge water on oil recovery by steamflooding in a steeply dipping reservoir. Ventura, CA, USA: Proceedings of the SPE California Regional Meeting: SPE-20021-MS. 1990: doi:10.2118/20021-MS
Khan, W. A., Ali, H., Shah, A. R., Ahmad, A., Jibran, A., and Baig, Z. (24–27 Nov 2014). Production forecast scenarios for shale gas and tight gas: How do they differ in terms of simulation? Proceedings of the PAPG/SPE Pakistan section Annual Technical Conference: SPE-174709-MS. Islamabad, Pakistan, 2014: doi:10.2118/174709-MS
Li, G. X., Tian, J., Duan, X. W., Yang, H. J., Tang, Y. L., and Bi, H. B., (16–18 Nov 2021). Research and practice on enhancing recovery of tight sandstone gas reservoir in kelasu gas field, tarim basin. SPE/AAPG/SEG asia pacific unconventional resources Technology conference. Virtual, Proceedings of the URTeC Technical Program Committee: URTEC-208304-MS. 2021: doi:10.15530/AP-URTEC-2021-208304
Li, X. P., and Wang, H. Q. (2008). Reasonable production pressure difference and production determination of gas wells in edge water drive gas reservoirs. Natur. Gas. Ind. 7, 85–86.
Li, X. P., and Yang, H. (2001). Study on seepage mechanics condition of stable movement of gas water interface. Drill. &Production Technol 3, 48–49.
Li, X. Z., Guo, Z. H., Hu, Y., Luo, R. L., Su, Y. H., and Sun, H. D. (2018). Efficient development strategies for large ultra-deep structural gas fields in China. Petroleum Explor. Dev. 45 (1), 118–126. doi:10.1016/s1876-3804(18)30011-9
Li, X. Z., Guo, Z. H., Hu, Y., Luo, R. L., Su, Y. H., and Sun, H. D. (2020). High-quality development of ultra-deep large gas fields in China: Challenges, strategies and proposals. Natur. Gas. Ind. 40 (2), 75–82.
Lin, T., Tan, C., Wang, T. S., Li, Q. F., Feng, M. Y., and Huang, S. W. (2022). Differential hydrocarbon accumulation and its influence on the formation of gas reservoirs in the Longwangmiao Formation, central Sichuan Basin. Petroleum Geol. Exp. 44 (4), 655–665.
Liu, C., Yu, Z. J., and Zhang, Y. (1999). Reasonable production allocation based on the analysis of benefit and output of oil region. Petroleum Explor. Dev. 1, 22–23.
Liu, Q. N., Wang, R. M., and Liu, Y. (1998). Stability of gas water interface (line) movement in edge water gas reservoirs. Acta Pet. Sin. 3, 89–94.
Liu, Q., Sun, L., Luo, P. Y., and Jia, W. (2013). The research on the proper production capacity evaluations on the west of sulige gas filed. J Southwest Petroleum Univ Sci Technol Ed 35 (3), 131–136.
Liu, X. J., Yan, J., and Yi, L. (9–11 Oct 2011). Slippage effect and quasi starting pressure in low permeability water-bearing gas reservoirs. Abu Dhabi, UAE: Proceedings of the SPE Reservoir Characterization and Simulation Conference and Exhibition: SPE-145803-MS. 2011: doi:10.2118/145803-MS
Liu, Y. R., Zhou, L. C., and Yang, B. M. (2022). Application of nodal system analysis method in reasonable production allocation of gas wells. China Petroleum Chem. Stand. Qual. 42 (13), 101–102.
Lv, Z. K., Tang, H. F., Liu, Q. M., Ning, B., and Mo, S. Y. (24 Jul 2017). New method of production proration determination of fractured horizontal wells in tight sand gas reservoirs. Proceedings of the 2017 International Field Exploration and Development Conference in Xi’an, 2017, Xi’an China
Lv, Z. Y., Wang, J., and Sun, Z. G. (2002). An experimental study on starting pressure gradient of fluids flow in low permeability sandstone porous media. Petroleum Explor. Dev 29 (2), 86–89.
Selemenev, S., Vasiliev, A., Kolesova, M., and Shekian, A., (28–30 Oct 2008). Integrated perspective assessment for complex low-permeability reservoir. Proceedings of the SPE Russian Oil and Gas Technical Conference and Exhibition: SPE-117084-MS. Moscow, Russia, 2008: doi:10.2118/117084-MS
Sergeychev, A. V., Toropov, K. V., Antonov, M. S., Fedorov, A. E., Povalyaev, A. A., and Dilmuhametov, I. R., (2020). Automated intelligent assistant in the selection of well placement when developing hard-to-recover reserves 76, 81, (Russian) . Neft khozyaystvo-Oil Ind. 10 doi:10.24887/0028-2448-2020-10-76-81
Taraskin, E., Ursegov, S., Gerasimov, I., and Ruzin, L. (26–28 Oct 2015). Results of thermo-hydrodynamic modeling of multiple cyclic steam stimulations of wells in the permian-carboniferous reservoir of the Usinsk Field. Moscow: Proceedings of the SPE Russian Petroleum Technology Conference: SPE-176709-MS. 2015: doi:10.2118/176709-MS
Temizel, C., Purwar, S., Abdullayev, A., Urrutia, K., and Tiwari, A. (9–12 Nov 2015). Efficient use of data analytics in optimization of hydraulic fracturing in unconventional reservoirs. Abu Dhabi, UAE: Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference: SPE-177549-MS. 2015: doi:10.2118/177549-MS
Wang, S., Tan, X. H., Zhang, S. H., Jiang, H. M., Jiang, D. L., and Ruan, H. J., (17–19 Oct 2017). Numerical simulation method and laboratory experiments of starting pressure gradient in tight sandstone oil reservoirs. Jakarta, Indonesia, Proceedings of the SPE/IATMI Asia Pacific Oil & Gas Conference and Exhibition: SPE-186349-MS. 2017: doi:10.2118/186349-MS
Wang, X. D., Hao, M. Q., and Han, Y. X. (2013). Implication of the threshold pressure gradient and its application. Acta Pet. Sin. 34 (1), 188–191.
Wang, Z. X., Hou, J. R., Hao, H. D., Zhao, F., L., and Yan, L. (15–18 Jul 2019). Laboratory investigation of sweeping efficiency by multiple horizontal wells CO2 huff and puff in fault-block reservoirs with an edge Aquife. Houston, TX, USA: Proceedings of the Carbon Management Technology Conference: CMTC-552102-MS. 2019, doi:10.7122/CMTC-552102-MS
Weijermans, P., Daniau, G., and Westerhof, D. (30 May 2016). Developing marginal near-tight gas fields in a mature area with long-reach hydraulically fractured wells - a case study: Proceedings of the SPE Europec featured at 78th EAGE Conference and Exhibition: SPE-180169-MS. 2016, Vienna, Austria: doi:10.2118/180169-MS
Yang, B., Luo, D., Zhang, X., Wu, D., and Shang, S. F. (2016). A study of stress sensitivity of abnormal high pressure shale gas reservoir and reasonable productivity allocation. J Southwest Petroleum Univ Sci Technol Ed 38 (2), 115–121.
Zhan, Z. D., Deng, W. F., Yan, H. R., and Yan, X. M. (2022). Research of production decline model dominated by late-boundary flow for tight gas reservoir under a constant flowing pressure. J Southwest Petroleum Univ Sci Technol Ed 44 (3), 85–92.
Keywords: tight gas reservoirs, edge-water gas reservoir, reasonable production allocation, starting pressure, production differential pressure
Citation: Huang W, Zhan Z, Niu N, Xiao Y and Shi Y (2023) Reasonable production allocation model of gas wells for deep tight gas reservoirs with the edge water. Front. Earth Sci. 11:1139663. doi: 10.3389/feart.2023.1139663
Received: 07 January 2023; Accepted: 13 March 2023;
Published: 30 March 2023.
Edited by:
Shengnan Chen, University of Calgary, CanadaReviewed by:
Zheng Sun, China University of Mining and Technology, ChinaWeichao Yu, PIPECHINA Oil & Gas Control Center, China
Qichen Zhang, China National Offshore Oil Corporation, China
Yanwei Wang, Jilin University, China
Copyright © 2023 Huang, Zhan, Niu, Xiao and Shi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zedong Zhan, superzzdxnyq@sina.com
 Weiting Huang
Weiting Huang