- 1Qinghai 906 Engineering Survey and Design Institute Co., Ltd., Xining, China
- 2Key Laboratory of Environmental Geology of Qinghai Province, Xining, China
- 3Qinghai Geological Environment Protection and Disaster Prevention Engineering Technology Research Center, Xining, China
- 4Sichuan Engineering Research Center for Mechanical Properties and Engineering Technology of Unsaturated Soils (Chengdu University), Chengdu, China
- 5School of Architecture and Civil Engineering, Chengdu University, Chengdu, China
- 6Qinghai Hydrogeology and Engineering Geology and Environgeology Survey Institute, Xining, China
- 7Southwestern Architectural Design Institute Co., Ltd., Chengdu, China
Landslides are geohazards of major concern that can cause casualties and property damage. Short-term landslide displacement prediction is one of the most critical and challenging tasks in landslide deformation analysis, and is beneficial for future hazard mitigation. In this research, a novel short-term displacement prediction approach using spatial-temporal correlation and a gated recurrent unit (GRU) is proposed. The proposed approach is a unified framework that integrates time-series instant displacements collected from multiple monitoring points on a failing slope. First, a spatial-temporal correlation matrix, including the pairwise Pearson’s correlation coefficients, was studied based on the temporal instant displacement data. Then, the extracted spatial features were integrated into the time-series prediction model using GRU. This approach combines both spatial and temporal features simultaneously and provides enhanced prediction performance. In the last step, a comparative analysis against other benchmark algorithms is performed in two case studies including the conventional time-series modeling approach and the spatial-temporal modeling approach. The computational results show that the proposed model performs best in terms of performance evaluation metrics.
Introduction
In mountainous regions, widely distributed landslides are a commonly observed phenomenon that threatens local people’s lives and properties (Zhou et al., 2021a; Zhou et al., 2021b; Zhou et al., 2022). Monitoring landslide displacement time series can directly reflect landslide deformation and slope stability (Gao and Meguid, 2018; Gao et al., 2021; Li et al., 2022). The prediction of landslide displacement is considered an essential part of an operational early warning system for future landslides. Thus, accurate and effective predictions of future displacements are valuable (Wang et al., 2020).
Existing studies on landslide displacement prediction can be roughly classified into three categories: physics models, statistical models, and artificial intelligence models (Gao and Meguid, 2021). According to the literature review, physics models were developed based on creep theory and validated via large-scale laboratory experiments. During this process, the physical parameters were estimated and monitored to forecast the incoming landslide displacements (Yang et al., 2019). Helmstetter et al. (2004) utilized a slider block friction model to analyze landslide displacement and velocity data. Corominas et al. (2005) developed a momentum equation in which a viscous term was added to predict the landslide displacements and velocities in water-triggered landslides. Mufundirwa et al. (2010) proposed an empirical physics model to forecast the failure time of landslides based on slope gradient and performed laboratory experiments for validation. Thiebes et al. (2014) proposed a physics-based model that combined hydrology and stability to provide an early warning for landslide occurrence. All physics-based models can provide clear physical explanations of landslides, but the implementation of sufficiently accurate models can be complex, time-consuming, and expensive.
On the other hand, statistical models are designed to discover statistical regularities or patterns in massive observed data points (Gao et al., 2020). Xu et al. (2011) constructed an autoregressive time-series model to fit temporal patterns in a landslide displacement dataset. Krkač et al. (2017) used a random forest regression model to forecast incoming landslide displacements. Zhao et al. (2018) optimized classification and regression trees to predict future landslide movements. Kavoura et al. (2020) used the Verhulst inverse function and residual correction to enhance the autoregressive integrated moving average (ARIMA) model for displacement time-series prediction. All statistical models investigate and extract statistical properties in the temporal domain, and construct corresponding models to forecast future displacement values. Promising results were obtained using statistical models fitted to the landslide displacement series.
Advances and applications of artificial intelligence (AI) have provided new ideas for landslide displacement prediction. Lian et al. (2015) initially applied an artificial neural network (ANN) to construct forecasting models for landslide displacement time-series datasets. Zhou et al. (2016) used the particle swarm optimization (PSO) algorithm to optimize the hyperparameter setting of a support vector machine (SVM) to further improve the prediction accuracy of the prediction model to forecast future displacements. Case studies of water-triggered landslides located in the Three Gorges Reservoir, China confirmed the validity of the proposed approach for field practice. Cao et al. (2016) introduced a single hidden layer feedforward (SHLF) neural network structure, the extreme learning machine (ELM), to predict landslide displacement series. Compared with conventional ANN, ELM is computationally effective and more reliable in terms of prediction performance. Li et al. (2018) incorporated the power of ELM with parametric copula models to study the patterns of seasonal step-like landslide displacements. Heavy precipitation and reservoir water level fluctuation are correlated with seasonal faster motion of slope failure, and thus are suggested to be utilized as input factors for modeling displacement time series. Li et al. (2020) trained a deep belief network (DBN) as a regression algorithm to forecast landslide displacement in the Three Gorges Reservoir, China. Exponential weighted moving average (EWMA) control charts were introduced as thresholds to classify between hazardous seasonal and faster seasonal displacements. The above work confirms the superior power of AI technologies in landslide displacement prediction tasks.
All studies cited above performed autoregressive time-series prediction of future landslide instant displacement. Their work considered the displacement data measured from a single point as a single autoregressive time series, but received no impact from outside factors. However, in practice, a landslide event with slope failure is a super-complex system that cannot be represented by a single time series. Multiple displacement time-series datasets vary owing to the different measurement locations on the slope. Intuitively, this refers to the different extents of deformation in various parts of the landslide region.
To overcome this limitation, in this study, we propose a novel spatial-temporal prediction framework for landslide displacement modeling. Instead of using a single measured displacement series, multiple displacement series from adjacent monitoring locations on the same slope were considered. A spatial-temporal correlation matrix was computed and applied as an input in the prediction model to estimate future displacement. The gated recurrent unit (GRU) algorithm was selected as the regression algorithm for the prediction tasks as it extracts both spatial and temporal features effectively (Minh et al., 2018; Becerra-Rico et al., 2020; Dutta et al., 2020; Bonassi et al., 2021; ur Rehman et al., 2021).
The major contributions of this study can be summarized as follows. First, it proposes a novel displacement prediction approach using spatial-temporal correlation from a dataset collected from multiple sensors. Second, GRU was trained as a time-series forecasting algorithm to perform short-term displacement forecasting.
The remainder of the manuscript is organized as follows: Case Study Region introduces the case study area and describes the landslide displacement data collection process. Prediction Methodology provides details about the spatial-temporal modeling process and the GRU model. Experimental Results presents the computational outcomes, and Conclusion concludes the study’s findings.
Case Study Region
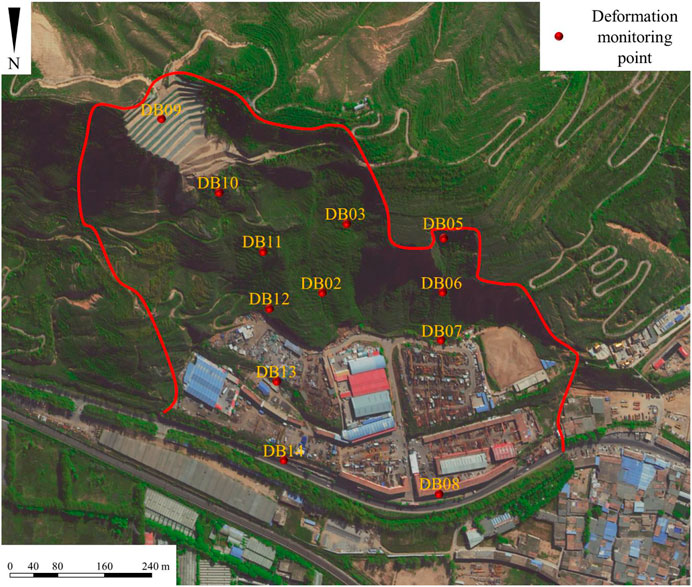
Our case study area, the Zhangjiawan landslide, is located in Pengjia Village, Chengxi County, central Qinghai Province, China. The slide is located at latitude 101°38′59″ and longitude 36°38′25″. The landslide event threatens the state road which passes through the front of the landslide. In total, more than 2000 residents live in the surrounding area. An overview of the Zhangjiawan landslide is shown in Figure 1.
As illustrated in Figure 1, the Zhangjiawan landslide is a colluvial landslide in which the slide body materials contain sandstone and mudstone interbeds. The entire landslide area is approximately 1,600 m long and 900 m wide. Meanwhile, the total area is approximately 1.26 km2. In total, 12 deformation monitoring (DB) points (see Figure 1) were configured by field engineers on the sliding region. All points are installed with global positioning system (GPS) in order to monitor the deformation process in real time from late July 2020. They collected daily instant displacement values in millimeters until the current time.
Prediction Methodology
Spatial-Temporal Sequence Modeling
Geographical scale is a critical component for discussing the spatial correlation of landslide displacement prediction tasks (Vega Orozco et al., 2012; Pathak et al., 2021; Li, 2022b). A large geographical scale is usually preferred in practice when the landslide is large scale. Thus, in this study, the geographical scale was set according to the boundaries of deformation (red line in Figure 1), and all monitoring points were included in the scale for prediction.
In our case study area, the relationship between the faster-moving part and the slower moving part is often not simple, owing to time delay, slope instability, and sliding materials. Moreover, various sliding directions exist for all GPS monitoring points. Therefore, it is challenging to analyze the displacement at a single point and use the obtained results to estimate the entire slope deformation process. Spatial-temporal correlation can offer a reliable solution for landslide displacement prediction based on multiple monitored time-series data.
In this study, a total of 12 GPS points that monitor displacement were considered for spatial-temporal correlation modeling. We support all points represented by a 12 × 12 matrix consisting of 12 rows and 12 columns. The location of each GPS point can be described by two-dimensional coordinates (i, j), where i denotes the row number, and j denotes the column number expressed in (1) as follows:
where
where
Gated Recurrent Unit
To strengthen the prediction power of the proposed spatial-temporal approach, GRU was applied as the regression algorithm in this study (Ravanelli et al., 2018). A GRU unit has similar architecture in comparison with a long short-term memory (LSTM) unit (Minh et al., 2018). They both have gates to extract temporal patterns from the dataset and pass relevant information for prediction making process. In comparison with LSTM, GRU does not have a forget gate or cell state (Li, 2022a). Consequently, GRU requires less memory and is more computationally effective than LSTM.
The GRU computation steps can be expressed by (3)–(5) below:
where
where
Training Strategy
The training strategy utilized in this study is the same approach used for training the LSTM-RNN in time-series tasks by other researchers. The size of the time window considers both the seasonality patterns and autocorrelation between the current and historic displacements. In total, almost 2 years of GPS-recorded daily displacement data in millimeters were utilized as the training and test datasets.
Within the dataset, the first 80% of the prepared dataset was used to train and validate the GRU model, and the remaining 20% was reserved as a held-out testing sample. In each training experiment, 10% of the training samples were further split for validation during the training process. To ensure the optimal parameter setting of the GRU, a grid search approach was applied to seek the best combination of hyperparameters via cross-validation. The loss function for training the GRU is the mean squared error loss which will be introduced in Performance Evaluation Metrics.
Benchmark Models
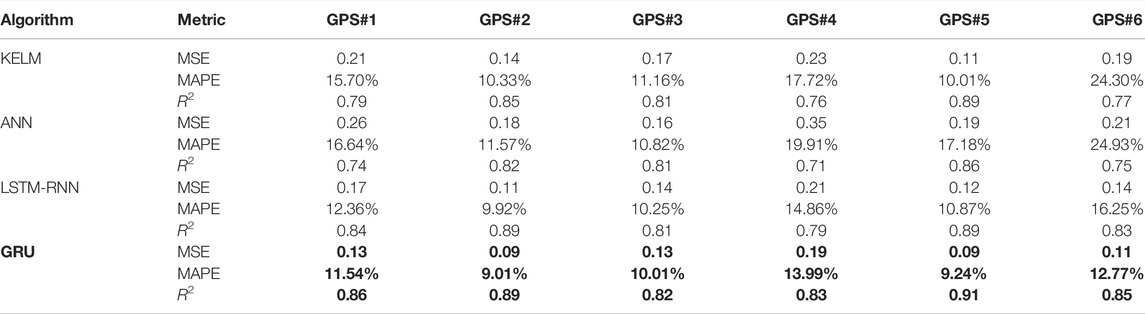
To demonstrate the superior power of the proposed GRU, three other benchmark time-series prediction algorithms were selected as benchmark algorithms for comparative analysis. These algorithms are also popular in landslide displacement prediction. They include kernel extreme learning machine (KELM), ANN, and LSTM-RNN.
KELM is an improved version of the original ELM. Similar to ELM, which is computationally efficient and robust, KELM proposes using a kernel function to enhance the generalization capacity and reduce possible overfitting issues (Iosifidis et al., 2015; He and Kusiak, 2017). Among the multiple kernel options, the most popular choices include the linear kernel, polynomial kernel, radial basis function (RBF) kernel, or exponential kernel. In this study, we consider the three most typical kernel functions, namely, the RBF kernel, hyperbolic tangent kernel, and wavelet kernel, for possible options in fitting displacement time series.
ANN is one of the most widely used machine-learning algorithms in both regression and classification tasks (Li et al., 2021a; Li et al., 2021b). It has a feedforward neural network architecture and involves three major components: the input, hidden, and output layers. By adaptively adjusting the weights and bias, meaningful features that are relevant to the target output can be extracted from the dataset.
LSTM is a special type of recurrent neural network with the capacity to remember values from the earlier stages (Gers et al., 2002; Greff et al., 2016). Each LSTM unit contains a set of cells in which data streams are captured and stored. The assembly of the cells results in an information transportation line that conveys data from the past and gathers them for the present timestamp. The memorization of earlier values assists in identifying both the trend and seasonality within the time-series dataset.
The hyperparameters that require tuning for the proposed GRU and other benchmark models are summarized in Table 1. KELM has two major hyperparameters: the selection of the kernel function and the number of hidden neurons within a single hidden layer. ANN has two hyperparameters that require tuning: the number of hidden layers and the number of hidden neurons inside the hidden layer. LSTM has the number of hidden nodes, learning rate, and sliding window steps as hyperparameters. GRU has the same hyperparameters that require tuning during the cross-validation process.
Performance Evaluation Metrics
To evaluate the performance of the landslide displacement models, three evaluation metrics, namely, mean squared error (MSE), mean absolute percentage error (MAPE), and predictive R-squared (R2), were selected in this study. MSE computes the squared error between the predicted and actual displacements. It is also utilized as a loss function for training all the algorithms. MAPE computes the average percentage error between the predicted and actual measured displacements. R2 determines how well the predicted displacements fit the actual displacement from a distribution perspective. Intuitively, it quantifies the percentage of variance within the test dataset explained by the prediction model. The formulas for computing these two metrics are summarized in Table 2.
Experimental Results
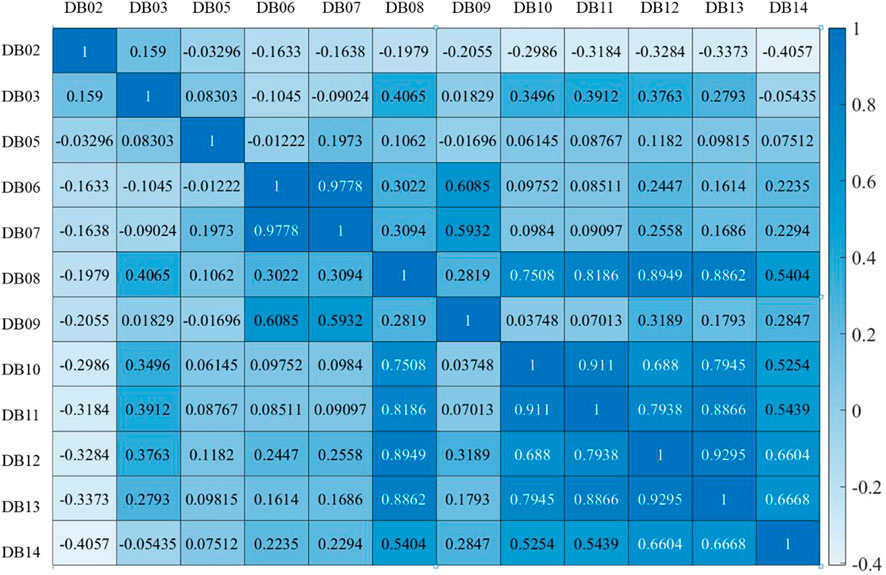
To predict the future displacement following the proposed approach, the spatial-temporal correlation is the foundation for the development of the prediction model. Following the methods introduced in Spatial-Temporal Sequence Modeling, we computed the average Pearson’s correlation coefficient in a pairwise manner for all 12 GPS points. The correlation coefficients ranged between -1 and 1. The computational results are displayed in Figure 2.
As shown in Figure 2, the spatial-temporal matrix containing correlation coefficients among the displacement time series in all GPS points differs from each other. The range varies between -1 and 1, where a positive value indicates a positive correlation and a negative value indicates the opposite scenario. All diagonal values in the spatial-temporal correlation matrix are 1, which represents a super positive correlation between the measured displacements and themselves. Furthermore, because it measures pairwise correlation, the entire spatial-temporal matrix is symmetric along the diagonal line. For the intra-GPS correlations, we applied a threshold of 0.5 to determine if the displacements measured in the neighborhood region are a valuable input for the prediction model. Thus, only a few neighboring displacements were considered in this study.
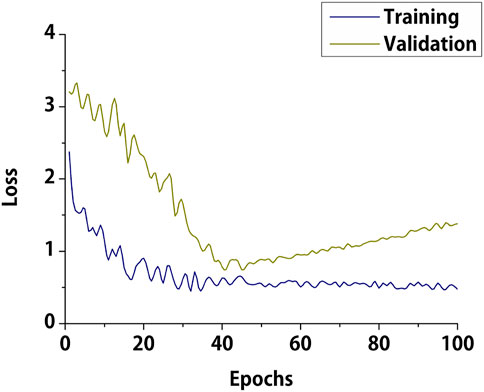
To train the proposed GRU model, the MSE loss was selected as the loss function, and the Adam optimizer was used to optimize the parameter settings within the GRU. The training process is illustrated in Figure 3. In total, 100 epochs were tested during the training and validation steps. It can be observed that the training loss is constantly reduced and converges around the 40th epoch. Meanwhile, the validation loss is significantly reduced before the 40th epoch but then starts to increase slowly. This phenomenon is a clear indication of overfitting after epoch 40. Thus, we extracted the weights at epoch 40 as our optimal model for displacement prediction.
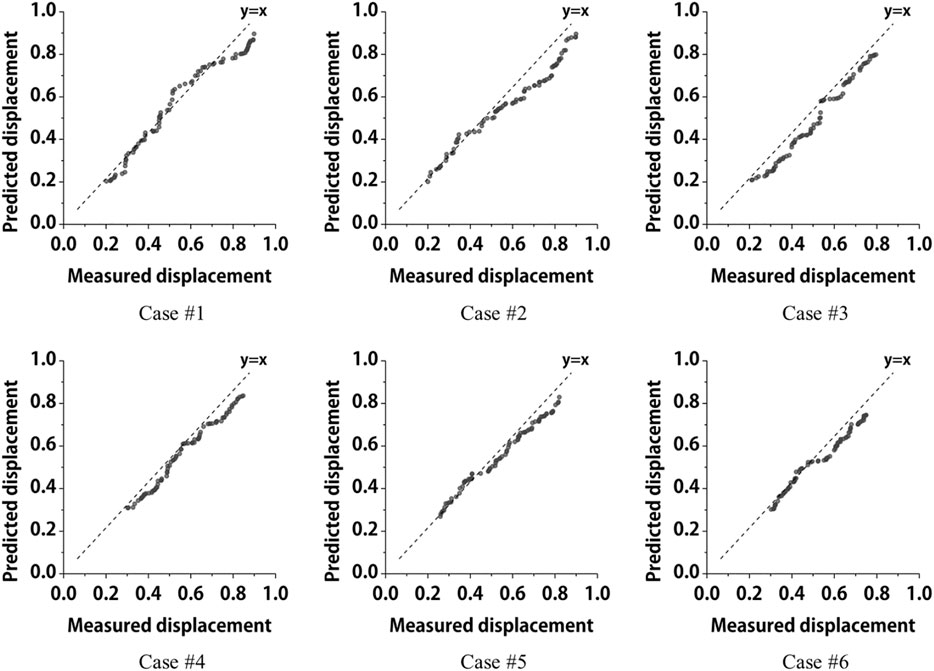
Figure 4 shows the predicted displacement versus the actual displacement within the reserved independent test dataset. For a fair comparison, we scaled all predictions and actual measured displacements between 0 and 1. The central diagonal dashed line denotes perfect prediction, which means that the predicted displacement values are exactly the same as the actual values for the displacement. The scattered points around the dashed line represent the predicted outcomes of the GRU algorithm. For our six case study GPS points, it can be observed that the majority of the points are scattered in the close neighborhood region of the dashed diagonal line. This indicates that the error between the prediction and actual measurement was within a small range, which confirms the accuracy of the prediction model. The quantitative prediction performance for all the algorithms tested is summarized in Table 3.
Furthermore, we compared the spatial-temporal modeling approach with the conventional time-series autoregression modeling approach. Here, the case number corresponds to the GPS point number. Unlike the spatial-temporal modeling approach, the conventional time-series approach only considers self-autocorrelation in the temporal domain for a single GPS-collected displacement series. The displacements collected from neighboring GPS points were not considered in the prediction model. As illustrated in Figure 5, the distributions of the absolute error from both the spatial-temporal and time-series approaches were compared at six selected GPS monitoring sites. All absolute errors compute the absolute difference between the predicted and actual values, and are then scaled between 0 and 1.
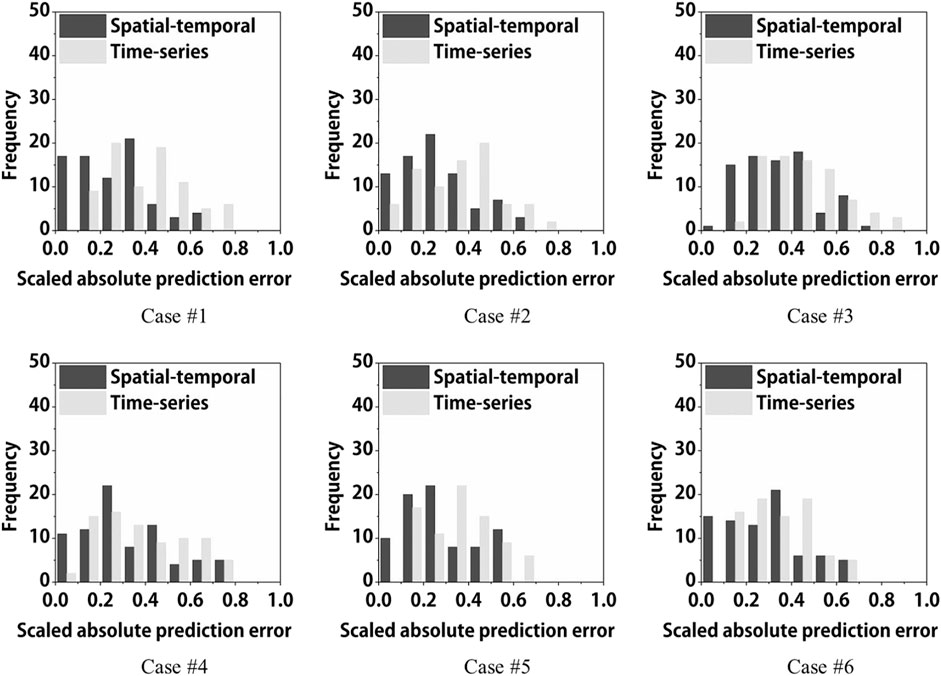
FIGURE 5. Comparison of absolute prediction error between spatial-temporal model and conventional time-series model.
As shown in Figure 5, the scaled absolute errors for both modeling approaches are skewed to the right with a long fat tail on the right-hand side. Same as Figure 4, the case numbers above refer to the same GPS number in our dataset. In the comparison between the two modeling approaches, the spatial-temporal approach is further skewed to the right with smaller mean and median values. This can be attributed to the spatial-temporal correlation among neighboring GPS points considered in the input of the proposed GRU model, whereas the conventional time-series model considers only autocorrelation and seasonality within a single GPS point. This confirms the outperformance of applying the spatial-temporal modeling approach in predicting landslide displacement.
Conclusion
In this study, we explored the possibility of using spatial-temporal correlation to enhance the prediction performance of landslide displacement at slope failure locations. GRU was applied as a time-series prediction algorithm to generate future landslide displacement. Comparative analysis against other benchmark algorithms, such as KELM, ANN, and LSTM-RNN, was performed in case studies for both traditional time-series forecasting and spatial-temporal forecasting. The experimental results support the conclusion that superior performance is achieved with the GRU and spatial-temporal modeling approach in the short-term landslide displacement prediction task. The utilization of the proposed approach can benefit field engineers in their landslide geohazard estimation tasks.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author Contributions
WM and JD conceptualized the study, contributed to the study methodology, and wrote the original draft. ZW, LP and QW contributed to the study methodology, data curation and investigation. CC contributed investigation. YW and FX contributed to software and formal analysis. JD and QW contributed to editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the Study on disaster prediction and risk assessment of mudstone landslide in Huangshui basin, Qinghai Province (2021-KJ-008), Scientific research fund project of Qinghai Bureau of Geology and mineral resources [(2022)32], and Qinghai provincial central leading local science and Technology Development Fund Project (2021ZY014).
Conflict of Interest
WM, ZW, and YW were employed by the Qinghai 906 Engineering Survey and Design Institute Co., Ltd., China. CC was employed by the Southwestern Architectural Design Institute Co., Ltd., China.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Becerra-Rico, J., Aceves-Fernández, M. A., Esquivel-Escalante, K., and Pedraza-Ortega, J. C. (2020). Airborne Particle Pollution Predictive Model Using Gated Recurrent Unit (GRU) Deep Neural Networks. Earth Sci. Inf. 13 (3), 821–834. doi:10.1007/s12145-020-00462-9
Bonassi, F., Farina, M., and Scattolini, R. (2021). On the Stability Properties of Gated Recurrent Units Neural Networks. Syst. Control Lett. 157, 105049. doi:10.1016/j.sysconle.2021.105049
Cao, Y., Yin, K., Alexander, D. E., and Zhou, C. (2016). Using an Extreme Learning Machine to Predict the Displacement of Step-Like Landslides in Relation to Controlling Factors. Landslides 13 (4), 725–736. doi:10.1007/s10346-015-0596-z
Corominas, J., Moya, J., Ledesma, A., Lloret, A., and Gili, J. A. (2005). Prediction of Ground Displacements and Velocities from Groundwater Level Changes at the Vallcebre Landslide (Eastern Pyrenees, Spain). Landslides 2 (2), 83–96. doi:10.1007/s10346-005-0049-1
Dutta, A., Kumar, S., and Basu, M. (2020). A Gated Recurrent Unit Approach to Bitcoin Price Prediction. J. Risk Financial Manag. 13 (2), 23. doi:10.3390/jrfm13020023
Gao, G., Meguid, M. A., Chouinard, L. E., and Xu, C. (2020). Insights into the Transport and Fragmentation Characteristics of Earthquake-Induced Rock Avalanche: Numerical Study. Int. J. Geomech. 20 (9), 04020157. doi:10.1061/(asce)gm.1943-5622.0001800
Gao, G., Meguid, M. A., Chouinard, L. E., and Zhan, W. (2021). Dynamic Disintegration Processes Accompanying Transport of an Earthquake-Induced Landslide. Landslides 18 (3), 909–933. doi:10.1007/s10346-020-01508-1
Gao, G., and Meguid, M. A. (2021). On the Role of Joint Roughness on the Micromechanics of Rock Fracturing Process: a Numerical Study. Acta Geotech., 1–26. doi:10.1007/s11440-021-01401-8
Gao, G., and Meguid, M. A. (2018). On the Role of Sphericity of Falling Rock Clusters-Insights from Experimental and Numerical Investigations. Landslides 15 (2), 219–232. doi:10.1007/s10346-017-0874-z
Gers, F. A., Schraudolph, N. N., and Schmidhuber, J. (2002). Learning Precise Timing with LSTM Recurrent Networks. J. Mach. Learn. Res. 3, 115–143.
Greff, K., Srivastava, R. K., Koutnik, J., Steunebrink, B. R., and Schmidhuber, J. (2016). LSTM: A Search Space Odyssey. IEEE Trans. Neural Netw. Learn Syst. 28 (10), 2222–2232. doi:10.1109/TNNLS.2016.2582924
He, Y., and Kusiak, A. (2017). Performance Assessment of Wind Turbines: Data-Derived Quantitative Metrics. IEEE Trans. Sustain. Energy 9 (1), 65–73. doi:10.1109/TSTE.2017.2715061
Helmstetter, A., Sornette, D., Grasso, J. R., Andersen, J. V., Gluzman, S., and Pisarenko, V. (2004). Slider Block Friction Model for Landslides: Application to Vaiont and La Clapiere Landslides. J. Geophys. Res. Solid Earth 109 (B2), 1–15. doi:10.1029/2002jb002160
Iosifidis, A., Tefas, A., and Pitas, I. (2015). On the Kernel Extreme Learning Machine Classifier. Pattern Recognit. Lett. 54, 11–17. doi:10.1016/j.patrec.2014.12.003
Kavoura, K., Konstantopoulou, M., Depountis, N., and Sabatakakis, N. (2020). Slow-Moving Landslides: Kinematic Analysis and Movement Evolution Modeling. Environ. Earth Sci. 79 (6), 1–11. doi:10.1007/s12665-020-8879-7
Krkač, M., Špoljarić, D., Bernat, S., and Arbanas, S. M. (2017). Method for Prediction of Landslide Movements Based on Random Forests. Landslides 14 (3), 947–960. doi:10.1007/s10346-016-0761-z
Li, H., Deng, J., Feng, P., Pu, C., Arachchige, D. D. K., and Cheng, Q. (2021a). Short-Term Nacelle Orientation Forecasting Using Bilinear Transformation and ICEEMDAN Framework. Front. Energy Res. 9, 780928. doi:10.3389/fenrg.2021.780928
Li, H., Deng, J., Yuan, S., Feng, P., and Arachchige, D. D. K. (2021b). Monitoring and Identifying Wind Turbine Generator Bearing Faults Using Deep Belief Network and EWMA Control Charts. Front. Energy Res. 9, 799039. doi:10.3389/fenrg.2021.799039
Li, H., He, Y., Xu, Q., Deng, j., Li, W., and Wei, Y. (2022). Detection and Segmentation of Loess Landslides via Satellite Images: A Two-Phase Framework. Landslides 19, 673–686. doi:10.1007/s10346-021-01789-0
Li, H. (2022b). SCADA Data Based Wind Power Interval Prediction Using LUBE-Based Deep Residual Networks. Front. Energy Res. 10, 920837. doi:10.3389/fenrg.2022.920837
Li, H. (2022a). Short-Term Wind Power Prediction via Spatial Temporal Analysis and Deep Residual Networks. Front. Energy Res. 10, 920407. doi:10.3389/fenrg.2022.920407
Li, H., Xu, Q., He, Y., and Deng, J. (2018). Prediction of Landslide Displacement with an Ensemble-Based Extreme Learning Machine and Copula Models. Landslides 15 (10), 2047–2059. doi:10.1007/s10346-018-1020-2
Li, H., Xu, Q., He, Y., Fan, X., and Li, S. (2020). Modeling and Predicting Reservoir Landslide Displacement with Deep Belief Network and EWMA Control Charts: A Case Study in Three Gorges Reservoir. Landslides 17 (3), 693–707. doi:10.1007/s10346-019-01312-6
Lian, C., Zeng, Z., Yao, W., and Tang, H. (2015). Multiple Neural Networks Switched Prediction for Landslide Displacement. Eng. Geol. 186, 91–99. doi:10.1016/j.enggeo.2014.11.014
Minh, D. L., Sadeghi-Niaraki, A., Huy, H. D., Min, K., and Moon, H. (2018). Deep Learning Approach for Short-Term Stock Trends Prediction Based on Two-Stream Gated Recurrent Unit Network. IEEE Access 6, 55392–55404. doi:10.1109/access.2018.2868970
Mufundirwa, A., Fujii, Y., and Kodama, J. (2010). A New Practical Method for Prediction of Geomechanical Failure-Time. Int. J. Rock Mech. Min. Sci. 47 (7), 1079–1090. doi:10.1016/j.ijrmms.2010.07.001
Pathak, S., Lu, C., Nagaraj, S. B., van Putten, M., and Seifert, C. (2021). STQS: Interpretable Multi-Modal Spatial-Temporal-seQuential Model for Automatic Sleep Scoring. Artif. Intell. Med. 114, 102038. doi:10.1016/j.artmed.2021.102038
Ravanelli, M., Brakel, P., Omologo, M., and Bengio, Y. (2018). Light Gated Recurrent Units for Speech Recognition. IEEE Trans. Emerg. Top. Comput. Intell. 2 (2), 92–102. doi:10.1109/tetci.2017.2762739
Thiebes, B., Bell, R., Glade, T., Jäger, S., Mayer, J., Anderson, M., et al. (2014). Integration of a Limit-Equilibrium Model into a Landslide Early Warning System. Landslides 11 (5), 859–875. doi:10.1007/s10346-013-0416-2
ur Rehman, S., Khaliq, M., Imtiaz, S. I., Rasool, A., Shafiq, M., Javed, A. R., et al. (2021). Diddos: An Approach for Detection and Identification of Distributed Denial of Service (Ddos) Cyberattacks Using Gated Recurrent Units (Gru). Future Gener. Comput. Syst. 118, 453–466. doi:10.1016/j.future.2021.01.022
Vega Orozco, C., Tonini, M., Conedera, M., and Kanveski, M. (2012). Cluster Recognition in Spatial-Temporal Sequences: The Case of Forest Fires. Geoinformatica 16 (4), 653–673. doi:10.1007/s10707-012-0161-z
Wang, H., Lv, Z., Qin, H., Yue, J., and Zhang, J. (2020). Deformation Control Method of the Antislide Pile under Trapezoidal Load in the Zhangjiawan Landslide. Adv. Civ. Eng. 2020, 1405610. doi:10.1155/2020/1405610
Xu, F., Wang, Y., Du, J., and Ye, J. (2011). Study of Displacement Prediction Model of Landslide Based on Time Series Analysis. Chin. J. Rock Mech. Eng. 30 (4), 746–751.
Yang, B., Yin, K., Lacasse, S., and Liu, Z. (2019). Time Series Analysis and Long Short-Term Memory Neural Network to Predict Landslide Displacement. Landslides 16 (4), 677–694. doi:10.1007/s10346-018-01127-x
Zhao, J., Liu, Y., and Hu, M. (2018). Optimisation Algorithm for Decision Trees and the Prediction of Horizon Displacement of Landslides Monitoring. J. Eng. 2018 (16), 1698–1703. doi:10.1049/joe.2018.8305
Zhou, C., Yin, K., Cao, Y., and Ahmed, B. (2016). Application of Time Series Analysis and PSO-SVM Model in Predicting the Bazimen Landslide in the Three Gorges Reservoir, China. Eng. Geol. 204, 108–120. doi:10.1016/j.enggeo.2016.02.009
Zhou, J., Wei, J., Yang, T., Zhang, P., Liu, F., and Chen, J. (2021a). Seepage Channel Development in the Crown Pillar: Insights from Induced Microseismicity. Int. J. Rock Mech. Min. Sci. 145, 104851. doi:10.1016/j.ijrmms.2021.104851
Zhou, Q., Xu, Q., Peng, D., Fan, X., Ouyang, C., Zhao, K., et al. (2021b). Quantitative Spatial Distribution Model of Site-Specific Loess Landslides on the Heifangtai Terrace, China. Landslides 18 (3), 1163–1176. doi:10.1007/s10346-020-01551-y
Keywords: GPS monitoring, slope deformation, spatial-temporal modeling, gated recurrent unit, time-series modeling
Citation: Ma W, Dong J, Wei Z, Peng L, Wu Q, Chen C, Wu Y and Xie F (2022) Landslide Displacement Prediction With Gated Recurrent Unit and Spatial-Temporal Correlation. Front. Earth Sci. 10:950723. doi: 10.3389/feart.2022.950723
Received: 23 May 2022; Accepted: 14 June 2022;
Published: 04 July 2022.
Edited by:
Yusen He, Grinnell College, United StatesReviewed by:
Ge Gao, McGill University, CanadaQi Zhou, GFZ German Research Centre for Geosciences, Germany
Copyright © 2022 Ma, Dong, Wei, Peng, Wu, Chen, Wu and Xie. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jianhui Dong, ZG9uZ2ppYW5odWlAY2R1LmVkdS5jbg==
 Wenli Ma1,2,3
Wenli Ma1,2,3 Jianhui Dong
Jianhui Dong