A New Numerical Procedure for the Excavation Response in Mohr–Coulomb Rock Mass Exhibiting Strain-Softening Behavior

A new numerical procedure for calculating the excavation response of the Mohr–Coulomb rock mass considering strain-softening behavior is proposed in this article. In this method, the plastic zone of the strain-softening rock mass is divided into the sufficient small plastic concentric annulus with constant radial stress increment, where the stress and strain distributions are characterized based on the existing analytical solutions of the brittle–plastic rock in the plastic zone. According to the equilibrium equation, geometric equation, and Mohr–Coulomb yield criterion, the stresses of each annulus can be calculated, and the explicit form of the displacement can also be determined by invoking the non-associated flow law and Hooke’s law. On this basis, the excavation disturbance-induced response and the ground reaction curve (GRC) in the strain-softening rock mass can be calculated by iterative computation. The proposed method is verified by comparing both the numerical simulation results and the existing theoretical solutions. Extensive computations are then carried out to clarify some practical questions, including the effect of ground condition, the computation efficiency, and the engineering applicability. It is found that the proposed numerical procedure behaves more efficiently and accurately than the previous one for the strain-softening rock mass. This might, therefore, provide convenience and benefits from a computation standpoint for the preliminary design of underground openings in rock masses with slight deformation.

Introduction

The prediction of the excavation response for the surrounding rock plays an important role in tunnel construction and support design (Huang et al., 2021; Qingke et al., 2021), and the convergence–confinement method (CCM) provides an effective way for analyzing the rock deformation by the ground reaction curve (GRC) and support capacity, in combination with the longitudinal deformation profile (LDP) of a tunnel. For the average quality rock mass with a geological strength index of between 30 and 60, the strain-softening behavior in the post-peak stage of the stress–strain curve is common. Obtaining the excavation-induced ground response in strain-softening rock mass remains a great interest to practical engineering, since it is beneficial to the determination of the rock-support interaction process within the framework of the CCM. The establishment of a proper prediction method for stability and deformation evolution of rock material is beneficial to the engineering design and disaster control (Cui et al., 2021; Li H, et al., 2022; Zhou et al., 2021; Li, et al., 2021a; Li, et al., 2021b; He and Kusiak 2018).

At present, many scholars have theoretically performed research on the elastic–plastic solutions of circular tunnels. When studying the post-peak mechanical behavior based on the elastic–plastic mechanics theory, the elastic–perfectly plastic, elastic–brittle–plastic, and strain-softening rock mass models are often adopted. On the basis of the previous studies on post-peak mechanical behavior, many factors have been considered. For an elastic–perfectly plastic model, Su et al. (2018) have presented analytical solutions for the stress and the displacement of a circular opening compatible with the Drucker–Prager yield criterion. The analysis considered the interaction between the ground response and the support characteristic. Kabwe et al. (2020) have presented solutions accounting for non-circular tunnels and intermediate principal stress based on Mohr–Coulomb (M–C) and Hoek–Brown (H–B) criteria. For an elastic–brittle–plastic model, Wang et al. (2012) have proposed stress and displacement distribution solutions around a circular tunnel in an M–C rock mass. Zareifard and Fahimifar (2016) have considered the damaged zone based on Park’s research in elastic–brittle–plastic rock masses. Among the three models, the strain-softening model is most widely used in practical engineering, and its special cases can be considered as the elastic–perfectly plastic and elastic–brittle–plastic models. Many scholars (Song and Rodriguez-Dono 2021; Cui et al., 2019; Wang and Zou 2018; Zareifard 2021) have used plastic variables, which characterize the strength deterioration for examining the GRC of a strain-softening rock mass. Meanwhile, there have been many strain-softening studies considering over-excavation and support systems (Song and Rodriguez-Dono 2021; Xue et al., 2021). Li et al. (2015) have used a simple strain-softening model with a brittleness coefficient to study the plastic radius, calculated using some assumptions and simplifications of non-expansion conditions.

Many studies have focused on numerical solutions in strain-softening rock masses based on the finite difference method. Lee and Pietruszczak (2008) have deduced numerical solutions in M–C and H–B rock masses based on the finite difference method. Compared with the work of Brown et al(1983), Lee and Pietruszczak (2008) have divided the plastic zone into assuming a constant radial stress between adjacent annuli instead of a constant radius. Wang et al. (2010) have proposed an analytical solution for strain-softening rock masses and established the corresponding program by dividing the strain-softening process into some elastic–brittle–plastic processes. Shen and Gu (2021) have calculated the displacement of a tunnel after excavation by a layer-wise summation method, which can provide accurate predictions. In order to investigate the influence of intermediate principal stress, Li J, et al. (2022) proposed a finite difference method to calculate the excavation response in Drucker–Prager rock mass exhibiting strain-softening behavior. Wang et al. (2021) developed a strain-softening numerical procedure considering the effects of confinement-dependent characteristic and the generalized 3D Hoek–Brown strength criterion. Yu-ming et al. (2021) established a numerical solution for strain-softening rock mass under three-dimensional principal stress condition, which is validated by numerical simulation results. Cui et al. (2015) have proposed a multistep brittle–plastic model with the assumption that the material properties follow a piecewise linear correction with plastic shear strain and proposed the critical value of shear modulus based on H–B and M–C yield criteria. Based on the previous studies, Zou et al. (2017) have proposed a new method for calculating the GRC in the strain-softening rock for a circular tunnel which starts with a constant radius increment and the plastic radius obtained by linear interpolation. However, the accuracy of this method depends on the initial plastic radius, and it is not convenient to calculate the stress field of each annulus. More recently, Zhang et al. (2021) and Guan et al. (2018) have defined the normalized radii for the plastic zone and proposed a novel numerical procedure for strain-softening rock mass, which provides convenience for obtaining GRC. Ghorbani and Hasanzadehshooiili (2019) have proposed strain-softening numerical procedure, considering unified strength criteria.

To improve calculation accuracy and efficiency, a new but simple method is developed here for calculating the ground response in an M–C rock mass exhibiting strain-softening behavior. First, the problem definition and the basic theory are introduced. During the theoretical derivation, the plastic zone is divided into some annuli, with the thickness determined by a constant radial stress increment. Then, the analytical solution of each annulus is obtained according to the equilibrium equation, geometric equation, and M–C yield criterion. The method is verified by numerical simulation. Finally, the effects of ground conditions, the computation efficiency, and the engineering applicability are examined.

Problem Definition

A circular tunnel of radius $r_0$ is excavated under the plane strain condition (see Figure 1). The rock mass is considered to be a continuous, homogenous, isotropic, and initially elastic before the excavation disturbance. Here, a hydrostatic stress ${\sigma }_0$ is imposed around the rock, and there is an internal support pressure $p_i$ on the inner tunnel surface. When the internal support pressure $p_i$ is lower than a critical value $p_{ic}$, a plastic zone appears around the tunnel. When the plastic zone develops, the strength parameters gradually decrease. When strain-softening behavior is considered, the plastic zone is divided into strain-softening and residual zones, and the interfacial radius between them is $R_s$.

FIGURE 1

FIGURE 1. Mechanical model for a circular tunnel in strain-softening rock mass.

The mechanical behavior and constitutive relationship of the rock mass can be determined by the definition of the plastic internal variable $\eta$, which can be calculated according to the plastic strain, expressed as follows (Zou, Li, and Wang 2017):

$\eta ={\epsilon }_{\theta }^p-{\epsilon }_r^p,(1)$

where ${\epsilon }_{\theta }^p$ and ${\epsilon }_r^p$ are the circumferential and radial plastic strain, respectively.

The strength parameters of the strain-softening rock mass are calculated according to the bilinear function as follows (Lee and Pietruszczak 2008; Zou, Li, and Wang 2017):

$\omega \left(\eta \right)=\{\begin{array}{c}{\omega }_p-\left({\omega }_p-{\omega }_r\right)\frac{\eta }{{\eta }_c}, 0<\eta <{\eta }_c\\ {\omega }_r,\eta \ge {\eta }_c\end{array},(2)$

where $\omega$ denotes a strength parameter, such as cohesion force $c$, friction angle $\phi$, and dilation angle $\psi$; ${\eta }_c$ denotes the critical plastic internal variable that the strength parameter transforms from strain-softening to the residual state; and subscripts $p$ and $r$ denote peak and residual values, respectively. In order to simplify the mechanical analysis, the deformation parameters (such as rock stiffness) are assumed to be constant once yielded.

The M–C yield criterion shows the relationship between the stress ${\sigma }_{\theta }$ and ${\sigma }_r$ as follows:

${\sigma }_{\theta }=\alpha \left(\eta \right)\cdot {\sigma }_r+Y\left(\eta \right),(3)$

where $\alpha \left(\eta \right)=\frac{1+sin\phi \left(\eta \right)}{1-sin\phi \left(\eta \right)}$ and $Y\left(\eta \right)=\frac{2c\left(\eta \right)cos\phi \left(\eta \right)}{1-sin\phi \left(\eta \right)}$ ,respectively.

To simplify the subsequent theoretical derivation and numerical programming, the dimensionless stress $\tilde{\sigma }$ is defined as follows:

$\tilde{\sigma }=\frac{1}{E}\left(\sigma +\frac{Y\left(\eta \right)}{\alpha \left(\eta \right)-1}\right),(4)$

where $E$ is the elastic modulus.

Combining Eqs 3, 4, the yield surface in the plastic zone can be expressed as follows:

${\tilde{\sigma }}_{\theta }-\alpha \left(\eta \right)\cdot {\tilde{\sigma }}_r=\mathrm{0,}(5)$

When the non-associated flow rule is adopted, the plastic potential function is given by the following equation:

$G\left({\tilde{\sigma }}_{\theta },{\tilde{\sigma }}_r,\eta \right)={\tilde{\sigma }}_{\theta }-\beta \left(\eta \right){\tilde{\sigma }}_r,(6)$

where $\beta \left(\eta \right)$ denotes the coefficient of dilation, which is expressed as follows:

$\beta \left(\eta \right)=\frac{1+sin\psi \left(\eta \right)}{1-sin\psi \left(\eta \right)},(7)$

Theoretical Derivations

The displacement and stress of the surrounding rock are derived, and the calculation is progressed and equations are presented in the following.

Solution for the Plastic Zone

To be convenient for the theoretical derivation and numerical programming of the plastic zone in the following parts, the following dimensionless radius $\rho$ and dimensionless displacement $U$ are defined as follows:

$\rho =\frac{r}{R_p},U=\frac{u}{R_p},(8)$

The strains can be expressed in terms of the previous dimensionless radial displacement and radius.

${\epsilon }_r=\frac{dU}{d\rho },{\epsilon }_{\theta }=\frac{U}{\rho },(9)$

The stress–strain field of the surrounding rock is solved by the finite difference method, with the plastic zone of the surrounding rock divided into n concentric annuli, and the stress increment $\text{Δ}{\sigma }_r$ is maintained constant between adjacent annuli (see Figure 2A). The radial stress at the elastic–plastic interface is ${\sigma }_{r\left(1\right)}$, while the stress at the tunnel wall is ${\sigma }_{r\left(n+1\right)}$. The locations at the outer and inner boundaries within the $j$ th annulus correspond to the dimensionless radius ${\rho }_{\left(j+1\right)}$ and ${\rho }_{\left(j\right)}$, respectively (see Figure 2B), and the radial stresses are denoted by ${\sigma }_{r\left(j+1\right)}$ and ${\sigma }_{r\left(j\right)}$, respectively. Therefore, the increment of radial stress $\Delta {\sigma }_r$ can be expressed as follows:

$\text{Δ}{\sigma }_r=\frac{{\sigma }_{r(n+1)}-{\sigma }_{r\left(1\right)}}{n},(10)$

where ${\sigma }_{r\left(n+1\right)}$ represents the internal support stress $p_i$ and ${\sigma }_{r\left(1\right)}$ is equal to the critical support stress $p_{ic}$.

FIGURE 2

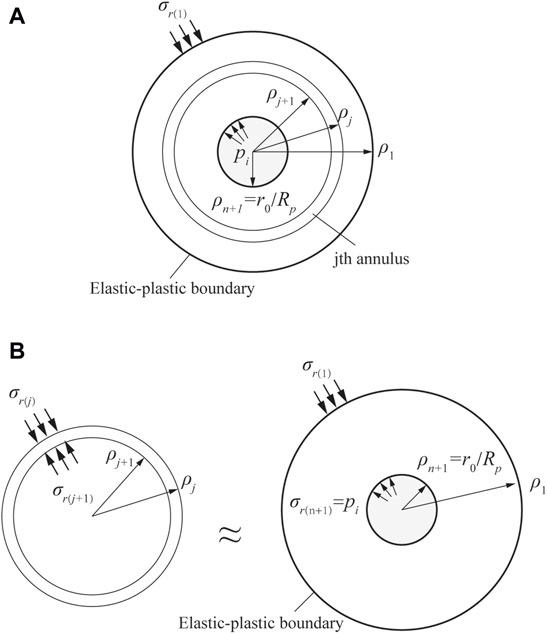
FIGURE 2. Schematic figure of numerical calculation strategy: (A) plastic region divided into the finite number of annuli and (B) stress boundary of the jth annulus.

When the internal support pressure is lower than the critical value $p_{ic}$, a plastic zone appears around the tunnel. For the rock mass which obeys the M–C yield criterion, the critical value $p_{ic}$ is calculated by the following equation:

$p_{ic}=\frac{2{\sigma }_0-Y_p}{{\alpha }_P+1},(11)$

where $Y_p=\frac{2c_{p}cos{\phi }_p}{1-sin{\phi }_p}$ and ${\alpha }_p=\frac{1+sin{\phi }_p}{1-sin{\phi }_p}$.

The radial stress at the inner radius of each annulus can be solved as follows:

${\sigma }_{r\left(j+1\right)}={\sigma }_{r\left(j\right)}+\text{Δ}{\sigma }_r,(12)$

For the $j^{th}$ annulus in the presented strain-softening model here, if the annulus number is large enough, the stresses within the $j^{th}$ annulus can be conveniently obtained by virtue of the existing brittle–plastic closed form solution (Park and Kim 2006), thus leading to the following stress expressions:

${\sigma }_{r\left(j\right)}=-\frac{Y_{\left(j\right)}}{{\alpha }_{\left(j\right)}-1}+({\sigma }_{r\left(j+1\right)}+\frac{Y_{\left(j\right)}}{{\alpha }_{\left(j\right)}-1}){\left(\frac{r_{\left(j\right)}}{r_{(j+1)}}\right)}^{({\alpha }_{\left(j\right)}-1)},(13)$

${\sigma }_{\theta \left(j\right)}=-\frac{{\alpha }_{\left(j\right)}\cdot Y_{\left(j\right)}}{{\alpha }_{\left(j\right)}-1}+\left({\sigma }_{r\left(j+1\right)}+\frac{Y_{\left(j\right)}}{{\alpha }_{\left(j\right)}-1}\right){\left(\frac{r_{\left(j\right)}}{r_{\left(j+1\right)}}\right)}^{\left({\alpha }_{\left(j\right)}-1\right)}+Y_{\left(j\right)},(14)$

where $Y_{\left(j\right)}=\frac{2c_{\left(j\right)}cos{\phi }_{\left(j\right)}}{1-sin{\phi }_{\left(j\right)}}$ and ${\alpha }_{\left(j\right)}=\frac{1+sin{\phi }_{\left(j\right)}}{1-sin{\phi }_{\left(j\right)}}$.

For convenience in the programming, the dimensionless radial and circumferential stress within the $j^{th}$ annulus can be also expressed integrating Eqs 13, 14 and Eqs 4, 8 as follows:

${\tilde{\sigma }}_{r\left(j\right)}={\tilde{\sigma }}_{r\left(j+1\right)}{\left(\frac{{\rho }_{\left(j\right)}}{{\rho }_{(j+1)}}\right)}^{{\alpha }_{\left(j\right)}-1},(15)$

${\tilde{\sigma }}_{\theta \left(j\right)}={\alpha }_{\left(j\right)}{\tilde{\sigma }}_{r\left(j\right)}={\alpha }_{\left(j\right)}{\tilde{\sigma }}_{r\left(j+1\right)}{\left(\frac{{\rho }_{\left(j\right)}}{{\rho }_{(j+1)}}\right)}^{{\alpha }_{\left(j\right)}-1},(16)$

where $\tilde{\sigma }$ is obtained according to Eq (4) with strength parameters ($Y$ and $\alpha$) corresponding to those at $\rho ={\rho }_{\left(j\right)}$.

Then, the dimensionless radius ${\rho }_{\left(j+1\right)}$ can be derived using Eq (15) as follows:

${\rho }_{\left(j+1\right)}={\rho }_{\left(j\right)}{\left(\frac{{\tilde{\sigma }}_{r\left(j\right)}}{{\tilde{\sigma }}_{r(j+1)}}\right)}^{\frac{1}{{\alpha }_{\left(j\right)}-1}},(17)$

If $n$ is large enough, the displacement within the $j^{th}$ plastic annulus can be given in a way similar to the brittle–plastic analytical expression (Park and Kim 2006) combining the non-associated flow law with Hooke’s law; that is,

$\frac{u_{(j+1)}}{r_{(j+1)}}=\frac{1}{2G}\left[\frac{U_{1(J+1)}}{{\beta }_{\left(j\right)}+1}+\frac{U_{2(j+1)}}{{\beta }_{\left(j\right)}+{\alpha }_{\left(j\right)}}-\frac{U_{1\left(j+1\right)}}{{\beta }_{\left(j\right)}+1}{\left(\frac{r_{\left(j\right)}}{r_{\left(j+1\right)}}\right)}^{{\beta }_{\left(j\right)}+1}-\frac{U_{2\left(j+1\right)}}{{\beta }_{\left(j\right)}+{\alpha }_{\left(j\right)}}{\left(\frac{r_{\left(j\right)}}{r_{\left(j+1\right)}}\right)}^{{\beta }_{\left(j\right)}+{\alpha }_{\left(j\right)}}+2G{\left(\frac{r_{\left(j\right)}}{r_{(j+1)}}\right)}^{{\beta }_{\left(j\right)}}\frac{u_{\left(j\right)}}{r_{(j+1)}}\right],(18)$

where $U_{1(j+1)}=(1+{\beta }_{\left(j\right)})(1-2\mu )(A-{\sigma }_0)$, $U_{2(j+1)}=\left[\left(1-\mu -{\beta }_{\left(j\right)}\mu \right)+\left({\beta }_{\left(j\right)}-{\beta }_{\left(j\right)}\mu -\mu \right){\alpha }_{\left(j\right)}\right]\mathrm{B,}$ $A=-Y_{\left(j\right)}/\left({\alpha }_{\left(j\right)}-1\right)$, and $B=p_i+\frac{Y_{\left(j\right)}}{\left({\alpha }_{\left(j\right)}-1\right)}$.

To simplify the numerical programming, the dimensionless radial displacement at $\rho ={\rho }_{\left(j+1\right)}$ is given by the following equation:

$U_{(j+1)}=\frac{1}{2G}{\rho }_{(j+1)}\left[\frac{{\text{Ω}}_{1(j+1)}}{{\beta }_{\left(j\right)}+1}+\frac{{\text{Ω}}_{2(j+1)}}{{\beta }_{\left(j\right)}+{\alpha }_{\left(j\right)}}-\frac{{\text{Ω}}_{1\left(j+1\right)}}{{\beta }_{\left(j\right)}+1}{\left(\frac{{\rho }_{\left(j\right)}}{{\rho }_{\left(j+1\right)}}\right)}^{{\beta }_{\left(j\right)}+1}-\frac{{\text{Ω}}_{2\left(j+1\right)}}{{\beta }_{\left(j\right)}+{\alpha }_{\left(j\right)}}{\left(\frac{{\rho }_{\left(j\right)}}{{\rho }_{\left(j+1\right)}}\right)}^{{\beta }_{\left(j\right)}+{\alpha }_{\left(j\right)}}+2G{\left(\frac{{\rho }_{\left(j\right)}}{{\rho }_{(j+1)}}\right)}^{{\beta }_{\left(j\right)}}\frac{U_{\left(j\right)}}{{\rho }_{(j+1)}}\right],(19)$

where ${\text{Ω}}_{1(j+1)}=\left(1+{\beta }_{\left(j\right)}\right)(1-2\mu )(-E{\tilde{\sigma }}_0)$ and ${\text{Ω}}_{2(j+1)}=\left[\left(1-\mu -{\beta }_{\left(j\right)}\mu \right)+\left({\beta }_{\left(j\right)}+{\beta }_{\left(j\right)}\mu -\mu \right){\alpha }_{\left(j\right)}\right]\left(E{\tilde{\sigma }}_{r(j+1)}\right)$.

The circumferential strain ${\epsilon }_{\theta \left(j+1\right)}$ and the radial strain ${\epsilon }_{r\left(j+1\right)}$ within the $j$ th plastic annulus is obtained by Eq (9) as follows:

${\epsilon }_{\theta (j+1)}=\frac{U_{(j+1)}}{{\rho }_{(j+1)}}(20)$

and

${\epsilon }_{r(j+1)}=\frac{d{U}_{(j+1)}}{d{\rho }_{(j+1)}}=\frac{1}{2G}\left[\frac{{\text{Ω}}_{1(j+1)}}{{\beta }_{\left(j\right)}+1}+\frac{{\alpha }_{\left(j\right)}\cdot {\text{Ω}}_{2(j+1)}}{{\beta }_{\left(j\right)}+{\alpha }_{\left(j\right)}}+\frac{{\beta }_{\left(j\right)}\cdot {\text{Ω}}_{1(j+1)}}{{\beta }_{\left(j\right)}+1}{\left(\frac{{\rho }_{\left(j\right)}}{{\rho }_{(j+1)}}\right)}^{{\beta }_{\left(j\right)}+1}+\frac{{\beta }_{\left(j\right)}\cdot {\text{Ω}}_{2(j+1)}}{{\beta }_{\left(j\right)}+{\alpha }_{\left(j\right)}}{\left(\frac{{\rho }_{\left(j\right)}}{{\rho }_{(j+1)}}\right)}^{{\beta }_{\left(j\right)}+{\alpha }_{\left(j\right)}}-2G\cdot {\beta }_{\left(j\right)}{\left(\frac{{\rho }_{\left(j\right)}}{{\rho }_{(j+1)}}\right)}^{{\beta }_{\left(j\right)}+1}\frac{U_{\left(j\right)}}{{\rho }_{\left(j\right)}}\right],(21)$

According to Hooke’s law, the radial and circumferential elastic strain at $\rho ={\rho }_{\left(j+1\right)}$ can be expressed as follows:

${\epsilon }_{r(j+1)}^e=\left(1+\mu \right)\left[\left(1-\mu \right)\left({\tilde{\sigma }}_{r(j+1)}-{\tilde{\sigma }}_0\right)-\mu \cdot \left({\tilde{\sigma }}_{\theta (j+1)}-{\tilde{\sigma }}_0\right)\right](22)$

and

${\epsilon }_{\theta (j+1)}^e=\left(1+\mu \right)\left[\left(1-\mu \right)\left({\tilde{\sigma }}_{\theta (j+1)}-{\tilde{\sigma }}_0\right)-\mu \cdot \left({\tilde{\sigma }}_{r(j+1)}-{\tilde{\sigma }}_0\right)\right],(23)$

Since the radial and circumferential strains are divided into elastic and plastic parts, combined with Eq (1), the plastic internal variable $\eta$ at $\rho ={\rho }_{\left(j+1\right)}$ can be expressed as follows:

${\eta }_{(j+1)}=\left({\epsilon }_{\theta (j+1)}-{\epsilon }_{\theta (j+1)}^e\right)-\left({\epsilon }_{r(j+1)}-{\epsilon }_{r(j+1)}^e\right),(24)$

Then, the strength parameters at $\rho ={\rho }_{\left(j+1\right)}$ can be updated according to Eq (2).

The radial displacement and the radius at $\rho ={\rho }_{\left(j+1\right)}$ can be obtained by Eq (8) as follows:

$u_{(j+1)}=R_p\cdot U_{(j+1)}(25)$

and

$r_{(j+1)}=R_p\cdot {\rho }_{(j+1)},(26)$

When $j=n$, $r=r_{\left(n+1\right)}=r_0$ at $\rho ={\rho }_{\left(n+1\right)}$. Thus, the plastic radius can be determined as follows:

$R_p=\frac{r_0}{{\rho }_{(n+1)}},(27)$

where ${\rho }_{\left(n+1\right)}$ is solved iteratively by Eq (17).

The wall convergence displacement can be expressed as follows:

$u_{\alpha }=u_{(n+1)}=R_p\cdot U_{(n+1)},(28)$

The deformation within the plastic zone can be computed by combining Eqs 25–27.

Solution for the Elastic Zone

The tunnel surrounding rock is elastic in the initial stage of excavation, and according to the research of Vrakas and Anagnostou (2014) and Yu and Houlsby (1995), the response in the elastic zone outside the plastic zone can be expressed as follows:

${\tilde{\sigma }}_r={\tilde{\sigma }}_0-\left({\tilde{\sigma }}_0-{\tilde{p}}_{ic}\right){\left(R_p/r\right)}^2{\tilde{\sigma }}_{\theta }={\tilde{\sigma }}_0+\left({\tilde{\sigma }}_0-{\tilde{p}}_{ic}\right){\left(R_p/r\right)}^{2}u=\left(1+\mu \right)\left({\tilde{\sigma }}_0-{\tilde{p}}_{ic}\right){\left(R_p/r\right)}^{2}r,(29)$

Once the plastic radius Rp is solved via Eq (27), the stresses and displacement in the elastic zone can be all obtained by Eq (29).

Calculation Progress

A flow chart summarizing the calculation process for obtaining the excavation response is shown in Figure 3, and the details are presented in the following steps:

FIGURE 3

FIGURE 3. Flow chart of the calculations.

Step 1:. The basic parameters are set first, including the excavation radius $r_0$, in situ hydrostatic field stress ${\sigma }_0$, internal support stress $p_i$, critical plastic internal variable ${\eta }_c$, and the peak and residual strength parameters of the rock mass ${\omega }_p$ and ${\omega }_r$. Moreover, accounting that the calculation process starts from the elastic–plastic interface, the initial values for the computation are set as: ${\omega }_1={\omega }_p$, ${\sigma }_{r\left(1\right)}=p_{ic}$, ${\rho }_1=1$, and ${\eta }_1=0$.

Step 2:. The thickness of each plastic annulus is determined by a constant radial stress increment as shown in Eq (10). Therefore, the radial stress ${\sigma }_{r\left(j+1\right)}$ at the dimensionless inner radius ${\rho }_{\left(j+1\right)}$ of the jth annulus is calculated using Eq (12), while the dimensionless radius ${\rho }_{\left(j+1\right)}$ is solved by Eq (17).

Step 3:. The dimensionless displacement within each annulus is obtained in a way similar to the brittle–plastic analytical expression. The total strain within each annulus is solved using Eq (9). The elastic strain is calculated using Hooke’s law, and plastic strain can be then determined.

Step 4:. The plastic internal variable ${\eta }_{j+1}$ at $\rho ={\rho }_{j+1}$ is calculated using Eq (24). The mechanical behavior of the rock mass is then determined by comparing the plastic internal variable ${\eta }_{j+1}$ with critical plastic internal variable ${\eta }_c$. The strength parameters of each annulus are updated using Eq (2).

Step 5:. Set $j=j+1$ and repeat the previous steps $n$ times.

Step 6:. When $j=n+1$, the plastic radius is determined by Eq (27). The displacement and stresses of each annulus in the plastic zone are calculated by Eq (25) and Eqs 15, 16, respectively.

Step 7:. The stresses and displacement in the elastic zone are calculated according to Eq (29).

Validation of the Numerical Procedure

Numerical Simulation Verification

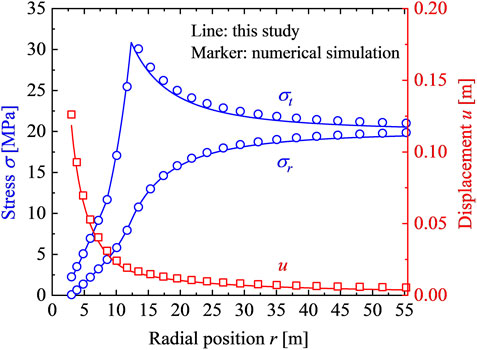
The GRC obtained by the proposed method is compared with the numerical simulation results from COMSOL Multiphysics to verify the validity of the numerical procedure. The parameters provided by Zou et al. (2017) are adopted, with $r_0$ = 3 m, ${\sigma }_0$ = 20 MPa, $p_i = 0$ MPa, $E$ = 10 GPa, μ = 0.25, $c_p$ = 1 MPa, $c_r$ = 0.7 MPa, ${\phi }_p$ = 30°, ${\phi }_r$ = 22°$,{\psi }_p$ = 3.75°, and ${\psi }_r$ = 3.75°.

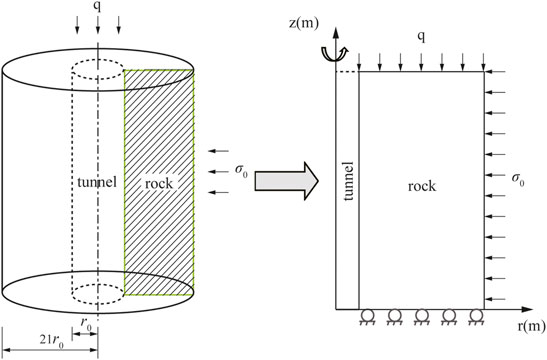
The two-dimensional rotational axisymmetric numerical model is shown in Figure 4. The in-plane axial in situ stress q is taken as $2\mu {\sigma }_0$ to satisfy the stress boundary conditions in the plane strain problem, which is exerted on top of the model. The right boundary is restrained by the confining stress ${\sigma }_0$, while the bottom end set as a roller, and left boundary is taken as a symmetrical boundary. The strain-softening constitutive model is used in the numerical simulation and the plastic zone radius $R_p$ is obtained by measuring the radius for $\eta >0$.

FIGURE 4

FIGURE 4. Two-dimensional axisymmetric numerical model.

The comparison results between the numerical simulation and the presented method with $n=50$ and ${\eta }_c$ = 0.008 are shown in Figure 5. It can be observed that, the stresses and displacement distribution of the strain-softening rock are in good agreement with the numerical simulation results, which indicates that the proposed numerical procedure is capable of predicting the ground response accurately.

FIGURE 5

FIGURE 5. Comparison results with numerical simulation.

Theoretical Verification

The procedure result is also compared with the work of Lee and Pietruszczak (2008). The relevant parameters are: $r_0$ = 2.5 m, ${\sigma }_0$ = 37.5 MPa, $n=50$, $E$ = 36.5 GPa, μ = 0.25, $c_p$ = 3.637 MPa, $c_r$ = 1.878 MPa, ${\phi }_p$ = 29.52°, ${\phi }_r$ = 20.64°, ${\psi }_p$ = 7.38°, ${\psi }_r$ = 7.38°, and ${\eta }_c=0.1190$. Figure 6 shows that the GRC obtained by the procedure is perfectly consistent with that by Lee and Pietruszczak (2008), which emphasizes the effectiveness of the proposed method in analyzing the excavation response.

FIGURE 6

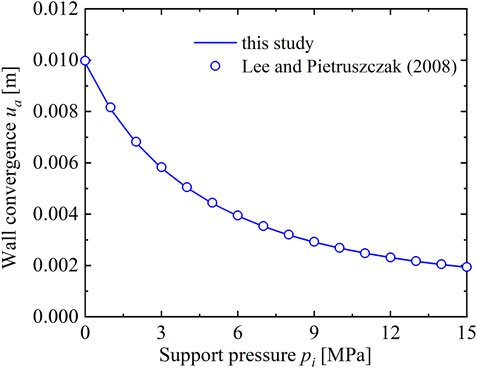
FIGURE 6. Comparison with theoretical solution of Lee and Pietruszczak (2008).

Analysis of the Excavation Response

This section examines the influence of some parameters on the ground response. The parameters are as follows: $r_0$ = 2.5 m, ${\sigma }_0$ = 37.5 MPa, $E$ = 36.5 GPa, μ = 0.25, $c_p$ = 3.637 MPa, $c_r$ = 1.878 MPa, ${\phi }_p$ = 29.52°, ${\phi }_r$ = 20.64°, ${\psi }_p$ = 7.38°, ${\psi }_r$ = 7.38°, and ${\eta }_c=0.1190$.

Influence of the Annulus Number

Figure 7 shows the GRCs under different annulus numbers in the plastic zone. It can be seen that the results are almost identical and a stable numerical solution can be achieved, despite of a quite small n = 50 assumed. It means that a rapid numerical convergence can be expected for the proposed procedure, which is beneficial in providing an accurate but a simple method in a preliminary tunneling design. For the purpose of ensuring the speed and accuracy of numerical calculation, the annulus number n in the plastic zone is taken as 50 in the following parts.

FIGURE 7

FIGURE 7. Influence of the annulus number.

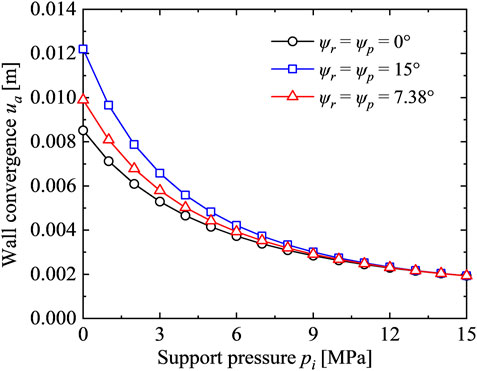
Influence of the Dilatancy Angle

In order to examine the influence of the dilatancy angle on ground response, three cases are compared, and those are ${\psi }_p={\psi }_r=$ 15°, ${\psi }_p={\psi }_r=$ 7.38°, and ${\psi }_p={\psi }_r=$ 0°. As shown in Figure 8, the rock displacement increases with the dilatancy angle, and it tends to be identical for big support pressure, which can be attributed to the pure elastic response in far field that is independent of the rock dilatancy.

FIGURE 8

FIGURE 8. Influence of the dilatancy angle.

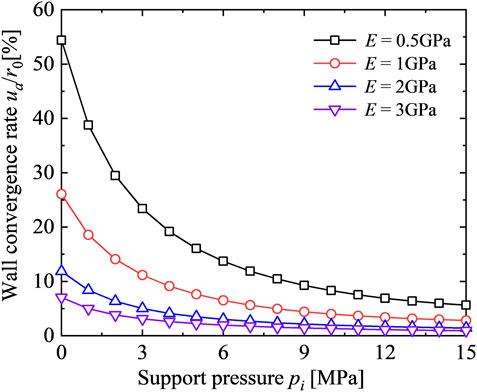
Influence of the Elastic Modulus

Figure 9 shows the influence of the elastic modulus E on GRC. It can be seen that the elastic modulus plays an important role on ground response. More specifically, the poorer quality of rock, the higher the displacement then more easily the rock mass deforms. Therefore, for the rock mass involving under adverse conditions, cautions should be paid due to the high squeezing potential and large deformation possibility.

FIGURE 9

FIGURE 9. Influence of the elastic modulus.

Discussion

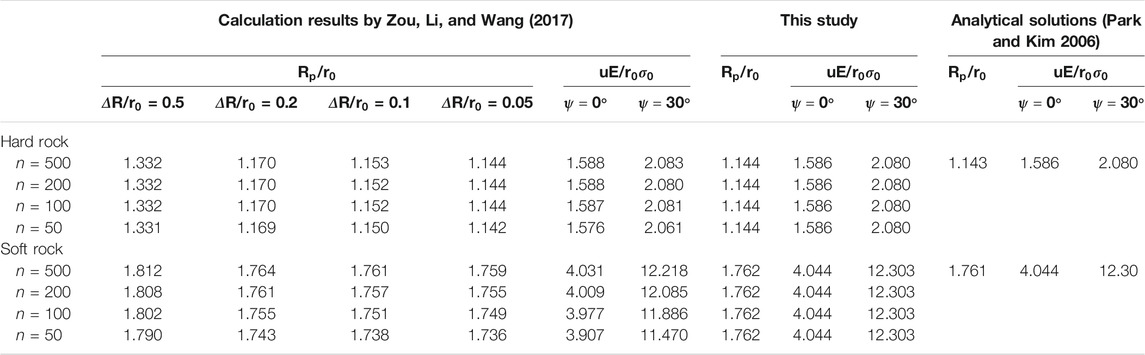
1) Zou et al. (2017) established the first strain-softening numerical procedure for GRC by resorting to existing analytical solutions, which is similar to the present method, so it would be beneficial here to discuss the present method with respect to that by Zou et al. (2017). In their approach, the computation starts with the assumption of constant radius increment within the plastic zone instead of constant radial stress increment in this study, which leads to the necessity to determine the actual radius Rp of the plastic zone based on a linear interpolation strategy in combination with the finite difference analysis. Despite that, this manipulation makes the calculation of GRC convenient, the accuracy and efficiency highly depend on not only the annulus number n but also the initially assumed value of the plastic radius and its increment ∆R, which may bring negative influence on the robustness of procedure. Moreover, the stress and displacement distributions in the surrounding rock are also difficult to be determined as stated by Zou et al. (2017), which makes the analysis of the fictitious support pressure and the rock-support interaction using the convergence–confinement method quite inconvenient. Conversely, our numerical procedure starts with constant radial stress increment assumption (see Equation 10), and the ground response including GRC and stresses and displacement can be all solved for without additional variables required except the annulus number, n.

In order to investigate the computation efficiency and accuracy, comparison results are given for the elastic–brittle–plastic rock mass. Table 1 lists the basic parameter values, and Table 2 shows the computation data by different methods. It can be observed that, the efficiency and accuracy of procedure by Zou et al. (2017) varies with plastic radius increment ∆R and annulus number n, while the present method in this study shows better accuracy and convergence, accounting that the results are perfectly consistent with the analytical solutions even when the value of n is small. Moreover, the distributions of stresses and displacement in the surrounding rock can be all obtained based on our numerical procedure, as shown in the previous Figure 5.

2) As shown in Figure 9, when the rock stiffness is low, significant deformation can be observed, with the wall convergence even reaching up to half of the designed radius $r_0$, which means that the undeformed (initial) and the deformed (current) tunnel configuration differs remarkably. This phenomenon can be magnified in weak rocks with high deformability and low strength, which makes the calculated wall convergence irrational within the framework of the infinitesimal strain theory adopted in this article, accounting that a slight configuration difference observed in tunneling is one of the main prerequisites. In fact, as emphasized by Vrakas and Anagnostou 2014; Vrakas and Anagnostou 2015; Vrakas 2016 and Guan et al., 2018, 2020a, 2020b;; Guan, Zhu, and Zhang 2021, when tunneling through rock masses under squeezing conditions with strains exceeding 10%, the characteristic of geometric non-linearity should be taken into consideration and the large deformation elasto–plastic theory is recommended. Nevertheless, our numerical procedure remains sufficiently accurate and high efficiency for the plane strain excavation problem, as long as the wall convergence rate is lower than 10%, and this aim ought to be kept in mind.

TABLE 1

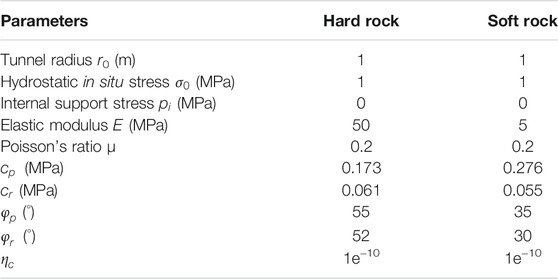
TABLE 1. Basic parameters for the elastic–brittle–plastic rock mass (Zou, Li, and Wang 2017).

TABLE 2

TABLE 2. Calculation results for different elasto-plastic analysis methods.

Conclusion

A new numerical procedure is presented to analyze the excavation-induced response in a strain-softening rock mass. During the calculation process, the plastic zone is divided into finite annuli, and thickness is determined by a constant radial stress increment. The ground behavior in the plastic zone is obtained explicitly by virtue of the existing analytical solutions of the brittle–plastic rock, which makes the derivation and calculation simple but effective. The comparison results with existing studies and numerical simulation show that the proposed method behaves more efficiently and accurately than the previous numerical procedure for strain-softening rock mass, and the ground response including GRC and stresses and displacement can be all calculated conveniently. However, more attention should be paid when the proposed strain-softening numerical procedure based on the infinitesimal strain theory is applied to a practical problem involving in large deformations with wall convergence over 10%.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

KG contributed to the implementation of the theoretical derivation and writing of the draft, QZ contributed to the data analysis and writing of the draft, HL contributed to the revision and approval of the draft, and WZ contributed to the discussion and implementation of the numerical procedure.

Funding

This work was supported by the National Natural Science Foundation of China (Grant Nos. 52004053 and U1906208), Natural Science Foundation of Liaoning Province (Grant No. 2021-BS-052), and Fundamental Research Funds for the Central Universities (Grant No. N2101028).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Brown, E. T., Bray, J. W., Ladanyi, B., and Hoek, E. (1983). Ground Response Curves for Rock Tunnels. J. Geotechnical Eng. 109 (1), 15–39. doi:10.1061/(asce)0733-9410(1983)109:1(15)

CrossRef Full Text | Google Scholar

Cui, L., Sheng, Q., Zheng, J.-j., Cui, Z., Wang, A., and Shen, Q. (2019). Regression Model for Predicting Tunnel Strain in Strain-Softening Rock Mass for Underground Openings. Int. J. Rock Mech. Mining Sci. 119, 81–97. doi:10.1016/j.ijrmms.2019.04.014

CrossRef Full Text | Google Scholar

Cui, L., Zheng, J.-J., Zhang, R.-J., and Dong, Y.-K. (2015). Elasto-plastic Analysis of a Circular Opening in Rock Mass with Confining Stress-dependent Strain-Softening Behaviour. Tunnelling Underground Space Tech. 50, 94–108. doi:10.1016/j.tust.2015.07.001

CrossRef Full Text | Google Scholar

Cui, S., Pei, X., Jiang, Y., Wang, G., Fan, X., Yang, Q., et al. (2021). Liquefaction within a Bedding Fault: Understanding the Initiation and Movement of the Daguangbao Landslide Triggered by the 2008 Wenchuan Earthquake (Ms = 8.0). Eng. Geology. 295, 106455. doi:10.1016/j.enggeo.2021.106455

CrossRef Full Text | Google Scholar

Ghorbani, A., and Hasanzadehshooiili, H. (2019). A Comprehensive Solution for the Calculation of Ground Reaction Curve in the crown and Sidewalls of Circular Tunnels in the Elastic-Plastic-EDZ Rock Mass Considering Strain Softening. Tunnelling Underground Space Tech. 84, 413–431. doi:10.1016/j.tust.2018.11.045

CrossRef Full Text | Google Scholar

Guan, K., Zhu, W. C., and Zhang, Q. Y. (2021). Application of the Convergence-Confinement Method to Excavation Response of Roadway in Rock Mass Considering Large Deformation. IOP Conf. Ser. Earth Environ. Sci. 861 (4), 042090. doi:10.1088/1755-1315/861/4/04209010.1088/1755-1315/861/4/042090

CrossRef Full Text | Google Scholar

Guan, K., Zhu, W., Liu, X., and Wei, J. (2020a). Finite Strain Analysis of Squeezing Response in an Elastic-Brittle-Plastic Weak Rocks Considering the Influence of Axial Stress. Tunnelling Underground Space Tech. 97, 103254. doi:10.1016/j.tust.2019.103254

CrossRef Full Text | Google Scholar

Guan, K., Zhu, W., Liu, X., Wei, J., and Niu, L. (2020b). Re-profiling of a Squeezing Tunnel Considering the post-peak Behavior of Rock Mass. Int. J. Rock Mech. Mining Sci. 125, 104153. doi:10.1016/j.ijrmms.2019.104153

CrossRef Full Text | Google Scholar

Guan, K., Zhu, W., Wei, J., Liu, X., Niu, L., and Wang, X. (2018). A Finite Strain Numerical Procedure for a Circular Tunnel in Strain-Softening Rock Mass with Large Deformation. Int. J. Rock Mech. Mining Sci. 112, 266–280. doi:10.1016/j.ijrmms.2018.10.016

CrossRef Full Text | Google Scholar

He, Y., and Kusiak, A. (2018). Performance Assessment of Wind Turbines: Data-Derived Quantitative Metrics. IEEE Trans. Sustain. Energ. 9 (1), 65–73. doi:10.1109/TSTE.2017.2715061

CrossRef Full Text | Google Scholar

Huang, X., Li, L., Zhang, C., Liu, B., Li, K., Shi, H., et al. (2021). Multi-Step Combined Control Technology for Karst and Fissure Water Inrush Disaster during Shield Tunneling in Spring Areas. Front. Earth Sci. 9, 1–16. doi:10.3389/feart.2021.795457

CrossRef Full Text | Google Scholar

Kabwe, E., Karakus, M., and Chanda, E. K. (2020). Proposed Solution for the Ground Reaction of Non-circular Tunnels in an Elastic-Perfectly Plastic Rock Mass. Comput. Geotechnics 119, 103354. doi:10.1016/j.compgeo.2019.103354

CrossRef Full Text | Google Scholar

Lee, Y.-K., and Pietruszczak, S. (2008). A New Numerical Procedure for Elasto-Plastic Analysis of a Circular Opening Excavated in a Strain-Softening Rock Mass. Tunnelling Underground Space Tech. 23 (5), 588–599. doi:10.1016/j.tust.2007.11.002

CrossRef Full Text | Google Scholar

Li, H., Deng, J., Feng, P., Pu, C., Arachchige, D. D. K., and Cheng, Q. (2021a). Short-Term Nacelle Orientation Forecasting Using Bilinear Transformation and ICEEMDAN Framework. Front. Energ. Res. 9, 1–14. doi:10.3389/fenrg.2021.780928

CrossRef Full Text | Google Scholar

Li, H., Deng, J., Yuan, S., Feng, P., Arachchige, D. D. K., and Arachchige, K. (2021b). Monitoring and Identifying Wind Turbine Generator Bearing Faults Using Deep Belief Network and EWMA Control Charts. Front. Energ. Res. 9, 39. doi:10.3389/fenrg.2021.799039

CrossRef Full Text | Google Scholar

Li, H., He, Y., Xu, Q., Deng, J., Li, W., and Wei, Y. (2022). Detection and Segmentation of Loess Landslides via Satellite Images: a Two-phase Framework. Landslides 19 (3), 673–686. doi:10.1007/s10346-021-01789-010.1007/s10346-021-01789-0

CrossRef Full Text | Google Scholar

Li, Jinwang., He, Xiufeng., Shen, Caihua., and Zheng, Xiangtian. (2022). A Proposed Algorithm to Compute the Stress-Strain Plastic Region and Displacement of a Deep-Lying Tunnel Considering Intermediate Stress and Strain-Softening Behavior. Appl. Sci. 12 (1), 85. doi:10.3390/app12010085

CrossRef Full Text | Google Scholar

Li, Y., Cao, S., Fantuzzi, N., and Liu, Y. (2015). Elasto-plastic Analysis of a Circular Borehole in Elastic-Strain Softening Coal Seams. Int. J. Rock Mech. Mining Sci. 80, 316–324. doi:10.1016/j.ijrmms.2015.10.002

CrossRef Full Text | Google Scholar

Park, K.-H., and Kim, Y.-J. (2006). Analytical Solution for a Circular Opening in an Elastic-Brittle-Plastic Rock. Int. J. Rock Mech. Mining Sci. 43 (4), 616–622. doi:10.1016/j.ijrmms.2005.11.004

CrossRef Full Text | Google Scholar

Qingke, N., Guang, S., Siyuan, G., Hongtao, L., Lichao, Z., and Jianpeng, H. (2021). Disturbance Process of Sandy Gravel Stratum Caused by Shield Tunneling and Ground Settlement Analysis. Front. Earth Sci. 9, 782927 doi:10.3389/feart.2021.782927

CrossRef Full Text | Google Scholar

Shen, C., and Gu, W. (2021). An Improved Analytical Approach for Analyzing a Circular Opening Excavated in a Strain-Softening Rock Mass. Arab J. Geosci. 14 (19), 2050. doi:10.1007/s12517-021-08402-7

CrossRef Full Text | Google Scholar

Song, F., and Rodriguez-Dono, A. (2021). Numerical Solutions for Tunnels Excavated in Strain-Softening Rock Masses Considering a Combined Support System. Appl. Math. Model. 92, 905–930. doi:10.1016/j.apm.2020.11.042

CrossRef Full Text | Google Scholar

Su, T., Peng, H., and Liu, H. (2018). Mechanical Analysis of the Circular Tunnel Considering the Interaction between the Ground Response Curve and Support Response Curve. Math. Probl. Eng. 2018, 1–8. doi:10.1155/2018/7892010

CrossRef Full Text | Google Scholar

Vrakas, A., and Anagnostou, G. (2014). A Finite Strain Closed-form Solution for the Elastoplastic Ground Response Curve in Tunnelling. Int. J. Numer. Anal. Meth. Geomech. 38 (11), 1131–1148. doi:10.1002/nag.2250

CrossRef Full Text | Google Scholar

Vrakas, A., and Anagnostou, G. (2015). A Simple Equation for Obtaining Finite Strain Solutions from Small Strain Analyses of Tunnels with Very Large Convergences. Géotechnique 65, 936–944. doi:10.1680/jgeot.15.P.036

CrossRef Full Text | Google Scholar

Vrakas, Apostolos. (2016). Analysis of Ground Response and Ground-Support Interaction in Tunnelling Considering Large Deformations. Zurich, Switzerland: ETH Zürich. doi:10.3929/ethz-a-010778160

CrossRef Full Text | Google Scholar

Wang, R., Bai, J.-b., Yan, S., Chang, Z.-g., Song, Y.-b., Zhang, W.-g., et al. (2021). The Elastoplastic Solutions of Deep Buried Roadway Based on the Generalized 3D Hoek-Brown Strength Criterion Considering Strain-Softening Properties. Geofluids 2021, 1–15. doi:10.1155/2021/557537610.1155/2021/5575376

CrossRef Full Text | Google Scholar

Wang, S., Wu, Z., Guo, M., and Ge, X. (2012). Theoretical Solutions of a Circular Tunnel with the Influence of Axial In Situ Stress in Elastic-Brittle-Plastic Rock. Tunnelling Underground Space Tech. 30, 155–168. doi:10.1016/j.tust.2012.02.016

CrossRef Full Text | Google Scholar

Wang, S., Yin, X., Tang, H., and Ge, X. (2010). A New Approach for Analyzing Circular Tunnel in Strain-Softening Rock Masses. Int. J. Rock Mech. Mining Sci. 47 (1), 170–178. doi:10.1016/j.ijrmms.2009.02.011

CrossRef Full Text | Google Scholar

Wang, Y., Xu, X., Xu, P., Feng, X., Zhang, Y., Fu, F., et al. (2018). Controllable Self-Assembly of Polystyrene-Block -Poly(2-Vinylpyridine). Polym. Int. 67 (6), 619–626. doi:10.12989/GAE.2018.16.6.61910.12989/GAE.2018.16.6.61910.1002/pi.5550

CrossRef Full Text | Google Scholar

Xue, D., Zhang, Z., Chen, C., Zhou, J., Lu, L., Sun, X., et al. (2021). Spatial Correlation-Based Characterization of Acoustic Emission Signal-Cloud in a Granite Sample by a Cube Clustering Approach. Int. J. Mining Sci. Tech. 31 (4), 535–551. doi:10.1016/j.ijmst.2021.05.008

CrossRef Full Text | Google Scholar

Yu, H. S., and Houlsby, G. T. (1995). A Large Strain Analytical Solution for Cavity Contraction in Dilatant Soils. Int. J. Numer. Anal. Methods Geomech. 19 (11), 793–811. doi:10.1002/nag.1610191104

CrossRef Full Text | Google Scholar

Yu-ming, S., Chao, L., Ming-yao, X., and Jin-feng, Z. (2021). Numerical Solutions for Strain-Softening Surrounding Rock under Three-Dimensional Principal Stress Condition. Int. J. Nonlinear Sci. Numer. Simulation, 1–16. doi:10.1515/ijnsns-2019-0253

CrossRef Full Text | Google Scholar

Zareifard, M. R., and Fahimifar, A. (2016). Analytical Solutions for the Stresses and Deformations of Deep Tunnels in an Elastic-Brittle-Plastic Rock Mass Considering the Damaged Zone. Tunnelling Underground Space Tech. 58, 186–196. doi:10.1016/j.tust.2016.05.007

CrossRef Full Text | Google Scholar

Zareifard, M. R. (2021). Ground Response Curve of Deep Circular Tunnel in Rock Mass Exhibiting Hoek-Brown Strain-Softening Behaviour Considering the Dead Weight Loading. Eur. J. Environ. Civil Eng. 25 (14), 2509–2539. doi:10.1080/19648189.2019.163274510.1080/19648189.2019.1632745

CrossRef Full Text | Google Scholar

Zhang, Q., Wang, X.-F., Jiang, B.-S., Liu, R.-C., and Li, G.-M. (2021). A Finite Strain Solution for Strain-Softening Rock Mass Around Circular Roadways. Tunnelling Underground Space Tech. 111, 103873. doi:10.1016/j.tust.2021.103873

CrossRef Full Text | Google Scholar

Zhou, J., Wei, J., Yang, T., Zhang, P., Liu, F., and Chen, J. (2021). Seepage Channel Development in the crown Pillar: Insights from Induced Microseismicity. Int. J. Rock Mech. Mining Sci. 145, 104851. doi:10.1016/j.ijrmms.2021.104851

CrossRef Full Text | Google Scholar

Zou, J.-f., Li, C., and Wang, F. (2017). A New Procedure for Ground Response Curve (GRC) in Strain-Softening Surrounding Rock. Comput. Geotechnics 89, 81–91. doi:10.1016/j.compgeo.2017.04.009

CrossRef Full Text | Google Scholar