Pore-Water Pressure Model for Carbonate Fault Materials Based on Cyclic Triaxial Tests

Pore-water pressure generation in the saturated carbonate fault zone plays a key role in the initiation of the Daguangbao landslide, which is the largest landslide triggered by the 2008 Wenchuan earthquake in China. This paper examines the pore-water pressure behavior and the influence of cyclic stress and initial stress state, and establishes a pore-water pressure model of carbonate fault materials. A series of cyclic triaxial tests of saturated carbonate fault materials were carried out, covering a broad range of frequencies, cyclic shear stress ratios and confining pressures. The test results show that the pore-water pressure in the materials increases rapidly under cyclic loading, revealing a significant liquefaction potential. The generation of pore-water pressure is barely affected by frequency. The higher cyclic shear stress ratio accelerates the generation of the pore-water pressure, while the higher confining pressure increases liquefaction resistance. Furthermore, an energy method is proposed to evaluate the development behavior of the pore-water pressure. An energy-based pore-water pressure model that accounts for the effects of frequency, cyclic shear stress ratio and confining pressure is established. The generation of the pore-water pressure is attributed to the grain crushing in the special fault materials with low-strength calcareous cementation. This work provides a novel model and some innovative observations for better understanding the pore-water pressure behavior of carbonate fault materials under seismic loading.

Highlights

• The pore-water pressure behavior of the saturated carbonate fault materials was investigated.

• The influences of cyclic stress and initial stress state on the pore-water pressure generation and dissipated energy were revealed.

• An energy-based pore-water pressure model was established.

Introduction

During the long-term tectonic activities, the bedding fault was formed and developed (Wang, 2009). The strength of bedding fault materials is very low. The bedding fault is widely distributed in the mountains, and the strength degradation of bedding faults often determine the slope stability. It has been previously reported that some large landslides initiated along the bedding fault, such as the Chiu-fen-erh-shan landslide (Wang et al., 2003), Daguangbao (DGB) landslide (Cui et al., 2018; Cui et al., 2020), and Qiyangou landslide (Fan et al., 2019), etc. In addition, the generation of pore-water pressure under seismic loading resulted in the strength degradation in the sliding zone, which was the key factor for the initiation and movement of landslide. Wang et al. (2014) proposed that liquefaction of the runout path material enhanced the mobility of the Donghekou landslide through the ring shear test. Pei et al. (2017) reported that the steady-state strength of the sliding zone was close to 0 due to the generation of pore-water pressure, which was the reason for the long-distance and fluidized movement of the Shibeiyuan landslide. Zhu et al. (2022) proposed that the sliding surface liquefaction caused complex surface landforms and long-runout movement of the LSB landslide. Therefore, it is crucial to investigate the pore-water pressure behavior of the sliding zone and establish a pore-water pressure model to evaluate the slope stability.

For a long time, the generation law of pore-water pressure and the pore-water pressure model under cyclic loading have been studied based on the results of field measurement and laboratory tests. Seed et al. (1976) first proposed the pore-water pressure development model of sand under cyclic loading based on isobaric consolidation undrained test. Polito et al. (2013) established an energy-based pore pressure generation model for use in predicting in situ pore pressures in soils subjected to nonsinusoidal loadings. Wang et al. (2013) proposed a formula to characterize the relationship between the peak axial strain and the peak pore-water pressure after 1,000 cycles. Chen et al. (2013) effectively evaluated the field liquefaction potential during the 1999 Chi-Chi earthquake by means of hysteresis loop energy and the proposed neural network. Liu et al. (2015) presented a fluid coupled-DEM model to investigate the generation mechanism of pore-water pressure. Azeiteiro et al. (2017) suggested that standard cyclic triaxial tests using uniform loads could be used for realistic energy-based assessment of in-situ liquefaction potential. Javdanian et al. (2017) derived an NF-GMDH-based model based on laboratory results that can be successfully used for strain energy-based estimation of liquefaction potential. Amini and Noorzad (2018) proposed an energy-based method to evaluate the liquefaction potential of fiber-reinforced sands. Yang and Pan (2018) investigated a unique relationship between the residual pore pressure and dissipated energy for isotropic and anisotropic consolidated sand with different densities and cyclic stress amplitudes. Chen et al. (2019) proposed a new strain-based model to assess the residual excess pore-water pressure generation in fully saturated sands. Javdanian (2019) proposed a strain energy-based method to accurately predict the energy required for liquefaction of sandy soil and silty sand samples in cyclic triaxial tests. Shan et al. (2020) reported that the dynamic strength of artificial marine clays with different mineral compositions was illustrated by VEDR cyclic strength from the perspective of energy dissipation. Ni et al. (2020) evaluated the effects of the initial deviatoric stress and cyclic stress amplitude on the liquefaction potential based on the energy-based method. Pan and Yang (2020) proposed an energy approach based on the energy density concept for liquefaction assessment, which could better capture the effect of loading randomness on sand liquefaction behavior. Zhang et al. (2020) established a three-parameter pore-water pressure model of fiber-reinforced sands that accounts for the effects of fiber content, fiber length, relative density, cyclic stress ratio, and sand particle diameter.

The pore-water pressure generation law of different materials under cyclic loading has been extensively investigated (Chang et al., 1983; Mitchell and Dubin 1986; Charlie et al., 1989; Sitharam and Govindaraju 2007; Polito et al., 2008; Hazirbaba and Rathje, 2009; Wang et al., 2010; Pan and Yang 2018; Balreddy et al., 2019; Zhang et al., 2020). However, energy is a scalar and can be directly iterated to reflect the generation process of pore-water pressure under complex stress paths, thus the energy-based pore-water pressure model is more reliable than the other pore-water pressure models. In addition, most studies only focus on some ideal materials, which is quite different from the real site situation. In this paper, a detailed field investigation and a series of saturated triaxial tests of carbonate fault materials were carried out. The pore-water pressure behavior in the materials was investigated. An energy-based pore-water pressure model is established considering the effect of frequencies, cyclic shear stress ratios, and confining pressures. The generation mechanism of pore-water pressure was investigated. This study is beneficial to evaluate the stability variability of the DGB landslide during the 2008 Wenchuan earthquake.

Characteristics of Carbonate Fault Materials

Geological Background

The 2008 Wenchuan earthquake triggered 112 large landslides with an area of more than 50,000 m² (Xu et al., 2011), of which the DGB landslide with a volume of about 1.2 × 109 m³ is located in Gaochuan Township, Mianyang City, and it is the largest landslide triggered by the 2008 Wenchuan earthquake (Figure 1A). The maximum thickness of the landslide mass is 570 m (Huang et al., 2012). The source area of DGB landslide is composed of a main scarp and two lateral flanks (Figure 2). A sliding surface with a length of 1.8 km is exposed in the southern flank. The exposed rocks in the sliding surface were highly weathered and extensively fractured. A bedding fault was found at the intersection of the main scarp and the sliding surface in the southern flank (Figure 3A). To investigate its formation mechanism, a tunnel was excavated along the sliding surface at the back of the mountain (Figure 1B).

FIGURE 1

FIGURE 1. The location (A) and 3D topography (B) of the DGB landslide.

FIGURE 2

FIGURE 2. The source area of the DGB landslide.

FIGURE 3

FIGURE 3. Bedding fault characteristic (A), groundwater in the tunnel (B) and saturated carbonate fault materials (C).

As shown in Figures 3A,B 3∼5 m thick bedding fault was found in the tunnel, indicating that the sliding surface was formed within the pre-existing bedding fault. The zone is mainly composed of carbonate fault materials. In addition, the bedding fault is below the groundwater level (Pei et al., 2018; Cui et al., 2021), and there is abundant groundwater in the tunnel. Due to long-term tectonic compression and shear, the materials in the bedding fault are seriously fragmented, similar to soil. Moreover, the groundwater seepage on the section of the bedding fault can be seen. The natural water content of the materials reaches 11.94% (Figure 3C). The carbonate fault materials mainly consisted of 5.68% breccia, 53.98% sand, 29.8% silt, and 10.54% clay. The non-uniform coefficient and curvature coefficient were 57.34 and 1.92, respectively. The plastic limit and liquid limit were 7.41 and 11.87, respectively. The plastic index and permeation coefficient were 4.46 and 8.1 × 10⁻⁵, respectively. The tested materials were obtained in the tunnel, and it is not disturbed by the landslide movement. Therefore, it is appropriate to investigate the generation law of pore-water pressure in the bedding fault under seismic loading.

Test Sample and Scheme

A cylindrical sample with a diameter of 50 mm and a height of 100 mm is used in this test. Due to the limitation of test conditions, particles larger than 5 mm are removed, and the sample is mainly composed of sand particles (0.075–2 mm), accounting for about 56% of the total mass. The content of breccia (>5 mm) in the materials is less than 10%. According to Kuenza et al. (2004), the mechanical behavior of the samples was mainly controlled by the matrix material when the content of particles larger than 5 mm in the material is less than 40%. The pore-water pressure behavior may not be influenced by the removed breccias. Therefore, this test result can reflect the generation characteristic of pore-water pressure in the bedding fault. Figure 4A shows the particle size distribution of the sample. The composition of the carbonate fault materials is similar to the residual soils on the sliding surface, which is mainly composed of dolomite. This result further demonstrates that the DGB landslide triggered along the bedding fault, which was mainly composed of carbonate fault materials. Figure 4B illustrates the X-ray diffraction (XRD) results.

FIGURE 4

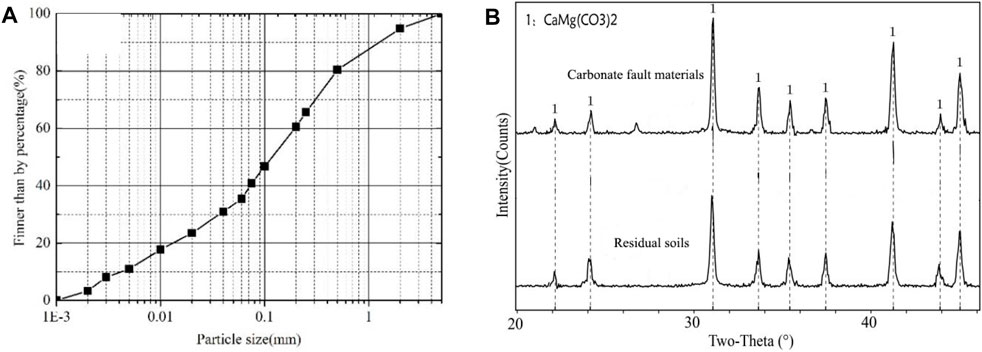
FIGURE 4. (A) Particle size distributions and (B) the XRD results of carbonate fault materials and residual soils on the sliding surface.

The materials with an initial water content of 5% were allowed to stand in a closed surroundings for 24 h. The initial density of the sample with a diameter of 50 mm and a height of 100 mm is 1.8 kg/m³. The samples were saturated by de-aired water with the assistance of carbon dioxide. The degree of saturation was checked by B_D, which is the ratio between the increment of excess pore water pressure (Δu) and the increment of confining pressure (Δσ₃) under undrained conditions (B_D = Δu/Δσ₃) (Skempton 1954; Tokimatsu et al., 1990). When this parameter is greater than 0.95, the sample is considered to be saturated. After saturation, consolidation pressures of 100, 150, and 200 kPa were separately applied in both lateral and axial directions. Due to the limitation of the cyclic triaxial test apparatus, it is impossible to apply the real 2008 Wenchuan earthquake loading, Cui et al. (2017) reported that the dominated seismic wave frequencies during the Wenchuan earthquake were 2–3 Hz. The sinusoidal loadings with different frequencies of 1, 2 and 3 Hz and cyclic shear stress ratios of 0.238, 0.325, and 0.411 were separately implemented. The sample is failed when the axial strain reaches 5%. The test scheme is shown in Table 1.

TABLE 1

TABLE 1. Test scheme.

Test Results

Figure 5A shows the time-series records of the pore-water pressure, axial strain, deviator stress under the confining pressure of 100 kPa. it can be seen from Figure 5A that the pore-water pressure increases rapidly at the initial stage, and pore-water pressure reaches 20 kPa at ∼20 s. Gradually, the generation rate of pore-water pressure slows down slightly, and the pore-water pressure is about 35 kPa at 40 s. The generation rate of pore-water pressure gradually increases after that and the pore-water pressure reaches 90 kPa at 80 s. Finally, the pore-water pressure is approximately equal to confining pressure when the axial strain reaches 5%. The axial strain increases slowly at 0–70 s, only reaching 1.5%. After the pore-water pressure ratio exceeded 0.7, the axial strain increases rapidly and reaches 5% in a very short time. In addition, the cyclic deviator stress is stable at 0–60 s, then decreases slightly. The peak deviator stress decreases to only 40 kPa at 90 s. The hysteresis curve widens gradually with increasing cycles, as presented in Figure 5B. Figure 5C shows the effective stress path. Effective average principal stress (p′ = 1/3(σ₁+2σ₃)) decreases continuously. The effective stress path reaches the original point at the end of the test. As a result, the materials show high liquefaction potential.

FIGURE 5

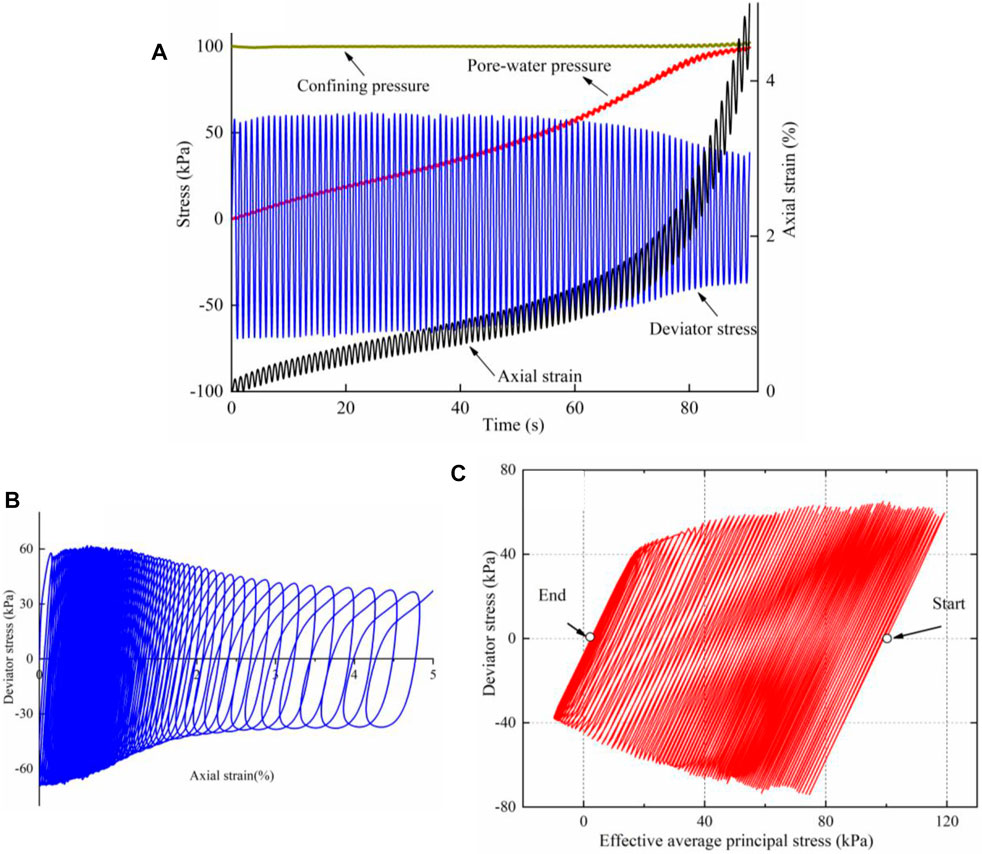
FIGURE 5. Test results of cyclic triaxial test: (A) time-series data of pore-water pressure, axial strain, confining pressure and deviator stress (B) stress-strain hysteresis curve, and (C) effective stress path.

Figure 6A indicates the pore-water pressure ratio (u_d/σ₃) versus cycles (N) curve under various frequencies. From Figure 6A, the generation law of the u_d/σ₃ is similar under different frequencies, and the u_d/σ₃ increases rapidly. Finally, the u_d/σ₃ is approximately equal to 1 and liquefaction occurs. To achieve 5% axial strain, 91, 198, and 264 cycles are required at frequencies of 1, 2 and 3 Hz, respectively. It can be found that the time required for liquefaction (∼90 s) is almost the same, indicating that the frequency has little impact on the generation rate of the pore-water pressure. Figure 6B shows the u_d/σ₃ versus N curves under a variety of cyclic shear stress ratios (CSR = 0.238, 0.325, and 0.411). From Figure 6B, the pore-water pressure increases rapidly under different cyclic shear stress ratios. The u_d/σ₃ is greater than 0.95 when the axial strain reaches 5%. All samples exhibit the same pattern. However, the greater cyclic shear stress ratio accelerates the generation of the pore-water pressure, and fewer cycles are required for liquefaction. As shown in Figure 6B, for the cyclic shear stress ratios of 0.238, 0.325, and 0.411, the number of cycles required to cause sample liquefaction are correspondingly 257, 91, and 44, respectively. This result reveals that the cyclic shear stress ratios change the generation rate of pore-water pressure. In addition, the u_d/σ₃ versus N curves under different confining pressures (σ₃ = 100, 150, and 200 kPa) are shown in Figure 6C. The u_d/σ₃ increases rapidly in the initial stage, and then the u_d/σ₃ slows down slightly. The generation rate of u_d/σ₃ gradually accelerates with increasing cycles. The samples can be liquefied under different confining pressures.

FIGURE 6

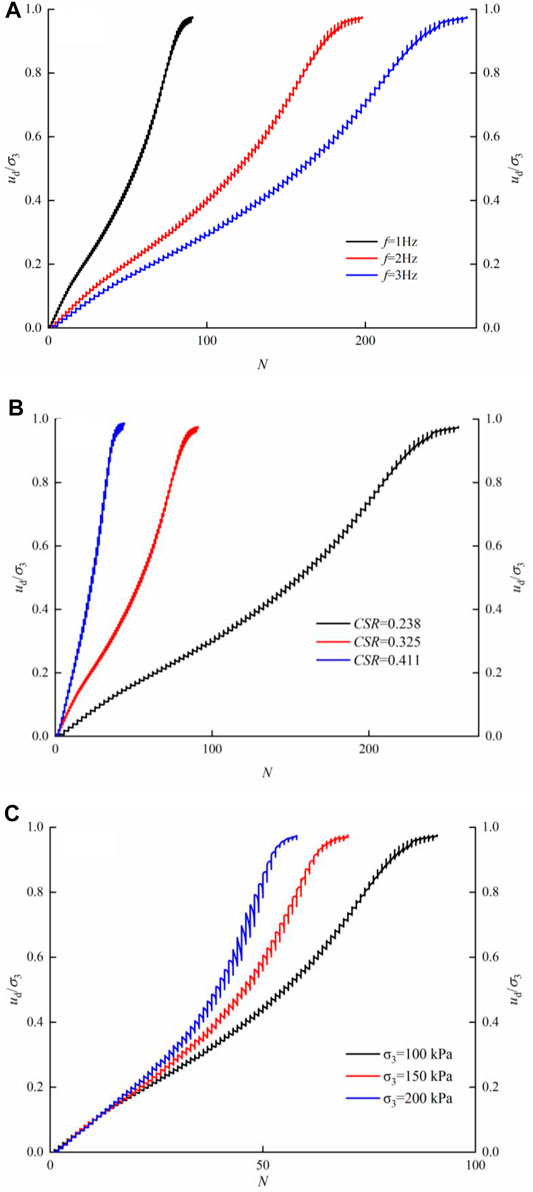
FIGURE 6. Relations between u_d/σ₃ and N under different frequencies (A), cyclic shear stress ratios (B) and confining pressures (C).

Pore-water Pressure Generation Model

The applied cyclic loading causes the generation of pore-water pressure in the sample, and an amount of energy is dissipated in this process. It can be summarized as input energy (E_i), output energy (E₀) and dissipated energy (W) (He and Cao, 1990). The formula is expressed as $E_i=E_0+W$. Saturated soil is composed of soil particles and pore water. During the cyclic loading, the dissipated energy is an important index to reveal the generation process of pore-water pressure. Therefore, in this paper, an energy analysis method is used to evaluate the generation of pore-water pressure in carbonate fault materials, and an energy-based pore-water pressure model is established.

Dissipated Energy

The area of the hysteresis curve can properly represent the dissipated energy of single cycle. Most previous studies simplified the hysteresis curve into an ellipse, and the dissipated energy was obtained by calculating the area of the ellipse. However, due to the hysteresis curve is not a standard ellipse, this calculation method has significant shortcomings. Therefore, a new method is proposed here to accurately calculate the area of the hysteresis curve. The hysteresis curve is divided into several tiny polygons by the stress and strain of adjacent data. The sum of all polygon areas is the area of the hysteretic curve (Figure 7A).

FIGURE 7

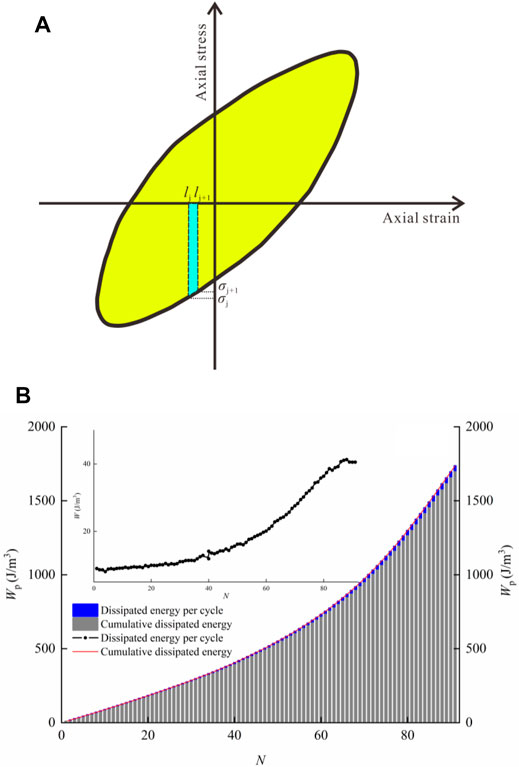
FIGURE 7. Energy calculation (A) and cumulative dissipated energy and dissipated energy per cycle versus cycle of sample S1 (B).

To precisely calculate the hysteresis curve area, 40 group stress-strain data in a cycle are obtained. The calculation formula of hysteresis curve area is as $W_i=S_i={\displaystyle \sum _{j=1}^{39}\frac{1}{2}({\sigma }_j+{\sigma }_{j+1})({\text{l}}_{j+1}-l_j)}$. Where $W_{\text{i}}$ is the dissipated energy of the ith cycle, S_i is the hysteresis curve area of the ith cycle, σ_j and l_j are the axial stress and axial strain of the jth cycle. Therefore, the cumulative dissipated energy ($W_{\text{pi}}$) is the sum of the hysteresis curve area from 1st to ith cycles, and the cumulative dissipated energy is obtained by $W_{\text{pi}}={\displaystyle \sum _1^i{W}_i}$. We introduce the average pore-water pressure (u₀), defined as the average of the maximum and minimum pore-water pressures per cycle, to clearly illustrate the generation behavior of pore-water pressure, and the formula is as ${\mu }_{0,i}=\left({\mu }_{\max ,i}+{\mu }_{\min ,i}\right)/2$. Where u_0,i is the average pore-water pressure of the ith cycle, u_max,i and u_min,i are the maximum pore-water pressure and minimum pore-water pressure of the ith cycle, respectively.

Figure 7B shows the cumulative dissipated energy ($W_{\text{pi}}$), dissipated energy per cycle ($W_{\text{i}}$) versus cycle (N) of sample S1. As shown in Figure 7B, the dissipated energy per cycle gradually increases with growing cycles. However, it is noted that the dissipated energy per cycle is basically the same (about 9.15 J/m³) in the first 30 cycles. After that, the dissipated energy per cycle increases, and the dissipated energy per cycle is basically stable towards the end of the test, about 40.55 J/m³. The cumulative dissipated energy throughout the cyclic loading process demonstrates an accelerated generation trend.

Figure 8 shows the dissipated energy per cycle and cumulative dissipated energy versus cycle under different frequencies. From Figure 8A, the dissipated energy per cycle is lower at higher frequencies, and the increased rate of dissipated energy per cycle with increasing cycles is faster at low frequencies. However, the frequency has little effect on the total dissipated energy required to trigger liquefaction, as shown in Figure 8B. Figure 9 shows the dissipated energy per cycle and cumulative dissipated energy versus cycle under different cyclic shear stress ratios. Under the condition of a larger cyclic shear stress ratio, the cyclic loading causes greater dissipated energy per cycle (Figure 9A). However, the cumulative dissipated energy required to trigger liquefaction is essentially the same for different cyclic shear stress ratios (Figure 9B). Figure 10 shows the dissipated energy per cycle and cumulative dissipated energy versus cycle under different confining pressures. The dissipated energy per cycle is great at large confining pressure (Figure 10A). The increase of the confining pressure leads to a rise in the cumulative dissipated energy required to liquefy (Figure 10B). Based on the above test results, it is noted that the dissipated energy per cycle increases with increasing cycles for all samples, with the maximum dissipated energy per cycle near the time of sample liquefaction, after which it remains stable or decreases slightly. In addition, frequency and cyclic shear stress ratio have little effect on the total dissipated energy required to trigger liquefaction, while the confining pressure has a significant effect.

FIGURE 8

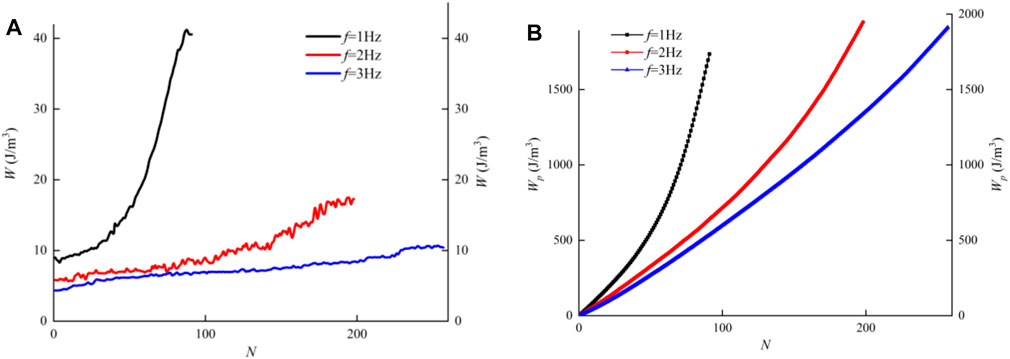
FIGURE 8. Evolution characteristics of dissipated energy under different frequencies: (A) dissipated energy per cycle and (B) cumulative dissipated energy.

FIGURE 9

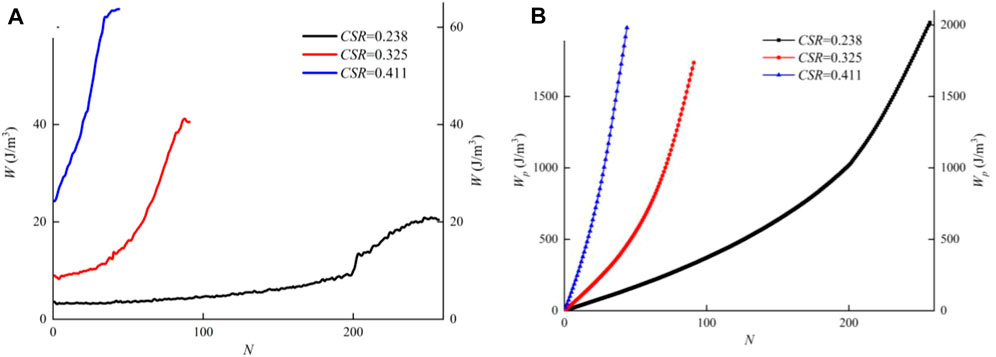
FIGURE 9. Evolution characteristics of dissipated energy under different cyclic shear stress ratios: (A) dissipated energy per cycle and (B) cumulative dissipated energy.

FIGURE 10

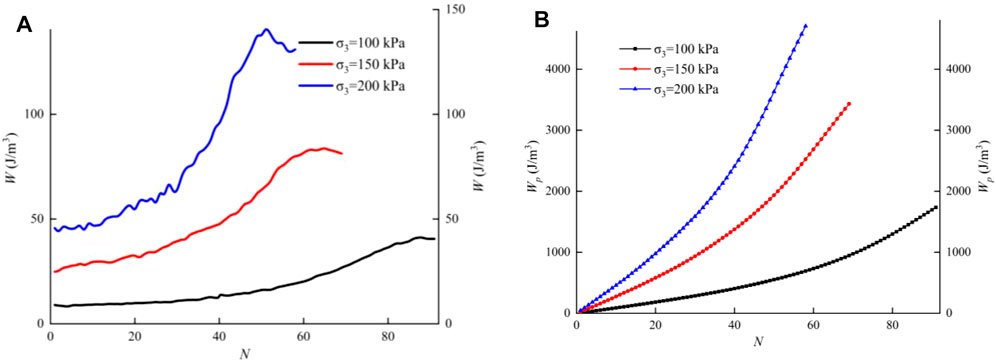
FIGURE 10. Evolution characteristics of dissipated energy under different confining pressures: (A) dissipated energy per cycle and (B) cumulative dissipated energy.

Relationship Between Pore-water Pressure Ratio and Cumulative Dissipated Energy

The pore-water pressure ratio versus cumulative dissipated energy curves under different frequencies and cyclic shear stress ratios show the same development characteristic, as shown in Figures 11A,B. The pore-water pressure ratio increases with increasing cumulative dissipated energy. According to the generation characteristics of pore-water pressure, the curve can be divided into two stages. Before the pore-water pressure ratio is 0.9, the pore-water pressure ratio and cumulative dissipated energy increase rapidly, and the slope of the curve is large. After that, the cumulative dissipated energy continuously increases while the pore-water pressure ratio remains stable. Figure 11C shows the pore-water pressure ratio versus cumulative dissipated energy curves under different confining pressures. It can be seen that the pore-water pressure ratio shows the same development characteristic. The pore-water pressure increases rapidly in the initial stage, and then tends to be stable. However, the contribution of cumulative dissipated energy to pore-water pressure generation is significantly influenced by the confining pressure, and the greater dissipated energy is required to trigger liquefaction in the higher confining pressure.

FIGURE 11

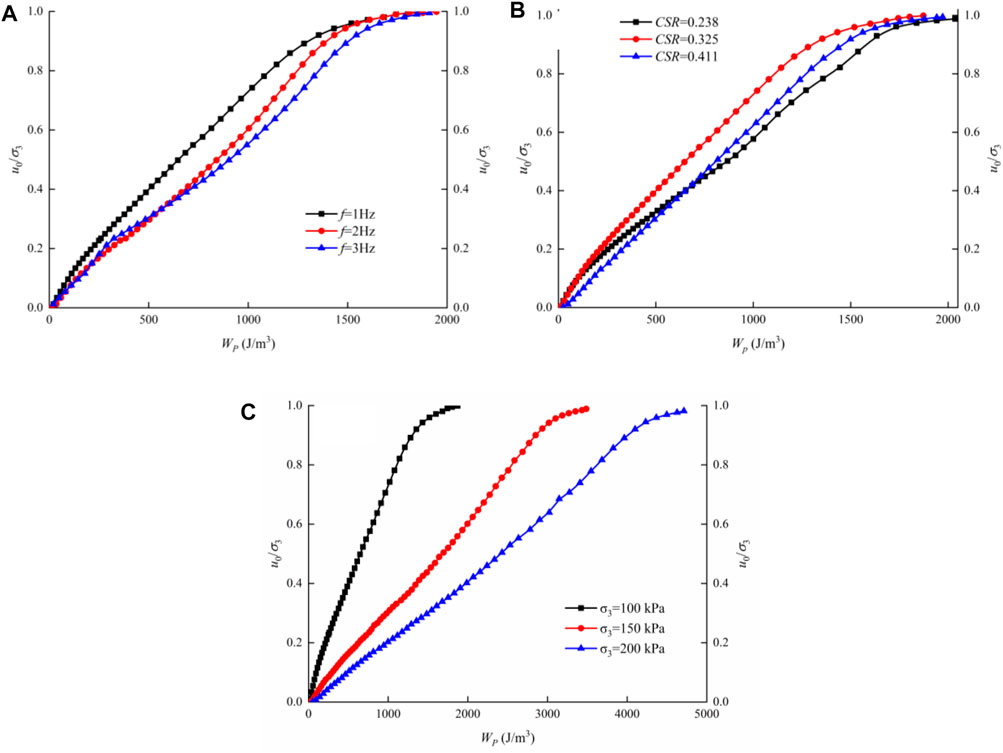
FIGURE 11. Relation between pore-water pressure ratio and cumulative dissipated energy under different frequencies (A), cyclic shear stress ratios (B) and confining pressures (C).

Normalized Model of Pore-water Pressure Ratio and Cumulative Dissipated Energy

To establish an energy-based pore-water pressure model considering the effect of frequency, cyclic shear stress ratio and confining pressure. The cumulative dissipated energy and cycles are normalized. The normalization results are shown in Figure 12. From Figure 12, the pore-water pressure ratio versus cumulative dissipated energy ratio (W_p/W_pf) are properly fitted by the exponential function,

$\log \left({\mathrm{\mu }}_d\text{/}{\mathrm{\sigma }}_3\right)=1-e^{\left(1-a^{\left(W_p\text{/}{W}_{p\mathrm{f}}\right)}\right)}(1)$

where W_pf is the cumulative dissipated energy trigger sample liquefaction, a is the test parameter. The fitting results are shown in Table. 2.

FIGURE 12

FIGURE 12. Relation between pore-water pressure ratio and cumulative dissipated energy.

TABLE 2

TABLE 2. Fitting results.

Discussion

Previous studies have attributed the soils liquefaction to the movement and rearrangement of grains (Lade and Yamamuro, 1997; Ovando-Shelley and Perez, 1997; Yamamuro and Covert, 2001). Afterwards, it is recognized that for loose sandy soils, the generation of pore-water pressure is mainly caused by the movement and rearrangement of grains, while in medium to dense sandy soils, and the generation of pore-water pressure is mainly due to grain crushing (Wang and Sassa, 2000; Wang and Sassa, 2002; Fukuoka et al., 2007). In addition, grain crushing susceptibility varies significantly for different materials. Under shear loading, siliceous sands exhibit shear dilatancy behavior due to low grain crushing susceptibility. Weathered granite sand with short transport distance exhibits a high susceptibility to grain crushing. Thus weathered dense granite sand properties under shear loading undergo three stages, 1) initial negative dilatancy due to grain movement and rearrangement, 2) dilatancy, and 3) negative dilatancy due to grain crushing (Wang and Sassa, 2000). The bedding fault of the DGB landslide is composed of special geological materials, which is formed by dolomite subjected to long-term tectonic shear and compression, so its structure is poor (Cui et al., 2021). In addition, the material grains are filled with a large amount of calcareous and argillaceous cementations, and the strength of these cementations is lower than the dolomite (Zhu et al., 2019) (Figures 13A,B). Therefore, for these special materials, it is noted that a special liquefaction mechanism of the bedding fault materials under cyclic loading, that is, liquefaction caused by cementation breakage. Under cyclic loading, when the cyclic loading exceeds the strength of the cementation, the grain crushing occurs, resulting in a reduction of the volume, so that the load originally borne by the particle skeleton is borne by the pore water, resulting in a rise in the pore-water pressure, and as illustrated in Figure 14. The low-strength calcareous and argillaceous cementations are easily broken by cyclic loading, thus this special material is more prone to occur in grain crushing than conventional soil. The pore-water pressure rise in the bedding fault caused by grain crushing plays a major role due to the high grain crushing susceptibility.

FIGURE 13

FIGURE 13. Carbonate fault materials with low-strength cementation from microscope. 2 × 10 (A), 4 × 10 (B).

FIGURE 14

FIGURE 14. Schematic diagram of liquefaction mechanism.

Conclusion

The tests on bedding fault material shows that the pore-water pressure increases rapidly during cyclic loading, and the carbonate fault materials have a high liquefaction potential. Frequency has little effect on the generation of the pore-water pressure. The higher cyclic shear stress ratio accelerates the generation of the pore-water pressure, while the higher confining pressure increases liquefaction resistance. Frequency and cyclic shear stress ratio have little effect on the total dissipated energy required to trigger liquefaction, while the confining pressure has a significant effect. We establish an energy-based pore-water pressure model of carbonate fault materials considering the effect of frequency, cyclic shear stress ratio and confining pressure.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

LZ designed the conceptualization, methodology, data curation, and original draft preparation. QY performed data curation and formal analysis. LL was responsible for data curation and Language. SC designed the methodology.

Funding

This study was financially sponsored by the National Natural Science Foundation of China (Grant Nos. 41931296), the National Key R&D Program of China (No. 2017YFC1501002) and the National Nature Science Foundation of China (Grant Nos. 41907254 and 41521002).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Azeiteiro, R. J. N., Coelho, P. A. L. F., Taborda, D. M. G., and Grazina, J. C. D. (2017). Energy-based Evaluation of Liquefaction Potential under Non-uniform Cyclic Loading. Soil Dyn. Earthquake Eng. 92, 650–665. doi:10.1016/j.soildyn.2016.11.005

CrossRef Full Text | Google Scholar

Balreddy, M. S., Dinesh, S. V., and Sitharam, T. G. (2019). “Effect of Fines on Pore Pressure Development during Cyclic Loading,” in Soil Dynamics and Earthquake Geotechnical Engineering (Singapore: Springer), 83–90. doi:10.1007/978-981-13-0562-7_10

CrossRef Full Text | Google Scholar

Chang, C. S., Kuo, C. L., and Selig, E. T. (1983). Pore Pressure Development during Cyclic Loading. J. Geotechnical Eng. 109 (1), 103–107. doi:10.1061/(asce)0733-9410(1983)109:1(103)

CrossRef Full Text | Google Scholar

Charlie, W. A., Veyera, G. E., and Doehring, D. O. (1989). Dilatational-wave-induced Pore-Water Pressure in Soil. Exp. Mech. 29 (4), 437–442. doi:10.1007/bf02323864

CrossRef Full Text | Google Scholar

Chen, G., Zhao, D., Chen, W., and Juang, C. H. (2019). Excess Pore-Water Pressure Generation in Cyclic Undrained Testing. J. Geotech. Geoenviron. Eng. 145 (7), 04019022. doi:10.1061/(asce)gt.1943-5606.0002057

CrossRef Full Text | Google Scholar

Chen, Y.-R., Chen, J.-W., Hsieh, S.-C., and Chang, Y.-T. (2013). Evaluation of Soil Liquefaction Potential Based on the Nonlinear Energy Dissipation Principles. J. Earthquake Eng. 17 (1), 54–72. doi:10.1080/13632469.2012.691256

CrossRef Full Text | Google Scholar

Cui, S., Pei, X., and Huang, R. (2018). Effects of Geological and Tectonic Characteristics on the Earthquake-Triggered Daguangbao Landslide, China. Landslides 15 (4), 649–667. doi:10.1007/s10346-017-0899-3

CrossRef Full Text | Google Scholar

Cui, S., Pei, X., Jiang, Y., Wang, G., Fan, X., Yang, Q., et al. (2021). Liquefaction within a Bedding Fault: Understanding the Initiation and Movement of the Daguangbao Landslide Triggered by the 2008 Wenchuan Earthquake (Ms = 8.0). Eng. Geology 295, 106455. doi:10.1016/j.enggeo.2021.106455

CrossRef Full Text | Google Scholar

Cui, S., Wang, G., Pei, X., Huang, R., and Kamai, T. (2017). On the Initiation and Movement Mechanisms of a Catastrophic Landslide Triggered by the 2008 Wenchuan (Ms 8.0) Earthquake in the Epicenter Area. Landslides 14 (3), 805–819. doi:10.1007/s10346-016-0754-y

CrossRef Full Text | Google Scholar

Cui, S., Yang, Q., Pei, X., Huang, R., Guo, B., and Zhang, W. (2020). Geological and Morphological Study of the Daguangbao Landslide Triggered by the Ms. 8.0 Wenchuan Earthquake, China. Geomorphology 370, 107394. doi:10.1016/j.geomorph.2020.107394

CrossRef Full Text | Google Scholar

Fan, W., Lv, J., Cao, Y., Shen, M., Deng, L., and Wei, Y. (2019). Characteristics and Block Kinematics of a Fault-Related Landslide in the Qinba Mountains, Western China. Eng. Geology 249, 162–171. doi:10.1016/j.enggeo.2018.12.019

CrossRef Full Text | Google Scholar

Fardad Amini, P., and Noorzad, R. (2018). Energy-based Evaluation of Liquefaction of Fiber-Reinforced Sand Using Cyclic Triaxial Testing. Soil Dyn. Earthquake Eng. 104, 45–53. doi:10.1016/j.soildyn.2017.09.026

CrossRef Full Text | Google Scholar

Fukuoka, H., Sassa, K., and Wang, G. (2007). Influence of Shear Speed and normal Stress on the Shear Behavior and Shear Zone Structure of Granular Materials in Naturally Drained Ring Shear Tests. Landslides 4 (1), 63–74. doi:10.1007/s10346-006-0053-0

CrossRef Full Text | Google Scholar

Hazirbaba, K., and Rathje, E. M. (2009). Pore Pressure Generation of Silty Sands Due to Induced Cyclic Shear Strains. J. Geotech. Geoenviron. Eng. 135 (12), 1892–1905. doi:10.1061/(asce)gt.1943-5606.0000147

CrossRef Full Text | Google Scholar

He, G., and Cao, Y. (1990). Fundamentals and Applications of the Energy Method in Soil Dynamics. China Civil Eng. J. 23 (3), 2–10. (In Chinese).

Google Scholar

Huang, R., Pei, X., Fan, X., Zhang, W., Li, S., and Li, B. (2012). The Characteristics and Failure Mechanism of the Largest Landslide Triggered by the Wenchuan Earthquake, May 12, 2008, China. Landslides 9 (1), 131–142. doi:10.1007/s10346-011-0276-6

CrossRef Full Text | Google Scholar

Javdanian, H. (2019). Evaluation of Soil Liquefaction Potential Using Energy Approach: Experimental and Statistical Investigation. Bull. Eng. Geol. Environ. 78 (3), 1697–1708. doi:10.1007/s10064-017-1201-6

CrossRef Full Text | Google Scholar

Javdanian, H., Heidari, A., and Kamgar, R. (2017). Energy-based Estimation of Soil Liquefaction Potential Using GMDH Algorithm. Iran J. Sci. Technol. Trans. Civ. Eng. 41 (3), 283–295. doi:10.1007/s40996-017-0061-4

CrossRef Full Text | Google Scholar

Kuenza, K., Towhata, I., Orense, R. P., and Wassan, T. H. (2004). Undrained Torsional Shear Tests on Gravelly Soils. Landslides 1 (3), 185–194. doi:10.1007/s10346-004-0023-3

CrossRef Full Text | Google Scholar

Lade, P. V., and Yamamuro, J. A. (1997). Effects of Nonplastic Fines on Static Liquefaction of Sands. Can. Geotech. J. 34 (6), 918–928. doi:10.1139/t97-052

CrossRef Full Text | Google Scholar

Liu, G., Rong, G., Peng, J., and Zhou, C. (2015). Numerical Simulation on Undrained Triaxial Behavior of Saturated Soil by a Fluid Coupled-DEM Model. Eng. Geology 193, 256–266. doi:10.1016/j.enggeo.2015.04.019

CrossRef Full Text | Google Scholar

Mitchell, R. J., and Dubin, B. I. (1986). Pore Pressure Generation and Dissipation in Dense Sands under Cyclic Loading. Can. Geotech. J. 23 (3), 393–398. doi:10.1139/t86-055

CrossRef Full Text | Google Scholar

Ni, X., Ye, B., Cheng, Z., and Ye, G. (2020). Evaluation of the Effects of Initial Deviatoric Stress and Cyclic Stress Amplitude on Liquefaction Potential of Loose and Medium-Dense Sands: An Energy-Based Method. Soil Dyn. Earthquake Eng. 136, 106236. doi:10.1016/j.soildyn.2020.106236

CrossRef Full Text | Google Scholar

Ovando-Shelley, E., and Pérez, B. E. (1997). Undrained Behaviour of Clayey Sands in Load Controlled Triaxial Tests. Géotechnique 47 (1), 97–111. doi:10.1680/geot.1997.47.1.97

CrossRef Full Text | Google Scholar

Pan, K., and Yang, Z. X. (2018). Effects of Initial Static Shear on Cyclic Resistance and Pore Pressure Generation of Saturated Sand. Acta Geotechnica 13 (2), 473–487.

Google Scholar

Pan, K., and Yang, Z. X. (2020). Evaluation of the Liquefaction Potential of Sand under Random Loading Conditions: Equivalent Approach versus Energy-Based Method. J. Earthquake Eng. 24 (1), 59–83. doi:10.1080/13632469.2017.1398693

CrossRef Full Text | Google Scholar

Pei, X. J., Cui, S. H., and Huang, R. Q. (2018). A Model of Initiation of Daguangbao Landslide: Dynamic Dilation and Water Hammer in Sliding Zone during strong Seismic Shaking. Chin. J. Rock Mech. Eng. 37 (2), 430–448. (In Chinese).

Google Scholar

Pei, X., Zhang, X., Guo, B., Wang, G., and Zhang, F. (2017). Experimental Case Study of Seismically Induced Loess Liquefaction and Landslide. Eng. Geology 223, 23–30. doi:10.1016/j.enggeo.2017.03.016

CrossRef Full Text | Google Scholar

Polito, C., Green, R. A., Dillon, E., and Sohn, C. (2013). Effect of Load Shape on Relationship between Dissipated Energy and Residual Excess Pore Pressure Generation in Cyclic Triaxial Tests. Can. Geotech. J. 50 (11), 1118–1128. doi:10.1139/cgj-2012-0379

CrossRef Full Text | Google Scholar

Polito, C. P., Green, R. A., and Lee, J. (2008). Pore Pressure Generation Models for Sands and Silty Soils Subjected to Cyclic Loading. J. Geotech. Geoenviron. Eng. 134 (10), 1490–1500. doi:10.1061/(asce)1090-0241(2008)134:10(1490)

CrossRef Full Text | Google Scholar

Seed, H. B., Martin, P. P., and Lysmer, J. (1976). Pore-water Pressure Changes during Soil Liquefaction. J. Geotech. Engrg. Div. 102 (4), 323–346. doi:10.1061/ajgeb6.0000258

CrossRef Full Text | Google Scholar

Shan, Y., Meng, Q., Yu, S., Mo, H., and Li, Y. (2020). Energy Based Cyclic Strength for the Influence of mineral Composition on Artificial marine clay. Eng. Geology 274, 105713. doi:10.1016/j.enggeo.2020.105713

CrossRef Full Text | Google Scholar

Sitharam, T. G., and Govindaraju, L. (2007). Pore Pressure Generation in Silty Sands during Cyclic Loading. Geomechanics and Geoengineering 2 (4), 295–306. doi:10.1080/17486020701670460

CrossRef Full Text | Google Scholar

Skempton, A. W. (1954). The Pore-Pressure Coefficients A and B. Géotechnique 4 (4), 143–147. doi:10.1680/geot.1954.4.4.143

CrossRef Full Text | Google Scholar

Tokimatsu, K., Yoshimi, Y., and Ariizumi, K. (1990). Evaluation of Liquefaction Resistance of Sand Improved by Deep Vibratory Compaction. Soils and Foundations 30 (3), 153–158. doi:10.3208/sandf1972.30.3_153

CrossRef Full Text | Google Scholar

Wang, B., Chen, G., and Jin, D. (2010). Pore Water Pressure Increment Model for Saturated Nanjing fine Sand Subject to Cyclic Loading. Earthq. Eng. Eng. Vib. 9 (4), 569–576. doi:10.1007/s11803-010-0038-9

CrossRef Full Text | Google Scholar

Wang, F., and Sassa, K. (2000). Relationship between Grain Crushing and Excess Pore Pressure Generation by sandy Soils in Ring-Shear Tests. J. Nat. Disaster Sci. 22 (2), 87–96. doi:10.2328/jnds.22.87

CrossRef Full Text | Google Scholar

Wang, G., Huang, R., Lourenço, S. D. N., and Kamai, T. (2014). A Large Landslide Triggered by the 2008 Wenchuan (M8.0) Earthquake in Donghekou Area: Phenomena and Mechanisms. Eng. Geology 182, 148–157. doi:10.1016/j.enggeo.2014.07.013

CrossRef Full Text | Google Scholar

Wang, G., and Sassa, K. (2002). Post-failure Mobility of Saturated Sands in Undrained Load-Controlled Ring Shear Tests. Can. Geotech. J. 39 (4), 821–837. doi:10.1139/t02-032

CrossRef Full Text | Google Scholar

Wang, J., Guo, L., Cai, Y., Xu, C., and Gu, C. (2013). Strain and Pore Pressure Development on Soft marine clay in Triaxial Tests with a Large Number of Cycles. Ocean Eng. 74, 125–132. doi:10.1016/j.oceaneng.2013.10.005

CrossRef Full Text | Google Scholar

Wang, S. (2009). Geological Nature of Rock and its Deduction for Rock Mechanics. Chin. J. Rock Mech. Eng. 28 (3), 433–450. (In Chinese).

Google Scholar

Wang, W. N., Chigira, M., and Furuya, T. (2003). Geological and Geomorphological Precursors of the Chiu-Fen-Erh-Shan Landslide Triggered by the Chi-Chi Earthquake in central Taiwan. Eng. Geology 69 (1-2), 1–13. doi:10.1016/s0013-7952(02)00244-2

CrossRef Full Text | Google Scholar

Xu, Q., Zhang, S., and Li, W. (2011). Spatial Distribution of Large-Scale Landslides Induced by the 5.12 Wenchuan Earthquake. J. Mt. Sci. 8 (2), 246–260. doi:10.1007/s11629-011-2105-8

CrossRef Full Text | Google Scholar

Yamamuro, J. A., and Covert, K. M. (2001). Monotonic and Cyclic Liquefaction of Very Loose Sands with High silt Content. J. Geotech. Geoenviron. Eng. 127 (4), 314–324. doi:10.1061/(asce)1090-0241(2001)127:4(314)

CrossRef Full Text | Google Scholar

Yang, Z. X., and Pan, K. (2018). Energy-based Approach to Quantify Cyclic Resistance and Pore Pressure Generation in Anisotropically Consolidated Sand. J. Mater. Civ. Eng. 30 (9), 04018203. doi:10.1061/(asce)mt.1943-5533.0002419

CrossRef Full Text | Google Scholar

Zhang, H., Zhang, J., Zhang, Z., Zhang, M., and Cao, W. (2020). Variation Behavior of Pore-Water Pressure in Warm Frozen Soil under Load and its Relation to Deformation. Acta Geotech. 15 (3), 603–614. doi:10.1007/s11440-018-0736-4

CrossRef Full Text | Google Scholar

Zhu, L., Cui, S., Pei, X., Zhang, X., Wang, H., He, S., et al. (2022). Investigation of the Characteristics and Long-Runout Movement Mechanisms of the Luanshibao Landslide on the Eastern Margin of the Qinghai-Tibet Plateau. Soil Dyn. Earthquake Eng. 153, 107094. doi:10.1016/j.soildyn.2021.107094

CrossRef Full Text | Google Scholar

Zhu, L., Pei, X., Cui, S., Liang, Y., and Luo, L. (2019). Experimental Study on Dynamic Damage and Strength Characteristics of Rock with Vein Mass. Chin. J. Rock Mech. Eng. 38 (05), 900–911. (In Chinese).

Google Scholar