
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
METHODS article
Front. Earth Sci. , 19 January 2023
Sec. Geohazards and Georisks
Volume 10 - 2022 | https://doi.org/10.3389/feart.2022.1107252
This article is part of the Research Topic Spatial Modelling and Failure Analysis of Natural and Engineering Disasters through Data-based Methods - Volume II View all 36 articles
To examine the strength and mechanical characteristics of self-compacting tailings, a direct shear test was conducted under various consolidation states and moisture contents to determine the cohesion and internal friction angle of the tailings. The degree of cohesion and the internal friction angle of unsaturated tailings increased initially before declining as the moisture content rose. The maximum cohesion and internal friction angle were reached when the moisture content was around 14%. When combined with the Coulomb shear strength formula and the tailings self-weight compaction model, the expressions for the active pressure and passive pressure of tailings at any height on the lateral restraint were obtained. An improvement in cohesion and the internal friction angle of unsaturated tailings was seen with increased consolidation stress, which became stable when the consolidation stress was greater than 1 MPa. The limited equilibrium method was used to establish the three-dimensional mechanical equilibrium of the cemented body. A strength model of cementation at the open stoping stage with subsequent filling was developed after the three-dimensional strength analytical model of cementation in step 1 was modified. The difference between the design value and the measured value was 0.2 MPa. The strength of the one-step cemented backfill design, as well as the design and erection of the backfill retaining wall, was supported technically and theoretically by this study.
The demand for mineral products in the national economy has continued to rise with China’s rapid industrialization and technological development, while production of solid waste, mullock, and tailings has also increased significantly. Long-term resource use and development can cause irreversible damage to the environment and the ecosystems that produce the natural resources. The idea of “green” development calls for the mining industry to develop in ways that utilize resources wisely, include recycling, and focuses on environmental protection. Promoting research and development on mine filling technology is therefore crucial (Zhang, 2014). According to the modern mining concept that “lucid waters and lush mountains are invaluable assets,” mine filling is frequently used as a supporting technology for green mining (Qiao et al., 2011; Chen et al., 2013; Qi et al., 2019). This satisfies the national directives.
Tailings are a structurally porous medium that is commonly used as the primary mine filling material (Edraki, 2014; Wu et al., 2016). Under pressure, tailings are easily deformable and the relationship between their compaction characteristics and the pressure of the overburden is nonlinear. Digital image technology was used by Cao et al. (2012) to examine the displacement development and evolution of sand compression under confinement. They stated that the displacement isolines were axisymmetrically distributed and that the sand displacement field resembled a parabola. Studies by Zhao (2020), Aursudkij B (2009), Wang and Qiao (2016a), Tian (2020), Li (2021), and Fall M (2005) showed that under conditions of unidirectional stepwise compression, the axial plastic strain of sand and tailings gradually increased. Because the characteristics of the early stage appeared more rapidly than the gradual changes of the late stage, stabilization was achieved. In their research on the density-compressibility of sand and tailings, Tian (2020) and Zhang et al. (2020a) showed that density had a significant impact on compressibility: as the material’s density improved, the compressibility increased. As Wu (2018) and Zhang et al. (2020b) noted, the confining pressure had a more significant impact than density on the compression characteristics of tailings. By examining the correlation between the density of the bulk material and the pressure, Wang et al. (2016b) and Han (2019) reported that the density increased as a power function with increases in pressure.
The self-compacting lateral expansion and tailings flow would invariably create active pressure (lateral pressure) on the structures (retaining walls and cement bodies), which could increase the stability of the structure. Several researchers, including Song (2020), Li (2017), and Yuan (2011), directly monitored the active pressure of tailings acting on a retaining wall. With increasing stability, the pressure on the backfilled retaining wall showed a nonlinear growth relationship with filling height. The pressure of earth on the retaining wall was simulated by Xiao (2020) using the discrete element method, and the pressure on the retaining wall was shown to have a nonlinear growth relationship with the increase in height. Wang (2015) and Wang et al. (2016b) performed a theoretical derivation for calculating the tailings lateral pressure and found a linear growth relationship between tailings active pressure and filling height. The effect of tailings active pressure on the stability of a cemented body was assessed by Cao (2015), (2017), (2018), Yang et al. (2018), Liu (2005), and others. These authors treated the tailings active pressure as a linear distribution. Through experimental research on the lateral pressure of rigid earth walls, Dou (2017) demonstrated that the lateral pressure coefficient improved with the increase of soil compression deformation. Cai (2020) investigated the factors influencing the lateral pressure coefficient and discovered that as the soil’s relative density increased, the lateral pressure coefficient value of sandy soil of the same particle size gradually increased. With increasing particle size, the lateral pressure coefficient for sand at the same density decreased. Yu (2020) suggested a nonlinear calculation method for the static earth pressure coefficient of coarse-grained soil based on a nonlinear distribution law of earth pressure. Gao et al. (2022) analyzed the layered cement tailings backfill using PFC 3D simulation. Cabalar (2021) ran tests to determine the characteristics of how waste rock powder inclusion affected consolidation at varying rates. The results showed a substantial decrease in compression index (cc), swelling index (cs), initial void ratio (eo), and volumetric compressibility (mv) and an increase in the coefficient of consolidation (cv) up to about 25%. Zhou (2020) showed that the cubic compressive strength, axial compressive strength, splitting tensile strength, and plastic modulus of solid concrete with self-compacting iron tailings all decreased with an increase in the iron tailings powder replacement rate.
The current tailings flow characteristics are adequately distinguished by active pressure (Zhai et al., 2010; Li et al., 2020). The distribution law and the factors affecting the influence of active pressure on tailings and other bulk media have been the subject of numerous studies, but some inconsistency still exists in the research. The effect of the self-compacting behavior of tailings on their physical and mechanical properties has been disregarded, which causes errors in the calculation and faulty designs of backfill retaining walls, ore pillars, and fillers. Previous studies have not adequately explored the relationship between height under self-gravity stress and physical and mechanical properties of tailings backfill such as porosity, water content, cohesion, and internal friction angle. A specific theoretical reference can be provided from the physical and mechanical characteristics of self-compacting tailings to facilitate secondary mining of lost pillars or residual pillars left over from initial mining.
In this paper, the relationship between cohesion and internal friction was assessed using the consolidation test and the direct shear test, and the angle of tailings and consolidation stress at various moisture contents were examined. A model of the strength of a cemented tailing body was constructed using this information as a foundation. The model offers some technical assistance and theoretical guidance for the design and construction of the backfill retaining wall and the one-step cemented backfill cube. In addition, this study provides a foundation for future research on the stability of the entire stope as well.
Unclassified mine tailings were selected as the test material, and their basic physical and mechanical parameters are shown in Table 1. The grading of unclassified tailings is shown in Table 2. The gradation curve of tailings particles is shown in Figure 1. From the results of grading tests, it can be calculated that the effective particle size is 0.0381 mm, the continuous particle size is 0.0674 mm, the average particle size is 0.1116 mm, and the control particle size is 0.1414 mm.
The tailings backfill was compressed under its own weight to yield a certain density, so the self-compacting behavior was simulated under conditions of confining compression and the shear strength indicators (cohesion and internal friction angle) were determined by a direct shear test (Chen et al., 2014). The main part of the direct shearing instrument was the shearing box, which was divided into a fixed upper box and a movable lower box. For the test, the tailings sample was put into the shearing box, a normal compressive stress was applied to the sample first, and then a horizontal shear force was applied to the lower box for shearing. The shear stress of the sample was obtained by determining when the shear plane between the upper and lower boxes failed. The shear strength, cohesion, and internal friction angle of the backfill tailings were then determined according to Coulomb’s law.
The strength characteristics of tailing sand were determined by the direct shear test under uniaxial compression and consolidation conditions (Liang et al., 2018; Ming et al., 2016; Jiang et al., 2018). The tailing sand filling in the extraction area had been left in place for a sufficient time. The water content of the tailing sand filling in the different extraction areas varied because of the different dewatering conditions, while the self-compacting tailing sand filling was in a non-saturated state. The water content of the non-cementing tailing sand filling was generally below 20%. The pore water in this range existed in the form of combined water and capillary water, which could not be dewatered by compression. In accordance with the pore ratio, the initial water content of the specimen was configured, and the prepared specimen was put into a plastic bag for 24 h to ensure that the moisture was evenly distributed, and then it was put into the configured ring knife. A specimen with a bottom area of 30 cm2 and a height of 2 cm was formed. The consolidation test was carried out over a range of pressures: 0.1, 0.2, 0.3, 0.4, 0.6, 0.8, 1.0, and 1.2 MPa. The loading time was defined for a compression deformation of ≤.01 mm. The specimens were put into a ZJ-type strain-controlled straight shear apparatus (Figure 2) after consolidation, and positive stresses of 0.1, 0.2, 0.3, and 0.4 MPa were applied from left to right. The shear stress at a shear rate of 0.8 mm/min was obtained by direct rapid shear without drainage. Three parallel tests were carried out for each group, and the means of the test data were recorded as the final results (Figure 3).
Water content and consolidation stress are important factors affecting the shear strength index of tailing sand (Lin et al., 2019). Different water contents and consolidation pressures led to significant differences in the shear strength index of tailing sand Under each consolidation pressure on the confined tailings, the normal stress and shear stress were linearly regressed according to the Coulomb formula. As an example, direct shear test data were collected from tailings at 0% water content under a consolidation stress of 0.1 MPa. The abscissa represented normal stress, while the ordinate showed the shear stress, and a linear regression was performed (Figure 4).
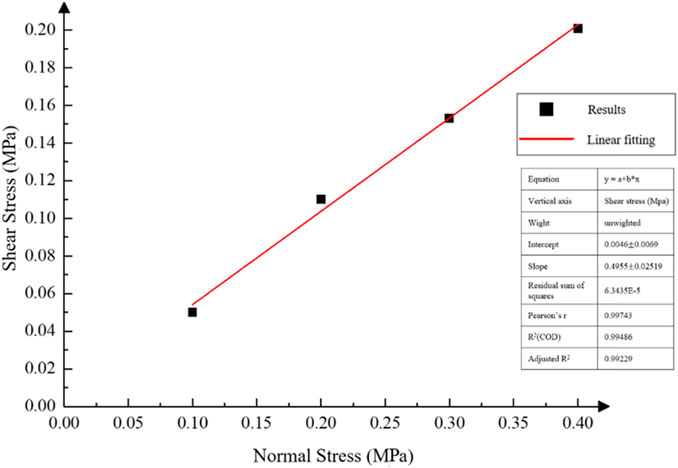
FIGURE 4. Shear strength line of tailings with 0% moisture content under the consolidation stress of 0.1 MPa.
The relationship between cohesion and angle of internal friction and moisture content is shown in Figures 5, 6. The cohesion and internal friction angle of unsaturated tailing sand followed a variation law of increasing then decreasing with increasing moisture content. The cohesion and internal friction angle of tailing sand were the highest at a moisture content of about 14%. When the moisture level was <14%, the cohesion and internal friction angle increased with increasing of moisture content; however, when moisture content was >14%, the cohesion force and the internal friction angle decreased with increasing moisture. The decreasing range gradually increased, until the angle of internal friction was the same (Zhang et al., 2021). The increasing water content of the tailing sand indicated that it had reached saturation. The high moisture content of the tailing sand triggered the alternative pore structure that resulted in a reduction in its ability to withstand shear. The water content had a significant impact on the particle viscosity of the tailing sand and the pore water pressure, which also changed the shear strength index.
When the moisture content in the tailing sand was low (0%–6%), water could be adsorbed by the particles. With a large amount of air and a small amount of liquid in the pore structure, the viscosity and pore water pressure of the tailing sand particles were lower and the cohesion and internal friction angle were relatively small. When the moisture content increased from 6% to 14%, the pores were partially filled with water, increasing the ratio of liquid to gas in the pores and the thickness of the water film on the particles. The higher water content increased the pore water pressure within the tailing sand skeleton, while its density gradually increased. The pore water linked the tailing sand particles together, thus improving cohesion and the internal friction angle. A high water content (>14%) increased the pore water pressure even further, while the water film became thinner as the pore water tension decreased. The viscosity between the tailing sand particles gradually weakened, which resulted in decreased shear strength. When the moisture content was increased even more, including the combined water in the pores, the tailing sand particles were separated by free water, and their ability to withstand shear was weak.
Combined with the consolidation test results, the relationship between cohesion and internal friction angle and consolidation stress is shown in Figures 7, 8. In Figures 7, 8, the cohesion and internal friction angle of unsaturated tailing sand generally showed an increasing variation law with the application of consolidation stress, and the increasing proportion of particles in contact with each other increased the contact area. The cohesion force and internal friction angle of tailing sand increased significantly in the early stages of consolidation stress during the whole compressive consolidation process. However, the cohesion force and internal friction angle showed a smaller growth trend with improvement in consolidation stress, which indicated that the tailing sand had become denser and more difficult to compress and consolidate. The cohesion and internal friction angle changed the most during the first stage of consolidation stress (0.1 MPa). Because the tailing sample before the first stage consolidation stress was in a naturally loose state, the pore volume between particles was the largest, and the cohesion and internal friction angle were the smallest. The cohesion and internal friction angle decreased rapidly when subjected to the first stage of compressive stress. Contacts between particles continued to increase, and the friction state was strengthened, so that the shear strength of the first stage 0.1 MPa consolidation changed the most. With increasing consolidation stress, the solid particles continuously migrated and were squeezed, causing the particle contact area to increase. The meshing effect between the particles was strengthened, while the friction and resistance between them increased, making it harder for the particles to move. The shear stress required to produce shear damage increased, and the shear strength of the tailing sand increased together with the cohesion and internal friction angle. The shear strength parameter of the tailing sand was basically in a stable state at 1 MPa pressure with the increase in consolidation stress. The development of cohesion and internal friction angle of the tailing sand was very low, reflecting the fact that the tailing sand sample was very dense. The change in pore volume was lower and tended to be stable, along with the cohesion and internal friction angle.
When the moisture content was equal, the shear capacity of the tailing sand increased as consolidation stress increased. The ultimate shear strength at the time of damage was increased due to the strengthening of the compressed particles linked to the tailing sand. The shear strength index followed a characteristic power function with increasing consolidation stress (Figures 6 and 7). In order to describe the relationship between cohesion, internal friction angle, and overburden stress (consolidation stress) of tailing sand under the different moisture content states utilized, a power function was constructed (Eq. 1):
The relationship between cohesion, c, and overlying consolidation stress is shown in Eq. 2:
The relationship between the angle of internal friction, φ, and the overlying consolidation stress is shown in Eq. 3:
where c is the cohesion of the tailing sand under consolidation stress in MPa; φ is the internal friction angle in degrees of the tailing sand under consolidation stress; σv is the consolidation stress on the tailing sand in MPa; σm is the critical stress when the tailing sand is stable, under a pressure of 1 MPa; vc and vφ are the coefficients related to compressive consolidation; zc and zφ are the coefficients related to initial pore space; uc is the cohesion force in MPa related to initial cohesion; and uφ is the internal friction angle in degrees relative to the initial internal friction angle.
Wu et al. (2018) constructed a relationship between the vertical consolidation stress of the water-bearing tailing sand and the depth of burial height as:
Substituting Eq. 4 and 2 into Eq. 3, we obtain the cohesion of the tailing sand, the angle of internal friction, and the height of burial depth as a function of:
Restricting the flow of tailings and carrying the lateral pressure was one of the key functions of the cemented body for filling an empty field. Tailings side pressure was employed as active pressure. In Figure 9, the maximum principal stress, σ1tailing, was the weight of the overlying tailings on the tailings unit at any height on the contact surface between the tailings and the cemented backfill. The minimum principal stress, σ3tailing, was the stress between the tailings and the cemented backfill, i.e., the lateral pressure of the tailings to the cemented backfill. It was assumed that the unit body on the contact surface between the tailings and the cemented backfill was in a limit equilibrium state under the stress conditions of σ1tailing and σ3tailing. Then, in a Cartesian coordinate system composed of normal stress and shear stress, the strength curve of the unit body was tangent to the stress Mohr circle, as shown in Figure 10.
In the right triangle, ABO’, in Figure 10, AB is trigonometrically related to O'A to obtain Eq. 7:
The aforementioned equation was simplified and organized by using the following trigonometric relationships (Eq. 8):
Eq. 7was simplified into Eq. 9:
The angle between the slip plane of the tailings and the maximum principal stress action surface (horizontal plane) is 45°+φ/2, and the limit equilibrium condition of the tailings active pressure state is simplified to Eq. 10:
The resultant active pressure of tailings at any height, h, on the contact length, L, gives the lateral restraint as Eq. 11:
When the lateral restraint was displaced or rotated relative to the direction of the tailings packing body under the action of an external force, the tailings packing body was squeezed, resulting in a tendency to upward sliding failure. When the horizontal stress exerted by the outside was greater than the vertical self-weight stress of the tailings and becomes the maximum principal stress, the tailings were compressed in the horizontal direction and their damage was affected by the resistance of the shearing force of the tailings. The tailings were in a passive state, and as the relative displacement of the confinement constraint increased, the horizontal stress of the tailings increased accordingly until the shear stress on the sliding surface reached the shear strength of the tailings. Consequently, the tailings were in a passive limit equilibrium state as shown in Figure 11. The angle between the slip plane of the tailings and the maximum principal stress action surface (vertical plane) was 45°+φ/2, and the angle between the slip plane and the horizontal plane was 45°-φ/2.
The ultimate equilibrium condition of the passive pressure of the tailings is shown in Eq. 12:
The resultant passive pressure force of tailings at any height, h, on the contact length, L, with lateral restraint is given by Eq. 13:
We provided a detailed analysis and discussion of the law of the self-weight compaction of tailings (the relationship between tailings density and height) (Edraki 2014). Thus, the variation in the relationship between tailings density and height satisfies a power function as shown in Eq. 14. Tailings density increased with increasing height, and the growth rate decreased.
The relationship between the bulk density of the tailings and the height is as follows:
In
where i, j, and l are constants related to the tailings density, a and d are compressibility constants, ε0 is the porosity in the natural loose state of tailings, and g is the acceleration of gravity.
In the continuous mining method with subsequent filling in an empty field, a II-step mine room was mined under a I-step colluvial artificial ore pillar. The I-step colluvial artificial ore pillar possesses a certain bearing capacity and has self-supporting strength, and in a stable state, it supports a certain exposure area and self-supporting height under its own self-supporting strength (Yang et al., 2018; Li et al., 2021a; Li et al., 2021b). The I-step colluvium was subjected to the most unfavorable state of a II-step mine room excavation exposure on one side, while the other side faced the active pressure effects of non-colluvial tailing sand (Liu et al., 2022). A three-dimensional analytical model of the self-supporting strength of the cemented fill in the most unfavorable state was established in the literature (Han et al., 2019; Liu et al., 2019) as shown in Figure 12.
In Figure 12, the limit equilibrium method was used to establish the three-dimensional mechanical equilibrium of the cemented body:
In Eq. 17:
It can be deduced that
The two coefficients in Eq. 19are
The influence of the tailings on the stability of the cemented body under pressure was increased under ideal conditions within height h0 (the influence of the tailings cohesion and internal friction angle with the depth of burial on the active pressure and the effect of the cemented body on the fracture of the tailings were ignored). Therefore, the results of the derivation of tailings active pressure in which the cohesion and internal friction angle change with the burial depth under the aforementioned pressure conditions were used to modify the three-dimensional strength model of the cemented body in step I (Edraki 2014; Guo et al., 2019), and the cohesion of the cement in step I was calculated. When φ = 5°∼45°, both parameters in Eq. 20 are approximately equal to 1. Therefore, Eq. 19 can be simplified to
The corrected result of the uniaxial compressive strength of the cemented body in step I is shown in formula (22):
The corrected result of the shear strength of the cemented body in step I is shown in formula (23):
The parameters in the formula are as follows:
In
In the formula, Ccemented is the cohesive force required for the self-supporting strength of the cemented filling body in MPa; σc(cemented) is the uniaxial compressive strength required for the self-supporting strength of the cemented filling body in MPa; τcemented is the shearing strength required for the self-supporting strength of the cemented filling body in MPa; γ is the bulk density of the cemented backfill in MN/m3; γ1 is the bulk density of the loose rock overlaying the top of the cemented backfill in MN/m3; γ2 is the bulk density of the surrounding rock on the sidewall of the cemented backfill in MN/m3; changed bulk density of self-compacting tailings in MN/m3; F is the resultant force of the non-cemented tailings on the lateral active pressure of the cemented backfill in MN; Ns is the force of the surrounding sidewall rock on the cemented backfill in MN; α is the backfill body sliding angle in degrees; θ is the sliding angle of the side rock in degrees; f is the general hardness coefficient of the side rock; H is the height of the cemented backfill in m; HA is the height of the cemented backfill on the potential slip surface in m; W is the contact width between the cemented backfill body and the sidewall surrounding rock in m; L is the contact length of the cemented backfill body and the self-compacting tailings in m; c(h) is the tailings cohesion that varies with burial depth and height in MPa; and φ(h) is the internal friction angle of tailings that changes with the height of burial depth in degrees.
To overcome the effects of high dilution rate, high loss rate, and low mining efficiency of the thick, gently sloping ore bodies in the Dahongshan Copper Mine, a two-step empty field was adopted on the lines B49-54 of the I2 and I3 ore bodies in the middle section of 285. The backfill mining method provided continuous mechanized mining without pillars in the panel. The ore body in this panel was relatively regular, high-grade, and continuous. A certain amount of engineering has been invested, which was more convenient for industrial testing and better reflects the advantages of continuous mechanized mining. The plan view of the continuous mining scheme is shown in Figure 13. (1), (2), and (4) show the one-step mine stopes that were cemented and filled, as shown in Figure 14.
To confirm the effects of the lateral pressure of the mine house self-compacting tailings on the cemented ore pillar in the aforementioned stopes, the cemented ore pillar of the second section B 49–51 in the middle section of 285 was selected as the test stope with on-site real-time tracking and monitoring of vertical pressure. In order to eliminate the need to place the pressure cell under the surrounding rock, a #9 pressure cell (TGH type pressure cell) was embedded at a horizontal distance of about 5 m from the retaining wall. The pressure cell was placed on the bottom 500 mm, and a #10 pressure cell was embedded in the 35 m cemented body (Figure 15).
The strength design of the cemented body in step I in the section adopted the revised formula (19), and the design of the cemented body strength model (for convenience called the original strength design) was carried out by ignoring the cohesive force and the internal friction angle and only considering the compression conditions. Based on the mine filling system and filling multiplier, the layer height was set at 10 m for calculation, and the relationship between strength and height was found to be inversely related. In the mining sequence (2), the cemented ore pillar in the second section of B49–51 in the middle section of 285 was the filling design of the test stope, as shown in Table 3. The relationship between the measured compressive stress of the #9 pressure cell and time is shown in Figure 16, and the relationship of the measured compressive stress of the #10 pressure cell with time is shown in Figure 17. The acquisition time was counted from the beginning of the packing of the cemented ore column.
The trend of the measured pressure values of the #9 and #10 pressure cells with time were consistent. The vertical stress of the cemented filling body increased with the improvement in filling height. The strength of the cemented body was designed by utilizing the modified step I filling strength model, and the safety factor was 1.2. In the revised design, the strength at the bottom of the cemented ore pillar of line 49–51 in Section II was 2.06 MPa, and the measured maximum vertical pressure at the bottom was 1.82 MPa. The designed strength according to the layer height of 35 m was 1.36 MPa, and the actual measurement of the maximum vertical pressure at the corresponding height was 1.17 MPa, which means that the measured value of the cemented pillar strength was less than the design strength.
By comparing the design value of this model with the empirical model of the Anqing Copper Mine and the model of Liu Zhixiang, it can be seen that the design value of the Anqing Copper Mine model was lower than the measured value, which is quite dangerous in practical terms. In addition, the calculated value of the Liu Zhixiang model is obviously larger than the design value of the model in this paper, which is significantly different from the measured value. The model in this paper not only returned a design value in a reasonable range but also provided a safety space, which enhanced its practical advantages.
Artificial intelligence is the future development direction of the mining industry, and engineering mechanics is necessary in mining engineering. Therefore, using an artificial intelligence algorithm to solve practical problems of engineering mechanics is one of the current goals of mining engineering development. If the artificial intelligence algorithm can be integrated into the scientific research of mining engineering, a large number of complicated test processes will be saved, and the results will be safer and more reliable. The machine learning models have higher LSP performance than general statistical and heuristic models due to their high AUC accuracy and reasonable LSI distribution features (Huang et al., 2020a). The ultimate purpose of strength design is to ensure the safety of underground mining. It is also crucial for predicting the instability and failure of pillars. There are various methods of prediction, such as deep learning (Huang et al., 2020b), semi-supervised learning (Huang et al., 2020c), and unsupervised learning (Chang et al., 2020). In the next stage, the research focus will be on the development of a prediction model for the strength of cemented backfill in various mining methods, to find out which machine learning algorithm can best reflect the strength law of cemented backfill.
Unsaturated tailings exhibit a first-order increase in cohesive force and internal friction angle that decreases with increasing moisture content; the maximum cohesive force and internal friction angle were observed at 14% moisture content. When the consolidation stress was greater than 1 MPa, the cohesive force and internal friction angle tended to be stable and increased with consolidation stress. The analytical model of a cemented body’s three-dimensional strength was altered, and the cemented body’s cohesive force correction result was resolved. The cemented backfill’s uniaxial compressive strength was then measured. In the second section of the B49–51 line of the I2 and I3 ore bodies in the middle of section 285 of the Dahongshan Copper Mine, the research findings were used to produce cemented pillars. The measured results of the ore pillar’s vertical stress and the cemented body’s strength value, which has been adjusted for the tailing self-compaction law, differed only slightly. At about 0.2 MPa, the difference was under control. The modified strength model is reasonable, ensures individual safety, and can increase mining production efficiency, as demonstrated by the industrial application.
The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.
WJ carried out the main writing of the article. YT-Y undertook the experiments and formula derivations of this paper. QD-P provided technical guidance and review for this article. CJ provided the materials needed for the experiments. LZ-L acquired the references and created the layout of the article.
This research was supported by Yunnan Fundamental Research Projects (grant no. 202001AU070062). In addition, part of the funds came from the Talent Training Fund of Kunming University of Science and Technology (No. KKZ3202021040).
Author CJ was employed by the company Yunnan Tin Industry Datun Tin Mine. Author LZ-L was employed by the company Baoshan Jinchanghe Mining Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Aursudkij, B., Mcdowell, G. R., and Collop, A. C. (2009). Cyclic loading of railway ballast under triaxial conditions and in a railway test facility. Granul. Matter 11 (6), 391–401. doi:10.1007/s10035-009-0144-4
Cabalar, A. F., and Alosman, S. O. (2021). Influence of rock powder on the behaviour of an organic soil. Bull. Eng. Geol. Environ. 80 (11), 8665–8676. doi:10.1007/s10064-021-02457-2
Cai, Z.-Y., Dai, Y.-Z., Xu, G.-M., Ren, G.-F., et al. (2020). Effect of particle size and compaction on K0 value of sand by centrifugal model test. Rock Soil Mech. 41 (12), 3882–3888. doi:10.16285/j.rsm.2020.0669
Cao, L., Liu, W.-B., Li, X.-Z., Zhao, X. B., Li, Y. X., et al. (2012). Experimental study of compression deformation patterns in sands based on digital image analysis. Rock Soil Mech. 33 (4), 1018–1024. doi:10.16285/j.rsm.2012.04.040
Cao, S., Du, C.-F., Tan, Y.-Y., Jian-xin, F., et al. (2015). Mechanical model analysis of consolidated filling pillar using stage-delayed backfill in metal mines. Rock Soil Mech. 36 (08), 2370–2376. doi:10.16285/j.rsm.2015.08.033
Cao, S., Erol, Yilmaz., and Song, W.-D. (2018). Evaluation of viscosity, strength and microstructural properties of cemented tailings backfill. Backfill. Miner. 8 (8), 352. doi:10.3390/min8080352
Cao, S. (2017). Research on structural characteristics and dynamic effects of cemented tailing backfilling and its application. Beijing China: University of Science and Technology Beijing.
Chang, Z., Du, Z., Zhang, F., Huang, F., Chen, J., Li, W., et al. (2020). Landslide susceptibility prediction based on remote sensing images and GIS: Comparisons of supervised and unsupervised machine learning models. Remote Sens. 12, 502. doi:10.3390/rs12030502
Chen, O., Qiao, D.-P., and etal, (2013). An introductive discussion of filling mining method. Min. Metallurgy 22 (3), 30–32+35.
Chen, R., Lei, R.-D., and Li, Z.-H. (2014). Anisotropic shear strength characteristics of a tailings sand. Environ. EARTH Sci. 71 (12), 5165–5172. doi:10.1007/s12665-013-2918-6
Dou, G.-T., Xia, J.-W., Yang, Y.-Z., Zhang, H.-W., Qiu, H., et al. (2017). Experiment study of lateral Earth pressure on rigid wall in mining area. J. China Univ. Min. Technol. 46 (1), 215–221. doi:10.13247/j.cnki.jcumt.000635
Edraki, M., Baumgartl, T., Manlapig, E., Bradshaw, D., Franks, D. M., and Moran, C. J. (2014). Designing mine tailings for better environmental, social and economic outcomes: A review of alternative approaches. J. Clean. Prod. 84, 411–420. doi:10.1016/j.jclepro.2014.04.079
Fall, M., Benzaazoua, M., and Ouellet, S. (2005). Experimental characterization of the influence of tailings fineness and density on the quality of cemented paste backfill. Miner. Eng. 18 (1), 41–44. doi:10.1016/j.mineng.2004.05.012
Gao, T., Sun, W., Liu, Z., and Cheng, H. Y. (2022). Investigation on fracture characteristics and failure pattern of inclined layered cemented tailings backfill. Rochester, NY: Social Science Electronic Publishing.
Guo, L., Liu, G., and Yang, X. (2019). Models of three-dimensional arching stress and strength requirement for the backill in open stoping with subsequent backfill mining. J. China Coal Soc. 44 (5), 1391–1403. doi:10.13225/j.cnki.jccs.2019.6025
Han, L., Shu, J.-S., Shang, T., Chen, S.-Z., Gerson, S. V. T., et al. (2019). Experiment study on the physical and mechanical parameters of soft rock remolding in waste dump. J. Min. Saf. Eng. 36 (4), 820–826. doi:10.13545/j.cnki.jmse.2019.04.022
Huang, F., Cao, Z., JianfeiGuo, S. H. J., Guo, Z., and Guo, Z. (2020c). Comparisons of heuristic, general statistical and machine learning models for landslide susceptibility prediction and mapping. CATENA 191, 104580. doi:10.1016/j.catena.2020.104580
Huang, F., Cao, Z., Jiang, S., Zhou, C., Guo, Z., and Guo, Z. (2020a). Landslide susceptibility prediction based on a semi-supervised multiple-layer perceptron model. Landslides 17, 2919–2930. doi:10.1007/s10346-020-01473-9
Huang, F., Zhang, J., Zhou, C., Wang, Y., Huang, J., and Zhu, L. (2020b). A deep learning algorithm using a fully connected sparse autoencoder neural network for landslide susceptibility prediction. Landslides 17 (1), 217–229. doi:10.1007/s10346-019-01274-9
Jiang, S. H., Huang, J., Huang, F., Yang, J., Yao, C., and Zhou, C. (2018). Modelling of spatial variability of soil undrained shear strength by conditional random fields for slope reliability analysis. Appl. Math. Model. 63, 374–389. doi:10.1016/j.apm.2018.06.030
Li, G.-T., and Qiao, D.-P. (2017). Filling retaining wall strength model of tailing and lts application in large goaf. Nonferrous Met. Eng. 7 (3), 88–92.
Li, J.-J., Erol, Y., and Cao, S. (2020). Influence of solid content, cement/tailings ratio, and curing time on rheology and strength of cemented tailings backfill. Minerals 10 (10), 922. doi:10.3390/min10100922
Li, X.-L., Tao, Z.-H., Wang, J.-G., Zuo, T., Ma, J., and Li, Q. (2021a). Strain rate effect on mechanical properties of cemented backfill under dynamic and static combined loading. Shock Vib. 2021, 1–11. doi:10.1155/2021/2196838
Li, X.L., Chen, S. J., and Wang, S. (2021b). Study on in situ stress distribution law of the deep mine taking Linyi Mining area as an example. Advances in Materials Science and Engineering 9 (4), 5594181. doi:10.1155/2021/5594181
Liang, B., Wang, K., and Jiang, L.-G. (2018). Experimental research on compressibility and consolidation characteristics of tailings and e-P curve model analysis. J. Disaster Prev. Mitig. Eng. 38 (1), 109–117. doi:10.13409/j.cnki.jdpme.2018.01.015
Lin, H., Zhou, C.-B., Chen, F., and Jiang, Q.-H. (2019). Shear strength and macro-micro analysis of copper tailingsand tungsten tailings. J. Eng. Geol. 27 (2), 317–324. doi:10.13544/j.cnki.jeg.2017-576
Liu, Z.-X. (2005). Mechanics of high tailings backfillandnonlinear optimal design in deep mining. Hu Nan Sheng, China: Central South University.
Liu, H. Y., Zhang, B. Y., and Li, X. L. (2022). Research on roof damage mechanism and control technology of gob-side entry retaining under close distance gob. Engineering Failure Analysis 138 (5), 106331. doi:10.1016/j.engfailanal.2022.106331
Ming, J., Hu, N.-L., Sun, J.-H., and Wang, Li. (2016). Experimental study on filling technology of full tailings method with compression and consolidation. Exp. Technol. Manag. 33 (9), 53–56+65. doi:10.16791/j.cnki.sjg.2016.09.015
Qi, C.-C., and Fourie, A. (2019). Cemented paste backfill for mineral tailings management: Review and future perspectives. Miner. Eng. 144, 106025. doi:10.1016/j.mineng.2019.106025
Qiao, D.-P., Cheng, W.-H., Zhang, W.-H., Yao, W.-X., Wang, X.-L., and Wang, H. (2011). Modern mining concepts and filling technique. Nonferrous Metal Sci. Eng. 2 (02), 7–14. doi:10.13264/j.cnki.ysjskx.2011.02.008
Song, H.-Y., Zhou, L., Liu, L.-Q., Chen, W.-W., et al. (2020). Study on the simulation test of the pressure variation rules of the filling retaining wall. Gold 41 (5), 40–45.
Tian, Y., Che, G.-F., and Zhang, W.-Q. (2020). Study on compressive characteristics of different dry density tailings. Fly. Ash Compr. Util. 34 (2), 72–76.
Wang, J., and Qiao, D.-P. (2016a). Strength model of cementing filling body under lateral pressure. Int Conf Mach. 853–859
Wang, J., Qiao, D.-P., Li, G.-T., Sun, H.-S., Tong, R.-Y., et al. (2016b). Dead weight compression model and application of tailings filling body in large goaf. Rock Soil Mech. 37 (S2), 403–409. doi:10.16285/j.rsm.2016.S2.052
Wang, J., Qiao, D.-P., Li, G.-T., Sun, H.-S., Tong, R.-Y., et al. (2016c). Computing method of lateral pressure of incompact milltailings with subsequent filling. J. Kunming Univ. Sci. Technol. Sci. Ed. 41 (5), 27–32. doi:10.16112/j.cnki.53-1223/n.2016.05.005
Wu, A.-X., Wang, Y., and Wang, H.-J. (2016). Status and prospects of the paste backfill technology. Metal. Mine 481 (7), 1–9.
Wu, J.-Y., Feng, M.-M., Chen, Z.-Q., Mao, X.-B., Han, G.-S., and Wang, Y.-M. (2018). Particle size distribution effects on the strength characteristic of cemented paste backfill. Backfill. Miner. 8 (8), 322. doi:10.3390/min8080322
Xiao, X.-D., Li, M.-G., and Wu, H. (2020). DEM simulation of earth pressure exerted on rigid retaining wall subjected to confined soil. Chin. J. Undergr. Space Eng. 16 (1), 288–294.
Yang, L., Qiu, J.-P., Sun, X.-G., Xing, J., et al. (2018). Research and application on strength model of cemented backfill pillar for stage subsequent filling mining method. J. Central South Univ. Sci. Technol. 49 (9), 2316–2322.
Yu, Z.-S., Chen, X.-B., Zhang, J.-S., Dong, L., Abdoulkarder, M. S., et al. (2020). Analysis of the nonlinearity of coefficient of Earth pressure at rest and its calculation method for coarse-grained soils. Rock Soil Mech. 41 (6), 1923–1932. doi:10.16285/j.rsm.2019.1280
Yuan, S.-L. (2011). Study on mechanical property of whole tailing filling retaining wall in panel large hole mining stope. China Mine Eng. 40 (4), 9–12.
Zhao, Y.-Z. (2020). Research of nonlinear MechanicalProperityfor granular ballast bed. Railw. Surv. Des. 2, 72–76.
Zhai, Y.-G., Wu, A.-X., Wang, H.-J., Qin-Rui, C. H. E. N., Hang-Kong, L. I., Jia-Long, Y. A. N., et al. (2010). Study on rheological properties of the unclassified-tailings paste. Metal. Mine 414 (12), 30–32+57.
Zhang, J.-B., Che, G.-F., and Zhang, W.-Q. (2021). Variation of shear strength parameters of lron tailings with the degree of consolidation. China Earthq. Eng. J. 43 (2), 453–458.
Zhang, W.-J. (2014). Adhering to the basic national policy of saving resources and protecting the environment and striving to move towards a new era of socialist ecological civilization. Shaanxi Water Resour. 4, 4–5.
Zhang, Y.-J., Chen, S.-S., and Fu, Z.-Z. (2020b). Experimental study on microstructure and compressibility of iron ore tailings. Chin. J. Geotechnical Eng. 42 (S2), 61–66.
Zhang, Z.-J., Guo, Y.-H., Tian, Y.-K., Hu, L., Wang, X. x., Zheng, H. M., et al. (2020a). Macroscopic and mesoscopic mechanical properties of mine tailings with different dry densities under different confining pressures. GEOFLUIDS 2020, 1–12. doi:10.1155/2020/8832335
Keywords: self-compacting tailings, cemented filling, strength model, active pressure, passive pressure
Citation: Jun W, Tian-Yu Y, Deng-Pan Q, Jie C and Zheng-Liang L (2023) Strength model of a cemented body based on self-compacting characteristics of tailings. Front. Earth Sci. 10:1107252. doi: 10.3389/feart.2022.1107252
Received: 24 November 2022; Accepted: 30 December 2022;
Published: 19 January 2023.
Edited by:
Zizheng Guo, Hebei University of Technology, ChinaReviewed by:
Roohollah Kalatehjari, Auckland University of Technology, New ZealandCopyright © 2023 Jun, Tian-Yu, Deng-Pan, Jie and Zheng-Liang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yang Tian-Yu, MTAxMjUxMzYzM0BxcS5jb20=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.