Study on triaxial test and constitutive prediction model of frozen silty clay

With the increasing demand for engineering construction in the seasonal frozen area and the background of the Belt and Road Initiative, the frozen soil constitutive model should be studied in depth. At present, the constitutive prediction model of frozen silty clay has many problems, such as complex formula, single model application and poor prediction ability. Random forest optimal model hyperparameter input was very difficult. Particle Swarm Optimization (PSO) was used to optimize the parameters of the number of neurons, dropout and batch_size in the Long-term and Short-Term Memory network (LSTM) structure. The optimization results were 61, 0.09 and 95 respectively. The results showed that the strength tended to be stable after 6,9,6,9 and 9 freeze-thaw cycles under initial moisture content = 25, 22.5, 20, 17.5, and 15%, respectively. After 18 freeze-thaw cycles, the strength decreased by 2.66%, 11.85%, 18.83%, 16.79, and 29.02%, respectively. The predicted values of frozen soil binary medium model (BM), random forest model (RF) and PSO-LSTM model were compared with the measured values under different working conditions, and good accuracy was obtained. The R² of the PSO-LSTM model test set was trained to more than 98%, and RMSE, MAE and MAPE were also trained to the lowest under the same working conditions. The influencing factors of deviator stress of frozen silty clay were given in order from strong to weak: initial moisture content>strain>confining pressure>number of freeze-thaw cycles. The LSTM optimal combination input parameters were searched by PSO, and the parameter adjustment speed of the model for the data learning process of frozen silty clay was greatly increased, which was conducive to the promotion of other soil constitutive prediction models. A new constitutive prediction model of frozen silty clay was developed using PSO-LSTM algorithm. 15 working conditions had been verified, and the optimal model had high accuracy in the constitutive prediction of frozen silty clay, which provided a good reference for the application of frozen soil engineering in cold regions.

1 Introduction

The world’s cold regions can be divided by air temperature, snow thickness and frozen soil depth. The distribution area of global frozen soil accounts for about 24% of the total land. Seasonal and intermittent frozen soil regions account for 50.6% and 6.6% of the land area in the Northern Hemisphere, respectively (Zhang et al., 2003), indicating that more than half of the land in the Northern Hemisphere experiences a freeze-thaw cycle every year (Li et al., 2021). The freezing damage of soil around building foundation, road foundation and pipeline is controlled by soil mechanical properties under freezing state. Frozen silty clay is widely distributed in cold regions of the Northern Hemisphere. In order to study the engineering properties of soil in cold regions, it is of great significance to study the constitutive relationship of frozen silty clay. Constitutive model is the key to analyze the stress-strain relationship of frozen soil, and also the basis for studying the stability of landslide (Huang et al., 2020; Li et al., 2022).

Soil elastic-plastic definite solution needs to be solved simultaneously with equilibrium differential equation, geometric equation, deformation coordination equation and known boundary. The constitutive model, as the deformation coordination equation, is an important theoretical basis for analyzing the soil stress-strain relationship. So far the most studied soil constitutive models can be divided into: elastic-plastic constitutive model (Zhang and Liu, 2019; Lai et al., 2010; Wang et al., 2020; Zhang et al., 2020; Zhang et al., 2020; Wang et al., 2021; Yu et al., 2022), nonlinear constitutive model (Yang et al., 2013; Jin et al., 2016; Loria et al., 2017), critical state constitutive model (Wu et al., 1996; Yao et al., 2004; Yang et al., 2010; Yin et al., 2010; Jin et al., 2016; Lai et al., 2016; Jin et al., 2017; Sun et al., 2020), hypoplastic constitutive model (Lai et al., 2014; Mašín, 2015; Chang et al., 2019) and the micromechanical constitutive model (Yin et al., 2010; Yin et al., 2014; Xiong et al., 2017; Qu et al., 2021; Qu et al., 2021; Wang et al., 2021). However, there are some problems in the above soil constitutive model: 1) the stress-strain relationship between frozen soil and thawed soil is proposed based on certain assumptions (Zhang et al., 2022; Yin et al., 2010). 2) Frozen soil and thawed soil models are generally only applicable to one soil type (Zhang et al., 2021). 3) The mathematical formula of stress and strain of frozen soil and thawed soil comes from data fitting, but the model prediction effect is not good (Yin et al., 2011). 4) With the increase of fitting parameters (Yin and Jin, 2021), the constitutive formula of frozen soil becomes increasingly complex.

The stiffness of frozen soil is between soft soil and rock, so a binary medium model can be used to describe the freeze-thaw-compression failure mechanism and stress evolution of frozen silty clay. In terms of the research on the frozen soil binary medium model and freeze-thaw damage mechanism, few articles have done relevant analysis. Zhang et al. (2019) verified the data obtained from the triaxial test of frozen soil through homogenization theory and binary medium theory.

In recent years, frozen soil constitutive theory has been being studied by some methods, such as experimental research, theoretical derivation, formula fitting, numerical simulation of particle flow, and data-driven deep learning. Numerous ML algorithms have been used to study thawing and frozen soil constitutive, such as Evolutionary Polynomial Regression (EPR) (Nassr et al., 2018), Support Vector Machine (SVM) (Zhao et al., 2014; Kohestani and Hassanlourad, 2016), Back Propagation Neural Network (BPNN) (Shahin and Indraratna, 2006; Johari et al., 2011; Rashidian and Hassanlourad, 2014; Stefanos and Gyan, 2015; Lin et al., 2019), radial basis function (RBF) neural network (Peng et al., 2008), recurrent neural network (RNN) (Zhu et al., 1998; Romo et al., 2001), long short-term memory (LSTM) neural network (Zhang et al., 2019; Zhang et al., 2020). Problems such as gradient explosion or gradient disappearance can be better avoided by LSTM neural network. However, the selection of the optimal model input parameter combination is still an urgent problem to be studied. However, for different frozen silty clay datasets, the optimal neuron numbers, dropout probability and batch_size combination corresponding to the minimum stress loss function should be different. Aiming at the problems of difficult parameter adjustment and poor fitting accuracy, a method based on long short-term memory neural network (LSTM) and particle swarm optimization (PSO) is proposed to predict the stress-strain evolution law of frozen silty clay.

The structure of this paper is as follows. In the first part of the experimental study, the stress-strain evolution process of frozen silty clay is qualitatively analyzed by mechanism. In the second part, the binary medium frozen silty clay constitutive model based on the simplification of freeze-thaw damage parameters is studied, and the fitted mathematical formula provides a reference for engineering design. The third part, frozen silty clay constitutive prediction model principle is introduced. In the fourth part, the relationship between the RF model, the frozen soil binary medium model and the PSO-LSTM model and the generalization value of the optimal model are discussed, and the mechanism of the influence of the three factors on the strength of frozen silty clay is deeply analyzed. Finally, this paper summarizes and puts forward the future work plan.

2 Materials

2.1 Test overview

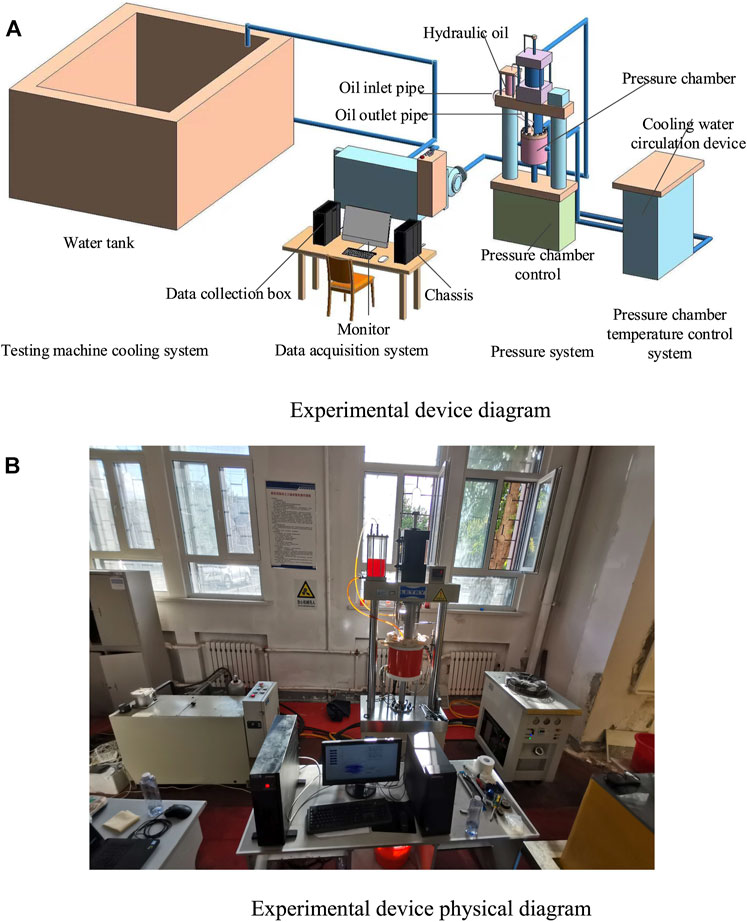
The test instrument adopts the frozen soil dynamic and static triaxial tester FST-250 designed by Xi’an Lichuang Material Testing Technology Co., Ltd. (see Figure 1). The instrument adopts displacement control mode and is mainly composed of triaxial pressure system, XT5718ULT-E2000 cooling water circulating device, data acquisition system, cooling system of testing machine, etc. The temperature control range is -70°C∼+90°C, the temperature control accuracy is 0.5°C, the confining pressure range is 0～40MPa, the accuracy is 1%, and the maximum axial pressure is 250KN.

FIGURE 1

FIGURE 1. (A). Experimental device diagram. (B). Experimental device physical diagram.

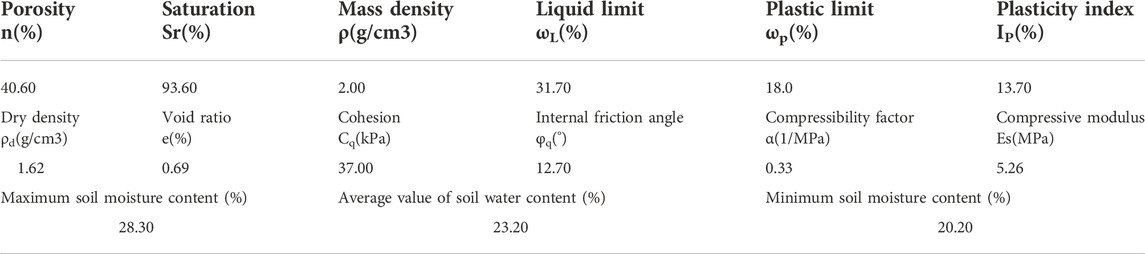
The microcomputer-controlled electro-hydraulic servo triaxial testing machine for frozen soil is mainly used for dynamic and static triaxial tests of conventional soil and frozen soil. The basic physical properties of the test soil are shown in Table 1. In order to reduce the heterogeneity and dispersion of natural silty clay, 1.25 mm sieve is used to screen out impurities such as plant fiber and gravel of natural silty clay. The distribution of soil with particle size less than 1.25 mm is shown in Table 2. Direct shear test is used to measure cohesion and internal friction angle of soil samples. The liquid limit and plastic limit in Table 1 are measured by LP-100D digital display soil liquid and plastic limit tester. The standard consolidation method is adopted in the consolidation test, and the compressibility factor and modulus are obtained. The maximum and minimum values are obtained from experiments, and the average values are obtained from calculation. According to the liquid plastic limit and particle size distribution, the test soil can be classified as silty clay.

TABLE 1

TABLE 1. Basic physical properties of natural silty clay.

TABLE 2

TABLE 2. Particle size distribution of soil.

2.2 Soil preparation

The dry soil that has passed through 1 mm sieve is sprayed and mixed with soil according to the initial moisture content (15%, 17.5%, 20%, 22.5%, and 25%). Then the soil samples are sealed with plastic wrap for 24 h. The dry density of soil sample is controlled to 1.62 g/cm3. Soil samples with different water contents are divided into five layers and compacted into a three-part mold with an inner diameter of 61.8 mm and a height of 125 mm. After standing for a certain time, soil samples with different initial moisture contents are demolded. Then, the soil samples are packaged and labelled with plastic wrap. Finally, the soil samples are put into the high and low temperature alternating test chamber TEMP880.

2.3 Freeze-thaw cycles test

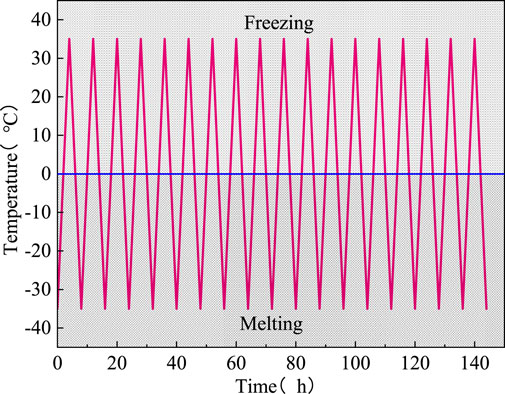
The high and low temperature alternating test chamber TEMP880 designed by Shanghai-Huayi Equipment Co., Ltd. is used for the freeze-thaw cycle test. The test chamber is set at -35°C–35°C. The specific temperature time history curve in the high and low temperature alternating test chamber during the experiment is shown in Figure 2 below. The soil samples undergoe 4 h of freezing and 4 h of thawing, that is, a freeze-thaw cycle is performed every 8 h (Teng et al., 2022). Then, the soil samples are packaged with a thin latex sleeve, and place in a constant temperature test chamber with the same design temperature for 24 h after sticking the label. YH-10 aviation hydraulic oil in the triaxial pressure chamber is used to apply confining pressure and maintain temperature stability. Next, the soil samples with sufficient temperature control in the constant temperature test chamber are placed in the triaxial pressure chamber. When the temperature of the soil sample and hydraulic oil is coupled to the design temperature, the design confining pressure is applied for the test.

FIGURE 2

FIGURE 2. Temperature variation of soil sample.

2.4 Time scaling principle of freeze-thaw cycle

Because the time scale of soil freezing and thawing process in seasonally frozen soil area is considerably large, the reduced similarity ratio is adopted in the test. The similarity criteria based on the similarity theoretical model are as follows (Guo et al., 2010):

$F_o=\frac{a{L}^2}{\mathrm{\Gamma }}(1)$

Where L represents the characteristic length, m. $\Gamma$ represents the period of surface temperature change, h a represents the proportional coefficient.

The physical simulation characteristics of frozen silty clay are consistent with the test process and the actual process. The experiment lasted 8 h (4 h of freezing and 4 h of thawing), and the 1-year change process under the action of freezing and thawing cycles was simulated. The similarity calculation process is shown in Table 3:

TABLE 3

TABLE 3. Test time simulation time conversion.

2.5 Shear test

Constant deformation loading is adopted during the test, and the shear rate is 1 mm·min-1. The test is terminated when the specimen strain reached 20% or when it failed. At -15°C, Triaxial tests are carried out on frozen silty clay nuder five freeze-thaw cycles, five initial moisture contents and three confining pressures. The change of soil sample stress is monitored in real time and recorded. After the triaxial test, the frozen soil sample is convex in the upper part and has expansion deformation in the radial direction. The frozen silty clay generally presents an oblique crack failure form (Xu et al., 2020; Niu et al., 2022; Zhang et al., 2022).

3 Methods

3.1 Long short-term memory neural network structure and implementation

Long short-term memory neural network (LSTM) was created primarily to solve the problem of gradient disappearance and explosion. The biggest difference between LSTM and traditional neural network is the introduction of Forget gate, Input gate and Output gate. Another key is the change in the internal state, which is the core of each activated neuron and can be seen as a carrier for adding information or deleting information.

Step 1. Some information is selectively discarded by the forget gate, and LSTM receives the input of $C_{\mathrm{t}}$ and $h_{t-1}$. And output a number between 0 and 1 to the internal state $S_t$.

$f^{\left(t\right)}=\sigma \left(W^{fC}{C}^{\left(t\right)}+W^{fh}{h}^{\left(t-1\right)}+b_f\right)(2)$

Step 2. Some information in the internal state is determined to be stored. The input gate determines which values are updated, and then a candidate state ${\mathrm{S}}^{\left(\mathrm{t}\right)}$ is built by the input node $g^{\left(t\right)}$.

$i^{\left(t\right)}=\sigma \left(W^{iC}{C}^{\left(t\right)}+W^{ih}{h}^{\left(t-1\right)}+b_i\right)(3)$

$g^{\left(t\right)}=\mathit{tanh}\left(W^{gC}{C}^{\left(t\right)}+W^{gh}{h}^{\left(t-1\right)}+b_g\right)(4)$

The original internal state is updated to ${\mathrm{S}}^{\left(\mathrm{t}\right)}$ by Eqs 2–4.

$S^{\left(t\right)}=g^{\left(t\right)}\times i^{\left(t\right)}+S^{\left(t-1\right)}\times f^{\left(t\right)}(5)$

Step 3. The output information is determined by the output gate.

$o^{\left(t\right)}=\sigma \left(W^{oC}{C}^{\left(t\right)}+W^{oh}{h}^{\left(t-1\right)}+b_o\right)(6)$

Step 4. Based on the output gate and the new internal state, the new hidden layer state ${\mathrm{h}}^{\left(\mathrm{t}\right)}$ is output.

$h^{\left(t\right)}=\mathit{tan}h{S}^{\left(t\right)}\times o^{\left(t\right)}(7)$

where W and b represent the weight and bias, respectively, ${\mathrm{W}}^{\mathrm{f}\mathrm{C}}$ is the weight of ${\mathrm{C}}^{\left(\mathrm{t}\right)}$ in the forget gate, and ${\mathrm{b}}_{\mathrm{f}}$ is the forget gate bias.

3.2 Introducing dropout to prevent overfitting

L1 and L2 regularization methods are often used in neural networks to prevent model overfitting. Some parameters in the loss function are limited by this method (Jiang et al., 2018; Huang et al., 2020). Neurons and fully connected layers are randomly deleted through Dropout technology to form new samples (Srivastava et al., 2014). The overfitting problem is effectively solved by this sample replacement effect. At the same time, the entire network is no longer very sensitive to the specific weights of neurons. Therefore, the generalization ability of the model has been greatly improved (Huang et al., 2020; Chang et al., 2022).

3.3 Particle swarm Optimization(PSO)-LSTM process

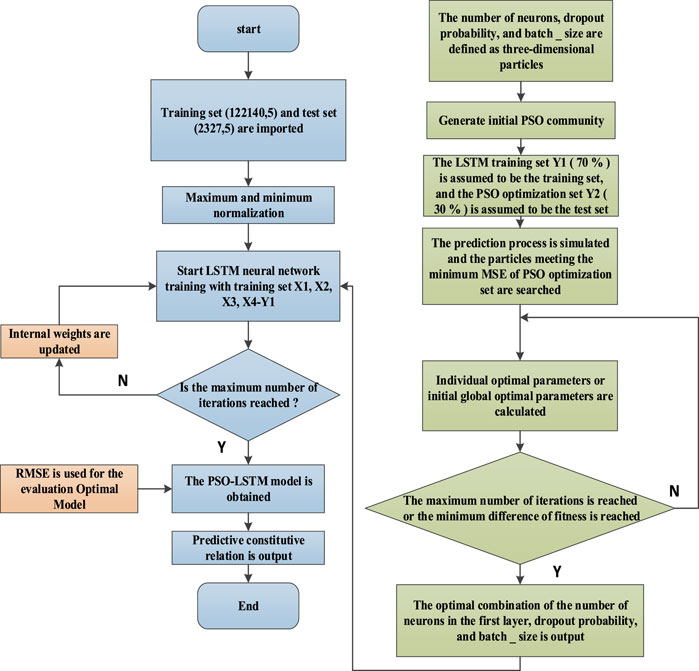
The steps of PSO-LSTM are as follows, and the flow chart is shown in Figure 3.

1) The dataset is divided into LSTM training set, validation set and test set.

2) Initialize the PSO algorithm: parameters such as the number of iterations, inertia weight, learning factor and iteration step range are initialized. Then, the position and velocity of each particle are randomly initialized.

3) The three-dimensional particle swarm composed of Neurons, dropout and batch_size is randomly generated.

4) In each iteration, the LSTM training set is used as the training set, and the PSO optimization set is used as the test set. Therefore, the LSTM prediction process is simulated and the solution (particle) with the smallest prediction error in iterations is selected.

5) When the end condition is reached, the historical optimal solution of the swarm is output. The optimal number of neurons, dropout probability and batch_size are input to the next LSTM prediction. Then MSE is used to evaluate the fitting effect of stress-strain curve of frozen silty clay.,Finally, the optimized prediction results are obtained.

FIGURE 3

FIGURE 3. PSO-LSTM process.

3.4 Optimization process analysis

According to the optimization parameters and constraints set above, the particle swarm optimization algorithm operation is performed. The fitness change curve is shown in Figure 4. It can be seen from Figure 4A that when the iteration exceeds 4 times, the fitness value quickly reaches the maximum. Therefore, the optimal solution is selected when the number of iterations (search steps) is 0–4, and the local optimal solution and the global optimal solution are output for each cycle. After 20 iterations, the global optimal solution can be obtained: [Number of neurons in the first layer, dropout, batch_size]=[61, 0.09, 95]. Therefore, PSO-LSTM structure optimization combination parameters are obtained and input.

FIGURE 4

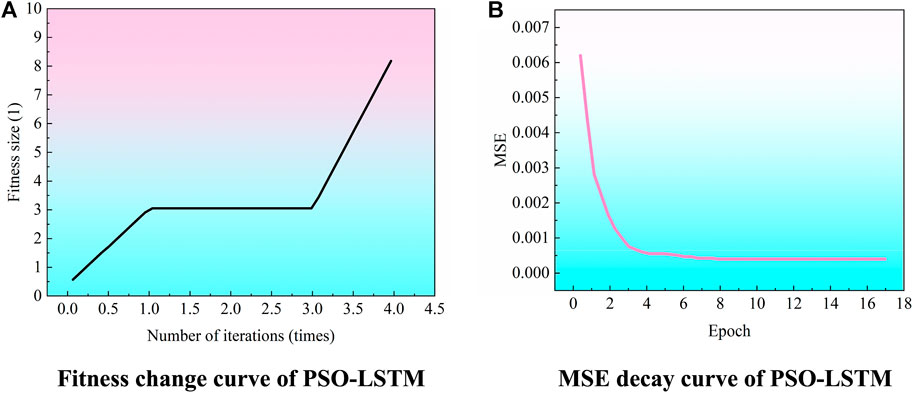
FIGURE 4. Optimization process curve (A) Fitness change curve of PSO-LSTM (B) MSE decay curve of PSO-LSTM.

It can be seen from the MSE attenuation curve of PSO-LSTM model in Figure 4B above that when the sample reaches 7.5 epochs, the MSE value tends to be stable. It shows that the validation set of the model has reached a good accuracy at this time. After determining the structural optimal parameters of PSO-LSTM, the weights and thresholds of each model are iteratively trained using the training set to obtain the final model. The test set is used to predict and compare each model (Chang et al., 2020; Huang et al., 2022).

4 Results

4.1 Test results analysis

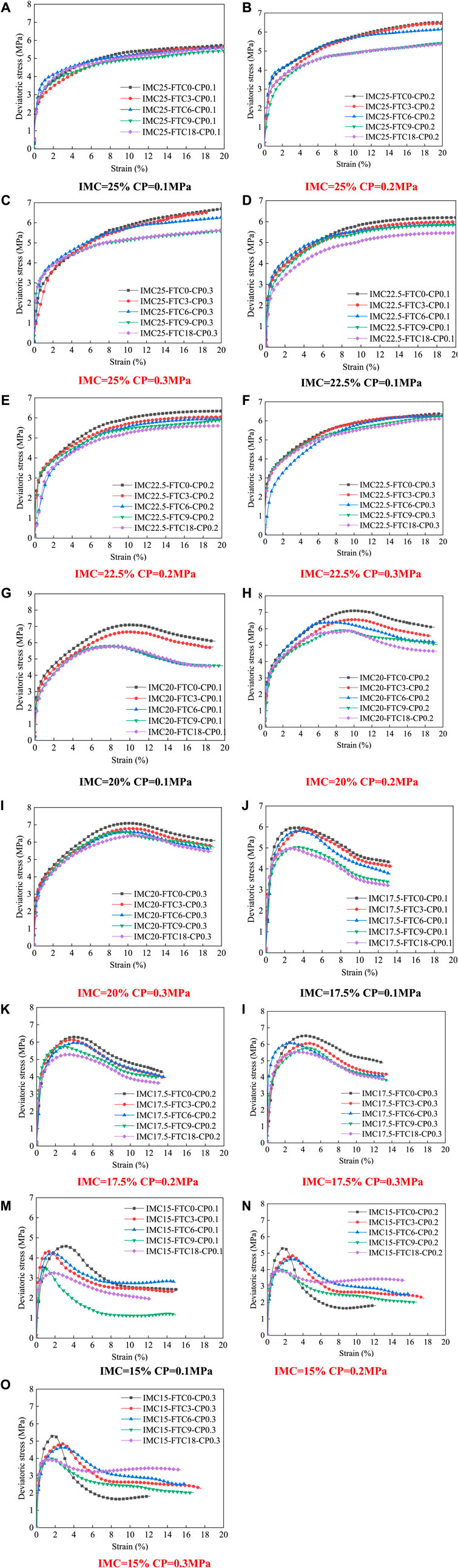
75 groups of triaxial tests are conducted on frozen silty clay with initial moisture content(IMC) of 25%, 22.5%, 20%, 17.5%, 15%, freeze-thaw cycles (FTC) of 0, 3, 6, 9, 18 times and confining pressure(CP) of 0.1Mpa, 0.2Mpa, 0.3Mpa. It can be seen from Figure 5 that freeze-thaw cycles and confining pressure do not change the strain characteristics of frozen silty clay. With the increase of initial moisture content, there is hysteresis phenomenon in the failure strain of frozen silty clay.

FIGURE 5

FIGURE 5. (Continued).

It can be seen from Figure 5 that when the initial moisture content is 22.5% and 25%, the deviatoric stress shows three development stages with the increase of the axial strain: linear elastic growth stage, elastic-plastic development stage, and strain hardening stage. In the linear elastic growth stage, the deviatoric stress is dominated by cementation elements composed of pore ice and soil particles. Due to the strain is small, the pore ice does not crush and melt, and the structure does not have cracks. At this time, the overall deformation modulus is large, and the deviatoric stress increases linearly.

In the elastic-plastic stage, due to the large strain at this time, micro-cracks are generated in the pore ice. Accompanied by the pressure-melting phenomenon at the ice crack, part of the cementation element structure is destroyed and transformed into friction elements. Since the deformation modulus of friction element is smaller than that of cementation element, the overall deformation modulus decreases. The deviatoric stress increases slowly with the increase of axial strain. During the strain hardening stage, the number of cementation elements remains stable, and the friction element, as the main bearing structure, show linear growth trend with the increase of strain.

It can be seen from Figure 5 that when the initial moisture content is 15%, 17.5%, and 20%, the frozen silty clay shows strain softening properties. The pore ice is broken and local shear bands are formed. The number of cementing elements decreases rapidly, the number of friction elements increases, and the integrity of the structural block is destroyed. The soil samples shows strain softening state. And with the decrease of initial water content, the strain softening phenomenon is more obvious. And under the same working condition, different confining pressures do not change the evolution law of deviatoric stress.

4.2 Binary medium constitutive model of frozen silty clay

The simplified frozen soil binary medium model based on damage parameters is shown in formula (8). The symbolic interpretation and derivation process of formula (8) are given (Zhang et al., 2022).

${\sigma }_1-{\sigma }_3=\left(1-\frac{E_i-E}{E_i-\alpha E_f}\right)E_i{\epsilon }_1+\frac{E_i-E}{E_i-\alpha E_f}\cdot \frac{{\epsilon }_1}{a+bc{\epsilon }_1}(8)$

Since the research object in this paper is frozen silty clay, the local strain coefficient c is obtained from the stress-strain curve. The comparison between the fitted value of the formula and the actual test value is shown in Figure 6.

FIGURE 6

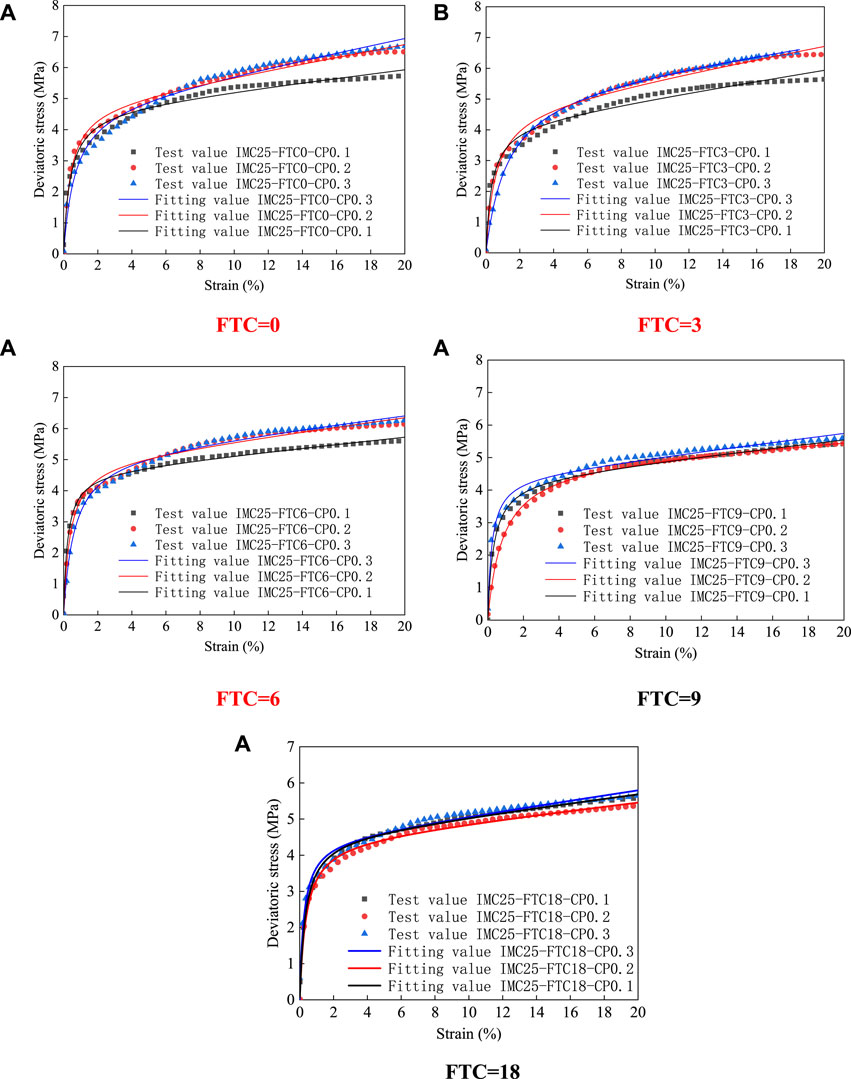
FIGURE 6. Comparison between the fitting values of the formula and the test results for different confining pressures: (A) FTC=9 (B) FTC=18. Note: Each working condition corresponds to other evaluation indexes (RMSE, MAE, MSE), which are given in the following comparative analysis of random forest model, frozen soil binary medium model, and PSO-LSTM model.

It can be seen from Figure 6 that the theoretical values of the constitutive model of frozen soil binary medium are very close to the measured values under different parameters. In addition, there is a high matching degree in the linear elastic stage, elastic-plastic stage and strain hardening stage of the stress strain curve. Therefore, it is further verified that the model can better simulate the curve relationship between stress and axial strain of silty clay in the low-temperature triaxial test. The process parameters of the binary medium model fitted by the frozen silty clay test are shown in Table 4.

TABLE 4

TABLE 4. Parameters of binary medium model of frozen silty clay.

4.3 Optimal model selection

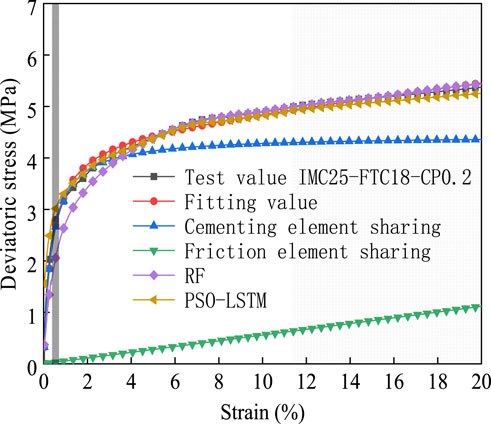
In order to compare the calculation accuracy of the model and select the optimal model, the frozen silty clay binary medium model, random forest model, PSO-LSTM model proposed in this paper and the frozen soil triaxial test are compared and analyzed. The stress sharing curve of the cementation element and the friction element is made by Formula (1), and the specific comparison is shown in Figure7. The deviatoric stress-strain curve under IMC25-FTC18-CP0.2 is shown in Figure 7. It can be seen from Figure 7 and formula (1) that the deviatoric stress curve of frozen silty clay is formed by superposition of the stress sharing curve of cementation element and the stress sharing curve of friction element.

FIGURE 7

FIGURE 7. Comparison of model calculated values and test results.

In the linear elastic stage, the evolution trend of deviatoric stress of frozen silty clay is more consistent with the sharing curve of cementation element. At this time, the deviatoric stress shared by the friction elements is less than 0.039 MPa. Therefore, the pore ice inside the cementation element is not crushed and melted in the linear elastic stage. The integrity of cementation element is good, and the cementation element mainly plays the role of bearing force under low temperature triaxial action.

In the elastic-plastic stage, the stress sharing curve of friction element shows a linear growth trend, and the stress sharing curve of cementation element begins to grow slowly. When the strain exceeds 2.7%, the difference between the stress sharing curve of cementation element and the total stress curve gradually increases. In the strain hardening stage, the stress sharing curve of cementation element tends to be stable. It shows that cementation element has yielded and stabilized at this time, and the stress sharing curve of the friction element still maintains linear growth trend. It shows that pore ice in the cemented element is crushed and melted under the action of low temperature triaxial. The local shear bands are formed, and the soil sample presents the failure form of oblique crack. In addition, it can be seen from Figure 7 that in the range of axial strain of 20%, the stress sharing curve of cementation element is always larger than stress sharing curve of the friction element. The peak value of the total stress is also the maximum value of the superposition of the stress sharing curve of the cementation element and the friction element.

It can be seen from Figure 7 that the calculated values of the frozen silty clay binary medium model and PSO-LSTM model are completely close to the test values. The constitutive relation of frozen silty clay can be better simulated by PSO-LSTM model. Because excellent matching degree can be achieved in linear elastic stage, elastic-plastic stage and strain hardening stage. The calculated values of the RF model and the test values show a high consistency in the strain hardening stage, but there is a large difference between the linear elastic stage and the elastic-plastic stage, which indicates that the model has a large error and still needs to be adjusted.

4.4 Model evaluation

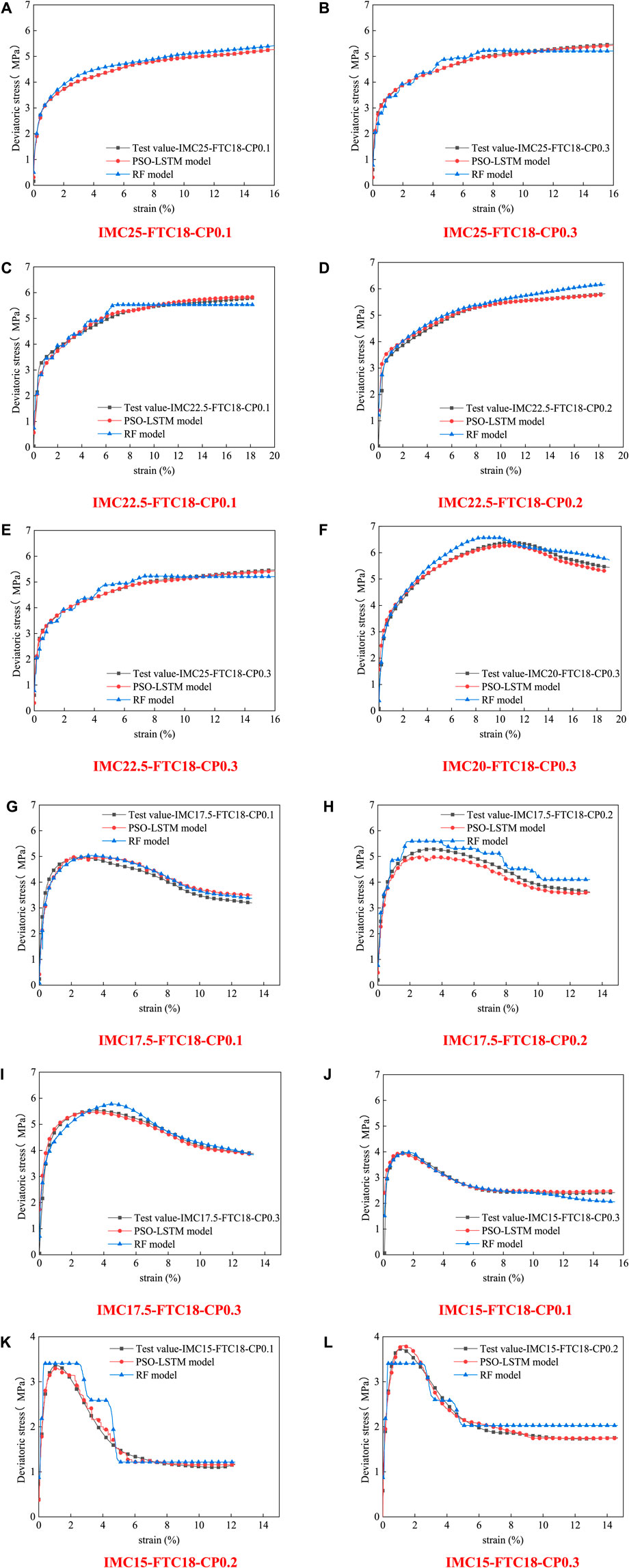
Based on the random forest model test set, the stress-strain relationship of frozen silty clay with different moisture content after the 18th freeze-thaw cycles is obtained In the constitutive relation curve obtained by selecting the random forest model, the working condition with lower R² is only shown in Figure 8. Therefore, the worst fitting condition of random forest model is selected as the test set of PSO-LSTM model. Finally, the universality and applicability of PSO-LSTM model can be well verified.

FIGURE 8

FIGURE 8. (Continued).

It can be seen from the results in Figure 8 that the strains corresponding to the maximum deviatoric stress errors of the RF model are 18.18%, 7.92%, 4.79%, and 15.04% under the initial moisture contents of 22.5, 20, 17.5, and 15%. The deviatoric stresses corresponding to the RF model are 6.16, 6.50, 5.76, and 2.07 MPa respectively, and the deviatoric stresses corresponding to the test are 5.80, 6.10, 5.45, and 2.41MPa respectively. The errors are 5.8%, 6.1%, 5.38%, and 16.4% respectively. Therefore, the trend of the random forest model curve is consistent with that of the test curve, but there is always a large deviation in the whole evolution process of the partial stress. The evaluation indexes of the initial training set and test set of the RF model are significantly different, and the training set is more excellent. It shows that RF model has over-fitting phenomenon in the training process, and the unsatisfactory test results are generated. Therefore, cross-validation is added to avoid overfitting. In the end, the maximum error of the model is still 16.4%.

The maximum error of PSO-LSTM model is only 1.56% under IMC20FTC18CP0.3 working condition. Compared with RF, the predicted value of the PSO-LSTM model constructed in this paper fits better with the actual measured value, and the relative error is smaller and more stable.

As can be seen from Figure 8, the evolution of deviatoric stress under each condition can be well simulated. The constitutive relationship predicted by the random forest model will have fluctuation segments, and it is prone to the problem of low strain sensitivity. The PSO-LSTM model can well simulate the evolution trend of deviatoric stress in each working condition.

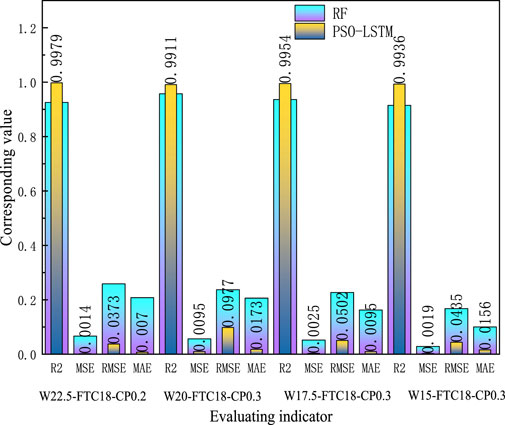
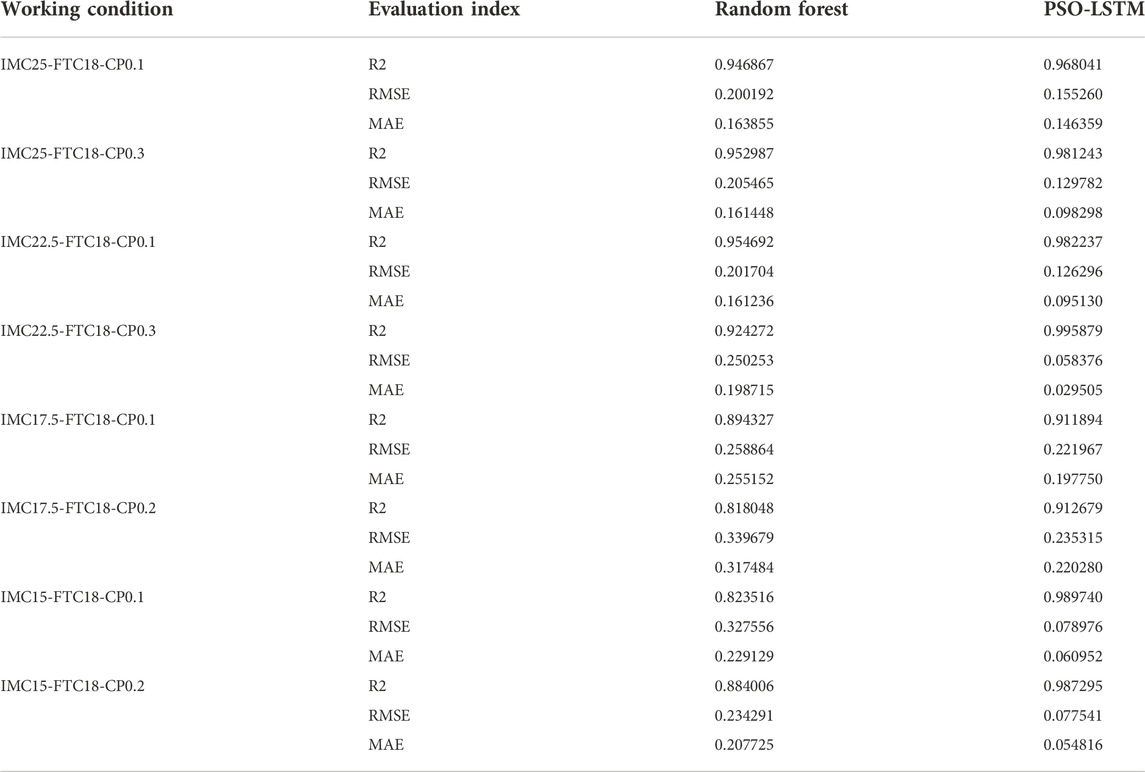
Analysis of the data in Table 5 shows that the R² of the deviatoric stress prediction data of the frozen silty clay obtained by the RF model, the binary medium model and the PSO-LSTM model are all above 94%. Therefore, in the process of iterative training, the internal test laws of initial moisture content, freeze-thaw degradation effect and confining pressure are well excavated, and more reasonable constitutive prediction values are output. However, compared with the RF model and frozen soil binary medium model, the R² obtained by the PSO-LSTM model reaches 98.44%. At the same time, MSE and MAE are the lowest, which are 0.0078 and 0.01778 respectively, indicating that the model prediction effect is the best. The evaluation index of the initial moisture content of 25 is only shown in Table 5. Therefore, the evaluation index of the model test set under other conditions is given in the following Figure 9.

TABLE 5

TABLE 5. Evaluation indicators of RF, theoretical calculation, PSO-LSTM model prediction and real data.

FIGURE 9

FIGURE 9. RF model and PSO-LSTM model evaluation index.

It can be seen from Table 6 that the accuracy of the optimal model under each working condition is above 90%. It can be seen from the comparison model that the accuracy of the PSO-LSTM model in each working condition is higher than that of the RF model. At the same time, RMSE and MAE errors are lower than RF model in all conditions, which is enough to show that the optimal model can well simulate the constitutive relation of frozen silty clay in all conditions.

TABLE 6

TABLE 6. Evaluation indicators of RF and PSO-LSTM model prediction and real data.

The evaluation indicators of the RF and PSO-LSTM models on the validation set and the test set are relatively consistent, so the evaluation indicators of the validation set are omitted here. At the same time, the RF model and the PSO-LSTM model have not been fitted. In addition, the R² of PSO-LSTM for frozen silty clay constitutive prediction in the test set are all greater than 0.99. At the same time, RMSE, MSE and MAE are the smallest under each water content working condition, and they are the best in all networks. The better fitting accuracy and prediction performance of this model have been fully proved, and it is very accurate for the constitutive prediction of frozen silty clay. It also provides a new method for the prediction of frozen silty clay constitutive model.

5 Discussion

5.1 Effect of freeze-thaw cycles, confining pressure and initial moisture content on strength of frozen silty clay

As shown in Figure 10, the strength tends to be stable after 6, 9, 6, 9, and 9 freeze-thaw cycles at initial moisture content of 25, 22.5, 20, 17.5, and 15%, respectively. After 18 freeze-thaw cycles, the shear strength of frozen silty clay decreased by 2.66%, 11.85%, 18.83%, 16.79, and 29.02%, respectively. Under the same confining pressure, the shear strength of frozen silty clay decreases first and then tends to be stable with the increase of freeze-thaw cycles. With the increase of freeze-thaw cycles, the bearing structure of frozen silty clay changes from initial coarse particles and pore ice to more deteriorated fine particles and pore ice. That is, the positions of the pore ice in frozen silty clay are occupied by more fine particles. On the one hand, the thickness of pore ice is reduced, and thin pore ice is more likely to expand cracks under low temperature triaxial stress. On the other hand, the unfrozen water film on the particle surface shows lubrication effect. And with the increase of freeze-thaw cycles, the rolling friction and sliding friction between particles increase more, which makes the shear strength decrease more obviously. Under a certain confining pressure, the rolling friction and sliding friction between particles tend to be stable after 6 and 9 freeze-thaw cycles. So the connection, arrangement and stress history of the soil particles are changed by the freeze-thaw cycles. This deterioration effect decreases with the increase of freeze-thaw cycles and tends to be stable after a certain number of freeze-thaw cycles (6 or 9 times).

FIGURE 10

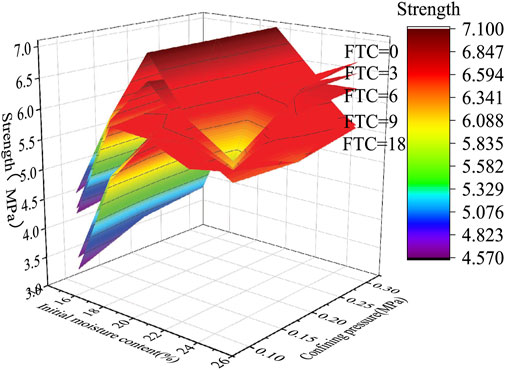
FIGURE 10. Three dimensional changes of confining pressure, initial moisture content and strength under different freeze-thaw conditions.

As shown in Figure 11, the deviatoric stress of frozen silty clay increases with the increase of confining pressure. This is very consistent with the actual project. And with the increase of the initial moisture content, the effect of confining pressure on the strength increase is no longer obvious. This is because in the third stage, the stress sharing curve of the friction element shows a linear growth trend. The stress sharing of the cemented element keeps the yield stable, and with the increase of the confining pressure, the strength of the cemented element for the yield stability is also greater. When the optimum moisture content is reached, the pore ice of cementation element tends to be saturated. At this time, with the increase of the initial moisture content, the expansion of the cracks generated by the thin pore ice is not obvious. Therefore, the influence of the confining pressure on the yield stability of the cemented element is gradually reduced.

FIGURE 11

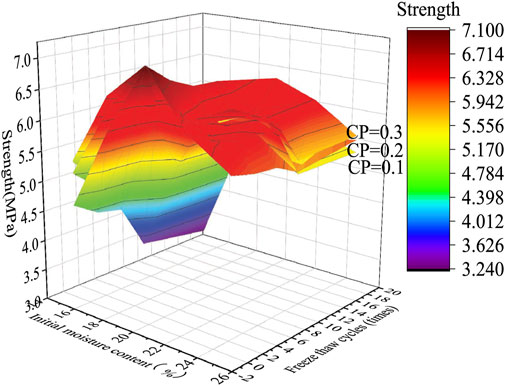
FIGURE 11. Three dimensional changes of freeze-thaw cycles, initial moisture content and strength under different confining pressures.

As shown in Figure 12, the strength of frozen silty clay is the highest near the initial moisture content of 20%. With the increase of freeze-thaw times and the decrease of confining pressure, the strength of frozen silty clay decreases. Therefore, the most unfavorable working condition is IMC15-FTC18-CP0.1, and the highest strength working condition is IMC20-FTC18-CP0.3.

FIGURE 12

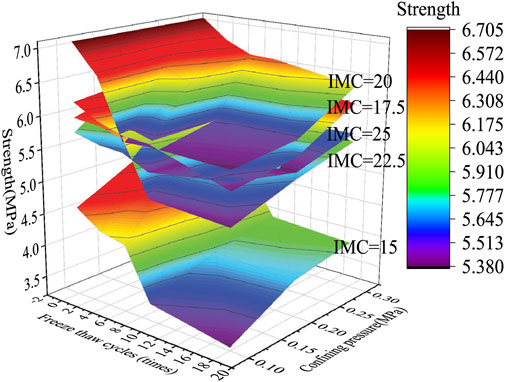
FIGURE 12. Three dimensional changes of freeze-thaw cycles, confining pressure and strength under different initial moisture content.

Compared with Figures 10, 11, it is obvious that the strength difference of frozen silty clay is the largest under different initial moisture content. That is, the initial moisture content has greater influence on the strength of frozen silty clay (Cao et al., 2022; Teng et al., 2022). This is because the effects of freezing and thawing and confining pressure on the connection and arrangement of soil particles and the stress history are not as significant as the initial moisture content. The bearing structures of soils with different initial moisture contents are quite different. As a result, the difference of pore ice thickness is large, and the difference of crack germination and expansion mode is increased. On the other hand, the difference of rolling friction and sliding friction between frozen silty clay particles under different initial moisture content is large, resulting in a large difference in shear strength.

5.2 Frozen soil structure model

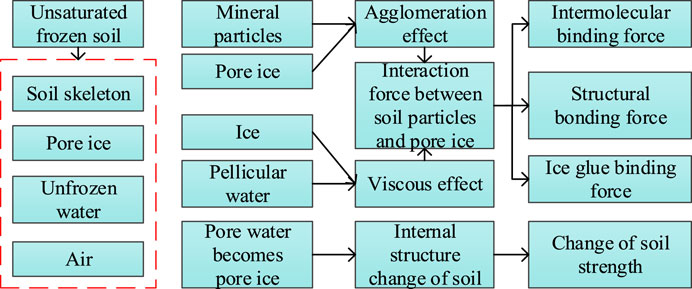
The structural composition of unsaturated frozen soil (Teng et al., 2022) which influences factors of soil particle and pore ice force and soil strength change process is shown in Figure 13 below.

FIGURE 13

FIGURE 13. Influencing factors of soil particle and pore ice force.

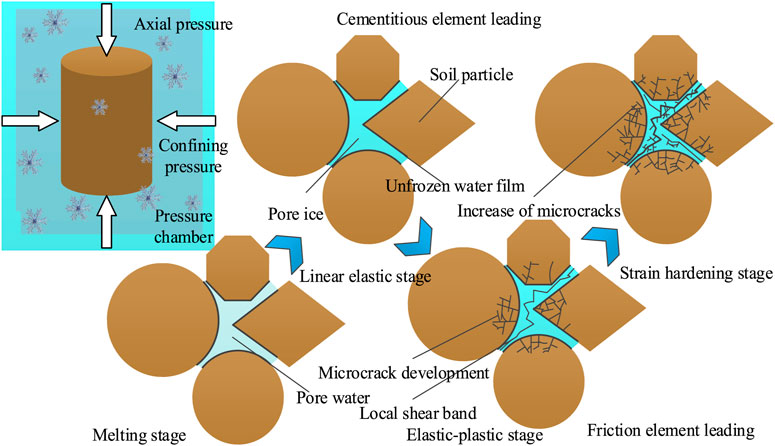
The structural model of frozen silty clay can be seen in Figure 14. According to the concept of the binary medium model (Zhang et al., 2022), cementation element is a stable ice-soil skeleton composed of clay particles and pore ice. The deformation modulus of cementation element is large, and it usually shows better integrity in case of small deformation. Under triaxial stress or low temperature, the pore ice inside the cemented element may be crushed and melted. Even soil particles can be broken. Local shear bands are gradually formed under deviatoric stress. At the same time, the cementation element transforms into the friction element.

FIGURE 14

FIGURE 14. Structural model of frozen silty clay.

There are a large number of cemented elements and friction elements in the frozen silty clay. And under the action of triaxial stress and low temperature, cementation element is gradually transformed into friction element. The strength characteristic difference of frozen soil is closely related to the quantity difference between cementation elements and friction elements.

The cementation element plays a major role in linear elastic stage, and the stress sharing curve of friction element can be ignored. In the elastic-plastic stage, the bearing capacity of the cementation element reaches the yield stability and continuously transforms into the friction element. During the strain hardening stage, the stress sharing curve of the cementation element remains stable, and the stress sharing curve of the friction element continues to increase linearly.

5.3 Contribution weight analysis of stress-strain curve of frozen silty clay

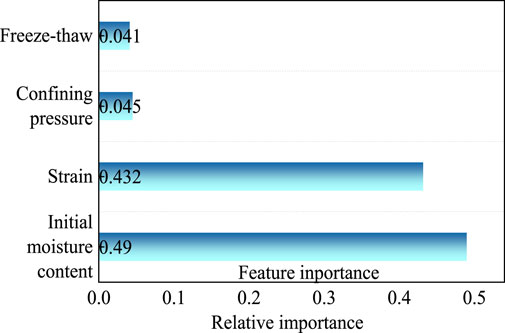
Compared with confining pressure and freeze-thaw cycles, the initial moisture content has the greatest influence on the evolution trend of deviatoric stress. Therefore, machine learning method is used to study the importance of features. It provides a new method for the study of the contribution weight of different factors to frozen silty clay constitutive curve. The contribution weight of deviatoric stress is shown in Figure 15.

FIGURE 15

FIGURE 15. Distribution of feature importance.

The contribution weight of the four factors to the deviatoric stress can be seen from the importance map of random forest characteristics. According to the above experimental study, the trend of the stress-strain relationship curve will be changed by the different initial moisture content. The state of frozen silty clay before the failure will be determined by the initial moisture content, and the position of peak strain will also be changed. With the increase of initial moisture content, the failure stage changes from strain softening to strain stabilization, and then to strain hardening. At the same time, the failure stress will also lag. This also verifies the strong connection between the moisture water content and the stress evolution law.

In a certain range (IMC = 25, 22.5, 20, 17.5, 15%, FTC = 0, 3, 6, 9, 18 times, CP = 0.1, 0.2, 0.3 MPa), the influence factors of frozen silty clay stress from strong to weak are: initial moisture content > strain > confining pressure > freeze-thaw cycles. The contribution of confining pressure to the stress evolution law is small, which is because the freezing depth of the seasonal frozen area is less than 2 m. Therefore, the gradient and range of the confining pressure setting in this paper are small, so the contribution weight is small.

5.4 Comparison and promotion of frozen silty clay binary constitutive model, RF model and PSO-LSTM model

Although the binary constitutive model of frozen silty clay has obtained a good prediction effect. And the reference formula is provided, which is beneficial to the application in practical engineering. However, there are some shortcomings in the model. For example, the binary constitutive model of frozen silty clay in this paper is only suitable for the fitting of the constitutive relationship under the condition of IMC=25%, but it can not achieve a good fitting effect for the IMC=22.5%, 20%, 17.5%, and 15%. Therefore, the formula fitting model still needs to find the constitutive formula of similar curve law. The formula fitting software 1STOPT can also be used to perform a random search of constitutive relations. But some parameters in the formula cannot be explained mathematically and physically. Therefore, in-depth research and promotion are limited.

Based on the shortcoming that the above model is applicable to a single working condition, the RF model is established in this paper. The RF model can be applied to all initial moisture content conditions, but the model prediction accuracy is not satisfactory.

The PSO-LSTM model is established in this paper to solve the problems of the above models. There are many advantages, such as high prediction accuracy, wide application range, and no need to propose based on certain assumptions. The LSTM optimal combination input parameters are searched by PSO, and the parameter adjustment speed of the model for the data learning process of other soil types is greatly increased, which is conducive to popularization. Therefore, it is only necessary to carry out frozen soil triaxial tests of different soil types in various regions. PSO-LSTM model has extremely high accuracy in constitutive prediction, which can provide reference for frozen soil engineering application in cold regions.

Moreover, the deep learning algorithm has a strong fitting ability for multiple operating conditions and multiple factors. The data driven deep learning method will have an excellent fitting effect for more dimensional sample data. For other soil types, the triaxial test data are imported, and the high-precision constitutive relation curve can be obtained by modifying the training set.

In the Code for Design of Soil and Foundation of Building in Frozen Soil Region, the characteristic value fa of foundation bearing capacity is selected based on temperature and soil type. Only four types of frozen soil with ground bearing capacity characteristic values at -3°C∼-0.5°C are given in the specification. However, it is not suitable for saline frozen soil and frozen peat soil, and a large number of experiments need to be carried out to revise the specification. Therefore, the optimal model proposed in this paper has important generalization significance.

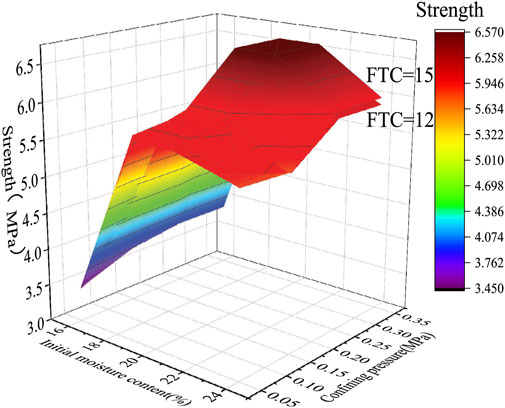
That is, a more comprehensive reference table of characteristic values of frozen soil bearing capacity is given by carrying out different working conditions tests on soils in various regions. The working conditions that have not been tested (IMC=16, 19, 21, 24%, FTC=12, 15 times, CP=0.05, 0.15, 0.25, 0.35Mpa) are predicted by the PSO-LSTM model to demonstrate the advantages of the model. As shown in Figure 16, the predicted strength law is consistent with the actual situation. It provides a new method for the constitutive study of frozen soil engineering in cold regions, and provides a favorable reference for the strength of remolded soil in seasonal frozen regions. Therefore, it is of great significance to carry out the model study in this paper.

FIGURE 16

FIGURE 16. Prediction of unknown working conditions by PSO-LSTM model.

Random forest and PSO-LSTM can provide a new method for frozen soil constitutive research. The constitutive model of frozen soil is developed based on mathematical skills, which can deeply learn the data of frozen soil triaxial test. Machine learning model has strong nonlinear mapping ability, and is not limited by frozen soil constitutive formula In the process of deep mining of multi-dimensional large sample data, there is usually a better fitting effect. Therefore, machine learning shows extremely high accuracy and wide applicability in frozen soil constitutive model prediction. It can be used to modify the characteristic value fa of foundation bearing capacity of the Code for Design of Soil and Foundation of Building in Frozen Soil Region.

6 Conclusion

The study of constitutive model is of great significance to the construction of frozen soil engineering. In this paper, 75 sets of experiments are carried out, and a comparative study of the constitutive models of frozen silty clay is carried out. The following conclusions are drawn:

1) Under the same confining pressure, the shear strength of frozen silty clay decreases first and then tends to be stable with the increase of freeze-thaw cycles. The strength tends to be stable after 6, 9, 6, 9, and 9 times freeze-thaw cycles at initial moisture content of 25, 22.5, 20, 17.5, and 15%, respectively. After 18 freeze-thaw cycles, the shear strength of frozen silty clay decreased by 2.66%, 11.85%, 18.83%, 16.79, and 29.02%, respectively.

2) Compared with RF model and frozen soil binary medium model, the R² obtained by the PSO-LSTM model reaches 98.44%. At the same time, MSE and MAE are the lowest, which are 0.0078 and 0.01778 respectively, indicating that the model prediction effect is the best. In the process of iterative training, the internal test laws of initial moisture content, freeze-thaw degradation effect and confining pressure are well excavated, and more reasonable constitutive prediction values are output.

3) In a certain range (IMC = 25, 22.5, 20, 17.5, 15%, FTC = 0, 3, 6, 9, 18 times, CP = 0.1, 0.2, 0.3 MPa), the influence factors of frozen silty clay stress from strong to weak are: initial moisture content > strain > confining pressure > freeze-thaw cycles. Tongming et al., 2021, Yuanming et al., 2010.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

Y-CT: Design, Experiment, Algorithm, Data Processing, Writing; Z-CT: writing, translation; J-LL: Experiment, Writing; Y-DZ: Experiment, Writing, X-YL: Writing, Z-WL: Experiment, C-YT: Experiment. All authors contributed to the article and approved the submitted version.

Acknowledgments

The authors gratefully acknowledge the financial support of this study by the National Natural Science Foundation of China (Grant No. 52076036).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cao, Y., Rong, C., Wang, Z., Shi, X., Wang, B., and Long, W. (2022). Experimental study on true triaxial mechanical properties of frozen calcareous clay under the influence of multiple factors. Crystals 12 (3), 328. doi:10.3390/cryst12030328

CrossRef Full Text | Google Scholar

Chang, D., Lai, Y., and Gao, J. (2019). An investigation on the constitutive response of frozen saline coarse sandy soil based on particle breakage and plastic shear mechanisms. Cold Regions Sci. Technol. 159, 94–105. doi:10.1016/j.coldregions.2018.12.011

CrossRef Full Text | Google Scholar

Chang, Z., Catani, F., Huang, F., Liu, G., Meena, S. R., Huang, J., et al. (2022). Landslide susceptibility prediction using slope unit-based machine learning models considering the heterogeneity of conditioning factors. J. Rock Mech. Geotechnical Eng. doi:10.1016/j.jrmge.2022.07.009

CrossRef Full Text | Google Scholar

Chang, Z., Du, Z., Zhang, F., Huang, F., Chen, J., Li, W., et al. (2020). Landslide susceptibility prediction based on remote sensing images and GIS: Comparisons of supervised and unsupervised machine learning models. Remote Sens. 12 (3), 502. doi:10.3390/rs12030502

CrossRef Full Text | Google Scholar

Guo, X. F., Xia, Z. Z., Wu, J. Y., and Wang, R. Z. (2010). Numerical analysis and similarity experiment on temperature field of underground pipe. Acta Energiae Solaris Sin. 31 (6), 727–731. Available at: https://CNKISUN:TYLX.0.2010-06-016.

Google Scholar

Huang, F., Cao, Z., Guo, J., Jiang, S. H., Li, S., and Guo, Z. (2020a). Comparisons of heuristic, general statistical and machine learning models for landslide susceptibility prediction and mapping. Catena 191, 104580. doi:10.1016/j.catena.2020.104580

CrossRef Full Text | Google Scholar

Huang, F., Cao, Z., Jiang, S. H., Zhou, C., Huang, J., and Guo, Z. (2020b). Landslide susceptibility prediction based on a semi-supervised multiple-layer perceptron model. Landslides 17 (12), 2919–2930. doi:10.1007/s10346-020-01473-9

CrossRef Full Text | Google Scholar

Huang, F., Tao, S., Li, D., Lian, Z., Catani, F., Huang, J., et al. (2022). Landslide susceptibility prediction considering neighborhood characteristics of landslide spatial datasets and hydrological slope units using remote sensing and GIS technologies. Remote Sens. 14 (18), 4436. doi:10.3390/rs14184436

CrossRef Full Text | Google Scholar

Huang, F., Zhang, J., Zhou, C., Wang, Y., Huang, J., and Zhu, L. (2020). A deep learning algorithm using a fully connected sparse autoencoder neural network for landslide susceptibility prediction. Landslides 17 (1), 217–229. doi:10.1007/s10346-019-01274-9

CrossRef Full Text | Google Scholar

Jiang, S. H., Huang, J., Huang, F., Yang, J., Yao, C., and Zhou, C. B. (2018). Modelling of spatial variability of soil undrained shear strength by conditional random fields for slope reliability analysis. Appl. Math. Model. 63, 374–389. doi:10.1016/j.apm.2018.06.030

CrossRef Full Text | Google Scholar

Jin, Y. F., Wu, Z. X., Yin, Z. Y., and Shen, J. S. (2017). Estimation of critical state-related formula in advanced constitutive modeling of granular material. Acta Geotech. 12 (6), 1329–1351. doi:10.1007/s11440-017-0586-5

CrossRef Full Text | Google Scholar

Jin, Y. F., Yin, Z. Y., Shen, S. L., and Hicher, P. Y. (2016). Investigation into MOGA for identifying parameters of a critical-state-based sand model and parameters correlation by factor analysis. Acta Geotech. 11 (5), 1131–1145. doi:10.1007/s11440-015-0425-5

CrossRef Full Text | Google Scholar

Jin, Y. F., Yin, Z. Y., Shen, S. L., and Hicher, P. Y. (2016). Selection of sand models and identification of parameters using an enhanced genetic algorithm. Int. J. Numer. Anal. Methods Geomech. 40 (8), 1219–1240. doi:10.1002/nag.2487

CrossRef Full Text | Google Scholar

Johari, A., Javadi, A. A., and Habibagahi, G. (2011). Modelling the mechanical behaviour of unsaturated soils using a genetic algorithm-based neural network. Comput. Geotechnics 38 (1), 2–13. doi:10.1016/j.compgeo.2010.08.011

CrossRef Full Text | Google Scholar

Kohestani, V. R., and Hassanlourad, M. (2016). Modeling the mechanical behavior of carbonate sands using artificial neural networks and support vector machines. Int. J. Geomech. 16 (1), 04015038. doi:10.1061/(asce)gm.1943-5622.0000509

CrossRef Full Text | Google Scholar

Lai, Y., Liao, M., and Hu, K. (2016). A constitutive model of frozen saline sandy soil based on energy dissipation theory. Int. J. Plasticity 78, 84–113. doi:10.1016/j.ijplas.2015.10.008

CrossRef Full Text | Google Scholar

Lai, Y., Xu, X., Yu, W., and Qi, J. (2014). An experimental investigation of the mechanical behavior and a hyperplastic constitutive model of frozen loess. Int. J. Eng. Sci. 84, 29–53. doi:10.1016/j.ijengsci.2014.06.011

CrossRef Full Text | Google Scholar

Li, T., Chen, Y. Z., Han, L. J., Cheng, L. H., Lv, Y. H., Fu, B. J., et al. (2021). Shortened duration and reduced area of frozen soil in the Northern Hemisphere. Innovation 2 (3), 100146. doi:10.1016/j.xinn.2021.100146

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, X., Wang, Y., Hu, Y., Zhou, C., and Zhang, H. (2022). Numerical investigation on stratum and surface deformation in underground phosphorite mining under different mining methods. Front. Earth Sci. (Lausanne). 10. doi:10.3389/feart.2022.831856

CrossRef Full Text | Google Scholar

Lin, P., Ratnam, R., Sankari, H., and Garg, A. (2019). Mechanism of microstructural variation under cyclic shearing of shantou marine clay: Experimental investigation and model development. Geotech. Geol. Eng. (Dordr). 37 (5), 4163–4210. doi:10.1007/s10706-019-00900-6

CrossRef Full Text | Google Scholar

Loria, A. R., Frigo, B., and Chiaia, B. (2017). A non-linear constitutive model for describing the mechanical behaviour of frozen ground and permafrost. Cold regions Sci. Technol. 133, 63–69. doi:10.1016/j.coldregions.2016.10.010

CrossRef Full Text | Google Scholar

Mašín, D. (2005). A hypoplastic constitutive model for clays. Int. J. Numer. Anal. Methods Geomech. 29 (4), 311–336. doi:10.1002/nag.416

CrossRef Full Text | Google Scholar

Nassr, A., Esmaeili-Falak, M., Katebi, H., and Javadi, A. (2018). A new approach to modeling the behavior of frozen soils. Eng. Geol. 246, 82–90. doi:10.1016/j.enggeo.2018.09.018

CrossRef Full Text | Google Scholar

Niu, Y., Wang, X., Liao, M., and Chang, D. (2022). Strength criterion for frozen silty clay considering the effect of initial water content. Cold Regions Sci. Technol. 196, 103521. doi:10.1016/j.coldregions.2022.103521

CrossRef Full Text | Google Scholar

Peng, X. H., Wang, Z. C., Luo, T., Yu, M., and Luo, Y. S. (2008). An elasto-plastic constitutive model of moderate sandy clay based on BC-RBFNN. J. Cent. South Univ. Technol. 15 (1), 47–50. doi:10.1007/s11771-008-0312-4

CrossRef Full Text | Google Scholar

Qu, T., Di, S., Feng, Y. T., Wang, M., and Zhao, T. (2021). Towards data-driven constitutive modelling for granular materials via micromechanics-informed deep learning. Int. J. Plasticity 144, 103046. doi:10.1016/j.ijplas.2021.103046

CrossRef Full Text | Google Scholar

Rashidian, V., and Hassanlourad, M. (2014). Application of an artificial neural network for modeling the mechanical behavior of carbonate soils. Int. J. Geomech. 14 (1), 142–150. doi:10.1061/(asce)gm.1943-5622.0000299

CrossRef Full Text | Google Scholar

Romo, M. P., García, S. R., Mendoza, M. J., and Taboada-Urtuzuástegui, V. (2001). Recurrent and constructive-algorithm networks for sand behavior modeling. Int. J. Geomech. 1 (4), 371–387. doi:10.1061/(asce)1532-3641(2001)1:4(371)

CrossRef Full Text | Google Scholar

Shahin, M. A., and Indraratna, B. (2006). Modeling the mechanical behavior of railway ballast using artificial neural networks. Can. Geotech. J. 43 (11), 1144–1152. doi:10.1139/t06-077

CrossRef Full Text | Google Scholar

Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. (2014). Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 15 (1), 1929–1958.

Google Scholar

Stefanos, D., and Gyan, P. (2015). On neural network constitutive models for geomaterials. J. Civ. Eng. Res. 5 (5), 106–113. doi:10.5923/j.jce.20150505.02

CrossRef Full Text | Google Scholar

Sun, K., Tang, L., Zhou, A., and Ling, X. (2020). An elastoplastic damage constitutive model for frozen soil based on the super/subloading yield surfaces. Comput. Geotechnics 128, 103842. doi:10.1016/j.compgeo.2020.103842

CrossRef Full Text | Google Scholar

Teng, Y. C., Teng, Z. C., Liu, Y., Liu, X. Y., Zhou, Y. D., Liu, J. L., et al. (2022). A review of the research on thermo-hydro-mechanical coupling for the frozen soil. Geofluids 2022, 1–11. doi:10.1155/2022/8274137

CrossRef Full Text | Google Scholar

Teng, Z. C., Teng, Y. C., Li, B., Liu, X. Y., Liu, Y., and Zhou, Y. D. (2022). Pipeline stress test simulation under freeze-thaw cycling via the XGBoost-based prediction model. Front. Earth Sci. (Lausanne). 319. doi:10.3389/feart.2022.839549

CrossRef Full Text | Google Scholar

Tongming, Q., Yuntian, F., Mengqi, W., Tingting, Z., and Shaocheng, D. (2021). Constitutive relations of granular materials by integrating micromechanical knowledge with deep learning. J. Mech. 53 (7), 1–12. doi:10.6052/0459-1879-21-221

CrossRef Full Text | Google Scholar

Wang, D., Liu, E., Zhang, D., Yue, P., Wang, P., Kang, J., et al. (2021). An elasto-plastic constitutive model for frozen soil subjected to cyclic loading. Cold Regions Sci. Technol. 189, 103341. doi:10.1016/j.coldregions.2021.103341

CrossRef Full Text | Google Scholar

Wang, P., Liu, E., Zhang, D., Liu, X., Zhang, G., and Song, B. (2020). An elastoplastic binary medium constitutive model for saturated frozen soils. Cold Regions Sci. Technol. 174, 103055. doi:10.1016/j.coldregions.2020.103055

CrossRef Full Text | Google Scholar

Wang, P., Liu, E., and Zhi, B. (2021). An elastic-plastic model for frozen soil from micro to macro scale. Appl. Math. Model. 91, 125–148. doi:10.1016/j.apm.2020.09.039

CrossRef Full Text | Google Scholar

Wu, W., Bauer, E., and Kolymbas, D. (1996). Hypoplastic constitutive model with critical state for granular materials. Mech. Mater. 23 (1), 45–69. doi:10.1016/0167-6636(96)00006-3

CrossRef Full Text | Google Scholar

Xiong, H., Nicot, F., and Yin, Z. Y. (2017). A three-dimensional micromechanically based model. Int. J. Numer. Anal. Methods Geomech. 41 (17), 1669–1686. doi:10.1002/nag.2692

CrossRef Full Text | Google Scholar

Xu, X., Wang, B., Fan, C., and Zhang, W. (2020). Strength and deformation characteristics of silty clay under frozen and unfrozen states. Cold Regions Sci. Technol. 172, 102982. doi:10.1016/j.coldregions.2019.102982

CrossRef Full Text | Google Scholar

Yang, Y., Gao, F., and Lai, Y. (2013). Modified Hoek–Brown criterion for nonlinear strength of frozen soil. Cold Regions Sci. Technol. 86, 98–103. doi:10.1016/j.coldregions.2012.10.010

CrossRef Full Text | Google Scholar

Yang, Y., Lai, Y., Dong, Y., and Li, S. (2010). The strength criterion and elastoplastic constitutive model of frozen soil under high confining pressures. Cold Regions Sci. Technol. 60 (2), 154–160. doi:10.1016/j.coldregions.2009.09.001

CrossRef Full Text | Google Scholar

Yao, Y. P., Sun, D. A., and Luo, T. (2004). A critical state model for sands dependent on stress and density. Int. J. Numer. Anal. Methods Geomech. 28 (4), 323–337. doi:10.1002/nag.340

CrossRef Full Text | Google Scholar

Yin, Z. Y., Chang, C. S., and Hicher, P. Y. (2010a). Micromechanical modelling for effect of inherent anisotropy on cyclic behaviour of sand. Int. J. Solids Struct. 47 (14-15), 1933–1951. doi:10.1016/j.ijsolstr.2010.03.028

CrossRef Full Text | Google Scholar

Yin, Z. Y., Chang, C. S., Karstunen, M., and Hicher, P. Y. (2010b). An anisotropic elastic-viscoplastic model for soft clays. Int. J. Solids Struct. 47 (5), 665–677. doi:10.1016/j.ijsolstr.2009.11.004

CrossRef Full Text | Google Scholar

Yin, Z. Y., and Jin, Y. F. (2019). Practice of optimisation theory in geotechnical engineering. Singapore: Springer, 199–241. doi:10.1007/978-981-13-3408-5

CrossRef Full Text | Google Scholar

Yin, Z. Y., Karstunen, M., Chang, C. S., Koskinen, M., and Lojander, M. (2011). Modeling time-dependent behavior of soft sensitive clay. J. Geotech. Geoenviron. Eng. 137 (11), 1103–1113. doi:10.1061/(asce)gt.1943-5606.0000527

CrossRef Full Text | Google Scholar

Yin, Z. Y., Zhao, J., and Hicher, P. Y. (2014). A micromechanics-based model for sand-silt mixtures. Int. J. solids Struct. 51 (6), 1350–1363. doi:10.1016/j.ijsolstr.2013.12.027

CrossRef Full Text | Google Scholar

Yu, F., Guo, P., and Na, S. (2022). A framework for constructing elasto-plastic constitutive models for frozen and unfrozen soils. Int. J. Numer. Anal. Methods Geomech. 46 (2), 436–466. doi:10.1002/nag.3306

CrossRef Full Text | Google Scholar

Yuanming, L., Yugui, Y., Xiaoxiao, C., and Shuangyang, L. (2010). Strength criterion and elastoplastic constitutive model of frozen silt in generalized plastic mechanics. Int. J. Plasticity 26 (10), 1461–1484. doi:10.1016/j.ijplas.2010.01.007

CrossRef Full Text | Google Scholar

Zhang, D., and Liu, E. (2019). Binary-medium-based constitutive model of frozen soils subjected to triaxial loading. Results Phys. 12, 1999–2008. doi:10.1016/j.rinp.2019.02.029

CrossRef Full Text | Google Scholar

Zhang, D., Liu, E., and Huang, J. (2020c). Elastoplastic constitutive model for frozen sands based on framework of homogenization theory. Acta Geotech. 15 (7), 1831–1845. doi:10.1007/s11440-019-00897-5

CrossRef Full Text | Google Scholar

Zhang, D., Liu, E., and Yu, D. (2020a). A micromechanics-based elastoplastic constitutive model for frozen sands based on homogenization theory. Int. J. Damage Mech. 29 (5), 689–714. doi:10.1177/1056789519891519

CrossRef Full Text | Google Scholar

Zhang, N., Shen, S. L., Zhou, A., and Xu, Y. S. (2019). Investigation on performance of neural networks using quadratic relative error cost function. IEEE Access 7, 106642–106652. doi:10.1109/ACCESS.2019.2930520

CrossRef Full Text | Google Scholar

Zhang, P., Yin, Z. Y., and Jin, Y. F. (2021). State-of-the-art review of machine learning applications in constitutive modeling of soils. Arch. Comput. Methods Eng. 28 (5), 3661–3686. doi:10.1007/s11831-020-09524-z

CrossRef Full Text | Google Scholar

Zhang, P., Yin, Z. Y., Jin, Y. F., and Ye, G. L. (2020b). An AI-based model for describing cyclic characteristics of granular materials. Int. J. Numer. Anal. Methods Geomech. 44 (9), 1315–1335. doi:10.1002/nag.3063

CrossRef Full Text | Google Scholar

Zhang, Q., Wang, Q., Fang, J., Zhao, X., Li, J., and Li, S. (2022b). Study of the characteristics mechanical damage and constitutive model of crushed-rocks from high-grade highway in permafrost region. Geofluids 2022, 1–17. doi:10.1155/2022/7439860

CrossRef Full Text | Google Scholar

Zhang, S., Jiang, G., Cai, J., Ye, X., Luo, B., and Yuan, S. (2022c). A binary medium model for frozen silty sand simplified by breakage parameter. Geofluids 2022, 1–14. doi:10.1155/2022/6988812

CrossRef Full Text | Google Scholar

Zhang, T., Barry, R. G., Knowles, K., Ling, F., and Armstrong, R. L. (2003 July). Distribution of seasonally and perennially frozen ground in the Northern Hemisphere. In Proceedings of the Proceedings of the 8th International Conference on Permafrost (Vol. 2, pp. 1289-1294). Zürich, Switzerland: Boulder, Unites States: AA Balkema Publishers.

Google Scholar

Zhang, Y., Tang, J., Cheng, Y., Huang, L., Guo, F., Yin, X., et al. (2022d). Prediction of landslide displacement with dynamic features using intelligent approaches. Int. J. Min. Sci. Technol. 32, 539–549. doi:10.1016/j.ijmst.2022.02.004

CrossRef Full Text | Google Scholar

Zhao, H., Huang, Z., and Zou, Z. (2014). Simulating the stress-strain relationship of geomaterials by support vector machine. Math. Problems Eng. 2014, 1–7. doi:10.1155/2014/482672

CrossRef Full Text | Google Scholar

Zhu, J. H., Zaman, M. M., and Anderson, S. A. (1998). Modeling of soil behavior with a recurrent neural network. Can. Geotech. J. 35 (5), 858–872. doi:10.1139/t98-042

CrossRef Full Text | Google Scholar