
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci. , 20 January 2023
Sec. Geohazards and Georisks
Volume 10 - 2022 | https://doi.org/10.3389/feart.2022.1029420
This article is part of the Research Topic A Multi-Disciplinary Study of Dynamic Triggering: Field Observations, Numerical Simulations, and Laboratory Experiments View all 6 articles
Due to the long-term overdraft of groundwater in Fuyang, silty clay in this area has been in an unsaturated state for a long time, which caused ground subsidence and threatened the safety of engineering construction. Creep is an important part of ground subsidence, but it is easily ignored in ground subsidence caused by groundwater overdraft. Therefore, in order to explore the creep behavior in this environment, a series of triaxial creep tests of unsaturated soil were conducted to research the effects of deviator stress, matrix suction and net confining pressure on creep. Then, based on analysis results of the geometric characteristics of the test creep curves, an improved fractional order Nishihara model of unsaturated soil under triaxial stress conditions was constructed by using fractional calculus theory. Finally, the effectiveness of improved fractional order Nishihara model was verified based on cooperation search algorithm and minimum mean square error principle. The simulation results show that the fitting curves of improved fractional order Nishihara model are in good agreement with the test curves, and it is feasible and effective to describe the creep characteristics of unsaturated silty clay in Fuyang.
Fuyang is located at the southern end of the Huang-Huai-Hai Plain in China as shown in Figure 1, and its territory is widely covered with silty clay. Since the 1980s, water for domestic use in Fuyang has gradually dependent on middle and deep groundwater due to the contamination of surface water flowing through the city (Bai, 2018). According to the investigation report (Chen, 2021), the groundwater mining amount of Fuyang in 1981, 1999 and 2019 was 24.41 million m3, 46.58 million m3 and 74.19 million m3, respectively, which overdraft 2–3 times the extractable amount in the same period, and the groundwater has been seriously overdraft in some years. Excessive groundwater mining has caused the groundwater level in Fuyang to drop continuously and formed a ground-water cone of depression (Yixiang and Guanhua, 2004), resulting in the silty clay in Fuyang being unsaturated for a long time. Besides, the decrease of groundwater level will also lead to the decrease of pore water pressure and the increase of effective stress, resulting in the soil consolidation and ground subsidence. Ground subsidence is a progressive geological hazard. Its damages, directly or indirectly, will increase with the development of the subsidence. As groundwater mining is concentrated in the urban area, the damages caused by ground subsidence are more severe. However, volume loss by the creep of “soft sediments” (clay, silt, peat) is also a well-known and crucial factor of the ground subsidence (Kooi and Erkens, 2020), but it is confusion that this important factor is usually ignored in ground subsidence caused by groundwater overdraft. What’s more, the existed case (Wen et al., 2019) shows that special properties of soil or rock mass will affect engineering situation furtherly. Therefore, to optimize engineering designs and prevent geologic hazard, it is necessary to conduct intensive studies on the creep characteristics of unsaturated silty clay in this region.
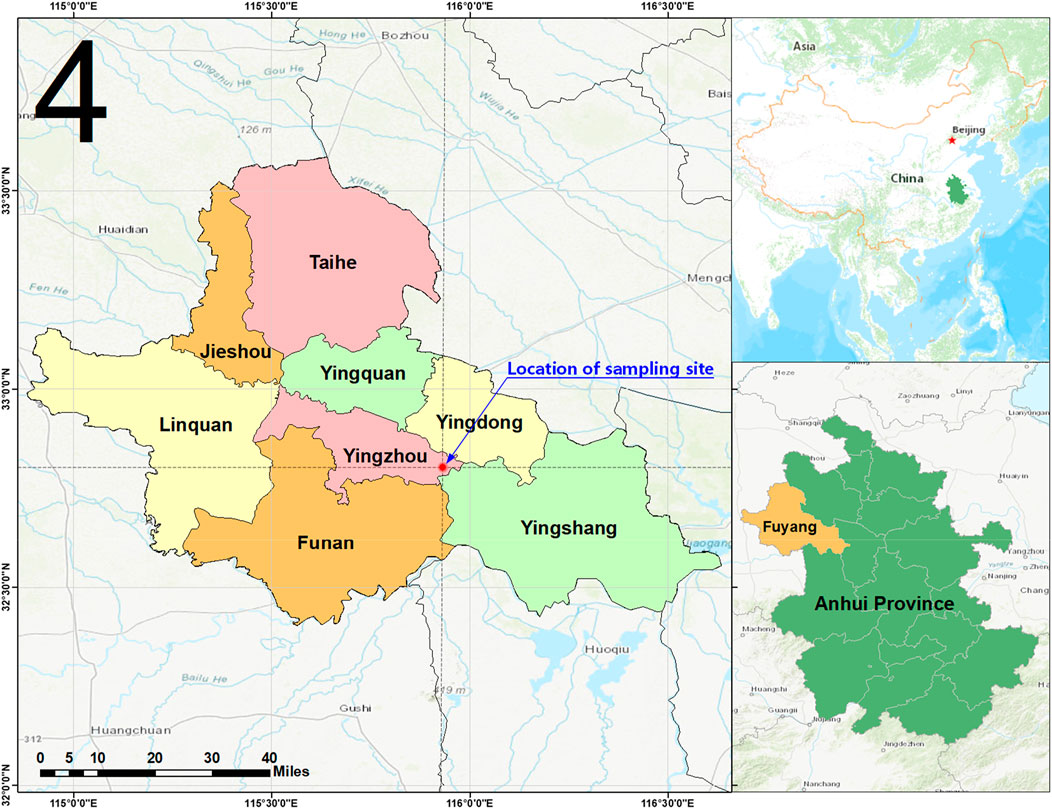
FIGURE 1. Location map of Fuyang (Xiaoguozhuang, Yuanji Town, Yingzhou District, Fuyang City, Anhui Province).
At present, there are several methods used to describe the creep properties of soils, among which the component model is widely used with the advantages of visualization, fewer parameters, and clear physical meaning, etc. For example, Ma et al. (2014) introduced the Burgers creep model to fit the properties of soil with deep-sea sediment; Cao et al. (2016) used non-linear damage creep constitutive model to research the creep properties of research objects in Jinchuan No.2 Mine in the northwest of China, the model consists of several classic basic elements, which is similar to Burgers models; Chang et al. (2020) studied the creep properties of loess in Malan by using the modified Burgers model; Yao et al. (2021) studied the characteristics of frozen silt in Nantong metro freezing construction process by optimized Burgers model; Besides Burges model series, Xu and Cui (2020) proposed a fractional component model to describe the creep behavior of Shanghai marine clay; Yang et al. (2015) analyzed the creep properties of Wangjiang silty clay by using the generalized Kevin model; Deng et al. (2020) proposed a modified Merchant model based on the fractional derivative theory to describe the creep properties of coastal soft clay. All the component models proposed in the above studies can fit the creep tests curves well and have made useful progress, but the above creep tests and models were established to focus on saturated soils and cannot describe the accelerating creep stage of soils. To describe accelerating creep of soil, Song (Song et al., 2021) proposed an improved Nishihara model to simulate the accelerating creep of frozen mixed soils, Liu (Liu et al., 2022) proposed a new model based on kinetic energy theorem to simulate the accelerating creep of tunnel surrounding rock, Wu (Wu et al., 2022) proposed a novel creep model based on fractional calculus and acoustic emission theory to describe accelerating creep of salt rock. Since the silty clay in China has regional differences, it is necessary to carry out targeted unsaturated creep tests and model studies on silty clay in Fuyang.
In this paper, we take the remodeled silt clay in Fuyang as the research object, firstly, we carried out the triaxial creep test of unsaturated soil to obtain the creep curves and isochronous stress-strain curves under different stress conditions. Then, by analyzing the curve variation characteristics, the creep law of Fuyang silty clay was summarized. Besides, an improved fractional order Nishihara model (IFNM) was proposed based on the geometric features of test curves, and the creep constitutive equations of IFNM for unsaturated soil under triaxial stress state was derived by considering the influence of matrix suction. Finally, based on the minimum mean square error (MSE) principle, we used cooperation search algorithm (CSA) to identify the parameters of IFNM and fit the test curves, and compared the fitting results with Burgers model to verify the feasibility and effectiveness of IFNM.
The test apparatus is FSR-20 duplex unsaturated triaxial creep test apparatus, which is illustrated in Figure 2. The test soil is the foundation soil at 12–14 m undergrounds of a project site in southern Fuyang, which is grayish yellow. The basic physical properties can be obtained through a series of laboratory tests as showed in Table 1. According to the Code for the Design of Building Foundations (China, 2012) (GB 50007-2011), test soil can be classified as silt clay in plastic state.
The duplex unsaturated soil triaxial creep apparatus can only test two groups of samples simultaneously, and because of the large number of test groups, long creep test duration, and the lack of customized in-situ soil extractor, the collected in-situ soil samples are disturbed and difficult to store for a long time. Therefore, after considering the above factors, this paper finally adopts the reshaped soil samples with water content w=20% and wet density ρ=1.9g/cm3 to conduct the consolidation and drainage triaxial creep test.
Due to the existence of pore air pressure, the stress state of unsaturated soil is much more complex than that of saturated soil. To describe the stress state of unsaturated soil more reasonably, Fredlund D.G (Fredlund and Rahardjo, 1993) suggested using net normal stress (σ-ua) and matrix suction (s=ua-uw) as the stress state variables of unsaturated soil. Therefore, in order to explore the influence of net normal stress and matric suction on the creep properties of unsaturated silty clay in Fuyang, we have developed a step loading test scheme as shown in Table 2.
The measured creep curve of the step loading creep test is shown in Figure 3.
At present, the method of converting step loading creep curves into creep curve clusters is mainly based on the Boltzmann superposition principle, but the traditional Boltzmann superposition principle (Shukla and Joshi, 2017) requires that the next step of loading can be applied only after the former step of loading enters the steady state creep, otherwise large redundant deformation would be calculated by this method. In order to overcome the defects of the above method, this paper applies the “correction technique based on Boltzmann superposition principle” proposed by Wang (Wang, 2008) to transform the step loading creep curves in Figure 3 into a creep curve cluster as shown in Figure 4.
From Figure 4, the effect of deviator stress on creep properties of unsaturated silty clay in Fuyang can be obtained as follows:
• A certain amount of transient deformation will occur at the moment of loading, and the deformation will gradually increase with time and eventually stabilize. When the deviator stress is too large, the sample will gradually yield and enter the accelerating creep stage. From the creep curve of sample 3 at deviator stress q=300 kPa, it can be seen that the creep curve in the accelerating creep stage will increase rapidly with time, and the strain rate will increase with time, and it can also be seen from Figure 5 that sample 3 appeared bulging deformation phenomenon.
• When the samples did not yield, the geometric features of the creep curves at different matrix suction or different net confining pressure were similar, and they all showed a non-linear characteristic of strain rate decreasing gradually with time.
In order to investigate the effects of net confining pressure and matrix suction on creep properties of unsaturated silt clay in Fuyang, the axial strain variation curves when matrix suction or net confining pressure is the only stress state variable are illustrated in Figure 6.
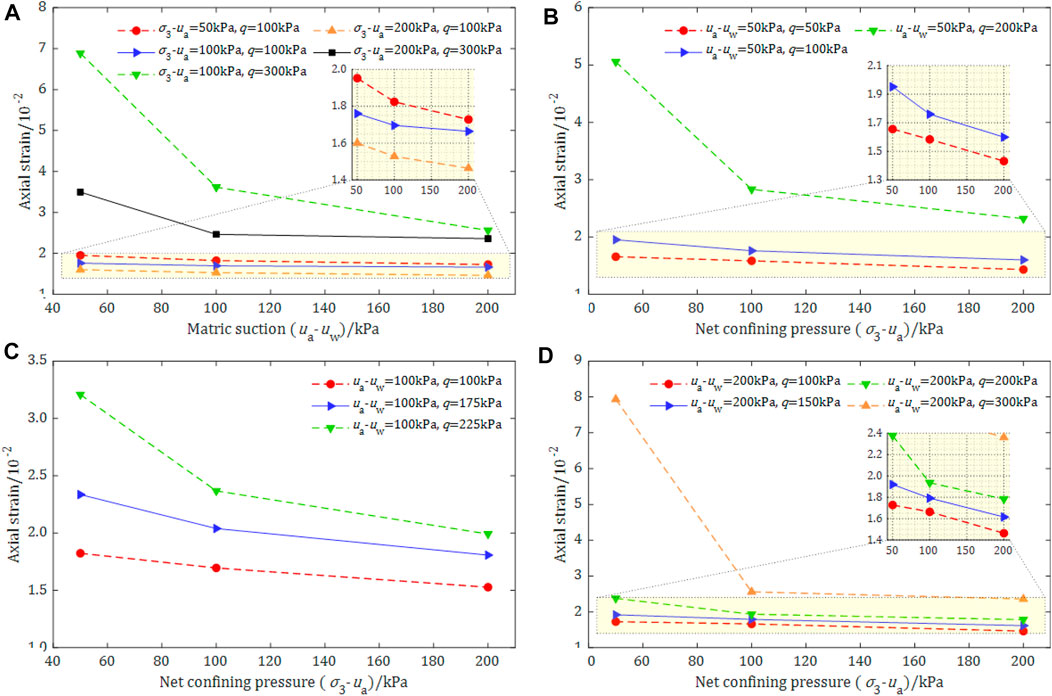
FIGURE 6. Final creep value comparison under different stress conditions. (A) The effect of matric suction on axial strain; (B–D) The effect of net confining pressure on axial strain.
From Figure 6A, it can be seen that the axial strain decreases with the increase of matrix suction when the net confining pressure and deviator stress are certain. Meanwhile, the curves all show the trend of gradually decreasing with the increase of matrix suction, and the curves gradually tend to be horizontal, which shows that the matrix suction has a certain hardening effect on the soil, but this hardening effect gradually tends to be stable with the increase of matrix suction. As seen in Figures 6B–D, when the deviator stress and matrix suction are constant, the curve gradually decreases with the increase of net confining pressure, which indicates that the axial strain and the net confining pressure are negatively correlated, and the lower the net confining pressure is, the larger axial strain when creep is stable.
To further research the creep characteristics of the soil, seven-time nodes of 5min, 30min, 60min, 120min, 360min, 1440min and 2880min were selected in this paper, and the isochronous stress-strain curves (ISSCs) of the above-mentioned different time nodes are shown in Figure 7 through the isochronous sampling process of the creep test data.
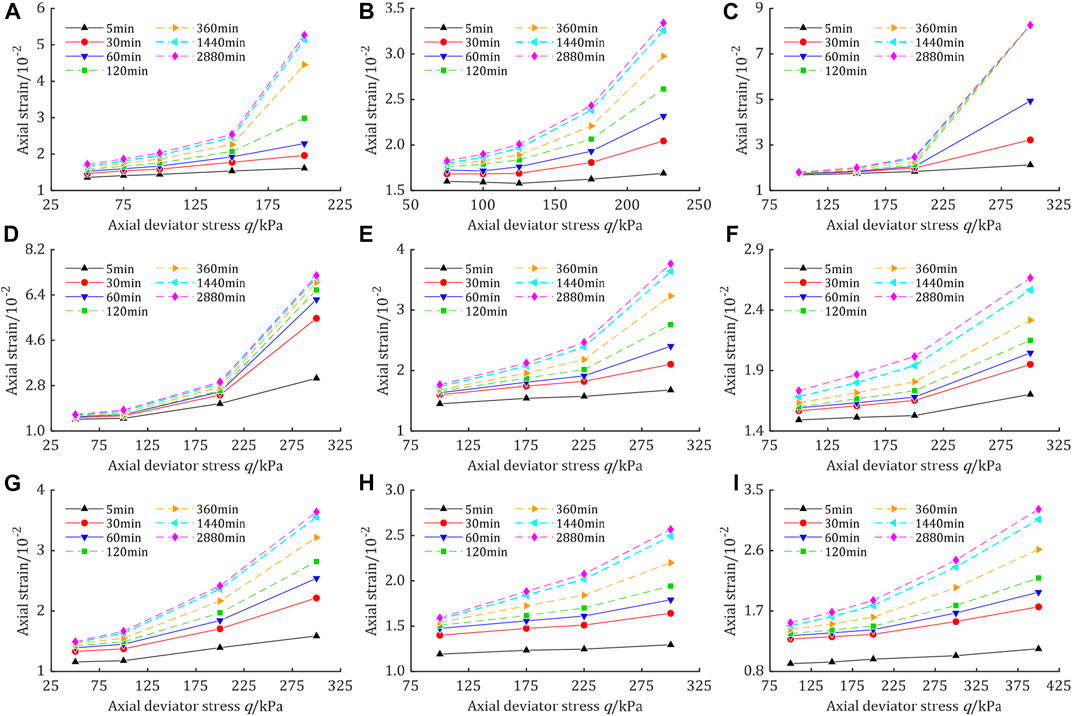
FIGURE 7. Isochronous stress-strain curves. (A) σ3-ua=50kPa, s=50kPa; (B) σ3-ua=50kPa, s=100kPa; (C) σ3-ua=50kPa, s=200kPa; (D) σ3-ua=100kPa, s=50kPa; (E) σ3-ua=100kPa, s=100kPa; (F) σ3-ua=100kPa, s=200kPa; (G) σ3-ua=200kPa, s=50kPa; (H) σ3-ua=200kPa, s=100kPa; (I) σ3-ua=200kPa, s=200 kPa.
From the ISSCs in Figure 7, it can be obtained that:
1) The ISSCs under different stress states have good similarity, so the simulated stress-strain-time relationships under different stress states can be expressed using the same component model.
2) All the ISSCs have a tendency to gradually approach to the strain axis with time, which indicates that the creep effect causes the soil to gradually soften and the stress required for further deformation gradually decreases compared with that before.
3) The ISSCs show an obvious downward convex shape. When the deviator stress is low, the ISSCs is approximately a straight line, which indicates that the soil creep shows approximately linear characteristics when the deviator stress is low. When the deviator stress is high, all ISSCs show obvious inflection points, and the slope of the ISSCs before and after the inflection point has obvious changes, which shows obvious non-linear characteristics.
4) As seen in Figure 7, except for Figures 7C,D, the ISSCs at 5 min and other time node under the remaining seven stress conditions show different degrees of separation, which may be due to the fact that the instantaneous rate of loading in the creep test is much larger than the creep rate, resulting in the mechanical properties of the soil showing much larger instantaneous strength and modulus of elasticity than the long-term strength and modulus of elasticity. Therefore, the deformation at the early stage of loading is small, but under the constant deviator stress, the mechanical properties of the soil gradually return to the long-term strength and modulus of elasticity with time, and its deformation increases rapidly, so the stress-strain curves at the early stage of loading and after a period of loading are separated.
In order to investigate the effect of matrix suction on creep, the ISSCs under different matrix suction conditions at 100 min and 2,500 min, are given in Figure 8. The curves show that when the matrix suction is constant, the axial strain increases with the increase of the deviator stress, and the stress-strain relationship is non-linear; when the deviator stress is constant, the axial strain increases with the decrease of the matrix suction, and this phenomenon is more obvious when the deviator stress is larger.
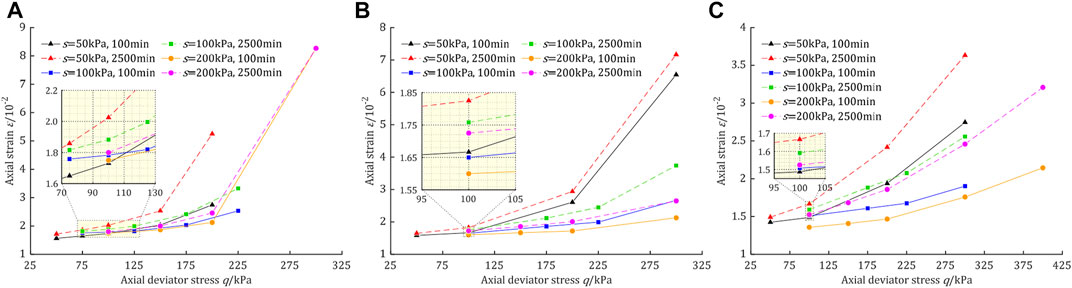
FIGURE 8. The isochronous stress-strain curves under different matric suctions. (A) σ3-ua=50kPa; (B) σ3-ua=100kPa; (C) σ3-ua=200 kPa.
Comprehensive analysis of the creep test curves obtained above shows that creep can be divided into three stages, as shown in Figure 9. Most of the common component models such as Maxwell model and Kevin model can only describe stage I and II, while the integral order Nishihara model (Yu et al., 2020) as shown in Figure 10 can describe the creep properties of the accelerating creep (stage III) due to the introduction of Newtonian dashpot as frictional element. When the creep enters stage II and III, the test curve is nearly linear, but in fact, it still has slight non-linear characteristics, and this slight non-linearity is difficult to be described in the traditional integer order Nishihara model.
Unlike the integer order Nishihara model, IFNM introduces non-linear Hooke body (Lin et al., 2022) and Abel dashpot (Guo et al., 2014) instead of traditional Hooke body and Newtonian dashpot, respectively, where the constitutive equations of the Abel dashpot element are:
where ξ denotes the viscosity coefficient and β denotes the fractional order. As seen in Eq. 1, when β = 1, the element is a conventional dashpot element, representing the Newtonian fluid; when β = 0, the element is a conventional Hooke body, representing the ideal elastomer. When the axial stress is a constant value (i.e., σ(t) = σ0) in the above equation, the element state is expressed as the creep state of corresponding material. For both sides of Eq. 1 simultaneously fractional order integration, according to the R-L fractional order calculus method described in previous section, the expression of strain ε(t) under constant stress σ(t) = σ0 can be denoted as:
If we assume σ0 =200 kPa and ξ=200 kPa min, respectively, by controlling the magnitude of the element order β, a series of strain curves based on Eq. 2 can be obtained as shown in Figure 10A.
As can be seen from Figure 11A, the Abel dashpot under constant stress, the strain can increase slowly with time like the material in between ideal fluid and ideal solid, neither increasing linearly like the Newtonian fluid nor remaining constant like the linear elastomer, indicating that the fractional order Abel dashpot can reflect the non-linear process for creep; The creep behavior of the material between the elastomer and the Newtonian body can be well described only by changing the order β. Therefore, it can be considered that the Abel dashpot is a joint element combining the elastic and damping elements. Compared with the classical integer order damping element, the Abel dashpot can control both the deformation rate and strain, while the traditional integer order Newtonian dashpot element can only control the deformation rate through the viscosity coefficient.
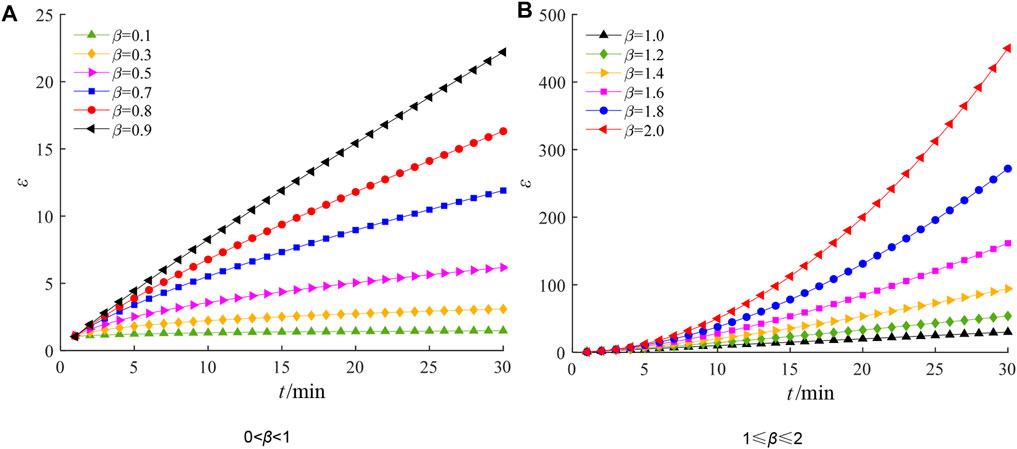
FIGURE 11. Creep curves of fractional Abel dashpot with different orders: (A) when order 0<β<1, (B) when order 1≤β≤2.
Although the Abel dashpot can better describe the non-linear properties of creep, it can only well describe the non-linear properties of the transient creep to steady state creep (i.e., stage I-II) in Figure 9, while the “convexity upward” characteristic of the accelerating creep (stage III) is not reflected at all in Figure 11A. Therefore, the Abel dashpot based on Eq. 2 cannot describe the accelerating creep stage.
By observing the change of the curve with the fractional order β in Figure 11A, we can see that the creep curve of the Abel dashpot is gradually approaching from the time axis to the strain axis when β increase from 0 to 1, but the slope of the curve is gradually decreasing with time, while the slope of the curve in the accelerating creep stage is gradually increasing with time. Here we still assume σ0 =200 kPa and ξ=200 kPa min, respectively, by controlling the order β, the creep curve variation law of β from 1 to 2 can be obtained as shown in Figure 11B.
As seen in Figure 11B, when fractional order β >1, the creep curve of the Abel dashpot will be like the accelerating creep stage (stage III) curve in Figure 9, with rapid “up”, “lower convex” and gradually increasing slope characteristics. The above geometrical characteristics of the Abel dashpot creep curve at β >1 provide a feasible way to describe the accelerating creep stage. Therefore, this paper adopts the Abel dashpot with order β >1 as the sliding frictional element to describe the plastic properties of the soil, and the strain expression under constant stress σ0 can be obtained according to Eq. 2 as follows:
where σs is the flow limit; η and γ (1 ≤ γ ≤ 2) a re the coefficient of viscosity and fractional order of the frictional element, respectively.
Considering that hardening or softening effects occur during soil loading, a non-linear Hooke body constructed based on Harris distribution function (Xie et al., 2020) is introduced in IFNM instead of the conventional Hooke body. Unlike the conventional Hooker body, the long-term elastic modulus of the non-linear Hooker body based on the Harris distribution function increases or decays with time, and the long-term elastic modulus
where E0 is the initial elastic modulus; a and b are the construction parameters of Harris function, when ab ≤ 0, EL is an increasing function about time t, which can describe the soil hardening phenomenon; when ab > 0, EL is a decreasing function about time t, which can describe the soil softening phenomenon.
1) When σ0 ≤σs
Under this condition, IFNM is a three-element fractional order creep model, which consists of two components connected in series, one part is the Harris non-linear Hooke body (E0) and the other part is a parallel structure (E1|N1) composed of the conventional Hooke body (E1) and the Abel dashpot (N1). According to the law of connection of components, it obtains that:
where, ε1(t) and ε2(t) are the strains of E0 and E1|N1, respectively; σ1(t) and σ2(t) are the stresses of E0 and E1|N1, respectively.
Introducing the R-L fractional order calculus operator (Ortigueira, 2011), we can get,
Among the above two equations, ε1(t) in Eq. 6 is easy to solve, while Eq. 7 is a binomial fractional order differential equation, and it is difficult to solve. Laplace transformation of the output signal of Eq. 7 can be shown as follows:
An essential inverse Laplace transformation (Ortigueira, 2011) is introduced here for all equations similar to Eq. 8:
Based on (8) and 9,
In summary, the ε(t) can be written as:
2) When σ0 >σs.
Under this condition, the IFNM is fractional order Burgers model, which consists of three parts: the non-linear Harris Hooke body (E0), the parallel structure (E1|N1), and the fractional order frictional element (N2). According to the law of connection of components, we can get,
where, σ1(t), ε1(t) are the stress and strain of the E0; σ2(t), ε2(t) are the stress and strain of the (E1|N1); σ3(t), ε3(t) are the stress and strain of the N2. The ε(t) can be written as follows:
In engineering practice, the soil is in complex three-dimensional stress state, and the creep tests of unsaturated soil described in this paper is also conducted in the triaxial stress state, so it is necessary to deduce the three-dimensional constitutive equation of IFNM. According to the theory of elasticity mechanics (Zou et al., 2013), the stress state of one point can be expressed in terms of the stress tensor. In the three-dimensional stress state, the stress tensor σij and the strain tensor εij of the soil can be denoted as follows:
where σm, εm and δij are spherical stress, spherical strain and Kronecker symbol respectively. σkk is the principal stress, and can also be simply denoted as σk. Sij is the deviator stress tensor. In the elastic state, the above variables satisfy:
Thus, the constitutive equation of IFNM in three-dimensional stress state is obtained as follows:
1) When Sij ≤ σs.
Further, by substituting Eqs 21, 22 into Eq. 18, we can get the strain-time relationship as follows:
Since the test soil is unsaturated soil, so the influence of pore air pressure ua should be considered in the above equation. Fredlund D.G. (Fredlund et al., 2012). believed that the net confining pressure (σ3-ua) and matric suction (ua -uw) should be used as the stress state variables in unsaturated soil, so we can replace the confining pressure σk with the net confining pressure, the creep constitutive equation of unsaturated soil considering pore air pressure can be obtained as follows:
2) When Sij > σs
After substituting Eq. 25 into Eq. 18, we get,
To verify the effectiveness of the IFNM proposed in this paper, a total of 12 creep test curves of sample 1, sample 3 and sample 7 are selected as three case studies for parameter identification and curve fitting. Parameter identification is an important link in the modeling and control of fractional order systems, which will directly determine whether the fractional order system can be involved in practical applications. At present, the parameter identification of fractional order system is mainly by applying swam intelligence optimization algorithm (Yang et al., 2017; Peng et al., 2019; Li et al., 2020; You et al., 2021). Due to the existence of Mittag–Leffler function and other hypergeometric functions with infinite series summation, the parameter identification of fractional order system has the characteristics of strong non-linearity and complex calculation, which also causes the difficulty of parameter identification. Therefore, it is necessary to select a swam intelligent algorithm with high accuracy, good stability and strong serviceability. In this paper, we selects seven current mainstream swarm intelligence optimization algorithms as shown in Table 3: Harris Hawks Optimization (HHO) (Heidari et al., 2019), Whale Optimization Algorithm (WOA) (Mirjalili and Lewis, 2016), Sparrow Search Algorithm (SSA) (Xue and Shen, 2020), Cooperation Search Algorithm (CSA) (Feng et al., 2021), Improved Grey Wolf Optimization (IGWO) (Nadimi-Shahraki et al., 2021), Coot Optimization Algorithm (COOT) (Naruei and Keynia, 2021) and Fruit fly Optimization Algorithm based on Cloud Model (CMFOA) (Wu et al., 2015), to identify the parameters of IFNM, and compares their performances in solving the parameter identification problem of fractional order system.
The parameter identification problem is essentially a non-linear fitting optimization problem. In this paper, the fitness function is defined as the minimum mean square error (MSE) of the sample strain test data and the model calculation data, which is transformed into the optimization problem with constraints. The principal expression is: If there are m observations and n parameters to be identified, the optimization problem is:
where P is the parameters set, LBj and UBj represent the search lower limit and upper boundary of the jth parameter.
It can be seen from Eqs 24, 26 that the IFNM has seven parameters when Sij ≤ σs, and nine parameters when Sij > σs. The search upper and lower boundaries of the above parameters are determined according to the trial calculation and experience, as shown in Table 4.
In order to show the feasibility and effectiveness of the IFNM more clearly, this section introduces the Nishihara model and Burgers model as a comparison, their construction are shown in Figure 12.
According to the derivation process of the constitutive equation of the Nishihara model (Yan et al., 2010) and Burgers model in (Zheng et al., 2019) and (Chen et al., 2003), the corresponding three-dimensional axial strain-time expression is as follows:
• Nishihara model three-dimensional axial strain-time expression:
• Burgers model three-dimensional axial strain-time expression:
where σ0 is deviator stress, σ0 = σ1-σ3; σm is the average stress, σm= (σ1+2σ3)/3. It can be seen from Eq. 29 that there are five parameters to be identified in the Nishihara model and Burgers model, which are G0, G1, ξ1, ξ2 and K. The upper and lower boundaries of their parameters search are shown in Table 5 and Table 6.
Considering the stringency of comparison, complex calculation and time-consuming of parameter identification in fractional order system, the maximum iteration times T and the population size pop of all algorithms were set to the same for parameter identification of IFNM and Burgers model, namely T=200 and pop=100. The unique computational parameters (α, β and M) of CSA are set as 0.1, 0.15 and 3. The order of normal cloud model α=10 in CMFOA. In the SSA, the number of the producers (PD) and the sparrows who perceive the danger (SD) accounts for 20% and 10%, respectively, and the security threshold ST=0.6. In summary, the flow chart of parameter identification for IFNM based on the swarm intelligence optimization algorithm is shown in Figure 13, and based on this process, the MSE convergence curves of seven different swarm intelligence algorithms in three case studies were obtained as shown in Figure 14.
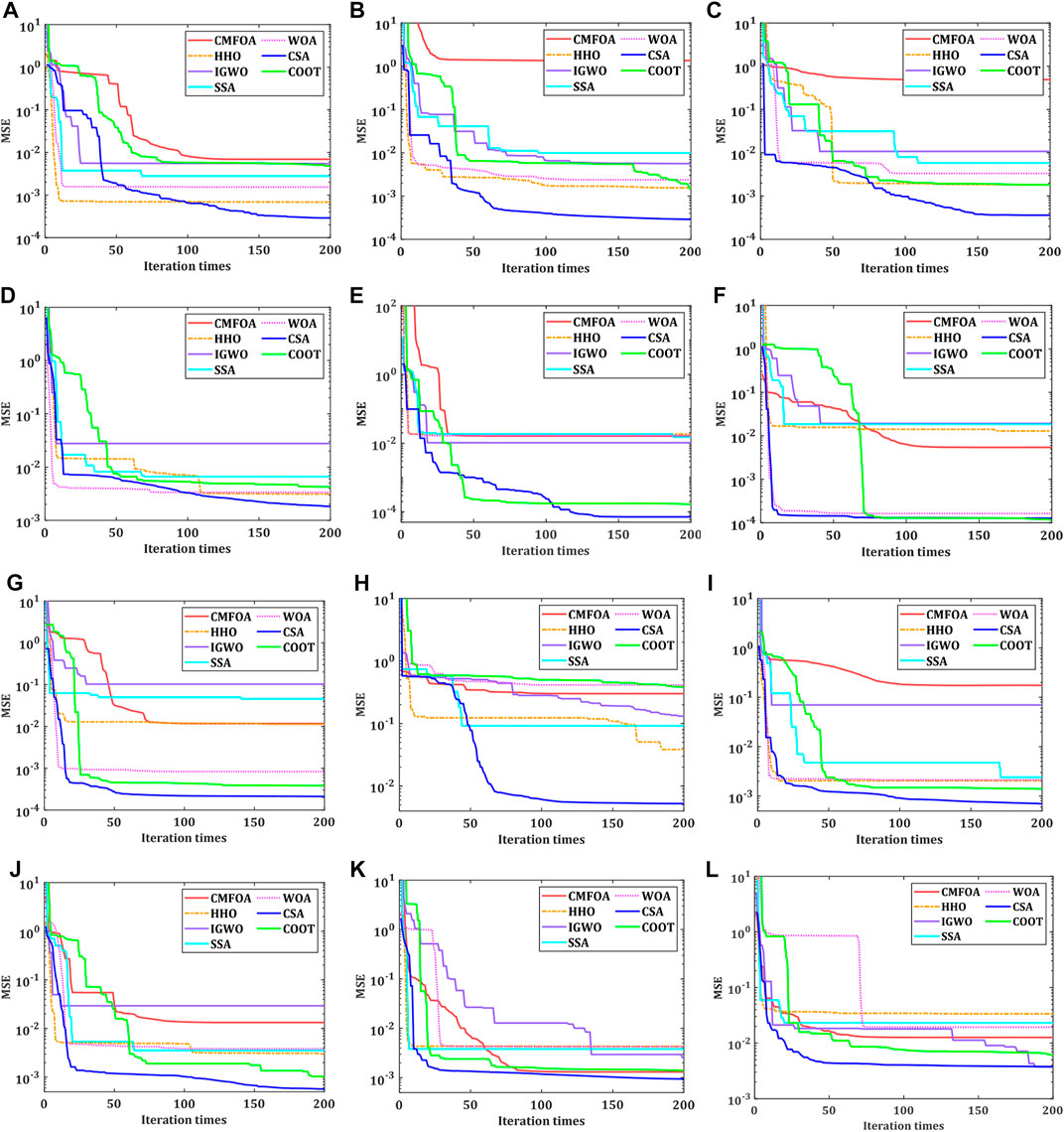
FIGURE 14. Comparison plots of MSE convergence curves under different algorithms: (A) Sample1, q=50kPa; (B) Sample1, q=75kPa; (C) Sample1, q=100kPa; (D) Sample1, q=150kPa; (E) Sample3, q=100kPa; (F) Sample3, q=150kPa; (G) Sample3, q=200kPa; (H) Sample3, q=300kPa; (I) Sample7, q=50kPa (J) Sample7, q=100kPa (K) Sample7, q=200kPa (L) Sample7, q=300 kPa.
It can be seen from Figures 14A–D that the parameter identification of sample 1, the MSE calculated by CSA under four different stress conditions is better than the other six algorithms. As seen from Figures 14E–H that the parameter identification of sample 3, when q = 150 kPa, MSE=1.2705×10–4 calculated by CSA is slightly worse than that calculated by COOT (MSE=1.1193×10–4), and under the other stress conditions, the MSE obtained by CSA is better than that of the other six algorithms. For sample 7, from Figures 14I–L we can see that when q = 300kPa, MSE = 3.7472×10–3 calculated by CSA is slightly better than MSE = 3.7632×10–3 calculated by IGWO, and under the other stress condition, MSE obtained by CSA is significantly better than the other six algorithms. Therefore, CSA has better convergence accuracy than the other six algorithms in solving the fractional order parameter identification problem, which can get satisfactory results in the face of different stress conditions, and shows excellent optimization performance, anti-interference and wide applicability, so this paper decided to use CSA to identify the parameters of IFNM and Burgers model.
In this section, the test creep curves of sample 1, sample 3 and sample 7, as shown in Figure 4, are used as three case studies to test the effectiveness of IFNM. Sample 1 and 7 are mainly used to verify the fitting performance of the IFNM on the two non-linear stages of transient creep and steady state creep, and sample 3 was used to verify the fitting performance of the accelerating creep stage. Finally, based on CSA, the parameter identification results of three case studies under IFNM, Nishihara model and Burgers model are shown in Table 7, Table 8 and Table 9, respectively. The comparison results of fitting curve and test curve are shown in Figure 15.
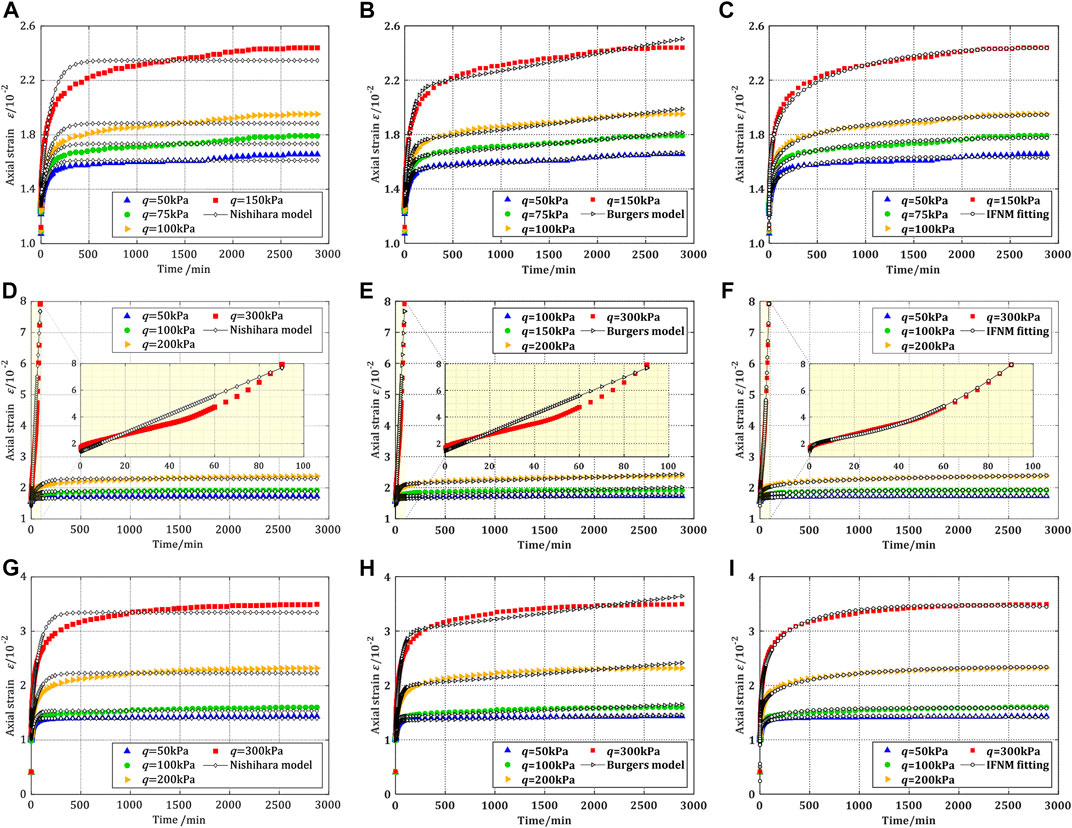
FIGURE 15. Comparison of fitting curves and test curves of IFNM, Nishihara model and Burgers models under different cases: (A–C) Sample 1 (D–F) Sample 3 (G–I) Sample 7.
It can be seen from Table 7, Table 8 and Table 9 that the fitting accuracy of IFNM on the samples is better than Nishihara model and Burgers model. The fitting accuracy of IFNM on sample 1 is basically closed to the Burgers model, but IFNM on sample 3 and sample 7 is 1–2 orders of magnitude better than that of the Burgers model, indicating that IFNM has better fitting performance for the whole creep process of unsaturated soil. Compared with the IFNM and the Burgers model, the MSE performance of the Nishihara model is the worst, and under some stress conditions of sample 1, sample 3 and sample 7, the MSE performance of the Burgers model is about one order of magnitude better than the Nishihara model, while the IFNM is about one or two orders of magnitude better than that of the Nishihara model.
It can be seen from Figures 15A–C that the Nishihara model, Burgers model and IFNM all can well describe the approximate linear characteristics of the transient creep stage on sample 1, but the fitting performance of the IFNM is significantly better than Nishihara model and Burgers model in the time domain from the end of the transient creep to the steady creep (100 min–500 min). In this time domain, Burgers model curve and the test curve appear ‘intersect’ and ‘separation’ phenomena, and this phenomenon is more obvious when the deviator stress is larger, such as when q=150 kPa, it is obvious that the Burgers model curve and the test curve are separated. When the creep enters the steady state creep (500 min–2880 min), the Burgers model curve is a slope almost unchanged oblique line, which also leads to the better fitting effect of the Burgers model for the case of small deviator stress, while the fitting performance for the case of large deviator stress is poor, and the non-linear characteristics of the steady creep cannot be simulated. This phenomenon is particularly obvious in the test curve at q =150 kPa in Figure 15B, when t =2500min, the Burgers model curve is significantly deviated from the test curve, and this deviation trend would continue to increase with the increase of time, resulting in greater error in the prediction of creep axial strain after 2,500 min by the Burgers model. The above similar phenomena also appear in sample 3 and 7.
Compared with the Burgers model, the ‘intersect’ and ‘separation’ phenomenon of between Nishihara model curves and test curves is more obvious than Burgers model in the time interval of 100 min–500 min. As shown in Figures 15A,G, there is a big error between the model curve and the test curve. In the 500 min–3,000 min stage, the strain of the test curve is still increasing in a weak non-linear trend, while the Nishihara model curve has approached with a slope of approximately zero, which obviously has a large error with the test curves, and contrary to common sense.
When the deviator stress q of sample 3 is 300 kPa, the IFNM can also well depict the accelerating creep characteristics of soil, especially in the yield germination stage of 0–10 min, the model curve and the test curve are highly coincident, which is difficult to be achieved by the traditional integer order model. It can be seen from Figure 15F that the IFNM fitting curve is basically consistent with the accelerating creep test curve, which shows the non-linear characteristics of the strain rate gradually increasing with time, but the Nishihara model and Burgers model in Figures 15D,E cannot show this feature, and only an approximate oblique line can be used to simulate the accelerating creep stage, which does not reflect non-linear characteristics and has a large error. Therefore, IFNM is far superior to the Nishihara model and Burgers model in describing the accelerating creep characteristics of unsaturated soil.
Through the above analysis of the model fitting curves, it can be seen that IFNM is superior to the Nishihara model and Burgers model in describing the creep of unsaturated silty clay in Fuyang, but what causes this phenomenon? Through the analysis of Eqs 28 and 29, we can get the creep geometrical characteristics curve of the Nishihara model and Burgers model as shown in Figure 16.
It can be seen from Eqs 28 and 29 that the non-linearity of Nishihara model and Burgers model all controlled by
Through the triaxial creep test of unsaturated soil, we obtained the creep curves of Fuyang unsaturated silty clay under different stress conditions, and established the improved fractional order Nishihara model (IFNM) containing non-linear Hooke body and Abel dashpot. Finally, three case studies based on cooperation search algorithm (CSA) verify the effectiveness of IFNM, through detailed analysis, some conclusions can be drawn as follows:
1) Fuyang unsaturated silty clay has strong creep behavior. When the deviator stress is low, creep presents approximate linear viscoelasticity. When the deviator stress is high, creep presents obvious non-linear viscoelasticity. When the deviator stress is large, the creep shows obvious non-linear viscoelasticity, and the test soil is softened. The increase of matric suction would inhibit axial strain development, which shows that matric suction has hardening effect on test soil, but this hardening effect would gradually stabilize with the increase of matric suction. There is a negative correlation between net confining pressure and axial strain, the larger net confining pressure is, the lower the axial strain is.
2) From the MSE convergence curves of IFNM of different swarm intelligence algorithms, it can be seen that CSA has the advantages of high convergence accuracy and strong anti-interference ability for parameter identification of fractional order system.
3) By comparing the fitting results of IFNM, Nishihara model and Burgers model, the fitting accuracy of IFNM is better than Nishihara model and Burgers model, which can not only overcome the defect of poor fitting of integer-order model at the inflection point of creep curve, but also simulate the non-linear characteristics of creep and accelerating creep stage well.
In addition, in engineering construction, the strong creep property of Fuyang unsaturated silty clay should be concerned. When constructing general buildings, drainage consolidation, rolling, cushion, vibration, compaction and other engineering treatment measures can be used to improve the foundation and foundation bearing capacity. Meanwhile, the corresponding construction quality monitoring should be strengthened to minimize the ground subsidence after project completion. Finally, it is suggested that the relevant departments establish a ground subsidence monitoring network, and timely feedback the monitoring results every year to the relevant government departments to provide a geological basis for urban construction and development planning.
Although IFNM can better describe the creep characteristics of unsaturated silty clay in Fuyang than the integer-order element model, IFNM has more than six parameters, which increases the difficulty of parameters identification and makes it difficult to apply in practical engineering. Therefore, how to achieve a balance between simulation precision and computational complexity and streamlining the number of parameters is one of our next research directions. In addition, this paper only uses the test curve fitting method to verify the feasibility and effectiveness of IFNM, which is still a long way from practical engineering applications. Therefore, the secondary development of IFNM in Flac3D is our another research direction. The non-linear Hooke body and Abel dashpot in IFNM is a series system, but for describing the creep phenomenon, a parallel system is a better choice. However, the abstract fractional order delay evolution equation generated by the parallel system composed of non-linear Hooke body and Abel dashpot is extremely complex and difficult to solve, so if we can obtain a simple numerical solution technique for abstract fractional order delay evolution equation, it will promote the generation of many new fractional element models.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Conceptualization, DW and GC; methodology, DW and GC; software, GC; validation, GC and DW; formal analysis, GC; investigation, DW and JP; resources, DW and JP; data curation, GC; writing—original draft preparation, DW and GC; writing—review and editing, GC, ZX and JM; visualization, GC; project administration, DW and JP; funding acquisition, DW and JP; All authors have read and agreed to the published version of the manuscript.
This research was funded by Youth Science and Technology Innovation Fund of the Anhui and Huaihe River Institute of Hydraulic Research (KY202004).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Bai, L. L. (2018). Groundwater overdraft problem in Fuyang City and analysis of proper exploiting mode. Guangxi Water Resour. Hydropower Eng. 4, 78–80. doi:10.16014/j.cnki.1003-1510.2018.04.023
Cao, P., Youdao, W., Yixian, W., Haiping, Y., and Bingxiang, Y. (2016). Study on nonlinear damage creep constitutive model for high-stress soft rock. Environ. Earth Sci. 75, 1–8. doi:10.1007/s12665-016-5699-x
Chang, Z., Gao, H., Huang, F., Chen, J., Huang, J., and Guo, Z. (2020). Study on the creep behaviours and the improved Burgers model of a loess landslide considering matric suction. Nat. Hazards (Dordr). 103, 1479–1497. doi:10.1007/s11069-020-04046-0
Chen, X. C. (2021). Groundwater limiting overdraft measures and effect analysis in land subsidence area of Fuyang City. Ground water 43, 78–80. doi:10.16014/j.cnki.1003-1510.2018.04.023
Chen, Y. J., Pan, C. L., Cao, P., and Wang, W. X. (2003). Endochronic rheological constitutive model of soft rock. Chin. J. Nonferrous Metals 13, 742–747. doi:10.19476/j.ysxb.1004.0609.2003.03.041
China, T. M. O. H. a. U.-R. D. O. T. P. S. R. O. (2012). Code for design of buliding foundation : GB 50007-2011. Beijing, China: China Architecture & Building Press.
Deng, H., Dai, G., and Azadi, M. R. (2020). Fractional time-dependent Merchant model for coastal soft clay. J. Coast. Res. 104, 825–831. doi:10.2112/JCR-SI104-141.1
Feng, Z.-K., Niu, W.-J., and Liu, S. (2021). Cooperation search algorithm: A novel metaheuristic evolutionary intelligence algorithm for numerical optimization and engineering optimization problems. Appl. Soft Comput. 98, 106734. doi:10.1016/j.asoc.2020.106734
Fredlund, D. G., Rahardjo, H., and Fredlund, M. D. (2012). Unsaturated soil mechanics in engineering practice. John Wiley & Sons.
Guo, F., Du, C.-B., and Li, R.-P. (2014). Viscoelastic parameter model of magnetorheological elastomers based on abel dashpot. Adv. Mech. Eng. 6, 629386. doi:10.1155/2014/629386
Heidari, A. A., Mirjalili, S., Faris, H., Aljarah, I., Mafarja, M., and Chen, H. (2019). Harris hawks optimization: Algorithm and applications. Future gener. Comput. Syst. 97, 849–872. doi:10.1016/j.future.2019.02.028
Kooi, H., and Erkens, G. (2020). Creep consolidation in land subsidence modelling; integrating geotechnical and hydrological approaches in a new MODFLOW package (SUB-CR). Proc. IAHS. 382, 499–503. doi:10.5194/piahs-382-499-2020
Lai, X. L., Ye, W.-M., and Wang, S. M. (2012). Experimental study on unsaturated creep characteristics of landslide soils. Yantu Gongcheng Xuebao. Chin. J. Geotechnical Eng. 34, 286–293.
Li, L., Zhu, H., Zhou, A., Hu, M., Fu, C., and Qin, D. (2020). A novel online parameter identification algorithm for fractional-order equivalent circuit model of lithium-ion batteries. Int. J. Electrochem. Sci. 15, 6863–6879. doi:10.20964/2020.07.29
Lin, H., Feng, J., Cao, R., and Xie, S. (2022). Comparative analysis of rock damage models based on different distribution functions. Geotech. Geol. Eng. (Dordr). 40, 301–310. doi:10.1007/s10706-021-01899-5
Liu, W., Zhou, H., Zhang, S., Jiang, S., and Yang, L. (2022). A nonlinear creep model for surrounding rocks of tunnels based on kinetic energy theorem. J. Rock Mech. Geotechnical Eng. doi:10.1016/j.jrmge.2022.04.015
Ma, W.-B., Rao, Q.-H., Li, P., Guo, S.-C., and Feng, K. (2014). Shear creep parameters of simulative soil for deep-sea sediment. J. Cent. South Univ. 21, 4682–4689. doi:10.1007/s11771-014-2477-3
Mirjalili, S., and Lewis, A. (2016). The Whale optimization algorithm. Adv. Eng. Softw. 95, 51–67. doi:10.1016/j.advengsoft.2016.01.008
Nadimi-Shahraki, M. H., Taghian, S., and Mirjalili, S. (2021). An improved grey wolf optimizer for solving engineering problems. Expert Syst. Appl. 166, 113917–113924. doi:10.1016/j.eswa.2020.113917
Naruei, I., and Keynia, F. (2021). A new optimization method based on COOT bird natural life model. Expert Syst. Appl. 183, 115352. doi:10.1016/j.eswa.2021.115352
Ortigueira, M. D. (2011). Fractional calculus for scientists and engineers. Berlin: Springer Science & Business Media.
Peng, Y., Sun, K., He, S., and Peng, D. (2019). Parameter identification of fractional-order Discrete chaotic systems. Entropy 21, 27–15. doi:10.3390/e21010027
Shukla, A., and Joshi, Y. M. (2017). Boltzmann superposition principle for a time-dependent soft material: Assessment under creep flow field. Rheol. Acta 56, 927–940. doi:10.1007/s00397-017-1044-x
Song, B.-T., Liu, E.-L., Shi, Z.-Y., Wang, P., and Yu, Q.-H. (2021). Creep characteristics and constitutive model for frozen mixed soils. J. Mt. Sci. 18, 1966–1976. doi:10.1007/s11629-020-6463-y
Wang, Z. J. (2008). Rheological Experimental study and mechanism research on gentle-dipped landslides of Jurassic red Strata in Wanzhou city. China Univ. Geoscience.
Wen, T., Tang, H., Ma, J., and Liu, Y. (2019). Energy analysis of the deformation and Failure process of Sandstone and damage constitutive model. KSCE J. Civ. Eng. 23, 513–524. doi:10.1007/s12205-018-0789-9
Wu, F., Zhou, X., Ying, P., Li, C., Zhu, Z., and Chen, J. (2022). A study of Uniaxial acoustic emission creep of salt rock based on improved fractional-order derivative. Rock Mech. Rock Eng. 55, 1619–1631. doi:10.1007/s00603-021-02741-3
Wu, L., Zuo, C., and Zhang, H. (2015). A cloud model based fruit fly optimization algorithm. Knowledge-Based Syst. 89, 603–617. doi:10.1016/j.knosys.2015.09.006
Xie, S., Lin, H., Wang, Y., Cao, R., Yong, R., Du, S., et al. (2020). Nonlinear shear constitutive model for peak shear-type joints based on improved Harris damage function. Arch. Civ. Mech. Eng. 20, 95–14. doi:10.1007/s43452-020-00097-z
Xu, X.-B., and Cui, Z.-D. (2020). Investigation of a fractional derivative creep model of clay and its numerical implementation. Comput. Geotechnics 119, 103387. doi:10.1016/j.compgeo.2019.103387
Xue, J., and Shen, B. (2020). A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 8, 22–34. doi:10.1080/21642583.2019.1708830
Yan, Y., Wang, S.-J., and Wang, E.-Z. (2010). Creep equation of variable parameters based on Nishihara model. Rock Soil Mech. 31, 3025–3035. doi:10.3969/j.issn.1000-7598.2010.10.001
Yang, C., Dai, G., Gong, W., Mao, Y., and Qing, W. (2015). Experimental research on creep properties of typical mucky silty in region of Wangjiang. China Civ. Eng. J. 48, 47–52.
Yang, Q., Xu, J., Cao, B., and Li, X. (2017). A simplified fractional order impedance model and parameter identification method for lithium-ion batteries. PLoS One 12, e0172424. doi:10.1371/journal.pone.0172424
Yao, Y., Cheng, H., Lin, J., and Ji, J. (2021). Optimization of Burgers creep damage model of frozen silty clay based on fuzzy random particle swarm algorithm. Sci. Rep. 11, 1–12. doi:10.1038/s41598-021-98374-1
Yixiang, L., and Guanhua, G. (2004). Ground subsidence in areas of loose porous aquifers. Acta Geol. Sinica-English Ed. 78, 829–837. doi:10.1111/j.1755-6724.2004.tb00203.x
You, T., Lei, D., Cai, L., and Li, P. (2021). Parameter identification of fractional order chaotic system via opposition based learning bare-bones imperialist competition algorithm. Int. J. Comput. Intell. Syst. 14, 453–460. doi:10.2991/ijcis.d.201223.001
Yu, M., Liu, B., Sun, J., Feng, W., and Wang, Q. (2020). Study on improved nonlinear Viscoelastic-plastic creep model based on the Nishihara model. Geotech. Geol. Eng. (Dordr). 38, 3203–3214. doi:10.1007/s10706-020-01217-5
Zheng, J., Wang, S. M., Zhou, H., Wang, L., Zou, L. C., Hui-Yuan, X. U., et al. (2019). A creep model of unsaturated soil based on Burger's model. Journal of Yangtze River Scientific Research Institute. doi:10.11988/ckyyb.20180096
Keywords: creep, unsaturated silty clay, fractional calculus, nishihara model, swam intelligence algorithm, parameter identification
Citation: Wu D, Chen G, Xia Z, Peng J and Mao J (2023) Fractional creep model and experimental study of unsaturated silty clay in Fuyang. Front. Earth Sci. 10:1029420. doi: 10.3389/feart.2022.1029420
Received: 27 August 2022; Accepted: 18 November 2022;
Published: 20 January 2023.
Edited by:
Dongdong Yao, China University of Geosciences Wuhan, ChinaCopyright © 2023 Wu, Chen, Xia, Peng and Mao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Guangyao Chen, Y2hlbmd5QHNldS5lZHUuY24=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.